Abstract
Many problems in science, engineering, and economics require solving of nonlinear equations, often arising from attempts to model natural systems and predict their behavior. In this context, iterative methods provide an effective approach to approximate the roots of nonlinear functions. This work introduces five new parametric families of multipoint iterative methods specifically designed for solving nonlinear equations. Each family is built upon a two-step scheme: the first step applies the classical Newton method, while the second incorporates a convex mean, a weight function, and a frozen derivative (i.e., the same derivative from the previous step). The careful design of the weight function was essential to ensure fourth-order convergence while allowing arbitrary parameter values. The proposed methods are theoretically analyzed and dynamically characterized using tools such as stability surfaces, parameter planes, and dynamical planes on the Riemann sphere. These analyses reveal regions of stability and divergence, helping identify suitable parameter values that guarantee convergence to the root. Moreover, a general result proves that all the proposed optimal parametric families of iterative methods are topologically equivalent, under conjugation. Numerical experiments confirm the robustness and efficiency of the methods, often surpassing classical approaches in terms of convergence speed and accuracy. Overall, the results demonstrate that convex-mean-based parametric methods offer a flexible and stable framework for the reliable numerical solution of nonlinear equations.
Keywords:
iterative methods; nonlinear equations; convergence order; optimal methods; dynamical analysis MSC:
65H05; 37C25
1. Introduction
In mathematics and engineering, many real-world and physical phenomena are modeled using nonlinear equations or systems. Solving such problems has led to the development of numerous numerical methods, which serve as fundamental tools for approximating solutions that cannot be found exactly or analytically.
Among these, iterative methods play a crucial role in finding the roots of nonlinear equations . Since a variety of iterative strategies exist, it becomes essential to evaluate their convergence order, stability, and computational efficiency. These aspects allow us to compare methods and choose the most appropriate one for a given problem.
Iterative methods are typically classified based on whether they are single-step or multi-step, are with or without memory, and require derivatives or not. In this context, we present new multipoint iterative methods aimed at approximating the zeros of nonlinear functions. These methods are inspired by the work in [1], which investigates and enhances Newton-type methods by incorporating convex combinations of classical means, achieving third-order convergence.
Motivated by these results, as well as by the contributions of Chun (2005) [2], King [3], Ostrowski [4], and more recently Artidiello [5], Abdullah et al. [6], and Zein [7], who designed multipoint schemes by starting from Newton’s method and then applying suitable correction steps, we introduce new families of iterative schemes based on composition and weight functions. These weight functions combine data from multiple evaluations of the function and its derivatives across iterations, improving both accuracy and efficiency. The proposed methods achieve fourth-order convergence and satisfy the optimality condition postulated by the Kung–Traub conjecture [8], which states
The order of convergence p of an iterative method without memory cannot exceed , where d is the number of functional evaluations per iteration.
A method that reaches this bound is called optimal. This and other criteria described below allow us to classify the iterative methods.
Building upon these foundations, this paper introduces a unified theoretical and dynamical framework for mean-based iterative methods with weight functions. The main contributions are summarized as follows:
- We propose five new parametric families of two-step, fourth-order, multipoint iterative methods. Each family combines (i) a Newton predictor, (ii) a convex-mean-based corrector, (iii) a frozen derivative, and (iv) a flexible weight function with a free parameter .
- We derive explicit conditions on that guarantee fourth-order convergence for various symmetric means (arithmetic, harmonic, counterharmonic).
- We conduct a detailed dynamical analysis on the Riemann sphere, including stability surfaces, parameter planes, and dynamical planes, to study how the free parameter affects convergence and stability.
- We identify safe regions for the parameter that ensure convergence to the root and prevent undesirable attractors, offering practical guidelines for parameter selection.
- Finally, we present extensive numerical comparisons with recent optimal fourth-order methods (e.g., Artidiello [5], Zein [7], Zhao et al. [9,10]), showing that the proposed schemes exhibit comparable or superior accuracy and robustness.
One of the most widely used and foundational approaches in nonlinear root-finding is Newton’s method. It is defined as
provided . Under appropriate smoothness conditions and for simple roots, the method exhibits quadratic convergence, meaning
for some constant , with being a root of .
In 2000, Weerakoon and Fernando [11] proposed a third-order variant of Newton’s method. This method replaces the rectangular approximation in the integral form of Newton’s method with a trapezoidal approximation, reducing truncation error and improving convergence. Their method, known as the trapezoidal or arithmetic mean method, is defined as
This method laid the seed for subsequent generalizations using other types of means. Researchers such as Chicharro et al. [12] and Cordero et al. [1] expanded this idea by incorporating various mathematical means to construct families of third-order methods:
where denotes the Newton step and represents the chosen mean applied to the values x and y.
1.1. Types of Means
Below are the different types of convex averages used in the literature for the design and analysis of various iterative methods. These concepts constitute a fundamental reference and will serve as a methodological basis for the development of our own iterative procedures.
Arithmetic Mean : The arithmetic mean of two real numbers x and y is given by
This mean appears in the trapezoidal scheme (2).
Harmonic Mean : The harmonic mean of two positive real numbers x and y is defined as
This mean is particularly sensitive to small values and is known for its use in rates and resistances. In the context of iterative methods, its reciprocal nature often yields improved stability under specific conditions. The following scheme arises by replacing the arithmetic mean in (2) with the harmonic one, as carried out in [13]:
Counterharmonic Mean : The counterharmonic mean is given by
and is always greater than or equal to the arithmetic mean. It accentuates larger values, making it suitable when higher magnitudes dominate the behavior of the function. When this mean is incorporated into iterative schemes, the obtained method, presented in [1,14], is
Different authors have proven that all these schemes have an order of convergence of three.
1.2. Some Characteristics of the Iterative Methods
To analyze an iterative method in depth, it is essential to understand certain concepts related to the mathematical notation used, the order of convergence, the efficiency index, and the computational order of convergence, as well as the fundamental theorems and conjectures that support the correct formulation of the proposed new multipoint methods. Each of these aspects is detailed below.
Order of convergence
The speed at which a sequence approaches a solution is quantified by the order of convergence p. Formally, the sequence is said to converge to with order and asymptotic error constant if
This limit establishes an asymptotic relation that describes how the errors decay as the number of iterations increases. Specifically,
- If and , the convergence is linear;
- If , the convergence is quadratic;
- If , the convergence is cubic;
- For , the method has higher-order convergence.
In practice, a high value of p implies faster convergence toward the root of , assuming that the constant C remains reasonably small. However, higher-order methods often require more functional evaluations per iteration, increasing the computational cost.
The error equation of an iterative method can be expressed as
where C is the asymptotic error constant and denotes higher-order terms that become negligible as n increases. This expression is central to the local convergence analysis of iterative schemes.
Numerical estimation of the order of convergence
Since the exact root is typically unknown, practical estimation of the convergence order relies on approximate values of the iterates. Two widely used techniques are
- The computational order of convergence (COC), defined in [11];
- The approximate computational order of convergence (ACOC), defined in [15].
These tools are commonly used in numerical experimentation to assess the performance of iterative schemes.
The classical estimate (COC) [11], assuming knowledge of the root , is given by
When is unknown, the ACOC [15] formula provides a root-free estimate using only the iterates:
This tool allows us to approximate the theoretical order of convergence p without requiring knowledge of the exact solution. Its reliability increases as the iterates approach the root, provided that the errors remain sufficiently small to avoid numerical cancellation or round-off issues.
Efficiency index of an iterative method
To assess the computational efficiency of an iterative method, one must consider its convergence order and the number of functional evaluations per iteration. Ostrowski (1973) [4] introduced the efficiency index I, defined as
where p is the order of convergence and d is the total number of functional evaluations per iteration (including derivatives, if applicable). This index provides a comparative efficiency measure across methods with varying orders and computational demands.
More recently, the concept has been extended to the computational efficiency index (CEI) [16], which includes not only functional evaluations but also the products/quotients of the iterative method.
where refers to the number of products/quotients produced in each iteration.
These indicators allow different iterative methods to be compared regarding convergence speed and total computational cost.
In this manuscript, Section 2 presents some known fourth-order iterative methods used in the numerical section for comparison. In Section 3, the new schemes are presented and their order of convergence is proven. Section 4 deals with the dynamical analysis of one of the proposed families of iterative schemes and a general result showing that the performance of all the fourth-order families is equivalent under conjugation. The best method in terms of stability is compared in the numerical section with known schemes. Two academic examples and two applied problems confirm the theoretical results. With some conclusions and references, we conclude the manuscript.
2. Some Fourth-Order Methods in the Literature
In recent decades, there has been an urgent need to develop iterative methods with high orders of convergence that do not require new functional evaluations or derivatives. Since Traub’s initial contributions [17] with his method, various approaches have been proposed to address this challenge. The following iterative expression defines Traub’s method:
This scheme achieves cubic convergence without the need to evaluate the second derivative. Similarly, Jarratt [18] introduced a two-step iterative scheme:
This also avoids evaluating second derivatives and achieves fourth-order convergence.
Based on these ideas, many multipoint methods have been developed to achieve even higher convergence orders. The specialized literature, including the works of Chun [2], Ostrowski [4], and King [3], among others, offers a wide range of fourth-order schemes based on the adjustment of parameters and weight functions. These schemes will serve as benchmarks for comparison with the methods proposed in this work.
Among them, it is worth highlighting the family of fourth-order methods introduced by Artidiello [5]. It is based on a weight function that generalizes several known schemes. Its formulation follows a two-step scheme:
where .
Theorem 1
([5]). Let be a sufficiently differentiable function on an open interval I containing a simple root α of , and be any sufficiently differentiable function satisfying
Then, for an initial estimate close enough to α, method (7) converges with an order of at least 4 and its error equation is
where and .
This theoretical framework not only unifies classical methods (such as those of Ostrowski or Chun) through specific choices of , but also provides a rigorous basis for designing new schemes.
Likewise, Zein [7] proposed a generalized two-step multipoint method that extends classical approaches by introducing additional free parameters. The scheme is given by
where and B are parameters, and .
Theorem 2
([7]). Let be a simple root of a sufficiently differentiable function for an open interval I. If is sufficiently close to α, and the weight function satisfies
then the scheme (8) converges to α with order four and satisfies the error equation
where provided that and .
By selecting appropriate values for the parameters , A, and B, and ensuring the necessary conditions on the weight function , the general method (8) achieves fourth-order convergence. It also encompasses methods such as those of Chun [2], Jarratt [18], Sharma and Bahl [19], Özban and Kaya [10], and Khirallah and Alkhomsan [20] as special cases.
Using expression (7), Table 1 summarizes several iterative methods that achieve fourth-order convergence thanks to the appropriate consideration of weight functions.

Table 1.
Summary of fourth-order iterative methods.
Each of these weight functions satisfies the conditions , achieving the corresponding scheme, a fourth-order convergence.
On the other hand, by using (8), the iterative methods that achieve fourth-order convergence by appropriately choosing the values of the parameters , A, and B, as well as the values of the weight functions, are summarized below. All methods have as their predictor step and as their correction step the one shown in each of the tables in the following items:
- If , , and , the conditions in (9) imply , , and . Using these values, different weight functions can be defined, appearing in Table 2.
 Table 2. Known methods corresponding to , , and .
Table 2. Known methods corresponding to , , and .  Table 3. Known methods corresponding to , , and .
Table 3. Known methods corresponding to , , and .- If , , and , the weight function must satisfy , , and . Table 4 shows the resulting scheme.
 Table 4. Known methods corresponding to , , and .
Table 4. Known methods corresponding to , , and . - New methods introduced in [7]:
3. General Framework of Mean-Based Iterative Methods
As discussed in Section 1.1, the mean-based iterative schemes introduced by [1] exhibit cubic convergence and are therefore not optimal under the Kung–Traub conjecture. Recent studies, such as those by [5,7], have demonstrated that this order of convergence can be increased from three to four by employing appropriate weight functions, without requiring additional functional or derivative evaluations.
In this work, five new families of mean-based iterative methods are proposed, all following this same principle. Each family incorporates a specifically designed weight function to raise the order of convergence from three to four, thereby producing optimal schemes according to the Kung–Traub conjecture. Moreover, the stability analysis of these families shows that there exists a conjugation that makes equivalent the qualitative performance of all the optimal methods coming from the different means. In these terms, the dependence on the initial estimation of all these methods has been unified.
In the following sections, a bounded real parameter is introduced within the weight function, with the aim of defining parametric families of methods and analyzing their dynamical richness. In particular, we study the effect of replacing the bounded weight function with its parametric version , where the parameter introduces an additional degree of freedom that enriches the dynamical behavior of the methods. Through this analysis, we identify fixed and critical points, parameter planes, and dynamical planes, making it possible to determine the values of that provide greater stability and efficiency in solving nonlinear equations.
We propose a general multipoint method involving as the Newton step, is an arbitrary mean applied to and , and is a weight function, with .
By choosing different symmetric means , such as the arithmetic means () and (), the harmonic mean (), and the counterharmonic means () and (), we obtain several iterative schemes with different correction steps, as summarized in Table 8.

Table 8.
Iterative methods defined via different symmetric means , along with their abbreviations and corresponding correction steps.
Theorem 3.

Let be a sufficiently differentiable function on an open interval I, holding its simple root , that is, and . The multipoint iterative method is defined by a Newton step
followed by a corrector step
where
- is a symmetric bivariate function representing a mean (, , , , or );
- , which is the variable of the weight function H;
- is a weight function with a Taylor expansion around :
If the coefficients satisfy specific conditions given in Table 9, then the methods achieve fourth-order convergence.

Table 9.
Coefficients of and error equations.
All methods achieve fourth-order convergence, with the generalized error equation
where
and represents the n-th iteration error. The constants and depend on the chosen mean and on the coefficients of the weight function appearing in Table 9.
Proof.
Let denote the error at the n-th iteration. Since f is sufficiently differentiable and is a simple root, we can use Taylor expansions of and around . In terms of , we have
Since , it follows that
We simplify the calculations using the expression of the constants (12):
In a similar way,
Therefore,
and the error in the approximation of becomes
Therefore,
We calculate, by direct division,
Since as , we expand the weight function in a Taylor series around :
Substituting the expression in terms of , we obtain:
Now, we detail the expansion of using the arithmetic mean in Table 8. For the rest of the means, all calculations are analogous.
Thus, the error equation of in Table 8 expands to
By solving the system obtained from eliminating the first-, second-, and third-order error terms, we get
so, the error equation of the method based on the arithmetic mean becomes
This finishes the proof for the case of the arithmetic mean. The order of convergence of the remaining methods is obtained in a similar way, replacing the mean function and using the corresponding values of the coefficients of presented in Table 9. Proceeding in this manner, the convex-mean-based methods indicated in Table 8 achieve an optimal fourth-order convergence. This can be checked by using the available Supplementary Material of the manuscript. □
4. Dynamical Analysis
The order of convergence of an iterative method is not the only relevant criterion when evaluating its performance. In fact, the dynamics of the method, that is, the behavior of its orbits under different initial estimations, plays a fundamental role in its overall analysis. In this section, we analyze the qualitative properties of the different mean-based optimal families designed, finding the best performance in terms of wideness of the basins of attraction and finding the similarities among them. To achieve this aim, tools from complex analysis are used [21,22,23].
We start from a rational function resulting from the application of an iterative method to a polynomial of low degree , denoted by , where denotes the Riemann sphere. The orbit of a point is given by the sequence
We are interested in studying the asymptotic behavior of the orbits of the rational operator R. A point is k-periodic if
We say that it is a fixed point of R if . If this fixed point is not a root of the polynomial , it is called a strange fixed point. These points are numerically undesirable, since the iterative method can converge on them under certain initial guesses [22].
The asymptotical performance of these fixed points is classified according to the . If , the fixed point is an attractor; if , it is called parabolic or indifferent; if , it is repellent; and if , it is a superattractor.
On the other hand, the study of the basin of attraction of an attractor is defined by
The Fatou set F is the union of the basins of attraction. The Julia set J is its topological complement in the Riemann sphere and represents the union of the boundaries of the basins of attraction.
A point is critical for R if . The following classical result, given by Fatou [24] and Julia [25], includes both periodic points (of any period) and fixed points, considered periodic points of unit period.
Theorem 4.
Let R be a rational function. The immediate basins of attraction of each attractive periodic point contain at least one critical point.
Using this key result, any attracting behavior can be found using the critical points as seeds of the iterative process [26].
In order to obtain global results, we prove a Scaling Theorem for the iterative methods designed.
4.1. Conjugacy Classes
Let f and g be two analytic functions defined on the Riemann sphere. An analytic conjugacy between f and g is a diffeomorphism h on the Riemann sphere such that .
We now state a general result that holds for all types of symmetric means described in Table 8.
Theorem 5.
Let be an analytic function on the Riemann sphere, and let be an affine transformation with , and , with . Let us consider the iterative scheme defined by
where is Newton’s method, with being one of the means that provide the schemes , , or , . Here, satisfies the conditions indicated in Table 9.
Then, (17) is analytically conjugate to the analogous method applied to g, that is
sharing the same essential dynamics.
Proof.
To prove the general result, we consider a particular case of the mean. For the rest of the methods, the proof is analogous. We choose the case of , whose scheme is given by
As can be seen, its structure is representative of the methods included in Table 8. We know that the affine function has an inverse given by .
By hypothesis, . By the chain rule, we obtain
Defining the operator as
and evaluated at , we obtain
Now, we apply the transformation h:
Using (23), we observe that the term transforms as
The same reasoning extends directly to the methods in Table 8, since
- In each case, the correction term maintains the form , with symmetric combinations based on means;
- The affine transformation h acts compatibly on both and , preserving the functional structure of the correction;
- The identity holds, since it depends only on the ratio , scaled by .
Therefore, the result holds for the entire family of iterative methods based on symmetric means, as described in Table 8.
4.2. Dynamics of Fourth-Order Classes
As shown in Table 8, five different parametric families of iterative methods are identified, each associated with specific conditions of the weight function . To satisfy these conditions, polynomial weight functions have been selected in this section. However, other functional forms could also be considered, provided that they meet the required smoothness and boundness conditions. This framework also allows for the introduction of an additional real parameter . The inclusion of this parameter provides greater flexibility and allows for a more in-depth dynamic analysis of the proposed schemes.
Table 10 presents the chosen polynomials for the development of this section.

Table 10.
Families of fourth-order iterative methods based on means.
Here, and is a free complex parameter.
To analyze the dynamics of these iterative methods, we start with the arithmetic mean family , which is defined as
The other cases are studied later in a similar way. This can be checked by using the available Supplementary Material of the manuscript.
4.3. Rational Operator
Proposition 1.
Let us consider the quadratic polynomial , of roots a and b. The rational operator related to family given in (26) on after a Möbius map, is
with being an arbitrary parameter.
Proof.
We apply the iterative scheme to and obtain a rational function that depends on the roots a and b and the parameter . Then, we apply a Möbius transformation [23,27,28] on with
which satisfies and . This transformation maps the roots a and b to the points 0 and ∞, respectively, and the divergence of the method to 1. Thus, the new conjugate rational operator is defined as
which no longer depends on the parameters a and b. □
Thus, this transformation facilitates the analysis of the dynamics of iterative methods by allowing the standardization of roots and the structural study of dynamical planes and their stability regions [16].
4.4. Fixed Points of the Operator
Now, we calculate all the fixed points of , to subsequently analyze their character (attractive, repulsive, neutral, or parabolic). Taking into account that the method has order four, the points and are always superattractor fixed points, since they come from the roots of the polynomial.
It is easy to prove that the fixed points of are , , and nine strange fixed points:
- is a strange fixed point if , and
- The roots of the polynomial:denoted by , , for any .
Now, we study the stability of the strange fixed point .
Proposition 2.
The strange fixed point of , , has the following character:
- If , is not a fixed point.
- If , is an attractor.
- If , is parabolic.
- If , is repulsive.
Proof.
As seen in the previous section, the behavior of a fixed point can be determined according to the value of the stability function . The expression of operator is
Therefore,
If , then is not a fixed point. To determine whether it is attractive or repulsive, we solve
Expressing the right side in terms of and ,
So,
By simplifying, we get
and thus,
□
Graphically, the behavior of the fixed point is visualized in Mathematica using the graph of the function . For each stability function, its 3D representation (called stability surface) is constructed. In this context, the graphical representation distinguishes the orange regions as zones of the complex plane where the strange fixed point is attracting , the gray regions as zones of repulsion , where the point is superattracting in the vertex of the cone , and parabolic zones at the boundary .
In Figure 1, the attraction zones are the yellow area and the repulsion zone corresponds to the gray area. That is, for values of within the disk, is repulsive, while for values of outside the gray disk, becomes attractive. Therefore, it is natural to select values within the gray disk, since repulsive divergence improves the performance of the iterative scheme.
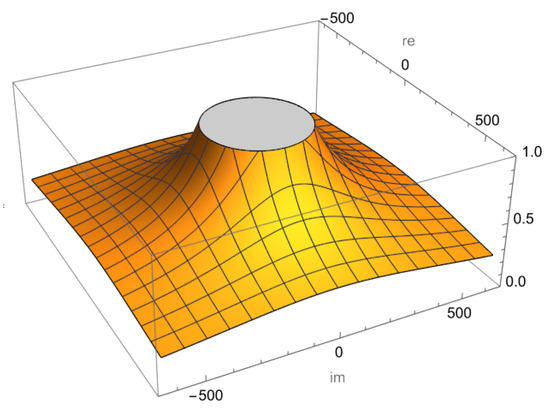
Figure 1.
Stability function of .
For the eighth roots , , of polynomial , we obtain the following results:
- , for all values;
- , for and ;
- , for ;
- , for all values;
- , for .
In Figure 2, we represent the stability functions of the strange fixed points , .
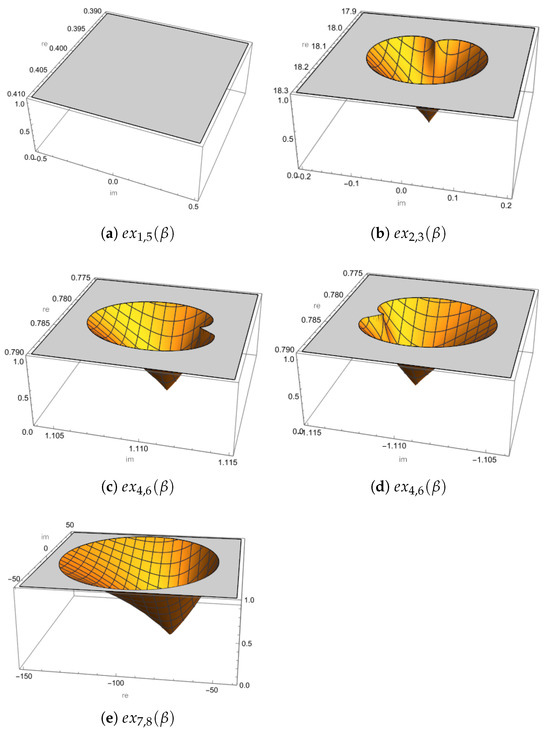
Figure 2.
Stability surface of strange fixed points in attraction zones.
From Figure 2, the following conclusions are drawn:
- As the derivative operator associated with the strange fixed points cannot be zero, it can be seen in Figure 2a that the resulting surface has only one gray region. This indicates that these fixed points are repulsive throughout the analyzed range, which is desirable, as it prevents convergence to these strange fixed points.
- Furthermore, at points , we obtain and . Figure 2b shows an inverted cone-shaped surface (normally yellow), representing an attractor inside the cone and a superattractor at its vertex (that of is similar, so it is omitted). The associated unstable domain is approximately , indicating a small but localized region. Similarly, by setting the derivative operator associated with the roots to zero, we obtain and . Figure 2c,d show behavior qualitatively similar to that of , with a comparable domain.
- By setting the derivative operator associated with the roots to zero, we obtain . As illustrated in Figure 2e, a considerably wider region of attraction appears, approximately , indicating that the method shows marked instability for these values of .
Therefore, to ensure the robustness of the method, values of where some root is an attractor or superattractor should be avoided. In contrast, values of where all strange fixed points are repulsors are preferable to ensure stable numerical behavior.
Just as we have studied strange fixed points, we must also analyze critical points, since, recalling Theorem 4, it turns out that each basin of attraction of an attractive periodic point (of any period) holds at least one critical point.
4.5. Critical Points of
Proposition 3.
The critical points of the rational operator are and , directly related to the zeros of the polynomial , and , , and are free critical points, where the auxiliary functions , , , , and are algebraic simplifications used for ease of notation:
Thus, there are five free critical points, except for , , and , where only three free critical points exist.
Proof.
To prove the result, we recall that was presented in (31). It is easily observed that its roots are , , , and four roots and of the fourth-degree polynomial in the numerator of .
Now, let us observe that for certain values of , only three free critical points exist. One such case is , where the derivative of the operator simplifies to
Here, the strange critical points are , and the conjugate pair
When , the derivative operator becomes
In this scenario, the strange critical points are , and the conjugate pair
And finally, when , the derivative operator becomes
whose zeros are and the conjugate pair
□
To visualize the behavior of the free critical points that depend on , we plot the parameter planes. In each parameter plane, we use each free critical point as an initial estimation. A mesh of points is defined in the complex plane. Each point of the mesh corresponds to a value of , that is, a member of the iterative method family, and for each one, we iterate the rational function . If the orbit of the critical point converges to or in a maximum of 100 iterations, the point is represented in red color; otherwise, it is colored black.
For the free critical point , we have , which is a strange fixed point. So, the parameter plane associated with the critical point is not of much interest, since we already know the stability of .
As a first step, we graph in Figure 3 the parameter plane of the conjugate pair , with both in the domain . In it, a broad stable performance region around the origin is observed, and in , we see a black area related to the stability of strange fixed points .
Figure 3.
Plane of parameters of in domain and a detail in .
Likewise, in Figure 4, the parameter plane of the conjugate pair is shown, with both in the domain , and a detail in the domain , which represents a complex region of values for with no convergence to the roots, nor to strange fixed points, but to periodic orbits of different periods.
Figure 4.
Plane of parameters of in domain and a detail in .
4.6. Dynamical Planes
In the case of dynamical planes, each point in the defined mesh of the complex plane is considered as a starting point of the iterative scheme and is represented with different colors depending on the point it converges to. In this case, points that converge to are colored blue, and those that converge to are colored orange. These dynamical planes have been generated using a grid of points and a maximum of 100 iterations per point. In these planes, the fixed points are represented by a white circle, the critical points by a white square, and the attracting points by an asterisk.
Next, the dynamical planes are plotted based on the values for obtained from the stability analysis of the strange fixed points of and from the observations in the parameter plane.
In Figure 5, methods with stable behavior can be found for and , with convergence only to the roots.
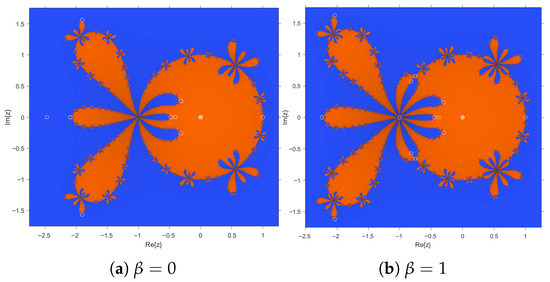
Figure 5.
Dynamical planes corresponding to methods with stable performance.
A notable case is , since in Proposition 2 it was established that when takes that value, is not a fixed point, as observed in Figure 6.
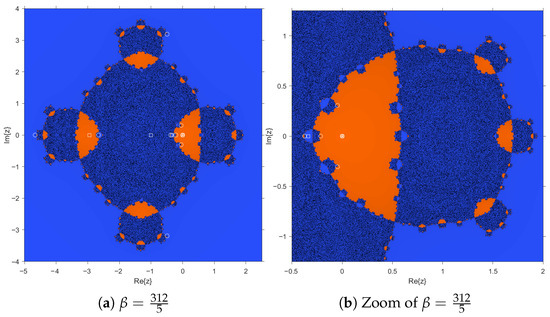
Figure 6.
Dynamical plane when is not a fixed point.
In Figure 6b, it can be clearly seen that is no longer characterized as a strange fixed point of the method. Moreover, we recall that when , is repulsive, as shown in Figure 5a,b, and when , is an attractor (with a green basin of attraction), as shown in Figure 7.
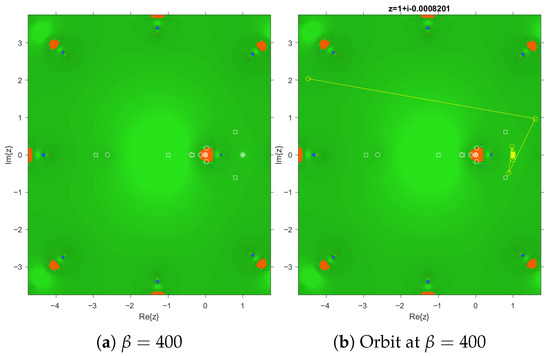
Figure 7.
Green basin of attraction of .
Based on the previous study (see Figure 2e), when considering the value , complex dynamical behavior is observed in Figure 8. It is seen that this basin of attraction is related to the parameter plane of the conjugate critical point and the superattracting character of strange fixed points for this value of , with their own basins of attraction (in red and green color). In this scenario, the method converges to elements different from the roots 0 and ∞, indicating that it is not suitable for root-finding. Therefore, values such as should be avoided when applying this method. Likewise, as another example of divergence, . Figure 8b represents a value of inside , in the parameter plane of Figure 4. In this case, the black area corresponds to the basin of attraction of a periodical orbit of period 2.
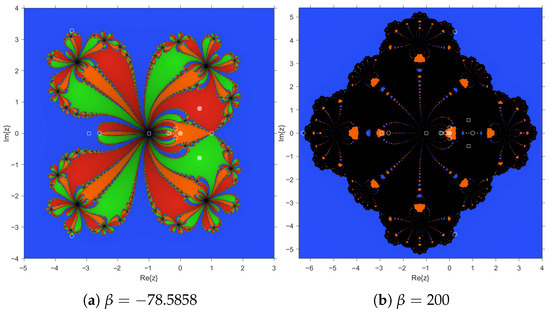
Figure 8.
Dynamical planes corresponding to methods with unstable performance.
The analysis of the remaining iterative methods presented in Table 10 has been carried out in an analogous way to that described for the iterative arithmetic mean scheme defined in Equation (27). However, a more detailed study reveals that all methods based on convex means exhibit essentially equivalent dynamical behavior. In particular, in the next section, it is proven that the rational transformations associated with each method are affine conjugate, which implies that they share the same structure of basins of attraction and Julia sets except for scale transformations. This is, as far as we know, the first time this has been proven for a set of designed families. This result of dynamical equivalence is presented below in general terms, and the rational operators associated with each family of methods are shown explicitly.
4.7. Dynamic Equivalence Between Methods Based on Convex Means
The study of the dynamic behavior of iterative families constructed using convex means is performed on the generic quadratic polynomial , of simple roots . For each family, a rational operator dependent on a complex parameter is defined, which describes the qualitative performance of the iterative method applied to . In what follows, the five rational operators associated with the different convex means considered are presented explicitly.
Proposition 4.
Let be the reference quadratic polynomial and a free parameter. The normalized rational operators associated with the five iterative families considered are as follows:
(1) Method , defined in (27):
(2) Method :
(3) Method :
(4) Method :
where
and
(5) Method :
where
and
Each of these operators represents the rational map induced by the corresponding iterative method on the Riemann sphere. The performance of these operators is analyzed by studying the parameter planes and the associated basins of attraction.
Now we introduce the characteristic quantities that allow us to establish the relationship between the different families: the scale r is defined by the stability function of in each family of methods, while the relative scale factor corresponds to the ratio between each scale and that of the arithmetic family .
Theorem 6.
Let be the rational operator associated with each of the five iterative families considered and the base operator corresponding to the arithmetic mean method . Let us define the characteristic quantities (obtained from the stability analysis of for each of the iterative methods):
Let the relative scale factor also be
Then, for each i, there exists an affine homothety such that
which proves that the rational operators are affine conjugate. Consequently, the five iterative families are dynamically equivalent: they share the same topology of fixed points, basins of attraction, and Julia sets, differing only by a scale transformation controlled by .
The relative scale factors are given explicitly by
Each function is strictly increasing on its domain, which implies that the relative scale factor varies monotonically with the parameter β.
Proof.
The result follows from the structural relationship among the rational operators associated with each iterative family. The proof is organized in three complementary steps.
(i) Construction of the rational operators. Applying each method to the generic quadratic polynomial yields a rational operator after a Möbius map, whose algebraic form depends on the convex mean employed and on the complex parameter . All these operators have the same rational nature and algebraic degree, differing only in the coefficients associated with higher-order terms, which act as scale factors in the dynamical plane.
(ii) Establishment of the affine relation. The quantities characterize the dynamical scale of each method, as they describe the stability function of as a strange fixed point (coming from the divergence before Möbius transformation). From them, the area of the complex plane for a repulsive performance of is defined. This is the bound of the red area of the parameter planes where the stable performance of the methods is defined. Defining the relative scale factor
one observes that substituting in the base operator , and multiplying by , reproduces exactly the rational structure of . That is,
where is an affine map. This identity proves that all operators are affine conjugate, sharing the same algebraic and dynamical structure and differing only by a global scale transformation controlled by .
(iii) Monotonicity of the scale factor. From the explicit expressions of , the scale factors take the following closed forms:
Differentiation yields
So, each is strictly increasing on its domain. Therefore, the affine transformation varies continuously and monotonically with the parameter .
So, the rational operators and are affine conjugate, implying full dynamical equivalence: they share the same structure of fixed points, basins of attraction, and Julia sets, differing only by a uniform scale factor . Hence, all five iterative families belong to a single affine conjugacy class, and the analysis of one representative (e.g., ) suffices to characterize the global dynamics of the entire family. □
The explicit forms of the scale factors and their numerical reference values for are summarized in Table 11. These results numerically confirm the relations observed in the parameter plane of each family.

Table 11.
Relative scale factors and numerical reference values ().
Figure 9 presents the unified parameter planes obtained for each iterative family. The unified parameter plane [29] is presented, where the white color represents those values of the parameter that are simultaneously red in all parameter planes of the same family. Meanwhile, in the black color appears those that are black in any of the parameter planes.
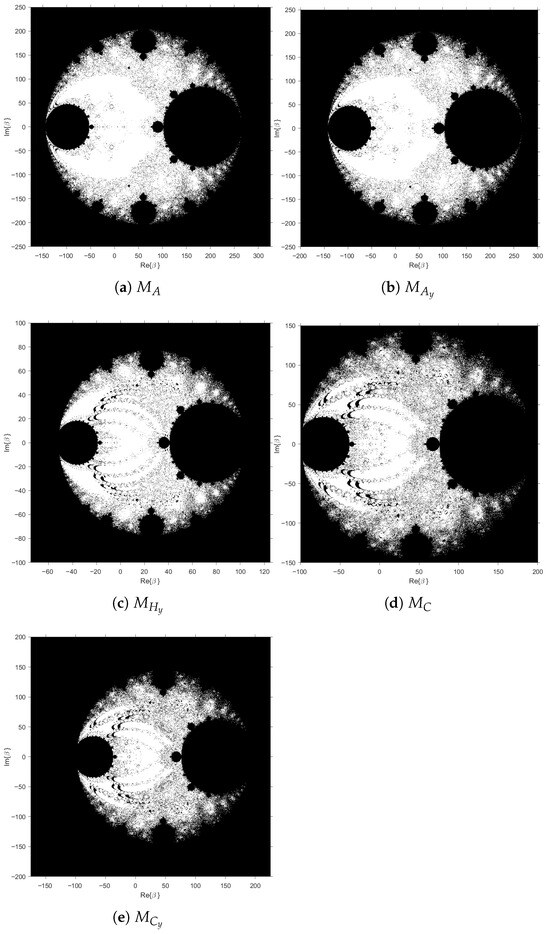
Figure 9.
Unified parameter planes for the iterative families.
The visual relationship between them is evident: the limit sets remain invariant except for the scale dictated by the factors . This geometric correspondence provides an empirical verification of the affine conjugacy proven in Theorem 6.
Theorem 6 thus provides a rigorous mathematical foundation for the empirical evidence observed in the parameter spaces: all rational operators derived from the convex means considered are dynamically equivalent by affine conjugation. This equivalence justifies the reduction of the global analysis to a single representative method and establishes a unified framework for classifying convex-mean-based iterative schemes according to their affine dynamical equivalence.
5. Numerical Examples
The iterative methods used in this section are presented in Table 10. This table takes into account all the conditions established in Table 9 with respect to , with the aim of guaranteeing fourth-order convergence. In particular, the parameter is selected, given its favorable behavior observed in the dynamical analysis.
To evaluate the efficiency of the new iterative methods proposed, a comparison is made with classical and new algorithms in the literature, presented in Section 2.
This section evaluates the performance of the newly proposed multipoint iterative methods in comparison with several well-established fourth-order methods. The comparison includes the following performance indicators:
- Number of iterations required for convergence (Iter).
- Approximate computational order of convergence (ACOC).
- Estimations of the errors (Incr, Incr2), where
- Efficiency index (EI), calculated with ACOC instead of p;
- Execution time (Time), measured in seconds.
All the numerical tests have been conducted in Matlab R2024a, with variable-precision arithmetics of 200 digits of mantissa. The implemented algorithm uses as stopping criteria
If neither of these criteria is met, the procedure ends when the maximum number of 100 iterations is reached. In each table, the best results are marked in bold, for the indicators Incr, Incr2, and Time.
5.1. Academic Example 1:
The target root of the problem considered is , obtained from the proposed nonlinear function. For the iterative process, was taken as the initial estimate. The results obtained under these conditions are presented in Table 12.

Table 12.
Performance comparison for . The best results are marked in bold.
The results reported in Table 12 underscore the strong competitiveness of the newly developed methods when compared with classical and recent schemes. The proposed approaches exhibit comparable, and in several cases superior, performance in terms of both accuracy and computational efficiency. This is reflected not only in the reduced number of iterations required to approximate the root, but also in the exact convergence order of four achieved by several of the new methods. In particular, tiny residual errors were obtained, such as for method and exactly zero for method .
Nevertheless, it is important to acknowledge the effective performance of the classical iterative schemes. For instance, the MEDJA4 method demonstrated remarkable robustness and efficiency, reaching errors of the order of with relatively low computational cost.
On the other hand, the MED44 method, despite its high estimated order of convergence (ACOC ), produced significantly larger final errors (). This behavior may indicate the presence of numerical instabilities or sensitivity to the transcendental nature of the problem.
5.2. Academic Example 2:
The real root of this function is , with an initial estimate . The results are given in Table 13.

Table 13.
Performance comparison for . The best results are marked in bold.
In this nonlinear and rapidly varying function, exhibits the most outstanding precision, with final error on the order of , confirming its high robustness. The classical methods MEDJA4, MEDOS4, and MED44 maintain excellent convergence behavior with very low errors () and lower execution times.
Overall, methods and achieve almost the theoretical order of convergence with a low number of iterations, and their performance may improve with adaptive strategies. In contrast, methods such as offer a balance between precision and convergence, suggesting their suitability for problems demanding extremely high accuracy.
The proposed methods , , and demonstrate solid fourth-order behavior, but exhibit larger errors compared to Example 1, indicating sensitivity to the exponential component of .
5.3. Applied Problems
Problem 1.
Chemical Equilibrium in Ammonia Synthesis
The analysis of chemical equilibrium systems using numerical methods has been widely addressed in the scientific literature. Solving complex nonlinear equations that model fractional conversions in reactive processes such as ammonia synthesis requires robust and efficient techniques.
This work analyzes the chemical equilibrium corresponding to the ammonia synthesis reaction from nitrogen and hydrogen, in a molar ratio of 1:3 [30], under standard industrial conditions (500 °C and 250 atm). The equation that describes this reaction is the following:
where x is the fractional conversion. Of the four real roots of this equation, only one lies within the physical interval , and therefore it is the only one with chemical significance.
In Table 14, it can be seen that all methods converge rapidly to the physically meaningful root, demonstrating high efficiency for this type of problem. For these results, we can use and the same stopping criteria as in the previous examples.

Table 14.
Comparison of iterative methods for the chemical equilibrium problem. The best results are marked in bold.
Method exhibits the best performance in terms of accuracy, reaching a residual on the order of , positioning it as the most precise among the set, at the cost of one additional iteration.
Among the classical methods, MEDOS4 and MEDZ4 stand out due to their excellent accuracy, with very small errors ( and , respectively) and ACOC.
Regarding the proposed methods , , , and , a consistent stability in the order of convergence and a good approximation in the errors can be observed, with results close to the classical methods, though without systematically surpassing them. Their computational performance is acceptable, although slightly inferior in terms of time.
In summary, for this chemical equilibrium problem, the methods with the best overall performance considering accuracy, efficiency, and stability are , MEDOS4, and MEDZ4, all offering an ideal combination of minimal errors, fulfilled theoretical order of convergence, and low execution times.
Problem 2.
Determination of the Maximum in Planck’s Radiation Law
The study of blackbody radiation through numerical methods has been fundamental in the development of quantum physics. As noted in [31], determining the spectral maximum in Planck’s distribution requires advanced techniques to solve nonlinear transcendental equations.
We analyze the equation derived from Planck’s radiation law that determines the wavelength corresponding to the maximum energy density:
where . Among the possible solutions, only has physical meaning in this context.
Table 15 shows that all proposed methods and converge to the physically valid root , even when starting from a distant initial condition ().

Table 15.
Comparison of iterative methods for the Planck problem with . The best results are marked in bold.
Method stands out for its quartic convergence (ACOC = 4.0) and a final error of exactly 0 (with 200 digits) in only five iterations, making it the most accurate method. Although it is slightly more computationally expensive, it achieves the highest relative efficiency (EI ≈ 1.587) among the proposed methods.
Methods show quadratic convergence with errors of the order in only four iterations, with low execution times. The method slightly improves the order of convergence , which represents a good compromise between efficiency and robustness.
In contrast, several classical methods converge to values that do not represent the physically significant root. For example, MEDCH4 converges to a negative value () with a clear divergence (Incr2 ). Meanwhile, the other methods diverge completely, presenting values with no physical meaning.
This highlights that, under unfavorable initial conditions, the proposed methods remain stable, while the classical ones are sensitive. Therefore, for problems such as Planck’s, methods based on the mean offer a more robust and reliable alternative.
In summary, all the analyzed methods proved to be efficient from a distant initial point, with standing out for its stability and performance.
6. Conclusions
This manuscript presents a new perspective on the design, analysis, and dynamical behavior of fourth-order multipoint iterative methods, constructed through convex combinations of classical means and parameterized weight functions. By extending the Newton-type scheme and incorporating arithmetic, harmonic, and contraharmonic means, a versatile family of optimal methods is developed, complying with the Kung–Traub conjecture by achieving order four with a minimal number of functional evaluations. Other means such as Heronian and centroidal means, have been used without positive results. The resulting iterative methods do not reach order four, so they are not optimal schemes.
The general formulation, grounded in a solid theoretical framework (Taylor expansions, affine conjugation, and local error analysis), enabled the derivation of explicit conditions on the weight functions to ensure fourth-order convergence. This has been complemented by a rigorous discrete dynamical system analysis using tools such as conjugated rational operators, stability surfaces, parameter planes, and dynamical planes on the Riemann sphere.
The results reveal that the proposed parametric families, particularly those associated with the modified arithmetic mean (), exhibit stable convergence behavior over large regions of the complex parameter space . Nevertheless, several regions of unstable performance have been identified, including attraction basins unrelated to the roots or convergence toward strange fixed points. Such zones, often visualized as black or green regions in the parameter and dynamical planes, must be avoided in practice. In this context, the detailed study of free critical points is fundamental, as each attractive basin must contain at least one critical point. The behavior of these points has provided early insights into the method’s stability and convergence characteristics. Noteworthy cases such as or illustrate convergence toward undesirable fixed points (e.g., ), despite proximity to the root , emphasizing the importance of well-informed parameter selection.
A key contribution of this work is the discovery that all iterative families constructed from convex means are conjugate to each other. That is, their associated rational operators are affine conjugate, sharing identical topological structures of fixed points, basins of attraction, and Julia sets, differing only by a global scale factor. This remarkable equivalence implies that the dynamical behavior of the entire class of convex-mean methods can be completely represented by studying a single representative operator, such as . Consequently, this finding provides a unified dynamical framework and reinforces the theoretical coherence of the proposed construction.
Finally, numerical experiments have confirmed the competitiveness of the proposed schemes. In various tests, both academic and applied, methods based on convex means have shown efficient performance comparable to classical and new methods. In most of the problems considered, the proposed methods managed to converge to the root in approximately three to five iterations. The only exception is the first applied example, which requires a greater number of iterations; however, it also reaches the root with errors of the order of ∼10−208. Likewise, in the second applied problem, their robustness is evident, as they are the only methods that converge to the root.
So, the proposed class of parametric iterative methods based on convex means not only achieves high computational efficiency but also, under the light of affine dynamical equivalence, constitutes a geometrically consistent and theoretically unified framework for the stable and predictive solution of nonlinear equations.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math13213525/s1.
Author Contributions
Validation, A.C. and J.R.T.; Formal analysis, J.R.T.; Investigation, M.E.M.M.; Resources, M.E.M.M.; Writing—original draft, M.E.M.M.; Writing—review & editing, A.C. and J.R.T.; Supervision, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the European Research Council (ERC) via Horizon Europe Advanced Grant, grant agreement nº 101097688 (“PeroSpiker”).
Data Availability Statement
The Original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cordero, A.; Franceschi, J.; Torregrosa, J.R.; Zagati, A.C. A Convex Combination Approach for Mean-Based Variants of Newton’s Method. Symmetry 2019, 11, 1106. [Google Scholar] [CrossRef]
- Chun, C. Some fourth-order iterative methods for solving nonlinear equations. Appl. Math. Comput. 2008, 195, 454–459. [Google Scholar] [CrossRef]
- King, R.F. A family of fourth order methods for nonlinear equations. SIAM J. Numer. Anal. 1973, 10, 876–879. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of Equations in Euclidean and Banach Spaces; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Artidiello Moreno, S.D.J. Diseño, Implementación y Convergencia de métodos Iterativos para Resolver Ecuaciones y Sistemas no Lineales Utilizando Funciones Peso. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2014. [Google Scholar]
- Abdullah, S.; Choubey, N.; Dara, S.; Junjua, M.U.D.; Abdullah, T. A robust and optimal iterative algorithm employing a weight function for solving nonlinear equations with dynamics and applications. Axioms 2024, 13, 675. [Google Scholar] [CrossRef]
- Zein, A. A New Family of Optimal Fourth-Order Iterative Methods for Solving Nonlinear Equations With Applications. J. Appl. Math. 2024, 2024, 9955247. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. ACM (JACM) 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Guo, W. New families of eighth-order methods with high efficiency index for solving nonlinear equations. WSEAS Trans. Math. 2012, 11, 283–293. [Google Scholar]
- Özban, A.Y.; Kaya, B. A new family of optimal fourth-order iterative methods for nonlinear equations. Results Control. Optim. 2022, 8, 100157. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Cordero, A.; Martínez, T.H.; Torregrosa, J.R. Mean-based iterative methods for solving nonlinear chemistry problems. J. Math. Chem. 2020, 58, 555–572. [Google Scholar] [CrossRef]
- Özban, A.Y. Some new variants of Newton’s method. Appl. Math. Lett. 2004, 17, 677–682. [Google Scholar] [CrossRef]
- Ababneh, O.Y. New Newton’s method with third-order convergence for solving nonlinear equations. World Acad. Sci. Eng. Technol. 2012, 61, 1071–1073. [Google Scholar]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Zúñiga, A.G.; Cordero, A.; Torregrosa, J.R.; Soto, J.P. Diseño y análisis de la convergencia y estabilidad de métodos iterativos para la resolución de ecuaciones no lineales. Rev. Digit. MatemÁtica Educ. Inter. 2021, 21, 1–27. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; American Mathematical Society: Providence, RI, USA, 1982; Volume 312. [Google Scholar]
- Jarratt, P. Some fourth order multipoint iterative methods for solving equations. Math. Comput. 1966, 20, 434–437. [Google Scholar] [CrossRef][Green Version]
- Sharma, R.; Bahl, A. An optimal fourth order iterative method for solving nonlinear equations and its dynamics. J. Complex Anal. 2015, 2015, 259167. [Google Scholar] [CrossRef]
- Khirallah, M.; Alkhomsan, A. Convergence and stability of optimal two-step fourth-order and its expanding to sixth order for solving nonlinear equations. Eur. J. Pure Appl. Math. 2022, 15, 971–991. [Google Scholar] [CrossRef]
- Blanchard, P. The dynamics of Newton’s method. In Proceedings of Symposia in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 1994; Volume 49, pp. 139–154. [Google Scholar]
- Maimo, J.G. Análisis Dinámico y Numérico de Familias de Métodos Iterativos para la Resolución de Ecuaciones no Lineales y su Extensión a Espacios de Banach. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2017. [Google Scholar]
- Blanchard, P. Complex analytic dynamics on the Riemann sphere. Bull. Am. Math. Soc. 1984, 11, 85–141. [Google Scholar] [CrossRef]
- Fatou, P. Sur les frontières de certains domaines. Bull. Soc. Math. Fr. 1923, 51, 16–22. [Google Scholar] [CrossRef][Green Version]
- Julia, G. Mémoire sur l’itération des fonctions rationnelles. J. Math. Pures Appl. 1918, 1, 47–245. [Google Scholar][Green Version]
- Moscoso-Martínez, M.; Chicharro, F.I.; Cordero, A.; Torregrosa, J.R.; Ureña-Callay, G. Achieving optimal order in a novel family of numerical methods: Insights from convergence and dynamical analysis results. Axioms 2024, 13, 458. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Review of some iterative root-finding methods from a dynamical point of view. Scientia 2004, 10, 35. [Google Scholar]
- Scott, M.; Neta, B.; Chun, C. Basin attractors for various methods. Appl. Math. Comput. 2011, 218, 2584–2599. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. On the choice of the best members of the Kim family and the improvement of its convergence. Math. Method Appl. Sci. 2020, 43, 8051–8066. [Google Scholar] [CrossRef]
- Nuevo, D. La síntesis de Amoniaco. Publicado el 19 de Marzo de 2024 en TECPA Formación de Ingenieros. 2024. Available online: https://www.tecpa.es/la-sintesis-de-amoniaco/ (accessed on 20 July 2025).
- González, S.L. Procedimiento didáctico para el estudio de la fórmula de Planck en carreras de ingeniería. Cad. Bras. Ensino Física 2021, 38, 270–292. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).