1. Preliminaries
The concept of graph labeling has experienced significant popularity over the past six decades, owing to its practical applications. A groundbreaking paper addressing graph labeling problems was published by Rosa [
1]. Subsequently, numerous papers on various graph labeling methods have been published, and Gallian’s survey [
2] elegantly categorizes and organizes these diverse labeling methods published by various mathematicians all over the world. ‘Cordial labeling’ is one of the popular labelings introduced by Cahit [
3]. Inspired by this notion, ‘product cordial labeling’ was proposed in [
4]. In 2012, this concept was extended further, and a new concept called ‘
k-product cordial labeling’ [
5] was introduced. In the same year, Vaidya et al. [
6] introduced a variation of product cordial labeling called ‘edge product cordial labeling’. In this variant, the roles of vertices and edges in ‘product cordial labeling’ are interchanged. Since then, some more results on ‘edge product cordial labeling’ have been published by the same authors; see [
6,
7,
8,
9]. Building on this, Thamizharasi et al. [
10] demonstrated the existence of ‘edge product cordial labeling’ of regular digraphs in 2015. In the subsequent years, Prajapati and Aboshady et al. [
11,
12,
13,
14] contributed additional results on ‘edge product cordial labeling’. Motivated by the concepts of ‘
k-product cordial labeling’ and ‘edge product cordial labeling’ and the established results, we put forth a new labeling, namely ‘edge
k-product cordial labeling’, which extends the concept of edge product cordial labeling by expanding the set of labels from
to
. Let
be a graph without isolated vertices and
. Let
be an edge labeling. The induced vertex labeling
is defined by
is called the induced labeling of
f. For convenience, let
be the complete residue system modulo
k. Also, an edge is called
i-edge if it is labeled by
i; and a vertex is called
j-vertex if its induced label is
j. Let
and
denote the number of
i-edges and
i-vertices, respectively, for
.
f is said to be an
edge k-product cordial labeling of
G if
and
for
. Also,
G is called an
edge k-product cordial graph.
Let L be a set of labels. For an edge labeling of a graph , if for all , then we say that the edges of the graph labeled by labels in Levenly (under f).
In this paper, we use this notation, these concepts, and the following definitions unless otherwise stated.
Definition 1. For , let be the path of order n. For , let the vertex set and the edge set of the star graph be and , respectively. For , let the graph with identifying c with . Such a graph is called a comet [15]. Definition 2. For , let the graph with the vertex set and the edge set and , respectively. Such a graph is called a double comet [16]. Notation and concepts, which are not defined in this paper, are referred to in [
17]. All graphs considered here are simple and connected.
We use the next section to show the structure of the subtree induced by all edges labeled by 0 of an edge k-product cordial tree. In the consecutive sections, we investigate the edge k-product cordial behavior of comet and double comet graphs for , and 5.
2. Properties of Edge -Product Cordial Trees
Lemma 1. Let be an edge labeling of a tree , where . Then , where is the induced labeling of f.
Proof. Let and , the edge induced subgraph of T. Let , p, and q be the number of components, the order and the size of , respectively. Since is a forest, . Since all its vertices are 0-vertices, . □
Corollary 1. Let f be an edge k-product cordial labeling of a tree T of order n, where . If is the set of 0 edges under f, then is a tree and Proof. For each
i, we have
By Lemma 1, we obtain this corollary. □
Example 1. Suppose and . Then T contains 7 vertices and 6 edges. We keep all notation defined in the proof of Lemma 1 and Corollary 2. For any edge 3-product cordial labeling f, and for . From the proof of Lemma 1, . Since and , and hence .
Lemma 2. Let G be a graph of order k. If k is a prime, then G is not an edge k-product cordial graph.
Proof. Let f be an edge k-product cordial labeling of G. Then for . In particular, . Suppose there is a 0-edge, then it induces two 0-vertices, which is a contradiction. Suppose there are no 0-edges. Since k is a prime, there is no induced 0-vertex, which is also a contradiction. □
Corollary 2. Let T be a tree of order k. If k is a prime or , then T is not an edge k-product cordial.
Proof. When k is a prime, by Lemma 2, T is not edge k-product cordial. For , let f be an edge 4-product cordial labeling of T. Then and for each i. Let u be the 0-vertex. By Lemma 2, there is no 0-edge in T. Thus, for . This results in , which is a contradiction. □
3. Edge 3-Product Cordial Trees
In order to establish the edge 3-product cordial behavior of the comet, we prove the following two lemmas.
Lemma 3. The path graph is an edge 3-product cordial for .
Proof. We define an edge labeling for recursively, and this labeling is represented by if , . We will use this representation for a labeling of in the whole paper.
The edge 3-product cordial labeling for
,
, is shown in
Table 1.
For
, define
recurrently as
, where
and
. Note that
. Clearly,
,
,
, where
. Thus,
Hence, is an edge 3-product cordial labeling of . Note that and . □
From [
18], we have the following result.
Lemma 4. The star graph is an edge 3-product cordial for .
Definition 3. Suppose G and H are the two edge-disjoint graphs with edge labelings g and h, respectively. We say that ϕ is a combination of g and h (or combine g with h) if Theorem 1. The comet graph is edge 3-product cordial for and .
Proof. Note that . Let . We label by , which was defined in the proof of Lemma 3. Define labeling , for as follows:
Suppose .
If , then , .
If , then , , .
If , then , , , .
Suppose .
If , then , .
If , then , , .
If , then , , , .
Suppose .
If , then , .
If , then , , .
If , then , , , .
Let be the combination of and . We can check that and ; and .
Note that with the common vertex . If is an edge 3-product cordial labeling of , , then combine for and for to obtain an edge 3-product cordial labeling for .
This completes the proof. □
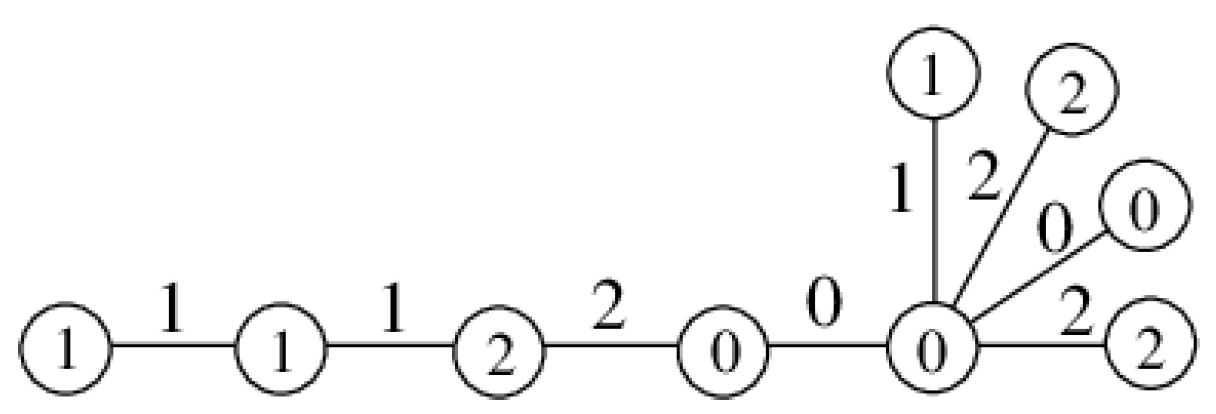
Example 2. Here is an example to illustrate the proof of Theorem 1. Suppose and . Firstly, we label . According to the labeling defined in the proof above, we have the following labeling (Figure 1): Here we can see that , ; . Now, we combine the labeling of to the labeling ϕ of . We have (see Figure 2) Here we can see that the number of 0-edges is 3, the number of i-edges is 4, , and the number of j-vertices is 4, .
Remark 1. By Lemma 3, when and when are edge 3-product cordial graphs. Again by Lemma 4, for and for are edge 3-product cordial graphs.
Also, note that under the labeling defined in Lemma 3, the vertex is always a 1-vertex and is always 0-vertex.
Consequently, if is not isomorphic to , , or , then admits an edge 3-product cordial labeling ϕ such that and .
Theorem 2. The double comet graph is edge 3-product cordial for and .
Proof. Let with the center and with the center . Then .
For , we label the edges of and the selected edges of by 0,1,2 evenly as shown below and denote this labeling by .
When , , and .
When , , , and .
When , , , .
When , , , and .
Note that and . Also, .
Now, consider , where and . We split into and with the common vertex . We label , and the selected edges of by as defined above, and all the edges of by 1 and 2 evenly. Again, we label the edges of an unlabeled subgraph of , which is isomorphic to by 0. We denote this labeling by . Then we have and ; ; and all are the same for .
Here, the unlabeled subgraph, say H, of is isomorphic to , where , which depends on q. That is,
When , if .
When , .
When , .
When , .
If , then by Theorem 1 there exists an edge 3-product cordial labeling for H. Note that , , and . When we combine with , the number of j-vertices () are , and . So the combination of and results in an edge 3-product cordial labeling for .
The detailed labeling for receiving edge 3-product cordial of
for
are moved to
Appendix A. This completes the proof. □
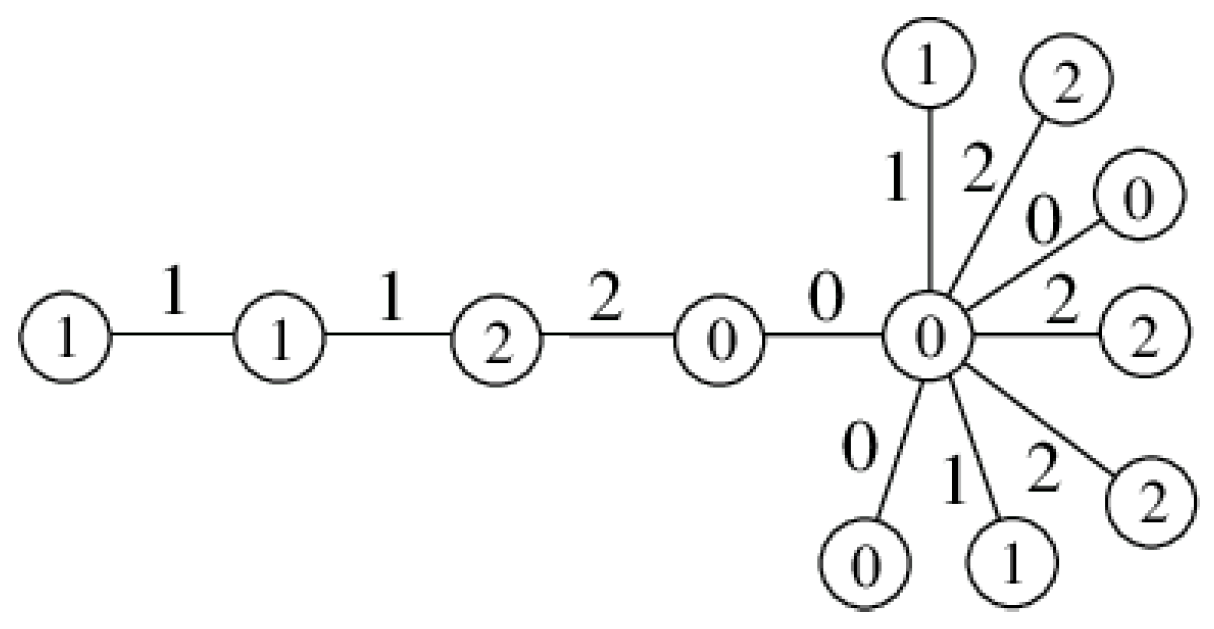
Example 3. The following Figure 3 illustrates the proof of Theorem 2. We combine α and ϕ to get an edge 3-product cordial labeling for .
4. Edge 4-Product Cordial Trees
We begin this section with the necessary condition on the number of vertices and leaves for a tree to admit an edge 4-product cordial labeling.
Theorem 3. Let T be a tree with n vertices, and S be the set of all the leaves of T. If T is an edge 4-product cordial graph, thenMoreover, the bound is sharp. Proof. Let f be an edge 4-product cordial labeling of T, and be the set of edges labeled by i, where . Let . By Corollary 1, is a tree and . This implies that each vertex in is not labeled by 0.
Now, consider forest . If , then ; and if , then . If and , then . If , then .
Let be the edges in such that and , . Note that are distinct, but may not be distinct. Then, there are edges in , and their end vertices are labeled by 2. Then , equivalently .
- (1)
If , then for all i and . Thus, . Therefore, .
- (2)
If , then for all i, and . Therefore, for . Hence, .
- (3)
If , then .
We merge the tree
into a vertex
r to receive the resultant graph
. Then
is a rooted tree with root
r and
. So
has at least
q leaves, which are also the leaves of
T. Since
S is the set of all leaves of
T and
T contains at least
q leaves,
. Hence,
□
The following remark demonstrates that the bound in Theorem 3 is sharp.
Remark 2. If is an edge 4-product cordial, thenClearly, , , and are not edge 4-product cordial graphs. An edge 4-product cordial labeling for , , is shown in Table 2. Corollary 3. is an edge 4-product cordial if and only if .
Note that in the following lemmas and corollary, all the induced vertex labelings work in the complete residues class modulo 4, .
Lemma 5. Suppose and are the trees such that . Let the order of and be a and b, respectively, such that for some positive integer n. Let and be the edge labeling, which satisfy the following conditions:
- (1)
and ;
- (2)
and ;
- (3)
only if , where .
Let ϕ be the combination of f and g. Then ϕ is an edge 4-product cordial labeling of .
Proof. Suppose the order of is . Then the order of is either or . Thus, by conditions 1 and 2, we obtain for all .
Since or 2, we have . Thus, the number of 0-vertices and 2-vertices does not change, and they are equal to n.
If the order of is and , then and . Hence, and .
If the order of is and , then and . Hence, and .
If the order of is , then . Hence, and if ; and if .
Suppose the order of is . Then the order of is . By conditions 1 and 2, the number of i-edges are n under for . In this case and , where and . Similarly, we have and . □
Lemma 6. Let be an edge labeling of tree T of order n, which satisfies the condition (2) of Lemma 5, then .
Proof. Let be the set of all 3-edges in T, and let . Since any 3-vertex must be incident to three edges, all 3-vertices are in . Also, each 3-vertex is of odd degree in . Thus, is even. Hence, . If is odd, then . If is even, then . Hence, . □
By Lemma 5, we have the following corollary.
Corollary 4. Suppose and are the trees such that . Let the order of be or and the order of be , where . Let and be the edge labeling, which satisfy the following conditions:
- (a)
and ;
- (b)
;
- (c)
and , where .
Let ϕ be the labeling of by combining f and g. Then ϕ is an edge 4-product cordial labeling of .
A vertex that satisfies the condition (3) in Lemma 5 or the conditions (b) and (c) in Corollary 4 is called a major vertex under g.
Lemma 7. If and , then there exists a labeling that satisfies the condition (2) of Lemma 5. If and , then there exists a labeling that satisfies the condition (c) of Corollary 4.
Proof. We label the edges of a path by 1,3,3,1 evenly and denote this required labeling by g. □
Lemma 8. If and , , then there exists a labeling that satisfies the condition (2) of Lemma 5. If and , , then there exists a labeling that satisfies the condition (c) of Corollary 4. Moreover, is the major vertex under g.
Proof. We will define a labeling
by the following approach. We first suitably label the edge
for
. And then label the edge of the path
. There are four cases. We put the details in
Appendix B. Hence, we have the theorem. □
Now, we consider the comet graph
, which has
leaves. From Theorem 3, we have
When , we have , which is a star. It is easy to check that is edge 4-product cordial when .
Theorem 4. For , the comet graph is edge 4-product cordial if and only if Proof. The necessary part is shown in the discussion above. Now we have to show the sufficient part. Let . We can check that when ; and when .
We split the graph
into two subgraphs,
and
, with a common vertex
x. Then, we define the labelings
f and
g for
and
, respectively, such that
f and
g satisfy all the conditions of Lemma 5 or Corollary 4. The details are referred to
Appendix C.
Hence, we have the theorem. □
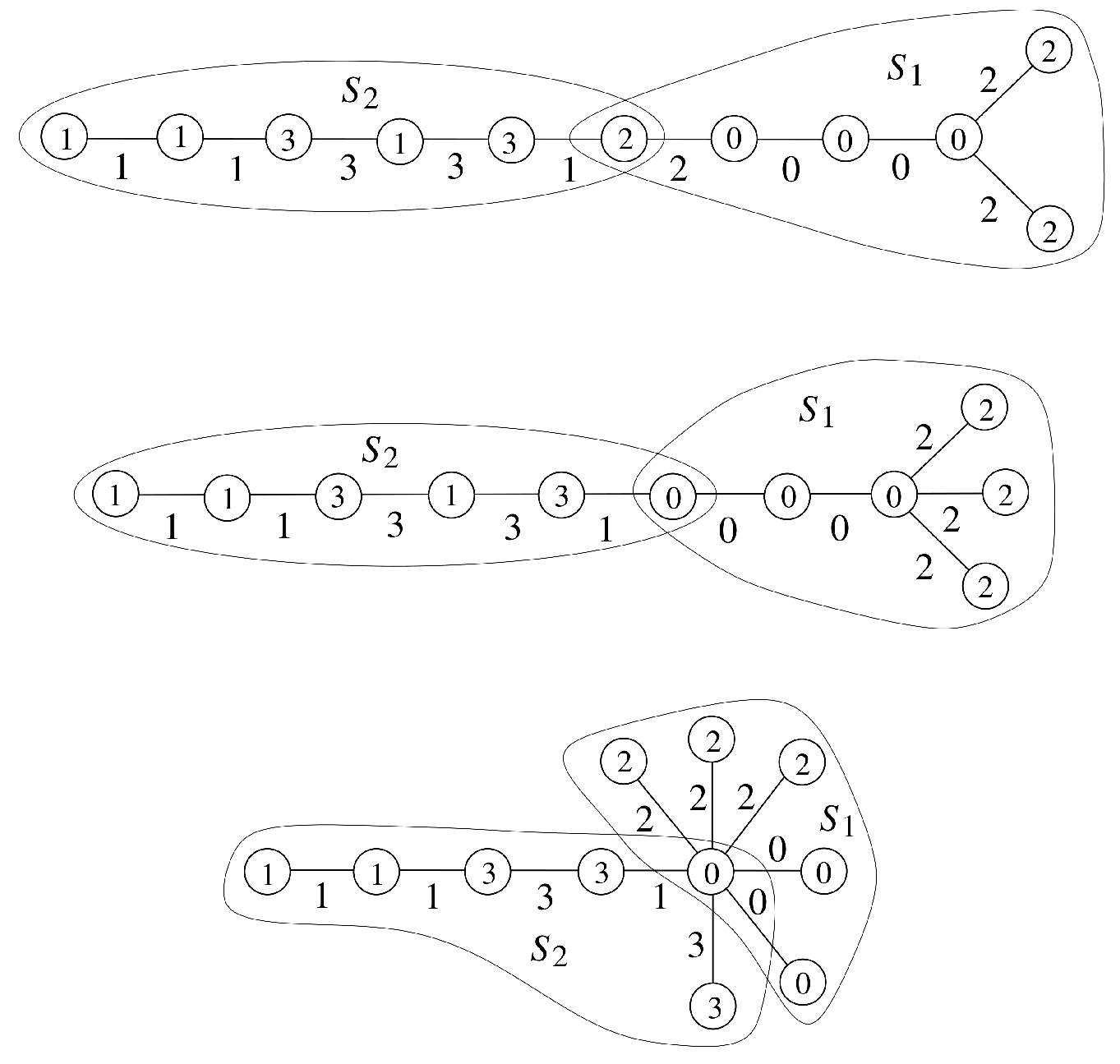
Example 4. Edge 4-product labelings for , , and are shown in Figure 4. Example 5. Edge 4-product labelings for , and are provided in Figure 5. Example 6. Edge 4-product labelings for and are shown in Figure 6. Remark 3. Suppose T is a tree of order , which admits an edge 4-product cordial labeling f, where . Let be the set of edges labeled by i, where and . By Theorem 3 we obtain the following results.
- (A)
If , then . Thus, H is a tree that has at least N leaves.
- (B)
If , then . Clearly, . Also, we have and .
- B1.
Suppose . Clearly, and . Then H is a tree of order that has at least leaves.
- B2.
Suppose . Recall that . Since , we have . Thus, and . Then H is a tree of order that has at least N leaves.
- B3.
Suppose . Since , we have and . Then H is a disjoint union of a tree of order with . Moreover, has at least leaves.
Theorem 5. Suppose , and , where .
- A.
When . The graph is an edge 4-product cordial if and only if .
- B.
When . The graph is an edge 4-product cordial if and only if .
Proof. Suppose there is an edge 4-product cordial labeling f for . Let H be the edge-induced subgraph defined in Remark 3.
- (A)
Suppose . By Remark 3, H is a tree of order that has at least N leaves. Suppose . Then . Thus, . Since H has at least N leaves, we have , where . But the order of H is at least , which is a contradiction. Thus, if , then is not an edge 4-product cordial graph.
- (B)
Suppose . Then and .
Suppose . Then H is a subtree of of order that has leaves. Suppose . Similarly to Case A, we obtain a contradiction. Thus, if , then is not an edge 4-product cordial graph.
Suppose . Then H is a subtree of of order that has N leaves. Suppose . Similarly to Case A, we obtain a contradiction. Thus, if , then is not an edge 4-product cordial graph.
Suppose . Then H is a disjoint union of a tree of order with . Moreover, has at least leaves. Thus, must be a comet such that and . Thus, if , then is not an edge 4-product cordial.
Consequently, if is an edge 4-product cordial, then when ; and when .
For the sufficient part, we split the graph into two subgraphs and with one or two common vertices. We label by 0 and 2, and by 1 and 3, respectively, such that these labelings induce an edge 4-product cordial labeling for .
Since
, we have
. This guarantees that the comets
and
defined below are well-defined. The details are referred to
Appendix D.
This completes the proof. □
Example 7. Edge 4-product labelings for and are shown in Figure 7. 5. Edge 5-Product Cordial Trees
In order to prove the main theorems, first we prove the following lemma. Note that, by Lemma 2, the path is not an edge 5-product cordial.
Lemma 9. The path graph is an edge 5-product cordial for and .
Proof. We define an edge labeling for recurrently, and this labeling is represented by if , .
We present the edge 5-product cordial labeling for
,
, except
in
Table 3.
For , we define recurrently as , where and . When , we have and . Thus, , , .
For , , , , , .
For , , , , , .
For , for all .
For , and for all .
Thus, is an edge 5-product cordial labeling of for . Moreover, and are the required labelings for and , respectively.
This completes the proof. □
Theorem 6. The comet graph is an edge 5-product cordial for and , except .
Proof. Let , where . In order to obtain an edge 5-product cordial labeling of for and , except for , we split into two subgraphs, and , with a common vertex . Note that when , does not appear; when , . For the last case, it has been proved in Lemma 9.
First, we label
by using
, which is defined below. For
, we label
to balance the number of
i-edges and
i-vertices, as shown in
Table 4.
For , we label , where . Then the difference between the number of i-edges and j-vertices does not change for all . Hence, according to the table above, we have an edge 5-product cordial labeling for , where and .
For , we label the edges of by 0, 1, 2, 3, and 4 evenly and denote this labeling by . Thus, is an edge 5-product labeling for for and , except for . By Corollary 2, is not an edge 5-product cordial graph. This completes the proof. □
Example 8. For the comet , we separate it into two edge-disjoint graphs, and . From the table above, we label as 1, 3, 3, 4, 4, 2, 2, 1, 0, and label the edges of by 0, 1, and 2. The resulting labeling is an edge labeling for . The numbers of 1-and 2-edges are 3, and the numbers of 0-, 3- and 4-edges are 2. The numbers of 0-, 1-, and 2- vertices are 3, and the numbers of 3- and 4- vertices are 2.
Finally, we label the edges of evenly by . We obtain three 0-vertices and two i-vertices, where . The centers of and will be merged; thus, we obtain an edge 5-product cordial labeling ϕ for . We can check that , , , , ; , , , , .
Theorem 7. The double comet graph is an edge 5-product cordial for and .
Proof. Let with center and with center . Then .
We define an edge labeling for and the selected edges of by 0,1,2,3,4 evenly. Consider , where . First, we assume .
For , we label the edges of by 1, 2, 3 evenly and edges of by , respectively.
For , we label edges of by , respectively, and edges of by , respectively.
For , we label edges of by , respectively, and edges of by , respectively.
Note that . Also for all i and for .
Now the unlabeled edges form
, where
Hence,
except for
. By Theorem 6, there is an edge 5-product cordial labeling for
for
.
For , . We label this by the labeling defined in Lemma 9. Now we check the number of i-vertices.
Before labeling , we have , , , , and . Suppose . After labeling , the vertex is still 0-vertex and the vertex changes from 1-vertex to . Thus and do not count towards the number of 0-vertices and 1-vertices. Thus, the combined labeling is an edge 5-product cordial labeling for .
For , the required labeling is shown in the following example.
Suppose . If , then , , , and . The unlabeled edges form . The argument is similar to the cases above. If , let , , , and . The unlabeled edges form . If , then we have an edge 5-product cordial labeling for . If , then label by 1. We have an edge 5-product cordial labeling for . If , then the labeling is the same as . □
Example 9. An edge 5-product cordial labelings for , where are shown in Figure 8.