Abstract
The concepts of k-product cordial labeling and edge product cordial labeling were introduced in 2012 and further explored by various researchers. Building on these ideas, we define a new concept called ‘edge k-product cordial labeling’ as follows: For a graph , which does not have isolated vertices, an edge labeling , where is an integer, is said to be an edge k-product cordial labeling of G if it induces a vertex labeling defined by , which satisfies and for , where and denote the number of edges and vertices, respectively, having label i for . In this paper, we study the edge k-product cordial behavior of trees, a comet, and a double comet.
Keywords:
cordial labeling; edge product cordial labeling; edge k-product cordial labeling; comet graph; double comet graph MSC:
05C78
1. Preliminaries
The concept of graph labeling has experienced significant popularity over the past six decades, owing to its practical applications. A groundbreaking paper addressing graph labeling problems was published by Rosa [1]. Subsequently, numerous papers on various graph labeling methods have been published, and Gallian’s survey [2] elegantly categorizes and organizes these diverse labeling methods published by various mathematicians all over the world. ‘Cordial labeling’ is one of the popular labelings introduced by Cahit [3]. Inspired by this notion, ‘product cordial labeling’ was proposed in [4]. In 2012, this concept was extended further, and a new concept called ‘k-product cordial labeling’ [5] was introduced. In the same year, Vaidya et al. [6] introduced a variation of product cordial labeling called ‘edge product cordial labeling’. In this variant, the roles of vertices and edges in ‘product cordial labeling’ are interchanged. Since then, some more results on ‘edge product cordial labeling’ have been published by the same authors; see [6,7,8,9]. Building on this, Thamizharasi et al. [10] demonstrated the existence of ‘edge product cordial labeling’ of regular digraphs in 2015. In the subsequent years, Prajapati and Aboshady et al. [11,12,13,14] contributed additional results on ‘edge product cordial labeling’. Motivated by the concepts of ‘k-product cordial labeling’ and ‘edge product cordial labeling’ and the established results, we put forth a new labeling, namely ‘edge k-product cordial labeling’, which extends the concept of edge product cordial labeling by expanding the set of labels from to . Let be a graph without isolated vertices and . Let be an edge labeling. The induced vertex labeling is defined by
is called the induced labeling of f. For convenience, let be the complete residue system modulo k. Also, an edge is called i-edge if it is labeled by i; and a vertex is called j-vertex if its induced label is j. Let and denote the number of i-edges and i-vertices, respectively, for . f is said to be an edge k-product cordial labeling of G if and for . Also, G is called an edge k-product cordial graph.
Let L be a set of labels. For an edge labeling of a graph , if for all , then we say that the edges of the graph labeled by labels in Levenly (under f).
In this paper, we use this notation, these concepts, and the following definitions unless otherwise stated.
Definition 1.
For , let be the path of order n. For , let the vertex set and the edge set of the star graph be and , respectively. For , let the graph with identifying c with . Such a graph is called a comet [15].
Definition 2.
For , let the graph with the vertex set and the edge set and , respectively. Such a graph is called a double comet [16].
Notation and concepts, which are not defined in this paper, are referred to in [17]. All graphs considered here are simple and connected.
We use the next section to show the structure of the subtree induced by all edges labeled by 0 of an edge k-product cordial tree. In the consecutive sections, we investigate the edge k-product cordial behavior of comet and double comet graphs for , and 5.
2. Properties of Edge -Product Cordial Trees
Lemma 1.
Let be an edge labeling of a tree , where . Then , where is the induced labeling of f.
Proof.
Let and , the edge induced subgraph of T. Let , p, and q be the number of components, the order and the size of , respectively. Since is a forest, . Since all its vertices are 0-vertices, . □
Corollary 1.
Let f be an edge k-product cordial labeling of a tree T of order n, where . If is the set of 0 edges under f, then is a tree and
Proof.
For each i, we have
By Lemma 1, we obtain this corollary. □
Example 1.
Suppose and . Then T contains 7 vertices and 6 edges. We keep all notation defined in the proof of Lemma 1 and Corollary 2. For any edge 3-product cordial labeling f, and for . From the proof of Lemma 1, . Since and , and hence .
Lemma 2.
Let G be a graph of order k. If k is a prime, then G is not an edge k-product cordial graph.
Proof.
Let f be an edge k-product cordial labeling of G. Then for . In particular, . Suppose there is a 0-edge, then it induces two 0-vertices, which is a contradiction. Suppose there are no 0-edges. Since k is a prime, there is no induced 0-vertex, which is also a contradiction. □
Corollary 2.
Let T be a tree of order k. If k is a prime or , then T is not an edge k-product cordial.
Proof.
When k is a prime, by Lemma 2, T is not edge k-product cordial. For , let f be an edge 4-product cordial labeling of T. Then and for each i. Let u be the 0-vertex. By Lemma 2, there is no 0-edge in T. Thus, for . This results in , which is a contradiction. □
3. Edge 3-Product Cordial Trees
In order to establish the edge 3-product cordial behavior of the comet, we prove the following two lemmas.
Lemma 3.
The path graph is an edge 3-product cordial for .
Proof.

We define an edge labeling for recursively, and this labeling is represented by if , . We will use this representation for a labeling of in the whole paper.
The edge 3-product cordial labeling for , , is shown in Table 1.

Table 1.
Edge 3-product cordial labeling for .
For , define recurrently as , where and . Note that . Clearly, , , , where . Thus,
Hence, is an edge 3-product cordial labeling of . Note that and . □
From [18], we have the following result.
Lemma 4.
The star graph is an edge 3-product cordial for .
Definition 3.
Suppose G and H are the two edge-disjoint graphs with edge labelings g and h, respectively. We say that ϕ is a combination of g and h (or combine g with h) if
Theorem 1.
The comet graph is edge 3-product cordial for and .
Proof.
Note that . Let . We label by , which was defined in the proof of Lemma 3. Define labeling , for as follows:
- Suppose .If , then , .If , then , , .If , then , , , .
- Suppose .If , then , .If , then , , .If , then , , , .
- Suppose .If , then , .If , then , , .If , then , , , .
Let be the combination of and . We can check that and ; and .
Note that with the common vertex . If is an edge 3-product cordial labeling of , , then combine for and for to obtain an edge 3-product cordial labeling for .
This completes the proof. □
Example 2.
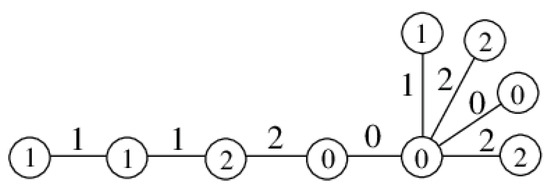
Here is an example to illustrate the proof of Theorem 1. Suppose and . Firstly, we label . According to the labeling defined in the proof above, we have the following labeling (Figure 1):

Figure 1.
Edge 3-product cordial labeling of .
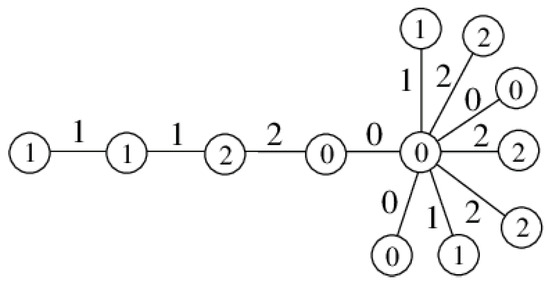
Here we can see that , ; . Now, we combine the labeling of to the labeling ϕ of . We have (see Figure 2)

Figure 2.
Edge 3-product cordial labeling of .
Here we can see that the number of 0-edges is 3, the number of i-edges is 4, , and the number of j-vertices is 4, .
Remark 1.
By Lemma 3, when and when are edge 3-product cordial graphs. Again by Lemma 4, for and for are edge 3-product cordial graphs.
Also, note that under the labeling defined in Lemma 3, the vertex is always a 1-vertex and is always 0-vertex.
Consequently, if is not isomorphic to , , or , then admits an edge 3-product cordial labeling ϕ such that and .
Theorem 2.
The double comet graph is edge 3-product cordial for and .
Proof.
Let with the center and with the center . Then .
For , we label the edges of and the selected edges of by 0,1,2 evenly as shown below and denote this labeling by .
- When , , and .
- When , , , and .
- When , , , .
- When , , , and .
Note that and . Also, .
Now, consider , where and . We split into and with the common vertex . We label , and the selected edges of by as defined above, and all the edges of by 1 and 2 evenly. Again, we label the edges of an unlabeled subgraph of , which is isomorphic to by 0. We denote this labeling by . Then we have and ; ; and all are the same for .
Here, the unlabeled subgraph, say H, of is isomorphic to , where , which depends on q. That is,
- When , if .
- When , .
- When , .
- When , .
If , then by Theorem 1 there exists an edge 3-product cordial labeling for H. Note that , , and . When we combine with , the number of j-vertices () are , and . So the combination of and results in an edge 3-product cordial labeling for .
The detailed labeling for receiving edge 3-product cordial of for are moved to Appendix A. This completes the proof. □
Example 3.
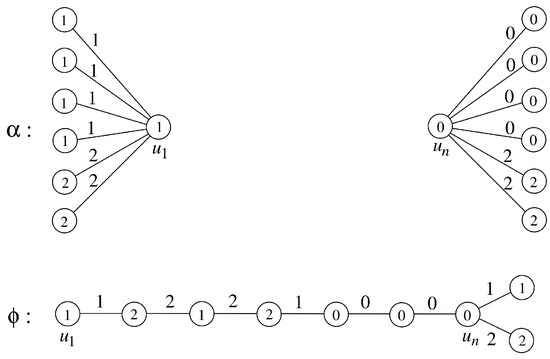
The following Figure 3 illustrates the proof of Theorem 2.

Figure 3.
Illustration of edge 3-product cordial labeling of .
We combine α and ϕ to get an edge 3-product cordial labeling for .
4. Edge 4-Product Cordial Trees
We begin this section with the necessary condition on the number of vertices and leaves for a tree to admit an edge 4-product cordial labeling.
Theorem 3.
Let T be a tree with n vertices, and S be the set of all the leaves of T. If T is an edge 4-product cordial graph, then
Moreover, the bound is sharp.
Proof.
Let f be an edge 4-product cordial labeling of T, and be the set of edges labeled by i, where . Let . By Corollary 1, is a tree and . This implies that each vertex in is not labeled by 0.
Now, consider forest . If , then ; and if , then . If and , then . If , then .
Let be the edges in such that and , . Note that are distinct, but may not be distinct. Then, there are edges in , and their end vertices are labeled by 2. Then , equivalently .
- (1)
- If , then for all i and . Thus, . Therefore, .
- (2)
- If , then for all i, and . Therefore, for . Hence, .
- (3)
- If , then .
We merge the tree into a vertex r to receive the resultant graph . Then is a rooted tree with root r and . So has at least q leaves, which are also the leaves of T. Since S is the set of all leaves of T and T contains at least q leaves, . Hence,
□
The following remark demonstrates that the bound in Theorem 3 is sharp.
Remark 2.

If is an edge 4-product cordial, then
Clearly, , , and are not edge 4-product cordial graphs. An edge 4-product cordial labeling for , , is shown in Table 2.

Table 2.
Edge 4-product cordial labeling for .
Corollary 3.
is an edge 4-product cordial if and only if .
Note that in the following lemmas and corollary, all the induced vertex labelings work in the complete residues class modulo 4, .
Lemma 5.
Suppose and are the trees such that . Let the order of and be a and b, respectively, such that for some positive integer n. Let and be the edge labeling, which satisfy the following conditions:
- (1)
- and ;
- (2)
- and ;
- (3)
- only if , where .
Let ϕ be the combination of f and g. Then ϕ is an edge 4-product cordial labeling of .
Proof.
Suppose the order of is . Then the order of is either or . Thus, by conditions 1 and 2, we obtain for all .
Since or 2, we have . Thus, the number of 0-vertices and 2-vertices does not change, and they are equal to n.
If the order of is and , then and . Hence, and .
If the order of is and , then and . Hence, and .
If the order of is , then . Hence, and if ; and if .
Suppose the order of is . Then the order of is . By conditions 1 and 2, the number of i-edges are n under for . In this case and , where and . Similarly, we have and . □
Lemma 6.
Let be an edge labeling of tree T of order n, which satisfies the condition (2) of Lemma 5, then .
Proof.
Let be the set of all 3-edges in T, and let . Since any 3-vertex must be incident to three edges, all 3-vertices are in . Also, each 3-vertex is of odd degree in . Thus, is even. Hence, . If is odd, then . If is even, then . Hence, . □
By Lemma 5, we have the following corollary.
Corollary 4.
Suppose and are the trees such that . Let the order of be or and the order of be , where . Let and be the edge labeling, which satisfy the following conditions:
- (a)
- and ;
- (b)
- ;
- (c)
- and , where .
Let ϕ be the labeling of by combining f and g. Then ϕ is an edge 4-product cordial labeling of .
A vertex that satisfies the condition (3) in Lemma 5 or the conditions (b) and (c) in Corollary 4 is called a major vertex under g.
Lemma 7.
If and , then there exists a labeling that satisfies the condition (2) of Lemma 5. If and , then there exists a labeling that satisfies the condition (c) of Corollary 4.
Proof.
We label the edges of a path by 1,3,3,1 evenly and denote this required labeling by g. □
Lemma 8.
If and , , then there exists a labeling that satisfies the condition (2) of Lemma 5. If and , , then there exists a labeling that satisfies the condition (c) of Corollary 4. Moreover, is the major vertex under g.
Proof.
We will define a labeling by the following approach. We first suitably label the edge for . And then label the edge of the path . There are four cases. We put the details in Appendix B. Hence, we have the theorem. □
Now, we consider the comet graph , which has leaves. From Theorem 3, we have
When , we have , which is a star. It is easy to check that is edge 4-product cordial when .
Theorem 4.
For , the comet graph is edge 4-product cordial if and only if
Proof.
The necessary part is shown in the discussion above. Now we have to show the sufficient part. Let . We can check that when ; and when .
We split the graph into two subgraphs, and , with a common vertex x. Then, we define the labelings f and g for and , respectively, such that f and g satisfy all the conditions of Lemma 5 or Corollary 4. The details are referred to Appendix C.
Hence, we have the theorem. □
Example 4.
Edge 4-product labelings for , , and are shown in Figure 4.

Figure 4.
Edge 4-product labelings for , , and .
Example 5.
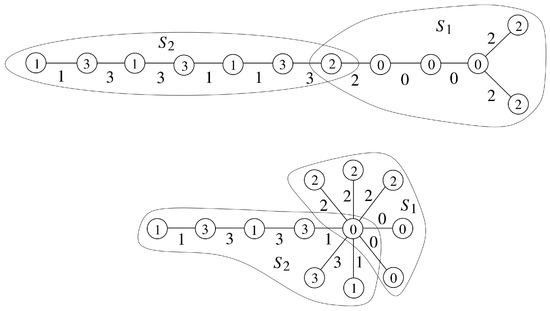
Edge 4-product labelings for , and are provided in Figure 5.

Figure 5.
Edge 4-product labelings for and .
Example 6.
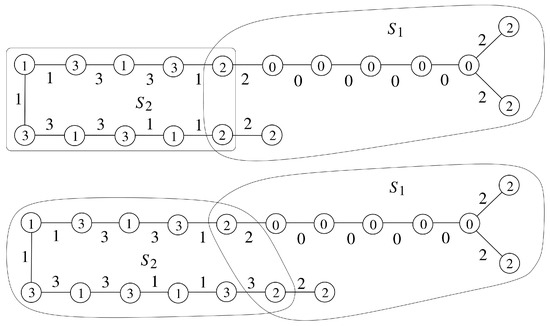
Edge 4-product labelings for and are shown in Figure 6.

Figure 6.
Edge 4-product labelings for and .
Remark 3.
Suppose T is a tree of order , which admits an edge 4-product cordial labeling f, where . Let be the set of edges labeled by i, where and . By Theorem 3 we obtain the following results.
- (A)
- If , then . Thus, H is a tree that has at least N leaves.
- (B)
- If , then . Clearly, . Also, we have and .
- B1.
- Suppose . Clearly, and . Then H is a tree of order that has at least leaves.
- B2.
- Suppose . Recall that . Since , we have . Thus, and . Then H is a tree of order that has at least N leaves.
- B3.
- Suppose . Since , we have and . Then H is a disjoint union of a tree of order with . Moreover, has at least leaves.
Theorem 5.
Suppose , and , where .
- A.
- When . The graph is an edge 4-product cordial if and only if .
- B.
- When . The graph is an edge 4-product cordial if and only if .
Proof.
Suppose there is an edge 4-product cordial labeling f for . Let H be the edge-induced subgraph defined in Remark 3.
- (A)
- Suppose . By Remark 3, H is a tree of order that has at least N leaves. Suppose . Then . Thus, . Since H has at least N leaves, we have , where . But the order of H is at least , which is a contradiction. Thus, if , then is not an edge 4-product cordial graph.
- (B)
- Suppose . Then and .
- Suppose . Then H is a subtree of of order that has leaves. Suppose . Similarly to Case A, we obtain a contradiction. Thus, if , then is not an edge 4-product cordial graph.
- Suppose . Then H is a subtree of of order that has N leaves. Suppose . Similarly to Case A, we obtain a contradiction. Thus, if , then is not an edge 4-product cordial graph.
- Suppose . Then H is a disjoint union of a tree of order with . Moreover, has at least leaves. Thus, must be a comet such that and . Thus, if , then is not an edge 4-product cordial.
Consequently, if is an edge 4-product cordial, then when ; and when .
For the sufficient part, we split the graph into two subgraphs and with one or two common vertices. We label by 0 and 2, and by 1 and 3, respectively, such that these labelings induce an edge 4-product cordial labeling for .
Since , we have . This guarantees that the comets and defined below are well-defined. The details are referred to Appendix D.
This completes the proof. □
Example 7.
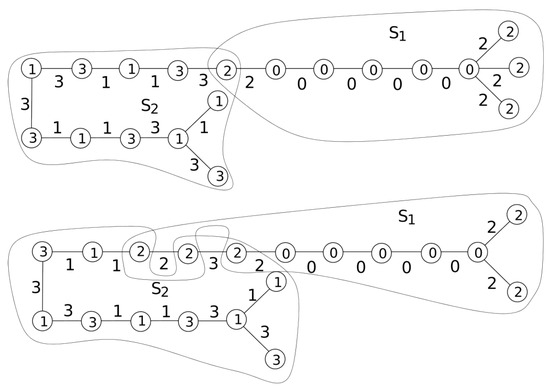
Edge 4-product labelings for and are shown in Figure 7.

Figure 7.
Edge 4-product labelings for and .
5. Edge 5-Product Cordial Trees
In order to prove the main theorems, first we prove the following lemma. Note that, by Lemma 2, the path is not an edge 5-product cordial.
Lemma 9.
The path graph is an edge 5-product cordial for and .
Proof.

We define an edge labeling for recurrently, and this labeling is represented by if , .
We present the edge 5-product cordial labeling for , , except in Table 3.

Table 3.
Edge 5-product cordial labeling for , except .
For , we define recurrently as , where and . When , we have and . Thus, , , .
- For , , , , , .
- For , , , , , .
- For , for all .
- For , and for all .
Thus, is an edge 5-product cordial labeling of for . Moreover, and are the required labelings for and , respectively.
This completes the proof. □
Theorem 6.
The comet graph is an edge 5-product cordial for and , except .
Proof.

Let , where . In order to obtain an edge 5-product cordial labeling of for and , except for , we split into two subgraphs, and , with a common vertex . Note that when , does not appear; when , . For the last case, it has been proved in Lemma 9.
First, we label by using , which is defined below. For , we label to balance the number of i-edges and i-vertices, as shown in Table 4.

Table 4.
Edge labeling for and .
For , we label , where . Then the difference between the number of i-edges and j-vertices does not change for all . Hence, according to the table above, we have an edge 5-product cordial labeling for , where and .
For , we label the edges of by 0, 1, 2, 3, and 4 evenly and denote this labeling by . Thus, is an edge 5-product labeling for for and , except for . By Corollary 2, is not an edge 5-product cordial graph. This completes the proof. □
Example 8.
For the comet , we separate it into two edge-disjoint graphs, and . From the table above, we label as 1, 3, 3, 4, 4, 2, 2, 1, 0, and label the edges of by 0, 1, and 2. The resulting labeling is an edge labeling for . The numbers of 1-and 2-edges are 3, and the numbers of 0-, 3- and 4-edges are 2. The numbers of 0-, 1-, and 2- vertices are 3, and the numbers of 3- and 4- vertices are 2.
Finally, we label the edges of evenly by . We obtain three 0-vertices and two i-vertices, where . The centers of and will be merged; thus, we obtain an edge 5-product cordial labeling ϕ for . We can check that , , , , ; , , , , .
Theorem 7.
The double comet graph is an edge 5-product cordial for and .
Proof.
Let with center and with center . Then .
We define an edge labeling for and the selected edges of by 0,1,2,3,4 evenly. Consider , where . First, we assume .
- For , we label the edges of by 1, 2, 3 evenly and edges of by , respectively.
- For , we label edges of by , respectively, and edges of by , respectively.
- For , we label edges of by , respectively, and edges of by , respectively.
Note that . Also for all i and for .
Now the unlabeled edges form , where
Hence, except for . By Theorem 6, there is an edge 5-product cordial labeling for for .
For , . We label this by the labeling defined in Lemma 9. Now we check the number of i-vertices.
Before labeling , we have , , , , and . Suppose . After labeling , the vertex is still 0-vertex and the vertex changes from 1-vertex to . Thus and do not count towards the number of 0-vertices and 1-vertices. Thus, the combined labeling is an edge 5-product cordial labeling for .
For , the required labeling is shown in the following example.
Suppose . If , then , , , and . The unlabeled edges form . The argument is similar to the cases above. If , let , , , and . The unlabeled edges form . If , then we have an edge 5-product cordial labeling for . If , then label by 1. We have an edge 5-product cordial labeling for . If , then the labeling is the same as . □
Example 9.
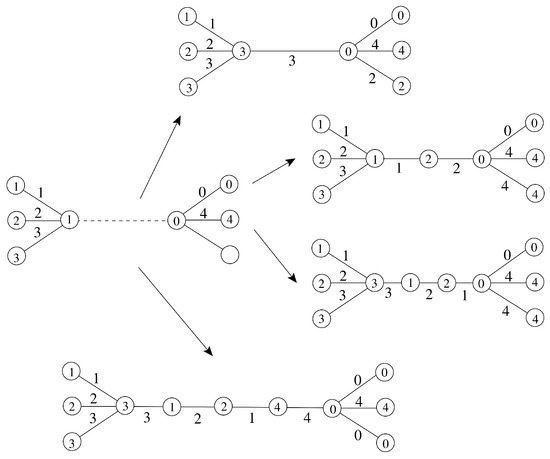
An edge 5-product cordial labelings for , where are shown in Figure 8.

Figure 8.
Edge 5-product labelings for , , , and .
6. Conclusions
The notion of edge k-product cordial labeling was introduced only in the year 2025, and the authors showed that star, bistar, and path unions of star graphs admit edge k-product cordial labeling. They also investigated the edge k-product cordial behavior of the shadow and the splitting graph of a star. In this work, we further explore the relationship between the number of edges and vertices labeled with 0 in edge k-product cordial trees and investigate the edge k- product cordiality of trees of order k. Also, we establish the edge k-product cordial properties of comet and double comet trees for , and 5. It is noted that edge k-product cordial labeling is a recent concept, and only a limited study has been carried out. Future researchers have ample scope to identify the families of graphs that admit or do not admit edge k-product cordial labeling, and also to investigate the edge k-product cordial behavior of a larger number of standard graphs.
Author Contributions
Conceptualization, J.D.K.; Validation, M.Z.Y.; Writing—original draft, J.J.; Writing—review and editing, J.P. and W.-C.S.; Visualization, I.A.-D.; Supervision, J.P.; Funding acquisition, M.Z.Y. and I.A.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors sincerely thank the referees for their valuable suggestions to improve the presentation of the paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
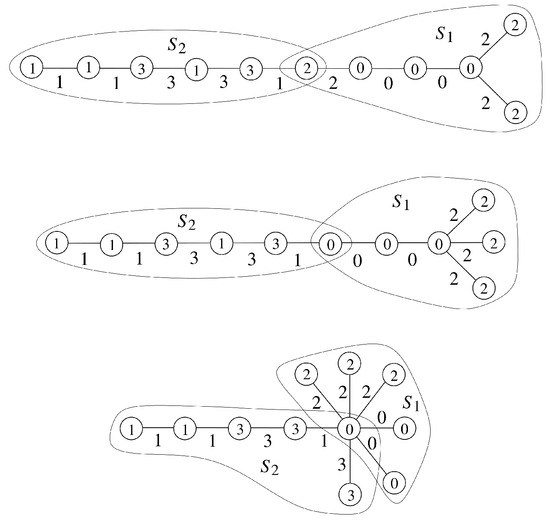
Appendix A. The Details About the Labelings for the Proof of Theorem 2
- When , , which implies . That is, .If and , then .
- (i)
- Suppose and . Let , and . Then . Also, . We form a path from the unlabeled edges. We combine and to get an edge 3-product cordial labeling for , where is defined in the proof of Lemma 3. For , the required labeling is shown in Figure A1.
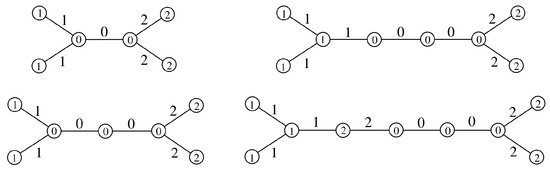 Figure A1. Edge 3-product cordial labelings of , and .
Figure A1. Edge 3-product cordial labelings of , and . - (ii)
- Suppose and . Let , , and . Then . Also, . We form a path from the unlabeled edges. Combine and to get an edge 3-product cordial labeling for , where is defined in the proof of Lemma 3. For , the required labeling is shown in Figure A2.
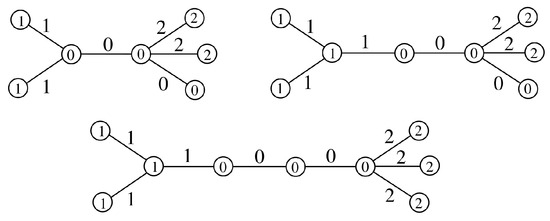 Figure A2. Edge 3-product cordial labeling of , and .
Figure A2. Edge 3-product cordial labeling of , and . - (iii)
- Suppose . If , then by Remark 1, admits an edge 3-product cordial labeling. So we have to consider only . Let , , . Also, if , then and if , then , . Hence, is an edge 3-product labeling for .
- (iv)
- Suppose . If , then by Remark 1, admits an edge 3-product cordial labeling. So we have to consider only . Let , , . Hence, is an edge 3-product labeling for .
When , . If , then similar to the above case, is an edge 3-product cordial. Therefore, we must consider only .- (i)
- Suppose . We have to consider only . By a similar method for labeling , we obtain an edge 3-product labeling for .
- (ii)
- Suppose . We have to consider only . By a similar method for labeling , we obtain an edge 3-product labeling for .
- When , we have . This implies that is, . Now, . We have to consider only .
- (i)
- Suppose . We have to consider only . By a similar method for labeling , we obtain an edge 3-product labeling for .
- (ii)
- Suppose . We have to consider only . By a similar method for labeling , we obtain an edge 3-product labeling for .
- When , we have , which is not possible.
- When , we have . This implies that is, . Now . We need to consider only and . By a similar method for labeling , we obtain an edge 3-product labeling for .
Appendix B. The Details About the Labelings for the Proof of Lemma 8
We define the labeling as follows:
- Suppose . We label by 1 for and by 3 for . Here, the induced vertex label for is 1. Also, we label by 1, 3, 3, 1 evenly.If , then and .If , then and .If , then and .If , then and .
- Suppose . If , we label by 1 for and by 3 for . Here, the induced vertex label for is 1 (if ) and an edge is not labeled. Label the path by 1, 3, 3, 1 evenly. Here, .If , then and .If , then and .If , then and .If , then and .
- Suppose . We label by 1 for and by 3 for ; and label and by 3 and 1, respectively. Also, we label the path by 1, 3, 3, 1 evenly. Here, the induced vertex label for and are 1.If , then and .If , then and .If , then and .If , then and .
- Suppose . We label by 1 for , by 3 for and by 3. Then and . We label the path by 1, 3, 3, 1 evenly.If , then and .If , then and .If , then and .If , then and .
Appendix C. The Details About the Labelings for the Proof of Theorem 4
- Suppose . When , we split into two subgraphs, namely and with a common vertex . Note that, since , has at least N leaves. When , we split into two subgraphs, namely and with a common vertex . Recall that and .We label N pendant edges of by 2 and the remaining edges by 0 and denote this labeling by f. Then , and .By Lemmas 7 and 8, we have a labeling g of , which satisfies the conditions (2) and (3) of Lemma 5.
- Suppose . When , we split into two subgraphs, namely and with a common vertex . Note that, since , has at least N leaves. When , we split into two subgraphs, namely and with a common vertex . Similar to Case 1, we have the labelings f and g of and , respectively, which satisfies all the conditions of Lemma 5.
- Suppose . Then, . First, we assume . When , we split into two subgraphs, namely and with a common vertex . Note that, since , has at least N leaves. When , we split the graph into two subgraphs, namely and with a common vertex .We label N pendant edges of by 2 and the remaining N edges by 0. By Lemmas 7 and 8, we have a labeling g of satisfying the condition s (2) and (3) of Lemma 5 or the conditions (b) and (c) of Corollary 4.Suppose . we split the graph into two subgraphs, namely and such that , where . Now label N pendant edges of by 2 and the remaining N edges by 0. Also, label the edges of by 1,3,3,1 evenly, denoted by g. Finally, we have and are 2-vertices. Consequently, the number of 0-vertices and 2-vertices are and those of 1-vertices and 3-vertices are N.
- Suppose . Then, . First, we assume . When , we split into two subgraphs, namely and with a common vertex . When , we split into two subgraphs, namely and with a common vertex . Note that, the order of is . We label N pendant edges of by 2 and the remaining N edges by 0. By Lemmas 7 and 8, we have a labeling g of satisfying the conditions (2) and (3) of Lemma 5 or the conditions (b) and (c) of Corollary 4. We can check that the number of 0-vertices is and the number of 2-vertices is N.Suppose . We split into two subgraphs, namely and such that , where . Now label N pendant edges of by 2 and the remaining N edges by 0. Also, label the edges of by 1,3,3,1 evenly, denoted by g. Finally, we have and are 2-vertices. Consequently, the number of 0-vertices and 2-vertices are ; and the number of 1-vertices and 3-vertices are either N or and not both.
Appendix D. The Details About the Labelings for the Proof of the Sufficient Part of Theorem 5
- Suppose . We assume that .
- 1a.
- Suppose . We split the graph into two subgraphs, namely and with a common vertex . Note that the order of and are and , respectively.We label N pendant edges of by 2 and the other edges of by 0. Consequently, we obtain N 2-vertices and N 0-vertices. By Lemma 8, we have a labeling g for such that is the major vertex. Combine these two labelings to get the required labeling for .
- 1b.
- Suppose . We split into two subgraphs, namely and with a common vertex . Note that the order of and are . Similarly to the Case 1a, we have the required labeling for .
- Suppose . Now, we assume that .
- 2a.
- Suppose .If , then we split into two subgraphs, namely and with a common vertex . Note that the orders of and are and . Similarly to Case 1a, we get the required labeling for .If , let be the disjoint union of with and is the disjoint union of with .We label all the N pendant edges in by 2 and the other N edges by 0. Here, the induced labels of , and are 2. By Lemma 8, we have a labeling for such that is the major vertex. Now we label the edge by 1 or 3 to have the edge labels evenly. Hence, we obtain the required labeling.
- 2b.
- Suppose .If , then we split into two subgraphs, namely and with a common vertex . Note that the orders of and are and , respectively. We label N pendant edges of by 2 and the other edges by 0. By Lemma 8, we have a labeling such that is the major vertex. We combine these two labelings to obtain the required labeling for .If , let be the disjoint union of with and is the disjoint union of with . Similarly to Case 2a, we obtain the required labeling for .
References
- Rosa, A. On Certain Valuations of the Vertices of a Graph, Theory of Graphs. In International Symposium, Rome, July 1966; Dunod Gordon & Breach Science Publishers, Inc.: Dunod, Paris, 1967; pp. 349–355. [Google Scholar]
- Gallian, J.A. A Dynamic Survey of Graph Labeling. Electron. J. Comb. 2023, #DS6. [Google Scholar]
- Cahit, I. Cordial graphs: A Weaker Version of Graceful and Harmonious Graphs. Ars Comb. 1987, 23, 201–207. [Google Scholar]
- Sundaram, M.; Ponraj, R.; Somasundaram, S. Product cordial labeling of graphs. Bull. Pure Appl. Sci. 2004, 23E, 155–163. [Google Scholar]
- Ponraj, R.; Sivakumar, M.; Sundaram, M. k-product cordial labeling of graphs. Int. J. Contemp. Math. Sci. 2012, 7, 733–742. [Google Scholar]
- Vaidya, S.K.; Barasara, C.M. Edge product cordial labeling of graphs. J. Math. Comput. Sci. 2012, 2, 1436–1450. [Google Scholar]
- Vaidya, S.K.; Barasara, C.M. On Edge product cordial Labeling of Some Product Related Graphs. Int. J. Math. Appl. 2014, 2, 15–22. [Google Scholar]
- Vaidya, S.K.; Barasara, C.M. Some Edge product cordial Graphs. Int. J. Math. Soft Comput. 2013, 3, 49–53. [Google Scholar] [CrossRef]
- Vaidya, S.K.; Barasara, C.M. Some New Families of Edge product cordial Graphs. Adv. Model. Optim. 2013, 15, 103–111. [Google Scholar]
- Thamizharasi, R.; Rajeswari, R. Edge Product Cordial Labeling and Total Magic Cordial Labeling of Regular Digraphs. Int. J. Inf. Sci. Comput. 2015, 9, 1–4. [Google Scholar] [CrossRef][Green Version]
- Aboshady, M.; Elbarkouky, R.; Roshdy, E.; Abdel-Azim Seoud, M. Further Results on Edge Product Cordial Labeling. Proc. Pak. Acad. Sci. 2020, 57, 23–32. [Google Scholar][Green Version]
- Prajapati, U.M.; Patel, N.B. Edge Product Cordial Labeling of Some Cycle Related Graphs. Open J. Discret. Math. 2016, 6, 268–278. [Google Scholar] [CrossRef][Green Version]
- Prajapati, U.M.; Patel, N.B. Edge Product Cordial Labeling of Some Graphs. J. Appl. Math. Comput. Mech. 2019, 18, 69–76. [Google Scholar] [CrossRef]
- Prajapati, U.M.; Patel, N.B. Edge Product Cordial Labeling of Switching Operations on Some Graphs. TWMS J. Appl. Eng. Math. 2022, 12, 191–199. [Google Scholar]
- Bagga, K.S.; Beineke, L.W.; Goddard, W.D.; Lipman, M.J.; Pippert, R.E. A survey of integrity. Discret. Appl. Math. 1992, 37, 13–28. [Google Scholar] [CrossRef]
- Antalan, J.R.M.; Tagle, R.P. Some Reverse Topological Indices of Comet and Double Comet Graphs. Commun. Appl. Nonlinear Anal. 2025, 32, 71–83. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; MacMillan: New York, NY, USA, 1976. [Google Scholar]
- NourEldeen, N.M.; Jenisha, J.; Jeya Daisy, K.; Jeyanthi, P.; Abdel-Aal, M.E. Edge k-Product Cordial Labeling of Graphs. Eur. J. Pure Appl. Math. 2025, 18, 5887. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).