A New Index for Quantifying the Peakedness of a Probability Distribution

Abstract

Peakedness is an important characteristic of probability distributions, and an effective method for quantifying peakedness is essential for statistical modeling and comparing different probability distributions in many practical applications. However, there has long been a misconception that kurtosis (or excess kurtosis) serves as a measure of peakedness. In this paper, we propose a new measure for quantifying peakedness, named the “peakedness index”. For a discrete distribution, the peakedness index is defined as the ratio of the maximum (peak) probability to its discrete informity; for a continuous distribution, it is defined as the ratio of the maximum (peak) density to its continuous informity, where “informity” is a concept introduced in the recently developed theory of informity. The peakedness indices for ten well-known distributions are presented and compared with the traditional kurtosis measure.

1. Introduction

Peakedness is an important characteristic of probability distributions. An effective measure of peakedness can provide insights into the concentration of probability mass. It is useful to analysts and researchers when building statistical models and comparing different probability distributions in many practical applications.

There has been a long-standing misconception that kurtosis (or excess kurtosis) serves as a measure of the peakedness of a probability distribution. Kurtosis is the fourth standardized moment, defined as follows:

$$\kappa \left(Y\right)=\mathrm{E}\left[{\left({\displaystyle \frac{Y-\mu }{\sigma }}\right)}^4\right]={\displaystyle \frac{\mathrm{E}\left[{\left(Y-\mu \right)}^4\right]}{{\left\{\mathrm{E}\left[{\left(Y-\mu \right)}^2\right]\right\}}^2}}={\displaystyle \frac{{\mu }_4}{{\sigma }^4}},$$

(1)

where $\mathrm{E}[·]$ represents the mathematical expectation, ${\mu }_4=\mathrm{E}\left[{\left(Y-\mu \right)}^4\right]$ is the fourth central moment, and $\sigma$ is the standard deviation.

The misconception appears in many statistics textbooks, ranging from those used in introductory courses to those used in advanced graduate courses [1]. Westfall [2] examined this misconception and provided insights through examples of distributions with the same kurtosis but different peaks. He concluded,

“As I have shown, kurtosis tells you very little about the peak or center of a distribution. Thus, kurtosis should never be defined in terms of peakedness. To do so is counterproductive to the aim of fostering statistical literacy. The relationship of peakedness with kurtosis is now officially over.”

If kurtosis is ruled out as a measure of peakedness, then the next question is: “What is the appropriate measure of the peakedness of a probability distribution?” This motivates consideration of alternative approaches.

Several quartile-based measures of peakedness have been proposed, including those by Hogg [3], Ruppert [4], Groeneveld and Meeden [5], and Horn [6]. However, because these measures depend on the specific quartile chosen, they do not provide a unique numerical assessment of a distribution’s peakedness. Moreover, some quartile-based measures, such as the one proposed by Horn [6], are limited to symmetric distributions, which further restricts their general applicability as universal measures of peakedness.

In this paper, we propose a new measure for quantifying the peakedness of a probability distribution, named the “peakedness index”. We consider both discrete and continuous distributions, but place more emphasis on continuous distributions. For a discrete distribution, the peakedness index is defined as the ratio of the maximum (peak) probability to its discrete informity; for a continuous distribution, it is defined as the ratio of the maximum (peak) density to its continuous informity, where “informity” is a concept in informity theory, recently proposed by Huang [7].

In the following sections, Section 2 describes the proposed peakedness index in detail. Section 3 explains the meaning of the proposed peakedness index for continuous distributions. Section 4 derives the peakedness index for the t-distribution. Section 5 presents the peakedness index for the binomial distribution. Section 6 presents the Discussion and Conclusion.

2. The Proposed Peakedness Index

2.1. Discrete Distributions

Definition 1. 

Consider a discrete random variable X with probability mass function (PMF) $P\left(X\right)$. The proposed peakedness index, denoted by $\rho \left(X\right)$, is defined as follows:

$$\rho \left(X\right)={\displaystyle \frac{P_{\max }}{\beta \left(X\right)}},$$

(2)

where $P_{\max }$ is the maximum value in the PMF, and $\beta \left(X\right)$ is the discrete informity of the distribution, given by ([7])

$$\beta \left(X\right)={{\displaystyle \sum }}_{i=1}^N{\left[P\left(x_i\right)\right]}^2=\mathrm{E}\left[P\left(X\right)\right],$$

(3)

where N is the number of possible outcomes.

The discrete informity $\beta \left(X\right)$ is the mean probability of the distribution, serving as a baseline for comparison with the peak probability. Therefore, ρ(X) measures how pronounced the maximum (peak) probability is relative to the mean probability of the distribution.

For a uniform distribution with the PMF $1/N$, $P_{\max }=\beta \left(X\right)=1/N$, and $\rho \left(X\right)=1$. For any other unimodal distribution, its peakedness index will be greater than 1. This is because the maximum value in a probability mass function is always greater than the average value of that function.

2.2. Continuous Distributions

Definition 2. 

Consider a continuous random variable Y with probability density function (PDF) p(Y). The proposed peakedness index, denoted by $\rho \left(Y\right)$, is defined as follows:

$$\rho \left(Y\right)={\displaystyle \frac{p_{\max }\left(y\right)}{\beta \left(Y\right)}},$$

(4)

where $p_{\max }\left(y\right)$ is the maximum value in the PDF $p\left(Y\right)$, and $\beta \left(Y\right)$ is the continuous informity of the distribution, given by ([7]):

$$\beta \left(Y\right)={\displaystyle \int }{\left[p\left(y\right)\right]}^{2}dy=\mathrm{E}\left[p\left(Y\right)\right],$$

(5)

The continuous informity $\beta \left(Y\right)$ is the mean density of the distribution, serving as a baseline for comparison with the peak density. Therefore, $\rho \left(Y\right)$ measures how pronounced the maximum (peak) density is relative to the mean density of the distribution.

In principle, the definition of the proposed peakedness index given by Equation (4) is valid for any type of distribution: symmetric, asymmetric, and even multimodal. In the case of a unimodal distribution, the maximum density is attained at the mode, denoted as $p\left(\mathrm{mode}\right)$. Then, the proposed peakedness index becomes

$$\rho \left(Y\right)={\displaystyle \frac{p\left(\mathrm{mode}\right)}{\beta \left(Y\right)}}$$

(6)

Table 1. PDFs, continuous informities, maximum densities, peakedness indices, and kurtoses for eight well-known distributions.

Distribution	PDF	$\mathbf{Continuous} \mathbf{Informity} \mathit{\beta }\left(\mathit{Y}\right)$	$\mathbf{Maximum} \mathbf{Density} {\mathit{p}}_{\mathbf{max}}\left(\mathit{y}\right)$	$\mathbf{Peakedness} \mathbf{Index} \mathit{\rho }\left(\mathit{Y}\right)$	$\mathbf{Kurtosis} \mathit{\kappa }\left(\mathit{Y}\right)$
Uniform	${\displaystyle \frac{1}{2a}}$	${\displaystyle \frac{1}{2a}}$	${\displaystyle \frac{1}{2a}}$	1	1.8
Triangular	$\{\begin{array}{c}{\displaystyle \frac{\left(y+a\right)}{a^2}}, -a\le y\le 0\\ {\displaystyle \frac{\left(a-y\right)}{a^2}}, 0\le y\le a\\ \end{array}$	${\displaystyle \frac{2}{3a}}$	${\displaystyle \frac{1}{a}}$	1.5	2.4
Raised cosine	${\displaystyle \frac{1}{2a}}\left[1+\cos \left({\displaystyle \frac{\pi }{a}}y\right)\right]$	${\displaystyle \frac{3}{4a}}$	${\displaystyle \frac{1}{a}}$	1.333	2.406
Normal	${\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right]$	${\displaystyle \frac{1}{2\sigma \sqrt{\pi }}}$	${\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}$	1.414	3
Exponential	$\lambda \exp \left(-\lambda y\right)$	${\displaystyle \frac{\lambda }{2}}$	$\lambda$	2	9
Cauchy	${\displaystyle \frac{1}{\pi \gamma \left[1+\frac{1}{{\gamma }^2}{\left(y-y_0\right)}^2\right]}}$	${\displaystyle \frac{1}{2\pi \gamma }}$	${\displaystyle \frac{1}{\pi \gamma }}$	2	Undefined
Rayleigh	${\displaystyle \frac{y}{{\sigma }^2}}\exp \left(-{\displaystyle \frac{y^2}{2{\sigma }^2}}\right)$	${\displaystyle \frac{\sqrt{\pi }}{4\sigma }}$	${\displaystyle \frac{1}{\sigma }}\exp \left(-{\displaystyle \frac{1}{2}}\right)$	1.369	3.245
Laplace	${\displaystyle \frac{1}{2b}}\exp \left(-{\displaystyle \frac{\left|y-\mu \right|}{b}}\right)$	${\displaystyle \frac{1}{4b}}$	${\displaystyle \frac{1}{2b}}$	2	9

presents the PDFs, continuous informities, maximum densities, peakedness indices, and kurtoses for eight well-known distributions. The continuous informities for these distributions are reported by Huang [7]. This table allows for a direct comparison between the proposed peakedness index and the traditional kurtosis measure.

As can be seen from Table 1, the proposed peakedness index is well defined for all eight distributions, including the Cauchy distribution. The peakedness index is 2 for the Cauchy distribution and 1.414 for the normal distribution, indicating that the Cauchy distribution is more peaked than the normal distribution, which aligns with our intuition. In contrast, the kurtosis of the Cauchy distribution is undefined because its moments do not exist, making comparison with other distributions (such as the normal distribution) impossible. In fact, the proposed peakedness index is applicable to any distribution, regardless of whether its moments exist. This is because both the peak density and the continuous informity of a distribution always exist and can be determined numerically. Therefore, the peakedness index provides a robust and universally applicable measure of the peakedness of a distribution.

It should be noted that we did not compare the proposed peakedness index with an existing non-kurtosis measure of peakedness. This is because existing non-kurtosis measures are primarily based on quartiles, and their calculated values depend on the specific choice of quartiles, which makes the comparison less consistent and meaningful. Therefore, in this study, we compare the proposed peakedness index only with the traditional kurtosis measure.

3. Meaning of the Proposed Peakedness Index for Continuous Distributions

Note that the continuous informity $\beta \left(Y\right)$ is the mean density of the PDF p(Y). It can be interpreted as the density of an equivalent uniform distribution with the same continuous informity on an interval of length $\delta$, where $\delta$ is referred to as the uncertainty length and is defined by the inverse of $\beta \left(Y\right)$ ([7])

$$\delta ={\displaystyle \frac{1}{\beta \left(Y\right)}}={\displaystyle \frac{1}{{\displaystyle \int }{\left[p\left(y\right)\right]}^{2}dy}}.$$

(7)

If the original distribution is symmetric about zero, then the support of its equivalent uniform distribution is $\left(-{\displaystyle \frac{\delta }{2}}, +{\displaystyle \frac{\delta }{2}}\right)$. If the original distribution is defined on the support $\left(0, q\right)$, where q > 0, the support of its equivalent uniform distribution becomes $\left(0, \delta \right)$.

Therefore, the proposed peakedness index quantifies the degree of peakedness of a probability distribution relative to its equivalent uniform distribution with the same continuous informity. As shown in Table 1, the peakedness index for the uniform distribution is 1, while the peakedness index for any other continuous unimodal distribution is greater than 1. The higher the peakedness index, the more pronounced the peak, while the lower the peakedness index, the flatter the distribution. This interpretation aligns with common-sense expectations regarding the shape of distributions.

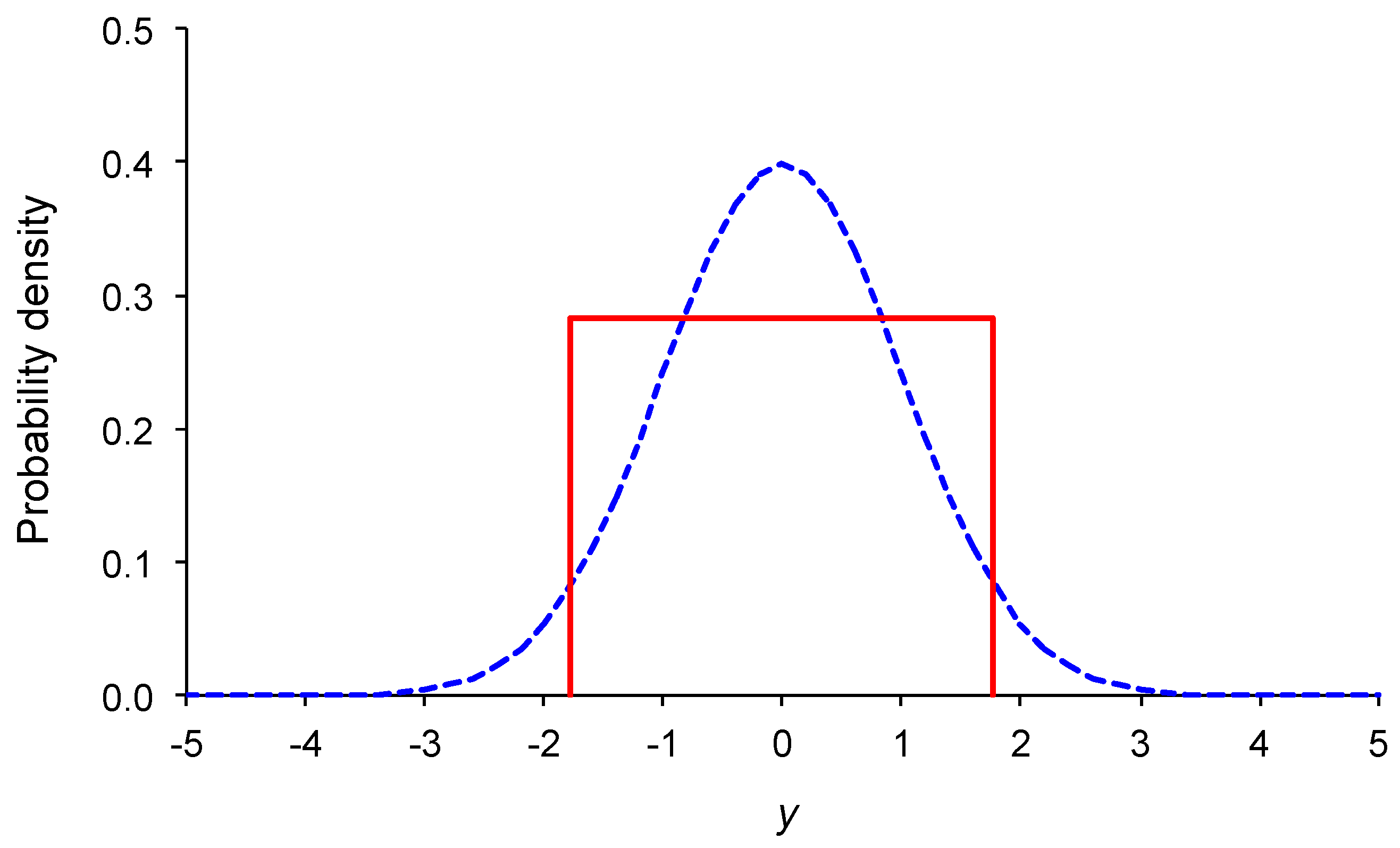
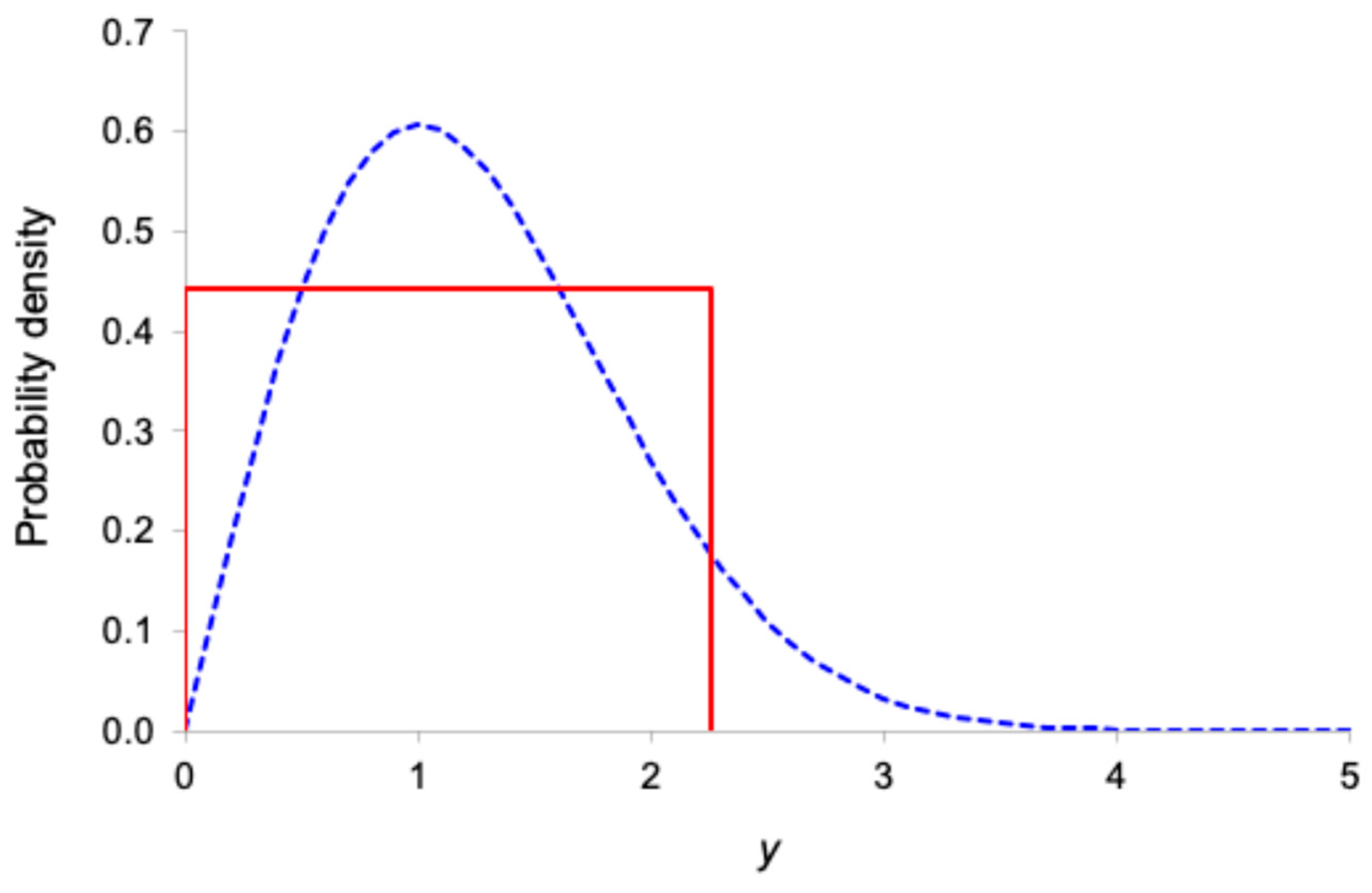
To further illustrate the meaning of the peakedness index for continuous distributions, we consider three distributions: the standard normal distribution N(0,1), the Cauchy distribution with y₀ = 0 and γ = 1, and the Rayleigh distribution with σ = 1.

Table 2. Values of the continuous informity, uncertainty length, and support of the equivalent uniform distribution for three distributions.

Distribution	$\mathbf{Continuous} \mathbf{Informity} \mathit{\beta }\left(\mathit{Y}\right)$	$\mathbf{Uncertainty} \mathbf{Length} \mathit{\delta }$	Support of Equivalent Uniform Distribution
Standard normal: N(0,1)	0.282	3.545	(−1.772, 1.772)
Cauchy: y0 = 0 and γ = 1	0.159	6.283	(−3.145, 3.145)
Rayleigh: σ = 1	0.443	2.257	(0, 2.257)

shows the numerical values of the continuous informity, uncertainty length, and support of the equivalent uniform distribution for these three distributions. Figure 1, Figure 2 and Figure 3 display the standard normal, Cauchy, and Rayleigh distributions alongside their corresponding equivalent uniform distributions. This visualization helps to better understand the meaning of the proposed peakedness index by comparing the shape of the original distribution with the shape of its equivalent uniform distribution.

4. Peakedness Index for the t-Distribution

The peakedness index for the t-distribution is a function of its degrees of freedom and is derived as follows.

The PDF of the t-distribution is written as

$$p\left(y\right)={\displaystyle \frac{\mathsf{\Gamma }\left(\frac{\nu +1}{2}\right)}{\sqrt{\pi \nu }\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}}{\left(1+{\displaystyle \frac{y^2}{\nu }}\right)}^{-{\displaystyle \frac{\nu +1}{2}}},$$

(8)

where $\nu$ is the degrees of freedom.

The continuous informity of the t-distribution is given by

$$\beta \left(Y\right)={\displaystyle \int }{\left[p\left(y\right)\right]}^{2}dy={\displaystyle \frac{{\mathsf{\Gamma }}^2\left(\frac{\nu +1}{2}\right)}{\nu \pi {\mathsf{\Gamma }}^2\left(\frac{\nu }{2}\right)}}{{\displaystyle \int }}_{-\infty }^{\infty }{\displaystyle \frac{1}{{\left(1+\frac{y^2}{\nu }\right)}^{\nu +1}}}dy.$$

(9)

The maximum density of the t-distribution is at y = 0. Thus, the maximum density is given by

$$p_{\max }\left(y=0\right)={\displaystyle \frac{\mathsf{\Gamma }\left(\frac{\nu +1}{2}\right)}{\sqrt{\pi \nu }\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}},$$

(10)

Then, the peakedness index for the t-distribution is given by

$$\rho \left(Y\right)={\displaystyle \frac{p_{\max }\left(y=0\right)}{\beta \left(Y\right)}}=\sqrt{\pi \nu }{\displaystyle \frac{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu +1}{2}\right)}}{\displaystyle \frac{1}{{{\displaystyle \int }}_{-\infty }^{\infty }\frac{1}{{\left(1+\frac{y^2}{\nu }\right)}^{\nu +1}}dy}}.$$

(11)

The solution for $\rho \left(Y\right)$ can be obtained by using the following integrals:

$${{\displaystyle \int }}_{-\infty }^{\infty }{\displaystyle \frac{1}{{\left(1+c{y}^2\right)}^n}}dy={\displaystyle \frac{\left(2n-3\right)}{2\left(n-1\right)}}{{\displaystyle \int }}_{-\infty }^{\infty }{\displaystyle \frac{1}{{\left(1+c{y}^2\right)}^{n-1}}}dy,\mathrm{and}$$

(12)

$${{\displaystyle \int }}_{-\infty }^{\infty }{\displaystyle \frac{1}{1+c{y}^2}}dy={\displaystyle \frac{\pi }{\sqrt{c}}}.$$

(13)

where $n=\nu -1$ and $c={\displaystyle \frac{1}{\nu }}$.

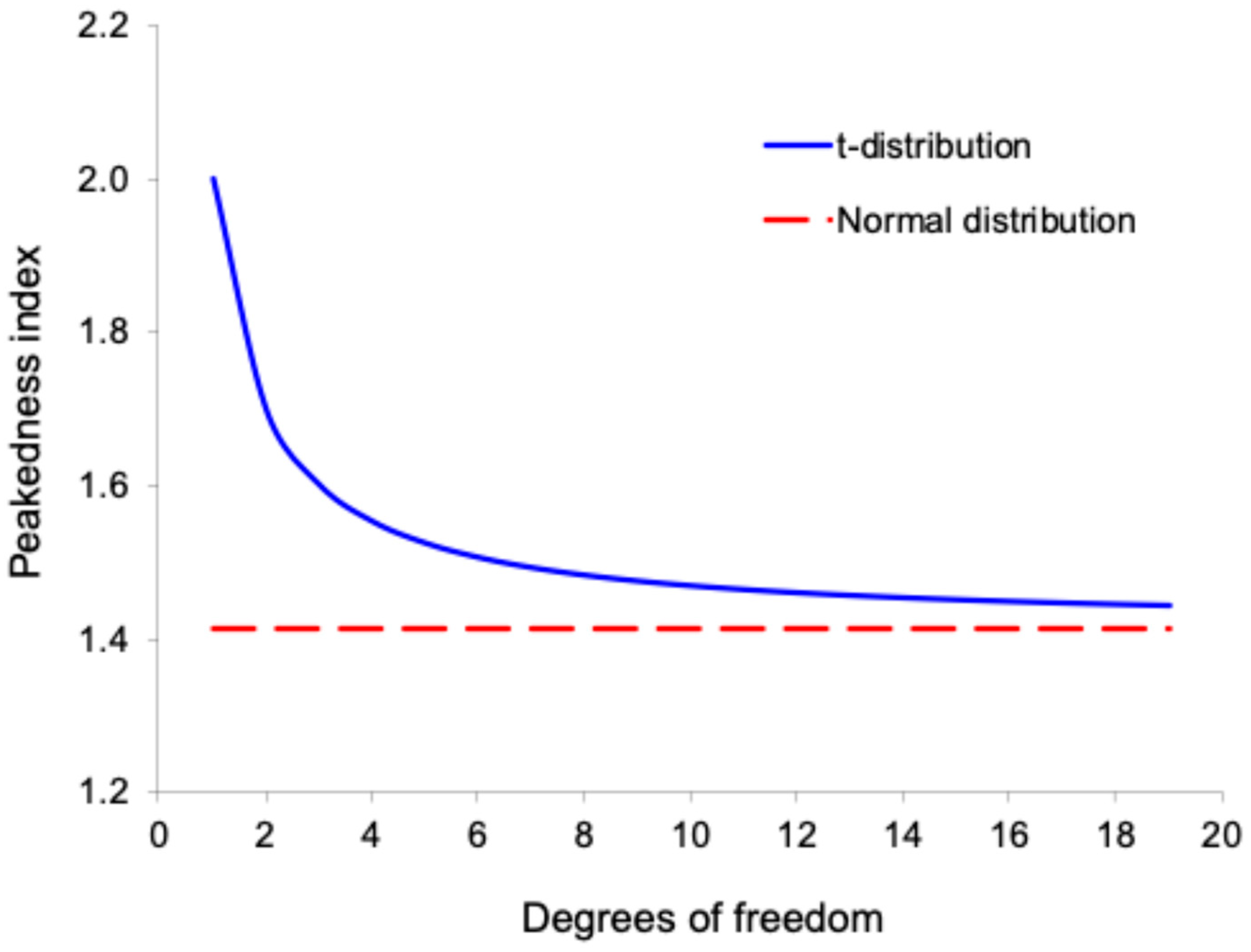
Figure 4 shows the peakedness index for the t-distribution as a function of the degrees of freedom, alongside that of the normal distribution. At ν = 1, which corresponds to the Cauchy distribution, the peakedness index is 2. As the degrees of freedom increase, the peakedness index decreases. In the limit case that the degrees of freedom approach infinity, the t-distribution converges to the standard normal distribution, and its peakedness index approaches $\sqrt{2}\approx 1.414$. This trend reflects the fact that t-distributions become less peaked and closer to the standard normal distribution as the degrees of freedom increase.

It is important to note that the peakedness index for the t-distribution is always defined, regardless of the degrees of freedom. In contrast, the kurtosis of the t-distribution is undefined for $\nu \le 4$.

For comparison, we also calculated the kurtosis of the t-distribution using the formula $\kappa \left(Y\right)={\displaystyle \frac{6}{\nu -4}}+3$. The resulting kurtosis values are 9 for $\nu =5$, 4 for $\nu =10$, and 3.063 for $\nu =100$, showing a similar decreasing trend as the degrees of freedom increase. In the limit case that $\nu \to \infty$, the kurtosis approaches 3, consistent with the normal distribution.

5. Peakedness Index for the Binomial Distribution

The binomial distribution $X~B\left(n,p\right)$ is a well-known discrete distribution. Its probability mass function (PMF) is expressed as

$$P\left(k,n,p\right)=\mathrm{Pr}\left(X=k\right)=\left(\begin{array}{c}n\\ k\end{array}\right)p^k{\left(1-p\right)}^{n-k},$$

(14)

where p is the success probability, n is the number of trials, $k=0, 1, 2, \dots , n$, and

$$\left(\begin{array}{c}n\\ k\end{array}\right)={\displaystyle \frac{n!}{k!\left(n-k\right)!}}$$

(15)

The discrete informity of the binomial distribution is

$$\beta \left(X\right)=\mathrm{E}\left[P\left(k,n,p\right)\right]={{\displaystyle \sum }}_{k=0}^n{\left(\begin{array}{c}n\\ k\end{array}\right)}^2{p}^{2k}{\left(1-p\right)}^{2\left(n-k\right)}.$$

(16)

The maximum probability is attained at the following mode:

$$k_{\mathrm{mode}}=\left(n+1\right)p, \mathrm{or} \left(n+1\right)p-1.$$

(17)

Thus, the peakedness index for the binomial distribution is

$$\rho \left(X\right)={\displaystyle \frac{P\left(k_{\mathrm{mode}},n,p\right)}{\beta \left(X\right)}}={\displaystyle \frac{P\left(k_{\mathrm{mode}},n,p\right)}{{{\displaystyle \sum }}_{k=0}^n{\left(\begin{array}{c}n\\ k\end{array}\right)}^2{p}^{2k}{\left(1-p\right)}^{2\left(n-k\right)}}}.$$

(18)

As a numerical example, consider the binomial distribution $X~B\left(n,0.5\right)$ (p = 0.5). Because p = 0.5, the distribution is symmetric. Figure 5 shows its peakedness index as a function of the number of trials, alongside that of the normal distribution. As the number of trials increases, the peakedness index also increases. In the limit case that the number of trials approaches infinity, the binomial distribution $X~B\left(n,0.5\right)$ can be approximated by a normal distribution $X~N\left(0.5n,0.25n\right)$, and its peakedness index converges to $\sqrt{2}\approx 1.414$. This trend indicates that, as the number of trials increases, the binomial distribution becomes increasingly peaked and progressively closer to the normal distribution.

For comparison, we also calculated the kurtosis of the binomial distribution $X~B\left(n,0.5\right)$ using the formula $\kappa \left(X\right)={\displaystyle \frac{1-6pq}{npq}}+3$, where $q=1-p$. The resulting kurtosis values are 2.333 for n = 3, 2.895 for n = 10, and 2.980 for n = 101, showing a similar increasing trend as the number of trials increases. In the limit case that $n\to \infty$, the kurtosis approaches 3, consistent with the normal distribution.

6. Discussion and Conclusions

The proposed peakedness index has two major advantages over the traditional kurtosis measure. First, the peakedness index is always well defined. This is because, for any discrete distribution, the maximum probability and the discrete informity (i.e., the mean probability) always exist; similarly, for any continuous distribution, the peak density and the continuous informity (i.e., the mean density) always exist. Therefore, the peakedness index can be used to compare the shapes of any distributions. In contrast, kurtosis is undefined when a distribution’s second and/or fourth central moments do not exist. For example, the kurtosis of the Cauchy distribution is undefined, making it impossible to compare the Cauchy distribution with other distributions (such as the normal distribution) in this regard.

Second, the proposed peakedness index is intuitive and straightforward to interpret. This is because it directly compares the peak probability or density with the average probability or density of the distribution. A uniform distribution has a peakedness index of 1, while any unimodal distribution has a peakedness index greater than 1. A higher peakedness index indicates a more pronounced peak, whereas a lower value indicates a flatter distribution. This interpretation aligns naturally with the common-sense understanding of the shapes of distributions. In contrast, kurtosis does not provide an intuitive and easily interpretable measure of peakedness. For example, as shown in Table 1, the kurtosis of the uniform distribution on the interval $\left[-a,a\right]$ is 1.8. It is unclear why this value corresponds to a completely flat distribution.

The calculation of the peakedness index requires knowledge of the underlying probability distribution, specifically its probability mass function (PMF) or probability density function (PDF). Therefore, it may not be directly applicable to raw experimental data. This limitation can be addressed by fitting the observed data to one or more candidate distribution models and selecting the best-fitting model. Such model selection is a standard and widely accepted practice in many statistical applications.

In principle, the proposed peakedness index is applicable to all types of distributions: symmetric, asymmetric, and even multimodal. In this study, the peakedness indices for ten well-known distributions have been derived. Further work is needed to extend the derivations to additional distributions.

In summary, the proposed peakedness index provides a robust and intuitive alternative to kurtosis for quantifying the peakedness of a probability distribution. Its universality and interpretability make it a valuable tool for statistical modeling, data analysis, and scientific research involving probability distributions.