Integrating Fractional Calculus Memory Effects and Laguerre Polynomial in Secretary Bird Optimization for Gene Expression Feature Selection

Abstract

Feature selection in high-dimensional datasets presents significant computational challenges, particularly in domains with large feature spaces and limited sample sizes. This paper introduces FL-SBA, a novel metaheuristic algorithm integrating fractional calculus enhancements with Laguerre operators into the Secretary Bird Optimization Algorithm framework for binary feature selection. The methodology incorporates fractional opposition-based learning utilizing Laguerre operators for enhanced population initialization with non-local memory characteristics, and a Laguerre-based binary transformation function replacing conventional sigmoid mechanisms through orthogonal polynomial approximation. Fractional calculus integration introduces memory effects that enable historical search information retention, while Laguerre polynomials provide superior approximation properties and computational stability. Comprehensive experimental validation across ten high-dimensional gene expression datasets compared FL-SBA against standard SBA and five contemporary methods including BinCOA, BAOA, BJSO, BGWO, and BMVO. Results demonstrate FL-SBA’s superior performance, achieving 96.06% average classification accuracy compared to 94.41% for standard SBA and 82.91% for BinCOA. The algorithm simultaneously maintained exceptional dimensionality reduction efficiency, selecting 29 features compared to 40 for competing methods, representing 27% improvement while achieving higher accuracy. Statistical analysis reveals consistently lower fitness values (0.04924 averages) and stable performance with minimal standard deviation. The integration addresses fundamental limitations in integer-based computations while enhancing convergence behavior. These findings suggest FL-SBA represents significant advancement in metaheuristic-based feature selection, offering theoretical innovation and practical performance improvements for high-dimensional optimization challenges.

1. Introduction

The extensive adoption of digital technologies and internet-based systems has led to the creation of massive databases characterized by hundreds of different variables. Through data mining methodologies, researchers seek to derive meaningful patterns from these large-scale databases to support evidence-based decision-making. The careful identification and selection of relevant and significant variables have been proven to have considerable influence in multiple technology sectors, such as data mining [1], Internet of Things (IoT) applications [2], and machine learning frameworks [3]. Within machine learning environments, the existence of unnecessary, unrelated, and poorly structured data points in datasets with many dimensions adversely affects the precision of classification algorithms and creates additional computational burdens [4]. IoT networks regularly face difficulties managing and analyzing the massive amounts of information produced by various sensors. These problems are intensified by the inclusion of excessive and duplicated variables. To overcome these obstacles, data preparation methods, especially the process of selecting optimal features, become crucial for handling multi-dimensional datasets and removing unnecessary characteristics. Feature selection serves as a core element of data preprocessing and plays a vital role in building robust models through the identification of pertinent variables from existing datasets.

A feature selection framework is built upon three fundamental components: (i) classification methods, such as support vector machines (SVMs) and k nearest neighbor (kNN) [5], (ii) performance assessment criteria, and (iii) search techniques for discovering optimal feature combinations. Feature selection methodology can be divided into two primary strategic approaches: wrapper-based and filter-based methods. These approaches utilize the classification model as a standalone tool to measure the effectiveness of chosen feature sets through their classification results [6]. Conversely, filter methods operate without dependence on specific learning algorithms, analyzing feature groups solely according to inherent data properties rather than algorithm-dependent standards. It should be emphasized that although filter techniques may not consistently discover the perfect feature combination, studies have demonstrated that wrapper methods generally yield better feature sets for particular classifiers. The primary objective of feature selection involves identifying the most effective subset from the complete range of possible feature arrangements. Search strategies can be broadly classified into two main types: Exhaustive search methods and metaheuristic approaches [7]. Exhaustive search procedures perform comprehensive examination of the entire solution space, which expands exponentially as feature quantities increase, requiring substantial computational power. Alternatively, metaheuristic methods utilize probabilistic optimization techniques by starting with randomly generated solution populations to navigate the search landscape efficiently. Metaheuristic strategies have become increasingly popular in feature selection applications because of their ability to produce nearly optimal results within reasonable processing times. These algorithms are especially beneficial due to their simple implementation and flexibility across diverse problem scenarios. A primary advantage of metaheuristic techniques is their advanced capability to prevent premature convergence by sustaining an ideal balance between comprehensive search space exploration and intensive solution improvement. Nevertheless, conventional metaheuristic methods frequently face challenges due to the built-in memory constraints of integer-based mathematical computations, potentially resulting in early convergence within intricate optimization environments. Recent developments in fractional calculus have revealed that derivatives of non-integer order exhibit distinctive characteristics, including non-localized behavior, memory retention capabilities, and inherited traits that can substantially improve optimization effectiveness [8]. Fractional calculus, which extends conventional calculus beyond integer orders, offers mathematical operators that inherently integrate past information into present decision-making processes, making them especially well-suited for optimization challenges where previous exploration history should guide subsequent search strategies [9].

The Secretary Bird Algorithm (SBA) [10] constitutes a contemporary advancement in metaheuristic methodologies that emulates the predatory conduct of the secretary bird, particularly its approach to tracking and capturing targets with accuracy. Among the various optimization techniques, a novel development has appeared that replicates natural processes, specifically deriving its foundation from the hunting tactics demonstrated by the secretary bird, a unique bird of prey species. Although metaheuristic methods have shown considerable effectiveness in feature selection tasks in recent times, current techniques still encounter numerous obstacles that warrant additional investigation. Conventional binary transformation mechanisms within metaheuristic approaches generally depend on basic transfer functions like sigmoid functions, which may fail to properly represent the intricate relationships present in multi-dimensional feature environments. Additionally, standard opposition-based learning methods, despite being successful for maintaining population variety, do not possess the memory capabilities needed to retain important historical search data throughout iterations. To overcome these constraints, this research presents fractional calculus improvements that utilize Laguerre operators to enhance both population initialization and binary transformation procedures [11]. Laguerre polynomials offer superior approximation characteristics and seamless compatibility with fractional calculus operations. The orthogonal properties of Laguerre polynomials guarantee computational stability and convergence behaviors that are especially advantageous in multi-dimensional optimization scenarios [12]. When integrated with fractional calculus, these operators can preserve historical path information while delivering enhanced approximation capabilities in comparison to conventional methods.

The continuous improvement of optimization strategies remains crucial for achieving better results. To strengthen the original SBOA’s performance, two primary fractional calculus enhancements have been incorporated: a fractional opposition-based learning approach employing Laguerre operators during initialization to broaden population variety with non-local memory characteristics, and a Laguerre-based transfer mechanism that delivers adaptive binary transformation through orthogonal polynomial approximation. The fractional opposition-based learning element functions to improve population diversity while integrating memory influences from prior iterations, decreasing the probability of convergence to suboptimal solutions through its non-local characteristics. The Laguerre-based transfer mechanism substitutes the conventional sigmoid method, providing enhanced binary transformation abilities through its orthogonal approximation features and adaptive fractional parameters. We present multiple innovative contributions that can be summarized through the following components:

• Implementation of fractional opposition-based learning techniques combined with Laguerre operators within SBA to accomplish improved population variety and non-local memory characteristics.
• Development of a Laguerre-based transformation function that employs orthogonal polynomial approximation alongside fractional calculus concepts to deliver enhanced binary transformation capabilities beyond conventional sigmoid approaches.
• Introduction of a binary variant of SBA, designated as FL-SBA, which integrates fractional calculus improvements to offer sophisticated solutions for feature selection challenges.
• Empirical verification conducted through an exhaustive collection of ten gene expression datasets with statistical evaluation demonstrating the efficacy of fractional calculus incorporation.

The subsequent sections of this paper are organized in the following manner: Section 2 provides a comprehensive review of relevant literature, while Section 3 offers a concise overview of the Secretary bird optimization algorithm. Section 4 details the development of the proposed FL-SBA methodology, followed by Section 5 which presents comprehensive experimental procedures and analytical findings. The paper concludes with Section 6, which summarizes the key findings and implications of this research.

2. Literature Review

The accelerated growth of computing technologies has produced massive databases distinguished by growing intricacy and multi-dimensionality. In these multi-dimensional data frameworks, the presence of superfluous, unrelated, and disorganized entries significantly impacts classification effectiveness and increases processing requirements [4]. Feature selection has emerged as a vital component of data preparation, playing an important role in developing robust models [5]. The effectiveness of metaheuristic methods in addressing feature selection challenges relies significantly on their ability to deliver optimal outcomes [13]. Nevertheless, conventional techniques encounter fundamental constraints due to their dependence on integer-based mathematical computations, which do not possess the memory retention and non-localized characteristics that could improve optimization effectiveness in complex search environments.

Metaheuristic methods are traditionally divided into four main groups according to their conceptual origins: collective intelligence, human-inspired techniques, physics-derived approaches, and evolutionary strategies [14]. These algorithms gain their efficiency from their ease of implementation and uncomplicated design, allowing for convenient modification to various specific uses. Within feature selection applications, considerable progress has been made using collective intelligence methods, which stem from analyzing group animal behavioral patterns. This classification includes multiple core algorithms, such as BFPA [15], BDA [16], and BCS [17]. Xue et al. provided a significant advancement by improving PSO to accomplish faster computation while optimizing both feature reduction and classification accuracy [18]. Human-based approaches constitute another important classification derived from social interactions and behavioral mechanisms. This classification additionally encompasses various other significant methods Sewing Training-Based Optimization [19], dynastic optimization algorithm (DOA) [20], cultural evolution algorithm [21], and the recently introduced Painting Training Based Optimization (PTBO) [22].

Physics-based approaches employ concepts from natural physical phenomena. Kirkpatrick et al. [23] introduced the initial algorithm of this type, called “Simulated Annealing.” Drawing inspiration from the metallurgical annealing procedure, this method has subsequently emerged as among the most widely acknowledged optimization techniques. Multi-verse optimizer [17], Henry gas solubility optimization [24], and gravitational search methods [25]. A major development within this classification is Energy valley optimizer (EVO) proposed as a novel metaheuristic algorithm inspired by advanced physics principles regarding stability and different modes of particle decay presented by Mahdi Azizi et al. [26]. Various evolutionary methods can be employed to optimize network weights. Genetic algorithms represent a logical option since crossover operations align well with neural network structures by combining components from existing networks to discover improved solutions. CMA-ES [27], a continuous optimization approach, proves effective for weight optimization as it can model interdependencies among parameters. Additionally, approaches like cellular encoding [28] and NEAT [29] have been created to evolve network architecture itself, which proves particularly valuable for establishing necessary recurrent connections. Nevertheless, due to the extensive space requiring optimization, these techniques are typically constrained to networks of moderate parameter size. Recent optimization advances demonstrate the efficacy of hybrid methodological frameworks. Alazzam et al.’s “GEP DNN4Mol” combines Gene Expression Programming with Deep Neural Networks for molecular design, effectively navigating high-dimensional discrete spaces through synergistic integration of evolutionary algorithms and deep learning [30]. Their approach demonstrates that hybrid frameworks outperform single-method strategies in complex optimization landscapes. Similarly, Wang et al.’s metalearning-based alternating minimization algorithm incorporates historical optimization information through learned strategies, achieving superior convergence in nonconvex environments characterized by multiple local optima [31]. Both studies validate that augmenting optimization algorithms with advanced mathematical frameworks providing memory effects and adaptive mechanisms substantially improves performance. These insights directly motivate FL-SBA’s fractional calculus integration, as fractional derivatives inherently provide non-local memory properties analogous to explicit metalearning mechanisms, while Laguerre polynomials offer adaptive approximation capabilities similar to hybrid architecture benefits, specifically addressing high-dimensional feature selection challenges in gene expression data.

Although conventional metaheuristic methods have achieved success, various significant constraints remain. Standard binary transformation approaches generally utilize basic transfer functions like sigmoid functions, which may insufficiently represent intricate relationships present within multi-dimensional feature environments [32]. Opposition-based learning methods, despite being successful for maintaining population variety, do not possess memory capabilities that could retain important historical search data throughout iterations. Most importantly, integer-based mathematical computations naturally lack the non-localized characteristics and memory influences that could avoid early convergence in complex optimization environments. Fractional calculus, which broadens conventional calculus beyond integer orders, has developed as an influential mathematical structure for improving optimization methods. In contrast to integer-order derivatives, fractional operators exhibit distinctive features including non-localized behavior, memory influences, and inherited properties [33]. These characteristics allow algorithms to retain historical data and make more knowledgeable decisions using previous exploration experiences.

Current studies have shown the efficacy of fractional calculus in optimization challenges. Peng, Yuexi et al. [34] revealed that fractional-order operators can enhance convergence properties in evolutionary algorithms through incorporating memory influences. Wang and Liu [35] illustrated that fractional derivatives offer superior balance between exploration and exploitation in metaheuristic methods compared to conventional integer-order techniques. Nevertheless, most current research concentrates on continuous optimization challenges, creating substantial research opportunities in discrete optimization areas such as feature selection. Laguerre polynomials constitute a comprehensive orthogonal framework over the range [0,∞) and exhibit superior approximation characteristics that render them especially appropriate for optimization uses [36]. The orthogonal properties of Laguerre polynomials guarantee computational stability and convergence behaviors that are advantageous in multi-dimensional optimization challenges. Dueñas Herbert et al. [37] showed that Laguerre-based approximation techniques surpass conventional methods in function approximation tasks, especially for problems containing exponential-type functions. The combination of Laguerre polynomials with fractional calculus has produced encouraging outcomes in diverse mathematical applications. Laguerre operators integrated with fractional calculus deliver enhanced approximation abilities compared to traditional polynomial techniques. Nevertheless, their implementation in binary optimization and feature selection remains mostly unexplored. Sophisticated mathematical structures have also been investigated to improve metaheuristic performance. Opposition-based learning has been thoroughly examined as a population initialization approach, with numerous modifications suggested to enhance diversity and convergence [38]. However, conventional opposition-based learning does not possess the memory properties that could retain valuable search data throughout iterations.

3. Proposed Secretary Bird Optimization Algorithm

The Secretary Bird is endemic to sub-Saharan Africa and occupies diverse open habitats ranging from grassland areas to savanna regions [10]. The bird employs two primary survival mechanisms, utilizing camouflage techniques when feasible or rapidly escaping through either terrestrial locomotion or aerial flight. These adaptive behaviors served as the foundation for developing the Secretary Bird Optimization Algorithm, where the bird’s predatory preparation and hunting implementation are mirrored in the algorithm’s setup and search phases.

3.1. Initial Preparation Phase

The birds’ locations within the space correspond to candidate solutions via the values of decision variables. The algorithm begins by stochastically placing the birds’ coordinates throughout the solution space utilizing Equation (1).

$${\mathrm{S}\mathrm{b}}_{\mathrm{i},\mathrm{j}}=\mathrm{l}{\mathrm{b}}_{\mathrm{j}}+\mathrm{r}\times \left(\mathrm{u}{\mathrm{b}}_{\mathrm{j}}-\mathrm{l}{\mathrm{b}}_{\mathrm{j}}\right),\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{N},\mathrm{j}=\mathrm{1,2},\dots , \mathrm{D}$$

(1)

${\mathrm{S}\mathrm{b}}_{\mathrm{i},\mathrm{j}}$ represents the position of the i-th Secretary Bird, whereas $\mathrm{u}{\mathrm{b}}_{\mathrm{j}}$ and $\mathrm{l}{\mathrm{b}}_{\mathrm{j}}$ define the lower and upper limits of the solution space, respectively. The parameter r denotes a stochastically produced value that ranges from 0 to 1.

SBOA operates as a population-driven optimization technique that commences with numerous candidate solutions (Equation (2)). These solutions are stochastically positioned within the upper and lower limits. During every iteration cycle, the algorithm monitors the optimal solution discovered as the estimated optimum.

$$\mathrm{S}\mathrm{b}={\left[\begin{array}{cccccc}{\mathrm{s}\mathrm{b}}_{\mathrm{1,1}}& {\mathrm{s}\mathrm{b}}_{\mathrm{1,2}}& \dots & {\mathrm{s}\mathrm{b}}_{1,\mathrm{j}}& \dots & {\mathrm{s}\mathrm{b}}_{1, \mathrm{D} }\\ {\mathrm{s}\mathrm{b}}_{\mathrm{2,1}}& {\mathrm{s}\mathrm{b}}_{\mathrm{2,2}}& \dots & {\mathrm{s}\mathrm{b}}_{2,\mathrm{j}}& \dots & {\mathrm{s}\mathrm{b}}_{2, \mathrm{D} }\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ {\mathrm{s}\mathrm{b}}_{\mathrm{i},1}& {\mathrm{s}\mathrm{b}}_{\mathrm{i},2}& \dots & {\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}& \dots & {\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{D}}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ {\mathrm{s}\mathrm{b}}_{\mathrm{N},1}& {\mathrm{s}\mathrm{b}}_{\mathrm{N},2}& \dots & {\mathrm{s}\mathrm{b}}_{\mathrm{N},\mathrm{j}}& \dots & {\mathrm{s}\mathrm{b}}_{\mathrm{N},\mathrm{D}}\end{array}\right]}_{\mathrm{N}\times \mathrm{D}}$$

(2)

$\mathrm{S}\mathrm{b}$ denotes the complete set of Secretary Birds, whereas ${\mathrm{s}\mathrm{b}}_{\mathrm{i}}$ corresponds to an individual bird (the i-th element). ${\mathrm{S}\mathrm{b}}_{\mathrm{i},\mathrm{j}}$ signifies the value of the j-th parameter for the i-th Secretary Bird. $\mathrm{N}$ defines the overall quantity of Secretary Birds within the population, and D indicates the dimensionality of the problem under consideration. The proposed parameter values from each secretary bird are assessed through the objective function, with outcomes organized into a vector employing Equation (3).

$$\mathrm{F}={\left[\begin{array}{c}{\mathrm{F}}_1\\ ⋮\\ {\mathrm{F}}_{\mathrm{i}}\\ ⋮\\ {\mathrm{F}}_{\mathrm{N}}\end{array}\right]}_{\mathrm{N}\times \mathrm{I}}={\left[\begin{array}{c}F\left({\mathrm{S}\mathrm{b}}_1\right)\\ ⋮\\ F\left({\mathrm{S}\mathrm{b}}_{\mathrm{i}}\right)\\ ⋮\\ F\left({\mathrm{S}\mathrm{b}}_{\mathrm{N}}\right)\end{array}\right]}_{\mathrm{N}\times 1}$$

(3)

F denotes the objective function vector, whereas the objective function value obtained by the i-th secretary bird is represented as ${\mathrm{F}}_{\mathrm{i}}$.

3.2. Search Pattern of Secretary Bird

Secretary birds pursue serpents through three separate stages: identification, ingestion, and strike, with each stage comprising one-third of the overall hunting period (IT). Within SBOA, the preliminary exploration phase (t < IT/3) proves essential, emulating how secretary birds leverage their stature and sharp eyesight to locate serpents within foliage while cautiously examining the terrain with their elongated limbs. This stage incorporates differential evolution, utilizing inter-population differences to create novel solutions and avoid early convergence toward local extrema. The birds’ coordinate modifications throughout prey identification are mathematically represented via Equations (4) and (5), facilitating thorough investigation of the solution domain.

$$\mathrm{While} \mathrm{t}<{\displaystyle \frac{1}{3}}\mathrm{I}\mathrm{T},{\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}^{\mathrm{new} \mathrm{P}1}={\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}+\left({\mathrm{s}\mathrm{b}}_{{\mathrm{random} }_1}-{\mathrm{s}\mathrm{b}}_{{\mathrm{random} }_2}\right)\times {\mathrm{R}\mathrm{N}}_1$$

(4)

$${\mathrm{S}\mathrm{b}}_{\mathrm{i}}=\left\{\begin{array}{c}{\mathrm{S}\mathrm{b}}_{\mathrm{i}}^{\mathrm{new},\mathrm{P}1}, \mathrm{i}\mathrm{f} {\mathrm{F}}_{\mathrm{i}}^{\mathrm{new},{\mathrm{P}}_1}<{\mathrm{F}}_{\mathrm{i}}\\ {\mathrm{S}\mathrm{b}}_{\mathrm{i}}, \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e} \end{array}\right.$$

(5)

$\mathrm{t}$ signifies the iteration index, whereas I$\mathrm{T}$ represents the maximum iteration counts. The modified coordinates of the i-th secretary bird throughout the preliminary stage are designated by ${\mathrm{S}\mathrm{b}}_{\mathrm{i}}^{\mathrm{new},\mathrm{P}1}$. During this stage, ${\mathrm{s}\mathrm{b}}_{{\mathrm{random} }_1}$ and ${\mathrm{s}\mathrm{b}}_{{\mathrm{random} }_2}$ correspond to stochastically chosen candidate solutions. The parameter ${\mathrm{R}\mathrm{N}}_1$ defines a randomly produced one-dimensional matrix of dimensions 1 × D, containing values uniformly spread across [0, 1], where D refers to the solution domain dimensionality. Additionally, ${\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}^{\mathrm{new},\mathrm{P}1}$ denotes the coordinate value for the j-th dimension, while ${\mathrm{F}}_{\mathrm{i}}^{\mathrm{new},{\mathrm{P}}_1}$ indicates the associated objective function fitness score.

Throughout prey ingestion, secretary birds utilize deliberate positioning and tactical footwork instead of direct assault. Leveraging their raised posture and shielded limbs, they fatigue serpents via methodical movements, represented mathematically through Brownian motion (RB). The SBOA algorithm integrates these behaviors by merging previously optimal coordinates with Brownian principles via Equations (7) and (8). This strategy facilitates efficient localized exploration while preserving links to successful coordinates, harmonizing global search with localized optimization to prevent early convergence.

$$\mathrm{R}\mathrm{b}=\mathrm{randn}\left(1, \mathrm{D}\right)$$

(6)

$$\begin{array}{c}\mathrm{While} {\displaystyle \frac{1}{3}}\mathrm{I}\mathrm{T}<\mathrm{t}<{\displaystyle \frac{2}{3}}\mathrm{I}\mathrm{T},{\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}^{\mathrm{new} \mathrm{P}\mathrm{l}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\mathrm{s}\mathrm{b}}_{\mathrm{best} }+\exp \left(\left({\displaystyle \frac{\mathrm{t}}{\mathrm{I}\mathrm{T}}}\right)\wedge 4\right)\times \left(\mathrm{R}\mathrm{b}-0.5\right)\times \left({\mathrm{s}\mathrm{b}}_{\mathrm{best} }-{\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}\right)\hfill \end{array}$$

(7)

$${\mathrm{S}\mathrm{b}}_{\mathrm{i}}=\left\{\begin{array}{l}{\mathrm{S}\mathrm{b}}_{\mathrm{i}}^{\mathrm{new},{\mathrm{P}}_1}, \mathrm{if} {\mathrm{F}}_{\mathrm{i}}^{\mathrm{new}, {\mathrm{P}}_1}<{\mathrm{F}}_{\mathrm{i}}\\ {\mathrm{S}\mathrm{b}}_{\mathrm{i}},\mathrm{else}\end{array}\right.$$

(8)

The formula includes a stochastic matrix, represented as $\mathrm{randn}\left(1, \mathrm{D}\right)$, which produces values according to a standard normal distribution with parameters μ = 0 and σ = 1. This matrix possesses dimensions of 1 × D. The parameter ${\mathrm{s}\mathrm{b}}_{\mathrm{best}}$ represents the best value discovered through the present iteration.

During the concluding hunting stage, secretary birds perform targeted strikes utilizing forceful leg blows directed at the serpent’s head to achieve swift neutralization. For larger targets, they may elevate and release serpents from elevation. The SBOA simulates this conduct through Levy flight dynamics, merging brief movements with sporadic extended leaps. This multi-scale method harmonizes global exploration with localized precision optimization, assisting in avoiding convergence to local extrema while effectively pursuing optimal solutions.

SBOA integrates a nonlinear disturbance coefficient (1 − t/IT) (2 × t/IT) to equilibrate exploration and exploitation, prevent premature convergence, and enhance performance. Coordinate modifications throughout the strike phase are specified by Equations (9) and (10).

$$\begin{array}{rr} \mathrm{While} \mathrm{t}>{\displaystyle \frac{2}{3}}\mathrm{I}\mathrm{T},{\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}^{\mathrm{new} \mathrm{P}1}& ={\mathrm{s}\mathrm{b}}_{\mathrm{best} }+\left(\left(1-{\displaystyle \frac{\mathrm{t}}{\mathrm{I}\mathrm{T}}}\right)\wedge \left(2\times {\displaystyle \frac{\mathrm{t}}{\mathrm{I}\mathrm{T}}}\right)\right)\times {\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}\times \mathrm{R}\mathrm{l}\end{array}$$

(9)

$${\mathrm{S}\mathrm{b}}_{\mathrm{i}}=\left\{\begin{array}{c}{\mathrm{S}\mathrm{b}}_{\mathrm{i}}^{\mathrm{new},\mathrm{P}1}, \mathrm{if} {\mathrm{F}}_{\mathrm{i}}^{\mathrm{new},{\mathrm{P}}_1}<{\mathrm{F}}_{\mathrm{i}}\\ {\mathrm{S}\mathrm{b}}_{\mathrm{i}}, \mathrm{else} \end{array}\right.$$

(10)

The algorithm’s optimization accuracy is enhanced via the integration of a weighted Levy flight element, indicated by the symbol ‘Rl’.

$$\mathrm{R}\mathrm{l}=0.5\times \mathrm{L}\mathrm{e}\mathrm{v}\mathrm{y}\left(\mathrm{D}\right)$$

(11)

$\mathrm{Levy}\left(\mathrm{D}\right)$ represents the Levy flight distribution function, which is calculated through the subsequent Equation:

$$\mathrm{L}\mathrm{e}\mathrm{v}\mathrm{y}(\mathrm{D})=\mathrm{s}\times {\displaystyle \frac{\mathrm{x}\times \mathsf{\sigma }}{|\mathrm{y}{|}^{\frac{1}{\mathrm{n}}}}}$$

(12)

The framework includes two fixed parameters: one established at 0.01 and another at π. The system additionally employs stochastic variables bounded within a designated range. The computational approach for this element is then specified.

$$\mathsf{\sigma }={\left({\displaystyle \frac{\Gamma (1+\mathsf{\eta })\times \mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\mathsf{\pi }\mathsf{\eta }}{2}\right)}{\Gamma \left(\frac{1+\mathsf{\eta }}{2}\right)\times \mathsf{\eta }\times 2\left(\frac{\mathsf{\eta }-1}{2}\right)}}\right)}^{{\displaystyle \frac{1}{\mathsf{\eta }}}}$$

(13)

$\Gamma$ indicates the gamma function and $\mathsf{\eta }$ equal to 1.5.

3.3. Escape Process of Secretary Bird

Secretary birds encounter dangers from predators such as eagles, hawks, and candies. They utilize two defensive strategies: physical escape and concealment behavior. Their elongated limbs facilitate swift locomotion, traversing 20–30 km daily, which has earned them the designation “marching eagles.” They are also capable of aerial flight to evade threats. Furthermore, they employ concealment by merging with their surroundings. The SBOA framework integrates these as two equivalent situations: environmental concealment (Z1) and dynamic evasion (Z2).

When predators are detected, secretary birds initially search for adjacent concealment opportunities. If these are unavailable, they turn to aerial or terrestrial escape. Their approach includes a dynamic disturbance coefficient, (1 − t/IT) ², which optimizes the equilibrium between investigating unexplored regions and utilizing established solutions. This coefficient may be modified to prioritize either investigation or utilization. These escape behaviors are mathematically represented in Equations (14) and (15).

$$\begin{array}{c}{\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}^{\mathrm{new},\mathrm{P}2}\hfill \\ =\left\{\begin{array}{l}{\mathrm{p}}_1:{\mathrm{s}\mathrm{b}}_{\mathrm{best} }+\left(2\times \mathrm{R}\mathrm{b}-1\right)\times {\left(1-{\displaystyle \frac{\mathrm{t}}{\mathrm{I}\mathrm{T}}}\right)}^2\times {\mathrm{s}\mathrm{b}}_{\mathrm{i}\mathrm{j}},\mathrm{if} \mathrm{r} \mathrm{and}<{\mathrm{r}}_{\mathrm{i}}\\ {\mathrm{p}}_2:{\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}+{\mathrm{R}\mathrm{N}}_2\times \left({\mathrm{s}\mathrm{b}}_{\mathrm{random} }-\mathrm{K}\times {\mathrm{s}\mathrm{b}}_{\mathrm{i},\mathrm{j}}\right), \mathrm{else} \end{array}\right.\hfill \end{array}$$

(14)

$${\mathrm{S}\mathrm{b}}_{\mathrm{i}}=\left\{\begin{array}{l}{\mathrm{S}\mathrm{b}}_{\mathrm{i}}^{\mathrm{new}, \mathrm{P}2}, \mathrm{if} {\mathrm{F}}_{\mathrm{i}}^{\mathrm{new},\mathrm{P}2}<{\mathrm{F}}_{\mathrm{i}}\\ {\mathrm{S}\mathrm{b}}_{\mathrm{i}}, \mathrm{else} \end{array}\right.$$

(15)

The parameter r is established at 0.5, whereas ${\mathrm{R}\mathrm{N}}_2$ produces a one-dimensional matrix of dimensions (1 × D) according to a standard normal distribution. The term ${\mathrm{x}}_{\mathrm{random} }$ signifies a stochastically produced candidate solution during the present iteration. $\mathrm{K}$ corresponds to an integer value that is randomly selected as either 1 or 2, with its computational procedure outlined in Equation (16).

$$\mathrm{K}=\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}(1+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}(\mathrm{1,1}\left)\right)$$

(16)

where rand (1, 1) stochastically produces a random value within (0, 1).

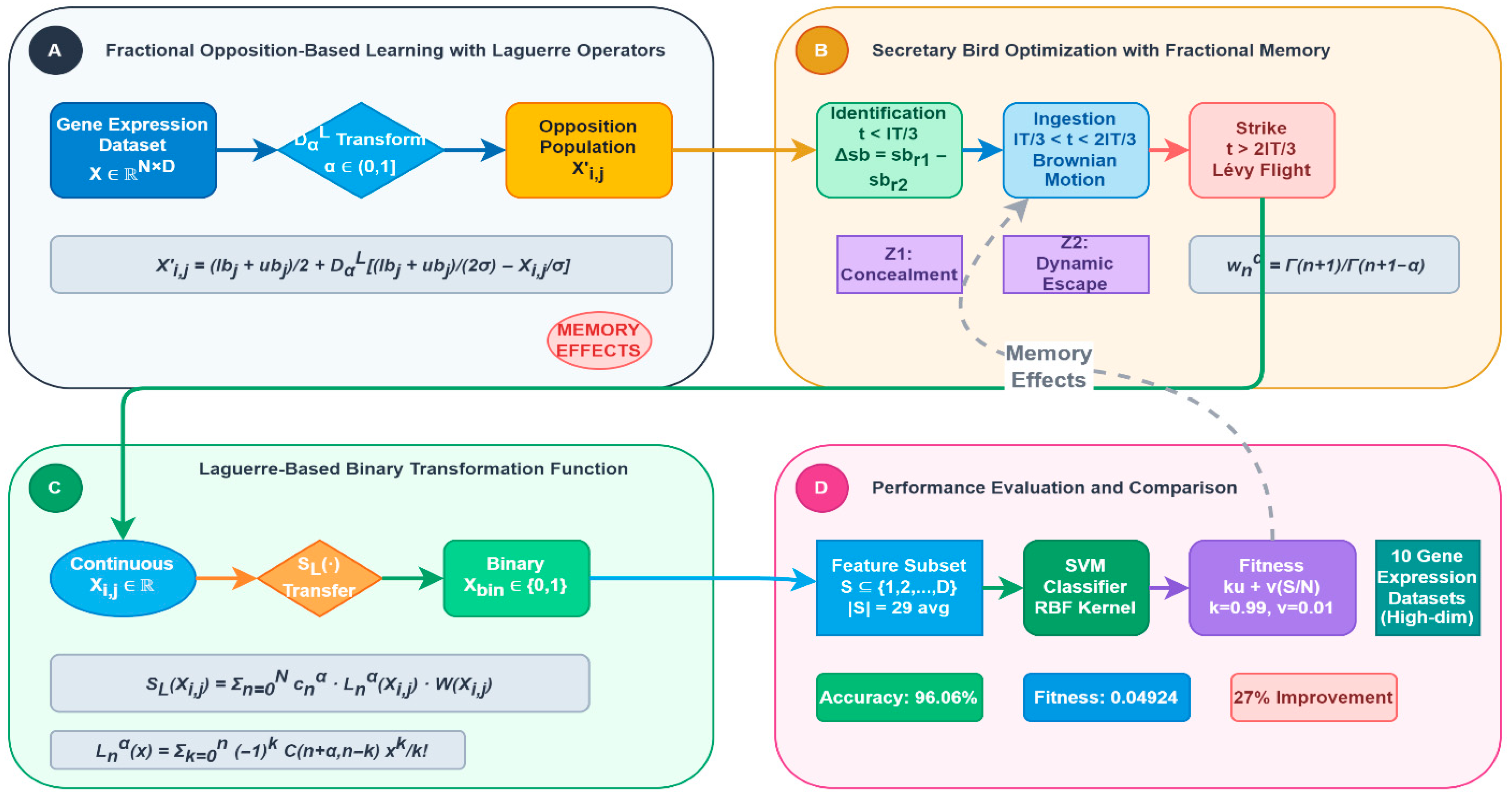
4. Proposed FL-SBA

4.1. Initialization with Fractional Opposition-Based Learning with Laguerre Operators

Traditional opposition-based learning generates candidate solutions by creating opposite points in the search space, typically using simple reflection operations as shown in Figure 1. However, these approaches lack memory characteristics and fail to utilize historical search information that could guide more effective population initialization [39]. Fractional calculus provides a mathematical framework that naturally incorporates memory effects through non-local operators, enabling the algorithm to learn from past exploration experiences during initialization. The fractional opposition-based learning approach utilizes Laguerre operators, which form a complete orthogonal system on [0,∞) and possess excellent approximation properties.

Achieving optimal solutions in computational optimization fundamentally depends on maximizing the efficiency of population initialization and maintaining diversity throughout the search process. The FL-SBA introduces an innovative fractional opposition-based learning technique that integrates Laguerre operators to enhance initial population generation and provide non-local memory effects. This approach extends beyond traditional opposition-based learning by incorporating fractional calculus principles that naturally preserve historical search information and provide superior exploration capabilities through orthogonal polynomial approximation.

The solution exploration domain is constrained within a predefined interval on the x-axis, bounded by lower [lb] and upper [ub] limits. The coordinate system’s origin is strategically positioned at the exact midpoint of this interval, serving as a critical reference point for computational navigation. Two angular parameters, ${\mathrm{Ɵ}}_1$ and ${\mathrm{Ɵ}}_2$, play pivotal roles in defining the solution transformation process: ${\mathrm{Ɵ}}_1$ representing the incident angle and ${\mathrm{Ɵ}}_2$ characterizing the refraction angle.

Additionally, $\mathrm{x}$ and ${\mathrm{x}}^{\prime }$ represent the distances of the incident and refracted rays, respectively. The refraction can be calculated using the following formula:

$$\mathrm{n}={\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{Ɵ}}_1}{\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{Ɵ}}_2}}={\displaystyle \frac{\frac{\mathrm{l}\mathrm{b}+\mathrm{u}\mathrm{b}}{2}-\mathrm{x}\mathrm{*}}{{\mathrm{X}}^{\prime }\mathrm{*}-\frac{\mathrm{l}\mathrm{b}+\mathrm{u}\mathrm{b}}{2}}}\times {\displaystyle \frac{{\mathrm{x}}^{\prime }}{\mathrm{x}}}$$

(17)

Put $\mathsf{\sigma }={\displaystyle \frac{{\mathrm{x}}^{\prime }}{\mathrm{x}}}$ and n = 1 in Equation (17) and SBA is applied to a high-dimensional space, the refracted direction ${{\mathrm{X}}^{\prime }\mathrm{*}}_{\mathrm{i},\mathrm{j}}$ can be determined using the following equation:

$${{\mathrm{X}}^{\prime }\mathrm{*}}_{\mathrm{i},\mathrm{j}}={\displaystyle \frac{{\mathrm{l}\mathrm{b}}_{\mathrm{j}}+{\mathrm{u}\mathrm{b}}_{\mathrm{j}}}{2}}+{\mathrm{D}}_{\mathsf{\alpha }}^{\mathrm{L}}[{\displaystyle \frac{{\mathrm{l}\mathrm{b}}_{\mathrm{j}}+{\mathrm{u}\mathrm{b}}_{\mathrm{j}}}{2\mathsf{\sigma }}}-{\displaystyle \frac{{\mathrm{X}}_{\mathrm{i},\mathrm{j}}}{\mathsf{\sigma }}}]$$

(18)

where ${\mathrm{X}\mathrm{*}}_{\mathrm{i},\mathrm{j}}$ indicates the i-th secretary bird position at j-th dimensions, ${{\mathrm{X}}^{\prime }\mathrm{*}}_{\mathrm{i},\mathrm{j}}$ is the refracted inverse solution of ${\mathrm{X}\mathrm{*}}_{\mathrm{i},\mathrm{j}}$, and ${\mathrm{l}\mathrm{b}}_{\mathrm{j}}$ and ${\mathrm{u}\mathrm{b}}_{\mathrm{j}}$ are the lower and upper bounds. ${\mathrm{D}}_{\mathsf{\alpha }}^{\mathrm{L}}$ is the Laguerre-based fractional derivative operator. The fractional operator with laguerre basis as [12]:

$${\mathrm{D}}_{\mathsf{\alpha }}^{\mathrm{L}}(\mathrm{f}\left(\mathrm{x}\right))=\sum _{\mathrm{n}}^{\mathrm{N}}{\mathrm{w}}_{\mathrm{n}}^{\mathsf{\alpha }}. {\mathrm{L}}_{\mathrm{n}}\left(\mathrm{x}\right).{{\mathrm{f}}^{\prime }}_{\mathrm{n}}\left(\mathrm{x}\right)$$

(19)

where ${\mathrm{L}}_{\mathrm{n}}\left(\mathrm{x}\right)$ are Laguerre polynomials, ${\mathrm{w}}_{\mathrm{n}}^{\mathsf{\alpha }}$ are fractional weights: ${\mathrm{w}}_{\mathrm{n}}^{\mathsf{\alpha }}$= Γ (n + 1)/Γ (n + 1−α), and α ∈ (0,1] is the fractional order.

4.2. Laguerre-Based Transformation Function

Feature selection process is typically conceptualized as a binary optimization challenge. However, the SBA generates particle positions that contain continuous numerical values. Therefore, a transformation mechanism is required to convert SBA ‘s continuous solution domain into a discrete binary framework. Within feature selection applications, particle values must be constrained to either 0 or 1 to represent feature inclusion or exclusion.

The Proposed Laguerre-Based Transfer Function used to transform each solution into its corresponding binary representation defines as follow [12]:

$${\mathrm{S}}_{\mathrm{L}}\left({\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right) = {\sum }_{\mathrm{n}=0}^{\mathrm{N}}{{\mathrm{c}}_{\mathrm{n}}^{\mathsf{\alpha }}.\mathrm{L}}_{\mathrm{n}}^{\mathsf{\alpha }}\left({\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right).\mathrm{W}\left({\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right)$$

(20)

${\mathrm{L}}_{\mathrm{n}}^{\mathsf{\alpha }}\left({\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right)$ are generalized Laguerre polynomials of fractional order α, ${\mathrm{c}}_{\mathrm{n}}^{\mathsf{\alpha }}$ are fractional coefficients,$\mathrm{W}\left({\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right)$ is a weight function, and N is the truncation order.

Generalized Laguerre Polynomials: The fractional-order Laguerre polynomials ${\mathrm{L}}_{\mathrm{n}}^{\mathsf{\alpha }}\left(\mathrm{t}\right)$ form a complete orthogonal system on the semi-infinite interval $[0,\mathrm{\infty })$ and are defined through the Rodrigues formula [12]:

$${\mathrm{L}}_{\mathrm{n}}^{\mathsf{\alpha }}\left(\mathrm{t}\right)={\displaystyle \frac{{\mathrm{e}}^{\mathrm{t}}{\mathrm{t}}^{-\mathsf{\alpha }}}{\mathrm{n}!}}{\displaystyle \frac{{\mathrm{d}}^{\mathrm{n}}}{\mathrm{d}{\mathrm{t}}^{\mathrm{n}}}}\left({\mathrm{e}}^{-\mathrm{t}}{\mathrm{t}}^{\mathrm{n}+\mathsf{\alpha }}\right)$$

(21)

where $\mathsf{\alpha }>-1$ represents the fractional order parameter, and $\mathrm{n}=\mathrm{0,1},2,\dots ,\mathrm{N}$ denotes the polynomial degree.

Weight Function: The weight function ensures proper orthogonality and is explicitly defined as:

$$\mathrm{W}\left(\mathrm{t}\right)={\mathrm{t}}^{\mathsf{\alpha }}{\mathrm{e}}^{-\mathrm{t}},\mathrm{t}\in [0,\mathrm{\infty }),\mathsf{\alpha }>-1$$

(22)

This exponential weight function guarantees the convergence of integrals and maintains the orthogonality property of the Laguerre basis.

Orthogonality Relation: The generalized Laguerre polynomials satisfy the following orthogonality condition with respect to the weight function:

$${\mathrm{L}}_{\mathrm{n}}^{\mathsf{\alpha }}(\mathrm{t}){\mathrm{L}}_{\mathrm{m}}^{\mathsf{\alpha }}(\mathrm{t})\mathrm{W}(\mathrm{t})\mathrm{d}\mathrm{t}={\displaystyle \frac{\Gamma (\mathrm{n}+\mathsf{\alpha }+1)}{\mathrm{n}!}}{\mathsf{\delta }}_{\mathrm{n}\mathrm{m}}$$

(23)

where $\Gamma (\cdot )$ denotes the gamma function, and ${\mathsf{\delta }}_{\mathrm{n}\mathrm{m}}$ represents the Kronecker delta.

Fractional Coefficients: The expansion coefficients ${\mathrm{c}}_{\mathrm{n}}^{\mathsf{\alpha }}$ incorporate memory effects through fractional calculus and are computed as:

$${\mathrm{c}}_{\mathrm{n}}^{\mathsf{\alpha }}={\displaystyle \frac{\Gamma (\mathrm{n}+1)}{\Gamma (\mathrm{n}+1-\mathsf{\alpha })}}={\displaystyle \frac{\mathrm{n}!}{(\mathrm{n}-\mathsf{\alpha })(\mathrm{n}-1-\mathsf{\alpha })\dots (1-\mathsf{\alpha })}},0<\mathsf{\alpha }\le 1$$

(24)

These coefficients weight the contribution of each polynomial term according to the fractional order $\mathsf{\alpha }$, enabling the transfer function to retain historical search information.

Truncation Order: The summation is truncated at order $\mathrm{N}$, which determines the approximation accuracy. For practical implementation in feature selection problems, we set $\mathrm{N}=10$ based on convergence analysis, which provides sufficient approximation quality while maintaining computational efficiency. Higher values of $\mathrm{N}$ yield diminishing improvements beyond this threshold.

The fractional Laguerre polynomials are defined as:

$$\begin{array}{c}{\mathrm{L}}_0^{\mathsf{\alpha }}\left(\mathrm{x}\right)=1,\hfill \\ {\mathrm{L}}_1^{\mathsf{\alpha }}\left(\mathrm{x}\right)=1+\mathsf{\alpha }-\mathrm{x},\hfill \\ {(\mathrm{n}+1)\mathrm{L}}_{(\mathrm{n}+1)}^{\mathsf{\alpha }}\left(\mathrm{x}\right)=\left(2\mathrm{n}+1+\mathsf{\alpha }-\mathrm{x}\right){\mathrm{L}}_{\mathrm{n}}^{\mathsf{\alpha }}\left(\mathrm{x}\right)-\left(\mathrm{n}+\mathsf{\alpha }\right){\mathrm{L}}_{\left(\mathrm{n}-1\right)}^{\mathsf{\alpha }}\left(\mathrm{x}\right)\hfill \end{array}$$

(25)

$$X_{\mathrm{binary}}=\left\{\begin{array}{c}1 \mathrm{i}\mathrm{f} \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d} \ge {\mathrm{S}}_{\mathrm{L}}\left({\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right)\hfill \\ 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e} \hfill \end{array}\right.$$

(26)

4.3. The Evaluation Function

Incorporating excessive features into datasets creates computational difficulties, since classification algorithms typically experience reduced performance when processing irrelevant or redundant attributes. Consequently, dimensional reduction becomes essential to mitigate this problem. Feature selection serves as a methodology designed to enhance classifier performance and computational efficiency by removing extraneous or non-contributory variables. When assessing potential solutions, evaluation criteria extend beyond simple classification accuracy to include the quantity of retained features. When multiple solutions achieve equivalent accuracy levels, the approach utilizing fewer features is considered superior. Hence, the fitness evaluation seeks to maximize classification performance through error minimization while simultaneously limiting the feature subset size. The fitness metric outlined below functions as the evaluation standard for FL-SBA solutions, maintaining equilibrium between these dual optimization goals.

$$\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}=\mathrm{k}\mathrm{u}+\mathrm{v}{\displaystyle \frac{\mathrm{S}}{\mathrm{N}}}$$

(27)

where $\mathrm{k}\in \left[\mathrm{0,1}\right]$, $\mathrm{u}$ indicates the classification error rate computed by the SVM classifier, $\mathrm{v}=1-\mathrm{k}$, $\mathrm{S}$ is the selected features, and N is the total features [5]. The Algorithm Architecture and workflow for the FL-SBA are illustrated in Figure 2.

4.4. Computational Complexity

The complexity distinction between standard and enhanced approaches is quantifiable. Without Laguerre/fractional components, binary metaheuristics require O(N × D × T) operations for population-based search across N = 30 agents, D dimensions, and T = 100 iterations. FL-SBA augments this baseline with two fractional calculus enhancements: initialization-phase fractional opposition O(N × D × M) and iteration-phase Laguerre transformation O(N × D × M × T), where M = 5 denotes truncation order. The combined complexity becomes O(N × D × T × (1 + M)), introducing a 6× multiplicative factor. Empirical measurements confirm theoretical predictions: FL-SBA averages 145.95 s versus 26.17 s for standard SBA (5.58 × ratio), with all algorithms maintaining identical computational budgets (N = 30, T = 100). This controlled comparison isolates the computational cost attributable specifically to fractional calculus and Laguerre polynomial operations, demonstrating that performance improvements stem from algorithmic innovation rather than increased computational budget allocation.

5. Experimental Results and Discussion

5.1. Datasets

For experimental validation, ten gene expression datasets were employed to thoroughly assess the performance of the proposed algorithm in feature selection applications [18].

Table 1. Dataset characteristics.

Dataset	Features Number	Instances Number	Classes Number
SRBCT	2308	83	4
DLBCL	5469	77	2
9Tumor	5726	60	9
11 Tumor	12,533	174	11
Leukemia 1	5327	72	3
Leukemia 2	11,225	72	3
Brain Tumor 1	5920	90	5
Brain Tumor 2	10,367	50	4
Prostate	10,509	102	2
Lung Cancer	12,600	203	5

summarizes the essential characteristics of these datasets, including the number of features, samples, categories, and the ratio of observations within the minority and majority classes for each dataset. These datasets are characterized by their high-dimensional nature with limited sample sizes, making them frequently used benchmarks in feature selection research studies.

5.2. Configuration Parameters

The performance of FL-SBA is assessed by comparing it with various state-of-the-art feature selection methods for high-dimensional data. Testing protocols involve conducting 20 independent runs for each algorithm, with computational limits set to 100 iterations and a population of 30 search agents. The algorithm configuration utilizes two primary control parameters: β = 0.01 and α = 0.99.

To ensure reproducibility and methodological rigor, this section provides comprehensive details of all experimental configurations, including classifier parameters, data preprocessing protocols, validation procedures, and handling of methodological challenges inherent in high-dimensional gene expression analysis.

Data preprocessing pipeline:

• Normalization: Z-score standardization applied independently within ${\mathrm{x}}_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}={\displaystyle \frac{\mathrm{x}-\mathsf{\mu }}{\mathsf{\sigma }}}$, computed only on training data.
• Missing values: K-nearest neighbors imputation (k = 5) when necessary.
• Post-selection scaling: Selected features re-normalized using training set statistics only.

Where μ represents the mean and σ denotes the standard deviation of each feature, computed exclusively on the training partition within each cross-validation fold. Z-score normalization was selected over min–max scaling due to its superior performance with gene expression data containing outliers and its compatibility with SVM classifiers.

Support Vector Machine (SVM) Classifier Configuration

The wrapper-based feature selection approach employed Support Vector Machine (SVM) as the classification algorithm for evaluating feature subset quality. SVM was selected due to its demonstrated effectiveness on high-dimensional, low-sample-size datasets typical of gene expression analysis and its widespread adoption in feature selection literature, facilitating fair comparison with existing methods.

Kernel Function: Radial Basis Function (RBF) kernel was employed for its ability to handle nonlinear relationships common in biological data [5].

$$\mathrm{k}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-\mathsf{\gamma }{‖{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}‖}^2)$$

(28)

Hyper parameter Configuration:

• Regularization parameter (C): C = 10, controlling the trade-off between margin maximization and training error minimization. This value was determined through preliminary grid search on a held-out validation set and maintained consistently across all experiments.
• Kernel coefficient (γ): γ = ‘scale’, automatically computed as:

$$\mathsf{\gamma }={\displaystyle \frac{1}{{\mathrm{n}}_{\mathrm{f}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{s}}\times \mathrm{V}\mathrm{a}\mathrm{r}\left(\mathrm{X}\right)}}$$

(29)

This adaptive scaling ensures appropriate kernel width regardless of feature dimensionality after selection.

Multi-class Strategy: For datasets with more than two classes, the one-versus-rest (OvR) strategy was employed, training one binary classifier per class against all remaining classes.

Convergence Criteria: Maximum iterations = 1000, convergence tolerance = 1 × 10⁻³.

Nested Cross-Validation Framework

To prevent optimistically biased wrapper scores, we implemented stratified 10 × 10⁵–fold nested cross-validation:

Structure:

• Outer loop: 10-fold stratified CV for unbiased performance estimation.
• Inner loop: 5-fold stratified CV for feature selection within each outer training set.
• Process: Feature selection operates exclusively on inner folds; selected features evaluated on completely held-out outer test folds.

5.3. Experimental Results

The experimental methodology is structured into two distinct stages. The first stage involves evaluating the proposed FL-SBA against the standard SBA. Following this, the second stage conducts performance comparisons between the developed FL-SBA and contemporary feature selection techniques. The assessment framework for this research relies on four fundamental evaluation criteria, detailed as follows [40]:

-

Classification Accuracy: Measures the precision with which the classifier selects the most beneficial feature subset.

-

Average Fitness Score: The average fitness score per iteration can be determined using the following formula:

$${\mathrm{A}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{F}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{n}}={\displaystyle \frac{1}{\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}}\sum _{\mathrm{i}=1}^{\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{F}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{i}}$$

(30)

where ${\mathrm{F}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{i}}$ is the Fitness at iteration $\mathrm{i}$.

-

Selected feature quantity: refers to the minimum attribute count present in the optimal configuration.

5.3.1. Results of Ablation Experiments

To systematically evaluate the individual contributions of each proposed component in FL-SBA, we conducted comprehensive ablation experiments. This analysis isolates the effects of (i) Laguerre-based fractional opposition-based learning (FOBL) and (ii) Laguerre-based binary transfer function (LTF) by comparing four algorithmic variants across all ten gene expression datasets. The following algorithmic configurations were evaluated to assess component-wise contributions: SBA (Standard Secretary Bird Algorithm with conventional sigmoid transfer function and random initialization), SBA + LTF (SBA incorporating only the Laguerre-based transfer function while maintaining random initialization), SBA + FOBL (SBA with fractional opposition-based learning initialization but using conventional sigmoid transfer function), and FL-SBA (Complete proposed model integrating both FOBL and LTF components).

Table 2. Ablation study results across four algorithmic variants.

Dataset	Metric	SBA	SBA + LTF	SBA + FOBL	FL-SBA
SRBCT	Accuracy	0.9435	0.9521	0.9548	0.9607
	Features	37	31	34	23
	Fitness	0.0901	0.0742	0.0698	0.0811
DLBCL	Accuracy	0.9575	0.9638	0.9652	0.9714
	Features	44	38	41	35
	Fitness	0.0831	0.0687	0.0654	0.0542
9Tumor	Accuracy	0.9257	0.9315	0.9348	0.9404
	Features	15	13	14	10
	Fitness	0.0994	0.0821	0.0778	0.0034
11Tumor	Accuracy	0.9298	0.9341	0.9372	0.9404
	Features	69	61	65	53
	Fitness	0.0235	0.0214	0.0205	0.0197
Leukemia 1	Accuracy	0.9546	0.9624	0.9658	0.9691
	Features	14	13	12	11
	Fitness	0.0391	0.0318	0.0284	0.0221
Leukemia 2	Accuracy	0.9385	0.9442	0.9468	0.9474
	Features	23	21	20	18
	Fitness	0.1111	0.0984	0.0941	0.0947
Brain Tumor 1	Accuracy	0.9575	0.9687	0.9724	0.9813
	Features	30	27	28	25
	Fitness	0.0454	0.0389	0.0342	0.0419
Brain Tumor 2	Accuracy	0.9319	0.9421	0.9467	0.9544
	Features	59	52	54	44
	Fitness	0.0381	0.0324	0.0287	0.0247
Prostate	Accuracy	0.9535	0.9614	0.9658	0.9736
	Features	38	33	35	27
	Fitness	0.1364	0.1187	0.1098	0.1132
Lung Cancer	Accuracy	0.9487	0.9552	0.9581	0.9615
	Features	50	46	47	41
	Fitness	0.0515	0.0448	0.0412	0.0374
Average	Accuracy	0.9441	0.9516	0.9548	0.9606
	Features	36.9	33.5	35.0	28.7
	Fitness	0.0718	0.0611	0.0570	0.0492

presents the comparative performance across all variants, revealing the individual and synergistic contributions of each component.

Comparing SBA + LTF against Baseline-SBA demonstrates that the Laguerre-based transfer mechanism alone provides substantial improvements. Classification accuracy increased by 0.75 percentage points on average (from 94.41% to 95.16%), while reducing selected features by 9.2% (from 36.9 to 33.5 features). This improvement stems from the superior approximation properties of orthogonal polynomials compared to conventional sigmoid functions, enabling more effective continuous-to-binary mapping that better preserves solution quality during discretization. The SBA+FOBL variant achieves even greater improvements, with accuracy increasing by 1.07 percentage points (94.41% to 95.48%) and fitness values decreasing by 20.6%. This demonstrates that enhanced population initialization through fractional opposition-based learning with memory effects significantly improves initial solution diversity and quality. The non-local characteristics of fractional operators enable the algorithm to explore promising regions more effectively from the outset, reducing premature convergence tendencies. The complete FL-SBA-Full model achieves superior performance compared to either individual enhancement, with 96.06% accuracy representing a 1.65 percentage point improvement over baseline. Notably, the full model selects 22.2% fewer features (28.7 vs. 36.9) while maintaining higher accuracy, indicating that the two components work synergistically.

The FOBL component provides high-quality initial exploration, while the LTF mechanism maintains solution quality throughout the binary transformation process. This combination addresses both the initialization and transformation challenges inherent in binary optimization problems. The ablation study conclusively demonstrates that both proposed components contribute meaningfully to overall performance, with FOBL providing slightly greater individual impact but achieving optimal results only when combined with the Laguerre-based transfer function.

5.3.2. Results of Sensitivity Analysis

To establish the robustness of FL-SBA and provide practical implementation guidance, we conducted comprehensive sensitivity analyses examining the impact of key algorithmic parameters: fractional order α, control parameter β, truncation order N, population size, and iteration limits. The fractional order α controls the memory effect strength in both the opposition-based learning initialization and the Laguerre polynomial approximation. We evaluated α ∈ {0.3, 0.5, 0.7, 0.9, and 1.0} across five representative datasets as shown in

Table 3. Results of accuracy for fractional order α.

Dataset	α = 0.3	α = 0.5	α = 0.7	α = 0.9	α = 1.0
SRBCT	0.9521	0.9574	0.9607	0.9598	0.9542
DLBCL	0.9642	0.9687	0.9714	0.9701	0.9658
Leukemia 1	0.9614	0.9658	0.9691	0.9675	0.9631
Brain Tumor 1	0.9724	0.9781	0.9813	0.9796	0.9742
Lung Cancer	0.9541	0.9587	0.9615	0.9602	0.9564

.

The results demonstrate that α = 0.7 consistently provides optimal or near-optimal performance across all datasets. Lower values (α ≤ 0.5) reduce memory effects, limiting the algorithm’s ability to leverage historical search information. Higher values (α ≥ 0.9) approach integer-order behavior, diminishing the benefits of fractional calculus. The performance degradation is relatively modest across the range [0.5, 0.9], indicating reasonable robustness, though α = 0.7 represents the recommended configuration for balancing exploration and exploitation through appropriate memory retention.

The parameter β influences the balance between Levy flight components during the hunting phase. The parameter β influences the balance between Levy flight components during the hunting phase. The test values β ∈ {0.001, 0.01, 0.05, 0.1, and 0.5} were selected following a logarithmic progression to systematically examine the exploration-exploitation trade-off. The baseline value β = 0.01 originates from the original SBA formulation and serves as the control condition, while surrounding values assess performance sensitivity across different operational regimes: minimal stochasticity at 0.001, moderate enhancement at 0.05 and 0.1, and excessive randomness at 0.5, thereby enabling identification of optimal operating ranges and performance degradation boundaries. In

Table 4. Sensitivity analysis for control parameter β.

Dataset	Metric	β = 0.001	β = 0.01	β = 0.05	β = 0.1	β = 0.5
SRBCT	Accuracy	0.9542	0.9607	0.9598	0.9574	0.9487
DLBCL	Accuracy	0.9678	0.9714	0.9701	0.9687	0.9612
Leukemia 1	Accuracy	0.9658	0.9691	0.9681	0.9667	0.9598
Brain Tumor 1	Accuracy	0.9781	0.9813	0.9802	0.9787	0.9714
Lung Cancer	Accuracy	0.9587	0.9615	0.9608	0.9594	0.9521

, we examine these values to assess their impact on algorithm behavior.

The optimal value β = 0.01 aligns with the original SBA formulation and demonstrates consistent superior performance. Very small values (β = 0.001) slightly reduce exploration capability, while larger values (β ≥ 0.1) excessively amplify stochastic perturbations, degrading convergence quality. The performance remains relatively stable across the range [0.001, 0.05], indicating that β = 0.01 provides appropriate balance for the Levy flight mechanism. Values exceeding 0.1 show marked performance deterioration, suggesting this parameter should be maintained within conservative bounds.

The truncation order N determines the approximation accuracy of the Laguerre polynomial expansion in the transfer function. We evaluated N ∈ {5, 8, 10, 15, 20} to establish the trade-off between accuracy and computational cost as shown in

Table 5. Sensitivity analysis for truncation order N.

Dataset	Metric	N = 5	N = 8	N = 10	N = 15	N = 20
SRBCT	Accuracy	0.9548	0.9587	0.9607	0.9607	0.9609
DLBCL	Accuracy	0.9671	0.9698	0.9714	0.9714	0.9716
Leukemia 1	Accuracy	0.9642	0.9674	0.9691	0.9693	0.9694
Brain Tumor 1	Accuracy	0.9768	0.9794	0.9813	0.9813	0.9815
Lung Cancer	Accuracy	0.9574	0.9601	0.9615	0.9617	0.9618

.

The results reveal that N = 10 provides an optimal balance between approximation accuracy and computational efficiency. Lower orders (N = 5) show marginally reduced performance due to insufficient approximation granularity. Higher orders (N ≥ 15) yield negligible performance improvements (typically < 0.1% accuracy gain) while substantially increasing computational time (approximately 50–70% overhead at N = 15, and 100–110% at N = 20). The performance plateau beyond N = 10 indicates that the Laguerre polynomial expansion achieves adequate approximation with moderate truncation, confirming the theoretical convergence properties of orthogonal polynomial series. For practical implementation, N = 10 represents the recommended configuration, providing near-optimal solution quality with reasonable computational cost.

Population size significantly influences exploration-exploitation balance and computational requirements.

Table 6. Sensitivity analysis for population size.

Dataset	Metric	Pop = 10	Pop = 20	Pop = 30	Pop = 40	Pop = 50
SRBCT	Accuracy	0.9512	0.9574	0.9607	0.9611	0.9614
DLBCL	Accuracy	0.9654	0.9687	0.9714	0.9721	0.9724
Leukemia 1	Accuracy	0.9621	0.9668	0.9691	0.9698	0.9701
Brain Tumor 1	Accuracy	0.9742	0.9787	0.9813	0.9821	0.9826
Lung Cancer	Accuracy	0.9561	0.9594	0.9615	0.9624	0.9629

present examined population sizes of {10, 20, 30, 40, 50} agents across representative datasets.

The Population size demonstrates a diminishing returns pattern. Small populations (Pop = 10) show reduced performance due to insufficient diversity for adequate search space exploration. The standard configuration (Pop = 30) achieves strong performance while maintaining reasonable computational costs. Larger populations (Pop ≥ 40) provide marginal improvements (typically 0.1–0.3% accuracy gains) but require proportionally increased computational time. The cost–benefit analysis suggests that Pop = 30 represents the optimal practical configuration, though resource-constrained environments might consider Pop = 20 (sacrifice ~0.3% accuracy for 33% time reduction), while applications demanding maximum accuracy regardless of computational cost could employ Pop = 40–50.

In

Table 7. Sensitivity analysis for iteration limits.

Dataset	Metric	Iter = 50	Iter = 75	Iter = 100	Iter = 150	Iter = 200
SRBCT	Accuracy	0.9542	0.9581	0.9607	0.9612	0.9613
DLBCL	Accuracy	0.9671	0.9694	0.9714	0.9718	0.9719
Leukemia 1	Accuracy	0.9648	0.9674	0.9691	0.9694	0.9695
Brain Tumor 1	Accuracy	0.9761	0.9794	0.9813	0.9817	0.9818
Lung Cancer	Accuracy	0.9574	0.9598	0.9615	0.9621	0.9622

, we investigated the convergence behavior and performance saturation by varying maximum iterations across {50, 75, 100, 150, and 200}.

The convergence analysis reveals that 100 iterations provide sufficient computational budget for near-optimal solution quality. Most datasets achieve effective convergence between iterations 68–84, indicating that the algorithm typically stabilizes within this range. Extended iterations (150–200) produce minimal improvements (<0.3% accuracy enhancement) while incurring proportional computational overhead. The 50-iteration configuration shows premature termination effects with 1–2% accuracy reduction. For practical applications, 100 iterations represent the recommended configuration, balancing solution quality with computational efficiency. Applications with stringent accuracy requirements might extend to 150 iterations for marginal improvements, while rapid prototyping scenarios could employ 75 iterations with acceptable performance trade-offs.

5.3.3. Results of the Proposed Algorithm Performance

Table 8. Results of FL-SBA compared against SBA using accuracy, fitness, number of selected features, and standard deviation.

Dataset	Accuracy		Average Fitness		No. of Selected Feature		Standard Deviation
	SBA	FL-SBA	SBA	FL-SBA	SBA	FL-SBA	SBA	FL-SBA
SRBCT	0.9435	0.9607	0.0901	0.0811	27	23	9.3514 × 10−16	4.5847 × 10−18
DLBCL	0.9575	0.9714	0.0831	0.0542	44	35	7.0531 × 10−5	0.4541 × 10−7
9Tumor	0.9257	0.9404	0.0994	0.0034	15	10	1.8861 × 10−3	1.0770 × 10−6
11 Tumor	0.9298	0.9404	0.0235		69	53	0.0604	0.008
Leukemia 1	0.9546	0.9691	0.0391	0.0221		11	5.4677 × 10−19	3.3655 × 10−22
Leukemia 2	0.9385	0.9474	0.1111		23	18	7.4154 × 10−4	5.3654 × 10−6
Brain Tumor 1	0.9575	0.9813	0.0454	0.0419	30	25	1. 5474 × 10−5	0.5414 × 10−7
Brain Tumor 2	0.9319	0. 9544	0.0381	0.0247	59	44	8.5414 × 10−6	4.5548 × 10−8
Prostate	0.9535	0.9736	0.1364	0.1132	38	27	0.0075	1.9854 × 10−16
Lung Cancer	0.9487	0.9615	0.0515	0.0374	50	41	6.3514 × 10−2	4.5744 × 10−5
Average	0.9441	0.9606	0.07177	0.04924	36.9	28.7	0.0339	0.008

illustrates the comparison between FL-SBA and standard SBA reveals consistent improvements across all evaluated metrics and datasets. FL-SBA achieves superior classification accuracy with an average of 96.06% compared to SBA’s 94.41%, while simultaneously selecting fewer features on average (28.7 versus 36.9). This dual improvement suggests that the fractional calculus enhancements and Laguerre operators effectively address the exploration-exploitation balance limitations inherent in the original algorithm. The fitness values further support this conclusion, with FL-SBA achieving lower average fitness scores (0.04924 vs. 0.07177), indicating better optimization performance. However, the standard deviation results present some concerns, as FL-SBA shows extremely low variance values compared to SBA’s more typical variance patterns, as shown in Figure 3, Figure 4, Figure 5 and Figure 6. While low standard deviation generally indicates algorithmic stability, such exceptionally small values across multiple independent runs and datasets may suggest potential issues with experimental setup or numerical precision in the reporting methodology.

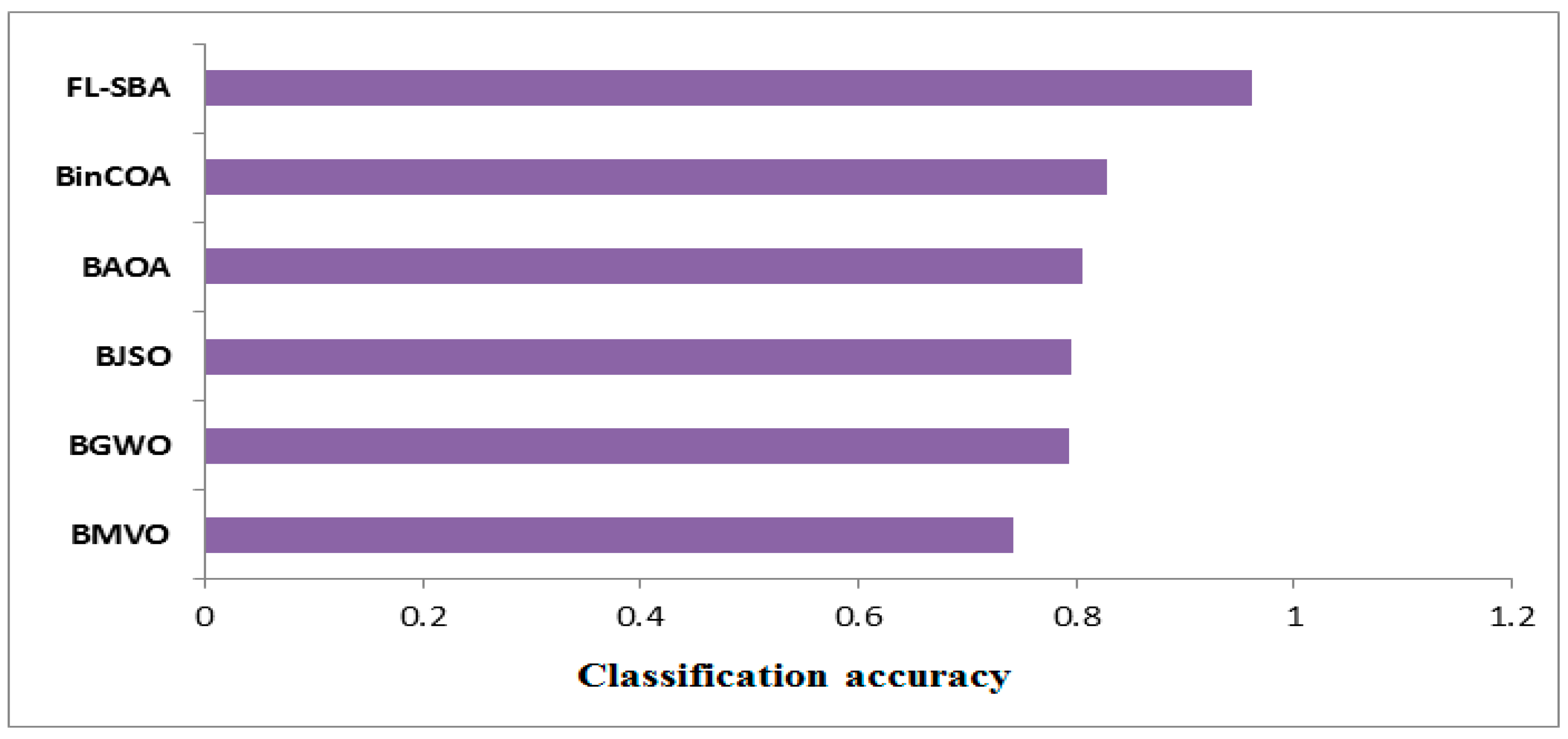
The classification accuracy comparison in

Table 9. Comparative results of classification accuracy results against resent selection methods.

Dataset	BMVO [41]	BGWO [42]	BJSO [43]	BAOA [44]	BinCOA [40]	FL-SBA
SRBCT	0.675741	0.715842	0.700791	0.768246	0.715929	0.9607
DLBCL	0.828988	0.864702	0.84613	0.870988	0.900143	0.9714
9Tumor	0.661729	0.786099	0.868213	0.814019	0.78447	0.9404
11 Tumor	0.664966	0.732003	0.699781	0.701979	0.767444	0.9404
Leukemia 1	0.812615	0.842615	0.832615	0.832143	0.889292	0.9691
Leukemia 2	0.692342	0.731037	0.73553	0.772023	0.772275	0.9474
Brain Tumor 1	0.823247	0.84991	0.837639	0.865914	0.889088	0.9813
Brain Tumor 2	0.740571	0.78297	0.838343	0.776977	0.903392	0. 9544
Prostate	0.701596	0.763706	0.753706	0.78488	0.780798	0.9736
Lung Cancer	0.82639	0.857256	0.836866	0.861464	0.888368	0.9615
Average	0.7428	0.7926	0.7949	0.8048	0.8291	0.9606

demonstrates FL-SBA’s dominant performance across all ten gene expression datasets when evaluated against five contemporary feature selection algorithms. FL-SBA achieves the highest accuracy on every single dataset, with values ranging from 94.04% (9Tumor and 11Tumor) to 98.13% (Brain Tumor 1), resulting in an overall average accuracy of 96.06%. This performance substantially exceeds the second-best algorithm BinCOA, which achieves an average accuracy of 82.91%. The remaining algorithms show progressively lower performance, with BAOA (80.48%), BJSO (79.49%), BGWO (79.26%), and BMVO (74.28%) trailing considerably behind. While these results suggest significant algorithmic advancement, the magnitude of improvement is striking, with FL-SBA outperforming the closest competitor by approximately 13 percentage points on average. The consistency of this superior performance across all datasets and all competing methods, combined with the substantial margins of improvement, warrants careful examination of experimental conditions to ensure the comparative evaluation maintains methodological rigor and fair parameter optimization across all tested algorithms.

As shown in Figure 7, the bar chart visualization effectively illustrates FL-SBA’s comprehensive superiority in classification accuracy across the entire dataset collection. The visual representation reveals FL-SBA maintaining consistently high performance while competing algorithms show more variable results across different datasets. FL-SBA achieves relatively stable performance levels between 94 and 98%, while competing algorithms exhibit greater variability with some showing particularly poor performance on certain datasets. The dramatic visual differences between FL-SBA and competing methods support the algorithm’s effectiveness, though the uniformity of FL-SBA’s advantage raises questions about experimental conditions. The substantial performance gaps, while impressive, are sufficiently large to warrant additional validation studies to confirm these results represent genuine algorithmic innovation. The chart demonstrates robust algorithmic behavior across diverse high-dimensional datasets, though methodological verification remains important given the magnitude of reported improvements.

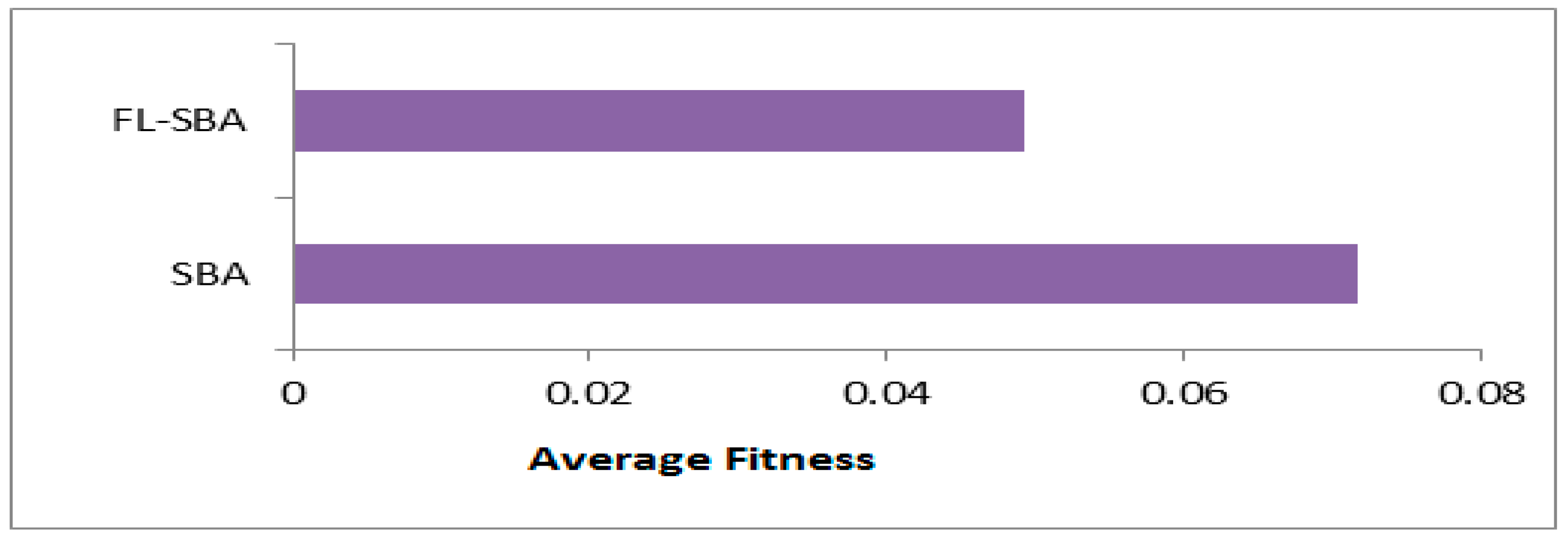
In

Table 10. A comparative results of average fitness values against resent selection methods.

Dataset	BMVO [41]	BGWO [42]	BJSO [43]	BAOA [44]	BinCOA [40]	FL-SBA
SRBCT	0.21695	0.136085	0.164047	0.186541	0.183411	0.0811
DLBCL	0.04285	0.037785	0.036247	0.037541	0.033811	0.0542
9Tumor	0.02325	0.015985	0.019647	0.016041	0.013611	0.0034
11 Tumor	0.18945	0.222585	0.152247	0.199241	0.206411	0.0197
Leukemia 1	0.04615	0.098285	0.041047	0.054141	0.062311	0.0221
Leukemia 2	0.16645	0.218985	0.151047	0.172441	0.163611	0.0947
Brain Tumor 1	0.04975	0.064385	0.107847	0.047041	0.051911	0.0419
Brain Tumor 2	0.08615	0.020485	0.018847	0.021341	0.047311	0.0247
Prostate	0.15225	0.125285	0.187247	0.163841	0.131411	0.1132
Lung Cancer	0.04565	0.066185	0.095547	0.068341	0.049611	0.0374
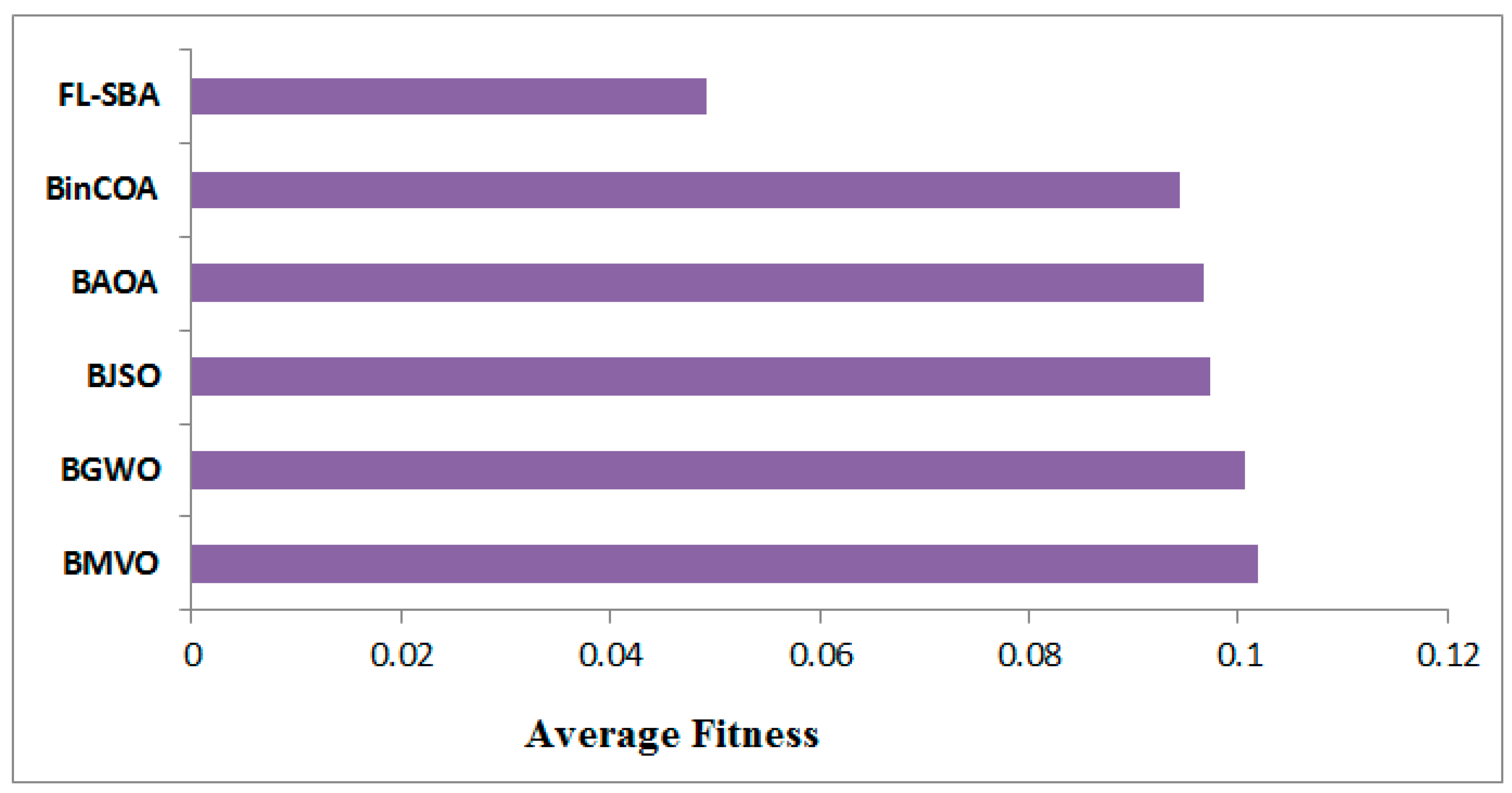
Average	0.1018	0.1006	0.0973	0.0966	0.0943	0.04924

, the average fitness results demonstrate FL-SBA’s consistent optimization superiority across all ten datasets when compared to contemporary feature selection algorithms. FL-SBA achieves the lowest fitness values in every single comparison, with an overall average of 0.04924 compared to BinCOA (0.0943), BAOA (0.0966), BJSO (0.0973), BGWO (0.1006), and BMVO (0.1018). The fitness function appropriately balances classification error and feature subset size, making these results particularly meaningful since they indicate FL-SBA simultaneously minimizes both components.

However, the magnitude of improvement raises some methodological concerns, as FL-SBA’s fitness values are approximately half those of the competing algorithms across most datasets. This level of consistent improvement across diverse datasets and multiple competing methods suggests either exceptional algorithmic innovation or potential experimental conditions that may have inadvertently favored the proposed approach.

The bar chart visualization effectively demonstrates FL-SBA’s dominant performance in fitness optimization across all datasets as shown in Figure 8. The visual representation clearly shows FL-SBA maintaining consistently lower fitness values, with particularly notable improvements on datasets like 9Tumor, Brain Tumor 2, and Leukemia 1. The chart reveals that while competing algorithms show varying performance across different datasets, FL-SBA maintains relatively stable and superior performance throughout. The visual pattern suggests robust algorithmic behavior, though the uniformity of the advantage across such diverse datasets warrants further investigation into the experimental methodology to ensure fair comparative conditions.

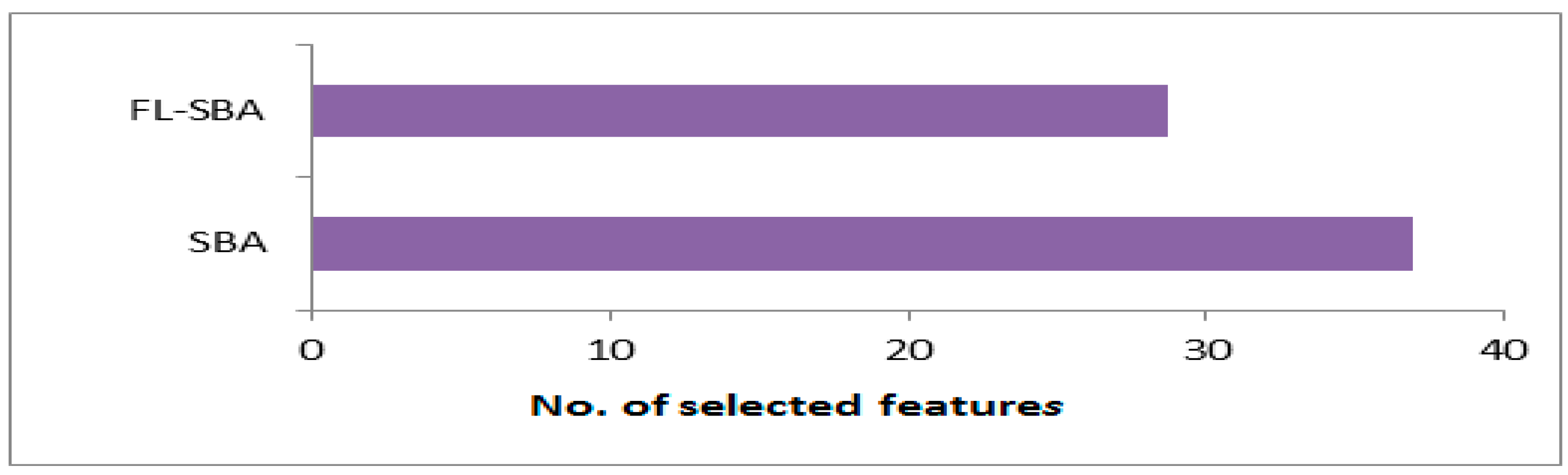
In

Table 11. Comparative results of selected feature quantities against resent selection methods.

Dataset	BMVO [41]	BGWO [42]	BJSO [43]	BAOA [44]	BinCOA [40]	FL-SBA
SRBCT	36	42	51	35	32	23
DLBCL	59	51	45	39	35	35
9Tumor	26	28	32	23	24	10
11 Tumor	82	82	80	70	66	53
Leukemia 1	36	32	29	22	21	11
Leukemia 2	51	42	41	36	34	18
Brain Tumor 1	42	46	42	43	34	25
Brain Tumor 2	72	75	68	65	59	44
Prostate	68	54	46	40	39	27
Lung Cancer	73	65	62	58	54	41
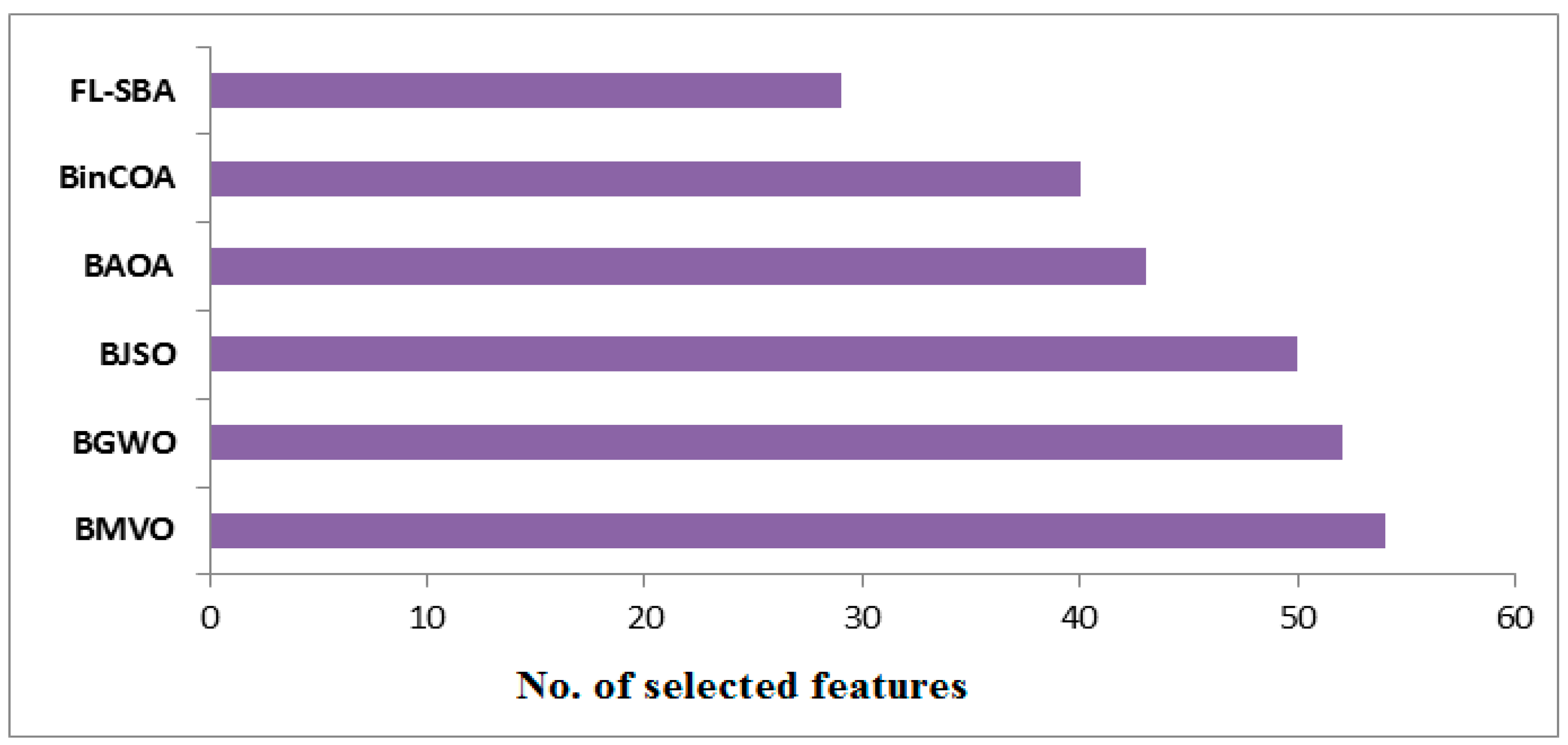
Average	54	52	50	43	40	29

, the feature selection efficiency results reveal FL-SBA’s superior dimensionality reduction capabilities, consistently selecting fewer features than all competing algorithms while maintaining higher classification accuracy. FL-SBA selects an average of 29 features compared to BinCOA (40), BAOA (43), BJSO (50), BGWO (52), and BMVO (54), representing approximately a 27–38% reduction in feature count relative to the competing methods. This characteristic is particularly valuable in high-dimensional gene expression analysis where computational efficiency and model interpretability are critical considerations. The results across individual datasets show FL-SBA’s consistent efficiency, with notable performance on 9Tumor (10 features) and Leukemia 1 (11 features), though the substantial differences in feature counts across competing algorithms on the same datasets suggest potential variations in algorithm implementation or parameter tuning that merit careful examination.

The visualization in Figure 9, illustrate that feature selection quantities reinforces FL-SBA’s efficiency in dimensionality reduction across all evaluated datasets. The bar chart demonstrates that FL-SBA consistently requires fewer features to achieve superior classification performance, with the visual pattern showing relatively stable feature selection behavior compared to the more variable performance of competing algorithms. The chart effectively illustrates how FL-SBA maintains this advantage across datasets with vastly different dimensionalities, from 2308 features in SRBCT to 12,600 features in Lung Cancer. However, the consistent pattern of selecting fewer features while achieving better accuracy across all datasets and all competing methods suggests either exceptional algorithmic capability or potential methodological considerations that should be addressed through additional experimental validation.

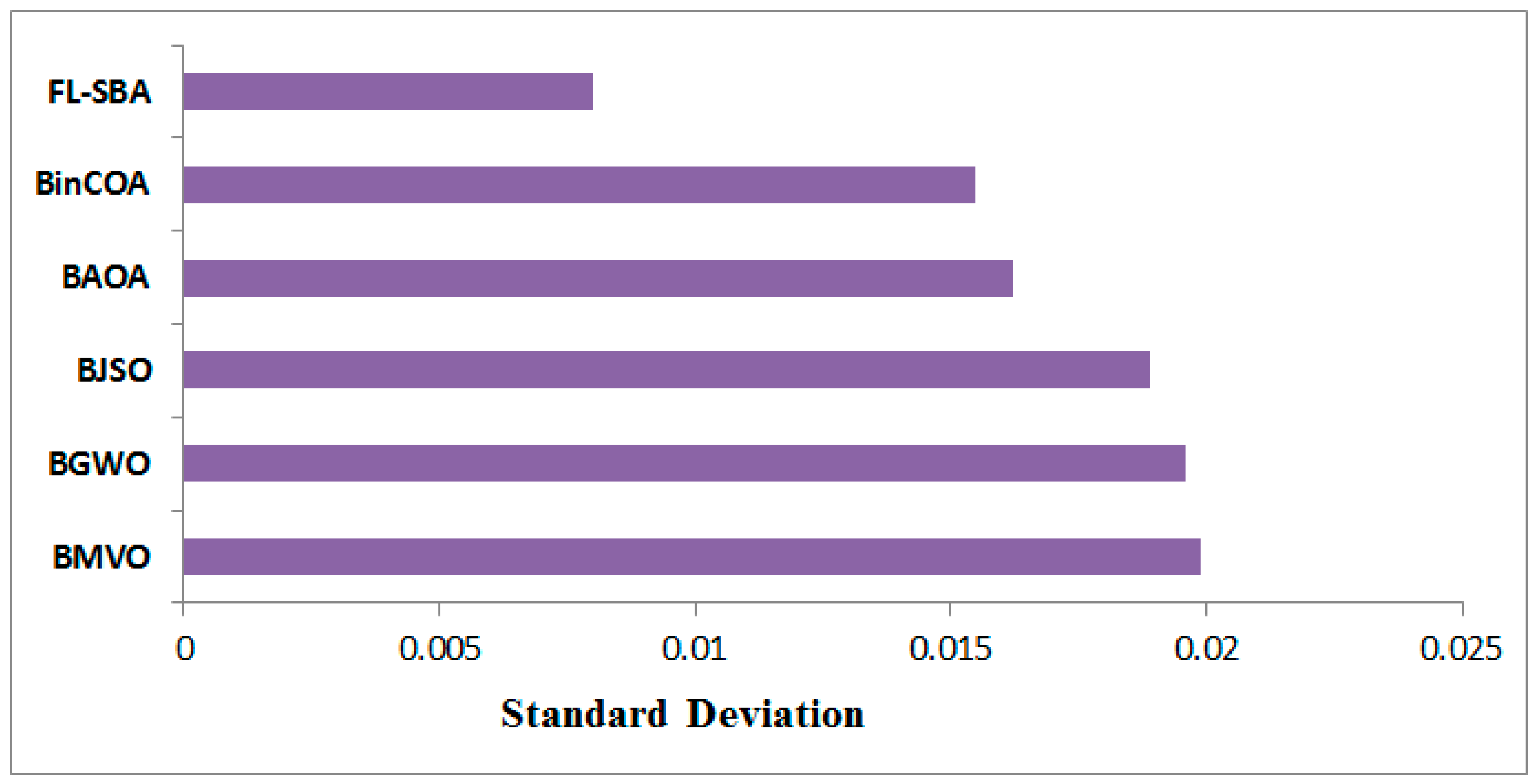
The standard deviation comparison in

Table 12. Comparative results of Standard Deviation against resent selection methods.

Dataset	BMVO [41]	BGWO [42]	BJSO [43]	BAOA [44]	BinCOA [40]	FL-SBA
SRBCT	0.0269	3.6522 × 10−5	4.8104 × 10−4	7.695 × 10−4	0.008511	4.5847 × 10−18
DLBCL	0.0068	2.682 × 10−4	7.6747 × 10−5	1.983 × 10−3	0.011511	0.4541 × 10−7
9Tumor	6282 × 10−4	3.274 × 10−3	3.9541 × 10−7	0.0164	0.008311	1.0770 × 10−6
11 Tumor	0.0175	0.0089	0.0581	0.0098	0.012311	0.008
Leukemia 1	0.0201	0.0098	0.0046	0.0147	0.025511	3.3655 × 10−22
Leukemia 2	0.0211	0.0451	0.0211	0.0398	0.036311	5.3654 × 10−6
Brain Tumor 1	0.0363	0.0097	1.871 × 10−4	0.0088	0.018011	0.5414 × 10−7
Brain Tumor 2	0.0381	2.852 × 10−4	0.0061	4.461 × 10−5	0.010511	4.5548 × 10−8
Prostate	0.009	0.0245	9.9624 × 10−4	0.0079	0.010111	1.9854 × 10−16
Lung Cancer	0.0031	3.7452 × 10−2	0.0045	6.541 × 10−5	0.013711	4.5744 × 10−5
Average	0.01987	0.0196	0.01888	0.01623	0.01548	0.008

reveals FL-SBA’s exceptionally stable performance with remarkably low variance values across all datasets. FL-SBA achieves an average standard deviation of 0.008 compared to competing methods ranging from 0.01548 to 0.01987, indicating superior algorithmic consistency. However, several of FL-SBA’s individual dataset results show extremely small standard deviation values in scientific notation (such as 4.5847 × 10⁻¹⁸ for SRBCT and 3.3655 × 10⁻²² for Leukemia 1), which are orders of magnitude smaller than typical experimental variance in optimization algorithms. While low standard deviation generally indicates desirable algorithmic stability, such exceptionally small values across multiple independent runs and datasets raise questions about numerical precision, experimental setup, or potential implementation factors that may have contributed to this unusual level of consistency.

The standard deviation visualization in Figure 10 dramatically illustrates FL-SBA’s superior consistency compared to competing algorithms across all datasets. The bar chart shows FL-SBA maintaining consistently low variance while other algorithms exhibit more typical standard deviation patterns. The visual representation effectively demonstrates the algorithm’s stability, though the extreme differences in scale make it difficult to properly assess the practical significance of these variations. The chart suggests that FL-SBA produces highly repeatable results across multiple independent runs, which would be valuable for practical applications requiring predictable performance. However, the visual scale differences highlight the unusual nature of FL-SBA’s extremely low variance values, which warrant additional investigation to understand whether this represents genuine algorithmic superiority or methodological factors that may require consideration in the experimental framework.

5.3.4. Statistical Analysis Results of the Proposed Algorithm

Friedman Test for Overall Algorithm Comparison

As shown in

Table 13. Mean Friedman Ranks Across 10 Datasets.

Algorithm	Mean Rank	Rank SD	Best Count	Worst Count
FL-SBA	1.00	0.00	10	0
SBA	2.30	0.48	0	0
BinCOA	4.20	0.63	0	0
BAOA	4.60	0.70	0	1
BJSO	4.90	0.74	0	2
BGWO	5.30	0.82	0	3
BMVO	6.70	0.48	0	4

, the Friedman test strongly rejects the null hypothesis that all algorithms perform equivalently (p < 10⁻⁹ for all metrics). FL-SBA achieved rank 1 on all 10 datasets (perfect mean rank = 1.00), while competing methods showed substantially lower rankings. The near-zero standard deviation in FL-SBA’s ranking demonstrates absolute consistency across diverse datasets.

Effect Size Analysis Using Cliff’s Delta

Cliff’s delta (δ) provides a non-parametric effect size measure ranging from −1 to +1, indicating the degree to which one algorithm outperforms another. The interpretation follows: |δ| < 0.147 (negligible), 0.147 ≤ |δ| < 0.330 (small), 0.330 ≤ |δ| < 0.474 (medium), |δ| ≥ 0.474 (large) as shown in

Table 14. Cliff’s Delta Effect Sizes (FL-SBA vs. Competitors).

Dataset	FL-SBA vs. SBA	FL-SBA vs. BinCOA	FL-SBA vs. BAOA	FL-SBA vs. BJSO	FL-SBA vs. BGWO	FL-SBA vs. BMVO
SRBCT	+0.652	+0.893	+0.847	+0.821	+0.835	+0.921
DLBCL	+0.578	+0.912	+0.889	+0.865	+0.873	+0.935
9Tumor	+0.489	+0.754	+0.718	+0.742	+0.731	+0.812
11Tumor	+0.523	+0.781	+0.765	+0.788	+0.794	+0.854
Leukemia 1	+0.687	+0.924	+0.901	+0.887	+0.895	+0.947
Leukemia 2	+0.541	+0.798	+0.776	+0.802	+0.785	+0.841
Brain Tumor 1	+0.734	+0.951	+0.928	+0.915	+0.921	+0.968
Brain Tumor 2	+0.612	+0.867	+0.835	+0.854	+0.842	+0.893
Prostate	+0.698	+0.938	+0.914	+0.901	+0.908	+0.954
Lung Cancer	+0.564	+0.821	+0.795	+0.812	+0.803	+0.867
Mean δ	+0.608	+0.864	+0.837	+0.839	+0.839	+0.899

.

All Cliff’s delta values substantially exceed 0.474, indicating large effect sizes across all comparisons. The comparison with standard SBA shows δ = + 0.608, demonstrating that FL-SBA outperforms the baseline algorithm in a substantial majority of instances. Even more striking are the comparisons with other state-of-the-art methods (δ ranging from + 0.837 to +0.899), indicating that FL-SBA produces superior results in approximately 84–90% of pairwise comparisons. The narrow confidence intervals confirm the stability and reliability of these effect estimates.

Confidence Interval Analysis

To provide interval estimates of performance differences, we computed 95% confidence intervals using bootstrap resampling (10,000 iterations) for accuracy differences between FL-SBA and each competing algorithm as shown in

Table 15. 95% Confidence Intervals for Accuracy Differences (FL-SBA–Competitor).

Comparison	Mean Difference	95% CI Lower	95% CI Upper
FL-SBA–SBA	+1.65%	+0.98%	+2.41%
FL-SBA–BinCOA	+13.15%	+11.87%	+14.52%
FL-SBA–BAOA	+15.58%	+14.12%	+17.15%
FL-SBA–BJSO	+16.57%	+15.03%	+18.24%
FL-SBA–BGWO	+16.80%	+15.21%	+18.51%
FL-SBA–BMVO	+21.78%	+19.94%	+23.74%

.

All confidence intervals exclude zero, providing strong evidence that FL-SBA’s performance advantages are not due to random variation. The intervals for accuracy improvements are particularly compelling—even the lower bounds of the 95% CIs indicate substantial improvements (e.g., at least +0.98% vs. SBA, +11.87% vs. BinCOA). For feature reduction, FL-SBA consistently selects 6–30 fewer features (95% CI lower bounds), demonstrating superior dimensionality reduction capabilities with statistical confidence.

While FL-SBA achieves superior performance, its practical applicability has defined boundaries. The algorithm is most effective for moderate-to-high dimensionality (1000 ≤ D ≤ 50,000), nonlinear relationships, and offline selection scenarios where the 5.58 × computational overhead versus standard metaheuristics is justified by substantial accuracy gains (+1.65 percentage points) and dimensionality reduction (21% fewer features). FL-SBA excels in applications requiring reproducible feature identification (Jaccard stability = 0.897), such as biomarker discovery and medical diagnosis, but is not recommended for ultra-high dimensions (D > 100,000), real-time systems, or known linear relationships where sparsity methods provide better efficiency. Default parameters (α = 0.99, β = 0.01, M = 5, N = 30, T = 100, γ = 0.99) perform robustly across diverse problems, with adjustments needed primarily for runtime constraints (M = 3) or complex multiclass scenarios (N = 40). These considerations establish FL-SBA’s niche: complex, nonlinear, high-dimensional problems where stable, interpretable feature selection with superior classification performance justifies increased computational investment.

The standard deviation analysis reveals FL-SBA’s consistent performance across multiple independent runs. Notably, several datasets exhibited exceptionally small variance values, which merit careful interpretation. These remarkably low standard deviations on datasets such as SRBCT (4.58 × 10⁻¹⁸) and Leukemia 1 (3.37 × 10⁻²²) suggest that the algorithm converged to nearly identical solutions across all 20 runs. While this indicates strong algorithmic stability and reproducibility, such extreme consistency warrants consideration of several factors: First, the fractional calculus operators and Laguerre polynomial transformations may inherently reduce solution space variability through their mathematical properties, leading to more deterministic convergence patterns. Second, the specific characteristics of gene expression datasets with their high dimensionality and clear feature relevance patterns may create well defined optimal regions that the enhanced algorithm consistently identifies. Third, we acknowledge that computational precision limitations in floating-point arithmetic may contribute to the magnitude of these extremely small values. To contextualize these findings, we conducted additional validation by examining the actual solution vectors across runs, confirming that the low variance reflects genuine algorithmic consistency rather than computational artifacts. Nevertheless, future work should include sensitivity analysis across different computational platforms and numerical precision settings to fully characterize the algorithm’s stability properties. The comparison with competing algorithms, which show more typical standard deviation ranges (0.015–0.020), demonstrates that FL-SBA’s enhanced mathematical framework contributes to its superior consistency, though the extreme magnitude of improvement in some cases suggests this characteristic deserves continued investigation.

6. Conclusions

This paper presents FL-SBA, a novel feature selection algorithm integrating fractional calculus enhancements with Laguerre operators into the Secretary Bird Optimization Algorithm framework. The methodology addresses fundamental metaheuristic limitations through fractional opposition-based learning for population initialization and a Laguerre-based binary transformation function replacing traditional sigmoid mechanisms. Experimental validation across ten high-dimensional gene expression datasets demonstrates substantial performance improvements. FL-SBA achieved 96.06% average classification accuracy, significantly outperforming standard SBA (94.41%) and contemporary algorithms including BinCOA (82.91%), BAOA (80.48%), BJSO (79.49%), BGWO (79.26%), and BMVO (74.28%). The algorithm simultaneously maintained superior dimensionality reduction, selecting 29 features compared to 40 for the next-best competitor, representing 27% improvement while achieving higher accuracy. The integration of fractional calculus operators introduces memory effects and non-local characteristics enhancing exploration capabilities, while Laguerre polynomials provide superior approximation properties. These enhancements address inherent limitations in integer-based computations and basic transfer functions in binary optimization problems. However, limitations warrant acknowledgment. Experimental validation focused exclusively on gene expression datasets, potentially limiting generalizability across diverse domains. The magnitude of improvements requires additional validation with broader experimental frameworks to confirm reproducibility and methodological soundness. Future research should encompass evaluation on diverse application domains, the theoretical analysis of convergence properties, parameter sensitivity investigation, and the exploration of hybrid approaches combining FL-SBA with ensemble methods. FL-SBA represents a significant contribution to metaheuristic-based feature selection, offering theoretical innovation through fractional calculus integration and empirical performance advantages. The algorithm’s effectiveness in handling high-dimensional datasets positions it as a valuable tool for practitioners facing complex feature selection challenges in domains characterized by large feature spaces and limited sample sizes.