AORO: Auto-Optimizing Reasoning Order for Multi-Hop Question Answering

Abstract

Answering multi-hop questions requires first retrieving a sequence of supporting facts, and the order in which these facts are retrieved significantly affects retriever performance. To achieve a clearer reasoning order, it is beneficial to address the easier facts first then move to the more difficult ones. However, current orders are usually pre-defined during data construction or specified manually, which restricts the model’s reasoning potential. This paper proposes Auto-Optimizing Reasoning Order (AORO), a method to automatically optimize the reasoning order for each sample, where difficulty is determined by a retrieval model trained with carefully curated data. First, a retriever is trained using data that encompasses all combinations of the possible reasoning orders. The trained retriever is then used to assess the difficulty of each fact, placing the fact with the least difficulty at the beginning of the sequence. Next, the retrieval model is retrained based on these optimized sequences, which are empirically better suited to its capabilities. This process creates an iterative self-debiasing paradigm, and these steps are repeated until all facts are reordered. Experiments conducted on two multi-hop QA benchmarks, QASC and MultiRC, demonstrate the effectiveness of AORO, which outperforms strong baselines using the same PTM, and further enables advanced PTMs to achieve improvements of up to 1.6 points in Recall@10 and 3.7 points in F1 score. Additional case analyses reveal empirical patterns in the optimal reasoning order: the pattern appears independent of the dataset and the underlying pre-trained model; and the sequence proceeds by confirming the truth of the question, answering the question, and filling in any gaps, which aligns with human reasoning.

1. Introduction

Multi-hop Question Answering (QA) is a challenging and complex form of QA [1,2,3] that requires addressing information needs that cannot be satisfied by a single query [4,5,6]. In such tasks, the answer cannot be derived from a single piece of fact [7]; rather, it must be obtained by retrieving, integrating, and reasoning over multiple factual statements to produce the correct answer [8,9]. A key advantage [10,11,12] of multi-hop QA is its ability to address questions that require complex reasoning or a deep understanding of the context [13,14]. In particular, gathering multiple facts typically requires several retrieval steps and can take the form of iterative single-hop retrieval [15,16,17]. During iterations, each subsequent retrieval step is guided by the initial question and the previously retrieved facts [18,19], producing a sequence of retrieved evidence referred to as the reasoning order [20].

Figure 1 presents an example of multi-hop multi-choice QA. The question is What makes food easier to chew? and the correct choice is liquids. The retriever is required to collect both ${\widehat{f}}_{\mathrm{a}}$ and ${\widehat{f}}_{\mathrm{b}}$. In the single-hop setting, ${\widehat{f}}_{\mathrm{b}}$ ranks 1st and ${\widehat{f}}_{\mathrm{a}}$ ranks 16th. In the multi-hop setting, the first hop is identical to the single-hop result, and the second hop, conditioned on Q and ${\widehat{f}}_{\mathrm{b}}$, promotes ${\widehat{f}}_{\mathrm{a}}$ to the first place. Compared with the single-hop setting, the multi-hop setting includes an additional search step, which can use the clue saliva in the single-hop result ${\widehat{f}}_{t}extb$ to find ${\widehat{f}}_{\mathrm{a}}$ more easily. Consequently, the multi-hop setting can outperform the single-hop setting by retrieving and combining newly emerged content that contains the necessary information.

However, a phenomenon usually arises in multi-hop retrieval: differences in reasoning order. As shown in Figure 1, the retriever outputs the order {${\widehat{f}}_{\mathrm{b}}$, ${\widehat{f}}_{\mathrm{a}}$}, whereas the ground-truth order in the training set is {${\widehat{f}}_{\mathrm{a}}$, ${\widehat{f}}_{\mathrm{b}}$}. The retrieved information is the same, but the orders differ. Naturally, two questions arise: Question 1 (Q1): What is the better reasoning order? and Question 2 (Q2): How can that order be obtained? Inspired by curriculum learning [22], this work posits that the reasoning process should progress from easier to harder retrieval steps. In this context, “easier” refers to the high probability of a fact being correctly retrieved at the current step. Addressing the “easier” facts first mitigates the risk of error propagation across subsequent reasoning steps [15]. Specifically, in AORO, “easier” is indicated by the retrieval model itself; the item that receives a higher rank under the current query state is deemed easier.

Based on the above assumption, in Q1, the highest-ranked item at a given hop is considered easier to retrieve at that retrieval step. For instance, in the multi-hop retrieval example illustrated in Figure 1, for hop 1, based on the query (Q), item ${\widehat{f}}_{\mathrm{b}}$ is ranked higher than the item ${\widehat{f}}_{\mathrm{a}}$. This suggests that retrieving ${\widehat{f}}_{\mathrm{b}}$ first and then ${\widehat{f}}_{\mathrm{a}}$ is better, whereas trying to retrieve ${\widehat{f}}_{\mathrm{a}}$, which ranks 16th in the first hop, would make retrieval more challenging.

For Q2, a retrieval model is required to produce a superior reasoning order by placing the easier item earlier in the sequence. The central task is therefore to construct such a “unbiased” model that can determine whether an item is easier. To this end, a retrieval model is trained on a consistency-based curated training set as the unbiased model. As shown in Figure 2, an illustrative procedure is as follows.

Step ①: Enumerate all feasible reasoning orders for a given sequence, namely Order 1 and Order 2. Step ②: Identify consistency samples across different orders and remove conflicting samples to avoid biased or confusing training data. For example, Order 1 yields three samples, which are marked with ②-a (in blue), and Order 2 yields three samples as well, marked with ②-b (in orange). The first sample in Order 1 conflicts with the first sample in Order 2, and the second and third samples are identical across the two orders. Step ③: Merge the samples that share identical input and output components to form a curated training set. The PTM-based retrieval model is then trained PTM-based retrieval model in Step ④. The resulting retrieval model is subsequently used to rank the candidate facts in Step ⑤. This result indicates that ${\widehat{f}}_{\mathrm{b}}$ ranks higher than ${\widehat{f}}_{\mathrm{a}}$, suggesting that the model finds ${\widehat{f}}_{\mathrm{b}}$ easier to retrieve. Consequently, ${\widehat{f}}_{\mathrm{b}}$ is designated as the first retrieval target (renamed to ${\widehat{f}}_1$), and ${\widehat{f}}_{\mathrm{a}}$ is set as the second target (renamed to ${\widehat{f}}_2$), following Order 2. This entire process represents the Auto-Optimizing Reasoning Order (AORO) framework.

AORO is evaluated on the multi-hop QA datasets QASC and MultiRC. The results show that AORO can improve the search performance over the strong baselines on both datasets, indicating that AORO yields a more effective reasoning order. Furthermore, AORO not only surpasses manual methods in optimizing orders but also produces reasoning sequences with high similarity across different PTMs. This similarity remains stable across datasets, suggesting that the optimal reasoning order is largely independent of the particular PTM or dataset. Case studies further reveal a consistent pattern in the induced order.

The contributions of this paper can be summarized as follows:

• This paper presents AORO to automatically optimize the reasoning order by iteratively training the model and selecting the better retrieval target.
• On two multi-hop QA datasets, QASC and MultiRC, AORO outperforms both non-ranking and rule-based ranking methods, demonstrating its effectiveness.
• Analysis across different PTMs and datasets indicates that the learned order is consistently superior and that the easier to harder retrieval strategy generalizes, underscoring the importance of selecting an appropriate reasoning order before launching the reasoning process.

This article is organized as follows. Section 2 briefly reviews related work. Section 3 presents the proposed approach, AORO. Specifically, Section 3.1 defines the concepts and symbols used throughout this paper. Section 3.2 introduces the process for automatically optimizing the reasoning order. Then, Section 3.3 describes the use of the optimized reasoning order to finetune the PTMs in the retrieval models. Section 4 describes the experimental procedures, and Section 5 presents the results and analysis of the findings. Finally, this paper concludes with an outline of directions for future work.

2. Background and Related Work

2.1. Multi-Hop Task

The initial component of multi-hop QA is multi-hop retrieval [23], which aims to gather the relevant facts needed for the subsequent answering phase [24,25]. Unlike single-hop retrieval tasks, such as MS MARCO [26] and WikiQA [27], the multi-hop retrieval requires the collection of more than one fact. Typical examples of multi-hop tasks are HotpotQA [8] and 2WikiMultiHopQA [10], where the questions are related to multiple extensive Wikipedia pages. This task demands not only effective search capabilities but also the ability to handle long texts [28,29], which adds complexity to the study of reasoning order. To simplify the problem, the datasets used in this paper are QASC [21] and MultiRC [30]. Both datasets consist of short sentences, making the management of reasoning order the primary issue to address.

2.2. Multi-Hop Retrieval

Methods for both datasets take into account the multi-hop structure. AIR (Alignment-based Iterative Retriever) [31] employs the similarity computation of AHE (Alignment over Heterogeneous Embeddings) [32] to eliminate irrelevant sentences while retaining the top 80 candidates. AHE uses word embeddings, such as GloVe [33] and BERT [34], to create an alignment cosine-similarity matrix between the words in the query and the candidate set. This matrix calculates the maximum alignment score, weighted by the Inverse Document Frequency (IDF) of the query words, along with summary scores. The AHE matrix simultaneously filters out retrieved words while keeping those that were not retrieved for further processing. However, AHE does not account for the meaning of entire sentences, which limits its effectiveness. To address this limitation, SingleRR and JointRR [35] utilize AHE as a filter and include a re-ranking component to better understand sentence meanings. In order to accommodate complete semantics, Beam Retrieval [36] models the multi-hop retrieval process in an end-to-end manner by jointly optimizing an encoder and two classification heads across all hops. In addition, RPA (Reasoning Path Augmentation) [14] employs RoBERTa-Large [37] to embed the sentences based on the same candidate set. The approach discussed in this paper uses the same multi-hop retrieval candidates with RPA, aiming for a fair comparison of multi-hop retrieval methods with the aforementioned techniques.

2.3. Reasoning Order

Reasoning orders are intended to be optimized so that easier facts are located first while more difficult ones are tackled later [14,38,39]. To achieve this, RPA [14] introduces reasoning-path augmentation to optimize the order of reasoning by extracting overlaps between sentences. The RPA consist of three optimization rules: (i) a set of query words, (ii) the set union of the query and retrieved facts, and (iii) the set intersection of the query and retrieved facts, with the third option yielding better results. However, when the number of set-intersection words among different facts is the same, it can be challenging to sort the ground-truth facts. Additionally, the priority of fact retrieval is often determined by manual rules, raising the question of whether a better order exists. To address this issue, this paper proposes an auto-optimization approach for reasoning order, which generates the order by training a model rather than relying on predefined rules.

3. Methods

This section first introduces the definitions of the task and notation used in this paper. Next, the automatic optimization process for the reasoning order is described. Finally, the obtained order is used to train a retrieval model and examine how changes in order affect the outcomes.

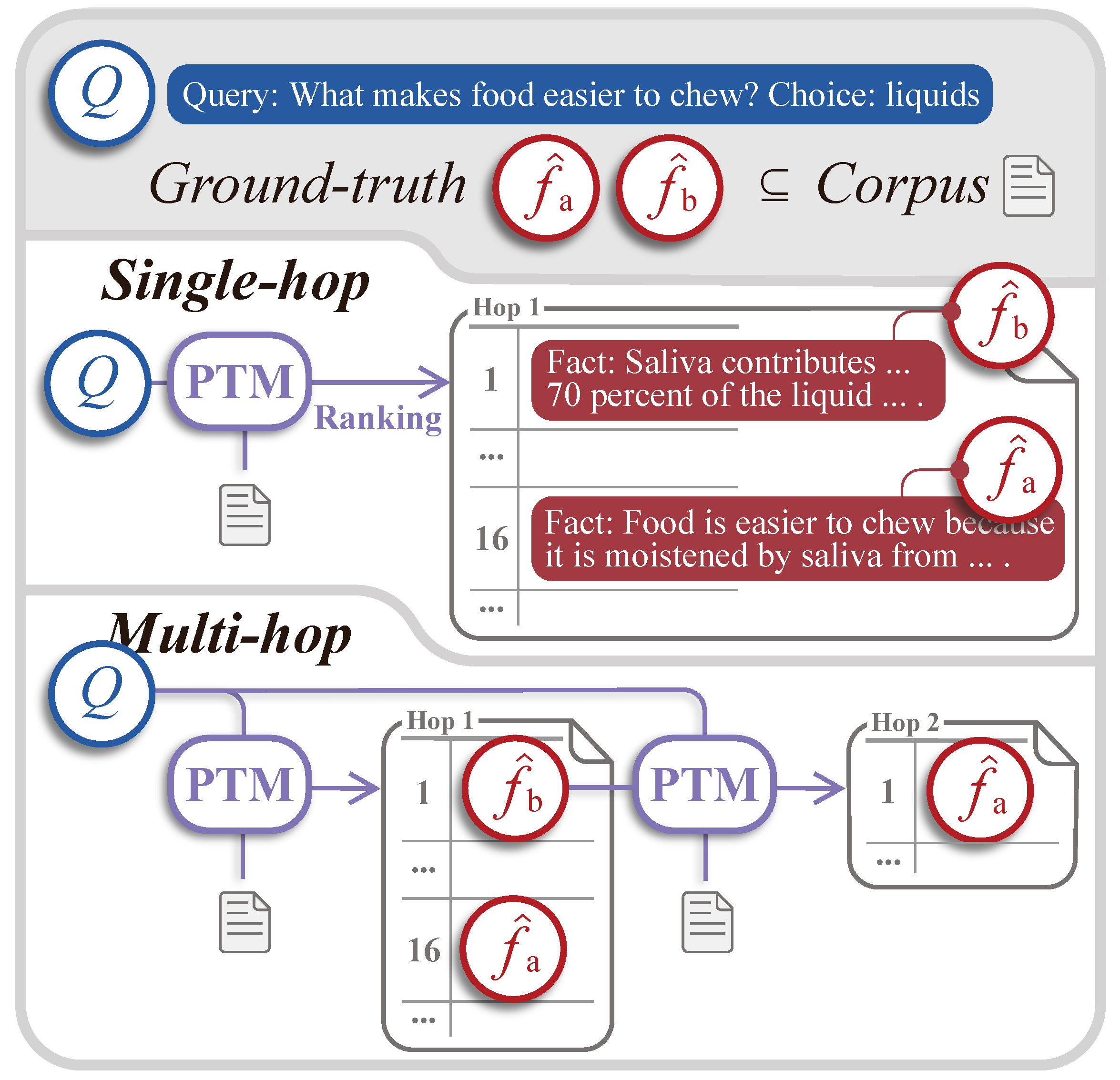
3.1. Task and Notation Definition

Given a query Q, a retrieval model is designed to gather all ground-truth facts $\widehat{F}=\{$${\widehat{f}}_{\mathrm{a}}$, ${\widehat{f}}_{\mathrm{b}}$, ⋯, ${\widehat{f}}_{\mathrm{x}}$, $\cdots \}$ ($|\widehat{F}|=N$) from the corresponding candidate corpus $\mathit{C}$. The optimized reasoning order, denoted as ${\widehat{F}}^{\mathrm{Opt}}$, is initially set to ⌀. The process of automatically optimizing the reasoning order involves using the retrieval model to extract the facts from $\widehat{F}$ in a specific sequence and append them to ${\widehat{F}}^{\mathrm{Opt}}$. In the end, $\widehat{F}$ is emptied (i.e., $\widehat{F}=⌀$) and ${\widehat{F}}^{\mathrm{Opt}}$ will contain the facts in the optimized order: $\{{\widehat{f}}_1,{\widehat{f}}_2,\cdots ,{\widehat{f}}_N\}$. To indicate the optimized order and distinguish it from $\widehat{F}$, the subscript of $\widehat{f}$ in ${\widehat{F}}^{\mathrm{Opt}}$ uses numbers instead of letters.

This section outlines two Information Retrieval (IR) processes: training and prediction. Their corresponding formulations differ as follows:

$$\begin{array}{cc}\hfill & \mathrm{Train}:max\mathrm{IR}(Q,{\widehat{f}}_1,\cdots ;{\widehat{f}}_{\mathrm{x}}),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \mathrm{Predict}:{\widehat{f}}_{\mathrm{x}}=\underset{{\widehat{f}}_{\mathrm{i}}\in \widehat{F}}{argmax}\mathrm{IR}(Q,{\widehat{f}}_1,\cdots ;{\widehat{f}}_{\mathrm{i}}).\hfill \end{array}$$

(2)

Equation (1) states that when the input is {Q, ${\widehat{f}}_1$, ⋯}, the training objective is to maximize the probability of obtaining ${\widehat{f}}_{\mathrm{x}}$. For example, in the middle term of ②-a in Figure 2, “In” denotes {Q, ${\widehat{f}}_{\mathrm{a}}$} and “Out” denotes ${\widehat{f}}_{\mathrm{b}}$. This relationship can be expressed as $max\mathrm{IR}(Q,{\widehat{f}}_{\mathrm{a}};{\widehat{f}}_{\mathrm{b}})$. Equation (2) indicates that when the input is $\{Q,{\widehat{f}}_1,\cdots \}$, ${\widehat{f}}_{\mathrm{x}}$ is the fact with the highest predicted probability among the non-input ground-truth facts. For instance, the ⑤ in Figure 2 is represented by ${\widehat{f}}_{\mathrm{b}}=arg{max}_{{\widehat{f}}_{\mathrm{i}}\in \{{\widehat{f}}_{\mathrm{a}},{\widehat{f}}_{\mathrm{b}}\}}\mathrm{IR}(Q;{\widehat{f}}_{\mathrm{i}})$. For simplicity, Equation (3) (Training) is used in place of Equations (1) and (4) (Prediction) replaces Equation (2) in the following discussion.

$$\begin{array}{c}\hfill Q+{\widehat{f}}_1+\cdots \stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{x}},\end{array}$$

(3)

$$\begin{array}{c}\hfill Q+{\widehat{f}}_1+\cdots \stackrel{\mathrm{P}}{\to }{\widehat{f}}_{\mathrm{x}}.\end{array}$$

(4)

In the equations above, “+” denotes sentence concatenation. Therefore, in Figure 2, the training process in ④ can be represented as $Q+{\widehat{f}}_{\mathrm{a}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}$ and $Q+{\widehat{f}}_{\mathrm{b}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}$. Additionally, the reasoning order in ⑥ of Figure 2 can be expressed as $Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$, where the subscripts “b” and “a” are replaced with “2” and “1,” respectively, to indicate the optimized order.

The AORO involves iteratively selecting the fact that is easiest to retrieve based on the query while simultaneously updating the query itself. Algorithm 1 illustrates this process. The algorithm consists of three main components: building unbiased training data, training the model, and making predictions. Each of these components is described in detail in this section.

Algorithm 1 Automatic optimization of reasoning order.

Input: Q, $\widehat{F}=\{{\widehat{f}}_{\mathrm{a}},{\widehat{f}}_{\mathrm{b}},\cdots \}$, PTM

Output:  ${\widehat{F}}^{\mathrm{Opt}}=\{{\widehat{f}}_1,{\widehat{f}}_2,\cdots \}$

1: ${\widehat{F}}^{\mathrm{Opt}}\leftarrow ⌀$ 2: while $\widehat{F}\ne ⌀$ do 3:     $Q^{\prime }\leftarrow Q+{\widehat{f}}_1+\cdots ,({\widehat{f}}_1,\cdots \in {\widehat{F}}^{\mathrm{Opt}})$          ▹ Collect the feasible orders 4:     $\mathrm{orders}\leftarrow \mathrm{Permutation}\left(\widehat{F}\right)$ 5:     $\mathrm{order}2\mathrm{data}\leftarrow \mathrm{Mapping}\left(\right)$ 6:     foreach ${\mathrm{order}}_{\mathrm{i}}\in \mathrm{orders}$ do 7:         ${\mathrm{ori}\_\mathrm{data}}_{\mathrm{i}}\leftarrow \mathrm{TrainingData}\left({\mathrm{order}}_{\mathrm{i}}\right)$ 8:         ${\mathrm{aug}\_\mathrm{data}}_{\mathrm{i}}\leftarrow \mathrm{AugmentationData}\left({\mathrm{order}}_{\mathrm{i}}\right)$ 9:         ${\mathrm{data}}_{\mathrm{i}}\leftarrow {\mathrm{ori}\_\mathrm{data}}_{\mathrm{i}}\cup {\mathrm{aug}\_\mathrm{data}}_{\mathrm{i}}$ 10:         add $\langle {\mathrm{order}}_{\mathrm{i}},{\mathrm{data}}_{\mathrm{i}}\rangle$ into $\mathrm{order}2\mathrm{data}$ 11:     end for 12:     $\mathrm{data}\leftarrow \mathrm{Merge}\left(\mathrm{order}2\mathrm{data}\right)$           ▹ Select the unbiased samples 13:     $\mathrm{PTM}\leftarrow \mathrm{Train}(\mathrm{PTM},\mathrm{data})$                 ▹ Training retrieval model 14:     ${\widehat{f}}_{\mathrm{x}}\stackrel{\mathrm{P}}{\leftarrow }{Q}^{\prime },({\widehat{f}}_{\mathrm{x}}\in \widehat{F})$                   ▹ Prediction with retrieval model 15:     $\widehat{F}\leftarrow \widehat{F}\setminus \left\{{\widehat{f}}_{\mathrm{x}}\right\}$ 16:     ${\widehat{F}}^{\mathrm{Opt}}\leftarrow {\widehat{F}}^{\mathrm{Opt}}\cup \left\{{\widehat{f}}_{\mathrm{x}}\right\}$ 17: end while 18: return ${\widehat{F}}^{\mathrm{Opt}}$

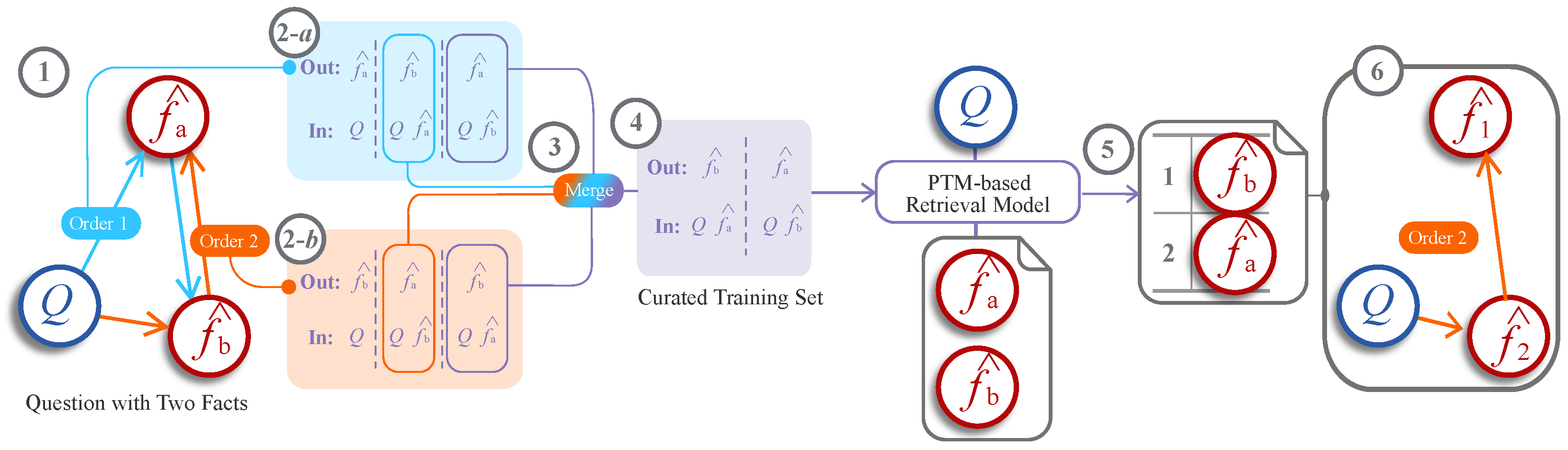
3.2. Automatic Optimization of Reasoning Order

3.2.1. Building Unbiased Training Data

The core objective of this stage is to eliminate the bias introduced by the predefined reasoning order formed in the original training data. Constructing an unbiased dataset enables the retrieval model to assess the intrinsic difficulty of retrieving each fact on its own merits. The procedure unfolds in three main steps: (Step 1) fact permutation, (Step 2) data generation for each permutation, and (Step 3) curation via merging. This process corresponds to Lines 2–12 in Algorithm 1 and is illustrated in steps ① to ③ of Figure 2.

Step 1: Fact Permutation. The initial step in mitigating order bias is to consider all potential reasoning orders. This is achieved by enumerating every possible permutation of the facts in $\widehat{F}$ (Line 4 of Algorithm 1). For a set of N facts, this results in $N!$ possible orderings.

Step 2: Data Generation for Each Permutation. For each permutation, a set of training samples is generated to teach the model how to follow that specific reasoning path (Lines 7–8 of Algorithm 1). This set includes two types of samples:

• Standard samples, which are generated based on the reasoning orders. For a given order, each fact is treated as the target output, with the query and all preceding facts serving as the input.
• Augmented samples, which are created by inserting a different fact into the reasoning order. This simulates a scenario where a different fact was mistakenly retrieved in a previous step, thereby training the retrieval model to recover from the error. The objective is to guide the model back to the correct target for the current stage.

Step 3: Curation via Merging. The final step is to create the unbiased dataset by retaining only the training samples that are consistent across all permutations (Line 12 of Algorithm 1). This is achieved by taking the intersection of the sample sets generated in Step 2. This merging process naturally filters out conflicting training samples, and the resulting curated dataset is agnostic to any specific order.

To make this process concrete, consider the example from Figure 2 where the set of ground-truth facts is $\widehat{F}=\{{\widehat{f}}_{\mathrm{a}},{\widehat{f}}_{\mathrm{b}}\}$. First, the two facts yield $2!=2$ possible reasoning orders: Order 1 ($Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_{\mathrm{a}}\stackrel{\mathrm{P}}{\to }{\widehat{f}}_{\mathrm{b}}$) and Order 2 ($Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_{\mathrm{b}}\stackrel{\mathrm{P}}{\to }{\widehat{f}}_{\mathrm{a}}$). Second, the full set of standard and augmented samples is generated for both the above orders:

$$\begin{array}{cc}\hfill & <\mathrm{Order}1,\left\{\begin{array}{cc}Q\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}\hfill & \left(\mathrm{Standard}\right)\hfill \\ Q+{\widehat{f}}_{\mathrm{a}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}\hfill & \left(\mathrm{Standard}\right)\hfill \\ Q+{\widehat{f}}_{\mathrm{b}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}\hfill & \left(\mathrm{Augmented}\right)\hfill \end{array}\right.>,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & <\mathrm{Order}2,\left\{\begin{array}{cc}Q\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}\hfill & \left(\mathrm{Standard}\right)\hfill \\ Q+{\widehat{f}}_{\mathrm{b}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}\hfill & \left(\mathrm{Standard}\right)\hfill \\ Q+{\widehat{f}}_{\mathrm{a}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}\hfill & \left(\mathrm{Augmented}\right)\hfill \end{array}\right.>.\hfill \end{array}$$

(6)

The samples labeled as (Augmented) are generated by inserting different samples into the original reasoning order. Third, by taking the intersection of the two datasets above, the conflicting first-hop samples ($Q\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}$ and $Q\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}$) are discarded. The final, unbiased training data consists only of the two samples common to both sets: $Q+{\widehat{f}}_{\mathrm{a}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}$ and $Q+{\widehat{f}}_{\mathrm{b}}\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}$. The above process effectively filters out the conflicting first-hop samples (e.g., $Q\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{a}}$ and $Q\stackrel{\mathrm{T}}{\to }{\widehat{f}}_{\mathrm{b}}$), as they are inconsistent across the possible permutations. The resulting curated dataset can prevent the model from developing a bias toward any single, predefined reasoning path. Training on such unbiased data enables the model to more accurately assess the intrinsic difficulty of retrieving each fact.

3.2.2. Training

In Line 13 of Algorithm 1, the model is trained on the merged training data. In the training process, let $Q^{\prime }=Q+{\widehat{f}}_1+\cdots$ (Equation (3)), and let F ($F\subseteq C,F\cap \widehat{F}=⌀,F\cap {\widehat{F}}^{\mathrm{Opt}}=⌀$) represent the negative information set. The training loss is the following.

$$\mathcal{L}=-{\displaystyle \frac{1}{\left|F\right|}}{\displaystyle \sum _{f\in F}}log{\displaystyle \frac{e^{h(Q^{\prime },{\widehat{f}}_{\mathrm{x}})}}{e^{h(Q^{\prime },{\widehat{f}}_{\mathrm{x}})}+e^{h(Q^{\prime },f)}}}.$$

(7)

The function $h(·,·)$ in the equation denotes the dot product of the [CLS] embeddings from the last layer of the two inputs. $Q^{\prime }$ represents the dynamic query context, which is formed by concatenating the original query Q with any facts that have already been identified (${\widehat{f}}_1$, etc.). This updated context provides the model with the accumulated information needed to retrieve the next piece of evidence. Meanwhile, ${\widehat{f}}_{\mathrm{x}}$ is the target fact for the current reasoning step. In the contrastive loss formulation, ${\widehat{f}}_{\mathrm{x}}$ serves as the positive instance that the model must learn to score higher than all other negative facts f from the set F, given the current context $Q^{\prime }$. The [CLS] token is a special input token used by Transformer-based models to capture an aggregate sequence representation. The PTMs used in this paper, specifically RoBERTa and DeBERTa, provide this embedding from their final layer. This resulting vector is then used to compute the similarity score between the two texts.

3.2.3. Prediction

By Line 14 of Algorithm 1, the model has been trained on unbiased data, which suggests that it does not favor any particular order of inference. The predicted order then can be determined by the model’s learned preferences. In the prediction step (see Equation (2)), the model assumes that when the input is $Q^{\prime }=Q+{\widehat{f}}_1+\cdots$, the fact ${\widehat{f}}_{\mathrm{x}}$ is the most easily searchable ground-truth fact, i.e.,

$$\begin{array}{cc}\hfill {\widehat{f}}_{\mathrm{x}}& =\underset{{\widehat{f}}_{\mathrm{i}}\in \widehat{F}}{argmax}\mathrm{IR}(Q,{\widehat{f}}_1,\cdots ;{\widehat{f}}_{\mathrm{i}})\hfill \\ \hfill & =\underset{{\widehat{f}}_{\mathrm{i}}\in \widehat{F}}{argmax}h(Q^{\prime },{\widehat{f}}_{\mathrm{i}}).\hfill \end{array}$$

(8)

Since ${\widehat{f}}_{\mathrm{x}}$ is selected by the model, it indicates that ${\widehat{f}}_{\mathrm{x}}$ should be retrieved now, reflecting the preference for the better reasoning order at this time.

3.3. Retraining Based on Orders

Algorithm 1 automatically optimizes the original reasoning order from $\widehat{F}=\{{\widehat{f}}_{\mathrm{a}},{\widehat{f}}_{\mathrm{b}},\cdots \}$ to ${\widehat{F}}^{\mathrm{Opt}}=\{{\widehat{f}}_1,{\widehat{f}}_2,\cdots \}$. This process yields two orders: naive order and optimized order. To assess the impact of order on performance, the PTM must be retrained using these orders. The data used for retraining includes the training data and the augmentation data. For example, if the order is determined to be Order 1, the retraining data is specified in Equation (5). Therefore, the actual performance of AORO is based on retraining after the order has been established, rather than on the effects during the optimization process.

4. Experiments

This section introduces the datasets used, establishes the baselines for comparison, selects the core PTMs in AORO, and defines the metric for comparing different reasoning orders. Additionally, several methods are designed to imitate the other optimized orders for comparative evaluation. This allows for direct acquisition of a better order in the future without needing to perform the AORO process.

4.1. Datasets

In contrast to the lengthy text of HotpotQA [8] and the single fact from MS MARCO [26], this work focuses on the search order across multiple facts by selecting the multi-fact datasets of shorter texts: QASC and MultiRC.

• QASC [21]: This dataset consists of an 8-choice QA task (https://allenai.org/data/qasc (accessed on 4 January 2024)) with a knowledge base containing 17 million facts. For each question, there are always two ground-truth facts, denoted as $\{{\widehat{f}}_1,{\widehat{f}}_2\}$. Following the evaluation protocol of prior work on this dataset [31,35], performance is primarily measured using Recall@10 (both found and at least one found). This means that in the top ten retrieved facts, the recall is measured for both facts being found as well as for at least one fact being found. The candidate set C on QASC is extracted from the knowledge base using Heuristic+IR [21], resulting in an upper bound for the validation set of 81.8 for Recall@10 at least one found and 61.3 for Recall@10 both found. After training, each sample in the validation set retrieves one fact in the first hop and nine facts in the second hop, resulting in a total of ten facts collected over the two hops.
• MultiRC [30]: This dataset is a multiple-choice QA task, where each sample includes a question, a set of 2 to 14 answer choices, 2 to 4 ground-truth facts for the validation set, 2 to 6 ground-truth facts for the training set, and a corresponding paragraph. The version of MultiRC used in this paper is the original MultiRC (https://cogcomp.seas.upenn.edu/multirc/ (accessed on 4 January 2024)) and not the one included in SuperGLUE [40]. The candidate set, denoted as C, is derived from all the facts within the paragraph. In the training phase, the maximum number of ground-truth facts is six, which also restricts the maximum number of iterations for auto-optimization to six. To ensure a fair comparison with RPA, AORO utilizes the same dynamic hop-stopping method during the MultiRC validation process. Specifically, for each query, the query’s non-stop words that appear in the retrieved facts are removed. Once all applicable words have been removed, the process of hopping stops. Given that the validation set contains a maximum of four facts, the maximum number of hops allowed is also four. Since the number of hops changes dynamically, the F1 score is used as the evaluation metric.

4.2. Baselines

For the iterative retrieval of multiple facts, there are two types: ignoring the order and considering the order, which correspond to no order and optimized order, respectively. The methods discussed in this paper are as follows.

• BM25 [41] (no order): The traditional BM25 retrieval algorithm ranks a set of facts based on query terms that appear within each fact, without considering their proximity.
• AutoROCC [41] (no order): This method introduces an unsupervised strategy for selecting facts. It is an enhanced version of BM25 that aims to (i) maximize the relevance of the selected facts, (ii) minimize the overlap between the selected facts, and (iii) maximize the coverage of both the question and the answer. Based on these principles, which are tailored for multi-hop QA, AutoROCC delivers better search results compared to BM25.
• AIR [31] (no order): This is a straightforward, fast, and unsupervised iterative evidence retrieval method known as AIR (Alignment-based Iterative Retriever). AIR is based on three key concepts: (i) an unsupervised alignment method that soft-aligns questions and answers with facts using embeddings, such as GloVe; (ii) an iterative process that reformulates queries to emphasize terms not addressed by the existing facts; (iii) a stopping criterion that halts retrieval when the terms in the question and candidate answers have been covered by the retrieved facts. Because AIR uses an iterative approach, facts are gathered one at a time, which establishes a specific reasoning order. Although the primary objective of AIR is collection rather than sequence, it can also incorporate a method for reordering research. In this context, one of its alignment methods, GloVe, is discussed in Section 4.6, focusing on training-free techniques.
• RPA [14] (optimized order): Reasoning Path Augmentation (RPA) is a method that adjusts the order of facts based on the number of overlapping words, which is an artificial rule. This method operates under the assumption that the more overlapping terms a fact has with the query, the more relevant it is to that query. By prioritizing these relevant facts, RPA can help reduce complexity and enhance retrieval results. However, it is uncertain whether the artificially determined order is indeed the most effective one. For the sake of comparison, RPA’s order is replicated and tested in the AORO environment.

4.3. PTMs

To explore the relationship between the order obtained through automatic optimization and PTM, AORO employs the following two PTMs in the experiment:

• RoBERTa [37]: RoBERTa has the same model structure as BERT, but it differs in several important ways. RoBERTa utilizes more data, a larger batch size, and a dynamic masking method, all of which enhance its performance on downstream tasks. To compare with RPA, which also optimizes reasoning orders, AORO employs the same RoBERTa model.
• DeBERTa [42]: DeBERTa encodes the content and positional information of words separately and employs disentangled matrices to calculate attention weights. This approach distinguishes it from BERT and RoBERTa. As a result, DeBERTa outperforms both RoBERTa and BERT in various downstream tasks.

The purpose of using RoBERTa is to enable a comparison with the RPA method, while DeBERTa is employed to assess the effectiveness of AORO when applied with different PTMs and to determine whether the order of optimization for various PTMs yields consistent results.

4.4. Training Details

AORO Retriever. The AORO retriever was trained on the QASC and MultiRC datasets, which have candidate set sizes of 80 and an average of 15, respectively. To balance the sampling of negative samples, the value of $\left|F\right|$ in QASC is set at 5, whereas in MultiRC, it is set at 2, as shown in Equation (7). Additionally, since a batch contains multiple samples during training, each sample in QASC includes two facts, while MultiRC can contain a maximum of six facts. This results in a smaller batch size for MultiRC, as illustrated in

Table 1. Configurations of PTMs.

Pretrained Models	RoBERTa-Large	DeBERTa-Large
Parameters (M)	355	405
Batch size (QASC)	32	4
Batch size (MultiRC)	12	2

. Table 1 also highlights that, due to the large number of parameters in DeBERTa, its batch size is relatively small. Base on AORO, the Lamb optimizer [43] is employed in the experiments with the following hyperparameters: a learning rate of 5 × 10⁻⁶ and beta values of (0.9, 0.999) [44]. The framework used is Lightning (https://lightning.ai/ (accessed on 19 May 2024)). The minimum epoch for QASC is set at 100, with a maximum of 500 epochs, where one checkpoint is stored per epoch. For MultiRC, the minimum epoch is 24, and the maximum is also 500, with a checkpoint saved every 1000 steps. An early stopping strategy is in place: if the metrics (Recall@10 both found for QASC and F1 for MultiRC) do not improve after reaching the minimum epoch, Lightning will wait for 30 checkpoints saving before halting the training.

Reader Models. The reader models were finetuned for the multiple-choice question answering task. The training objective was to minimize the cross-entropy loss using the AdamW optimizer with a learning rate of 2 × 10⁻⁵. A linear scheduler with a warm-up phase constituting 10% of the total training steps was used to adjust the learning rate. All experiments were performed on two NVIDIA RTX 3090 Ti GPUs.

4.5. Similarity Metric for Orders

There are two categories of ${\widehat{F}}^{\mathrm{Opt}}$ orders used for training, as detailed below:

• RPA’s optimized order (${\widehat{F}}^{\mathrm{RPA}}$): The reasoning order is optimized by RPA. Since RPA uses RoBERTa, ${\widehat{F}}^{\mathrm{RPA}}={\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{RPA}}$.
• AORO’s optimized order (${\widehat{F}}^{\mathrm{AORO}}$): The reasoning order is optimized by the AORO algorithm. It is further divided into ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$ and ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$, reflecting the differences between the models.

To illustrate the gap between the above categories, a straightforward similarity calculation method (sim) is defined, which constructs the similarity between sentences based on the edit distance (dist):

$$\mathit{sim}({\widehat{F}}^{\mathrm{Order} \mathrm{i}},{\widehat{F}}^{\mathrm{Order} \mathrm{j}})={\displaystyle \frac{N-\mathit{dist}({\widehat{F}}^{\mathrm{Order} \mathrm{i}},{\widehat{F}}^{\mathrm{Order} \mathrm{j}})}{N}}.$$

(9)

For example, $\mathit{sim}(\{{\widehat{f}}_{\mathrm{a}},{\widehat{f}}_{\mathrm{b}}\},\{{\widehat{f}}_{\mathrm{b}},{\widehat{f}}_{\mathrm{a}}\})=(2-2)/2=0\%$; sim(${\widehat{F}}^{\mathrm{RPA}}$,${\widehat{F}}^{\mathrm{AORO}}$) refers to the measure of similarity between the two order categories: RPA and AORO. The term $sim({\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{RPA}},{\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}})$ indicates the similarity between two sequences when utilizing RoBERTa as PTM. In comparison to measuring the exact sameness of each position, similarity based on edit distance more accurately reflects the differences and similarities in order.

4.6. Training-Free Methods

In the previous experiments, AORO needs to be executed to establish a specific order among the facts. This process requires extensive iterative training time, and the final sequence must be run again to evaluate actual inference performance. Therefore, it is essential to employ a training-free method to generate an inference order that closely resembles AORO, allowing for its direct application in search and reducing the iterative training phase of AORO. To achieve this, four types of training-free methods are utilized, TF-IDF Term Frequency-Inverse Document Frequency [45], RPA [14], GloVe of AIR [31], and spaCy (https://spacy.io/ (accessed on 23 May 2024)), to generate the orders. These training-free methods can be categorized into three distinct types: word weight calculation, overlapping words, simple word vectors, and an integrated tool. These methods are discussed further in Section 5.4.

The AORO optimization process, utilizing large PTMs (RoBERTa-Large and DeBERTa-Large), is computationally intensive. For each of the ~9000 training samples in QASC ($N=2$ facts), the process requires one ($N-1$) full fine-tuning round. This expands for MultiRC, which demands up to five ($N-1$) fine-tuning rounds for samples with $N=6$ facts. The complete one-time optimization for both datasets consumed approximately 72 h on a dual NVIDIA RTX 3090 Ti platform. While this represents a significant upfront resource investment, it is a direct trade-off for achieving a superior, model-aware reasoning order. The resulting performance improvements, as demonstrated in the detailed results in the Section 5.4, validate that this resource-intensive approach is crucial for discovering the effective reasoning paths that lead to better results.

5. Experimental Results

5.1. Performance

The effectiveness of AORO’s order optimization is evaluated using a comprehensive set of metrics appropriate for each dataset. For QASC, performance is measured using Recall@10. For the more dynamic MultiRC dataset, a granular analysis using Precision, Recall, and the F1 score is provided to fully characterize retrieval quality. The results, categorized into three settings (AORO with RoBERTa, with DeBERTa, and a hybrid RoBERTa on DeBERTa), demonstrate that AORO consistently outperforms the baseline methods. The detailed analysis is as follows:

• AORO (RoBERTa): When the PTM is RoBERTa, AORO generates ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$, which is then used to train RoBERTa to achieve improved search performance. In the QASC dataset (see

  Table 2. Recall@10 on the QASC dataset. “RoBERTa on DeBERTa” indicates that the PTM RoBERTa utilizes the order achieved through the DeBERTa optimization during training. The others utilize their own PTMs and orders.

  Method	Both Found	At Least One Found
  No order
  BM25 [31]	27.8	65.7
  Heuristics [21]	41.6	64.6
  BERT-LC [21]	41.6	64.4
  AIR (parallel = 5) [31]	44.8	68.6
  SingleRR [35]	44.4	69.6
  Two-step IR [21]	44.4	69.9
  SupA + QA [46]	47.8	-
  Optimized order
  RPA (RoBERTa) [14]	52.7	77.5
  AORO (RoBERTa)	53.1	77.8
  AORO (RoBERTa on DeBERTa)	53.3	78.1
  AORO (DeBERTa)	54.3	78.4

  ), when using the same RoBERTa as the training PTM, AORO outperforms the RPA by 0.4 in the Recall@10 both found metric and shows an improvement of 0.3 in Recall@10 at least one found. On the MultiRC dataset (see

  Table 3. AORO’s performance on MultiRC. “RoBERTa on DeBERTa” indicates that AORO uses the RoBERTa PTM for training with the order derived from DeBERTa. The other models utilize their own PTMs and orders.

  Methods	Hop(s)	Precision	Recall	F1
  No order
  Entire passage [31]	-	17.4	100.0	29.6
  BM25 [41]	Single	43.8	61.2	51.0
  AutoROCC [41]	Single	48.2	68.2	56.4
  RoBERTa-retriever (All passages) [31]	Single	63.4	61.1	62.3
  SingleRR (RoBERTa) [35]	Multiple	-	-	64.0
  AIR top chain [31]	Multiple	66.2	63.1	64.2
  Optimized order
  RPA (RoBERTa) [14]	Multiple	60.2	69.7	64.6
  AORO (RoBERTa)	Multiple	61.1	70.8	65.6
  AORO (RoBERTa on DeBERTa)	Multiple	61.5	71.7	66.2
  AORO (DeBERTa)	Multiple	63.8	73.5	68.3

  ), AORO also exceeds RPA by 1.0 in the F1 metric. This indicates that the proposed AORO provides a more search-friendly reasoning order than RPA. Specifically, ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$ is superior to ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{RPA}}$, confirming that automatic reasoning optimization can achieve a more logical order compared to the manual rules used in RPA. However, it is evident that the improvement observed on QASC is less significant than that on MultiRC, which is analyzed in detail in Section 5.3.
• AORO (DeBERTa): Similar to AORO (RoBERTa), AORO utilizes ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$ to train DeBERTa for the search task. Given that AORO outperforms RPA (RoBERTa) in search performance, DeBERTa further enhances the results of AORO. For instance, on the QASC dataset, as shown in Table 2, DeBERTa achieves a 1.2 improvement in Recall@10 both found over AORO (RoBERTa). Additionally, on the MultiRC dataset, as demonstrated in Table 3, it shows a 3.3 point increase in F1 score. This improvement is not only attributable to the advantages of ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$ compared to ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$ but also to DeBERTa’s superior model architecture and its powerful encoding capabilities in search tasks.
• AORO (RoBERTa on DeBERTa): To further investigate why AORO (DeBERTa) outperforms AORO (RoBERTa), AORO (RoBERTa on DeBERTa) is introduced, which utilizes ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$ to train RoBERTa. In this experiment, the performance of AORO (RoBERTa on DeBERTa) is compared using the same RoBERTa. If AORO (RoBERTa on DeBERTa) surpasses AORO (RoBERTa), it would indicate that ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$ is more effective than ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$ in reasoning tasks. As expected, AORO (RoBERTa on DeBERTa) performs 0.2 better on Recall@10 both found for the QASC dataset (see Table 2) and achieves a 0.6 increase in F1 score for the MultiRC dataset (see Table 3). Although these improvements are modest, they support the observation that ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$ outperforms ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$. This suggests that the stronger the pre-trained model, the more effective its reasoning capabilities become. It also implies that even weaker models can achieve better results when using an effective reasoning order.

To provide a more comprehensive evaluation of the AORO retriever, its performance was evaluated in a standard retriever–reader pipeline when paired with various reader models [47]. In this standard retriever–reader pipeline, the reader is the component responsible for the final answer selection. For each of the eight multiple-choice options in a QASC question, the reader’s input consists of the original question, the retrieved evidence sentences, and the text of that specific answer choice. The reader assigns a score to each choice, indicating the probability of that answer is correct. The AORO retriever is paired with three distinct reader models against corresponding baselines. First, for a fair comparison with the Two-step IR baseline, a bert-large-cased reader was utilized, achieving 76.1% accuracy representing a 2.9% improvement over the baseline’s 73.2%. Second, to align with more recent baselines such as SingleRR and SupA + QA, a RoBERTa-base reader was employed. This pairing reached 76.01% accuracy, surpassing the 73.9% baseline by 2.11%. Finally, to establish state-of-the-art performance, the AORO retriever was combined with a powerful DeBERTa-large reader, attaining 80.3% accuracy and outperforming the other baselines. These results demonstrate both the standalone improvement of the AORO retriever against comparable baselines and its maximum potential when paired with a powerful reader model.

5.2. Quantitative Analysis of $sim$

To further investigate the impact of reasoning order on search performance, some reasoning orders are randomized to create Order x. The similarity is then calculated ${\widehat{F}}^{\mathrm{Order} \mathrm{x}}$ and ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$, denoted as $sim({\widehat{F}}^{\mathrm{Order} \mathrm{x}},{\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}})$. The similarity value ranges from 0 to 100, with increments of 10. When using RoBERTa as PTM, the training results for QASC are illustrated in Figure 3.

In the figure, as $sim$ increases, Recall@10 both found shows an overall upward trend. When $sim$ is at 70, there is a brief drop in Recall, which then continues to rise. Surprisingly, Recall reaches 53.4 when $sim$ is at 90, exceeding the 53.1 observed when $sim$ is at 100. This phenomenon, where some results exceed those obtained with a $sim$ value of 100, also occurs in the quantitative experiments with DeBERTa’s $sim$. This suggests that there exists a better order of reasoning than ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$. These observations align with the last hypothesis regarding weaker models and their effective ordering discussed in Section 5.1. For a more detailed analysis of the relationship between $sim$ and results, please refer to Section 5.3.

5.3. Qualitative Analysis

Figure 4a,b illustrates the $sim$ between orders in the QASC and MultiRC datasets, respectively. The figures are examined from three perspectives: the absolute magnitude of $sim$, the reasons behind the differences in $sim$, and the implications of these differences. The details are presented below:

The greater the $sim({\widehat{F}}^{\mathrm{Order} \mathrm{x}},{\widehat{F}}^{\mathrm{Excellent}})$, the better the performance. The reasoning order that has achieved the highest result achieved so far is ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$, which is referred to as ${\widehat{F}}^{\mathrm{Excellent}}\mathrm{order}$ in this paper. Therefore, the larger the $sim({\widehat{F}}^{\mathrm{Order} \mathrm{x}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})$, the higher the metric value. Specifically, Figure 4 shows that $sim({\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})>sim({\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})>sim({\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{RPA}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})$. This order corresponds to the Recall values in Table 2, indicating that AORO (DeBERTa) > AORO (RoBERTa) > RPA (RoBERTa). A similar pattern is observed for F1 in Table 3. Additionally, since $sim({\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})>sim({\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})$, it can be concluded that AORO (RoBERTa on DeBERTa) > AORO (RoBERTa), as shown in Table 2 on QASC.

The greater the number of facts, the larger the $sim$ difference. In the QASC datasets, there are always two facts, whereas in MultiRC, there can be up to six facts in the training set. As discussed in the permutation paragraph of Section 3.2.1, QASC has $2!$ (which equals to 2) possible orderings, while MultiRC has $6!$ (which equals to 720) possible orderings. More possible orderings lead to a lower probability that the orders will be identical, resulting in a greater similarity difference. This is reflected in Figure 4a, where the $sim$ generally shows little difference, while in Figure 4b, the $sim$ difference is more pronounced.

The greater the $sim$ difference, the wider the variation in performance. As shown in Figure 4a (QASC), the $sim$ values are generally greater than 80, resulting in comparable Recall@10 scores. This means that Recall@10 is quite similar for RPA (RoBERTa), AORO (RoBERTa), and AORO (RoBERTa on DeBERTa), as seen in Table 2. The most significant improvement is observed with AORO (DeBERTa), where Recall increases by 1.0. However, in the case of MultiRC (Table 3), the maximum $sim$ between the optimization orders is $sim({\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})=76.4$ (Figure 4b). Here, the F1 score of AORO (DeBERTa) increases by 1.9 compared to AORO (RoBERTa on DeBERTa), indicating a more substantial improvement.

5.4. Regularities in Reasoning Orders

There is a notable empirical pattern in AORO: the similarity value $sim({\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})$ is consistently large both in QASC (89.7) and MultiRC (74.6), as depicted in Figure 4. After the trained retrieval model automatically selects the reasoning order by itself (AORO), the orders generated by the two PTMs with different structures consistently exhibit higher similarities. This observation suggests that, within the conducted experiments, the preferred reasoning order could be relatively insensitive to the choice of PTM. Moreover, high $sim$ values are observed across datasets, indicating thatthe preferred order may also be robust to dataset variation. This consistency can be referred to as regularities in reasoning orders.

In this section, training-free methods are employed to generate reasoning orders and calculate their similarities with ${\widehat{F}}^{\mathrm{Excellent}}$ (as referenced by ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$) to explore the relevant factors underlying these empirical regularities. The four training-free methods include TF-IDF, RPA, GloVe, and spaCy, which can be categorized into two groups:

• TF-IDF, RPA, GloVe: First, Q and $\widehat{f}$s are processed in three steps: (i) they are split using the word_tokenize from NLTK (Natural Language ToolKit) as tokenizer, (ii) stop words are removed, and (iii) stems are extracted using the Porter Stemmer. This results in lists of words that are used for similarity calculations. The ranking process involves the following steps: (i) identifying the fact ${\widehat{f}}_i$ that has the highest sentence similarity with Q, (ii) removing overlapping words between Q and ${\widehat{f}}_i$, and (iii) using the remaining words as a new Q to compute similarity with the remaining $\widehat{f}$s. This ranking process continues iteratively until no $\widehat{f}$s remain.
• spaCy: When using spaCy’s similarity method, it is important to note that once the sentence is split into individual words, spaCy cannot compute inter-sentence similarity. As a result, the new Q is created by combining the old Q and the retrieved $\widehat{f}$.

The TF-IDF score for the i-th fact in $\widehat{F}$ is calculated as follows:

$${\mathrm{TF}-\mathrm{IDF}}_i={\displaystyle \sum _{word\in Q}}\mathrm{TF}(word,{\widehat{f}}_i)\times {\mathrm{IDF}}_{word}$$

(10)

Here, TF refers to the Term Frequency of $word$ in ${\widehat{f}}_i$, and ${\mathrm{IDF}}_{word}$ is the standard Inverse Document Frequency, which remains constant despite the reconfiguration of Q. Thus, a higher TF-IDF value for $\widehat{f}$ indicates that it contains more important words that are present in Q, leading to a higher ranking. Additionally, the dependence on GloVe to calculate scores in AIR is illustrated in Figure 5.

Specifically, the cosine similarity matrix is computed based on the word vectors from GloVe, and the final Query-IDF ${\mathrm{IDF}}_{word}^{\mathrm{GloVe}}$ is a modified version of ${\mathrm{IDF}}_{word}$, defined as follows:

$${\mathrm{IDF}}_{word}^{\mathrm{GloVe}}=log{\displaystyle \frac{|Q+\widehat{F}|-|word\in Q,\widehat{F}|+0.5}{|word\in Q,\widehat{F}|+0.5}}.$$

(11)

In this equation, $|Q+\widehat{F}|$ denotes the total number of texts of Q and $\widehat{F}$, and $word\in Q,\widehat{F}$ refers to the texts containing the specified $word$.

After determining the reasoning order using a training-free method, $sim({\widehat{F}}^{\mathrm{Training}-\mathrm{free}},$ ${\widehat{F}}^{\mathrm{Excellent}})$ is calculated, followed by using DeBERTa to evaluate the performance based on ${\widehat{F}}^{\mathrm{Training}-\mathrm{free}}$. The results are presented in

Table 4. $sim({\widehat{F}}^{\mathrm{Training}-\mathrm{free}},{\widehat{F}}^{\mathrm{Excellent}})$ and the critical metrics for training with DeBERTa.

Training-Free Method	QASC $\mathit{sim}$/Recall@10 Both Found	MultiRC $\mathit{sim}$/F1
AORO (DeBERTa)	100/54.3	100/68.3
TF-IDF	82.2/52.0 (↓2.3)	67.2/64.5 (↓3.8)
RPA	83.1/52.7 (↓1.6)	67.1/64.6 (↓3.7)
GloVe	78.0/51.6 (↓2.7)	65.7/64.3 (↓4.0)
spaCy	74.1/51.7 (↓2.6)	59.7/63.5 (↓4.8)

.

In Table 4, the least reduction in ${\widehat{F}}^{\mathrm{Excellent}}$ is achieved by RPA, with $sim$s of 83.1 and 67.1 on QASC and MultiRC, respectively, followed by TF-IDF. In contrast, GloVe and spaCy demonstrate relatively poorer performance. Although zero reduction of ${\widehat{F}}^{\mathrm{Excellent}}$ was not achieved, it appears that lexicon-level statistical methods currently yield better order-optimization results than word vectors. Therefore, it is not yet feasible to fully replace the automatic optimization process of AORO with a training-free approach. Further exploration of the regularities in reasoning orders is still necessary.

5.5. Case Studies

This section analyzes cases from the QASC and MultiRC datasets to evaluate the results of reasoning-order optimization, as presented in

Table 5. Analysis of QASC and MultiRC cases. Possible reasoning connections between search sources and targets are included.

QASC	Q with 2 Ground-Truth Facts
Q	Query: What are invaluable for soil health? Choice: annelids.
${\widehat{f}}_1$	Fact: Annelids are worms such as the familiar earthworm.
${\widehat{f}}_2$	Fact: Earthworms are invaluable for soil health.
	${\widehat{F}}^{\mathrm{AORO}}$ ($?\stackrel{\mathrm{Reasoning}\mathrm{connection}}{\to }?$)
${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$	$$\begin{gathered} Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1(Q\stackrel{\mathrm{What}\mathrm{are}“\mathrm{invaluable}\mathrm{for}\mathrm{soil}\mathrm{health}?”“\mathrm{Earthworms}.”}{\to }{\widehat{f}}_2,Q+ \\ {\widehat{f}}_2\stackrel{\mathrm{Are}“\mathrm{earthworms}”\mathrm{related}\mathrm{to}“\mathrm{annelids}?”}{\to }{\widehat{f}}_1) \end{gathered}$$
${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)
	${\widehat{F}}^{\mathrm{Training}-\mathrm{free}}$
TF-IDF	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)
RPA	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)
GloVe	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)
spaCy	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)
MultiRC	$\mathit{Q}$ with 4 Ground-Truth Facts
Q	Query: Why did the writer think he was going crazy? Choice: He heard a sound and saw a light in a vacuum.
${\widehat{f}}_1$	Fact: Hotel California My first thought: I was going crazy.
${\widehat{f}}_2$	Fact: Twenty-four hours of silence (vacuum, remember); was I hallucinating noises now?
${\widehat{f}}_3$	Fact: It was a fine bell, reminiscent of ancient stone churches and the towering cathedrals I’d seen in documentaries.
${\widehat{f}}_4$	Fact: And accompanying the bell, I saw a light.
	${\widehat{F}}^{\mathrm{AORO}}$ ($?\stackrel{\mathrm{Reasoning}\mathrm{connection}}{\to }?$)
${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$	$$\begin{gathered} Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3(Q\stackrel{\mathrm{Did}\mathrm{he}“\mathrm{think}”\mathrm{he}\mathrm{is}“\mathrm{going}\mathrm{crazy}”?\mathrm{Yes}.}{\to } \\ {\widehat{f}}_1,Q\stackrel{\mathrm{Did}\mathrm{he}“\mathrm{see}\mathrm{a}\mathrm{light}?”\mathrm{Yes}.}{\to }{\widehat{f}}_4,Q\stackrel{\mathrm{Why}“\mathrm{thought}”“\mathrm{crazy}?”“\mathrm{Hallucinating}\mathrm{noises}.”}{\to } \\ {\widehat{f}}_2,Q+{\widehat{f}}_4\stackrel{\mathrm{Are}“\mathrm{sounds}”\mathrm{or}“\mathrm{noises}“\mathrm{related}\mathrm{to}“\mathrm{bell}?”}{\to }{\widehat{f}}_3) \end{gathered}$$
${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)
	${\widehat{F}}^{\mathrm{Training}-\mathrm{free}}$/For samples whose $|\widehat{F}|\ge 4$, $sim({\widehat{F}}^{\mathrm{Training}-\mathrm{free}},{\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}})$
TF-IDF	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)/50.0
RPA	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3$ (same with ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$)/51.2
GloVe	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$/45.5
spaCy	$Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2$/42.4

.

In the QASC case, the naive reasoning order is $\widehat{F}=Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2$. After optimization, all methods adopt the new order $Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$, aligning with the observation that all similarity scores on QASC are greater than 80. However, as noted in Section 5.3, when $|\widehat{F}|$ is small, the differences in $sim$ scores are minimal. The consistently high similarity scores and uniform orders obscure the analysis of the strengths and weaknesses of the different methods. To illustrate the variations more effectively, the subsequent analysis focuses on a MultiRC sample with $|\widehat{F}|\ge 4$, which includes the query Q and its four corresponding ground-truth facts.

In the MultiRC sample, both ${\widehat{F}}_{\mathrm{RoBERTa}}^{\mathrm{AORO}}$ and ${\widehat{F}}_{\mathrm{DeBERTa}}^{\mathrm{AORO}}$ follow the order $Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3$, while the training-free methods, TF-IDF and RPA, also produce the same order ($sim=100$). In contrast, GloVe and spaCy produce entirely different orders, resulting in similarity scores of 0. The notable discrepancies in similarity appear to stem from the specific sample. Indeed, when analyzing all samples with $|\widehat{F}|\ge 4$, it is observed that as the number of reasoning steps increases, the similarities for TF-IDF (50.0) and RPA (51.2) significantly surpass those of GloVe (45.5) and spaCy (42.4). This suggests that the training-free methods TF-IDF and RPA are more effective in optimizing the inference order for long sequences.

In terms of content, the MultiRC sample demonstrates that AORO (DeBERTa) initiates each reasoning process from Q and systematically analyzes and verifies each detail within it, addressing Q and ultimately clarifying the relationships among these details. The reasoning steps undertaken by AORO are as follows:

• Confirm the query going crazy ($Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_1$).
• Validate the choice see a light ($Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_4$).
• Investigates the cause of crazy, identifying it as hallucinating noises ($Q\stackrel{\mathrm{P}}{\to }{\widehat{f}}_2$).
• Combines Q and ${\widehat{f}}_4$ to establish the relationship that sound comes from bell ($Q+{\widehat{f}}_4\stackrel{\mathrm{P}}{\to }{\widehat{f}}_3$).

This sequence aligns with a logical thinking order: first confirming the query, then answering the question, and finally providing additional details. Looking back at the QASC sample, it can be observed that AORO (DeBERTa) follows a similar approach: it initially seeks the conceptual definition of the query (clarifying what it is) before supplementing the remaining content.

6. Conclusions

This paper introduces AORO, a method designed to automatically optimize the reasoning order for multi-hop QA. AORO operates by iteratively selecting the most appropriate target at each inference step, constructing an optimized reasoning order for each sample. Its performance is validated on the QASC and MultiRC datasets. The results demonstrate that the method improves upon strong baselines with the same PTM, while the synergy with advanced PTMs yields further gains of up to 1.6 points in Recall@10 and 3.7 points in F1 score. Additionally, the conducted experiments reveal that the optimized reasoning orders generated by AORO, based on various pre-trained models, exhibit a high degree of similarity across datasets. This suggests that the reasoning process may follow a stable, model- and dataset-agnostic principle. While the implementation of training-free methods to approximate the optimized order still requires improvement, a consistent reasoning pattern is observed: verifying the authenticity of the question content, answering the question, and providing supplementary details. Future work will aim to utilize more advanced models to achieve even better reasoning orders and to develop more effective training-free methods for approximating these orders. Future work will also seek to explore the fundamental factors that determine the optimal reasoning order.