A Hybrid Strategy for Achieving Robust Matching Inside the Binocular Vision of a Humanoid Robot

Abstract

Binocular vision is a core module in humanoid robots, and stereo matching is one of the key challenges in binocular vision, relying on template matching techniques and mathematical optimization methods to achieve precise image matching. However, occlusion significantly affects matching accuracy and robustness in practical applications. To address this issue, we propose a novel hybrid matching strategy. This method does not require network training and has high computational efficiency, effectively addressing occlusion issues. First, we propose the Inverse Template Matching Mathematical Method (ITM), which is based on optimization theory. This method generates multiple new templates from the image to be matched using mathematical segmentation techniques and then matches them with the original template through an inverse optimization process, thereby effectively improving matching accuracy under mild occlusion conditions. Second, we propose the Iterative Matching Mathematical Method (IMM), which repeatedly executes ITM combined with optimization strategies to continuously refine the size of matching templates, thereby further improving matching accuracy under complex occlusion conditions. Concurrently, we adopt a local region selection strategy to selectively target areas related to occlusion regions for inverse optimization matching, significantly enhancing matching efficiency. Experimental results show that under severe occlusion conditions, the proposed method achieves a 93% improvement in accuracy compared to traditional template matching methods and a 37% improvement compared to methods based on convolutional neural networks (CNNs), reaching the current state of the art in the field. Our method introduces a reverse optimization paradigm into the field of template matching and provides an innovative mathematical solution to address occlusion issues.

1. Introduction

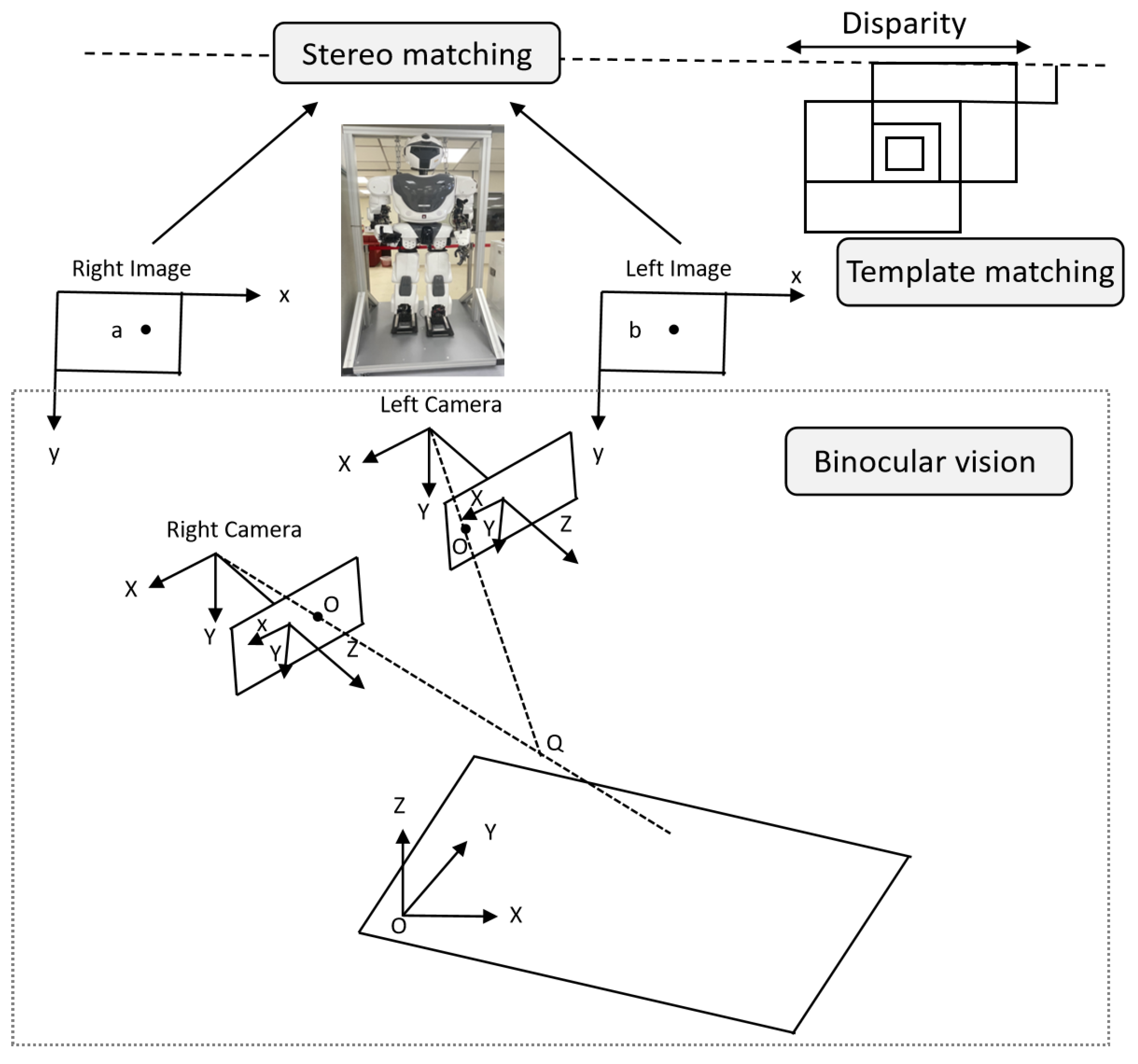
In the binocular vision system of humanoid robots, template matching is a key task for achieving stereoscopic matching, as shown in Figure 1. Template matching uses mathematical optimization methods to find the region in the target image that is most similar to the template image. Given a template image T and a target image I, the goal of template matching is to use mathematical optimization techniques to find the best match between the template image T and the target image I by calculating a similarity metric function at each candidate window position in the target image I. This process typically involves three basic steps: first, a search strategy is used to divide the target image I into candidate windows $W_{ij}$ of the same size as the template image T, with the center of each candidate window $W_{ij}$ located at $(i,j)$ in the target image I; second, feature vectors are extracted from the template image T and the candidate windows $W_{ij}$; and finally, the similarity between the template image T and the candidate window $W_{ij}$ features is calculated, with the window having the highest similarity value identified as the matched region. Template matching plays a crucial role in various fields, including object detection [1,2], object tracking [3], face recognition [4], feature extraction [5], and robotics applications [6].

Traditional template matching methods, such as Sum of Squared Distance (SSD), Sum of Absolute Distance (SAD), and Normalized Cross-Correlation (NCC) [7,8], perform very effectively in most scenarios. However, when encountering complex situations, such as occlusion or scale changes, the performance of these methods is often limited, and they are unable to maintain good matching accuracy.

Specifically, the SSD measures similarity by minimizing the sum of squared differences between pixels in the template T and candidate windows $W_{ij}$ using the following equation:

$$SSD(T,W_{i,j})=\sum _{p=1}^M\sum _{q=1}^N{\left(T(p,q)-W_{i,j}(p,q)\right)}^2.$$

(1)

The SAD measures similarity by minimizing the sum of the absolute values of the pixel differences between the template T and the candidate window $W_{ij}$. The equation is as follows:

$$SAD(T,W_{i,j})=\sum _{p=1}^M\sum _{q=1}^N\left|T(p,q)-W_{i,j}(p,q)\right|.$$

(2)

The NCC calculates the correlation between the template T and the candidate window $W_{ij}$ to measure their similarity. It is often used to process brightness changes in images. NCC is a standard similarity measure that calculates the correlation between two image patches while remaining invariant to linear illumination changes. The equation is as follows:

$$NCC(T,W_{i,j})={\displaystyle \frac{{\sum }_{p=1}^M{\sum }_{q=1}^N\left(T(p,q)-\overline{T}\right)\left(W_{i,j}(p,q)-{\overline{W}}_{i,j}\right)}{\sqrt{{\sum }_{p=1}^M{\sum }_{q=1}^N{\left(T(p,q)-\overline{T}\right)}^2{\sum }_{p=1}^M{\sum }_{q=1}^N{\left(W_{i,j}(p,q)-{\overline{W}}_{i,j}\right)}^2}}},$$

(3)

where $\overline{T}$ and ${\overline{W}}_{i,j}$ are the means of the template and candidate windows, respectively.

Traditional mathematical methods are unable to effectively handle occlusions, scale transformations, and other non-rigid transformations when calculating correlations, resulting in a significant decrease in matching accuracy. To address these issues, methods based on nearest neighbor (NNF) have been proposed [9,10] and have been proven to achieve good results in complex situations, becoming the state-of-the-art technology in this field. NNF provides a general mathematical framework for image matching, enhancing its robustness in handling non-rigid transformations, occlusion, and background noise by focusing on matching subsets between the template and query subwindows [11,12]. Based on this, NNN-based template matching methods improve matching accuracy by matching template point sets and query point sets and defining similarity metrics based on matching statistics. However, NNN-based methods may still face issues with reduced matching accuracy when handling extreme scenarios, especially large-scale occlusions and extremely complex backgrounds, and their high computational complexity limits their widespread adoption in real-time applications.

Deep learning-based template matching methods have made significant progress in recent years, particularly in addressing object detection and tracking problems in complex scenes. Unlike traditional template matching methods, deep learning approaches utilize convolutional neural networks (CNNs) [13] or Siamese networks [14] to automatically learn feature representations in images, thereby enabling efficient matching. Among these methods, CNNs learn both local and global features through multiple layers of convolutional operations, enabling precise matching in more complex and dynamic environments. Siamese networks, on the other hand, perform template matching by comparing the similarity between two input images, demonstrating strong robustness. Specifically, the CNN model minimizes the difference between the template image T and the target window $W_{i,j}$ by optimizing the objective function $L={\sum }_{i=1}^N\mathcal{L}(f\left(T_i\right),f\left(W_i\right))$, where $f(·)$ represents the feature map extracted by the CNN network and $\mathcal{L}$ is the loss function, typically cross-entropy or mean squared error. By optimizing these loss functions, CNNs can effectively adjust the feature map to improve matching accuracy. However, deep learning-based template matching methods still face challenges in practical applications, particularly in terms of their reliance on large amounts of labeled data and computational resources. Deep learning models [15] typically require a large amount of labeled data for training, which is particularly challenging in real-world applications where target features are highly variable or images are complex.

Occlusion is a major challenge in computer vision, and solving the template matching problem is crucial for advancing binocular stereovision matching and 3D reconstruction, while also improving the accuracy of mathematical models in depth perception and spatial localization. Therefore, this paper proposes a robust template matching method for achieving cognitive stereovision. For mild occlusion problems, we proposed the ITM mathematical method, which generates new templates by mathematically segmenting the target image and performs inverse matching between these new templates and the original templates. This process effectively improves matching accuracy by reducing the size of the matching region. For severe occlusion problems, we proposed the IMM mathematical method, which performs ITM multiple times to generate new templates of different sizes and performs inverse matching, thereby enhancing the robustness of the matching. In this process, we introduced a local region selection strategy to optimize the selection of relevant regions and reduce the computational complexity of the matching process. Experimental results show that our method achieves state-of-the-art performance in current research and effectively addresses template matching problems in complex occlusion environments.

The main contributions of this paper are as follows:

• We propose an Inverse Template Matching Mathematical Method (ITM), an image processing method based on mathematical segmentation, which divides the input image into multiple sub-images. This method can effectively improve the accuracy of template matching by reducing errors caused by occlusion.
• We propose an Iterative Matching Mathematical Method (IMM), an optimization method based on an iterative process that gradually optimizes matching results by repeatedly executing ITM and dynamically adjusting template sizes. Through repeated iterations, IMM can adjust templates during each matching process to optimize matching accuracy in complex occlusion scenarios.
• We propose a local region selection strategy that employs mathematical techniques, such as accuracy measurement and threshold setting, to identify the optimal matching region from all sub-images. This strategy reduces redundant computations and significantly improves matching efficiency.
• Compared to the traditional template matching method, our method improves the average accuracy by 93% in the case of severe occlusion. When compared to neural network-based matching methods, our method achieves a 37% improvement in average accuracy under the same conditions, reaching state-of-the-art performance.

2. Related Work

2.1. Traditional Template Matching

Traditional template matching methods are usually categorized into pixel-based matching methods and feature-based matching methods. Pixel-based matching methods determine the matching location by calculating the similarity between the image region and the template. Feature-based template matching methods rely on salient features extracted from the image for matching.

The pixel-based template matching method [16] is one of the most traditional and widely used techniques in the field of image matching. Common similarity measures include SSD, SAD, and NCC [17]. Recently, a new fast and robust template matching method was proposed in [18], which combines the Most Neighbor Similarity (MNS) and Annular Projection Transformation (APT). By adopting a coarse-to-fine matching strategy and MNS measurement, this method avoids the traditional sliding window scan, enabling efficient matching and also estimating the rotation angle of the target object. It effectively addresses challenges such as background noise and occlusion. A new RGB-T Siamese tracker was proposed in [19], which enhances the recognition ability of background distractors and ensures real-time performance by introducing a target enhancement module, a multi-modal feature fusion module based on intra- and inter-modality attention, and a hard-focus online classifier. In [20], a novel coarse-to-fine pattern parsing network based on Capsule Networks was introduced to mitigate the issue of severe pixel imbalance in pattern parsing tasks. A new Adaptive Radial Ring Code Histogram image descriptor was proposed in [21], which uses radial gradient codes as rotation-invariant features and can solve template matching under both scale and rotation transformations of images.

Feature-based matching methods have better robustness by extracting key feature points (e.g., corner points, edges, and textures) in the image, and common methods include Scale-Invariant Feature Transform (SIFT) [22], Speeded-Up Robust Features (SURF) [23], and Oriented FAST and Rotated BRIEF (ORB) [24]. The SIFT method maintains a better matching effect under different scales and rotations by extracting scale-invariant keypoints and descriptors. The ORB method combines FAST corner detection and BRIEF descriptors, which improves the computational efficiency and maintains a high matching accuracy. In order to achieve robust template matching at multiple scales, a new rotation-invariant template matching method is proposed in [25], which realizes multi-scale search and partially occluded robust template matching by using the complex coefficients of the discrete Fourier transform of the radial projection for extracting the local features and using the Hough transform and the features of the stabilized sub-templates for fast matching. When SIFT is used for remote sensing image alignment, image intensity differences lead to a large number of keypoints mismatched. For this reason, the study by [26] proposed a joint scale-orientation restriction criterion and an improved feature descriptor, which significantly improved the matching performance of multi-date, multi-spectral, and multi-sensor remote sensing images, as well as increasing the correct matching rate and alignment accuracy compared with the traditional methods. Feature-based methods are widely used in the fields of autonomous driving, robot vision, and image retrieval, and they perform well in dealing with target recognition and localization in dynamic environments.

Traditional pixel matching methods perform well in simple scenes but are prone to mismatching and accuracy degradation when confronted with real-world scenarios, such as image noise, scale variations, rotation and occlusion. In addition, these methods ignore the higher-order semantic information in images, which limits their application in complex scenes.

2.2. Deep Learning-Based Template Matching

In recent years, deep learning techniques have been gradually applied to the template matching problem, especially methods such as CNNs [27] and Siamese networks [28], which address some of the limitations in the traditional methods by learning the feature representations of images. In order to overcome the influence of complex scenes on the results in template matching methods, in [29], a visible and infrared image matching network based on the structure of a Siamese network is proposed, which extracts feature maps from the input image through a residual network with an attentional mechanism and fuses these feature maps for classification and regression to achieve image matching with excellent mean-averaged accuracy. In [30], an efficient high-resolution template matching method is proposed to improve the matching accuracy and computational efficiency by using vector quantized nearest neighbor fields. The method can effectively handle large-scale datasets and reduce the computational complexity while maintaining the matching quality. In [31], a novel adaptive edge deletion network is proposed for subgraph matching, which improves the matching accuracy and speed by introducing an adaptive edge deletion mechanism to remove redundant edges in order to maintain the consistency of the neighboring structure of the matching nodes, and at the same time ensures the consistency of the features of the matching nodes by using a one-way cross-propagation mechanism.

Although deep learning methods have made some progress in improving robustness, they still face challenges in terms of computational complexity and real-time performance, especially on resource-constrained devices. Although researchers have proposed various optimization strategies, such as model compression and hardware acceleration [32,33], how to optimize computational efficiency while improving robustness remains a key issue in current research.

2.3. Similarity Metrics in Template Matching

The similarity measure between the template and the sub-window of the target image is the core part of template matching. Commonly used methods are pixel-level, such as NCC [34]. The basic idea of normalized cross-correlation is to compare the template with each part of the image on a pixel-by-pixel basis and compute their correlation. The formula for calculating normalized cross-correlation is usually as follows:

Although NCC can provide an effective similarity measure in many contexts, the method usually only satisfies a necessary condition for similarity, not a sufficient condition. NCC does not adequately account for complex image variations, such as occlusion, lighting changes, or deformation. Therefore, in complex scenes, these methods often do not cope well with occlusion and deformation situations.

To improve the robustness of template matching in the case of occlusion, many researchers have proposed different methods to find the similarity between a given template and the input image. For instance, the work reported in [35] proposes the use of Best-Buddies Similarity (BBS) as a method to find the similarity in place of the widely used Normalized Cross-Correlation or the Sum-of-Squared-Distances method. Since BBS only makes use of a subset of points of the nearest neighbor matches and compares the features of the input and the template image, it only detects the relevant features. It proves to be partially effective in the case of occluded images. Further extending the approach of BBS, the author in [36] introduces another novel feature-based and parameter-free similarity index named Deformable Diversity Similarity to find the similarity. Moreover, the work listed in [37] makes use of Sum of Absolute Differences as a method to find the similarity. This makes template matching capable of partially handling occlusions and enables the algorithm to manage transformations on the input images.

Although existing similarity methods have achieved good results in many cases, they still face many challenges when dealing with complex scenes, such as occlusion, distortion, and lighting changes. Therefore, exploring and selecting appropriate similarity methods is always a key and challenging difficulty in template matching.

2.4. Positioning of the Proposed Method

The proposed ITM and IMM methods share a high-level goal with patch-based and correspondence-based methods like BBS and Deformable Diversity Similarity [36]: to achieve robust template matching under challenging conditions like occlusion. However, a fundamental philosophical and methodological distinction exists, which forms the core novelty of our work.

Methods like BBS and Deformable Diversity Similarity operate within an enhanced forward matching paradigm. They take the original template T and search for mutual or “best-buddy” correspondences within the input image I. Their primary innovation lies in defining a robust similarity measure that is resistant to outliers caused by occlusion. Nevertheless, the fundamental process remains centered on comparing the template T to regions within I, maintaining the traditional roles where T is the active searcher and I is the passive target.

In contrast, our ITM/IMM method introduces a genuine inverse matching paradigm. The core innovation is the systematic role reversal between the template and the search image. Instead of deconstructing the template or designing a robust global metric, we systematically deconstruct the input image I into a set of sub-templates $\{I_1,I_2,\dots ,I_z\}$. The matching process is fundamentally reversed: we evaluate how well each of these sub-templates, representing potential unoccluded parts of the scene, matches the original, intact template T. In this framework, T serves as the immutable reference model, and the algorithm’s task is to identify which segments of the cluttered scene I best instantiate this model. This approach naturally prioritizes any visible, matchable part of the object without being inherently biased by occluded portions of the template itself.

Furthermore, the iterative process in IMM is distinct. It is not merely about refining correspondence matches or features but about systematically and recursively reducing the scale of the search space itself. Each iteration generates smaller, more focused sub-templates from promising regions, allowing the matching to converge on an optimal, occlusion-free match at a finer granularity. This represents a unique application of iterative optimization to the specific inverse matching problem we define, differing from the traditional coarse-to-fine search in image pyramids or feature spaces.

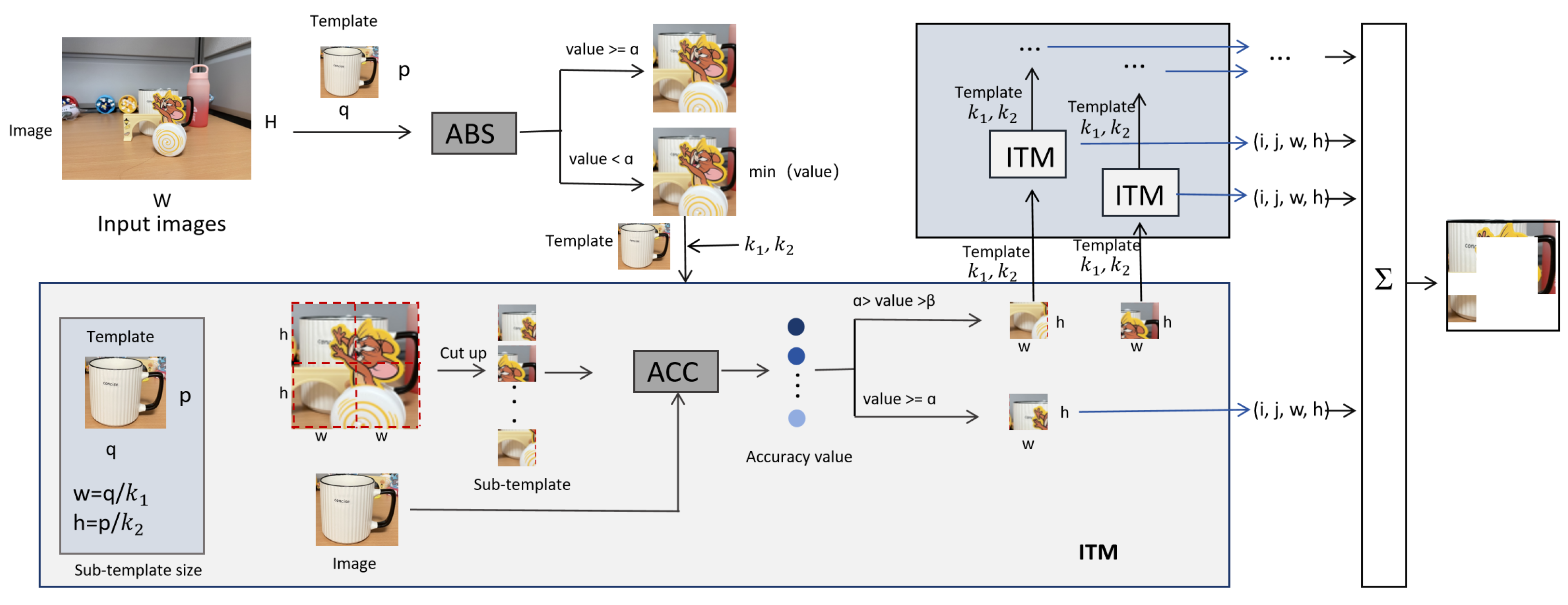
3. Method

In this section, we provide a detailed introduction to the core content of our proposed strategy, i.e., “A Hybrid Strategy for Achieving Robust Matching Inside the Binocular Vision of a Humanoid Robot”. This method proposes two mathematical methods, ITM and IMM, to solve the occlusion problem in template matching. First, in Section 3.1, we introduced the Forward Template Matching (FTM). Then, in Section 3.2, we introduced a detailed description of the ITM method, which segmented the original input image into multiple sub-templates for inverse matching against the initial template. However, when the occlusion problem was more complex, a single inverse match could not fully handle the detail areas. To address this, in Section 3.3, we proposed the IMM method, which overcame the limitations of single matching by iterating ITM multiple times and adjusting the template size, significantly improving matching accuracy. Finally, in Section 3.4, we introduced a local region selection strategy, utilizing the optimal local region from the forward matching as the input image for inverse matching, further optimizing matching efficiency and accuracy, with particularly significant results in complex occlusion scenarios. The overall flowchart is shown in Figure 2.

3.1. Forward Template Matching (FTM)

Template matching algorithms are used to identify and locate images by searching for the region in the target image I that most closely matches the template image T. Given an input image I and a template image T, with pixel values $I(i,j)$ and $T(m,n)$, respectively, the objective of forward template matching is to find the best matching position between I and T. The template is slid over each position in the target image $I(i,j)$, forming sub-images $W_{ij}$ in the target image I, and the similarity or dissimilarity between the current template T and the sub-images $W_{ij}$ of the target image I is calculated to determine the best matching position.

Specifically, the optimization objective of FTM can be expressed as follows:

$$(i^{*},j^{*})=arg\underset{i,j}{max}\mathrm{NCC}(W_{ij},T),$$

(4)

where NCC($W_{ij},T$) represents the normalized cross-correlation between the template T and the sub-image $W_{ij}$ at position $(i,j)$. This measures the similarity between the template and the sub-image, and the location that maximizes this value is selected as the best match.

Additionally, we can express the matching problem as an optimization of the mean squared error (MSE) between the template and sub-image:

$$E=\sum _{i,j}{|W_{ij}(i,j)-T(i,j)|}^2,$$

(5)

where E is the matching error, and minimizing this error leads to the optimal alignment of the template with the image.

3.2. Inverse Template Matching Mathematical Method (ITM)

We propose an inverse matching mathematical method to solve the template matching problem in cases of slight occlusion. In ITM, the input image i is divided into multiple sub-images that act as candidate templates, while the original template T is treated as the query image to be matched. This reverse formulation enables the algorithm to capture fine-grained structural correspondences and to remain robust under partial occlusion.

Let the input image be

$$I:{\Omega }_I\subset {\mathbb{Z}}^2\to \mathbb{R},{\Omega }_I=\{1,\dots ,p\}\times \{1,\dots ,q\},$$

(6)

where p and q represent the width and height of the image, respectively, and the co-domain is typically the intensity range $[0,255]$ for grayscale images.

Moreover, let the original template be

$$T:{\Omega }_T\subset {\mathbb{Z}}^2\to \mathbb{R},{\Omega }_T=\{1,\dots ,w\}\times \{1,\dots ,h\},$$

(7)

where w and h denote the template dimensions.

The input image I is systematically partitioned into z rectangular sub-images (also called candidate templates) $I_z$, each having smaller dimensions than T. Formally, the z-th sub-image is defined as

$$I_z(i,j)=I(i+{\Delta }_i^{\left(z\right)},j+{\Delta }_j^{\left(z\right)}),\forall (i,j)\in {\Omega }_I,$$

(8)

where $({\Delta }_i^{\left(z\right)},{\Delta }_j^{\left(z\right)})$ represents the spatial offset of the z-th window within the image domain ${\Omega }_I$.

The collection of all such sub-images forms the candidate template set:

$$\mathcal{P}\left(I\right)=\{I_1,I_2,\dots ,I_z\}.$$

(9)

For each candidate template $I_z\in \mathcal{P}\left(I\right)$, we compute a dissimilarity measure $D(I_z,T)$ and corresponding similarity score $C(I_z,T)$ as follows:

$$D(I_z,T)=\sum _{i=1}^w\sum _{j=1}^h|I_z(i,j)-T(i,j)|,$$

(10)

$$C(I_z,T)=1-{\displaystyle \frac{1}{w·h·L_{\max }}}D(I_z,T),$$

(11)

where $L_{\max }=255$ is the maximum possible pixel intensity.

The ITM method uses this reverse matching strategy to effectively extract the areas that best represent template T from the original image and improve matching accuracy through difference value calculations, as shown in Figure 3. This method is particularly suitable for scenes with slight occlusions, as it concentrates the calculation accuracy of the matching area on a smaller area, thereby avoiding large-scale mismatches caused by occlusions.

We intentionally employ a simple subtraction-based similarity measure to maximize computational efficiency, a design choice that is fundamental to the scalability of our inverse matching paradigm. This approach not only enables the real-time processing of numerous sub-templates but also ensures stability and interpretability throughout the iterative refinement process, offering a practical and efficient alternative to computationally intensive traditional metrics.

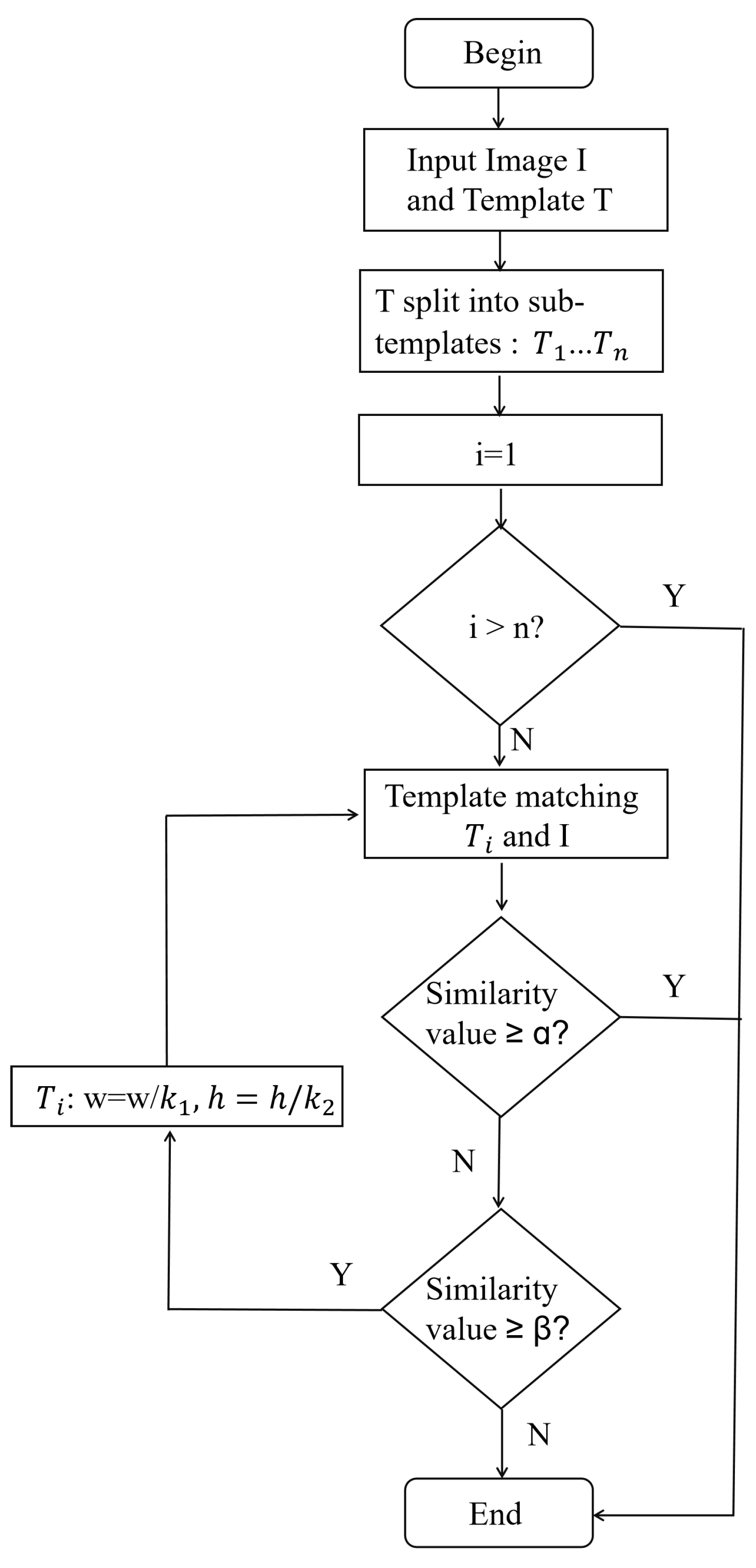
3.3. Iterative Matching Mathematical Method (IMM)

In Section 3.2, we proposed ITM, which effectively solved the occlusion problem in binocular vision and enabled basic template matching. However, when occlusion is severe or complex, a single reverse template matching operation does not cover a sufficient area, resulting in imprecise matching of details. Therefore, to address this issue, we proposed the IMM, which improves matching accuracy by iteratively optimizing template size and similarity thresholds through multiple iterations.

The relationship between ITM and IMM can be summarized as an extension from a single-scale inverse matching to a multi-scale iterative framework. In ITM, the input image is divided into several fixed-size sub-images that are each compared with template T to locate the most similar region. Although this approach effectively handles mild occlusion, it relies on a constant template size, which limits its adaptability to variations in scale and occlusion extent. IMM addresses this limitation by repeatedly executing the ITM process while dynamically adjusting the template size and similarity thresholds in each iteration. Formally, IMM can be interpreted as a recursive application of ITM under adaptive scaling parameters $({\lambda }_w^{\left(n\right)},{\lambda }_h^{\left(n\right)})$.

To better understand the structure and flow of the algorithm, we present the overall framework in Figure 4. The following are the mathematical derivations and algorithmic steps:

1. 

Definition of Input Image and Template:

Let the input image with size $p\times q$ be

$$I:{\Omega }_I\subset {\mathbb{Z}}^2\to [0,255],$$

(12)

Let the original template with size $w\times h$ be

$$T:{\Omega }_T\subset {\mathbb{Z}}^2\to [0,255].$$

(13)

At iteration n, the current sub-template extracted from I is denoted by

$$I_z^{\left(n\right)}:{\Omega }_{I^{\left(n\right)}}\to [0,255],$$

(14)

with dimensions $w^{\left(n\right)}\times h^{\left(n\right)}$. Initially, $w^{\left(0\right)}=w$ and $h^{\left(0\right)}=h$. Each iteration evaluates the similarity between $I_z^{\left(n\right)}$ and T to determine whether refinement is necessary.

2. 

Difference Metric and Similarity Calculation:

For the z-th sub-image at iteration n, the pixel-wise absolute difference is defined as

$$D_z^{\left(n\right)}=\sum _{i=1}^{w^{\left(n\right)}}\sum _{j=1}^{h^{\left(n\right)}}|I_z^{\left(n\right)}(i,j)-T(i,j)|.$$

(15)

The normalized similarity coefficient is given by

$$C_z^{\left(n\right)}=1-{\displaystyle \frac{D_z^{\left(n\right)}}{255w^{\left(n\right)}{h}^{\left(n\right)}}}.$$

(16)

A higher $C_z^{\left(n\right)}$ indicates stronger correspondence between $I_z^{\left(n\right)}$ and T. The overall IMM objective can thus be expressed as

$$\underset{z,n}{max}{C}_z^{\left(n\right)}.$$

(17)

3. 

Iterative Process:

Given the similarity thresholds $\alpha$ and $\beta$ ($0\le \beta <\alpha \le 1$), the decision process for each region is as follows:

$$\left\{\begin{array}{cc}{C}_z^{\left(n\right)}\ge \alpha ,\hfill & \mathrm{region}\mathrm{accepted}\mathrm{as}\mathrm{a}\mathrm{valid}\mathrm{match},\hfill \\ \beta <C_z^{\left(n\right)}<\alpha ,\hfill & \mathrm{region}\mathrm{retained}\mathrm{for}\mathrm{next}\mathrm{iteration},\hfill \\ C_z^{\left(n\right)}\le \beta ,\hfill & \mathrm{region}\mathrm{discarded}.\hfill \end{array}\right.$$

For each retained region, the template size is refined using adaptive scaling factors:

$$w^{(n+1)}={\lambda }_w^{\left(n\right)}{w}^{\left(n\right)},h^{(n+1)}={\lambda }_h^{\left(n\right)}{h}^{\left(n\right)},$$

(18)

where ${\lambda }_w^{\left(n\right)},{\lambda }_h^{\left(n\right)}\in (0,1)$ control the granularity of refinement.

Equivalently, using the input image dimensions p and q, we have

$$w^{\left(n\right)}={\displaystyle \frac{p}{k_1^{\left(n\right)}}},h^{\left(n\right)}={\displaystyle \frac{q}{k_2^{\left(n\right)}}},$$

(19)

where $k_1^{\left(n\right)}$ and $k_2^{\left(n\right)}$ denote the adaptive scaling parameters at iteration n. Thus, the refinement process can be represented recursively as

$$I_z^{(n+1)}=\Phi \left(I_z^{\left(n\right)},C_z^{\left(n\right)},{\lambda }_w^{\left(n\right)},{\lambda }_h^{\left(n\right)}\right),$$

(20)

where $\Phi (·)$ denotes the spatial subdivision and rescaling operator acting on each sub-image.

4. 

Optimal Matching Output:

At each iteration, the algorithm selects the sub-template with the highest similarity score:

$$I_{\mathrm{best}}^{\left(n\right)}=arg\underset{I_z^{\left(n\right)}}{max}{C}_z^{\left(n\right)}.$$

(21)

After all iterations, the final optimal match is obtained as

$$I^{*}=I_{z^{*}}^{\left(n^{*}\right)},(z^{*},n^{*})=arg\underset{z,n}{max}{C}_z^{\left(n\right)}.$$

(22)

All sub-templates with similarity values above the threshold $\alpha$ are combined to form the final matching region:

$$R^{*}=\bigcup _{C_z^{\left(n\right)}\ge \alpha }{S}_z^{\left(n\right)}.$$

(23)

By iteratively refining both template size and similarity thresholds, IMM progressively improves local accuracy and robustness. This adaptive, coarse-to-fine procedure enables automatic adjustment to variable occlusion, converging toward the most accurate unobstructed region:

$$\underset{n\to n^{*}}{lim}{C}_{z^{*}}^{\left(n\right)}=\underset{z,n}{max}{C}_z^{\left(n\right)},$$

(24)

where the similarity value $C_{z^{*}}^{\left(n\right)}$ of the optimal sub-template $S_{z^{*}}^{\left(n\right)}$ approaches the global maximum as the iteration index n tends to its final state $n^{*}$.

This expression mathematically represents the algorithm’s stability: through successive refinement, IMM gradually maximizes the similarity score, ensuring convergence to the most accurate and unobstructed matching region despite variations in occlusion or illumination. Therefore, IMM provides a mathematically grounded iterative optimization framework that enhances both precision and adaptability for complex occluded template matching scenarios.

Figure 4. Iterative Matching Method Framework. We iterate over the detection image and divide it into sub-templates for matching with the original template. The image width of the input image is divided into $k_1$ parts, and the height of the input image is divided into $k_2$ parts, obtaining the width and height of the template image, denoted as w and h, respectively. $\alpha$ and $\beta$ represent the minimum and maximum values of the accuracy, respectively.

Figure 4. Iterative Matching Method Framework. We iterate over the detection image and divide it into sub-templates for matching with the original template. The image width of the input image is divided into $k_1$ parts, and the height of the input image is divided into $k_2$ parts, obtaining the width and height of the template image, denoted as w and h, respectively. $\alpha$ and $\beta$ represent the minimum and maximum values of the accuracy, respectively.

3.4. Local Region Selection Strategy

In traditional template matching, using the entire input image for matching increases the computational load, which can lead to reduced matching accuracy, especially for complex images or those containing irrelevant information. To address this issue, we propose a local region selection strategy that integrates IMM. This strategy further enhances the efficiency and accuracy of template matching by selecting the most representative regions for matching in each iteration.

Specifically, in the region selection process, a sub-template is inputted into the next iteration based on the results of the similarity measure within a certain range defined by thresholds $\alpha$ and $\beta$.

Mathematically, we define the similarity distance $C_z$ between the sub-template $I_z$ and the template image T in the region selection process. The similarity distance $C_z$ is calculated based on the predicted thresholds $\alpha$ and $\beta$. If the similarity distance $C_z$ falls within the range $\beta <C_z<\alpha$, we regard it as a valid sub-template for the next iteration. In this way, the overall matching efficiency improves as we refine the matching process for each region.

The mathematical significance of this strategy lies in updating the template by precisely selecting the appropriate region, enabling each iteration to focus more effectively on the potential target areas within the image. By progressively narrowing the matching range and focusing on key regions, the IMM method can better handle complex occlusion scenarios and improve matching accuracy within occluded areas. During the optimization of matching, selecting appropriate similarity thresholds $\alpha$ and $\beta$ grants the local region selection strategy greater flexibility, enabling it to adjust the sensitivity of matching based on different occlusion scenarios or image characteristics.

In practical applications, this strategy significantly improves the accuracy of identifying occluded regions while reducing computations on irrelevant regions. This not only improves the overall efficiency of template matching but also enhances the robustness of the algorithm, particularly when processing images with complex occlusions or noise, thereby avoiding matching failures caused by interference from irrelevant regions. Therefore, the local region selection strategy effectively optimizes the template matching process, further enhancing the accuracy and computational efficiency of the IMM method, especially demonstrating high adaptability when addressing occlusion issues.

4. Experiments

The main objective of this paper is to propose and validate a new template matching solution designed to address the presence of occlusion in humanoid binocular vision. To enhance the persuasiveness of this paper, we show experimental results in different real-world scenarios in this section. Through these experiments, we verify the effectiveness of ITM and IMM in real applications, especially in the case of complex occlusions.

In order to comprehensively evaluate the performance of the proposed methods, we take pictures in several scenes as experimental datasets, covering both mild occlusion and severe occlusion environments. In Section 4.1, we first introduce the evaluation metrics. In Section 4.2, we outline the effect of ITM in the mild occlusion case. In Section 4.3, we describe the effect of the FTM algorithm in the case of severe occlusion. In Section 4.4, we provide comparison tests in mild and severe occlusion cases, respectively, and the quantitative comparison results are outlined in Section 4.4.2, as shown in

Table 1. Quantitative Results for Real Scenarios. We compared NCC, SIFT, ORB, CNNs and Siamese Net algorithms. All the experimental results of our method are obtained by IMM.

Method	Mild Occlusion				Severe Occlusion
	Cup	Bus	Apple	Average	Cup	Bus	Apple	Average
NCC	0.51	0.41	0.46	0.46	0.32	0.16	0.41	0.30
SIFT	0.61	0.53	0.48	0.54	0.65	0.53	0.56	0.58
ORB	0.55	0.50	0.65	0.57	0.51	0.50	0.59	0.53
CNNs	0.57	0.97	0.61	0.72	0.58	0.61	0.59	0.59
Siamese Net	0.92	0.86	0.91	0.90	0.37	0.54	0.73	0.55
Ours	0.96	0.91	0.95	0.94	0.94	0.91	0.93	0.93

. In Section 4.4.3, we provide the qualitative comparison results.

4.1. Evaluation Metrics

We use Mean Absolute Error (MAE) as the primary metric to evaluate the accuracy of template matching. MAE can effectively quantify the difference between the target image and the template image, making it particularly suitable for error evaluation in template matching tasks.

The specific difference calculation method is as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n|I(i,j)-T(i,j)|,$$

(25)

where $I(i,j)$ and $T(i,j)$ represent the pixel values at the i-th row and j-th column of the target image and template image, respectively, and n is the total number of pixels in the image.

Template matching accuracy, i.e., similarity is

$$ACC=1-{\displaystyle \frac{MAE}{255}}.$$

(26)

Through this evaluation criterion, we can effectively quantify the similarity between the template and the target image. A smaller $MAE$ value represents higher similarity between the images, which leads to better matching results and an improved algorithm performance.

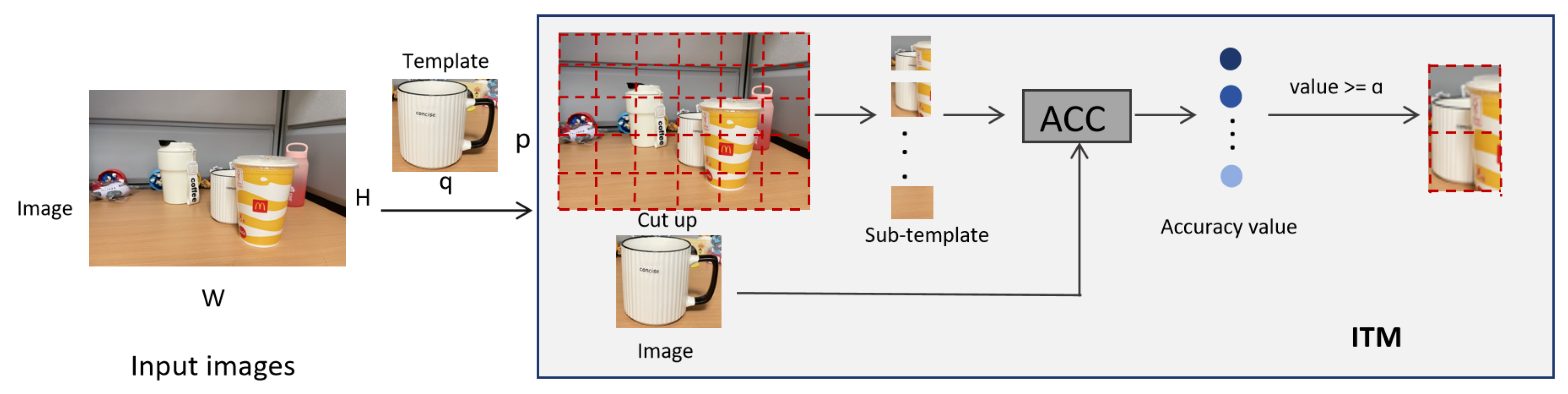
4.2. Experimental Procedure of Inverse Template Matching

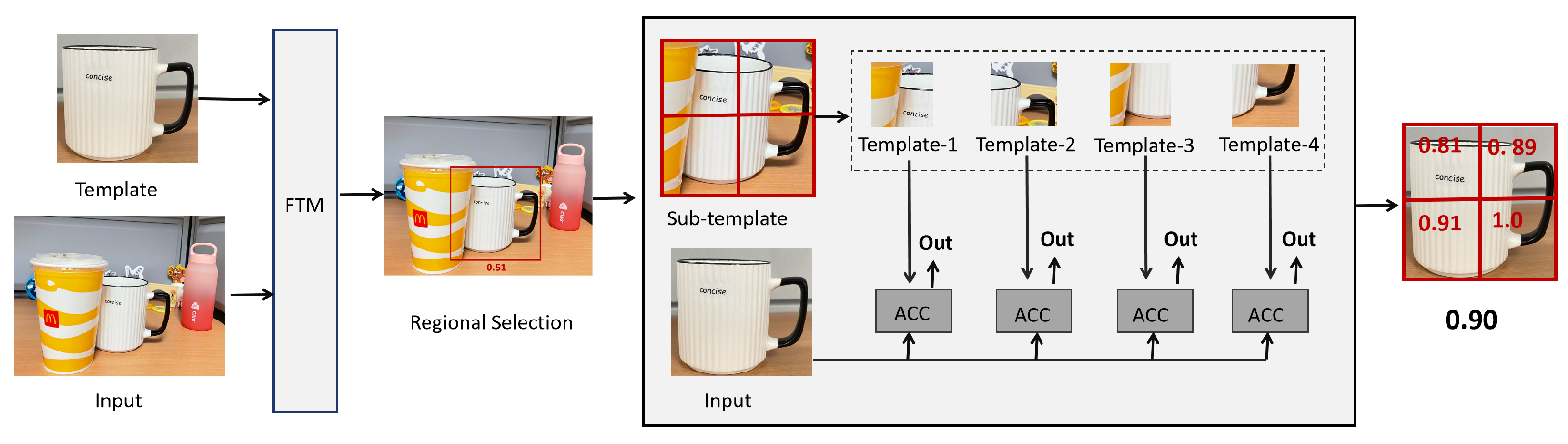
In this section, we verify the performance of ITM in dealing with mild occlusion scenarios. ITM is able to effectively identify regions similar to the template image by segmenting the input image into multiple sub-images and matching each sub-image with the template image. The smallest value of the similarity value matrix corresponds to a region that is highly similar to the template image. Each sub-template image will have a minimum difference value when matched with the original template image, and the average of the difference values obtained from all sub-template images is the difference value of the entire region to be detected. As shown in Figure 5, we input a template image and the input image, after the FTM algorithm is used, to obtain a similarity matrix. If the maximum in the similarity value matrix is considered to be the best matching region, we will take this part of the region as a sub-template image and template image for ITM. The sub-template image is partitioned into four templates, comprising each template and the original template image for ITM, retaining the minimum difference value of each with the sub-template image. Eventually, the average of the similarity values of the matched regions of the four sub-templates is the similarity value of the ITM output. In Figure 5, the similarity values we obtained for the four sub-template images are 0.81, 0.89, 0.91, and 1.0, respectively, and their average value is 0.90.

In order to show the effect of the ITM algorithm compared with FTM more intuitively, we first set light masking in the image to be matched, i.e., part of the target region is masked but the rest remains intact. We use the ITM and FTM algorithms to template match the same image separately, and the reverse template matching algorithm processes the input image and calculates the similarity value between each sub-image and the template image; the results are shown in Figure 6. The results in Figure 6 demonstrate that when there is an occlusion situation, the FTM algorithm does not obtain as values as accurately as the ITM; for example, in the first row of Figure 6, the FTM algorithm obtains a similarity value of 0.51, while the ITM algorithm obtains a similarity value of 0.90, and the ITM algorithm obtains a more accurate match. Thus, reverse template matching shows significantly better performance than forward matching in this case and it is able to identify the target area more accurately, especially in the processing of an occluded part. Moreover, Figure 7 presents a comparison of the evaluation metrics for our approach against the conventional method NCC.

4.3. Experimental Process of Iterative Matching Method

In this section, we verify that using the hybrid template matching algorithm in the case of complex occlusion can be better for template matching, and adjusting the size of the template and the difference value threshold through several iterations can result in matching inaccuracies due to occlusion being dealt with more optimally. The flow of the IMM algorithm can be seen in Figure 4. The ITM method is very effective for the case of mild occlusion and can better cope with the simple occlusion in the image and the more obvious image differences. However, when faced with complex occlusion, the accuracy of single ITM decreases, leading to a failure of dealing with the matching of details effectively. Figure 8 illustrates the similarity scores generated by selecting different template sizes for ITM, which can assist in effectively choosing an appropriate template size to iterative.

In order to more intuitively show the comparative effect of the ITM algorithm and IMM in complex environments, we conducted experiments in complex environments in different scenarios separately, and the results are shown in Figure 9. In the experiments, we set the threshold of each ITM to 0.9. When the similarity value is less than 0.9, it will continue to iterate the ITM process. When the similarity value is greater than or equal to 0.9, then the matching is considered successful, and the region is retained. When encountering occlusion complexity, the accurate value obtained from one ITM operation is not very good and the region obtained is not precise enough. After many iterations of ITM, the selected region keeps becoming smaller and the accuracy increases continuously. For example, for the first row of data in Figure 9, the similarity value obtained when iterating through one ITM is 0.81. When iterating through the IMM, the ITM will continue to be performed for a similarity value less than 0.9. Finally, the overall similarity value obtained is 0.94, and, at the same time, the selected region is more accurate.

The experimental results show that IMM is able to identify the target region more accurately by adjusting the template size threshold in the case of complex occlusion. The algorithm gradually improves the accuracy of matching regions through iterative optimization. Regardless of how complex the occlusion is, the detection of all occlusion cases can be recognized by setting the threshold and template size.

4.4. Comparisons

In order to validate the effectiveness of our algorithms, we conducted qualitative and quantitative analyses, we experimented with mildly occluded and severely occluded datasets in real scenes, and we compared our methods with pixel-based template matching methods, feature-based template matching methods, and deep learning-based template matching algorithms. In the quantitative analysis, for pixel-based template matching, we compared the NCC similarity calculation method; for feature-based template matching method, we compared the SIFT and ORB methods; and for deep learning-based template matching, we compared the CNN-based and Siamese network-based matching algorithms, respectively. The specific comparison results are shown in Table 1.

In addition, in order to show the effect of our algorithms more comprehensively, we also selected mildly occluded and severely occluded datasets in real scenes for a qualitative comparison under different algorithms, as shown in Figure 10 and Figure 11. Through these qualitative analyses and comparisons, we further validated the superiority and effectiveness of our algorithms in a visual reconstruction task.

4.4.1. Comprehensive Evaluation Metrics

We employ Precision, Recall, F1-score, and IoU to quantitatively validate the effectiveness of our method under occluded scenarios.

Precision measures the reliability of positive matches, i.e., the proportion of correctly matched templates among all reported matches.

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}.$$

(27)

Recall measures the completeness of detection, i.e., the proportion of successfully matched templates among all ground-truth templates.

$$\mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}}.$$

(28)

F1-score provides a balanced measure between Precision and Recall, evaluating the overall effectiveness of the template matching algorithm.

$$\mathrm{F}1-\mathrm{score}=2\times {\displaystyle \frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}.$$

(29)

The Intersection over Union (IoU) measures the spatial accuracy of the matched region against the ground-truth template location. It is defined as

$$\mathrm{IoU}(B_p,B_{gt})={\displaystyle \frac{\mathrm{Area}(B_p\cap B_{gt})}{\mathrm{Area}(B_p\cup B_{gt})}}.$$

(30)

where a higher IoU indicates better alignment between the predicted match $B_p$ and the true template position $B_{gt}$.

4.4.2. Quantitative Results

We quantitatively analyzed the dataset collected from real scenarios and used the ACC method to calculate the similarity as an evaluation metric. The results show that our algorithm exhibits significant advantages. We compare it with traditional pixel-based template matching, feature-based template matching, and deep learning-based template matching methods.

For pixel-based template matching, we compare NCC similarity calculation methods; for feature-based template matching methods, we compare SIFT and ORB methods; for deep learning-based template matching, we compare CNN-based and Siamese network-based matching algorithms, respectively. All the experimental results of our methods are obtained with IMM.

The deep learning-based template matching methods we compare use CNNs and Siamese networks for model training, respectively, and template image datasets taken in different environments are selected. All the captured photos of the three scenes are assigned as training, test, and validation sets. In the case of the convolutional neural network, the accuracy of the test set is 0.77 and the loss value is 0.56; in the case of the Siamese network, the accuracy of the test set is 0.88 and the loss value of the test set is 0.1. Eventually, we applied the trained model to the to-be-detected image pairs and obtained corresponding similarity results, as shown in Table 1.

The CNN model processes image pairs through two parallel but independent branches, each containing three convolutional layers (64, 128, and 256 filters with $3\times 3$ kernels) and each followed by $2\times 2$ max-pooling. The outputs are flattened, passed through a 512-unit dense layer, concatenated, and finally fused by a sigmoid output unit for binary classification.

The Siamese network utilizes a single shared-weight convolutional backbone, which processes both inputs through three convolutional layers (64, 128, and 256 filters with $3\times 3$ kernels), each followed by $2\times 2$ max-pooling. The extracted features are flattened and passed through a 512-unit dense layer, and the L1 distance between the two embeddings is computed before a final sigmoid output unit.

As can be seen from Table 1, our method improves the average accuracy by 51% in the case of mild occlusion and 93% in the case of severe occlusion compared to the traditional pixel-based NCC method. Compared to the feature-based ORB matching method, our method improves the average accuracy by 46% in the mild occlusion case and 43% in the severe occlusion case. Compared to the CNN matching method, our method improves the average accuracy by 23% in the mild occlusion case and 37% in the severe occlusion case.

To empirically evaluate the computational efficiency within the domain of training-free methods, we benchmarked the runtime of our IMM algorithm against three established and representative traditional baselines: NCC as a pixel-based method, SIFT as a robust feature-based method, and ORB as a highly optimized feature-based method. We deliberately excluded deep learning-based approaches from this efficiency comparison for two principled reasons. First, they operate in a fundamentally different paradigm, requiring extensive offline training on large datasets, which incurs a significant and one-time computational cost that is not directly comparable to our instant-deployment, training-free approach. Second, the primary contribution of our work is to advance the capabilities of model-free template matching. The results in

Table 2. Computational Efficiency Comparison Under Severe Occlusion. Execution time of a matching box in the complex “Cup” dataset.

Method	Time (ms)	Accuracy	Time/Accuracy Ratio
ORB	100	0.51	196
SIFT	650	0.65	1000
NCC	230	0.32	719
Ours	180	0.97	186

demonstrate that our method achieves superior robustness under severe occlusion at a computationally feasible cost within this relevant and comparable domain of algorithms.

The results under severe occlusion, presented in

Table 3. Performance Benchmark Under Severe Occlusion. Results evaluated on the Cup dataset, with metrics averaged over multiple matching trials across all test images.

Method	Precision	Recall	F1-Score	IoU
NCC	0.45	0.52	0.48	0.65
SIFT	0.73	0.76	0.74	0.81
ORB	0.60	0.65	0.62	0.69
CNNs	0.61	0.54	0.57	0.63
Siamese Net	0.55	0.50	0.52	0.45
Ours	0.98	0.92	0.95	0.91

, unequivocally demonstrate the superior robustness of our proposed IMM method. It achieves the highest scores across all metrics, with a near-perfect Precision (0.98) and the best F1-score (0.92), significantly outperforming all baseline approaches. This indicates that our method is not only highly reliable in identifying correct matches with minimal false positives but also excels in accurately localizing the target template, establishing a new state-of-the-art procedure for robust template matching.

4.4.3. Qualitative Results

In order to demonstrate the effectiveness of our algorithm more intuitively, we qualitatively analyzed the mild occlusion and severe occlusion in real scenes, respectively. We chose to compare our algorithm with NCC and ORB. The results for the mild occlusion case are shown in Figure 10, and the severe occlusion case is shown in Figure 11.

According to Figure 10 and Figure 11, it can be seen that our method pays more attention to the precise matching of details in the feature matching process, and it can accurately identify and match the correct region. Meanwhile, compared with other methods, our method performs better in matching accuracy. Compared with the traditional pixel-based NCC method, our method nearly doubles the accuracy. Although feature-based matching methods have achieved better improvements, feature matching methods may somewhat suffer when dealing with occluded scenes, resulting in a decrease in matching accuracy and failure to capture the complete details of the matching region. Our method is able to maintain high stability and accuracy under different levels of occlusion using inverse and iterative matching strategies.

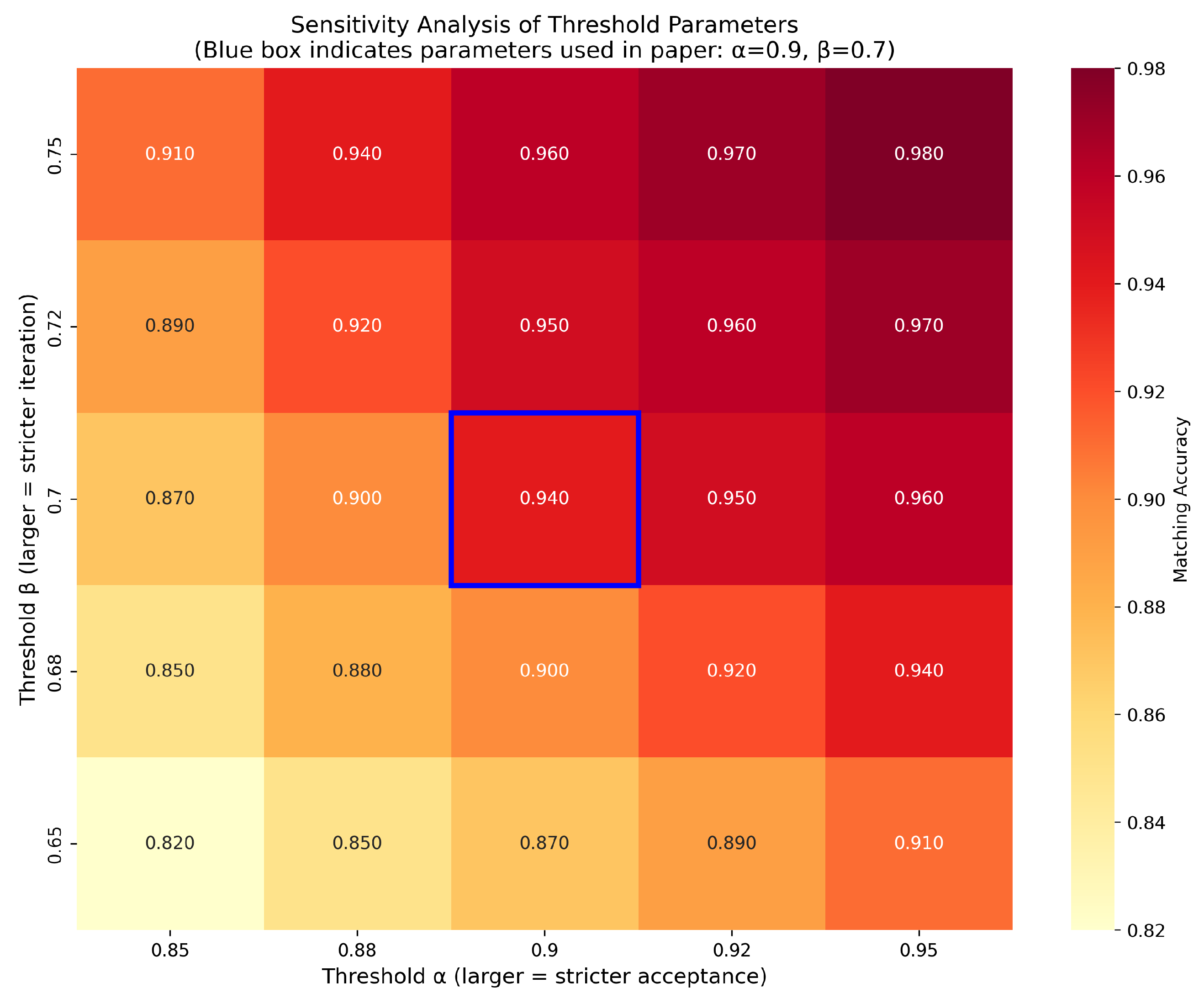
4.5. Sensitivity Analysis of Thresholds $\alpha$ and $\beta$

The thresholds $\alpha$ and $\beta$ are pivotal in governing the iterative refinement process of our IMM method. To rigorously assess the robustness of our method to these parameters, we conducted a systematic sensitivity analysis.

We evaluated the IMM algorithm across a comprehensive grid of parameter values: $\alpha$ varied from 0.85 to 0.95, and $\beta$ varied from 0.65 to 0.75. This resulted in 25 distinct parameter combinations, each tested on our severe occlusion dataset. The average matching accuracy for each combination is presented in the form of a heatmap in Figure 12.

This sensitivity analysis was conducted to rigorously validate our empirical selection of thresholds $\alpha =0.9$ and $\beta =0.7$. As visualized in the heatmap, these parameters achieve a high accuracy of 0.94 and are situated within a stable, high-performance region, confirming their robustness. Furthermore, while peak accuracy (0.98) occurs at stricter settings ($\alpha =0.95$, $\beta =0.75$), our chosen values represent a deliberate and optimal balance, delivering state-of-the-art performance while avoiding the computational inefficiency and over-restrictive matching associated with excessively high thresholds, thus ensuring greater practical utility.

In conclusion, this sensitivity analysis conclusively demonstrates that the performance of our IMM framework is stable across a broad range of its key parameters, thereby solidifying the reliability and practical utility of our method.

5. Conclusions

This paper presents a hybrid strategy for achieving robust matching inside the binocular vision of a humanoid robot, which aims to improve template matching accuracy in occlusion situations. The method avoids the high computational burden of deep learning models and provides a more efficient and real-time solution. The first step of Robust Template Matching is Inverse Template Matching Mathematical Method (ITM), which splits the original input image into multiple sub-images and acts as a new template image to the The method splits the original input image into multiple sub-images and matches the original template as a new template image in reverse, thus solving the problem that the forward template matching method cannot recognize the target object effectively under occlusion. However, when the occlusion situation is more complex, the accuracy of single ITM may decrease. Therefore, we propose an Iterative Matching Mathematical Method (IMM). IMM continuously improves the matching effect of the original template by repeatedly executing the ITM, which generates a template image with a more appropriate size at each iteration, in order to improve the recognition accuracy of image details. In addition, we propose a local selection strategy to improve the efficiency of image matching by selecting the optimal region as the image for the next iteration during the IMM. By combining ITM and IMM, the robust template matching method is able to adapt to the template matching task in any complex scenario, enhance the recognition accuracy of image details, and significantly improve the overall accuracy of template matching. Experimental results demonstrate that the proposed method achieves an average accuracy of 0.94 under mild occlusion and 0.93 under severe occlusion, representing a 93% improvement over traditional pixel-based methods and a 37% improvement over CNN-based methods under severe occlusion.

Limitations and Future Work

Limitations: While the proposed IMM framework has demonstrated exceptional robustness in handling severe occlusions, this study is subject to several limitations. First, the scope of validation is constrained by the scale and diversity of the experimental datasets used. Second, the current method is primarily validated under controlled conditions focusing on geometric occlusions, and its performance can be adversely affected by challenging visual appearances, such as regions with similar colors or textures, which may lead to a reduced matching accuracy. These factors define the current boundary conditions of our work.

Future Work: To address these limitations and advance current research, we outline the following directions. Our immediate priority is to conduct extensive evaluations on large-scale public benchmarks (e.g., COCO and KITTI) to verify generalization across diverse objects, scenes, and lighting conditions. We also plan to enhance the method’s discriminative capability against appearance-based ambiguities by integrating learnable deep feature representations. Furthermore, we will comprehensively assess robustness to a broader spectrum of challenges, including photometric variations (e.g., noise and illumination changes) and geometric transformations (e.g., scaling and rotation). Finally, efforts will be made to optimize the framework for real-time performance on embedded robotic platforms to solidify its practical utility.