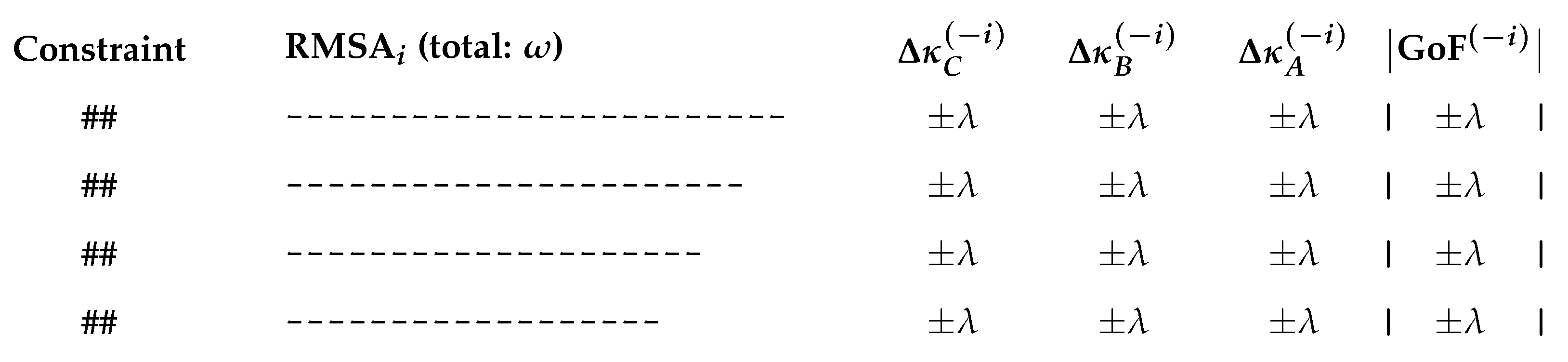CLSP: Linear Algebra Foundations of a Modular Two-Step Convex Optimization-Based Estimator for Ill-Posed Problems

Abstract

This paper develops the linear-algebraic foundations of the Convex Least Squares Programming (CLSP) estimator and constructs its modular two-step convex optimization framework, capable of addressing ill-posed and underdetermined problems. After reformulating a problem in its canonical form, ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$, Step 1 yields an iterated (if $r>1$) minimum-norm least-squares estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}$ on a constrained subspace defined by a symmetric idempotent $\mathbf{Z}$ (reducing to the Moore–Penrose pseudoinverse when $\mathbf{Z}=\mathbf{I}$). The optional Step 2 corrects ${\widehat{\mathbf{z}}}^{\left(r\right)}$ by solving a convex program, which penalizes deviations using a Lasso/Ridge/Elastic net-inspired scheme parameterized by $\alpha \in [0,1]$ and yields ${\widehat{\mathbf{z}}}^{*}$. The second step guarantees a unique solution for $\alpha \in (0,1]$ and coincides with the Minimum-Norm BLUE (MNBLUE) when $\alpha =1$. This paper also proposes an analysis of numerical stability and CLSP-specific goodness-of-fit statistics, such as partial $R^2$, normalized RMSE (NRMSE), Monte Carlo t-tests for the mean of NRMSE, and condition-number-based confidence bands. The three special CLSP problem cases are then tested in a 50,000-iteration Monte Carlo experiment and on simulated numerical examples. The estimator has a wide range of applications, including interpolating input–output tables and structural matrices.

1. Introduction

As the existing literature on optimization—for example, Nocedal and Wright [1] (pp. 1–9) and Boyd and Vandenberghe [2] (pp. 1–2)—points out, constrained optimization plays an important role not only in natural sciences, where it was first developed by Euler, Fermat, Lagrange, Laplace, Gauss, Cauchy, Weierstrass, and others, but also in economics and its numerous applications, such as econometrics and operations research, including managerial planning at different levels, logistics optimization, and resource allocation. The history of modern constrained optimization began in the late 1940s to 1950s, when economics, already heavily reliant on calculus since the marginalist revolution of 1871–1874 [3] (pp. 43–168), and the emerging discipline of econometrics, standing on the shoulders of model fitting [4] (pp. 438–457), internalized a new array of quantitative methods referred to as programming after the U.S. Army’s logistic jargon. Programming—including classical, linear, quadratic, and dynamic variants—originated with Kantorovich in economic planning in the USSR and was independently discovered and developed into a mathematical discipline by Dantzig in the United States (who introduced the bulk of the terminology and the simplex algorithm) [5] (pp. 1–51, [6]). Since the pivotal proceedings published by Koopmans [7], programming has become an integral part of mathematical economics [8,9,10], in both microeconomic analysis (an overview is provided in Intriligator and Arrow [11] (pp. 76–91) and macroeconomic modeling, such as Leontief’s input–output framework outlined in Koopmans [7] (pp. 132–173) and, in an extended form, in Dorfman et al. [12] (pp. 204–264).

Calculus, model fitting, and programming are, however, subject to strong assumptions, including function smoothness, full matrix ranks, well-posedness, well-conditionedness, feasibility, non-degeneracy, and non-cycling (in the case of the simplex algorithm) as summarized by Nocedal and Wright [1] (pp. 304–354, 381–382) and Intriligator and Arrow [11] (pp. 15–76). These limitations have been partially circumvented by developing more strategy-based than analysis-based, computationally intensive constraint programming algorithms; consult Frühwirth and Abdennadher [13] and Rossi et al. [14] for an overview. Still, specific cases of constrained optimization problems in econometric applications, such as incorporating the textbook two-quarter business-cycle criterion into a general linear model [15] or solving underdetermined linear programs to estimate an investment matrix [16], remain unresolved within the existing methodologies and algorithmic frameworks. In response, this text develops a modular two-step convex programming methodology to formalize such problems as a linear system of the form $\mathbf{A}\mathbf{z}=\mathbf{b}$, including linear(ized) constraints $\mathbf{C}\mathbf{x}+\mathbf{S}{\mathbf{y}}^{*}={\mathbf{b}}_{1:k}$, with $k\le m$, where $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ is a partitioned matrix, $\mathbf{C}\in {\mathbb{R}}^{k\times p}$ and $\mathbf{S}\in {\mathbb{R}}^{k\times (n-p)}$ are its submatrices, $\mathbf{b}\in {\mathbb{R}}^m$ is a known vector, and $\mathbf{z}\in {\mathbb{R}}^n$ is the vector of unknowns, which includes both the target solution subvector $\mathbf{x}\in {\mathbb{R}}^p$ and an auxiliary slack-surplus subvector ${\mathbf{y}}^{*}\in {\mathbb{R}}^{n-p}$, introduced to accommodate inequalities in constraints.

The methodology (Convex Least Squares Programming, or CLSP, framework) comprises selectively omittable and repeatable actions for enhanced flexibility—and consists of two steps: (a) the first, grounded in the theory of (constrained) pseudoinverses as summarized in Rao and Mitra [17], Ben-Israel and Greville [18], Lawson and Hanson [19], and Wang et al. [20], is iterable to refine the solution and serves as a mandatory baseline in cases where the second step becomes infeasible (due to mutually inconsistent constraints)—as exemplified by Whiteside et al. [21] for regression-derived constraints and by Blair [22,23] in systems with either too few or too many effective constraints; and (b) the second, grounded in the theory of regularization and convex programming as summarized in Tikhonov et al. [24], Gentle [4], Nocedal and Wright [1], and Boyd and Vandenberghe [2], provides an optional correction of the first step, drawing on the logic of Lasso, Ridge, and Elastic Net to address ill-posedness and compensate for constraint violations or residual approximation errors resulting from the first-step minimum-norm LS estimate. Hence, it can be claimed that the proposed framework is grounded in the general algorithmic logic of Wolfe [25] and Dax [26] as further formalized by Osborne [27], who were among the first to introduce an additional estimation step into simplex-based solvers, and is comparable to the algorithms of Übi [28,29,30,31,32], the closest and most recent elaborations on the topic.

The aim of this work is to define the linear algebra foundations (the theoretical base) of the CLSP framework, present supporting theorems and lemmas, develop tools for analyzing numerical stability of matrix $\mathbf{A}$, and discuss the goodness of fit of vector ${\widehat{\mathbf{z}}}^{*}$, illustrating them on simulated examples. Topics such as the maximum likelihood estimation of ${\widehat{\mathbf{z}}}^{*}$ and corresponding information criteria (Akaike and Bayesian) are beyond its present scope. The text is organized as follows. Section 2 summarizes the historical development and recent advances in convex optimization, motivating the formulation of a new methodology. Section 3 presents the formalization of the estimator, while Section 4 develops a sensitivity analysis for $\mathbf{C}$. Section 5 introduces goodness-of-fit statistics, including the normalized root mean square error (NRMSE) and its sample-mean test. Section 6 presents special cases, and Section 7 reports the results of a Monte Carlo experiment and solves simulated problems via CLSP-based Python 3 modules. Section 8 concludes with a general discussion. Throughout, the following notation is used: bold uppercase letters (e.g., $\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{G},\mathbf{M},$ and $\mathbf{S}$) denote matrices; bold lowercase letters (e.g., $\mathbf{b},\mathbf{x},\mathbf{y},$ and $\mathbf{z}$) denote column vectors; italic letters (e.g., $i,j,k,m,n,p,\lambda ,\omega$) denote scalars; the transpose of a matrix is denoted by the superscript ⊤ (e.g., ${\mathbf{X}}^{\top }$); the inverse by $-1$ (e.g., ${\mathbf{Q}}^{-1}$); generalized inverses are indexed using curly braces (e.g., ${\mathbf{G}}^{\{1,2\}}$); the Moore–Penrose pseudoinverse is denoted by dagger (e.g., ${\mathbf{A}}^{†}$); ${\ell }_p$ norms, where $1\le p\le \infty$, are denoted by double bars (e.g., ${\parallel ·\parallel }_2$); and condition numbers by $\kappa (·)$. All functions, scalars, vectors, and matrices are defined over the real numbers ($\mathbb{R}$).

2. Historical and Conceptual Background of the CLSP Framework

The methodology of convex optimization—formally, ${\mathbf{x}}^{*}=\arg {\min }_{\mathbf{x}\in {\mathbb{R}}^n}f\left(\mathbf{x}\right)$, subject to convex inequality constraints $g_i\left(\mathbf{x}\right)\le 0$ and affine equality constraints $h_j\left(\mathbf{x}\right)=0$ as defined by Boyd and Vandenberghe [2] (pp. 7, 127–129)—has evolved over more than two centuries through several milestones, including generalized inverses and linear and (convex) quadratic programming, each relaxing the strong assumptions of its predecessors. As documented in the seminal works of Rao and Mitra [17] (pp. vii–viii) and Ben-Israel and Greville [18] (pp. 4–5, 370–374), the first pseudoinverses (original term, now typically reserved for ${\mathbf{A}}^{†}$) or generalized inverses (current general term) emerged in the theory of integral operators—introduced by Fredholm in 1903 and further developed by Hurwitz in 1912—and, implicitly, in the theory of differential operators by Hilbert in 1904, whose work was subsequently extended by Myller in 1906, Westfall in 1909, Bounitzky in 1909, Elliott in 1928, and Reid in 1931. The cited authors attribute their first application to matrices to Moore in 1920 under the term general reciprocals [33] (though some sources suggest he may have formulated the idea as early as 1906), with independent formulations by Siegel in 1937 and Rao in 1955, and generalizations to singular operators by Tseng in 1933, 1949, and 1956, Murray and von Neumann in 1936, and Atkinson in 1952–1953. A theoretical consolidation occurred with Bjerhammar’s [34] rediscovery of Moore’s formulation, followed by Penrose’s [35,36] introduction of four conditions defining the unique least-squares minimum-norm generalized inverse $\mathbf{G}\equiv {\mathbf{A}}^{†}$, which, such that $\mathbf{G}\in {\mathbb{R}}^{n\times m}$, can be expressed in Equation (1):

$$\left(\mathrm{i}\right)\mathbf{A}\mathbf{G}\mathbf{A}=\mathbf{A}\left(\mathrm{ii}\right)\mathbf{G}\mathbf{A}\mathbf{G}=\mathbf{G}\left(\mathrm{iii}\right){\left(\mathbf{A}\mathbf{G}\right)}^{\top }=\mathbf{A}\mathbf{G}\left(\mathrm{iv}\right){\left(\mathbf{G}\mathbf{A}\right)}^{\top }=\mathbf{G}\mathbf{A}$$

(1)

In econometrics, it led to conditionally unbiased (minimum bias) estimators [37] and a redefinition of the Gauss–Markov theorem [38] in the 1960s, superseding earlier efforts [39].

Further contributions to the theory, calculation, and diverse applications of $\mathbf{G}$ were made in the 1950s to early 1970s by Rao and Mitra [17,40] (a synthesis of the authors’ previous works from 1955–1969), Ben-Israel and Greville [18], Greville [41,42,43,44], Cline [45], Cline and Greville [46], Golub and Kahan [47], Ben-Israel and Cohen [48], and Lewis and Newman [49] (the most cited sources on the topic in the Web of Science database, although the list is not exhaustive; consult Rao and Mitra [17] (pp. vii–viii) for an extended one), which, among others, introduced the concept of a $\{·\}$-generalized inverse $\mathbf{G}\in {\mathbf{A}}^{\{·\}}$, where ${\mathbf{A}}^{\{·\}}\subseteq {\mathbb{R}}^{n\times m}$ is the space of the $\{·\}$-generalized inverses of $\mathbf{A}\in {\mathbb{R}}^{m\times n}$— hereafter, $\{i,j\}$-inverses for $i>1$, $\{i,j,k\}$-inverses, Drazin inverses, and higher-order $\mathbf{G}$ are disregarded because of their inapplicability to the CLSP framework—by satisfying a subset or all of the (i)–(iv) conditions in Equation (1) as described in

Table 1. Selected types of generalized inverses $\mathbf{G}\in {\mathbf{A}}^{\{·\}}$, where ${\mathbf{A}}^{\{·\}}\subseteq {\mathbb{R}}^{n\times m}$, $\mathbf{x}\in {\mathbb{R}}^n$, and $\mathbf{b}\in {\mathbb{R}}^m$.

Type of Inverse	Terminology	Properties
$\left\{1\right\}$	Equation Solving Inverse	$\mathbf{G}\in {\mathbf{A}}^{\left\{1\right\}}$ iff $\mathbf{A}\mathbf{G}\mathbf{A}=\mathbf{A}$. Hence, $\mathbf{G}\mathbf{b}$ is a solution to $\mathbf{A}\mathbf{x}=\mathbf{b}$ for all $\mathbf{b}\in \mathcal{R}\left(\mathbf{A}\right)$.
$\{1,2\}$	Reflexive Inverse	$\mathbf{G}\in {\mathbf{A}}^{\{1,2\}}$ iff $\mathbf{A}\mathbf{G}\mathbf{A}=\mathbf{A}$ and $\mathbf{G}\mathbf{A}\mathbf{G}=\mathbf{G}$. Each $\{1,2\}$-inverse defines a direct sum $\mathcal{N}\left(\mathbf{A}\right)\oplus \mathcal{R}\left(\mathbf{G}\right)={\mathbb{R}}^n$, $\mathcal{R}\left(\mathbf{A}\right)\oplus \mathcal{N}\left(\mathbf{G}\right)={\mathbb{R}}^m$. For complementary subspaces $(\mathcal{N},\mathcal{R})$, ${\mathbf{G}}_{\mathcal{N},\mathcal{R}}$ is unique, with $\mathcal{R}\left({\mathbf{G}}_{\mathcal{N},\mathcal{R}}\right)=\mathcal{R}$ and $\mathcal{N}\left({\mathbf{G}}_{\mathcal{N},\mathcal{R}}\right)=\mathcal{N}$.
$\{1,3\}$	Least Squares Inverse	$\mathbf{G}\in {\mathbf{A}}^{\{1,3\}}$ iff $\mathbf{A}\mathbf{G}\mathbf{A}=\mathbf{A}$ and ${\left(\mathbf{A}\mathbf{G}\right)}^{\top }=\mathbf{A}\mathbf{G}$. Hence, $\mathbf{G}\mathbf{b}$ is the least-squares solution minimizing the norm ${∥\mathbf{A}\mathbf{x}-\mathbf{b}∥}_2^2$.
$\{1,4\}$	Minimum Norm Inverse	$\mathbf{G}\in {\mathbf{A}}^{\{1,4\}}$ iff $\mathbf{A}\mathbf{G}\mathbf{A}=\mathbf{A}$ and ${\left(\mathbf{G}\mathbf{A}\right)}^{\top }=\mathbf{G}\mathbf{A}$. Hence, $\mathbf{G}\mathbf{b}$ is the minimum-norm solution of $\mathbf{A}\mathbf{x}=\mathbf{b}$ for all $\mathbf{b}\in \mathcal{R}\left(\mathbf{A}\right)$.
$\{1,2,3,4\}$	Moore–Penrose Inverse	The unique $\mathbf{G}\equiv {\mathbf{A}}^{†}\in {\mathbf{A}}^{\{1,2,3,4\}}$ is the least-squares minimum-norm solution.

Source: Adapted from Campbell and Meyer (2009, Table 6.1, p. 96) [51] (pp. 91–119) as a summary of Rao and Mitra [17] (pp. 44–71), Rao and Mitra [40], Ben-Israel and Greville [18] (pp. 40–51), and Wang et al. [20] (pp. 10–19, 33–42).

. Formally, for ${\mathbf{G}}^{\left\{1\right\}}\in {\mathbf{A}}^{\left\{1\right\}}$, ${\mathbf{I}}_n\in {\mathbb{R}}^{n\times n}$, ${\mathbf{I}}_m\in {\mathbb{R}}^{m\times m}$, and arbitrary matrices $\mathbf{U},\mathbf{V}\in {\mathbb{R}}^{n\times m}$, any $\left\{1\right\}$-inverse, including all $\{1,j\}$-inverses and ${\mathbf{A}}^{†}$, can be expressed as $\mathbf{G}={\mathbf{G}}^{\left\{1\right\}}+({\mathbf{I}}_n-{\mathbf{G}}^{\left\{1\right\}}\mathbf{A})\mathbf{U}+\mathbf{V}({\mathbf{I}}_m-\mathbf{A}{\mathbf{G}}^{\left\{1\right\}})$, out of which only $\mathbf{G}\equiv {\mathbf{A}}^{†}$ and a constrained $\mathbf{G}\equiv {\mathbf{G}}^{\{1,2\}}\in {\mathbb{R}}^{n\times m}$—here, the Bott–Duffin inverse [50], expressed in modern notation as ${\mathbf{A}}_{\mathbf{S}}^{†}={\mathbf{P}}_{\mathbf{S}}^L{\left({\mathbf{P}}_{\mathbf{S}}^L\mathbf{A}{\mathbf{P}}_{\mathbf{S}}^R\right)}^{†}{\mathbf{P}}_{\mathbf{S}}^R$, where ${\mathbf{P}}_{\mathbf{S}}^L\in {\mathbb{R}}^{m\times m}$ and ${\mathbf{P}}_{\mathbf{S}}^R\in {\mathbb{R}}^{n\times n}$ are orthogonal (perpendicular) projectors onto the rows and columns defined by an orthonormal matrix $\mathbf{S}$—can be uniquely defined (${\mathbf{A}}_{\mathbf{S}}^{†}$ under certain conditions) and qualify as minimum-norm unbiased estimators in the sense of Chipman [37] and Price [38].

Starting from the early 1960s, Cline [45], Rao and Mitra [17] (pp. 64–71), Meyer [52], Ben-Israel and Greville [18] (pp. 175–200), Hartwig [53], Campbell and Meyer [51] (pp. 53–61), Rao and Yanai [54], Tian [55], Rakha [56], Wang et al. [20] (pp. 193–210), and Baksalary and Trenkler [57], among others, extended the formulas for ${\mathbf{A}}^{†}$ to partitioned matrices, including the general row-wise case, ${\mathbf{A}}_1\in {\mathbb{R}}^{m_1\times n}$, ${\mathbf{A}}_2\in {\mathbb{R}}^{m_2\times n}$, $m_1+m_2=m$—and, equivalently, column-wise one, ${\mathbf{A}}_1\in {\mathbb{R}}^{m\times n_1}$, ${\mathbf{A}}_2\in {\mathbb{R}}^{m\times n_2}$, and $n_1+n_2=n$ (Equation (2), used in the numerical stability analysis of the CLSP estimator for ${\mathbf{C}}_{\mathrm{canon}}=\left[\mathbf{C}\mathbf{S}\right]$ in the decomposition $\mathbf{A}=\mathbf{B}{\mathbf{C}}_{\mathrm{canon}}+\mathbf{R}$ given $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, ${\mathbf{C}}_{\mathrm{canon}}\in {\mathbb{R}}^{k\times n}$, and $\mathbf{B}=\mathbf{A}{\mathbf{C}}_{\mathrm{canon}}^{†}=\mathbf{A}{\left[\mathbf{C}\mathbf{S}\right]}^{†}\in {\mathbb{R}}^{m\times k}$):

$${\left[\begin{array}{cc}{\mathbf{A}}_1& {\mathbf{A}}_2\end{array}\right]}^{†}={\left({\left[\begin{array}{cc}{\mathbf{A}}_1& {\mathbf{A}}_2\end{array}\right]}^{\top }\left[\begin{array}{cc}{\mathbf{A}}_1& {\mathbf{A}}_2\end{array}\right]\right)}^{†}{\left[\begin{array}{cc}{\mathbf{A}}_1& {\mathbf{A}}_2\end{array}\right]}^{\top }={\left[\begin{array}{cc}{\mathbf{A}}_1^{\top }{\mathbf{A}}_1& {\mathbf{A}}_1^{\top }{\mathbf{A}}_2\\ {\mathbf{A}}_2^{\top }{\mathbf{A}}_1& {\mathbf{A}}_2^{\top }{\mathbf{A}}_2\end{array}\right]}^{†}\left[\begin{array}{c}{\mathbf{A}}_1^{\top }\\ {\mathbf{A}}_2^{\top }\end{array}\right]$$

(2)

where $rank\left(\left[{\mathbf{A}}_1{\mathbf{A}}_2\right]\right)\le rank\left({\mathbf{A}}_1\right)+rank\left({\mathbf{A}}_2\right)$, with equality iff $\mathcal{R}\left({\mathbf{A}}_1\right)\cap \mathcal{R}\left({\mathbf{A}}_2\right)=\left\{\mathbf{0}\right\}$, and strict inequality iff $\mathcal{R}\left({\mathbf{A}}_1\right)\cap \mathcal{R}\left({\mathbf{A}}_2\right)\ne \left\{\mathbf{0}\right\}$. For the original definitions and formulations, consult Rao and Mitra [17] (pp. 64–66) and Ben-Israel and Greville [18] (pp. 175–200).

To sum up, $\mathbf{G}$ (especially ${\mathbf{A}}^{†}$), SVD, and regularization techniques—namely, Lasso (based on the ${\ell }_1$-norm), Tikhonov regularization (hereafter, referred to as Ridge regression, based on the ${\ell }_2$-norm), and Elastic Net (a convex combination of ${\ell }_1$ and ${\ell }_2$ norms) [4] (pp. 477–479)—have become an integral part of estimation (model-fitting), where ${\mathbf{A}}^{†}$ can be defined as a minimum-norm best linear unbiased estimator (MNBLUE), reducing to the classical BLUE in (over)determined cases. These methods have been applied in (a) natural sciences since the 1940s [24] (pp. 68–156) [34,50] (pp. 85–172, [58]) [59,60,61], and (b) econometrics since the 1960s (pp. 36–157, 174–232, [19]) [37,38] (pp. 61–106, [62]) (pp. 37–338, [63]) in both unconstrained and equality-constrained forms, thereby relaxing previous rank restrictions.

The incorporation of inequality constraints into optimization problems during the 1930s–1950s (driven by the foundational contributions of Kantorovich [64], Koopmans [7], and Dantzig [6], along with the later authors [5]) marked the next milestone in the development of convex optimization under the emerging framework of programming, namely for linear cases (LP)—formally, ${\mathbf{x}}^{*}=\arg {\max }_{\mathbf{x}\in {\mathbb{R}}^n}{\mathbf{c}}^{\top }\mathbf{x}$ subject to $\mathbf{A}\mathbf{x}\le \mathbf{b}$, $\mathbf{x}\ge \mathbf{0}$ (with the dual ${\mathit{\lambda }}^{*}=\arg {\min }_{\mathit{\lambda }\in {\mathbb{R}}^m}{\mathbf{b}}^{\top }\mathit{\lambda }$ subject to ${\mathbf{A}}^{\top }\mathit{\lambda }\ge \mathbf{c})$, where $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, $\mathbf{b}\in {\mathbb{R}}^m$, and $\mathbf{c}\in {\mathbb{R}}^n$—and convex quadratic ones (QP)—formally, ${\mathbf{x}}^{*}=\arg {\min }_{\mathbf{x}\in {\mathbb{R}}^n}\left\{\frac{1}{2}{\mathbf{x}}^{\top }\mathbf{Q}\mathbf{x}+{\mathbf{c}}^{\top }\mathbf{x}\right\}$ subject to $\mathbf{A}\mathbf{x}\le \mathbf{b}$ (with the dual ${\mathit{\lambda }}^{*}=\arg {\max }_{\mathit{\lambda }\in {\mathbb{R}}_{+}^m}\left\{-\frac{1}{2}{({\mathbf{A}}^{\top }\mathit{\lambda }+\mathbf{c})}^{\top }{\mathbf{Q}}^{-1}({\mathbf{A}}^{\top }\mathit{\lambda }+\mathbf{c})-{\mathbf{b}}^{\top }\mathit{\lambda }\right\}$), where $\mathbf{Q}\in {\mathbb{R}}^{n\times n}$ is symmetric positive definite, $\mathbf{c}\in {\mathbb{R}}^n$, $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, and $\mathbf{b}\in {\mathbb{R}}^m$—[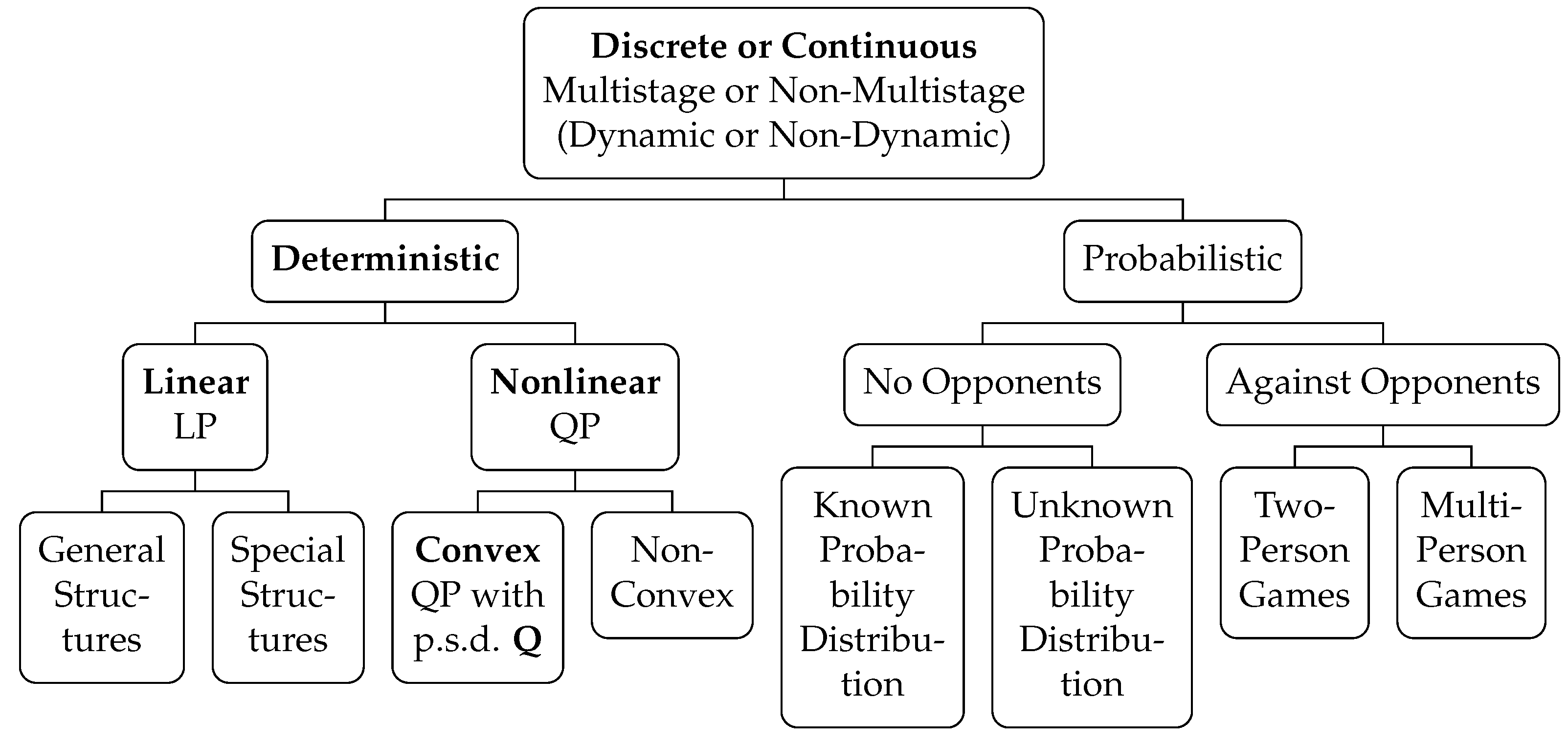2] (pp. 146–213) (for a classification of programming, consult Figure 1) (pp. 355–597, [1]) (pp. 1–31, [6]), with Dantzig’s simplex and Karmarkar’s interior-point algorithms being efficient solvers [65,66].

In the late 1950s–1970s, the application of LP and QP extended to LS problems (which can be referred to as a major generalization of mainstream convex optimization methods; consult Boyd and Vandenberghe [2] (pp. 291–349) for a comprehensive modern overview) with the pioneering works of Wagner [67] and Sielken and Hartley [68], expanded by Kiountouzis [69] and Sposito [70], who first substituted LS with LP-based (${\ell }_1$-norm) least absolute (LAD) and (${\ell }_{\infty }$-norm) least maximum (LDP) deviations and derived unbiased (${\ell }_p$-norm, $1<p<\infty$) estimators with non-unique solutions, whilst, in the early 1990s, Stone and Tovey [66] demonstrated algorithmic equivalence between LP algorithms and iteratively reweighted LS. Judge and Takayama [71] and Mantel [72] reformulated (multiple) LS with inequality constraints as QP, and Lawson and Hanson [19] (pp. 144–147) introduced, among others, the non-negative least squares (NNLS) method. These and further developments are reflected in the second step of the CLSP framework, where $\widehat{\mathbf{z}}=\mathbf{G}\mathbf{b}$ is corrected under a regularization scheme inspired by Lasso ($\alpha =0$), Ridge ($\alpha =1$), and Elastic Net ($0<\alpha <1$) regularization, where ${\widehat{\mathbf{z}}}^{*}=\arg {\min }_{\mathbf{z}\in {\mathbb{R}}^n}\left\{(1-\alpha ){∥\mathbf{z}-\widehat{\mathbf{z}}∥}_1+\alpha {∥\mathbf{z}-\widehat{\mathbf{z}}∥}_2^2\right\}$, subject to $\mathbf{A}\mathbf{z}=\mathbf{b}$.

The final frontier that motivates the formulation of a new framework is the class of ill-posed problems in Hadamard’s sense [4] (pp. 143, 241), i.e., systems with no (i) feasibility, $\mathbf{x}\notin \mathcal{F}:=\left\{\mathbf{x}\right|{\forall }_{i,j}{g}_i\left(\mathbf{x}\right)\le 0,h_j\left(\mathbf{x}\right)=0\}$, (ii) uniqueness, $\exists {\mathbf{x}}_1\ne {\mathbf{x}}_2:\mathbf{A}{\mathbf{x}}_1=\mathbf{A}{\mathbf{x}}_2$, (iii) stability, $\forall \epsilon >0,\exists \delta >0:∥\mathbf{b}-{\mathbf{b}}_{\delta }∥<\delta \Rightarrow ∥{\mathbf{A}}^{†}\mathbf{b}-{\mathbf{A}}^{†}{\mathbf{b}}_{\delta }∥\ge \epsilon$, or formulation—as a well-posed LS, LP, or QP problem—of solution under mainstream assumptions, where $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, $\mathbf{x}\in {\mathbb{R}}^n$, and $\mathbf{b}\in {\mathbb{R}}^m$, such as the ones described in Bolotov [15], Bolotov [16]: namely, (a) underdetermined, $rank\left(\mathbf{A}\right)<min(m,n)$, and/or ill-conditioned linear systems, $\kappa \left(\mathbf{A}\right)={\parallel \mathbf{A}\parallel }_2{\parallel {\mathbf{A}}^{†}\parallel }_2\gg 1$, $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, in cases of LS and LP, where solutions are either non-unique or highly sensitive to perturbations [22,73]; and (b) degenerate, $\#\left\{\mathrm{active}\mathrm{constraints}\mathrm{at}\mathbf{x}\right\}>dim\left(\mathbf{x}\right)=n$, with cycling behavior, $c^{\top }{\mathbf{x}}^{(k+1)}=c^{\top }{\mathbf{x}}^{\left(k\right)}$, and ${\mathbf{x}}^{(k+1)}\ne {\mathbf{x}}^{\left(k\right)}$, $\mathbf{x}\in {\mathbb{R}}^n$, in all LP and QP problems, where efficient methods, such as the simplex algorithm, may fail to converge [27,74]. Such problems have been addressed since the 1940s–1970s by (a) regularization (i.e., a method of perturbations) and (b) problem-specific algorithms [2] (pp. 455–630). For LS cases, the list includes, among others, Lasso, Ridge regularization, and Elastic Net [4] (pp. 477–479), constrained LS methods [75], restricted LS [76], LP-based sparse recovery approaches [73], Gröbner bases [77], as well as derivatives of eigenvectors and Nelson-type, BD-, QR- and SVD-based algorithms [78]. For LS and QP, among others, we have Wolfe’s regularization-based technique for simplex [25] and its modifications [27,74], Dax’s LS-based steepest-descent algorithm [26], a primal-dual NNLS-based algorithm (LSPD) [79], as well as modifications of the ellipsoid algorithm [80]. A major early attempt to unify (NN)LS, LP, and QP within a single framework to solve both well- and ill-posed convex optimization problems was undertaken by Übi [28,29,30,31,32], who proposed a series of problem-specific algorithms (VD, INE, QPLS, and LS1). Figure 2 compares all the mentioned methods by functionality.

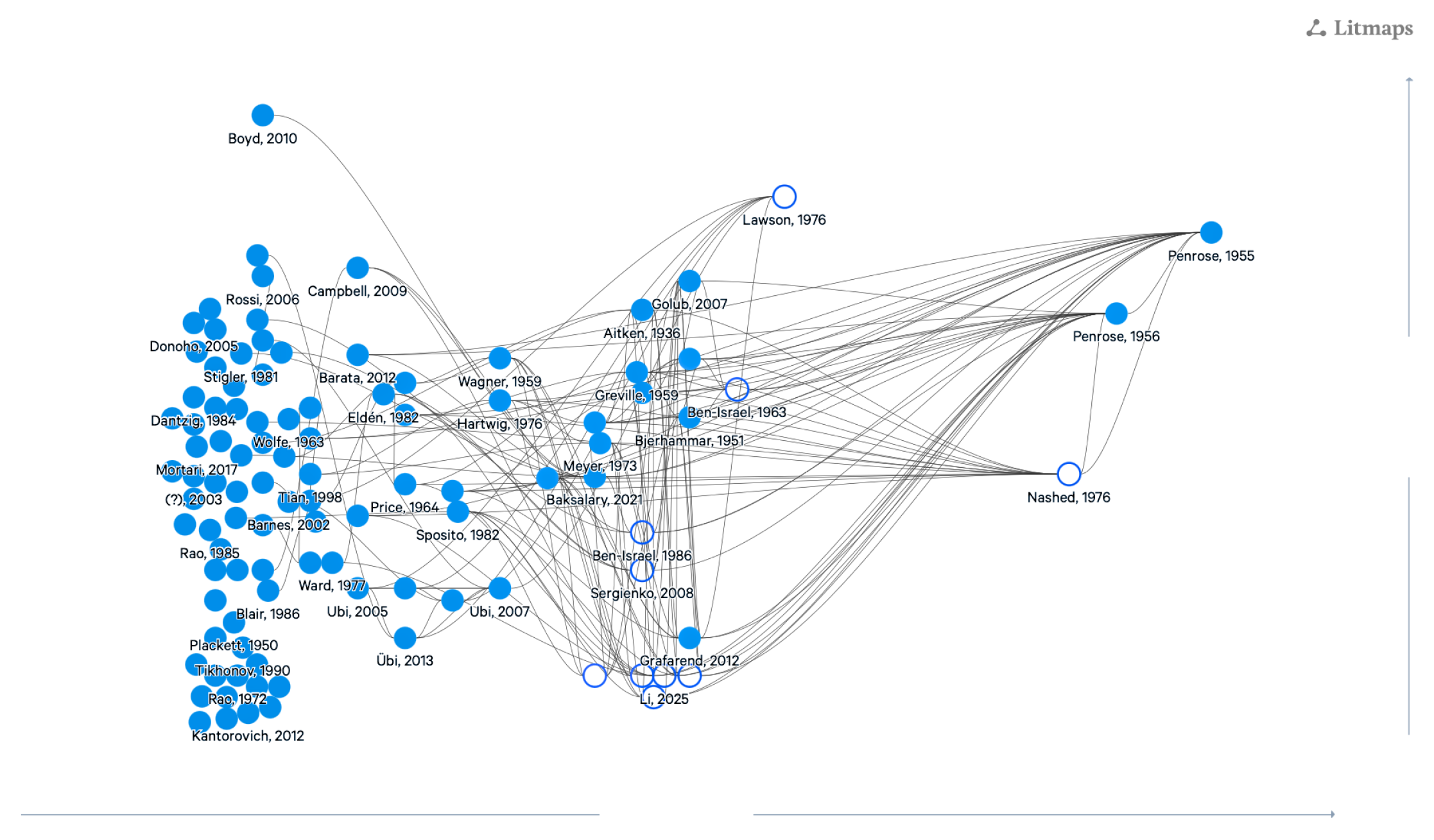
To sum up, based on the citation and reference counts in modern literature mapping software (here, Litmaps), as well as in-group relevance (i.e., the number of citations within the collection) of the above-cited works (consult Figure 3), this text incorporates the seminal studies and an almost exhaustive representation of prior research on the topic in question.

3. Construction and Formalization of the CLSP Estimator

To accommodate the above-described problem classes, a modular two-step CLSP consists of a first (compulsory) step—minimum-norm LS estimation, based on ${\mathbf{A}}^{†}$ or ${\mathbf{A}}_{\mathbf{S}}^{†}$ (hereafter denoted as ${\mathbf{A}}_{\mathbf{Z}}^{†}$ to match $\mathbf{z}$)—followed by a second (optional) step, a regularization-inspired correction. This structure ensures that CLSP is able to yield a unique solution under a strictly convex second-step correction and extends the classical LS framework in both scope and precision, providing a generalized approach that reduces the reliance on problem-specific algorithms [28,29,30,31,32]. 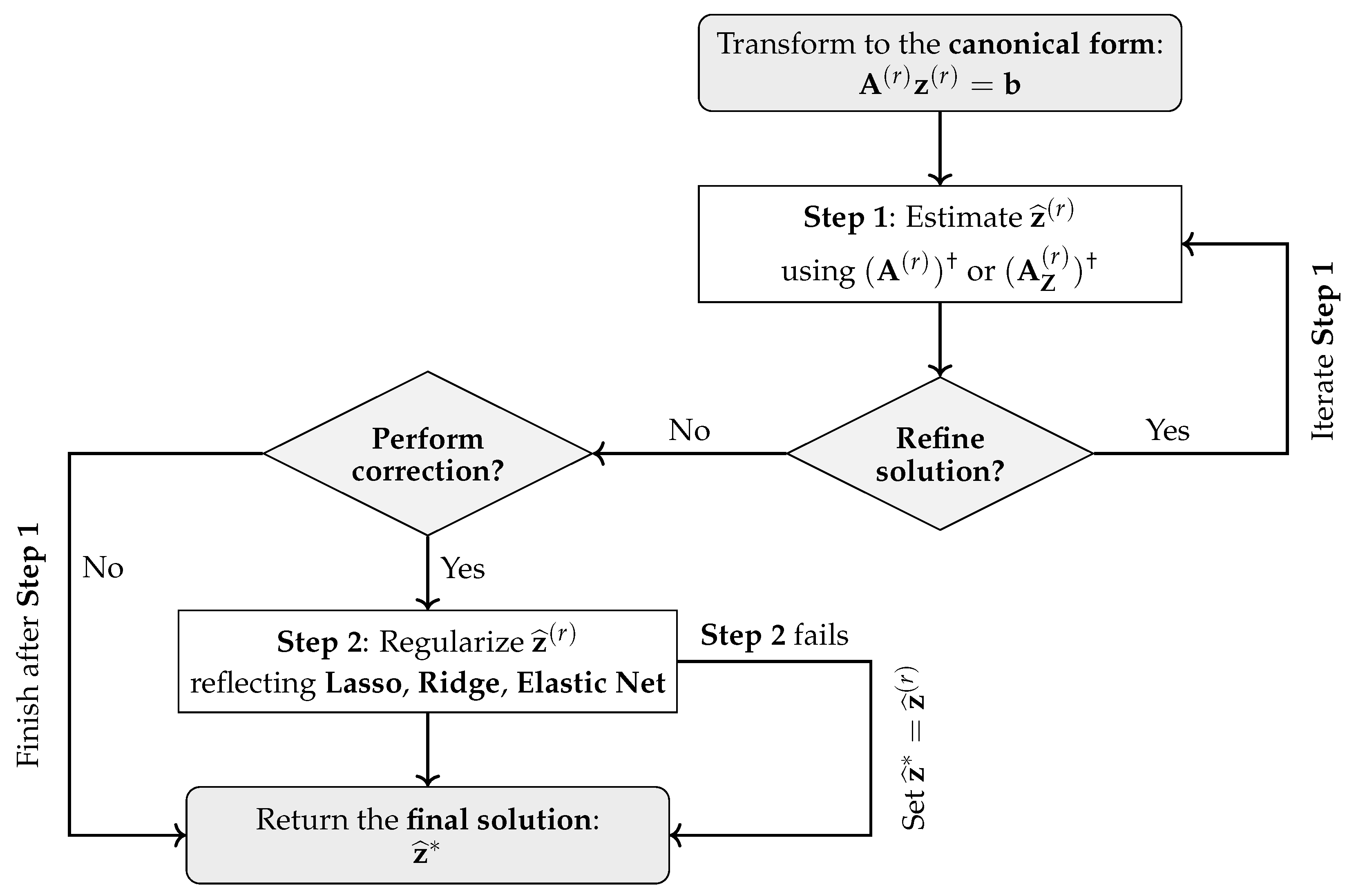The estimator’s algorithmic flow is illustrated in Figure 4 and formalized below.

The first process block in the CLSP algorithmic flow denotes the transformation of the initial problem—${\widehat{\mathbf{x}}}_M^{*}={Proj}_{{\mathbf{x}}_M}\left\{{\mathbf{Q}}_X\left[\begin{array}{c}{\mathbf{x}}_M\\ {\mathbf{x}}_L\end{array}\right]\in {\mathbb{R}}^p:{\forall }_{1\le i\le s}{g}_i({\mathbf{x}}_M,{\mathbf{x}}_L)⋛{\gamma }_i,{\forall }_j{h}_j({\mathbf{x}}_M,{\mathbf{x}}_L)={\eta }_j\right\}$, where ${Proj}_{{\mathbf{x}}_M}$ is the projection onto the ${\mathbf{x}}_M$ coordinates, ${\mathbf{x}}_M\in {\mathbb{R}}^{p-l}$ is the vector of model (target) variables to be estimated (${\widehat{\mathbf{x}}}_M^{*}$), ${\mathbf{x}}_L\in {\mathbb{R}}^l$, $l\ge 0$, is a vector of latent variables that appear only in the constraint functions $g_i(·)$ and $h_j(·)$, such that ${\mathbf{Q}}_X\left[\begin{array}{c}{\mathbf{x}}_M\\ {\mathbf{x}}_L\end{array}\right]=\mathbf{x}\in {\mathbb{R}}^p$, ${\mathbf{Q}}_X$ is the permutation matrix, and $g_i(·)⋛{\gamma }_i$ and $h_j(·)={\eta }_j$ are the linear(ized) inequality and equality constraints, ${\forall }_{i,j}{\gamma }_i,{\eta }_j\in \mathbf{b}$—to the canonical form ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$ (a term first introduced in LP [6] (pp. 75–81)), where (a) ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{m\times n}$ is the block design matrix consisting of a ${\forall }_i{g}_i(·)$-and-${\forall }_j{h}_j(·)$ constraints matrix $\mathbf{C}\in {\mathbb{R}}^{k\times p}$, a model matrix $\mathbf{M}={\mathbf{Q}}_M^L\left[\begin{array}{c}{\mathbf{M}}_{\mathrm{partial}}\\ \mathbf{0}\end{array}\right]{\mathbf{Q}}_M^R\in {\mathbb{R}}^{(m-k)\times p}$, a sign slack matrix $\mathbf{S}={\mathbf{Q}}_S^L\left[\begin{array}{c}{\mathbf{S}}_s\subseteq {\forall }_{{\sigma }_1,\dots ,{\sigma }_s\in \{-1,+1\}}diag\left({\sigma }_1,\dots ,{\sigma }_s\right)\\ \mathbf{0}\end{array}\right]{\mathbf{Q}}_S^R\in {\mathbb{R}}^{k\times (n-p)}$, and either a zero matrix $\mathbf{0}$ (if $r=1$) or a reverse-sign slack matrix ${\mathbf{S}}_{\mathrm{residual}}=\left[\mathbf{0}diag\left(-sign\left({(\mathbf{b}-{\mathbf{A}}^{(r-1)}{\widehat{\mathbf{z}}}^{(r-1)})}_{k+1:m}\right)\right)\right]\in {\mathbb{R}}^{(m-k)\times (n-p)}$ (if $r>1$) (see Equation (3)):

$${\mathbf{A}}^{\left(r\right)}=\left[\begin{array}{cc}\mathbf{C}& \mathbf{S}\\ \mathbf{M}& \left\{\begin{array}{cc}\mathbf{0},\hfill & \mathrm{initial}\mathrm{iteration},r=1\hfill \\ {\mathbf{S}}_{\mathrm{residual}},\hfill & \mathrm{subsequent}\mathrm{iterations},r>1\hfill \end{array}\right.\end{array}\right]$$

(3)

and (b) ${\mathbf{z}}^{\left(r\right)}=\left[\begin{array}{c}{\mathbf{x}}^{\left(r\right)}\\ {\left({\mathbf{y}}^{\left(r\right)}\right)}^{*}\end{array}\right]\in {\mathbb{R}}^n$ is the full vector of unknowns, comprising (model) ${\mathbf{x}}^{\left(r\right)}\in {\mathbb{R}}^p$ and (slack) ${\left({\mathbf{y}}^{\left(r\right)}\right)}^{*}=\left[\begin{array}{c}{\mathbf{y}}^{\left(r\right)}\\ {\mathbf{y}}_{\mathrm{residual}}^{\left(r\right)}\end{array}\right]\in {\mathbb{R}}^{n-p}$, $y_i^{\left(r\right)}\ge 0$ and $y_j^{\left(r\right)}=0$—an equivalent problem [2] (pp. 130–132), where $g_i{(·)}^a=g_i(·)+{\mathbf{S}}_{ii}{y}_i^{\left(r\right)}=0$ and $h_j{(·)}^a=h_j(·)$. The constraint functions $g_i{(·)}^a$ and $h_j{(·)}^a$ must be linear(ized), so that $\mathbf{C},\mathbf{S}\subseteq {\mathbf{A}}^{\left(r\right)}\iff \mathbf{C}{\mathbf{x}}^{\left(r\right)}+\mathbf{S}{\left({\mathbf{y}}^{\left(r\right)}\right)}^{*}={\mathbf{b}}_{1:k}$, $k\le m$.

In practical implementations, for problems with $(m>m_E)\vee (n>n_E)$, where E is an estimability limit, a block-wise estimation can be performed through the partitioning ${\mathbf{A}}^{\left(r\right)}=\left\{{\mathbf{A}}_{subset,i_E,j_E}^{\left(r\right)}\right\}$, $m_{\mathrm{subset}}=m_{\mathrm{reduced}}-1$, $n_{\mathrm{subset}}=n_{\mathrm{reduced}}-1$, $i_E\in \{1,\dots ,⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉\}$, and $j_E\in \{1,\dots ,⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\}$, leading to a total of $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉·⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\right)$ matrices ${\mathbf{A}}_{\mathrm{reduced}}^{\left(r\right)}\in {\mathbb{R}}^{m_{\mathrm{reduced}}\times n_{\mathrm{reduced}}}$, composed of ${\mathbf{A}}_{\mathrm{subset}}^{\left(r\right)}$ and $\sum a_{i,j}^{\left(r\right)}$, $i\notin {\mathcal{I}}_{\mathrm{subset}}\subset \{1,\dots ,m\}$, $j\notin {\mathcal{J}}_{\mathrm{subset}}\subset \{1,\dots ,n\}$, and a total of $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉\right)$ vectors ${\mathbf{b}}_{\mathrm{r}.}\in {\mathbb{R}}^{m_{\mathrm{reduced}}}$ (as formalized in Equation (4)):

$${\mathbf{A}}_{\mathrm{reduced}}^{\left(r\right)}={\mathbf{Q}}_A^{\mathcal{I}}\left[\begin{array}{cc}{\mathbf{A}}_{{\mathcal{I}}_{\mathrm{subset}},{\mathcal{J}}_{\mathrm{subset}}}^{\left(r\right)}& \sum _{j\notin {\mathcal{J}}_{\mathrm{subset}}}{a}_{i,j}^{\left(r\right)}\\ \sum _{i\notin {\mathcal{I}}_{\mathrm{subset}}}{a}_{i,j}^{\left(r\right)}& \sum _{i\notin {\mathcal{I}}_{\mathrm{subset}}}\sum _{j\notin {\mathcal{J}}_{\mathrm{subset}}}{a}_{i,j}^{\left(r\right)}\end{array}\right]{\mathbf{Q}}_A^{\mathcal{J}},{\mathbf{b}}_{\mathrm{r}.}={\mathbf{Q}}_b^{\mathcal{I}}\left[\begin{array}{c}{\mathbf{b}}_{{\mathcal{I}}_{\mathrm{subset}}}\\ \sum _{i\notin {\mathcal{I}}_{\mathrm{subset}}}{b}_i\end{array}\right]$$

(4)

$\sum a_{i,j}^{\left(r\right)}$ are then treated as slack rows/columns, i.e., incorporated into $\mathbf{S}$, to act as balancing adjustments since the reduced model, by construction, tends to inflate the estimates ${\widehat{a}}_{i_E,j_E}$. However, full compensation of information loss, caused by aggregation, is infeasible; hence, estimable (smaller) full models are always preferred over reduced (per parts) estimation.

The second process block, i.e., the first step of the CLSP estimator, denotes obtaining an (iterated if $r>1$) estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}={\mathbf{G}}^{\left(r\right)}\mathbf{b}$ (alternatively, $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉·⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\right)$-times ${\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{\left(r\right)}={\mathbf{G}}_{\mathrm{reduced}}^{\left(r\right)}{\mathbf{b}}_{\mathrm{r}.}$ with ${\widehat{\mathbf{z}}}_{i_E,j_E}^{\left(r\right)}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{\left(r\right),(i_E,j_E)}\right\}$) through the (constrained) Bott–Duffin inverse ${\mathbf{G}}^{\left(r\right)}\equiv {\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\in {\mathbb{R}}^{n\times m}$ [50] (pp. 49–64, [20]), defined on a subspace specified by a symmetric idempotent matrix $\mathbf{Z}\in {\mathbb{R}}^{n\times n}$ (regulating solution-space exclusion through binary entries 0/1, such that ${\mathbf{P}}_{\mathbf{Z}}^L=\mathbf{Z}$ restricts the domain of estimated variables to the selected subspace, while ${\mathbf{P}}_{\mathbf{Z}}^R={\mathbf{I}}_m$ leaves the data vector, i.e., the input $\mathbf{b}$, unprojected). ${\mathbf{G}}^{\left(r\right)}\equiv {\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}$ reduces to the Moore–Penrose pseudoinverse ${\mathbf{G}}^{\left(r\right)}\equiv {\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}\in {\mathbb{R}}^{n\times m}$ when $\mathbf{Z}={\mathbf{I}}_n$, and equals the standard inverse ${\mathbf{G}}^{\left(r\right)}\equiv {\left({\mathbf{A}}^{\left(r\right)}\right)}^{-1}$ iff $\mathbf{Z}={\mathbf{I}}_n\wedge rank\left({\mathbf{A}}^{\left(r\right)}\right)=m=n$ (the application of a left-sided Bott–Duffin inverse to ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$ is given by Equation (5)):

$${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}=\left[{\left(\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)}^{†}\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }\right]\mathbf{b},{\mathbf{Z}}^2=\mathbf{Z}={\mathbf{Z}}^{\top }$$

(5)

The number of iterations (r) increases until a termination condition is met, such as error $\left|{\displaystyle \frac{1}{\sqrt{m}}}{∥(\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)})∥}_2-{\displaystyle \frac{1}{\sqrt{m}}}{∥(\mathbf{b}-{\mathbf{A}}^{(r-1)}{\widehat{\mathbf{z}}}^{(r-1)})∥}_2\right|<\epsilon$ or $r>r_{\mathrm{limit}}$, whichever occurs first—implemented in CLSP-based software—although any goodness-of-fit metric can be employed. The described condition, maximizing the fit quality—especially under a missing second step—is, however, heuristic, with a formal proof of convergence lying beyond the scope of this work. In practical implementations, ${\widehat{\mathbf{z}}}^{\left(r\right)}$ is efficiently computed using the SVD (see Appendix A.1) with optional Ridge regularization to stabilize a nearly singular system.

The third process block, i.e., the second step of the CLSP estimator, denotes obtaining a corrected final solution ${\widehat{\mathbf{z}}}^{*}$ (alternatively, $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉·⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\right)$-times ${\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{*}$ with ${\widehat{\mathbf{z}}}_{i_E,j_E}^{*}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{*,(i_E,j_E)}\right\}$)—unless the algorithmic flow terminates after Step 1, in which case ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}$—by penalizing deviations from the (iterated if $r>1$) estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ reflecting Lasso ($\alpha =0\iff {\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}+\widehat{\mathbf{u}}$, where $\widehat{\mathbf{u}}=\arg {\min }_{\mathbf{u}}{\parallel \mathbf{u}\parallel }_1,\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}({\widehat{\mathbf{z}}}^{\left(r\right)}+\mathbf{u})=\mathbf{b}$), Ridge ($\alpha =1\iff {\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}+{\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}{\mathbf{A}}^{\left(r\right)}\widehat{\mathbf{u}}$, where ${\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}{\mathbf{A}}^{\left(r\right)}={\mathbf{P}}_{\mathcal{R}\left({\mathbf{A}}^{\top }\right)}$, a projector equal to $\mathbf{I}$ iff ${\mathbf{A}}^{\left(r\right)}$ is of full column rank, and $\widehat{\mathbf{u}}=\arg {\min }_{\mathbf{u}}{\parallel \mathbf{u}\parallel }_2^2,\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}({\widehat{\mathbf{z}}}^{\left(r\right)}+\mathbf{u})=\mathbf{b}$), and Elastic Net ($0<\alpha <1\iff {\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}+(1-\alpha )\widehat{\mathbf{u}}+\alpha {\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}{\mathbf{A}}^{\left(r\right)}\widehat{\mathbf{u}}$, where $\widehat{\mathbf{u}}=\arg {\min }_{\mathbf{u}}\left\{{(1-\alpha )\parallel \mathbf{u}\parallel }_1+\alpha {\parallel \mathbf{u}\parallel }_2^2\right\},\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}({\widehat{\mathbf{z}}}^{\left(r\right)}+\mathbf{u})=\mathbf{b}$) (pp. 306–310, [2]) (pp. 477–479, [4]) (the combination of Lasso, Ridge, and Elastic Net corrections of ${\widehat{\mathbf{z}}}^{*}$ is given by Equation (6)):

$${\widehat{\mathbf{z}}}^{*}=\arg \underset{\mathbf{z}\in {\mathbb{R}}^n}{\min }\left\{(1-\alpha ){∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_1+\alpha {∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2\right\},\alpha \in [0,1],\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$$

(6)

where the parameter $\alpha$ may be selected arbitrarily or determined from the input $\mathbf{b}$ using an appropriate criterion, such as minimizing prediction error via cross-validation, satisfying model-selection heuristics (e.g., AIC or BIC), or optimizing residual metrics under known structural constraints. Alternatively, $\alpha$ may be fixed at benchmark values, e.g., $\alpha \in \{0,{\displaystyle \frac{1}{2}},1\}$, or based on an error rule, e.g., $\alpha =min\left({\displaystyle \frac{{\left(\frac{1}{\sqrt{m}}{∥(\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*})∥}_2\right)}_{\alpha =0}}{{\left(\frac{1}{\sqrt{m}}{∥(\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*})∥}_2\right)}_{\alpha =0}+{\left(\frac{1}{\sqrt{m}}{∥(\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*})∥}_2\right)}_{\alpha =1}+\epsilon }},1\right)$, $\epsilon \to 0^{+}$—in CLSP-based software. In practical implementations, ${\widehat{\mathbf{z}}}^{*}$, obtained from solving a convex optimization problem, is efficiently computed with the help of numerical solvers.

To sum up, the definition of the process blocks ensures that the CLSP estimator yields a unique final solution ${\widehat{\mathbf{z}}}^{*}$ under regularization weight $\alpha \in (0,1]$ owing to the strict convexity of the objective function; see Theorem 1 (although Theorem 1 is mathematically straightforward, it is included for completeness because its corollaries establish the conditions for uniqueness and convergence that underlie special cases). For $\alpha =0$, the solution remains convex but may not be unique unless additional structural assumptions are imposed. In the specific case of $\alpha =1$, the estimator reduces to the Minimum-Norm Best Linear Unbiased Estimator (MNBLUE), or, alternatively, to a block-wise $m_{\mathrm{subset}}\times n_{\mathrm{subset}}$-MNBLUE across $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉·⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\right)$ reduced problems (for a proof, consult Theorem 2 and its corollaries). It is, however, important to note that—when compared to the classical BLUE—the CLSP, as an MNBLUE estimator, by definition, is not constrained by the same Gauss–Markov conditions and remains well-defined under rank-deficient or underdetermined systems ($m<n$) by introducing the minimum-norm condition as a substitute for the homoscedasticity and full-rank assumptions of the original theorem. Therefore, the MNBLUE represents a generalized or, for ill-posed cases, a problem-class-specific extension of the BLUE, applicable to systems which violate one or more Gauss–Markov requirements while still preserving (a) linearity, (b) unbiasedness, and (c) minimum variance (as demonstrated in Theorem 2, although a formal theoretical treatment of the MNBLUE is beyond the scope of this work).

Theorem 1. 

Let ${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}$ be the r-iterated estimate obtained in the first step of the CLSP algorithm, and let ${\widehat{\mathbf{z}}}^{*}$ be the second-step correction obtained through convex programming by solving ${\widehat{\mathbf{z}}}^{*}=\arg {\min }_{\mathbf{z}\in {\mathbb{R}}^n}\left\{(1-\alpha ){∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_1+\alpha {∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2\right\},\alpha \in (0,1],\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$ (i.e., the regularization parameter excludes a pure Lasso-type correction), then the final solution ${\widehat{\mathbf{z}}}^{*}$ is unique.

Proof. 

Let ${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}$ denote the linear estimator obtained via the Bott–Duffin inverse, defined on a subspace determined by a symmetric idempotent matrix $\mathbf{Z}$, and producing a conditionally unbiased estimate over that subspace. The Bott–Duffin inverse ${\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}$ is given by ${\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}={\left(\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)}^{†}\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }$, and the estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ is unique if $rank\left({\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)=dim\left(\mathcal{R}\left(\mathbf{Z}\right)\right)$. In this case, ${\widehat{\mathbf{z}}}^{\left(r\right)}$ is the unique minimum-norm solution in $\mathcal{R}\left(\mathbf{Z}\right)$. In all other cases, the solution set is affine and given by ${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}+\left[ker\left({\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)\cap \mathcal{R}\left(\mathbf{Z}\right)\right]$, where the null-space component represents degrees of freedom not fixed by the constraint ${\mathbf{A}}^{\left(r\right)}\mathbf{Z}$, and hence ${\widehat{\mathbf{z}}}^{\left(r\right)}$ is not unique. At the same time, the second-step estimate ${\widehat{\mathbf{z}}}^{*}$ is obtained by minimizing the function $(1-\alpha ){∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_1+\alpha {∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2$ over the affine (hence convex and closed) constraint set ${\mathcal{F}}^{\left(r\right)}=\left\{\mathbf{z}\in {\mathbb{R}}^n|{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}\right\}$. Under $\alpha \in (0,1]$, the quadratic term $\alpha {∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2$ contributes a positive-definite Hessian $2\alpha \mathbf{I}\succ 0$ to the objective function, making it a strictly convex parabola-like curvature, and, given ${\mathcal{F}}^{\left(r\right)}\ne \varnothing$, the minimizer ${\mathbf{z}}^{*}$ exists and is unique. Therefore, the CLSP estimator with $\alpha \in (0,1]$ yields a unique ${\widehat{\mathbf{z}}}^{*}$.    □

Corollary 1. 

Let the final solution be ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}$, where ${\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}$ denotes the Bott–Duffin inverse on a subspace defined by a symmetric idempotent matrix $\mathbf{Z}$. Then (one-step) ${\widehat{\mathbf{z}}}^{*}$ is unique iff $rank\left({\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)=dim\left(\mathcal{R}\left(\mathbf{Z}\right)\right)$. Else, the solution set is affine and given by ${\widehat{\mathbf{z}}}^{*}\in {\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}+\left[ker\left({\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)\cap \mathcal{R}\left(\mathbf{Z}\right)\right]$, which implies that the minimizer ${\mathbf{z}}^{*}$ is not unique, i.e., $\#\arg \min (·)>1$.

Corollary 2. 

Let ${\widehat{\mathbf{z}}}^{*}$ be the final solution obtained in the second step of the CLSP estimator by solving ${\widehat{\mathbf{z}}}^{*}=\arg {\min }_{\mathbf{z}\in {\mathbb{R}}^n}\left\{{∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_1\right\},\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$ (i.e., the regularization parameter is set to $\alpha =0$, corresponding to a Lasso correction). Then the solution ${\widehat{\mathbf{z}}}^{*}$ exists and the problem is convex. The solution is unique iff the following two conditions are simultaneously satisfied: (1) the affine constraint set ${\mathcal{F}}^{\left(r\right)}=\left\{\mathbf{z}\in {\mathbb{R}}^n|{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}\right\}$ intersects the subdifferential of $\parallel \mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}{\parallel }_1$ at exactly one point, and (2) the objective function is strictly convex on ${\mathcal{F}}^{\left(r\right)}$, which holds when ${\mathcal{F}}^{\left(r\right)}$ intersects the interior of at most one orthant in ${\mathbb{R}}^n$. In all other cases, the minimizer ${\mathbf{z}}^{*}$ is not unique, and the set of optimal solutions forms a convex subset of the feasible region ${\mathcal{F}}^{\left(r\right)}$; that is, the final solution ${\widehat{\mathbf{z}}}^{*}\in \arg {\min }_{\mathbf{z}\in {\mathcal{F}}^{\left(r\right)}}{∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_1$, where $\arg \min (·)$ is convex and $\#\arg \min (·)>1$.

Theorem 2. 

Let ${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}$ be the r-iterated estimate obtained in the first step of the CLSP algorithm, and let ${\widehat{\mathbf{z}}}^{*}$ be the second-step correction obtained through convex programming by solving ${\widehat{\mathbf{z}}}^{*}=\arg {\min }_{\mathbf{z}\in {\mathbb{R}}^n}\left\{{∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2\right\},\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$ (i.e., the regularization parameter is $\alpha =1$, corresponding to a Ridge correction), then ${\widehat{\mathbf{z}}}^{*}$ is the Minimum-Norm Best Linear Unbiased Estimator (MNBLUE) of $\mathbf{z}$ under the linear(ized) constraints set by the canonical form of the CLSP.

Proof. 

Let ${\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}$ denote the linear estimator obtained via the Bott–Duffin inverse, defined on a subspace determined by a symmetric idempotent matrix $\mathbf{Z}$, and producing a conditionally unbiased estimate over that subspace. The Bott–Duffin inverse is ${\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}={\left(\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)}^{†}\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }$ and the estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ is unique if $rank\left({\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)=dim\left(\mathcal{R}\left(\mathbf{Z}\right)\right)$. Given the linear model derived from the canonical form $\mathbf{b}={\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}+\epsilon$, where $\epsilon$ are residuals with $\mathbb{E}\left[\epsilon \right]=\mathbf{0}$, it follows that $\mathbb{E}\left[{\widehat{\mathbf{z}}}^{\left(r\right)}\right]=\mathbb{E}\left[{\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbf{b}\right]={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}\mathbb{E}\left[\mathbf{b}\right]={\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}{\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}$. Substituting ${\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}$ yields $\mathbb{E}\left[{\widehat{\mathbf{z}}}^{\left(r\right)}\right]={\left(\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\mathbf{Z}\right)}^{†}\mathbf{Z}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}$. By the generalized projection identity ${\left({\mathbf{A}}_{\mathbf{Z}}^{\left(r\right)}\right)}^{†}{\mathbf{A}}^{\left(r\right)}\mathbf{Z}=\mathbf{Z}$, one obtains $\mathbb{E}\left[{\widehat{\mathbf{z}}}^{\left(r\right)}\right]=\mathbf{Z}{\mathbf{z}}^{\left(r\right)}$, which proves conditional unbiasedness on $\mathcal{R}\left(\mathbf{Z}\right)$ (and full unbiasedness if $\mathbf{Z}=\mathbf{I}$). Subsequently, the second-step estimate ${\widehat{\mathbf{z}}}^{*}$ is obtained by minimizing the squared Euclidean distance between ${\widehat{\mathbf{z}}}^{\left(r\right)}$ and $\mathbf{z}$, subject to the affine constraint ${\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$, which corresponds, in geometric and algebraic terms, to an orthogonal projection of ${\widehat{\mathbf{z}}}^{\left(r\right)}$ onto the affine (hence convex and closed) subspace ${\mathcal{F}}^{\left(r\right)}=\left\{\mathbf{z}\in {\mathbb{R}}^n|{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}\right\}$. By Theorem 1, the unique minimizer ${\mathbf{z}}^{*}$ exists and is given explicitly by ${\mathbf{z}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}+{\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}\left(\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}\right)$. This expression satisfies the first-order optimality condition of the convex program and ensures that ${\mathbf{z}}^{*}$ is both feasible and closest (in the examined ${\ell }_2$-norm) to ${\widehat{\mathbf{z}}}^{\left(r\right)}$ among all solutions in ${\mathcal{F}}^{\left(r\right)}$. Therefore, ${\mathbf{z}}^{*}$ is (1) linear (being an affine transformation of a linear estimator), (2) unbiased (restricted to the affine feasible space), (3) minimum-norm (by construction), and (4) unique (by strict convexity). By the generalized Gauss–Markov theorem (Chapter 7, Definition 4, p. 139, [17]) (Chapter 8, Section 3.2, Theorem 2, p. 287, [18]), it follows that ${\widehat{\mathbf{z}}}^{*}$ is the Minimum-Norm Best Linear Unbiased Estimator (MNBLUE) under the set of linear(ized) constraints ${\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$—i.e., the one with the smallest dispersion (in the Löwner sense) among the class of unbiased minimum second-norm least-squares estimators ${\widehat{\mathbf{z}}}^{*}=\arg {\min }_{\mathbf{z}}{∥\mathbf{b}-\mathbf{A}\mathbf{z}∥}_2^2={\mathbf{G}}^{\{1,3,4\}}\mathbf{b}+\mathbf{\epsilon }$, where $\mathbf{E}\left(\mathbf{\epsilon }\right)=0$ and $\mathrm{Var}\left(\mathbf{\epsilon }\right)=0$ given the Ridge-inspired convex programming correction (residual sterilization), ${\widehat{\mathbf{z}}}^{*}=\arg {\min }_{\mathbf{z}\in {\mathbb{R}}^n}\left\{{∥\mathbf{z}-{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2\right\},\mathrm{s}.\mathrm{t}.{\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$, ensuring strict satisfaction of the problem constraints ${\mathbf{A}}^{\left(r\right)}\mathbf{z}=\mathbf{b}$, under the assumption of a feasible Step 2.    □

Corollary 3. 

Let the canonical system ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$ be consistent and of full column rank, ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{m\times n}$, $m\ge n$, and $rank\left({\mathbf{A}}^{\left(r\right)}\right)=n$. Suppose that the CLSP algorithm terminates after Step 1 and that $\mathbf{Z}={\mathbf{I}}_n$, such that ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}={\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}\mathbf{b}={\left({\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\right)}^{-1}{\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }\mathbf{b}$. Then, provided the classical linear model $\mathbf{b}={\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}+\epsilon$, where $\mathbb{E}\left[\epsilon \right]=\mathbf{0}$ and $Cov\left(\epsilon \right)={\sigma }^2{\mathbf{I}}_m$, holds, the CLSP estimator is equivalent to OLS while ${\widehat{\mathbf{z}}}^{*}$ is the Best Linear Unbiased Estimator (BLUE).

Corollary 4. 

Let ${\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{\left(r\right)}={\mathbf{A}}_{{\mathbf{Z}}_{\mathrm{reduced}},\mathrm{reduced}}^{†}{\mathbf{b}}_{\mathrm{r}.}$ be the r-iterated estimate obtained via the Bott–Duffin inverse, defined on a subspace determined by a symmetric idempotent matrix ${\mathbf{Z}}_{\mathrm{reduced}}$, and producing a conditionally unbiased estimate over that subspace. Subsequently, the estimate ${\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{*}$ is obtained by minimizing the squared Euclidean distance between ${\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{\left(r\right)}$ and ${\mathbf{z}}_{\mathrm{reduced}}$, subject to the affine constraint ${\mathbf{A}}_{\mathrm{reduced}}^{\left(r\right)}{\mathbf{z}}_{\mathrm{reduced}}={\mathbf{b}}_{\mathrm{r}.}$, such that ${\widehat{\mathbf{z}}}_{i_E,j_E}^{*}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{*,(i_E,j_E)}\right\}$. Then each ${\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{*}$ is the Minimum-Norm Best Linear Unbiased Estimator (MNBLUE) under the linear(ized) constraints defined by the canonical form of each reduced system of the CLSP, and ${\widehat{\mathbf{z}}}^{*}$ is a block-wise$m_{\mathrm{subset}}\times n_{\mathrm{subset}}$-MNBLUE corresponding to each of the $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉·⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\right)$ reduced problems.

4. Numerical Stability of the Solutions ${\widehat{\mathbf{z}}}^{\left(\mathit{r}\right)}$ and ${\widehat{\mathbf{z}}}^{*}$

The numerical stability of solutions, potentially affecting solver convergence in practical implementations, at each step of the CLSP estimator—both the (iterated if $r>1$) first-step estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ (alternatively, ${\widehat{\mathbf{z}}}_{i_E,j_E}^{\left(r\right)}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{\left(r\right),(i_E,j_E)}\right\}$) and the final solution ${\widehat{\mathbf{z}}}^{*}$ (alternatively, ${\widehat{\mathbf{z}}}_{i_E,j_E}^{*}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{*,(i_E,j_E)}\right\}$)—depends on the condition number of the design matrix, $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)$, which, given its block-wise formulation in Equation (3), can be analyzed as a function of the “canonical” constraints matrix ${\mathbf{C}}_{\mathrm{canon}}=\left[\mathbf{C}\mathbf{S}\right]\in {\mathbb{R}}^{k\times n}$ as a fixed, r-invariant, part of ${\mathbf{A}}^{\left(r\right)}$. For both full and reduced problems, sensitivity analysis of $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)$with respect to constraints (i.e., rows) in ${\mathbf{C}}_{\mathrm{canon}}$, especially focused on their reduction (i.e., dropping), is performed based on the decomposition (Equations (7) and (8)):

$${\mathbf{A}}^{\left(r\right)}={\mathbf{B}}^{\left(r\right)}{\mathbf{C}}_{\mathrm{canon}}+{\mathbf{R}}^{\left(r\right)}={\mathbf{B}}^{\left(r\right)}\left[\begin{array}{cc}\mathbf{C}& \mathbf{S}\end{array}\right]+{\mathbf{R}}^{\left(r\right)},{\mathbf{R}}^{\left(r\right)}={\mathbf{A}}^{\left(r\right)}(\mathbf{I}-{\mathbf{P}}_{\mathcal{R}\left({\left[\mathbf{C}\mathbf{S}\right]}^{\top }\right)})$$

(7)

where ${\mathbf{B}}^{\left(r\right)}={\mathbf{A}}^{\left(r\right)}{\mathbf{C}}_{\mathrm{canon}}^{†}\in {\mathbb{R}}^{m\times k}$ denotes the constraint-induced, r-variant, part of $\mathbf{A}$, and, when the rows of ${\mathbf{A}}^{\left(r\right)}$ lie entirely within $\mathcal{R}\left({\mathbf{C}}_{\mathrm{canon}}\right)$, i.e., ${\mathbf{A}}^{\left(r\right)}={\mathbf{A}}^{\left(r\right)}{\mathbf{P}}_{\mathcal{R}\left({\left[\mathbf{C}\mathbf{S}\right]}^{\top }\right)}\iff {\mathbf{R}}^{\left(r\right)}=\mathbf{0}$,

$$\begin{array}{cc}\hfill \kappa \left({\mathbf{A}}^{\left(r\right)}\right)& \le \kappa \left({\mathbf{B}}^{\left(r\right)}\right)·\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)\hfill \\ \hfill \kappa \left({\mathbf{A}}^{\left(r\right)}\right)+\Delta {\kappa }_A& \le \left(\kappa \left({\mathbf{B}}^{\left(r\right)}\right)+\Delta {\kappa }_B\right)·\left(\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)+\Delta {\kappa }_C\right)\hfill \\ \hfill & =\kappa \left({\mathbf{B}}^{\left(r\right)}\right)·\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)+\Delta {\kappa }_B·\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)+\kappa \left({\mathbf{B}}^{\left(r\right)}\right)·\Delta {\kappa }_C+\Delta {\kappa }_B·\Delta {\kappa }_C\hfill \end{array}$$

(8)

i.e., a change in $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)$ consists of a (lateral) constraint-side effect, $\kappa \left({\mathbf{B}}^{\left(r\right)}\right)·\Delta {\kappa }_C$, induced by structural modifications in ${\mathbf{C}}_{\mathrm{canon}}$, an (axial) model-side effect, $\Delta {\kappa }_B·\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)$, reflecting propagation into ${\mathbf{B}}^{\left(r\right)}$—where ${\mathbf{B}}^{\left(r\right)}={\mathbf{A}}^{\left(r\right)}{\mathbf{C}}_{\mathrm{canon}}^{†}$ and ${\mathbf{A}}^{\left(r\right)}=f\left({\mathbf{C}}_{\mathrm{canon}},{\mathbf{M}}_{\mathrm{canon}}^{\left(r\right)}\right)$, ${\mathbf{M}}_{\mathrm{canon}}^{\left(r\right)}=g\left(\mathbf{M},{\epsilon }^{(r-1)}\right)$, and ${\epsilon }^{(r-1)}=\mathbf{b}-{\mathbf{A}}^{(r-1)}{\widehat{\mathbf{z}}}^{(r-1)}$ (for a “partitioned” decomposition of ${\mathbf{B}}^{\left(r\right)}$ given the structure of ${\mathbf{C}}_{\mathrm{canon}}^{†}$, see Appendix A.2)—and the (non-linear) term, $\Delta {\kappa }_B·\Delta {\kappa }_C$.

The condition number of ${\mathbf{C}}_{\mathrm{canon}}\in {\mathbb{R}}^{k\times n}$, $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)$, the change of which determines the constraint-side effect, $\kappa \left({\mathbf{B}}^{\left(r\right)}\right)·\Delta {\kappa }_C$, can itself be analyzed with the help of pairwise angular measure between row vectors ${\mathbf{c}}_i^{\top },{\mathbf{c}}_j^{\top }\in {\mathbf{C}}_{\mathrm{canon}}$, where $i,j\in \{1,\dots ,k\}$. For any two ${\mathbf{c}}_i^{\top },{\mathbf{c}}_j^{\top }\in {\mathbb{R}}^{1\times n}$ (alternatively, in a centered form, ${\tilde{\mathbf{c}}}_i^{\top }={\mathbf{c}}_i^{\top }-{\overline{c}}_i,{\tilde{\mathbf{c}}}_j^{\top }={\mathbf{c}}_j^{\top }-{\overline{c}}_j\in {\mathbb{R}}^{1\times n}$, with ${\overline{c}}_i={\displaystyle \frac{1}{n}}{\sum }_{k=1}^n{c}_{i,k},{\overline{c}}_j={\displaystyle \frac{1}{n}}{\sum }_{k=1}^n{c}_{j,k}$), $i\ne j$, the cosine of the angle between them $cos\left({\theta }_{i,j}\right)$ (alternatively, the Pearson correlation coefficient $\rho =cos\left({\tilde{\theta }}_{i,j}\right)$) captures their angular alignment—values close to $\pm 1$ indicate near-collinearity and potential ill-conditioning, whereas values near 0 imply near-orthogonality and improved numerical stability (for the pairwise definition and its potential aggregated measures, consult Equations (9) and (10)):

$${\forall }_{{\mathbf{c}}_i^{\top },{\mathbf{c}}_j^{\top }\in {\mathbf{C}}_{\mathrm{canon}},i\ne j}cos\left({\theta }_{i,j}\right)={\displaystyle \frac{{\mathbf{c}}_i^{\top }·{\mathbf{c}}_j}{\parallel {\mathbf{c}}_i^{\top }{\parallel }_2·{\parallel {\mathbf{c}}_j^{\top }\parallel }_2}}\in [-1,1]$$

(9)

The pairwise angular measure can be aggregated across j (i.e., for each row ${\mathbf{c}}_i^{\top }$) and jointly across $i,j$ (i.e., for the full set of $\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)={\displaystyle \frac{k(k-1)}{2}}$ unique row pairs of ${\mathbf{C}}_{\mathrm{canon}}$), yielding a scalar summary statistic of angular alignment, e.g., the Root Mean Square Alignment (RMSA):

$${\mathrm{RMSA}}_i=\sqrt{{\displaystyle \frac{1}{k-1}}\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^k{cos}^2\left({\theta }_{i,j}\right)},\mathrm{RMSA}=\sqrt{{\displaystyle \frac{2}{k(k-1)}}\sum _{i=1}^{k-1}\sum _{j=i+1}^k{cos}^2\left({\theta }_{i,j}\right)}$$

(10)

where ${\mathrm{RMSA}}_i$ captures the average angular alignment of constraint i with the rest, while RMSA evaluates the overall constraint anisotropy of ${\mathbf{C}}_{\mathrm{canon}}$. As with individual cosines $cos\left({\theta }_{i,j}\right)$ (alternatively, $\rho =cos\left({\tilde{\theta }}_{i,j}\right)$), values near 1 suggest collinearity and potential numerical instability, while values near 0 reflect angular dispersion and reduced condition number $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)$. The use of squared cosines ${cos}^2\left({\theta }_{i,j}\right)$ (alternatively, ${\rho }^2={cos}^2\left({\tilde{\theta }}_{i,j}\right)$) in contrast with other metrics (e.g., absolute values) maintains consistency with the Frobenius norms in $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)$ and assigns greater penalization to near-collinear constraints in ${\mathbf{C}}_{\mathrm{canon}}$. Furthermore, a combination of ${\mathrm{RMSA}}_i$, $i\in \{1,\dots ,k\}$, and the above-described marginal effects, obtained by excluding row i from ${\mathbf{C}}_{\mathrm{canon}}$—namely, $\kappa \left({\mathbf{B}}^{\left(r\right)}\right)·\Delta {\kappa }_C^{(-i)}$, $\Delta {\kappa }_B^{(-i)}·\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)$, and $\Delta {\kappa }_B^{(-i)}·\Delta {\kappa }_C^{(-i)}$ if ${\mathbf{R}}^{\left(r\right)}=\mathbf{0}$—together with the corresponding changes in the goodness-of-fit statistics from the solutions ${\widehat{\mathbf{z}}}^{\left(r\right)(-i)}$ and ${\widehat{\mathbf{z}}}^{*(-i)}$ (consult Section 5), can be visually presented over either all i, or a filtered subset, such that ${\mathrm{RMSA}}_i\ge \mathrm{threshold}$ as depicted in Figure 5.

To sum up, in the CLSP estimator, a feasible solution ${\widehat{\mathbf{z}}}^{*}$ (in limiting cases, ${\widehat{\mathbf{z}}}^{*}\equiv {\widehat{\mathbf{z}}}^{\left(r\right)}$), by the theoretical definition of the Bott–Duffin (Moore–Penrose) inverse (consult Section 2), always exists for the canonical form ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$ (therefore, there is no threshold value $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)>\kappa {\left({\mathbf{A}}^{\left(r\right)}\right)}_{\mathrm{threshold}}$ that would imply the nonexistence of a solution). Still, ill-conditioning of the design matrix ${\mathbf{A}}^{\left(r\right)}$ might hinder the software-dependent computation of (a) the SVD in Step 1 and (b) the convex optimization problem in Step 2 on an ad hoc basis, thereby manifesting the ill-posedness of the problem. The proposed decomposition and ${\mathrm{RMSA}}_i$ (RMSA) metric, quantifying the anisotropy of ${\mathbf{C}}_{\mathrm{canon}}$, provide a means to analyze the origin of instability and optimize the constraint structure of ${\mathbf{A}}^{\left(r\right)}$—e.g., by mitigating the (numerical) issues discussed in Whiteside et al. [21] and Blair [22,23]—before re-estimation can be performed.

5. Goodness of Fit of the Solutions ${\widehat{\mathbf{z}}}^{\left(\mathit{r}\right)}$ and ${\widehat{\mathbf{z}}}^{*}$

Given the hybrid structure of the CLSP estimator—comprising a least-squares-based (iterated if $r>1$) initial estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ (or ${\widehat{\mathbf{z}}}_{i_E,j_E}^{\left(r\right)}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{\left(r\right),(i_E,j_E)}\right\}$), followed by a regularization-inspired final solution ${\widehat{\mathbf{z}}}^{*}$ (or ${\widehat{\mathbf{z}}}_{i_E,j_E}^{*}=\left\{{\widehat{\mathbf{z}}}_{\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{*,(i_E,j_E)}\right\}$)—and the potentially ill-posed or underdetermined nature of the problems it addresses, standard goodness-of-fit methodology of classical regression—such as explained variance measures (e.g., the coefficient of determination, $R^2$), error-based metrics (e.g., Root Mean Square Error, RMSE, for comparability with the above-described RMSA), hypothesis tests (e.g., F-tests in the analysis of variance and t-tests at the coefficient level), or confidence intervals (e.g., based on Student’s t- and the normal distribution)—are not universally applicable (with the exception of RMSE, these measures are valid only under classical Gauss–Markov assumptions, i.e., for overdetermined problems where ${\widehat{\mathbf{z}}}^{*}\equiv {\widehat{\mathbf{z}}}^{\left(r\right)}$). The same limitation applies to model-selection criteria, such as $R_{\mathrm{adjusted}}^2$, AIC, and BIC, that presuppose the existence of a maximizable likelihood function and well-defined (i.e., greater than zero) degrees of freedom, not satisfied in the examined class of problems (equally, the formulation of a likelihood function for the two-step CLSP estimator lies beyond the scope of this work). This text, therefore, discusses the applicability of selected alternative statistics, most of which are robust to underdeterminedness: partial $R^2$ (i.e., the adaptation of $R^2$ to the CLSP structure), normalized RMSE, t-test for the mean of the NRMSE, and a diagnostic interval based on the condition number of ${\mathbf{A}}^{\left(r\right)}$—implemented in CLSP-based software (see Equations (11)–(18)).

For the explained variance measures, the block-wise formulation of the full vector of unknowns ${\mathbf{z}}^{\left(r\right)}=\left[\begin{array}{c}{\mathbf{x}}^{\left(r\right)}\\ {\left({\mathbf{y}}^{\left(r\right)}\right)}^{*}\end{array}\right]\in {\mathbb{R}}^n$—obtained from ${\mathbf{x}}^{\left(r\right)}={\mathbf{Q}}_X\left[\begin{array}{c}{\mathbf{x}}_M^{\left(r\right)}\\ {\mathbf{x}}_L^{\left(r\right)}\end{array}\right]\in {\mathbb{R}}^p$ (where ${\mathbf{x}}_M^{\left(r\right)}\in {\mathbb{R}}^{p-l}$ is the vector of model (target) variables and ${\mathbf{x}}_L^{\left(r\right)}\in {\mathbb{R}}^l$, $l\ge 0$, is a vector of latent variables present only in the constraints) and a vector of slack variables ${\left({\mathbf{y}}^{\left(r\right)}\right)}^{*}\in {\mathbb{R}}^{n-p}$—the design matrix ${\mathbf{A}}^{\left(r\right)}=\left[\begin{array}{c}{\mathbf{C}}_{\mathrm{canon}}\\ {\mathbf{M}}_{\mathrm{canon}}^{\left(r\right)}\end{array}\right]\in {\mathbb{R}}^{m\times n}$, where ${\mathbf{M}}_{\mathrm{canon}}^{\left(r\right)}=\left[\mathbf{M}\{\mathbf{0},r=1;{\mathbf{S}}_{\mathrm{residual}},r>1\}\right]\in {\mathbb{R}}^{(m-k)\times n}$ is the “canonical” model matrix, and the input $\mathbf{b}=\left[\begin{array}{c}{\mathbf{b}}_C\\ {\mathbf{b}}_M\end{array}\right]\in {\mathbb{R}}^m$, all necessitate a “partial” ${\mathit{R}}^{\mathbf{2}}$ (hereafter, the term “partial” will be reserved for statistics related to vector ${\mathbf{x}}^{*}\subseteq \mathbf{z}$) to isolate the estimated variables ${\widehat{\mathbf{x}}}^{*}$, where, given the vector of ones $\mathbf{1}={\{1,\dots ,1\}}^{\top }$,

$$R_{\mathrm{partial}}^2=1-{\displaystyle \frac{{∥{\mathbf{b}}_M-\mathbf{M}{\widehat{\mathbf{x}}}^{*}∥}_2^2}{{∥{\mathbf{b}}_M-{\overline{b}}_M\mathbf{1}∥}_2^2}},{\overline{b}}_M={\displaystyle \frac{1}{m-k}}\sum _{i=1}^{m-k}{b}_{M,i}$$

(11)

provided that $rank\left({\mathbf{A}}^{\left(r\right)}\right)=n$, $m\ge n$, i.e., applicable strictly to (over)determined problems. If $\mathbf{C}=\varnothing \iff k=0\wedge \mathbf{y}=\varnothing \iff n=p$, then ${\mathbf{A}}^{\left(r\right)}\equiv \mathbf{M}$ and $R_{\mathrm{partial}}^2$ reduces to the classical $R^2$. Overall, $R_{\mathrm{partial}}^2$ has limited use for the CLSP estimator and is provided for completeness.

Next, for the error-based metrics, independent of $rank\left({\mathbf{A}}^{\left(r\right)}\right)$ and thus more robust across underdetermined cases (in contrast to $R_{\mathrm{partial}}^2$), a Root Mean Square Error (RMSE) can be defined for both (a) the full solution ${\widehat{\mathbf{z}}}^{*}$, via $\mathrm{RMSE}={\displaystyle \frac{1}{\sqrt{m}}}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}∥}_2$, serving as an overall measure of fit, and (b) its variable component ${\widehat{\mathbf{x}}}^{*}$, via ${\mathrm{RMSE}}_{\mathrm{partial}}^{\left(r\right)}={\displaystyle \frac{1}{\sqrt{m-k}}}{∥{\mathbf{b}}_{k+1:m}-\mathbf{M}{\widehat{\mathbf{x}}}^{*}∥}_2$, quantifying the fit quality with respect to the estimated target variables only (in alignment with $R_{\mathrm{partial}}^2$). Then, to enable cross-model comparisons and especially its use in hypothesis testing (see below), RMSE must be normalized—typically by the standard deviation of the reference input, ${\sigma }_{\mathbf{b}}$ or ${\sigma }_{{\mathbf{b}}_M}$—yielding the Normalized Root Mean Square Error (NRMSE) comparable across datasets and/or models (e.g., in the t-test for the mean of the NRMSE):

$$\mathrm{NRMSE}={\displaystyle \frac{\frac{1}{\sqrt{m}}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}∥}_2}{{\sigma }_{\mathbf{b}}}},{\mathrm{NRMSE}}_{\mathrm{partial}}={\displaystyle \frac{\frac{1}{\sqrt{m-k}}{∥{\mathbf{b}}_{k+1:m}-\mathbf{M}{\widehat{\mathbf{x}}}^{*}∥}_2}{{\sigma }_{{\mathbf{b}}_M}}}$$

(12)

The standard deviation is preferred in statistical methodology over the alternatives (e.g., max-min scaling or range-based metrics) because it expresses residuals in units of their variability, producing a scale-free measure analogous to the standard normal distribution. It is also more common in practical implementations (such as Python’s sklearn or MATLAB).

Also, for the hypothesis tests, classical ANOVA-based F-tests and coefficient-level t-tests—relying on variance decomposition and residual degrees of freedom—are applicable exclusively to the least-squares-based (iterated if $r>1$) first-step estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ and to the final solution ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}$, given a strictly overdetermined ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$, i.e., $rank\left({\mathbf{A}}^{\left(r\right)}\right)=n$, $m>n$ (an OLS case), and under the assumption of homoscedastic and normally distributed residuals. Then, in the case of the F-tests, the test statistics follow the distributions (a) $F\sim \mathcal{F}(q,m-n)$ and (b) $F_{\mathrm{partial}}\sim \mathcal{F}(q_{\mathrm{partial}},m-n)$, a Wald-type test on a linear restriction—with the degrees of freedom $q=n-1$ and $q_{\mathrm{partial}}=p-1$ if ${\mathbf{x}}^{\left(r\right)}$ is a vector of coefficients from a linear(ized) model with an intercept and $q=n$ and $q_{\mathrm{partial}}=p$ otherwise—yielding (a) $H_0:{\widehat{\mathbf{z}}}^{\left(r\right)}=\mathbf{0}$ and (b) $H_0^{\mathrm{partial}}:{\widehat{\mathbf{x}}}^{\left(r\right)}=\mathbf{R}{\widehat{\mathbf{z}}}^{\left(r\right)}=\mathbf{0}$, where $\mathbf{R}\in {\mathbb{R}}^{p\times n}$ is a restriction matrix:

$$F={\displaystyle \frac{\frac{1}{q}{∥{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2}{\frac{1}{m-n}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2}},F_{\mathrm{partial}}={\displaystyle \frac{\frac{1}{q_{\mathrm{partial}}}{\left(\mathbf{R}{\widehat{\mathbf{z}}}^{\left(r\right)}\right)}^{\top }{\left[\mathbf{R}{\left({\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\right)}^{-1}{\mathbf{R}}^{\top }\right]}^{-1}\left(\mathbf{R}{\widehat{\mathbf{z}}}^{\left(r\right)}\right)}{\frac{1}{m-n}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2^2}}$$

(13)

In the case of the t-tests, (a) ${\forall }_{i\in \{1,\dots ,n\}}{t}_i\sim t_{m-n}$ (n test statistics) and (b) ${\forall }_{i\in \{1,\dots ,p\}}$$t_{\mathrm{partial},i}\equiv t_i$ (p test statistics), given that the partial result ${\widehat{\mathbf{x}}}^{\left(r\right)}$ or ${\widehat{\mathbf{x}}}^{*}={\widehat{\mathbf{x}}}^{\left(r\right)}$ is a subvector of length p of ${\widehat{\mathbf{z}}}^{\left(r\right)}$ (also ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}$), yielding (a) ${\forall }_{i\in \{1,\dots ,n\}}{H}_0:{\widehat{z}}_i^{\left(r\right)}=0$ and (b) ${\forall }_{i\in \{1,\dots ,p\}}{H}_0^{\mathrm{partial}}:{\widehat{x}}_i^{\left(r\right)}=0$:

$${\forall }_{i\in \{1,\dots ,n\}}{t}_i={\displaystyle \frac{{\widehat{z}}_i^{\left(r\right)}}{\left(\frac{1}{\sqrt{m-n}}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2\right)·\sqrt{{\left[{\left({\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\right)}^{-1}\right]}_{ii}}}},{\forall }_{i\in \{1,\dots ,p\}}{t}_{\mathrm{partial},i}\equiv t_i$$

(14)

An alternative hypothesis test—robust to both $rank\left({\mathbf{A}}^{\left(r\right)}\right)$ and the step of the CLSP algorithm, i.e., valid for the final solution ${\widehat{\mathbf{z}}}^{*}$ (in contrast to the classical ANOVA-based F-tests or coefficient-level t-tests)—can be a $\mathbf{t}$-test for the mean of the NRMSE, comparing the observed ${\mathrm{NRMSE}}_{\mathrm{obs}}$ (as ${\mu }_0$), both full and partial, to the mean of a simulated sample ${\mathrm{NRMSE}}_{\mathrm{sim}}^{\left(\tau \right)}$, generated via Monte Carlo simulation, typically from a uniformly (a structureless flat baseline) or normally (a “canonical” choice) distributed random input ${\mathbf{b}}^{\left(\tau \right)}\sim \mathcal{U}(\mathbf{0},{\mathbf{I}}_m)$ or ${\mathbf{b}}^{\left(\tau \right)}\sim \mathcal{N}(\mathbf{0},{\mathbf{I}}_m)$—both the distributions being standard (the choice of distributions is, therefore, analogous to employing standard weakly or non-informative priors, with the exception of Jeffrey’s prior, in Bayesian inference)—for $\tau =1,\dots ,T$, where T is the sample size, yielding $t\sim t_{T-1}$ with $H_0:{\mathrm{NRMSE}}_{\mathrm{obs}}={\overline{\mathrm{NRMSE}}}_{\mathrm{sim}}$ and $H_1:{\mathrm{NRMSE}}_{\mathrm{obs}}\ne {\overline{\mathrm{NRMSE}}}_{\mathrm{sim}}$ for the two-sided test and $H_1:{\mathrm{NRMSE}}_{\mathrm{obs}}\gtrless {\overline{\mathrm{NRMSE}}}_{\mathrm{sim}}$ for the one-sided one:

$$t={\displaystyle \frac{{\overline{\mathrm{NRMSE}}}_{\mathrm{sim}}-{\mathrm{NRMSE}}_{\mathrm{obs}}}{\sqrt{\frac{1}{T(T-1)}{\sum }_{\tau =1}^T{\left({\mathrm{NRMSE}}_{\mathrm{sim}}^{\left(\tau \right)}-{\overline{\mathrm{NRMSE}}}_{\mathrm{sim}}\right)}^2}}},{\overline{\mathrm{NRMSE}}}_{\mathrm{sim}}={\displaystyle \frac{1}{T}}\sum _{\tau =1}^T{\mathrm{NRMSE}}_{\mathrm{sim}}^{\left(\tau \right)}$$

(15)

justified when ${\mathbf{b}}^{\left(\tau \right)}$ is normally distributed or approximately normally distributed based on the Lindeberg–Lévy Central Limit Theorem (CLT), i.e., when $T>30$ (as a rule of thumb) for ${\mathbf{b}}^{\left(\tau \right)}\sim \mathcal{U}(\mathbf{0},{\mathbf{I}}_m)$. Then, $H_0$ denotes a good fit for ${\widehat{\mathbf{z}}}^{*}$ in the sense that ${\mathrm{NRMSE}}_{\mathrm{obs}}$ does not significantly deviate from the simulated distribution, i.e., $H_0$ should not be rejected for the CLSP model to be considered statistically consistent. In practical implementations (such as Python 3, R 3, Stata 14, SAS 9.4, Julia 1.0, and MATLAB 2015a/Octave 4), T typically ranges from 50 to 50,000.

Finally, for the confidence intervals, classical formulations for (a) $z_i^{\left(r\right)}$, $i\in \{1,\dots ,n\}$, and (b) $x_i^{\left(r\right)}$, $i\in \{1,\dots ,p\}$—based on Student’s t- and, asymptotically, the standard normal distribution, $t\sim t_{m-n}$ and $z\sim \mathcal{N}(0,1)$—are equivalently exclusively applicable to the least-squares-based (iterated if $r>1$) first-step estimate ${\widehat{\mathbf{z}}}^{\left(r\right)}$ and to the final solution ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}$ under a strictly overdetermined ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$, i.e., $rank\left({\mathbf{A}}^{\left(r\right)}\right)=n$, $m>n$ (an OLS case), and assuming homoscedastic and normally distributed residuals. Then, provided $\alpha \in (0,1)$, such as $\alpha \in \{0.01,0.05,0.1\}$, the confidence intervals for (a) $z_i^{\left(r\right)}$ and (b) $x_i^{\left(r\right)}$ are

$$\begin{array}{cc}\hfill & {\forall }_{i\in \{1,\dots ,n\}}{z}_i^{\left(r\right)}\in {\widehat{z}}_i^{\left(r\right)}\pm t_{m-n,1-\alpha /2}·{\displaystyle \frac{1}{\sqrt{m-n}}}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2·\sqrt{{\left[{\left({\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\right)}^{-1}\right]}_{ii}},\hfill \\ \hfill & {\forall }_{i\in \{1,\dots ,p\}}{x}_i^{\left(r\right)}\equiv z_i^{\left(r\right)}\hfill \end{array}$$

(16)

given that the partial result ${\widehat{\mathbf{x}}}^{\left(r\right)}$ or ${\widehat{\mathbf{x}}}^{*}={\widehat{\mathbf{x}}}^{\left(r\right)}$ is a subvector of length p of ${\widehat{\mathbf{z}}}^{\left(r\right)}$ or ${\widehat{\mathbf{z}}}^{*}={\widehat{\mathbf{z}}}^{\left(r\right)}$. For $n>30$, the distribution of the test statistic, $t_{m-n,1-\alpha /2}$, approaches a standard normal one, $Z_{1-\alpha /2}$, based on the CLT, yielding an alternative notation for the confidence intervals:

$$\begin{array}{cc}\hfill & {\forall }_{i\in \{1,\dots ,n\}}{z}_i^{\left(r\right)}\in {\widehat{z}}_i^{\left(r\right)}\pm Z_{1-\alpha /2}·{\displaystyle \frac{1}{\sqrt{m-n}}}{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{\left(r\right)}∥}_2·\sqrt{{\left[{\left({\left({\mathbf{A}}^{\left(r\right)}\right)}^{\top }{\mathbf{A}}^{\left(r\right)}\right)}^{-1}\right]}_{ii}},\hfill \\ \hfill & {\forall }_{i\in \{1,\dots ,p\}}{x}_i^{\left(r\right)}\equiv z_i^{\left(r\right)}\hfill \end{array}$$

(17)

An alternative “confidence interval”—equivalently robust to both $rank\left({\mathbf{A}}^{\left(r\right)}\right)$ and the step of the CLSP algorithm, i.e., valid for the final solution ${\widehat{\mathbf{z}}}^{*}$ (in contrast to the classical Student’s t- and, asymptotically, the standard normal distribution-based formulations)—can be constructed deterministically via condition-weighted bands, relying on componentwise numerical sensitivity. Let the residual vector $\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}$ be a (backward) perturbation in $\mathbf{b}$, i.e., $\Delta \mathbf{b}=\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}$. Then, squaring both sides of the classical first-order inequality ${\displaystyle \frac{\parallel \Delta {\widehat{\mathbf{z}}}^{*}{\parallel }_2}{\parallel {\widehat{\mathbf{z}}}^{*}{\parallel }_2}}\le \kappa \left({\mathbf{A}}^{\left(r\right)}\right)·{\displaystyle \frac{{\parallel \Delta \mathbf{b}\parallel }_2}{{\parallel \mathbf{b}\parallel }_2}}$ yields ${\displaystyle \frac{{\sum }_{i=1}^n{(\Delta {\widehat{z}}_i^{*})}^2}{{\sum }_{i=1}^n{\left({\widehat{z}}_i^{*}\right)}^2}}\le \kappa {\left({\mathbf{A}}^{\left(r\right)}\right)}^2·{\displaystyle \frac{{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}∥}_2^2}{{\parallel \mathbf{b}\parallel }_2^2}}$, where $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)=\parallel {\mathbf{A}}^{\left(r\right)}{\parallel }_2{\parallel {\left({\mathbf{A}}^{\left(r\right)}\right)}^{†}\parallel }_2={\displaystyle \frac{{\sigma }_{\max }\left({\mathbf{A}}^{\left(r\right)}\right)}{{\sigma }_{rank\left({\mathbf{A}}^{\left(r\right)}\right)}\left({\mathbf{A}}^{\left(r\right)}\right)}}$—${\sigma }_{\max }$ and ${\sigma }_{rank\left({\mathbf{A}}^{\left(r\right)}\right)}$ being the biggest and smallest singular values of ${\mathbf{A}}^{\left(r\right)}$—iff ${\sigma }_{rank\left({\mathbf{A}}^{\left(r\right)}\right)}>0\wedge {\parallel \mathbf{b}\parallel }_2>0$. Under a uniform relative squared perturbation (a heuristic allocation of error across components as a simplification, not an assumption) of ${\mathbf{z}}^{*}$, rearranging terms and taking square roots of both sides gives ${\forall }_{i\in \{1,\dots ,n\}}|\Delta {\widehat{z}}_i^{*}|\le |{\widehat{z}}_i^{*}|·\kappa \left({\mathbf{A}}^{\left(r\right)}\right)·{\displaystyle \frac{{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}∥}_2}{{\parallel \mathbf{b}\parallel }_2}}$ and a condition-weighted “confidence” band:

$${\forall }_{i\in \{1,\dots ,n\}}{z}_i^{*}\in {\widehat{z}}_i^{*}·\left(1\pm \kappa \left({\mathbf{A}}^{\left(r\right)}\right)·{\displaystyle \frac{{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}∥}_2}{{\parallel \mathbf{b}\parallel }_2}}\right),{\forall }_{i\in \{1,\dots ,p\}}{x}_i^{*}\equiv z_i^{*}$$

(18)

which is a diagnostic interval based on the condition number for ${\mathbf{z}}^{*}$, consisting of (1) a canonical-form system conditioning, $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)$, (2) a normalized model misfit, ${\displaystyle \frac{{∥\mathbf{b}-{\mathbf{A}}^{\left(r\right)}{\widehat{\mathbf{z}}}^{*}∥}_2}{{\parallel \mathbf{b}\parallel }_2}}$, and (3) the “scale” of the final solution, ${\widehat{\mathbf{z}}}^{*}$, without probabilistic assumptions. A perturbation in one or more of these three components, e.g., caused by a change in RMSA resulting from dropping selected constraints (consult Section 4), will affect the limits of ${\mathbf{z}}^{*}$. Under a perfect fit, the interval collapses to $z_i^{*}\in {\widehat{z}}_i^{*}\pm 0$ and, for $\kappa \left({\mathbf{A}}^{\left(r\right)}\right)\gg 1$, tends to be very wide. Overall, in practical implementations, where the squared perturbations may violate the uniformity simplification, an aggregated (e.g., average) width of the diagnostic interval for vectors ${\mathbf{z}}^{*}$ and ${\mathbf{x}}^{*}$ becomes more informative, as it represents an adjusted goodness-of-fit statistic—normalized error weighted by the condition number of the design matrix ${\mathbf{A}}^{\left(r\right)}$.

To sum up, the CLSP estimator requires a goodness-of-fit framework that reflects both its algorithmic structure and numerical stability. Classical methods remain informative but are valid only under strict overdetermination ($m>n$), full-rank design matrix ${\mathbf{A}}^{\left(r\right)}$, and distributional assumptions (primarily, homoscedasticity and normality of residuals). In contrast, the proposed alternatives—(a) NRMSE and ${\mathrm{NRMSE}}_{\mathrm{partial}}$, (b) t-tests for the mean of NRMSE with the help of Monte Carlo sampling, and (c) condition-weighted confidence bands—are robust to underdeterminedness and ill-posedness, making them preferable in practical implementations (e.g., in existing CLSP-based software for Python, R, and Stata).

6. Special Cases of CLSP Problems: APs, CMLS, and LPRLS/QPRLS

The structure of the design matrix ${\mathbf{A}}^{\left(r\right)}$ in the CLSP estimator, as defined in Equation (3) (consult Section 3), allows for accommodating a selection of special-case problems, out of which three cases are covered (each case will use modified notation for i, j, m, and p), but the list may not be exhaustive. Among others, the CLSP estimator is, given its ability to address ill-posed or underdetermined problems under linear(ized) constraints, efficient in addressing what can be referred to as allocation problems (APs) (or, for flow variables, tabular matrix problems, TMs)—i.e., in most cases, underdetermined problems involving matrices of dimensions $m\times p$ to be estimated, subject to known row and column sums, with the degrees of freedom (i.e., nullity) equal to $n-rank\left({\mathbf{A}}^{\left(r\right)}\right)\ge mp+s^{*}-({\displaystyle \frac{m}{i}}+{\displaystyle \frac{p}{j}})-q$, where $0\le s^{*}\le ({\displaystyle \frac{m}{i}}+{\displaystyle \frac{p}{j}})+q$ is the number of active (non-zero) slack variables and $0\le q\le rank\left({\mathbf{M}}_{\mathrm{partial}}\right)\le min(k,mp)$ is the number of known model (target) variables (e.g., a zero diagonal)—whose design matrix, ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{({\displaystyle \frac{m}{i}}+{\displaystyle \frac{p}{j}}+k)\times n}$, comprises a (by convention) row-sum-column-sum constraints matrix $\mathbf{C}={\left[{\left(\left({\mathbf{I}}_{{\displaystyle \frac{m}{i}}}\otimes {\mathbf{1}}_i\right)\otimes {\mathbf{1}}_p\right)}^{\top }|{\left({\mathbf{1}}_m\otimes \left({\mathbf{I}}_{{\displaystyle \frac{p}{j}}}\otimes {\mathbf{1}}_j\right)\right)}^{\top }\right]}^{\top }\in {\mathbb{R}}^{({\displaystyle \frac{m}{i}}+{\displaystyle \frac{p}{j}})\times mp}$ (where $\mathbf{1}=\{1,\dots ,1\}$), a model matrix $\mathbf{M}={\mathbf{Q}}_M^L\left[\begin{array}{c}{\mathbf{M}}_{\mathrm{partial}}\\ \mathbf{0}\end{array}\right]{\mathbf{Q}}_M^R\in {\mathbb{R}}^{k\times mp}$—in a trivial case, ${\mathbf{M}}_{\mathrm{partial}}\subseteq {\mathbf{I}}_{mp}$—a sign slack matrix $\mathbf{S}={\mathbf{Q}}_S^L\left[\begin{array}{c}{\mathbf{S}}_s\subseteq {\forall }_{{\sigma }_1,\dots ,{\sigma }_s\in \{-1,+1\}}diag\left({\sigma }_1,\dots ,{\sigma }_s\right)\\ \mathbf{0}\end{array}\right]{\mathbf{Q}}_S^R\in {\mathbb{R}}^{({\displaystyle \frac{m}{i}}+{\displaystyle \frac{p}{j}})\times (n-mp)}$, and either a zero matrix $\mathbf{0}$ (if $r=1$) or a (standard) reverse-sign slack matrix ${\mathbf{S}}_{\mathrm{residual}}\in {\mathbb{R}}^{k\times (n-mp)}$ (provided $r>1$) (as given by Equation (19) extending Equation (3)):

$${\mathbf{A}}^{\left(r\right)}=\left[\begin{array}{cc}\left[\begin{array}{c}\left({\mathbf{I}}_{{\displaystyle \frac{m}{i}}}\otimes {\mathbf{1}}_i\right)\otimes {\mathbf{1}}_p\\ {\mathbf{1}}_m\otimes \left({\mathbf{I}}_{{\displaystyle \frac{p}{j}}}\otimes {\mathbf{1}}_j\right)\end{array}\right]& \mathbf{S}\\ \mathbf{M}& \left\{\begin{array}{cc}\mathbf{0},\hfill & \mathrm{initial}\mathrm{iteration},r=1\hfill \\ {\mathbf{S}}_{\mathrm{residual}},\hfill & \mathrm{subsequent}\mathrm{iterations},r>1\hfill \end{array}\right.\end{array}\right]$$

(19)

where ${\displaystyle \frac{m}{i}}$ and ${\displaystyle \frac{p}{j}}$ denote groupings of the m rows and p columns, respectively, into i and j homogeneous blocks (when no grouped row or column sums are available, $i=j=1$); with real-world examples including: (a) input–output tables (national, inter-country, or satellite); (b) structural matrices (e.g., trade, country-product, investment, or migration); (c) financial clearing and budget-balancing; and (d) data interpolations (e.g., quarterly data from annual totals). Given the available literature in 2025, the first pseudoinverse-based method of estimating input–output tables was proposed in Pereira-López et al. [81] and the first APs (TMs)-based study was conducted in Bolotov [16], attempting to interpolate a world-level (in total, 232 countries and dependent territories) “bilateral flow” matrix of foreign direct investment (FDI) for the year 2013, based on known row and column totals from UNCTAD data (aggregate outward and inward FDI). The estimation employed a minimum-norm least squares solution under APs (TMs)-style equality constraints, based on the Moore–Penrose pseudoinverse of a “generalized Leontief structural matrix”, rendering it equivalent to the initial (non-corrected) solution in the CLSP framework, ${\widehat{\mathbf{z}}}^{\left(1\right)}={\mathbf{A}}_{\mathbf{Z}}^{\left(1\right)†}\mathbf{b}$. As a rule of thumb, AP (TM)-type problems are rank deficient for $m>2\wedge p>2$ with the CLSP being a unique (if $\alpha \in (0,1]$) and an MNBLUE (if $\alpha =1$) estimator (consult Section 3).

In addition to the APs (TMs), the CLSP estimator is also efficient in addressing what can be referred to as constrained-model least squares (CMLS) (or, more generally, regression problems, RPs)—i.e., (over)determined problems involving vectors of dimension p to be estimated with (standard) OLS degrees of freedom, subject to, among others, linear(ized) data matrix $\mathbf{D}\in {\mathbb{R}}^{k\times p}$-related (in)equality constraints, ${\forall }_{i\in \{1,\dots ,t\}}{\mathbf{C}}_i\equiv {\mathbf{T}}_i\mathbf{D}\in {\mathbb{R}}^{m_i\times p}$, where ${\mathbf{T}}_i\in {\mathbb{R}}^{m_i\times k}$ is a transformation matrix of $\mathbf{D}$, such as the i-th difference or shift (lag/lead), and ${\mathbf{C}}_i\mathbf{x}⋛{\mathbf{\gamma }}_i$—whose design matrix, ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{({\sum }_{i=1}^u{m}_i+k)\times n}$, consists of a u-block constraints matrix $\mathbf{C}=\left[\begin{array}{c}{\mathbf{C}}_1\\ \dots \\ {\mathbf{C}}_u\end{array}\right]\in {\mathbb{R}}^{\left({\sum }_{i=1}^u{m}_i\right)\times p}$ (${\forall }_{i\in \{1,\dots ,u\}}{\mathbf{C}}_i\in {\mathbb{R}}^{m_i\times p}$), $u\ge t$, a data matrix as the model matrix $\mathbf{M}\equiv \mathbf{D}\in {\mathbb{R}}^{k\times p}$, a (standard) sign slack matrix $\mathbf{S}\in {\mathbb{R}}^{\left({\sum }_{i=1}^u{m}_i\right)\times (n-p)}$, and either a zero matrix $\mathbf{0}$ (if $r=1$) or a (standard) reverse-sign slack matrix ${\mathbf{S}}_{\mathrm{residual}}\in {\mathbb{R}}^{k\times (n-p)}$ (when $r>1$) (as given by Equation (20) extending Equation (3), with $\mathbf{M}$ substituted by data matrix $\mathbf{D}$):

$${\mathbf{A}}^{\left(r\right)}=\left[\begin{array}{cc}\left[\begin{array}{c}{\mathbf{C}}_1\\ \dots \\ {\mathbf{C}}_u\end{array}\right]& \mathbf{S}\\ \mathbf{D}& \left\{\begin{array}{cc}\mathbf{0},\hfill & \mathrm{initial}\mathrm{iteration},r=1\hfill \\ {\mathbf{S}}_{\mathrm{residual}},\hfill & \mathrm{subsequent}\mathrm{iterations},r>1\hfill \end{array}\right.\end{array}\right]$$

(20)

with real-world examples including (a) previously infeasible textbook-definition econometric models of economic (both micro and macro) variables (e.g., business-cycle models), and (b) additional constraints applied to classical econometric models (e.g., demand analysis). Given the available literature in 2025, the first studies structurally resembling CMLS (RPs) were conducted in Bolotov [15,82], focusing on the decomposition of the long U.S. GDP time series into trend ($y_t$) and cyclical ($c_t$) components—using exponential trend, moving average, Hodrick-Prescott filter, and Baxter-King filter—under constraints on its first difference, based on the U.S. National Bureau of Economic Research (NBER) delimitation of the U.S. business cycle. $c_t$ was then modeled with the help of linear regression (OLS), based on an n-th order polynomial with extreme values smoothed via a factor of ${\displaystyle \frac{1}{{10}^{n-i}}}$ and simultaneously penalized via an n-th or ($n+1$)-th root, $c_t={\beta }_0+{\beta }_1\int \left(\sqrt[\{n,n+1\}]{{\prod }_{i=1}^{i=n}(t-t_i)·{\displaystyle \frac{1}{{10}^{n-i}}}}\right)dt+{\epsilon }_t$, where ${\beta }_0,{\beta }_1$ are the model parameters, ${\forall }_{1\le i\le n}{t}_i$ are the values of the (externally given) stationary points, and ${\epsilon }_t$ is the error. The order of the polynomial and the ad hoc selection of smoothing and penalizing factors, however, render such a method inferior to the CLSP. Namely, the unique (if $\alpha \in (0,1]$) and an MNBLUE (if $\alpha =1$) CLSP estimator (consult Section 3) allows (a) the presence of inequality constraints and (b) their ill-posed formulations.

Finally, the CLSP estimator can be used to address (often unsolvable using classical solvers) underdetermined and/or ill-posed—caused by too few and/or mutually inconsistent or infeasible constraints as in the sense of Whiteside et al. [21] and Blair [22,23]—LP and QP problems, an approach hereafter referred to as linear/quadratic programming via regularized least squares (LPRLS/QPRLS): CLSP substitutes the original objective function of the LP/QP problem with the canonical form ${\mathbf{A}}^{\left(r\right)}{\mathbf{z}}^{\left(r\right)}=\mathbf{b}$ (i.e., focusing solely on the problem’s constraints, without distinguishing between the LP and QP cases) with ${\widehat{\mathbf{x}}}_M^{*}={Proj}_{{\mathbf{x}}_M^{\left(r\right)}}\left\{{\mathbf{Q}}_X\left[\begin{array}{c}{\mathbf{x}}_M^{\left(r\right)}\\ {\mathbf{x}}_L^{\left(r\right)}\end{array}\right]\in {\mathbb{R}}^p:{\forall }_{1\le i\le s}{g}_i({\mathbf{x}}_M^{\left(r\right)},{\mathbf{x}}_L^{\left(r\right)})⋛{\gamma }_i,{\forall }_j{h}_j({\mathbf{x}}_M^{\left(r\right)},{\mathbf{x}}_L^{\left(r\right)})={\eta }_j\right\}\subseteq {\mathbf{z}}^{*}$ being the solution of the original problem, where ${\mathbf{Q}}_X$ is a permutation matrix and $g_i(·)⋛{\gamma }_i$ and $h_j(·)={\eta }_j$ represent the linear(ized) inequality and equality constraints, ${\forall }_{i,j}{\gamma }_i,{\eta }_j\in \mathbf{b}$, and the degrees of freedom are equal, under the classical formalization of a primal LP/QP problem (consult Section 2), to $n-rank\left({\mathbf{A}}^{\left(r\right)}\right)\ge (p+s)-(m_{ub}+m_{eq}+m_{nn})=p-m_{eq}$, where p is the length of ${\mathbf{x}}_M^{\left(r\right)}$, $s=m_{ub}+m_{nn}$ is the number of introduced slack variables, while $m_{ub}\ge 0$, $m_{eq}\ge 0$, and $m_{nn}\equiv p$ denote the numbers of upper-bound, equality, and non-negativity constraints, respectively (under the standard assumption that all model variables are constrained to be non-negative). In the LPRLS/QPRLS, the design matrix, ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{(m_{ub}+m_{eq}+m_{nn})\times n}$, by the definition of LP/QP, is r-invariant and consists of a block constraints matrix $\mathbf{C}=\left[\begin{array}{c}{\mathbf{C}}_{ub}\\ {\mathbf{C}}_{eq}\\ {\mathbf{C}}_{nn}\end{array}\right]\in {\mathbb{R}}^{(m_{ub}+m_{eq}+m_{nn})\times p}$, where ${\mathbf{C}}_{ub}\in {\mathbb{R}}^{m_{ub}\times p}$, ${\mathbf{C}}_{eq}\in {\mathbb{R}}^{m_{eq}\times p}$, and ${\mathbf{C}}_{nn}\equiv {\mathbf{I}}_p\in {\mathbb{R}}^{p\times p}$, a (standard) sign slack matrix $\mathbf{S}\in {\mathbb{R}}^{(m_{ub}+m_{eq}+m_{nn})\times (n-p)}$, and ${\mathbf{M}}_{\mathrm{canon}}=\varnothing$ (as given by Equation (21) extending Equation (3), under the condition $\mathbf{M}={\mathbf{S}}_{\mathrm{residual}}=\varnothing$):

$${\mathbf{A}}^{\left(r\right)}={\mathbf{A}}^{\left(1\right)}=\left[\begin{array}{cc}\left[\begin{array}{c}{\mathbf{C}}_{ub}\\ {\mathbf{C}}_{eq}\\ {\mathbf{C}}_{nn}\end{array}\right]& \mathbf{S}\end{array}\right]$$

(21)

Given the available literature in 2025, the first documented attempts to incorporate LS into LP and QP included, among others, Dax’s LS-based steepest-descent algorithm [26] and the primal-dual NNLS-based algorithm (LSPD) [79], whose structural restrictions—in terms of well-posedness and admissible constraints—can be relaxed through LPRLS/QPRLS, still guaranteeing a unique (if $\alpha \in (0,1]$) and an MNBLUE (if $\alpha =1$) solution (consult Section 3).

To sum up, the CLSP framework can be applied to three special classes of problems—allocation (APs (TMs)), constrained-model least squares (CMLS (RPs)), and regularized linear or quadratic programming (LPRLS/QPRLS)—differing only in the nature of their constraint blocks, the treatment of slack or residual components, and rank properties of their design matrix ${\mathbf{A}}^{\left(r\right)}$, while the estimation method and goodness-of-fit statistics remain identical. The three examined cases correspond to the overwhelming majority of potential real-world uses of the estimator, whereas custom (non-described) problem types are relatively scarce. The AP (TM) case is of particular methodological importance as a means of estimating, among others, input–output tables (without reliance on historical observations).

7. Monte Carlo Experiment and Numerical Examples

This work will finally demonstrate the capability of the CLSP estimator to undergo large-scale Monte Carlo experiments across its special cases—namely, the AP (TM), CMLS (RP), and LPRLS/QPRLS problems (illustrated below on the example of the APs (TMs))—which can be replicated to assess its explanatory power and to calibrate key parameters (r and $\alpha$) for real-world applications in future research. However, the construction of a complete econometric framework—requiring not only the results of such calibration but also the formal derivation of its maximum likelihood function (for model selection) and an extension of the Gauss–Markov theorem (to explicitly incorporate MNBLUE cases)—lies beyond the scope of this theoretical text, whose aim is to establish the linear-algebraic foundations of the estimator and to discuss its numerical stability and potential measures of its goodness of fit. Therefore, the Monte Carlo experiment is complemented by simulated numerical examples serving as a proof of the estimator’s practical implementability and the estimability of its diagnostic metrics (i.e., RMSA, NRMSE, t-tests, and diagnostic intervals).

Proceeding to the Monte Carlo experiment, the standardized form of $\mathbf{C}$ in the APs (TMs), i.e., $\mathbf{C}=f(m,i,p,j)$, with given $\mathbf{S}$ and r, enables the large-scale simulation of the distribution of NRMSE—a robust goodness-of-fit metric for the CLSP—through repeated random trials under varying matrix dimensions $m\times p$, row and column group sizes i and j, and composition of $\mathbf{M}$, inferring asymptotic percentile means and standard deviations for practical implementations (e.g., the t-test for the mean). This text presents the results of a simulation study on the distribution of the NRMSE from the first-step estimate ${\widehat{\mathbf{z}}}^{\left(1\right)}$ (implementable in standard econometric software without CLSP modules) for $i=1$, $j=1$, $\mathbf{S}=\varnothing$, $\mathbf{Z}={\mathbf{I}}_{m+p+k}\iff {\left({\mathbf{A}}_{\mathbf{Z}}^{\left(1\right)}\right)}^{†}={\left({\mathbf{A}}^{\left(1\right)}\right)}^{†}$, and $r=1$, conducted in Stata/MP (set to version 14.0) with the help of Mata’s 128-bit floating-point cross-product-based quadcross() for greater precision and SVD-based svsolve() with a strict tolerance of c("epsdouble") for increased numerical stability, and a random-variate seed 123456789 (see Listing A1 containing a list of dependencies [83] and the Stata .do-file). In this 50,000-iterations Monte Carlo simulation study, spanning matrix dimensions from 1 × 2 and 2 × 1 up to 50 × 50, random normal input vectors $\mathbf{b}\sim \mathcal{N}(\mathbf{0},{\mathbf{I}}_{m+p+k})$ were generated for each run, applied with and without zero diagonals (i.e., if, under $l=0\iff {\mathbf{x}}_L=\varnothing$, ${\mathbf{x}}_M=\mathbf{x}={\mathbf{z}}_{1:mp}\in {\mathbb{R}}^{mp}$ is reshaped into a ($m\times p$)-matrix ${\mathbf{X}}_M=\mathbf{X}\in {\mathbb{R}}^{m\times p}$, then ${\forall }_{i\in \{1,\dots ,min(m,p\left)\right\}}{\mathbf{X}}_{ii}=0$). Thus, a total of 249.9 million observations ($=(50·50-1)·2·50,000$) was obtained via the formula $\mathrm{NRMSE}={\displaystyle \frac{1}{\sqrt{m}}}{\parallel \mathbf{b}-{\mathbf{A}}^{\left(1\right)}\left({\left({\mathbf{A}}^{\left(1\right)}\right)}^{†}\mathbf{b}\right)\parallel }_2/{\sigma }_{\mathbf{b}}$, resulting in 4998 aggregated statistics of the asymptotic distribution, assuming convergence: mean, sd, skewness, kurtosis, min, max, as well as 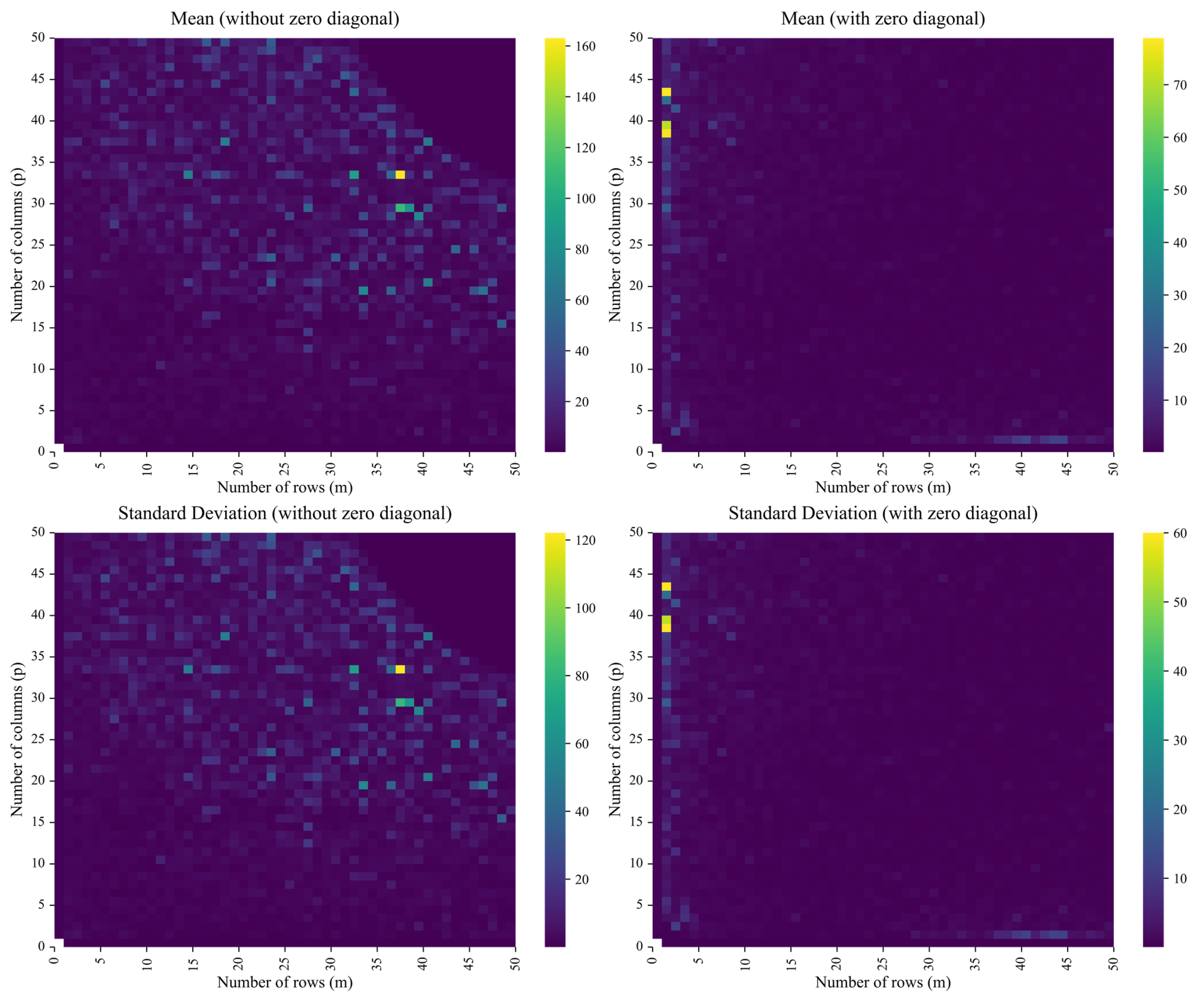p1–p99 as presented in Figure 6 (depicting the intensity of its first two moments, mean and sd) and

Table 2. Subset (at $m,pmod10=0$) of the summary statistics for NRMSE from the simulation study.

m	p	Mean	sd	Skewness	Kurtosis	Min	Max	p1	p5	p25	p50	p75	p95	p99
Without Zero Diagonal
10	10	000.81	000.59	000.82	003.24	000.00	003.52	000.01	000.06	000.33	000.70	001.18	001.94	002.47
10	20	001.53	001.14	000.92	003.60	000.00	008.10	000.02	000.12	000.62	001.31	002.21	003.70	004.80
10	30	005.30	003.96	000.95	003.69	000.00	027.25	000.09	000.41	002.13	004.51	007.65	012.95	016.90
10	40	007.56	005.67	000.97	003.77	000.00	046.23	000.12	000.61	003.02	006.45	010.90	018.59	024.18
10	50	025.08	018.95	000.99	003.84	000.00	127.63	000.39	001.98	009.99	021.10	036.31	061.64	080.75
20	10	000.57	000.43	000.93	003.60	000.00	002.73	000.01	000.04	000.23	000.49	000.83	001.39	001.79
20	20	007.90	005.85	000.89	003.48	000.00	040.71	000.13	000.64	003.18	006.77	011.48	019.17	024.57
20	30	004.10	003.03	000.92	003.61	000.00	021.59	000.06	000.33	001.68	003.50	005.92	009.92	012.87
20	40	005.85	004.37	000.95	003.71	000.00	031.73	000.09	000.47	002.36	005.00	008.44	014.27	018.65
20	50	008.52	006.36	000.94	003.63	000.00	043.37	000.14	000.68	003.44	007.22	012.36	020.73	026.90
30	10	002.89	002.16	000.97	003.78	000.00	015.48	000.05	000.23	001.16	002.47	004.17	007.05	009.19
30	20	002.85	002.11	000.92	003.58	000.00	014.28	000.05	000.23	001.16	002.43	004.12	006.88	008.93
30	30	004.44	003.32	000.94	003.66	000.00	022.66	000.07	000.35	001.78	003.76	006.43	010.85	014.08
30	40	008.73	006.50	000.95	003.69	000.00	048.55	000.14	000.69	003.56	007.47	012.61	021.13	027.85
30	50	005.61	004.22	000.96	003.69	000.00	031.96	000.09	000.44	002.25	004.75	008.10	013.70	017.94
40	10	000.55	000.41	000.98	003.80	000.00	003.10	000.01	000.04	000.22	000.47	000.79	001.35	001.76
40	20	004.67	003.48	000.93	003.66	000.00	025.54	000.07	000.35	001.87	003.97	006.74	011.34	014.83
40	30	001.39	001.04	000.95	003.69	000.00	006.70	000.02	000.11	000.56	001.18	002.01	003.40	004.39
40	40	000.27	000.20	000.96	003.71	000.00	001.48	000.00	000.02	000.11	000.23	000.39	000.67	000.87
40	50	000.29	000.21	000.95	003.69	000.00	001.58	000.00	000.02	000.11	000.24	000.41	000.70	000.91
50	10	003.74	002.82	000.99	003.84	000.00	023.34	000.06	000.29	001.50	003.16	005.37	009.20	012.13
50	20	001.65	001.24	000.95	003.68	000.00	008.17	000.03	000.13	000.67	001.40	002.39	004.05	005.26
50	30	005.24	003.90	000.94	003.69	000.00	028.36	000.08	000.42	002.12	004.47	007.56	012.74	016.54
50	40	000.47	000.35	000.97	003.73	000.00	002.40	000.01	000.04	000.19	000.40	000.67	001.15	001.49
50	50	000.23	000.17	000.94	003.64	000.00	001.21	000.00	000.02	000.09	000.20	000.33	000.56	000.73
10	10	000.71	000.52	000.85	003.37	000.00	003.20	000.01	000.06	000.29	000.62	001.04	001.71	002.20
10	20	000.69	000.51	000.92	003.60	000.00	003.54	000.01	000.05	000.28	000.59	001.00	001.67	002.16
10	30	001.93	001.44	000.95	003.74	000.00	010.17	000.03	000.15	000.78	001.64	002.77	004.69	006.13
10	40	004.65	003.50	000.97	003.76	000.00	023.68	000.07	000.37	001.86	003.92	006.72	011.43	014.89
10	50	001.94	001.47	000.98	003.84	000.00	012.42	000.03	000.15	000.77	001.64	002.81	004.75	006.25
20	10	000.70	000.52	000.92	003.59	000.00	003.70	000.01	000.06	000.28	000.60	001.02	001.70	002.20
20	20	000.70	000.52	000.93	003.57	000.00	003.68	000.01	000.05	000.28	000.60	001.01	001.71	002.21
20	30	000.42	000.31	000.94	003.68	000.00	002.24	000.01	000.03	000.17	000.36	000.61	001.02	001.34
20	40	000.27	000.20	000.94	003.64	000.00	001.27	000.00	000.02	000.11	000.23	000.39	000.65	000.85
20	50	002.06	001.55	000.97	003.81	000.00	011.72	000.03	000.16	000.83	001.75	002.98	005.04	006.64
30	10	000.45	000.34	000.95	003.67	000.00	002.40	000.01	000.04	000.18	000.38	000.65	001.10	001.43
30	20	000.42	000.32	000.95	003.71	000.00	002.16	000.01	000.03	000.17	000.36	000.61	001.03	001.34
30	30	000.45	000.34	000.96	003.76	000.00	002.53	000.01	000.03	000.18	000.38	000.65	001.10	001.43
30	40	000.34	000.26	000.97	003.73	000.00	001.88	000.01	000.03	000.14	000.29	000.50	000.85	001.10
30	50	000.57	000.43	000.96	003.75	000.00	003.21	000.01	000.05	000.23	000.48	000.82	001.39	001.81
40	10	000.34	000.26	000.96	003.76	000.00	001.83	000.01	000.03	000.14	000.29	000.49	000.84	001.08
40	20	000.33	000.25	000.98	003.77	000.00	001.68	000.01	000.03	000.13	000.28	000.47	000.80	001.05
40	30	000.63	000.47	000.97	003.80	000.00	003.36	000.01	000.05	000.25	000.53	000.90	001.52	001.99
40	40	000.38	000.28	000.98	003.82	000.00	002.23	000.01	000.03	000.15	000.32	000.54	000.92	001.20
40	50	000.30	000.23	000.97	003.78	000.00	001.76	000.00	000.02	000.12	000.26	000.44	000.75	000.98
50	10	000.61	000.46	000.97	003.74	000.00	003.16	000.01	000.05	000.24	000.52	000.88	001.48	001.95
50	20	000.17	000.13	000.97	003.76	000.00	000.87	000.00	000.01	000.07	000.14	000.24	000.41	000.54
50	30	000.32	000.24	000.97	003.82	000.00	002.10	000.00	000.03	000.13	000.28	000.47	000.80	001.03
50	40	000.61	000.46	000.95	003.67	000.00	003.04	000.01	000.05	000.24	000.52	000.89	001.49	001.95
50	50	000.68	000.51	000.96	003.70	000.00	003.76	000.01	000.05	000.27	000.58	000.98	001.66	002.16

Source: self-prepared.

(reporting a subset of all thirteen statistics for $m,pmod10=0$).

From the results of the Monte Carlo experiment, it is observable that (1) the NRMSE from the first-step estimate ${\widehat{\mathbf{z}}}^{\left(1\right)}$ and its distributional statistics exhibit increasing stability and boundedness as matrix dimensions $m\times p$ increase—specifically, for $m,p\gg 1$, both the mean and sd of NRMSE tend to converge, indicating improved estimator performance (e.g., under no diagonal restrictions, at $m=p=5$, $\mathtt{mean}=1.84$ and $\mathtt{sd}=1.29$, while at $m=p=45$, $\mathtt{mean}=0.21$ and $\mathtt{sd}=0.16$); (2) the zero-diagonal constraints (${\forall }_{i\in \{1,\dots ,min(m,p\left)\right\}}{\mathbf{X}}_{ii}=0$) reduce the degrees of freedom and lead to a much more uniform and dimensionally stable distribution of NRMSE across different matrix sizes (e.g., at $m=p=5$, mean drops to $1.17$ and sd to $0.85$, while at $m=p=45$, mean rises slightly to $0.26$ and sd to $0.19$); and (3) the distribution of NRMSE exhibits mild right skew and leptokurtosis—less so for the zero-diagonal case: under no diagonal restriction, the average skewness is $0.97$ with a coefficient of variation of $38.16\%$ (i.e., >0.00), and the average kurtosis is $4.15$ with a variation of $304.61\%$, whereas under the zero-diagonal constraint, skewness averages $0.95$ with only $8.57\%$ variation, and kurtosis averages $3.76$ with $25.94\%$ variation (i.e., >3.00). To sum up, the larger and less underdetermined (i.e., in an AP (TM) problem, the larger the ${\mathbf{M}}^{\left(1\right)}$ block of ${\mathbf{A}}^{\left(1\right)}$) the canonical system ${\mathbf{A}}^{\left(1\right)}{\mathbf{z}}^{\left(1\right)}=\mathbf{b}$, the lower the estimation error (i.e., the mean NRMSE) and its variance, and, provided a stable limiting law for NRMSE exists, the skewness and kurtosis from the simulations drift toward 0 and 3, respectively, consistent with—though not proving—a convergence toward a standard-normal distribution. This leads to a straightforward conclusion that the CLSP estimator’s Step 1 performance improves monotonically with increasing problem size and rank, indicating that larger and better-conditioned systems yield more stable normalized errors, thereby allowing future research to concentrate on the calibration of the parameters r and, on the inclusion of Step 2, $\alpha$.

For an illustration of the implementability of the estimator for the APs (TMs), CMLS (RPs), and LPRLS/QPRLS, the author’s cross-platform Python 3 module, pyclsp (version ≥ 1.6.0, available on PyPI) [84]—together with its interface co-modules for the APs (TMs), pytmpinv (version ≥ 1.2.0, available on PyPI) [85], and the LPRLS/QPRLS, pylppinv (version ≥ 1.3.0, available on PyPI) [86] (a co-module for the CMLS (RPs) is not provided, as the variability of ${\forall }_{i\in \{1,\dots ,t\}}{\mathbf{C}}_i\equiv {\mathbf{T}}_i\mathbf{D}$ within the $\mathbf{C}=\left[\begin{array}{c}{\mathbf{C}}_1\\ \dots \\ {\mathbf{C}}_u\end{array}\right]$, $u\ge t$, block of ${\mathbf{A}}^{\left(r\right)}$ prevents efficient generalization)—is employed for a sample (dataset) of i random elements ${\mathcal{X}}_i$ (scalars, vectors, or matrices depending on context) and their transformations, drawn independently from the standard normal distribution, i.e., $\{{\mathcal{X}}_1,\dots ,{\mathcal{X}}_i\}\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, under the mentioned random-variate seed 123456789 (configured for consistency with the above-described Monte Carlo experiment). Thus, using the cases of (a) a (non-negative symmetric) input–output table and (b) a (non-negative) zero-diagonal trade matrix as two AP (TM) numerical examples, this text simulates problems similar to the ones addressed in Pereira-López et al. [81] and Bolotov [16]: an underdetermined $\mathbf{X}\in {\mathbb{R}}^{m\times p}$ is estimated—from row sums, column sums, and k known values of two randomly generated matrices (a) ${\mathbf{X}}_{\mathrm{true}}=0.5·\left(|{\mathcal{X}}_1|+|{\mathcal{X}}_1{|}^{\top }\right)$ and (b) ${\mathbf{X}}_{\mathrm{true},i,j}=\left(|{\mathcal{X}}_1\right|{)}_{i,j}\left(1-{\mathbb{1}}_{\{i=j\le min(m,p\left)\right\}}\right)$, ${\left({\mathcal{X}}_1\right)}_{i,j}\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, subject to (a) ${\mathbf{X}}_{i,j}\ge 0$ and (b) ${\mathbf{X}}_{i,j}\ge 0\wedge {\forall }_{i\in \{1,\dots ,min(m,p\left)\right\}}{\mathbf{X}}_{ii}=0$—via CLSP assuming $\mathbf{x}=vec\left(\mathbf{X}\right)\subseteq \mathbf{z}$, $\mathbf{M}\equiv {\left({\mathbf{I}}_{mp}\right)}_{\mathcal{I}}$, $\mathbf{b}=\left[\begin{array}{c}{\mathbf{b}}_{\mathrm{row}\mathrm{sums}}\\ {\mathbf{b}}_{\mathrm{column}\mathrm{sums}}\\ {\mathbf{b}}_{\mathrm{known}\mathrm{values}}\end{array}\right]=\left[\begin{array}{c}{\mathbf{X}}_{\mathrm{true}}\mathbf{1}\\ {\left({\mathbf{1}}^{\top }{\mathbf{X}}_{\mathrm{true}}\right)}^{\top }\\ {\left(vec\left({\mathbf{X}}_{\mathrm{true}}\right)\right)}_{\mathcal{I}}\end{array}\right]$, and $\mathcal{I}\sim \mathcal{U}\left\{1,\dots ,mp\right\}\wedge \left|\mathcal{I}\right|=k$. The Python 3 code, based on pytmpinv and two other modules, installable by executing pip install matplotlib numpy pytmpinv==1.2.0, for (a) $m=p=20$ and $k=0.1·mp=40$ and (b) $m=p=40$—estimated with the help of $m_{\mathrm{subset}}\times n_{\mathrm{subset}}$-MNBLUE across $\left(⌈{\displaystyle \frac{m}{m_{\mathrm{subset}}}}⌉·⌈{\displaystyle \frac{n}{n_{\mathrm{subset}}}}⌉\right)=\left(⌈{\displaystyle \frac{40}{20-1}}⌉·⌈{\displaystyle \frac{40}{20-1}}⌉\right)=9$ reduced models $m_{\mathrm{reduced}}=p_{\mathrm{reduced}}\le 20$ assuming an estimability constraint of $mp\le 400$—and $k=0.2·mp=320$, with a non-iterated ($r=1$), unique ($\alpha >0$), and MNBLUE ($\alpha =1$) (two-step) CLSP solution, is implemented in (a) Listing 1 and (b) Listing 2 (e.g., to be executed in a Jupyter Notebook 6.5 or later).

Listing 1. Simulated numerical example for a symmetric input-output-table-based AP (TM) problem.

In case (a) (see Listing 1 for code), the number of model (target) variables $\#{\widehat{\mathbf{x}}}_M^{*}$ is $mp=400$ with a nullity of $dim(ker\left({\mathbf{A}}^{\left(1\right)}\right))=n-rank\left({\mathbf{A}}^{\left(1\right)}\right)=321$, corresponding to 80.25% of the total unknowns. Given the simulation of ${\mathbf{X}}_{\mathrm{true}}\in {\mathbb{R}}^{20\times 20}$, a matrix unknown in real-world applications—i.e., CLSP is used to estimate the elements of an existing matrix from its row sums, ${\mathbf{X}}_{\mathrm{true}}\mathbf{1}\in {\mathbb{R}}^{20}$, column sums, ${\left({\mathbf{1}}^{\top }{\mathbf{X}}_{\mathrm{true}}\right)}^{\top }\in {\mathbb{R}}^{20}$, and a randomly selected 10% of its entries, ${\left(vec\left({\mathbf{X}}_{\mathrm{true}}\right)\right)}_{\mathcal{I}}\in {\mathbb{R}}^{40}$—the model’s goodness of fit can be measured by a user-defined $R^2\approx max\left(0,1-{\displaystyle \frac{{∥vec\left({\mathbf{X}}_{\mathrm{true}}\right)-{\widehat{\mathbf{x}}}_M^{*}∥}_2^2}{{∥vec\left({\mathbf{X}}_{\mathrm{true}}\right)-\mathbf{1}\frac{1}{400}{\sum }_{i=1}^{400}\left(vec{\left({\mathbf{X}}_{\mathrm{true}}\right)}_i\right)∥}_2^2}}\right)\approx 0.278256$ (i.e., CLSP achieves an improvement of $\Delta R^2=0.178256$ over a hypothetical naïve predictor reproducing the known 10% entries of ${\mathbf{X}}_{\mathrm{true},\mathcal{I}}$ and yielding a $R^2\approx 0.1$ but still a modest value of $R^2$, i.e., a relatively large error, $\mathrm{NRMSE}=12.649111$) with ${\widehat{\mathbf{x}}}_M^{*}$ lying within wide condition-weighted diagnostic intervals ${\widehat{\mathbf{x}}}_M^{*}\in \left[min\left({\widehat{\mathbf{x}}}_{M,\mathrm{lower}}^{*}\right),max\left({\widehat{\mathbf{x}}}_{M,\mathrm{upper}}^{*}\right)\right]=\left[-8.0847\times {10}^{15},8.0847\times {10}^{15}\right]$ reflecting the ill-conditioning of the strongly rectangular ${\mathbf{A}}^{\left(1\right)}\in {\mathbb{R}}^{80\times 400}$, $\kappa \left({\mathbf{A}}^{\left(1\right)}\right)=4.9968\times {10}^{14}$, and only the left-sided Monte Carlo-based t-test for the mean of the NRMSE (on a sample of 30 NRMSE values obtained by substituting $\mathbf{b}$ with ${\left({\mathbf{b}}^{\left(\tau \right)}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$) suggesting consistency with expectations (i.e., with the $p-\mathrm{value}\approx 1$). In terms of numerical stability, $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)=4.8023\times {10}^{14}\approx \kappa \left({\mathbf{A}}^{\left(1\right)}\right)$ with a low ${\mathrm{RMSA}}_{i\in \{1,\dots ,40\}}=\mathrm{RMSA}=0.0400$, as confirmed by the correlogram produced in matplotlib, indicating a well-chosen constraints matrix, even given the underdeterminedness of the model (which also prevents a better fit).

Listing 2. Simulated numerical example for a (non-negative) trade-matrix-based AP (TM) problem.

In case (b) (see Listing 2 for code), the corresponding number of model (target) variables in each of the $\left(⌈{\displaystyle \frac{40}{19}}⌉·⌈{\displaystyle \frac{40}{19}}⌉\right)=9$ reduced design submatrices ${\mathbf{A}}_{\mathrm{subset}}^{\left(1\right)}\subset {\mathbf{A}}_{\mathrm{reduced}}^{\left(1\right)}$, $\#{\widehat{\mathbf{x}}}_{M,\mathrm{reduced}}^{*}$, is $m_{\mathrm{subset}}{p}_{\mathrm{subset}}\le 361$—where $m_{\mathrm{subset}}\le 20-1=19$ and $p_{\mathrm{subset}}\le 20-1=19$, one row and one column being reserved for ${\sum }_{j\notin \mathcal{J}}{a}_{i,j}^{\left(1\right)}$ and ${\sum }_{i\notin \mathcal{I}}{a}_{i,j}^{\left(1\right)}$, which enter ${\mathbf{A}}_{\mathrm{reduced}}^{\left(1\right)}$ as $\mathbf{S}=\left[\begin{array}{c}{\mathbf{I}}_{m-m_{\mathrm{subset}}}\mathbf{0}\\ \mathbf{0}{\mathbf{I}}_{p-p_{\mathrm{subset}}}\end{array}\right]$ and the vector of slack variables ${\left({\widehat{\mathbf{y}}}_{\mathrm{reduced}}^{*}\right)}^{*}=\left[\begin{array}{c}{\widehat{\mathbf{y}}}_{\mathrm{reduced}}^{*}\\ {\widehat{\mathbf{y}}}_{\mathrm{residual},\mathrm{reduced}}^{*}\end{array}\right]\subset {\widehat{\mathbf{z}}}_{\mathrm{reduced}}^{*}$, so that ${\mathbf{C}}_{\mathrm{reduced}}{\mathbf{x}}_{\mathrm{reduced}}+{\mathbf{S}}_{\mathrm{reduced}}{\mathbf{y}}_{\mathrm{reduced}}^{*}={\mathbf{b}}_{\mathrm{r}.,1:k}$ (i.e., the slack matrix compensates for the unaccounted row and column sums in the reduced models as opposed to the full one, such as case (a))—with a nullity $dim(ker\left({\mathbf{A}}_{\mathrm{reduced}}^{\left(1\right)}\right))=n_{\mathrm{reduced}}-rank\left({\mathbf{A}}_{\mathrm{reduced}}^{\left(1\right)}\right)\in [2,290]$ (per reduced model), corresponding to 25.00–72.68% of the total unknowns (per reduced model)—to compare, a full model, under the same inputs and no computational constraints (i.e., $mp\nleqq m_E{p}_E$), would have a nullity $dim(ker\left({\mathbf{A}}^{\left(1\right)}\right))=n-rank\left({\mathbf{A}}^{\left(1\right)}\right)=1168$, corresponding to 73.00% of the total unknowns. In the examined example—based on ${\mathbf{X}}_{\mathrm{true}}\mathbf{1}\in {\mathbb{R}}^{40}$, ${\left({\mathbf{1}}^{\top }{\mathbf{X}}_{\mathrm{true}}\right)}^{\top }\in {\mathbb{R}}^{40}$, and a randomly selected 20% of entries of the true matrix ${\mathbf{X}}_{\mathrm{true}}\in {\mathbb{R}}^{40\times 40}$—the reduced-model block solution’s goodness of fit could not be efficiently measured by a user-defined $R^2\approx max\left(0,1-{\displaystyle \frac{{∥vec\left({\mathbf{X}}_{\mathrm{true}}\right)-vec\left(\left\{{\widehat{\mathbf{x}}}_{M,\mathrm{reduced},1:m_{\mathrm{subset}},1:n_{\mathrm{subset}}}^{*,(i_E,j_E)}\right\}\right)∥}_2^2}{{∥vec\left({\mathbf{X}}_{\mathrm{true}}\right)-\mathbf{1}\frac{1}{1600}{\sum }_{i=1}^{1600}\left(vec{\left({\mathbf{X}}_{\mathrm{true}}\right)}_i\right)∥}_2^2}}\right)\approx 0$ (i.e., the block matrix constructed from $\left(⌈{\displaystyle \frac{40}{19}}⌉·⌈{\displaystyle \frac{40}{19}}⌉\right)=9$ reduced-model estimates led to $R^2\approx max(0,-5.435377)$ but to an error proportionate to the one in case (a), ${\mathrm{NRMSE}}_{\mathrm{reduced}}\in [3.464102,15.748016]$ (per reduced model))—in contrast, a full model would achieve $R^2\approx max\left(0,1-{\displaystyle \frac{{∥vec\left({\mathbf{X}}_{\mathrm{true}}\right)-{\widehat{\mathbf{x}}}_M^{*}∥}_2^2}{{∥vec\left({\mathbf{X}}_{\mathrm{true}}\right)-\mathbf{1}\frac{1}{1600}{\sum }_{i=1}^{1600}\left(vec{\left({\mathbf{X}}_{\mathrm{true}}\right)}_i\right)∥}_2^2}}\right)\approx 0.278427$ but at a cost of a greater error, $\mathrm{NRMSE}=29.427878$—with ${\widehat{\mathbf{x}}}_{M,\mathrm{reduced}}^{*}$ lying within strongly varying condition-weighted diagnostic intervals ${\widehat{\mathbf{x}}}_{M,\mathrm{reduced}}^{*}\in \left[min\left({\widehat{\mathbf{x}}}_{M,\mathrm{lower},\mathrm{reduced}}^{*}\right),max\left({\widehat{\mathbf{x}}}_{M,\mathrm{upper},\mathrm{reduced}}^{*}\right)\right]$, where $min\left({\widehat{\mathbf{x}}}_{M,\mathrm{lower},\mathrm{reduced}}^{*}\right)\in [-330.638753,-2.5009\times {10}^{-19}]$ (per reduced model) and $max\left({\widehat{\mathbf{x}}}_{M,\mathrm{upper},\mathrm{reduced}}^{*}\right)\in [-2.5456\times {10}^{-19},336.547225]$ (per reduced model), and varying results of Monte Carlo-based t-tests for the mean of the ${\mathrm{NRMSE}}_{\mathrm{reduced}}$ (on a sample of 30 ${\mathrm{NRMSE}}_{\mathrm{reduced}}$ values obtained by substituting ${\mathbf{b}}_{\mathrm{r}.}$ with ${\left({\mathbf{b}}_{\mathrm{r}.}^{\left(\tau \right)}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$), where the p-values range is $4.8022\times {10}^{-09}$–1.000000 (left-sided), 0.000000–1.000000 (two-sided), and $3.7021\times {10}^{-20}$–1.000000 (right-sided) (per reduced model)—alternatively, a full model would lead to wider condition-weighted diagnostic intervals ${\widehat{\mathbf{x}}}_M^{*}\in \left[min\left({\widehat{\mathbf{x}}}_{M,\mathrm{lower}}^{*}\right),max\left({\widehat{\mathbf{x}}}_{M,\mathrm{upper}}^{*}\right)\right]=\left[-1.5357\times {10}^{16},1.5357\times {10}^{16}\right]$ (i.e., reflecting the ill-conditioning of the strongly rectangular ${\mathbf{A}}^{\left(1\right)}\in {\mathbb{R}}^{400\times 1600}$, $\kappa \left({\mathbf{A}}^{\left(1\right)}\right)=2.2196\times {10}^{14}$) and only the left-sided Monte Carlo-based t-test for the mean of the NRMSE (on a sample of 30 NRMSE values obtained by substituting $\mathbf{b}$ with ${\left({\mathbf{b}}^{\left(\tau \right)}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$) suggesting consistency with expectations (i.e., with the $p-\mathrm{value}\approx 1$). In terms of numerical stability, $\kappa \left({\mathbf{C}}_{\mathrm{canon},\mathrm{reduced}}\right)\in [2.236068,6.244998]<\kappa \left({\mathbf{A}}_{\mathrm{reduced}}^{\left(1\right)}\right)\in [4.509742,9.325735]$ (per reduced model), which indicates well-conditioning of all the reduced models—conversely, in a full model, $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)=1.0907\times {10}^{14}<\kappa \left({\mathbf{A}}^{\left(1\right)}\right)$ (therefore, a full model ensures an overall better fit but a lower fit quality, i.e., a trade-off).

As the CMLS (RP) numerical example, this text addresses a problem similar to the one solved in Bolotov [15,82]: a coefficient vector $\mathit{\beta }$ from a (time-series) linear regression model in its classical (statistical) notation $y_t={\mathbf{x}}_t\mathit{\beta }+{ϵ}_t,\mathrm{s}.\mathrm{t}.{\sum }_{j=1}^{i+1}{\beta }_j=c\wedge {\forall }_{t\in \mathbf{P}}\Delta y_t=0\wedge {\forall }_{t\in \mathbf{P}}{\Delta }^2{y}_t⪌0$ with ${\Delta }^n{y}_t$ denoting n-th order differences (i.e., the discrete analogue of ${\displaystyle \frac{d^n{y}_t}{d{t}^n}}$)—where $y_t$ is the dependent variable, ${\mathbf{x}}_t=\left[1,x_{t,1},\dots ,x_{t,i}\right]$ is the vector of regressors with a constant, ${ϵ}_t$ is the model’s error (residual), c is a constant, and $\mathbf{P}⫋\{t_j:j=1,\dots ,k\}$ is the set of stationary points—is estimated on a simulated sample (dataset) with the help of CLSP assuming ${\mathbf{x}}_M\equiv \mathit{\beta }\in {\mathbb{R}}^p$ and $\mathbf{D}\equiv \mathbf{X}=\left[\mathbf{1},{\mathbf{x}}_1,\dots ,{\mathbf{x}}_i\right]\in {\mathbb{R}}^{k\times p}$, $p=i+1$. The Python 3 code, based on numpy and pyclsp modules, installable by executing pip install numpy pyclsp==1.6.0, for $k=500$, $p=6$, $c=1$, $\mathbf{y}=\mathbf{D}{\mathit{\beta }}_{\mathrm{true}}+\mathbf{ϵ}$, where ${\forall }_{j\in \{2,\dots ,6\}}{\mathbf{D}}_{·,j}\equiv {\mathcal{X}}_j$, ${\left({\mathcal{X}}_j\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, ${\mathcal{X}}_j\in {\mathbb{R}}^{500}$, ${\mathit{\beta }}_{\mathrm{true}}={\displaystyle \frac{{\mathcal{X}}_{\mathbf{\beta }}}{{\mathbf{1}}^{\top }{\mathcal{X}}_{\mathbf{\beta }}}}$, ${\left({\mathcal{X}}_{\mathbf{\beta }}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, ${\mathcal{X}}_{\mathit{\beta }}\in {\mathbb{R}}^6$, $\mathit{ϵ}\equiv {\mathcal{X}}_{\mathbf{ϵ}}$, ${\left({\mathcal{X}}_{\mathbf{ϵ}}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, ${\mathcal{X}}_{\mathbf{ϵ}}\in {\mathbb{R}}^{500}$, and $\mathbf{P}=\{t:\Delta \mathbf{y}=0\}$, with a non-iterated ($r=1$), unique ($\alpha >0$), and MNBLUE ($\alpha =1$) two-step CLSP solution (consistent with the ones from cases (a) and (b) for APs (TMs)), is implemented in Listing 3 (e.g., for a Jupyter Notebook).

Listing 3. Simulated numerical example for a (time-series) stationary-points-based CMLS (RP) problem.

Compared to the true values ${\mathit{\beta }}_{\mathrm{true}}=[0.1687,-0.3593,0.5969,-0.0628,-0.1742,0.8307]$, the CMLS (RP) estimate is $\widehat{\mathit{\beta }}={\widehat{\mathbf{x}}}_M^{*}=[0.2024,-0.1121,0.2095,-0.0396,-0.0296,0.2611]$ with a modest $R_{\mathrm{partial}}^2=0.293328$ (i.e., a greater error, ${\mathrm{NRMSE}}_{\mathrm{partial}}=0.840638$), moderate condition-weighted diagnostic intervals ${\widehat{\mathbf{x}}}_M^{*}\in [-29.7780,30.3003]$, and only the right-sided Monte Carlo-based t-test for the mean of the ${\mathrm{NRMSE}}_{\mathrm{partial}}$ (on a sample of 30 ${\mathrm{NRMSE}}_{\mathrm{partial}}$ values obtained by substituting $\mathbf{b}$ with ${\left({\mathbf{b}}^{\left(\tau \right)}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$)—in the example under scrutiny, ${\mathrm{NRMSE}}_{\mathrm{partial}}$ is preferable to NRMSE due to ${\widehat{\mathbf{y}}}^{*}\gg {\widehat{\mathbf{x}}}^{*}$—suggesting consistency with expectations (i.e., with the $p-\mathrm{value}\approx 1$). Similarly, in terms of numerical stability, $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)=138.6109>\kappa \left({\mathbf{A}}^{\left(1\right)}\right)=127.8287$, indicating that the constraint block is ill-conditioned, most likely, because of the imposed data- (rather than theory-) based definition of stationary points, which rendered Step 2 infeasible (${\widehat{\mathbf{x}}}_M^{*}={\widehat{\mathbf{x}}}_M^{\left(1\right)}$) (limiting the fit quality).

Finally, in the case of a LPRLS/QPRLS numerical example, this text simulates potentially ill-posed LP (QP) problems, similar to the ones addressed in Whiteside et al. [21] and Blair [22,23]: a solution ${\widehat{\mathbf{x}}}^{*}⋛0$ in its classical LP (QP) notation ${\mathbf{x}}^{*}=\arg {\max }_{\mathbf{x}\in {\mathbb{R}}^p}{\mathbf{c}}^{\top }\mathbf{x}$ (${\mathbf{x}}^{*}=\arg {\min }_{\mathbf{x}\in {\mathbb{R}}^p}\left\{\frac{1}{2}{\mathbf{x}}^{\top }\mathbf{Q}\mathbf{x}+{\mathbf{c}}^{\top }\mathbf{x}\right\}$), $\mathrm{s}.\mathrm{t}.\mathbf{A}\mathbf{x}\le \mathbf{b}\equiv {\mathbf{A}}_{ub}\mathbf{x}\le {\mathbf{b}}_{ub}\wedge {\mathbf{A}}_{eq}\mathbf{x}={\mathbf{b}}_{eq}$—where $\mathbf{Q}\in {\mathbb{R}}^{p\times p}$ is a symmetric positive definite matrix, $\mathbf{c}\in {\mathbb{R}}^p$, $\mathbf{A}=\left[\begin{array}{c}{\mathbf{A}}_{ub}\\ {\mathbf{A}}_{eq}\end{array}\right]\in {\mathbb{R}}^{(m_{ub}+m_{eq})\times p}$, and $\mathbf{b}=\left[\begin{array}{c}{\mathbf{b}}_{ub}\\ {\mathbf{b}}_{eq}\end{array}\right]\in {\mathbb{R}}^{m_{ub}+m_{eq}}$ —is estimated from two randomly generated (coefficient) matrices ${\mathbf{A}}_{ub}\equiv {\mathcal{X}}_1$, ${\left({\mathcal{X}}_1\right)}_{i,j}\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, and ${\mathbf{A}}_{eq}\equiv {\mathcal{X}}_2$, ${\left({\mathcal{X}}_2\right)}_{i,j}\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, and two (right-hand-side) vectors ${\mathbf{b}}_{ub}\equiv {\mathcal{X}}_3$, ${\left({\mathcal{X}}_3\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, and ${\mathbf{b}}_{eq}\equiv {\mathcal{X}}_4$, ${\left({\mathcal{X}}_4\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$, via CLSP assuming $\mathbf{C}=\left[\begin{array}{c}{\mathbf{A}}_{ub}\\ {\mathbf{A}}_{eq}\end{array}\right]$, $\mathbf{S}={\mathbf{Q}}_S^L\left[\begin{array}{c}{\mathbf{S}}_s\subseteq {\mathbf{I}}_{m_{ub}}\\ \mathbf{0}\end{array}\right]{\mathbf{Q}}_S^R$, and $\mathbf{b}=\left[\begin{array}{c}{\mathbf{b}}_{ub}\\ {\mathbf{b}}_{eq}\end{array}\right]$, where ${\mathbf{Q}}_S^L$ and ${\mathbf{Q}}_S^R$ are permutation matrices, while omitting $\mathbf{Q}$ and $\mathbf{c}$. The Python 3 code, based on numpy and pylppinv modules, installable by executing pip install numpy pylppinv==1.3.0, for $m_{ub}=50$, $m_{eq}=25$, and $p=500$, with a non-iterated ($r=1$), unique ($\alpha >0$), and MNBLUE ($\alpha =1$) (two-step) CLSP solution (analogously consistent with the ones from cases (a) and (b) for APs (TMs) and the one from CMLS (RPs)), is implemented in Listing 4 (e.g., for a Jupyter Notebook).

Listing 4. Simulated numerical example for a underdetermined and potentially infeasible LP (QP) problem.

The nullity (i.e., underdeterminedness) of the CLSP design matrix, ${\mathbf{A}}^{\left(1\right)}$, is $dim(ker\left({\mathbf{A}}^{\left(1\right)}\right))=n-rank\left({\mathbf{A}}^{\left(1\right)}\right)=475$, corresponding to 86.36% of the total unknowns, accompanied by a greater (relatively high) error, $\mathrm{NRMSE}=12.247449$, moderate condition-weighted diagnostic intervals ${\widehat{\mathbf{x}}}_M^{*}\in [-1.2919,1.3918]$, and only the right-sided Monte Carlo-based t-test for the mean of the NRMSE (on a sample of 30 NRMSE values obtained by substituting $\mathbf{b}$ with ${\left({\mathbf{b}}^{\left(\tau \right)}\right)}_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,1)$) suggesting consistency with expectations (i.e., with the $p-\mathrm{value}\approx 1$). Similarly, in terms of numerical stability, $\kappa \left({\mathbf{C}}_{\mathrm{canon}}\right)=2.2168=\kappa \left({\mathbf{A}}^{\left(1\right)}\right)=2.2168$, indicating that the constraint block is well-conditioned despite a strongly rectangular ${\mathbf{A}}^{\left(1\right)}\in {\mathbb{R}}^{75\times 550}$. Hence, CLSP can be efficiently applied to AP (TM), CMLS (RP), and LPRLS/QPRLS special cases using Python 3, and the reader may wish to experiment with the code in Listings 1–4 by relaxing its uniqueness (setting $\alpha =0$) or the MNBLUE characteristic (setting $\alpha \in [0,1)$).

To sum up, while the simulated numerical examples for the APs (TMs), CMLS (RPs), and LPRLS/QPRLS problems successfully illustrate the theoretical assumptions and numerical behavior of the CLSP estimator (as described in Section 3, Section 4 and Section 5 of this work), they remain limited by simplification and a priori construction. First, each estimation was performed under a fixed $r=1$ (i.e., without iterative refinement) and a unique MNBLUE configuration ($\alpha =1$), thus omitting the calibration of these parameters. Second, in the AP (TM) case with 10% known values and a non-zero diagonal, similar to the CMLS (RP) one, the estimator achieved a modest $R^2\approx 0.3$, consistent with the degree of underdeterminedness, while the reduced models (e.g., zero-diagonal, block-decomposed) performed substantially worse due to aggregation and block-wise estimation (backing the recommendation to prefer full models over reduced ones). Finally, the estimator, given its formalization, is computationally demanding, with the SVD-based Step 1 complexity of $O(max(m,n)min{(m,n)}^2)$ for ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{m\times n}$ in each iteration (in CLSP-based software built on Python’s SciPy, R, and Stata) and convex-programming-based Step 2 complexity of $O\left(knnz\left({\mathbf{A}}^{\left(r\right)}\right)\right)$ or $O\left(n^3\right)$, where k is the number of solver iterations and $nnz(·)$ is the number of non-zero elements in ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{m\times n}$, (in CLSP-based software built on Python’s CVXPY and R’s CVXR), not including eventual repeated estimations for ${\mathrm{RMSA}}_i$ (in which ${\mathbf{A}}^{\left(r\right)}$ is reduced by one row) and Monte Carlo-based t-test—to exemplify, a $20\times 20$ AP (TM) problem with 10% known values and a non-zero diagonal has an ${\mathbf{A}}^{\left(r\right)}\in {\mathbb{R}}^{80\times 400}$ requiring r-times 2.56 million floating-point operations in Step 1 and up to 320 million under the SCS solver in Step 2, both eventually repeated twenty times to calculate ${\mathrm{RMSA}}_i$ and at least thirty times (per CLT) for Monte Carlo-based t-test. Despite its complexity, the CLSP framework remains practically viable and is ready for parameter calibration with subsequent application to real-world problems.

8. Discussion and Conclusions

The proposed modular two-step Convex Least Squares Programming (CLSP) estimator represents an attempt to unify historical efforts developed mainly in the 1960s–1990s to address ill-posed problems in both LS and LP (QP)—namely, the mentioned Wolfe [25], Stoer [75], Waterman [76], Dax [26], Osborne [27], George and Osborne [74], Barnes et al. [79], Donoho and Tanner [73], Grafarend and Awange [77], Bei et al. [80], and Qian et al. [78]—by correcting (1) the estimation, based on a Moore–Penrose pseudoinverse ${\mathbf{A}}^{†}$ (which has been applied in an ad hoc manner in the field, particularly in econometrics in the 2010s; consult Pereira-López et al. [81] and Bolotov [16]) and a Bott–Duffin inverse ${\mathbf{A}}_{\mathbf{Z}}^{†}$ (based on the literature research, this text may be the first to consider a constrained generalized inverse to generalize an ${\mathbf{A}}^{†}$-based estimator) with the help of a (2) regularization-inspired correction [4] (pp. 477–479), achieving greater fit quality in terms of ensuring strict satisfaction of problem constraints (previously infeasible under an ${\mathbf{A}}^{†}$-based solution), while yielding a (potentially) unique and MNBLUE solution (by setting $\alpha =1$). At the same time, CLSP is well grounded in the algorithmic logic of the works in question, such as Wolfe [25] and Dax [26], as further formalized by, e.g., Osborne [27]. However, the primary strength of the framework in question lies in its “generality”: in contrast to the (individual) problem-specific algorithms, such as the ones developed by Übi [28,29,30,31,32]—routines combining (NN)LS, LP, and QP within a single framework to solve both well- and ill-posed convex optimization problems—CLSP provides a unified estimator with a proper methodology for numerical stability and goodness-of-fit assessment, centered around RMSA and NRMSE. A secondary strength is its practical “versatility”: through at least three classes of special cases—APs (TMs), CMLS (RPs), and LPRLS/QPRLS—it allows estimation of (rectangular) input–output tables (national, inter-country, or satellite), structural matrices (such as trade, country-product, investment, or migration data), and previously infeasible textbook-definition models of economic variables and/or LP (QP) problems. Furthermore, the inclusion of ${\mathbf{A}}_{\mathbf{Z}}^{†}$ allows probabilistic and Bayesian applications since its subspace restrictions can be interpreted in terms of random variables and prior distributions, as well as Monte Carlo-based inference. To conclude, CLSP has already been fully implemented in Python 3 (pyclsp, pytmpinv, and pylppinv) and is to be ported into R and Stata in the future, making it a readily available alternative to purely theoretical or not freely accessible algorithms or proprietary packages, and applicable in a real-world setting (such as econometric research, replacing [15,16,81] with the two-step corrected estimation).