Simulation Teaching of Adaptive Fault-Tolerant Containment Control for Nonlinear Multi-Agent Systems

Abstract

An adaptive fault-tolerant containment control approach is developed for nonlinear multi-agent systems to address issues related to both communication link and actuator faults. This approach achieves fault-tolerant containment control through the introduction of a convex hull signal estimator and a fault compensation mechanism. First, a leader–follower network model with communication link faults is constructed, and distributed containment errors are established. The proposed framework involves three key components: the design of an adaptive backstepping control law, the introduction of a nonlinear filter for boundary error elimination, and the application of a radial basis function neural network (RBFNN) for the approximation of unknown nonlinear terms. Meanwhile, an adaptive convex hull estimator is designed to estimate the signals formed by the leaders, and an actuator fault estimator is constructed to compensate for fault signals online. Additionally, Lyapunov stability analysis demonstrates that all containment errors remain uniformly bounded. To support simulation teaching and validation, numerical simulations and autonomous underwater vehicle (AUV) simulations are used to not only to confirm the efficacy of the presented control technique but also to provide illustrative cases for educational purposes.

1. Introduction

The significant application potential of multi-agent systems in unmanned devices has driven enduring research interest in their cooperative control. Among them, underwater vehicles stand out as key tools for ocean exploration. Their cooperative control is highly useful for tasks like resource prospecting and ocean monitoring [1,2,3]. The objective of containment control, a key cooperative problem, is to ensure that the states of all followers reside within the convex hull spanned by the leaders’ states, achieved via a distributed strategy [4]. This framework perfectly fits complex task scenarios such as multi-target enclosure, cooperative escort, and safe area coverage. Especially for autonomous underwater vehicles (AUVs), in such tasks, challenges such as limited communication [5] and complex environment [6] are faced. How to achieve effective containment control has always been the focus of research in the field.

The research on containment control has been extended from linear systems to complex nonlinear systems. Early work focused on linear models. Reference [7] laid the theoretical foundation of linear containment control under fixed topology based on algebraic graph theory and matrix theory. For the more general nonlinear dynamic models in the real world, backstepping [8,9], adaptive control [10,11] and intelligent optimization algorithms have been widely used. The inherent adaptive approximation capability of neural networks enabled references [12,13] to effectively handle the unknown nonlinearities in the follower dynamics, while reference [14,15] adopted fuzzy logic systems to address similar challenges. To further improve the robustness of the system, techniques such as disturbance observers [16] and sliding mode control [17] have been successfully integrated into the containment control framework to suppress external disturbances and model uncertainties. Most of the above research is based on ideal communication assumptions. However, practical communication networks often face non-ideal factors such as bandwidth limitations, time delays, and packet loss. This reality has thus prompted the development of communication-aware control strategies. Reference [18] studied containment control under switching topology, and reference [19] further explored consensus under random communication noise. However, these works usually model faults as disturbances with known statistical characteristics or fixed patterns, and research on completely unknown, time-varying weight faults for communication links (such as caused by malicious network attacks [20,21]) is not sufficient. Such faults can destroy the inherent properties of the topology structure, making traditional Laplacian matrix-based analysis methods ineffective.

On the other hand, as the final execution unit of control, the reliability of the actuator is of crucial importance. Actuator faults mainly include partial faults (multiplicative faults), jams, and offsets (additive faults), among others. One of the most important technologies for guaranteeing the system’s safe functioning is fault-tolerant control. Existing fault-tolerant strategies can be divided into passive [22,23] and active [24,25] types. Although the passive method has a simple structure but is conservative, the active online method estimates the fault information through a fault diagnosis module and compensates for it, with better performance. Regarding fault-tolerant control, some studies have developed adaptive controllers to compensate for actuator faults [26,27], and in [28], an interval observer was used to detect and isolate system faults. However, an obvious trend is that most fault-tolerant control studies deal with actuator faults or communication problems in isolation.

Although the existing achievements have enriched the theoretical system of multi-agent fault-tolerant control, through systematic review, an important research gap can still be found: currently, very few works can comprehensively handle the complex scenario where there are coexisting unknown time-varying weight faults in the communication link and mixed actuator faults (that is, multiplicative faults and additive faults coexist), and this situation is particularly common in reality. For example, in the cooperative operation of AUVs, underwater communication is limited, and link quality fluctuations or even interruptions can easily occur. At the same time, the actuator faces multiple faults such as hydrodynamic uncertainties, actuator jams, or thrust losses. These two types of faults are coupled with each other: communication faults lead to distorted information of neighbors and leaders, destroying the information basis for cooperative control; actuator faults directly cause execution deviations, resulting in the degradation of the system’s dynamic performance. The superposition of simultaneous faults in both communication and execution greatly increases the difficulty of controller design and also poses serious challenges to system stability and security. In response to the issues above, this work focuses on the adaptive containment control problem under a complex scenario involving both unknown communication link faults and mixed actuator faults in nonlinear multi-agent systems. The contributions of this paper are summarized as follows:

• Aiming at addressing the problem whereby the leader reference signal cannot be directly obtained due to time-varying faults in the communication link, a new distributed adaptive estimator is designed to reconstruct the required convex hull signal online, laying a foundation for the realization of containment control.
• A nonlinear filter with a dynamic compensation term is introduced. Compared with traditional linear filters, it can more effectively handle the differential explosion problem and suppress the filtering error in backstepping design, and enhance the system’s resilience and transient performance.
• A unified adaptive framework is proposed, which can simultaneously estimate the multiplicative fault- and additive fault-related values of the actuator online and generate an active compensation signal, effectively eliminating the negative impact of hybrid faults on the system performance.

To confirm the efficacy and capacity for generalization of the suggested approach, in addition to the conventional numerical simulation, this paper also adds a simulation experiment of AUV containment control to simulate the situation where communication link faults and actuator thrust faults occur simultaneously in a complex marine environment, further reflecting the practical value of the theoretical results in the application of typical unmanned systems.

In fault-tolerant control of nonlinear multi-agent systems, simulations are essential to complement theoretical designs. Physical fault injection is often costly, unsafe, and hard to reproduce. Simulations offer three key advantages: safe and low-cost virtual testing under extreme faults; full control over fault timing and type, ensuring repeatability; and complete, noise-free data to reveal system dynamics. Through stability analysis [29] and comprehensive simulations, this paper validates the effectiveness and generality of the proposed adaptive fault-tolerant containment scheme.

The remainder of this paper is organized as follows: Section 2 gives preliminaries and problem formulation; Section 3 details adaptive fault-tolerant containment controller design; Section 4 provides simulation results and analysis; and Section 5 summarizes the full paper.

2. Preliminaries and Problem Formulation

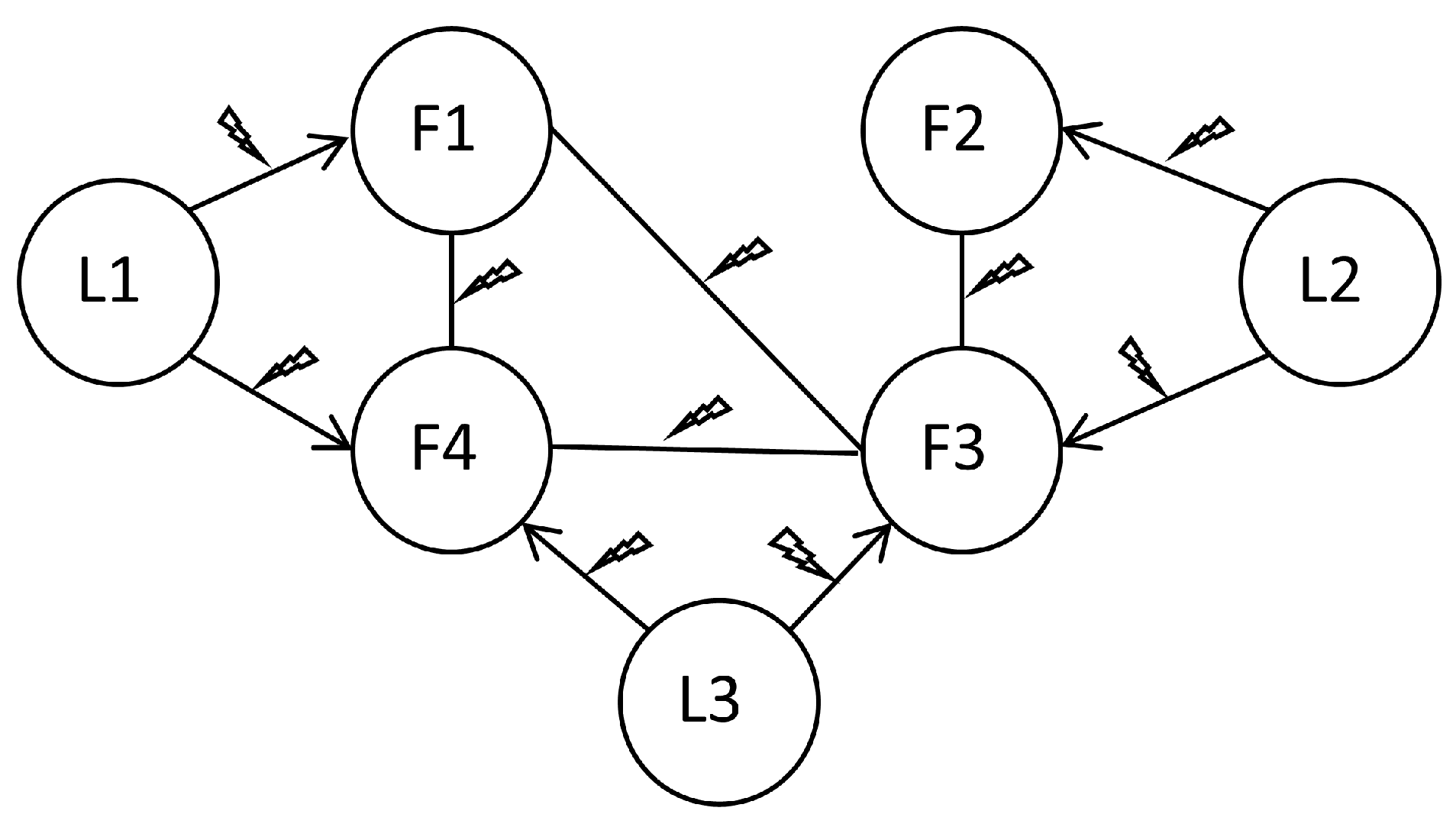
2.1. Graph Theory

The communication topology can be described by the graph $G=(V,E,A)$, with the following components: the node set $V=\{1,2,\dots ,N+M\}$; the edge set $E\subseteq V\times V$; the adjacency matrix $A=\left[a_{ij}\right]$. Furthermore, the in-degree matrix is given by $D=\mathrm{diag}\left\{d_i\right\}$, and the Laplacian matrix by $L=D-A$.

Consider a multi-agent system populated by N followers and M leaders, interconnected via a communication network. The adjacency weight $a_{ij}$ is greater than zero if and only if $\left(v_j,v_i\right)\in E$; otherwise, $a_{ij}$ equals to zero and, at the same time, $d_i={\displaystyle \sum _{i=1}^N}{a}_{ij}$. In this paper, the communication among N followers is considered to be undirected.

Assumption 1.

There is no direct communication link among the leaders; and each follower can at least establish a communication connection with one of the leaders.

Definition 1

([30]). The convex hull of a set $\mathcal{A}\subset {\mathbb{R}}^P$ can be expressed as

$$Co\left(\mathcal{A}\right)=\left\{\left.\sum _i{\omega }_i{\mathbf{y}}_i \right| {\mathbf{y}}_i\in \mathcal{A}, {\omega }_i\ge 0, \sum {\omega }_i=1\right\}$$

where the summation index runs over any finite subset of $\mathcal{A}$.

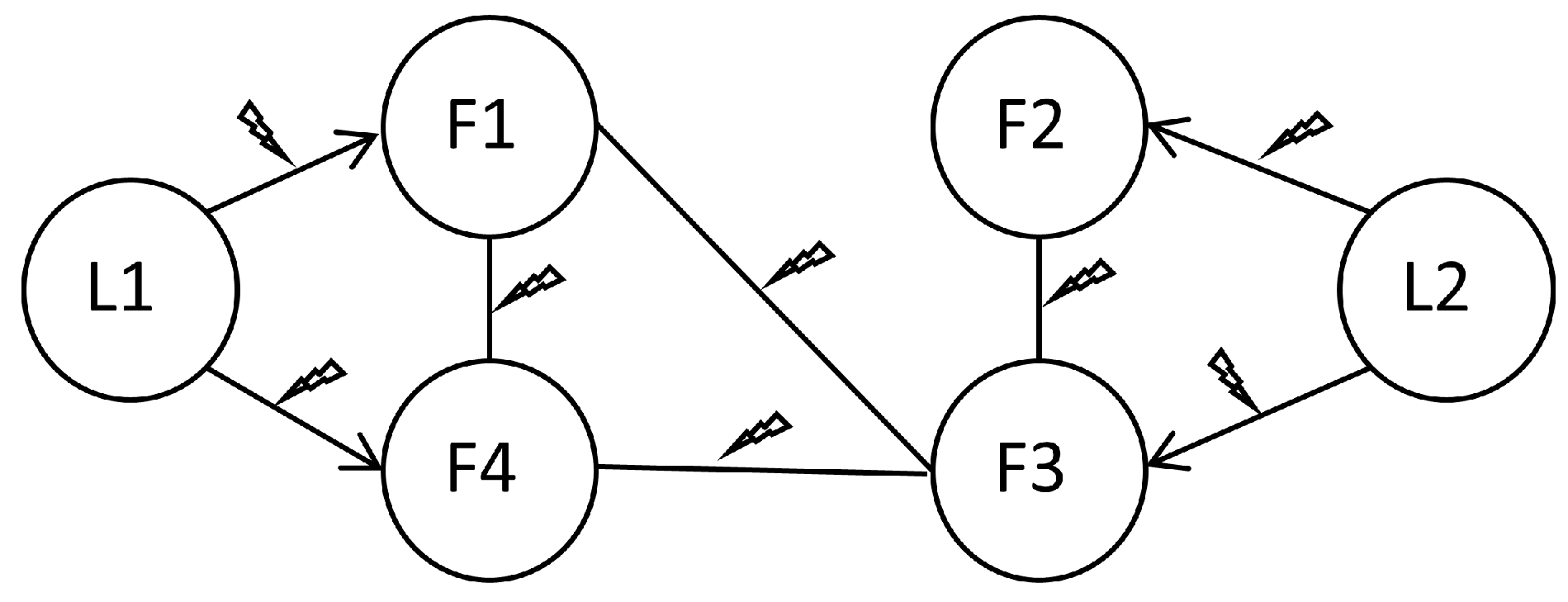
2.2. Communication Link Faults

In this paper, given a G (undirected graph) representing communication link faults, these faults can be expressed as

$$\begin{array}{cc}\hfill {\tilde{a}}_{ij}^F\left(t\right)& =a_{ij}+{\delta }_{ij}^F\left(t\right), j=1,2,\dots ,N\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\tilde{a}}_{ij}^L\left(t\right)& =a_{ij}+{\delta }_{ij}^L\left(t\right), j=N+1,\dots ,N+M\hfill \end{array}$$

(2)

where $a_{ij}>0$ is the weight in the ideal communication link, defined as the connection matrix A, while ${\delta }_{ij}^F\left(t\right)$ and ${\delta }_{ij}^L\left(t\right)$ are time-varying weights caused by faults. It can be seen from (1) and (2) that the communication link’s weight changes from the constant $a_{ij}$ to the unknown time-varying functions ${\tilde{a}}_{ij}^F\left(t\right)$ and ${\tilde{a}}_{ij}^L\left(t\right)$. In this case, the designed Laplacian coefficient matrix is

$$\tilde{L}\left(t\right)=\left\{{\tilde{l}}_{ij}\left(t\right)\mid {\tilde{l}}_{ij}\left(t\right)\in {\mathbb{R}}^{\left(M+N\right)}\right\}$$

The elements of the matrix are defined as

$$\left\{\begin{array}{c}{\tilde{l}}_{ii}\left(t\right)=\sum _{j\ne i}{\tilde{a}}_{ij}\left(t\right)\hfill \\ {\tilde{l}}_{ij}\left(t\right)=-{\tilde{a}}_{ij}\left(t\right),i\ne j\hfill \end{array}\right.$$

Assumption 2.

In an undirected graph, ${\delta }_{ij}^F\left(t\right)$ and ${\delta }_{ij}^L\left(t\right)$ are the communication link faults. They have bounded derivatives. Assume ${\delta }_{ij}^F\left(t\right)={\delta }_{ji}^F\left(t\right)$.

Assumption 3.

${\tilde{a}}_{ij}^F\left(t\right)$ and ${\tilde{a}}_{ij}^L\left(t\right)$ are the same as the sign of $a_{ij}$.

With respect to Assumptions 1 and 2, the following is an expression for the Laplacian matrix $\tilde{L}\left(t\right)$:

$$\tilde{L}\left(t\right)=\left[\begin{array}{cc}{\tilde{L}}_1\left(t\right)\hfill & {\tilde{L}}_2\left(t\right)\hfill \\ 0_{M\times N}\hfill & 0_{M\times M}\hfill \end{array}\right]$$

2.3. Problem Formulation

The following can be written for a network system with M leaders and N followers:

$$\begin{array}{cc}\hfill {\dot{x}}_{i,k}=& x_{i,k+1}+f_{i,k}\left({\mathcal{X}}_{i,k}\right)\hfill \\ \hfill {\dot{x}}_{i,n}=& b_i{u}_i^f+f_{i,n}\left({\mathcal{X}}_{i,n}\right)\hfill \end{array}$$

where the system’s state variable is ${\mathcal{X}}_{i,k}={\left[x_{i,1},x_{i,2},\dots ,x_{i,k}\right]}^T$, $i\in \{1,2,\dots ,N\},k\in \{1,2,\dots ,n-1\}$. The i-th follower’s output signal is represented by $y_i$. The nonlinear function $f_{i,k}\left({\mathcal{X}}_{i,k}\right)$ is unknown and continuously differentiable. $b_i$ satisfies $0<b_i\le Q_i$. Among them, an indeterminate positive constant is $Q_i$. ${u_i}^f$ is the input with faults, characterized by

$$u_i^f=s_i{u}_i\left(t\right)+u_i^b\left(t\right)$$

(3)

where the actual control input is $u_i\left(t\right)$. $0<s_i\le 1$ represents the unknown control effectiveness during faults, and $s_i$ is an unknown positive constant. The time-varying deviation fault function $u_i^b\left(t\right)$ is unknown, and it satisfies $\left|u_i^b\left(t\right)\right|\le u_i^b$, whereas a positive constant that is unknown is $u_i^b$.

For the following controller design, some structural characteristics of the undirected graph with communication link faults are derived.

Lemma 1

([30]). A symmetric positive definite matrix is ${\tilde{L}}_1\left(t\right)$ if Assumptions 1 and 3 are true.

Lemma 2

([30]). The sum of the elements in each row of $-{\tilde{L}}_1{\left(t\right)}^{-1}{\tilde{L}}_2\left(t\right)$ is still equal to 1, and each element of $-{\tilde{L}}_1{\left(t\right)}^{-1}{\tilde{L}}_2\left(t\right)$ is greater than or equal to zero.

Lemma 3

([31]). For any ϕ (real variable), the following can be found:

$$\left|\varphi \right|-\varphi tanh{\displaystyle \frac{\varphi }{\delta }}\le 0.2785\delta$$

where $\delta >0$.

2.4. Control Objective

The purpose of this study is to construct a nonlinear multi-agent system’s adaptive fault-tolerant containment controller, such that in the event of actuator and communication link faults, the leader $y_{rj}\left(j=N+1,N+2,\dots ,N+M\right)$ can drive the follower’s output $y_i\left(i=1,2,\dots ,N\right)$ to converge into the convex hull spanned by it with enough accuracy.

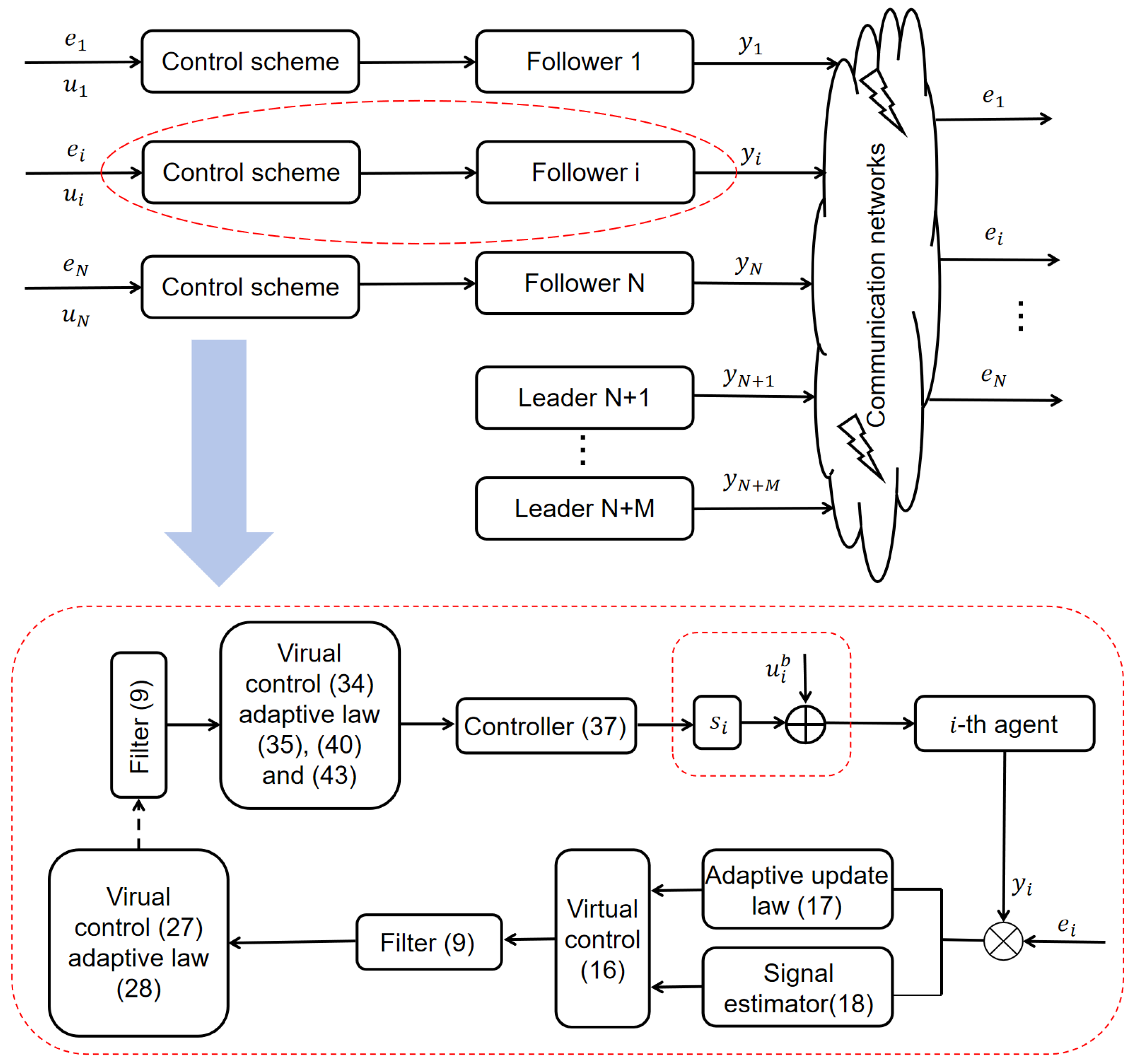
3. Adaptive Fault-Tolerant Containment Controller Design

The controller is derived using the backstepping method in this section. The nonlinear terms are estimated using a neural network and a nonlinear filter at each step, and ultimately, the system’s stability is demonstrated by creating a Lyapunov function. The control architecture diagram of the system is presented in Figure 1.

3.1. Recursive Design

Define vectors $Y_F={\left[y_1,y_2,\dots ,y_N\right]}^T\in {\mathbb{R}}^N$ and $Y_L=$${\left[y_{rN+1},y_{rN+2},\dots ,y_{rN+M}\right]}^T\in {\mathbb{R}}^M$. The distributed containment error with communication link faults is defined as

$$e_i=\sum _{j\in N_i^F}{\tilde{a}}_{ij}^F\left(t\right)\left(y_i-y_j\right)+\sum _{j\in N_i^L}{\tilde{a}}_{ij}^L\left(t\right)\left(y_i-y_{rj}\right)$$

(4)

Its compact form can be written as

$$e={\tilde{L}}_1\left(t\right)Y_F+{\tilde{L}}_2\left(t\right)Y_L$$

(5)

where $N_i^F$ and $N_i^L$ represent the sets of followers and leaders connected to the i-th agent, respectively.

${\tilde{L}}_1\left(t\right)$ remains an invertible matrix in accordance with Lemma 1; then, we obtain

$$e={\tilde{L}}_1\left(t\right)\left[Y_F-\left(-{\tilde{L}}_1{\left(t\right)}^{-1}{\tilde{L}}_2\left(t\right)Y_L\right)\right]$$

where $Y_d={\left[y_{d1},\dots ,y_{di},\dots ,y_{dN}\right]}^T=-{\tilde{L}}_1{\left(t\right)}^{-1}{\tilde{L}}_2\left(t\right)Y_L$. Then, from Lemma 2 and Definition 1, when $Y_F\to Y_d$ ($e\to 0$), $y_i\left(i\in N_i^F\right)$ converges towards the convex hull $Co\left\{y_{rj},j\in N_i^L\right\}$.

It is assumed that the reference signals $y_{rj}$ of the leaders are continuously differentiable and their derivatives $y_{rj},{\dot{y}}_{rj},{\ddot{y}}_{rj},j=N+1,\dots ,N+M$ are bounded in this paper.

Remark 1.

From Lemmas 1 and 2, it can be seen that some properties in the static undirected graph still hold in the time-varying case. Then, even if the graph information is time-varying, the convex hull that the leaders traverse still contains the signal $Y_d$.

Assumption 4.

For every agent, it is assumed that the distributed containment error $e_i$ is measurable.

Remark 2.

Although the specific values of the time-varying weights ${\tilde{a}}_{ij}^F\left(t\right)$ and ${\tilde{a}}_{ij}^L\left(t\right)$ cannot be directly obtained, the tracking error $e_i$ in the formation system can still be effectively constructed. Consider an underwater vehicle formation system that implements distributed control based on a wireless local area network, where the control instructions are generated by a central computer server. When the output signal is transmitted through a network with potential link faults, the server stores the data ${\tilde{a}}_{ij}^F\left(t\right)y_i$ and ${\tilde{a}}_{ij}^L\left(t\right)y_{rj}$ after weight adjustment. Through the distributed calculation on the server side, the relative error between adjacent vehicles can be reconstructed into the form of ${\tilde{a}}_{ij}^F\left(t\right)\left(y_i-y_j\right)$ and ${\tilde{a}}_{ij}^L\left(t\right)\left(y_i-y_{rj}\right)$. Extending this reconstruction process to the entire communication topology graph, even if the weight coefficients ${\tilde{a}}_{ij}^F\left(t\right)$ and ${\tilde{a}}_{ij}^L\left(t\right)$ are unknown, the error signal $e_i$ for the controller design can still be obtained through data fusion.

The following equations describe a coordinate transformation:

$$\begin{array}{cc}\hfill z_{i,1}& =y_i-{\widehat{y}}_{di}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill z_{i,k}& =x_{i,k}-{\alpha }_{i,k}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill s_{i,k}& ={\beta }_{i,kf}-{\alpha }_{i,k-1}\hfill \end{array}$$

(8)

where the convex hull signal $y_{di}$ of the i-th agent is estimated by ${\widehat{y}}_{di}$. ${\beta }_{i,kf},k=2,3,\dots ,N,$ is the filtered output signal, whereas ${\alpha }_{i,k-1}$ is the input signal and virtual control signal of the filter. The design of the nonlinear filter is as follows:

$$\begin{array}{c}\hfill {\tau }_{i,k}{\dot{\beta }}_{i,kf}=-{\tau }_{i,k}{\widehat{B}}_{i,k}tanh\left[{\displaystyle \frac{{\widehat{B}}_{i,k}\left({\beta }_{i,kf}-{\alpha }_{i,k-1}\right)}{{\epsilon }_{i,k}}}\right]-\left({\beta }_{i,kf}-{\alpha }_{i,k-1}\right)\end{array}$$

(9)

where ${\tau }_{i,k}>0$ represents the time constant; ${\epsilon }_{i,k}>0$ is an adjustment parameter; the estimate of $B_{i,k}$ is ${\widehat{B}}_{i,k}$. The initial conditions satisfy ${\beta }_{i,kf}\left(0\right)=$${\alpha }_{i,k-1}\left(0\right)$.

Step 1: Using the coordinate transformation (6), the following relationship is obtained:

$$z_{i,1}=y_i-{\widehat{y}}_{di}=y_i-y_{di}+y_{di}-{\widehat{y}}_{di}={\delta }_i+{\tilde{y}}_{di}$$

(10)

where ${\delta }_i=y_i-y_{di}$ and ${\tilde{y}}_{di}=y_{di}-{\widehat{y}}_{di}$.

This is how the derivative of $z_{i,1}$ is computed:

$${\dot{z}}_{i,1}={\dot{y}}_i-{\dot{\widehat{y}}}_{di}={\dot{z}}_{i,2}+{\alpha }_{i,1}+s_{i,2}+f_{i,1}\left({\mathcal{X}}_{i,1}\right)-{\dot{\tilde{y}}}_{di}$$

(11)

Due to the existence of uncertainties, the function $f_{i,1}\left({\mathcal{X}}_{i,1}\right)$ cannot be directly used for the controller. Since the radial basis function neural network (RBFNN) has excellent approximation ability, it is applied to estimate the function $f_{i,1}\left({\mathcal{X}}_{i,1}\right)$. Then, there exists a neural network $M_{i,1}^{\ast }{U}_{i,1}\left({\mathcal{X}}_{i,1}\right)$ that satisfies

$$f_{i,1}\left({\mathcal{X}}_{i,1}\right)=M_{i,1}^{\ast T}{U}_{i,1}\left({\mathcal{X}}_{i,1}\right)+{\iota }_{i,1}\left({\mathcal{X}}_{i,1}\right)$$

(12)

where $M_{i,1}^{\ast }\in R^{l\times m}$ represents the ideal weight vector, ${\iota }_{i,1}\left({\mathcal{X}}_{i,1}\right)$ is the estimated error that meets $\left|{\iota }_{i,1}\right|\le {\overline{\iota }}_{i,1}$, and $U_{i,1}=\left[U_{i,1}^1,U_{i,1}^2,\dots ,U_{i,1}^l\right]\in R^l$ represents having

$$U_{i,1}^k=exp\left({\displaystyle \frac{-{∥\begin{array}{c}{\mathcal{X}}_{i,1}-c_{\epsilon }\end{array}∥}^2}{w_{\epsilon }^2}}\right),\epsilon =1,2,\dots ,l$$

(13)

where in the Gaussian function, the center and width are specified by $c_{\epsilon }$ and $w_{\epsilon }$ which correspond to these two key parameters, respectively.

Consider the Lyapunov function candidate, defined by

$$V_1=\sum _{i=1}^N\left[{\displaystyle \frac{1}{2}}{z}_{i,1}^2+{\displaystyle \frac{1}{2{\kappa }_{M_{i1}}}}{\tilde{M}}_{i,1}^T{\tilde{M}}_{i,1}+{\displaystyle \frac{1}{2{\kappa }_{y_{di}}}}{\tilde{y}}_{di}^2\right]$$

(14)

where ${\tilde{M}}_{i,1}=M_{i,1}^{\ast }-{\widehat{M}}_{i,1},{\kappa }_{M_{i1}}$ and ${\kappa }_{y_{di}}$ represent positive design parameters.

Differentiating $V_1$ gives

$$\begin{array}{cc}\hfill {\dot{V}}_1=& \sum _{i=1}^N{z}_{i,1}\left[-{\widehat{y}}_{di}+z_{i,2}+s_{i,2}+M_{i,1}^{\ast T}{U}_{i,1}+{\alpha }_{i,1}+{\iota }_{i,1}\right]\hfill \\ \hfill & -\sum _{i=1}^N\left[{\displaystyle \frac{{\tilde{M}}_{i,1}^T{\widehat{M}}_{i,1}}{{\kappa }_{M_{i1}}}}+{\displaystyle \frac{{\tilde{y}}_{di}\left({\dot{y}}_{di}-{\dot{\tilde{y}}}_{di}\right)}{{\kappa }_{y_{di}}}}\right]\hfill \end{array}$$

(15)

The following designs for the virtual controller, adaptive update law, and adaptive estimator are derived:

$$\begin{array}{cc}\hfill {\alpha }_{i,1}=& -k_i{e}_i-c_{i,1}{z}_{i,1}-{\displaystyle \frac{3}{2}}{z}_{i,1}-{\widehat{M}}_{i,1}^T{U}_{i,1}+{\dot{\widehat{y}}}_{di}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\dot{\widehat{M}}}_{i,1}=& {\kappa }_{M_{i1}}{z}_{i,1}{U}_{i,1}-{\mu }_{M_{i1}}{\widehat{M}}_{i,1}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\dot{\widehat{y}}}_{di}=& -{\kappa }_{y_{di}}{k}_i{e}_i-{\mu }_{y_{di}}{\widehat{y}}_{di}\hfill \end{array}$$

(18)

where $k_i,c_{i,1},{\mu }_{M_{i1}}$ and ${\mu }_{y_{di}}$ are positive design parameters.

Substituting Equations (16)–(18) into Equation (15) gives

$$\begin{array}{cc}\hfill {\dot{V}}_1=-& \sum _{i=1}^N{c}_{i,1}{z}_{i,1}^2+\sum _{i=1}^N-k_i{e}_i\left(z_{i,1}+{\tilde{y}}_{di}\right)+\sum _{i=1}^N{z}_{i,1}\left[z_{i,2}+s_{i,2}+{\iota }_{i,1}-{\displaystyle \frac{3}{2}}{z}_{i,n}\right]\hfill \\ \hfill -& \sum _{i=1}^N\left[{\displaystyle \frac{{\tilde{M}}_{i,1}^T{\widehat{M}}_{i,1}}{{\kappa }_{M_{i1}}}}+{\displaystyle \frac{{\tilde{y}}_{di}{\dot{y}}_{di}}{{\kappa }_{y_{di}}}}+{\displaystyle \frac{{\mu }_{y_{di}}}{{\kappa }_{y_{di}}}}{\tilde{y}}_{di}{\widehat{y}}_{di}\right]\hfill \end{array}$$

(19)

From Young’s inequality comes the following result:

$$\begin{array}{cc}\hfill z_{i,1}{z}_{i,2}& \le {\displaystyle \frac{1}{2}}{z}_{i,1}^2+{\displaystyle \frac{1}{2}}{z}_{i,2}^2\hfill \\ \hfill z_{i,1}{s}_{i,2}& \le {\displaystyle \frac{1}{2}}{z}_{i,1}^2+{\displaystyle \frac{1}{2}}{s}_{i,2}^2\hfill \\ \hfill z_{i,1}{l}_{i,1}& \le {\displaystyle \frac{1}{2}}{z}_{i,1}^2+{\displaystyle \frac{1}{2}}{l}_{i,1}^2\hfill \\ \hfill {\tilde{y}}_{di}{\widehat{y}}_{di}& \le {\displaystyle \frac{1}{2}}{\tilde{y}}_{di}^2+{\displaystyle \frac{1}{2}}{\widehat{y}}_{di}^2\hfill \end{array}$$

(20)

Substituting Equation (20) into (19) gives

$$\begin{array}{cc}\hfill {\dot{V}}_1\le -& \sum _{i=1}^N{c}_{i,1}{z}_{i,1}^2+\sum _{i=1}^N-k_i{e}_i\left(z_{i,1}+{\tilde{y}}_{di}\right)+\sum _{i=1}^N\left[z_{i,2}^2+s_{i,2}^2+{\iota }_{i,1}^2\right]\hfill \\ \hfill -& \sum _{i=1}^N\left[{\displaystyle \frac{{\tilde{M}}_{i,1}^T{\widehat{M}}_{i,1}}{{\kappa }_{M_{i1}}}}+{\displaystyle \frac{{\tilde{y}}_{di}^2}{2{\kappa }_{y_{di}}}}+{\displaystyle \frac{{\dot{y}}_{di}^2}{2{\kappa }_{y_{di}}}}+{\displaystyle \frac{{\mu }_{y_{di}}}{{\kappa }_{y_{di}}}}{\tilde{y}}_{di}{\widehat{y}}_{di}\right]\hfill \end{array}$$

(21)

It can be inferred that

$$\begin{array}{cc}\hfill -\sum _{i=1}^N{k}_i{e}_i\left(z_{i,1}+{\tilde{y}}_{di}\right)=& -\sum _{i=1}^N{k}_i{e}_i{\delta }_i=-{\delta }^{T}K\left({\tilde{L}}_1{Y}_F+{\tilde{L}}_2{Y}_L\right)=-{\delta }^{T}K{\tilde{L}}_1\left(Y_F-Y_d\right)\hfill \\ \hfill \le & -{\lambda }_{min}\left(K{\tilde{L}}_1\right){\delta }^T\delta <0\hfill \end{array}$$

(22)

where ${\lambda }_{min}\left(K{\tilde{L}}_1\right)$ represents the minimum eigenvalue, and $K=$$diag\left\{k_1,k_2,\dots ,k_N\right\}$.

Since the derivatives ${\dot{\delta }}_{ij}^F\left(t\right),{\dot{\delta }}_{ij}^L\left(t\right)$ and ${\dot{y}}_{rj}$ are bounded, thus, according to Lemma 2, there is $\left|{\dot{y}}_{di}\right|\le Y_{di}$, where $Y_{di}$ is a positive constant. At the same time, there is $\left|l_{i,1}\right|\le {\overline{l}}_{i,1}$.

Equation (22) gives the following form for ${\dot{V}}_1$:

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & -{\lambda }_{min}\left(K{\tilde{L}}_1\right){\delta }^T\delta -\sum _{i=1}^N{c}_{i,1}{z}_{i,1}^2+\sum _{i=1}^N{\displaystyle \frac{{\mu }_{M_{i1}}}{{\kappa }_{M_{i1}}}}{\tilde{M}}_{i,1}^T{\widehat{M}}_{i,1}+\sum _{i=1}^N{\displaystyle \frac{{\mu }_{y_{di}}}{{\kappa }_{y_{di}}}}{\tilde{y}}_{di}{\dot{y}}_{di}\hfill \\ \hfill & +\sum _{i=1}^N{\displaystyle \frac{Y_{di}^2}{2{\kappa }_{y_{di}}}}+\sum _{i=1}^N{\displaystyle \frac{{\tilde{y}}_{di}^2}{2{\kappa }_{y_{di}}}}+\sum _{i=1}^N{\displaystyle \frac{1}{2}}{\overline{\iota }}_{i,1}^2+\sum _{i=1}^N\left[{\displaystyle \frac{1}{2}}{z}_{i,2}^2+{\displaystyle \frac{1}{2}}{s}_{i,2}^2\right]\hfill \end{array}$$

(23)

Step $k\left(k=2,3,n-1\right)$: Based on the coordinate transformations in (6) and (7) and the system dynamics, the following equation is obtained:

$${\dot{z}}_{i,k}=f_{i,k}\left({\mathcal{X}}_{i,k}\right)+z_{i,k+1}-{\dot{\beta }}_{i,kf}+{\alpha }_{i,k}+s_{i,k+1}$$

(24)

Similar to step $1, f_{i,1}\left({\mathcal{X}}_{i,1}\right)$, it can be approximated by RBFNN. Satisfy

$$f_{i,k}\left({\mathcal{X}}_{i,k}\right)=M_{i,k}^{\ast T}{U}_{i,k}\left({\mathcal{X}}_{i,k}\right)+{\iota }_{i,k}\left({\mathcal{X}}_{i,k}\right)$$

From the filter (9), it is obtained that

$${\dot{\beta }}_{i,kf}=-{\displaystyle \frac{s_{i,k}}{{\tau }_{i,k}}}-{\widehat{B}}_{i,k}tanh{\displaystyle \frac{1}{{\epsilon }_{i,k}}}{\widehat{B}}_{i,k}{s}_{i,k}$$

The Lyapunov function can be described as

$$V_k=\sum _{i=1}^N\left[{\displaystyle \frac{1}{2}}{z}_{i,k}^2+{\displaystyle \frac{1}{2{\kappa }_{M_{i,k}}}}{\tilde{M}}_{i,k}^T{\tilde{M}}_{i,k}\right]$$

(25)

Differentiating yields

$${\dot{V}}_k=\sum _{i=1}^N\left\{\left[{\alpha }_{i,k}+s_{i,k+1}+M_{i,k}^{\ast T}S\left({\mathcal{X}}_{i,k}\right)+{\iota }_{i,k}-{\dot{\beta }}_{i,kf}+z_{i,k+1}\right]z_{i,k}-{\displaystyle \frac{1}{K_{M_{i,k}}}}{\tilde{M}}_{i,k}^T{\dot{\widehat{M}}}_{i,k}\right\}$$

(26)

The virtual control ${\alpha }_{i,k}$ is designed alongside its corresponding adaptive update law ${\dot{\widehat{M}}}_{i,k}$, given below:

$$\begin{array}{cc}\hfill {\alpha }_{i,k}=& -c_{i,k}{z}_{i,k}-2z_{i,k}-{\widehat{M}}_{i,k}^T{U}_{i,k}-{\dot{\beta }}_{i,kf}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\dot{\widehat{M}}}_{i,k}=& {\kappa }_{M_{i,k}}{z}_{i,k}{U}_{i,k}-{\mu }_{M_{i,k}}{\widehat{M}}_{i,k}\hfill \end{array}$$

(28)

where $c_{i,k}$ and ${\mu }_{M_{i,k}}$ are defined as positive design constants.

Based on Young’s inequality, it can be derived that

$$\begin{array}{cc}\hfill z_{i,k}{z}_{i,k+1}\le & {\displaystyle \frac{1}{2}}{z}_{i,k}^2+{\displaystyle \frac{1}{2}}{z}_{i,k+1}^2\hfill \\ \hfill z_{i,k}{s}_{i,k+1}\le & {\displaystyle \frac{1}{2}}{z}_{i,k}^2+{\displaystyle \frac{1}{2}}{s}_{i,k+1}^2\hfill \\ \hfill z_{i,k}{\iota }_{i,k}\le & {\displaystyle \frac{1}{2}}{z}_{i,k}^2+{\displaystyle \frac{1}{2}}{\iota }_{i,k}^2\hfill \end{array}$$

(29)

Substituting Equations (27)–(29) into ${\dot{V}}_k$ yields

$${\dot{V}}_k\le -\sum _{i=1}^N{c}_{i,k}{z}_{i,k}^2+\sum _{i=1}^N{\displaystyle \frac{{\mu }_{M_{i,k}}}{{\kappa }_{M_{i,k}}}}{\tilde{M}}_{i,k}^T{\widehat{M}}_{i,k}+\sum _{i=1}^N{\displaystyle \frac{1}{2}}{\overline{\iota }}_{i,k}^2+\sum _{i=1}^N{\displaystyle \frac{1}{2}}{z}_{i,k+1}^2+\sum _{i=1}^N{\displaystyle \frac{1}{2}}{s}_{i,k+1}^2-\sum _{i=1}^N{\displaystyle \frac{1}{2}}{z}_{i,k}^2$$

(30)

3.2. Fault-Tolerant Controller Design

Step n: The coordinate transformations (6) and (7) yield

$${\dot{z}}_{i,n}=b_i{s}_i{u}_i+b_i{u}_i^b+M_{i,n}^{\ast T}{U}_{i,n}\left({\mathcal{X}}_{i,n}\right)-{\dot{\beta }}_{i,nf}+{\iota }_{i,n}$$

(31)

Consider the Lyapunov function candidate, defined by

$$V_n=\sum _{i=1}^N\left[{\displaystyle \frac{1}{2{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\tilde{M}}_{i,n}+{\displaystyle \frac{1}{2}}{z}_{i,n}^2\right.\left.+{\displaystyle \frac{b_i{s}_i}{2{\kappa }_{{\varpi }_i}}}{\tilde{\varpi }}_i^2+{\displaystyle \frac{1}{2{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_{i,n}^2\right]$$

(32)

where ${\kappa }_{M_{i,n}}$, ${\kappa }_{{\varpi }_i}$, and ${\kappa }_{{\rho }_i}$ are positive constants. The estimation errors are defined as ${\tilde{\varpi }}_i={\varpi }_i^{\ast }-{\widehat{\varpi }}_i$ and ${\tilde{\rho }}_{i,n}={\rho }_{i,n}^{\ast }-{\widehat{\rho }}_{i,n}$, with ${\widehat{\varpi }}_i$ and ${\widehat{\rho }}_{i,n}$ being the estimates of ${\varpi }_i^{\ast }=1/\left|b_i\right|s_i$ and ${\rho }_{i,n}^{\ast }=Q_i{\overline{u}}_i^b$, respectively.

Combining Equations (31) and (32) yields

$$\begin{array}{cc}\hfill {\dot{V}}_n=& \sum _{i=1}^M\left[z_{i,n}\right(b_i{s}_i{u}_i+u_i^b+M_{i,n}^{\ast T}{s}_{i,n}\left({\mathcal{X}}_{i,n}\right)-{\dot{\beta }}_{i,nf}\hfill \\ \hfill & +{\iota }_{i,n})+{\displaystyle \frac{1}{{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\dot{\tilde{M}}}_{i,n}+{\displaystyle \frac{b_i{s}_i}{{\kappa }_{{\varpi }_i}}}{\tilde{\varpi }}_i{\dot{\tilde{\varpi }}}_i+{\displaystyle \frac{1}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_i{\dot{\tilde{\rho }}}_i]\hfill \\ \hfill =& \sum _{i=1}^M[-c_{i,n}{z}_{i,n}^2+z_{i,n}{b}_i{s}_i{u}_i+z_{i,n}{b}_i{u}_i^b+z_{i,n}{\iota }_{i,n}\hfill \\ \hfill & +z_{i,n}(c_{i,n}{z}_{i,n}+M_{i,n}^{\ast T}{s}_{i,n}\left({\mathcal{X}}_{i,n}\right)-{\dot{\beta }}_{i,nf}\hfill \\ \hfill & +{\widehat{\rho }}_{i}tanh\left({\displaystyle \frac{z_{i,n}}{{ϵ}_i}}\right)+z_{i,n})-{\displaystyle \frac{1}{{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\dot{\widehat{M}}}_{i,n}-z_{i,n}^2\hfill \\ \hfill & -{\displaystyle \frac{b_i{s}_i}{{\kappa }_{{\varpi }_i}}}{\tilde{\varpi }}_i{\dot{\widehat{\varpi }}}_i-{\displaystyle \frac{1}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_i{\dot{\widehat{\rho }}}_i-z_{i,n}{\widehat{\rho }}_{i}tanh\left({\displaystyle \frac{z_{i,n}}{{ϵ}_i}}\right)]\hfill \end{array}$$

(33)

Create the following neural weight update law and virtual controller:

$$\begin{array}{cc}\hfill {\alpha }_{i,n}=& c_{i,n}{z}_{i,n}+{\widehat{M}}_{i,n}^T{U}_{i,n}\left({\mathcal{X}}_{i,n}\right)-{\dot{\beta }}_{i,nf}\hfill \\ \hfill & +{\widehat{\rho }}_{i}tanh\left({\displaystyle \frac{z_{i,n}}{{\epsilon }_i}}\right)+z_{i,n}\hfill \end{array}$$

(34)

$${\dot{\widehat{M}}}_{i,n}={\kappa }_{M_{i,n}}{z}_{i,n}{U}_{i,n}-{\mu }_{M_{i,n}}{\widehat{M}}_{i,n}$$

(35)

Equations (34) and (35) can be substituted into Equation (33) to obtain

$$\begin{array}{cc}\hfill {\dot{V}}_n=& \sum _{i=1}^M\left[-c_{i,n}{z}_{i,n}^2+z_{i,n}{b}_i{s}_i{u}_i+z_{i,n}{b}_i{u}_i^b+z_{i,n}{l}_{i,n}\right.+z_{i,n}{\alpha }_{i,n}+{\displaystyle \frac{{\mu }_{M_{i,n}}}{{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\widehat{M}}_{i,n}\hfill \\ \hfill & -{\displaystyle \frac{b_i{s}_i}{{\kappa }_{{\varpi }_i}}}{\tilde{\varpi }}_i{\dot{\widehat{\varpi }}}_i\left.-{\displaystyle \frac{1}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_i{\dot{\widehat{\rho }}}_i-z_{i,n}{\widehat{\rho }}_{i}tanh\left({\displaystyle \frac{z_{i,n}}{{\epsilon }_i}}\right)-z_{i,n}^2\right]\hfill \end{array}$$

(36)

The final controller $u_i$ and the adaptation law of parameter ${\widehat{\varpi }}_i$ are designed as follows:

$$u_i=-sgn\left(b_i\right){\displaystyle \frac{z_{i,n}{\widehat{\varpi }}_i^2{\alpha }_{i,n}^2}{\sqrt{z_{i,n}^2{\widehat{\varpi }}_i^2{\alpha }_{i,n}^2+{\eta }_i^2}}}$$

(37)

$${\dot{\widehat{\varpi }}}_i=z_{i,n}{\kappa }_{{\varpi }_i}{\alpha }_{i,n}-{\mu }_{{\varpi }_i}{\widehat{\varpi }}_i$$

(38)

Application of the designed control law (37) and the inequality $0\le \left|a\right|-\left({\displaystyle \frac{a^2}{\sqrt{a^2+b^2}}}\right)<b$ leads to

$$\begin{array}{c}\hfill z_{i,n}{b}_i{s}_i{u}_i\le -\left|b_i\right|s_i{\displaystyle \frac{z_{i,n}{\widehat{\varpi }}_i^2{\alpha }_{i,n}^2}{\sqrt{s_{i,n}^2{\widehat{\varpi }}_i^2{\alpha }_{i,n}^2+{\eta }_i^2}}}\le \left|b_i\right|s_i{\eta }_i-z_{i,n}\left|b_i\right|s_i{\widehat{\varpi }}_i{\alpha }_{i,n}\end{array}$$

(39)

Since ${\varpi }_i^{\ast }={\widehat{\varpi }}_i+{\tilde{\varpi }}_i$ and ${\varpi }_i^{\ast }={\displaystyle \frac{1}{|b_i|s_i}}$, then

$$z_{i,n}{\alpha }_{i,n}=|b_i|s_i{\varpi }_i^{\ast }{z}_{i,n}{\alpha }_{i,n}=\left|b_i\right|s_i({\widehat{\varpi }}_i+{\tilde{\varpi }}_i)z_{i,n}{\alpha }_{i,n}$$

That is,

$$z_{i,n}{\alpha }_{i,n}-\left|b_i\right|s_i{z}_{i,n}{\widehat{\varpi }}_i{\alpha }_{i,n}-\left|b_i\right|s_i{z}_{i,n}{\tilde{\varpi }}_i{\alpha }_{i,n}=0$$

(40)

Considering Equations (39) and (40) together yields

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & \sum _{i=1}^N[-c_{i,n}{z}_{i,n}^2+z_{i,n}{s}_i{u}_i^b+z_{i,n}{\iota }_{i,n}-z_{i,n}^2\hfill \\ \hfill & +{\displaystyle \frac{{\mu }_{M_{i,n}}}{{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\widehat{M}}_{i,n}+{\displaystyle \frac{b_i{s}_i{\mu }_{{\varpi }_i}}{{\kappa }_{{\varpi }_i}}}{\widehat{\varpi }}_{i,n}{\widehat{\varpi }}_{i,n}-{\displaystyle \frac{1}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_i{\dot{\widehat{\rho }}}_i]\hfill \end{array}$$

(41)

The following can be obtained from the properties of the system:

$$z_{i,n}{b}_i{u}_i^b\le \left|z_{i,n}\right|Q_i{\overline{u}}_i^b\le \left|z_{i,n}\right|{\rho }_i^{\ast }$$

(42)

Design the following adaptive estimation law:

$${\dot{\widehat{\rho }}}_i=z_{i,n}{\kappa }_{{\rho }_i}tanh\left({\displaystyle \frac{z_{i,n}}{{\epsilon }_i}}\right)-{\mu }_{{\rho }_i}{\widehat{\rho }}_i$$

(43)

Young’s inequality ensures that

$$z_{i,n}{\iota }_{i,n}\le {\displaystyle \frac{1}{2}}{z}_{i,n}^2+{\displaystyle \frac{1}{2}}{\overline{\iota }}_{i,n}^2$$

(44)

Combining Equations (42)–(44) yields

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & \sum _{i=1}^N\left[-c_{i,n}{z}_{i,n}^2-{\displaystyle \frac{1}{2}}{z}_{i,n}^2+{\displaystyle \frac{{\mu }_{M_{i,n}}}{{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\widehat{M}}_{i,n}\right.+{\rho }_i\left(|z_{i,n}|-z_{i,n}tanh\left({\displaystyle \frac{z_{i,n}}{{ϵ}_i}}\right)\right)\hfill \\ \hfill & \left.+{\displaystyle \frac{b_i{s}_i{\mu }_{{\varpi }_i}}{{\kappa }_{{\varpi }_i}}}{\widehat{\varpi }}_{i,n}{\widehat{\varpi }}_{i,n}+{\displaystyle \frac{1}{2}}{\overline{\iota }}_{i,n}^2+{\displaystyle \frac{{\mu }_{{\rho }_i}}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_i{\widehat{\rho }}_i\right]\hfill \end{array}$$

(45)

Lemma 3 indicates that

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & \sum _{i=1}^N\left[-c_{i,n}{z}_{i,n}^2-{\displaystyle \frac{1}{2}}{z}_{i,n}^2+{\displaystyle \frac{{\mu }_{M_{i,n}}}{{\kappa }_{M_{i,n}}}}{\tilde{M}}_{i,n}^T{\widehat{M}}_{i,n}+{\displaystyle \frac{1}{2}}{\overline{\iota }}_{i,n}^2\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{b_i{s}_i{\mu }_{{\varpi }_i}}{{\kappa }_{{\varpi }_i}}}{\widehat{\varpi }}_{i,n}{\widehat{\varpi }}_{i,n}+{\displaystyle \frac{{\mu }_{{\rho }_i}}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_i{\widehat{\rho }}_i+0.2785{\rho }_i{ϵ}_i\right]\hfill \end{array}$$

(46)

3.3. Stability Analysis

Theorem 1.

For an N-follower and M-leader multi-agent system satisfying Assumptions 1–4 and initial conditions $V\left(0\right)\le \Psi$ ($\Psi >0$), consider the application of the adaptive laws (17), (18), (28), (35), (38), (43), (50), the virtual controllers (16), (27), (34) and the fault-tolerant controller (37). Then, all containment errors are ultimately bounded within a small region around the origin.

Proof. 

The transformation $s_{i,k}={\beta }_{i,kf}-{\alpha }_{i,k-1}$ in (8) yields

$${\dot{s}}_{i,k}=-\frac{s_{i,k}}{{\tau }_{i,k}}-{\widehat{B}}_{i,k}tanh\left({\displaystyle \frac{{\widehat{B}}_{i,k}{s}_{i,k}}{{\epsilon }_{i,k}}}\right)-{\dot{\alpha }}_{i,k-1}$$

(47)

From Equations (16), (27) and (34), it can be obtained that ${\dot{\alpha }}_{i,k}$ is a function of variables $z_{i,1},\dots ,z_{i,k+1},{\widehat{y}}_{di},{\widehat{\widehat{y}}}_{di},{\ddot{\widehat{y}}}_{di},{\delta }_{ij}^F,{\delta }_{ij}^L,{\dot{\delta }}_{ij}^F,{\dot{\delta }}_{ij}^L,{\widehat{M}}_{i,1},\dots ,{\widehat{M}}_{i,k}$ and $s_{i,1},\dots ,s_{i,k},{\widehat{B}}_{i,1},\dots ,{\widehat{B}}_{i,k},{\widehat{\rho }}_i$.

The total Lyapunov function is

$$V=V_1+V_2+\dots +V_n+{\displaystyle \frac{1}{2}}\sum _{i=1}^N\sum _{k=2}^n{s}_{i,k}^2+{\displaystyle \frac{1}{2{\kappa }_{B_{ik}}}}\sum _{i=1}^N\sum _{k=2}^n{\tilde{B}}_{i,k}^2$$

(48)

where ${\tilde{B}}_{i,k}=B_{i,k}-{\widehat{B}}_{i,k}$, with ${\widehat{B}}_{i,k}$ estimating $B_{i,k}$ and ${\kappa }_{B_{i,k}}>0$ is a design parameter.

Consider the compact sets ${\Omega }_1$ and ${\Omega }_2$ given by

$$\begin{array}{cc}\hfill {\Omega }_1=& \{\sum _{i=1}^N\sum _{k=1}^n\left[z_{i,k}^2+{\displaystyle \frac{{\tilde{M}}_{i,k}^T{\tilde{M}}_{i,k}}{{\kappa }_{M_{i,k}}}}\right]+\sum _{i=1}^N\sum _{k=2}^n\left[s_{i,k}^2+{\displaystyle \frac{{\tilde{B}}_{i,k}^2}{{\kappa }_{B_{i,k}}}}\right]\hfill \\ \hfill & +\sum _{i=1}^N\left[{\displaystyle \frac{{\tilde{y}}_{di}^2}{{\kappa }_{y_{di}}}}+{\displaystyle \frac{b_i{s}_i}{{\kappa }_{{\varpi }_i}}}{\tilde{\varpi }}_i^2+{\displaystyle \frac{1}{{\kappa }_{{\rho }_i}}}{\tilde{\rho }}_{i,n}^2\right]\le 2\Psi \}\hfill \\ \hfill {\Omega }_2=& \{{\left[y_{rN+1},\dots ,y_{rN+M}, {\dot{y}}_{rN+1},\dots ,{\dot{y}}_{rN+M}, {\ddot{y}}_{rN+1},\dots ,{\ddot{y}}_{rN+M}\right]}^T: \hfill \\ \hfill & \sum _{j=N+1}^{N+M}{y}_{rj}^2+\sum _{j=N+1}^{N+M}{\dot{y}}_{rj}^2+\sum _{j=N+1}^{N+M}{\ddot{y}}_{rj}^2\le \Gamma \}\hfill \end{array}$$

whereby, with $\Gamma$ as a positive constant and ${\delta }_{ij}^{\left(F\right)}\left(t\right)$, ${\delta }_{ij}^{\left(L\right)}\left(t\right)$, and with continuous and bounded derivatives on ${\Omega }_1\times {\Omega }_2$, the functions satisfy $|{\dot{\alpha }}_{i,k}|\le B_{i,k}$ for some unknown positive constant $B_{i,k}$.

Computing the time derivative of V yields

$$\begin{array}{cc}\hfill \dot{V}\le & -\sum _{i=1}^N\sum _{k=1}^n{c}_{i,k}{z}_{i,k}^2+\sum _{i=1}^N\sum _{k=1}^n{\displaystyle \frac{{\mu }_{M_{ik}}}{{\kappa }_{M_{ik}}}}{\tilde{M}}_{i,k}^T{\widehat{M}}_{i,k}-\sum _{i=1}^N\sum _{k=2}^n\left({\displaystyle \frac{1}{{\tau }_{i,k}}}-{\displaystyle \frac{1}{2}}\right)s_{i,k}^2\hfill \\ \hfill & +\sum _{i=1}^N\sum _{k=2}^n\left|s_{i,k}\right|B_{i,k}-\sum _{i=1}^N\sum _{k=2}^n{\displaystyle \frac{{\tilde{B}}_{i,k}}{{\kappa }_{B_{ik}}}}{\dot{\widehat{B}}}_{i,k}+\sum _{i=1}^N\sum _{k=1}^n{\displaystyle \frac{1}{2}}{\overline{i}}_{i,k}^2+\sum _{i=1}^{N}0.2785{\rho }_i{\epsilon }_i\hfill \\ \hfill & +\sum _{k=1}^n{\displaystyle \frac{{\mu }_{y_{di}}}{{\kappa }_{y_{di}}}}{\tilde{y}}_{di}{\widehat{y}}_{di}+\sum _{k=1}^n{\displaystyle \frac{Y_{di}^2}{2{\kappa }_{y_{di}}}}+\sum _{k=1}^n{\displaystyle \frac{{\tilde{y}}_{di}^2}{2{\kappa }_{y_{di}}}}-\sum _{i=1}^N\sum _{k=2}^n{s}_{i,k}{\widehat{B}}_{i,k}tanh\left({\displaystyle \frac{{\widehat{B}}_{i,k}{s}_{i,k}}{{\epsilon }_{i,k}}}\right)\hfill \end{array}$$

(49)

The adaptive update law for ${\widehat{B}}_{i,k}$ takes the following form:

$${\dot{\widehat{B}}}_{i,k}={\kappa }_{B_{i,k}}\left|s_{i,k}\right|-{\mu }_{B_{ik}}{\widehat{B}}_{i,k}$$

(50)

where the design parameters ${\kappa }_{B_{i,k}}$ and ${\mu }_{B_{i,k}}$ are selected as positive constants.

Young’s inequality yields

$$\begin{array}{cc}\hfill {\tilde{y}}_{di}{\widehat{y}}_{di}\le & -{\displaystyle \frac{1}{2}}{\tilde{y}}_{di}^2+{\displaystyle \frac{1}{2}}{y}_{di}^2\hfill \\ \hfill {\tilde{M}}_{i,k}^T{\widehat{M}}_{i,k}\le & -{\displaystyle \frac{1}{2}}{\tilde{M}}_{i,k}^T{\tilde{M}}_{i,k}+{\displaystyle \frac{1}{2}}{M}_{i,k}^{\ast T}{M}_{i,k}^{\ast }\hfill \\ \hfill {\tilde{B}}_{i,k}{\widehat{B}}_{i,k}\le & -{\displaystyle \frac{1}{2}}{\tilde{B}}_{i,k}^2+{\displaystyle \frac{1}{2}}{B}_{i,k}^2\hfill \end{array}$$

(51)

Substituting (50) and (51) into inequality (49) and applying Lemma 3 yields

$$\begin{array}{cc}\hfill \dot{V}\le & -\sum _{i=1}^N\sum _{k=1}^n{c}_{i,k}{z}_{i,k}^2-\sum _{i=1}^N\sum _{k=1}^n{\displaystyle \frac{{\mu }_{M_{ik}}}{2{\kappa }_{M_{ik}}}}{\tilde{M}}_{i,k}^T{\tilde{M}}_{i,k}-\sum _{i=1}^N\sum _{k=2}^n\left({\displaystyle \frac{1}{{\tau }_{i,k}}}-{\displaystyle \frac{1}{2}}\right)s_{i,k}^2\hfill \\ \hfill & -\sum _{i=1}^N\sum _{k=2}^n{\displaystyle \frac{{\mu }_{B_{ik}}}{2{\kappa }_{B_{ik}}}}{\tilde{B}}_{i,k}^2-\sum _{i=1}^N{\displaystyle \frac{\left({\mu }_{y_{di}}-1\right)}{2{\kappa }_{y_{di}}}}{\tilde{y}}_{di}^2+\Delta \le -CV+\Delta \hfill \end{array}$$

(52)

where $C=min\left\{c_{i,k},{\mu }_{B_{ik}},\left(\left(2/{\tau }_{i,k}\right)-1\right),\left({\mu }_{y_{di}}-1\right),{\mu }_{M_{ik}}\right\}$ with ${\mu }_{y_{di}}>1$ and

$$\begin{array}{cc}\hfill \Delta =& \sum _{i=1}^N\sum _{k=1}^n\left[\left(1/2\right){\overline{\iota }}_{i,k}^2+\left({\mu }_{M_{ik}}/2{\kappa }_{M_{ik}}\right)M_{i,k}^{\ast }{}^{T}M_{i,k}^{\ast }\right]\hfill \\ \hfill & +\sum _{i=1}^N\sum _{k=2}^n\left[0.2785{\epsilon }_{i,k}+\left({\mu }_{B_{ik}}/2{\kappa }_{B_{ik}}\right)B_{i,k}^2\right]\hfill \\ \hfill & +\sum _{i=1}^N\left[0.2785{\rho }_i{\epsilon }_i+\left(Y_{di}^2/2{\kappa }_{y_{di}}\right)+\left({\mu }_{y_{di}}/2{\kappa }_{y_{di}}\right)y_{di}^2\right]\hfill \end{array}$$

From inequality (52), it can be seen that $z_{i,k},{\tilde{y}}_{di},{\tilde{B}}_{i,k}$ and ${\tilde{M}}_{i,k}$ are bounded. Then, it can be concluded that ${\delta }_i$, that is, $y_i-y_{di}$ is bounded, which implies the boundedness of the containment error, thus completing the proof. □

Remark 3.

Based on the proposed fault-tolerant containment controller, it is theoretically feasible to achieve adaptive estimation of the desired trajectory and adaptive compensation for actuator faults when both communication link faults and actuator faults are considered.

4. Simulation Results and Analysis

To validate the proposed method, this study employs both numerical simulation and autonomous underwater vehicle (AUV) simulation. These two simulations validate the efficacy of the fault-tolerant containment control approach.

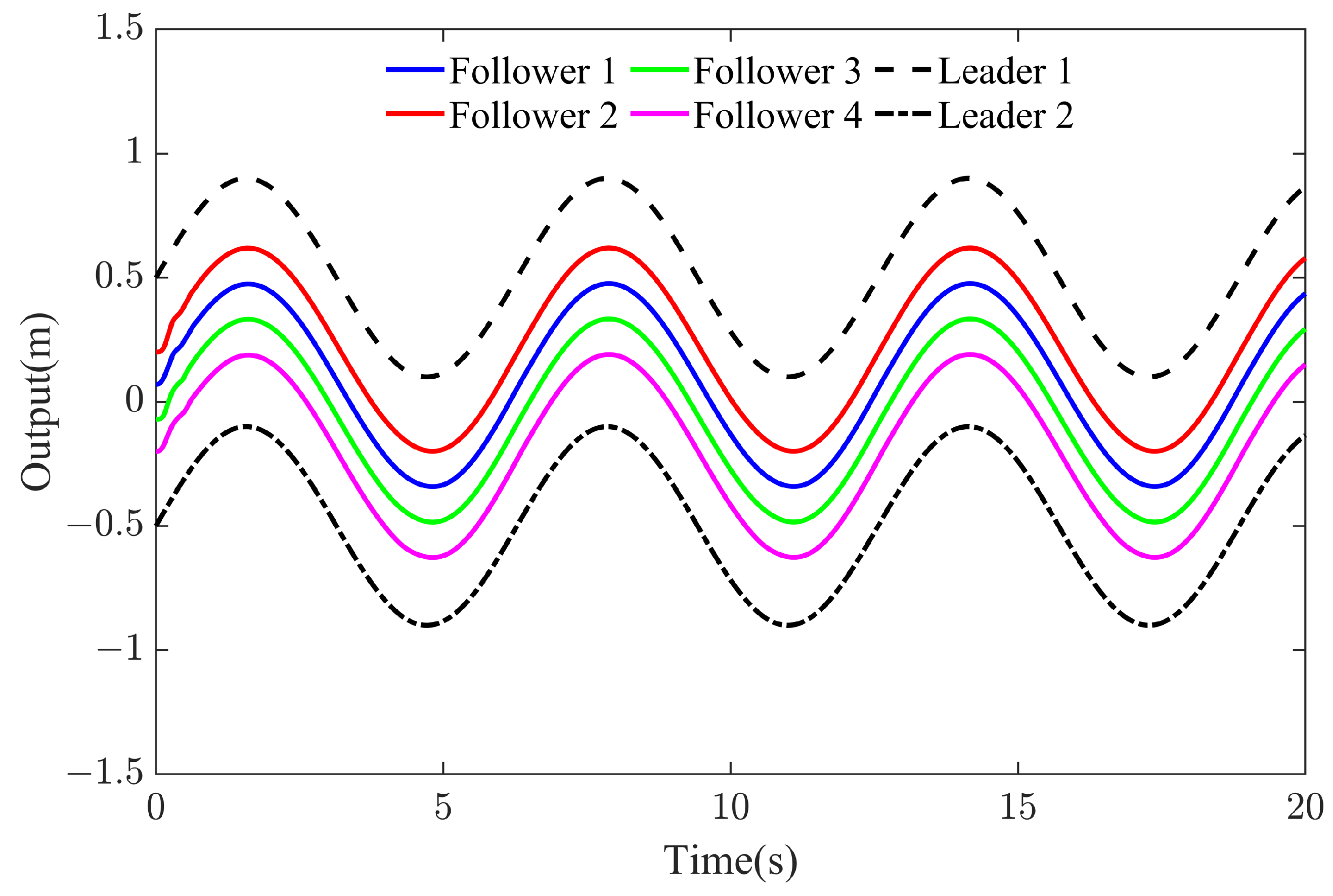
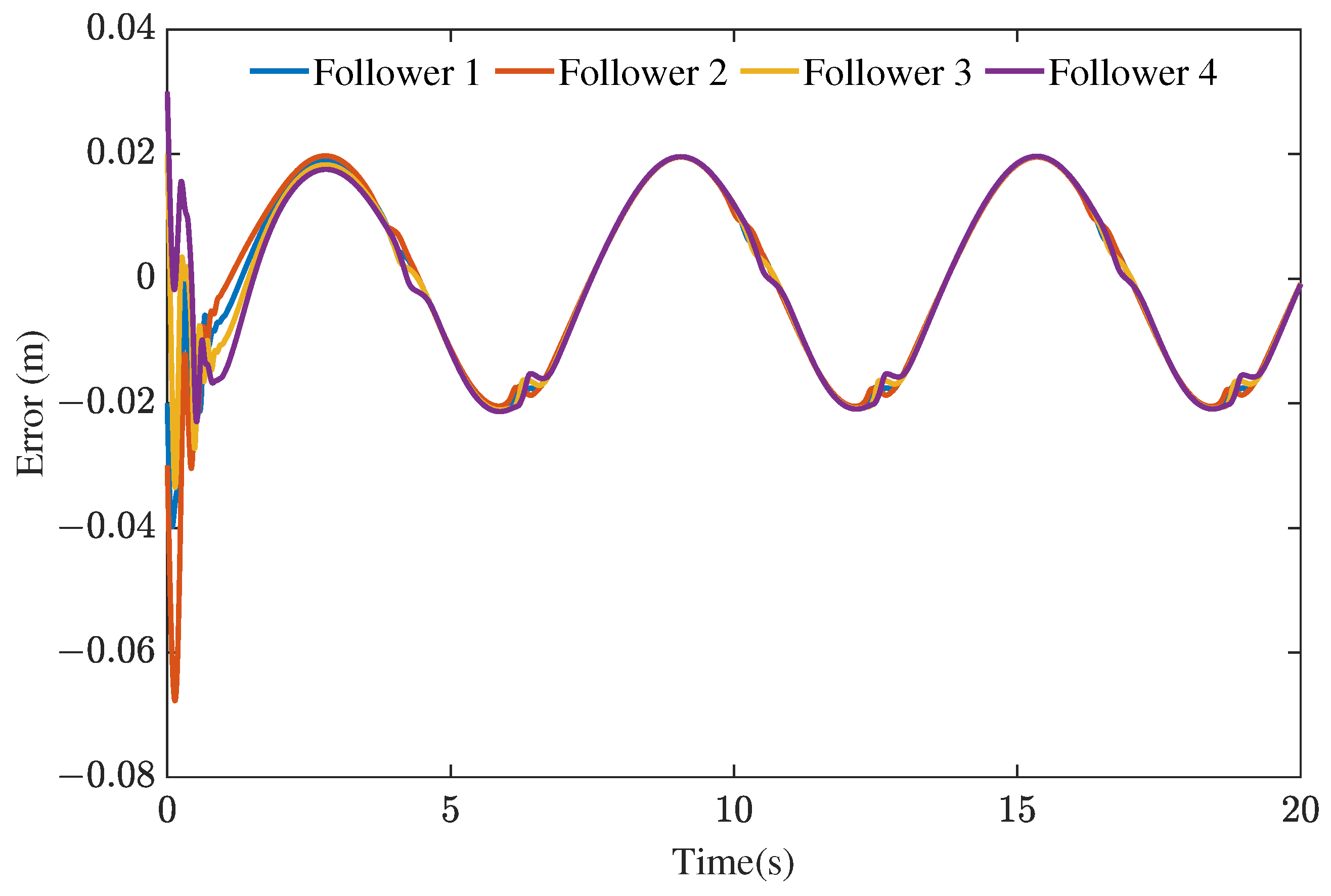
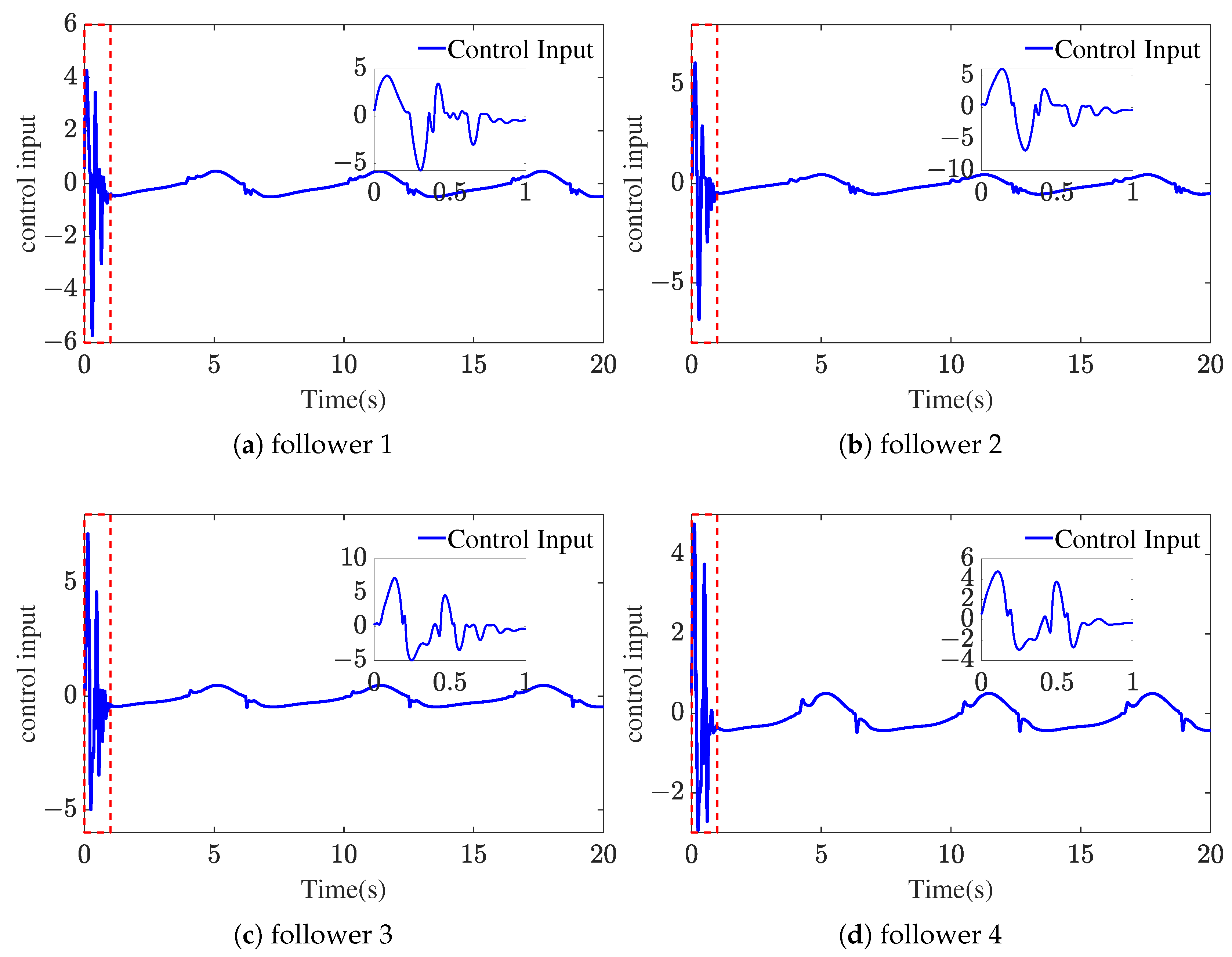
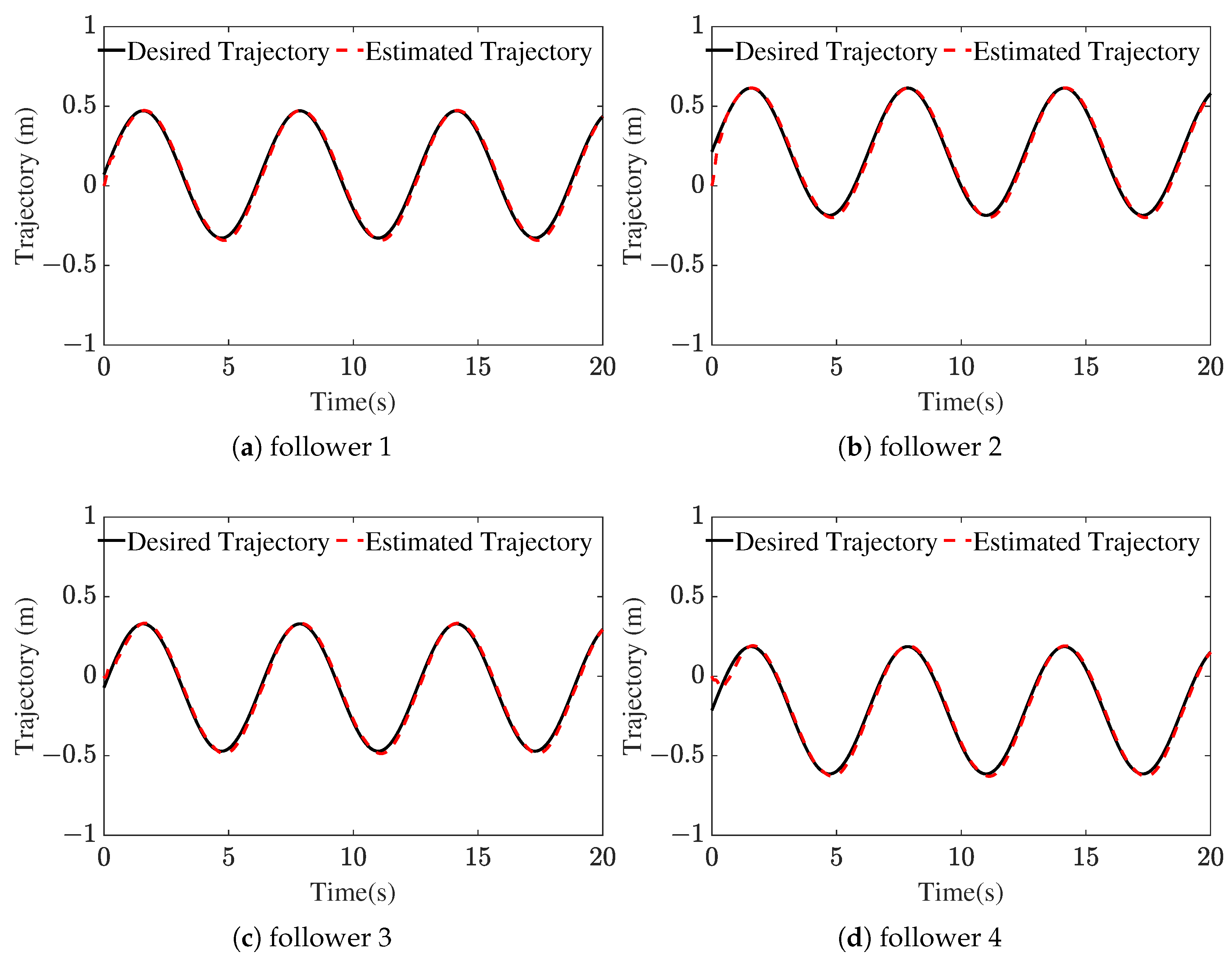
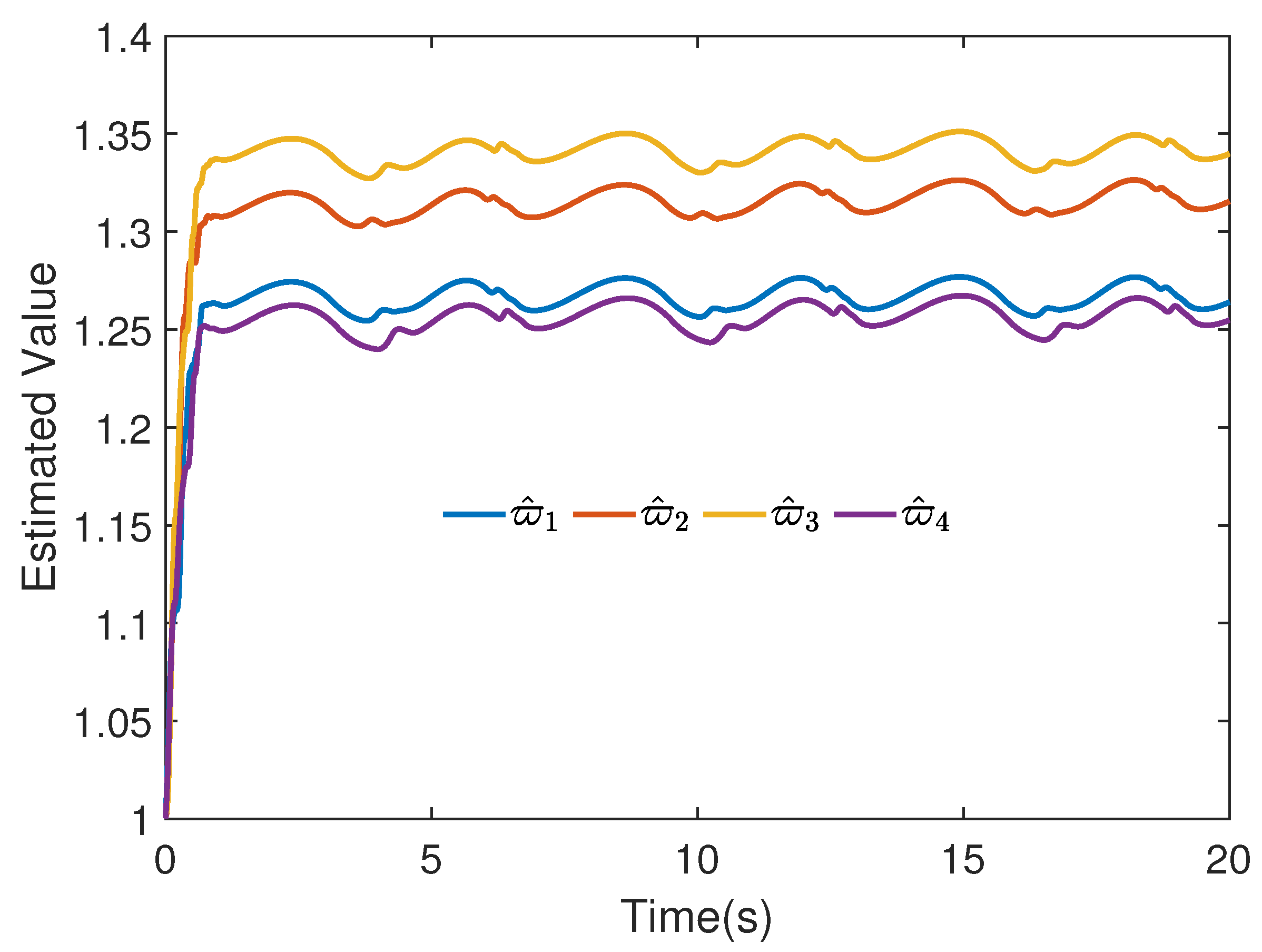
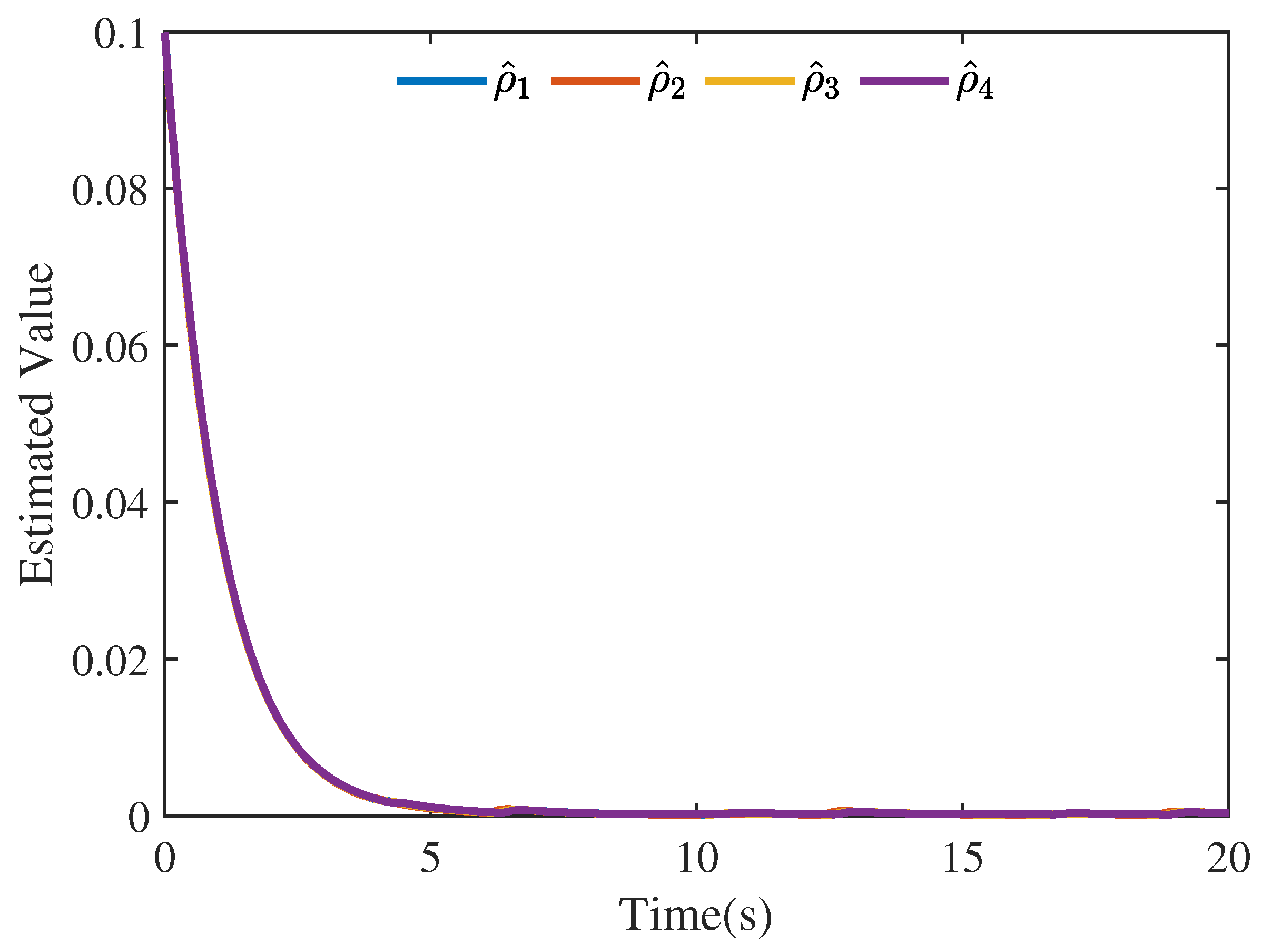
4.1. Numerical Simulation

The studied network system, illustrated in Figure 2, is composed of four followers and two leaders. The follower dynamics are described by

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_{i,1}& =x_{i,2}+x_{i,1}\hfill \\ \hfill {\dot{x}}_{i,2}& =b_i{u}_i^f\left(t\right)+x_{1,2}sin\left(x_{i,1}\right)+x_{i,2}^2\hfill \\ \hfill y_i& =x_{i,1}\hfill \end{array}\right.$$

The reference trajectories for the leaders are given by $y_{r1}=0.4sin\left(t\right)+0.5$ and $y_{r2}=0.4sin\left(t\right)-0.5$. The actuator fault parameters are defined as $s_i=$$0.5, u_i^b\left(t\right)=0.1exp\left(-0.1t\right)$. Other parameters are set as ${\epsilon }_{i,k}=$$0.1, c_{i,j}=2, k_i=0.2, {\epsilon }_i=0.2, {\tau }_{i,j}=0.1, b_i=1$ and ${\epsilon }_i=exp\left(-0.01t\right)$. The neural network is configured with parameters ${\kappa }_{M_{i,k}}=5$ and ${\mu }_{M_{i,k}}=1$; the expected trajectory estimation parameters are set as ${\kappa }_{y_{di}}=12, {\mu }_{y_{di}}=$$0.1,B_i$; the estimation parameters are set as ${\kappa }_{B_i}=12,{\mu }_{B_i}=0.01$; the multiplicative fault estimation parameters are set as ${\kappa }_{{\varpi }_i}=10, {\mu }_{{\varpi }_i}=0.003$; and the additive fault estimation parameters are set as ${\kappa }_{{\rho }_i}=0.1, {\mu }_{{\rho }_i}=1$. The Gaussian function is configured with center $c_{\epsilon }=0$ and width $w_{\epsilon }={\left[-2,2\right]}^T$.

The followers are assigned the initial conditions $x_{1,1}\left(0\right)=0.4, x_{1,2}\left(0\right)=$$0, x_{2,1}\left(0\right)=0.5, x_{2,2}\left(0\right)=0, x_{3,1}\left(0\right)=0.2, x_{3,2}\left(0\right)=$$0, x_{4,1}\left(0\right)=0.1, x_{4,2}\left(0\right)=0, {\widehat{B}}_i\left(0\right)=1, {\widehat{\varpi }}_i\left(0\right)=0$, ${\widehat{\rho }}_i\left(0\right)=0.1, {\widehat{M}}_{i,k}\left(0\right)=0$ and ${\widehat{y}}_{di}\left(0\right)=0$. The original communication weights are set as $a_{i,j}=1$, while the time-varying weights ${\delta }_{ij}^F\left(t\right)$ and ${\delta }_{ij}^L\left(t\right)$ are chosen as $0.5sin\left(t\right)$.

The efficacy of the proposed containment control scheme is validated through simulation results in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Figure 3 demonstrates successful convergence of all follower trajectories into the leaders’ convex hull, verifying containment achievement under simultaneous communication and actuator faults. Figure 4 shows the bounded containment errors converging to a small region around zero, confirming system stability. The control inputs in Figure 5 remain smooth and bounded, ensuring physical implementability. Figure 6 presents accurate online estimation of desired trajectories, overcoming communication faults. Figure 7 and Figure 8 demonstrate effective fault estimation, with multiplicative fault estimates converging near theoretical values and additive fault estimates properly tracking the decaying fault profile. These results collectively confirm the controller’s robustness and fault-tolerant capability in practical scenarios.

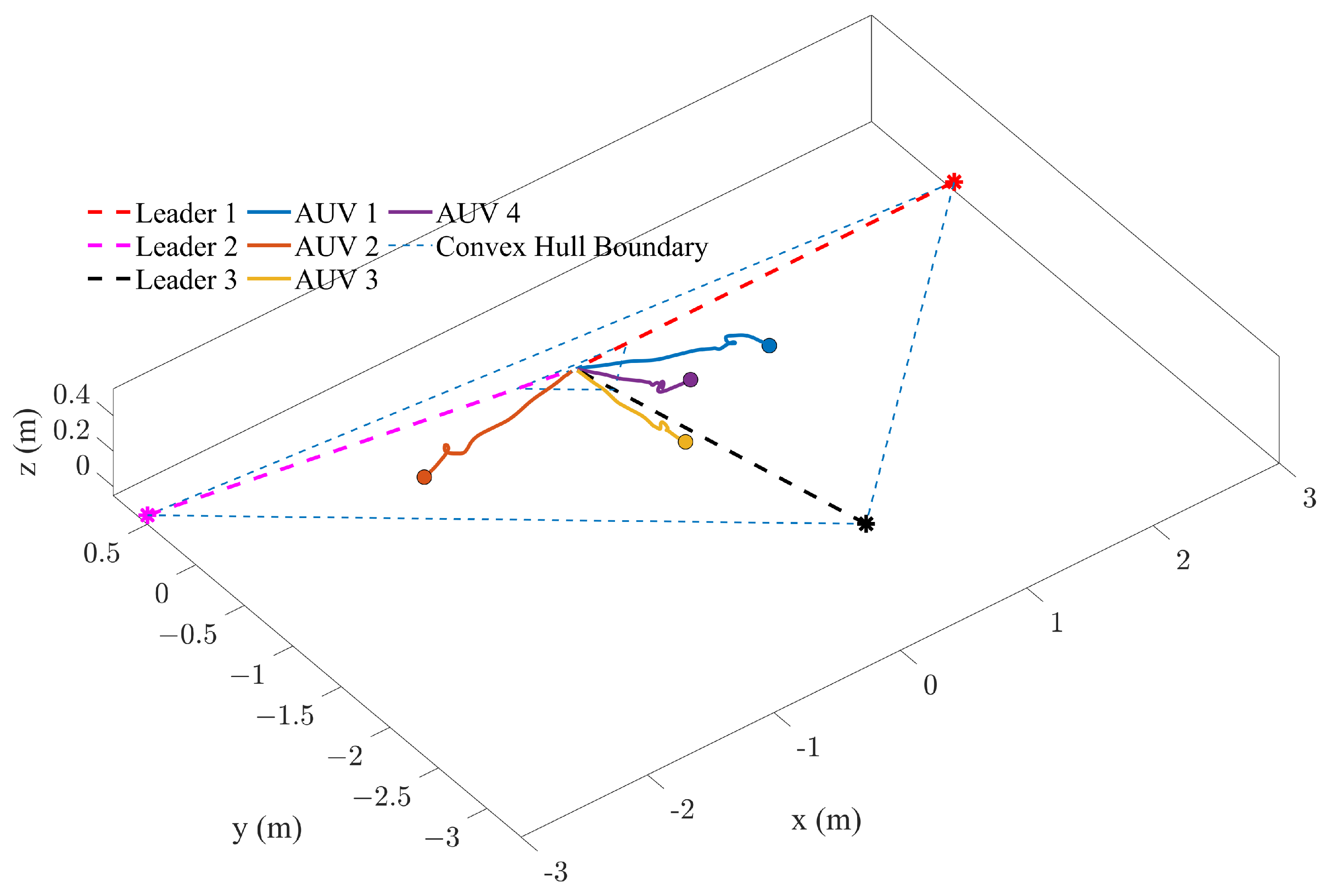
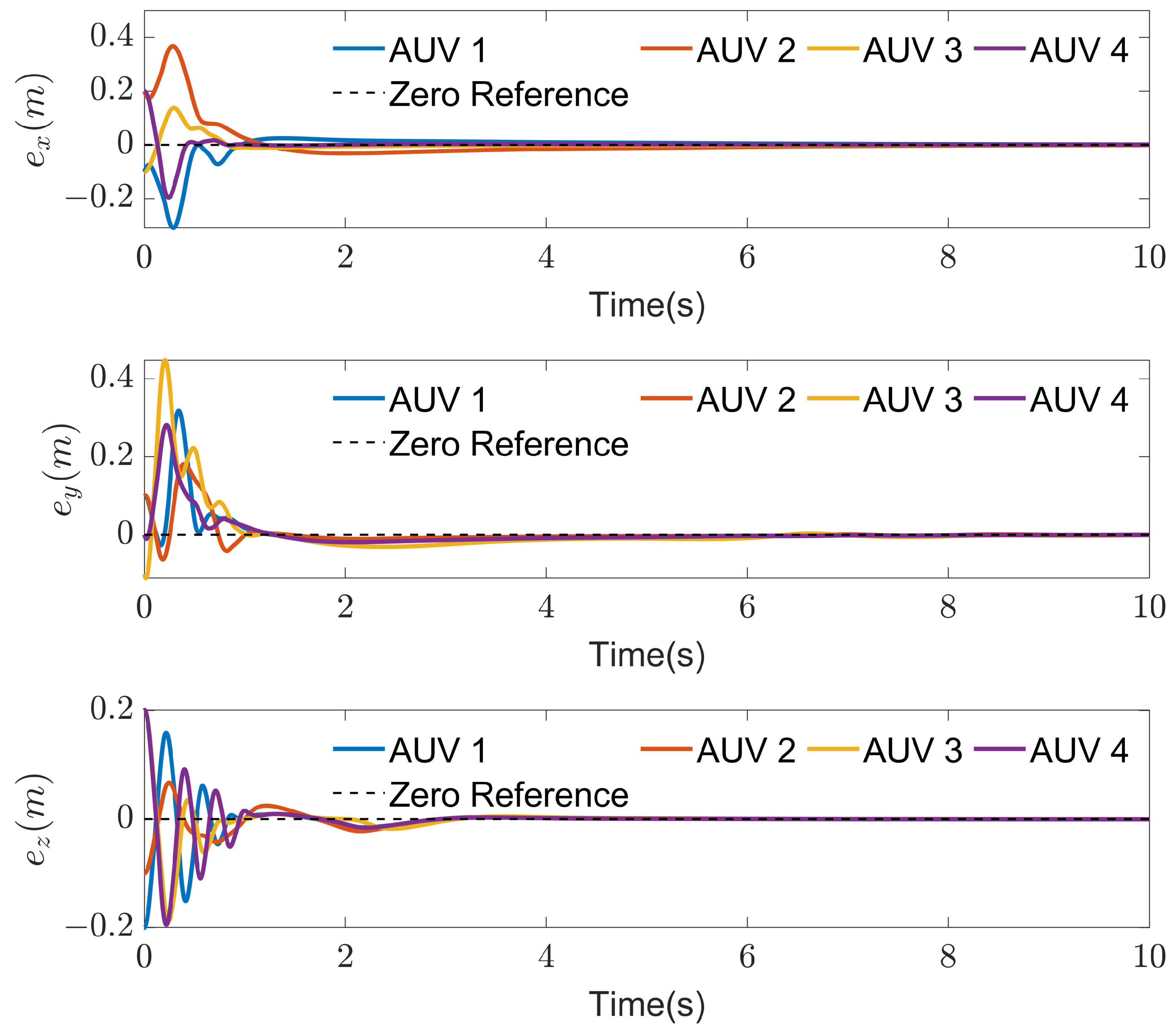
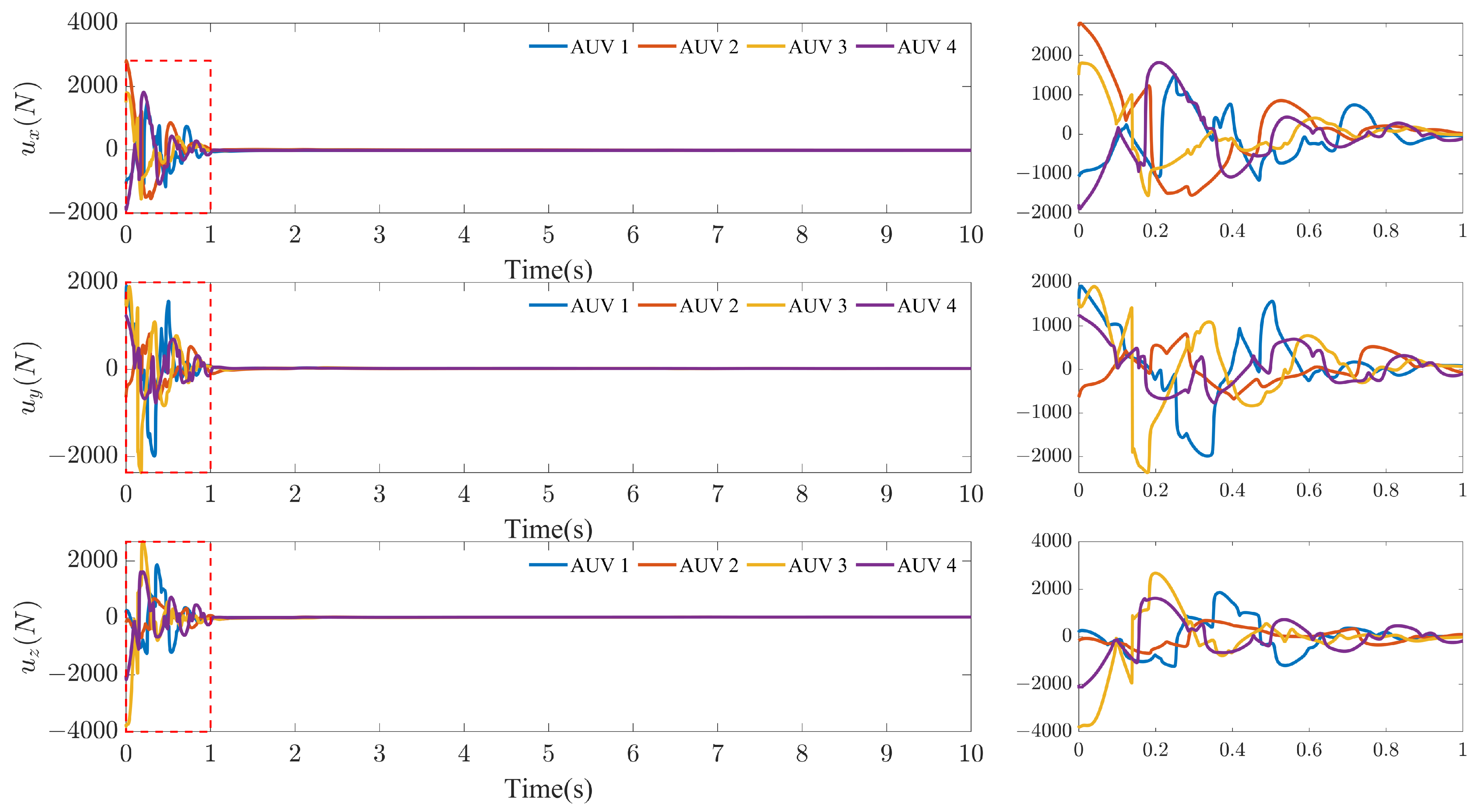
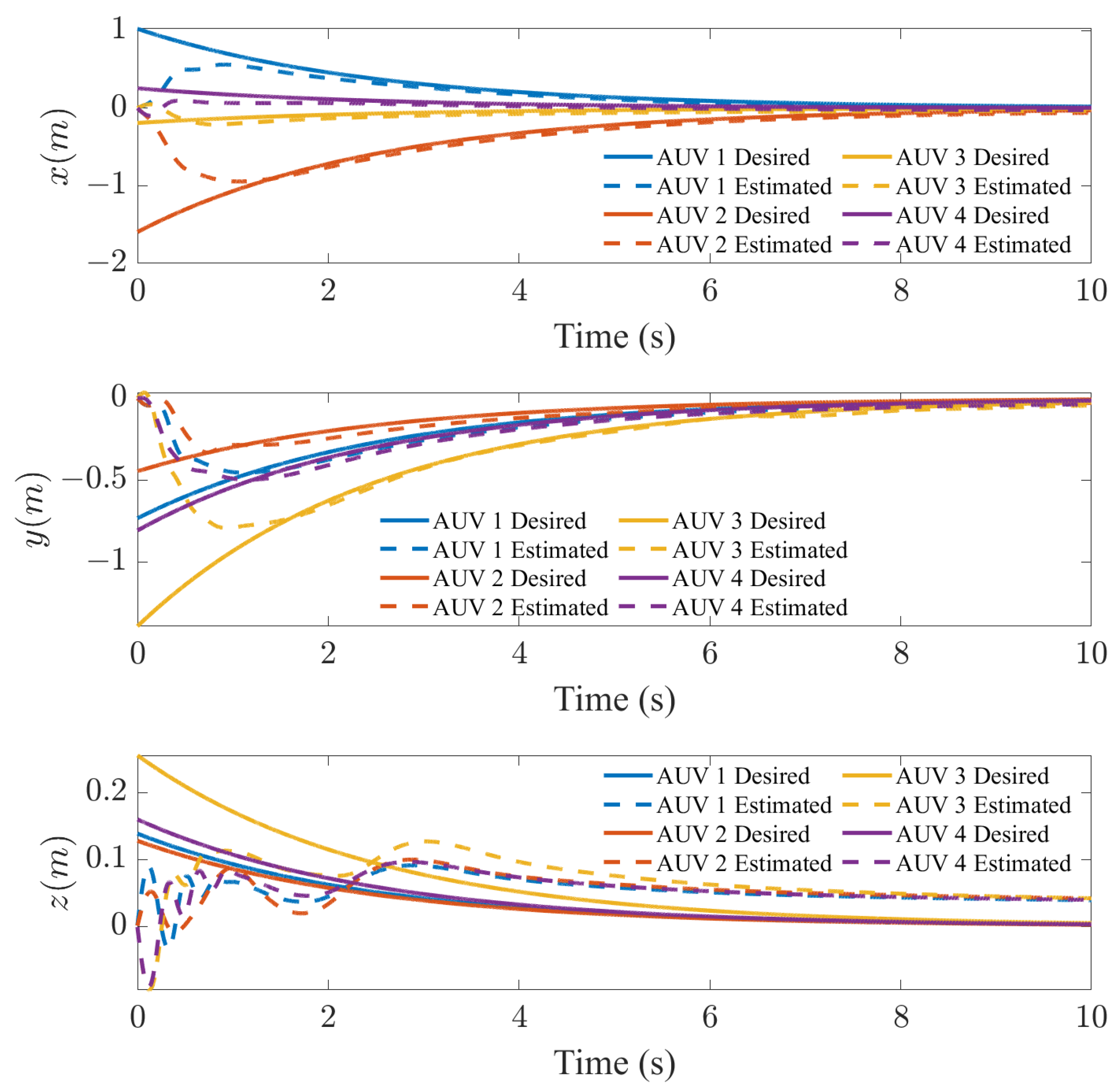
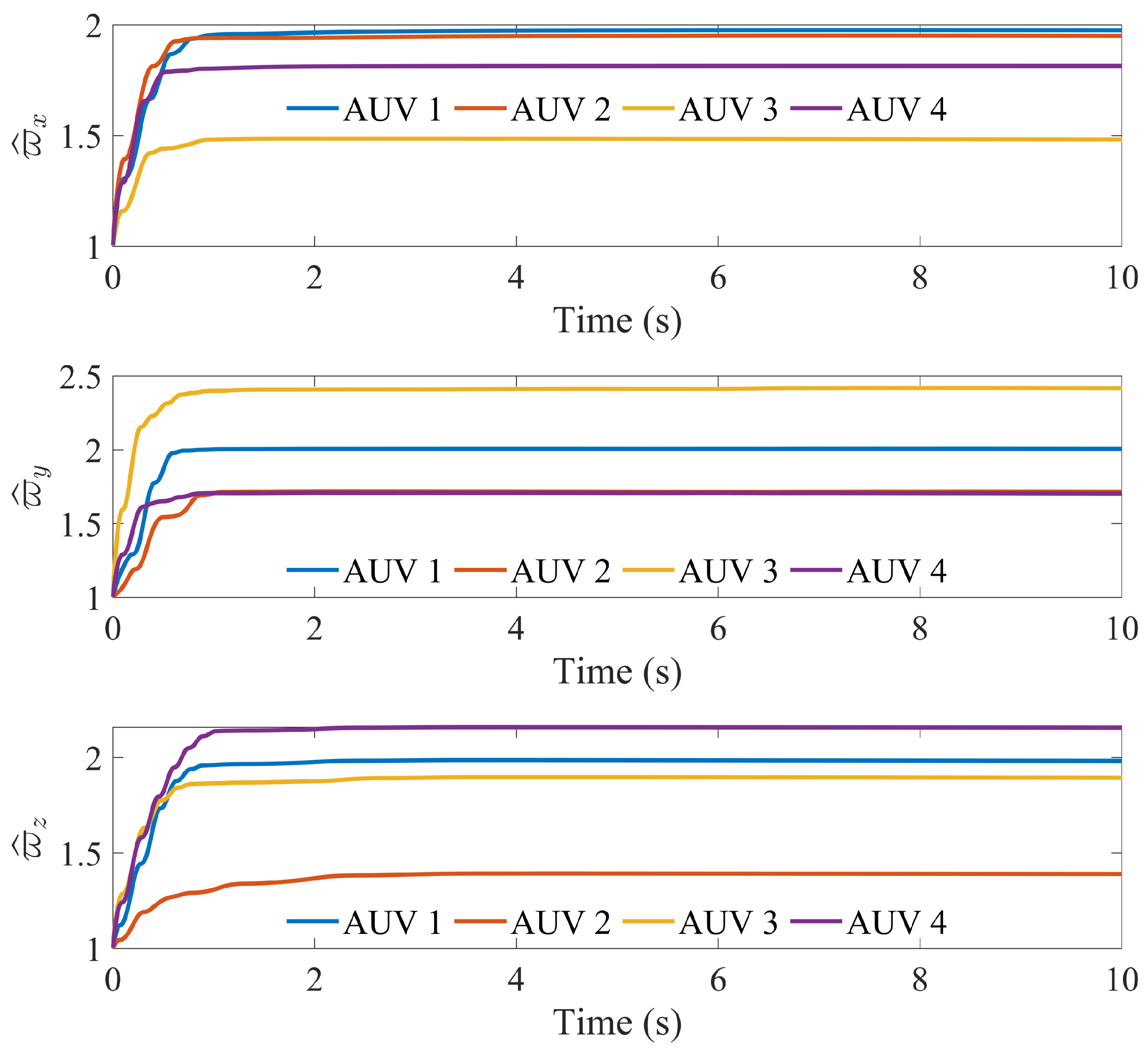
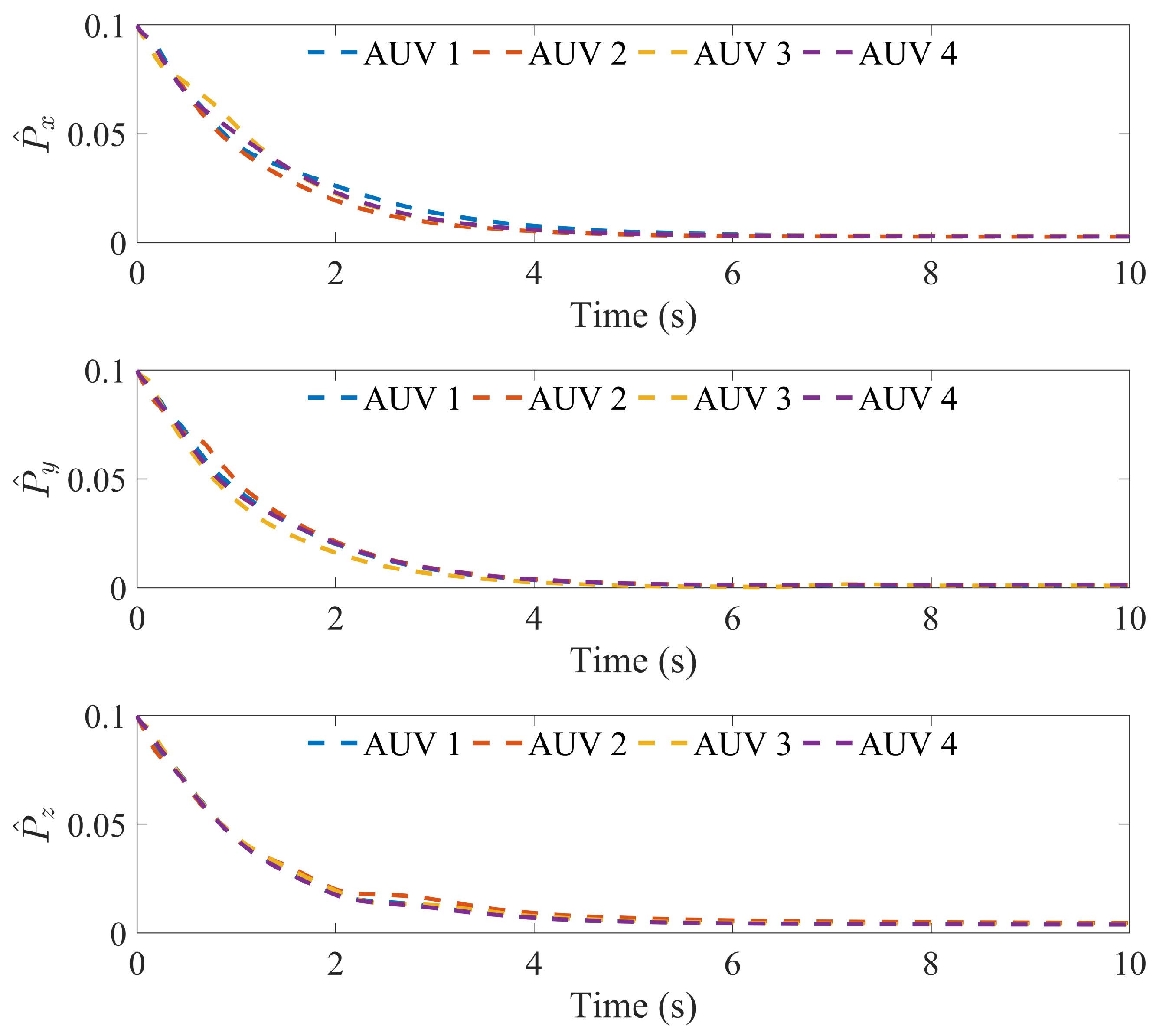
4.2. Simulation of AUV

To validate the practical efficacy of the proposed method, a simulation of a group of AUVs subjected to both communication link and actuator faults is conducted. The communication topology among the AUVs is shown in Figure 9. Their dynamic models and parameters follow the definitions in [32].

$$\begin{array}{cc}\hfill {\dot{p}}_i=& J_i\left({\Theta }_i\right)v_i\hfill \\ \hfill M_i{\dot{v}}_i=& -D_i\left(v_i\right)v_i-G_i\left({\Theta }_i\right)+u_i^f\hfill \end{array}$$

(53)

where $p_i={[x_i,y_i,z_i]}^T$ and $v_i={[u_i,v_i,w_i]}^T$ are the displacement and velocity vectors, respectively; ${\Theta }_i={[{\varphi }_i,{\theta }_i,{\psi }_i]}^T$ is the attitude vector (roll, pitch, yaw); and $J_i\left({\Theta }_i\right)\in {\mathbb{R}}^{3\times 3}$ is the Jacobian matrix. The system matrices are $M_i\in {\mathbb{R}}^{3\times 3}$ (inertia), $D_i\left(v_i\right)\in {\mathbb{R}}^{3\times 3}$ (damping), and $G_i\left({\Theta }_i\right)\in {\mathbb{R}}^{3\times 1}$ (restoring force). $u_i^f={\left[u_{ix}^f,u_{iy}^f,u_{iz}^f\right]}^T={\left[s_{ix}{u}_{ix}+u_{ix}^b, s_{iy}{u}_{iy}+u_{iy}^b, s_{iz}{u}_{iz}+u_{iz}^b\right]}^T$ are the actuator output vectors of each autonomous underwater vehicle, where $u_{ix},u_{iy}$ and $u_{iz}$ are the designed actual control commands for surge, sway, and heave, respectively. By defining the state variables $x_{i1}=p_i$ and $x_{i2}={\dot{p}}_i$, and taking the time derivative of ${\dot{p}}_i=J_i\left({\Theta }_i\right)v_i$, the original equation can be rewritten as

$$\begin{array}{cc}\hfill {\dot{x}}_{i1}=& x_{i2}\hfill \\ \hfill {\dot{x}}_{i2}=& f_i+B_i{u}_i^f\hfill \end{array}$$

where $f_i={\dot{J}}_i\left({\Theta }_i\right)v_i-J_i\left({\Theta }_i\right)M_i^{-1}{D}_i\left(v_i\right)v_i-J_i\left({\Theta }_i\right)M_i^{-1}{G}_i\left({\Theta }_i\right)$ and $B_i=J_i\left({\Theta }_i\right)M_i^{-1}$.

The signal of the leader is

$$\begin{array}{cc}\hfill y_1^T=& {\left[y_1^{rx},y_1^{ry},y_1^{rz}\right]}^T={\left[3e^{-\alpha t},0,0\right]}^T\hfill \\ \hfill y_2^T=& {\left[y_2^{rx},y_2^{ry},y_2^{rz}\right]}^T={\left[-3e^{-\alpha t},0.5e^{-\alpha t},0\right]}^T\hfill \\ \hfill y_3^T=& {\left[y_3^{rx},y_3^{ry},y_3^{rz}\right]}^T={\left[0,-3e^{-\alpha t},0.5e^{-\alpha t}\right]}^T\hfill \end{array}$$

where the attenuation coefficient is $\alpha =0.1$. The unknown actuator fault parameters are $s_i=[0.5,0.5,0.5]$ and $u_i^b\left(t\right)=0.1exp\left(t\right)$.

The system (53) is in the form of a nonlinear second-order multi-input multi-output, containing unknown control gains $B_i$ and actuator fault parameters $S_i=\left[s_{ix},s_{iy},s_{iz}\right]$. Therefore, autonomous underwater vehicles with actuator and communication connection faults will be able to use the fault-tolerant control approach that this study proposes.

In the simulation, the initial values are selected as the state of AUV1 $x_{11}\left(0\right)={\left[0.8,0.5,-0.2\right]}^T, x_{12}\left(0\right)=0.1I_0$, the state of AUV 2 $x_{21}\left(0\right)={\left[1.0,0.3,-0.1\right]}^T, x_{22}\left(0\right)=0.2I_0$, the state of AUV3 $x_{31}\left(0\right)={\left[-0.2,-0.4,0.3\right]}^T, x_{32}\left(0\right)=0.3I_0$, the state of AUV 4 $x_{41}\left(0\right)={\left[-0.8,0.5,0.2\right]}^T, x_{42}\left(0\right)=0.4I_0, {\widehat{B}}_i\left(0\right)=I_1$, ${\varpi }_i\left(0\right)=I_1, {\rho }_i\left(0\right)=0.1I_1$ and ${\widehat{y}}_{di}\left(0\right)=I_0$. The actuator fault parameters are set as $s_i=0.5I_1$, $u_i^f=0.1exp\left(-0.1t\right)I_1$. The original weights are set as $a_{i,j}=1$, while the time-varying weights ${\delta }_{ij}^F\left(t\right)$ and ${\delta }_{ij}^L\left(t\right)$ are also selected as $0.5sin\left(t\right)$. The controller is configured with design parameters ${\epsilon }_{i,j}=0.1$, $c_{i,j}=2, k_i=0.2, {\kappa }_{M_{i,k}}=5I_1, {\mu }_{M_{i,k}}=1I_1, {\kappa }_{y_{di}}=12I_1$, ${\mu }_{y_{di}}=0.1I_1, {\kappa }_{M_i}=3I_1, {\mu }_{M_i}=0.01I_1, {\kappa }_{{\varpi }_i}=0.1I_1, {\mu }_{{\varpi }_i}=$$0.001I_1, {\kappa }_{{\rho }_i}=0.1I_1, {\mu }_{{\rho }_i}=I_1, {\epsilon }_i=0.2, {\tau }_{i,j}=0.1$, ${\epsilon }_i=exp\left(-0.01t\right)$, where $I_0={\left[0,0,0\right]}^T, I_1={\left[1,1,1\right]}^T$.

Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 present the simulation results of the multi-AUV system, validating the containment control performance and adaptive estimation strategies in 3D space. Figure 10 shows the 3D trajectories of three leader and four follower AUVs, along with the convex hull formed by the leaders. All followers successfully converge into this hull, confirming effective containment. Figure 11 displays the distributed containment errors $e_i$ along the X, Y, and Z axes, which converge to a bounded region near zero, demonstrating system stability. Figure 12 presents the control inputs in surge, sway, and heave. The inputs are smooth and bounded, confirming practical implementability. Figure 13 shows the accurate estimation of desired trajectories, with errors within 0.1. Figure 14 confirms effective multiplicative fault estimation, converging to a positive constant, while Figure 15 shows additive fault estimates converging to zero. These results collectively validate the robustness and fault-tolerant capability of the proposed framework under complex AUV dynamics.

The numerical and AUV simulations validate that the proposed fault-tolerant control strategy enables the multi-agent system to achieve containment control despite concurrent communication link and actuator faults.

Remark 4.

Based on the simulation results, the proposed containment control scheme demonstrates excellent performance. All followers successfully converge into the leaders’ dynamic convex hull in both 2D and 3D spaces, despite simultaneous communication and actuator faults. The containment errors are uniformly ultimately bounded, confirming theoretical predictions. The control signals are smooth and feasible, while the adaptive laws effectively estimate unknown leader references and fault parameters online, validating the key contributions of the method.

5. Conclusions

This paper studied the fault-tolerant containment control problem of nonlinear multi-agent systems suffering from actuator and communication link faults. An adaptive convex hull signal estimator is designed to effectively compensate for the influence of unknown global information caused by uncertain communication link faults. To further eliminate the boundary layer error, a nonlinear filter with a compensation term is applied. Considering actuator faults, an adaptive fault estimator is designed to compensate for the fault signal. Numerical and AUV simulations have been conducted, and the resulting simulation cases can serve as effective teaching materials for graduate-level courses helping students intuitively understand the design and validation process of fault-tolerant control scheme. In the future, an event-triggered mechanism can be considered to be introduced based on this study to reduce the system burden by reducing unnecessary communication while ensuring the control performance, thereby improving the resource utilization rate.