Interactions and Soliton Dynamics for a (2+1)-Dimensional Nonlinear Integrable Model Arising in Shallow Water
Abstract
1. Introduction
2. Interactions Solutions
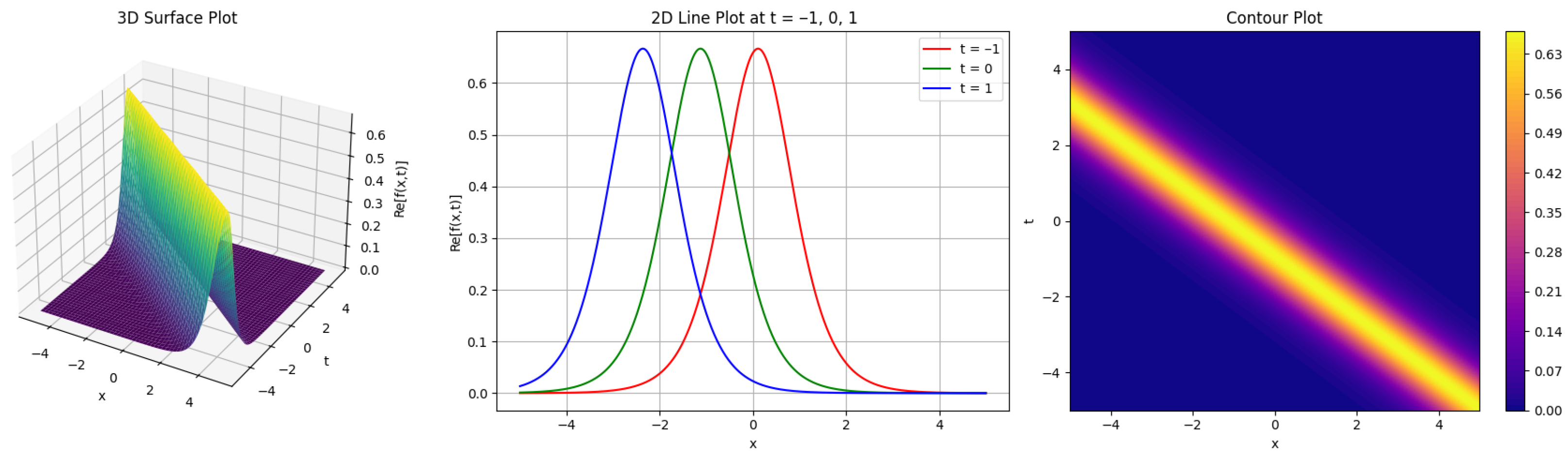
2.1. The Breather Solution
2.2. The Two-Waves Solution
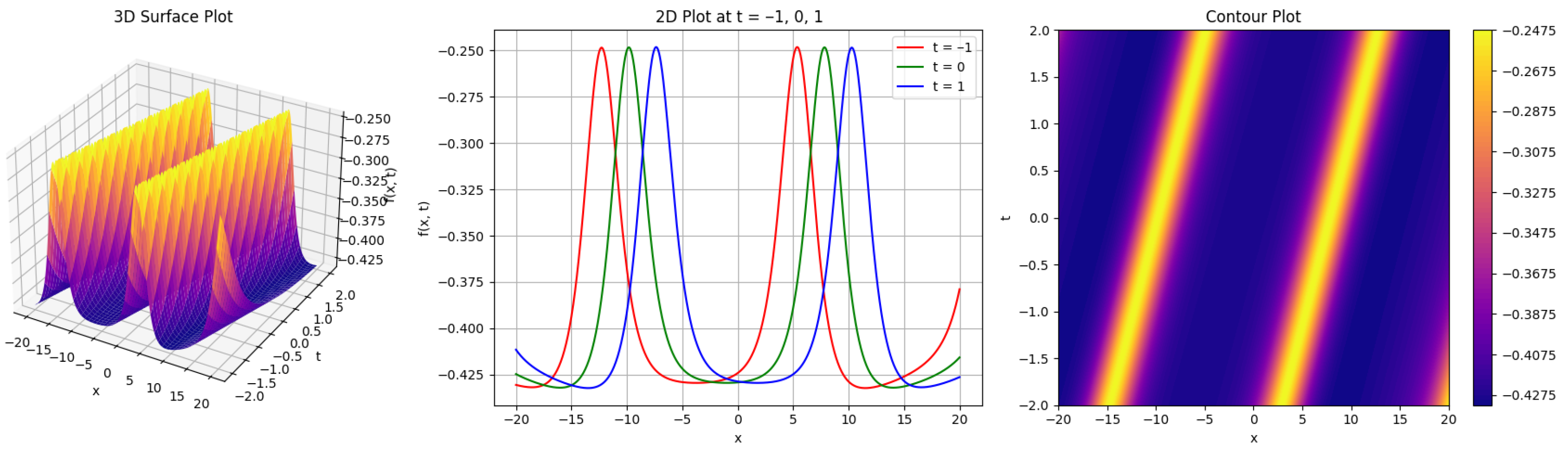
2.3. The Lump-Periodic Solution
2.4. The New Interaction Solution
3. Solitary, Kink/Antikink and Periodic Wave Solution
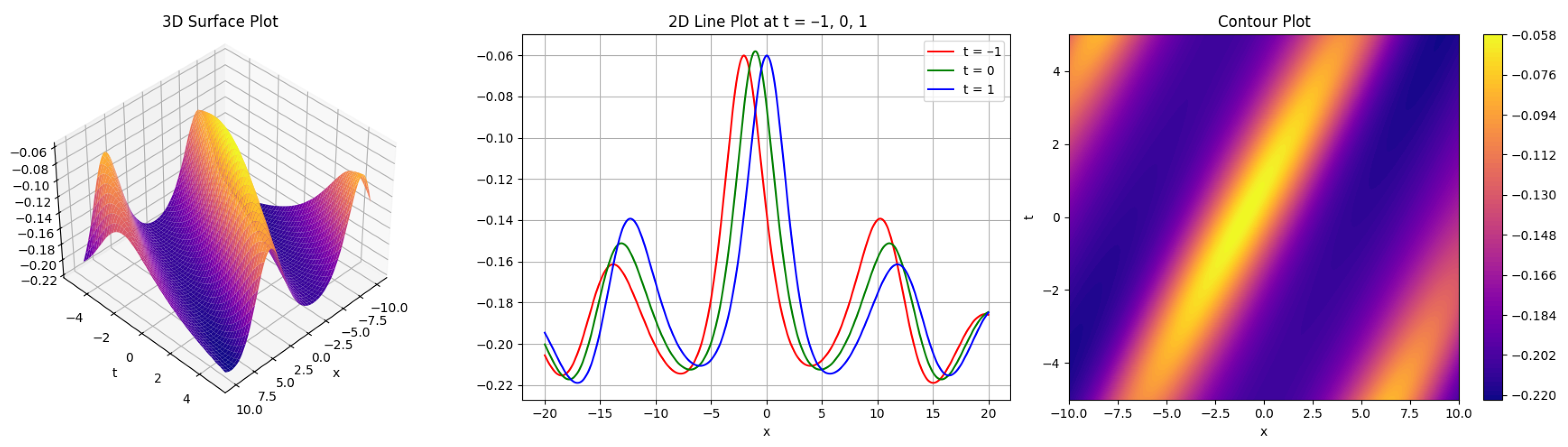
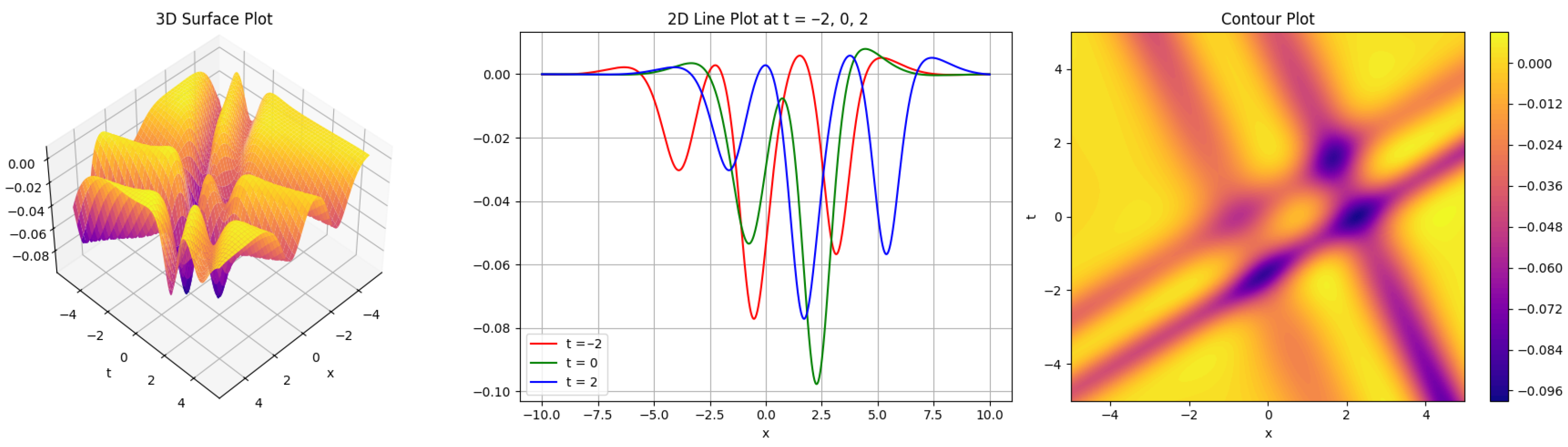
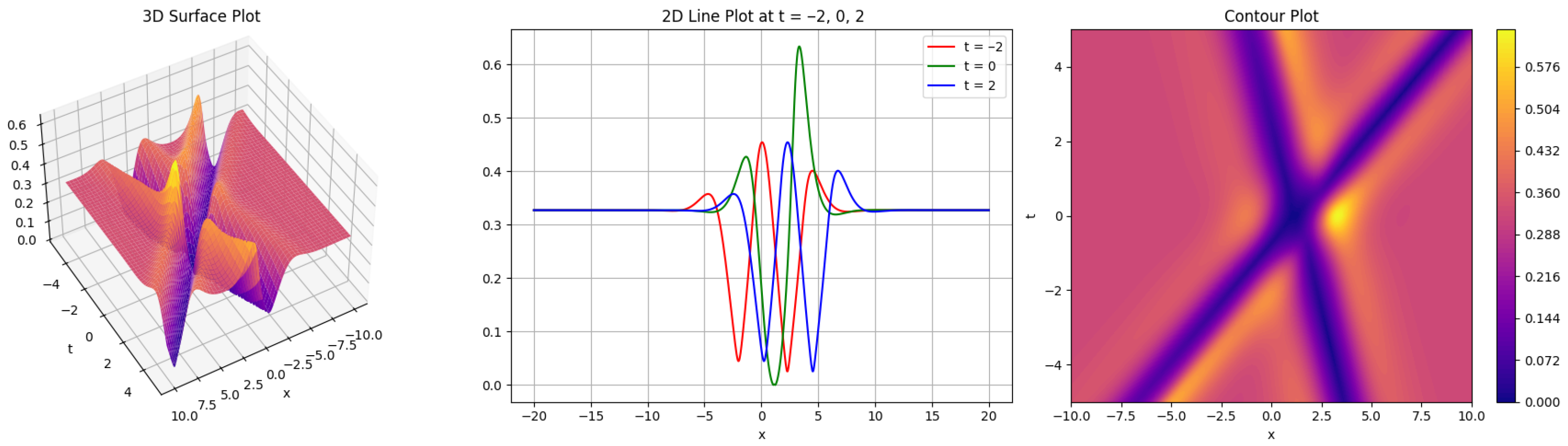
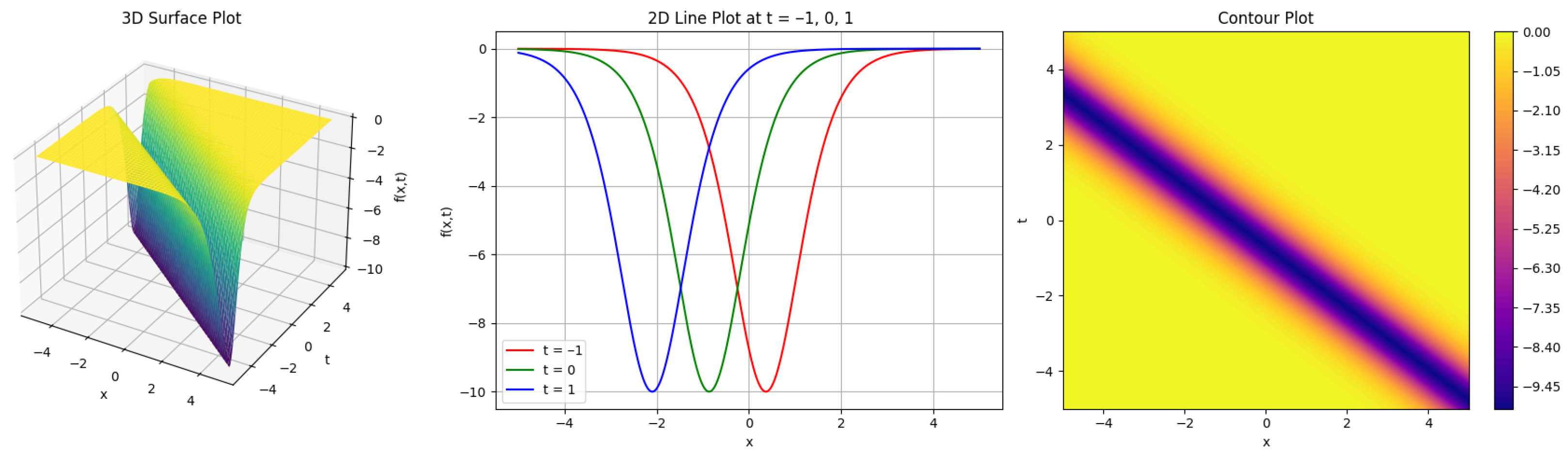
4. Graphical Representation
5. Modulation Instability Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boussinesq, J. Essai sur la Théorie des Eaux Courantes; Imprimerie Nationale: Paris, France, 1877. [Google Scholar]
- Darvishi, M.T.; Najafi, M.; Wazwaz, A.M. Soliton solutions for Boussinesq-like equations with spatio-temporal dispersion. Ocean. Eng. 2017, 130, 228–240. [Google Scholar] [CrossRef]
- McKean, H.P. Boussinesq’s equation as a Hamiltonian system. In Advances in Mathematics Supplementary Studies; Academic Press: San Diego, CA, USA, 1978; Volume 3, pp. 217–226. [Google Scholar]
- McKean, H.P. Boussinesq’s equation on the circle. Commun. Pure Appl. Math. 1981, 34, 599–691. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Kruskal, M.D. New similarity reductions of the Boussinesq equation. J. Math. Phys. 1989, 30, 2201–2213. [Google Scholar] [CrossRef]
- Zhu, J.Y. Line-soliton and rational solutions to (2+1)-dimensional Boussinesq equation by Dbar-problem. arXiv 2017, arXiv:1704.02779. [Google Scholar]
- Hirota, R.; Ito, M. Resonance of solitons in one dimension. J. Phys. Soc. Jpn. 1983, 52, 744–748. [Google Scholar] [CrossRef]
- Hereman, W.; Nuseir, A. Symbolic methods to construct exact solutions of nonlinear partial differential equations. Math. Comput. Simul. 1997, 43, 13–27. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Springer and Higher Education Press: Berlin, Germany, 2009. [Google Scholar]
- Wazwaz, A.M. Two kinds of multiple wave solutions for the potential YTSF equation and a potential YTSF-type equation. J. Appl. Nonlinear Dyn. 2012, 1, 51–58. [Google Scholar] [CrossRef]
- Leblond, H.; Mihalache, D. Models of few optical cycle solitons beyond the slowly varying envelope approximation. Phys. Rep. 2013, 523, 61–126. [Google Scholar] [CrossRef]
- Adem, A.R.; Khalique, C.M. New exact solutions and conservation laws of a coupled Kadomtsev-Petviashvili system. Comput. Fluids 2013, 81, 10–16. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple kink solutions for the (2+1)-dimensional Sharma-Tasso-Olver and the Sharma-Tasso-Olver-Burgers equations. J. Appl. Nonlinear Dyn. 2013, 2, 95–102. [Google Scholar] [CrossRef]
- Su, T. Explicit solutions for a modified (2+1)-dimensional coupled Burgers equation by using Darboux transformation. Appl. Math. Lett. 2017, 69, 15–21. [Google Scholar] [CrossRef]
- Mihalache, D. Multidimensional localized structures in optical and matter-wave media: A topical survey of recent literature. Rom. Rep. Phys. 2017, 69, 403–420. [Google Scholar]
- Xing, Q.; Wu, Z.; Mihalache, D.; He, Y. Smooth positon solutions of the focusing modified Korteweg-de Vries equation. Nonlinear Dyn. 2017, 89, 2299–2310. [Google Scholar] [CrossRef]
- Wazwaz, A.M. One kink solution for a variety of nonlinear fifth-order equations. Discontinuity Nonlinearity Complex. 2012, 1, 161–170. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Abundant solutions of distinct physical structures for three shallow water waves models. Discontinuity Nonlinearity Complex. 2017, 6, 295–304. [Google Scholar]
- Wazwaz, A.M. A variety of distinct kinds of multiple soliton solutions for a (3+1)-dimensional nonlinear evolution equations. Math. Methods Appl. Sci. 2013, 36, 349–357. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple real and multiple complex soliton solutions for the integrable Sine-Gordon equation. Optik 2018, 172, 622–627. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two-wave mode higher-order modified KdV equations: Essential conditions for multiple soliton solutions to exist. J. Numer. Methods Heat Fluid Flow 2017, 27, 2223–2230. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property of partial differential equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.M. Painlevé analysis and invariant solutions of generalized fifth-order nonlinear integrable equation. Nonlinear Dyn. 2018, 94, 2469–2477. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.M. Einstein’s vacuum field equation: Painlevé analysis and Lie symmetries. In Waves in Random and Complex Media; Taylor & Francis: Milton Park, UK, 2019. [Google Scholar]
- Yang, Z.; Zhong, W.P.; Belić, M. Dark localized waves in shallow waters: Analysis within an extended Boussinesq system. Chin. Phys. Lett. 2024, 41, 044201. [Google Scholar] [CrossRef]
- Cao, Y.; He, J.; Mihalache, D. Families of exact solutions of a new extended (2+1)-dimensional Boussinesq equation. Nonlinear Dyn. 2018, 91, 2593–2605. [Google Scholar]
- Khizar, F.; Ejaz, H.; Usman, Y.; Herbert, M.; Tamer, M.K.; Abdul, M.; Syed, A.A.S. Exploring the wave’s structures to the nonlinear coupled system arising in surface geometry. Sci. Rep. 2025, 15, 11624. [Google Scholar] [CrossRef] [PubMed]
- Farooq, K.; Alshammari, F.S.; Li, Z.; Hussain, E. Soliton dynamics and stability in the Boussinesq equation for shallow water applications. Front. Phys. 2025, 13, 1637491. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Kaur, L. New integrable Boussinesq equations of distinct dimensions with diverse variety of soliton solutions. Nonlinear Dyn. 2019, 97, 83–94. [Google Scholar] [CrossRef]
- Yin, Y.H.; Ma, W.X.; Liu, J.G.; Lu, X. Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction. Comput. Math. Appl. 2018, 76, 1275–1283. [Google Scholar]
- Gao, L.N.; Zi, N.N.; Yin, Y.H.; Ma, W.X.; Lu, X. Bäcklund transformation, multiple wave solutions and lump solutions to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 2017, 89, 2233–2240. [Google Scholar] [CrossRef]
- Lu, X.; Ma, W.X. Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation. Nonlinear Dyn. 2016, 85, 1217–1222. [Google Scholar] [CrossRef]
- Lu, X.; Chen, S.T.; Ma, W.X. Constructing lump solutions to a generalized Kadomtsev-Petviashvili-Boussinesq equation. Nonlinear Dyn. 2016, 86, 523–534. [Google Scholar] [CrossRef]
- Lu, X.; Ma, W.X.; Khalique, C.M. A direct bilinear Bäcklund transformation of a (2+1)-dimensional Korteweg-de Vries-like model. Appl. Math. Lett. 2015, 50, 37–42. [Google Scholar]
- Lu, X.; Ma, W.X.; Yum, J.; Khalique, C.M. Solitary waves with the Madelung fluid description: A generalized derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 2016, 31, 40–46. [Google Scholar] [CrossRef]
- Hussain, E.; Arafat, Y.; Malik, S.; Alshammari, F.S. The (2+1)-Dimensional Chiral Nonlinear Schrödinger Equation: Extraction of Soliton Solutions and Sensitivity Analysis. Axioms 2025, 14, 422. [Google Scholar] [CrossRef]
- Beenish; Hussain, E.; Younas, U.; Tapdigoglu, R.; Garayev, M. Exploring Bifurcation, Quasi-Periodic Patterns, and Wave Dynamics in an Extended Calogero-Bogoyavlenskii-Schiff Model with Sensitivity Analysis. Int. J. Theor. Phys. 2025, 64, 146. [Google Scholar] [CrossRef]
- Zhao, L.; Ejaz, H. Qualitative analysis and traveling wave solutions of a (3+1)-dimensional generalized nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt system. Fractal Fract. 2025, 9, 285. [Google Scholar] [CrossRef]
- Clarkson, P.; Dowie, E. Rational solutions of the Boussinesq equation and applications to rogue waves. Trans. Math. Its Appl. 2017, 1, tnx003. [Google Scholar] [CrossRef]
- Kumar, D.; Nuruzzaman, M.; Paul, G.C.; Hoque, A. Novel localized waves and interaction solutions for a dimensionally reduced (2+1)-dimensional Boussinesq equation from N-soliton solutions. Nonlinear Dyn. 2022, 107, 2717–2743. [Google Scholar] [CrossRef]
- Nuruzzaman, M.; Kumar, D. Lumps with their some interactions and breathers to an integrable (2+1)-dimensional Boussinesq equation in shallow water. Results Phys. 2022, 38, 105642. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Atangana, A. New lump, lump-kink, breather waves and other interaction solutions to the (3+1)-dimensional soliton equation. Commun. Theor. Phys. 2020, 72, 085004. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Hincal, E.; Baleanu, D.; Bayram, M. Two-wave, breather wave solutions and stability analysis to the (2+1)-dimensional Ito equation. J. Ocean. Eng. Sci. 2022, 7, 467–474. [Google Scholar] [CrossRef]
- Alquran, M.; Alhami, R. Analysis of lumps, single-stripe, breather-wave, and two-wave solutions to the generalized perturbed-KdV equation by means of Hirota’s bilinear method. Nonlinear Dyn. 2022, 109, 1985–1992. [Google Scholar] [CrossRef]
- Younas, U.; Sulaiman, T.A.; Ismael, H.F.; Muke, P.Z. Exploring the generalized fifth-order (2+1)-dimensional KdV equation: The lump structures and collision phenomena to the shallow water under gravity and nonlinear lattice. High Energy Density Phys. 2025, 55, 101186. [Google Scholar] [CrossRef]
- Muhammad, J.; Rehman, S.U.; Nasreen, N.; Bilal, M.; Younas, U. Exploring the fractional effect to the optical wave propagation for the extended Kairat-II equation. Nonlinear Dyn. 2025, 113, 1501–1512. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danladi, A.; Abdullah, A.R.; Hussain, E.; Li, Z. Interactions and Soliton Dynamics for a (2+1)-Dimensional Nonlinear Integrable Model Arising in Shallow Water. Mathematics 2025, 13, 3474. https://doi.org/10.3390/math13213474
Danladi A, Abdullah AR, Hussain E, Li Z. Interactions and Soliton Dynamics for a (2+1)-Dimensional Nonlinear Integrable Model Arising in Shallow Water. Mathematics. 2025; 13(21):3474. https://doi.org/10.3390/math13213474
Chicago/Turabian StyleDanladi, Ali, Aljethi Reem Abdullah, Ejaz Hussain, and Zhao Li. 2025. "Interactions and Soliton Dynamics for a (2+1)-Dimensional Nonlinear Integrable Model Arising in Shallow Water" Mathematics 13, no. 21: 3474. https://doi.org/10.3390/math13213474
APA StyleDanladi, A., Abdullah, A. R., Hussain, E., & Li, Z. (2025). Interactions and Soliton Dynamics for a (2+1)-Dimensional Nonlinear Integrable Model Arising in Shallow Water. Mathematics, 13(21), 3474. https://doi.org/10.3390/math13213474





