GIS-Integrated Data Analytics for Optimal Location-and-Routing Problems: The GD-ARISE Pipeline

Abstract

Optimizing the siting and servicing of urban facilities is a core operations research problem that must reconcile heterogeneous demand, spatial constraints, and network-realistic travel. We present GD-ARISE, a GIS-integrated and data analytics pipeline that maintains a pedestrian–road network metric from demand inference through siting to routing. The workflow has three modules: (i) GIS integration that unifies spatial layers on one network and distance metric; (ii) data analytics that builds multi-criteria suitability via the Analytic Hierarchy Process (AHP) and maps scores to adaptive service radii; (iii) optimal location-and-routing that selects nonoverlapping sites with a transparent greedy rule (SCASS) and computes depot-to-depot routes via simulated annealing on the same metric. A case study in Seoul’s Gangnam District yields a high-coverage portfolio and feasible collection routes. We add a theoretical framework that casts SCASS as a conflict-graph problem, document the AHP elicitation with consistency checks, and report robustness analyses including sensitivity to AHP weights and to radius bounds. Results indicate that core hotspots remain stable to weighting, whereas mid-range corridors shift as criteria priorities or spatial parameters change.

1. Introduction

1.1. Motivation

Urban waste disposal and storage can be framed as a rigorously defined operations research location-and-routing problem that is driven by demand data analytics and is GIS-native [1]. In megacities, rapid urbanization and rising population density intensify pressure on municipal services; public waste management often struggles to keep pace. A core cause is geometric mismatch: bins are not where people generate waste, and service routes ignore how people and vehicles actually move [1,2]. The result is a network-based operations research problem in which demand must be inferred, sites must be chosen, and service must be routed using a coherent metric and data stack. This is now feasible at the city scale because municipalities publish high-frequency geospatial datasets (e.g., floating populations, transit nodes, and points of interest), and open platforms such as OpenStreetMap, with OSMnx, enable the computation of network-consistent distances [3]. Planners increasingly require transparent analytics that map directly to policy levers—how many bins to deploy, where to place them, and how to service them given fleet and budget constraints—so there is a timely opportunity to connect demand estimation, siting, and routing under one geometry and one metric [2,4]. Despite practical need, algorithms for urban amenity siting that integrate heterogeneous demand data with geometry-consistent spatial and operational constraints have received limited attention. Few studies, to our knowledge, claim an end-to-end algorithm that explicitly integrates GIS-based geometry, demand-driven multi-criteria scoring that feeds back into spatial parameters, nonoverlap enforced with adaptive radii on a network metric, and routing on the same metric. Most prior workflows stop at ranking without altering geometry, mix Euclidean screening with network routing, or impose fixed buffers that ignore local demand. As a result, geometry-consistent siting-and-routing pipelines remain rare in the literature, leaving a gap for methods that are both operationally credible and analytically transparent.

1.2. Related Works

The literature on multi-criteria decision-making (MCDM), the maximal covering location problem (MCLP), and routing has been extensively developed for facility location in operations research. GIS strengthens these models by linking geospatial data and network analysis [3,5], enabling city-scale location allocation, coverage, and access studies [6]. For multi-criteria synthesis, the Analytic Hierarchy Process (AHP) [7] and related MCDM methods are widely used to build suitability surfaces for siting and infrastructure planning [6]. This approach typically involves weighting heterogeneous GIS layers to derive a composite suitability index. It has been widely applied across various domains, including landfill siting [8,9], healthcare facility planning [10], and renewable energy projects [11,12]. These studies formalize how multi-criteria weighting translates spatially into suitability gradients, underscoring MCDM’s capacity to operationalize complex environmental and social criteria.

Church and ReVelle introduced MCLP, which chooses sites to cover as much demand as possible within a set distance [13]. Many studies have extended this idea to include budgets, fairness goals, and changes over time or uncertainty [14,15,16,17]. Ref. [18] investigated model placement as a single goal of maximizing coverage. In solid-waste systems, recent reviews summarize how covering models are used and point out that results can change a lot depending on the distance measure and the service radius assumed [19,20]. A primary critique of the classical MCLP concerns its rigid, binary definition of coverage. Berman et al. (2003) [21] addressed the model’s unrealistic “all-or-nothing” assumption by introducing a gradual decay function, where service quality diminishes with distance rather than ceasing abruptly. Complementing this, Karasakal and Karasakal (2004) [22] highlighted that strict binary formulations can yield unjustified solutions where partial service is plausible, thereby motivating variants that permit partial coverage. More recent extensions have broadened the MCLP’s focus from pure efficiency to include equity. Blanco and Gázquez (2023) [23] formalized the integration of fairness, employing concepts such as $\alpha$-fairness and ordered-weighted objectives. Their work underscores that distributional equity is not inherent in the basic model and must be incorporated as an explicit objective. Despite these theoretical advancements, practical siting decisions increasingly rely on spatial data and multi-criteria integration. However, using such derived scores to dynamically adjust geometric or operational parameters, such as service radii or coverage decay, remains limited [24,25,26]. Spatial feasibility often requires nonoverlap [27,28], which connects to disk packing [29] and independent set formulations [30]; in practice, spacing is frequently enforced with ad hoc buffers rather than with network metric optimization. In algorithms, greedy heuristics are common for NP-hard location models because they are fast and transparent [31], though not globally optimal [14,15,32].

For routing, simulated annealing [33,34] and other local search methods perform well on the traveling salesman problem (TSP) [35] and on modern VRP variants [36]. Recent applied work also moves toward joint decisions on where to locate facilities and how to route the service.

Rahmanifar et al. (2024) [37] present a non-linear multiobjective model that integrates warehouse location with vehicle routing in cold-chain logistics, and Hashemi-Amiri et al. (2023) [38] propose a tri-objective mixed-integer linear program (MILP) that unifies facility location, crew scheduling, and routing for municipal solid waste. These studies advance integrated planning, but they do not maintain a single, GIS-consistent distance metric from multi-criteria demand aggregation through siting constraints to downstream routing.

1.3. Contributions

This paper introduces GD-ARISE (GIS-integrated and Data analytic Adaptive Radius Integrated Siting and rEservicing), an end-to-end, GIS-integrated pipeline that maintains geometric consistency from demand analytics to operations. First, all spatial layers—administrative boundaries, pedestrian–road networks, floating populations, transit nodes, and waste-related points of interest—are reconciled onto a single pedestrian–road network and one distance metric, ensuring that measurements and decisions are expressed in the same geometry. Second, multi-criteria demand is constructed via AHP into a composite suitability score, and then mapped to geometry as an adaptive service radius, so that high-suitability areas receive smaller radii while lower-suitability areas receive larger radii to preserve access. Third, spatially constrained selection is formulated with site-specific radii on the network metric and implemented via a transparent greedy rule (SCASS) to produce a maximal nonoverlapping portfolio; the associated conflict structure admits an interpretation as a graph independent set problem. Fourth, depot-to-depot service routes are generated using simulated annealing on the identical network metric used upstream, closing the loop without changing geometry. Finally, the pipeline is demonstrated on waste bin siting and servicing in Seoul’s Gangnam District, where the walkable network is sampled at fine resolution, composite scores and adaptive radii are computed, a nonoverlapping portfolio of sites is selected, and operational routes are produced, including a single depot case in Samsung 1–dong. By maintaining one geometry and one metric across all stages, GD-ARISE turns GIS analytics into operations research decisions about counts, placement, spacing, and service effort under realistic constraints.

2. An Integrated Planning Algorithm: GD-ARISE

We present GD-ARISE, a unified, GIS-integrated workflow for optimal location-and-routing. Figure 1 shows the workflow of the GD-ARISE algorithm, which has three modules: GIS integration, data analytics, and optimal location-and-routing. All steps use one network distance metric on the pedestrian–road network. This keeps geometry and units consistent. In GIS integration, load the administrative boundaries, the pedestrian–road network, floating population layers, transit nodes, and waste-related points of interest. Harmonize coordinate reference systems, clean fields, and clip layers to the study region. In data analytics, generate dense candidate sites along walkable streets. For each candidate site, compute criterion scores from the GIS layers such as population, transit access, and proximity to points of interest. Normalize all scores to $[0,1]$. Use AHP to set weights and combine the criteria into a composite suitability. In optimal location-and-routing, first select sites with SCASS. Sort candidates by suitability and add a site if its radius does not overlap any already selected radius. Then route service to build depot-to-depot tours. The workflow also reports the coverage attained, the number of selected sites, the route length, and the route time. Because all steps share one metric and one GIS substrate, results are easy to audit, map, and reproduce.

We work on a single geographic region $L\subset {\mathbb{R}}^2$ with a pedestrian–road network-induced distance $d:{\mathbb{R}}^2\times {\mathbb{R}}^2\to {\mathbb{R}}_{\ge 0}$ (shortest path on the network). The region is discretized into candidate sites $J=\{j_1,\dots ,j_N\}$ sampled from the network at resolution $\delta >0$, so adjacent samples are at most $\delta$ apart under d. A set of criteria $\mathcal{C}=\{C_1,\dots ,C_M\}$ evaluates each site. We assign to every $j\in J$ a composite suitability $S_j^{*}\in [0,1]$ and an adaptive service radius $r_j\in [R_{\min },R_{\max }]$ with $0<R_{\min }<R_{\max }<\infty$. Then, we select a subset $J_{\mathrm{sel}}\subseteq J$ of size $P_{\mathrm{target}}\in \mathbb{N}$ while enforcing nonoverlap based on d and $\left\{r_j\right\}$. Finally, we route the service from a designated depot $D_0\in L$. When routing is required, each served site carries demand $q_j\ge 0$, the fleet has $m\in \mathbb{N}$ vehicles, and each vehicle has capacity $Q>0$. All distances and constraints use the same metric d.

Multi-criteria demand assessment will be performed by mapping heterogeneous raw measurements into a composite demand suitability score $S_j^{*}$ and a site-specific spatial footprint $r_j$. The inputs are the raw criterion values or proximity-based syntheses for each $C_k\in \mathcal{C}$, together with a pairwise comparison matrix that encodes decision priorities. Each criterion is normalized to $[0,1]$ via a monotone transformation so that larger values consistently mean greater desirability, and AHP weights are extracted from the principal eigenvector of the comparison matrix, subject to a consistency check. Aggregation by a convex combination yields $S_j^{*}={\sum }_k{\alpha }_k{S}_{j,k}$. This first stage resolves two design tensions in a data-driven yet interpretable way: it fuses many incommensurate predictors of demand into a single, dimensionless score, and it ties spatial influence to local desirability so that high-value sites are modeled with tighter catchments while low-value sites expand to preserve access.

For every criterion $C_k\in \mathcal{C}$ and site $j\in J$, the non-negative value $V_{j,k}\in {\mathbb{R}}_{\ge 0}$ quantifies the magnitude of $C_k$ at j. Two constructions cover the settings of interest. When $C_k$ is directly observed at the site—such as floating population, footfall, or local demand intensity—we set $V_{j,k}=P_j$, where $P_j$ denotes the measured quantity at j. When $C_k$ reflects the influence of external features distributed in space, we let $F_k={\left\{f_s\right\}}_{s=1}^{S_k}\subset L$ denote the relevant feature set and assign non-negative weights ${\left\{{\omega }_{k,s}\right\}}_{s=1}^{S_k}$ that sum to one and encode the relative importance of individual features or subtypes. A influence kernel $K:{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$ then maps distances to contributions so that

$$V_{j,k}=\sum _{s=1}^{S_k}{\omega }_{k,s}K\left(d(j,f_s)\right).$$

(1)

In the case study, we adopt $K\left(\rho \right)=\rho$ with $d(j,f_s)$, measured as Euclidean distance.

Because the criteria are measured in heterogeneous units, each raw value is transformed to a standardized unit-interval score via a criterion-specific monotone standardization map $f_k:{\mathbb{R}}_{\ge 0}\to [0,1]$ defined by $S_{j,k}=f_k\left(V_{j,k}\right)$. When $C_k$ is a benefit-type attribute for which larger values are more desirable, a min–max mapping places all sites on a common scale,

$$S_{j,k}=\left\{\begin{array}{cc}{\displaystyle \frac{V_{j,k}-{\min }_{\ell \in J}{V}_{\ell ,k}}{{\max }_{\ell \in J}{V}_{\ell ,k}-{\min }_{\ell \in J}{V}_{\ell ,k}}},\hfill & \mathrm{if}\underset{\ell \in J}{\max }{V}_{\ell ,k}>\underset{\ell \in J}{\min }{V}_{\ell ,k},\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(2)

sending the empirical minimum to 0 and the empirical maximum to 1. To translate composite suitability into a spatial service footprint, two design constants $0<R_{\min }<R_{\max }$ specify the admissible range of coverage radii. The adaptive coverage radius at site j is then defined by the affine mapping:

$$r_j=R_{\max }-(R_{\max }-R_{\min })S_j^{*}.$$

(3)

Because $S_j^{*}\in [0,1]$, this definition guarantees $r_j\in [R_{\min },R_{\max }]$. Differentiating shows that $\mathsf{\partial }{r}_j/\mathsf{\partial }{S}_j^{*}=-(R_{\max }-R_{\min })<0$, so sites with higher suitability are assigned proportionally smaller catchments by concentrating service in areas of strong demand while allowing sites in weaker areas to expand their reach to preserve access. The use of a network-based metric d is essential in urban contexts when it captures the true impedance of travel.

Now, we design an algorithm for selecting locations via adaptive coverage and greedy nonoverlap, so-called SCASS, in the spirit of MCLP. The aim is to choose the optimal number of target sites $P_{\mathrm{target}}$ that maximizes the amount of demand covered within the heterogeneous radii ${\left\{r_j\right\}}_{j\in J}$.

Proposition 1 

(SCASS). Let $L\subset {\mathbb{R}}^2$ be a geographic region endowed with a network metric d, let $J=\{j_1,\dots ,j_N\}\subset L$ be candidate sites with adaptive radii ${\left\{r_j\right\}}_{j\in J}$ determined from composite scores ${\left\{S_j^{*}\right\}}_{j\in J}$, and let $U\subseteq L$ be finite demand nodes with weights ${\left\{w_u\right\}}_{u\in U}$. For each $j\in J$ define the coverage set:

$$C\left(j\right)=\{u\in U:d(u,j)\le r_j\},\mathit{and}\mathit{the}\mathit{service}\mathit{disk}{\mathbb{D}}_j=\{x\in L:d(x,j)\le r_j\}.$$

Construct the conflict graph $G_c=(J,\mathcal{E})$ with an edge $\{i,j\}\in \mathcal{E}$ iff $d(i,j)<r_i+r_j$.

(i) 

Nonoverlap ⟺ Independence. A subset $J_{\mathrm{sel}}\subseteq J$ satisfies the SCASS nonoverlap requirement ${\mathbb{D}}_i\cap {\mathbb{D}}_j=⌀$ for all distinct $i,j\in J_{\mathrm{sel}}$, if and only if $J_{\mathrm{sel}}$ is an independent set in $G_c$.

(ii) 

Adaptive radius MCLP with exclusions. For a given cardinality $P_{\mathrm{target}}\in \mathbb{N}$, the problem of choosing $J_{\mathrm{sel}}\subseteq J$ with $|J_{\mathrm{sel}}|=P_{\mathrm{target}}$ to maximize covered demand,

$$\sum _{u\in U}{w}_u\mathbf{1}\left\{u\in \bigcup _{j\in J_{\mathrm{sel}}}C\left(j\right)\right\}$$

subject to SCASS nonoverlap is equivalent to the maximal covering location problem on U with site-specific radii $\left\{r_j\right\}$ and the additional constraint that $J_{\mathrm{sel}}$ is an independent set of $G_c$.

(iii) 

Maximum-weight independent set (MWIS). If the siting objective is to maximize ${\sum }_{j\in J_{\mathrm{sel}}}{S}_j^{*}$ subject to nonoverlap and $|J_{\mathrm{sel}}|=P_{\mathrm{target}}$, then the problem is a cardinality-constrained MWIS on $G_c$:

$$\underset{J_{\mathrm{sel}}\subseteq J}{\max }\sum _{j\in J_{\mathrm{sel}}}{S}_j^{*}\mathrm{s}.\mathrm{t}.\left|J_{\mathrm{sel}}\right|=P_{\mathrm{target}},J_{\mathrm{sel}}\mathit{independent}\mathit{in}{G}_c.$$

Equivalently, with binaries $x_j\in \{0,1\}$,

$$\begin{array}{cc}\hfill \underset{x\in {\{0,1\}}^N}{\max }& \sum _{j=1}^N{S}_j^{*}{x}_j\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& x_i+x_j\le 1\forall \{i,j\}\in \mathcal{E},\hfill \\ & \sum _{j=1}^N{x}_j=P_{\mathrm{target}}.\hfill \end{array}$$

Proof. 

For (i), if ${\mathbb{D}}_i\cap {\mathbb{D}}_j\ne ⌀$, then there exists x with $d(i,j)\le d(i,x)+d(x,j)\le r_i+r_j$ by the triangle inequality; hence $\{i,j\}\in \mathcal{E}$ and the pair cannot be jointly selected. Conversely, if $d(i,j)\ge r_i+r_j$, then no x can lie in both disks, so ${\mathbb{D}}_i\cap {\mathbb{D}}_j=⌀$. This establishes the equivalence between nonoverlap and independence in $G_c$. Statement (ii) inserts this feasibility into the adaptive radius MCLP coverage objective, so a feasible solution is exactly an independent set of prescribed size. Statement (iii) is a direct translation of the selection objective into a cardinality-constrained MWIS, yielding the stated 0–1 formulation. □

Finally, we optimize the service route problem over the selected sites and depot using a capacitated vehicle-routing model. The node set is $V=\{0,1,\dots ,K\}$ with $K=|J_{\mathrm{sel}}|$. The node 0 means the depot $D_0$ of an operations center or garage, and node i corresponds to site $j_i\in J_{\mathrm{sel}}$. Edge costs are the network distances $d_{ij}=d(j_i,j_j)$ with $j_0\equiv D_0$. Demands ${\left\{q_{j_i}\right\}}_{i=1}^K$ and a common capacity Q define feasibility, and the goal is to partition $J_{\mathrm{sel}}$ into at most m depot-to-depot tours minimizing total travel cost while serving each site exactly once and respecting capacity. Because exact mixed-integer formulations are NP-hard at realistic scales, we adopt a simulated annealing search over permutations augmented with depot separators. A candidate solution is encoded as a sequence that starts and ends at 0 and contains each customer once, together with $m-1$ additional depot symbols; cutting at the depot symbols yields the m routes. The total cost is the sum of $d_{ij}$ along the sequence, and capacity feasibility amounts to verifying that the sum of demands on each between-depot segment does not exceed Q. This stage converts a strategic siting outcome into operationally feasible tours that coincide with the same network metric d used in the first two stages.

Routing operates on these selected sites and the designated depot $D_0\in L$. To harmonize indexing, fix an arbitrary bijection between $\{1,\dots ,K\}$ and $J_{\mathrm{sel}}$ and write $j_i$ for the site associated with index i. Define the node set $V=\{0,1,\dots ,K\}$, where node 0 corresponds to the depot $D_0$ and node $i\in \{1,\dots ,K\}$ corresponds to site $j_i$. For any pair $(i,j)\in V\times V$, define $d_{ij}=d(j_i,j_j)$ with the convention $j_0\equiv D_0$ and exclude self-loops via $x_{ii}=0$. Each customer node $i\in \{1,\dots ,K\}$ is assigned a non-negative service demand $q_i\ge 0$ (e.g., expected daily pickups or deliveries), and vehicles have a common capacity $Q>0$ in the same units as the $q_i$. Let $m\in \mathbb{N}$ be the available fleet size. A vehicle route is a directed cycle that starts and ends at the depot, visits a subset of customers exactly once, and respects capacity. We encode routing decisions with binary arc variables $x_{ij}\in \{0,1\}$ that indicate whether a vehicle travels directly from node i to node j. To enforce capacity and eliminate subtours, we introduce continuous load–flow variables using the classical single-commodity formulation: let $y_i$ denote the cumulative load delivered up to and including customer i on the route that visits i, measured from zero at the depot. The capacitated vehicle routing problem on $(V,d_{ij})$ is then

$$\underset{x,y}{\min }\sum _{i=0}^K\sum _{j=0}^K{d}_{ij}{x}_{ij}$$

(4)

subject to the depot degree constraints ${\sum }_{j=1}^K{x}_{0j}=m$ and ${\sum }_{i=1}^K{x}_{i0}=m$, the customer in- and out-degree constraints ${\sum }_{i=0}^K{x}_{ih}=1$ and ${\sum }_{j=0}^K{x}_{hj}=1$ for every $h\in \{1,\dots ,K\}$, and the load–flow constraints

$$y_j\ge y_i+q_j-Q(1-x_{ij})\mathrm{for}\mathrm{all}i\in V,j\in \{1,\dots ,K\},$$

(5)

together with the bounds $y_0=0$ and $q_i\le y_i\le Q$ for all $i\in \{1,\dots ,K\}$, and the binary and no-nnegativity restrictions $x_{ij}\in \{0,1\}$ and $y_i\ge 0$. The degree constraints ensure that every customer is entered and left exactly once and that exactly m tours depart from and return to the depot. The load–flow inequalities propagate cumulative load along used arcs: if $x_{ij}=1$, then $y_j\ge y_i+q_j$. So, when a vehicle traverses $(i,j)$, it must have delivered an additional $q_j$ units by the time it leaves j; if $x_{ij}=0$, the constraint is slack by at most Q. The bounds $y_0=0$ and $y_i\le Q$ enforce vehicle capacity and, together with flow propagation, preclude subtours disconnected from the depot, since any positive delivery in a closed customer-only cycle would force y to grow without the possibility of resetting to 0. This mixed-integer program is NP-hard; indeed, when $m=1$ and $Q\ge {\sum }_{i=1}^K{q}_i$, the problem reduces to the classical traveling salesman problem on $\{0,1,\dots ,K\}$.

3. Application

Typical applications of the proposed algorithm include siting clinics, fire stations, micro-mobility docks, or public waste bins, each requiring a coherent pipeline. We illustrate the approach on public waste bin siting and servicing in the Gangnam District of Seoul, a dense mixed-use environment in which pedestrian flows, transit access, and commercial intensity co-produce spatially and temporally concentrated litter generation. Figure 2 presents the detailed computational workflow to apply the proposed GD-ARISE with the case study on public waste-bin siting and servicing in Seoul’s Gangnam District.

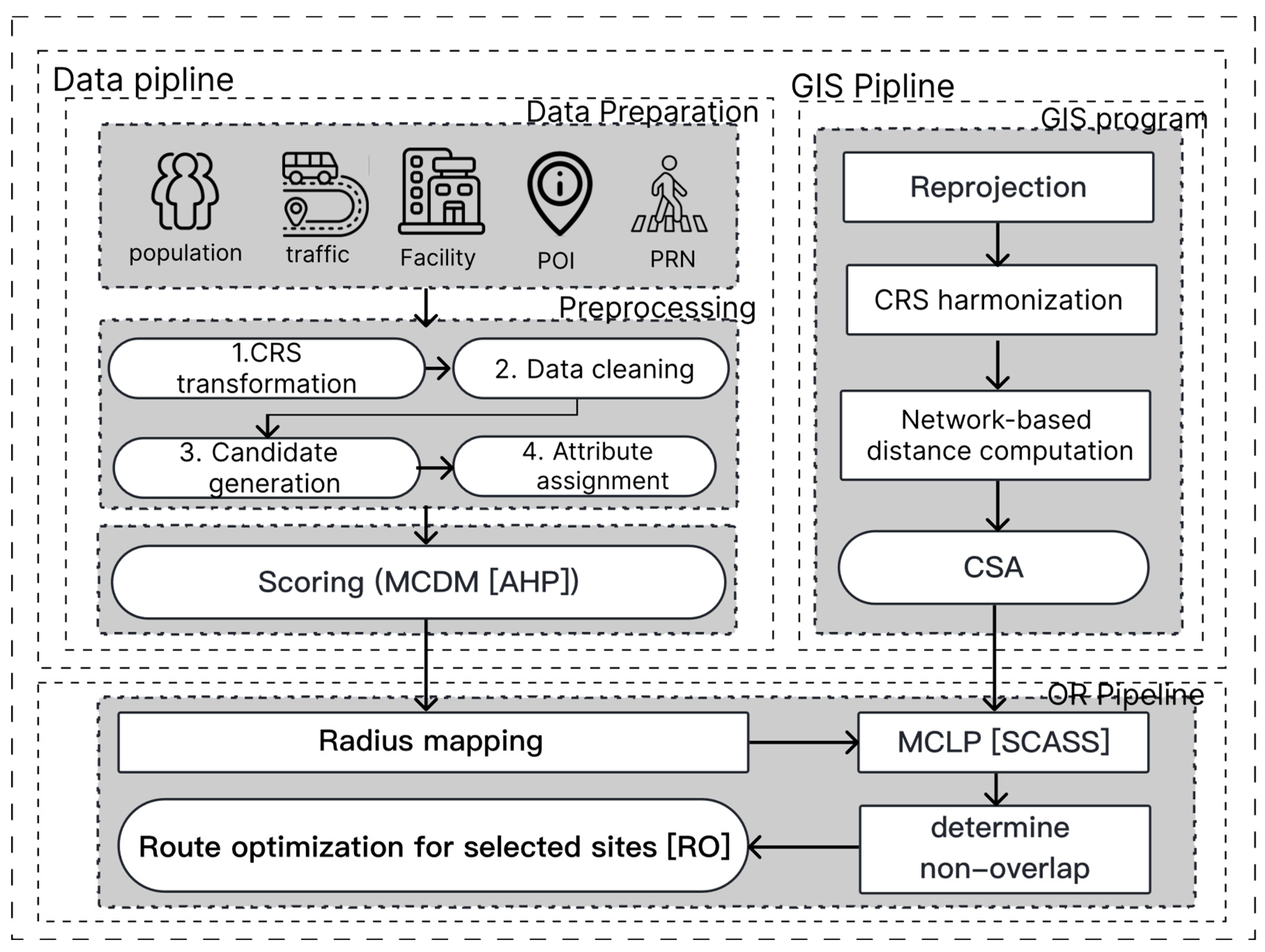
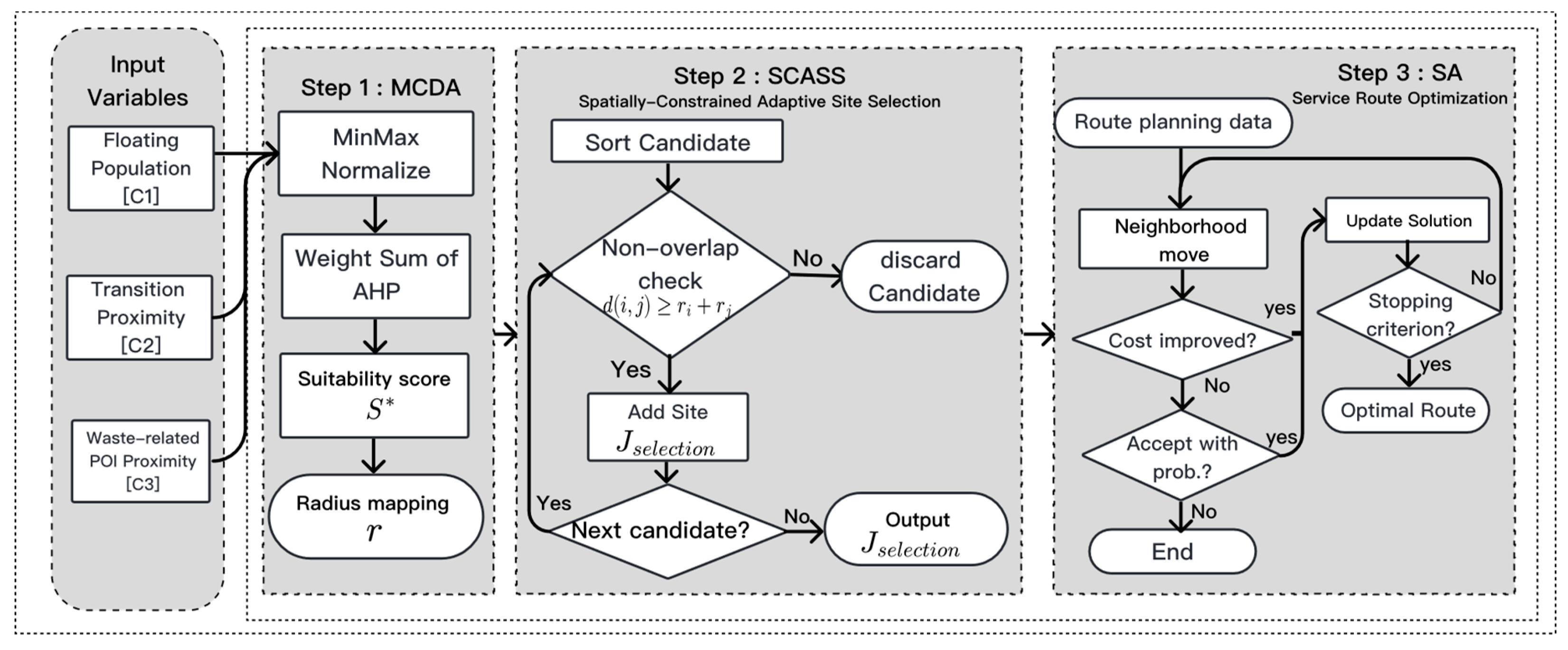
3.1. GIS Analytics

The application domain is the Gangnam District of Seoul. We set the study region of the framework to $L=G\subset {\mathbb{R}}^2$, and we use a single distance metric $d:{\mathbb{R}}^2\times {\mathbb{R}}^2\to {\mathbb{R}}_{\ge 0}$ throughout all stages, instantiated in practice as the shortest-path metric induced by the pedestrian–road network $\mathcal{G}$ so that distances reflect walk times and barriers rather than straight lines. Gangnam’s land incorporates corridors along Teheran–ro, high-street retail near Gangnam Boulevard, entertainment clusters in Apgujeong and Cheongdam, and multiple subway interchanges induce marked spatiotemporal variation in footfall. We represent this with a non-negative pedestrian density field $P:G\times [0,T]\to {\mathbb{R}}_{\ge 0}$ over a representative horizon $[0,T]$ (e.g., one day). Administrative boundaries for G were obtained as polygonal census layers and ingested into a GeoPandas workflow. To ensure geometric consistency across heterogeneous sources, all layers were reprojected to the common geographic CRS EPSG:4326 (WGS84) for integration with web data, and then to EPSG:5186 (Korea 2000/Central Belt) for all computations that require metric accuracy. All geoprocessing and network analyses were performed in Python (v3.11.11) using GeoPandas (v1.0.1) for spatial data handling, OSMnx (v2.0.2) for extracting the pedestrian network from OpenStreetMap, Shapely (v2.1.0) for geometric operations (e.g., buffering and distance), and Folium (v0.19.5) for interactive map visualization.

Table 1. GIS integration workflow for Gangnam case.

Variable Category	Source and Preprocessing	Role in Model
Administrative boundaries	Census polygons; reproject WGS84 → EPSG:5186; spatial joins to points	Study region G, attribution of J and U
Pedestrian network $\mathcal{G}$	OSM walkable edges via OSMnx; simplification; snapping tolerance	Distance metric d; candidate sampling; routing graph
Candidate locations J	Points every $\delta =10$ m along $\mathcal{G}$; $N=32,890$	Feasible siting set
Demand nodes U	Network vertices or grid centroids within G	Coverage evaluation, calibration, validation

summarizes the GIS integration for the Gangnam case. It shows each spatial layer, how we prepare it, and how it is used in the model.

Candidate facility sites are drawn from the walkable subgraph of OpenStreetMap within G. We extracted footways, pedestrian paths, sidewalks, and low-speed residential links using OSMnx, simplified the network to retain unique traversable edges, and then sampled points along these edges at a fixed network spacing $\delta =10$ m. The result is a finite candidate set $J=\{j_1,\dots ,j_N\}\subset G$ with $N=\mathrm{32,890}$ points for feasible bin locations. Each $j\in J$ inherits attributes from intersecting administrative polygons via spatial join (e.g., sub-district codes) and is snapped to the nearest network node to avoid topological artifacts when computing $d(·,·)$. 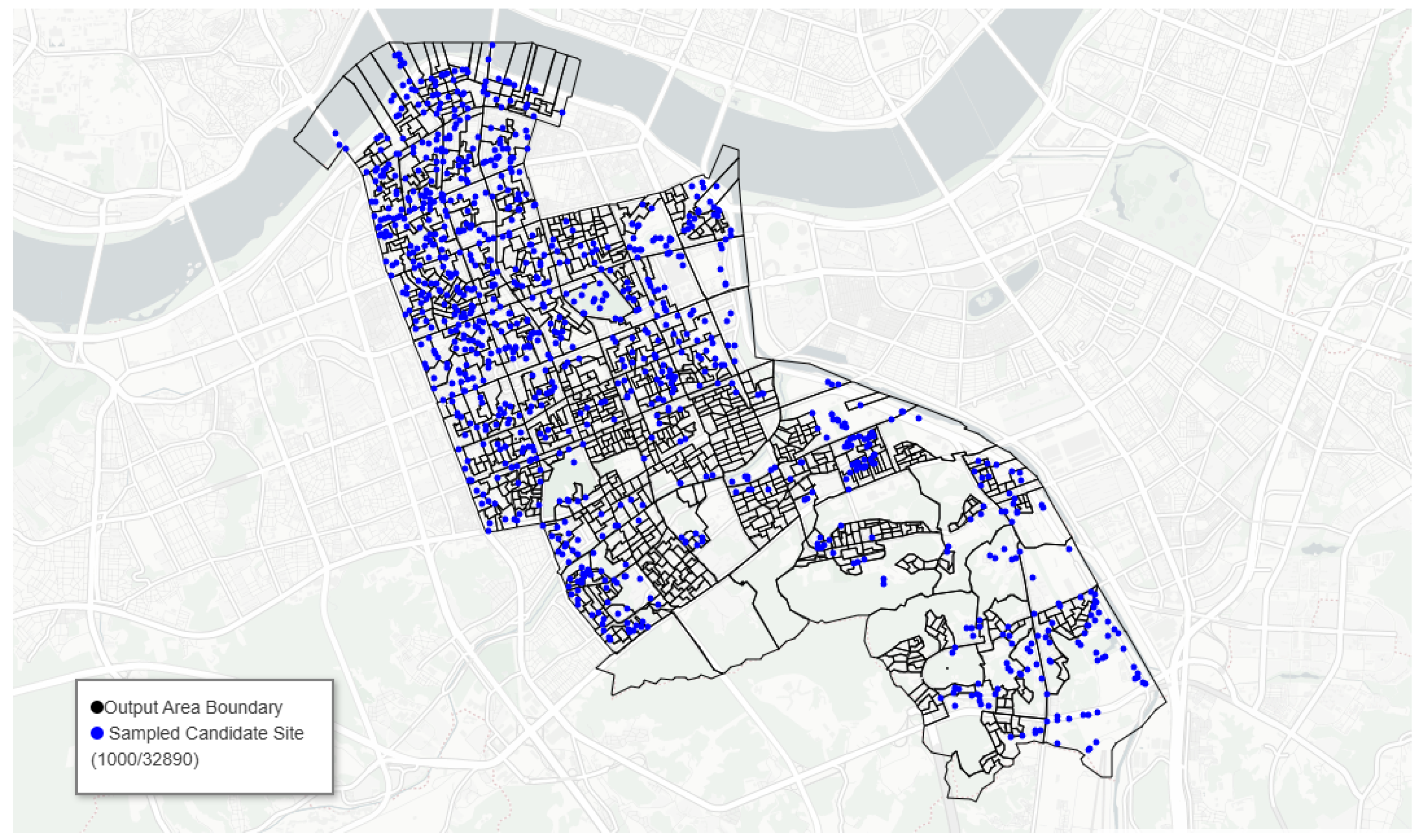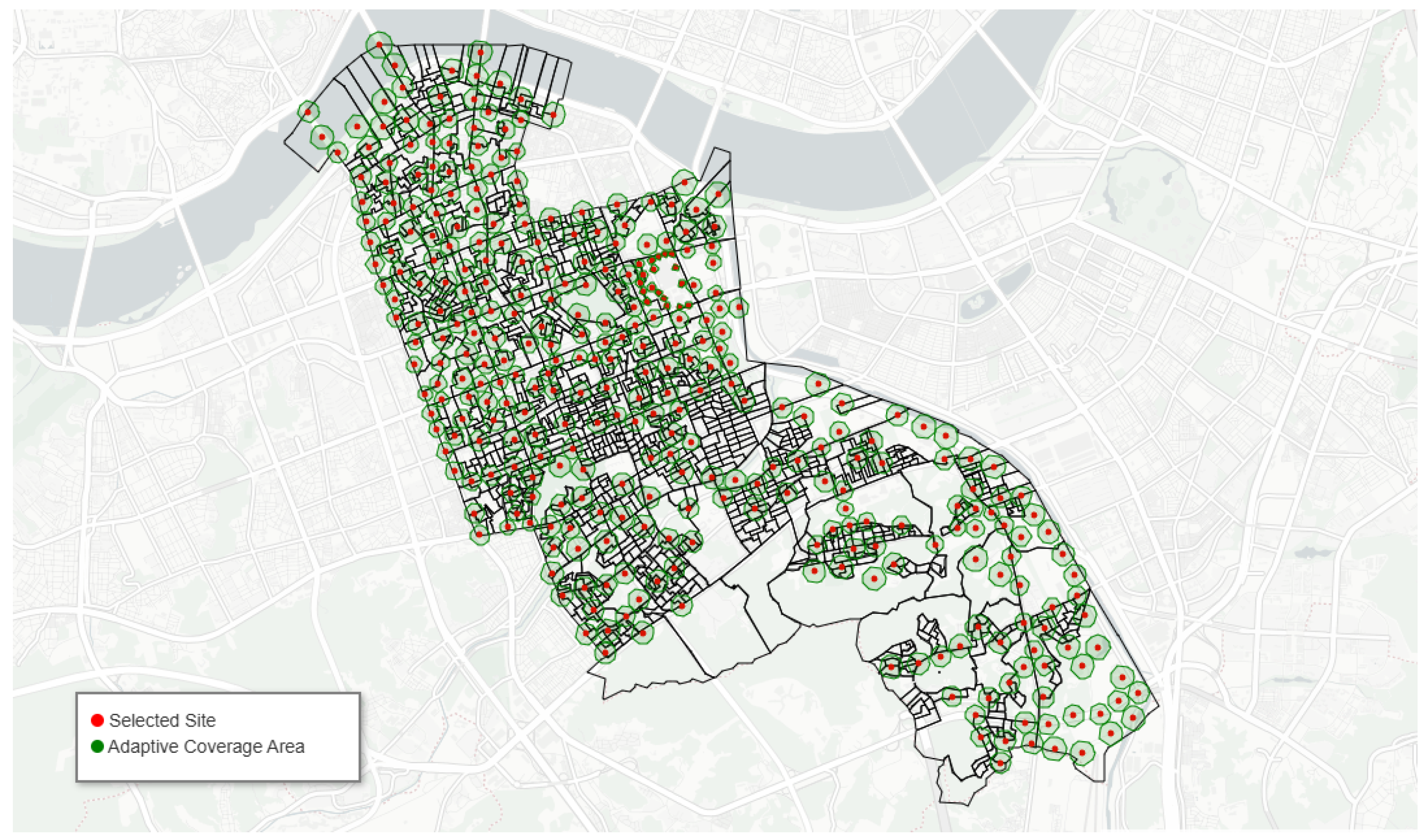As shown in Figure 3, a random sample of candidate waste bin sites illustrates the spatial spread of the full feasible set across the walkable network. Blue points depict a random subset of 1000 candidates drawn from the full set of $32,890$ network-anchored sites (black lines: pedestrian–road network; grey polygons: output-area boundaries). The sample visualizes coverage of feasible placements prior to scoring and selection.

3.2. Data Analytics: Demand Criteria and Feature Construction

Waste bin demand is driven by cumulative exposure to pedestrians and by proximity to attractors such as transit nodes or retail frontages. To support coverage modeling and validation, we also assemble a demand representation that is consistent with the framework’s notation. Let $U\subset G$ denote a set of demand nodes at which pedestrian exposure and ancillary variables are tabulated; in practice, U may consist of network vertices in $\mathcal{G}$ inside G or centroids of census micro-polygons. All exogenous point datasets (e.g., transit stops and points of interest) are cleaned, deduplicated within a tolerance in EPSG:5186, and converted to GeoDataFrame for nearest-neighbor and kernel computations. Where a dataset is temporally indexed, we aggregate to representative daily means so that demand scores represent a typical day on the planning horizon. The dense sampling of the pedestrian network at $\delta =10$ m yields $\left|J\right|=32,890$ feasible bin locations, allowing the adaptive radii $\left\{r_j\right\}$ to respond to fine-scale variation in the built environment. Distances used in all subsequent computations—spatial-exclusion checks $d(i,j)\ge r_i+r_j$ and routing costs $d_{ij}=d(j_i,j_j)$—are evaluated with the same network metric d on $\mathcal{G}$.

Table 2. Data analytics workflow for Gangnam District case.

Variable Category	Source and Preprocessing	Role in Model
Floating population	Daily counts by block; temporal mean; areal join to J and U	Criterion $C_1$: raw $V_{j,1}\to S_{j,1}$
Transit nodes	Bus stops and subway exits; nearest-neighbor on $\mathcal{G}$	Proximity criterion $C_2$: raw via kernel $\to S_{j,2}$
Waste-related POIs	Convenience stores, cafés, food trucks, parks; subtype weights $\omega$	Proximity criterion $C_3$: raw via kernel $\to S_{j,3}$
Depot $D_0$, fleet and service params	Operations center location; $(m,Q,v_{\mathrm{speed}},\tau )$	Routing inputs and constraints

summarizes the data analytics used in the Gangnam district case, which lists each variable category, how the data are sourced and preprocessed, and how they enter the model as criteria scores $S_{j,k}$ or routing inputs.

In connection with open data acquisition provided by the Seoul Open Data platform, first,

Table 3. Population and boundary datasets used for demographic analysis ($C_1$).

Dataset	Format/Unit	Description	Source
Seoul Living Population (Domestic Residents)	CSV (by census block)	Daily population counts (15–21 May 2025) Variables: DateID, TimeType, DistrictCode, CensusBlockCode, TotalPopulation Estimated using public data (resident registry, transport, business, and building DBs) combined with KT telecom big data	https://data.seoul.go.kr/dataList/OA-14979/F/1/datasetView.do (accessed on 2 July 2025) (Seoul Open Data)
Seoul Living Population (Short-term Foreign Residents)	CSV (by census block)	Estimated short-term foreign resident population by census block Method identical to domestic dataset; includes mobility-based estimation using transport and telecom data	https://data.seoul.go.kr/dataList/OA-14980/F/1/datasetView.do (accessed on 2 July 2025) (Seoul Open Data)
Seoul Living Population (Long-term Foreign Residents)	CSV (by census block)	Long-term foreign residents measured via public and telecom data integration Same variable structure as domestic dataset	https://data.seoul.go.kr/dataList/OA-14978/F/1/datasetView.do (accessed on 2 July 2025) (Seoul Open Data)
Census Block Boundary	SHP/SBN (EPSG:5186)	Geospatial boundaries of census blocks where living population is estimated Spatial unit for integrating demographic data	https://data.seoul.go.kr/dataVisual/seoul/seoulLivingPopulation.do (accessed on 2 July 2025) (Seoul Open Data)

summarizes the demographic datasets integrated into the GD-ARISE pipeline for the Gangnam district case study. The datasets include Seoul’s living-population estimates for domestic and foreign residents, and each living-population dataset represents the estimated number of people present in a specific location and time, derived by combining administrative records (resident registry, transport, business, and building databases) with KT (Korea Telecom) big data. The census-block boundary layer (EPSG:5186) provides the spatial framework for aggregating and visualizing these population estimates. Together, these layers constitute the demographic foundation for quantifying spatial patterns of pedestrian exposure and population density within the GD-ARISE framework.

Table 4. Transit-related datasets used for transit proximate disposal $C_2$.

Dataset	Format/Unit	Description	Source
Seoul Bus Stop Locations	CSV (EPSG:5186)	NodeID, StopID StopName Coordinates (X, Y) StopType	https://data.seoul.go.kr/dataList/OA-15067/S/1/datasetView.do (accessed on 2 July 2025) (Seoul Open Data)
Subway Entrance Coordinates	CSV (manual extraction)	Latitude–Longitude pairs (manual extraction) Subway entrance locations for accessibility criterion $C_2$	http://map.esran.com/ (accessed on 2 July 2025) (Seoul Open Data)

summarizes the transit-related GIS layers integrated into the GD-ARISE pipeline to represent multimodal accessibility across Gangnam District. The datasets include bus stop locations and subway entrance coordinates, each obtained from verified public sources and re-projected to a unified coordinate reference system (EPSG:5186) for geometric consistency. The bus stop layer provides detailed node attributes, such as stop IDs, names, and coordinates, while the subway entrance layer contains manually extracted latitude–longitude pairs for all access points within the study area. Together, these layers constitute the transit node component of criterion $C_2$, serving as the spatial foundation for the proximity-based accessibility analysis in subsequent stages of the GD-ARISE framework. In addition,

Table 5. POI datasets used for waste source facilities $C_3$.

Dataset	Format / Unit	Description	Source
Gangnam Food-Service Licensing (cafe_conv_stfood)	CSV (EPSG:5186)	Fields: business name, type, address, coordinates (X, Y) Filtered to cafés, convenience stores, food trucks; active only Updated: 26 May 2025	https://data.seoul.go.kr/dataList/OA-18699/S/1/datasetView.do (accessed on 2 July 2025) (Seoul Open Data)
Gangnam Urban Parks	CSV (EPSG:5186)	Fields: park name, type, latitude–longitude Subtype of $C_3$ (parks; weight $=0.10$) Updated: 1 July 2024	https://data.seoul.go.kr/dataList/OA-15004/F/1/datasetView.do (accessed on 2 July 2025) (Seoul Open Data)

details the source datasets and preprocessing for the waste-related POIs criterion $C_3$.

Now, we discretize G by sampling $\mathcal{G}$ at the spatial resolution $\delta >0$ to obtain a candidate set of feasible bin sites $J=\{j_1,\dots ,j_N\}\subset G$, and, independently, a demand lattice $U=\{u_1,\dots ,u_M\}\subset G$. The criterion collection $\mathcal{C}=\{C_1,\dots ,C_M\}$ is expressed for waste bin siting, with observable correlates of litter pressure and disposal opportunity, in a manner that matches the demand formulation. A floating population is treated as a direct, site-specific magnitude: block-level counts from the observation period are averaged to obtain a mean daily exposure and then spatially joined to both J and U. When a candidate point or demand node falls within overlapping administrative polygons, the exposure is taken as the mean of the overlapping values, which yields well-defined raw measurements $V_{j,k}$ for the population criterion and preserves mass under areal interpolation. Public transit proximity is encoded via proximity to bus stops and subway exits. After loading both datasets and projecting to EPSG:5186, we compute for each $j\in J$ the shortest path distance along $\mathcal{G}$ to the nearest stop and to the nearest exit. Local waste generation potential is represented by proximity to POIs that tend to generate street litter, such as convenience stores, cafés, food trucks, and public parks. Each POI set is harmonized into a single layer with subtype weights ${\omega }_{k,s}\ge 0$ that sum to one within the criterion.

As shown in Figure 4, population scores are highly right-skewed, indicating many low-exposure segments and a small fraction of hotspots that dominate the upper tail. Most candidates have low values, with a long tail and few very high-exposure locations created by concentrated corridors. A floating population $C_1$ is a direct site-specific magnitude derived from block-level daily counts aggregated over the observation period. Let $P_j$ denote the mean daily floating population assigned to site j via areal interpolation from its containing (or overlapping) census blocks. To place $P_j$ on a unit scale while preserving ranks, we apply the benefit of min–max normalization over all candidates,

$$S_{j,\mathrm{pop}}={\displaystyle \frac{P_j-{\min }_{i\in J}{P}_i}{{\max }_{i\in J}{P}_i-{\min }_{i\in J}{P}_i}},$$

(6)

which yields $S_{j,\mathrm{pop}}\in [0,1]$ and encodes relative pedestrian exposure.

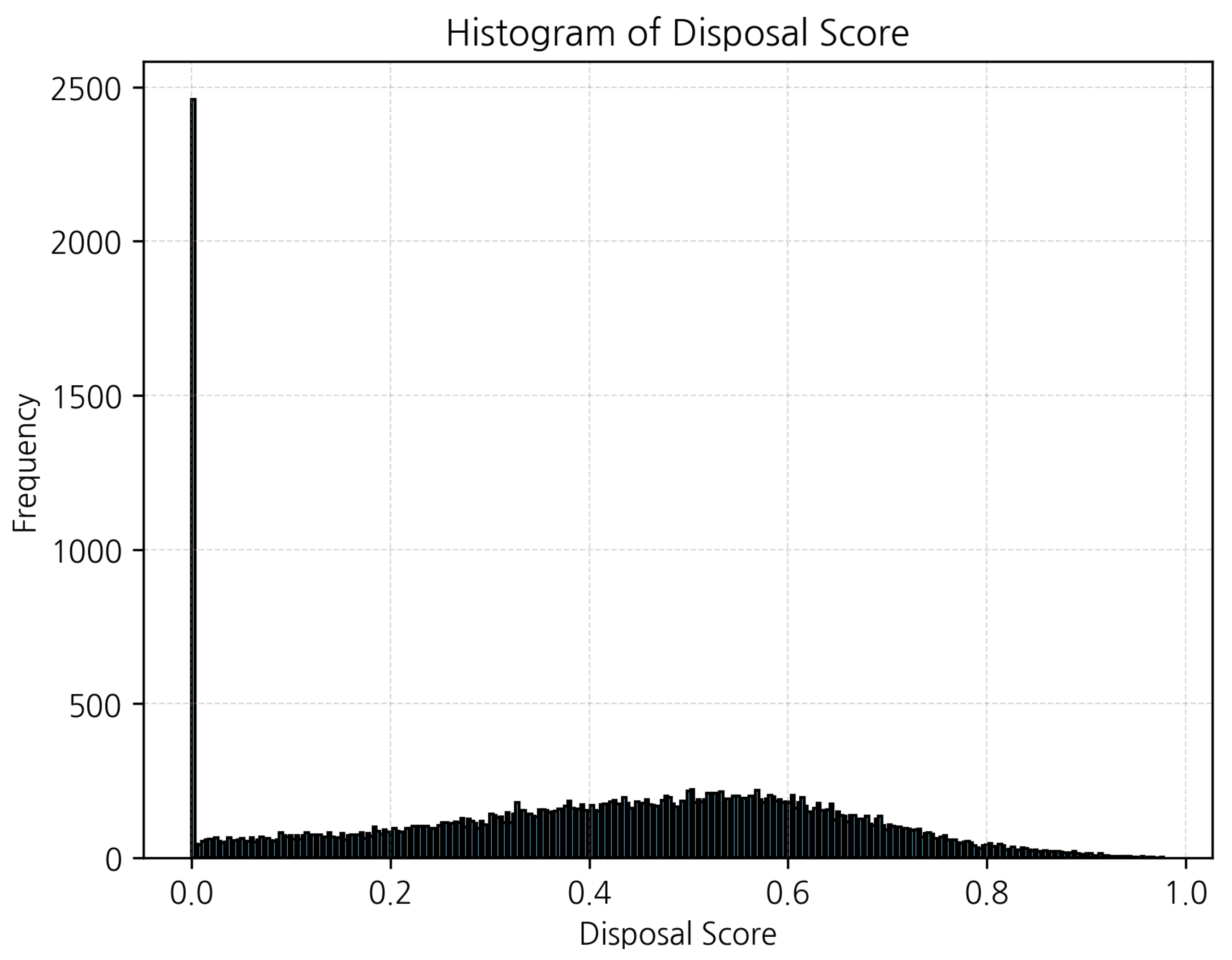
As shown in Figure 5, disposal scores are mostly moderate with a broad mode around the mid-range, plus a spike at zero for candidates far from transit. The distribution is broadly spread with a mid-range mode and a mass at zero reflecting locations beyond the 300 m influence of both bus stops and subway exits. Transit proximate disposal opportunity $C_2$ is modeled as proximity to the nearest bus stop and the nearest subway exit, recognizing that on–off flows around stations correlate with both waste generation and appropriate placement of receptacles. Let $d_{j,\mathrm{bus}}$ and $d_{j,\mathrm{sub}}$ denote the network distances from j to the nearest bus stop and the nearest subway exit, respectively. A convex combination of linear distance decay kernels with a common maximum influence range $D_{\max ,\mathrm{disp}}=300$ m produces a unit-interval score

$$\begin{array}{cc}\hfill S_{j,\mathrm{disp}}& ={\omega }_{\mathrm{bus}}\max \left\{0,1-\frac{d_{j,\mathrm{bus}}}{300}\right\}+{\omega }_{\mathrm{sub}}\max \left\{0,1-\frac{d_{j,\mathrm{sub}}}{300}\right\},\hfill \\ \hfill & \mathrm{where}{\omega }_{\mathrm{bus}}=0.75\mathrm{and}{\omega }_{\mathrm{sub}}=0.25.\hfill \end{array}$$

(7)

which reflects the stronger baseline frequency of bus stops relative to subway exits, while allowing both to contribute when they are nearby.

As shown in Figure 6, shop proximity scores exhibit two masses: a spike at zero for sites with no nearby POIs and a broad peak around 0.5–0.6 where multiple POIs lie within walking range. The spike at zero reflects POI-sparse areas; the main peak indicates neighborhoods with several POIs inside the decay radius. Waste source proximity $C_3$ aggregates the influence of POIs associated with street litter. Let $\mathcal{K}=\{\mathrm{conv},\mathrm{cafe},\mathrm{truck},\mathrm{park}\}$ index convenience stores, cafés, food trucks, and parks, and let $d_{j,k}$ denote the network distance from j to the nearest POI of subtype k. Subtype weights ${\left\{w_k\right\}}_{k\in \mathcal{K}}$ encode relative propensities for waste exposure and satisfy ${\sum }_k{w}_k=1$. Using the same 300 m influence range, we set

$$\begin{array}{cc}\hfill S_{j,\mathrm{shop}}& =\sum _{k\in \mathcal{K}}{w}_k\max \left\{0,1-\frac{d_{j,k}}{300}\right\},\hfill \\ \hfill & \mathrm{where}(w_{\mathrm{conv}},w_{\mathrm{cafe}},w_{\mathrm{truck}},w_{\mathrm{park}})=(0.35,0.35,0.20,0.10).\hfill \end{array}$$

(8)

so that co-location near multiple waste-related attractors increases the score while contributions taper linearly to zero at 300 m.

The empirical distributions of the component scores and the composite reveal substantial spatial heterogeneity across Gangnam’s pedestrian network and inform the subsequent radius mapping. The floating population score $S_{j,\mathrm{pop}}$ spans $[0,1]$ and is right-skewed, with a mean of $0.1133$, a standard deviation of $0.1380$, and a 75th percentile of $0.1339$, reflecting concentrated corridors of high exposure. The transit disposal score $S_{j,\mathrm{disp}}$ ranges over $[0,0.9780]$ and is more uniform, with a mean of $0.4170$, a standard deviation of $0.2257$, and a median of $0.4450$, consistent with the dense but heterogeneous distribution of bus stops and subway exits. The POI proximity score $S_{j,\mathrm{shop}}$ is generally small, with a maximum of $0.0987$, a mean of $0.0275$, a standard deviation of $0.0288$, and a 75th percentile of $0.0515$, indicating that only a minority of network points lie within short walks of multiple waste-generating attractors.

We specify three criteria $\mathcal{C}=\{C_1,C_2,C_3\}$ that capture complementary drivers of litter pressure and disposal opportunity: $C_1$ encodes floating population intensity, $C_2$ captures transit-proximate disposal likelihood, and $C_3$ reflects proximity to waste-generating points of interest (POIs). For each $j\in J$ and criterion $C_k$, a raw, non-negative measurement $V_{j,k}$ is constructed and mapped to a unit-interval score $S_{j,k}\in [0,1]$ via a monotone transformation $f_k$ so that larger values consistently indicate greater suitability for siting a bin at j. With the criterion scores in hand, the relative importance of population exposure, transit opportunity, and POI proximity is computed via the AHP. To clarify the AHP elicitation, we provide the pairwise comparison scale and the exact questions used for expert judgments. AHP pairwise comparison scale used for expert elicitation.

Scale	Definition
1	Equally important
3	Slightly more important
5	Moderately more important
7	Strongly more important
9	Absolutely more important
2, 4, 6, 8	Intermediate between adjacent judgments
Reciprocals	Inverse when criterion B is preferred over A

Pairwise comparison questions used for expert elicitation were as follows:

Q1.

How much more important is distance to waste-source facilities (cafés, convenience stores) than floating population? Answer: $1/5$ (population is moderately more important than shop).

Q2.

How much more important is disposal likelihood near transit stops (bus, subway) than floating population? Answer: $1/5$ (population is moderately more important than disposal).

Q3.

How much more important is disposal likelihood near transit stops than waste-source proximity? Answer: 3 (disposal is slightly more important than shop).

Two municipal officers completed the elicitation independently. Their responses were aggregated into the following pairwise comparison matrix:

$$A=\left[\begin{array}{ccc}1& 5& 5\\ {\displaystyle \frac{1}{5}}& 1& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{5}}& 3& 1\end{array}\right].$$

This matrix indicates that population was judged substantially more important than both disposal likelihood and shop proximity, and that disposal likelihood was moderately more important than shop proximity. Using the normalized average method on A, we obtain the AHP weights,

$${\alpha }_{\mathrm{pop}}=0.6864,{\alpha }_{\mathrm{disp}}=0.2114,{\alpha }_{\mathrm{shop}}=0.1022,$$

reported to four decimal places. The composite suitability at site j is the convex combination given by

$$\begin{array}{cc}\hfill S_j^{*}& ={\alpha }_{\mathrm{pop}}{S}_{j,\mathrm{pop}}+{\alpha }_{\mathrm{disp}}{S}_{j,\mathrm{disp}}+{\alpha }_{\mathrm{shop}}{S}_{j,\mathrm{shop}}\hfill \\ \hfill & =0.6864S_{j,\mathrm{pop}}+0.2114S_{j,\mathrm{disp}}+0.1022S_{j,\mathrm{shop}}\hfill \end{array}$$

(9)

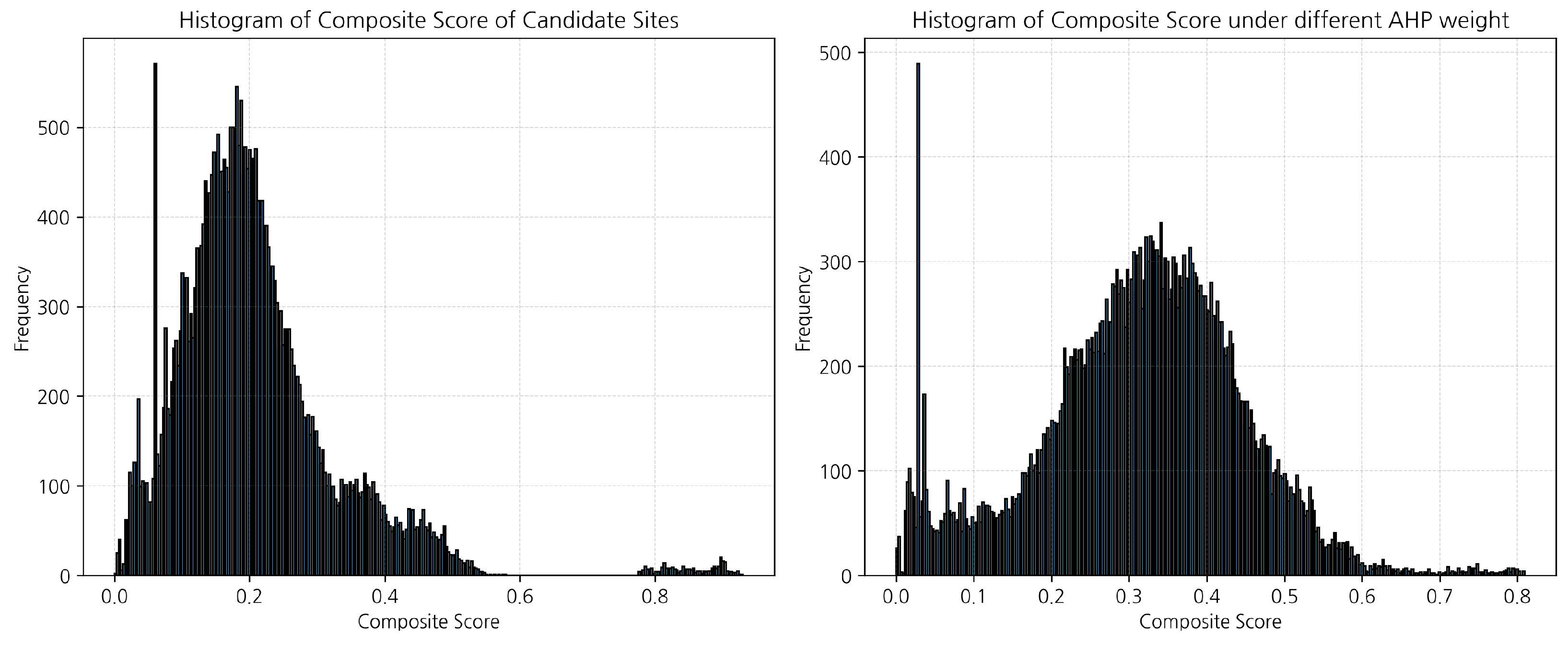
which, by construction, lies in $[0,1]$ and is strictly increasing in each constituent score. This $S_j^{*}$ serves as the demand score output used downstream to assign adaptive radii and to prioritize candidates during siting. Aggregation by the AHP weights produces a composite $S_j^{*}$ that remains right-skewed, with a mean of $0.2083$, a standard deviation of $0.1199$, a median of $0.1883$, a maximum of $0.9301$, and a 75th percentile of $0.2551$. Under the adaptive radius map $r_j=R_{\max }-(R_{\max }-R_{\min })S_j^{*}$, these statistics translate into smaller service radii in the highest-scoring corridors and larger radii in peripheral or residential areas, ensuring fine spatial granularity where litter pressure is greatest while preserving baseline access elsewhere. All distances entering the kernels are evaluated with the same network metric d as used in the siting and routing stages, maintaining geometric consistency across the full GD-ARISE pipeline.

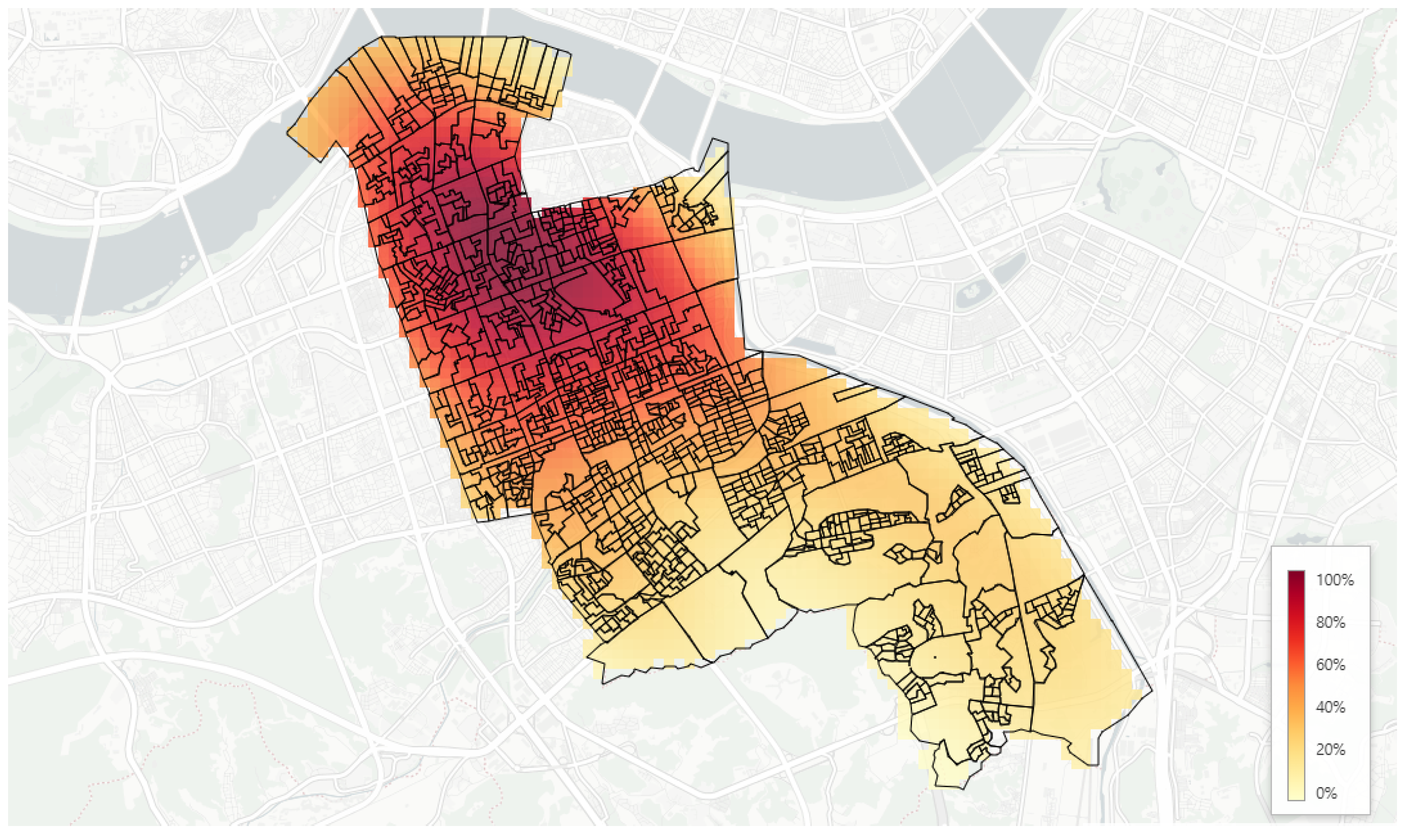
Figure 7 shows a heatmap for the composite demand surface that is highly clustered with the highest percentiles concentrated along the northern–central corridors and decreasing toward the periphery. Colors show percentile ranks from low (light) to high (dark); road segments and administrative polygons are overlaid for reference. The surface reveals pronounced high-demand bands in the northern–central corridors, tapering toward the southeast and peripheral areas.

3.3. SCASS

This stage specializes the SCASS formulation to the Gangnam candidate set $J=\{j_1,\dots ,j_N\}$ with $N=32,890$ points sampled every $\delta =10$ m along the pedestrian–road network $\mathcal{G}$, using the same network-based distance metric d as in the scoring stage. The input at each site $j\in J$ is the composite suitability $S_j^{*}\in [0,1]$ obtained from the AHP-based demand assessment. Two preprocessing choices are made to align data coverage with plausible service contexts while preserving the mathematical structure of SCASS. First, a proximity sanity check is applied to screen out isolated candidates: for each j we test whether there exists at least one demand facility (bus stop, subway exit, or waste-related POI) within 1 km under d. In the Gangnam dataset, every candidate satisfies this condition, so the working set remains J. Second, each candidate is assigned an adaptive coverage radius $r_j$ via the affine map

$$r_j=R_{\max }-(R_{\max }-R_{\min })S_j^{*},$$

(10)

so that higher suitability implies a smaller catchment, consistent with dense placement in demand hotspots, while lower suitability enlarges catchments to preserve baseline access elsewhere. Applied to Gangnam with $(R_{\min },R_{\max })=(30\mathrm{m},150\mathrm{m})$ and $P_{\mathrm{target}}=500$, the greedy procedure selects $|J_{\mathrm{sel}}|=347$ sites before all remaining candidates conflict with at least one already-selected site; this binding of nonoverlap rather than the numerical target determines the achieved count. The realized $J_{\mathrm{sel}}$ concentrates in high-scoring corridors around major commercial and transit axes, while respecting minimum separations implied by the adaptive radii and thereby avoiding redundant service areas.

As shown in Figure 8, the final set of selected sites for this analysis is displayed. Network edges are shown in black; selections were obtained by the SCASS greedy nonoverlap procedure on the pedestrian–road network.

Table 6. Parameters and outcomes for adaptive site selection.

Quantity	Value	Definition/Role
Candidate set size N	$32,890$	Points sampled every $\delta =10$ m along $\mathcal{G}$ within G
Proximity sanity radius	1000 m	Filter to exclude candidates with no nearby facilities under d
Adaptive radius bounds	$R_{\min }=30$ m, $R_{\max }=150$ m	Affine map $r_j=R_{\max }-(R_{\max }-R_{\min })S_j^{*}$
Target portfolio $P_{\mathrm{target}}$	500	Desired number of nonoverlapping bins
Selected sites $|J_{\mathrm{sel}}|$	347	Maximal nonoverlapping set obtained by greedy scan under d
Distance metric d	Network shortest path	Used for radii, nonoverlap checks, coverage, and routing

summarizes key parameters and resulting outcomes for the SCASS stage. It lists the candidate set size and sampling, the proximity filter, the adaptive radius bounds and mapping, the target portfolio size, the number of selected sites, and the shared network distance metric.

3.4. Collection Route Optimization: Samsung 1–dong

To instantiate routing optimization on a concrete sub-area, we focus on Samsung 1–dong within Gangnam and route a single collection vehicle to visit the $K=37$ waste–bin sites that were previously selected there. The depot is fixed at $D_0$ = (37.50867° N, 127.086466° E), and we retain the notation of the main framework by labeling the selected bins $\{j_1,\dots ,j_{37}\}$ and defining the node set $V=\{0,1,\dots ,37\}$ with $j_0\equiv D_0$. Consistent with the end-to-end pipeline, inter-node travel costs are evaluated using the same distance metric d induced by the pedestrian–road network $\mathcal{G}$ restricted to the Samsung 1–dong extent. Because all bins must be serviced exactly once and, for this small cluster, a single vehicle is sufficient, we solve the capacitated vehicle routing model in the special case $m=1$ and $Q\ge {\sum }_{i=1}^{37}{q}_i$, which reduces to a traveling salesman problem on the node set V. A route is represented by a closed walk $({\pi }_0,{\pi }_1,\dots ,{\pi }_{37},{\pi }_{38})$ with ${\pi }_0={\pi }_{38}=0$ and $\{{\pi }_1,\dots ,{\pi }_{37}\}=\{1,\dots ,37\}$. Its network cost is

$$C\left(\pi \right)=\sum _{t=0}^{37}{d}_{{\pi }_t,{\pi }_{t+1}},$$

(11)

and the optimization objective is to find $\pi$ that minimizes $C\left(\pi \right)$.

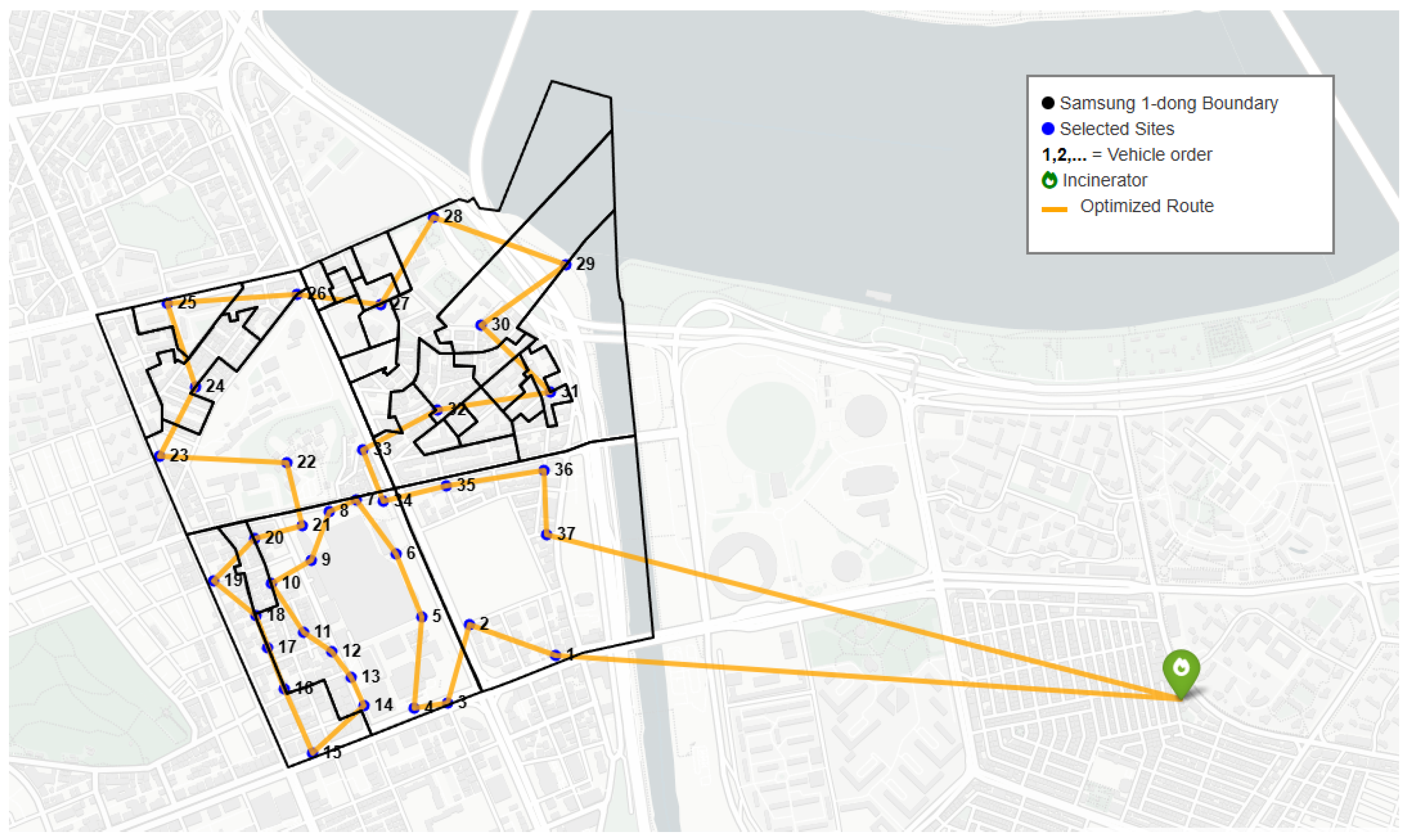
As shown in Figure 9, simulated annealing produces a single depot-to-depot tour that visits all selected Samsung 1–dong sites in sequence on the same network used for siting. The green marker denotes the depot; blue points mark the 37 selected sites labeled in visit order; orange lines depict the annealed tour; the black polygon outlines the Samsung 1–dong boundary. The route is the outcome of simulated annealing, evaluated using the network metric consistent with location selection. The resulting annealed tour visits each of the 37 Samsung 1–dong bins exactly once and returns to the depot. Because the encoding, acceptance logic, and termination criteria conform exactly to the routing specification, this Samsung 1–dong case demonstrates that the GD-ARISE pipeline maintains geometric consistency from demand scoring through siting to routing, and that the final routing layer can be solved to high quality with modest computation even when distances respect real network impedances rather than idealized straight lines.

For the computation of the simulated annealing (SA) algorithm, the parameters of the number of nodes in the route (n), the number of iterations per temperature stage (M), the initial temperature ($T_0$), the stopping temperature ($T_{\mathrm{stop}}$), and the cooling rate ($\alpha$, $0<\alpha <1$) are considered, so that the total number of temperature stages ($L_a$) and the time complexity ($L_b$) are respectively computed as $L_a=⌊{\displaystyle \frac{ln(T_{\mathrm{stop}}/T_0)}{ln\left(\alpha \right)}}⌋$ and $L_b=O\left(L_a·(M·n+n^2)\right)$. For the single vehicle case, the parameters were set to $M=1000$, $n=39$, $T_0=1000$, $T_{\mathrm{stop}}={10}^{-8}$, and $\alpha =0.995$, yielding $L_a=5054$ and $L_b=\mathrm{204,793,134}$. The optimized SA route resulted in a total travel distance of approximately $11.43\mathrm{km}$, with a mean leg distance of about $301\mathrm{m}$. The self-intersection count was none, and the tortuosity was $2.44$ times the straight round-trip length from the depot. 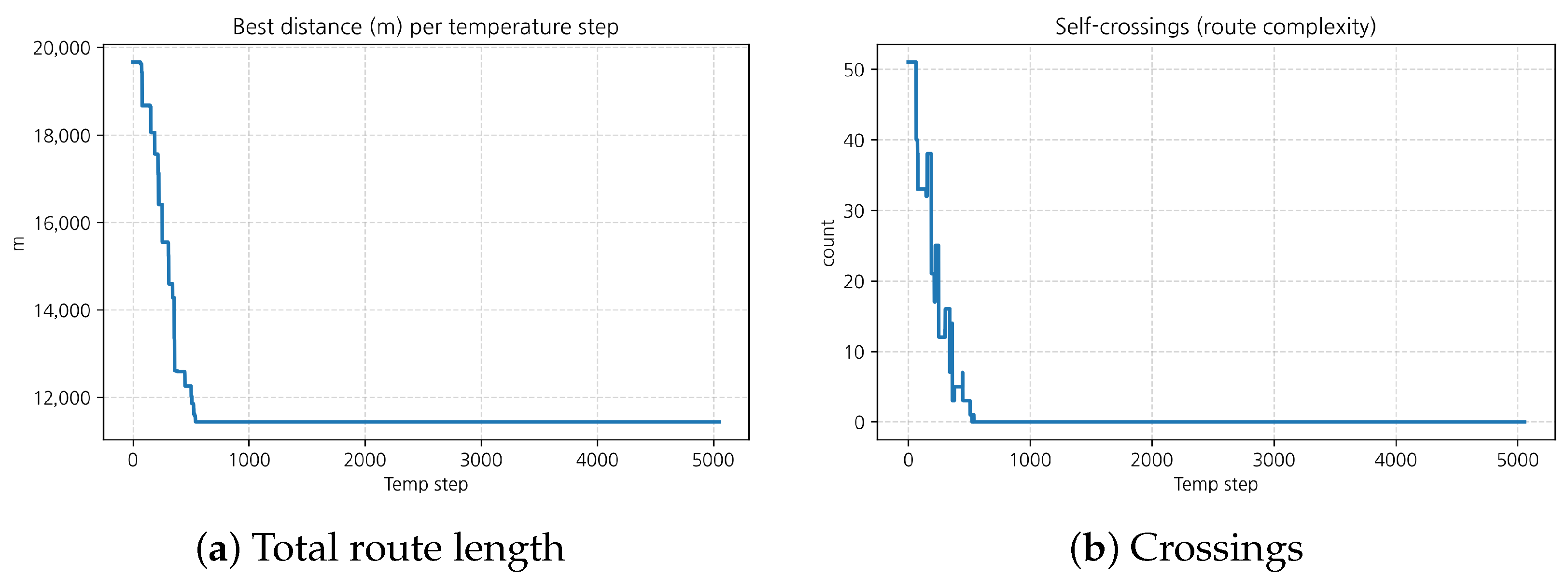Figure 10 shows the total route length decreased sharply before about 1000 steps, from approximately $19,500\mathrm{m}$ to $11,430\mathrm{m}$, and then stabilized.

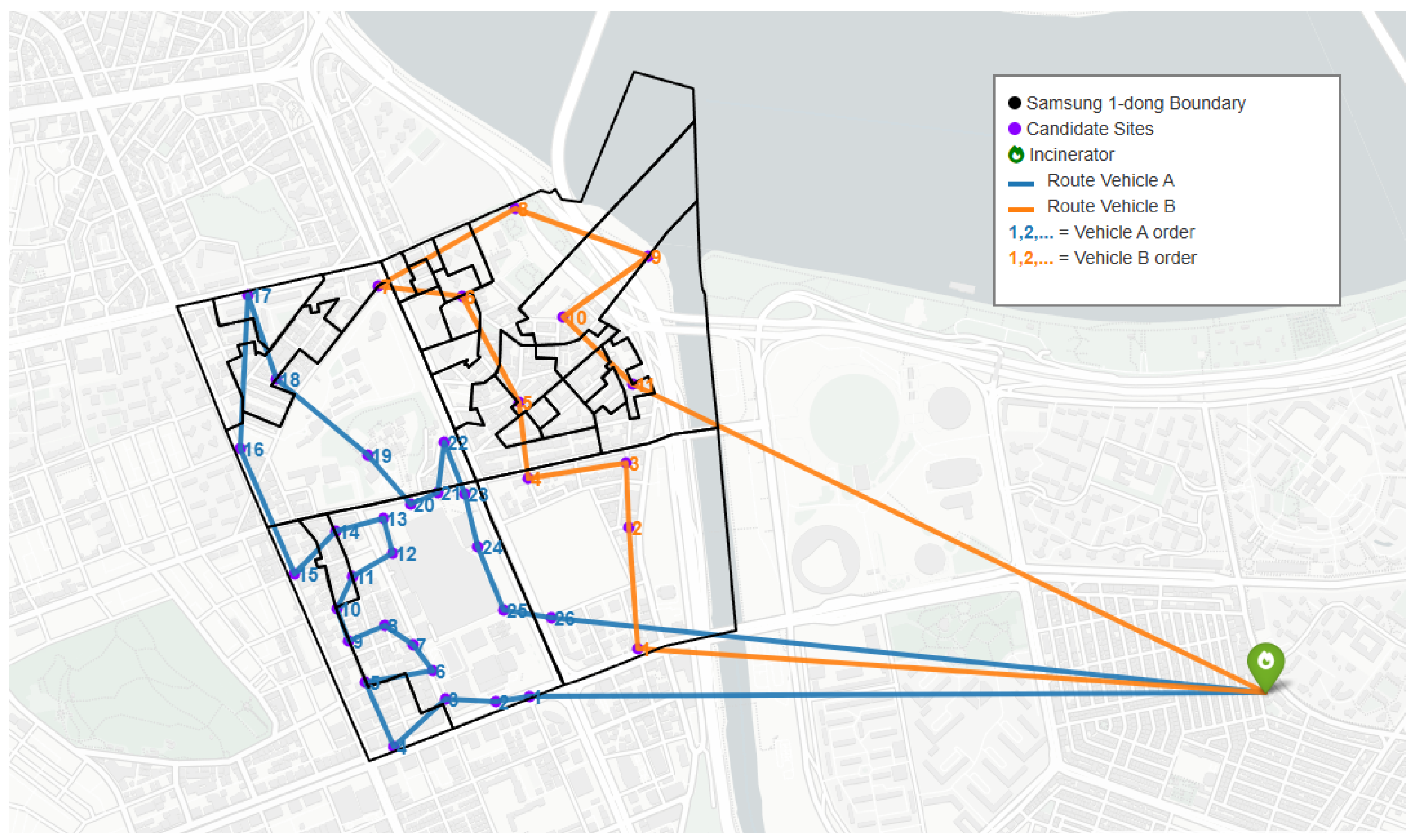
For the two-vehicle case, instead of one long tour (TSP), the route can first be divided into two subroutes, each optimized independently by SA. The sites were partitioned via the K-means clustering method to minimize overlap between vehicle coverages and to balance total travel distances, among many other alternative clustering methods. As shown in Figure 11, K-means clustering partitioned the candidate sites between the two vehicles, and inspection of the routes confirms that the two vehicles divided the four census blocks in Samsung 1–dong, with each vehicle traversing two blocks. This process results in two single depot-to-depot tours assigned to the two vehicles, each visiting all trash bins in Samsung 1–dong in sequence, as in the single vehicle case. The green marker denotes the depot; purple points mark the 37 selected sites; the blue lines depict the annealed tour of the 26 selected sites visited by Vehicle A, labeled in visit order; the orange lines depict the annealed tour of the 11 selected sites visited by Vehicle B, labeled in visit order; the black polygon outlines the Samsung 1–dong boundary.

After clustering, Vehicle A was assigned $n_A=28$ nodes and Vehicle B was assigned $n_B=13$ nodes, excluding the depot. All other SA parameters were kept identical to the single-vehicle case, except for n. The estimated number of operations was $\mathrm{145,474,336}$ for Vehicle A, and $\mathrm{66,556,126}$ for Vehicle B. When the two vehicles divided the candidate sites for collection, the total travel distance of both vehicles combined was approximately $15.81\mathrm{km}$, which is longer than the single-vehicle distance of about $11.43\mathrm{km}$. However, the individual travel burdens were reduced, with Vehicle A and Vehicle B traveling approximately $8.77\mathrm{km}$ and $7.04\mathrm{km}$, respectively. Each vehicle’s route had a mean leg distance of approximately $324.8\mathrm{m}$ and $587.0\mathrm{m}$, tortuosity values of $1.83$ and $1.84$, and a self-intersection count of zero for both.

Figure 12 shows the total route lengths of both vehicles decreased rapidly during the early temperature steps, with Vehicle A dropping from approximately $14,000\mathrm{m}$ to $8700\mathrm{m}$ and Vehicle B from about $7600\mathrm{m}$ to $7040\mathrm{m}$ within the first 1000 steps, after which both stabilized. The number of crossings followed a similar trend, falling from roughly 30 and 0 at the beginning to nearly zero within 1000 steps for Vehicle A and Vehicle B, respectively.

3.5. Sensitivity Analysis

We analyze the impact of parameter settings on GD-ARISE’s results. Two sensitivity experiments have been conducted by focusing on (i) the AHP weighting in the multi-criteria scoring stage and (ii) the adaptive coverage parameters in the SCASS site-selection stage. These experiments give ideas about how variations in subjective or geometric settings propagate through the pipeline and influence the resulting suitability distribution and selected facility portfolio.

3.5.1. AHP Sensitivity

To gauge the effect of AHP weighting, we repeated the analysis with near-uniform weights across the three criteria. Under uniform weights, the composite suitability distribution broadened and shifted upward (Figure 13), implying that more candidates attained moderate-to-high suitability. The feasible nonoverlapping selection also expanded and reconfigured, with changes concentrated in mid-range corridors while core hotspots remained stable (Figure 14). Overall, equal weighting increases admissible placements and shifts marginal sites rather than overturning the highest-demand areas.

3.5.2. SCASS Sensitivity

To assess sensitivity to spatial parameters in SCASS, we increased the adaptive-radius bounds from $(R_{\min },R_{\max })=(30\mathrm{m},150\mathrm{m})$ to $(100\mathrm{m},200\mathrm{m})$. Larger radii produced fewer but broader catchments: the feasible nonoverlapping set shrank (from 347 to 180 sites) while coverage areas grew across the entire distribution (range, mean, and quartiles all increased). Spatially, intensified exclusions reduced site density and shifted feasible locations, with removals and additions concentrated where spacing became binding (Figure 15). Overall, expanding $(R_{\min },R_{\max })$ trades off count for reach, yielding sparser deployments with larger service footprints.

3.6. Managerial Implications

The Gangnam application converts analytics into direct choices about how many bins to deploy, where to place them, and how to service them under real network constraints. The realized portfolio $J_{\mathrm{sel}}$ provides a defensible deployment count given nonoverlap and adaptive radii; managers can tune $P_{\mathrm{target}}$ and $(R_{\min },R_{\max })$ to meet coverage or budget targets. Adaptive radii yield a clear siting rule—smaller in high-pressure corridors, larger in quieter areas—so spacing reflects actual walkability rather than Euclidean distance, and nearby nonconflicting alternatives can be identified when frontage or regulations prevent a proposed point.

Two indicators support oversight: the share of demand nodes U covered by ${\bigcup }_{j\in J_{\mathrm{sel}}}{\mathbb{D}}_j$, and the distribution of separations relative to $r_i+r_j$, revealing where spacing is tight or slack. The routing layer turns network distance into service hours with average speed and per-stop time, enabling staffing and shift design and making comparisons to incumbent routes straightforward. Sensitivity to AHP weights highlights “swing” sites and shows whether small preference shifts change coverage or route time; robust outcomes ease stakeholder agreement, while sensitive zones can be prioritized for pilots or field checks. Because all stages share one metric and dataset, the pipeline can be re-run seasonally as demand or networks change, with re-routing for minor updates and re-siting reserved for larger deviations. The same geometry-consistent workflow transfers to curb-level assets, such as micro-mobility docks or hydration stations, by swapping criteria and data sources while retaining the sensitivity and monitoring protocol.

4. Conclusions

This paper framed public waste bin placement and servicing as a GIS-grounded operations research problem and developed a GD-ARISE data analytic pipeline that unifies multi-criteria demand assessment, spatially constrained site selection, and operational routing on a shared network metric. The Gangnam district case demonstrated that, with readily available administrative layers, pedestrian network data, floating population estimates, transit nodes, and points of interest, the pipeline can sample the walkable network at fine resolution, construct composite suitability scores, translate them into adaptive service radii, select a maximal nonoverlapping portfolio of facility sites, and generate depot-to-depot routes that are feasible on the actual network.

Methodologically, four elements define our contribution. First, GIS integration unifies all spatial layers on one pedestrian–road network and one distance metric. Second, demand data analytics converts heterogeneous inputs into transparent multi-criteria scores. Third, site selection is cast as coverage with nonoverlap on the same network. A fast greedy procedure enforces spacing with a degree-based performance guarantee and scales on GIS graphs. Fourth, routing closes the loop on the identical metric used upstream. Together, these steps form a reproducible, end-to-end pipeline for location-and-routing that is defensible, scalable, and operationally relevant for municipal planning. The Gangnam application highlights several substantive findings. Composite demand is highly skewed and spatially clustered along commercial corridors and transit interchanges; adaptive radii concentrate bins where pressure is greatest while preserving access in quieter areas; nonoverlap constraints prevent redundant service footprints and enforce minimum spacing that respects sidewalk conditions; and simulated annealing delivers shorter, operationally coherent tours once distances reflect real network impedances. These outcomes suggest that a GIS-integrated operations research approach can simultaneously improve perceived cleanliness, reduce reactive cleanup, and control service effort by aligning siting and routing with observed urban activity. While our case study centers on waste bins, the framework generalizes to other street-level amenities—micro-mobility docks, kiosks, sensors, hydration stations—where demand is heterogeneous, space is scarce, and operations matter.

The work also has limitations that point to avenues for extension. Criteria weights were elicited via AHP and calibrated to available data; while consistency checks were enforced, robustness to alternative weight sets and to additional criteria (e.g., complaints, street-furniture density, event schedules) merits further study. The adaptive radius mapping is intentionally simple and interpretable; in settings with strong regulatory or equity requirements, radius rules could be learned from outcomes, made time-dependent, or augmented with minimum-access guarantees. Finally, SCASS employs a greedy selection to ensure transparency and scalability, but we did not benchmark its potential suboptimality against exact or metaheuristic methods; future work should quantify optimality gaps (e.g., via MILP on subregions or lightweight local improvements) to bound performance under the stated constraints.