Abstract
In today’s volatile supply chain environment, organizations require flexible and collaborative procurement strategies. Swap contracts, originally developed as financial instruments, have recently been adopted to address inventory imbalances—such as the 2021 COVID-19 vaccine swap between South Korea and Israel. Despite its increasing adoption in the real world, theoretical studies on swap-based procurement remain limited. This study proposes an integrated model that combines buyer-to-buyer swap agreements with long-term wholesale contracts under demand uncertainty. The model quantifies the expected swap quantity between parties and embeds it into the profit function to derive optimal order quantities. Numerical experiments are conducted to compare the performance of the proposed strategy with that of a baseline wholesale contract. Sensitivity analyses are performed on key parameters, including demand asymmetry and swap prices. The numerical analysis indicates that the swap-integrated procurement strategy consistently outperforms procurement based on long-term wholesale contracts. Moreover, the results reveal that under the swap-integrated strategy, the optimal order quantity must be adjusted—either increased or decreased—depending on the demand scale of the counterpart and the specified swap price, deviating from the optimal quantity under traditional long-term contracts. These findings highlight the potential of swap-integrated procurement strategies as practical coordination mechanisms across both private and public sectors, offering strategic value in contexts such as vaccine distribution, fresh produce, and other critical products.
Keywords:
procurement strategy; swap contract; demand uncertainty; inventory coordination; supply chain risk management MSC:
90B06
1. Introduction
Global supply chains have been increasingly exposed to uncertainty due to external shocks such as the COVID-19 pandemic, geopolitical conflicts, and rapid demand fluctuations. In this context, procurement has emerged as a critical challenge for maintaining supply chain continuity and resilience. Ineffective procurement not only reduces operational efficiency and customer service levels but also undermines trust in supply reliability and overall supply chain resilience [1]. To mitigate these risks, the supply chain management (SCM) literature has proposed various contract-based procurement strategies. Notable examples include buyback contracts [2], revenue-sharing contracts [3], and option contracts [4]. However, these strategies primarily focus on vertical coordination between suppliers and retailers.
This paper introduces a swap-integrated procurement model that facilitates lateral cooperation between buyers. A swap is a financial derivative contract in which two parties agree to exchange streams of cash flow over a specified period, typically to manage interest rate, currency, or commodity price risks. Common types include interest rate swaps (exchanging fixed and floating payments) and currency swaps (exchanging payments in different currencies). Swaps are widely used in financial engineering as a tool for hedging against market volatility and aligning financial exposures with risk preferences. For example, during the 2008 Global Financial Crisis, South Korea entered into a USD 30 billion currency swap agreement with Japan to stabilize its financial markets by supplying short-term liquidity in foreign currencies. Under this agreement, Japan provided Japanese yen to South Korea in exchange for Korean won, with the option to swap the yen back into won at a later date. This swap agreement played a vital role in helping the two economies weather the financial storm during the 2008 crisis [5].
Recently, swap mechanisms have been adapted for use in supply chain procurement strategies to mitigate the risks associated with demand volatility. Unlike financial swaps, which are based on predefined cash flow exchanges over time, supply chain swaps refer to the post-demand reallocation of physical goods between buyers. In this context, a swap refers to an arrangement where buyers exchange surplus and shortage quantities of goods after demand uncertainty is realized. For instance, in 2021, Australia and Singapore executed a vaccine swap agreement: Australia received 500,000 near-expiry doses from Singapore to accelerate its domestic vaccination program, with the promise to return an equal quantity at a later date [6]. Similarly, India implemented an LNG swap tender in 2025 to exchange cargoes from the U.S. for future deliveries to meet seasonal demand fluctuations, thereby enhancing supply flexibility and reliability [7].
These examples highlight the practical value of swap contracts as flexible and collaborative mechanisms for resolving short-term supply–demand mismatches. However, despite their increasing adoption in supply chain practice, theoretical research on swap contracts remains at an early stage. In addition, most existing studies on swap contracts have primarily focused on logistics optimization from the supplier’s perspective—such as minimizing transportation distances, reducing logistics costs, and shortening lead times—by facilitating resource exchanges between inventory hubs prior to demand realization. While these approaches enhance operational efficiency, the application of swap strategies in broader supply chain contexts, particularly from the buyer’s perspective, has received limited attention [8]. In particular, there is a significant gap in theoretical and quantitative research on how buyers should optimally determine order quantities and evaluate procurement performance when swap-based sourcing options are available. This highlights the need for rigorous analytical investigation into the role and effectiveness of swaps as a collaborative procurement strategy under post-demand realization uncertainty.
This study proposes a swap-integrated procurement model that combines swap contracts with wholesale contracts and analyzes its performance in a single-period environment with uncertain demand. The analysis focuses on a setting in which two buyers, each having secured a long-term commitment contract—either with the same supplier or with different suppliers—determine their order quantities, and subsequently adjust surplus and shortage inventories through a swap contract after demand is realized. To the best of our knowledge, this study is the first to explore analytical models for the swap-integrated procurement strategy in supply chains, offering a novel contribution to the literature in three key aspects:
- (1)
- Formulating the expected swap inflows and outflows under the swap-integrated strategy and embedding them into the expected profit function to derive optimal order quantities;
- (2)
- Comparing the performance of the proposed strategy with a baseline wholesale contract to assess the structural benefits of swap integration;
- (3)
- Conducting sensitivity analyses on key parameters—such as demand asymmetry and swap prices—to identify the conditions under which the proposed strategy yields its greatest performance benefits.
This paper is organized as follows: Section 2 reviews the related literature on swap-based procurement contracts and identifies research gaps. Section 3 presents the supply chain structure and mathematical model for the swap-integrated procurement strategy. Section 4 presents the numerical results, including sensitivity analyses. Finally, Section 5 concludes with implications, limitations, and future research directions.
2. Literature Review
Demand uncertainty serves as a major procurement risk across the entire supply chain, and the information asymmetry between the procurement stage and the demand realization stage exposes buyers to two opposing risks: excess inventory and stockouts. Various contract-based procurement strategies have been proposed in the SCM literature to mitigate risks associated with highly volatile demand. Common examples include buyback contracts [2], revenue-sharing contracts [3], and option contracts [4], most of which are characterized as forms of vertical cooperation between suppliers and retailers.
Our literature study focuses on swap contracts, which can be characterized as lateral cooperation between buyers. Swap practice refers to the mutual exchange of goods or inventory between firms, typically under pre-agreed terms, to mitigate supply–demand mismatches. Unlike traditional procurement, it emphasizes flexibility and collaboration, allowing firms to reduce holding costs or address shortages without relying solely on upstream suppliers. Swap practices were initially adopted in the petroleum and energy industries, where they offered significant advantages due to the commodity-based nature of products [9]. In these sectors, customers typically prioritize product specifications and on-time delivery over the origin of the goods. By collaborating, they can reduce transportation and inventory costs while enhancing customer service. These alliances are particularly effective in improving overall supply chain efficiency. The transportation cost savings achieved through such cooperation are shared among the participating firms. Bidyarthi and Deshmukh [10] highlight the role of swap mechanisms as a strategic inventory handling tool in downstream petroleum supply chains. They illustrate how swap practices can be applied as an alternative to conventional inventory management in addressing regional supply–demand mismatches. Al-Husain and Khorramshahgol [11] conduct a comprehensive analysis of the determinants of swap problems in the petroleum industry. The study explores contract terms, inventory capacity, and operational flexibility as key drivers of effective swap execution, emphasizing the importance of operational structure in swap-based systems. Farahani and Rahmani [12] analyze the impact of swap strategies on the financial performance of supply chains in large-scale distribution networks, such as those found in the petrochemical industry. They develop a mixed integer linear programming model to capture the complexities of production and transportation decisions within an oil supply chain and design scenarios in which long-distance transportation is replaced with swaps between nearby production sites. Their experimental results show that implementing swap strategies can simultaneously reduce transportation costs and lead time risks by shortening delivery distances, thereby significantly improving the supply chain’s overall net present value.
Dizbay and Ozturkoglu [13] explore a product swapping mechanism among suppliers operating in a balanced supply network. The study investigates how transfer sales and swap agreements can help suppliers reallocate inventory to meet customer demand more effectively. By modeling supplier interactions, the research shows that swap-based coordination improves service levels and reduces total costs. Wang et al. [14] investigate the use of swap contracts in bunker fuel procurement for liner shipping companies. They develop a short-term procurement model that integrates fuel price uncertainty and the strategic use of swaps to hedge against price volatility. The study demonstrates that incorporating swap contracts can reduce procurement costs and financial risk under fluctuating market conditions. Park [15] explores the strategic inventory swapping between competing firms facing uncertain demand. The study models a two-stage game in which firms first determine inventory levels and then decide whether to swap inventory after demand is realized. The analysis shows that swap agreements can improve supply chain efficiency and profitability for both parties, even in competitive settings.
Kemper et al. [16] investigate the pricing of swaps and options in electricity markets by focusing on the market price of risk across different delivery periods. The study develops a risk-adjusted valuation model that captures the stochastic behavior of electricity prices and accounts for delivery-specific risk premia. Their findings show that incorporating delivery period-specific risks significantly improves the pricing accuracy of both swaps and options in volatile energy markets. Zhang and Thomspon [17] examine how product swaps can be optimized within an urban retail network under demand uncertainty. They propose a stochastic optimization model to determine when and where product swaps should occur between stores to minimize overall logistics costs and improve service levels. The study demonstrates that incorporating swap decisions into network planning can significantly enhance operational efficiency, especially under highly volatile demand. The existing literature has primarily focused on swap mechanisms from a logistics-oriented perspective, such as optimizing transportation or reallocating resources between production sites, while mathematical analyses of contract design and profit structures based on inventory adjustment between buyers are scarce. Accordingly, there is a clear need for a structural analysis of how swap-based strategies can mitigate procurement risks, improve performance, and inform the design of optimal ordering policies.
Swap-based procurement shares conceptual similarities with lateral transshipment, a widely used inventory management strategy designed to address stock imbalances across decentralized locations. Lateral transshipment aims to alleviate inventory discrepancies at local stores by enabling the transfer of goods between retail outlets, particularly in urban areas, to fulfill customer demand in regions facing stockouts. This approach seeks to reduce overall inventory costs and maintain desired service levels by reallocating surplus inventory from locations with excess stock to those experiencing shortages, typically within the same organization or integrated supply network. Diks and de Kok [18] find that such transshipments can reduce losses associated with excess inventory and stockouts, while Ekren and Arslan [8] emphasize that pre-planned transshipment policies are particularly effective in environments with high demand volatility. Paterson et al. [19] and Kumari et al. [20] provide a comprehensive review of lateral transshipments in inventory systems.
Existing studies on lateral transshipment generally focus on the internal transfer of resources or goods within the same organization or integrated system; they do not presuppose external cooperation or the exchange of resources between different stakeholders based on contractual agreements. In contrast, the swap-based procurement strategy proposed in this study is structured to enable the exchange of surplus and shortage inventories between different buyers based on contractual agreements after demand realization. This suggests that the swap strategy, as a post-realization collaboration mechanism, possesses structural characteristics that distinguish it from lateral transshipment and offers the potential to enhance supply chain flexibility through autonomous agreements among buyers.
This study addresses gaps in the existing literature by proposing a swap-integrated procurement strategy aimed at mitigating supply–demand mismatches that emerge after demand realization. The proposed strategy attempts to achieve both procurement flexibility and risk diversification—outcomes that are difficult to secure through a single contract structure—by facilitating the exchange of surplus and shortage inventories among buyers through contractual agreements. This approach not only enhances the practical efficiency of supply chain operations but also serves as a new collaborative procurement model for responding to demand uncertainty. Table 1 summarizes the key distinctions between this study and prior research.

Table 1.
Comparison between this study and existing studies.
3. Model Description
This study investigates a collaborative strategy between two buyers operating in a supply chain under demand uncertainty. Initially, both buyers independently determine their order quantities under a common procurement framework based on long-term wholesale contracts. While the demand for each buyer follows the same probability distribution, it differs in scale and is modeled as an independent random variable. The supplier is assumed to have unlimited production capacity, thereby imposing no constraints on order quantities, and procurement occurs only once within a single-period setting. Any excess inventory resulting from over-ordering is discarded without salvage value, whereas unmet demand incurs a penalty cost per unit. The retail price, wholesale price, and penalty cost are assumed to be exogenously given.
In this section, we first outline the procurement model based on long-term wholesale contracts, which serves as a benchmark. We then introduce the system configuration and mathematical formulation of the swap-integrated procurement strategy, which aims to enhance supply chain performance through buyer-to-buyer cooperation. Table 2 summarizes the key variables and notations used throughout this paper. The units of demand, order quantity, price, and cost are context-dependent and may, for instance, represent either individual units or thousands (for quantities), or dollars or thousands of dollars (for monetary values).

Table 2.
Notations and descriptions.
3.1. Baseline Model: Long-Term Wholesale (WH) Procurement Model
This section describes the procurement structure through a long-term wholesale contract that serves as a benchmark. In this structure, the buyer purchases the products at a predetermined wholesale price and sells them in the market. The model is similar to the newsvendor framework. When the procurement quantity is Q and the demand is X, the sales quantity equals min(X, Q), while the unmet demand is represented by (X − Q)+ where (X − Q)+ = max(X − Q, 0). The buyer’s expected profit function, , is obtained as follows:
The optimal order quantity that maximizes expected profit is obtained from the first-order condition, as follows:
While the long-term wholesale contract is simple and easy to operate from the buyer’s perspective, it may result in frequent losses due to excess inventory or stockouts in environments where demand is highly uncertain.
3.2. Swap-Integrated (SW) Procurement Model
This section presents an integrated procurement strategy that combines swap and wholesale contracts to address potential inventory imbalances inherent in long-term wholesale contract structures. The model is presented primarily from the perspective of Buyer 1, with a focus on the procurement process and inventory exchange mechanism. For clarity, Buyer 1 is referred to as the focal buyer, while Buyer 2 is referred to as the collaborating buyer (or counterpart) throughout the paper. A schematic illustration of the proposed strategy is shown in Figure 1.
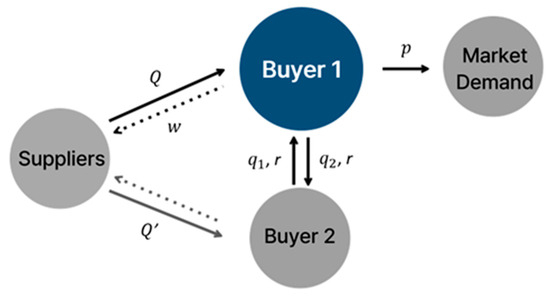
Figure 1.
Schematic of the swap-integrated procurement strategy. Solid lines represent the physical flows of products, while dotted lines indicate monetary transfers.
The primary objective of this strategy is to mitigate inventory risk by enabling the mutual adjustment of excess inventory between the two buyers once demand is realized—the risk that each buyer would otherwise bear. The two buyers procure identical goods from arbitrary—and potentially different—suppliers. The term “identical goods” is adopted as a simplifying assumption for theoretical purposes; in practice, this may encompass functionally equivalent substitutes. For example, products such as the Pfizer and AstraZeneca vaccines are considered equivalent goods, as they serve the same function despite differences in formulation.
Each buyer enters into a long-term wholesale-based contract with their respective supplier prior to demand realization, committing to quantities Q and Q′, respectively, and subsequently sells the products on the market. Due to demand uncertainty, mismatches between ordered and realized demand may result in either excess inventory or stockouts. For instance, if Buyer 1 holds excess inventory while Buyer 2 experiences a shortage, the surplus is transferred from Buyer 1 to Buyer 2 at a predetermined swap price. The swap transaction is triggered only after demand is realized and proceeds according to the conditions agreed upon in advance. This mechanism serves as a structural risk-sharing tool, reducing each firm’s exposure to individual inventory risks.
To facilitate the analysis of this swap-integrated procurement strategy, the following assumptions are introduced:
- (1)
- The two buyers are fully cooperative under the swap contract. If one buyer holds excess inventory and the other faces a shortage after demand is realized, the surplus is mandatorily transferred at the pre-agreed swap price, r.
- (2)
- The demand of Buyer 1 is represented by the random variable X, and Buyer 2’s demand is represented by Y, where Y follows the same distributional form as X but is scaled by a factor of c. For instance, if Buyer 1 represents the Korean market and Buyer 2 represents the Japanese market, c = 2.5 may reflect the population size ratio. The scaling factor, c, plays a central role in the sensitivity analysis conducted later in this study.
- (3)
- The swap price, r, is given exogenously. Sensitivity analyses with respect to varying values of r will be conducted in a following section.
3.2.1. Expected Profit Model for the Swap-Integrated Procurement Strategy
The swap-integrated procurement model aims to identify the optimal order quantity that maximizes the expected profit of the buyer: . (To follow the model development more easily, it may be helpful to refer to Figure 2 at this point.) As described previously, the demands of Buyers 1 and 2 are given as independent random variables, X and Y, respectively. Buyer 1 procures quantity Q at unit price w in advance and sells the product at price p upon demand realization. Throughout this process, excess demand and excess inventory arise, which are adjusted through the swap contract. Buyer 2 operates under the same structure, with an order quantity set as cQ reflecting the demand scaling factor. Accordingly, Buyer 2’s excess demand and excess inventory are defined as functions of , and . The swap contract is executed after demand realization when one buyer holds surplus inventory and the other experiences a shortage. The actual quantity exchanged is determined as the minimum of these two values. Accordingly, the swap quantity procured by Buyer 1 from Buyer 2 is expressed as follows:

Figure 2.
Procedure for deriving the optimal order quantity from a long-term supplier under uniform demand distribution conditions.
Conversely, the swap quantity supplied by Buyer 1 to Buyer 2 is expressed as follows:
The expected profit function for Buyer 1 is expressed as follows:
where and , with a given order quantity, Q.
Each term corresponds to revenue from market sales, cost of procurement under the wholesale contract, additional revenue from sales through the swap, penalty costs from unmet demand, and revenue from supplying surplus inventory via the swap. The expected profit is restated as follows:
Buyer 1 needs to determine the optimal order quantity that maximizes the expected profit above. To compute the expected profit, it is necessary to determine and , which is not trivial. The following section presents the procedure for calculating and :
3.2.2. Obtaining the Expected Swap Quantity
To obtain and , we apply the tail expectation formula, which states that for a non-negative random variable, z. The expected swap quantity is then derived as follows:
Expression (7) can be restated as follows:
Since we assume that X and Y are independent, we obtain the following equation:
This can be transformed in terms of the distribution function as follows:
Finally, we obtain the following function:
Given that Y follows the same distributional structure as X but scaled by factor c, the pdf and cdf of Y satisfy the following relationship:
By applying this relationship, the expected swap transfer quantity from Buyer 2 to Buyer 1 can be summarized as follows:
By applying a similar procedure, the expected swap transfer quantity from Buyer 1 to Buyer 2 can also be obtained as follows:
By embedding expressions (13) and (14) into expression (6), can be restarted as follows:
Finally, the order quantity, Q, is determined to maximize in expression (15). The expected profit function described above has a nonlinear structure with respect to order quantity Q and consists of integrals involving multiple probability distribution functions and joint probabilities, making it highly complex to compute derivatives and derive the optimal solution analytically.
3.2.3. Optimal Order Quantity Model Under Uniform Distribution Conditions
In this section, we develop the model by assuming that demand follows a uniform distribution, which facilitates the derivation of closed-form solutions for evaluating the buyer’s profitability. In the supply chain literature, this assumption is a well-established modeling convention that offers analytical simplicity while enabling insights into more complex and realistic demand settings [21]. Importantly, adopting a uniform distribution does not compromise the generality or validity of the results, as the model remains effective in capturing the structural characteristics and comparative performance of alternative procurement strategies. Let demand X and Y follow uniform distributions, U(a, b) and U(ca, cb), respectively. For the uniform distribution, the cdf is given by , and accordingly, and are expressed as follows:
Since the cdf in expression (13) are defined only within specific domains, and , the integral is valid only over the range that simultaneously satisfies these conditions. Let be the effective integration interval, , for . Expression (13) can be restated as follows:
By computing the integral above, is expressed in polynomial form as follows:
Using the same procedure as that used for obtaining , can be derived. In Equation (14), the integral is valid when the conditions and are simultaneously satisfied. Let be the effective integration interval, , for . Then, the following expression holds:
By utilizing the obtained values of and , the expected profit under the swap-integrated procurement strategy can be expressed as follows:
(Note that under U(a, b) distribution conditions.)
When making procurement decisions, Buyer 1 determines the optimal order quantity, Q*, that maximizes in expression (20). However, the complexity of the expected profit function makes it too challenging to derive the optimal order quantity in a closed form. This study adopts a numerical method, determining the optimal order quantity using the minimize_scalar function from Python’s scipy.optimize package (Python version 3.10.0). This function is based on Brent’s method, which combines bisection, linear interpolation, and quadratic interpolation. Brent’s method is particularly well-suited for this type of problem, as it efficiently locates the extremum of a continuous, nonlinear function of a single variable without requiring derivative information [22]. Moreover, it provides high numerical precision with no fixed time complexity, making it a robust and practical choice for solving the optimal ordering problem in this study.
Figure 2 illustrates the procedure for determining the optimal order quantity to be placed with the long-term contract supplier under the swap-integrated procurement strategy.
4. Numerical Studies
This section evaluates the performance of the procurement model proposed in the previous section by comparing it with a long-term wholesale contract. In addition, sensitivity analyses are conducted to examine the impact of key parameter variations on model performance.
The baseline demand scenario follows the setting of Koo [23], with some modification for swap settings. Buyer 1’s demand, denoted by X, is modeled as a uniform distribution X∼U(100, 300), while Buyer 2’s demand, Y, is defined as Y∼U(100c, 300c), reflecting the demand scaling factor, c. Initially, the value of c is fixed at 1. The main cost parameters are as follows: retail price p = 60, wholesale price w = 40, swap price r = 50, and penalty cost for unmet demand g = 30. Numerical experiments were conducted using Python.
4.1. Performance Comparison: Wholesale-Based vs. Swap-Integrated Procurement Strategies
This section compares the procurement performance between wholesale-based and swap-integrated procurement strategies under the same demand and cost structure. Figure 3 illustrates how the expected profit of the two procurement strategies changes with order quantity, identifies the profit-maximizing order quantity for each strategy, and shows the corresponding expected profit at that point. It shows that the SW strategy achieves higher expected profit while selecting a lower order quantity compared to the WH strategy. This suggests that the complementary mechanism of addressing excess and shortage demand through the swap mitigates the buyer’s procurement risk and ultimately enables a more efficient profit structure.
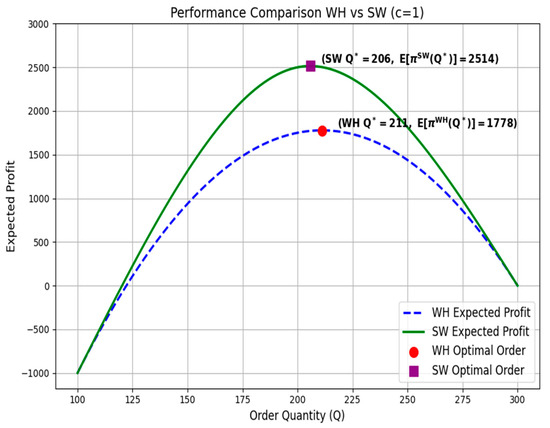
Figure 3.
Comparison of the optimal order quantity and expected profit under the wholesale-only (WH) and swap-integrated (SW) procurement strategies in the baseline scenario. The SW strategy yields a 41.4% increase in expected profit with a 2.4% reduction in order quantity by enabling buyer-to-buyer inventory swaps, thereby mitigating both shortage and surplus costs.
Specifically, in the WH strategy, the optimal order quantity is 211 units, with an expected profit of 1,778. In contrast, under the SW strategy, the order quantity is slightly decreased to 206 units (−2.4%), while the expected profit is significantly increased to 2514 (+41.4%). The relatively lower optimal order quantity under the SW strategy is primarily attributed to the flexibility provided by the swap mechanism, which enables effective responses to both excess inventory and shortages. The SW strategy allows a buyer to procure surplus inventory from another buyer when demand exceeds expectations, and conversely, to transfer surplus inventory to another buyer and earn additional revenue when demand falls short of expectations. This structure enables stable fulfillment of demand without excessive pre-ordering, thereby allowing for efficient operations even with a lower order quantity. However, it should be noted that a lower order quantity in the SW strategy should not be generalized, as it may vary depending on the demand structure, inter-buyer relationships, and the terms of the swap contract. Changes in the optimal order quantity may vary depending on factors such as demand structure, relationships between buyers, and swap conditions; these aspects are discussed in greater detail in the sensitivity analysis in Section 4.2 and Section 4.3.
Meanwhile, the notable improvement in expected profit under the SW strategy stems from the swap mechanism effectively mitigating costs associated with supply-demand mismatches. When demand exceeds the pre-ordered quantity, the WH strategy obliges the buyer to bear the full penalty cost for the shortage. In contrast, the SW strategy enables the buyer to cover the shortage through swaps, thereby reducing the financial burden. Conversely, when demand falls below the ordered quantity, the WH strategy results in the buyer absorbing the full cost of surplus inventory, whereas the SW strategy allows excess inventory to be transferred to another buyer and converted into revenue.
These results demonstrate that the SW strategy provides a structural advantage by enabling efficient resource reallocation through inter-buyer cooperation and by allowing for adaptive responses to fluctuating demand. Consequently, the strategy mitigates procurement risks and enhances supply chain stability in environments characterized by high demand uncertainty.
4.2. Effect of Demand Scaling Factor
This section examines the influence of demand asymmetry on the operational efficiency and performance of the SW strategy. To this end, the demand scaling factor, c, is designated as the key experimental variable. Sensitivity analyses are conducted with respect to three performance dimensions: the expected swap quantity, the optimal order quantity, and the expected profit. The analysis is performed by setting five scenarios in which c = 0.25, 0.5, 1, 2, and 4.
Figure 4 illustrates the expected swap quantities for Buyer 1 and Buyer 2 under the SW procurement strategy. As expected, the expected swap quantity reaches its minimum value of zero when the order quantity is equal to either the lower or upper bound of the demand. This result is intuitive, as either the inventory surplus or the inventory shortage becomes zero in such cases. It is also seen that both and exhibit a clear increasing trend as the demand scaling factor, c, increases. This result is also expected, as a larger demand scale of the collaborating partner implies greater potential for both surplus and shortage on their side. Consequently, when the focal buyer faces a shortage, the partner is more likely to have sufficient surplus to supply; conversely, when the focal buyer has excess inventory, the partner is more likely to absorb it due to higher unmet demand.
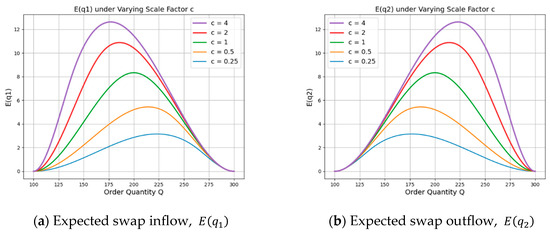
Figure 4.
Expected swap transfer quantity under varying sale factor c. As c increases, the expected swap quantity rises, and the peaks of and shift in opposite directions due to changes in swap feasibility.
An interesting observation is that the order quantity, Q, that maximizes and varies with the value of c. Specifically, as c increases, the value of Q that maximizes decreases, while the value that maximizes increases. This outcome can be explained as follows: The expected swap inflow, , represents the amount of shortage that the focal buyer can replenish from the collaborating buyer’s surplus inventory. The swap inflow is determined by the minimum of the focal buyer’s shortage and the collaborating buyer’s surplus. The peak of the curve occurs when these two quantities are equal. As c increases, the collaborating buyer’s demand becomes relatively larger, leading to more surplus inventory at a given order quantity. Consequently, the limiting factor for gradually shifts from the collaborating buyer’s surplus to the focal buyer’s own shortage. As a result, the point of equality between shortage and surplus occurs at a smaller Q, causing the peak of to shift leftward as c increases. Similarly, the peak of shifts rightward as c increases, since higher demand from the collaborating buyer leads to greater shortages on their side. To support more swap outflows, the focal buyer must order more to generate sufficient surplus. These opposing shifts intuitively illustrate how ordering decisions are structurally adjusted under the swap-integrated procurement strategy.
Figure 5 presents the optimal order quantity and expected profit under the SW strategy as the demand scaling factor, c, varies. Figure 5a shows that the optimal order quantity reaches a minimum near c = 1 and increases as the value of c deviates from this point in either direction. This pattern can be interpreted as the result of a combined effect of the structural feasibility of the swap mechanism and the associated economic incentives. When c < 1, the collaborating buyer, Buyer 2, has relatively small demand, which provides little opportunity for inventory contribution through swaps. Consequently, Buyer 1 adopts a more conservative strategy by procuring additional inventory in advance to hedge against potential shortages. In contrast, when , the collaborating partner is more likely to engage in substantial swap transactions, thereby reducing inventory risk for Buyer 1. As a result, it becomes advantageous for Buyer 1 to adopt a more relaxed ordering policy.
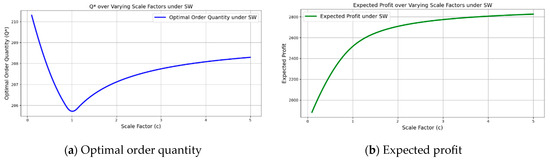
Figure 5.
Optimal order quantity and expected profit under the SW strategy across varying scale factors. (a) A pattern in which the optimal order quantity reaches its minimum around c = 1 and increases as c becomes either smaller or larger. (b) A gradual increase in expected profit with increasing values of c.
The expected profit results shown in Figure 5b exhibit an upward trend as c increases, with growth being particularly pronounced when . When the demand scaling factor, c, is low, the inventory surplus or shortage of the counterpart with lower demand is relatively small, resulting in a limited volume of swap transactions. Consequently, the focal buyer’s ability to compensate for inventory imbalances through swaps is constrained, leading to lower expected profits. On the other hand, as c increases, the inventory surplus or shortage of the counterpart becomes more significant, enhancing the potential for mitigating the focal buyer’s inventory imbalance through swap transactions. This leads to a steady increase in expected profit, although the rate of increase slows down. Note that the results presented here are based on an assumption of a swap price of 50. The next section investigates how variations in the swap price influence the model’s performance.
4.3. Effect of Swap Price
According to the results from the baseline scenario analysis, the SW strategy tends to yield a higher expected profit and a relatively lower optimal order quantity compared to the WH strategy. This is attributed to the fact that the swap mechanism enables buyers to complement excess and shortage demand through mutual adjustment, thereby encouraging a more conservative ordering strategy. However, whether this tendency holds consistently across different procurement environments requires further examination. In particular, if the swap terms are sufficiently favorable, buyers may instead be incentivized to adopt a more aggressive ordering strategy. In other words, it is uncertain whether the swap strategy always leads to a lower order quantity than the wholesale-only strategy.
To address this question, this section examines how changes in the swap price affect the decision-making behavior of swap participants and the performance of the proposed model, with particular focus on how performance varies according to the size of the counterpart. In the experiment, the demand scale factor, c, varies from 0.1 to 5, while the swap price, r, is set at five discrete levels: 30, 40, 50, 60, and 70.
Figure 6 illustrates how the optimal order quantity under the SW strategy is adjusted in response to changes in the demand scaling factor, c, for different levels of the swap price, r. Each solid line represents the ordering curve corresponding to a specific value of r under the SW strategy while the dotted line indicates the optimal order quantity under the WH strategy .
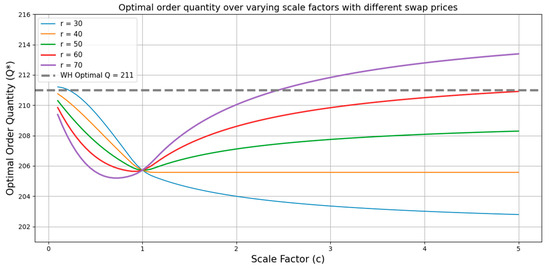
Figure 6.
Optimal order quantity across varying scale factors under different swap prices. The solid lines illustrate how optimal order decisions adjust in response to changes in demand asymmetry and swap pricing. Notably, the order quantity remains unchanged when c = 1 and shows opposing trends depending on whether swap price, r, is high or low. The dashed line represents the optimal order quantity under the WH strategy and is provided for comparison.
The experimental results reveal several noteworthy insights:
- (1)
- When c = 1, the focal and collaborating buyers have identical demand distributions, resulting in a symmetric setting. In this case, the probabilities of surplus and shortage are evenly balanced between the two parties, making the expected gains from swap transactions invariant to the swap price, r. As a result, the optimal order quantity under the SW strategy remains constant regardless of the value of r. Furthermore, this order quantity is consistently lower than that of the WH strategy, reflecting the risk-mitigating role of the swap mechanism. By enabling post-demand adjustments, the swap contract reduces the need for inventory buffers, thereby encouraging more conservative upfront procurement.
- (2)
- When c ≠ 1, the effect of the swap price, r, on the optimal ordering behavior diverges significantly depending on whether c < 1 or c > 1. This outcome is driven by the directional behavior of the expected swap quantities and their influence on the profit function. Recall that the r-dependent part of the expected profit in expression (5) is stated as −+ . Accordingly, the relative magnitude of and plays a critical role in shaping the impact of swap price changes. As shown in Figure 4, when c < 1, a lower order quantity, Q, tends to generate > , implying that an increase in r yields a net gain in the term −+ . Therefore, in this case, higher swap prices make lower Q values more desirable, leading to a decline in optimal order quantity as r increases. Conversely, applying a similar line of analysis reveals that when c > 1, the optimal order quantity tends to increase as the swap price, r, rises.
- (3)
- In most cases, the SW strategy yields a lower optimal order quantity than the WH strategy. However, when both c and r are sufficiently high, the SW strategy may induce a higher order quantity than the WH benchmark. For instance, when r = 70, the SW strategy begins to induce higher ordering quantities than the WH strategy for . This is because the incentive to dispose of excess inventory through swaps becomes stronger when the swap price is high. Also, a similar pattern emerges when and the swap price r is very low. In this case, even if surplus inventory occurs, it may be offloaded to the counterpart, which reduces the burden of holding excess stock. At the same time, the low swap price strengthens the collaborating buyer’s incentive to participate in swaps, thereby increasing the likelihood of successful transactions. As a result, it may be more profitable for the focal buyer to adopt a more aggressive ordering strategy. Accordingly, when the swap price is either sufficiently high or very low—depending on the demand structure—the SW strategy may actually lead to more aggressive ordering than the WH strategy.
- (4)
- When the swap price, r, is low, increasing the scale factor, c, does not lead to a higher order quantity under the SW strategy; instead, the focal buyer tends to adopt a more conservative ordering approach. This outcome reflects the interplay of two reinforcing factors. First, a low swap price provides the focal buyer with a cost-effective means of addressing potential shortages, as inventory can be secured post hoc at a price lower than the wholesale cost, w. This reduces the incentive for large initial orders. Second, the financial benefit from offloading surplus inventory through swaps is diminished at lower r values, limiting the upside of over-ordering. Together, these effects weaken the buyer’s motivation to place aggressive orders in advance and instead encourage strategic reliance on the swap mechanism as a flexible, lower-cost buffer against demand uncertainty.
The numerical findings, supported by Figure 6, show that the effectiveness of the SW strategy is highly sensitive to the interaction between the demand scaling factor, c, and the swap price, r. When demand asymmetry is high and swap conditions are favorable, the SW strategy can induce even more aggressive ordering than the traditional wholesale approach, transforming it from a risk-hedging mechanism into a tool for strategic profit optimization. However, under low swap prices or limited counterpart demand, the strategy encourages conservative procurement, highlighting the need for careful contract design and coordination. These results underscore the practical value of swap-integrated procurement, not only for balancing inventory risks but also for enabling adaptable sourcing decisions in both private and public sector supply chains.
The subsequent analysis examines how variations in the swap price, r, and the demand scaling factor, c, affect the expected profit under the SW strategy. Figure 7 presents a heatmap that visualizes the expected profit across different combinations of r and c, thereby illustrating how the profitability of the SW strategy varies depending on the procurement environment. The results reveal that the expected profit under the SW strategy generally increases with the demand scaling factor, c. A higher value of c implies greater demand from the collaborating buyer, which in turn increases the likelihood of successful swap transactions and enhances the opportunity to offload excess inventory under favorable conditions.
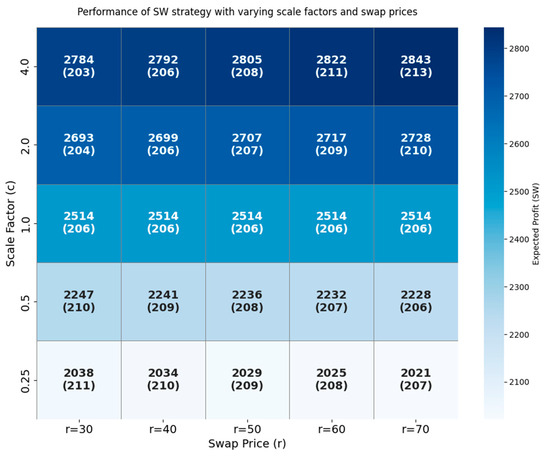
Figure 7.
Performance of the SW procurement strategy under varying scale factors and swap prices. Each cell presents the expected profit (upper value) and the corresponding optimal order quantity (in parentheses). As the demand scale factor, c, increases, the expected profits generally improve due to enhanced swap flexibility, while the optimal order quantity adjust accordingly based on the swap price, r.
However, the impact of the swap price, r, is not uniform and depends on the demand asymmetry. When , the expected swap inflow is larger than the expected swap outflow with order quantities above 200 (see Figure 4). Therefore, from the perspective of the focal buyer, a higher swap price leads to a lower expected profit compared to a lower swap price. This is because although a higher swap price increases the revenue gained from supplying surplus inventory through swaps, it also increases the cost of procuring inventory via swaps. The reduction in swap procurement cost outweighs the loss in swap revenue, resulting in a net gain in profit. However, since the counterpart’s surplus or shortage is relatively small, its contribution to the profit is limited. Conversely, when , the expected swap inflow is smaller than the expected swap outflow, which contrasts with the case of . One interesting observation is that the impact of r on the focal buyer’s expected profit is less pronounced than that of c. This can be attributed to the bidirectional nature of swap transactions, which involve both procuring shortages and supplying surpluses. As a result, the effect of the swap price tends to be largely offset.
Overall, these findings underscore that the expected profit from the SW strategy is shaped not by isolated parameters but by the interaction between demand structure and contractual terms. When demand asymmetry is high and swap prices are favorable, the SW strategy serves not only as a risk-mitigation mechanism but also as a tool for profit maximization. In contrast, when the collaborating buyer has limited demand and swap prices are high, the profitability of the strategy may decline. Therefore, aligning contract terms with the underlying demand structure is essential for the effective implementation of swap-integrated procurement.
5. Conclusions
This study proposed a swap-integrated procurement strategy that combines a long-term wholesale-based contract to enhance flexibility and risk mitigation under demand uncertainty. By enabling post-demand inventory exchanges between buyers, the strategy addresses limitations inherent in single-contract structures. The theoretical contributions of this study can be summarized in the following key points:
- (1)
- This study presents a novel application of swap mechanisms, traditionally used in financial sectors, to the context of buyer-to-buyer inventory reallocation. By modeling swaps as contractual exchanges of surplus and shortage inventory between buyers, this research reconceptualizes swaps as a post-demand coordination mechanism in supply chain operations.
- (2)
- A model is proposed to estimate the expected swap inflows and outflows resulting from swap transactions.
- (3)
- An analytical model is presented for the expected profit in a system that adopts a swap-integrated procurement policy.
- (4)
- Under the assumption that demand is uniformly distributed, a closed-form expression for the expected profit is derived, and a method for determining the optimal order quantity is presented.
- (5)
- Experimental analyses are conducted to quantify the strategic benefits of swap integration by comparing it to traditional wholesale-based procurement. The results highlight the influence of key parameters, such as demand asymmetry and swap price, on the strategy’s effectiveness.
The findings demonstrate that the proposed strategy consistently outperforms long-term wholesale contracts in terms of profitability and stability; under the baseline scenario, it achieves a 41.4% increase in expected profit compared to the wholesale-based strategy, which clearly supports the value of swap integration.
From a practical perspective, the study offers a strategic approach to mitigating inventory risk in supply chains with highly unpredictable demand, such as vaccines, fresh produce, or electronic components, by utilizing swap contracts. By analyzing performance variations across different levels of swap price and demand asymmetry, this study provides practical guidelines for contract design. For instance, the results indicate that swap contracts are particularly advantageous for the focal buyer when the counterpart has a relatively larger demand scale and the swap price is high. These results can guide decision-makers in structuring contract terms in various procurement environments and offer valuable insights for designing cooperative structures, including participant selection and prioritization in swap strategies. However, it should be noted that these results are derived from the specific parameter settings assumed in this study. In practice, different supply chain environments may yield different outcomes; therefore, careful consideration of the actual procurement context is essential when applying these insights in practice.
This study is subject to several limitations that offer directions for future research. First, the model adopts a single-period setting, which does not capture multi-period dynamics such as inventory rollover or learning effects. Second, it assumes that swaps are always executed when conditions are met, overlooking real-world frictions such as information asymmetry or negotiation failures. Third, the analysis is based on uniform demand; future studies may examine the model’s robustness under more realistic demand patterns. Fourth, the supply capacity is sufficient with fully reliable suppliers. Fifth, the current framework involves only two buyers in the swap contract. These assumptions may deviate from real-world supply chain conditions, highlighting the need for further research to relax or generalize them. In addition, future extensions could explore portfolio-based strategies that combine swap contracts with other mechanisms such as options or spot markets. Finally, in this study, the numerical analysis was conducted under a specific setting, in which parameters such as the selling price, wholesale price, and stockout penalty were fixed. Variations in these parameter values are expected to influence the performance of the proposed swap-integrated procurement strategy. Investigating how the model behaves across a broader set of parameter configurations remains a promising direction for future research.
Author Contributions
Conceptualization, P.-H.K.; methodology, M.-Y.R. and P.-H.K.; software, M.-Y.R.; validation, M.-Y.R. and P.-H.K.; formal analysis, M.-Y.R. and P.-H.K.; resources, P.-H.K.; data curation, M.-Y.R.; writing—original draft preparation, M.-Y.R.; writing—review and editing, M.-Y.R. and P.-H.K.; supervision, P.-H.K.; funding acquisition, P.-H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Korea (No. 2022R1I1A3070919).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; the collection, analysis, or interpretation of the data; the writing of the manuscript; or the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| WH | Long-term wholesale-based procurement strategy |
| SW | Swap-integrated procurement strategy |
References
- Alkhatib, S.F.; Momani, R.A. Supply Chain Resilience and Operational Performance: The Role of Digital Technologies in Jordanian Manufacturing Firms. Adm. Sci. 2023, 13, 40. [Google Scholar] [CrossRef]
- Choi, T.-M.; Li, D.; Yan, H. Mean–variance analysis of a single supplier and retailer supply chain under a returns policy. Eur. J. Oper. Res. 2008, 184, 356–376. [Google Scholar] [CrossRef]
- Cachon, G.P.; Lariviere, M.A. Supply Chain Coordination with Revenue-Sharing Contracts: Strengths and Limitations. Manag. Sci. 2005, 51, 30–44. [Google Scholar] [CrossRef]
- Zhao, Y.; Choi, T.-M.; Cheng, T.C.E.; Wang, S. Supply option contracts with spot market and demand information updating. Eur. J. Oper. Res. 2018, 266, 1062–1071. [Google Scholar] [CrossRef]
- The Bank of Korea. The Bank of Korea and the Bank of Japan Announce an Increase in the Size of the Won-Yen Swap Arrangement, 2008, Press Release. Available online: https://www.bok.or.kr/eng/bbs/E0000634/view.do?menuNo=400423&nttId=146770 (accessed on 15 July 2025).
- Australian Government Department of Health and Aged Care. COVID-19 Vaccine Rollout Update: International Dose Swap Arrangements. 2024. Available online: https://www.health.gov.au/our-work/covid-19-vaccines/about-rollout/vaccine-agreements (accessed on 26 June 2025).
- Reuters. India’s GAIL Issues Swap Tender for 12 LNG Cargoes. Available online: https://www.reuters.com/business/energy/indias-gail-issues-swap-tender-12-lng-cargoes-sources-say-2025-02-04/ (accessed on 26 June 2025).
- Ekren, B.Y.; Arslan, M.C. Simulation-based lateral transshipment policy optimization for s, S inventory control problem in a single-echelon supply chain network. Int. J. Optim. Control. Theor. Appl. 2020, 10, 9–16. [Google Scholar] [CrossRef]
- Al Husain, R.; Assavapokee, T.; Khumawala, B. Modelling the supply chain swap problem in the petroleum industry. Int. J. Appl. Decis. Sci. 2008, 1, 261. [Google Scholar] [CrossRef]
- Bidyarthi, H.M.J.; Deshmukh, L.B. Swap in downstream petroleum supply chain: An effective inventory handling tool. In Driving the Economy Through Innovation and Entrepreneurship; Mukhopadhyay, C., Akhilesh, K.B., Srinivasan, R., Gurtoo, A., Ramachandran, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 363–370. [Google Scholar] [CrossRef]
- Al-Husain, R.; Khorramshahgol, R. A comprehensive analysis of the determinants of swap problem in the supply chain of the petroleum industry. Int. J. Stat. Probab. 2016, 5, 97–108. [Google Scholar] [CrossRef]
- Farahani, M.; Rahmani, D. Production and distribution planning in petroleum supply chains regarding the impacts of gas injection and swap. Energy 2017, 141, 991–1003. [Google Scholar] [CrossRef]
- Dizbay, I.E.; Ozturkoglu, O. Product swapping and transfer sales between suppliers in a balanced network. In Proceedings of the 2013 Federated Conference on Computer Science and Information Systems, Krakow, Poland, 8–11 September 2013; pp. 1191–1194. [Google Scholar]
- Wang, Y.; Meng, Q.; Tan, Z. Short-term liner shipping bunker procurement with swap contracts. Marit. Policy Manag. 2017, 45, 211–238. [Google Scholar] [CrossRef]
- Park, S.J. Swapping inventory between competing firms. Int. J. Prod. Econ. 2018, 199, 26–46. [Google Scholar] [CrossRef]
- Kemper, A.; Schmeck, M.D.; Balci, A.K. The market price of risk for delivery periods: Pricing swaps and options in electricity markets. Energy Econ. 2022, 113, 106221. [Google Scholar] [CrossRef]
- Zhang, L.; Thomspon, R.G. Optimising product swaps in an urban retail network with uncertainty. Transp. Res. Procedia 2024, 79, 210–217. [Google Scholar] [CrossRef]
- Diks, E.B.; de Kok, A.G. Controlling a divergent two-echelon network with transshipments using linear programming. Eur. J. Oper. Res. 1996, 45, 369–379. [Google Scholar] [CrossRef]
- Paterson, C.; Kiesmüller, G.; Teunter, R.; Glazebrook, K. Inventory models with lateral transshipments: A review. Eur. J. Oper. Res. 2011, 210, 125–136. [Google Scholar] [CrossRef]
- Kumari, A.G.; Wijayanayake, A.; Niwunhella, H. Lateral Transshipment Inventory Models: A Systematic Literature Review of Models and Solution Approaches. Proc. Int. Conf. Bus. Manag. 2022, 18, 54–80. [Google Scholar] [CrossRef]
- Aggarwal, P.; Ganeshan, R. Using risk-management tools on B2Bs: An exploratory investigation. Int. J. Prod. Econ. 2007, 108, 2–7. [Google Scholar] [CrossRef]
- Zhang, Z. An Improvement to the Brent’s Method. Int. J. Exp. Algorithms 2011, 2, 21–26. [Google Scholar]
- Koo, P.-H. Exploring the relationship between buyback and revenue sharing contracts in channel coordination. J. Korean Inst. Ind. Eng. 2024, 50, 211–221. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).