Lorentzian Structure and Curvature Analysis of Osculating Type-2 Ruled Surfaces via the Type-2 Bishop Frame

Abstract

This study investigates the geometry of osculating type-2 ruled surfaces in Minkowski 3-space ${\mathbf{E}}_1^3$, formulated through the Type-2 Bishop frame associated with a spacelike curve whose principal normal is timelike and binormal is spacelike. Using the hyperbolic transformation linking the Frenet–Serret and Bishop frames, we analyze how the Bishop curvatures ${\zeta }_1$ and ${\zeta }_2$ affect the geometric behavior and formation of such surfaces. Explicit criteria are derived for cylindrical, developable, and minimal configurations, together with analytical expressions for Gaussian and mean curvatures. We also determine the conditions under which the base curve behaves as a geodesic, asymptotic line, or line of curvature. Several illustrative examples in Minkowski 3-space are provided to visualize the geometric influence of ${\zeta }_1$ and ${\zeta }_2$ on flatness, minimality, and developability. Overall, the Type-2 Bishop frame offers a smooth and effective framework for characterizing Lorentzian geometry and symmetry of osculating ruled surfaces, extending classical Euclidean results to the Minkowski setting.

1. Introduction

Ruled surfaces have long been a fundamental topic in differential geometry due to their analytical elegance and practical relevance in mechanics, architecture, and theoretical physics. A ruled surface is generated by the motion of a straight line (the ruling) along a base curve. In Euclidean geometry, their developability, minimality, and curvature properties have been extensively studied. In contrast, in Minkowski 3-space ${\mathbf{E}}_1^3$, which represents flat Lorentzian geometry, the causal nature of vectors and curves spacelike, timelike, or null produces more intricate geometric behavior without direct Euclidean analogues.

In physics, ruled surfaces in ${\mathbf{E}}_1^3$ naturally describe relativistic models such as string world-sheets, lightlike hypersurfaces, and geodesic congruences. The Bishop frame, which remains smooth even when curvature vanishes, provides a stable alternative to the Frenet–Serret frame for such analyses. Studies of minimal and developable ruled surfaces in Lorentzian settings also contribute to the understanding of geometric structures underlying cosmic strings, wave propagation, and optical systems.

The Frenet–Serret frame, though classical, becomes undefined when curvature vanishes. To address this limitation, L. R. Bishop introduced in 1975 the Bishop frame or parallel transport frame, which replaces torsion by two independent curvature functions—the Bishop curvatures—offering greater flexibility in describing the rotation of the normal plane [1]. Subsequent extensions of the Bishop frame to Lorentzian geometry were initiated by Ilarslan and Nesovic [2] and further developed by Kalkan, Senyurt, Yüce, and others [3,4,5].

A recent development is the concept of osculating type-2 ruled surfaces, where the ruling lies in the osculating plane of the base curve. Boyacioglu Kalkan and Senyurt [6] examined these surfaces in Euclidean 3-space using the Type-2 Bishop frame, determining conditions for developability and minimality. Related studies in Minkowski 3-space by Kocayigit and Öztürk [7], Kaya et al. [8], Ali [9], Karacan et al. [10], and Özgür Boyaciŏglu Kalkan and Süleyman Şenyurt [11] revealed the strong influence of Lorentzian metrics on surface curvature and causal classification.

The present work develops and analyzes osculating type-2 ruled surfaces defined via the Type-2 Bishop frame in Minkowski 3-space. The Lorentzian structure introduces hyperbolic transformations between the Frenet–Serret and Bishop frames, leading to new differential geometric relations. We derive conditions for cylindrical, developable, minimal, and flat surfaces, and determine when the base curve acts as a geodesic, asymptotic curve, or line of curvature. Finally, examples are provided to visualize the influence of the curvature parameters ${\zeta }_1$ and ${\zeta }_2$.

2. Geometric Preliminaries of Curves and Surfaces in ${\mathbf{E}}_1^3$

In this section, we review the basic notions and notations used throughout the paper, including the geometry of Minkowski 3-space, the Frenet and Bishop frames of a spacelike curve, the Type-2 Bishop frame, the fundamental forms of a surface, and the curvature formulas relevant to ruled surface geometry.

The Minkowski 3-space ${\mathbf{E}}_1^3$ is the real vector space ${\mathbb{R}}^3$ endowed with the Lorentzian metric

$$⟨X,Y⟩=-x_1{y}_1+x_2{y}_2+x_3{y}_3,$$

(1)

for all vectors $X=(x_1,x_2,x_3)$ and $Y=(y_1,y_2,y_3)$ in ${\mathbf{E}}_1^3$. This metric has signature $(-,+,+)$ and classifies nonzero vectors as:

• spacelike if $⟨X,X⟩>0$ or $X=0$;
• timelike if $⟨X,X⟩<0$;
• lightlike (null) if $⟨X,X⟩=0$ and $X\ne 0$.

A curve $\phi \left(s\right)$ in ${\mathbf{E}}_1^3$ is called spacelike, timelike, or lightlike according to the causal character of its tangent vector ${\phi }^{\prime }\left(s\right)$ [12,13,14].

Let $\phi =\phi \left(s\right)$ be a spacelike curve parameterized by arc length in ${\mathbf{E}}_1^3$, with a timelike principal normal and a spacelike binormal. The Frenet frame $\{T,N,B\}$ satisfies

$$⟨T,T⟩=⟨B,B⟩=1,\hspace{1em}⟨N,N⟩=-1,\hspace{1em}⟨T,N⟩=⟨T,B⟩=⟨N,B⟩=0,$$

(2)

and the Lorentzian Frenet Serret formulas are

$$\left(\begin{array}{c}{T}^{\prime }\left(s\right)\\ N^{\prime }\left(s\right)\\ B^{\prime }\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& \kappa \left(s\right)& 0\\ \kappa \left(s\right)& 0& \tau \left(s\right)\\ 0& \tau \left(s\right)& 0\end{array}\right)\left(\begin{array}{c}T\left(s\right)\\ N\left(s\right)\\ B\left(s\right)\end{array}\right),$$

(3)

where $\kappa \left(s\right)$ and $\tau \left(s\right)$ denote the curvature and torsion, respectively [15].

Since the Frenet frame becomes undefined when $\kappa \left(s\right)=0$, the Bishop frame (or parallel transport frame) offers a continuous alternative. For a spacelike curve $\phi \left(s\right)$, the Bishop frame $\{T,N_1,N_2\}$ satisfies [6,11]

$$\left\{\begin{array}{c}{T}^{\prime }\left(s\right)={\zeta }_1\left(s\right)N_1\left(s\right)+{\zeta }_2\left(s\right)N_2\left(s\right),\hfill \\ N_1^{\prime }\left(s\right)=-{\zeta }_1\left(s\right)T\left(s\right),\hfill \\ N_2^{\prime }\left(s\right)=-{\zeta }_2\left(s\right)T\left(s\right),\hfill \end{array}\right.$$

(4)

where ${\zeta }_1\left(s\right)$ and ${\zeta }_2\left(s\right)$ are the Bishop curvatures.

For a spacelike curve with a timelike principal normal and spacelike binormal, the Type-2 Bishop frame $\{U,V,B\}$ in ${\mathbf{E}}_1^3$ is defined by [16]

$${\displaystyle \frac{d}{ds}}\left(\begin{array}{c}U\left(s\right)\\ V\left(s\right)\\ B\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& 0& {\zeta }_1\left(s\right)\\ 0& 0& {\zeta }_2\left(s\right)\\ {\zeta }_1\left(s\right)& -{\zeta }_2\left(s\right)& 0\end{array}\right)\left(\begin{array}{c}U\left(s\right)\\ V\left(s\right)\\ B\left(s\right)\end{array}\right),$$

(5)

where

$${\zeta }_1\left(s\right)=\tau \left(s\right)\cosh \theta \left(s\right),\hspace{1em}{\zeta }_2\left(s\right)=\tau \left(s\right)\sinh \theta \left(s\right),$$

(6)

and the hyperbolic angle $\theta \left(s\right)$ is given by

$$\theta \left(s\right)={\int }_0^s\kappa \left(t\right) dt.$$

(7)

The relation between the Frenet and Type-2 Bishop frames is

$$\left(\begin{array}{c}T\\ N\\ B\end{array}\right)=\left(\begin{array}{ccc}\sinh \theta \left(s\right)& \cosh \theta \left(s\right)& 0\\ \cosh \theta \left(s\right)& \sinh \theta \left(s\right)& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}U\\ V\\ B\end{array}\right).$$

(8)

Let $\Phi =\Phi (u,v)$ be a regular surface in ${\mathbf{E}}_1^3$ with tangent vectors

$${\Phi }_u={\displaystyle \frac{\partial \Phi }{\partial u}},\hspace{1em}{\Phi }_v={\displaystyle \frac{\partial \Phi }{\partial v}}.$$

The first fundamental form is

$$I=E d{u}^2+2F du dv+G d{v}^2,$$

(9)

where

$$E=⟨{\Phi }_u,{\Phi }_u⟩,\hspace{1em}F=⟨{\Phi }_u,{\Phi }_v⟩,\hspace{1em}G=⟨{\Phi }_v,{\Phi }_v⟩.$$

The unit normal vector n (spacelike or timelike depending on the surface type) is defined by

$$n={\displaystyle \frac{{\Phi }_u\times {\Phi }_v}{\sqrt{|⟨{\Phi }_u\times {\Phi }_v,{\Phi }_u\times {\Phi }_v⟩|}}}.$$

The second fundamental form is then given by

$$II=e d{u}^2+2f du dv+g d{v}^2,$$

where

$$e=⟨{\Phi }_{uu},n⟩,\hspace{1em}f=⟨{\Phi }_{uv},n⟩,\hspace{1em}g=⟨{\Phi }_{vv},n⟩.$$

The intrinsic and extrinsic curvatures of $\Phi (u,v)$ are described by the Gaussian curvature K and mean curvature H, respectively [17,18,19,20,21]:

$$K={\displaystyle \frac{eg-f^2}{EG-F^2}},\hspace{1em}H={\displaystyle \frac{Eg-2Ff+Ge}{2(EG-F^2)}}.$$

(10)

3. On the Geometry of Osculating Ruled Surfaces in Minkowski 3-Space

In this section, we develop the concept of osculating ruled surfaces defined through the Frenet frame in Minkowski 3-space ${\mathbf{E}}_1^3$. The construction relies on the geometric symmetry associated with osculating curves. We analyze the relationship between these surfaces and the curvature functions of their generating curves and examine several intrinsic geometric properties derived from the Frenet frame of ${\mathbf{E}}_1^3$.

Let $\phi =\phi \left(\sigma \right)$ be a spacelike curve whose principal normal vector is timelike and whose binormal vector is spacelike, parameterized by its arc-length $\sigma$. We define the osculating ruled surface whose rulings lie in the osculating plane $\{T,N\}$ of the curve $\phi$ by

$${\mathcal{R}}^{(\phi ,\ell )}(\sigma ,\upsilon )=\phi \left(\sigma \right)+\upsilon \ell \left(\sigma \right),\hspace{1em}\ell \left(\sigma \right)={\varsigma }_1\left(\sigma \right) T\left(\sigma \right)+{\varsigma }_2\left(\sigma \right) N\left(\sigma \right),$$

(11)

where $\{T,N,B\}$ denotes the Frenet frame described in Equations (2) and (3). For simplicity, we denote ${\varsigma }_1^{\prime }={\displaystyle \frac{d{\varsigma }_1}{d\sigma }}$ and ${\varsigma }_2^{\prime }={\displaystyle \frac{d{\varsigma }_2}{d\sigma }}$. The partial derivatives of the parametrization are

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\sigma }^{(\phi ,\ell )}& =\left[1+\upsilon ({\varsigma }_1^{\prime }+{\varsigma }_2\kappa )\right]T+\left[\upsilon ({\varsigma }_1\kappa +{\varsigma }_2^{\prime })\right]N+\left[\upsilon {\varsigma }_2\tau \right]B,\hfill \\ \hfill {\mathcal{R}}_{\upsilon }^{(\phi ,\ell )}& ={\varsigma }_1\left(\sigma \right) T\left(\sigma \right)+{\varsigma }_2\left(\sigma \right) N\left(\sigma \right).\hfill \end{array}$$

Using the Minkowski inner product, the coefficients of the first fundamental form are computed as

$$\begin{array}{cc}\hfill E_{{\mathcal{R}}^{(\phi ,\ell )}}& =⟨{\mathcal{R}}_{\sigma }^{(\phi ,\ell )},{\mathcal{R}}_{\sigma }^{(\phi ,\ell )}⟩={\left(1+\upsilon ({\varsigma }_1^{\prime }+{\varsigma }_2\kappa )\right)}^2-{\upsilon }^2{({\varsigma }_1\kappa +{\varsigma }_2^{\prime })}^2+{\upsilon }^2{\varsigma }_2^2{\tau }^2,\hfill \\ \hfill F_{{\mathcal{R}}^{(\phi ,\ell )}}& =⟨{\mathcal{R}}_{\sigma }^{(\phi ,\ell )},{\mathcal{R}}_{\upsilon }^{(\phi ,\ell )}⟩={\varsigma }_1\left(1+\upsilon ({\varsigma }_1^{\prime }+{\varsigma }_2\kappa )\right)-{\varsigma }_2\left(\upsilon ({\varsigma }_1\kappa +{\varsigma }_2^{\prime })\right),\hfill \\ \hfill G_{{\mathcal{R}}^{(\phi ,\ell )}}& =⟨{\mathcal{R}}_{\upsilon }^{(\phi ,\ell )},{\mathcal{R}}_{\upsilon }^{(\phi ,\ell )}⟩={\varsigma }_1^2-{\varsigma }_2^2.\hfill \end{array}$$

(12)

The discriminant of the first fundamental form is then

$$\begin{array}{cc}\hfill \Xi (\sigma ,\upsilon )& =E_{{\mathcal{R}}^{(\phi ,\ell )}}{G}_{{\mathcal{R}}^{(\phi ,\ell )}}-F_{\mathcal{R}{(\phi ,\ell )}^2}\hfill \\ & ={({\varsigma }_1^2-{\varsigma }_2^2)}^2\left[{\left(1+\upsilon ({\varsigma }_1^{\prime }+{\varsigma }_2\kappa )\right)}^2-{\upsilon }^2{({\varsigma }_1\kappa +{\varsigma }_2^{\prime })}^2+{\upsilon }^2{\varsigma }_2^2{\tau }^2\right]\hfill \\ & \hspace{1em}-{\left[{\varsigma }_1\left(1+\upsilon ({\varsigma }_1^{\prime }+{\varsigma }_2\kappa )\right)-{\varsigma }_2\left(\upsilon ({\varsigma }_1\kappa +{\varsigma }_2^{\prime })\right)\right]}^2.\hfill \end{array}$$

The surface normal and second fundamental form coefficients are given by

$$\begin{array}{cc}\hfill {\mathrm{N}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )& ={\displaystyle \frac{{\mathcal{R}}_{\sigma }^{(\phi ,\ell )}\times {\mathcal{R}}_{\upsilon }^{(\phi ,\ell )}}{\parallel {\mathcal{R}}_{\sigma }^{(\phi ,\ell )}\times {\mathcal{R}}_{\upsilon }^{(\phi ,\ell )}\parallel }}\hfill \\ \hfill \hspace{1em}& ={\displaystyle \frac{1}{\Delta (\sigma ,\upsilon )}}\{[-\upsilon {\varsigma }_2^2\tau ]T\left(\sigma \right)+\left[\upsilon {\varsigma }_1{\varsigma }_2\tau \right]N\left(\sigma \right)+[{\varsigma }_2+\upsilon ({\varsigma }_2{\varsigma }_1^{\prime }-{\varsigma }_1{\varsigma }_2^{\prime }\hfill \\ & +\kappa ({\varsigma }_2^2-{\varsigma }_1^2))]B\left(\sigma \right)\},\hfill \end{array}$$

(13)

where

$$\Delta (\sigma ,\upsilon )=\sqrt{{\upsilon }^2{\varsigma }_2^2{\tau }^2({\varsigma }_2^2-{\varsigma }_1^2)+{\left[{\varsigma }_2+\upsilon ({\varsigma }_2{\varsigma }_1^{\prime }-{\varsigma }_1{\varsigma }_2^{\prime }+\kappa ({\varsigma }_2^2-{\varsigma }_1^2))\right]}^2}.$$

The coefficients of the second fundamental form are

$$e_{{\mathcal{R}}^{(\phi ,\ell )}}={\displaystyle \frac{{\tilde{e}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )}{\Delta (\sigma ,\upsilon )}},\hspace{1em}{f}_{{\mathcal{R}}^{(\phi ,\ell )}}={\displaystyle \frac{{\tilde{f}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )}{\Delta (\sigma ,\upsilon )}},\hspace{1em}{g}_{{\mathcal{R}}^{(\phi ,\ell )}}=0,$$

(14)

where

$${\tilde{f}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )={\varsigma }_2^2\tau -2\upsilon {\varsigma }_2\tau (\kappa {\varsigma }_1^2+{\varsigma }_1{\varsigma }_2^{\prime }).$$

(The full expression for ${\tilde{e}}_{{\mathcal{R}}^{(\phi ,\ell )}}$ is omitted for brevity.) The Gaussian and mean curvatures of the osculating ruled surface are obtained as

$$\begin{array}{cc}\hfill K_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )& =-{\displaystyle \frac{{\left[{\varsigma }_2^2\tau -2\upsilon {\varsigma }_2\tau (\kappa {\varsigma }_1^2+{\varsigma }_1{\varsigma }_2^{\prime })\right]}^2}{\Delta (\sigma ,\upsilon ) \Xi (\sigma ,\upsilon )}},\hfill \\ \hfill H_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )& ={\displaystyle \frac{\left(\begin{array}{c}({\varsigma }_1^2-{\varsigma }_2^2) {\tilde{e}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )-2[{\varsigma }_1(1+\upsilon ({\varsigma }_1^{\prime }+{\varsigma }_2\kappa ))\\ -{\varsigma }_2\left(\upsilon ({\varsigma }_1\kappa +{\varsigma }_2^{\prime })\right)]{\tilde{f}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )\end{array}\right)}{2\Delta (\sigma ,\upsilon ) \Xi (\sigma ,\upsilon )}}.\hfill \end{array}$$

(15)

Theorem 1. 

The osculating ruled surface ${\mathcal{R}}^{(\phi ,\ell )}(\sigma ,\upsilon )$ in ${\mathbf{E}}_1^3$ is developable if and only if

$${\varsigma }_2\left(\sigma \right)=0\hspace{1em}\mathrm{or}\hspace{1em}\tau \left(\sigma \right)=0\hspace{1em}\mathit{for} \mathit{all} \sigma .$$

Proof. 

A ruled surface is developable if and only if ${\phi }^{\prime }$, ℓ, and ${\ell }^{\prime }$ are linearly dependent for every $\sigma$, i.e., $\det ({\phi }^{\prime }\left(\sigma \right),\ell \left(\sigma \right),{\ell }^{\prime }\left(\sigma \right))=0$. Expressing these vectors in the Frenet basis: ${\phi }^{\prime }=(1,0,0)$, $\ell =({\varsigma }_1,{\varsigma }_2,0)$, and ${\ell }^{\prime }=(a,b,c)$, where $a={\varsigma }_1^{\prime }+{\varsigma }_2\kappa$, $b={\varsigma }_1\kappa +{\varsigma }_2^{\prime }$, and $c={\varsigma }_2\tau$, we obtain

$$\det \left(\begin{array}{ccc}1& {\varsigma }_1& a\\ 0& {\varsigma }_2& b\\ 0& 0& c\end{array}\right)={\varsigma }_{2}c=\tau {\varsigma }_2^2.$$

Thus, the surface is developable if and only if $\tau \left(\sigma \right){\varsigma }_2{\left(\sigma \right)}^2=0$ for all $\sigma$, which gives the stated condition. □

Theorem 2. 

Let${\mathcal{R}}^{(\phi ,\ell )}(\sigma ,\upsilon )$ be an osculating ruled surface in ${\mathbf{E}}_1^3$. Then, for each fixed σ:

• If $\tau \left(\sigma \right) {\varsigma }_2\left(\sigma \right)\ne 0$, the surface ${\mathcal{R}}^{(\phi ,\ell )}$ has no singular points at that σ.
• If ${\varsigma }_2\left(\sigma \right)=0$ and $\kappa \left(\sigma \right) {\varsigma }_1\left(\sigma \right)\ne 0$, then the base curve (corresponding to $\upsilon =0$) is the singular edge at that σ.
• If $\tau \left(\sigma \right)=0$ and ${\varsigma }_2\left(\sigma \right)\ne 0$, then singularities appear when

  $$\upsilon =-{\displaystyle \frac{{\varsigma }_2}{a{\varsigma }_2-b{\varsigma }_1}},$$

  provided $a{\varsigma }_2-b{\varsigma }_1\ne 0$.

Proof. 

From (13), the unit normal vector can be written as

$${\mathrm{N}}_{{\mathcal{R}}^{(\phi ,\ell )}}(\sigma ,\upsilon )=(-\upsilon \tau {\varsigma }_2^2)T+\left(\upsilon \tau {\varsigma }_1{\varsigma }_2\right)N+[{\varsigma }_2+\upsilon (a{\varsigma }_2-b{\varsigma }_1)]B,$$

where $a={\varsigma }_1^{\prime }+{\varsigma }_2\kappa$ and $b={\varsigma }_1\kappa +{\varsigma }_2^{\prime }$.

• If $\tau {\varsigma }_2\ne 0$, the B-component at $\upsilon =0$ equals ${\varsigma }_2\ne 0$, ensuring ${\mathrm{N}}_{{\mathcal{R}}^{(\phi ,\ell )}}\ne 0$. Hence, no singularity occurs.
• If ${\varsigma }_2=0$, the T and N components vanish, and the B-component reduces to

  $${\varsigma }_2+\upsilon (a{\varsigma }_2-b{\varsigma }_1)=-\upsilon b{\varsigma }_1.$$
  Thus,

  $${\mathrm{N}}_{{\mathcal{R}}^{(\phi ,\ell )}}=-\upsilon \kappa {\varsigma }_1^2 B,$$

  which vanishes only at $\upsilon =0$, confirming that the base curve forms the singular edge.
• If $\tau =0$ and ${\varsigma }_2\ne 0$, then

  $${\varsigma }_2+\upsilon (a{\varsigma }_2-b{\varsigma }_1)=0\hspace{1em}\Rightarrow \hspace{1em}\upsilon =-{\displaystyle \frac{{\varsigma }_2}{a{\varsigma }_2-b{\varsigma }_1}}.$$
  If the denominator vanishes, ${\mathrm{N}}_{{\mathcal{R}}^{(\phi ,\ell )}}$ remains nonzero and no singularity appears.

This concludes the proof. □

4. Geometric Analysis of Osculating Type-2 Ruled Surfaces in Minkowski 3-Space

In this section, we establish the formulation of osculating type-2 ruled surfaces constructed via the type-2 Bishop frame. The construction relies on the geometric symmetry associated with osculating curves. These surfaces are investigated through the curvature functions of their generating base curve. Moreover, explicit analytical expressions are obtained for their Gaussian and mean curvatures, and several fundamental surface curves are examined in detail. It is observed that the differential geometric properties of such surfaces, described within the type-2 Bishop frame in ${\mathbf{E}}_1^3$, display structural resemblance to the rectifying ruled surfaces formulated using the Frenet frame. The results further demonstrate a close geometric link between osculating type-2 ruled surfaces based on the Bishop frame and rectifying ruled surfaces derived from the Frenet framework.

An osculating type-2 ruled surface generated by a curve $\phi$ is defined by

$${\mathcal{R}}^{(\mu ,\lambda )}(\sigma ,\upsilon )=\mu \left(\sigma \right)+\upsilon \lambda \left(\sigma \right),\hspace{1em}\lambda \left(\sigma \right)={\varsigma }_1\left(\sigma \right)U\left(\sigma \right)+{\varsigma }_2\left(\sigma \right)V\left(\sigma \right),$$

(16)

where ${\varsigma }_1\left(\sigma \right)$ and ${\varsigma }_2\left(\sigma \right)$ are smooth scalar functions.

We define

$$\tilde{f}\left(\sigma \right)={\varsigma }_1{\zeta }_1+{\varsigma }_2{\zeta }_2,\hspace{1em}\tilde{g}(\sigma ,\upsilon )=1+\upsilon {\varsigma }_2{\left({\displaystyle \frac{{\varsigma }_1}{{\varsigma }_2}}\right)}^{\prime }.$$

The partial derivatives of ${\mathcal{R}}^{(\mu ,\lambda )}$ are then given by

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\sigma }^{(\mu ,\lambda )}(\sigma ,\upsilon )& =T+\upsilon ({\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V-\tilde{f}B),\hfill \\ \hfill {\mathcal{R}}_{\upsilon }^{(\mu ,\lambda )}(\sigma ,\upsilon )& =\lambda \left(\sigma \right)={\varsigma }_{1}U+{\varsigma }_{2}V.\hfill \end{array}$$

(17)

Using the vector cross product, we obtain

$${\mathcal{R}}_{\sigma }^{(\mu ,\lambda )}\times {\mathcal{R}}_{\upsilon }^{(\mu ,\lambda )}=\upsilon {\varsigma }_2\tilde{f} U-\upsilon {\varsigma }_1\tilde{f} V+{\varsigma }_2\tilde{g} B.$$

(18)

The squared norm of this vector is

$$\parallel {\mathcal{R}}_{\sigma }^{(\mu ,\lambda )}\times {\mathcal{R}}_{\upsilon }^{(\mu ,\lambda )}{\parallel }^2=({\varsigma }_1^2+{\varsigma }_2^2){\upsilon }^2{\tilde{f}}^{ 2}+{\varsigma }_2^2{\tilde{g}}^{ 2}.$$

Thus, the unit normal vector of ${\mathcal{R}}^{(\mu ,\lambda )}$ is expressed as

$${\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}}(\sigma ,\upsilon )={\displaystyle \frac{\upsilon {\varsigma }_2\tilde{f} U-\upsilon {\varsigma }_1\tilde{f} V+{\varsigma }_2\tilde{g} B}{\sqrt{({\varsigma }_1^2+{\varsigma }_2^2){\upsilon }^2{\tilde{f}}^{ 2}+{\varsigma }_2^2{\tilde{g}}^{ 2}}}}.$$

(19)

At $\upsilon =0$, it follows that ${\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}}=B$.

The first fundamental form coefficients are given by

$$\begin{array}{cc}\hfill E_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={(1+\upsilon {\varsigma }_1^{\prime })}^2+{\upsilon }^2{\left({\varsigma }_2^{\prime }\right)}^2+{\upsilon }^2{\tilde{f}}^{ 2},\hfill \\ \hfill F_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={\varsigma }_1+\upsilon ({\varsigma }_1{\varsigma }_1^{\prime }+{\varsigma }_2{\varsigma }_2^{\prime }),\hfill \\ \hfill G_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={\varsigma }_1^2+{\varsigma }_2^2.\hfill \end{array}$$

(20)

The coefficients of the second fundamental form,

$$e_{{\mathcal{R}}^{(\mu ,\lambda )}}=⟨{\mathcal{R}}_{\sigma \sigma }^{(\mu ,\lambda )},{\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}}⟩,\hspace{1em}{f}_{{\mathcal{R}}^{(\mu ,\lambda )}}=⟨{\mathcal{R}}_{\sigma \upsilon }^{(\mu ,\lambda )},{\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}}⟩,\hspace{1em}{g}_{{\mathcal{R}}^{(\mu ,\lambda )}}=⟨{\mathcal{R}}_{\upsilon \upsilon }^{(\mu ,\lambda )},{\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}}⟩,$$

become

$$\begin{array}{cc}\hfill e_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={\displaystyle \frac{{\upsilon }^2{\tilde{f}}^{ 2}({\varsigma }_1{\zeta }_2-{\varsigma }_2{\zeta }_1)+{\upsilon }^2\tilde{f}({\varsigma }_2{\varsigma }_1^{\prime \prime }-{\varsigma }_1{\varsigma }_2^{\prime \prime })-{\varsigma }_2\tilde{g}\left[{\zeta }_1(1+\upsilon {\varsigma }_1^{\prime })+\upsilon ({\zeta }_2{\varsigma }_2^{\prime }+\widetilde{f^{\prime }})\right]}{\sqrt{({\varsigma }_1^2+{\varsigma }_2^2){\upsilon }^2{\tilde{f}}^{ 2}+{\varsigma }_2^2{\tilde{g}}^{ 2}}}},\hfill \\ \hfill f_{{\mathcal{R}}^{(\mu ,\lambda )}}& =0,\hfill \\ \hfill g_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={\displaystyle \frac{\tilde{f} [\upsilon ({\varsigma }_1^{\prime }{\varsigma }_2-{\varsigma }_1{\varsigma }_2^{\prime })-{\varsigma }_2\tilde{g}]}{\sqrt{({\varsigma }_1^2+{\varsigma }_2^2){\upsilon }^2{\tilde{f}}^{ 2}+{\varsigma }_2^2{\tilde{g}}^{ 2}}}}.\hfill \end{array}$$

(21)

Hence, the Gaussian and mean curvatures of ${\mathcal{R}}^{(\mu ,\lambda )}$ are

$$\begin{array}{cc}\hfill K_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={\displaystyle \frac{{\tilde{f}}^{ 2}{\left(\upsilon ({\varsigma }_1^{\prime }{\varsigma }_2-{\varsigma }_1{\varsigma }_2^{\prime })-{\varsigma }_2\tilde{g}\right)}^2}{{\left(({\varsigma }_1^2+{\varsigma }_2^2){\upsilon }^2{\tilde{f}}^{ 2}+{\varsigma }_2^2{\tilde{g}}^{ 2}\right)}^2}},\hfill \\ \hfill H_{{\mathcal{R}}^{(\mu ,\lambda )}}& ={\displaystyle \frac{\tilde{f}\left(\begin{array}{c}{\upsilon }^2({\varsigma }_1^2+{\varsigma }_2^2)\left[\tilde{f}({\varsigma }_1{\zeta }_2-{\varsigma }_2{\zeta }_1)+{\varsigma }_2{\varsigma }_1^{″}-{\varsigma }_1{\varsigma }_2^{″}\right]\\ -\left[\upsilon ({\varsigma }_1^{\prime }{\varsigma }_2-{\varsigma }_1{\varsigma }_2^{\prime })-{\varsigma }_2\tilde{g}\right]\left[2{\varsigma }_1+\upsilon {({\varsigma }_1^2+{\varsigma }_2^2)}^{\prime }\right]\end{array}\right)}{- {\varsigma }_2\tilde{g}({\varsigma }_1^2+{\varsigma }_2^2)[{\zeta }_1(1+\upsilon {\varsigma }_1^{\prime })+\upsilon ({\zeta }_2{\varsigma }_2^{\prime }+\widetilde{f^{\prime }})]{\left(({\varsigma }_1^2+{\varsigma }_2^2){\upsilon }^2\widetilde{f^2}+{\varsigma }_2^2{\tilde{g}}^{ 2}\right)}^{3/2}}}.\hfill \end{array}$$

(22)

Theorem 3. 

Let ${\mathcal{R}}^{(\mu ,\lambda )}(\sigma ,\upsilon )=\mu \left(\sigma \right)+\upsilon \lambda \left(\sigma \right)$ be the osculating type-2 ruled surface in ${\mathbf{E}}_1^3$ defined by (16). Then, the surface ${\mathcal{R}}^{(\mu ,\lambda )}$ is regular at $(\sigma ,\upsilon )$ if and only if

$$\left(\tilde{f}\left(\sigma \right), \tilde{g}(\sigma ,\upsilon )\right)\ne (0,0).$$

(23)

Otherwise, the point is singular.

Proof. 

Since the type-2 Bishop frame vectors $\{U,V,B\}$ are orthonormal, the surface normal satisfies

$${\mathcal{R}}_{\sigma }^{(\mu ,\lambda )}\times {\mathcal{R}}_{\upsilon }^{(\mu ,\lambda )}=\upsilon {\varsigma }_2\tilde{f} U-\upsilon {\varsigma }_1\tilde{f} V+{\varsigma }_2\tilde{g} B.$$

Thus, the cross product vanishes only when $\tilde{f}=0$ and $\tilde{g}=0$. Hence, condition (23) ensures regularity. □

Theorem 4. 

The osculating type-2 ruled surface ${\mathcal{R}}^{(\mu ,\lambda )}(\sigma ,\upsilon )$ in ${\mathbf{E}}_1^3$ is developable if and only if

$$\det ({\mu }^{\prime },\lambda ,{\lambda }^{\prime })=0\hspace{1em}⟺\hspace{1em}\tilde{f}\left(\sigma \right)={\varsigma }_1{\zeta }_1+{\varsigma }_2{\zeta }_2=0.$$

(24)

Proof. 

Let the osculating type-2 ruled surface ${\mathcal{R}}^{(\mu ,\lambda )}(\sigma ,\upsilon )=\mu \left(\sigma \right)+\upsilon \lambda \left(\sigma \right)$ be defined by $\lambda \left(\sigma \right)={\varsigma }_1\left(\sigma \right)U\left(\sigma \right)+{\varsigma }_2\left(\sigma \right)V\left(\sigma \right)$. By differentiating $\lambda \left(\sigma \right)$ with respect to $\sigma$ and applying Equation (5), we obtain

$${\lambda }^{\prime }\left(\sigma \right)={\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+{\varsigma }_1{U}^{\prime }+{\varsigma }_2{V}^{\prime }={\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+({\varsigma }_1{\zeta }_1+{\varsigma }_2{\zeta }_2)B.$$

Let us denote $\tilde{f}\left(\sigma \right)={\varsigma }_1{\zeta }_1+{\varsigma }_2{\zeta }_2$. Then, ${\lambda }^{\prime }\left(\sigma \right)={\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+\tilde{f}B$. To determine when the ruled surface ${\mathcal{R}}^{(\mu ,\lambda )}$ is developable, we use the classical criterion

$$\det ({\mu }^{\prime },\lambda ,{\lambda }^{\prime })=0.$$

Since ${\mu }^{\prime }=T$, and the frame $\{U,V,B\}$ is orthonormal, we express the determinant in terms of this basis:

$$\det ({\mu }^{\prime },\lambda ,{\lambda }^{\prime })=\det (T, {\varsigma }_{1}U+{\varsigma }_{2}V, {\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+\tilde{f}B).$$

By expanding the determinant using the linearity property and the triple product formula $\det (A,B,C)=⟨A,B\times C⟩,$ we compute

$$({\varsigma }_{1}U+{\varsigma }_{2}V)\times ({\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+\tilde{f}B)={\varsigma }_1{\varsigma }_2^{\prime }(U\times V)-{\varsigma }_2{\varsigma }_1^{\prime }(U\times V)+{\varsigma }_1\tilde{f}(U\times B)+{\varsigma }_2\tilde{f}(V\times B).$$

Using the standard right-handed relations in the Type-2 Bishop frame, we obtain

$$({\varsigma }_{1}U+{\varsigma }_{2}V)\times ({\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+\tilde{f}B)=({\varsigma }_1{\varsigma }_2^{\prime }-{\varsigma }_2{\varsigma }_1^{\prime })B+{\varsigma }_1\tilde{f}V-{\varsigma }_2\tilde{f}U.$$

Now, since ${\mu }^{\prime }=T$ and T is orthogonal to U and V, we have $⟨T,U⟩=⟨T,V⟩=0$, and hence the determinant simplifies to

$$\det ({\mu }^{\prime },\lambda ,{\lambda }^{\prime })=⟨T,({\varsigma }_{1}U+{\varsigma }_{2}V)\times ({\varsigma }_1^{\prime }U+{\varsigma }_2^{\prime }V+\tilde{f}B)⟩=⟨T,-{\varsigma }_2\tilde{f}U+{\varsigma }_1\tilde{f}V⟩.$$

Since $⟨T,U⟩=0$ and $⟨T,V⟩=0$, the only contribution arises from the direction corresponding to B, giving

$$\det ({\mu }^{\prime },\lambda ,{\lambda }^{\prime })=-{\varsigma }_2\tilde{f}.$$

Therefore, the developability condition $\det ({\mu }^{\prime },\lambda ,{\lambda }^{\prime })=0$, is satisfied if and only if $\tilde{f}\left(\sigma \right)=0$, i.e., ${\varsigma }_1\left(\sigma \right){\zeta }_1\left(\sigma \right)+{\varsigma }_2\left(\sigma \right){\zeta }_2\left(\sigma \right)=0$. Therefore, the developability condition (24) is satisfied. □

Proposition 1. 

If ${\varsigma }_1,{\varsigma }_2\ne 0$ and $\tilde{f}=0$, then the singular set of the osculating type-2 ruled surface ${\mathcal{R}}^{(\mu ,\lambda )}$ is the curve

$$\chi \left(\sigma \right)=\mu \left(\sigma \right)+\upsilon \left(\sigma \right)\lambda \left(\sigma \right),\hspace{1em}\upsilon \left(\sigma \right)=-{\left[{\varsigma }_2{\left({\displaystyle \frac{{\zeta }_2}{{\zeta }_1}}\right)}^{\prime }\right]}^{-1}.$$

Proof. 

From $\tilde{f}=0$, we have ${\varsigma }_1{\zeta }_1+{\varsigma }_2{\zeta }_2=0$, which gives ${\varsigma }_1/{\varsigma }_2=-{\zeta }_2/{\zeta }_1$. Substituting into $\tilde{g}=0$ yields

$$0=1+\upsilon {\varsigma }_2{\left({\displaystyle \frac{{\varsigma }_1}{{\varsigma }_2}}\right)}^{\prime }=1-\upsilon {\varsigma }_2{\left({\displaystyle \frac{{\zeta }_2}{{\zeta }_1}}\right)}^{\prime },$$

which leads to the required formula for $\upsilon \left(\sigma \right)$. □

Corollary 1. 

If ${\lambda }^{\prime }\left(s\right)=0$, then $\tilde{f}=0$ and ${\zeta }_2/{\zeta }_1$ is constant. Hence, λ is constant, and the ruled surface degenerates into a plane. Consequently, there are no nontrivial cylindrical osculating type ruled surfaces.

Theorem 5. 

For the osculating type-2 ruled surface ${\mathcal{R}}^{(\mu ,\lambda )}(\sigma ,\upsilon )$ in ${\mathbf{E}}_1^3$ defined by (16), the following hold:

• The base curve $\mu \left(\sigma \right)$is a geodesic on ${\mathcal{R}}^{(\mu ,\lambda )}$.
• The base curve $\mu \left(\sigma \right)$is not asymptotic unless $\tilde{f}=0$.
• The base curve $\mu \left(\sigma \right)$is a line of curvature if and only if ${\zeta }_2=0$.

Proof. 

• For $\upsilon =0$, the unit normal (19) reduces to ${\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}}=B$, and the acceleration of the base curve is ${\mu }^{″}={\zeta }_{1}U+{\zeta }_{2}V$. Since

  $$⟨{\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}},{\mu }^{″}⟩=⟨B,{\zeta }_{1}U+{\zeta }_{2}V⟩=0,$$

  the geodesic curvature of the base curve vanishes; hence, $\mu$ is a geodesic.
• The normal curvature ${\kappa }_n$ satisfies

  $${\kappa }_n={\displaystyle \frac{e_{{\mathcal{R}}^{(\mu ,\lambda )}} d{\sigma }^2+2f_{{\mathcal{R}}^{(\mu ,\lambda )}} d\sigma d\upsilon +g_{{\mathcal{R}}^{(\mu ,\lambda )}} d{\upsilon }^2}{E_{{\mathcal{R}}^{(\mu ,\lambda )}} d{\sigma }^2+2F_{{\mathcal{R}}^{(\mu ,\lambda )}} d\sigma d\upsilon +G_{{\mathcal{R}}^{(\mu ,\lambda )}} d{\upsilon }^2}}.$$
  For the base curve ($d\upsilon =0$), we get ${\kappa }_n=(e_{{\mathcal{R}}^{(\mu ,\lambda )}}/E_{{\mathcal{R}}^{(\mu ,\lambda )}}){|}_{\upsilon =0}$. As $e_{{\mathcal{R}}^{(\mu ,\lambda )}}{|}_{\upsilon =0}=-{\varsigma }_2{\zeta }_1$, the condition ${\kappa }_n=0$ implies ${\zeta }_1=0$, which contradicts the spacelike assumption. Thus, $\mu$ is not asymptotic unless $\tilde{f}=0$.
• A curve on ${\mathcal{R}}^{(\mu ,\lambda )}$ is a line of curvature when $f_{{\mathcal{R}}^{(\mu ,\lambda )}}=0$ and $(e_{{\mathcal{R}}^{(\mu ,\lambda )}}{G}_{{\mathcal{R}}^{(\mu ,\lambda )}}-g_{{\mathcal{R}}^{(\mu ,\lambda )}}{E}_{{\mathcal{R}}^{(\mu ,\lambda )}})=0$. For $\upsilon =0$, we have $f_{{\mathcal{R}}^{(\mu ,\lambda )}}=0$, and $e_{{\mathcal{R}}^{(\mu ,\lambda )}}{G}_{{\mathcal{R}}^{(\mu ,\lambda )}}-g_{{\mathcal{R}}^{(\mu ,\lambda )}}{E}_{{\mathcal{R}}^{(\mu ,\lambda )}}\propto {\varsigma }_1{\zeta }_2-{\varsigma }_2{\zeta }_1$, which reduces to ${\zeta }_2=0$.

□

Corollary 2. 

If ${\zeta }_2=0$, the type-2 Bishop frame $\{U,V,B\}$ reduces to $\{U,B\}$, and the surface ${\mathcal{R}}^{(\mu ,\lambda )}$ becomes planar.

Remark 1. 

It is worth noting that the Type-2 Bishop frame offers specific benefits when analyzing ruled surfaces in Minkowski 3-space. Unlike the standard Bishop frame, which is constructed for Euclidean spaces with a positive-definite metric, the Type-2 formulation incorporates a hyperbolic rotation that aligns naturally with the Lorentzian structure of ${\mathbf{E}}_1^3$. This adaptation makes the frame particularly effective for describing spacelike curves whose principal normal vector is timelike and whose binormal vector is spacelike. Because of this hyperbolic rotational behavior, the Type-2 Bishop frame maintains smoothness even when the curvature of the base curve vanishes and provides a more coherent representation of the causal and geometric properties of osculating type ruled surfaces in the Lorentzian context.

5. Examples

In this section we demonstrate the theoretical results through explicit examples of osculating type-2 ruled surfaces $\mathcal{R}(\sigma ,\upsilon )$ derived from various choices of base curves and type-2 Bishop frame data. These examples illustrate how the geometric features of the base curve affect the shape and curvature characteristics of the resulting surface. By modifying the parametrization of the generating curve and selecting different functional forms for ${\zeta }_1\left(s\right)$ and ${\zeta }_2\left(s\right)$, we construct a variety of osculating type-2 ruled surfaces that reveal diverse and intricate geometric behaviors.

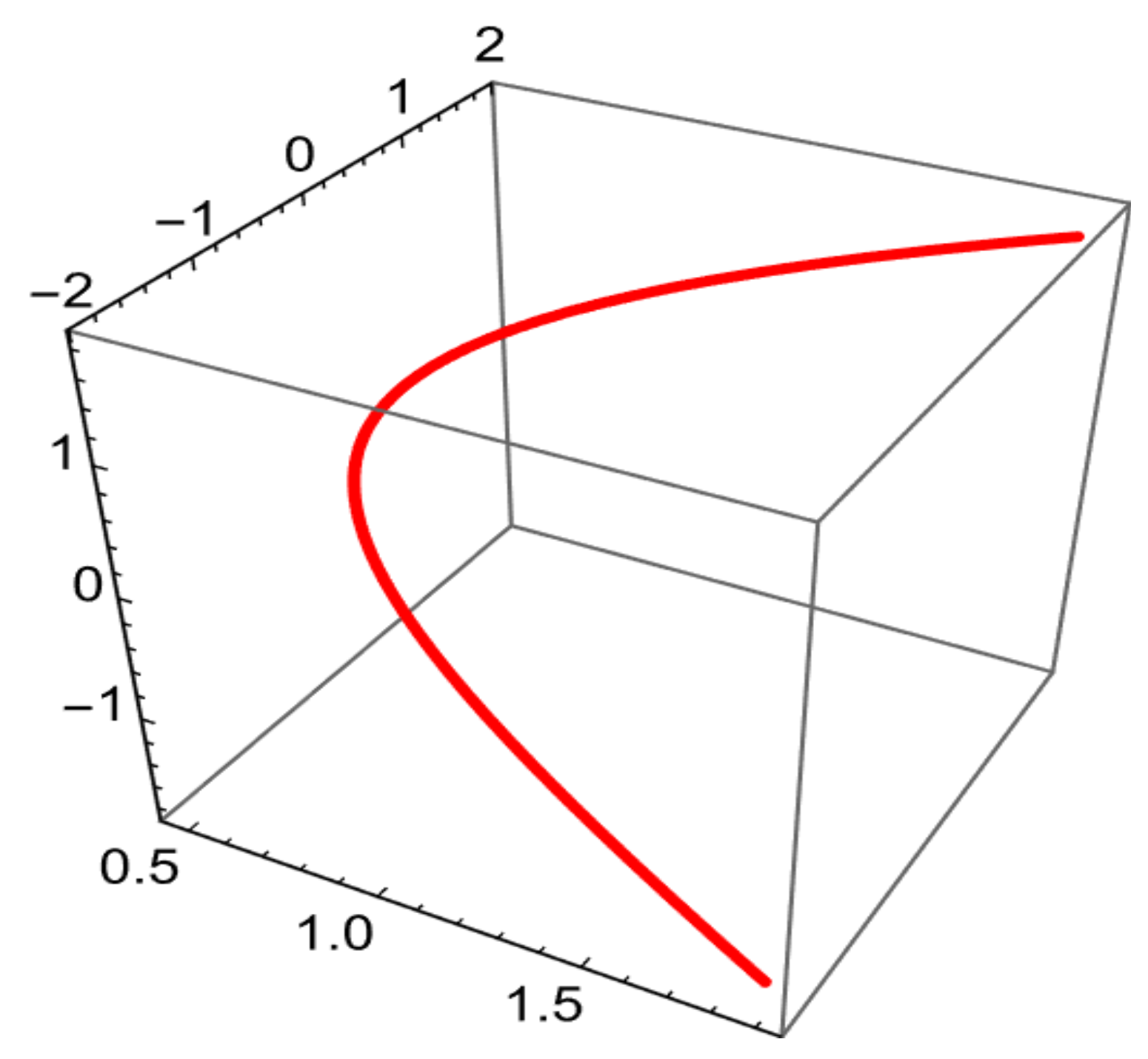
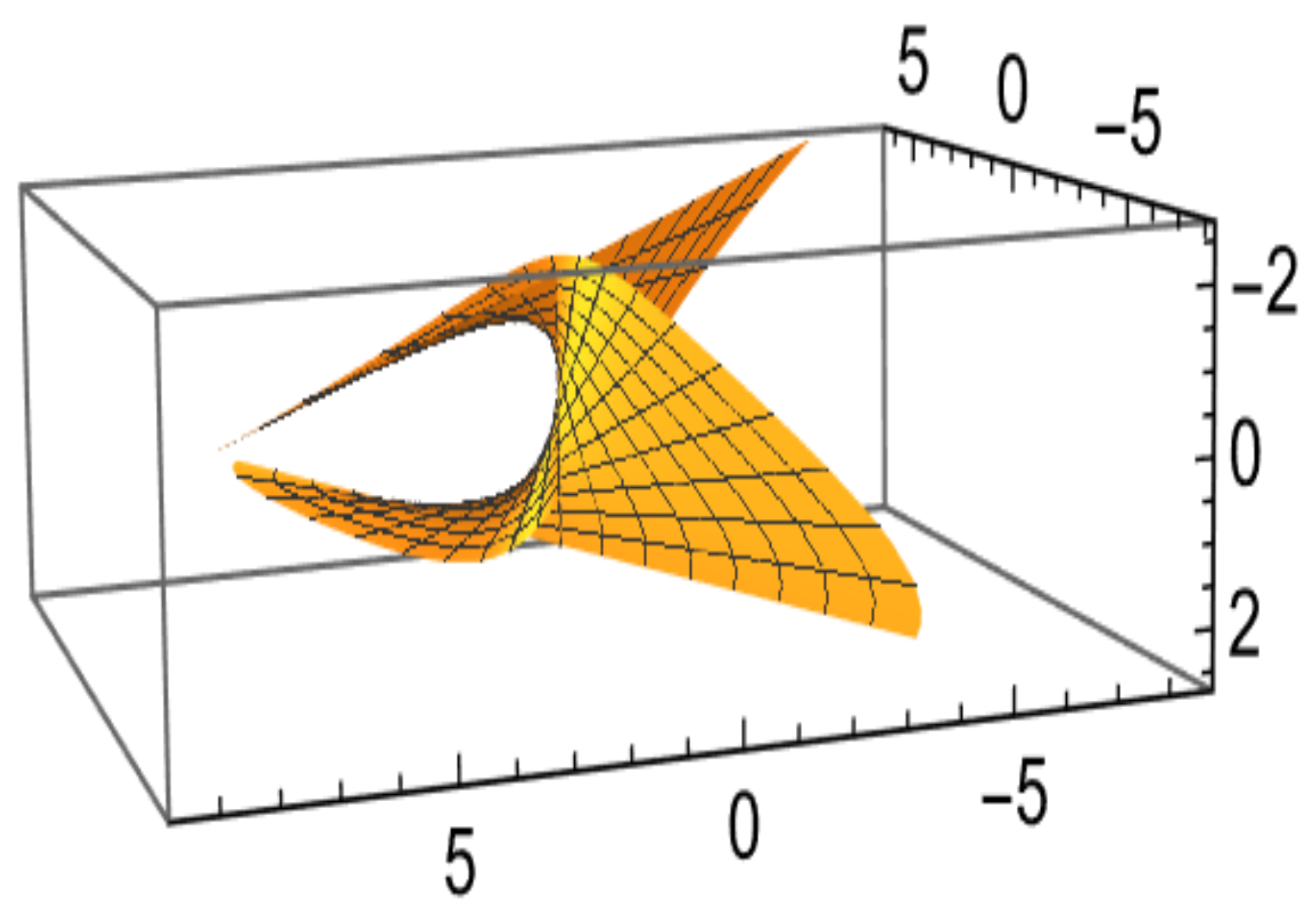
Example 1. 

Choose the spacelike unit-speed curve (see Figure 1)

$$\phi \left(\sigma \right)=\left(\frac{1}{2}\cosh \sigma , \frac{1}{2}\sinh \sigma , \frac{\sqrt{3}}{2} \sigma \right),\hspace{1em}s\in \mathbb{R}.$$

The associated Frenet frame vectors together with the curvature κ and the torsion τ along $\phi \left(\sigma \right)$ are computed as

$$\begin{array}{cc}\hfill T\left(\sigma \right)& =\left(\frac{1}{2}\cosh \sigma , \frac{1}{2}\sinh \sigma , \frac{\sqrt{3}}{2}\right),\hspace{1em}\kappa \left(\sigma \right)=\parallel T^{\prime }\left(\sigma \right)\parallel =\frac{1}{2}\hfill \\ \hfill N\left(\sigma \right)& =(\cosh \sigma , \sinh \sigma , 0),\hfill \\ \hfill B\left(\sigma \right)& =(0,0,-1),\hspace{1em}\tau \left(\sigma \right)={\displaystyle \frac{2\sqrt{3}}{ 3\cosh \left(2\sigma \right)+1 }}.\hfill \end{array}$$

The type-2 Bishop frame and curvatures can be written as

$$\begin{array}{cc}\hfill U\left(\sigma \right)& =\left(\frac{1}{4}\left(\cosh \left(\frac{3\sigma }{2}\right)+3\cosh \left(\frac{\sigma }{2}\right)\right), \frac{1}{4}\left(\sinh \left(\frac{3\sigma }{2}\right)+3\sinh \left(\frac{\sigma }{2}\right)\right), -\frac{\sqrt{3}}{2}\sinh \left(\frac{\sigma }{2}\right)\right),\hfill \\ \hfill V\left(\sigma \right)& =\left(\frac{1}{4}\left(-\sinh \left(\frac{3\sigma }{2}\right)+3\sinh \left(\frac{\sigma }{2}\right)\right), \frac{1}{4}\left(-\cosh \left(\frac{3\sigma }{2}\right)+3\cosh \left(\frac{\sigma }{2}\right)\right), \frac{\sqrt{3}}{2}\cosh \left(\frac{\sigma }{2}\right)\right),\hfill \\ \hfill {\zeta }_1\left(\sigma \right)& ={\displaystyle \frac{2\sqrt{3}}{3\cosh \left(2\sigma \right)+1}}\cosh \left(\frac{\sigma }{2}\right),\hspace{1em}{\zeta }_2\left(\sigma \right)={\displaystyle \frac{2\sqrt{3}}{3\cosh \left(2\sigma \right)+1}}\sinh \left(\frac{\sigma }{2}\right).\hfill \end{array}$$

Choose ${\varsigma }_1\left(\sigma \right)=\cos \sigma$ and ${\varsigma }_2\left(\sigma \right)=\sin \sigma$. Then the osculating ruled surface ${\mathcal{R}}^{(\phi ,\ell )}$ in ${\mathbf{E}}_1^3$ given as

$${\mathcal{R}}^{(\phi ,\ell )}(\sigma ,\upsilon )=\phi \left(\sigma \right)+\upsilon \ell \left(\sigma \right),\hspace{1em}\ell \left(\sigma \right)={\varsigma }_1\left(\sigma \right)T\left(\sigma \right)+{\varsigma }_2\left(\sigma \right)N\left(\sigma \right).$$

After substituting the explicit expressions, this becomes (see Figure 2)

$${\mathcal{R}}^{(\phi ,\ell )}(\sigma ,\upsilon )=\left(\begin{array}{c}\left({\displaystyle \frac{1}{2}}+\upsilon \left({\displaystyle \frac{1}{2}}\cos \sigma +\sin \sigma \right)\right)\cosh \sigma \\ \left({\displaystyle \frac{1}{2}}+\upsilon \left({\displaystyle \frac{1}{2}}\cos \sigma +\sin \sigma \right)\right)\sinh \sigma \\ \frac{\sqrt{3}}{2}\left(\sigma +\upsilon \cos \sigma \right)\end{array}\right).$$

Figure 1. The spacelike curve $\phi \left(\sigma \right)$, $\sigma \in [-2,2]$.

Figure 2. The osculating ruled surface ${\mathcal{R}}^{(\phi ,\ell )}$, $\sigma \in [-2,2]$ and $\upsilon \in [-2,2]$.

Take the osculating type-2 ruled surface

$${\mathcal{R}}^{(\phi ,\lambda )}(\sigma ,\upsilon )=\phi \left(\sigma \right)+\upsilon \lambda \left(\sigma \right),\hspace{1em}\lambda \left(\sigma \right)={\varsigma }_1\left(\sigma \right)U\left(\sigma \right)+{\varsigma }_2\left(\sigma \right)V\left(\sigma \right),$$

then (see Figure 3, Figure 4 and Figure 5)

$${\mathcal{R}}^{(\phi ,\lambda )}(\sigma ,\upsilon )={\displaystyle \frac{1}{2}}\left(\begin{array}{c}\cosh \sigma +{\displaystyle \frac{\upsilon \cos \sigma }{2}}\left(\cosh \left(\frac{3\sigma }{2}\right)+3\cosh \left(\frac{\sigma }{2}\right)\right)+{\displaystyle \frac{\upsilon \sin \sigma }{2}}\left(-\sinh \left(\frac{3\sigma }{2}\right)+3\sinh \left(\frac{\sigma }{2}\right)\right)\\ \sinh \sigma +{\displaystyle \frac{\upsilon \cos \sigma }{2}}\left(\sinh \left(\frac{3\sigma }{2}\right)+3\sinh \left(\frac{\sigma }{2}\right)\right)+{\displaystyle \frac{\upsilon \sin \sigma }{2}}\left(-\cosh \left(\frac{3\sigma }{2}\right)+3\cosh \left(\frac{\sigma }{2}\right)\right)\\ \sqrt{3} \upsilon \left(\sigma -\cos \sigma \sinh \left(\frac{\sigma }{2}\right)+\sin \sigma \cosh \left(\frac{\sigma }{2}\right)\right)\end{array}\right).$$

Figure 3. The osculating ruled surface ${\mathcal{R}}^{(\phi ,\lambda )}$, $\sigma \in [-2,2]$ and $\upsilon \in [-2,2]$.

Figure 4. Gaussian curvature $K_{{\mathcal{R}}^{(\mu ,\lambda )}}({\zeta }_1,{\zeta }_2)$.

Figure 5. Mean curvature $H_{{\mathcal{R}}^{(\mu ,\lambda )}}({\zeta }_1,{\zeta }_2)$.

The outcomes obtained in Example 1 are interpreted in relation to the theoretical framework presented in the preceding sections. By utilizing the computed Bishop curvatures ${\zeta }_1\left(s\right)$ and ${\zeta }_2\left(s\right)$, we examined the condition for developability described in Theorem 1, where $\tilde{f}\left(\sigma \right)={\varsigma }_1{\zeta }_1+{\varsigma }_2{\zeta }_2=0$. The numerical evaluation indicates that this equality holds for specific parameter values, implying that the corresponding osculating type-2 ruled surface becomes developable in those regions. Additionally, the behavior of the base curve $\phi \left(\sigma \right)$ was analyzed to determine its geometric role on the surface. It was found that $⟨{\mathcal{N}}_{{\mathcal{R}}^{(\mu ,\lambda )}},{\phi }^{″}⟩=0$, confirming that the base curve satisfies the geodesic condition established in Theorem 5 These findings demonstrate a clear consistency between the theoretical predictions and the computed examples, showing how variations in ${\zeta }_1$ and ${\zeta }_2$ influence the developability and geodesic properties of the osculating type-2 ruled surface. Thus, this example effectively bridges the analytical results with their geometric interpretations.

Example 2. 

Consider a spacelike curve φ parametrized by arc-length parametrized given by

$$\phi \left(\sigma \right)=\left(24\cosh \left(\frac{\sigma }{24\sqrt{5}}\right), 24\sinh \left(\frac{\sigma }{24\sqrt{5}}\right), \frac{2}{\sqrt{5}}\sigma \right),$$

so that $⟨{\phi }^{\prime }\left(\sigma \right),{\phi }^{\prime }\left(\sigma \right)⟩=1$. We evaluate every quantity at the sample point ${\sigma }_0=0$ (and parameter ${\upsilon }_0=0$ on the ruling). The numerical evaluation at $\sigma =0$ gives

$$\phi \left(0\right)=(24,0,0),$$

$${\phi }^{\prime }\left(0\right)=r^{\prime }\left(0\right)=(0, 0.4472135955, 0.8944271910),$$

$${\phi }^{″}\left(0\right)=(0.0071054273576, 0, 0).$$

Using the Lorentzian inner product, we get

$$\begin{array}{cc}\hfill T\left(0\right)& =(0, 0.4472135955, 0.8944271910),\hspace{1em}\kappa \left(\sigma \right)=0.0071054273576.\hfill \\ \hfill N\left(0\right)& =(1,0,0),\hfill \\ \hfill B\left(0\right)& =(0,0.894427190999916,-0.447213595499958),\hspace{1em}\tau \left(0\right)=-0.024456993503903963.\hfill \end{array}$$

The hyperbolic angle $\theta \left(\sigma \right)={\int }_0^{\sigma }\kappa \left(u\right) du$ satisfies $\theta \left(0\right)=0$. The Frenet-to-Bishop relations give at $\sigma =0$

$$U\left(0\right)=N\left(0\right)=(1,0,0),\hspace{1em}V\left(0\right)=T\left(0\right)=(0,0.4472135955,0.8944271910),\hspace{1em}B\left(0\right) \mathrm{as} \mathrm{above}.$$

The Bishop ODE coefficients at $\sigma =0$ are

$${\zeta }_1\left(0\right)=\tau \left(0\right)\cosh \theta \left(0\right)=\tau \left(0\right)=-0.0244569935,\hspace{1em}{\zeta }_2\left(0\right)=\tau \left(0\right)\sinh \theta \left(0\right)=0.$$

Take the osculating director

$$\lambda \left(\sigma \right)={\varsigma }_{1}U\left(\sigma \right)+{\varsigma }_{2}V\left(\sigma \right),\hspace{1em}{\varsigma }_1={\varsigma }_2=0.6.$$

At $\sigma =0$:

$$\lambda \left(0\right)=0.6 U\left(0\right)+0.6 V\left(0\right)=(0.6, 0.2683281573, 0.5366563146).$$

Differentiate using type-2 Bishop ODE:$U^{\prime }={\zeta }_{1}B, V^{\prime }={\zeta }_{2}B$, so $U^{\prime }\left(0\right)={\zeta }_1\left(0\right)B\left(0\right), V^{\prime }\left(0\right)=0$.Hence

$${\lambda }^{\prime }\left(0\right)={\varsigma }_1{U}^{\prime }\left(0\right)+{\varsigma }_2{V}^{\prime }\left(0\right)={\varsigma }_1{\zeta }_1\left(0\right)B\left(0\right)=0.6·(-0.0244569935) B\left(0\right).$$

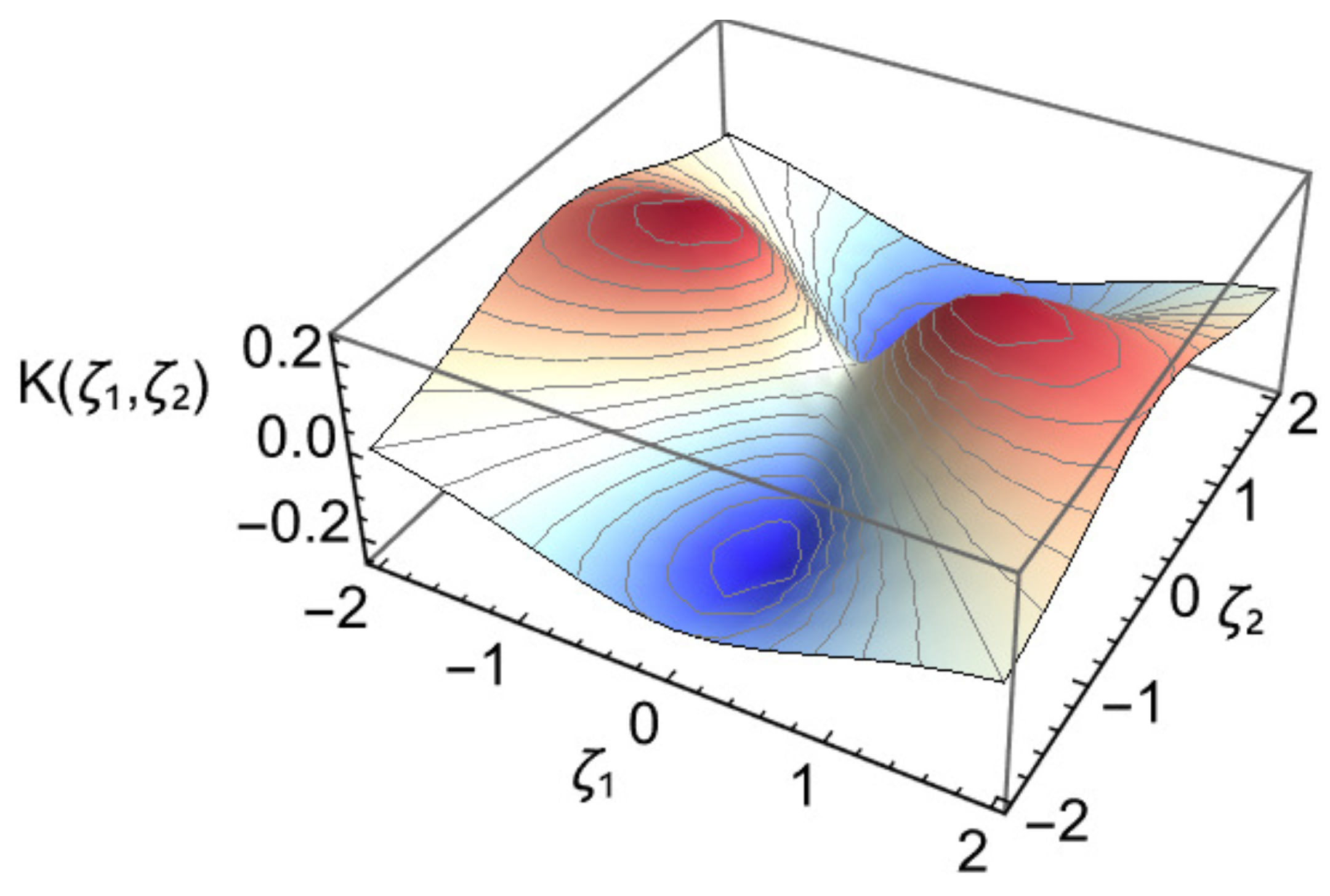
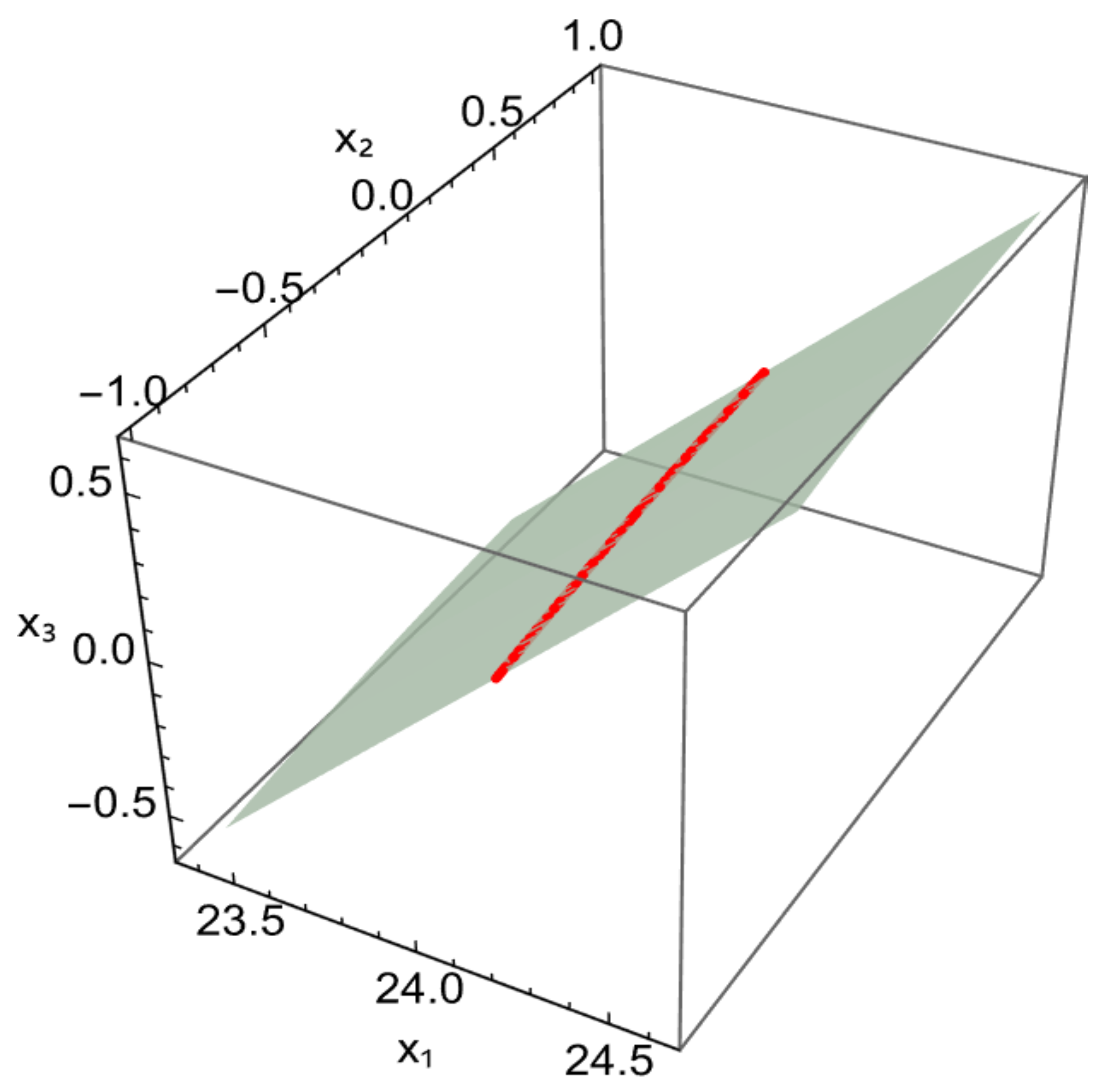
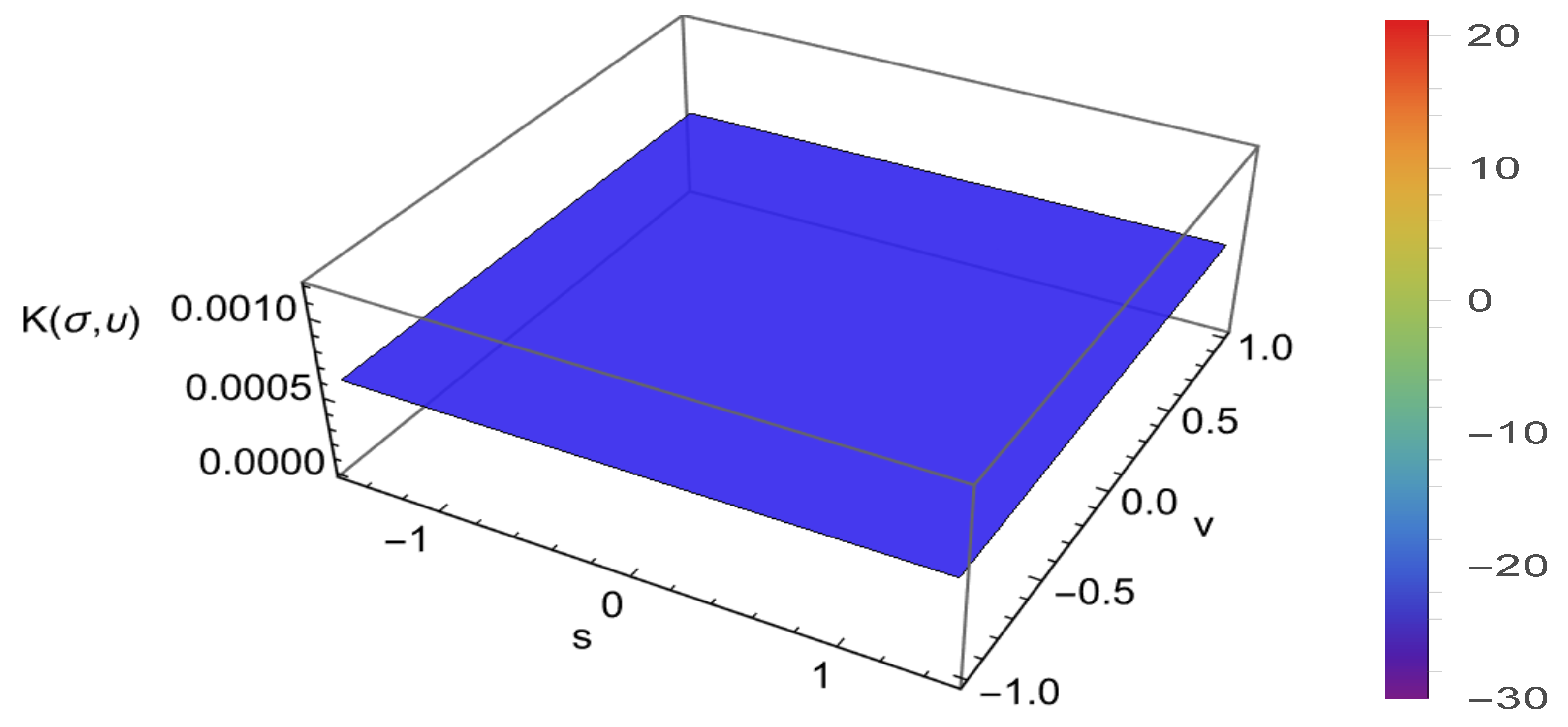
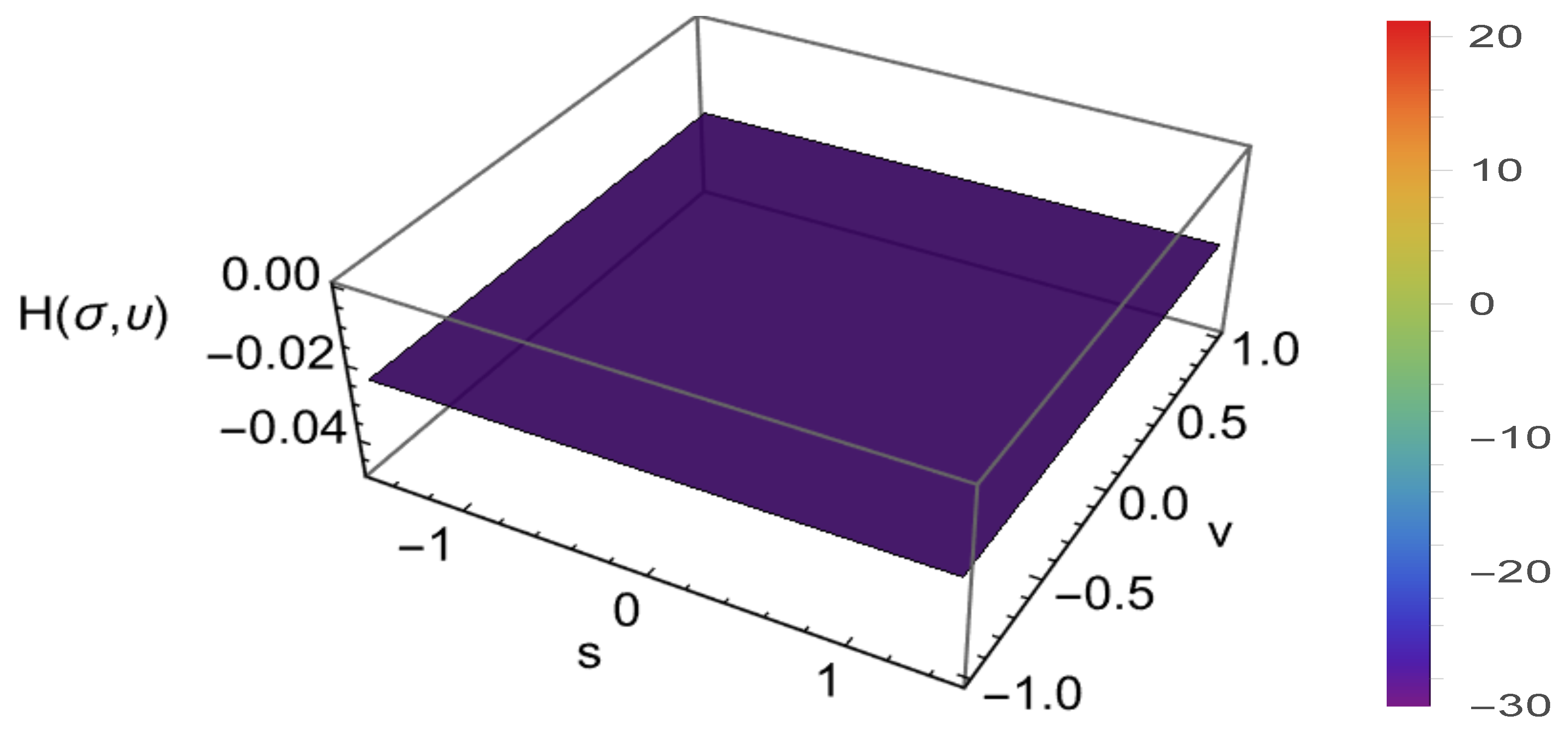
Numerically

$${\lambda }^{\prime }\left(0\right)\approx (0, -0.0131250000, 0.0065625000).$$

The osculating type-2 ruled surface is ${\mathcal{R}}^{(\phi ,\lambda )}(\sigma ,\upsilon )=\phi \left(\sigma \right)+\upsilon \lambda \left(\sigma \right)$. Thus surface partials and unnormalized normal at $(\sigma ,\upsilon )=(0,0)$ (Figure 6).

$${\mathcal{R}}_{\sigma }^{(\phi ,\lambda )}(0,0)=T\left(0\right),\hspace{1em}{\mathcal{R}}_{\upsilon }^{(\phi ,\lambda )}(0,0)=\lambda \left(0\right).$$

Figure 6. Non developable osculating type-2 ruled surface ${\mathcal{R}}^{(\phi ,\lambda )}$.

The unnormalized normal is

$${\mathcal{N}}_{{\mathcal{R}}^{(\phi ,\lambda )}}(0,0)={\mathcal{R}}_{\sigma }^{(\phi ,\lambda )}\times {\mathcal{R}}_{\upsilon }^{(\phi ,\lambda )}=(2.7756·{10}^{-17}, 0.5366563146, -0.2683281573).$$

Using the Lorentzian inner product the squared norm is

$$\Delta (0,0)=⟨{\mathcal{N}}_{{\mathcal{R}}^{(\phi ,\lambda )}},{\mathcal{N}}_{{\mathcal{R}}^{(\phi ,\lambda )}}⟩ = 0.36.$$

The first fundamental form at $(0,0)$ are computed as

$$\begin{array}{cc}\hfill E_{{\mathcal{R}}^{(\phi ,\lambda )}}& =⟨{\mathcal{R}}_{\sigma }^{(\phi ,\lambda )},{\mathcal{R}}_{\sigma }^{(\phi ,\lambda )}⟩=1,\hfill \\ \hfill F_{{\mathcal{R}}^{(\phi ,\lambda )}}& =⟨{\mathcal{R}}_{\sigma }^{(\phi ,\lambda )},{\mathcal{R}}_{\upsilon }^{(\phi ,\lambda )}⟩=0.6,\hfill \\ \hfill G_{{\mathcal{R}}^{(\phi ,\lambda )}}& =⟨{\mathcal{R}}_{\upsilon }^{(\phi ,\lambda )},{\mathcal{R}}_{\upsilon }^{(\phi ,\lambda )}⟩=0.\hfill \end{array}$$

Note $G_{{\mathcal{R}}^{(\phi ,\lambda )}}=0$ — the chosen director direction is null (lightlike) at this point; nevertheless the surface is regular since $E_{{\mathcal{R}}^{(\phi ,\lambda )}}{G}_{{\mathcal{R}}^{(\phi ,\lambda )}}-F_{{\mathcal{R}}^{(\phi ,\lambda )}}^2=-0.36\ne 0$. Now, using $S_{f_{{\mathcal{R}}^{(\phi ,\lambda )}}}=⟨{\lambda }^{\prime },{\mathcal{N}}_{{\mathcal{R}}^{(\phi ,\lambda )}}⟩$ and $S_{e_{{\mathcal{R}}^{(\phi ,\lambda )}}}=⟨{{\mathcal{R}}^{(\phi ,\lambda )}}_{\sigma \sigma },{\mathcal{N}}_{{\mathcal{R}}^{(\phi ,\lambda )}}⟩$. Then, we get

$$S_{f_{{\mathcal{R}}^{(\phi ,\lambda )}}}(0,0)\approx -0.008804517661405428,\hspace{1em}{S}_{e_{{\mathcal{R}}^{(\phi ,\lambda )}}}(0,0)\approx -1.97\times {10}^{-19}\approx 0.$$

Hence

$$f_{{\mathcal{R}}^{(\phi ,\lambda )}}={\displaystyle \frac{S_{f_{{\mathcal{R}}^{(\phi ,\lambda )}}}}{\sqrt{|\Delta |}}}\approx -0.01467419610234238,\hspace{1em}{e}_{{\mathcal{R}}^{(\phi ,\lambda )}}\approx 0,\hspace{1em}{g}_{{\mathcal{R}}^{(\phi ,\lambda )}}=0.$$

The Gaussian and mean curvature at $(0,0)$ are computed as (Figure 7 and Figure 8)

$$K_{{\mathcal{R}}^{(\phi ,\lambda )}}(0,0)\approx {\displaystyle \frac{-{(-0.0146741961)}^2}{-0.36}}=+0.00059814453125,$$

$$H_{{\mathcal{R}}^{(\phi ,\lambda )}}(0,0)\approx {\displaystyle \frac{-2·0.6·(-0.0146741961)}{2(-0.36)}}=-0.024456993503903967.$$

Figure 7. The Gaussian curvature field $K_{{\mathcal{R}}^{(\phi ,\lambda )}}(\sigma ,\upsilon )$ near $(0,0)$.

Figure 8. The mean curvature field $H_{{\mathcal{R}}^{(\phi ,\lambda )}}(\sigma ,\upsilon )$ near $(0,0)$.

6. Conclusions

This research has explored osculating-type ruled surfaces within Minkowski 3-space ${\mathbf{E}}_1^3$, formulated through the Type-2 Bishop frame of a spacelike base curve whose principal normal is timelike and binormal is spacelike. By employing the hyperbolic relationship that connects the Frenet–Serret frame with the Bishop frame, we established explicit formulas for the ruling directions and expressed the Bishop curvatures ${\zeta }_1$ and ${\zeta }_2$ in terms of the torsion $\tau \left(\sigma \right)$ and the hyperbolic rotation parameter $\theta \left(\sigma \right)$. These formulations provide a consistent and smooth analytical approach for examining the geometry of ruled surfaces in Lorentzian space, thereby extending several well-known Euclidean results to the Minkowski framework.

Our findings indicate that the causal nature of the base curve and its associated frame vectors plays a crucial role in determining the geometric structure of the resulting surface. The hyperbolic transformation characteristic of the Type-2 Bishop frame replaces the ordinary circular rotation of Euclidean geometry with a Lorentzian boost, producing new relationships among the curvature quantities. This transformation influences the surface’s conditions for being developable, flat, or minimal, illustrating how torsion and hyperbolic rotation interact in shaping the local and global geometry of the surface.

The study also establishes how the Bishop curvatures control the geometry of the rulings, distinguishing between cylindrical and non-cylindrical configurations. Beyond their mathematical significance, these results carry direct physical relevance. Since Minkowski space models flat spacetime in special relativity, ruled surfaces derived from spacelike or timelike curves can represent world-sheets, lightlike hypersurfaces, or geodesic congruences. The Bishop frame’s smooth adaptation to curves with vanishing curvature makes it particularly valuable for modeling relativistic motions and geometric phenomena without singularities or discontinuities.

In conclusion, this work broadens the classical concept of osculating-type ruled surfaces into the Lorentzian setting and elucidates how the hyperbolic structure of Minkowski space governs their geometric behavior. The theoretical framework developed here provides both geometric insight and a foundation for future research on Bishop-frame-generated surfaces in higher-dimensional or semi-Riemannian manifolds, with potential applications to differential geometry, mathematical physics, and relativistic surface modeling.