Characterization of Pomonoids by Properties of I-Regular S-Posets

Abstract

In 2005, Shi defined I-regular S-posets and used this concept to characterize $PP$-pomonoids and po-cancellable pomonoids. In this paper, we continued the development of the homological classification of pomonoids by using the I-regularity of S-posets. First, we characterized pomonoids over which all I-regular S-posets have one of the properties around projectivity or injectivity, and many known results were generalized. Moreover, some possible conditions on pomonoids that describe when their diagonal posets are I-regular were found. Finally, some characterizations of pomonoids by the I-regularity of their Rees factor posets were given.

1. Preliminaries

In this paper, unless otherwise specified, S is a partially ordered monoid (or simply a pomonoid). A nonempty poset A is called a left S-poset, usually denoted by _SA, if there exists a mapping $S\times A\to A$, $(s,a)⟼sa$ which satisfies the following conditions: (i) The action is monotonic in each variable; (ii) $t\left(sa\right)=\left(ts\right)a$ and $1a=a$ for all $a\in A$ and all $s,t\in S$. Right S-posets $B_S$ are defined analogously, and $\Theta =\left\{\theta \right\}$ denotes the one-element S-poset. In this paper, a left (right) ideal of S refers to a nonempty subset I of S satisfying $SI\subseteq I$ ($IS\subseteq I$).

A morphism of left S-posets is a monotonic mapping $f:{}_{S}A\to {}_{S}B$ which satisfies $f\left(sa\right)=sf\left(a\right)$ for every $a\in A$ and $s\in S$. Morphisms of right S-posets are defined similarly, and morphisms of posets are just monotonic mappings. In this way, the categories _SPos (left S-posets), ${\mathrm{Pos}}_S$ (right S-posets), and Pos (posets) are obtained. In these categories, the monomorphisms are the injective morphisms, whereas the regular monomorphisms are the order-embeddings, that is, morphisms $f:{}_{S}A\to {}_{S}B$, for which $f\left(a\right)\le f\left(a^{\prime }\right)$ implies $a\le a^{\prime }$ for all $a,a^{\prime }\in A$ (see [1]). Research on flatness properties of S-posets was initiated in the mid-1980s by S. Fakhruddin in [2], and this work has recently been continued in the articles [1,3,4,5,6,7,8].

An S-subposet _SB of an S-poset _SA is called convex if for any $a\in A$ and $b,b^{\prime }\in B$, $b^{\prime }\le a\le b$ implies $a\in B$. An element $c\in S$ is called right (left) po-cancellable if for all $s,s^{\prime }\in S$, $sc\le s^{\prime }c$ ($cs\le c{s}^{\prime }$) implies $s\le s^{\prime }$. A pomonoid is called left (right) collapsible if for all $s,t\in S$, there exists $u\in S$ such that $us=ut$ ($su=tu$). A pomonoid is called weakly right (left) reversible if for all $s,t\in S$, there exist $u,v\in S$ such that $us\le vt$ ($su\le tv$). A left S-poset is called simple if it has no proper subposets and completely reducible if it is a coproduct of simple posets.

An order congruence on an S-poset _SA is an S-act congruence $\rho$ such that the factor act $A/\rho$ can be equipped with a compatible order, making the natural map $A\to A/\rho$ an S-poset morphism. A left S-poset _SA is called cyclic if $A=Sa=\{sa\mid s\in S\}$ for some $a\in A$. In [9], an S-poset _SA is cyclic if and only if there exists an order congruence $\lambda$ on S such that $A\cong S/\lambda$. If K is a convex left ideal of a pomonoid S, then there exists an S-poset congruence where one of its classes is K and all the others are singletons. Moreover, the factor S-poset by this congruence is called the Rees factor S-poset of S by K and denoted $S/K$.

Various flatness properties of S-posets are defined in terms of tensor products. To define the tensor product $A{\otimes }_{S}B$ of a right S-poset $A_S$ and a left S-poset _SB (see [10]), we consider a preorder $\theta$ on the set $A\times B$, defined by $(a,b)\theta (a^{\prime },b^{\prime })$ if and only if

$$\begin{array}{cc}\hfill a& \le a_1{s}_1,\hfill \\ \hfill a_1{t}_1& \le a_2{s}_2,\hfill & \hfill s_{1}b& \le t_1{b}_2,\hfill \\ \hfill a_2{t}_2& \le a_3{s}_3,\hfill & \hfill s_2{b}_2& \le t_2{b}_3,\hfill \\ & ⋮\hfill & & ⋮\hfill \\ \hfill a_n{t}_n& \le a^{\prime },\hfill & \hfill s_n{b}_n& \le t_n{b}^{\prime }.\hfill \end{array}$$

for some $n\in \mathbb{N}$, $a_1,\dots ,a_n\in A$, $b_2,\dots ,b_n\in B$ and $s_1,t_1,\dots ,s_n,t_n\in S$. Then $\theta \cap {\theta }^{-1}$ is an equivalence relation on $A\times B$, and we denote the equivalence class of $(a,b)$ by $a\otimes b$. The quotient set

$$A{\otimes }_{S}B:=(A\times B)/(\theta \cap {\theta }^{-1})=\{a\otimes b\mid a\in A,b\in B\}$$

is a poset with respect to the order

$$a\otimes b\le a^{\prime }\otimes b^{\prime }\iff (a,b)\theta (a^{\prime },b^{\prime }).$$

This poset $A{\otimes }_{S}B$ is called the tensor product of A_S and _SB. Note that $as\otimes b=a\otimes sb$ for every $a\in A$, $b\in B$ and $s\in S$. In a natural way, one obtains a functor $A_S\otimes -$ of tensor multiplication from ${}_S\mathrm{Pos}$ to Pos.

In [4,9], the definitions of flatness, weak flatness, principally weak flatness, and weak torsion freeness are formulated as follows:

• A left S-poset _SB is called flat if for every right S-poset $A_S$ and all pairs $(a,b),(a^{\prime },b^{\prime })$ in $A\times B$, $a\otimes b=a^{\prime }\otimes b^{\prime }$ in $A{\otimes }_{S}B$ implies the same equality holds in $(aS\cup a^{\prime }S){\otimes }_{S}B$. Equivalently, the functor $-{\otimes }_{S}B$ takes embeddings in ${\mathrm{Pos}}_S$ to monomorphisms in Pos.
• A left S-poset _SB is called (principally) weakly flat if the functor $-{\otimes }_{S}B$ maps embeddings of (principal) right ideals $I\subseteq S$ in ${\mathrm{Pos}}_S$ to monomorphisms in Pos.
• A left S-poset _SB is called weakly torsion free if $cb=c{b}^{\prime }$ implies $b=b^{\prime }$ whenever $b,b^{\prime }\in B$ and c is a left po-cancellable element.
• A left S-poset _SB is said to satisfy Condition (P) if for all $b,b^{\prime }\in B$, and $s,s^{\prime }\in S,$$sb\le s^{\prime }{b}^{\prime }$ implies $b=u{b}^{\prime \prime },b^{\prime }=v{b}^{\prime \prime }$ for some $b^{\prime \prime }\in B$ and $u,v\in S$ with $su\le s^{\prime }v$.

For a more complete discussion of flatness properties of posets over pomonoids, the reader is referred to [4,11,12]. The following relations exist among flatness properties of S-posets:

We let _SA be an S-poset. An element $a\in A$ is called I-regular if there exists an S-morphism $f:{}_S\mathit{Sa}\to {}_{S}S$ such that $f\left(a\right)a=a$. An S-poset _SA is called I-regular if all elements of A are I-regular.

Example 1.

Let $S=\{1,0\}$ be a pomonoid, where the multiplication operation is defined as $1·1=1$ and $1·0=0·1=0·0=0$ (i.e., 1 is the identity element and 0 is the zero element), and the partial order is $0\le 1$. We take the trivial S-poset $A=\left\{a\right\}$, the left action of this poset is defined such that $s·a=a$ for all $s\in S$, and the partial order on it is trivial. Obviously, A is an I-regular S-poset.

It is clear that a regular pomonoid S was I-regular as a left S-poset, but the converse is not true. For example, if S is a right po-cancellable pomonoid, then S is an I-regular left S-poset without being a regular pomonoid. In the special case where S is an ordered group, S is not only a regular pomonoid but also an I-regular left S-poset.

In [10], Shi introduced the concept of I-regular S-posets and offered characterizations of two classes of pomonoids (left $PP$-pomonoid and right po-cancellable pomonoid) by the I-regularity of S-posets. However, the projectivity, injectivity, and the direct product properties of I-regular S-posets were not involved. In [13], the authors focused on the homological classification of pomonoids based on the flatness of Rees factor S-posets, but did not establish a connection with I-regularity. In this paper, we continue the development of I-regular S-posets. In Section 2, we characterize pomonoids over which all I-regular S-posets have one of the properties around projectivity or injectivity. In [10], characterizations of pomonoids over which all free (projective) S-posets are I-regular are given; in [9], the authors characterized pomonoids over which all strongly flat S-posets are I-regular. Consequently, we investigate pomonoids over which all left S-posets with one of the properties are I-regular in Section 3. In Section 4, we investigate the direct product of I-regular S-posets. Finally, we study the classification of pomonoids by the I-regularity property of right Rees factor S-posets and tabulate the results.

2. Characterizations of Pomonoids Where All I-Regular Left S-Posets Possess Projectivity or Injectivity-Related Properties

In this section, we investigate pomonoids over which all I-regular left S-posets have one of the properties introduced in Section 1. To achieve this goal, we need the following lemmas.

Lemma 1

([10], Proposition 4.2). Let A be an S-poset and $a\in A$. The following assertions are equivalent:

(1)

a is I-regular.

(2)

There exists an element $e\in E\left(S\right)$ such that $a=ea$ and $sa\le ta$ implies $se\le te$ for $s,t\in S$.

(3)

 $Sa\cong Se$ in _SPos for some $e\in E\left(S\right)$.

(4)

 $Sa$ is projective.

Proof. 

(3)⇒(4). For any surjective S-morphism $g:B\to C$ and any S-morphism $f:Se\to C$. Suppose $f\left(e\right)=c\in C$. Since g is surjective, there exists $b\in B$ with $g\left(b\right)=c.$ We define $h\left(te\right)=tb$, then $g\left(h\right(te\left)\right)=g\left(tb\right)=tg\left(b\right)=tc=tf\left(e\right)=f\left(te\right)$, so $gh=f$. Thus, $Se$ is projective, and $Sa\cong Se$ implies $Sa$ is projective. □

If $a\in A,e^2=e\in S$ as in Lemma 1 (2), then we call $\{a,e\}$ an I-regular pair (in A).

From [10], a pomonoid S is called left $PP$-pomonoid if the S-subposet $Sx$ is projective for all $x\in S$. (Note, however, that $Sx$ may be an ideal of S in the ordered sense.) By Lemma 1, an S-poset is I-regular if and only if all cyclic S-subposets of A are projective. Thus, we have

Lemma 2

([10], Lemma 4.7). A pomonoid S is I-regular if and only if S is a left $PP$ pomonoid.

Lemma 3.

${}_S\Theta$ is I-regular if and only if S contains a right zero element.

Proof. 

This follows from Theorem 1 of [4] and Lemma 1. □

Lemma 4

([10], Lemma 4.5). All S-subposets of I-regular S-poset are I-regular, and coproducts of I-regular S-posets are I-regular.

Lemma 5

([4]). Let S be a pomonoid, $a,a^{\prime }\in A,b,b^{\prime }\in B$. Then $a\otimes b\le a^{\prime }\otimes b^{\prime }$ in $A{\otimes }_{S}B$ if and only if there exist $a_1,\dots ,a_m\in A,b_2,\dots ,b_m\in B$, $s_1,t_1,\dots ,s_m,t_m\in S$ such that

$$\begin{array}{cc}\hfill a& \le a_1{s}_1,\hfill \\ \hfill a_1{t}_1& \le a_2{s}_2,\hfill & \hfill s_{1}b& \le t_1{b}_2,\hfill \\ \hfill a_2{t}_2& \le a_3{s}_3,\hfill & \hfill s_2{b}_2& \le t_2{b}_3,\hfill \\ & ⋮\hfill & & ⋮\hfill \\ \hfill a_m{t}_m& \le a^{\prime },\hfill & \hfill s_m{b}_m& \le t_m{b}^{\prime }.\hfill \end{array}$$

Similar to ([14], Lemma 3.2), we have

Lemma 6.

Let S be a pomonoid. If there exists an I-regular left S-poset, then there exist a largest I-regular left ideal of S.

In the following, $T\left(S\right)$ is always used to represent the largest I-regular left ideal of S.

Theorem 1.

For any pomonoid S, all I-regular left S-posets are principally weakly flat if and only if for every idempotent $e\in T\left(S\right)$ and every element $s\in S$ the product $se$ is a regular element in S.

Proof. 

We let $s\in S$ and $e^2=e\in T$. If $Sse=Se$, then there exists $t\in S$ such that $tse=e$, and then it follows that $setse=se$, hence $se$ is a regular element. In another case, we have $Sse\ne Se$. We can construct an S-act M as follows:

$$M=\left\{\right(x,te)\mid te\in Se\setminus Sse\}\cup \left\{\right(y,te)\mid te\in Se\setminus Sse\}\cup \left\{\right(z,te)\mid te\in Sse\}$$

where $x,y,z$ are three elements not belonging to S, and define a left S-action on M by

$$r(w,te)=\left\{\begin{array}{cc}(w,rte),\hfill & ifrte\in Se\setminus Sse,w\in \{x,y\},\hfill \\ (z,rte),\hfill & ifrte\in Sse,\hfill \end{array}\right.$$

$$r(z,te)=(z,rte).$$

The order on M is defined as

$$(w_1,s)\le (w_2,t)\iff (w_1=w_2\mathrm{and}s\le t)\mathrm{or}(w_1\ne w_2,s\le i\le t\mathrm{for}\mathrm{some}i\in Sse).$$

Then M is an S-poset according to the above definition. It is clear that there are isomorphisms $S(x,e)\simeq Se\simeq S(y,e)$. Since $Se\le T\left(S\right)$, $Se$ is I-regular by Lemma 4, thus $S(x,e)$ and $S(y,e)$ are also I-regular. From Lemma 4, it follows that $M=S(x,e)\cup S(y,e)$ is I-regular. By assumption, M is principally weakly flat. Clearly, $s(x,e)=(z,se)=s(y,e)$, then $se\otimes (x,e)=se\otimes (y,e)$ in $seS{\otimes }_{S}M$. By Lemma 5, there exist $s_1,\dots ,s_n,u_1,v_1,\dots u_n,v_n\in S,b_2,b_3,\dots ,b_n\in seS,w_1,\dots ,w_n\in \{x,y,z\}$ such that

$$\begin{array}{cccc}& \hfill & & (x,e)\le u_1(w_1,s_1),\hfill \\ & se{u}_1\le b_2{v}_1,\hfill & \hfill & v_1(w_1,s_1)\le u_2(w_2,s_2),\hfill \\ & b_2{u}_2\le b_3{v}_2,\hfill & & v_2(w_2,s_2)\le u_3(w_3,s_3),\hfill \\ & \dots \hfill & & \dots \hfill \\ & b_n{u}_n\le se{v}_n,\hfill & & v_n(w_n,s_n)\le (y,e).\hfill \end{array}$$

We denote 1 by $u_0{s}_0$ and $v_{n+1}{s}_{n+1}$; by the definition of M, there exist $k\in \{0,1,\dots ,n,n+1\}$ and $j\in Sse$ such that $v_k{s}_k\le j\le u_{k+1}{s}_{k+1}.$ So we have $se\le see\le se{u}_1{s}_1\le b_2{v}_1{s}_1\le b_2{u}_2{s}_2\le \dots \le b_{k+1}{v}_k{s}_k\le b_{k+1}j\le b_{k+1}{u}_{k+1}{s}_{k+1}\le \dots \le b_n{u}_n{s}_n\le b_n{v}_n{s}_n\le se{v}_n{s}_n\le se$, which implies that $se=b_{k+1}j$, hence $se\in seSse$. Now the result follows.

Conversely, we suppose _SA is an I-regular left S-poset and for $a,a^{\prime }\in A,s\in S$, $s\otimes a=s\otimes a^{\prime }$ in $S{\otimes }_{S}A$. Then there exist $a_2,a_3,\dots ,a_m,b_2,b_3,\dots ,b_k\in A,u_1,v_1,\dots ,u_m,v_m\in S$, $p_1,q_1,\dots ,p_k,q_k\in S,$ $s_1,\dots ,s_m,r_1,\dots ,r_k\in S$ such that

$$\begin{array}{cccc}& s\le s_1{u}_1,\hfill & \hfill & \hfill \\ & s_1{v}_1\le s_2{u}_2,\hfill & \hfill & u_{1}a\le v_1{a}_2,\hfill \\ & s_2{v}_2\le s_3{u}_3,\hfill & & u_2{a}_2\le v_2{a}_3,\hfill \\ & \dots \hfill & & \dots \hfill \\ \hfill & s_m{v}_m\le s,\hfill & \hfill & u_m{a}_m\le v_m{a}^{\prime },\hfill \\ & s\le r_1{p}_1,\hfill & \hfill & \hfill \\ & r_1{q}_1\le r_2{p}_2,\hfill & \hfill & p_1{a}^{\prime }\le q_1{b}_2,\hfill \\ & r_2{q}_2\le r_3{p}_3,\hfill & & p_2{b}_2\le q_2{b}_3,\hfill \\ & \dots \hfill & & \dots \hfill \\ & r_k{q}_k\le s,\hfill & \hfill & p_k{b}_k\le q_{k}a.\hfill \end{array}$$

Because _SA is I-regular, there exist $e,f\in E\left(S\right)$ such that $\{a,e\},\{a^{\prime },f\}$ are I-regular pairs and $Se$, $Sf$ are I-regular left ideals, thus $e,f\in T\left(S\right)$. By hypothesis, there exist $x,y\in S$ such that $se=sexse$ and $sf=sfysf$. From $s\otimes a=s\otimes a^{\prime }$, we obtain that $sa=s{a}^{\prime }$. We can now calculate

$$\begin{array}{cc}\hfill sexs{a}^{\prime }& \le sex{r}_1{p}_1{a}^{\prime }\le sex{r}_1{q}_1{b}_2\le sex{r}_2{p}_2{b}_2\hfill \\ & \le \dots \le sex{r}_k{p}_k{b}_k\le sex{r}_k{q}_{k}a\hfill \\ & \le sexsa=sexsea=sea=sa=s{a}^{\prime }.\hfill \end{array}$$

Thus, $sexsf\le sf$ (using the I-regular pair property). Hence

$$\begin{array}{cc}\hfill s\otimes a& =s\otimes ea=se\otimes a=sexse\otimes a\hfill \\ & =sex\otimes sa=sex\otimes s{a}^{\prime }=sex\otimes sf{a}^{\prime }\hfill \\ & =sexsf\otimes a^{\prime }\le sf\otimes a^{\prime }=s\otimes f{a}^{\prime }\hfill \\ & =s\otimes a^{\prime }\hfill \end{array}$$

in $sS{\otimes }_{S}A$. Similarly, using the I-regular pair property, we can obtain $sfyse\le se$. Therefore,

$$\begin{array}{cc}\hfill s\otimes a^{\prime }& =s\otimes f{a}^{\prime }=sf\otimes a^{\prime }=sfysf\otimes a^{\prime }\hfill \\ & =sfy\otimes sf{a}^{\prime }=sfy\otimes s{a}^{\prime }=sfy\otimes sa\hfill \\ & =sfyse\otimes a\le se\otimes a=s\otimes ea\hfill \\ & =s\otimes a\hfill \end{array}$$

in $sS\otimes A$. So _SA is principally weakly flat. □

Next, we give an example to apply the above theorem.

Example 2.

Let $S=\{1,e\}$ with multiplication defined as $1·1=1$, $1·e=e·1=e$, $e·e=e$ and partial order $e\le 1$; here, the set of idempotents $E\left(S\right)=\{1,e\}$. Checking Theorem 1’s condition, we find that for all $s\in S$ and $e\in E\left(S\right)$, the product se is regular. By Theorem 1, all I-regular left S-posets are principally weakly flat, which is verified by the I-regular S-poset $A=\{a,b\}$ (with action $1·a=a$, $1·b=b$, $e·a=b$, $e·b=b$ and order $a\le b$): for $s=e$, $e·a=b\le e·b=b$ implies $a\le b$, satisfying the principal weak flatness condition. In contrast, finite pomonoids violating Theorem 1’s condition (i.e., containing an idempotent $e\in E\left(S\right)$ and an element $s\in S$ such that se is non-regular) are rare, especially when $E\left(S\right)=S$ (all elements are idempotent), as idempotents inherently make se regular; for such pomonoids, some I-regular left S-posets fail to be principally weakly flat, though constructing a finite example requires a pomonoid with non-regular products of idempotents and elements, which is non-trivial due to the regularity of idempotent-generated products.

Corollary 1.

For any pomonoid S, the following statements are equivalent:

(1)

S is a regular pomonoid.

(2)

S is a left $PP$ pomonoid and all I-regular left S-posets are principally weakly po-flat.

(3)

S is a left $PP$ pomonoid and all I-regular left S-posets are principally weakly flat.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. We let S be a regular pomonoid. Then S is left $PP$ and all left S-posets are principally weakly po-flat by ([15], Theorem 2.3).

$\left(2\right)\Rightarrow \left(3\right)$. It is obvious.

$\left(3\right)\Rightarrow \left(1\right)$. From Proposition 4.6 of [10], it follows that S is a left $PP$ pomonoid if and only if S is an I-regular S-poset if and only if $T\left(S\right)=S$. So by Theorem 1, S is a regular pomonoid. □

Theorem 2.

Let S be a pomonoid. If all I-regular left S-posets are $GP$-flat, then for every idempotent $e\in T\left(S\right)$ and every element $s\in S$, there exist $n\in N,x\in S$ such that ${\left(se\right)}^n={\left(se\right)}^{n}xse$.

Proof. 

It is similar to that of Theorem 1. □

Theorem 3.

For any pomonoid S, the following statements are equivalent:

(1)

All I-regular left S-posets are weakly torsion free.

(2)

For every left po-cancellable element r and for every idempotent $e\in T\left(S\right)$, $re\mathcal{L}e$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. For left po-cancellable element $r\in S$ and $e^2=e\in T\left(S\right)$, if $Sre\ne Se$, then M is an I-regular S-poset constructed in Theorem 1. By assumption, M must be weakly torsion free. But now from $r(x,e)=(z,re)=r(y,e)$, we get $(x,e)=(y,e),$ a contradiction. Hence $Sre=Se$, which means that $re\mathcal{L}e$.

$\left(2\right)\Rightarrow \left(1\right)$. We let _SA be an I-regular S-poset and $ra=rb$ for any left po-cancellable element r, any $a,b\in A$. Since _SA is I-regular, there exist $e,f\in E\left(S\right)$ such that $\{a,e\},\{b,f\}$ are I-regular pairs. Thus, we have $rea=rfb$. Since $e\in T\left(S\right)$, we have $re\mathcal{L}e$, which implies there exists $t\in S$ such that $tre=e$. Therefore, $ea=trea=trfb$ and $rb=ra=rtrfb$, which implies $rf=rtrf$. Since r is a left po-cancellable element, then $f=trf$ and so $a=ea=trfb=fb=b$. Therefore, A is weakly torsion free. □

Theorem 4.

For any pomonoid S, the following statements are equivalent:

(1)

All I-regular left S-posets are projective.

(2)

All I-regular left S-posets are strongly flat.

(3)

All I-regular left S-posets satisfy Condition $\left(P\right)$.

(4)

Every idempotent of $T\left(S\right)$ generates a minimal left ideal.

Proof. 

The implications $\left(1\right)\Rightarrow \left(2\right)\Rightarrow \left(3\right)$ are obvious.

(3)⇒(4). We let $e^2=e\in T\left(S\right)$. Then $Se$ is I-regular by Lemma 4. Suppose I is a left ideal of S such that $I\subseteq Se,I\ne Se$. We let M be an I-regular S-poset constructed in Theorem 1. By assumption, M satisfies Condition $\left(P\right)$. By [9], Proposition 2.11, M must be a coproduct of cyclic S-subposets which is impossible because $S(x,e)\cap S(y,e)=\left\{\right(z,se\left)\right\}.$ Hence, $Se$ is a minimal left ideal.

(4)⇒(1). We let _SA be an I-regular left S-poset. For any $a\in A$, the cyclic subposet $Sa$ is, by Lemma 1, isomorphic to some left ideal $Se,e\in T\left(S\right)$. By assumption, all such ideals $Se$ are simple. Hence, _SA is a coproduct of simple subposets each of which is isomorphic to a left ideal generated by an idempotent. By Theorem 3.4 of [10], _SA is projective. □

Recall from [16,17] that a left S-poset _SA is called regular-injective if for any regular monomorphism $h:{}_{S}B\to {}_{S}C$ and morphism $f:{}_{S}B\to {}_{S}A$ there exists a morphism $g:{}_{S}C\to {}_{S}A$ such that $f=gh$. A left S-poset _SA is called regular-(principally) weakly injective if for any regular monomorphism $i:I\to S$ where I is a (principally) left ideal of S and for any S-poset morphism $f:{}_{S}I\to {}_{S}A$ there exists an S-poset morphism $g:{}_{S}S\to {}_{S}A$ such that $f=gi$. A left S-poset A is called regular-divisible if ${}_S\mathit{dA}={}_{S}A$ for every right po-cancellable element d of S.

Proposition 1.

For any pomonoid S, all regular-principally weakly injective S-posets are regular-divisible.

Proof. 

We let _SM be a regular-principally weakly injective S-poset and let d be any right po-cancellable element of S. We let $m\in M$. Since d is right po-cancellable, there exists an S-poset morphism $f:{}_S\mathit{Sd}\to {}_{S}M$ defined by $f\left(sd\right)=sm$ for all $s\in S$. Since _SM is regular-principally weakly injective, there exists an S-poset morphism $g:{}_{S}S\to {}_{S}M$ such that $f=gi$ where i is the regular monomorphism of $Sd$ into S. Now,

$$m=f\left(d\right)=\left(gi\right)\left(d\right)=g\left(d\right)=d\left(g\right(1\left)\right)\in dM.$$

Hence $M\subseteq dM$, and thus $dM=M$, which means that _SM is regular-divisible. □

From the previous definitions and proposition, we have following implications:

$$\begin{gathered} \mathrm{regular-injective}\Rightarrow \mathrm{regular-weakly}\mathrm{injective}\Rightarrow \\ \mathrm{regular-principally}\mathrm{weakly}\mathrm{injective}\Rightarrow \mathrm{regular-divisible}. \end{gathered}$$

Theorem 5.

Let S be a pomonoid. All I-regular left S-posets are regular-divisible if and only if all left ideals $Se$, $e^2=e\in T\left(S\right)$, are regular-divisible.

Proof. 

Necessity is obvious because $Se$ is I-regular by Lemma 4.

Regarding sufficiency, we let _SA be an arbitrary I-regular S-poset and let $a\in A$. Then by Lemma 1, $Sa$ is isomorphic to $Se$, $e\in T\left(S\right)$. Since $Se$ is regular-divisible, then for any right po-cancellable $d\in S$, we have $dSe=Se$ and thus $dSa=Sa$. But then

$$dA=d(\bigcup _{a\in A}Sa)=\bigcup _{a\in A}dSa=\bigcup _{a\in A}Sa=A$$

which shows that _SA is regular-divisible. □

For any $q\in S$, an element $p\in S$ is said to be q-po-cancellable if for any $s,t\in S$, $sp\le tp$ always implies $sq\le tq$.

Theorem 6.

Let S be a pomonoid. If all I-regular left S-posets are regular-principally weakly injective, then the largest left ideal $T\left(S\right)\subseteq S$ is regular and if $p\in S\setminus T\left(S\right)$ is e-po-cancellable for $e^2=e\in T\left(S\right)$, then $e\in pS$.

Proof. 

For any $t\in T\left(S\right)$, we have $St\subseteq T\left(S\right)$ and $St$ is I-regular. By assumption, $St$ is regular-principally weakly injective, and there exists a morphism $g:S\to St$ such that $gi=1_{St}$ where $i:St\to S$ is the inclusion morphism. So $st=g\left(1\right)$ for some $s\in S$. Now, $tst=tg\left(1\right)=g\left(t\right)=t$. Thus, t is regular.

We let $p\in S\setminus T\left(S\right)$ be e-po-cancellable for $e^2=e\in T\left(S\right)$. Then, by setting $f\left(p\right)=e$, we obtain an S-poset morphism f from $Sp$ into $Se$. Since $Se$ is I-regular, it is regular-principally weakly injective and there exists a morphism $g:S\to Se$ such that $f=gi$ where $i:Sp\to S$ is the inclusion homomorphism. Now, $e=f\left(p\right)=g\left(p\right)=pg\left(1\right)\in pS.$ □

Lemma 7.

S is a regular pomonoid if and only if all left S-posets are regular-principally weakly injective.

Proof. 

We let _SA be a left S-poset and $f:{}_S\mathit{Ss}\to {}_{S}A,s\in S$ be an S-homomorphism. If S is regular, then there exists $s^{\prime }\in S$ such that $s=s{s}^{\prime }s$. We set $f\left(s^{\prime }s\right)=a$ and define a mapping $g:S\to A$ by $g\left(1\right)=a$. Then, g is well defined and $g\left(s\right)=sg\left(1\right)=sa=sf\left(s^{\prime }s\right)=f\left(s\right)$. Since g is the extension of f to S, _SA is regular-principally weakly injective.

Conversely, suppose that all left S-posets are regular-principally weakly injective. Then, for every $s\in S$, the principal left ideal $Ss$ of S is a regular-principally weakly injective left S-poset. Hence the identity map i of $Ss$ to $Ss$ can extended to the S-homomorphism g of S onto $Ss$. We set $g\left(1\right)=s^{\prime }s$ for some $s^{\prime }\in S$. Then, $s=i\left(s\right)=g\left(s\right)=sg\left(1\right)=s{s}^{\prime }s$, hence s is a regular element. □

Theorem 7.

A pomonoid S is an I-regular left S-poset and all I-regular left S-posets are regular-principally weakly injective if and only if S is a regular pomonoid.

Proof. 

Regarding necessity, suppose that _SS is an I-regular left S-poset and all I-regular left S-posets are regular-principally weakly injective. Then $T\left(S\right)\subseteq S$ is regular by Theorem 6. We let $p\in S\setminus T\left(S\right)$. If _SS is an I-regular S-poset, then there exists an idempotent $e\in S$ such that $h:{}_S\mathit{Sp}\to {}_S\mathit{Se}$ is an isomorphism. Since _SSe is I-regular, it is regular-principally weakly injective and then there exists an S-homomorphism $g:{}_{S}S\to {}_S\mathit{Se}$ such that g is an extension of h. Hence $e=h\left(p\right)=g\left(p\right)=pg\left(1\right),$ and then $p=ep=pg\left(1\right)p,$ so p is also regular. Thus, S is a regular pomonoid.

Regarding sufficiency, if S is a regular pomonoid, then S is a left $PP$-pomonoid and so _SS an I-regular left S-poset by Lemma 2. Using Lemma 7, we determine that all left S-posets are regular-principally weakly injective. So the result follows. □

From [10], a left S-poset _SA is called faithful (strongly faithful) if from $sa\le ta,$$s,t\in S$, for all (some) $a\in A$ it follows that $s\le t$.

Theorem 8.

For any pomonoid S, the following statements are equivalent:

(1)

All I-regular left S-posets are faithful.

(2)

For any $e^2=e\in T\left(S\right)$, $Se$ is faithful.

Proof. 

The implication $\left(1\right)\Rightarrow \left(2\right)$ is obvious.

$\left(2\right)\Rightarrow \left(1\right)$. We let _SA be an I-regular left S -poset and $ux\le vx$, $u,v\in S$,$x\in A$. We take $a\in A$; there exists $e^2=e\in T\left(S\right)$ such that $\{a,e\}$ is an I-regular pair. For any $s\in S$, we have $usa\le vsa$; it follows that $use\le vse$. Since _SSe is faithful, $u\le v$. □

Example 3.

Let $S=\{1,e\}$ be the finite pomonoid, equipped with a discrete partial order (i.e., only reflexivity holds: $1\le 1$, $e\le e$, and no other order relations exist). The set of idempotents of S is $E\left(S\right)=\{1,e\}$, and the largest I-regular left ideal of S is $T\left(S\right)=S$. First, we verify that the left S-poset Se is faithful for all $e\in T\left(S\right)$: When $e=1$, $S·1=S=\{1,e\}$. By the definition of a faithful poset (if $s·b\le t·b$ for all $b\in B$, then $s\le t$), if $s·x\le t·x$ for all $x\in S$, taking $x=1$ gives $s·1=s\le t=t·1$, so $S·1$ is faithful. When $e=e$, $S·e=\left\{e\right\}$; if $s·e\le t·e$ (which simplifies to $e\le e$, a condition that always holds) for all $e\in S·e$, we note that in the discrete partial order, $s\le t$ if and only if $s=t$. Since $S·e=\left\{e\right\}$ is a singleton set, the condition “for all $b\in B$” is trivial, so $S·e$ is also faithful. Next, we present an example of a faithful I-regular left S-poset: We let $A=S·1=\{1,e\}$, which is I-regular as shown in Example 1. For any $s,t\in S$, if $s·a\le t·a$ for all $a\in A$, taking $a=1$ yields $s\le t$; in the discrete partial order, this implies $s=t$, so A is faithful.

Theorem 9.

Let S be a pomonoid. Then all I-regular left S-posets are strongly faithful if and only if S is right po-cancellable.

Proof. 

We let all I-regular left S-posets be strongly faithful and for any $s,t,z\in S$, $sz\le tz$. For $a\in A$, we have $s\left(za\right)\le t\left(za\right)$. Since _SA is strongly faithful, $s\le t$ and so S is right po-cancellable.

Conversely, suppose that _SA is an I-regular left S-poset and for $a\in A,s,t\in S$, $sa\le ta$. Then there exists $e\in E\left(S\right)$ such that $ea=a$ and $se\le te$. Since S is right po-cancellative, we have $s\le t$ and so _SA is strongly faithful as required. □

3. Characterizations of Pomonoids Where All Left S-Posets with Specific Properties Are I-Regular

In [10], characterizations of pomonoids over which all free (projective) S-posets are I-regular are given. In [9], the authors characterize pomonoids over which all strongly flat S-posets are I-regular. In this section, we continue to investigate pomonoids over which all left S-posets with one of the properties are I-regular.

Proposition 2.

For any pomonoid S, all strongly faithful S-posets are I-regular.

Proof. 

We let _SA be a strongly faithful S-poset. Then for any $a\in A$, there exists a morphism $f:{}_S\mathit{Sa}\to {}_{S}S$ defined by $f\left(sa\right)=s$ which satisfies $f\left(a\right)a=a$. Therefore, _SA is I-regular. □

Theorem 10.

For any pomonoid S, all completely reducible left S-posets are I-regular if and only if S contains a right zero element.

Proof. 

Regarding necessity, the one element left S-poset _SΘ is obviously completely reducible. Hence, by assumption, _SΘ is I-regular. By Lemma 1, _SΘ is projective, which implies that S contains a right zero element from ([4], Theorem 1).

Regarding sufficiency, from the existence of a right zero element, it follows that the only simple left S-poset is one-element S-poset. Obviously the one-element poset is projective and I-regular by Lemma 1. But then, by Lemma 3, every completely reducible left S-poset is I-regular. □

Lemma 8.

Let S be a left zero semigroup with 1 adjoined and _SA a weakly po-flat left S-poset. Suppose that $a\in A$ and $s,t\in S\setminus \left\{1\right\}$ are such that $sa\le ta$. Then, $s\le t.$

Proof. 

From $sa\le ta$, it follows that $s\otimes a\le t\otimes a$ in $S{\otimes }_{S}A.$ Thus, we have $s\otimes a\le t\otimes a$ in $(sS\cup tS){\otimes }_{S}A$, since _SA is weakly po-flat. Therefore, by Lemma 5, there exist $u_1,v_1,\dots ,u_n,v_n\in S,s_1,\dots ,s_n\in (sS\cup tS),a_2,\dots ,a_n\in A$ such that

$$\begin{array}{cc}& s\le s_1{u}_1,\hfill \\ & s_1{v}_1\le s_2{u}_2,\hfill & \hfill & u_{1}a\le v_1{a}_2,\hfill \\ & s_2{v}_2\le s_3{u}_3,\hfill & & u_2{a}_2\le v_2{a}_3,\hfill \\ & \dots \hfill & & \dots \hfill \\ & s_n{v}_n\le t,\hfill & & u_n{a}_n\le v_{n}a.\hfill \end{array}$$

Since $s_1,\dots ,s_n\in (sS\cup tS)$, where $s,t$ are left zero elements, it is easy to show that $s_1,s_2,\dots ,s_n$ are also left zero elements. Thus, $s\le t$ and the result follows. □

Theorem 11.

Let S be a left zero semigroup with 1 adjoined. Then all weakly po-flat left S-posets are I-regular.

Proof. 

If $S=\left\{1\right\}$, then the result is clear. Now we let S be a left zero semigroup with 1 adjoined. Suppose that ${}_{S}A$ is a weakly po-flat left S-poset and $a\in A$. By Lemma 1, we show that ${}_S\mathit{Sa}$ is a projective left S-poset.

Suppose that $sa\ne a$ for any $s\in S\setminus \left\{1\right\}$. We define a mapping $f:{}_S\mathit{Sa}\to {}_{S}S$ as follows: $f\left(ta\right)=t,t\in S.$

Suppose $ta=t^{\prime }a$. If $t,t^{\prime }\in S\setminus \left\{1\right\}$, then $t=t^{\prime }$ by Lemma 8. If $t\in S\setminus \left\{1\right\}$ and $t^{\prime }=1,$ then $ta=a$, it is a contradiction. If $t^{\prime }\in S\setminus \left\{1\right\}$ and $t=1$, the result is similar. This means that f is well defined. It is clear that f is an isomorphism of left S-posets. Thus, ${}_S\mathit{Sa}$ is projective.

Now suppose that there exists an element $s\in S\setminus \left\{1\right\}$ such that $sa=a$. We define a mapping $f:{}_S\mathit{Sa}\to {}_S\mathit{Ss}$ as follows:

$$f\left(a\right)=s,$$

$$f\left(ta\right)=t,t\in S\setminus \left\{1\right\}.$$

By Lemma 8, it is easy to see that f is well defined. Clearly, $f:{}_S\mathit{Sa}\to {}_S\mathit{Ss}$ is an isomorphism of left S-posets. Thus, _SSa is projective since s is an idempotent of S. □

Proposition 3.

All weakly torsion free left S-posets are I-regular if and only if S is right po-cancellable.

Proof. 

Regarding necessity, suppose all weakly torsion free left S-posets are I-regular. We let $s,t,c\in S$ where c is left po-cancellable and $sc\le tc$. Consider the left S-poset $A=S$, which is weakly torsion free. Since A is I-regular, for the element $c\in A$, there exists an idempotent $e\in E\left(S\right)$ such that:

• $c=ec$;
• For all $s,t\in S$, $sc\le tc$ implies $se\le te$.

By the given condition $sc\le tc$, the second property yields $se\le te$. If S were not right po-cancellable, there would exist $s\ne t\in S$ such that $sc\le tc$ but $s\nleqq t$, contradicting the weak torsion freeness of A. Thus, S must be right po-cancellable.

Regarding sufficiency, we let S be right po-cancellable and let A be a weakly torsion free left S-poset. For any $a\in A$, we define a map $f:Sa\to S$ by $f\left(sa\right)=s$ for all $s\in S$.

First, we verify that f is well defined: If $sa=ta$ for some $s,t\in S$, then the weak torsion freeness of A (together with right po-cancellability of S) implies $s=t$. Thus, $f\left(sa\right)=f\left(ta\right)$, so f is well defined.

Next, since $a=1·a$, we have $f\left(a\right)=f(1·a)=1$. It follows that $f\left(a\right)·a=1·a=a$. By the definition of I-regularity, a is I-regular. Since a was arbitrary, A is I-regular. □

Proposition 4.

All flat left S-posets are I-regular if and only if S is a regular pomonoid.

Proof. 

Regarding necessity, suppose all flat left S-posets are I-regular. The pomonoid S itself is a flat left S-poset. Thus, S is I-regular as a left S-poset. By Lemma 2, a pomonoid S is left PP if and only if it is I-regular as a left S-poset. Hence, S is left PP. Now, we take any $s\in S$. Since S is flat and I-regular, Theorem 1 implies that for every idempotent $e\in T\left(S\right)$ and every $s\in S$, $se$ is regular in S. Since $T\left(S\right)=S$ (as S is I-regular), $s=s·1$ must be regular. Thus, every element of S is regular, so S is a regular pomonoid.

Regarding sufficiency, we let S be a regular pomonoid and let A be a flat left S-poset. For any $a\in A$, we need to show a is I-regular.

Since S is regular, for every $s\in S$, there exists $s^{\prime }\in S$ such that $s=s{s}^{\prime }s$. We define a map $f:Sa\to S$ by $f\left(sa\right)=s{s}^{\prime }$ for all $s\in S$.

First, we verify f is well defined: If $sa=ta$ for $s,t\in S$, the flatness of A implies there exists $u\in S$ such that $su=tu$ and $ua=a$. Then, $s{s}^{\prime }=s{s}^{\prime }\left(su\right)u^{\prime }=\left(s{s}^{\prime }s\right)u{u}^{\prime }=su{u}^{\prime }$, and similarly $t{t}^{\prime }=tu{u}^{\prime }$. Since $su=tu$, we have $s{s}^{\prime }=t{t}^{\prime }$, so $f\left(sa\right)=f\left(ta\right)$. Thus, f is well defined.

Next, we compute $f\left(a\right)$: Since $a=1·a$, $f\left(a\right)=f(1·a)=1·1^{\prime }=1^{\prime }$ (where $1^{\prime }$ is the inverse of 1 in S, which is 1 itself, since $1=1·1·1$). Thus, $f\left(a\right)=1$, and $f\left(a\right)·a=1·a=a$.

Alternatively, we can use regularity directly. For $a\in A$, $a=1·a=(1·1^{\prime }·1)·a=1^{\prime }·(1·a)=1^{\prime }·a$. Thus, $f\left(a\right)=1^{\prime }$ and $f\left(a\right)·a=a$, so a is I-regular. Since a was arbitrary, A is I-regular. □

4. Direct Product of I-Regular $\mathbf{S}$-Posets

In the following, we first investigate I-regularity of $D\left(S\right)$. First, we remind the reader of some preliminaries.

First, notice that for $a\in A,{\rho }_a:{}_{S}A\to {}_{S}A$ denotes the right translation map defined by ${\rho }_a\left(s\right)=sa$ and $\overrightarrow{ker}{\rho }_a=\left\{(s,t)\right|sa\le ta\}$. We let _SA and _SB be left S-posets over a pomonoid S. It is known that _SA is I-regular if and only if for every $a\in A$ there exists an idempotent $e\in S$ such that $\overrightarrow{ker}{\rho }_a=\overrightarrow{ker}{\rho }_e$. It is also known that a pomonoid S is left $PP$ if and only if for each $s\in S,\overrightarrow{ker}{\rho }_s=\overrightarrow{ker}{\rho }_e$ for some idempotent $e\in S$. Therefore, each left $PP$-pomonoid as a left S-poset is I-regular. Furthermore, if we denote by $Co{n}_{S}A$ the set of all congruences on the poset _SA, the order relation on ${Con}_{S}A$ is defined by $\rho \le \lambda$ if and only if $\rho \cap \lambda =\rho$. Then clearly $(Co{n}_{S}A,\cap )$ is a pomonoid with identity ${(}_{S}A\times {}_{S}A)$. It can be routinely verified that for $(a,b)\in A\times B$, $\overrightarrow{ker}{\rho }_{(a,b)}=\overrightarrow{ker}{\rho }_a\cap \overrightarrow{ker}{\rho }_b$.

The next theorem gives a characterization of pomonoids over which $D\left(S\right)$ is I-regular.

Theorem 12.

Let S be a pomonoid. The diagonal S-poset $D\left(S\right)$ is I-regular if and only if

(1)

S is a left $PP$-pomonoid.

(2)

The set $R=\{\overrightarrow{ker}{\rho }_e|e\in E(S)\}\cup (S\times S)$ is a subpomonoid of $T=(Co{n}_{S}S,\cap )$.

Proof. 

Regarding necessity, we take $s\in S$. Since $D\left(S\right)$ is I-regular, $\overrightarrow{ker}{\rho }_s=\overrightarrow{ker}{\rho }_{(s,s)}=\overrightarrow{ker}{\rho }_e$ for some idempotent $e\in S$. Thus, S is a left $PP$ pomonoid. On the other hand, by assumption, for each pair of idempotents $e,f\in S$, $\overrightarrow{ker}{\rho }_e\cap \overrightarrow{ker}{\rho }_f=\overrightarrow{ker}{\rho }_{(e,f)}=\overrightarrow{ker}{\rho }_h$ for some idempotent $h\in S$, which complete the proof of necessity.

Regarding sufficiency, we let $(s,t)\in D\left(S\right)$ for $s,t\in S$. Since S is a left $PP$ pomonoid, S is I-regular by Lemma 2. Thus, there exist idempotents $e,f$ in S such that $\overrightarrow{ker}{\rho }_s=\overrightarrow{ker}{\rho }_e$ and $\overrightarrow{ker}{\rho }_t=\overrightarrow{ker}{\rho }_f$. Since R is a subpomonoid of T, there exists an idempotent $h\in S$ such that $\overrightarrow{ker}{\rho }_e\cap \overrightarrow{ker}{\rho }_f=\overrightarrow{ker}{\rho }_h$. Now, we get $\overrightarrow{ker}{\rho }_{(s,t)}=\overrightarrow{ker}{\rho }_s\cap \overrightarrow{ker}{\rho }_t=\overrightarrow{ker}{\rho }_e\cap \overrightarrow{ker}{\rho }_f=\overrightarrow{ker}{\rho }_h$. Hence, $D\left(S\right)$ is I-regular. □

Theorem 13.

The following are equivalent for a left $PP$-pomonoid S:

(1)

Every finite product of I-regular S-posets is I-regular.

(2)

$S^n$ is I-regular for every $n\in N$.

(3)

The diagonal S-poset $D\left(S\right)$ is I-regular.

Proof. 

The implications $\left(1\right)\Rightarrow \left(2\right)$ and $\left(2\right)\Rightarrow \left(3\right)$ are trivial.

$\left(3\right)\Rightarrow \left(1\right)$. We let _SA and _SB be two I-regular posets. We take $(a,b)\in A\times B$. Suppose that $\overrightarrow{ker}{\rho }_a=\overrightarrow{ker}{\rho }_e$ and $\overrightarrow{ker}{\rho }_b=\overrightarrow{ker}{\rho }_f$ for some idempotents $e,f\in S$. By Theorem 12, we have $\overrightarrow{ker}{\rho }_{(a,b)}=\overrightarrow{ker}{\rho }_a\cap \overrightarrow{ker}{\rho }_b=\overrightarrow{ker}{\rho }_e\cap \overrightarrow{ker}{\rho }_f=\overrightarrow{ker}{\rho }_h$ for some idempotent $h\in S$. Now, by induction, we obtain the desired result. □

Theorem 14.

Let S be a pomonoid, $E\left(S\right)$ the set of idempotents of S. Then, the following conditions are equivalent:

(1)

The diagonal S-poset $D\left(S\right)$ is I-regular and $\left|E\right(S\left)\right|=1$.

(2)

S is right po-cancellable.

Proof. 

(1)⇒(2). We let $su\le tu$, for $u,s,t\in S$. Then $(s,t)\in \overrightarrow{ker}{\rho }_u=\overrightarrow{ker}{\rho }_{(u,u)}$. Since $D\left(S\right)$ is I-regular, there exists $e\in E\left(S\right)$ such that $\overrightarrow{ker}{\rho }_{(u,u)}=\overrightarrow{ker}{\rho }_e$. But $\left|E\right(S\left)\right|=1$, that is $e=1$, then $s\le t$. Hence, S is right po-cancellable.

(2)⇒(1). If S is right po-cancellable, then $\left|E\right(S\left)\right|=1$ and S is a left PP pomonoid. For $(s,t)\in D\left(S\right)$, it is clear that $\overrightarrow{ker}{\rho }_s=\overrightarrow{ker}{\rho }_1$ and $\overrightarrow{ker}{\rho }_t=\overrightarrow{ker}{\rho }_1$. So $\overrightarrow{ker}{\rho }_{(s,t)}=\overrightarrow{ker}{\rho }_s\cap \overrightarrow{ker}{\rho }_t=\overrightarrow{ker}{\rho }_1\cap \overrightarrow{ker}{\rho }_1=\overrightarrow{ker}{\rho }_1$. Hence, $(s,t)$ is an I-regular element of $D\left(S\right)$ and it is I-regular. □

Proposition 5.

For a right collapsible pomonoid S, if ${\prod }_{i\in I}{A}_i$ is I-regular, then for every $i\in I$, $A_i$ is I-regular.

Proof. 

We let $s{a}_i\le t{a}_i$, for $a_i\in A_i$. Since S is right collapsible, there exists $r\in S$ such that $sr=tr$. We consider the fixed element $a_j\in A_j$, for $j\ne i$ and take

$$d_k=\left\{\begin{array}{cc}{a}_i,\hfill & k=i\hfill \\ r{a}_j,\hfill & k\ne i.\hfill \end{array}\right.$$

Then $s{\left(d_k\right)}_I\le t{\left(d_k\right)}_I$. Since ${\prod }_{i\in I}{A}_i$ is I-regular, by Lemma 1 there exists $e\in E\left(S\right)$ such that ${\left(d_k\right)}_I=e{\left(d_k\right)}_I$, $se\le te$. So $a_i=e{a}_i$ and $A_i$ is I-regular. □

Proposition 6.

For a left $PP$-pomonoid S, the following are equivalent:

(1)

If ${\prod }_{i\in I}{A}_i$ is I-regular, then $A_i$ is I-regular.

(2)

_SΘ is I-regular.

(3)

S has a right zero element.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. We let S be a left $PP$-pomonoid. From Lemma 2, it follows that S is I-regular as a left S-poset. Since $S\cong S\times$ _SΘ, we have, by assumption, that _SΘ is I-regular.

$\left(2\right)\Rightarrow \left(3\right)$. By Lemma 3, it is obvious.

$\left(3\right)\Rightarrow \left(1\right)$. If S has a right zero element, then S is right collapsible. By Proposition 5, the result follows. □

5. Classification of Pomonoids by I-Regularity Property of Right Rees Factor $\mathbf{S}$-Posets

In this section, we give a classification of pomonoids by I-regularity property of their right Rees factor S-posets.

Lemma 9

([13], Lemma 1.8). Let S be a pomonoid and K a convex, proper right ideal of S. The following assertions are equivalent:

(1)

$S/K$ is free.

(2)

$S/K$ is projective.

(3)

$S/K$ is strongly flat.

(4)

$S/K$ satisfies condition $\left(P\right)$.

(5)

$\left|K\right|=1$.

Lemma 10

([4], Theorem 1). Let S be a pomonoid. Then:

(1)

${\Theta }_S$ is free if and only if $\left|S\right|=1$.

(2)

${\Theta }_S$ is projective if and only if S has a left zero element.

(3)

${\Theta }_S$ satisfies condition $\left(E\right)$ if and only if S is left collapsible.

(4)

The following assertions are equivalent:

(a) 

${\Theta }_S$ satisfies condition $\left(P\right)$;

(b) 

${\Theta }_S$ satisfies condition $\left(P_w\right)$;

(c) 

${\Theta }_S$ is po-flat;

(d) 

${\Theta }_S$ is flat;

(e) 

${\Theta }_S$ is weakly po-flat;

(f) 

${\Theta }_S$ is weakly flat;

(g) 

S is weakly right reversible.

(5)

${\Theta }_S$ is (always) principally weakly (po-)flat and (po-)torsion free.

Theorem 15.

Let S be a pomonoid and K a convex, right ideal of S. Then $S/K$ is I-regular if and only if $\left|K\right|=1$ and S is right $PP$, or $K_S=S$ and S contains a left zero element.

Proof. 

Suppose that $S/K$ is I-regular for the convex right ideal $K_S$ of S. Then there are two cases as follows:

Case 1. $K_S=S$. Then $S/K\cong {\Theta }_S$ is I-regular and so by Lemma 3 S contains a left zero element.

Case 2. $K_S$ is a convex proper right ideal of S. Since $S/K$ is I-regular, $S/K$ is projective. Thus, by Lemma 9, $\left|K\right|=1$ and so $S/K\cong S_S$. Since $S/K$ is I-regular, $S_S$ is I-regular and so by Lemma 2, S is right $PP$ as required.

Conversely, suppose $\left|K\right|=1$ and S is right $PP$. Then $S/K\cong S_S$ and so by Lemma 2, $S/K$ is I-regular.

If $K_S=S$ and S contains a left zero element, then $S/K\cong {\Theta }_S$ and by Lemma 3, $S/K$ is I-regular. □

Theorem 16.

Let S be a pomonoid. The following statements are equivalent:

(1)

All projective right Rees factor S-posets are I-regular.

(2)

All free right Rees factor S-posets are I-regular.

(3)

If S has a left zero element, then S is right $PP$.

Proof. 

Implication $\left(1\right)\Rightarrow \left(2\right)$ is obvious.

$\left(2\right)\Rightarrow \left(3\right)$. Suppose that S contains a left zero element z. If $K_S=zS=\left\{z\right\}$, then $S/K_S\cong S_S$ and so $S/K_S$ is free, since $S_S$ is free. Thus, by assumption, $S/K_S$ is I-regular and by Lemma 2, S is right $PP$.

$\left(3\right)\Rightarrow \left(1\right)$. Suppose that $S/K$ is projective for the convex right ideal $K_S$ of S. Then there are two cases as follows:

Case 1. $K_S=S$. Then $S/K\cong {\Theta }_S$ is projective and so by Lemma 3, $S/K$ is I-regular.

Case 2. $K_S$ is a convex proper right ideal of S. Since $S/K$ is projective, by Lemma 9, $\left|K\right|=1$, and so $K_S=zS=\left\{z\right\}$ for some $z\in S$. Thus, z is a left zero element and so by assumption, S is right $PP$. From Lemma 2, it follows that $S/K\cong S_S$ is I-regular. □

Theorem 17.

Let S be a pomonoid. The following statements are equivalent:

(1)

All strongly flat right Rees factor S-posets are I-regular.

(2)

If S is left collapsible, then S contains a left zero element and S is right $PP$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. If S is left collapsible, then by Lemma 10, ${\Theta }_S$ satisfies Condition $\left(E\right)$ and so it is strongly flat. Thus, by assumption, ${\Theta }_S$ is I-regular and so by Lemma 3 S contains a left zero element. Thus, S is right $PP$ by Theorem 16.

$\left(2\right)\Rightarrow \left(1\right)$. Suppose that $S/K$ is strongly flat for the convex right ideal $K_S$ of S. Then there are two cases as follows:

Case 1. $K_S=S$. Then $S/K\cong {\Theta }_S$ is strongly flat and so by Lemma 10, S is left collapsible. By assumption, S contains a left zero element; thus, by Lemma 3, $S/K$ is I-regular.

Case 2. $K_S$ is a convex proper right ideal of S. Since $S/K$ is strongly flat, by Lemma 9, $\left|K\right|=1$ and so $K_S=zS=\left\{z\right\}$ for some $z\in S$. Thus, z is a left zero element and so S is left collapsible. By assumption, S is right $PP$. Hence, $S/K\cong S_S$ is I-regular by Lemma 2. □

Theorem 18.

Let S be a pomonoid. The following statements are equivalent:

(1)

All right Rees factor S-posets satisfying Condition $\left(P\right)$ are I-regular.

(2)

If S is weakly right reversible, then S contains a left zero element and S is right $PP$.

Proof. 

It is similar to that of Theorem 17. □

Recall from [13] that we let K be convex, proper right ideal of pomnoid S, $S/K$ is principally weakly flat if and only if K is left stabilizing. $S/K$ is principally po-flat if and only if K is strongly left stabilizing.

Theorem 19.

Let S be a pomonoid. The following statements are equivalent:

(1)

All weakly flat right Rees factor S-posets are I-regular.

(2)

If S is weakly right reversible, then S contains a left zero element and S is right $PP$, and S has no proper, left stabilizing convex right ideal K with $\left|K\right|>1$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. If S is weakly right reversible, then S contains a left zero element and also S is right $PP$ by Theorem 18. If S has a proper, left stabilizing convex right ideal K with $\left|K\right|>1$, then $S/K$ is weakly flat and by assumption $\left|K\right|=1$, a contradiction is obtained.

$\left(2\right)\Rightarrow \left(1\right)$. We let K be a convex right ideal of pomonoid S and $S/K$ is weakly flat. If K is convex, proper right ideal of S, by [13], Lemma 1.7, S is weakly right reversible and K is a proper, left stabilizing convex right ideal of S. By assumption, $\left|K\right|=1$ and S is right $PP$; then, $S/K\cong S$ is I-regular. But if $K=S$, $S/K\cong \Theta$ is weakly flat and by Lemma 10, S is weakly right reversible. By assumption, S has a left zero element and by Lemma 3, $S/K$ is I-regular. □

The following theorem can be proven by a similar argument of the proof of Theorem 19.

Theorem 20.

Let S be a pomonoid. The following statements are equivalent:

(1)

All weakly po-flat right Rees factor S-posets are I-regular.

(2)

If S is weakly right reversible, then S contains a left zero and S is right $PP$, and S has no proper, strongly left stabilizing convex right ideal K with $\left|K\right|>1$.

Theorem 21.

Let S be a pomonoid. The following statements are equivalent:

(1)

All principally weakly flat right Rees factor S-posets are I-regular.

(2)

S has a left zero element and S is right $PP$, and S has no proper, left stabilizing convex right ideal K with $\left|K\right|>1$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. Since $\Theta$ is principally weakly flat, by assumption, $\Theta$ is I-regular. Using Lemma 3, we deetermine that S has a left zero element and also S is right $PP$ by Theorem 16. Suppose that S has proper, left stabilizing convex right ideal K with $\left|K\right|>1$. Then $S/K$ is principally weakly flat and by assumption that $\left|K\right|=1$, a contradiction is obtained.

$\left(2\right)\Rightarrow \left(1\right)$. We let K be a convex right ideal of pomonoid S and $S/K$ be principally weakly flat. If K is convex, proper right ideal of S, then by [13], Lemma 1.7, K is a proper, left stabilizing convex right ideal of S. By assumption, $\left|K\right|=1$ and S is right $PP$; hence, $S/K\cong S$ is I-regular. But if $K=S$, then $S/K\cong \Theta$ is principally weakly flat. Since S has a left zero element and by Lemma 3, $S/K$ is I-regular. □

Similarly, one can prove the following theorem.

Theorem 22.

Let S be a pomonoid. The following statements are equivalent:

(1)

All principally weakly po-flat right Rees factor S-posets are I-regular.

(2)

S has a left zero element and S is right $PP$, and S has no proper, strongly left stabilizing convex right ideal K with $\left|K\right|>1$.

Theorem 23.

Let S be a pomonoid. The following statements are equivalent:

(1)

All I-regular right Rees factor S-posets are free.

(2)

If S has a left zero element, then $S=\left\{1\right\}$.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. Suppose that S has a left zero element. From Lemma 3, it follows that $\Theta$ is I-regular. By assumption that ${\Theta }_S$ is free, we determine that $S=\left\{1\right\}$ by Lemma 10.

$\left(2\right)\Rightarrow \left(1\right)$. Suppose that $S/K$ is I-regular for the convex right ideal K of S. Then there are two cases as follows:

Case 1. $K=S$. Then $S/K\cong \Theta$ and so by Lemma 3, S contains a left zero element. Hence, by assumption, $S=\left\{1\right\}$ and so $S/K\cong \Theta$ is free by Lemma 10.

Case 2. K is a proper, convex right ideal of S. Since $S/K$ is projective, by Lemma 9 we have $\left|K\right|=1$. Thus $S/K\cong S_S$ is free, since $S_S$ is free. □

Theorem 24.

Let S be a pomonoid. Then all I-regular right Rees factor S-posets are projective.

Proof. 

It follows from Lemma 1. □

Remark 1.

If the order of S is discrete (as an S-act), then by the main results in this paper, we can easily obtain all the characterization of monoids by properties of regular (Rees factor) S-acts.

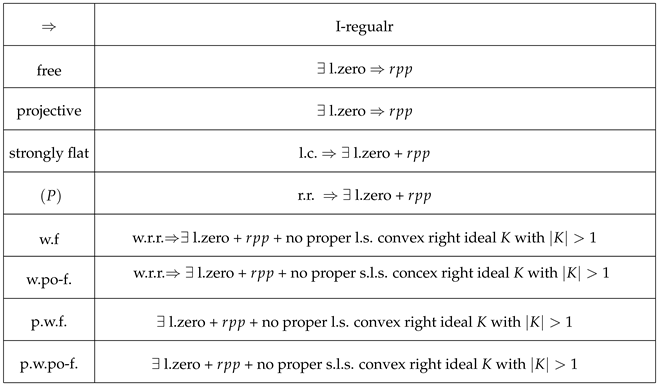
Below, we tabulate the results.

Abbreviations: l.c. = left collapsible; l.zero = left zero; w.r.r. = weakly right reversible; r.r. = right reversible; rpp = right $PP$; s.l.s. = strongly left stabilizing; l.s. = left stabilizing.

6. Conclusions and Limitations

6.1. Conclusions

This paper extends the homological classification of pomonoids using I-regular S-posets, with three key contributions:

• It characterizes pomonoids where all I-regular left S-posets possess projectivity (injectivity)-related properties (e.g., principally weakly flat, weakly torsion free), generalizing Shi’s 2005 results on $PP$-pomonoids and po-cancellable pomonoids.
• It establishes conditions for the I-regularity of diagonal posets $D\left(S\right)$ and Rees factor posets, linking I-regularity to idempotent behavior and pomonoid structure (e.g., right $PP$, left collapsible).
• It supplements results on I-regularity of posets with specific properties (e.g., strongly faithful, completely reducible), providing a more comprehensive framework for pomonoid classification.

6.2. Limitations and Future Directions

Despite these contributions, the work has several limitations that can guide future research:

• Restriction to Left S-posets: All results focus on left S-posets, with no analogous analysis for right S-posets. Future work could extend I-regularity to right S-posets and explore left–right duality in pomonoid classification.
• Finite Pomonoid Bias: While examples use finite pomonoids, the paper does not explicitly address infinite pomonoids (e.g., pomonoids over infinite semigroups). Infinite pomonoids may exhibit distinct I-regularity behavior (e.g., non-finite idempotent sets), requiring new techniques.
• Connection to Other Regularity Notions: I-regularity is not compared to other regularity concepts in S-poset theory (e.g., GP-regularity, strongly regular). Future work could explore hierarchies between these notions and their impact on pomonoid classification.