CoEGAN-BO: Synergistic Co-Evolution of GANs and Bayesian Optimization for High-Dimensional Expensive Many-Objective Problems

Abstract

Bayesian optimization (BO) struggles with data scarcity and poor scalability in high-dimensional many-objective optimization problems. To address this, we propose Co-Evolutionary GAN–Bayesian Optimization (CoEGAN-BO), a novel framework that synergizes generative adversarial networks (GANs) with Bayesian co-evolutionary search for data-driven optimization. The GAN module generates synthetic samples conditioned on promising regions identified by BO, while a co-evolutionary mechanism maintains two interacting populations: one explores the GAN’s latent space for diversity, and the other exploits BO’s probabilistic model for convergence. A bi-stage infilling strategy further enhances efficiency: early iterations prioritize exploration via $L_p$-norm-based candidate selection, later switching to a max–min distance criterion for Pareto refinement. Experiments on expensive multi/many-objective benchmarks show that CoEGAN-BO outperforms four state-of-the-art surrogate-assisted algorithms, achieving superior convergence and diversity under limited evaluation budgets.

1. Introduction

Evolutionary computation has increasingly focused on complex engineering problems characterized by multiple conflicting objectives [1,2] in recent years. These problems, prevalent in domains such as aerodynamic design optimization [3], control engineering systems [4], and drug design optimization [5], pose significant challenges due to their high-dimensional and computationally expensive nature. Each objective requires expensive computational costs, rendering the problem an expensive multi-objective optimization problem (EMOP) [6,7,8] as follows:

$$minF\left(\mathit{x}\right)=min(f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\dots ,f_m\left(\mathit{x}\right))$$

(1)

where $\mathit{x}=(x_1,x_2,\dots ,x_D)\in {\mathsf{\Omega }}^D$ is a D-dimensional variable vector in the decision space ${\mathsf{\Omega }}^D$, while m and D represent the number of objectives and the dimensions of the decision variables, respectively. When each objective function $f_i\left(\mathit{x}\right)$ requires exorbitant computational overhead, highlighting a scenario where $D\ge 30$ and $m\ge 3$, $F\left(\mathit{x}\right)$ is indicative of high-dimensional expensive many-objective optimization problems (HEMaOPs) [9,10,11,12].

Bayesian optimization algorithms (BOs) [13,14,15] have emerged as the predominant methods for addressing expensive optimization problems. BOs significantly economize fitness evaluations, which are an intensive and time-consuming aspect of traditional evolutionary algorithms (EAs) [16,17]. By utilizing surrogate models constructed from pre-processed historical data to approximate true models, BOs efficiently pre-screen candidate solutions, substantially reducing the need for expensive original fitness evaluations [13,14]. In essence, only those solutions predicted to be promising undergo expensive computational or physical resource consumption, while the rest benefit from less resource-intensive surrogate models [18]. This strategic approach effectively addresses expensive optimization problems by saving time and resources that would otherwise be spent on extensive fitness evaluations [19].

Furthermore, when traditional optimization problems encounter expensive, high-dimensional, multi-objective problems, the difficulty of optimization is further amplified.

• Constructing a high-fidelity model from limited sample data poses substantial challenges, encountering issues such as reduced optimization efficiency and compromised model precision [20]. Moreover, the time required for model construction escalates exponentially with rising dimensionality, further complicating the optimization process [21].
• As the dimension of the objective space increases, the number of non-dominated solutions tends to burgeon exponentially, thereby intensifying selection pressure throughout the evolutionary process [22].
• Inherently, the sparsity of samples in the high-dimensional decision spaces contributes to a significant level of uncertainty in the value of each predictive sample [23]. This uncertainty complicates the selection of the most advantageous solutions, which are critical for enhancing the precision of the model while concurrently providing more effective guidance for the population’s search trajectory.

There are currently three main approaches to addressing issues encountered when using BO. We provide a more detailed discussion in Table 1.

• Model-Construction-Based BO: In pursuit of refining the surrogate-assisted model’s fidelity, hybrid surrogate modeling has become a key technique [24]. This method capitalizes on the synergy of multiple models to better fit the real objective function, thereby reducing overreliance on the predictive power of any single model. Surrogate models such as the Radial Basis Function (RBF) model [25], Artificial Neural Networks (ANNs) [26], Gaussian process [27,28], and Support Vector Machine (SVM) models [29] are utilized for their respective strengths in various optimization contexts. This illustrates the tailored application of surrogates to different optimization problems.
• Model-Management-Based BO: As the complexity of the objective function increases, not only does the prediction error of the surrogate model intensify, but it also exacerbates the challenge of approaching the Pareto front, making the means of distinguishing between better individuals more difficult. These challenges can be addressed by adopting a more efficient infill criterion.
• Novel Search-Strategy-Based BO: Environment selection is an important part of multi-objective evolutionary algorithms [30]. Individuals with better fitness are selected as the next initial population from the mixed population. Existing methods still use the predicted value and uncertainty of the model to select the next initial population. However, the predicted value and uncertainty variance given by the surrogate model decrease rapidly with the increase in the dimensions. Therefore, the effectiveness of the evolutionary algorithm is also reduced.

Table 1. Summary table of Bayesian optimization (BO)-related methods.

Method Category	Algorithm	Summary of Algorithm Ideas
	MOEA/D-EGO [31]	Adopt fuzzy clustering-based modeling in the decision space; construct multiple local surrogate models for each objective function.
Model-Construction-Based BO	KTA2 [32]	Combine two point-insensitive models with the original Gaussian process to adaptively approximate each objective function, minimizing outlier impacts.
	CLBO [33]	Build several Gaussian processes; impose protocol constraints on all/part of them during training to ensure reasonable and accurate predictions.
	EI (Expected Improvement) [24,34]	A common infill criterion for selecting promising candidates. Loses effectiveness with increasing dimension (uncertainty differences shrink) and fails to optimize all problems.
Model-Management-Based BO	PI (Probability of Improvement) [35,36]	Another widely used infill criterion. Similar to EI: dimension growth reduces uncertainty distinction, leading to invalidation; not optimal for all problems.
	LCB (Lower Confidence Bound) [37,38]	A mainstream infill criterion. Faces the same issues as EI/PI: dimension increase weakens uncertainty measurement, and a single criterion cannot fit all scenarios.
Novel Search-Strategy-Based BO	NSGA-III [39]	Integrate Pareto dominance and decomposition strategies; balance convergence and diversity effectively in high-dimensional problems.
	Two-Arch2 [40]	Establish two updated archives (via metrics and Pareto dominance). Performs well in high dimensions by considering both convergence and diversity.

Table 1. Summary table of Bayesian optimization (BO)-related methods.

Method Category	Algorithm	Summary of Algorithm Ideas
	MOEA/D-EGO [31]	Adopt fuzzy clustering-based modeling in the decision space; construct multiple local surrogate models for each objective function.
Model-Construction-Based BO	KTA2 [32]	Combine two point-insensitive models with the original Gaussian process to adaptively approximate each objective function, minimizing outlier impacts.
	CLBO [33]	Build several Gaussian processes; impose protocol constraints on all/part of them during training to ensure reasonable and accurate predictions.
	EI (Expected Improvement) [24,34]	A common infill criterion for selecting promising candidates. Loses effectiveness with increasing dimension (uncertainty differences shrink) and fails to optimize all problems.
Model-Management-Based BO	PI (Probability of Improvement) [35,36]	Another widely used infill criterion. Similar to EI: dimension growth reduces uncertainty distinction, leading to invalidation; not optimal for all problems.
	LCB (Lower Confidence Bound) [37,38]	A mainstream infill criterion. Faces the same issues as EI/PI: dimension increase weakens uncertainty measurement, and a single criterion cannot fit all scenarios.
Novel Search-Strategy-Based BO	NSGA-III [39]	Integrate Pareto dominance and decomposition strategies; balance convergence and diversity effectively in high-dimensional problems.
	Two-Arch2 [40]	Establish two updated archives (via metrics and Pareto dominance). Performs well in high dimensions by considering both convergence and diversity.

Building on the insights gained from existing research and aiming to address the optimization bottlenecks inherent in high-dimensional expensive problems, this paper pivots towards enhancing the algorithm’s convergence capabilities when faced with numerous non-dominant solutions. Recognizing the necessity for a more efficient approach, we present a novel optimization framework—the Bi-Stage Infill Criterion Bayesian Co-evolutionary Optimization Algorithm (CoEGAN-BO). This algorithm is specifically tailored for many-objective, high-dimensional, and expensive optimization challenges. CoEGAN-BO leverages a cutting-edge generative adversarial network to adeptly select potential solutions that significantly propel the algorithm’s convergence. By doing so, it not only minimizes the need for expensive fitness evaluations but also accelerates the convergence rate, culminating in the attainment of better optimal solutions. The key contribution of our work lies in the selection mechanism following this secondary assessment. Specifically, we extract those individuals that the GAN identifies as “real” from the pool of predicted samples. This approach allows us to isolate and prioritize the high-fidelity samples, which are deemed by the trained GAN to closely resemble the distribution of the actual computed samples. By integrating the GAN-based selection process, we are able to mitigate the risks associated with the surrogate model’s inaccuracies. This is particularly critical in optimization tasks where the search path could be significantly altered due to misleading predictions. Thus, our approach ensures that the optimization process remains robust against such deviations, maintaining the integrity of the search trajectory toward the global optimum. The major contributions of this paper can be summarized as follows:

(1)

The proposed method adeptly extracts useful information from both real and predicted samples. It employs a secondary assessment of the current model’s predictive outcomes. This is designed to mitigate the deterioration in predictive accuracy that can arise due to the trajectory deviation of the surrogate model in the context of high-dimensional expensive optimization challenges.

(2)

We introduce an efficient model management strategy. This strategy synergistically combines the $L_p$-norm with a convergence criterion based on the extremities of distances (maximum and minimum). The main purpose is to significantly reduce computational complexity and to be able to accurately determine which individuals have high “potential”.

(3)

The proposed CoEGAN-BO exhibits considerable advantages when addressing the “curse of dimensionality” challenges in HEMaOPs. The CoEGAN-BO algorithm accelerates population evolution by conducting a secondary selection of more competitive predicted solutions from the non-dominated solutions by reducing non-dominated selection pressure.

(4)

The proposed CoEGAN-BO demonstrates outstanding performance; the experimental results clearly demonstrate that this method is highly competitive in solving high-dimensional problems of 50D and 100D, as well as many-objective problems with 3, 4, 6, 8, and 10 objectives.

The remainder of this paper is organized as follows: Section 2 provides a concise overview of the key techniques utilized in this research: Gaussian processes and generative adversarial networks. Within this context, Gaussian processes are employed for model construction, while generative adversarial networks are applied for the secondary estimation of predicted samples. Section 3 gives a detailed description of the proposed algorithm. The experimental results and analysis are presented in Section 4. The conclusions and future prospects are provided in Section 5.

2. Preliminaries

2.1. Gaussian Process

The Gaussian process (GP) [27,28] is a method renowned for its efficacy in enhancing the forecasting efficiency of engineering problems. Due to its effectiveness, the GP is extensively utilized across diverse engineering disciplines. Also referred to as the kriging model, this method reflects the spatial correlation between known and unknown points by making assumptions. Predictions at interpolation points are made using the GP, which is formulated as follows:

$$\widehat{y}\left(x\right)=\mu +\epsilon \left(x\right)$$

(2)

where $\widehat{y}\left(x\right)$ represents the predicted output at input location x; $\mu$ denotes the constant mean parameter, representing the global average of the process; and $\epsilon \left(x\right)$ signifies a zero-mean Gaussian process with the covariance function $k(x,x^{\prime })$, where $\epsilon \left(x\right)\sim \mathcal{N}(0,{\delta }^2)$.

Given N training points, the predictive distribution at any test point x is Gaussian, with the mean given by

$$\widehat{f}\left(x\right)=\widehat{\mu }+p^T{P}^{-1}(f-l\widehat{\mu })$$

(3)

where $\widehat{f}\left(x\right)$ is the predicted mean value at point x; $\widehat{\mu }$ is the estimated global mean, computed as $\widehat{\mu }={\left(l^T{P}^{-1}l\right)}^{-1}{l}^T{P}^{-1}f$; p is an $N\times 1$ correlation vector between the test point x and training points, with elements $p_i=\mathrm{corr}(x,x_i)$; P is an $N\times N$ correlation matrix among training points, where $P_{ij}=\mathrm{corr}(x_i,x_j)$; f is an $N\times 1$ vector of observed outputs at training points, where $f={[y_1,y_2,\dots ,y_N]}^T$; and l is an $N\times 1$ vector of ones, where $l={[1,1,\dots ,1]}^T$.

The prediction uncertainty is quantified by the variance:

$$s^2\left(x\right)={\widehat{\delta }}^2\left[1-p^T{P}^{-1}p+{\displaystyle \frac{{(1-l^T{P}^{-1}p)}^2}{l^T{P}^{-1}l}}\right]$$

(4)

where $s^2\left(x\right)$ represents the prediction variance at point x, measuring uncertainty; and ${\widehat{\delta }}^2$ is the estimated process variance, typically computed as ${\widehat{\delta }}^2={\displaystyle \frac{1}{N}}{(f-l\widehat{\mu })}^T{P}^{-1}(f-l\widehat{\mu })$. The term $p^T{P}^{-1}p$ accounts for the reduction in uncertainty due to proximity to training points. The fraction term ${\displaystyle \frac{{(1-l^T{P}^{-1}p)}^2}{l^T{P}^{-1}l}}$ represents additional uncertainty from estimating the mean parameter.

The Gaussian process framework assumes that the covariance between any two points is related through the correlation matrix P and correlation vector p. This spatial correlation structure enables the GP to provide both accurate predictions and reliable uncertainty estimates, making it particularly valuable for engineering applications requiring risk assessment and decision-making under uncertainty.

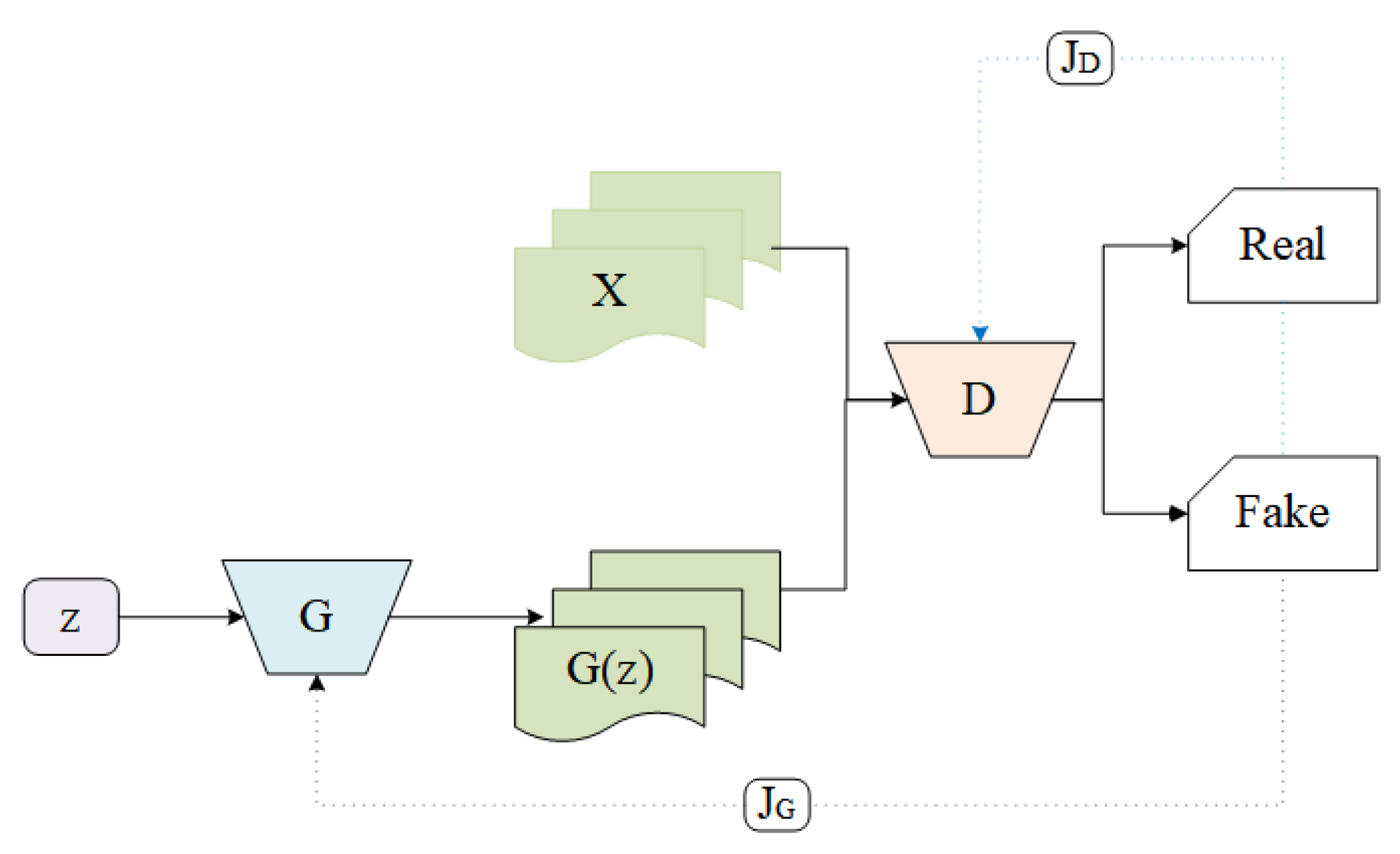
2.2. Generative Adversarial Networks

Generative adversarial networks (GANs) [41,42] offer a powerful framework for learning data representations even in the absence of extensive labeled training datasets. This innovative approach circumvents the need for explicit modeling of the probability density function and has achieved widespread application across various domains, including unsupervised representation learning, image synthesis, and image super-resolution enhancement.

The foundational structure of the GAN is depicted in Figure 1. At its core, the GAN is composed of two neural networks that are trained concurrently: the Generator (G) and the Discriminator (D). The Generator’s role is to approximate the distribution of real data by generating synthetic samples that are indistinguishable from actual data, thereby attempting to deceive the Discriminator into accepting the fabricated data as authentic. On the other hand, the Discriminator functions as a classifier that discerns whether a sample originates from the real dataset or has been concocted by the Generator.

Engaged in a continuous adversarial contest, both networks employ backpropagation to update their weights, thereby progressively honing their respective capabilities. The Generator strives to maximize the likelihood of creating convincing forgeries, while the Discriminator aims to minimize the chances of erroneously classifying fake data as real. Through this adversarial training process, both networks incrementally escalate their competencies, learning from each other’s weaknesses and thereby advancing the model’s overall performance.

The Discriminator within a generative adversarial network bears the crucial task of discerning the authenticity of data. It acts as a judge, evaluating each sample to ascertain whether it is genuine or a counterfeit produced by the Generator. The objectives of the Discriminator are twofold:

Accuracy in Classification: The Discriminator must accurately distinguish between real and generated (fake) samples, minimizing the likelihood of misclassification.

Adversarial Improvement: Through iterative training, the Discriminator seeks to refine its ability to identify subtle cues that differentiate authentic data from imitations, thereby providing a robust challenge to the Generator. These goals ensure that the Discriminator evolves in tandem with the Generator, maintaining a delicate balance where each component improves in response to the other’s advancements, driving the overall system towards more sophisticated data representation and generation capabilities.

$$max{E}_{x\sim p_{data}}[logD(x\left)\right]+E_{z\sim p_z}[log(1-D\left(G\right(z\left)\right)\left)\right]$$

(5)

In Equation (5), the first part is to make the Generator judge whether the real sample is real with high probability. The second part is to minimize the probability of the Generator discriminating the fake sample as true.

GANs learn the distribution of the given data by adversarial means. This makes the Generator fit the distribution close to the real data. It is the distribution of the PS (Pareto set), which provides convenience for us to find the true PF [43]. At the same time, the trained discriminator completes the binary classification task, making it possible to distinguish what is generator-generated data, in order to complete an effective control solution. GMOEA [44] proposes dividing the population into two different datasets based on the fitness evaluation criterion. It uses two datasets to train the GAN model. The GAN and genetic operators are used to generate some offspring to complete the optimization work. EGANS [45] proposes an evolutionary generator architecture search strategy. It employs a many-to-one adversarial training strategy to evolutionarily search for the optimal Generator. In this way, a generative network with good adaptability and stability is designed. EWSGAN [46] trains a weight-sharing super-network through GANs and identifies the optimal subnet. It can be seen that the GAN has great potential in the optimization field. We propose CoEGAN-BO, an efficient GAN-based environmental selection strategy to guide population evolution.

In this study, we leverage the power of generative adversarial networks (GANs) by utilizing samples that have undergone actual computation as the “real” samples while treating the predicted samples as the “generated” ones. We train the GAN in such a way that it becomes capable of conducting a secondary assessment of the predicted samples. Through this process, the GAN evaluates the authenticity of each predicted sample, akin to distinguishing between the genuine and the imitative.

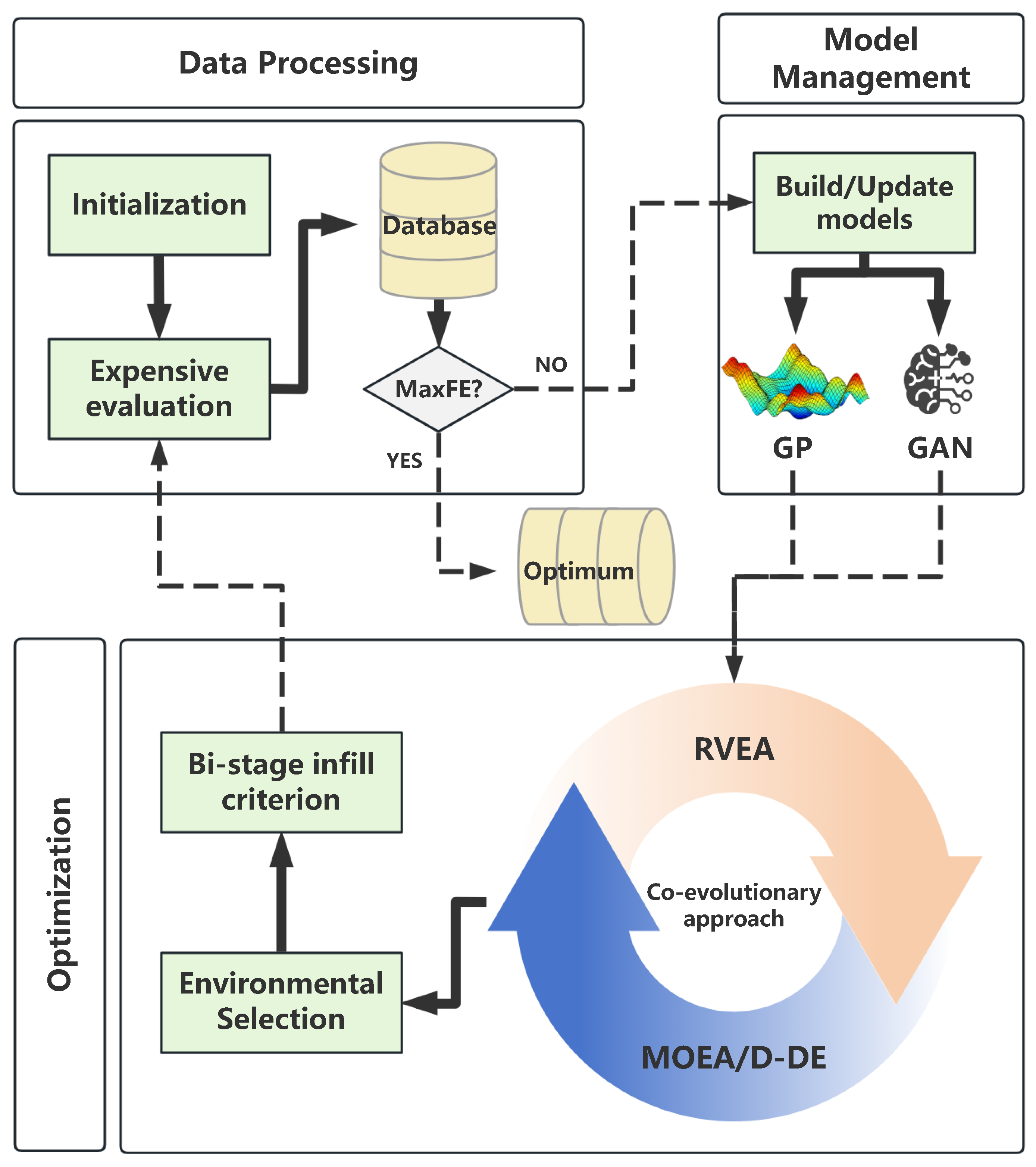
3. The Proposed CoEGAN-BO Algorithm

In this work, we introduce CoEGAN-BO, a novel strategy tailored for tackling HEMaOPs. Mirroring the structure of existing SAEAs, CoEGAN-BO is comprised of a triad of core components: an optimizer, a surrogate model, and an adaptive sampling criterion. Initially, this section outlines the overarching architecture of CoEGAN-BO. This is followed by an exposition on the innovative use of generative adversarial networks (GANs) for environmental selection, which plays a pivotal role in guiding the optimization process. Subsequently, we introduce a distinctive infilling criterion that holistically considers both the convergence and diversity of the algorithm, ensuring a balanced exploration and exploitation throughout the optimization process.

The computational framework of the proposed CoEGAN-BO is given in Algorithm 1. The algorithm adopts an individual-based model management strategy. This means that CoEGAN-BO will select several individuals for expensive fitness evaluation. These selected individuals are then utilized to iteratively refine both the Gaussian process and the GAN model with each successive generation. The flowchart in Figure 2 presents a comprehensive overview of an evolutionary algorithm that incorporates the GAN for environmental selection and uses surrogate models to facilitate the optimization process, especially in scenarios where evaluations are computationally expensive. Throughout the process, the database (DB) plays a central role by providing the necessary data for rebuilding the surrogate and GAN models, ensuring that they are kept up-to-date with the latest insights from the search space. Using the GAN for environment selection introduces a novel approach to guide the evolutionary process by selecting individuals that are not only high-performing according to surrogate models but also resemble authentic data points, potentially leading to more efficient and effective optimization.

The operational specifics of CoEGAN-BO are delineated in Algorithm 1. An initial sampling of candidates is generated via Latin hypercube sampling, with the evaluated samples stored in the database (DB). These samples form the foundation for constructing objective-wise surrogate-assisted and GAN models.

Algorithm 1 Framework of CoEGAN-BO

Require: $F{E}_{max}$ (maximum number of fitness evaluations); $NI$ (number of initialized solutions); N (population size); ${\omega }_{max}$ (maximum generations before Gaussian process update); $\eta$ (number of fitness evaluations in each generation). Ensure: $PS$ (Pareto set).    1: Initialization: Employ LHS to generate design samples and evaluate them; archive all of the evaluated solutions into the DB, set $FE=NI$;    2: Establish Gaussian process and $GAN$ for each objective function using the $DB$ samples;    3: From the initial design points, select $NP$ superior candidates to form the initial population P;    4: while  $FE<=F{E}_{max}$  do    5:     while $\omega <={\omega }_{max}$ do    6:           Select mating parents from $P^{\omega }$ and generate offspring $O^{\omega }$ via each optimizer;    7:           Estimate the offspring by the surrogate-assisted models;    8:           Select NP best individuals to be the next population $P^{\omega +1}$;    9:           Increment generation counter: $\omega =\omega +1$;  10:     end while  11:     Employ an infill criterion to identify $\eta$ optimal offspring;  12:     Execute original fitness evaluations for these candidates;  13:     Update $FE$ accordingly: $FE=FE+\eta$;  14:     Update surrogate models with new evaluated data;  15: end while

Within the CoEGAN-BO framework, popular multi-objective evolutionary algorithms such as MOEA/D-DE [47] and RVEA [48] are integrated as the baseline optimization engines. The algorithm employs genetic operators to spawn offspring, while a surrogate model is utilized to estimate the fitness value of each objective function.

Subsequently, selection for the next generation is conducted using the procedure outlined in Algorithm 2, which continues until the predefined population iteration limit is achieved. Integral to the process is Algorithm 3, which selectively pinpoints the most promising subset of solutions and subjects them to expensive fitness evaluations.

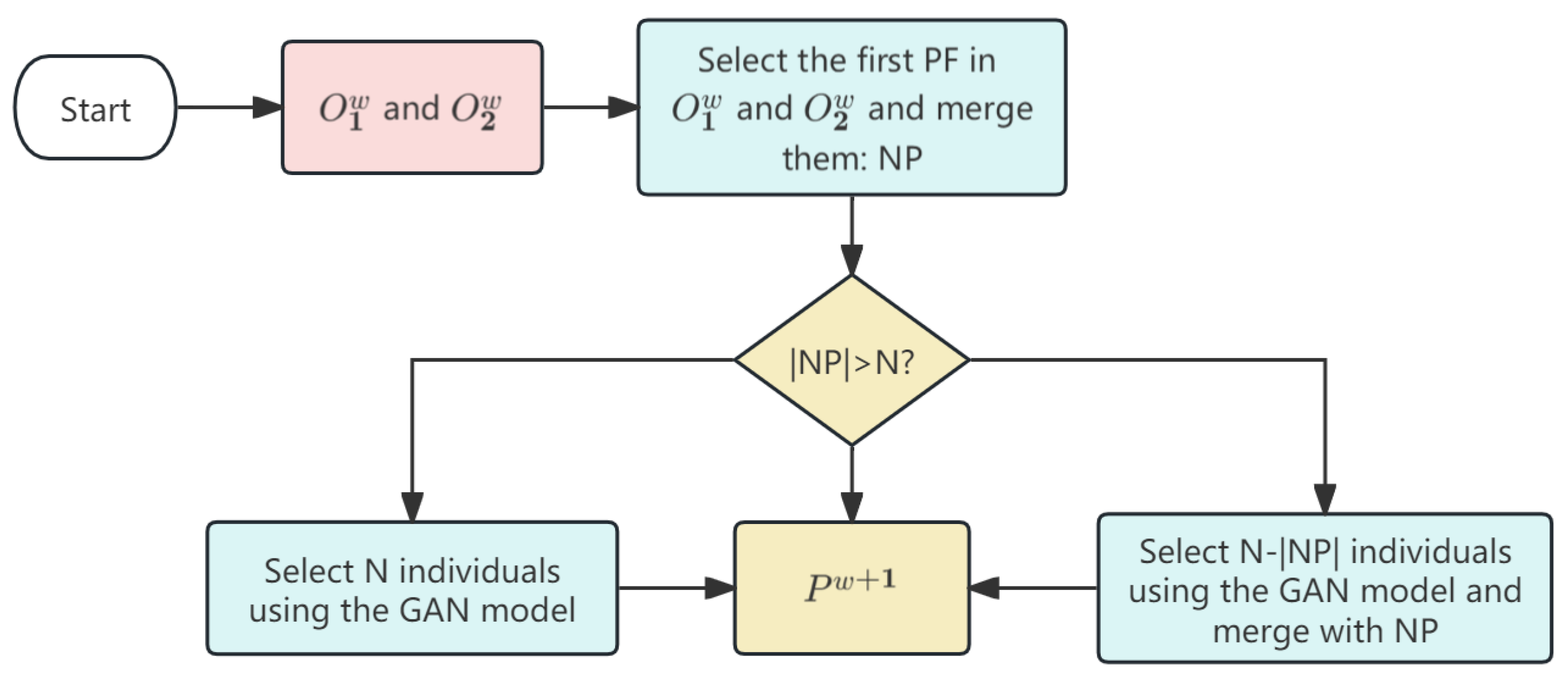
Algorithm 2 Environmental selection strategy using GAN

Require: N (population size); ${\omega }_{max}$ (maximum iterations of population evolution); $O_1^{\omega }$ (offspring of the first population); $O_2^{\omega }$ (offspring of the second population); $GAN$ (trained generative adversarial network). Ensure: $P^{\omega +1}$ (the next population).    1: while  $\omega <={\omega }_{max}$  do    2:     Perform non-dominated sorting on $O_1^{\omega }$ and $O_2^{\omega }$;    3:     $PF{1}_1\leftarrow$ Select individuals from the first Pareto front of $O_1^{\omega }$;    4:     $PF{1}_2\leftarrow$ Select individuals from the first Pareto front of $O_2^{\omega }$;    5:     if $\left|NP\right|>N$ then    6:         $P^{\omega +1}\leftarrow$ Select top N individuals most likely to be authentic using $GAN$;    7:     else    8:         $\mathsf{\Lambda }\leftarrow$ Select $N-\left|NP\right|$ individuals most likely to be authentic using $GAN$ from the remaining candidates by discriminator prediction probability;    9:         $P^{\omega +1}\leftarrow NP\cup \mathsf{\Lambda }$;  10:     end if  11:     $\omega \leftarrow \omega +1$;  12: end while

Algorithm 3 Bi-stage infill sampling criterion

Require: K (number of clusters for infill sampling); N (population size); $\gamma$ (bi-stage division threshold); $F{E}_{max}$ (maximum number of fitness evaluations). Ensure: $\mathsf{\Lambda }$ (candidate solutions for expensive re-evaluation).    1: Initialize set $\mathsf{\Lambda }$ as empty;    2: Perform K-means clustering on the solutions to form K clusters;    3: for $i=1$ to K do    4:     if $FE<\gamma \times F{E}_{max}$ then    5:         Select the solution with the minimum $L_p$-norm within the cluster;    6:     else    7:         Calculate $MD$;    8:         Select the solution with the maximum $MD$ from these solutions in the cluster;    9:     end if  10:     Add the selected solution to set $\mathsf{\Lambda }$;  11: end for

The iterative process of model refinement and solution evaluation via CoEGAN-BO strategically inserts new update points for expensive fitness evaluation. This systematic approach propels the algorithm towards identifying the optimal solution, ensuring that each update maximizes the efficacy of the expensive fitness evaluation process until the budget for such fitness evaluations is exhausted.

In the following sections, we will explore the details of the co-evolutionary algorithm and the new sampling criterion.

3.1. Environmental Selection Strategy Based on Generative Adversarial Network

For complex optimization challenges, one of the most efficacious approaches is to harness diverse heuristic search strategies to enhance the efficiency of identifying optimal solutions. By integrating additional search tactics and employing various operators, the rate of population convergence is expedited. Therefore, this study adopts a co-evolutionary guidance approach for populations to address such complex optimization issues. Our proposed algorithm operates on the basis of two distinct populations, and these populations evolve independently. Each population employs a specific optimizer, with one using MOEA/D-DE and the other utilizing RVEA. Evolution within each population is steered by disparate environment selection, crossover, and mutation techniques. The two populations have the same population size and generate different offspring to ensure the diversity of the offspring. Co-evolutionary dynamics between the two populations enhance the efficacy of the search process. Inter-population information exchange occurs via non-dominated solutions and those identified as promising by the GAN. The optimization process is guided by a secondary GAN-based screening that selects predictive samples that are more closely aligned with the distribution of the real sample (which is evaluated by the original expensive function) space. Both populations excel at identifying superior candidates within their local vicinities, thereby sustaining elevated search efficiency. The experimental results presented in Section 4.3 of this paper indicate that this search strategy not only effectively enhances population diversity but also improves the algorithm’s search capability and optimization speed.

The detailed procedure of Algorithm 2, which describes an environmental selection strategy using the GAN, is outlined below. The algorithm operates on offspring populations $O_1^{\omega }$ and $O_2^{\omega }$. Each iteration begins by performing non-dominated sorting on these offspring populations to identify the fittest individuals in the first Pareto front from each population.

The first Pareto fronts $PF{1}_1$ and $PF{1}_2$ are then merged into a single population $NP$. If the size of $NP$ is greater than the desired population size N, the GAN’s discriminative network is used to select the top N individuals that are most likely to be authentic. These individuals are chosen based on their estimated probabilities of resembling authentic samples, thereby ensuring the reliability of the selected population.

In the case where the number of individuals in $NP$ is less than N, additional individuals are chosen from the remaining candidates by the GAN to make up the shortfall. Once N individuals have been selected, they form the new parent population $P^{\omega +1}$ for the next generation.

This process iterates until the maximum number of generations ${\omega }_{max}$ has been reached. The goal throughout is to maintain a population size of N, filled with individuals that exhibit high fitness and authenticity, thus facilitating effective convergence of the population.

The rationale behind integrating a GAN within Algorithm 2 for environment selection lies in the Discriminator’s acute ability to discern the authenticity of samples, effectively evaluating the likelihood of a sample being representative of the real data distribution. By harnessing the Discriminator’s judgments, the algorithm preferentially selects individuals that are most likely to be authentic. This method seeks to minimize the deviation in the optimization trajectory caused by potential prediction errors, directing the evolutionary process more precisely toward the desired outcomes. Furthermore, this approach is robust even in scenarios like high-dimensional expensive multi-objective optimization problems (HEMaOPs), where sparse samples could potentially diminish model accuracy. The GAN provides valuable secondary information that can be utilized to refine the selection process, thus bolstering the algorithm’s ability to navigate the optimization landscape effectively.

Figure 3 illustrates the environmental selection process using a GAN model within an evolutionary algorithm framework. The overall goal of this process, as depicted in the diagram, is to maintain a population of individuals that not only exhibit high fitness levels but also align well with the authentic data distribution as determined by the GAN’s Discriminator. This approach seeks to enhance the evolutionary algorithm’s ability to converge towards optimal solutions effectively.

3.2. Bi-Stage Infill Criterion

Our method introduces a bi-stage infill criterion that utilizes both the $L_p$-norm distance and $max-min$ distances to identify more promising candidate solutions. This criterion efficiently leverages the surrogate model’s feedback. During the optimization process, sampling is performed according to the infill criterion, with the surrogate model undergoing continuous updates and optimization until the maximum number of evaluations is reached. The selection of individuals for costly fitness evaluations is pivotal within BO. The efficacy of this selection bears directly on the precision of the model post-update. The inherent uncertainty in model predictions sways the algorithm’s search trajectory, thereby influencing the solution quality of the algorithm. In this study, CoEGAN-BO introduces an infill sampling criterion propelled by both the $L_p$-norm distance [49] and max–min distances [50]. This criterion meticulously parses the feedback from the surrogate model to pinpoint more propitious samples. The proposed infill criterion is detailed in Algorithm 3. K-means [51] clustering arranges the candidate solutions into K groups, placing similar individuals within the same cluster. In the first stage, if the number of costly evaluations is below the threshold $\gamma \times F{E}_{max}$, the candidate solution with the minimum $L_p$-norm distance within each cluster is selected for re-evaluation. In the second stage, after the threshold is met, we calculate the minimum Euclidean distance ($MD$) in the objective space between each candidate and those already expensively evaluated. The candidate with the maximum $MD$ from the evaluated set in each cluster is then selected.

The impact of dimensionality on distance metrics is scrutinized [49]. In high-dimensional spaces, the disparity between the most distant and nearest individuals to the search probe is negligible, indicating the erosion of distance functions’ effectiveness as dimensionality escalates. Compared to the Manhattan distance ($L_1$-norm) [52] and the Euclidean distance ($L_2$-norm) [53], the Lp-norm distance demonstrates superior performance in high-dimensional spaces. A static distance may not be universally applicable across optimization problems with varying objective counts. Hence, experimentally, $p=1/m$ is set [40], where m is the number of objectives. This method takes into account the impact of dimensionality on distance metrics, which becomes particularly pertinent in high-dimensional spaces, where traditional distance measures may lose effectiveness. An experimental $L_p$-norm with $p=1/m$, where m is the number of objectives, is utilized to maintain the efficacy of distance measurement across different objective counts. Moreover, in the early stages of optimization in high-dimensional spaces, when candidate solutions are sparse, relying solely on the max–min distance criterion can reduce the population’s local search capability. Our bi-stage infill criterion addresses this issue.

The strategy enables potential solutions to oscillate between regions, circumventing local optima. Each update point is selected with the utmost deliberation, thoroughly assimilating the surrogate model’s feedback. By enabling the selection of multiple promising candidates near the current best solution and in regions with fewer samples, this method significantly improves both the accuracy of the surrogate model and the efficiency of the optimization process. It is well-suited for surrogate models that lack variance estimation, overcoming the limitations of a single sampling criterion and accelerating convergence.

3.3. Computational Complexity Analysis

The proposed CoEGAN-BO algorithm integrates multiple computational components, whose complexity is analyzed as follows:

The algorithm sequentially performs GP and GAN training in each generation. The computational complexity for training these two models is $O(n^2·d)$ for the GP training and $O(E·n·M^2)$ for the GAN, where n is the population size, d is the dimension of the decision space, E is the number of training epochs, and M is the number of objectives.

Following the surrogate modeling, the hybrid optimization combining MOEA/D-DE and RVEA is executed. The computational complexity of the hybrid optimization is $O(N·T·d·{\omega }_{max}+N_1^2·M)$, where N is the number of weight vectors in MOEA/D-DE, T is the neighborhood size, ${\omega }_{max}$ is the maximum iterations, and $N_1$ is the RVEA population size.

Finally, K-means clustering is applied for solution selection with complexity $O(K_e·Q·d)$, where $K_e$ is the number of clusters and $Q\approx O\left(N\right)$ is the candidate solution size.

The main optimization loop runs for T generations, where T is determined by the function evaluation budget. Therefore, the overall computational complexity of CoEGAN-BO is

$$T·\left[O(n^2·d+E·n·M^2)+O(N·T·d·{\omega }_{max}+N_1^2·M)+O(K_e·N·d)\right]$$

(6)

Considering that $N,N_1\approx O\left(n\right)$ and other parameters are constants, the overall complexity can be simplified to

$$T·O(n^2·(d+M))$$

(7)

4. Experimental Evaluation

This section assesses the effectiveness of our proposed method, referred to as CoEGAN-BO, in the context of many-objective optimization problems. An empirical comparison is made with notable SAEAs such as MOEA/D-EGO [31], K-RVEA [24], KTA2 [32], REMO [54], and EDN-ARMOEA [55]. All of the referenced algorithms have been realized within the PlatEMO framework [56]. Our experimental setup included instances from the DTLZ and MaF suite targeting 3, 4, 6, 8, and 10 objectives. Across all DTLZ cases, we set the count of decision variables to 50 and 100, while the MaF problem was on 50 dimensions. Importantly, every experimental setup underwent 20 independent runs.

To evaluate the performance of the SAEAs under comparison, we adopted the Inverted Generational Distance (IGD) metric [57], ensuring a comprehensive assessment of both convergence and diversity. Furthermore, we applied the Wilcoxon rank-sum (WRS) test for a statistical comparison between CoEGAN-BO and the other four SAEAs, establishing a significance threshold of 0.05. In our results, the symbols “+”, “−”, and “=” symbolize the statistical significance in superiority, inferiority, or approximate equivalence of a given algorithm relative to CoEGAN-BO, respectively.

Our GAN architecture employs lightweight feed-forward neural networks for both the Generator and Discriminator, each containing three hidden layers with 5 neurons, epoch = 100, learning rate = 0.001, and batch size equal to the number of training samples, and using the cross-entropy loss function. The number of actual samples and predicted samples is equal during training, and normalization is performed before training. This makes the GAN efficient in training, and it achieves good performance.

4.1. Experimental Settings

In our comparative experiment, all of the compared algorithms shared common parameter settings, which are outlined as follows:

• The initial population size was uniformly set to $100+D/10$ for consistency across all algorithms;
• The maximum allowable number of expensive function evaluations was limited to 300, ensuring a level playing field for evaluation;
• Parameters governing reproduction, including crossover and mutation, had values of $pc=1.0$, $\eta c=20$, $pm=1.0$, and $\eta m=20$ across all algorithms;
• To maintain uniformity, the maximum number of generations before updating the Gaussian process was uniformly established at $w_{max}=20$ for all considered algorithms.

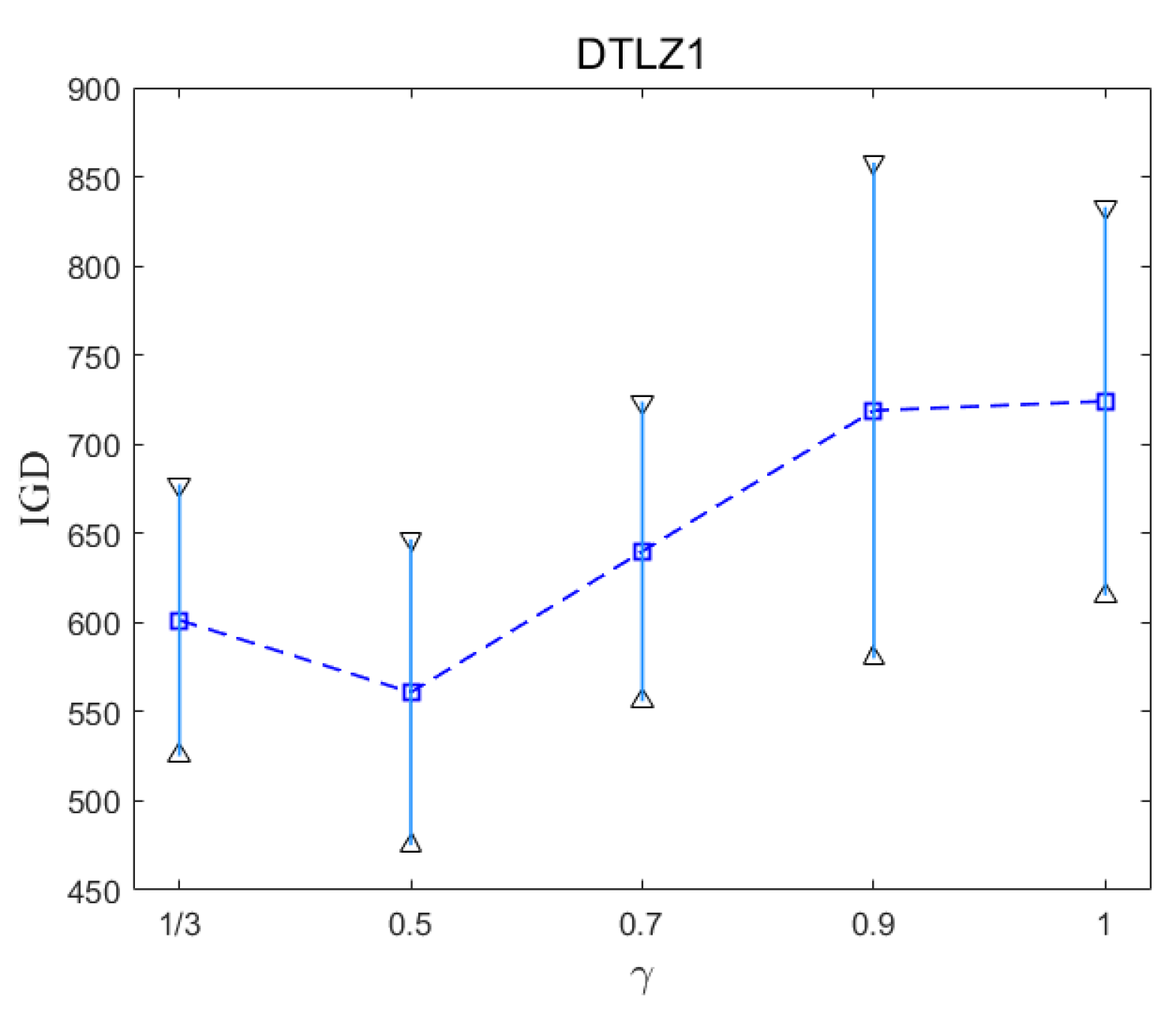
4.2. Sensitivity Analysis Based on Bi-Stage Division Threshold

In the experimental section, we emphasize the significance of the parameter $\gamma$, which is integral to the bi-stage filling criterion detailed in Algorithm 3. The selection of the $\gamma$ value is crucial, as it directly influences the efficacy of CoEGAN-BO. For the purpose of optimizing and refining the parameters of CoEGAN-BO, we chose DTLZ1 as the principal test case. DTLZ1 is renowned for its testing complexity, particularly due to the slow convergence that it typically presents. Success in optimizing DTLZ1 suggests that CoEGAN-BO is likely to perform well across a diverse array of test scenarios. To this end, we rigorously examined the sensitivity of $\gamma$ within the CoEGAN-BO by conducting a series of targeted experiments on the DTLZ1 benchmark.

To ascertain the impact of varying $\gamma$ values on performance, we tested a spectrum of $\gamma$ values within the set $\gamma \in 1/3,0.5,0.7,0.9,1$. The comparative results for the DTLZ1 problems with 3, 4, 6, 8, and 10 objectives are depicted in Figure 4. The results indicate that CoEGAN-BO performs optimally when $\gamma$ is set to 0.5, striking an effective balance between convergence and diversity.

The value $\gamma =1/3$ represents the lower bound of the parameter’s range. At this setting, the model relies exclusively on the max–min distance for sample selection. Despite enhancing the diversity of solutions, this setting leads to suboptimal results due to compromised convergence.

At the other extreme, $\gamma =1$ denotes the upper limit and involves the exclusive use of the $Lp$-norm distance for sample selection. However, this setting yields results that are inferior, even when compared to the $\gamma =1/3$ setting. The likely reason for this decline in performance is the diminished efficacy of the $Lp$-norm distance in high-dimensional spaces.

A discernible trend is observed, where performance gradually deteriorates as $\gamma$ increases from 0.5 to 1. A larger $\gamma$ value potentially causes the algorithm to converge more slowly. Consequently, we adopted $\gamma =0.5$ as the default value for all test instances, given its general effectiveness.

4.3. Impact of GAN-Based Environmental Selection

In our comparative analysis, we examine two distinct variants of CoEGAN-BO to isolate the impacts of different environmental selection strategies. The variant named CoEGAN-BO($N_p$) adopts only the non-dominated sorting technique, eschewing the proposed GAN-based environmental selection strategy. Conversely, CoEGAN-BO(GAN) exclusively utilizes the generative adversarial network, bypassing the traditional environmental selection approach.

Table 2. The statistical results of IGD values obtained after 300 function evaluations. The best results are highlighted in bold.

Problem	CoEGAN-BO (GAN)	CoEGAN-BO (${\mathit{N}}_{\mathit{p}}$)	CoEGAN-BO
DTLZ1	6.45 $\times {10}^2$	6.01 $\times {10}^2$	5.61$\times {\mathbf{10}}^{\mathbf{2}}$
DTLZ2	1.62 $\times {10}^0$	1.67 $\times {10}^0$	1.57$\times {\mathbf{10}}^{\mathbf{0}}$
DTLZ3	1.24 $\times {10}^3$	1.32 $\times {10}^3$	1.20$\times {\mathbf{10}}^{\mathbf{3}}$
DTLZ5	1.65 $\times {10}^0$	1.62 $\times {10}^0$	1.49$\times {\mathbf{10}}^{\mathbf{0}}$
DTLZ6	2.20$\times {\mathbf{10}}^{\mathbf{1}}$	2.21 $\times {10}^1$	2.24 $\times {10}^1$
DTLZ7	9.19 $\times {10}^0$	9.09 $\times {10}^0$	8.59$\times {\mathbf{10}}^{\mathbf{0}}$

shows the average Inverted Generational Distance (IGD) results for both CoEGAN-BO($N_p$) and CoEGAN-BO(GAN), as well as the standard CoEGAN-BO, with the best-performing results emphasized.

The empirical results indicate that the standard CoEGAN-BO, which integrates both non-dominated sorting and the GAN-based strategy, outperforms these variants on the DTLZ problems. This finding highlights the algorithm’s significant advantage in effectively identifying non-dominated solutions, which are instrumental in generating the next population.

Therefore, it is effective to propose the environment selection strategy based on a GAN to select effective non-dominant solutions. Firstly, the CoEGAN-BO($N_p$) version exclusively uses the non-dominated sorting technique, foregoing the proposed GAN-based environmental selection strategy. Non-dominated sorting is an important tool in traditional multi-objective and many-objective optimization problems, as it helps maintain solution diversity and guides the population towards Pareto front evolution. However, as the dimensionality of the problem increases and the limitations of surrogate models become apparent, non-dominated sorting may amplify these inadequacies, because it relies entirely on model predictions to evaluate the fitness of individuals. On the other hand, the CoEGAN-BO(GAN) version combines the advantages of non-dominated sorting with the GAN-based environmental selection strategy. In high-dimensional problems, the constraints of surrogate models imply that using model predictions for non-dominated sorting could lead to cumulative errors affecting the direction of population search and could even cause search bias. The introduction of GANs becomes particularly important at this juncture, as they improve the selection process by learning to differentiate between real samples and those generated by the surrogate models. In other words, GANs help CoEGAN-BO reduce the search bias that could arise due to model inaccuracies.

4.4. Comparison Results on DTLZ Test Problems

To discuss the performance of the proposed algorithm, CoEGAN-BO was compared with several other algorithms, including K-RVEA, MOEA/D-EGO, KTA2, REMO, and EDN-ARMOEA, on a set of 30 problems with varying numbers of objectives (3, 4, 6, 8, and 10). The comparison was based on the Inverted Generational Distance (IGD) metric, with the results summarized in

Table 3. Statistical IGD results of the four compared algorithms and CoEGAN-BO on 30 DTLZ test instances by Wilcoxon signed-rank test (the significance level is 0.05). The best results for each instance of 50-dimensional problems are highlighted in bold.

Problem	M	K-RVEA	MOEA/D-EGO	KTA2	REMO	EDN-ARMOEA	CoEGAN-BO
DTLZ1	3	1.1630 $\times {10}^3$ (7.89 $\times {10}^1$) −	9.8024 $\times {10}^2$ (8.76 $\times {10}^1$) −	1.1909 $\times {10}^3$ (1.30 $\times {10}^2$) −	8.9557 $\times {10}^2$ (8.73 $\times {10}^1$) −	1.1999 $\times {10}^3$ (5.50 $\times {10}^1$) −	5.6089$\times {\mathbf{10}}^{\mathbf{2}}$(8.58 $\times {\mathbf{10}}^{\mathbf{1}}$)
	4	1.0674 $\times {10}^3$ (5.90 $\times {10}^1$) −	8.7119 $\times {10}^2$ (5.75 $\times {10}^1$) −	9.6466 $\times {10}^2$ (1.63 $\times {10}^2$) −	8.8421 $\times {10}^2$ (8.66 $\times {10}^1$) −	1.0493 $\times {10}^3$ (6.44 $\times {10}^1$) −	5.5394 $\times {\mathbf{10}}^{\mathbf{2}}$ (1.22 $\times {\mathbf{10}}^{\mathbf{2}}$)
	6	9.0109 $\times {10}^2$ (7.09 $\times {10}^1$) −	7.7411 $\times {10}^2$ (6.08 $\times {10}^1$) −	8.0940 $\times {10}^2$ (3.22 $\times {10}^1$) −	7.3680 $\times {10}^2$ (7.20 $\times {10}^1$) −	9.0269 $\times {10}^2$ (6.09 $\times {10}^1$) −	5.3822 $\times {\mathbf{10}}^{\mathbf{2}}$ (9.80 $\times {\mathbf{10}}^{\mathbf{1}}$)
	8	7.9409 $\times {10}^2$ (7.25 $\times {10}^1$) −	7.0443 $\times {10}^2$ (5.89 $\times {10}^1$) −	7.6470 $\times {10}^2$ (1.41 $\times {10}^2$) −	6.6895 $\times {10}^2$ (7.95 $\times {10}^1$) −	8.4174 $\times {10}^2$ (4.86 $\times {10}^1$) −	5.4340 $\times {\mathbf{10}}^{\mathbf{2}}$ (9.26 $\times {\mathbf{10}}^{\mathbf{1}}$)
	10	6.5519 $\times {10}^2$ (8.55 $\times {10}^1$) −	6.0232 $\times {10}^2$ (6.57 $\times {10}^1$) −	7.9799 $\times {10}^2$ (9.15 $\times {10}^1$) −	5.6624 $\times {10}^2$ (7.74 $\times {10}^1$) −	7.6990 $\times {10}^2$ (5.12 $\times {10}^1$) −	4.1843 $\times {\mathbf{10}}^{\mathbf{2}}$ (1.20 $\times {\mathbf{10}}^{\mathbf{2}}$)
DTLZ2	3	3.0168 $\times {10}^0$ (1.26 $\times {10}^{-1}$) −	2.0717 $\times {10}^0$ (2.20 $\times {10}^{-1}$) −	2.5237 $\times {10}^0$ (3.08 $\times {10}^{-1}$) −	1.6689 $\times {10}^0$ (2.74 $\times {10}^{-1}$) =	2.7616 $\times {10}^0$ (1.19 $\times {10}^{-1}$) −	1.5716 $\times {\mathbf{10}}^{\mathbf{0}}$ (4.69 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	4	3.0025 $\times {10}^0$ (1.45 $\times {10}^{-1}$) −	2.4457 $\times {10}^0$ (2.16 $\times {10}^{-1}$) −	2.6122 $\times {10}^0$ (3.66 $\times {10}^{-1}$) −	2.1026 $\times {10}^0$ (2.43 $\times {10}^{-1}$) −	2.7210 $\times {10}^0$ (1.26 $\times {10}^{-1}$) −	1.5617 $\times {\mathbf{10}}^{\mathbf{0}}$ (2.91 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	6	2.9962 $\times {10}^0$ (1.18 $\times {10}^{-1}$) −	2.6470 $\times {10}^0$ (2.11 $\times {10}^{-1}$) −	2.5842 $\times {10}^0$ (3.72 $\times {10}^{-1}$) −	2.1645 $\times {10}^0$ (2.02 $\times {10}^{-1}$) −	2.7891 $\times {10}^0$ (1.09 $\times {10}^{-1}$) −	1.5619 $\times {\mathbf{10}}^{\mathbf{0}}$ (2.61 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	8	2.8051 $\times {10}^0$ (1.87 $\times {10}^{-1}$) −	2.6686 $\times {10}^0$ (1.31 $\times {10}^{-1}$) −	2.7268 $\times {10}^0$ (3.22 $\times {10}^{-1}$) −	2.0794 $\times {10}^0$ (1.65 $\times {10}^{-1}$) −	2.7682 $\times {10}^0$ (9.51 $\times {10}^{-2}$) −	1.5613 $\times {\mathbf{10}}^{\mathbf{0}}$ (2.98 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	10	2.7647 $\times {10}^0$ (1.67 $\times {10}^{-1}$) −	2.6465 $\times {10}^0$ (2.01 $\times {10}^{-1}$) −	2.5056 $\times {10}^0$ (2.99 $\times {10}^{-1}$) −	2.0173 $\times {10}^0$ (1.99 $\times {10}^{-1}$) −	2.6952 $\times {10}^0$ (9.71 $\times {10}^{-2}$) −	1.5378 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.87 $\times {\mathbf{10}}^{-\mathbf{1}}$)
DTLZ3	3	3.5193 $\times {10}^3$ (2.18 $\times {10}^2$) −	3.0694 $\times {10}^3$ (2.69 $\times {10}^2$) −	3.2725 $\times {10}^3$ (6.62 $\times {10}^2$) −	2.8104 $\times {10}^3$ (2.54 $\times {10}^2$) −	3.7080 $\times {10}^3$ (1.52 $\times {10}^2$) −	1.1958 $\times {\mathbf{10}}^{\mathbf{3}}$ (2.25 $\times {\mathbf{10}}^{\mathbf{2}}$)
	4	3.3967 $\times {10}^3$ (2.32 $\times {10}^2$) −	3.1343 $\times {10}^3$ (2.51 $\times {10}^2$) −	2.7809 $\times {10}^3$ (9.35 $\times {10}^2$) −	2.8618 $\times {10}^3$ (2.67 $\times {10}^2$) −	3.6016 $\times {10}^3$ (1.57 $\times {10}^2$) −	1.1265 $\times {\mathbf{10}}^{\mathbf{3}}$ (1.79 $\times {\mathbf{10}}^{\mathbf{2}}$)
	6	3.1608 $\times {10}^3$ (2.26 $\times {10}^2$) −	3.1859 $\times {10}^3$ (2.10 $\times {10}^2$) −	1.7952 $\times {10}^3$ (6.63 $\times {10}^2$) −	2.6210 $\times {10}^3$ (2.79 $\times {10}^2$) −	3.4518 $\times {10}^3$ (1.41 $\times {10}^2$) −	9.5895 $\times {\mathbf{10}}^{\mathbf{2}}$ (2.79 $\times {\mathbf{10}}^{\mathbf{2}}$)
	8	2.9514 $\times {10}^3$ (1.95 $\times {10}^2$) −	3.0723 $\times {10}^3$ (2.00 $\times {10}^2$) −	1.8546 $\times {10}^3$ (6.86 $\times {10}^2$) −	2.6058 $\times {10}^3$ (2.66 $\times {10}^2$) −	3.2543 $\times {10}^3$ (1.27 $\times {10}^2$) −	9.5564 $\times {\mathbf{10}}^{\mathbf{2}}$ (2.43 $\times {\mathbf{10}}^{\mathbf{2}}$)
	10	2.7507 $\times {10}^3$ (2.14 $\times {10}^2$) −	2.9255 $\times {10}^3$ (2.29 $\times {10}^2$) −	2.0252 $\times {10}^3$ (7.83 $\times {10}^2$) −	2.3794 $\times {10}^3$ (2.73 $\times {10}^2$) −	3.0955 $\times {10}^3$ (1.63 $\times {10}^2$) −	9.8153 $\times {\mathbf{10}}^{\mathbf{2}}$ (2.27 $\times {\mathbf{10}}^{\mathbf{2}}$)
DTLZ5	3	2.8829 $\times {10}^0$ (1.62 $\times {10}^{-1}$) −	2.1090 $\times {10}^0$ (1.75 $\times {10}^{-1}$) −	2.4662 $\times {10}^0$ (4.68 $\times {10}^{-1}$) −	1.7606 $\times {10}^0$ (1.59 $\times {10}^{-1}$) −	2.6462 $\times {10}^0$ (1.05 $\times {10}^{-1}$) −	1.4994 $\times {\mathbf{10}}^{\mathbf{0}}$ (3.39 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	4	2.8584 $\times {10}^0$ (1.49 $\times {10}^{-1}$) −	2.3209 $\times {10}^0$ (1.82 $\times {10}^{-1}$) −	2.4170 $\times {10}^0$ (4.70 $\times {10}^{-1}$) −	2.0165 $\times {10}^0$ (3.34 $\times {10}^{-1}$) −	2.6011 $\times {10}^0$ (1.22 $\times {10}^{-1}$) −	1.4336 $\times {\mathbf{10}}^{\mathbf{0}}$ (3.57 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	6	2.6142 $\times {10}^0$ (1.79 $\times {10}^{-1}$) −	2.5474 $\times {10}^0$ (1.50 $\times {10}^{-1}$) −	2.5377 $\times {10}^0$ (3.62 $\times {10}^{-1}$) −	1.8241 $\times {10}^0$ (3.11 $\times {10}^{-1}$) −	2.4741 $\times {10}^0$ (1.40 $\times {10}^{-1}$) −	1.2413 $\times {\mathbf{10}}^{\mathbf{0}}$ (2.84 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	8	2.3461 $\times {10}^0$ (1.33 $\times {10}^{-1}$) −	2.4404 $\times {10}^0$ (1.21 $\times {10}^{-1}$) −	2.2628 $\times {10}^0$ (1.98 $\times {10}^{-1}$) −	1.6780 $\times {10}^0$ (1.97 $\times {10}^{-1}$) −	2.3209 $\times {10}^0$ (9.32 $\times {10}^{-2}$) −	1.1171 $\times {\mathbf{10}}^{\mathbf{0}}$ (2.92 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	10	2.1783 $\times {10}^0$ (1.38 $\times {10}^{-1}$) −	2.3175 $\times {10}^0$ (1.63 $\times {10}^{-1}$) −	2.0085 $\times {10}^0$ (3.10 $\times {10}^{-1}$) −	1.6264 $\times {10}^0$ (2.26 $\times {10}^{-1}$) −	2.2470 $\times {10}^0$ (6.59 $\times {10}^{-2}$) −	9.1949 $\times {\mathbf{10}}^{-\mathbf{1}}$ (2.55 $\times {\mathbf{10}}^{-\mathbf{1}}$)
DTLZ6	3	3.7862 $\times {10}^1$ (6.27 $\times {10}^{-1}$) −	3.8309 $\times {10}^1$ (9.45 $\times {10}^{-1}$) −	2.9367 $\times {10}^1$ (3.59 $\times {10}^0$) −	3.8616 $\times {10}^1$ (1.44 $\times {10}^0$) −	4.1882 $\times {10}^1$ (2.91 $\times {10}^{-1}$) −	2.2441 $\times {\mathbf{10}}^{\mathbf{1}}$ (2.59 $\times {\mathbf{10}}^{\mathbf{0}}$)
	4	3.7501 $\times {10}^1$ (1.23 $\times {10}^0$) −	3.8952 $\times {10}^1$ (7.66 $\times {10}^{-1}$) −	2.8591 $\times {10}^1$ (3.71 $\times {10}^0$) −	3.8753 $\times {10}^1$ (1.16 $\times {10}^0$) −	4.1156 $\times {10}^1$ (1.09 $\times {10}^{-1}$) −	2.5876 $\times {\mathbf{10}}^{\mathbf{1}}$ (2.89 $\times {\mathbf{10}}^{\mathbf{0}}$)
	6	3.6577 $\times {10}^1$ (7.35 $\times {10}^{-1}$) −	3.8246 $\times {10}^1$ (4.90 $\times {10}^{-1}$) −	2.7463 $\times {10}^1$ (2.95 $\times {10}^0$) −	3.7040 $\times {10}^1$ (1.10 $\times {10}^0$) −	3.9301 $\times {10}^1$ (2.42 $\times {10}^{-1}$) −	2.4404 $\times {\mathbf{10}}^{\mathbf{1}}$ (1.82 $\times {\mathbf{10}}^{\mathbf{0}}$)
	8	3.5115 $\times {10}^1$ (8.54 $\times {10}^{-1}$) −	3.6498 $\times {10}^1$ (7.45 $\times {10}^{-1}$) −	2.5257 $\times {10}^1$ (4.64 $\times {10}^0$) −	3.5939 $\times {10}^1$ (9.76 $\times {10}^{-1}$) −	3.7511 $\times {10}^1$ (2.38 $\times {10}^{-1}$) −	2.2870 $\times {\mathbf{10}}^{\mathbf{1}}$ (2.42 $\times {\mathbf{10}}^{\mathbf{0}}$)
	10	3.3429 $\times {10}^1$ (1.01 $\times {10}^0$) −	3.4783 $\times {10}^1$ (5.58 $\times {10}^{-1}$) −	2.1562 $\times {10}^1$ (3.07 $\times {10}^0$) =	3.4070 $\times {10}^1$ (9.54 $\times {10}^{-1}$) −	3.5672 $\times {10}^1$ (2.05 $\times {10}^{-1}$) −	2.0519 $\times {\mathbf{10}}^{\mathbf{1}}$ (1.72 $\times {\mathbf{10}}^{\mathbf{0}}$)
DTLZ7	3	5.4355 $\times {\mathbf{10}}^{-\mathbf{1}}$ (7.98 $\times {\mathbf{10}}^{-\mathbf{2}}$) +	5.6601 $\times {10}^0$ (7.65 $\times {10}^{-1}$) +	9.3943 $\times {10}^0$ (8.12 $\times {10}^{-1}$) −	5.4656 $\times {10}^0$ (9.92 $\times {10}^{-1}$) +	9.2824 $\times {10}^0$ (5.35 $\times {10}^{-1}$) −	8.5884 $\times {10}^0$ (7.91 $\times {10}^{-1}$)
	4	8.6090 $\times {\mathbf{10}}^{-\mathbf{1}}$ (9.32 $\times {\mathbf{10}}^{-\mathbf{2}}$) +	9.1196 $\times {10}^0$ (1.44 $\times {10}^0$) +	1.1873 $\times {10}^1$ (9.73 $\times {10}^{-1}$) =	8.9490 $\times {10}^0$ (8.38 $\times {10}^{-1}$) +	1.2503 $\times {10}^1$ (5.41 $\times {10}^{-1}$) −	1.1532 $\times {10}^1$ (1.52 $\times {10}^0$)
	6	1.4746 $\times {\mathbf{10}}^{\mathbf{0}}$ (3.04 $\times {\mathbf{10}}^{-\mathbf{1}}$) +	1.5391 $\times {10}^1$ (1.75 $\times {10}^0$) +	1.9032 $\times {10}^1$ (1.66 $\times {10}^0$) −	1.5532 $\times {10}^1$ (1.36 $\times {10}^0$) +	1.9573 $\times {10}^1$ (9.33 $\times {10}^{-1}$) −	1.7448 $\times {10}^1$ (2.20 $\times {10}^0$)
	8	2.7182 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.20 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.2466 $\times {10}^1$ (2.36 $\times {10}^0$) =	2.5169 $\times {10}^1$ (2.93 $\times {10}^0$) −	2.2078 $\times {10}^1$ (1.84 $\times {10}^0$) =	2.6114 $\times {10}^1$ (1.49 $\times {10}^0$) −	2.3463 $\times {10}^1$ (2.54 $\times {10}^0$)
	10	5.2089 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.87 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.8486 $\times {10}^1$ (3.95 $\times {10}^0$) =	3.2039 $\times {10}^1$ (2.65 $\times {10}^0$) −	2.7666 $\times {10}^1$ (2.82 $\times {10}^0$) =	3.2454 $\times {10}^1$ (2.07 $\times {10}^0$) −	2.9126 $\times {10}^1$ (4.30 $\times {10}^0$)
+/−/=		5/25/0	3/25/2	0/28/2	3/24/3	0/29/1

and

Table 4. Statistical IGD results of the four compared algorithms and CoEGAN-BO on 30 DTLZ test instances by Wilcoxon signed-rank test (the significance level is 0.05). The best results for each instance are highlighted for 100-dimensional problems in bold.

Problem	M	K-RVEA	MOEA/D-EGO	KTA2	REMO	EDN-ARMOEA	CoEGAN-BO
DTLZ1	3	2.7400 $\times {10}^3$ (9.95 $\times {10}^1$) −	2.3905 $\times {10}^3$ (1.58 $\times {10}^2$) −	2.7076 $\times {10}^3$ (1.33 $\times {10}^2$) −	2.2310 $\times {10}^3$ (9.09 $\times {10}^1$) −	2.6023 $\times {10}^3$ (5.46 $\times {10}^1$) −	1.3536 $\times {\mathbf{10}}^{\mathbf{3}}$ (4.04 $\times {\mathbf{10}}^{\mathbf{2}}$)
	4	2.4209 $\times {10}^3$ (1.10 $\times {10}^2$) −	2.1237 $\times {10}^3$ (1.25 $\times {10}^2$) −	2.4253 $\times {10}^3$ (1.00 $\times {10}^2$) −	2.0944 $\times {10}^3$ (1.46 $\times {10}^2$) −	2.2831 $\times {10}^3$ (6.71 $\times {10}^1$) −	1.3482 $\times {\mathbf{10}}^{\mathbf{3}}$ (2.03 $\times {\mathbf{10}}^{\mathbf{2}}$)
	6	1.9867 $\times {10}^3$ (6.60 $\times {10}^1$) −	1.8757 $\times {10}^3$ (1.09 $\times {10}^2$) −	2.0993 $\times {10}^3$ (1.35 $\times {10}^2$) −	1.8480 $\times {10}^3$ (1.15 $\times {10}^2$) −	1.9940 $\times {10}^3$ (1.07 $\times {10}^2$) −	1.2423 $\times {\mathbf{10}}^{\mathbf{3}}$ (1.95 $\times {\mathbf{10}}^{\mathbf{2}}$)
	8	1.8175 $\times {10}^3$ (1.09 $\times {10}^2$) −	1.7335 $\times {10}^3$ (9.42 $\times {10}^1$) −	2.0243 $\times {10}^3$ (1.15 $\times {10}^2$) −	1.7154 $\times {10}^3$ (1.42 $\times {10}^2$) −	1.8348 $\times {10}^3$ (8.79 $\times {10}^1$) −	1.0897 $\times {\mathbf{10}}^{\mathbf{3}}$ (3.27 $\times {\mathbf{10}}^{\mathbf{2}}$)
	10	1.7690 $\times {10}^3$ (1.06 $\times {10}^2$) −	1.5889 $\times {10}^3$ (1.37 $\times {10}^2$) −	1.9312 $\times {10}^3$ (1.48 $\times {10}^2$) −	1.6480 $\times {10}^3$ (1.27 $\times {10}^2$) −	1.7663 $\times {10}^3$ (9.13 $\times {10}^1$) −	9.4570 $\times {\mathbf{10}}^{\mathbf{2}}$ (2.76 $\times {\mathbf{10}}^{\mathbf{2}}$)
DTLZ2	3	6.5568 $\times {10}^0$ (2.95 $\times {10}^{-1}$) −	5.5056 $\times {10}^0$ (3.00 $\times {10}^{-1}$) −	6.4772 $\times {10}^0$ (3.25 $\times {10}^{-1}$) −	4.9357 $\times {10}^0$ (4.93 $\times {10}^{-1}$) =	6.1443 $\times {10}^0$ (1.78 $\times {10}^{-1}$) −	4.6614 $\times {\mathbf{10}}^{\mathbf{0}}$ (9.00 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	4	6.4980 $\times {10}^0$ (3.25 $\times {10}^{-1}$) −	6.0500 $\times {10}^0$ (3.00 $\times {10}^{-1}$) −	6.5618 $\times {10}^0$ (2.50 $\times {10}^{-1}$) −	5.3265 $\times {10}^0$ (3.68 $\times {10}^{-1}$) −	6.0854 $\times {10}^0$ (2.08 $\times {10}^{-1}$) −	4.7588 $\times {\mathbf{10}}^{\mathbf{0}}$ (8.49 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	6	6.5986 $\times {10}^0$ (1.79 $\times {10}^{-1}$) −	6.1751 $\times {10}^0$ (2.37 $\times {10}^{-1}$) −	6.5517 $\times {10}^0$ (2.89 $\times {10}^{-1}$) −	5.1044 $\times {10}^0$ (3.36 $\times {10}^{-1}$) −	6.1155 $\times {10}^0$ (1.56 $\times {10}^{-1}$) −	4.1289 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.06 $\times {\mathbf{10}}^{\mathbf{0}}$)
	8	6.5548 $\times {10}^0$ (2.69 $\times {10}^{-1}$) −	6.1776 $\times {10}^0$ (3.83 $\times {10}^{-1}$) −	6.5600 $\times {10}^0$ (2.36 $\times {10}^{-1}$) −	5.2862 $\times {10}^0$ (4.16 $\times {10}^{-1}$) −	6.0762 $\times {10}^0$ (1.99 $\times {10}^{-1}$) −	4.5706 $\times {\mathbf{10}}^{\mathbf{0}}$ (9.46 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	10	6.3792 $\times {10}^0$ (3.22 $\times {10}^{-1}$) −	6.0196 $\times {10}^0$ (2.06 $\times {10}^{-1}$) −	6.4229 $\times {10}^0$ (3.74 $\times {10}^{-1}$) −	5.1812 $\times {10}^0$ (3.58 $\times {10}^{-1}$) −	6.0105 $\times {10}^0$ (1.60 $\times {10}^{-1}$) −	4.4632 $\times {\mathbf{10}}^{\mathbf{0}}$ (9.27 $\times {\mathbf{10}}^{-\mathbf{1}}$)
DTLZ3	3	8.3362 $\times {10}^3$ (3.61 $\times {10}^2$) −	7.8510 $\times {10}^3$ (2.23 $\times {10}^2$) −	8.2749 $\times {10}^3$ (4.88 $\times {10}^2$) −	7.1383 $\times {10}^3$ (4.10 $\times {10}^2$) −	8.4466 $\times {10}^3$ (1.83 $\times {10}^2$) −	2.6985 $\times {\mathbf{10}}^{\mathbf{3}}$ (1.36 $\times {\mathbf{10}}^{\mathbf{2}}$)
	4	8.3606 $\times {10}^3$ (2.67 $\times {10}^2$) −	8.0465 $\times {10}^3$ (3.08 $\times {10}^2$) −	8.1113 $\times {10}^3$ (9.15 $\times {10}^2$) −	7.3300 $\times {10}^3$ (4.70 $\times {10}^2$) −	8.2661 $\times {10}^3$ (2.00 $\times {10}^2$) −	2.4775 $\times {\mathbf{10}}^{\mathbf{3}}$ (2.79 $\times {\mathbf{10}}^{\mathbf{2}}$)
	6	8.2088 $\times {10}^3$ (2.68 $\times {10}^2$) −	8.0250 $\times {10}^3$ (3.06 $\times {10}^2$) −	7.4869 $\times {10}^3$ (9.23 $\times {10}^2$) −	7.1297 $\times {10}^3$ (2.84 $\times {10}^2$) −	7.9735 $\times {10}^3$ (2.59 $\times {10}^2$) −	2.1852 $\times {\mathbf{10}}^{\mathbf{3}}$ (5.92 $\times {\mathbf{10}}^{\mathbf{2}}$)
	8	8.0873 $\times {10}^3$ (2.09 $\times {10}^2$) −	7.8899 $\times {10}^3$ (2.56 $\times {10}^2$) −	6.8763 $\times {10}^3$ (1.58 $\times {10}^3$) −	7.0811 $\times {10}^3$ (5.28 $\times {10}^2$) −	7.8185 $\times {10}^3$ (2.58 $\times {10}^2$) −	1.9900 $\times {\mathbf{10}}^{\mathbf{3}}$ (8.30 $\times {\mathbf{10}}^{\mathbf{2}}$)
	10	7.7497 $\times {10}^3$ (3.33 $\times {10}^2$) −	7.5194 $\times {10}^3$ (3.35 $\times {10}^2$) −	6.8331 $\times {10}^3$ (1.51 $\times {10}^3$) −	6.8932 $\times {10}^3$ (4.77 $\times {10}^2$) −	7.7091 $\times {10}^3$ (2.35 $\times {10}^2$) −	2.3608 $\times {\mathbf{10}}^{\mathbf{3}}$ (7.12 $\times {\mathbf{10}}^{\mathbf{2}}$)
DTLZ5	3	6.4983 $\times {10}^0$ (2.24 $\times {10}^{-1}$) −	5.5380 $\times {10}^0$ (3.18 $\times {10}^{-1}$) −	6.4745 $\times {10}^0$ (2.86 $\times {10}^{-1}$) −	4.6592 $\times {10}^0$ (4.69 $\times {10}^{-1}$) =	5.9920 $\times {10}^0$ (1.61 $\times {10}^{-1}$) −	4.4818 $\times {\mathbf{10}}^{\mathbf{0}}$ (9.80 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	4	6.5053 $\times {10}^0$ (2.27 $\times {10}^{-1}$) −	5.6927 $\times {10}^0$ (3.17 $\times {10}^{-1}$) −	6.3412 $\times {10}^0$ (3.41 $\times {10}^{-1}$) −	5.4709 $\times {10}^0$ (4.64 $\times {10}^{-1}$) −	5.9715 $\times {10}^0$ (1.24 $\times {10}^{-1}$) −	4.5460 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.17 $\times {\mathbf{10}}^{\mathbf{0}}$)
	6	6.3855 $\times {10}^0$ (3.00 $\times {10}^{-1}$) −	5.9243 $\times {10}^0$ (2.10 $\times {10}^{-1}$) −	6.3203 $\times {10}^0$ (2.52 $\times {10}^{-1}$) −	5.1026 $\times {10}^0$ (4.31 $\times {10}^{-1}$) −	5.8540 $\times {10}^0$ (2.80 $\times {10}^{-1}$) −	4.1627 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.03 $\times {\mathbf{10}}^{\mathbf{0}}$)
	8	6.1416 $\times {10}^0$ (2.44 $\times {10}^{-1}$) −	5.9718 $\times {10}^0$ (3.16 $\times {10}^{-1}$) −	6.0392 $\times {10}^0$ (5.27 $\times {10}^{-1}$) −	5.0663 $\times {10}^0$ (3.82 $\times {10}^{-1}$) −	5.7729 $\times {10}^0$ (1.65 $\times {10}^{-1}$) −	3.7756 $\times {\mathbf{10}}^{\mathbf{0}}$ (9.71 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	10	6.1396 $\times {10}^0$ (1.96 $\times {10}^{-1}$) −	5.9373 $\times {10}^0$ (2.38 $\times {10}^{-1}$) −	5.7663 $\times {10}^0$ (5.84 $\times {10}^{-1}$) −	4.7344 $\times {10}^0$ (4.74 $\times {10}^{-1}$) −	5.6017 $\times {10}^0$ (1.35 $\times {10}^{-1}$) −	3.9932 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.12 $\times {\mathbf{10}}^{\mathbf{0}}$)
DTLZ6	3	8.2975 $\times {10}^1$ (1.05 $\times {10}^0$) −	8.4323 $\times {10}^1$ (8.88 $\times {10}^{-1}$) −	7.5523 $\times {10}^1$ (6.66 $\times {10}^0$) −	8.2203 $\times {10}^1$ (1.63 $\times {10}^0$) −	8.6402 $\times {10}^1$ (2.76 $\times {10}^{-1}$) −	4.6775 $\times {\mathbf{10}}^{\mathbf{1}}$ (4.12 $\times {\mathbf{10}}^{\mathbf{0}}$)
	4	8.2596 $\times {10}^1$ (8.57 $\times {10}^{-1}$) −	8.4379 $\times {10}^1$ (6.46 $\times {10}^{-1}$) −	7.8968 $\times {10}^1$ (5.13 $\times {10}^0$) −	8.3351 $\times {10}^1$ (9.80 $\times {10}^{-1}$) −	8.5521 $\times {10}^1$ (3.77 $\times {10}^{-1}$) −	4.7666 $\times {\mathbf{10}}^{\mathbf{1}}$ (4.08 $\times {\mathbf{10}}^{\mathbf{0}}$)
	6	8.1410 $\times {10}^1$ (7.52 $\times {10}^{-1}$) −	8.2948 $\times {10}^1$ (5.82 $\times {10}^{-1}$) −	7.5985 $\times {10}^1$ (6.10 $\times {10}^0$) −	8.1505 $\times {10}^1$ (1.23 $\times {10}^0$) −	8.3769 $\times {10}^1$ (2.57 $\times {10}^{-1}$) −	4.6297 $\times {\mathbf{10}}^{\mathbf{1}}$ (3.95 $\times {\mathbf{10}}^{\mathbf{0}}$)
	8	8.0194 $\times {10}^1$ (8.38 $\times {10}^{-1}$) −	8.1350 $\times {10}^1$ (8.09 $\times {10}^{-1}$) −	7.5311 $\times {10}^1$ (6.77 $\times {10}^0$) −	7.9948 $\times {10}^1$ (1.04 $\times {10}^0$) −	8.1799 $\times {10}^1$ (3.99 $\times {10}^{-1}$) −	4.4825 $\times {\mathbf{10}}^{\mathbf{1}}$ (4.25 $\times {\mathbf{10}}^{\mathbf{0}}$)
	10	7.8081 $\times {10}^1$ (8.25 $\times {10}^{-1}$) −	7.9716 $\times {10}^1$ (6.16 $\times {10}^{-1}$) −	7.0222 $\times {10}^1$ (1.05 $\times {10}^1$) −	7.7877 $\times {10}^1$ (7.50 $\times {10}^{-1}$) −	8.0155 $\times {10}^1$ (2.29 $\times {10}^{-1}$) −	4.3439 $\times {\mathbf{10}}^{\mathbf{1}}$ (3.77 $\times {\mathbf{10}}^{\mathbf{0}}$)
DTLZ7	3	4.2957 $\times {\mathbf{10}}^{\mathbf{0}}$ (7.69 $\times {\mathbf{10}}^{-\mathbf{1}}$) +	9.4168 $\times {10}^0$ (4.29 $\times {10}^{-1}$) +	1.0478 $\times {10}^1$ (4.20 $\times {10}^{-1}$) −	6.9445 $\times {10}^0$ (4.93 $\times {10}^{-1}$) +	9.9256 $\times {10}^0$ (3.47 $\times {10}^{-1}$) =	1.0015 $\times {10}^1$ (6.16 $\times {10}^{-1}$)
	4	4.8264 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.41 $\times {\mathbf{10}}^{\mathbf{0}}$) +	1.2636 $\times {10}^1$ (9.37 $\times {10}^{-1}$) +	1.3982 $\times {10}^1$ (9.53 $\times {10}^{-1}$) =	1.0970 $\times {10}^1$ (7.67 $\times {10}^{-1}$) +	1.3366 $\times {10}^1$ (5.16 $\times {10}^{-1}$) =	1.3532 $\times {10}^1$ (9.69 $\times {10}^{-1}$)
	6	7.3726 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.57 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.0451 $\times {10}^1$ (1.10 $\times {10}^0$) =	2.1300 $\times {10}^1$ (1.02 $\times {10}^0$) =	1.9530 $\times {10}^1$ (7.65 $\times {10}^{-1}$) +	2.0726 $\times {10}^1$ (5.75 $\times {10}^{-1}$) =	2.1114 $\times {10}^1$ (1.35 $\times {10}^0$)
	8	9.3152 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.38 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.8779 $\times {10}^1$ (1.34 $\times {10}^0$) =	2.9089 $\times {10}^1$ (1.53 $\times {10}^0$) =	2.7428 $\times {10}^1$ (1.09 $\times {10}^0$) +	2.8210 $\times {10}^1$ (1.08 $\times {10}^0$) =	2.8402 $\times {10}^1$ (1.46 $\times {10}^0$)
	10	1.1131 $\times {\mathbf{10}}^{\mathbf{1}}$ (1.62 $\times {\mathbf{10}}^{\mathbf{0}}$) +	3.5965 $\times {10}^1$ (1.51 $\times {10}^0$) =	3.6868 $\times {10}^1$ (1.21 $\times {10}^0$) −	3.4709 $\times {10}^1$ (1.19 $\times {10}^0$) +	3.5519 $\times {10}^1$ (1.13 $\times {10}^0$) =	3.6030 $\times {10}^1$ (1.31 $\times {10}^0$)
+/−/=		5/25/0	2/25/3	0/27/3	5/23/2	0/25/5

for 50-dimensional and 100-dimensional problems, respectively, derived from 20 independent runs. A Wilcoxon rank-sum (WRS) test was performed to statistically compare the performance of CoEGAN-BO against the other four algorithms. CoEGAN-BO consistently achieved the best IGD values among the 30 test instances for both 50- and 100-dimensional problems, with the highest number of best results (25 out of 30), followed by K-RVEA and KTA2. MOEA/D-EGO and ParEGO did not secure the best results on the DTLZ test suite.

DTLZ1 and DTLZ3 are known for their slow convergence characteristics. DTLZ1 has a linear Pareto-optimal front, while DTLZ3 challenges an algorithm’s ability to converge to the global Pareto front. The other algorithms may struggle with DTLZ1 and DTLZ3 due to these properties. However, CoEGAN-BO outperforms the competition on these problems, with REMO and MOEA/D-EGO following behind. DTLZ2 evaluates an algorithm’s computational power as the number of objectives increases. CoEGAN-BO shows strong performance on DTLZ2, particularly for problems with 8 and 10 objectives, highlighting the importance of maintaining diversity for this problem. The other algorithms also demonstrate satisfactory results for DTLZ2.

DTLZ5 and DTLZ6 test an algorithm’s ability to converge to a curved Pareto front, with DTLZ6 presenting a more complex challenge than DTLZ5. Overall, CoEGAN-BO outperforms the other algorithms for DTLZ1-6, while KTA2 shows the weakest performance, possibly due to its convergence and diversity mechanisms.

CoEGAN-BO achieves significantly better results on the DTLZ test suite, especially on the simpler problems such as DTLZ2, DTLZ5, and DTLZ7, compared to the more challenging DTLZ1, DTLZ3, and DTLZ6. Its superior exploratory capabilities allow CoEGAN-BO to excel on these problems, achieving the best IGD values for DTLZ1-6. CoEGAN-BO and REMO rank as the top two algorithms for these problems. Furthermore, as the number of decision variables and objectives increases, CoEGAN-BO’s performance continues to improve. For DTLZ7, K-RVEA achieves the best IGD value, while CoEGAN-BO ranks fourth.

Despite the challenges with problems like DTLZ1 and DTLZ3 that are difficult to converge, CoEGAN-BO manages to obtain the best convergence solution sets. However, it demonstrates poor diversity in solving DTLZ7, with its solutions tending to cluster in specific regions, which affects its ability to address problems with a discontinuous Pareto-optimal front.

4.5. Comparison Results on MaF Problems

We extended our evaluation to assess the performance of CoEGAN-BO on the complex ultra multi-objective optimization MaF benchmarks (

Table 5. Statistical IGD results of the four compared algorithms and CoEGAN-BO on 35 MaF test instances by the Wilcoxon signed-rank test (the significance level is 0.05). The best results for each instance are highlighted for 100-dimensional problems in bold.

Problem	M	K-RVEA	MOEA/D-EGO	KTA2	REMO	EDN-ARMOEA	CoEGAN-BO
MaF1	3	3.0630 $\times {10}^0$ (1.67 $\times {10}^{-1}$) −	2.0202 $\times {10}^0$ (2.83 $\times {10}^{-1}$) −	2.5657 $\times {10}^0$ (4.97 $\times {10}^{-1}$) −	1.7246 $\times {10}^0$ (2.73 $\times {10}^{-1}$) −	3.0720 $\times {10}^0$ (1.94 $\times {10}^{-1}$) −	1.0977 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.90 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	4	3.5592 $\times {10}^0$ (3.55 $\times {10}^{-1}$) −	2.3167 $\times {10}^0$ (4.56 $\times {10}^{-1}$) −	3.3756 $\times {10}^0$ (7.06 $\times {10}^{-1}$) −	2.0812 $\times {10}^0$ (3.14 $\times {10}^{-1}$) −	3.9069 $\times {10}^0$ (2.59 $\times {10}^{-1}$) −	1.4582 $\times {\mathbf{10}}^{\mathbf{0}}$ (3.63 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	6	4.4377 $\times {10}^0$ (4.79 $\times {10}^{-1}$) −	2.8709 $\times {10}^0$ (4.03 $\times {10}^{-1}$) −	4.6643 $\times {10}^0$ (7.89 $\times {10}^{-1}$) −	2.6182 $\times {10}^0$ (2.19 $\times {10}^{-1}$) =	5.1277 $\times {10}^0$ (2.72 $\times {10}^{-1}$) −	2.4861 $\times {\mathbf{10}}^{\mathbf{0}}$ (5.48 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	8	4.7617 $\times {10}^0$ (6.96 $\times {10}^{-1}$) −	3.2560 $\times {10}^0$ (6.56 $\times {10}^{-1}$) =	5.4752 $\times {10}^0$ (7.56 $\times {10}^{-1}$) −	3.0219 $\times {10}^0$ (4.76 $\times {10}^{-1}$) =	5.7178 $\times {10}^0$ (3.20 $\times {10}^{-1}$) −	3.2295 $\times {\mathbf{10}}^{\mathbf{0}}$ (6.66 $\times {\mathbf{10}}^{-\mathbf{1}}$)
	10	5.0680 $\times {10}^0$ (6.58 $\times {10}^{-1}$) −	3.2540 $\times {\mathbf{10}}^{\mathbf{0}}$ (4.78 $\times {\mathbf{10}}^{-\mathbf{1}}$) +	6.5188 $\times {10}^0$ (7.06 $\times {10}^{-1}$) −	3.0217 $\times {10}^0$ (5.44 $\times {10}^{-1}$) +	6.1669 $\times {10}^0$ (2.90 $\times {10}^{-1}$) −	3.6704 $\times {10}^0$ (7.31 $\times {10}^{-1}$)
MaF2	3	2.6263 $\times {10}^{-1}$ (7.31 $\times {10}^{-3}$) −	2.0954 $\times {10}^{-1}$ (1.12 $\times {10}^{-2}$) −	2.3592 $\times {10}^{-1}$ (1.09 $\times {10}^{-2}$) −	2.0265 $\times {10}^{-1}$ (1.65 $\times {10}^{-2}$) −	2.4247 $\times {10}^{-1}$ (5.19 $\times {10}^{-3}$) −	1.7090 $\times {\mathbf{10}}^{-\mathbf{1}}$ (1.09 $\times {\mathbf{10}}^{-\mathbf{2}}$)
	4	2.2340 $\times {10}^{-1}$ (7.35 $\times {10}^{-3}$) −	2.0269 $\times {10}^{-1}$ (5.54 $\times {10}^{-3}$) −	2.1383 $\times {10}^{-1}$ (8.81 $\times {10}^{-3}$) −	2.0096 $\times {10}^{-1}$ (9.29 $\times {10}^{-3}$) −	2.0679 $\times {10}^{-1}$ (3.01 $\times {10}^{-3}$) −	1.9284 $\times {\mathbf{10}}^{-\mathbf{1}}$ (9.25 $\times {\mathbf{10}}^{-\mathbf{3}}$)
	6	2.7449 $\times {10}^{-1}$ (1.60 $\times {10}^{-2}$) =	2.0713 $\times {\mathbf{10}}^{-\mathbf{1}}$ (7.43 $\times {\mathbf{10}}^{-\mathbf{3}}$) +	2.6282 $\times {10}^{-1}$ (1.40 $\times {10}^{-2}$) +	2.7039 $\times {10}^{-1}$ (1.58 $\times {10}^{-2}$) =	2.3129 $\times {10}^{-1}$ (6.94 $\times {10}^{-3}$) +	2.7770 $\times {10}^{-1}$ (1.27 $\times {10}^{-2}$)
	8	3.1911 $\times {10}^{-1}$ (1.68 $\times {10}^{-2}$) =	2.2804 $\times {\mathbf{10}}^{-\mathbf{1}}$ (8.30 $\times {\mathbf{10}}^{-\mathbf{3}}$) +	3.1711 $\times {10}^{-1}$ (2.36 $\times {10}^{-2}$) =	3.2468 $\times {10}^{-1}$ (2.07 $\times {10}^{-2}$) =	2.7502 $\times {10}^{-1}$ (1.15 $\times {10}^{-2}$) +	3.2753 $\times {10}^{-1}$ (2.52 $\times {10}^{-2}$)
	10	3.5788 $\times {10}^{-1}$ (2.58 $\times {10}^{-2}$) =	2.3443 $\times {\mathbf{10}}^{-\mathbf{1}}$ (1.09 $\times {\mathbf{10}}^{-\mathbf{2}}$) +	3.4783 $\times {10}^{-1}$ (2.28 $\times {10}^{-2}$) =	3.6012 $\times {10}^{-1}$ (2.22 $\times {10}^{-2}$) =	3.0043 $\times {10}^{-1}$ (1.09 $\times {10}^{-2}$) +	3.5505 $\times {10}^{-1}$ (2.44 $\times {10}^{-2}$)
MaF3	3	1.5968 $\times {\mathbf{10}}^{\mathbf{7}}$ (1.45 $\times {\mathbf{10}}^{\mathbf{6}}$) +	2.9779 $\times {10}^7$ (5.41 $\times {10}^6$) −	N/A	1.6799 $\times {10}^7$ (7.00 $\times {10}^6$) +	2.1325 $\times {10}^7$ (2.21 $\times {10}^6$) =	2.0445 $\times {10}^7$ (6.14 $\times {10}^6$)
	4	1.6168 $\times {\mathbf{10}}^{\mathbf{7}}$ (2.10 $\times {\mathbf{10}}^{\mathbf{6}}$) +	2.6638 $\times {10}^7$ (5.80 $\times {10}^6$) −	N/A	1.5377 $\times {10}^7$ (3.47 $\times {10}^6$) +	2.0561 $\times {10}^7$ (2.90 $\times {10}^6$) =	1.9783 $\times {10}^7$ (6.77 $\times {10}^6$)
	6	1.5305 $\times {10}^7$ (2.07 $\times {10}^6$) −	2.3244 $\times {10}^7$ (5.64 $\times {10}^6$) −	N/A	1.8147 $\times {10}^7$ (4.41 $\times {10}^6$) −	1.8280 $\times {10}^7$ (2.29 $\times {10}^6$) −	9.9529 $\times {\mathbf{10}}^{\mathbf{6}}$ (5.80 $\times {\mathbf{10}}^{\mathbf{6}}$)
	8	1.3950 $\times {10}^7$ (2.52 $\times {10}^6$) −	2.1341 $\times {10}^7$ (4.55 $\times {10}^6$) −	N/A	1.8048 $\times {10}^7$ (6.65 $\times {10}^6$) −	1.7721 $\times {10}^7$ (2.91 $\times {10}^6$) −	7.7932 $\times {\mathbf{10}}^{\mathbf{6}}$ (4.69 $\times {\mathbf{10}}^{\mathbf{6}}$)
	10	1.2835 $\times {10}^7$ (2.32 $\times {10}^6$) −	2.1700 $\times {10}^7$ (3.85 $\times {10}^6$) −	N/A	1.5644 $\times {10}^7$ (7.46 $\times {10}^6$) −	1.4193 $\times {10}^7$ (2.76 $\times {10}^6$) −	5.4190 $\times {\mathbf{10}}^{\mathbf{6}}$ (2.50 $\times {\mathbf{10}}^{\mathbf{6}}$)
MaF4	3	1.1714 $\times {10}^4$ (7.59 $\times {10}^2$) −	1.0856 $\times {10}^4$ (1.12 $\times {10}^3$) −	N/A	8.7103 $\times {10}^3$ (8.20 $\times {10}^2$) −	1.1913 $\times {10}^4$ (5.38 $\times {10}^2$) −	7.2791 $\times {\mathbf{10}}^{\mathbf{3}}$ (1.83 $\times {\mathbf{10}}^{\mathbf{3}}$)
	4	2.4369 $\times {10}^4$ (1.81 $\times {10}^3$) −	2.5217 $\times {10}^4$ (1.86 $\times {10}^3$) −	N/A	1.8465 $\times {10}^4$ (2.37 $\times {10}^3$) −	2.4869 $\times {10}^4$ (1.58 $\times {10}^3$) −	1.6300 $\times {\mathbf{10}}^{\mathbf{4}}$ (3.33 $\times {\mathbf{10}}^{\mathbf{3}}$)
	6	9.2871 $\times {10}^4$ (5.95 $\times {10}^3$) −	1.0140 $\times {10}^5$ (9.25 $\times {10}^3$) −	N/A	7.0090 $\times {10}^4$ (9.57 $\times {10}^3$) −	9.4063 $\times {10}^4$ (6.03 $\times {10}^3$) −	6.0758 $\times {\mathbf{10}}^{\mathbf{4}}$ (1.34 $\times {\mathbf{10}}^{\mathbf{4}}$)
	8	3.5739 $\times {10}^5$ (2.59 $\times {10}^4$) −	3.8744 $\times {10}^5$ (3.11 $\times {10}^4$) −	N/A	2.6748 $\times {10}^5$ (4.12 $\times {10}^4$) −	3.7234 $\times {10}^5$ (1.79 $\times {10}^4$) −	2.1231 $\times {\mathbf{10}}^{\mathbf{5}}$ (4.17 $\times {\mathbf{10}}^{\mathbf{4}}$)
	10	1.2808 $\times {10}^6$ (1.17 $\times {10}^5$) −	1.4273 $\times {10}^6$ (1.25 $\times {10}^5$) −	N/A	9.7701 $\times {10}^5$ (1.08 $\times {10}^5$) −	1.3940 $\times {10}^6$ (7.71 $\times {10}^4$) −	8.3542 $\times {\mathbf{10}}^{\mathbf{5}}$ (1.60 $\times {\mathbf{10}}^{\mathbf{5}}$)
MaF5	3	9.1984 $\times {10}^0$ (5.39 $\times {10}^{-1}$) =	9.5013 $\times {10}^0$ (2.21 $\times {10}^0$) =	1.0741 $\times {10}^1$ (2.91 $\times {10}^0$) =	6.3104 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.97 $\times {\mathbf{10}}^{\mathbf{0}}$) +	1.0056 $\times {10}^1$ (9.10 $\times {10}^{-1}$) =	1.0048 $\times {10}^1$ (2.18 $\times {10}^0$)
	4	1.0502 $\times {10}^1$ (8.87 $\times {10}^{-1}$) +	1.1610 $\times {10}^1$ (2.67 $\times {10}^0$) =	1.2108 $\times {10}^1$ (2.31 $\times {10}^0$) =	8.3278 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.13 $\times {\mathbf{10}}^{\mathbf{0}}$) +	1.3135 $\times {10}^1$ (1.66 $\times {10}^0$) −	1.1784 $\times {10}^1$ (1.86 $\times {10}^0$)
	6	1.7812 $\times {\mathbf{10}}^{\mathbf{1}}$ (2.67 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.8493 $\times {10}^1$ (7.96 $\times {10}^0$) −	2.5577 $\times {10}^1$ (6.56 $\times {10}^0$) =	1.9600 $\times {10}^1$ (3.15 $\times {10}^0$) +	2.8780 $\times {10}^1$ (6.34 $\times {10}^0$) −	2.3089 $\times {10}^1$ (2.94 $\times {10}^0$)
	8	4.6440 $\times {\mathbf{10}}^{\mathbf{1}}$ (6.74 $\times {\mathbf{10}}^{\mathbf{0}}$) +	6.0658 $\times {10}^1$ (1.04 $\times {10}^1$) −	5.7401 $\times {10}^1$ (1.22 $\times {10}^1$) =	5.2089 $\times {10}^1$ (9.93 $\times {10}^0$) =	8.0599 $\times {10}^1$ (2.57 $\times {10}^1$) −	5.3179 $\times {10}^1$ (6.30 $\times {10}^0$)
	10	1.5650 $\times {\mathbf{10}}^{\mathbf{2}}$ (1.73 $\times {\mathbf{10}}^{\mathbf{1}}$) +	1.8395 $\times {10}^2$ (4.56 $\times {10}^1$) =	1.6005 $\times {10}^2$ (2.10 $\times {10}^1$) +	1.8052 $\times {10}^2$ (2.02 $\times {10}^1$) =	2.3848 $\times {10}^2$ (4.50 $\times {10}^1$) −	2.1777 $\times {10}^2$ (9.91 $\times {10}^1$)
MaF6	3	2.7284 $\times {10}^2$ (2.66 $\times {10}^1$) −	1.6807 $\times {10}^2$ (2.61 $\times {10}^1$) −	N/A	1.3929 $\times {\mathbf{10}}^{\mathbf{2}}$ (2.58 $\times {\mathbf{10}}^{\mathbf{1}}$) =	2.4823 $\times {10}^2$ (1.99 $\times {10}^1$) −	1.3966 $\times {10}^2$ (4.21 $\times {10}^1$)
	4	2.6540 $\times {10}^2$ (1.65 $\times {10}^1$) −	2.1893 $\times {10}^2$ (2.74 $\times {10}^1$) −	N/A	1.4843 $\times {10}^2$ (2.54 $\times {10}^1$) =	2.4619 $\times {10}^2$ (1.58 $\times {10}^1$) −	1.4091 $\times {\mathbf{10}}^{\mathbf{2}}$ (3.31 $\times {\mathbf{10}}^{\mathbf{1}}$)
	6	2.4028 $\times {10}^2$ (2.04 $\times {10}^1$) −	2.2333 $\times {10}^2$ (2.28 $\times {10}^1$) −	N/A	1.5078 $\times {10}^2$ (2.87 $\times {10}^1$) −	2.2341 $\times {10}^2$ (1.12 $\times {10}^1$) −	1.2670 $\times {\mathbf{10}}^{\mathbf{2}}$ (3.65 $\times {\mathbf{10}}^{\mathbf{1}}$)
	8	2.1140 $\times {10}^2$ (1.78 $\times {10}^1$) −	2.1633 $\times {10}^2$ (1.99 $\times {10}^1$) −	N/A	1.3969 $\times {10}^2$ (2.67 $\times {10}^1$) −	2.1538 $\times {10}^2$ (1.37 $\times {10}^1$) −	1.1838 $\times {\mathbf{10}}^{\mathbf{2}}$ (3.60 $\times {\mathbf{10}}^{\mathbf{1}}$)
	10	2.0077 $\times {10}^2$ (1.70 $\times {10}^1$) −	2.0177 $\times {10}^2$ (1.70 $\times {10}^1$) −	N/A	1.2808 $\times {10}^2$ (2.75 $\times {10}^1$) −	2.0416 $\times {10}^2$ (1.56 $\times {10}^1$) −	9.6546 $\times {\mathbf{10}}^{\mathbf{1}}$ (5.06 $\times {\mathbf{10}}^{\mathbf{1}}$)
MaF7	3	5.9342 $\times {\mathbf{10}}^{-\mathbf{1}}$ (9.20 $\times {\mathbf{10}}^{-\mathbf{2}}$) +	6.0456 $\times {10}^0$ (7.44 $\times {10}^{-1}$) +	8.7173 $\times {10}^0$ (1.20 $\times {10}^0$) =	5.5385 $\times {10}^0$ (9.61 $\times {10}^{-1}$) +	9.4068 $\times {10}^0$ (4.46 $\times {10}^{-1}$) −	8.8519 $\times {10}^0$ (8.05 $\times {10}^{-1}$)
	4	8.9847 $\times {\mathbf{10}}^{-\mathbf{1}}$ (1.21 $\times {\mathbf{10}}^{-\mathbf{1}}$) +	8.5943 $\times {10}^0$ (1.72 $\times {10}^0$) +	1.1882 $\times {10}^1$ (1.72 $\times {10}^0$) =	9.1095 $\times {10}^0$ (1.33 $\times {10}^0$) +	1.2849 $\times {10}^1$ (4.94 $\times {10}^{-1}$) −	1.1682 $\times {10}^1$ (9.83 $\times {10}^{-1}$)
	6	1.6050 $\times {\mathbf{10}}^{\mathbf{0}}$ (4.26 $\times {\mathbf{10}}^{-\mathbf{1}}$) +	1.5978 $\times {10}^1$ (2.03 $\times {10}^0$) +	1.6023 $\times {10}^1$ (3.35 $\times {10}^0$) =	1.5290 $\times {10}^1$ (1.12 $\times {10}^0$) +	1.9694 $\times {10}^1$ (8.66 $\times {10}^{-1}$) −	1.7763 $\times {10}^1$ (2.96 $\times {10}^0$)
	8	2.7957 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.15 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.2782 $\times {10}^1$ (2.69 $\times {10}^0$) =	2.3852 $\times {10}^1$ (2.34 $\times {10}^0$) =	2.2239 $\times {10}^1$ (1.32 $\times {10}^0$) =	2.5877 $\times {10}^1$ (7.13 $\times {10}^{-1}$) −	2.4003 $\times {10}^1$ (2.83 $\times {10}^0$)
	10	4.6937 $\times {\mathbf{10}}^{\mathbf{0}}$ (1.63 $\times {\mathbf{10}}^{\mathbf{0}}$) +	2.8617 $\times {10}^1$ (3.45 $\times {10}^0$) =	3.0500 $\times {10}^1$ (2.86 $\times {10}^0$) =	2.8646 $\times {10}^1$ (2.56 $\times {10}^0$) =	3.2563 $\times {10}^1$ (1.30 $\times {10}^0$) −	2.8807 $\times {10}^1$ (4.67 $\times {10}^0$)
+/−/=		11/20/4	7/22/6	2/7/11	9/15/11	3/29/3

). It is imperative to note that not all of the algorithms yielded results across the full spectrum of MaF instances. Specifically, algorithms such as MOEA/D-EGO and ParEGO, incorporated within the PlatEMO framework, faced challenges when confronting some of the more intricate MaF scenarios, resulting in incomplete datasets in our comparative analysis. We use “N/A” to indicate missing data.

MaF1 is designed to test an algorithm’s ability to address inverted Pareto fronts (PFs). CoEGAN-BO exhibited superior performance on the 3-, 4-, 6-, and 8-objective variants of the MaF1 problem, but its efficacy diminished at the 10-objective level, where MOEA/D-EGO prevailed. MaF2, known for its irregularity and incomplete coverage of the objective space, saw CoEGAN-BO triumphing at 3 and 4 objectives, while MOEA/D-EGO outperformed the rest at 6, 8, and 10 objectives, likely due to its more effective convergence function in such contexts.

MaF3, characterized by its convex PF and multitude of local fronts, was another domain where CoEGAN-BO demonstrated best-in-class performance for 6-, 8-, and 10-objective settings. K-RVEA, however, stood out for the 3- and 4-objective cases. This may be attributed to CoEGAN-BO’s environmental selection strategy, which adeptly tackles the convex PF challenges in many-objective problems.

MaF4’s high multimodality, comprising numerous local PFs, tests an algorithm’s ability to navigate through severe PF landscapes. Here, CoEGAN-BO proved to be a robust solver, particularly in the 8- and 10-objective scenarios, showcasing significant improvements over its peers. CoEGAN-BO emerged as the preeminent solver for MaF4, with no other algorithm matching its performance.

On MaF5, where each objective function is scaled to distinctively different ranges, CoEGAN-BO did not emerge as the top contender. This suboptimal performance might be due to the limitations imposed by its bi-stage infilling criterion, which hinders its ability to effectively scale diverse objective functions. K-RVEA demonstrated the best performance on MaF5’s three objectives.

MaF6 features a degenerate PF and serves as a litmus test for an algorithm’s proficiency in tackling such challenges. It is evident that CoEGAN-BO has a commendable capacity to address degenerate PFs effectively. MaF7, which evaluates an algorithm’s prowess in managing disconnected PFs, highlighted K-RVEA as the superior solver, potentially owing to an environmental selection strategy that favors continuous local optima. In conclusion, K-RVEA, CoEGAN-BO, and REMO stand out as the leading algorithms for resolving the diverse range of challenges presented by the MaF suite.

4.6. Runtime

We compared the runtime performance of seven algorithms on DTLZ problems with 3 objectives and 50 decision variables.

Table 6. Average runtime (seconds) of all seven algorithms on DTLZ test problems.

Problem	K-RVEA	MOEA/D-EGO	KTA2	REMO	EDN-ARMOEA	CoEGAN-BO
DTLZ1	1.4427 $\times {10}^2$	3.7621 $\times {10}^2$	3.5105 $\times {10}^3$	3.7793 $\times {10}^2$	1.3358 $\times {10}^1$	5.1477 $\times {10}^2$
DTLZ2	1.5611 $\times {10}^2$	4.5886 $\times {10}^2$	8.7350 $\times {10}^2$	2.3010 $\times {10}^2$	1.3099 $\times {10}^1$	5.0543 $\times {10}^2$
DTLZ3	1.8730 $\times {10}^2$	4.3973 $\times {10}^2$	9.0765 $\times {10}^2$	4.4563 $\times {10}^2$	1.6600 $\times {10}^1$	5.0490 $\times {10}^2$
DTLZ5	1.3001 $\times {10}^2$	4.5142 $\times {10}^2$	9.2378 $\times {10}^2$	2.9397 $\times {10}^2$	1.5870 $\times {10}^1$	4.8810 $\times {10}^2$
DTLZ6	1.3371 $\times {10}^2$	4.6383 $\times {10}^2$	8.8606 $\times {10}^2$	3.1500 $\times {10}^2$	1.4933 $\times {10}^1$	4.6461 $\times {10}^2$
DTLZ7	1.4691 $\times {10}^2$	4.4943 $\times {10}^2$	8.5553 $\times {10}^2$	1.8000 $\times {10}^2$	1.5293 $\times {10}^1$	4.7112 $\times {10}^2$

presents the average computation time (in seconds) across 20 independent runs for each algorithm. Even though CoEGAN-BO does not execute rapidly, it is still in the same order of magnitude as the rest of the algorithms and fits into the range of expensive optimization.

Additionally, we evaluated the runtime of the algorithm’s BO and GAN modules with 3 objectives and 50 decision variables. In

Table 7. BO and GAN operational efficiency comparison results (seconds).

Problem	Bayesian optimization (BO)		Generative Adversarial Network (GAN)		Total Runtime
	Avg. Train Time	Total Train Time	Avg. Train Time	Total Train Time
DTLZ1	1.7787 $\times {10}^1$	6.9370 $\times {10}^2$	6.5291 $\times {10}^{-2}$	2.5464 $\times {10}^0$	5.1477 $\times {10}^2$
DTLZ2	1.6424 $\times {10}^1$	6.4054 $\times {10}^2$	7.6485 $\times {10}^{-2}$	2.9829 $\times {10}^0$	5.0543 $\times {10}^2$
DTLZ3	1.6385 $\times {10}^1$	6.3900 $\times {10}^2$	6.7070 $\times {10}^{-2}$	2.6157 $\times {10}^0$	5.0490 $\times {10}^2$
DTLZ5	1.5958 $\times {10}^1$	6.2237 $\times {10}^2$	6.8467 $\times {10}^{-2}$	2.6702 $\times {10}^0$	4.8810 $\times {10}^2$
DTLZ6	1.6909 $\times {10}^1$	6.5947 $\times {10}^2$	6.7778 $\times {10}^{-2}$	2.6433 $\times {10}^0$	4.6461 $\times {10}^2$
DTLZ7	1.7023 $\times {10}^1$	6.6392 $\times {10}^2$	7.5646 $\times {10}^{-2}$	2.9502 $\times {10}^0$	4.7112 $\times {10}^2$

, Avg. Train Time denotes the duration of a single training run, Total Train Time represents the cumulative runtime until the maximum number of genuine evaluations is exhausted, and Total Runtime indicates the overall execution time of the entire algorithm.

5. Conclusions

In this work, we have developed a cutting-edge bi-stage Bayesian co-evolutionary optimization algorithm underpinned by generative adversarial networks specifically designed to tackle HEMaOPs. Our proposed method, dubbed CoEGAN-BO, employs distinct search strategies to expedite convergence, allowing two independent populations to evolve while facilitating the exchange of superior individuals at strategic intervals to enhance the convergence speed. This approach ensures that the optimal solution is a composite of the individual optimal solutions, thereby refining the overall solution quality within the population. A novel bi-stage infill criterion is also introduced, ensuring that solution diversity is not solely reliant on the measure of uncertainty. Moreover, by fine-tuning the balance factor, our algorithm adeptly navigates the trade-off between diversity and convergence. In the realm of high-dimensional optimization, where sample sparsity is an issue, our algorithm adeptly sidesteps the local optimum problem, advancing towards a more precise identification of the global optimum. The efficacy and superior performance of our algorithm, with its integrated strategy, have been rigorously tested on a suite of established benchmark problems. The empirical results highlight our algorithm’s remarkable superiority over other comparative algorithms across most of the test scenarios. The algorithm is competitive in solving most of the test problems used in the experiments. However, the algorithm converges slowly in solving DTLZ7 test problems. This shows that CoEGAN-BO is not capable enough when the real PF is a degenerate curve and discontinuous. Future research should consider selecting more effective prediction samples from the optimization process of irregular PFs to guide the population evolution in the right direction.