Multi-Objective Batch Energy-Entropy Acquisition Function for Bayesian Optimization

Abstract

Bayesian Optimization (BO) provides an efficient framework for optimizing expensive black-box functions by employing a surrogate model (typically a Gaussian Process) to approximate the objective function and an acquisition function to guide the search for optimal points. Batch BO extends this paradigm by selecting and evaluating multiple candidate points simultaneously, which improves computational efficiency but introduces challenges in optimizing the resulting high-dimensional acquisition functions. Among existing acquisition functions for batch Bayesian Optimization, entropy-based methods are considered to be state-of-the-art methods due to their ability to enable more globally efficient while avoiding redundant evaluations. However, they often fail to fully capture the dependencies and interactions among the selected batch points. In this work, we propose a Multi-Objective Batch Energy–Entropy acquisition function for Bayesian Optimization (MOBEEBO), which adaptively exploits the correlations among batch points. In addition, MOBEEBO incorporates multiple types of acquisition functions as objectives in a unified framework to achieve more effective batch diversity and quality. Empirical results demonstrate that the proposed algorithm is applicable to a wide range of optimization problems and achieves competitive performance.

1. Introduction

Bayesian Optimization (BO) [1,2] has emerged as a powerful framework for solving global optimization problems involving expensive-to-evaluate and unknown objective functions. It is particularly well suited for scenarios where function evaluations are constrained by computational cost or time limitations [3]. Traditional BO operates sequentially, selecting one candidate point at each iteration and updating the surrogate model based on the observed outcome. However, many real-world applications, including materials discovery [4] and hyperparameter tuning of deep neural networks [5], allow for parallel function evaluations. In such settings, selecting and evaluating a batch of candidate points simultaneously can substantially reduce the total optimization time while maintaining or even improving the quality of the final solution.

The application of BO to deep neural network training has significantly expanded its research scope [6]. Subsequent studies have explored methods to handle noisy and multi-fidelity data [7,8], high-dimensional spaces [9], and batch evaluations [10]. These advancements typically involve improving one of two fundamental components of the BO: the surrogate model or the acquisition function. The surrogate model provides a probabilistic approximation of the unknown objective function, enabling uncertainty quantification for unexplored regions, with the Gaussian Process (GP) [11] being a common choice. Following this, the acquisition function uses this surrogate model to identify candidate points for evaluation in the next iteration, aiming to strike a balance between exploring high-uncertainty regions to improve the model and exploiting areas that currently appear promising [12].

Several acquisition functions have been proposed to guide the candidate selection process. Expected Improvement (EI) [13] is one of the most widely used due to its intuitive appeal and closed-form solution under Gaussian assumptions. It favors points that are expected to improve upon the current best observation. While the Upper Confidence Bound (UCB) [14] introduces a tunable parameter to control the exploration–exploitation balance, selecting points with high predictive mean and high uncertainty. These methods are efficient in the sequential single-point setting but face challenges when extended to batch parallel evaluations. To address this, more recent work has shifted toward entropy-based acquisition functions, such as Predictive Entropy Search (PES) [15] and Max-value Entropy Search (MES) [16], which directly aim to reduce the uncertainty about the location of the global optimum. More recently, the Batch Energy–Entropy Bayesian Optimization (BEEBO) method [17] has been introduced, offering precise control over the exploration–exploitation trade-off during the optimization process. As a result, entropy-based methods have been widely regarded as state-of-the-art for Batch Bayesian Optimization.

However, these entropy-based approaches inherently fail to capture the correlations among the selected batch points and often treat batch points independently, which can exacerbate redundancy and limit effective exploration of the objective function. While BEEBO partially addresses this issue by incorporating an energy–entropy term to capture global information, it still does not explicitly model the pairwise correlations among batch points. Consequently, the chosen points may be redundant or may not fully exploit the complementary information distributed across the batch. Therefore, in this work, we propose a Multi-Objective batch Energy–Entropy acquisition function for Bayesian Optimization (MOBEEBO) with an RBF kernel-based regularizer that directly quantifies pairwise similarities, promoting diversity and reducing redundancy in batch selection. The main contributions of this paper are the following:

• We develop a multi-objective framework that simultaneously integrates multiple acquisition function types, enabling adaptive exploration–exploitation trade-offs and more balanced batch selection decisions.
• We introduce an energy-based regularization term that explicitly models and exploits correlations among batch points, enhancing the diversity and quality of selected candidates.
• Through comprehensive empirical evaluation, we demonstrate that MOBEEBO overall achieves superior or competitive performance compared to state-of-the-art methods across a diverse range of optimization benchmarks.

MOBEEBO is broadly applicable to continuous, expensive, black-box optimization problems. It is particularly effective when evaluations are costly, where efficient use of each batch evaluation is critical. By building upon the general Bayesian optimization framework and incorporating multiple acquisition strategies, MOBEEBO remains versatile and robust across a wide spectrum of applications.

2. Related Work

Batch extensions of classical acquisition strategies have become a central focus in parallel Bayesian Optimization. These methods typically build upon well-established single-point acquisition functions such as EI [13], Knowledge Gradient (KG) [18], and UCB [14]. When adapted to select a batch of Q points per iteration, these functions yield batch variants such as q-EI and q-UCB [19]. While single-point formulations often possess closed-form expressions that enable efficient gradient-based optimization, extending them to the batch setting introduces significant computational challenges. In most cases, batch acquisition functions lack closed-form expressions and involve high-dimensional integrals over joint distributions, necessitating alternative optimization approaches such as greedy sequential selection, Monte Carlo approximations, or analytical approximations of joint expectations over multiple query points [20].

For example, the EI acquisition function selects the next query point by maximizing the expected gain over the best value observed so far, which is denoted as $f_t^{*}$. When using a GP as the surrogate model, EI can be computed in closed form based on the model’s predictive mean $\mu \left(\mathbf{x}\right)$ and variance $\Sigma \left(\mathbf{x}\right)$. However, extending EI to the batch setting (q-EI), where multiple points are simultaneously selected, the joint evaluation requires integrating over a multivariate Gaussian distribution, which quickly becomes intractable as the batch size increases. In such cases, Monte Carlo (MC) sampling [21] is commonly employed to approximate the acquisition value and its gradient. Yet, MC methods can be inefficient, especially in high-dimensional settings, due to the exponential increase in sample complexity [22]. To address this, Wilson et al. [19] applied the reparameterization trick [23] to reformulate the integrals involved in acquisition functions, enabling efficient gradient-based optimization. This approach has proven effective, particularly in problems with moderate to high dimensionality.

More recently, entropy-based acquisition functions have been proposed for batch BO due to their ability to directly and globally reduce uncertainty about the location or value of the global optimum, resulting in more informative, non-redundant, and sample-efficient batch selection. This viewpoint has motivated the development of approaches such as Entropy Search (ES) [24], PES [15], and MES [16]. A key distinction of MES is its focus on the mutual information [25] between the unknown optimum value and the observed data rather than on the location of the optimum itself. Building on MES, the General-purpose Information-Based Bayesian Optimization (GIBBON) method [26] introduces a scalable extension suitable for batch selection and more complex scenarios, such as multi-fidelity optimization. However, its performance declines for large batches (e.g., $Q>50$) due to approximation errors, necessitating the use of heuristic diversity-enhancing techniques. To mitigate this issue, Teufel et al. [17] proposed a BEEBO acquisition function, which incorporates an entropy term to balance information gain and diversity through an energy–entropy trade-off. This formulation does not require MC sampling and enables the efficient selection of batch points that are both informative and diverse.

3. The MOBEEBO Acquisition Function

Our proposed MOBEEBO addresses scalability and redundancy challenges through a combination of gradient-based batch optimization and explicit diversity regularization. Redundancy is mitigated via an RBF kernel-based regularizer that penalizes closely spaced batch points, while the integration of BEEBO, q-EI, and q-UCB in a unified framework which ensures that exploration, exploitation, and batch diversity are adaptively balanced.

Let $f_{\mathrm{true}}:\mathcal{X}\to \mathbb{R}$ denote an unknown objective function that maps inputs to the real-valued outputs. And also, suppose we are given a dataset with N samples $\mathcal{D}={\left\{(x_i^{train},y_i^{train})\right\}}_{i=1}^N$, and a batch of Q candidate query points $\mathbf{x}=(x_1,\dots ,x_Q)\in {\mathcal{X}}^Q$, for which we aim to compute an acquisition value. Following the BO paradigm, we place a posterior distribution over the GP surrogate function f evaluated at these query points as

$$f\left(\mathbf{x}\right)\sim P\left(f\right|\mathcal{D},\mathbf{x})=\mathcal{N}(f\left|\mu \right(\mathbf{x}),\Sigma (\mathbf{x}\left)\right)$$

(1)

where $\mathcal{N}\left(f\right|\mu \left(\mathbf{x}\right),\Sigma \left(\mathbf{x}\right))$ represents the multivariate Gaussian distribution with mean $\mu \left(\mathbf{x}\right)$ and covariance $\Sigma \left(\mathbf{x}\right)$. For GPs, both the posterior mean and covariance of Q queries can be computed in closed-form expressions as

$$\begin{array}{cc}\hfill \mu \left(\mathbf{x}\right)& =K(\mathbf{x},{\mathbf{x}}_{\mathcal{D}})K{({\mathbf{x}}_{\mathcal{D}},{\mathbf{x}}_{\mathcal{D}})}^{-1}{\mathbf{y}}_{\mathcal{D}}\hfill \\ \hfill \Sigma \left(\mathbf{x}\right)& =K(\mathbf{x},\mathbf{x})-K(\mathbf{x},{\mathbf{x}}_{\mathcal{D}})K{({\mathbf{x}}_{\mathcal{D}},{\mathbf{x}}_{\mathcal{D}})}^{-1}K({\mathbf{x}}_{\mathcal{D}},\mathbf{x})\hfill \end{array}$$

(2)

where ${\mathbf{x}}_{\mathcal{D}}={\left\{x_i\right\}}_{i=1}^N$ and ${\mathbf{y}}_{\mathcal{D}}={\left\{y_i\right\}}_{i=1}^N$ are the N observed inputs and observations, respectively, and $K(·,·)$ represents the kernel matrix computed using a GP kernel function (e.g., the RBF kernel [27]). Note that the augmented covariance ${\Sigma }_{\mathrm{aug}}\left(\mathbf{x}\right)$ for the Q candidate points can be readily computed using the augmented inputs ${\mathbf{x}}_{\mathrm{aug}}=({\mathbf{x}}_{\mathcal{D}},\mathbf{x})$, without requiring the true observations $\mathbf{y}$ corresponding to these Q inputs:

$${\Sigma }_{\mathrm{aug}}\left(\mathbf{x}\right)=K(\mathbf{x},\mathbf{x})-K(\mathbf{x},{\mathbf{x}}_{\mathrm{aug}})K{({\mathbf{x}}_{\mathrm{aug}},{\mathbf{x}}_{\mathrm{aug}})}^{-1}K({\mathbf{x}}_{\mathrm{aug}},\mathbf{x})$$

(3)

Based on this, BEEBO constructs a batch acquisition function to maximize Q points, introducing a temperature T to control the trade-off between exploration and exploitation. This temperature functions as a hyperparameter that scales the relative influence of uncertainty versus mean predictions when evaluating candidate points. A higher temperature encourages broader exploration by amplifying the contribution of uncertainty, whereas a lower temperature promotes exploitation of regions with higher predicted means. The corresponding acquisition function is defined as follows:

$$\begin{array}{cc}\hfill A_{\mathrm{BEEBO}}& =E\left(\mathbf{x}\right)+T·I\left(x\right)\hfill \\ \hfill & =\sum _{q=1}^Q\mu \left(x_q\right)+T·\left(H\left(f\right|\mathcal{D},\mathbf{x})-H_{\mathrm{aug}}\left(f\right|\mathcal{D},\mathbf{x})\right)\hfill \end{array}$$

(4)

where $E\left(\mathbf{x}\right)$ represents the energy term that drives exploitation, while the mutual information $I\left(x\right)$ serves as the entropy term promoting exploration. Specifically, $I\left(x\right)$ is derived from differential entropy H computed as

$$\begin{array}{cc}\hfill H\left(f\right|\mathcal{D},\mathbf{x})& =-{\int }_{f}P\left(f\right|\mathcal{D},\mathbf{x})ln\left(P\left(f\right|\mathcal{D},\mathbf{x})\right)df\hfill \\ \hfill & =-{\mathbb{E}}_f\left[ln\left(\mathcal{N}\right(f\left|\mu \right(\mathbf{x}),\Sigma (\mathbf{x}\left)\right))\right]\hfill \\ \hfill & ={\displaystyle \frac{Q}{2}}log\left(2\pi e\right)+{\displaystyle \frac{1}{2}}log\left|\Sigma \left(\mathbf{x}\right)\right|.\hfill \end{array}$$

(5)

where e is is the base of natural logarithms. Similarly, the augmented differential entropy $H_{\mathrm{aug}}\left(f\right|\mathcal{D},\mathbf{x})$ of f can be expressed as $H_{\mathrm{aug}}\left(f\right|\mathcal{D},\mathbf{x})={\displaystyle \frac{Q}{2}}log\left(2\pi e\right)+{\displaystyle \frac{1}{2}}log\left|{\Sigma }_{\mathrm{aug}}\left(\mathbf{x}\right)\right|$. As a result, the batch acquisition function of BEEBO can be simplified as

$$A_{\mathrm{BEEBO}}\left(\mathbf{x}\right)=\sum _{q=1}^Q\mu \left(x_q\right)+T·\left({\displaystyle \frac{1}{2}}log\left|\Sigma \left(\mathbf{x}\right)\right|-{\displaystyle \frac{1}{2}}log\left|{\Sigma }_{\mathrm{aug}}\left(\mathbf{x}\right)\right|\right)$$

(6)

The advantage of this acquisition function is that it does not require access to the true observations $\mathbf{y}$ for Q candidate points, which would otherwise incur significant computational costs if $f_{\mathrm{true}}$ is expensive to evaluate. However, it lacks the ability to capture correlations among Q batch points, thereby failing to fully exploit the complementary information distributed across the batch. To mitigate this limitation, we propose introducing an additional RBF-like repulsion regularization term with a bounded and smooth penalty, which is formulated as

$$R\left(\mathbf{x}\right)=\sum _{q<q^{\prime }\in Q}exp\left(-{\displaystyle \frac{{∥x_q-x_{q^{\prime }}∥}^2}{2{\ell }^2}}\right)$$

(7)

where ℓ is the length-scale hyperparameter that controls how quickly the function values change with respect to the input, and $x_q$ and $x_{q^{\prime }}$ are two different points belonging to Q batch points $\mathbf{x}$. In addition, while BEEBO balances exploration and exploitation through global uncertainty reduction, it may under-exploit areas near the current optimum. Conversely, q-EI and q-UCB focus on local improvement and uncertainty-guided exploitation. To combine their strengths, a multi-objective acquisition function integrating BEEBO, q-EI, and q-UCB is proposed as follows, enabling simultaneous global exploration, local refinement, and uncertainty-driven sampling:

$$A_{\mathrm{MOBEEBO}}\left(\mathbf{x}\right)=A_{\mathrm{BEEBO}}\left(\mathbf{x}\right)+A_{\mathrm{q}-\mathrm{EI}}\left(\mathbf{x}\right)+A_{\mathrm{q}-\mathrm{UCB}}\left(\mathbf{x}\right)+R\left(\mathbf{x}\right)$$

(8)

where $A_{\mathrm{q}-\mathrm{EI}}\left(\mathbf{x}\right)$ and $A_{\mathrm{q}-\mathrm{UCB}}\left(\mathbf{x}\right)$ can be efficiently estimated via MC sampling, enabling fast, gradient-based optimization as follows:

$$\begin{array}{cc}\hfill A_{\mathrm{q}-\mathrm{EI}}\left(\mathbf{x}\right)& =\mathbb{E}\left[max\left(maxf\left(\mathbf{x}\right)-f^{*},0\right)\right]\hfill \\ \hfill & \approx {\displaystyle \frac{1}{M}}\sum _{j=1}^{M}max\left(\underset{q}{max}{f}^{\left(j\right)}\left(x_q\right)-f^{*},0\right)\hfill \\ \hfill A_{\mathrm{q}-\mathrm{UCB}}\left(\mathbf{x}\right)& =\mathbb{E}\left[maxf\left(\mathbf{x}\right)\right]\hfill \\ \hfill & \approx {\displaystyle \frac{1}{M}}\sum _{j=1}^{M}max{f}^{\left(j\right)}\left(\mathbf{x}\right)\hfill \\ \hfill & \approx {\displaystyle \frac{1}{M}}\sum _{j=1}^M\underset{q}{max}\left(\begin{array}{c}\hfill \overline{f}\left(x_q\right)+\beta \left|f^{\left(j\right)}\left(x_q\right)-\overline{f}\left(x_q\right)\right|\end{array}\right)\hfill \end{array}$$

(9)

where M represents the number of MC samples, $\overline{f}\left(x_q\right)={\displaystyle \frac{1}{M}}{\sum }_{j=1}^M{f}^{\left(j\right)}\left(x_q\right)$ is the predictive mean of the q-th point across M samples, and $\beta$ is the hyperparameter controls the exploration–exploitation trade-off in q-UCB. By combining them, MOBEEBO leverages these diverse perspectives to achieve a more balanced search strategy that avoids the biases inherent in relying on a single criterion. Trade-offs among the components are naturally balanced by their shared probabilistic formulation and Monte Carlo estimation, which normalize contributions to comparable scales; in practice, this yields stable optimization without requiring problem-specific manual tuning.

The overall optimization process of our proposed MOBEEBO is shown in Algorithm 1, with the learning rate defined as $\gamma$. In this setup, the $\mathcal{GP}$ model incorporates both the training data $\mathcal{D}$ and the learned kernel function K, while the augmented covariance matrix ${\Sigma }_{\mathrm{aug}}\left(\mathbf{x}\right)$ is computed using a refitted $\mathcal{GP}$ model based on the augmented inputs ${\mathbf{x}}_{\mathrm{aug}}$. The batch of Q points $\mathbf{x}$ is optimized using a gradient ascent algorithm, rather than the heuristic search methods commonly used in multi-objective evolutionary optimization, to achieve faster convergence.

And convergence is achieved when the gradient norm $\left|\right|{▽}_{\mathbf{x}}{A}_{\mathrm{MOBEEBO}}\left(\mathbf{x}\right)\left|\right|$ falls below a small threshold, indicating that candidate point $\mathbf{x}$ has reached a local maximum of the acquisition function. Due to the non-convexity introduced by the combination of energy–entropy, expected improvement, upper confidence bound, and batch diversity terms, the algorithm generally converges to a locally optimal configuration rather than a global optimum. The MC estimation of q-EI and q-UCB introduces stochasticity, which can be mitigated by using a sufficiently large number of samples. Overall, upon convergence, MOBEEBO provides a batch of points that effectively balances exploration, exploitation, and diversity, thereby guiding efficient evaluation of expensive black-box functions.

Algorithm 1: MOBEEBO optimization.

Input:$\mathcal{GP}$ model, observed data $\mathcal{D}$, Q batch points $\mathbf{x}$

1: repeat   2:     Calculate $\mu \left(\mathbf{x}\right)$ and $\Sigma \left(\mathbf{x}\right)$ using $\mathcal{GP}$ given in Equation (2)   3:     $E\left(x\right)\leftarrow {\sum }_{q=1}^Q\mu \left(x_q\right)$   4:     Calculate ${\Sigma }_{\mathrm{aug}}\left(\mathbf{x}\right)$ using ${\mathbf{x}}_{\mathrm{aug}}=({\mathbf{x}}_{\mathcal{D}},\mathbf{x})$ given in Equation (3)   5:     Compute $A_{\mathrm{BEEBO}}\left(\mathbf{x}\right)$ using Equation (6)   6:     $R\left(\mathbf{x}\right)\leftarrow {\sum }_{q<q^{\prime }}exp\left(-{\displaystyle \frac{{∥x_q-x_{q^{\prime }}∥}^2}{2{\ell }^2}}\right)$   7:     $A_{\mathrm{q}-\mathrm{EI}}\left(\mathbf{x}\right)\leftarrow {\displaystyle \frac{1}{M}}{\sum }_{j=1}^{M}max\left({max}_q{f}^{\left(j\right)}\left(x_q\right)-f^{*},0\right)$   8:     $A_{\mathrm{q}-\mathrm{UCB}}\left(\mathbf{x}\right)\leftarrow {\displaystyle \frac{1}{M}}{\sum }_{j=1}^M{max}_q\left(\begin{array}{c}\hfill \overline{f}\left(x_q\right)+\beta \left|f^{\left(j\right)}\left(x_q\right)-\overline{f}\left(x_q\right)\right|\end{array}\right)$   9:     $A_{\mathrm{MOBEEBO}}\left(\mathbf{x}\right)\leftarrow A_{\mathrm{BEEBO}}\left(\mathbf{x}\right)+A_{\mathrm{q}-\mathrm{EI}}\left(\mathbf{x}\right)+A_{\mathrm{q}-\mathrm{UCB}}\left(\mathbf{x}\right)+R\left(\mathbf{x}\right)$ 10:     $\mathbf{x}\leftarrow \mathbf{x}+\gamma {▽}_{\mathbf{x}}{A}_{\mathrm{MOBEEBO}}\left(\mathbf{x}\right)$ 11: until Converged

Output: Optimized batch points $\mathbf{x}$

4. Experiments

4.1. Experimental Settings

We evaluated the performance of MOBEEBO on a diverse collection of benchmark optimization problems with varying input dimensions, as summarized in

Table 1. Summary of test problems.

Problems	Dimension (d)	Optimization Type	Global Optimum
Ackley	10	Minimization	0
Rastrigin	10	Minimization	0
Levy	10	Minimization	0
Shekel-10	4	Minimization	−10.536443
Hartmann	6	Minimization	−3.32237
Cosine	8	Maximization	0.8

. These benchmark functions were implemented in the BoTorch library [28], with several supporting flexible dimensional configurations. To evaluate performance in higher-dimensional settings, we configured the Ackley, Rastrigin, and Levy functions to operate in 10-dimensional search spaces, providing a representative set of moderately high-dimensional optimization challenges.

For each test function, we conducted 10 independent runs of BO using the proposed MOBEEBO algorithm and compare the results against baseline methods q-EI and q-UCB, as well as the state-of-the-art entropy-based method BEEBO. To ensure fair comparison, we adopted identical experimental settings across all methods. The temperature parameter T was set to 0.5, following the configuration in the original BEEBO work. And the length-scale ℓ of the regularizer in Equation (7) was set to 1 for moderate-strength repulsion. The Gaussian Process surrogate model was initialized with 100 randomly sampled points, each positioned at least 0.5 units away from the known global optimum to ensure challenging and unbiased starting conditions. For the Monte Carlo-based methods (q-EI and q-UCB), we used $M=1024$ samples for acquisition function evaluation. To eliminate random variation effects, identical random seeds were employed across all methods, ensuring that each independent run would begin from the same initial design points. All experiments were performed with a fixed batch size of $Q=100$, which represents a large-batch regime in the BO literature [29].

4.2. Results

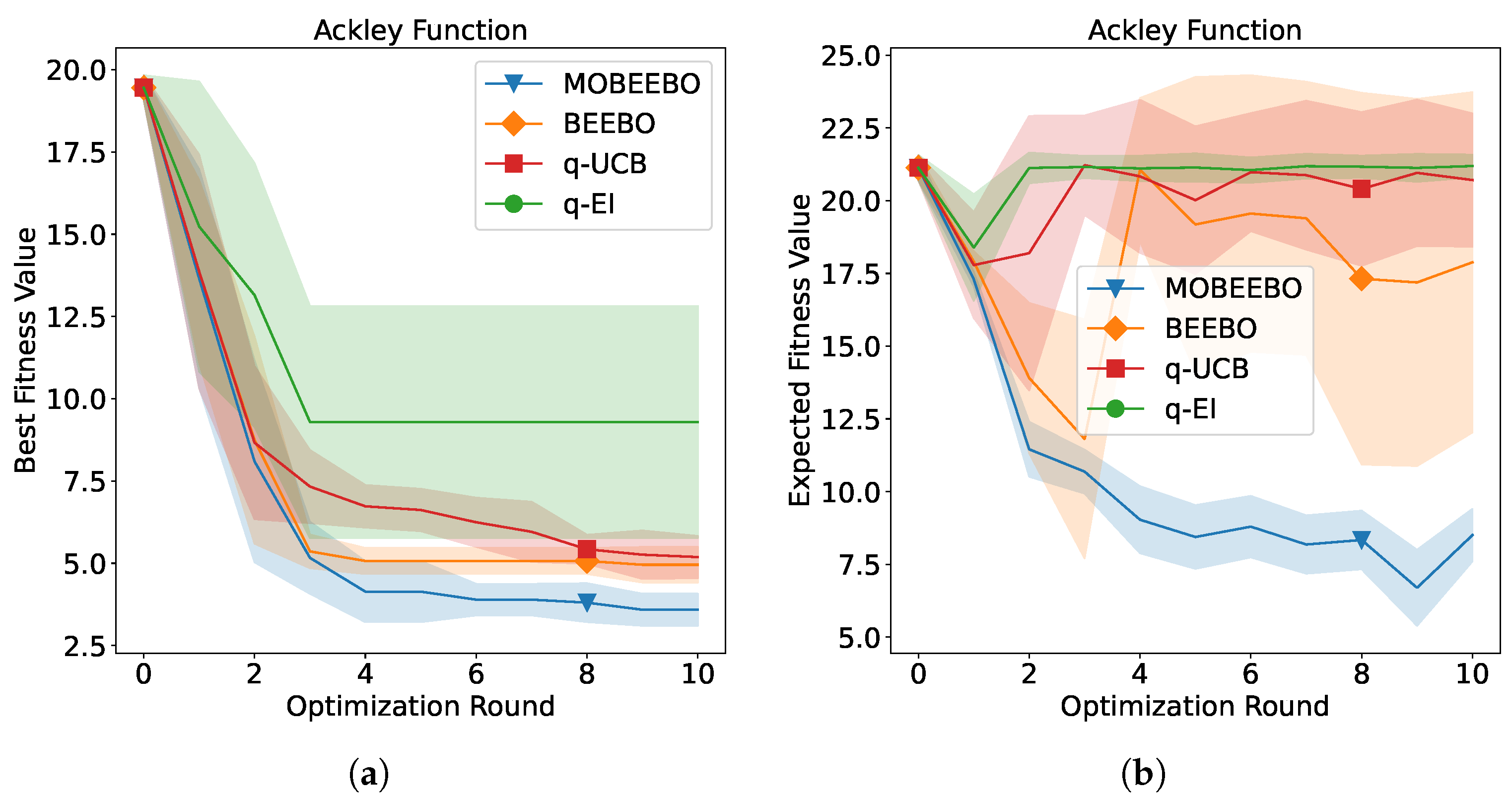
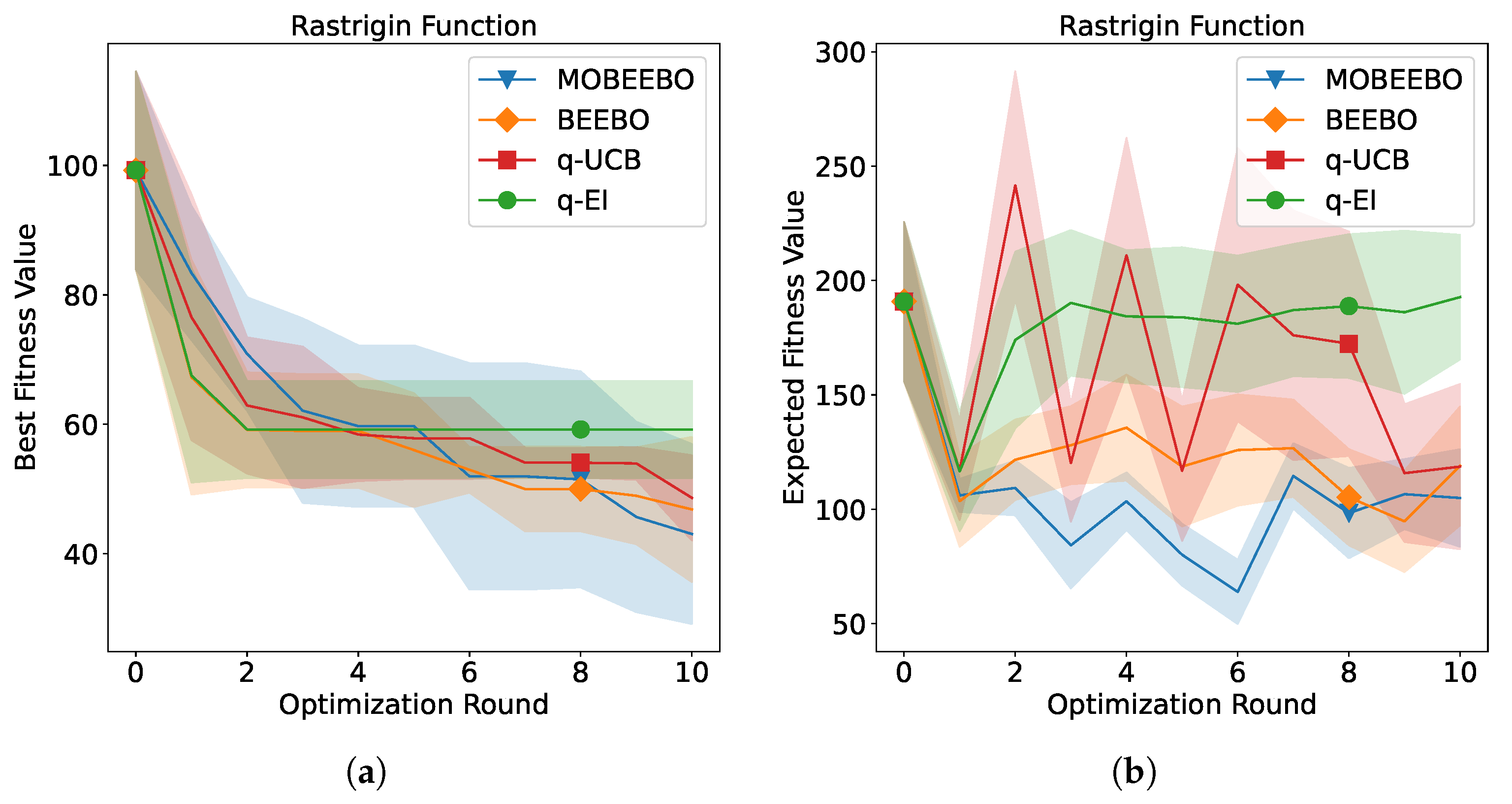
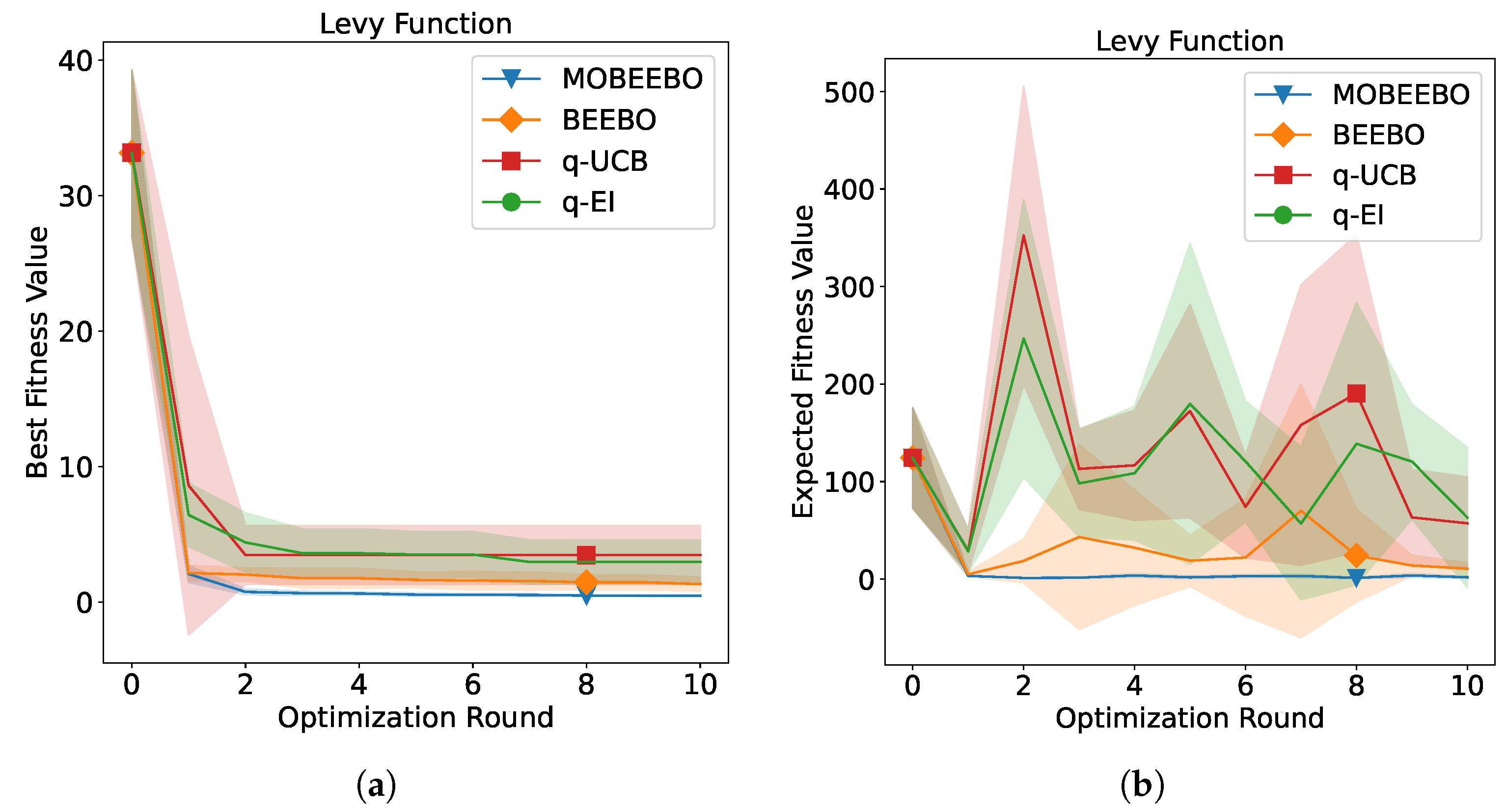
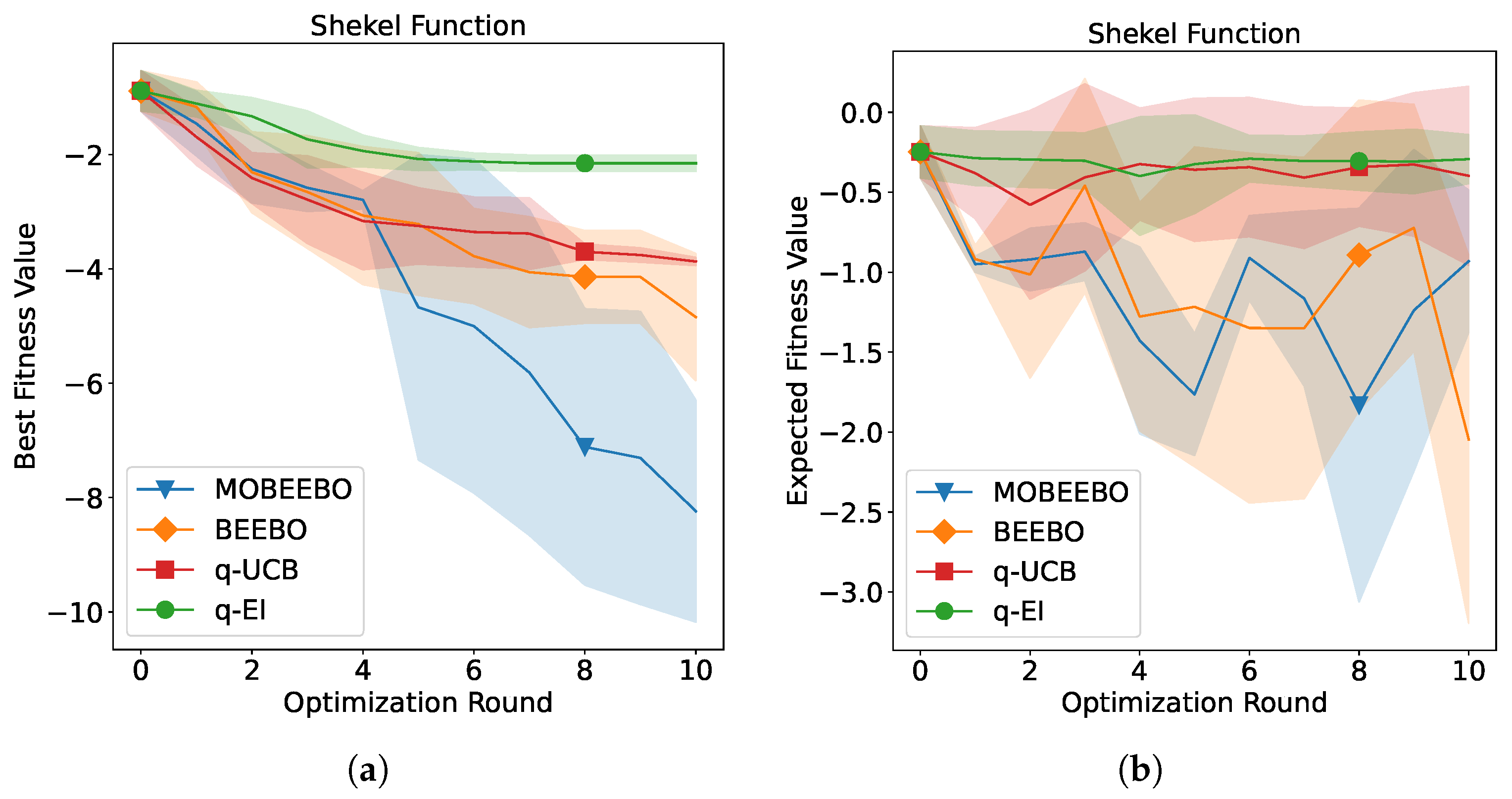
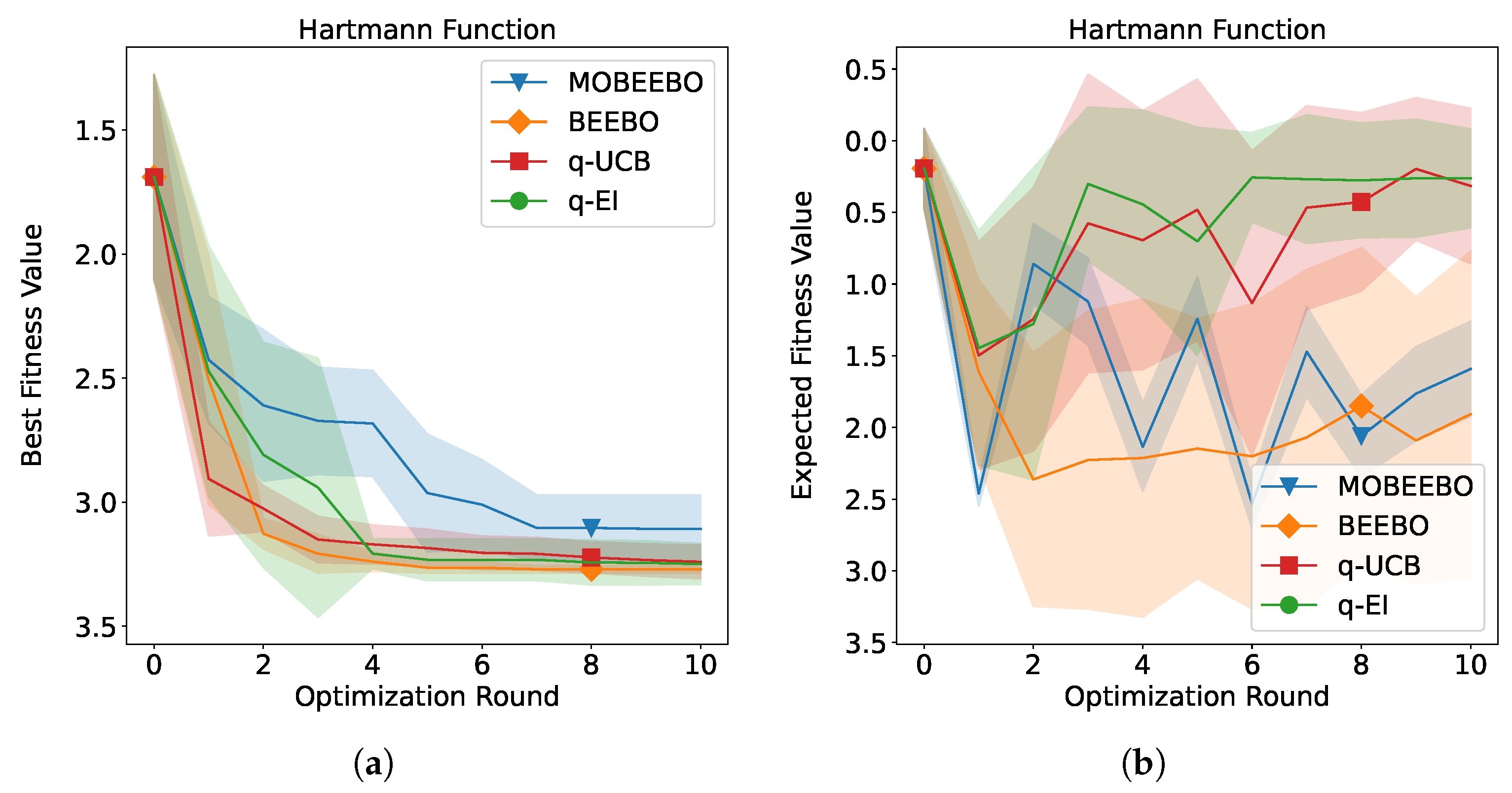
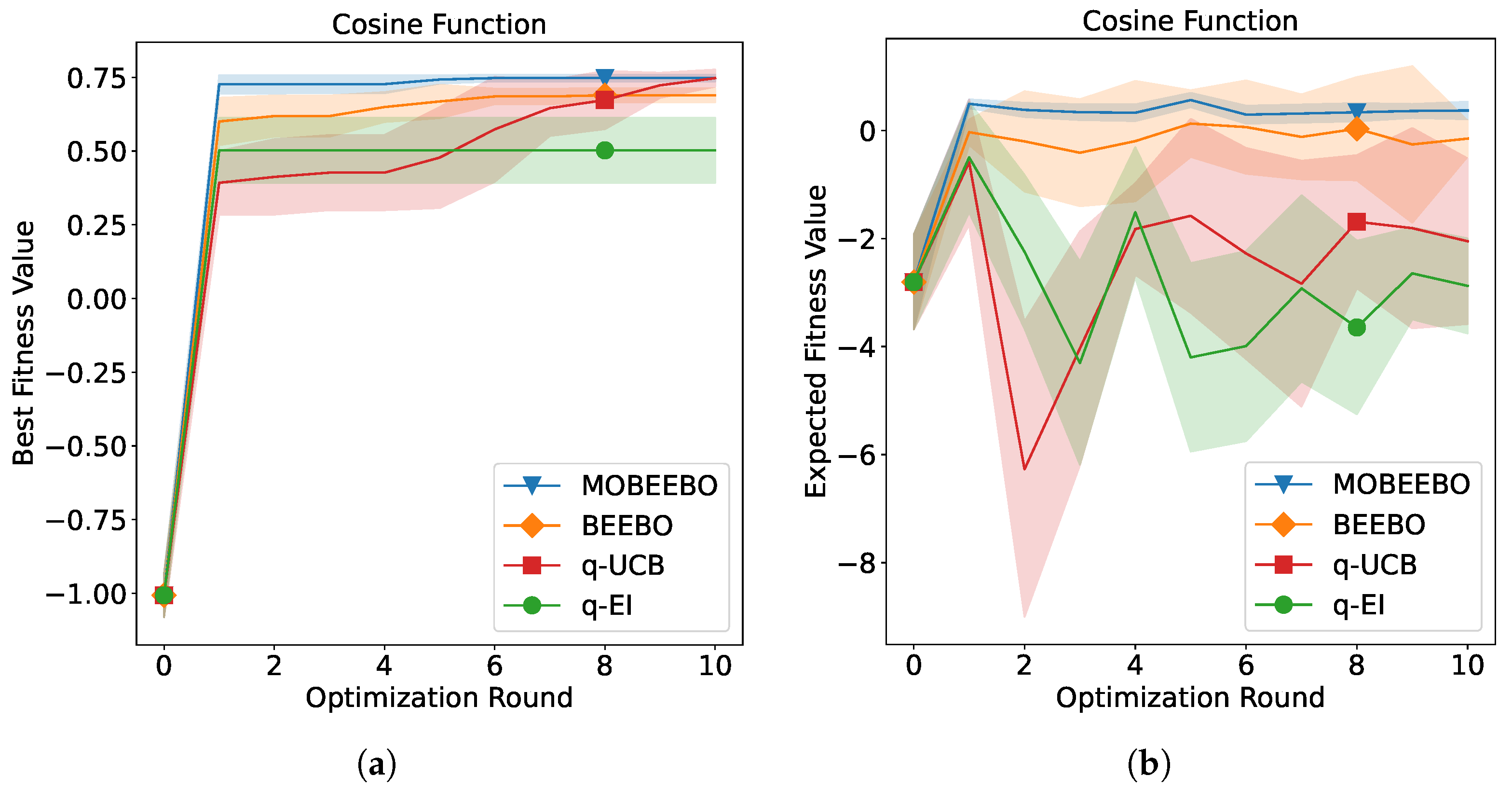
The optimization performance of the proposed MOBEEBO method compared with the three baseline methods over successive BO rounds is presented in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. Each figure contains two panels: the left panel displays the mean best objective value found up to each iteration (incumbent) across five independent runs, while the right panel shows the mean objective value of the Q points evaluated in each batch. Both shaded regions represent one standard deviation around the mean performance.

It is evident that the proposed MOBEEBO acquisition function generally outperformed the other approaches over the 10 BO rounds, with the exception of the embedded Hartmann test problem, where it performed slightly worse than the alternatives. This strong performance can be attributed to the low predictive uncertainty of MOBEEBO, which arises from the inclusion of the RBF-based regularization term $R\left(\mathbf{x}\right)$. By enhancing the correlation among the Q points within each batch, this term encourages more coherent exploitation of the search space, thereby reducing variance in the acquisition function and improving overall stability during optimization. And BEEBO achieved the second-best overall performance in the tests. The Q points it selects across rounds exhibit greater diversity but lower correlation, which can potentially encourage broader exploration of the search space. However, the resulting high uncertainty may hinder exploitation by allocating resources to less promising regions, leading to inefficient searches in unexpected areas.

Specifically, for the Ackley function, MOBEEBO exhibited the fastest convergence, reaching a value of approximately 3, which is closest to the optimal value of 0 among all methods. In contrast, q-UCB and BEEBO demonstrated similar convergence performance, while q-EI showed the poorest convergence, with a final optimization value of around 10. However, the trend differed for the Rastrigin function, where MOBEEBO converged the slowest during the initial BO rounds. Its performance curve then exhibited a sharp drop around the third round and continued to decline to nearly 40. BEEBO, q-UCB, and q-EI showed similar convergence patterns, with their performance stabilizing near the end of the optimization process. In addition, the search expectation for Rastrigin fluctuated minimally, indicating a relatively stable optimization process. Unlike the previous scenarios, all acquisition functions exhibited similar convergence performance, with MOBEEBO performing slightly better and q-EI performing slightly worse.

Similar to the Rastrigin problem, MOBEEBO initially showed only modest convergence performance for Shekel function, slightly better than q-EI, but experienced a performance boost in the fifth BO round, reaching approximately −7.8 and approaching the optimal value of −8. In contrast, MOBEEBO performed poorly on the embedded Hartmann function, achieving an optimal fitness value of around −3, whereas the other three acquisition functions converged to approximately −3.25, close to the optimal value of −3.32237. Moreover, all acquisition functions except MOBEEBO exhibited severe fluctuations across the Q batch points for this test problem. Finally, for the maximization problem of the Cosine Mixture test function, the proposed MOBEEBO exhibited both the fastest convergence speed and the best optimization performance across the rounds, while also maintaining the smallest fluctuations.

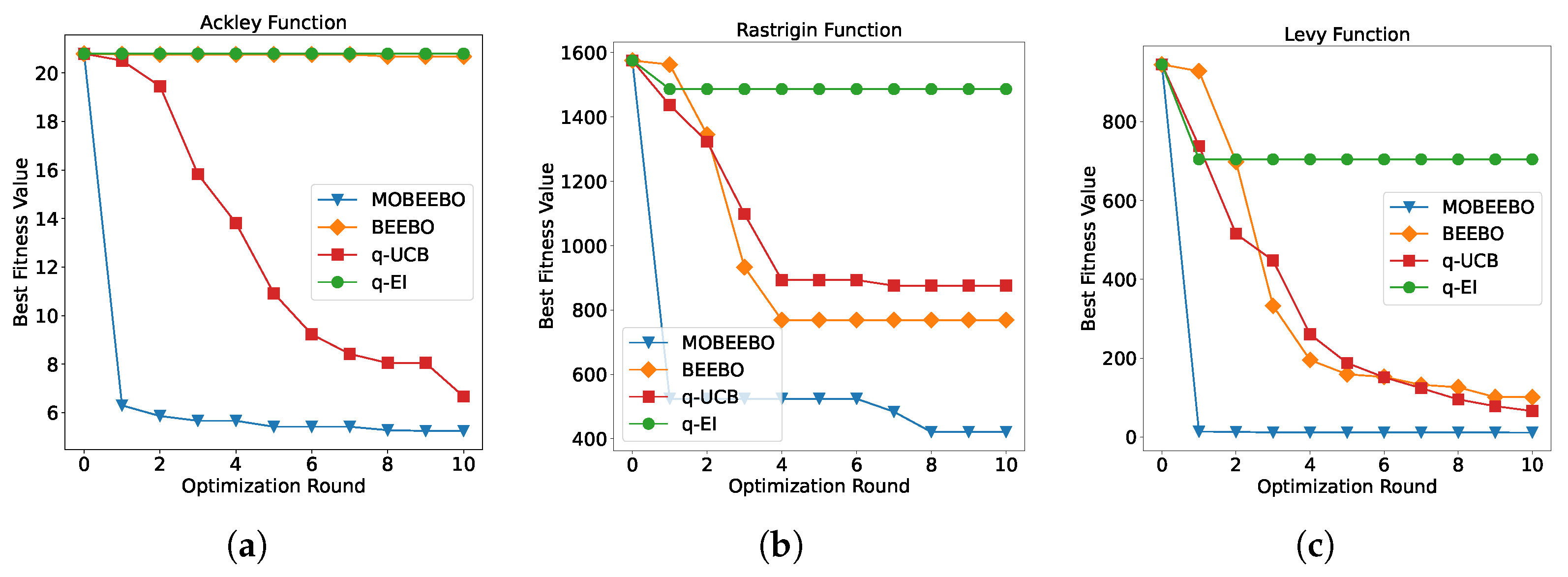
Finally, the test performance outcomes of all acquisition functions werre evaluated on the Ackley, Rastrigin, and Levy functions in extremely high-dimensional settings. The corresponding results for the 100-dimensional problems are shown in Figure 7. It can be clearly observed that our proposed MOBEEBO converged much faster than the other three acquisition functions in the early stages of the optimization and then stabilized, ultimately achieving the best optimization performance across all three test functions. In contrast, q-EI performed the worst, as it failed to converge in any of the test problems. A potential reason for this phenomenon is that, in extremely high dimensions, it is very difficult to attain the best evaluated fitness $f^{*}$, which serves as an anchor point for guiding the optimization direction. It is surprising to observe that BEEBO, similar to q-EI, failed to converge, with its final optimization result being almost indistinguishable from random initialization. This finding implicitly demonstrates that the redundancy introduced by batch optimization becomes more pronounced in high-dimensional problems.

To further validate the effectiveness of the MOBEEBO acquisition function, we conducted an additional 10 rounds of searches using the Q batch points selected in the previous rounds. For this scenario, the temperature T was set to 0 to enable full exploitation. Since the test problems vary widely in scale, we applied min-max normalization to the results for each problem. This normalization allows us to measure progress toward the true optimum on a standardized scale from 0 to 1. And the highest observed values averaged across multiple runs, together with the Wilcoxon test results after 10 BO rounds for all test functions, are presented in

Table 2. Highest observed value after 10 rounds of BO with $Q=100$. The best value is highlighted in bold, and both Mean and Median values are computed across test problems.

Problem	d	MOBEEBO	BEEBO	q-UCB	q-EI
Ackley	10	0.973	0.836 +	0.732 +	0.522 +
Rastrigin	10	0.523	0.497 +	0.449 +	0.385 +
Levy	10	0.985	0.961 +	0.894 +	0.905 +
Shekel-10	4	0.828	0.342 +	0.303 +	0.130 +
Hartmann	6	0.996	1.000−	0.938 +	0.955 +
Cosine	8	1.000	1.000 +	0.968 +	0.836 +
Mean		0.8842	0.7727	0.714	0.6222
Median		0.979	0.8985	0.813	0.679

, with the best value highlighted in bold. It is evident that MOBEEBO achieved the highest searched value for almost all test functions, except for the embedded Hartmann function, where its value of 0.996 was slightly lower than that of BEEBO. Specifically, for the Shekel test problem, MOBEEBO significantly outperformed all other methods, attaining a value of 0.828, which is approximately 0.5 higher than the second-best result achieved by BEEBO.

5. Conclusions

In this paper, we introduced MOBEEBO, a multi-objective batch energy–entropy acquisition function for BO that explicitly accounts for the correlations among batch points. By integrating multiple acquisition functions within a unified framework, MOBEEBO leverages the complementary strengths of different selection strategies, enabling both globally efficient and non-redundant exploration. Empirical evaluations across diverse optimization problems demonstrate that MOBEEBO overall achieved competitive or superior performance compared to SOTA methods, including entropy-based approaches. These results highlight the potential of multi-objective and correlation-aware acquisition strategies in advancing batch BO.

Nevertheless, MOBEEBO also has certain limitations. Its performance may be sensitive to the choice of hyperparameters, such as the temperature T, and the computational cost of evaluating multiple acquisition objectives can increase with batch size Q and problem dimension. Moreover, the current formulation assumes relatively noise-free settings, which may not fully reflect the challenges of real-world applications. Future research directions will therefore include providing a formal theoretical analysis of MOBEEBO’s convergence guarantees, which include investigating its robustness under noisy and constrained optimization scenarios and developing scalable approximations to improve efficiency with very large batch sizes and high-dimensional problems.