Three-Dimensional Discrete Echo-Memristor Map: Dynamic Analysis and DSP Implementation

Abstract

In recent years, with the development of novel hardware such as memristors, integrating chaotic systems with hardware implementations has enabled efficient and controllable generation of chaotic signals, providing new avenues for both theoretical research and engineering applications. In this work, we propose a novel memristor-based chaotic system, named the three-dimensional discrete echo-memristor map (3D-DEMM). The 3D-DEMM is capable of generating complex dynamic behaviors with self-similar attractor structures; specifically, under different parameters and initial conditions, the system produces similar attractor shapes at different amplitudes, which we refer to as an echo chaotic map. By incorporating the discrete nonlinear characteristics of memristors, the 3D-DEMM is systematically designed. We first conduct a thorough dynamic analysis of the 3D-DEMM, including attractor visualization, Lyapunov exponents, and NIST tests, to verify its chaoticity and self-similarity. Subsequently, the attractors of the 3D-DEMM are captured on a DSP platform, demonstrating discrete-time hardware simulation and real-time operation. Experimental results show that the proposed system not only exhibits highly controllable chaotic behavior but also demonstrates strong robustness in maintaining amplitude-invariant attractor shapes, providing a new theoretical and practical approach for memristor-based chaotic signal generation and applications in information security.

1. Introduction

In nonlinear dynamic systems, chaos has emerged as an important phenomenon due to its complexity and unpredictability [1,2,3,4], with wide-ranging applications in information security, random number generation, and signal processing [5,6,7,8,9]. In recent years, with the development of novel nonlinear devices such as memristors, researchers have increasingly incorporated them into the construction of chaotic systems [10,11].

Memristors not only possess non-volatility and strong nonlinearity but also enable the natural mapping of complex dynamic relationships in hardware circuits [12,13], providing a new physical foundation for the discretization and miniaturization of chaotic systems [14,15,16]. This opens up possibilities for addressing the limitations of traditional chaotic circuits, which are often complex in design and lack flexibility [17,18,19]. Meanwhile, the rapid progress of digital signal processors (DSPs) has made it possible for discrete-time chaotic systems to achieve real-time operation on hardware platforms, thereby further promoting the transition of chaos theory into practical engineering applications. Therefore, the design and implementation of memristor-based discrete chaotic systems not only hold significant theoretical research value but also have practical importance for applications in information security and signal processing [20,21,22].

In recent years, several memristor-based chaotic mapping systems have been proposed. Feali proposed a novel discrete memristor–hyperbolic sine map system that integrates a memristor model with the sinh chaotic map, generating complex chaotic and hyperchaotic dynamics with high entropy values and large Lyapunov exponents. Numerical simulations and experiments verified its potential applications in secure communications and random number generation [23]. Lu et al. introduced two memristor-based chaotic systems derived from the same fundamental structure, featuring multi-parameter amplitude modulation, large-scale offset enhancement, coexisting attractors, and robust chaos. Their potential applications were demonstrated through bifurcation diagrams, Lyapunov exponents, and circuit experiments [24]. Lin et al. constructed a memristor-coupled asymmetric neural network (MANN), revealing complex dynamics such as infinite-width hyperchaos, initial condition sensitivity enhancement, and multi-structured attractors. They further designed a color image encryption scheme, whose security and circuit feasibility were validated experimentally [25]. Demirkol et al. [26] proposed a novel locally active memristor-based chaotic circuit and implemented hybrid image encryption on a low-cost FPGA platform. The algorithm combines memristor chaos with DNA encryption, improving sequence randomness. Experiments and NIST tests verified its high security and real-time applicability. Di et al. [27] developed a memristor-based MMLC discrete map using a flux–charge discretization method, preserving the integral properties of the continuous system. They uncovered extreme multistability and computational chaos phenomena and analyzed the chaotic mechanism via Marotto’s theorem, confirming it as a unique dynamic behavior induced by discretization. These systems make full use of the nonlinear characteristics of memristors and exhibit rich chaotic behaviors in their dynamic performance, thereby meeting certain requirements for randomness and complexity.

Nevertheless, these existing studies still present certain limitations. First, most memristor-based chaotic systems focus on the complexity of attractors and the high-dimensional dynamic characteristics of the system, while the generated attractor shapes often lack structural self-similarity and multi-scale features [28,29,30,31,32]. Second, they fail to produce chaotic attractors with an “echo structure,” in which the attractors preserve similar geometric shapes under different parameters or initial conditions, differing only in amplitude. Unlike self-similar attractors, which exhibit repeating patterns across scales, or general chaotic attractors, which may vary unpredictably, echo attractors maintain a consistent shape while enabling amplitude scaling. This “echo chaos” property is not only theoretically valuable for understanding self-similarity and scale invariance in chaotic systems but also practically beneficial for improving the controllability and robustness of chaotic signals in engineering applications [33,34,35,36]. Therefore, designing a novel memristor-based chaotic map that combines both traditional chaotic properties and echo attractor characteristics has become an important problem to be addressed.

To address the limitation that existing memristor-based chaotic systems lack echo-structured attractors, this paper proposes a novel three-dimensional discrete echo-memristor map (3D-DEMM). First, leveraging the nonlinear characteristics of memristors, the 3D-DEMM system is designed and constructed, and a systematic dynamic analysis is carried out, including phase portraits, Lyapunov exponents, the 0–1 test, and NIST randomness tests, to verify its chaotic behavior and self-similarity. Second, the 3D-DEMM is implemented in real time on a DSP hardware platform, where its attractor shapes are captured, demonstrating the feasibility and practicality of discrete-time hardware realization.

The main contributions of this work are as follows:

1.

The 3D-DEMM is proposed, capable of generating chaotic attractors with echo structures, thereby enriching the theoretical class of chaotic systems.

2.

The chaotic properties of the 3D-DEMM are comprehensively revealed through attractor analysis, Lyapunov exponents, and NIST randomness evaluations.

3.

The attractors of the 3D-DEMM are successfully implemented on a DSP platform, demonstrating the realizability and application potential of echo chaos in discrete hardware systems.

The organization of this paper is as follows: Section 2 introduces the design of the 3D-DEMM. Section 3 analyzes the dynamic characteristics of the 3D-DEMM, including attractor analysis, bifurcation diagram analysis, NIST tests, and complexity analysis. Section 4 presents the implementation of the 3D-DEMM attractors using a DSP platform. Section 5 provides the conclusion.

2. Three-Dimensional Discrete Echo-Memristor Map

2.1. Discrete Memristor

The memristor, due to its unique nonlinear electrical characteristics and memory effect, is used to generate chaotic sequences and explain chaotic phenomena. Its resistance depends not only on the instantaneous voltage or current but also dynamic changes with the accumulation of past charge or current. This “history dependence” endows the system with strong nonlinear dynamic behavior. By exploiting this chaotic property, memristors can enable high-complexity and highly secure applications in fields such as information encryption, random number generation, and signal processing.

According to Chua’s definition [37], a charge-controlled memristor is described by

$$\left\{\begin{array}{c}v\left(t\right)=M\left(q\right)i\left(t\right)\hfill \\ dq\left(t\right)/\phantom{dq\left(t\right)dt}dt=i\left(t\right)\hfill \end{array}\right.$$

(1)

Using the forward Euler method, Equation (1) can be discretized as

$$\left\{\begin{array}{c}{v}_n=\phi \left(q_n\right)i_n\hfill \\ q_{n+1}=q_n+\delta i_n\hfill \end{array}\right.$$

(2)

By setting $\phi \left(q_n\right)=a_{1}sin\left(q_n\right)-a_{2}cos\left(q_n\right)$, the discrete memristive model becomes

$$\left\{\begin{array}{c}{v}_n=(a_{1}sin\left(q_n\right)-a_{2}cos\left(q_n\right))i_n\hfill \\ q_{n+1}=q_n+\delta i_n\hfill \end{array}\right.$$

(3)

where $v_n$ and $i_n$ denote the voltage across and current through the memristor at discrete time step n, respectively; $q_n$ represents the internal charge at time step n; and $q_{n+1}$ is the charge at the next step. The parameters $a_1$ and $a_2$ characterize the nonlinearity of the memristance. $\delta$ is the discrete step size used to update the charge from $q_n$ to $q_{n+1}$. This discrete model captures the memristor’s charge-dependent nonlinear behavior, which can give rise to complex or chaotic dynamics.

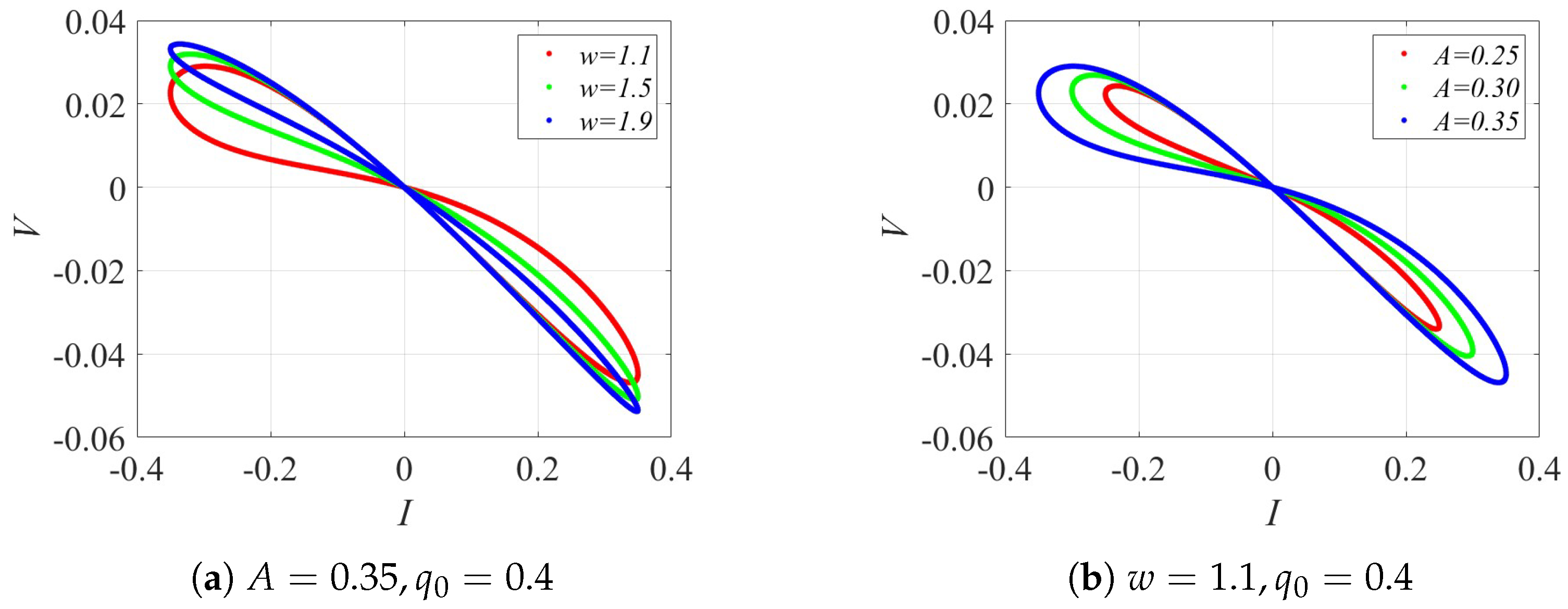
To verify whether Equation (3) is consistent with the characteristics of a memristor, the current through the memristor is set as $i\left(t\right)=Asin\left(\omega t\right)$. Assuming the internal parameters of the memristor are $\delta =0.9$, $a_1=0.1$, and $a_2=0.2$, the discrete-time input current ($i_n$) and output voltage ($v_n$) of the memristor are plotted in Figure 1.

As shown in Figure 1, the hysteresis curve of the proposed memristor exhibits a characteristic figure-eight shape at the origin, consistent with the fundamental definition of a memristor. The voltage across the memristor depends not only on the instantaneous current but also on the accumulated charge, reflecting its inherent memory effect. Moreover, the shape and area of the hysteresis loop vary with the input signal and internal parameters, confirming that the model accurately captures the nonlinear and history-dependent dynamics of the memristor.

2.2. Design of Three-Dimensional Discrete Echo-Memristor Map

Based on the discrete memristor model Equation (3), a novel 3D-DEMM is proposed:

$$\left\{\begin{array}{c}{x}_{i+1}=asin\left(y_i\right)\hfill \\ y_{i+1}=sin\left(x_i\right)+b(a_{1}sin\left(z_i\right)-a_{2}cos\left(z_i\right))y_i\hfill \\ z_{i+1}=\delta y_i+z_i\hfill \end{array}\right.$$

(4)

This system fully exploits the nonlinear and memory-dependent characteristics of the memristor. By coupling the state variables x, y, and z, it introduces strong feedback and complex dynamic behavior, resulting in rich chaotic properties. The system not only incorporates nonlinear functions but also leverages the memristor’s history-dependent behavior to realize dynamic memory effects, so that each state update is influenced by the accumulated states of previous steps.

The parameters a, b and the internal memristor parameters $a_1$, $a_2$, and $\delta$ can be used to adjust the coupling strength and the amplitude of nonlinearity, enabling tunable control of the chaotic behavior. By appropriately selecting these parameters, the system can exhibit a wide range of dynamics from periodic and quasi-periodic to fully chaotic, providing a flexible and efficient framework for applications such as information encryption, pseudo-random sequence generation, and signal processing.

3. Dynamic Analysis of Three-Dimensional Discrete Echo-Memristor Map

To analyze the dynamic behavior of the 3D-DEMM, the parameters in Equation (4) are fixed as $a_1=0.1$, $a_2=0.2$, and $\delta =0.9$. The effects of variations in the parameters a and b, as well as changes in the system’s initial conditions $x_0$, $y_0$, and $z_0$, on the 3D-DEMM are then investigated.

3.1. Attractor Analysis

3.1.1. Analysis of the Regular Attractor

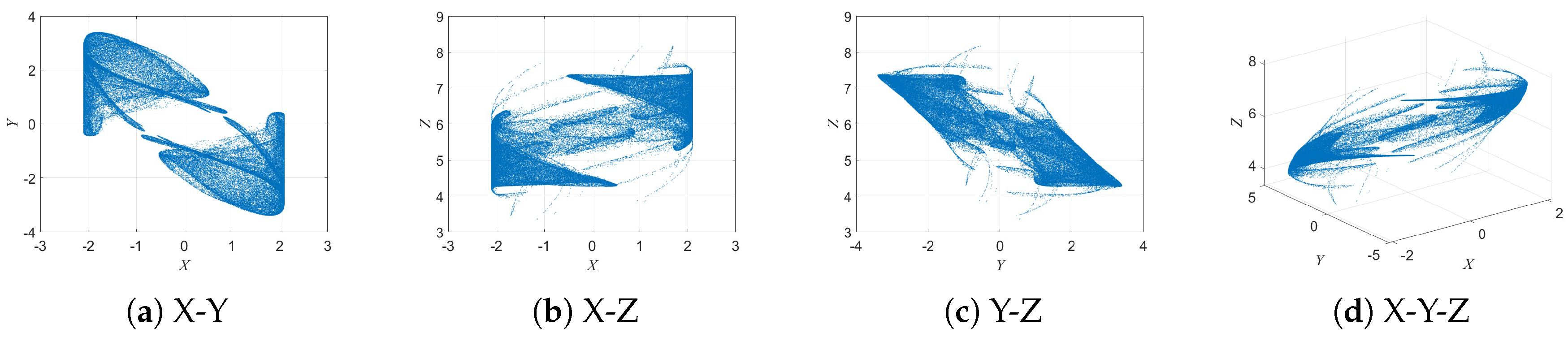
To investigate the long-term dynamic behavior of the system, the regular attractor of the 3D-DEMM is analyzed. By observing the evolution of the system’s state trajectories in phase space, the stability, periodicity, or quasi-periodicity of the system can be revealed, providing further insight into how parameter variations affect the system dynamics. The initial conditions are set as $x_0=0.8147$, $y_0=0.5468$, and $z_0=0.0975$. The regular attractor analysis of the 3D-DEMM is shown in Figure 2, Figure 3 and Figure 4.

By analyzing the regular attractors of the 3D-DEMM system, the evolutionary characteristics of the trajectories in phase space can be clearly observed. As shown in Figure 2, Figure 3 and Figure 4, under the initial conditions $x_0=0.8147$, $y_0=0.5468$, and $z_0=0.0975$, the system states gradually converge to a specific trajectory region over time, forming a stable attractor structure. As the parameters (a and b) vary, the shape of the attractor changes accordingly, reflecting the diversity of the 3D-DEMM dynamics.

3.1.2. Analysis of the Echo Attractor

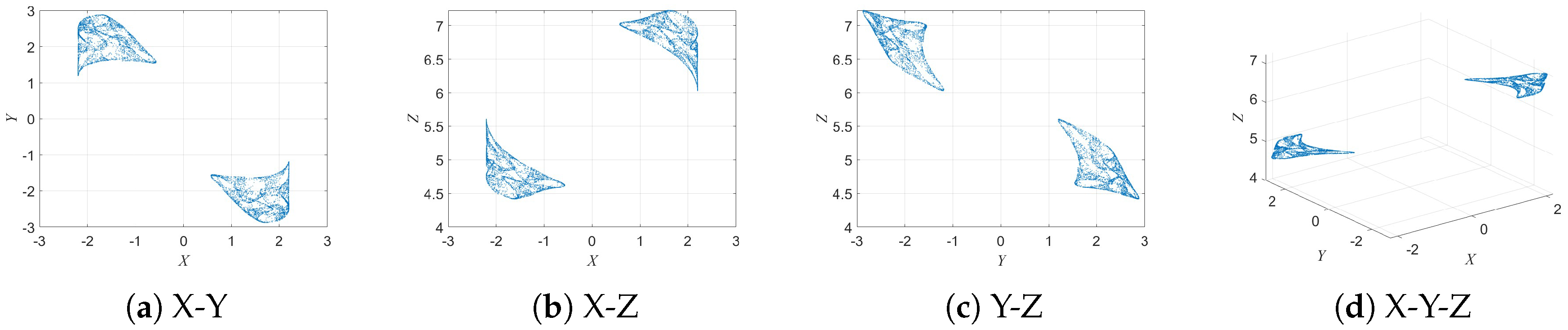
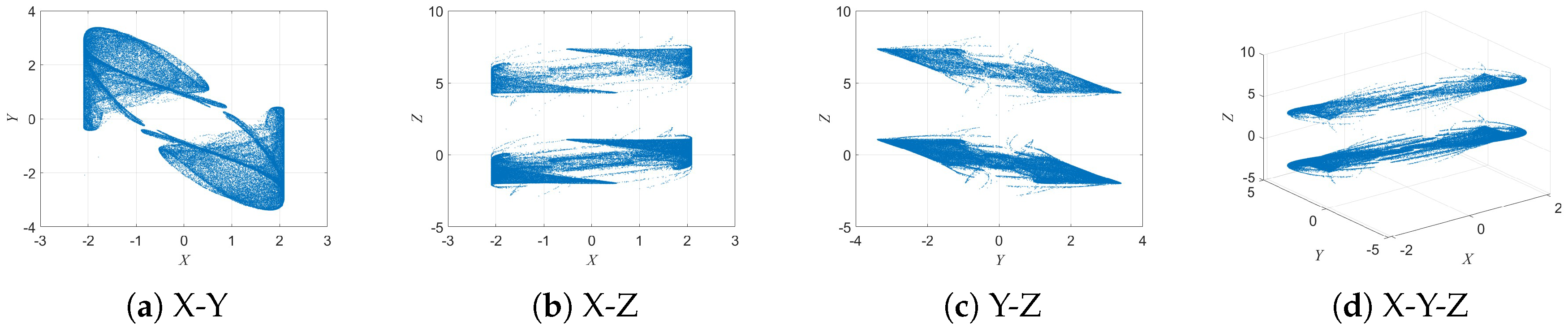
To verify the existence of echo attractor structures in the 3D-DEMM, the initial conditions were fixed as $x_0=0.8147$, $y_0=0.5468$, and $z_0=0.0975$, along with parameter a. Parameter b was then varied to observe the evolution of attractor patterns in the phase space. The results are illustrated in Figure 5, Figure 6 and Figure 7.

With parameter a fixed, the attractor patterns of the 3D-DEMM under different values of parameter b were analyzed. As shown in Figure 5, when $b=5.547$, the system exhibits a single independent attractor structure in both the $X-Z$ and $Y-Z$ planes, indicating relatively simple dynamic behavior at this stage.

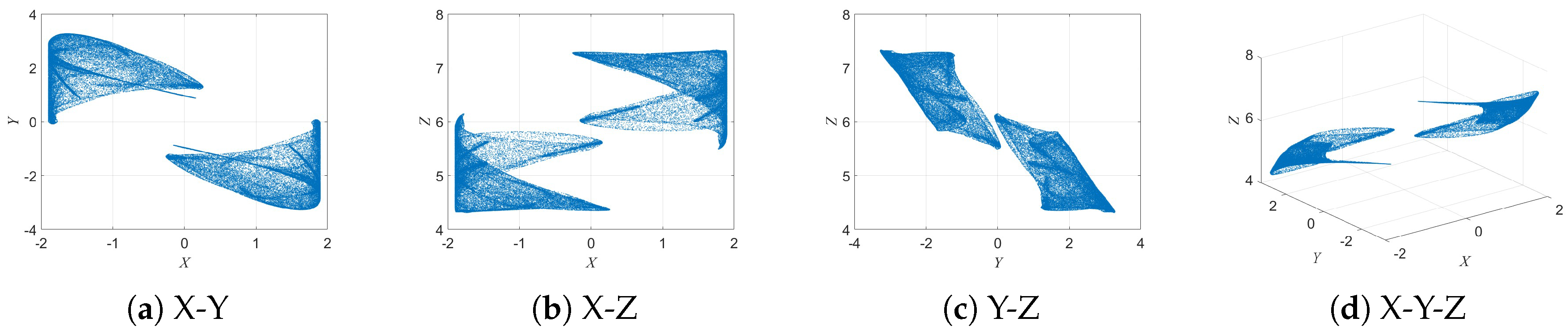
As parameter b increases to $5.476$, as illustrated in Figure 6, two independent and disconnected attractors emerge in the $X-Z$ and $Y-Z$ planes. These attractors share highly similar geometrical shapes and can therefore be regarded as typical echo attractors, reflecting the mirror symmetry and diversity of the system under parameter perturbations.

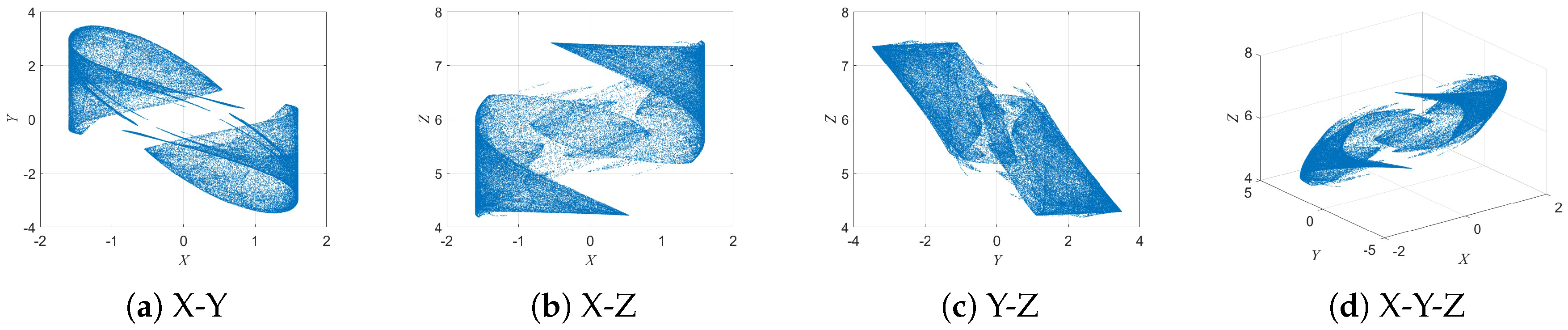
When parameter b is further increased to $5.548$, as shown in Figure 7, the system displays four independent and disconnected attractors in the $X-Z$ and $Y-Z$ planes, with all four maintaining similar geometric structures. This gradual evolution from a single attractor to multiple echo attractors reveals the complex bifurcation behavior of the 3D-DEMM and its strong sensitivity to parameter variations.

As parameter b continues to increase, the number of attractors generated by the system grows, while their geometrical structures remain highly consistent. This indicates that the 3D-DEMM can produce multiple attractor configurations with repeated echo characteristics under different parameter conditions. From the perspective of chaos theory, such “echo-like” behavior not only confirms the existence of echo attractors in the system but also demonstrates the complexity and self-similarity of its dynamic evolution. More importantly, the emergence of echo attractors implies that the system can maintain structural similarity across different scales or parameter conditions, which is closely related to fractal properties and scale invariance. This phenomenon not only reflects the richness and diversity of the system’s attractor set but also reveals the stable repetitive patterns embedded in its long-term evolution. Such characteristics hold potential application value in chaotic signal modeling, pattern recognition, and neuromorphic computing.

3.1.3. Analysis of the Coexisting Attractor

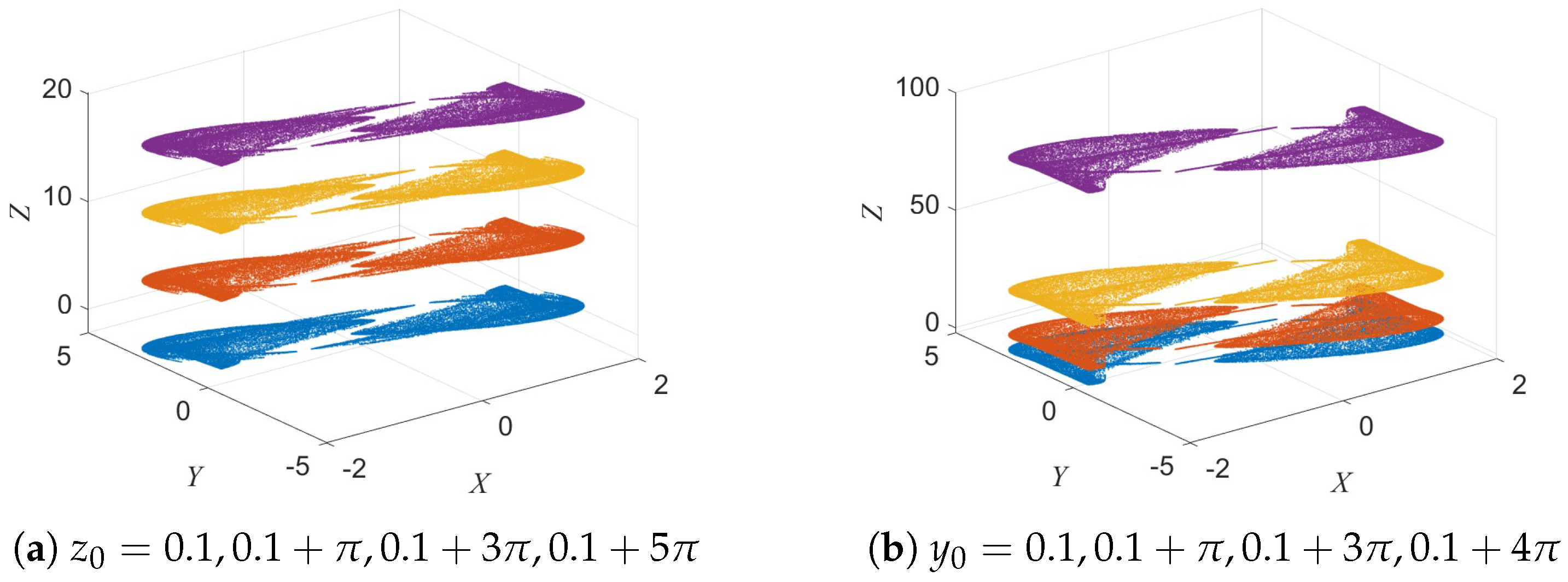
In nonlinear dynamic systems, coexisting attractors refer to the phenomenon where, under the same parameter conditions, the system may evolve into different attractor regions depending on the initial states, thereby exhibiting multiple dynamic behaviors simultaneously. In this section, the potential coexisting attractors of the 3D-DEMM system are analyzed to reveal its dynamic diversity. The initial conditions are set as $x_0=0.1$, $y_0=0.1$, and $z_0=0.1$, with parameters $a=1.9$ and $b=5.5$. By varying the initial values of $y_0$ and $z_0$, the attractor patterns of the 3D-DEMM are observed. The results are illustrated in Figure 8.

Figure 8 illustrates the formation of coexisting attractors in the 3D-DEMM system. Specifically, Figure 8a shows the attractor patterns under different initial values of $z_0$ ($z_0=0.1,z_0=0.1+\pi ,z_0=0.1+3\pi ,z_0=0.1+5\pi$), where it can be observed that the system evolves into different attractor regions depending on the initial conditions, exhibiting multiple coexisting dynamic behaviors.

Figure 8b presents the attractors for different initial values of $y_0$ ($y_0=0.1$, $y_0=0.1+\pi$, $y_0=0.1+3\pi ,y_0=0.1+4\pi$), further demonstrating the high sensitivity of the system to initial states, as different initial conditions lead the system to converge to distinct stable trajectories. These results clearly confirm the existence of coexisting attractors in the 3D-DEMM system and highlight its dynamic diversity.

3.2. Bifurcation Diagram Analysis

To investigate the dynamic evolution characteristics of the 3D-DEMM system, this section analyzes the system’s behavior under different parameter conditions using bifurcation diagrams. Bifurcation diagrams are an intuitive and effective tool for illustrating how the system transitions among stable states, periodic orbits, quasi-periodic orbits, and chaotic behavior as the parameters vary. The results of the bifurcation diagram analysis are shown in Figure 9, Figure 10 and Figure 11.

During the analysis, parameter b and the initial conditions were kept fixed, while the value of parameter a was gradually varied. The stable states or attractor trajectories of the system were recorded for each parameter value. From the bifurcation diagram, it can be clearly observed that the system gradually transitions from simple periodic orbits to complex quasi-periodic and even chaotic states. The system exhibits pronounced period-doubling bifurcations, eventually entering chaotic regions, where echo attractors and coexisting multiple attractors may also appear.

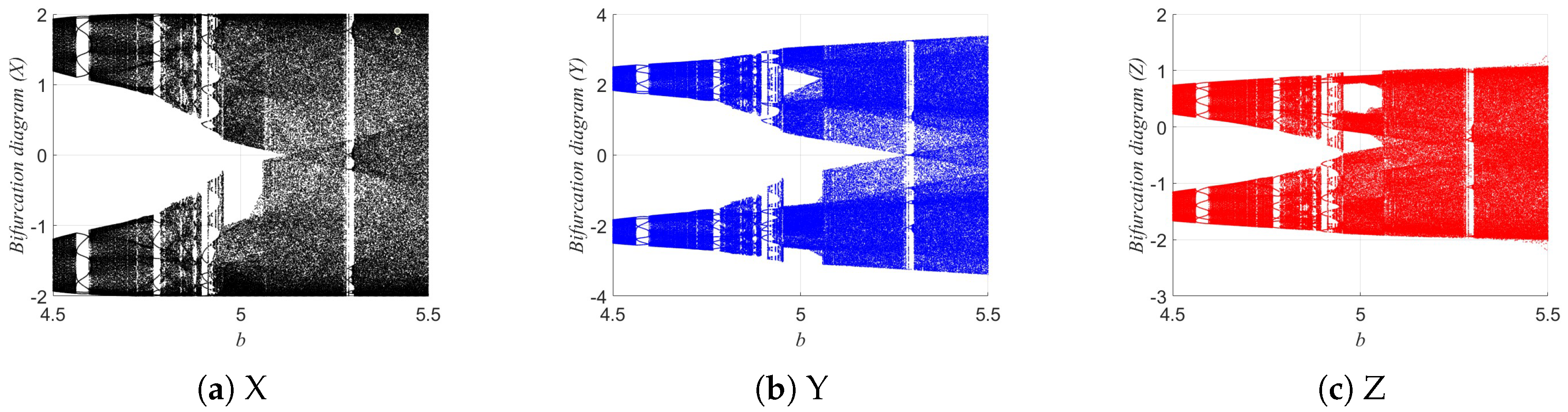
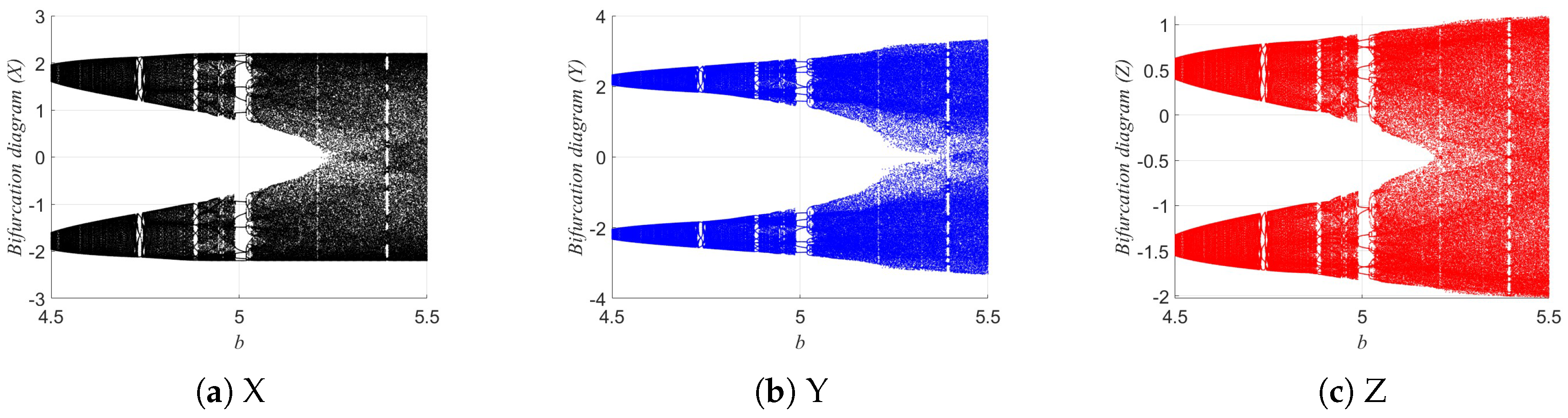
3.3. Lyapunov Exponent Analysis

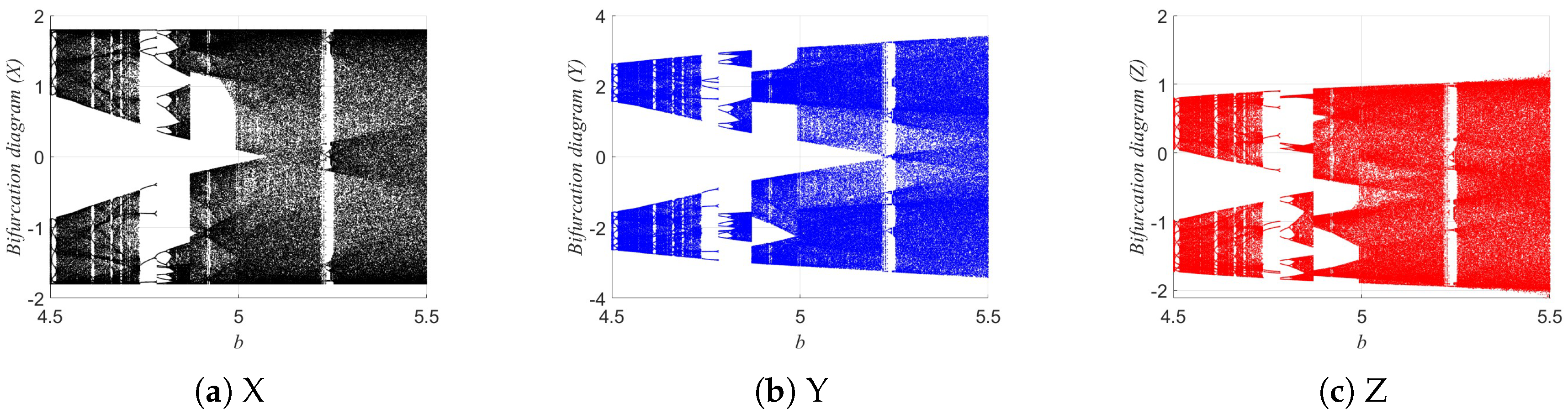
The Lyapunov exponents (LEs) of the 3D-DEMM were analyzed. The Lyapunov exponent is an important indicator for measuring a dynamic system’s sensitivity to initial conditions, reflecting whether system trajectories diverge or converge exponentially over time. If the system has a positive maximum Lyapunov exponent, it indicates typical chaotic behavior. The Lyapunov exponent analysis of the 3D-DEMM is shown in Figure 12. The value of b ranges from 4.5 to 5.5, with an iteration step size of $0.001$.

During the analysis, certain system parameters are fixed, while the Lyapunov exponents are calculated under different parameter conditions, and their variation with respect to the parameters is plotted. The results show that within a specific parameter range, the system’s maximum Lyapunov exponent is positive, indicating that the 3D-DEMM exhibits significant chaotic behavior. Moreover, when b is in the range of 5.3–5.5, the system shows two positive Lyapunov exponents, demonstrating hyperchaotic behavior. These results confirm the complex dynamic nature of the 3D-DEMM and its sensitivity to system parameters.

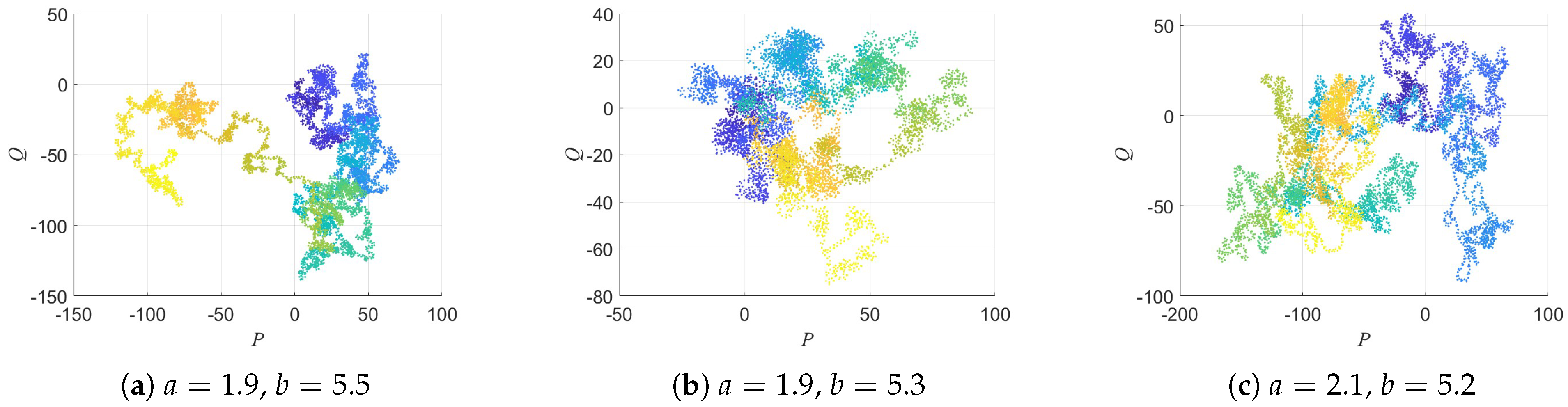
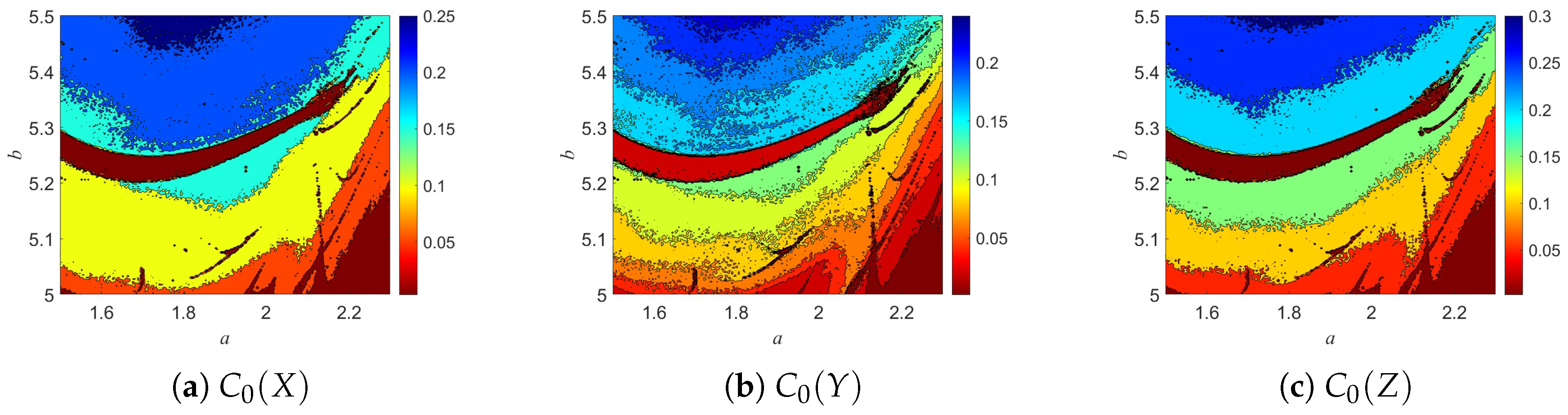
3.4. Gottwald–Melbourne 0–1 Test

The 0–1 test for chaos, proposed by Gottwald and Melbourne [38], is a tool that directly determines whether a system exhibits chaotic behavior based on time-series data. This method does not rely on the system’s differential equations or phase-space reconstruction; instead, it only requires the input time series to output a value close to either 0 or 1: a result close to 0 indicates that the system is in a periodic or quasi-periodic state, while a result close to one suggests that the system is chaotic. Moreover, if the system is chaotic, its trajectories exhibit a diffusion pattern similar to Brownian motion.

In the 0–1 test, the original time series generated by the system is first projected into two new sequences, $p\left(n\right)$ and $q\left(n\right)$, via specific transformation formulas. If the original sequence is periodic or quasi-periodic, the trajectory in the $(p,q)$ plane remains confined within a bounded region, displaying oscillatory behavior. In contrast, if the sequence is chaotic, the $(p,q)$ trajectory continuously diffuses outward, resembling the irregular wandering of Brownian motion. For example, taking sequence X, the 0–1 test results of the 3D-DEMM under different parameters are illustrated in Figure 13, while the quantitative results of the 0–1 test are presented in

Table 1. Gottwald–Melbourne 0–1 test results of the 3D-DEMM.

a	b	X	Y	Z	Average
1.83	5.12	0.9960	0.9965	0.9976	0.9967
2.07	5.48	0.9975	0.9974	0.9979	0.9976
1.56	5.21	0.9972	0.9976	0.9980	0.9976
2.21	5.36	0.9973	0.9978	0.9978	0.9976
1.72	5.09	0.9946	0.9957	0.9966	0.9956
1.95	5.42	0.9974	0.9979	0.9980	0.9977
2.32	5.36	0.9965	0.9932	0.9955	0.9950
1.63	5.33	0.9977	0.9973	0.9976	0.9975
2.11	5.25	0.9958	0.9962	0.9968	0.9962
1.87	5.47	0.9978	0.9974	0.9979	0.9977

.

Figure 13 shows the 0–1 test results of the 3D-DEMM system under different parameter combinations. It can be observed that the trajectory of sequence X in the $(p,q)$ plane exhibits diffusion, resembling a Brownian-motion-like random walk. This trajectory characteristic is a typical signature of chaotic dynamics. The results demonstrate that, under the tested parameters, the sequence of the 3D-DEMM system is in a chaotic state.

Table 1 presents the Gottwald–Melbourne 0–1 test results of the 3D-DEMM system under different parameter combinations $(a,b)$. As shown in the table, the test values for all parameter sets are close to 1 (mostly ranging from $0.9950$ to $0.9980$), indicating that the system is in a chaotic state under these parameter conditions.

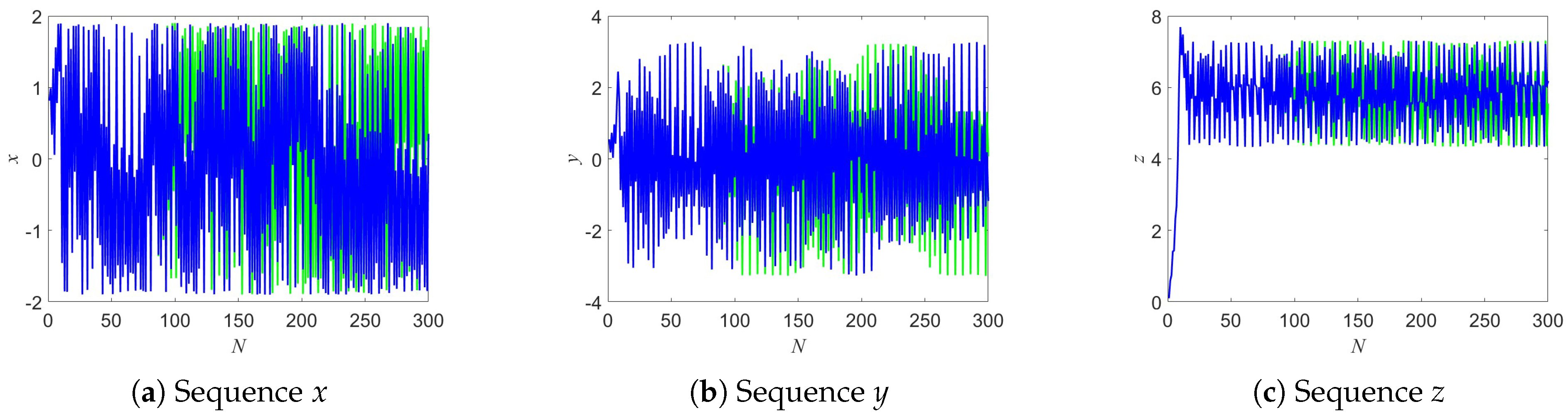
3.5. Sensitivity Analysis

In this section, we investigate both the initial value sensitivity and parameter sensitivity of the 3D discrete echo-memristor map (3D-DEMM). The system is initialized with fixed values $x\left(1\right)=0.8147$, $y\left(1\right)=0.5468$, $z\left(1\right)=0.0975$ and parameters $a=2.9$, $b=5.3$.

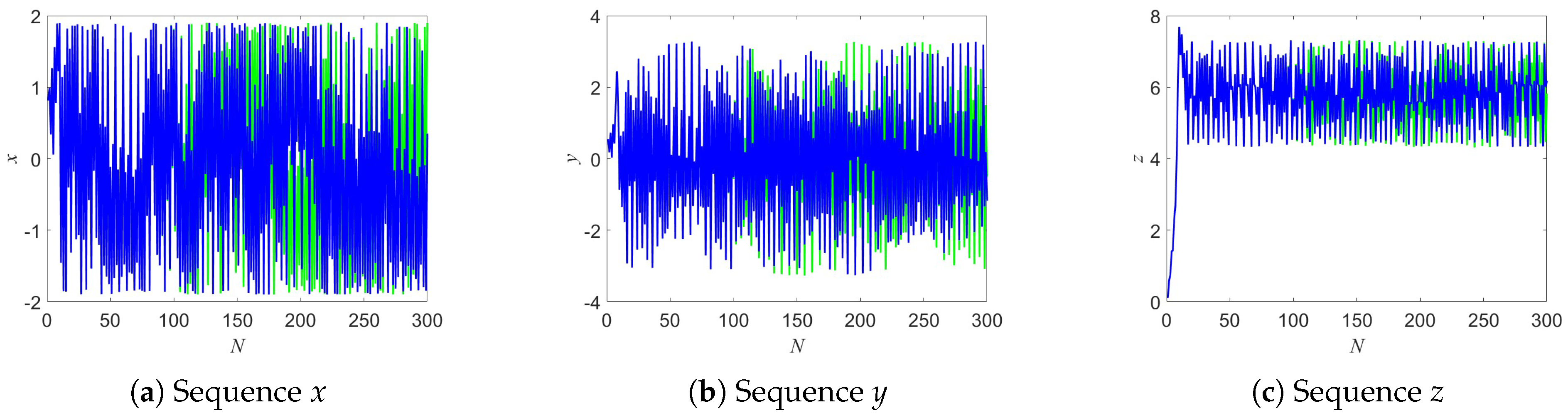
To examine the initial value sensitivity, a tiny perturbation is added to the initial condition of x, i.e., $x\left(1\right)=x\left(1\right)+{10}^{-10}$. The evolution of the three sequences under this perturbation is shown in Figure 14, illustrating the high sensitivity of the system to initial conditions, which is a hallmark of chaotic behavior.

Similarly, the parameter sensitivity is tested by introducing a small perturbation to the system parameter a, i.e., $a=a+{10}^{-10}$. Figure 15 presents the resulting trajectories of the three sequences, demonstrating that even an infinitesimal change in the system parameter can lead to significant deviations over time.

These results confirm that the 3D-DEMM exhibits strong sensitivity both to its initial conditions and to its parameters, highlighting its potential for applications in secure communications and chaotic encryption systems.

3.6. NIST Test

To verify the randomness and security of the output sequences generated by the proposed 3D-DEMM system, NIST randomness tests were conducted on the sequences. The NIST tests are important tools for evaluating whether the output sequences of cryptographic and chaotic systems meet statistical randomness criteria, including multiple subtests such as the frequency test, run test, cumulative sum test, and discrete Fourier transform test. The results of the NIST tests are summarized in

Table 2. NIST analysis of the 3D-DEMM.

Test Name	$\mathit{a}=2.1$, $\mathit{b}=5.2$			$\mathit{a}=1.9$, $\mathit{b}=5.3$
	X	Y	Z	X	Y	Z
	p-Value	p-Value	p-Value	p-Value	p-Value	p-Value
Rank	0.611108	0.663130	0.330628	0.151616	0.072289	0.199580
Universal	0.559523	0.098036	0.414525	0.199580	0.953553	0.131500
Random Excursions	0.242986	0.242986	0.186566	0.585209	0.437274	0.585209
Serial	0.509162	0.811993	0.113706	0.611108	0.953553	0.098036
Linear Complexity	0.663130	0.460664	0.663130	0.174249	0.174249	0.927083
Block Frequency	0.027405	0.371101	0.005659	0.330628	0.714660	0.509162
Cumulative Sums	0.714660	0.663130	0.953553	0.258961	0.414525	0.460664
Longest Run	0.559523	0.131500	0.953553	0.044942	0.002244	0.559523
Runs	0.460664	0.811993	0.509162	0.509162	0.113706	0.509162
Frequency	0.227773	0.894201	0.258961	0.953553	0.509162	0.199580
FFT	0.414525	0.663130	0.330628	0.764655	0.008120	0.013808
Approximate Entropy	0.052778	0.953553	0.714660	0.663130	0.509162	0.764655
Non-Overlapping Template	0.894201	0.811993	0.663130	0.509162	0.663130	0.611108
Random Excursions Variant	0.484646	0.311542	0.242986	0.392456	0.834308	0.689019
Overlapping Template	0.001050	0.663130	0.032381	0.509162	0.199580	0.113706

.

With parameters a and b fixed, the chaotic sequence is iterated 10,000,000 times. The generated sequence is first converted into pixel values and then further transformed into binary form as the input for the NIST test. In the NIST testing process, the binary sequence is divided into 45 groups, each containing 1,000,000 binary data points.

In the experiments, the system parameters and initial conditions were fixed, and the discrete sequences generated by the 3D-DEMM under different operating states were collected and analyzed using the NIST test suite. The results showed that the vast majority of the subtests passed the significance level of 0.001, indicating that the system’s output sequences possess good statistical randomness.

3.7. Complexity Analysis

In this section, the complexity of the 3D-DEMM system is analyzed. System complexity is an important indicator for measuring the degree of chaos and regularity in nonlinear dynamic systems, and commonly used methods include SE complexity analysis and $C_0$ complexity analysis. These methods can quantitatively characterize the dynamic complexity of a system.

$SE$ provides a measure of the complexity and unpredictability of a signal by quantifying the distribution of its frequency components. Chaotic signals typically exhibit high uncertainty and complexity, characterized by a broad frequency spectrum and a relatively uniform energy distribution. These properties result in higher $SE$ values, which reflect the richness and randomness of the signal’s frequency content. Therefore, $SE$ serves as an effective tool for revealing the dynamic behavior and complexity of signals, particularly for chaotic systems. The results of the SE complexity analysis are presented in Figure 16.

The $C_0$ complexity quantifies a signal’s complexity by comparing the mean squared error between an original signal $\Psi \left(n\right)$ and a reconstructed signal $\overline{\Psi }\left(n\right)$. Values closer to one indicate higher complexity, whereas lower values indicate simpler signals. The $C_0$ complexity analysis results of the 3D-DEMM are shown in Figure 17.

To further verify the performance of the 3D-DEMM system, its complexity metrics were compared with several classical memristor-based chaotic maps, as shown in

Table 3. Comparative analysis of complexity.

Chaotic Maps	Range of Parameters	$\mathit{SE}$	${\mathit{C}}_0$
3D-DEMM	$a\in [5.3,5.5],b\in [1.5,2.3]$	0.8649	0.2038
3D-HMBM [12]	$k\in [-4,-2]\cup [2,4],\epsilon \in [-8,8],\eta \in [-0.9,0.8]$	0.5977	0.3318
2D-MCSM [23]	$n\in [1,10],r\in [1.8,3.7]$	0.5590	0.0485
3D-IMHM [39]	$a\in [0.1,1.7],b\in [-0.2,0.7]$	0.1956	0.0440

.

It can be seen that the 3D-DEMM exhibits higher values in both $SE$ and $C_0$ complexity measures, indicating greater uncertainty in its dynamic behavior and richer structural complexity. Compared with other systems, the higher $SE$ value reflects a more uniform energy distribution across the frequency spectrum and more widely spread frequency components, demonstrating stronger randomness. The higher $C_0$ value indicates that the system trajectories cover the phase space more thoroughly and exhibit more complex structures. These comparative results fully demonstrate that the 3D-DEMM surpasses existing classical memristor-based chaotic maps in terms of chaotic complexity and dynamic diversity, providing a solid foundation for high-performance chaotic signal generation.

4. DSP Implementation

DSP is a processor specifically designed for real-time digital signal processing. Its architecture is deeply optimized for core operations such as multiply–accumulate and iterative computation and is particularly suited to the dynamic evolution requirements of continuous or discrete chaotic systems. Enabled by its real-time response capability and high-efficiency computing performance, the DSP platform is established as a core vehicle for facilitating the transition of chaotic systems from theoretical models to engineering applications.

To realize the engineering implementation of the chaotic map proposed in this paper, an experimental platform with TMS320F28335 DSP as the core is adopted. The real-time iterative computation of the chaotic map is undertaken by the DSP; the conversion from digital sequences to analog signals is accomplished by the DAC8552; the output waveforms are captured in real time by the oscilloscope; and algorithm debugging and data monitoring are synchronously implemented by the computer.

The experimental process of implementing the proposed chaotic system on the DSP platform is illustrated in Figure 18a, which provides a complete depiction of the signal flow and hardware interconnections. During the experiment, the system parameters were configured as $a=1.95$, $b=5.45$, with initial conditions $x_0=0.1$, $y_0=0.1$, and $z_0=0.1$. Under these settings, the DSP performed real-time iterative computations of the chaotic map, and the generated voltage signals were converted into analog waveforms through the DAC module.

As shown in Figure 18c, the chaotic attractor captured by the oscilloscope exhibits high morphological consistency with the MATLAB simulation results (https://www.mathworks.com/products/matlab.html) presented in Figure 18b. This close correspondence not only verifies the mathematical accuracy and dynamic authenticity of the proposed mapping model but also demonstrates its feasibility for real-time engineering realization.

The physical experimental setup of the DSP-based hardware platform is displayed in Figure 18d. From circuit board deployment and signal routing to the stable attractor waveforms displayed on the oscilloscope, each stage intuitively validates the successful hardware realization of the chaotic system. These results confirm that the proposed model can be effectively migrated from numerical simulation to physical implementation, providing a solid foundation for subsequent applications in secure communication and chaotic signal generation.

5. Conclusions

In this paper, a novel memristor-based three-dimensional discrete echo-memristor map (3D-DEMM) chaotic system was proposed, and its dynamic characteristics and hardware implementation were systematically investigated. The results demonstrate that the 3D-DEMM can generate complex dynamic behaviors with self-similar attractor structures under different parameters and initial conditions, producing attractors of similar shapes at different amplitudes, which reflects typical echo-chaotic characteristics. Through comprehensive analyses, including attractor visualization, Lyapunov exponent calculation, the 0–1 test, and NIST randomness tests, the chaoticity and self-similarity of the system were verified. Furthermore, the attractors of the 3D-DEMM were realized on a DSP platform for discrete-time hardware simulation and real-time operation. Overall, the proposed 3D-DEMM system provides new theoretical insights and practical methods for memristor-based chaotic signal generation, with potential applications in information security and signal processing.

In addition, although the proposed 3D-DEMM system exhibits promising performance, the current research is still limited to simulation and DSP-based implementation. Future work could further investigate its performance in large-scale hardware integration and energy efficiency under practical conditions. Beyond information security, the unique echo-chaotic characteristics of the system also hold potential for applications in random number generation, secure communications, and advanced signal processing. Future research may also extend the system to higher-dimensional or hybrid forms and explore its potential in neuromorphic computing and emerging hardware platforms.