Adaptive PPO-RND Optimization Within Prescribed Performance Control for High-Precision Motion Platforms
Abstract
1. Introduction
- An innovative PPO-RND algorithm is proposed, which integrates Proximal Policy Optimization (PPO) and Random Network Distillation (RND) methods by introducing an adaptive beta parameter to dynamically regulate the balance between exploration and convergence. Traditional PPO algorithms typically employ a fixed strategy for exploration-exploitation trade-offs, whereas the proposed method adaptively adjusts beta to optimize the degree of exploration in real-time based on the system’s learning progress and reward feedback.
- A dynamically optimized control framework is innovatively proposed by combining Prescribed Performance Control (PPC) with the adaptive beta PPO-RND algorithm, and implemented on a PMLSM platform. Unlike traditional PPC methods, this approach enables real-time optimization of controller parameters while simultaneously managing dynamic system errors. Experimental results indicate that the proposed method significantly improves control accuracy and enhances system stability and robustness in complex environments.
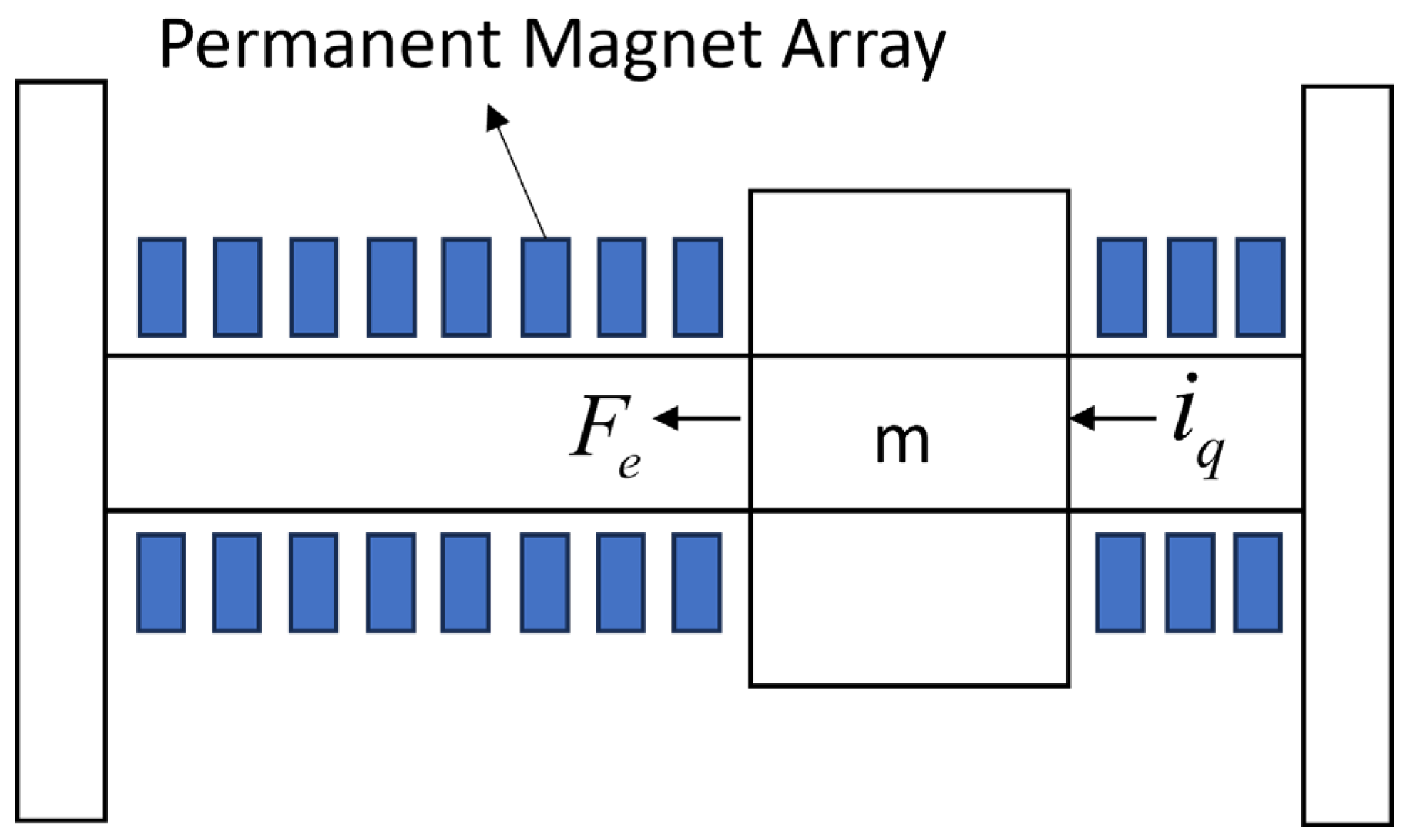
2. Modeling
3. Control Strategy
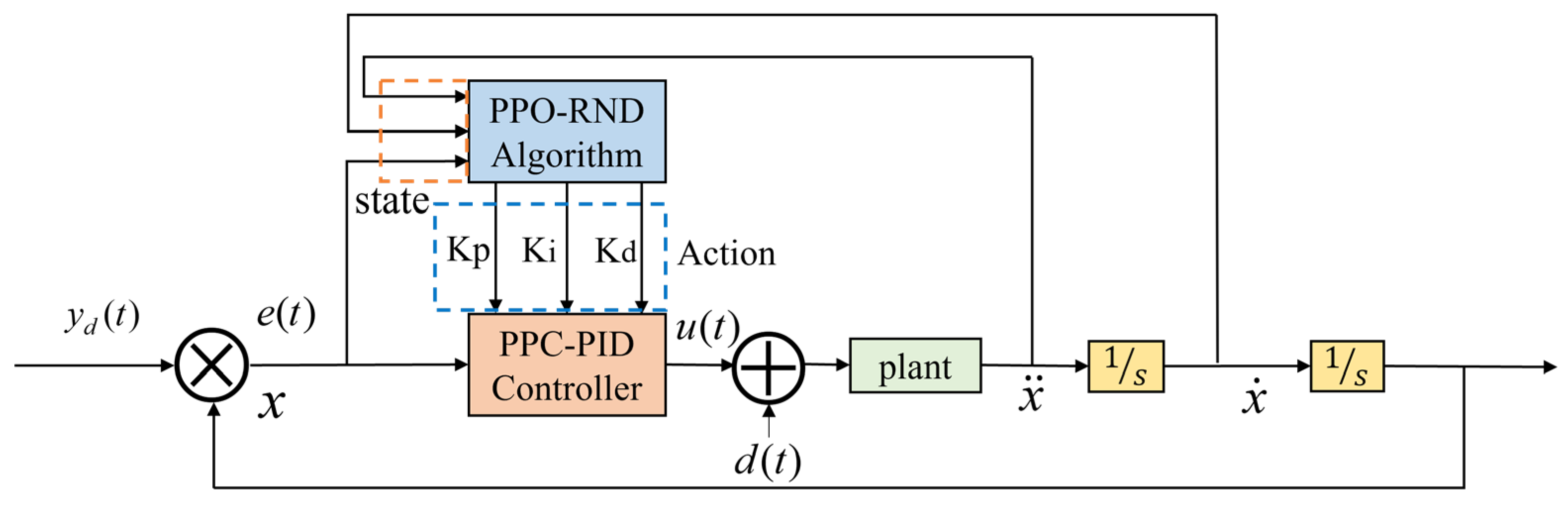
3.1. Based on the PPO-RND Prescribed Performance Control Architecture
3.2. The Structure of Prescribed Performance Control
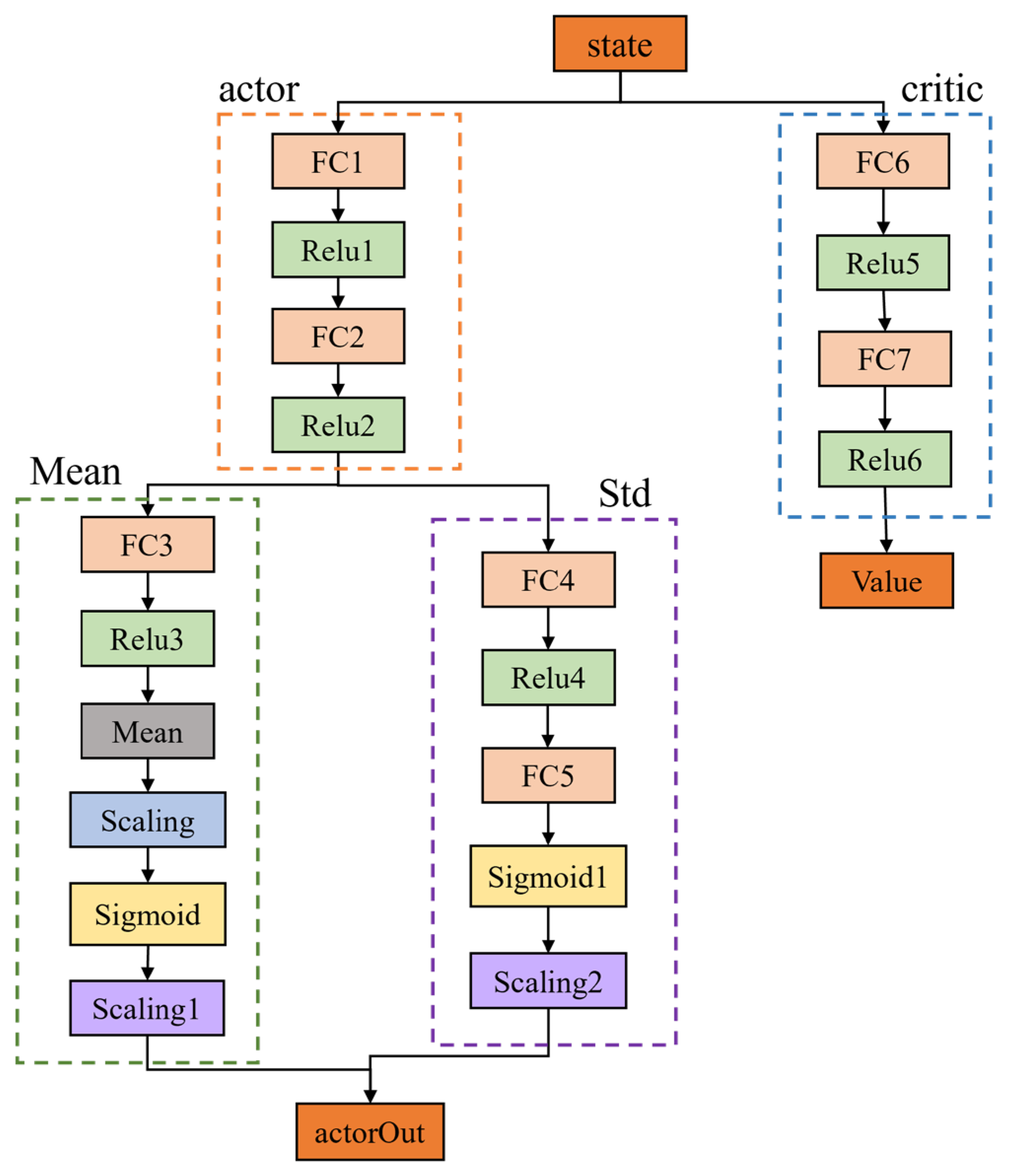
3.3. Proximal Policy Optimization
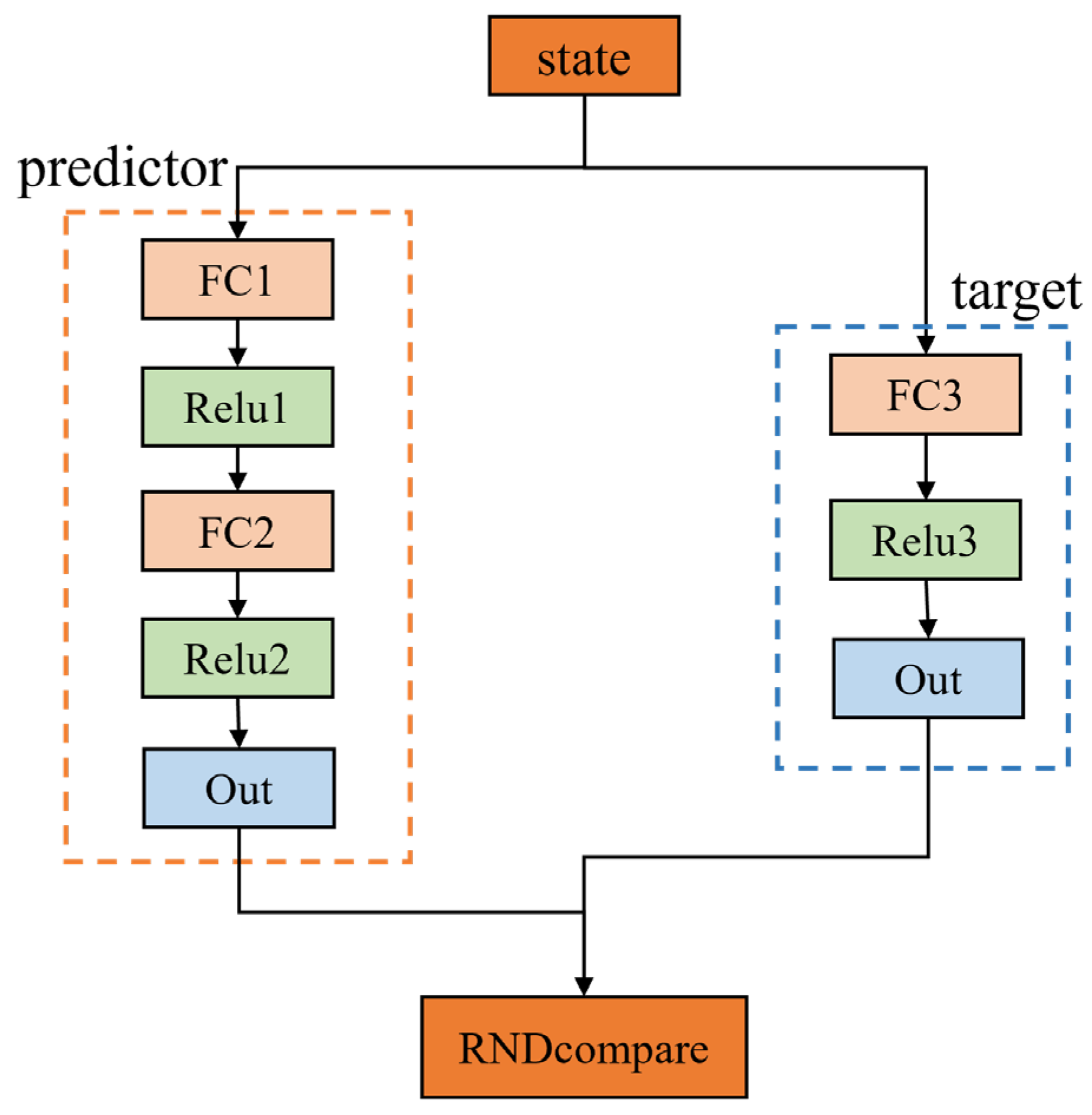
3.4. Random Network Distillation
4. Analysis of the Stability
5. Experiment
5.1. Experiment Platform
5.2. Reward
5.3. Experiment Results
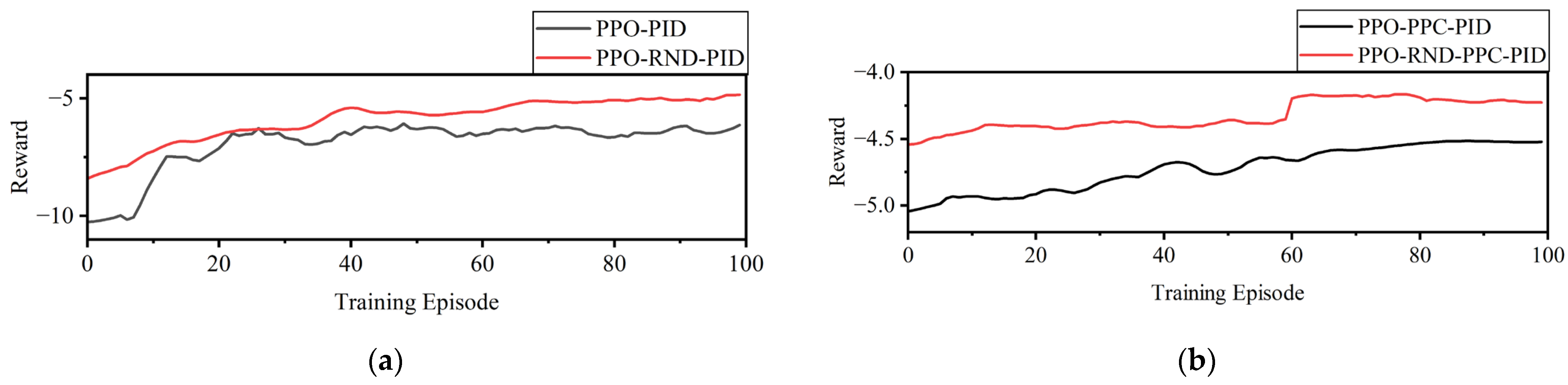
- First, the training reward curves of different methods are analyzed to evaluate convergence speed and stability.
- Second, control error metrics of various methods under identical reference trajectories are compared to validate the tracking performance of the proposed approach.
5.3.1. Reward Curves
5.3.2. System Performance
- The Mean Absolute Error (MAE) metric reflects the average deviation of the system throughout its entire operation, intuitively gauging the overall tracking accuracy, as given by Equation (33).
- The Root Mean Square Error (RMSE), which is more sensitive to large-magnitude errors, reflects the system’s control capability under extreme deviation conditions, as given by Equation (34).
- The metric represents an upper error bound at a high confidence level. It quantifies the maximum error within which the controller operates for the vast majority (95th percentile) of the time, reflecting the worst-case precision of the system under normal operating conditions. A smaller indicates that most of the time the controller maintains a low tracking deviation, as given by Equation (35).
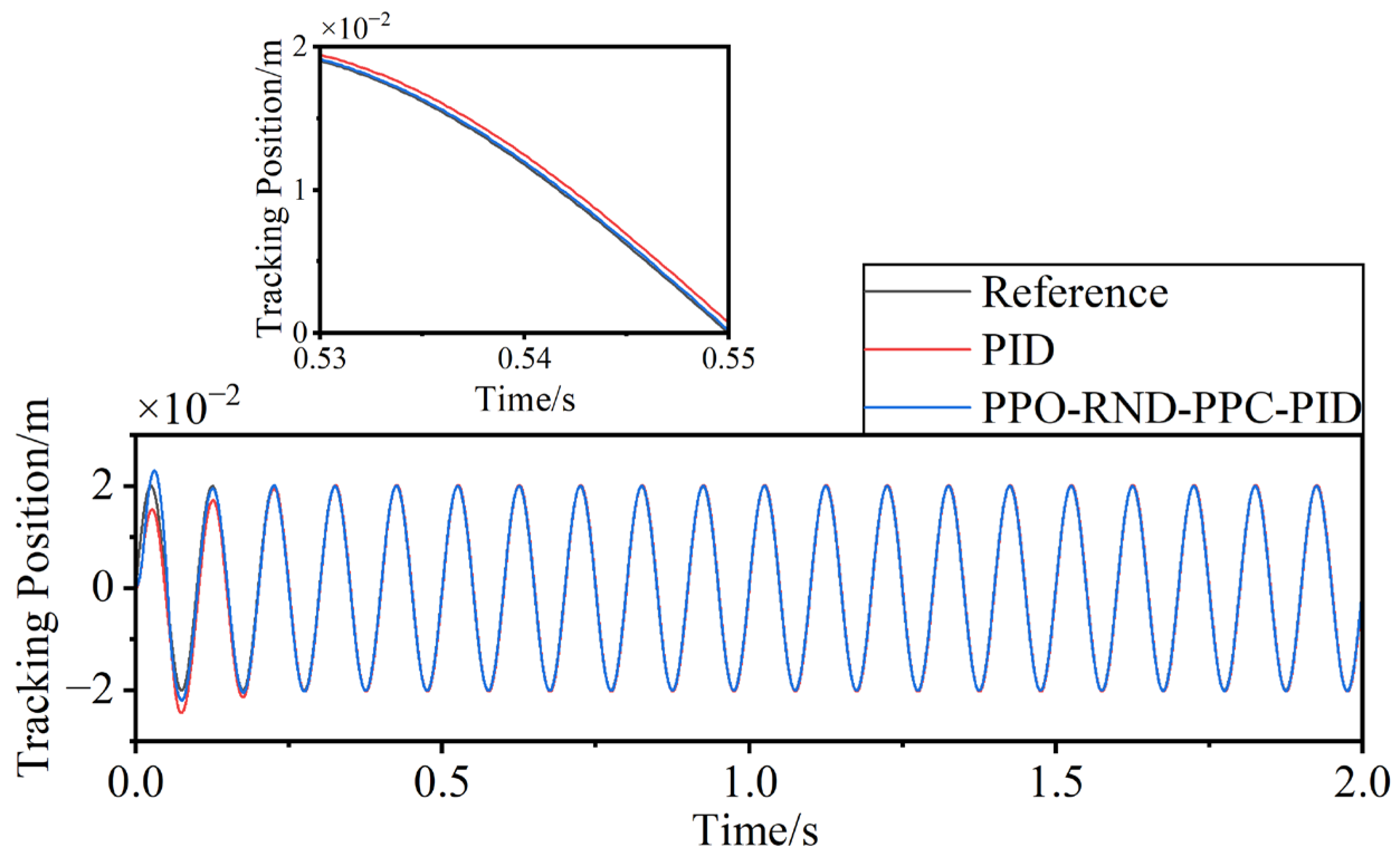
- The steady-state per-cycle root-mean-square error evaluates the periodic tracking consistency of the system during steady operation. For a reference trajectory with period T, the RMS error of the k-th cycle is computed as given by Equation (36).and the steady-state performance is expressed as the mean and standard deviation of the last cycles, as given by Equations (37) and (38).where T is the period of the reference trajectory, denotes the RMS error in the k-th cycle, and is the number of cycles used for steady-state evaluation. A smaller and indicate better steady-state precision and cycle-to-cycle stability. Under identical reference trajectories and simulation conditions, a comparative analysis of closed-loop tracking performance was conducted across six methods (PID, PID-PPC, PPO-PID, PPO-PPC-PID, PPO-RND-PID, PPO-RND-PPC-PID), with a focus on evaluating their steady-state error. To provide an intuitive visual comparison, Figure 8 contrasts the tracked trajectories of the basic PID controller and the proposed PPO-RND-PPC-PID controller against the reference path, clearly illustrating the improvement in tracking accuracy. The control error trajectories over time are illustrated in Figure 9, while the error statistics (MAE and RMSE) within the steady-state phase are summarized in Table 2.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kailath, T.; Schaper, C.; Cho, Y.; Gyugyi, P.; Norman, S.; Park, P.; Boyd, S.; Franklin, G.; Saraswat, K.; Moslehi, M.; et al. (Eds.) Control for advanced semiconductor device manufacturing: A case history. In Control System Applications; CRC Press: Boca Raton, FL, USA, 2019; pp. 67–83. [Google Scholar]
- Song, F.; Liu, Y.; Dong, Y.; Chen, X.; Tan, J. Motion control of wafer scanners in lithography systems: From setpoint generation to multistage coordination. IEEE Trans. Instrum. Meas. 2024, 73, 7508040. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Moreno-Valenzuela, J. PID control of quadrotor UAVs: A survey. Annu. Rev. Control 2023, 56, 100900. [Google Scholar] [CrossRef]
- Chai, T.; Zhou, Z.; Cheng, S.; Jia, Y.; Song, Y. Industrial metaverse-based intelligent PID optimal tuning system for complex industrial processes. IEEE Trans. Cybern. 2024, 54, 6458–6470. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.E. Precision Six Degrees of Freedom Magnetically-Levitated Photolithography Stage. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, UK, 1998. [Google Scholar]
- Butler, H. Position control in lithographic equipment: An enabler for current-day chip manufacturing. IEEE Control Syst. 2011, 31, 28–47. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, P.; Jiang, B.; Yan, H. Research trends in methods for controlling macro-micro motion platforms. Nanotechnol. Precis. Eng. 2023, 6, 035001. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H.; Wang, X. Fuzzy PID control of parallel 6-DOF motion platform. In Proceedings of the 2023 5th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), Chengdu, China, 19–21 May 2023. [Google Scholar]
- Liu, H.; Zeng, Z.; Yang, X.; Zou, Y.; Liu, X. A control strategy for shipboard stabilization platforms based on a fuzzy adaptive proportional–integral–derivative (PID) control architecture. Mech. Sci. 2025, 16, 325–342. [Google Scholar] [CrossRef]
- Tian, H.; An, J.; Ma, H.; Tian, B. Trajectory planning and adaptive fuzzy PID control for precision in robotic vertebral plate cutting: Addressing force dynamics and deformation challenges. J. Intell. Robot. Syst. Theory Appl. 2024, 110, 161. [Google Scholar] [CrossRef]
- Noordin, A.; Mohd Basri, M.A.; Mohamed, Z. Adaptive PID control via sliding mode for position tracking of quadrotor MAV: Simulation and real-time experiment evaluation. Aerospace 2023, 10, 512. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, H.; He, H. Research on genetic algorithm for feedforward parameter tuning in XY motion platform. In Proceedings of the 2023 24th International Conference on Electronic Packaging Technology (ICEPT), Shihezi, China, 8–11 August 2023. [Google Scholar]
- Aboud, H.; Amouri, A.; Cherfia, A.; Bouchelaghem, A.M. Fractional-order PID controller tuned by particle swarm optimization algorithm for a planar CDPR control. Indones. J. Electr. Eng. Comput. Sci. 2024, 33, 1500–1510. [Google Scholar] [CrossRef]
- Sabo, A.; Bawa, M.; Yakubu, Y.; Ngyarmunta, A.A.; Aliyu, Y.; Musa, A.; Katun, M. PID Controller Tuning for an AVR System Using Particle Swarm Optimisation Techniques and Genetic Algorithm Techniques: A Comparison-Based Approach. Vokasi Unesa Bull. Eng. Technol. Appl. Sci. 2025, 2, 270–280. [Google Scholar] [CrossRef]
- Ramadhani, N.; Ma’arif, A.; Çakan, A. Implementation of PID control for angular position control of dynamixel servo motor. Control Syst. Optim. Lett. 2024, 2, 8–14. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Song, X.; Zheng, Z.; Tao, W.; Che, J. A BP-neural-network-based PID control algorithm of shipborne stewart platform for wave compensation. J. Mar. Sci. Eng. 2024, 12, 2160. [Google Scholar] [CrossRef]
- Ghasemi, M.; Rahimnejad, A.; Gil, M.; Akbari, E.; Gadsden, S.A. A self-competitive mutation strategy for differential evolution algorithms with applications to proportional–integral–derivative controllers and automatic voltage regulator systems. Decis. Anal. J. 2023, 7, 100205. [Google Scholar] [CrossRef]
- Liu, H.; Yu, Q.; Wu, Q. PID control model based on back propagation neural network optimized by adversarial learning-based grey wolf optimization. Appl. Sci. 2023, 13, 4767. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, Q.; Xie, B. Application research of intelligent PID parameter optimization algorithm for XY linear motor motion platform in wire bonder. In Proceedings of the 2024 25th International Conference on Electronic Packaging Technology (ICEPT), Tianjin, China, 7–9 August 2024. [Google Scholar]
- Azeez, M.I.; Abdelhaleem, A.M.M.; Elnaggar, S.; Moustafa, K.A.F.; Atia, K.R. Optimization of PID trajectory tracking controller for a 3-DOF robotic manipulator using enhanced artificial bee colony algorithm. Sci. Rep. 2023, 13, 11164. [Google Scholar] [CrossRef]
- Suid, M.H.; Ahmad, M.A. Optimal Tuning of Sigmoid PID Controller Using Nonlinear Sine Cosine Algorithm for the Automatic Voltage Regulator System. ISA Trans. 2022, 128 Pt B, 265–286. [Google Scholar] [CrossRef]
- Tumari, M.Z.; Ahmad, M.A.; Suid, M.H.; Ghazali, M.R.; Tokhi, M.O. An Improved Marine Predators Algorithm Tuned Data-Driven Multiple-Node Hormone Regulation Neuroendocrine-PID Controller for Multi-Input–Multi-Output Gantry Crane System. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1666–1698. [Google Scholar] [CrossRef]
- Li, L. A novel optimization control of gas turbine based on a hybrid method using the belbic and adaptive multi input multi output feedback control. J. Intell. Fuzzy Syst. 2023, 45, 863–876. [Google Scholar] [CrossRef]
- Basil, N.; Marhoon, H.M.; Mohammed, A.F. Evaluation of a 3-DOF helicopter dynamic control model using FOPID controller-based three optimization algorithms. Int. J. Inf. Technol. 2024, 16, 1–10. [Google Scholar] [CrossRef]
- Mok, R.H.; Ahmad, M.A. Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Eng. Sci. Technol. Int. J. 2022, 35, 101264. [Google Scholar] [CrossRef]
- Yonezawa, H.; Yonezawa, A.; Kajiwara, I. Experimental verification of active oscillation controller for vehicle drivetrain with backlash nonlinearity based on norm-limited SPSA. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2024, 238, 134–149. [Google Scholar] [CrossRef]
- Ma, D.; Chen, X.; Ma, W.; Zheng, H.; Qu, F. Neural network model-based reinforcement learning control for AUV 3-D path following. IEEE Trans. Intell. Veh. 2024, 9, 893–904. [Google Scholar] [CrossRef]
- Blais, M.A.; Akhloufi, M.A. Reinforcement learning for swarm robotics: An overview of applications, algorithms and simulators. Cogn. Robot. 2023, 3, 226–256. [Google Scholar] [CrossRef]
- Yan, L.; Liu, Z.; Chen, C.L.P.; Zhang, Y.; Wu, Z. Reinforcement learning based adaptive optimal control for constrained nonlinear system via a novel state-dependent transformation. ISA Trans. 2023, 133, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Y.; Ma, C.; Yan, X.; Jiang, D. Path-following optimal control of autonomous underwater vehicle based on deep reinforcement learning. Ocean Eng. 2023, 268, 113407. [Google Scholar] [CrossRef]
- Del Rio, A.; Jimenez, D.; Serrano, J. Comparative analysis of A3C and PPO algorithms in reinforcement learning: A survey on general environments. IEEE Access 2024, 12, 146795–146806. [Google Scholar] [CrossRef]
- Raeisi, M.; Sesay, A.B. Power control of 5G-connected vehicular network using PPO-based deep reinforcement learning algorithm. IEEE Access 2024, 12, 96387–96403. [Google Scholar] [CrossRef]
- Zhou, Z.; Mo, F.; Zhao, K.; Hao, Y.; Qian, Y. Adaptive PID control algorithm based on PPO. J. Syst. Simul. 2024, 36, 1425–1432. [Google Scholar] [CrossRef]
- Zhang, J.; Rivera, C.E.O.; Tyni, K.; Nguyen, S. AirPilot: Interpretable PPO-based DRL auto-tuned nonlinear PID drone controller for robust autonomous flights. arXiv 2024, arXiv:2404.00204. [Google Scholar] [CrossRef]
- Mikhaylova, E.; Makarov, I. Curiosity-driven exploration in VizDoom. In Proceedings of the 2022 IEEE 20th Jubilee International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 15–17 September 2022. [Google Scholar]
- Zhang, X.; Dai, R.; Chen, W.; Qiu, J. Self-supervised network distillation for exploration. Int. J. Pattern Recognit. Artif. Intell. 2023, 37, 2351021. [Google Scholar] [CrossRef]
- Zhang, G.; Xing, Y.; Zhang, W.; Li, J. Prescribed performance control for USV-UAV via a robust bounded compensating technique. IEEE Trans. Control Netw. Syst. 2025, in press. [Google Scholar] [CrossRef]
- Sui, S.; Tong, S. Finite-time fuzzy adaptive PPC for nonstrict-feedback nonlinear MIMO systems. IEEE Trans. Cybern. 2023, 53, 732–742. [Google Scholar] [CrossRef] [PubMed]
- Han, N.; Ren, X.; Zhang, C.; Zheng, D. Prescribed performance control with input indicator for robot system based on spectral normalized neural networks. Neurocomputing 2022, 492, 201–210. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Gao, K.; Xing, J.; Liu, B. High-precision dynamic tracking control method based on parallel GRU–transformer prediction and nonlinear PD feedforward compensation fusion. Mathematics 2025, 13, 2759. [Google Scholar] [CrossRef]
- Bu, X. Prescribed performance control approaches, applications and challenges: A comprehensive survey. Asian J. Control 2023, 25, 241–261. [Google Scholar] [CrossRef]

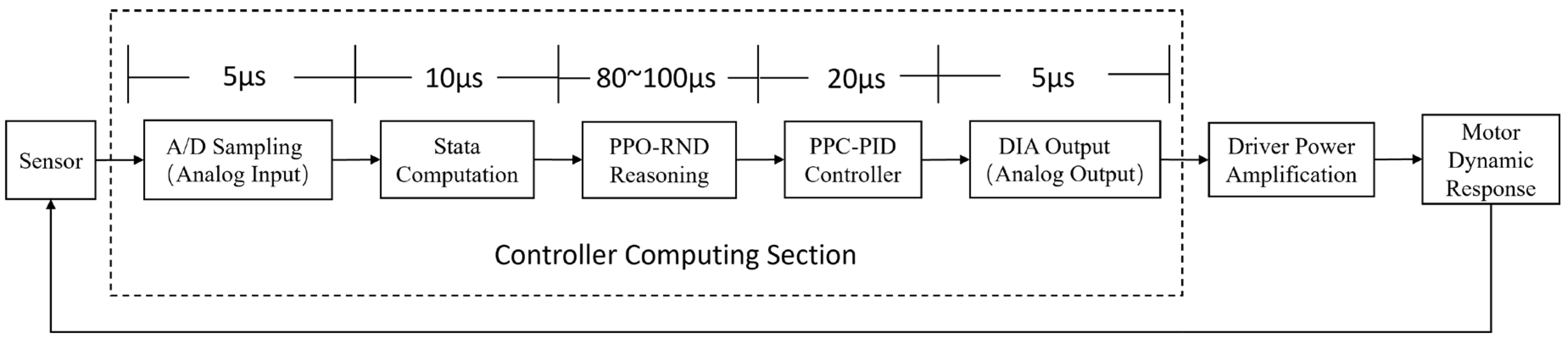


| Hardware | Parameter |
|---|---|
| Real-time simulation machine | CPU: Intel Core i9-9900KS@4.00GHz octa-core (Intel Corporation, Santa Clara, CA, USA), 8 GB DDR3 SDRAM, Operating system: RTOS |
| Analog output board | D/A conversion accuracy: 16-bit, voltage output: 16-channel, output range: +/−10 V, conversion rate: 25 V/μs, setup time: 2 μs |
| FPGA board | CPU: Kintex UltraScale XCKU040-2FFVA11561 (AMD, Santa Clara, CA, USA), Block RAM (Mb): 21.1, DSP Slices: 1920, DSP Slices: 1920 |
| Sensor | Effective accuracy: 0.5 μm |
| Driver | DC: 240 V, AC: 100–240 V, IC: 6 A, IP: 18 A |
| Algorithm | MAE (×10−3 m) | RMSE (×10−3 m) | P95 (×10−3 m) | Per-Cycle RMS (SS) (×10−3 m) |
|---|---|---|---|---|
| PID | 0.461 | 0.512 | 1.687 | 0.543 ± 0.00374 |
| PPO-PID | 0.434 | 0.482 | 1.763 | 0.522 ± 0.0105 |
| PPO-RND-PID | 0.431 | 0.501 | 0.894 | 0.457 ± 0.00425 |
| PPC-PID | 0.153 | 0.172 | 3.250 | 0.274 ± 0.046 |
| PPO-PPC-PID | 0.151 | 0.170 | 3.151 | 0.253 ± 0.353 |
| PPO-RND-PPC-PID | 0.135 | 0.154 | 0.844 | 0.158 ± 0.0148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, J.; Gao, K.; Wang, J.; Bu, S.; Liu, B.; Xing, J. Adaptive PPO-RND Optimization Within Prescribed Performance Control for High-Precision Motion Platforms. Mathematics 2025, 13, 3439. https://doi.org/10.3390/math13213439
Wang Y, Xu J, Gao K, Wang J, Bu S, Liu B, Xing J. Adaptive PPO-RND Optimization Within Prescribed Performance Control for High-Precision Motion Platforms. Mathematics. 2025; 13(21):3439. https://doi.org/10.3390/math13213439
Chicago/Turabian StyleWang, Yimin, Jingchong Xu, Kaina Gao, Junjie Wang, Shi Bu, Bin Liu, and Jianping Xing. 2025. "Adaptive PPO-RND Optimization Within Prescribed Performance Control for High-Precision Motion Platforms" Mathematics 13, no. 21: 3439. https://doi.org/10.3390/math13213439
APA StyleWang, Y., Xu, J., Gao, K., Wang, J., Bu, S., Liu, B., & Xing, J. (2025). Adaptive PPO-RND Optimization Within Prescribed Performance Control for High-Precision Motion Platforms. Mathematics, 13(21), 3439. https://doi.org/10.3390/math13213439






