A Stacking-Based Fusion Framework for Dynamic Demand Forecasting in E-Commerce

Abstract

In response to the growing complexity of e-commerce warehouse management driven by the expansion of live-streaming and cross-border businesses, this study tackles the critical challenge of product demand forecasting. We propose an intelligent forecasting approach based on a multi-model fusion framework, constructing a Stacking ensemble that integrates XGBoost, LightGBM, and CatBoost as base learners. Hyperparameter optimization is systematically conducted using grid search combined with cross-validation. To account for periodic trends, seasonal fluctuations are modeled as explicit temporal features, and a Seasonal Autoregressive Integrated Moving Average (SARIMA) model is incorporated to perform joint forecasting by capturing residual time-dependent patterns. Experimental results show that the proposed fusion model consistently outperforms all individual base learners across multiple metrics, including R², RMSE, MAE, MAPE, Precision, Recall, and Accuracy. Furthermore, the mean cosine similarity of the forecast sequences reaches 0.986, underscoring both the stability of seasonal representations and the model’s robustness in capturing demand variations. This method effectively improves the accuracy of e-commerce product demand forecasts, offering reliable data support for inventory management and allocation strategies.

1. Introduction

The exponential growth of live-streaming e-commerce and cross-border business has revolutionized retail paradigms but also placed unprecedented strain on supply chain logistics. This new retail landscape exacerbates challenges such as severe regional supply–demand imbalances and declining inventory turnover rates, largely due to the proliferation of long-tail products with sporadic and volatile demand patterns [1]. Traditional warehousing and forecasting systems, often reliant on historical averages or simple statistical models, struggle to adapt to this new reality. Consequently, developing intelligent, multi-scenario decision-support systems with a sharp focus on improving forecasting accuracy—particularly at the Stock-Keeping Unit (SKU) level for long-tail items—has become a critical imperative for operational efficiency and cost reduction [2].

Substantial research efforts have been dedicated to addressing these forecasting challenges, evolving from statistical methods to machine learning and ensemble techniques. On one hand, statistical time series models like the Seasonal Autoregressive Integrated Moving Average (SARIMA) are proficient in capturing linear trends and seasonal patterns. Their effectiveness has been demonstrated in fields ranging from traffic flow [3] to disease forecasting [4], and improved versions have been applied to retail inventory, significantly reducing prediction errors [5]. However, their fundamental limitation lies in handling the complex non-linearities induced by promotions, market shifts, and competition in e-commerce. To bridge this gap, hybrid models that combine SARIMA with non-linear models like Support Vector Machines (SVM) or Long Short-Term Memory (LSTM) networks have been proposed for water consumption [6] and freight volume [7], showing that synergistic combinations can outperform individual components.

On the other hand, machine learning (ML), particularly Gradient Boosting Decision Tree (GBDT) algorithms, has emerged as a powerful tool for modeling complex, non-linear relationships. XGBoost has shown remarkable success in financial [8,9] and rental markets [10]; LightGBM excels in scenarios requiring high efficiency [10,11]; and CatBoost is robust for categorical feature handling [5,12]. In the context of sales forecasting, comparative studies confirm that these ML techniques generally surpass traditional methods [2,13]. Nevertheless, a consensus indicates that no single GBDT model is universally optimal; their performance is highly dependent on data characteristics [2]. This underscores the need for a framework that leverages their collective strengths rather than relying on a single choice.

This realization has catalyzed the adoption of ensemble learning, with Stacking emerging as a premier strategy for building robust meta-models by integrating diverse base learners. The superiority of Stacking has been validated across domains, including customer churn prediction in banking [14], urban rent forecasting [15], building energy performance [16], and power load forecasting [17]. These studies collectively demonstrate that Stacking effectively mitigates model-specific biases and variances, yielding superior generalization ability. For instance, the integration of Prophet with Random Forest within a Stacking framework has shown excellent results on supply chain data [14,18], highlighting its potential for e-commerce applications.

Despite significant advancements, a research gap persists in developing robust forecasting frameworks that effectively integrate the strengths of multiple advanced algorithms, specifically tailored for SKU-level predictions in complex e-commerce environments. To address this gap and provide managerial decision-support, this paper proposes a novel multi-model fusion architecture based on a stacking paradigm. The proposed framework employs XGBoost, LightGBM, and CatBoost as base learners and introduces an innovative application of the naive bayes classification ensemble algorithm based on K-means algorithm to predictions generated on the validation set, thereby deriving distinct warehouse importance levels for subsequent performance optimization. Furthermore, the framework synergistically combines the Stacking model’s ability to capture complex nonlinear relationships and feature interactions with a Seasonal Autoregressive Integrated Moving Average (SARIMA) model, which specifically captures linear temporal dependencies within the Stacking residuals for joint forecasting. This integrated approach aims to significantly enhance forecasting accuracy at the Stock Keeping Unit (SKU) level, thereby establishing a reliable foundation for optimizing cross-regional inventory allocation strategies. To comprehensively evaluate the robustness of the Stacking framework, we conducted systematic sensitivity analyses under various feature configurations, revealing the model’s dependency on specific feature types and underscoring the critical importance of properly handling categorical features within the ensemble components.

2. Design of the Stacking Fusion Model

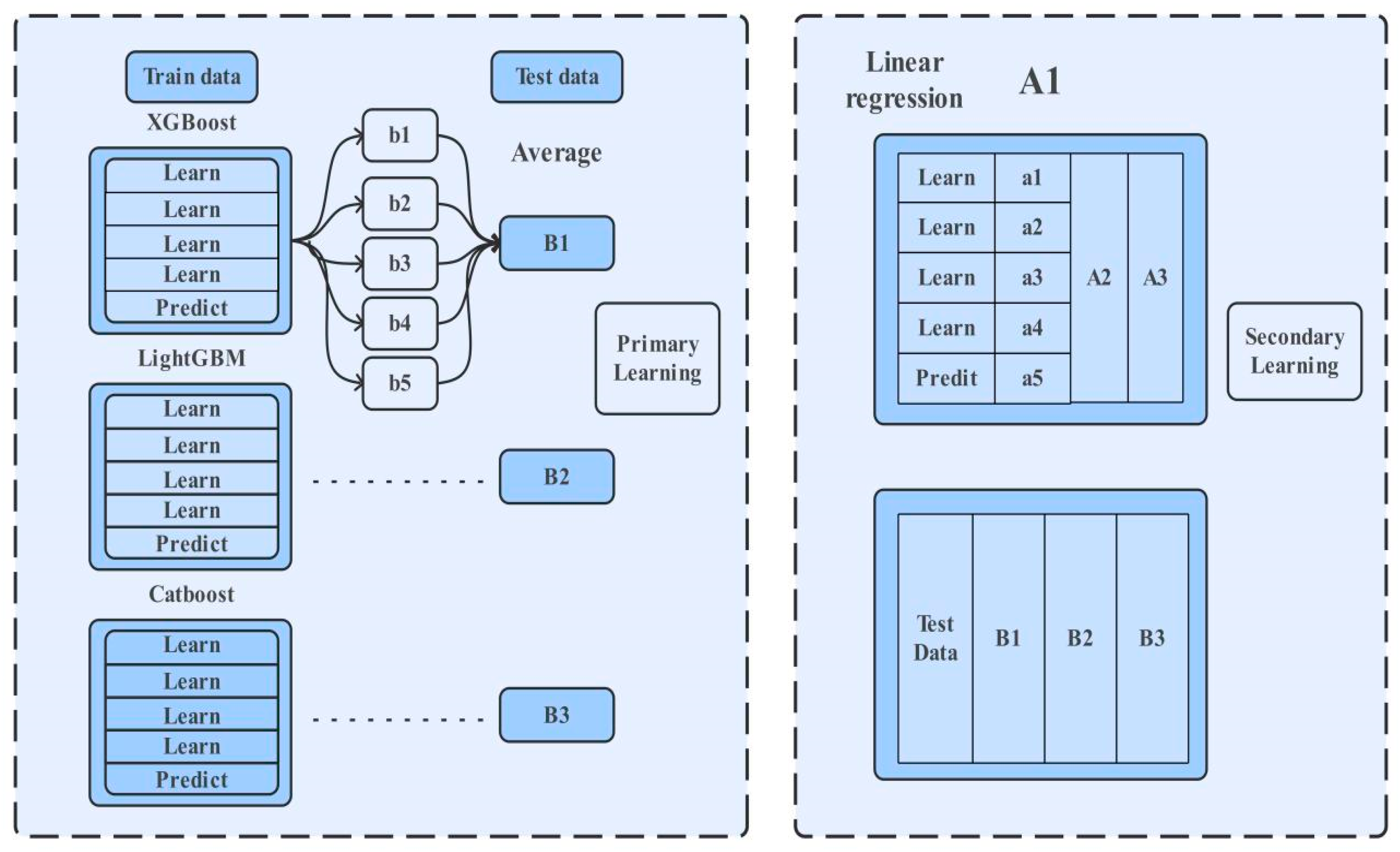
To address the multidimensional challenges in e-commerce supply chains, such as the vast heterogeneity in merchant attributes, divergent operational strategies, constraints on warehouse resources, and the dynamic nature of product demand., this paper proposes a hierarchical Stacking fusion modeling strategy to enhance forecasting accuracy. This strategy employs a meta-learner to integrate multiple base models, whereby the outputs of the base learners are used as new features to train the secondary learner (meta-learner). To mitigate the risk of overfitting, a structurally simple and stable model is selected for the meta-learner. The cross-validation framework employed within this Stacking architecture is illustrated in Figure 1.

In the construction of the base learner layer:

(1)

The XGBoost model, built on a gradient-boosting framework, is utilized to handle high-dimensional sparse features. It combines weak CART decision tree learners and approximates the optimal solution for the objective function by incorporating the first and second-order derivatives of the loss function along with a regularization term [9].

(2)

The LightGBM model enhances training efficiency through its histogram-based decision tree algorithm. By employing feature binning and histogram statistics, it optimizes split point selection, thereby significantly reducing computational overhead [19].

(3)

The CatBoost model effectively addresses the issue of prediction shift by introducing a prior probability weighting scheme. It automatically handles categorical feature encoding and captures multi-dimensional feature interactions [20].

(4)

An Ensemble analysis was performed using the K-means algorithm on the base learner predictions from the validation set [21,22,23]. The resulting represent different levels of warehouse importance, which serve as a basis for further optimization planning research.

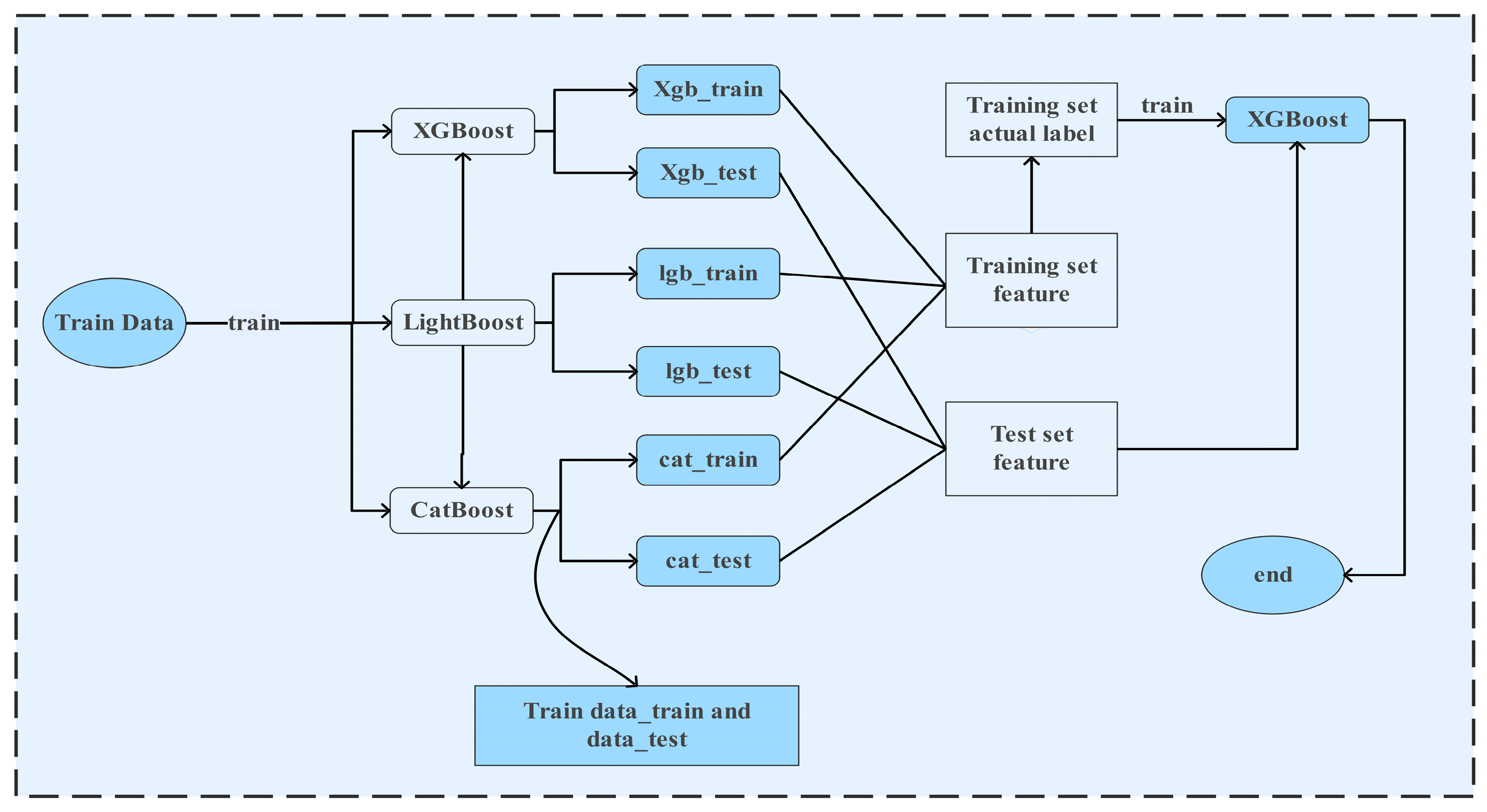
When stacking, outputs can act as class-conditional probability estimators given that each model is treated as independent, which serves to enhance classification accuracy while simultaneously accelerating the computational process. The overall model training workflow is presented in Figure 2, and the pseudo code for Naive Bayes Classification Ensemble Algorithm Based on K-means presented in Algorithm 1.

Algorithm 1. Pseudocode for Naive Bayes Classification Ensemble Algorithm Based on K-Means

3. Data Processing and Experimental Setup

3.1. Data Source and Preprocessing

To establish a joint analytical framework for product demand forecasting and warehouse allocation optimization, this study utilizes operational data sourced from E-commerce platform. The dataset encompasses daily sales data of a certain e-commerce platform for one years. Key information was extracted and categorized into the following four types:

(1)

Time Series Forecasting Data: This includes daily sales volumes, inventory dynamics, and promotional flags for 350 product categories.

(2)

Warehouse Constraint Data: Operational parameters for 12 regional warehouses are considered, covering storage costs and maximum capacity limits.

(3)

Affinity Data: A category affinity matrix, generated using a collaborative filtering algorithm, quantifies co-purchase rates and logistics coupling strength between product categories.

(4)

Attribute Encoding Data: This comprises categorical encodings, product dimensions/type parameters, and product lifecycle stage labels.

Meanwhile, descriptive statistical analysis was conducted on the overall dataset, and the results are shown in

Table 1. Descriptive Statistics of the Dataset.

Category	Metric	Value
Sales Data	Number of Sales Records	5,231,336
	Average Daily Sales	13
	Standard Deviation of Residuals	73.4181
	Variance of Sales	4162.976
	Missing Rate	0.18
Category Data	Number of Product Categories	2303
	Number of Merchants	37
	Number of Warehouses	57
	Number of Data Pairs	6416
	Number of Time Intervals	574

.

The raw data underwent a comprehensive preprocessing pipeline to form a structured dataset. The minimal analytical unit was defined as the “Merchant-Warehouse-Product” combination. Ultimately, this process resulted in 6416 independent forecasting sequences. A subset of these combinations is illustrated in

Table 2. Display Table of Sequence Quantity in Prediction Dataset.

Merchant	Warehouse	Product	Merchant	Warehouse	Product	Merchant	Warehouse	Product
M10	5	251	M21	6	184	M32	6	276
M11	6	123	M22	4	171	M33	4	164
M12	7	89	M23	6	56	M35	5	346
M13	3	218	M24	7	34	M36	10	216
M14	5	71	M25	8	254	M37	4	147
M15	8	259	M26	3	224	M4	5	229
M16	6	36	M27	4	334	M5	6	138
M17	6	349	M28	7	172	M6	6	338
M18	1	156	M29	5	125	M7	5	149
M19	7	247	M3	4	68	M8	5	229
M2	5	136	M30	7	142	M9	5	198
M20	2	63	M31	4	224

. For the convenience of subsequent prediction, the data will be divided with 70% used as the training set and 30% as the testing set.

3.2. Experimental Optimization

In this experiment, a combined approach of grid search and random search was employed, coupled with 5-fold cross-validation, to balance computational efficiency and search comprehensiveness. The complete hyperparameter search spaces for each model are as follows:

(1)

XGBoost: learning_rate: [0.01, 0.1, 0.2, 0.3], max_depth: [3, 5, 7, 9], n_estimators: [50, 100, 200, 500], reg_alpha: [0, 0.001, 0.005, 0.01, 0.1]

(2)

LightGBM: num_leaves: [7, 15, 31, 63], max_depth: [3, 5, 7, −1], learning_rate: [0.01, 0.05, 0.1, 0.2], n_estimators: [50, 100, 200]

(3)

CatBoost: iterations: [50, 100, 200, 500], learning_rate: [0.01, 0.05, 0.1, 0.2], depth: [4, 6, 8, 10]

The corresponding computational resource usage for each model is summarized in

Table 3. Corresponding Computational Resource Usage.

Metric	Description	Value
		Time (Seconds)	Memory Usage (MB)	Data Throughput (MB/s)
Computational Requirements	Data loading	0.0055	0.29	9,499,641
	Data preprocessing	0.0135	0.39	3,867,266
	Data normalization	0	0.46	0
	Data reshaping	0.006	0.51	8,695,781
	Model training	109.3641	9.05	344
	Model prediction	0.5003	10.09	14,392
	Inverse normalization	0	10.09	0
	Error calculation	0	10.1	0
	draw	12.6958	14.32	0
Hardware Configuration	Processor	Intel(R) Core(TM) i7-10875H
	Memory	16G
	Storage Device	SSD 1T

.

To achieve optimal performance for the Stacking fusion model, hyperparameter tuning was conducted during the training phase using a combination of grid search and cross-validation. This process iteratively adjusted the parameters to select the optimal configuration, thereby enhancing the model’s overall predictive capability. The finalized hyperparameter settings for each individual model are detailed in

Table 4. Display Table of Hyperparameter Results for Each Model.

Model	Hyperparameter
XGBoost	learningrate = 0.05, n estimators = 53, reg.alpha = 0.005
	njobs = 8, max. depth = 7, importance. type= ‘total cover’
LightGBM	numleaves= 9, maxdepth = 5, learningrate = 0.05
	nestimators= 80, njobs= −8
CatBoost	iterations = 60, learningrate = 0.05, depth = 10, silent = True
	threadcotasktype= ‘CPU’ unt = 8, cat_features = [‘product_category’, ‘warehouse_id’, ‘product_lifecycle_stage’]

.

3.3. Experimental Analysis

To validate the performance of the proposed fusion model, a comparative evaluation was carried out against the single models—LightGBM, XGBoost, and CatBoost. The assessment was based on standard metrics: Accuracy, Precision, Recall, Root Mean Square Error (RMSE), 5% accuracy rate (Accuracy₅), R-squared (R²), MAE, and MAPE. The results are summarized in

Table 5. Performance Display Table of Each Model.

Indicators	Accuracy	Precision	Recall	RMSE	Accuracy5	R2	MAE	MAPE (%)
LightBGM	0.601	0.578	0.609	318.57	0.458	0.617	254.86	25.49
CatBoost	0.592	0.582	0.598	289.63	0.412	0.608	231.7	23.17
XGBoost	0.621	0.612	0.634	257.15	0.378	0.637	205.72	20.57
Stacking	0.674	0.649	0.677	214.59	0.349	0.679	171.67	17.17

.

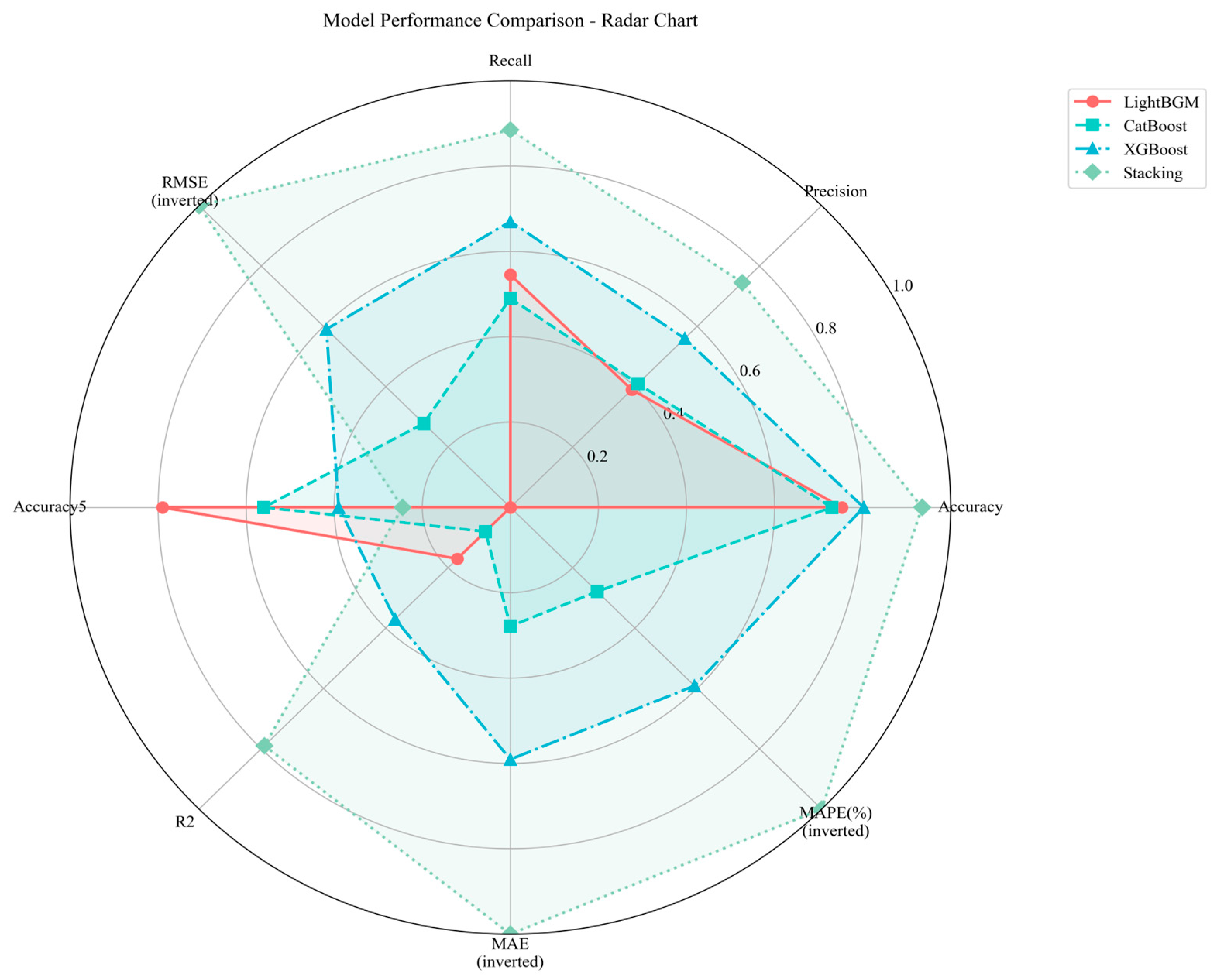
As shown in Table 5 and Figure 3, the Stacking fusion model achieved superior performance across all key metrics. It attained an Accuracy₅ of 0.674, a Precision of 0.649, and a Recall of 0.677, outperforming each individual benchmark algorithm. Furthermore, the model’s R² value reached 0.679, indicating a significantly better goodness-of-fit compared to the single models (LightGBM: 0.617, XGBoost: 0.637, CatBoost: 0.608). Concurrently, the RMSE was reduced to 214.59, which represents a 16.6% improvement over the second-best model (XGBoost). These results collectively demonstrate the higher predictive accuracy of the proposed Stacking framework.

The practical utility of the model is further evidenced by the replenishment forecasting results presented in

Table 6. Partial Results Display Table.

SellorNo	ProductNo	WarehouseNo	Predict Value
S19	P448	wh30	189
S11	P148	wh1	283
S11	P132	wh16	15
S11	P170	wh9	100
S11	P184	wh18	158
S11	P135	wh19	110
S16	P1187	wh33	52
S27	P668	wh13	48
S28	P807	wh43	281
S28	P818	wh45	182

. For instance, the forecast indicates a required replenishment quantity of 189 units for product P448 in warehouse wh30 for seller S19, showcasing the model’s direct applicability to real-world inventory management decisions.

3.4. Experimental Design for Sensitivity Evaluation

To comprehensively evaluate the robustness of the proposed Stacking framework, we conducted a systematic sensitivity analysis under multiple feature configurations. This analysis was designed to address two key aspects: the model’s dependency on specific types of features and the importance of appropriately handling categorical features within the ensemble components. Accordingly, five distinct experimental configurations were designed:

(1)

All available features, including categorical, temporal, numerical, and affinity matrix features;

(2)

Exclusion of categorical features to evaluate CatBoost’s capability in processing categorical data;

(3)

Removal of temporal features to assess time-series dependencies;

(4)

Only basic numerical features (sales and inventory data);

(5)

Exclusion of the affinity matrix to measure the importance of cross-product relationships.

All experiments maintained identical hyperparameter settings and employed 5-fold time-series cross-validation to ensure consistent evaluation conditions.

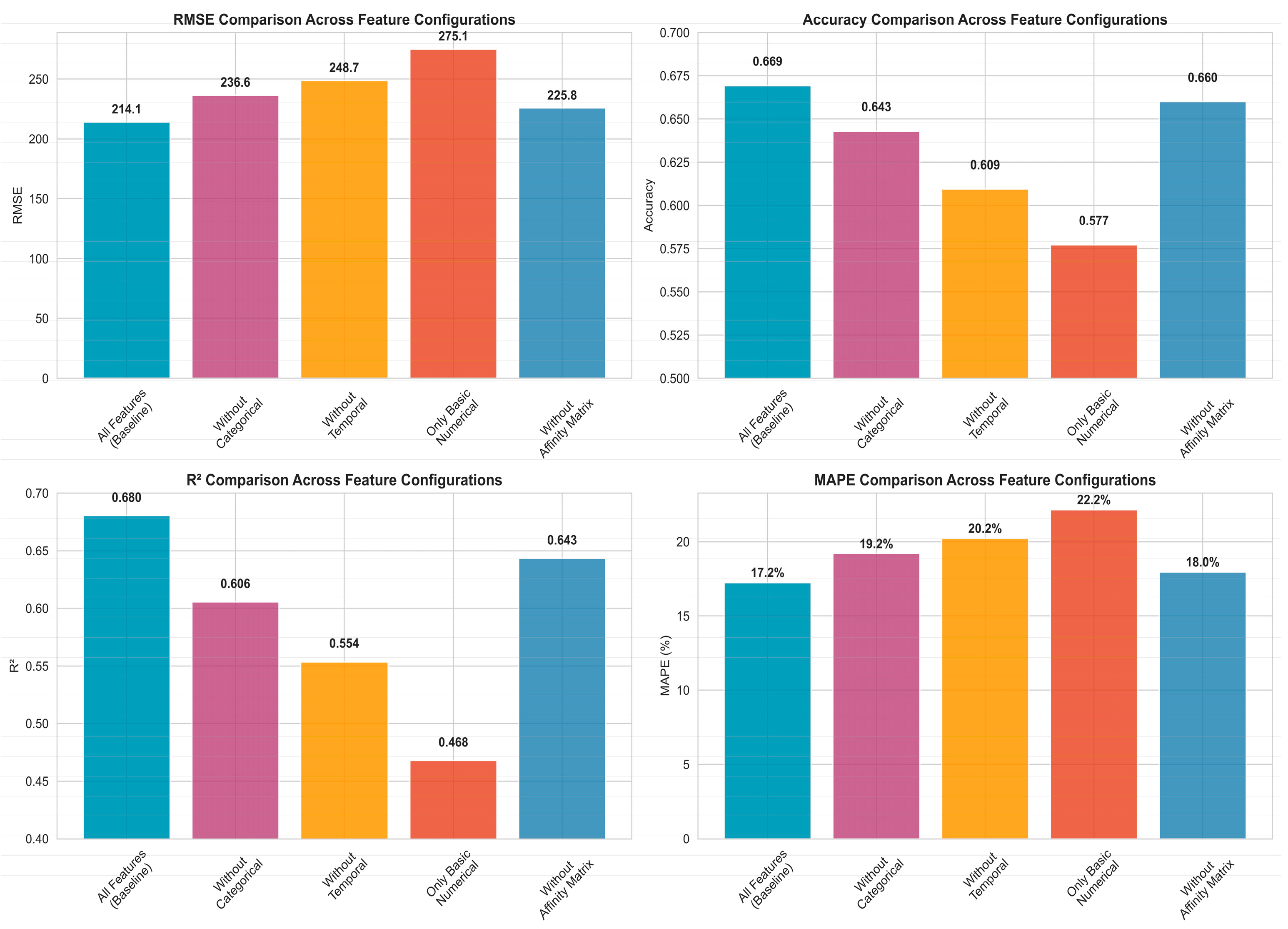
As illustrated in Figure 4, the configuration “Without Categorical” features, for example, shows that the RMSE increased from 214.1 to 236.6, while the R² value decreased from 0.690 to 0.606. These results further confirm the performance degradation and highlight the crucial role of categorical feature encoding in demand forecasting accuracy.

Figure 5 displays a heatmap of the relative performance degradation, illustrating the percentage changes in other configurations compared to the baseline. Shades of red indicate performance deterioration, whereas shades of blue represent performance improvement. The most pronounced performance decline is observed in the configurations excluding categorical features and using only basic numerical features. The heatmap clearly indicates that temporal features represent the second most critical feature category, with an average performance drop of 17% across all metrics. This finding aligns with the time-series nature of demand forecasting. Meanwhile, the removal of the affinity matrix resulted in the mildest performance impact (average decrease of 5.1%), suggesting that although cross-product relationships help improve prediction accuracy, their absence can be partially compensated by other feature types in the Stacking framework.

4. Modeling and Validation with Seasonal Factors

4.1. Model Construction

This study employs a Stacking ensemble model to capture complex nonlinear relationships and feature interactions, while utilizing a Seasonal Autoregressive Integrated Moving Average (SARIMA) time series model to account for the linear temporal dependencies present in the residuals of the Stacking predictions. The specific procedure is as follows: First, the Stacking ensemble model is trained on the training dataset. Predictions are then generated on the training set ${\widehat{y}}_t^S$, and the corresponding residuals are computed as shown in Equation (1).

$$e_t=y_t-{\widehat{y}}_t^S$$

(1)

Second, these residual series are subsequently treated as a new time series and used to train a SARIMA model. By incorporating seasonal hyperparameters (P,Q,D)and a period parameter m, the SARIMA framework extends the standard SARIMA (p,d,q) model [24,25], resulting in a composite (p,d,q) (P,Q,D,m) structure capable of effectively capturing seasonal variations. The construction of the seasonal factors (P,Q,D,m) model involves the following steps:

The model construction process involved the following steps:

(1)

Seasonal Differencing: Seasonal differencing of order D (with period m = 7 days) was applied to the original series to remove periodic effects.

(2)

Trend Differencing: Ordinary differencing of order d was performed to eliminate trend components, yielding the series described by Equation (2).

$${\phi }_{(p)}(V){\Phi }_{(p)}(V_m){(1-V)}^d{(1-V_m)}^D{y}_m={\varphi }_{(q)}(V){\Theta }_{(Q)}(V_m){\mu }_t$$

(2)

(3)

Additive Modeling: The differenced series was expressed as a linear combination of autoregressive and moving average terms, both seasonal and non-seasonal.

The trained models are subsequently applied to the test set. Specifically, the initial predictions ${\widehat{y}}_{test}^S$ are generated using the Stacking model, after which the corresponding residuals are forecasted by the SARIMA model to obtain values ${\widehat{e}}_{test}$. The final predictions are then computed as shown in Equation (3).

$${\widehat{y}}_{test}={\widehat{y}}_{test}^S+{\widehat{e}}_{test}$$

(3)

4.2. Results Analysis

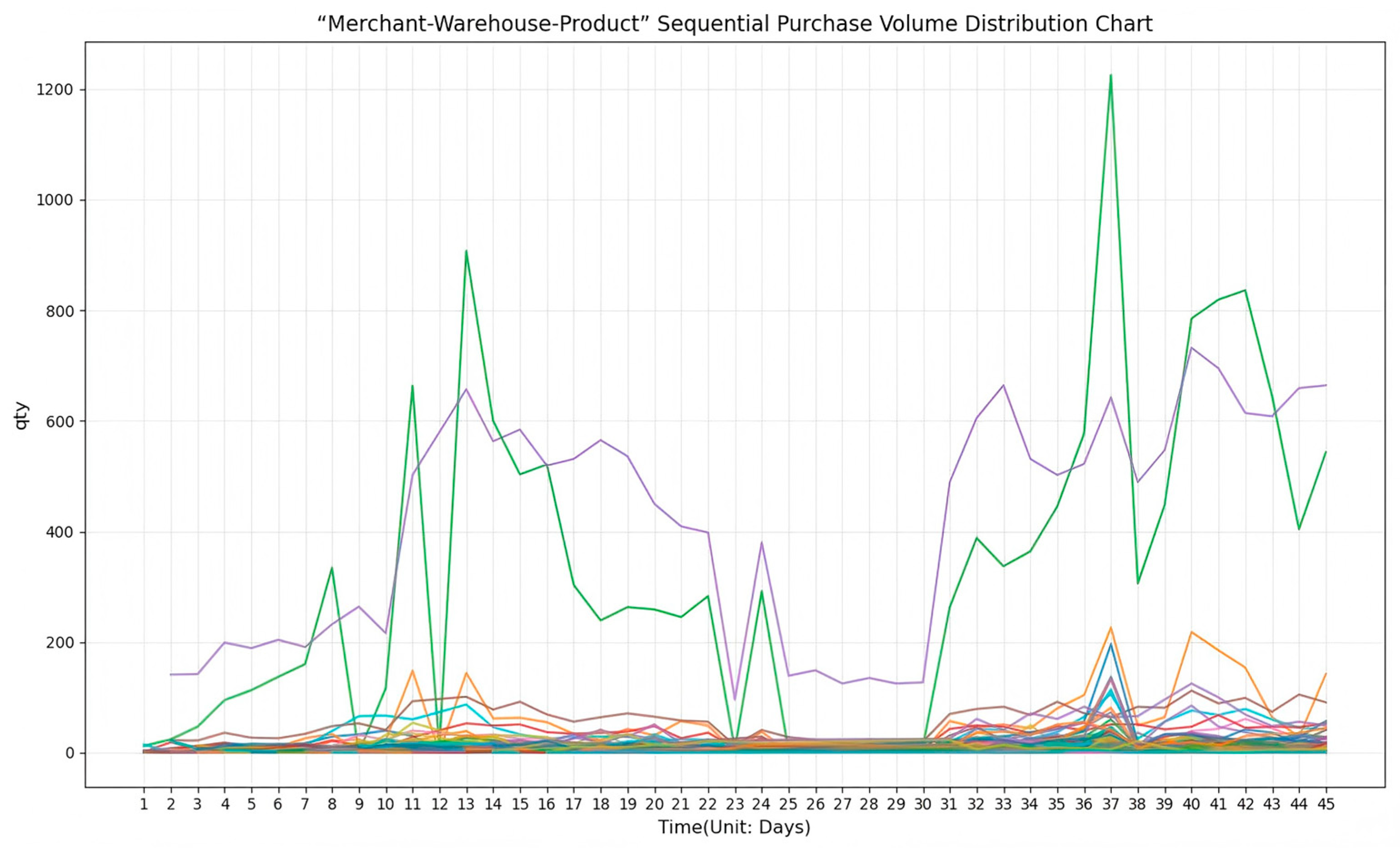
For each merchant-warehouse-product combination, daily data were analyzed. The investigation revealed the emergence of new product types within specific merchant-warehouse pairs. The visualized demand trends over time are presented in Figure 6, where each curve represents a unique warehouse-product sequence. Notably, the sequences exhibit convergent trend patterns.

To validate the model’s demand forecasting performance for replenishment quantities under seasonal influences against actual observations, the demand forecasts and actual values were treated as two separate sequences. The inner product of these sequences was computed using Equation (4), and their similarity was quantified via cosine similarity (Equation (5)). Sequences exhibiting redundant relationships within the dataset were eliminated prior to this analysis.

$$\alpha \cdot \beta =\left|\alpha \right|\left|\beta \right|\cos \theta ,(\theta \in [0,\pi ])$$

(4)

$$K=\cos \theta ={\displaystyle \frac{\alpha \cdot \beta }{‖\alpha ‖‖\beta ‖}}={\displaystyle \frac{{\displaystyle {\sum }_{\begin{array}{l}i=1996\\ j=210\end{array}}{\alpha }_i\times {\beta }_j}}{\sqrt{{\displaystyle \sum _{i=1}^{1996}{({\alpha }_i)}^2}}\times \sqrt{{\displaystyle \sum _{j=1}^{210}{({\beta }_j)}^2}}}}$$

(5)

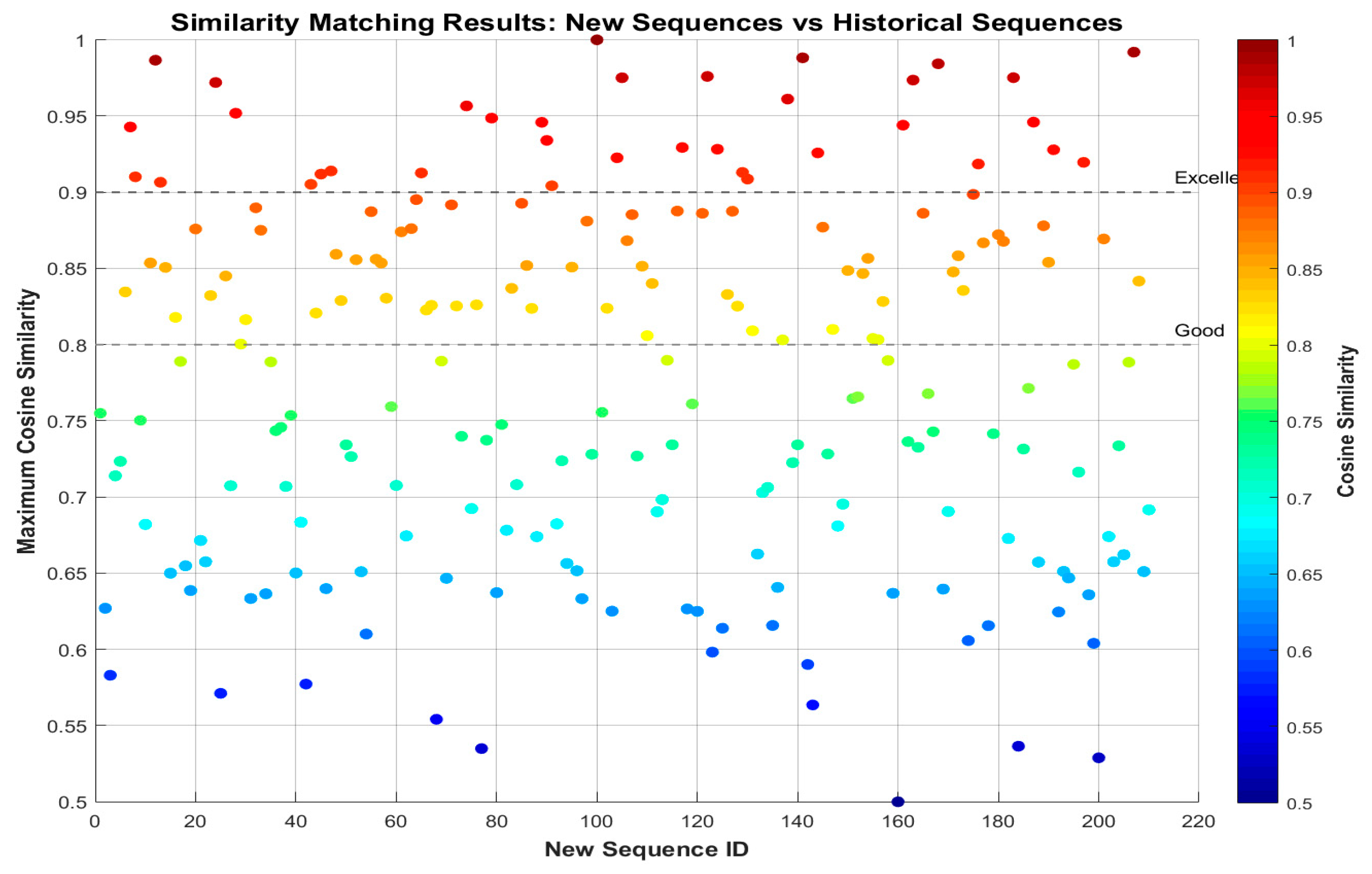
The experimental results indicate that by calculating the cosine similarity between the forecasted and actual sequence vectors, the historical sequence with the highest similarity to the forecast period can be identified. A scatter plot of these similarity matching results is shown in Figure 7. The plot clearly demonstrates that the cosine similarity values approach 1, indicating strong alignment between the sequences. For optimal matching, historical sequences temporally proximate to the forecast period were prioritized, showing consistent demand patterns. After removing redundant sequences, the feature vectors retained displayed a highly concentrated distribution of similarity scores, further corroborating the effectiveness of the proposed model in capturing seasonal variations.

Furthermore, the sequence indices were mapped back to their actual values. The corresponding cosine similarity metrics for selected sequences are listed in

Table 7. Sequence Similarity Display Table.

Predict Sequence			Match Similar Sequences			Cosine Similarity
SNO	ProductNO	WarehouseNO	SNO	ProductNO	WarehouseNO
12	1850	27	35	37	2252	0.998
30	994	36	29	19	922	1
30	1002	35	29	42	922	0.995
17	1277	14	15	47	2418	1
28	756	45	15	47	858	0.984
15	884	48	15	25	858	0.996
27	667	13	15	48	858	1
24	943	1	15	5	858	0.979

. The forecasting results for 210 merchant-warehouse-product sequences indicate synchronous demand trends across sequences, with a mean cosine similarity of 0.986 (range: [0.958, 1.00]). This high level of similarity validates the model’s stability in replicating seasonal characteristics.

4.3. Model Validation

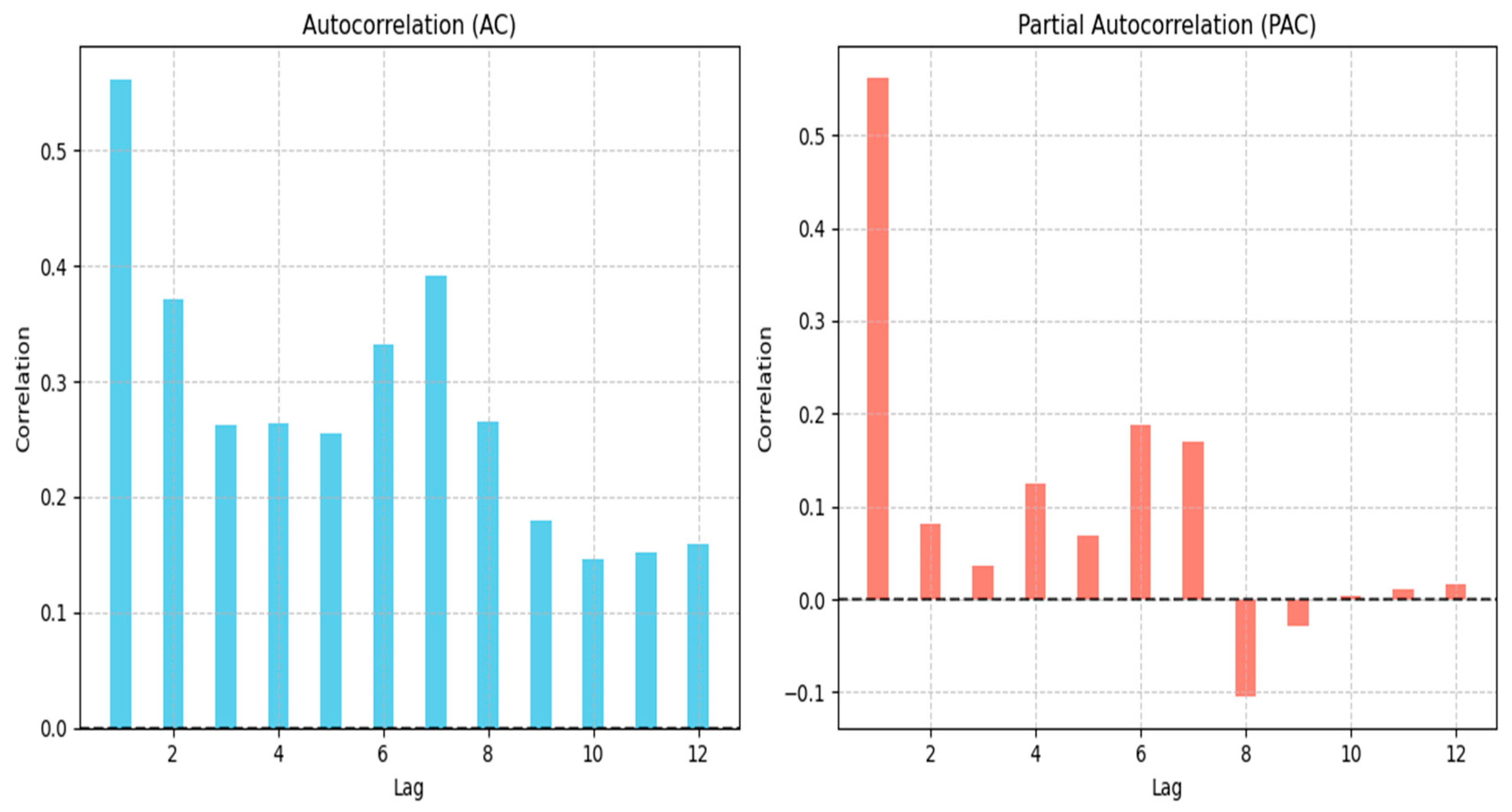
Given the extensive volume of data, this section presents the validation results for a representative case: Product 430 in Warehouse 23 belonging to Merchant 19. The autocorrelation function (AC) and partial autocorrelation function (PAC) plots against the lag order are shown in Figure 8 and

Table 8. Autocorrelation Test Simulation Diagram.

Autocorrelation	Partial Correlation		AC	PAC	Q-Stat	Prob
		1	0.562	0.562	341.12	0.000
		2	0.372	0.081	490.21	0.000
		3	0.263	0.037	564.86	0.000
		4	0.264	0.125	640.16	0.000
		5	0.255	0.069	710.69	0.000
		6	0.332	0.188	830.20	0.000
		7	0.391	0.169	996.00	0.000
		8	0.265	−0.105	1072.5	0.000
		9	0.180	−0.028	1107.8	0.000
		10	0.146	0.003	1130.9	0.000
		11	0.152	0.011	1156.1	0.000
		12	0.159	0.017	1183.7	0.000

, respectively.

A systematic analysis of the AC plot (Table 8) for this specific case reveals a significant autocorrelation of 0.562 at lag 1. The AC gradually decreases from lag 2 to lag 5, indicating strong short-term temporal dependencies. Secondary peaks observed at lags 6 and 7 (AC = 0.332 and 0.391, respectively) suggest the presence of seasonal patterns. Meanwhile, the PAC decays rapidly after lag 2 and even exhibits negative values, implying weak independent influences from higher-order lags. These characteristics collectively indicate stationarity in the time series for this merchant-warehouse-product combination.

The stationarity is further confirmed by the ARIMA diagnostic test (α= 0.01) results depicted in Figure 8. The autocorrelation coefficients decline gradually starting from lag 1 but do not truncate abruptly to zero, exhibiting a “trailing off “pattern. While some coefficients at specific lags fall outside the confidence bounds, the overall behavior confirms that the series meets the prerequisites for SARIMA modeling.

As indicated in

Table 9. Display of Prediction Results.

SellNo	ProductNo	WarehouseNo	PredictValue	SARIMA
S1	product3	wh5	5	(2,1,2)
S1	product4	wh1	60	(2,0,1)
S1	product8	wh3	4	(2,1,2)
S1	product9	wh2	28	(2,0,2)
S1	product9	wh5	30	(1,0,2)
S1	product24	wh2	45	(2,0,1)
S1	product2005	wh2	38	(2,1,1)
S1	product2072	wh5	39	(2,0,1)
S1	product2073	wh1	5	(2,1,2)
S1	product2073	wh1	60	(2,0,2)

, employing a SARIMA (2,1,2) model for forecasting yields a practical outcome: a recommended replenishment quantity of 5 units for Product 3 (S1) in Warehouse WH5. This result underscores the practical utility of the proposed model in addressing seasonal demand forecasting within supply chain management.

5. Discussion

This study successfully developed and validated a Stacking-based fusion model integrated with seasonal decomposition for dynamic e-commerce demand forecasting. A key finding is that the proposed ensemble framework consistently outperforms several strong baseline models—XGBoost, LightGBm, and CatBoost—across a comprehensive set of evaluation metrics. The higher R² values and lower RMSE indicate improved variance explanation and superior predictive accuracy. This performance gain can be attributed to the Stacking architecture’s ability to leverage the complementary strengths of multiple base learners, thereby capturing diverse patterns within the high-dimensional and complex feature space typical of e-commerce data [2,5]. By synthesizing these predictions through a meta-learner, the model effectively reduces individual biases and variances of base estimators, yielding more robust and generalizable forecasts.

Another important result is the model’s demonstrated capacity to identify and represent seasonal fluctuations. The high mean cosine similarity (0.986) between forecasted and actual demand sequences strongly suggests that the integrated SARIMA component successfully captured recurring seasonal trends. This was further corroborated by AC/PAC analyses, which revealed both short-term dependencies and weekly seasonal effects, formally incorporated via the SARIMA (p,d,q) (P,D,Q,m) formulation. These findings resonate with existing literature on the critical role of seasonality in retail forecasting [4,11], while extending prior work through the seamless integration of a classical time series model within a modern machine learning ensemble. The practical value of this hybrid approach is illustrated through SKU-level replenishment guidance, as exemplified by the case of Product P448 in Warehouse WH30, translating statistical gains into actionable inventory decisions—a crucial advantage in supply chain operations.

Nevertheless, several limitations warrant attention. First, model validation was conducted on data from a single platform over a limited period. Generalizability to other e-commerce contexts—such as those with differing product lifecycles or business models—and long-term stability under volatile conditions remain to be examined. Second, although the model incorporates a range of influential features, it omits certain external factors such as macroeconomic indicators, competitor actions, or granular marketing campaign data, which may enhance predictive realism. Third, while sensitivity analysis using 5-fold time-series cross-validation ensured evaluation consistency (Section 3.4), a more rigorous assessment of model robustness—such as repeated cross-validation with varying fold numbers (e.g., 10 or 15) or testing under noisy or adversarial conditions [26,27]—has not been conducted and represents an important area for future validation.

Looking forward, subsequent research could focus on integrating the aforementioned external variables and exploring advanced deep learning architectures (e.g., Temporal Fusion Transformers or LSTMs) to capture more intricate temporal dependencies. Additionally, developing adaptive mechanisms to handle concept drift in fast-evolving e-commerce settings would further enhance the model’s applicability. Systematic data perturbation tests—injecting noise into features or target variables—along with repeated SHAP analysis over multiple runs to ensure consistent feature attribution, will be essential to verify operational reliability prior to deployment.

It should also be noted that the proposed fusion architecture entails certain inherent constraints. The end-to-end complexity, arising from the cascade of a Stacking ensemble and a SARIMA model, introduces non-trivial computational overhead, potentially hindering deployment in high-frequency or near real-time forecasting scenarios. Moreover, interpretability is partially compromised. Despite the strong predictive performance of the Stacking ensemble, its black-box nature complicates traceability of specific prediction drivers. This issue is exacerbated when SARIMA corrects the ensemble’s residuals, further complicating output attribution. Such limited interpretability could restrict the model’s use in high-stakes or transparency-sensitive decision contexts. Finally, the framework’s adaptability to sudden market shifts—such as breaks in historical seasonal patterns—has not been thoroughly evaluated and remains an open question.

In conclusion, this study introduces an accurate and robust framework for e-commerce demand forecasting. The synergistic combination of a Stacking ensemble and a seasonal time series model yields clear improvements over conventional forecasting techniques. By delivering precise, SKU-level forecasts that account for seasonal behavior, this model lays a solid foundation for enhancing inventory allocation, reducing holding costs, and strengthening end-to-end supply chain agility.

6. Conclusions

To effectively support inventory cost control and goods allocation in e-commerce warehousing, this study developed a sophisticated demand forecasting framework based on a Stacking ensemble that integrates XGBoost, LightGBM, and CatBoost. Hyperparameters were systematically optimized using cross-validation, and experimental evaluations confirmed that the proposed model outperforms individual base learners, achieving accurate demand predictions at the merchant-warehouse-product level.

To explicitly capture seasonal fluctuations in the time series, a SARIMA component was incorporated into the modeling architecture. Validation results verify the model’s capability to handle short-term forecasts under seasonal influences. Moreover, its consistent performance across repeated cross-validation runs offers a positive indication of robustness.

While these outcomes are encouraging, further improvements are possible—particularly in enhancing the model’s generalizability and adaptability to more complex business environments. Future work will investigate advanced frameworks such as deep temporal neural networks, with the aim of delivering more robust and precise decision support for intelligent warehouse management in dynamic e-commerce settings.