Abstract
This paper proposes an enhanced hierarchical fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) integrated with the Analytic Network Process (ANP) for solving multi-criteria decision-making (MCDM) problems under uncertainty. Conventional fuzzy TOPSIS models often face significant challenges, such as restrictions to specific fuzzy number formats, difficulties in normalization when zero or very small values appear, and limited capacity to capture hierarchical interdependencies among criteria. To address these limitations, we develop a generalized fuzzy geometric mean approach for deriving weights from pairwise comparisons that can accommodate multiple fuzzy number types. Moreover, a novel normalization function is introduced, which ensures mathematically valid outcomes within the [0, 1] interval while avoiding division-by-zero and inconsistency issues. The proposed method is validated through both a numerical building selection problem and a practical supplier selection case study. Comparative analyses against established fuzzy MCDM models demonstrate the improved robustness, flexibility, and accuracy of the approach. Additionally, a sensitivity analysis confirms the stability of results with respect to variations in criteria weights, fuzzy number formats, and normalization techniques. These findings highlight the potential of the proposed fuzzy hierarchical TOPSIS-ANP framework as a reliable and practical decision support tool for complex real-world applications, including supply chain management and resource allocation under uncertainty.
MSC:
90B50; 03B52
1. Introduction
Decision-making in real-world contexts is rarely straightforward, as it often involves balancing multiple conflicting criteria under conditions of uncertainty. Multi-criteria decision-making (MCDM) provides systematic approaches for evaluating alternatives when both qualitative and quantitative factors must be considered simultaneously [1,2,3]. These techniques have been widely applied in diverse domains, including supplier selection [4], sustainable energy planning [5], healthcare decision-making [6], and transportation systems [7]. Among various MCDM approaches, the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) stands out due to its simplicity, intuitive logic, and ability to yield a complete ranking of alternatives [8,9]. Despite its popularity, classical TOPSIS is based on crisp numerical data and assumes independence among criteria, which often does not hold in practical decision-making contexts. For instance, supplier cost and quality may be interdependent, while environmental and social dimensions of sustainability often overlap. Moreover, decision-makers typically rely on linguistic judgments rather than precise numbers, making fuzziness unavoidable. To address these challenges, fuzzy extensions of TOPSIS have been developed, enabling the use of fuzzy numbers and categories representing selected levels of importance to better model uncertainty [10,11,12].
Hybrid models that integrate fuzzy TOPSIS with weighting techniques, such as the Analytic Hierarchy Process (AHP) and Analytic Network Process (ANP), have further enhanced applicability by capturing interdependencies and feedback among criteria [13,14,15]. However, these models are still constrained by several critical issues:
- (a)
- Restriction to specific fuzzy number formats: Most existing studies rely only on triangular or trapezoidal fuzzy numbers, whereas real-world judgments may require more diverse or generalized representations [16].
- (b)
- Normalization challenges: Conventional normalization formulas often lead to division-by-zero errors, negative values, or results outside the [0,1] range when dealing with uncertain or extreme data [17].
- (c)
- Hierarchical interdependencies: Many fuzzy TOPSIS approaches neglect hierarchical or network-based dependencies among criteria, leading to oversimplified weight assignments [18].
- (d)
- Limited robustness validation: Few studies provide comprehensive comparative analysis or sensitivity testing, making it difficult to evaluate the stability and practical reliability of proposed methods [19].
Addressing these gaps, this paper proposes an enhanced fuzzy hierarchical TOPSIS-ANP framework that makes the following contributions:
- (1)
- Introduction of a generalized fuzzy geometric mean method for deriving weights from fuzzy pairwise comparisons, which accommodates multiple types of fuzzy numbers beyond the triangular/trapezoidal cases.
- (2)
- Development of a new normalization function that guarantees mathematically valid outputs within the [0, 1] interval, avoiding division-by-zero and inconsistency issues.
- (3)
- Integration of hierarchical ANP-based weighting into fuzzy TOPSIS to capture interdependencies among criteria.
- (4)
- Empirical validation of the method using both numerical and real-world case studies, supplemented with comparative analysis and sensitivity analysis to demonstrate robustness, accuracy, and practical relevance.
The remainder of this paper is structured as follows. Section 2 reviews the related works on fuzzy MCDM and hierarchical TOPSIS approaches. Section 3 presents the preliminaries and fundamental concepts used in this study. Section 4 introduces the proposed fuzzy hierarchical TOPSIS-ANP method in detail. Section 5 demonstrates the applicability of the method through both numerical and real-world case studies, along with comparative and sensitivity analyses. Section 6 provides a discussion of the results, practical implications, and limitations. Finally, this section (Section 6) concludes the paper and outlines directions for future research.
2. Literature Review
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) and its fuzzy extensions have been extensively applied in multi-criteria decision-making (MCDM) problems, such as supplier selection, project prioritization, sustainable energy planning, and healthcare evaluation [20,21,22,23]. Fuzzy TOPSIS enables decision-makers to incorporate linguistic judgments and uncertain information, thus providing greater flexibility than classical TOPSIS.
To improve weighting and capture interdependencies among criteria, hybrid models that integrate fuzzy TOPSIS with methods such as the Analytic Hierarchy Process (AHP) and Analytic Network Process (ANP) have been proposed. For instance, Dağdeviren et al. [24] applied a fuzzy ANP–TOPSIS framework for occupational risk assessment, while Hadi-Vencheh and Mohamadghasemi [25] employed fuzzy AHP–DEA for inventory classification
Despite these developments, several limitations persist. First, most studies rely solely on triangular or trapezoidal fuzzy numbers, which restricts the representation of more diverse linguistic inputs [26]. Second, conventional normalization formulas in fuzzy TOPSIS may result in division-by-zero errors, negative values, or outcomes outside the [0,1] range, raising concerns of mathematical validity [27]. Third, although ANP integration has been attempted, hierarchical dependencies among criteria are often oversimplified or ignored [28]. Finally, many studies lack robustness validation through comparative benchmarking or sensitivity analysis, limiting confidence in their applicability to real-world problems [29].
Recent research has sought to address these issues. Nafei et al. [6] developed a neutrosophic triplet-based fuzzy TOPSIS for sustainable supplier selection, while Karbassi Yazdi et al. [1] introduced blockchain-enabled fuzzy MCDM for supply chain decision-making. Theilig et al. [9] compared hierarchical MCDM techniques for energy-efficient building renovation, emphasizing the role of interdependencies. Similarly, Roy et al. [11] and Baral et al. [14] identified normalization inconsistencies in existing fuzzy TOPSIS models. More advanced approaches include Liu et al. [30], who proposed a probabilistic hesitant fuzzy TOPSIS for smart city infrastructure planning, Zhang et al. [31], who developed a cloud model-based hierarchical MCDM for renewable energy evaluation, and Yang et al. [32], who integrated deep learning with fuzzy MCDM for supply chain risk assessment.
In light of these gaps, the present study contributes by (i) introducing a generalized fuzzy geometric mean for deriving weights from diverse fuzzy numbers, (ii) proposing a novel normalization method that ensures mathematically valid values within the [0,1] interval, and (iii) validating the approach through numerical and practical case studies, supported by comparative and sensitivity analyses. These contributions position the proposed fuzzy hierarchical TOPSIS–ANP framework as a robust and replicable decision support tool for complex applications under uncertainty.
Notation
denotes the vector of criteria weights;
represents the fuzzy pairwise comparison matrix;
denotes the set of fuzzy numbers;
A fuzzy number in parametric form is written as , with . In addition, we standardized the use of indices: refers to the criterion under evaluation, to the comparator, and α to the level parameter. These clarifications ensure that the notations are consistently defined and unambiguous before the matrices are introduced.
3. Preliminaries
Fuzzy set theory, originally introduced by Zadeh [16], provides a mathematical framework for modeling vagueness and imprecision inherent in real-world systems. Unlike classical sets with binary membership, fuzzy sets assign each element a membership grade in , making them well-suited for representing linguistic and subjective judgments such as preferences, importance, and satisfaction levels [10,17,18]. First of all, we need a definition of a fuzzy number or interval. We adopt -cut representation of fuzzy numbers (Figure 1).
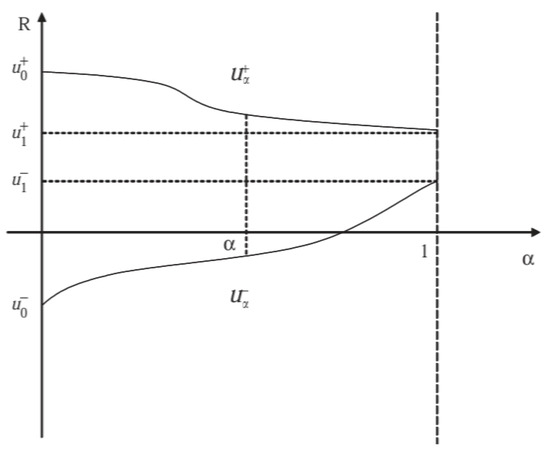
Figure 1.
The -cut representation.
Definition 1 (Continuous fuzzy number).
A fuzzy number is represented as a pair of functions with satisfying [19]:
- (1)
- is bounded, non-decreasing, and continuous on
- (2)
- is bounded, non-increasing, and continuous on
- (3)
- For all it holds that
The -cut of is the closed interval If the result is a fuzzy interval; if , the result is a fuzzy number. A commonly used fuzzy number is the trapezoidal fuzzy number, represented as à = , where and are defuzzified values, and and represent the left and right fuzziness, respectively. Its membership function is given as
The corresponding parametric form of this trapezoidal fuzzy number is:
3.1. Basic Operations
Let and be fuzzy numbers.
Definition 2 (Addition).
with -cut representation:
Definition 3 (Scalar multiplication).
For
At the -cut level: Special case: if , then
Definition 4 (Subtraction).
with
Definition 5 (Multiplication).
where
Definition 6 (Division).
If then with
3.2. Distance Measures on Fuzzy Numbers
Let denote the set of fuzzy numbers. A widely used distance on is the Hausdorff metric [19]:
The above distance is equivalent to the following [20]:
3.3. Ranking of Fuzzy Numbers
Various methods have been proposed in the literature for ranking fuzzy numbers. In this study, we employ a two-step approach: first, we defuzzify the fuzzy numbers, and then compare the resulting crisp values to establish a ranking. To perform the defuzzification, we utilize Equation (6), which is defined as follows [20]:
For , the ranking between and is defined by comparing their nearest crisp representatives in . We then define [20]:
3.4. Fuzzy Normalization
Normalization is a fundamental step in multi-criteria decision-making (MCDM), used to convert original values into a dimensionless form so that they can be compared on a common scale. Several normalization techniques have been proposed in the literature, including norm-based, linear, fuzzy, and Wang’s methods [24]. Despite their widespread use, each of these methods has its own limitations. To illustrate the challenges associated with these normalization techniques, consider the following example.
Example 1.


Suppose we have a set of four fuzzy numbers (FNs) given in Table 1. The normalized results of these FNs using different methods are shown in Table 2.

Table 1.
Data of Example 1.

Table 2.
The revised normalized FNs of Example 1.
As we see, using Ref. [24] led to the same normalized value for all four numbers. Here, we propose a novel normalization approach designed to address the shortcomings identified in existing methods. Conventional techniques may produce inconsistent or unbounded results, particularly when applied to fuzzy numbers with zero or near-zero values. To ensure mathematical consistency and preserve the integrity of fuzzy decision data, we introduce a new normalization function. Let , , be a collection of arbitrary of fuzzy numbers. The proposed normalization method is defined as follows:
This equation is applied component-wise to the fuzzy numbers, ensuring that the normalized values are always bounded between 0 and 1. Using Equation (7) we have:
3.5. Fuzzy Normal Geometry Average
In order to derive the weights of the criteria in MCDM problems with criteria, we begin with the fuzzy pairwise comparison matrix where each element denotes the fuzzy linguistic judgment of criterion relative to criterion . These judgments are expressed as trapezoidal fuzzy numbers derived from categories representing selected levels of importance (e.g., “equal,” “moderate,” “strong”), with corresponding membership functions. By construction, the matrix is reciprocal, i.e., Each fuzzy entry is represented in parametric form as where and are the lower and upper bounds of the membership function, respectively.
Step 1. Row-wise fuzzy geometric mean.
For each criterion , the geometric mean of all fuzzy comparisons in row j is computed using as below:
This aggregates the relative importance of with respect to all other criteria, while maintaining the fuzzy lower and upper bounds.
Step 2. Fuzzy weight formulation.
Using the following formula, the row-wise geometric mean is normalized against the cumulative contribution of all criteria. The denominator accounts for the integrals of the other rows, ensuring that the weight vector is scaled consistently across criteria.
Step 3. Defuzzification.
Since fuzzy weights are intervals, they are defuzzified by averaging the lower and upper bounds across the unit interval as given in Equation (10):
This produces a crisp scalar , representing the central tendency of the fuzzy weight for criterion .
Step 4. Final normalization.
Finally, the crisp weights are normalized so that their total equals one.
The resulting vector provides the priority distribution of criteria and can be directly used in the subsequent fuzzy TOPSIS procedure.
4. Extension of Fuzzy Hierarchical TOPSIS-ANP
In this section, we present the proposed extension of the fuzzy hierarchical TOPSIS integrated with the analytic network process (ANP). The methodology aims to capture interdependencies among criteria while addressing the limitations of classical TOPSIS in handling fuzziness and subjectivity. To enhance clarity and reproducibility, the mathematical formulations are presented step by step with explanatory notes. A flowchart summarizing the overall procedure is also provided (Figure 2).
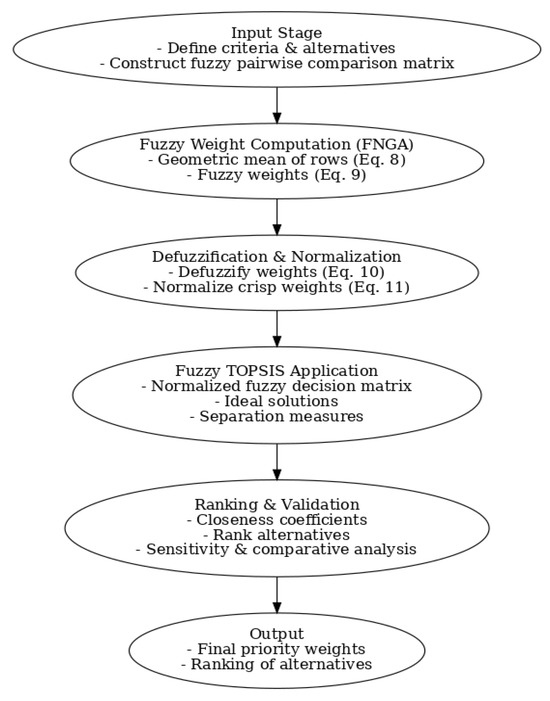
Figure 2.
Flowchart of the proposed methodology.
Step 1: Determination of Alternatives and Criteria.
In the first step of the proposed fuzzy hierarchical TOPSIS method, the decision-making problem is structured by identifying the set of alternatives and evaluation criteria. Let denote the number of alternatives and represent the number of criteria.
In hierarchical decision problems, criteria may be organized into multiple levels, where higher-level goals are decomposed into sub-criteria or sub-goals. This hierarchical structure can be represented in the form of a tree or network model, which facilitates pairwise comparisons and weight derivation in later steps.
Step 2: Construction of the Hierarchical Structure and Sub-Criteria Definition.
In this step, the decision-making problem is further refined by constructing a hierarchical structure that decomposes the overall goal into criteria and sub-criteria across multiple levels. Let denote the maximum number of levels in the hierarchy, where
- Level 0 represents the overall objective of the decision problem;
- Level 1 includes the main criteria;
- Levels 2 to consist of sub-criteria or sub-sub-criteria, depending on the complexity of the problem.
This hierarchical model enables a more detailed and structured evaluation of the alternatives, especially when criteria are interdependent or when decisions involve complex, multi-layered considerations. The result of this step is a tree-structured hierarchy where each criterion may branch into several sub-criteria. This structure serves as the foundation for the subsequent pairwise comparisons and weight derivation using fuzzy ANP or fuzzy AHP methods.
Step 3: Construction of Pairwise Comparison Matrices and Definition of Linguistic Scale.
In this step, decision-makers perform pairwise comparisons among criteria and sub-criteria to assess their relative importance using categories representing selected levels of importance. These comparisons form the foundation for determining the weights of criteria in the fuzzy hierarchical structure. Let represent the total number of fuzzy pairwise comparison matrices required in the hierarchy. Each matrix corresponds to a decision node (e.g., a set of criteria or sub-criteria under a specific parent criterion). To capture the inherent uncertainty and subjectivity in human judgments, a predefined linguistic scale is used for expressing preferences. A generic fuzzy pairwise comparison matrix for a given level or cluster is structured as:
Step 4: Derivation of Criteria Weights Using Fuzzy ANP and Geometric Mean Method.
In this step, the Fuzzy Analytic Network Process (FANP) is applied to derive the weights of criteria and sub-criteria based on the fuzzy pairwise comparison matrices constructed in Step 3. The integration with ANP is justified by the fact that many real-world decision problems involve interdependent criteria rather than independent ones. Although ANP is a subjective weighting method, its combination with fuzzy set theory mitigates the vagueness of expert judgments. To achieve this, we use Equations (8)–(11) to drive weights.
After computing the weights, the same procedure is applied to all fuzzy pairwise comparison matrices throughout the hierarchical structure. These calculations yield the local weights of sub-criteria at each level. Subsequently, the Fuzzy Analytic Hierarchy Process (FAHP) is applied to aggregate the local weights and determine the global weights of the main criteria. This hierarchical aggregation ensures that the final weights reflect both the local relative importance and the structural position of each criterion within the hierarchy. The outcome of this step is a complete set of normalized criteria weights, which will be used in the next stages of the fuzzy hierarchical TOPSIS method.
Step 5: Construction of the Fuzzy Decision Matrix.
In this step, the main fuzzy decision matrix is constructed based on the evaluations of alternatives with respect to each criterion. The approach varies depending on whether categories representing selected levels of importance are used in the evaluation process.
- If categories representing selected levels of importance are used:Each evaluation is expressed using categories representing selected levels of importance which must first be converted into corresponding fuzzy numbers by assigning an appropriate membership function. These membership functions are usually represented as triangular or trapezoidal fuzzy numbers, depending on the problem context. The linguistic scale and its associated fuzzy representations should be predefined and agreed upon by the decision-making team.
- If categories representing selected levels of importance are not used:The evaluations are directly expressed using fuzzy numbers, eliminating the need for transformation from categories representing selected levels of importance. In such cases, the fuzzy decision matrix is constructed by collecting these fuzzy evaluations across all alternatives and criteria.
Let the resulting fuzzy decision matrix be denoted as:
This matrix serves as the foundation for subsequent steps, including normalization, distance calculation, and ranking of alternatives.
Step 6: Construction of the Normalized Fuzzy Weighted Decision Matrix.
In this step, the normalized fuzzy weighted decision matrix is obtained. The procedure for normalization depends on whether categories representing selected levels of importance were used during the evaluation process:
If categories representing selected levels of importance are used:
All elements of the decision matrix are represented using a consistent fuzzy linguistic scale, and thus, further normalization is not required because the scale is inherently uniform and dimensionless.
If categories representing selected levels of importance are not used:
The fuzzy decision matrix must be normalized to eliminate the effect of differing units of measurement and to ensure comparability across criteria. In this case, normalization is essential for constructing a unit-free and scale-independent matrix.
To avoid the limitations associated with the Chen and Hwang [23], this study adopts the Wang normalization approach [21], which better preserves the properties of fuzzy numbers during the normalization process. By applying Equation (8), the fuzzy decision matrix can be reformulated to reflect the normalized fuzzy evaluations of each alternative with respect to all criteria. The resulting normalized fuzzy decision matrix is given as follows:
After obtaining the normalized fuzzy decision matrix, the next step is to construct the weighted normalized fuzzy decision matrix by incorporating the previously calculated fuzzy weights of criteria. This is achieved using the following fuzzy multiplication operation:
To proceed with the ranking of alternatives, we identify the Positive Ideal Solution (FPIS) and the Negative Ideal Solution (FNIS), defined as:
Since direct comparison of fuzzy numbers can be ambiguous, we first apply defuzzification to transform fuzzy values into crisp scores for ranking purposes. To derive the defuzzified value of each fuzzy number, we use Equation (6).
Step 8: Separation Measures and Final Ranking of Alternatives.
In the final step of the proposed fuzzy hierarchical TOPSIS method, we calculate the distance of each alternative from both the PIS and the NIS. These distances are referred to as the separation measures, and they form the basis for deriving the final ranking of alternatives. These distances are calculated using the fuzzy distance metric defined earlier Equation (5). The specific formulas for the separation measures are:
The relative closeness of each alternative to the ideal solution is computed as:
Based on the calculated closeness coefficients , all alternatives are ranked in descending order. The alternative with the highest relative closeness is considered the most preferred option according to the fuzzy hierarchical TOPSIS model.
The methodology proceeds as follows: (i) construct the fuzzy pairwise comparison matrix, (ii) compute fuzzy weights using FNGA, (iii) defuzzify and normalize the weights, (iv) apply fuzzy TOPSIS to rank the alternatives, and (v) analyze the results through sensitivity and comparative analysis.
A flowchart summarizing these steps is provided in Figure 2. The flowchart illustrates the stepwise process of the proposed approach. It begins with the construction of the fuzzy pairwise comparison matrix and proceeds to fuzzy weight computation via the fuzzy normal geometric average (FNGA). The fuzzy weights are then defuzzified and normalized to yield crisp priorities, which are subsequently incorporated into the fuzzy TOPSIS procedure. Finally, the method produces the ranking of alternatives along with sensitivity and comparative analyses to validate robustness.
5. Numerical Examples
To demonstrate the applicability and effectiveness of the proposed methodology, two case studies are conducted. These case studies have been carefully selected from real-world decision-making contexts to ensure both practical relevance and methodological rigor. Although only two applications are presented, the limitation stems from the availability of high-quality expert data. Nevertheless, the selected cases are sufficiently complex to illustrate the performance of the proposed approach and to highlight its advantages over conventional fuzzy MCDM methods.
Note: In what follows meaning of the symbol “–” in the pairwise comparison matrices. Specifically, in our tables the entry “–” does not mean that the element is missing; rather, it indicates the reciprocal value of the corresponding evaluation of element A with respect to element B.
Example 2.
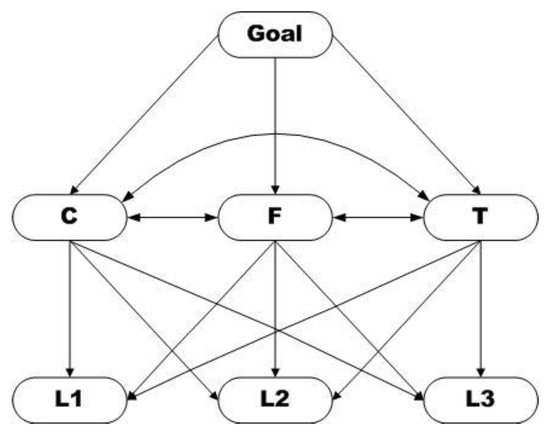
A decision-making scenario is considered in which a firm intends to select the most suitable building from three alternatives L1, L2, and L3. The evaluation is based on three main criteria: commercial position (C), transportation (T), and finance (F). Figure 3 shows the structure of this decision process. Two distinct sets of categories representing selected levels of importance are used in this example: For pairwise comparisons (fuzzy AHP/ANP weighting) they are Equal, Weak, Moderate, Strong, and for alternative evaluations (Decision Matrix) these are used: Extreme importance, Very low, Low, Fair, High, and Very high.

Figure 3.
The hierarchal structure of Example 2.
The goal is to rank the buildings L1, L2, and L3 based on how well they satisfy the three criteria, considering both the fuzzy nature of evaluations and the hierarchical importance of criteria. The procedure for selecting the most suitable location using the proposed fuzzy hierarchical TOPSIS algorithm is carried out in the following steps:
Step 1: The decision-maker begins by comparing the three criteria using categories representing selected levels of importance that reflect their relative importance. Each category representing selected levels of importance is associated with a corresponding fuzzy number representing its membership function. Table 3 presents the fuzzy numbers assigned to the category representing selected levels of importance used in the pairwise comparison process. Table 4 shows the pairwise comparison matrix created by the decision-maker to evaluate the relative importance of the three criteria with respect to the goal of selecting the most suitable building. This matrix serves as the input for calculating fuzzy weights using the geometric mean method, as described earlier in Section 4.

Table 3.
Fuzzy categories used in pairwise comparisons (Example 2).

Table 4.
Fuzzy pairwise comparison matrix.
Step 2: To determine the relative importance of the three criteria the fuzzy pairwise comparison matrix from Table 4 is processed using Equations (8) through (11), as outlined in Section 4. Table 5 represents the results.

Table 5.
Weight of criteria with geometry average method.
The final normalized crisp weights of the criteria are summarized as follows:
Dividing each by the sum:
Normalized weight vector =
Step 3: In this step, we construct the fuzzy decision matrix by evaluating the alternatives with respect to the four criteria. The evaluations are provided by the decision-maker using categories representing selected levels of importance to reflect the qualitative nature of the assessments. Each category representing selected levels of importance is associated with a corresponding fuzzy number that defines its membership function. These fuzzy scales ensure that the subjective judgments are systematically incorporated into the decision model. Table 6 represents the membership functions of categories representing selected levels of importance used in the decision matrix. Based on these definitions, the fuzzy decision matrix for the three alternatives is shown in Table 7.

Table 6.
Membership functions of categories representing selected levels of importance for Example 2.

Table 7.
Decision matrix.
Step 4: Since the evaluations in the decision matrix are expressed using categories representing selected levels of importance that share a common fuzzy scale (as shown in Table 6), normalization is not required. The fuzzy numbers are already dimensionless and directly comparable across all criteria. To incorporate the importance of each criterion into the decision-making process, we compute the weighted normalized decision matrix. The resulting matrix, which reflects both the performance of each alternative and the importance of each criterion, is shown in Table 8.

Table 8.
Weighted normalized decision matrix.
Step 5: In this step, we determine the PIS and NIS to evaluate how close each alternative is to the optimal and worst-case scenarios, respectively. Since direct comparison between fuzzy numbers is not straightforward, we first defuzzify the fuzzy values in the weighted normalized decision matrix using Equation (6). The resulting crisp scores for all values are presented in Table 9.

Table 9.
Defuzzified weighted normalized decision matrix for Example 2.
The PIS and NIS are obtained based on their respective definitions in Equations (19) and (20),
| PIS | (1.789 + 1.342α, 4.025 − 0.447α) | (1.515 + 1.136α, 3.409 − 0.379α) | (1.218 + 0.348α, 1.74) |
| NIS | (0.447 + 0.447α, 2.683 − 1.342α) | (0.379 + 0.379α, 2.273 − 1.136α) | (0.1740 + 0.174 α, 1.044 − 0.522 α) |
Step 6: To assess the relative performance of each alternative, we compute their separation distances from both the PIS and the NIS. These distances are calculated using Equations (18) and (19). The computed distances between each alternative and the PIS and NIS are summarized as follows:
These separation values are then used to compute the relative closeness coefficient of each alternative to the ideal solution. In practice, for defuzzified crisp values, the separation measures from the PIS and NIS can be obtained using Equations (16) and (17):
The final step in the proposed fuzzy hierarchical TOPSIS method involves calculating the relative closeness of each alternative to the Ideal Solution. This value indicates how close each option is to the optimal solution and serves as the basis for ranking the alternatives.
Based on the closeness values, Building L2 ranks highest and is thus identified as the most suitable location for the firm. The proposed method effectively integrates fuzzy judgment, hierarchical criteria, and linguistic evaluation to deliver a reliable decision-making outcome. This ranking highlights the dominance of L2 in financial and sustainability-related factors. To better illustrate the results, Figure 4 presents a bar chart of the closeness coefficients of the three alternatives. The graphical representation highlights the relative superiority of L2 compared to the others, while also showing the close performance of L1 relative to L2.
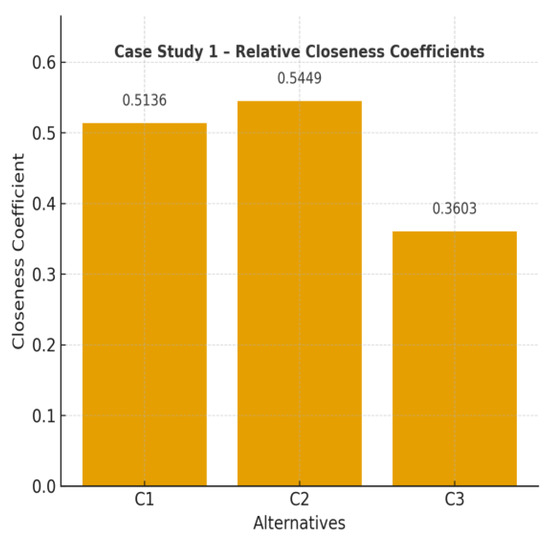
Figure 4.
Relative closeness coefficients of Example 2.
5.1. Comparative and Sensitivity Analysis—Example 2
In this subsection, a comparative analysis and sensitivity analysis are conducted in order to evaluate the robustness and reliability of the proposed FNGA–TOPSIS–ANP method. The comparative analysis contrasts the ranking results of the proposed approach with those obtained from other well-established MCDM techniques, including Classical TOPSIS, VIKOR, and ELECTRE. This ensures that the superiority of the identified best alternative is not method-dependent. Furthermore, a sensitivity analysis is performed by varying the criteria weights by ±10% to assess the stability of the final ranking against fluctuations in the decision parameters. These examinations provide further evidence of the consistency and validity of the proposed methodology.
5.1.1. Comparative Analysis—Example 2
Table 10 presents the comparative analysis of alternatives (L1, L2, L3) using four methods: FNGA–TOPSIS–ANP (proposed), Classical TOPSIS, VIKOR, and ELECTRE I. The results indicate that alternative L2 consistently achieves the highest rank across all methods, demonstrating the robustness of the proposed approach.

Table 10.
Comparative analysis of alternatives (Example 2).
5.1.2. Sensitivity Analysis-Example 2
Table 11 summarizes the sensitivity analysis of the TOPSIS method under ±10% variations in the criteria weights. In all scenarios, the ranking order remains unchanged (L2 L3 L1), which confirms the stability and reliability of the decision-making results. This demonstrates that minor perturbations in the weight distribution do not affect the superiority of alternative L2.

Table 11.
Summarizes the sensitivity analysis of Example 2.
Example 3.
(Case Study: Supplier Selection Using Cost Attributes).
In this section, the proposed fuzzy hierarchical TOPSIS method is applied to a real decision-making problem involving the selection of the most appropriate supplier. The decision-maker evaluates three alternatives S1, S2, and S3. The selection is based on three cost-related criteria C1 (Purchase Price), C2 (Transportation Cost), and C3 (Delivery Time). To construct the fuzzy pairwise comparison matrix, the decision-maker uses categories representing selected levels of importance to express preferences between criteria. Each term is mapped to a fuzzy number representing its membership function. These terms and their corresponding fuzzy values are presented in Table 12.

Table 12.
Fuzzy categories and their membership functions (Example 3).
These fuzzy values are then used to populate the pairwise comparison matrix of the criteria, which forms the basis for deriving fuzzy weights in the next step. Using the corresponding fuzzy numbers from Table 12, we construct the fuzzy pairwise comparison matrices as shown in Table 13.

Table 13.
Fuzzy pairwise comparison matrices.
To determine the relative importance of the criteria, we apply the fuzzy normal geometric average method, which improves upon the traditional extent analysis by addressing its known limitations (as highlighted in Wang et al., 2008 [21]).
| Goal | Weight | C1 | Weight | C3 | Weight | C2 | Weight |
| C1 | 0.708810 | C2 | 0.971127 | C1 | 0.084587 | C1 | 0.915413 |
| C2 | 0.195834 | C3 | 0.028873 | C2 | 0.915413 | C3 | 0.084587 |
| C3 | 0.095356 |
Normalized weight:
The decision matrix is shown as follows (Table 14):

Table 14.
Decision matrix of Example 3.
The parametric form of decision matrix is as follows (Table 15):

Table 15.
Parametric form of decision matrix in Example 2.
Next, we build the normalized decision matrix as given in Table 16.

Table 16.
Normalized decision matrix for Example 2.
Using these, we compute the weighted normalized fuzzy decision matrix in Table 15.
To compare fuzzy performance scores and identify the best and worst levels for each criterion, we must first defuzzify each fuzzy number in the weighted normalized decision matrix in Table 17 and the results are given in Table 18.

Table 17.
Weighted normalized decision matrix for Example 2.

Table 18.
Defuzzified weighted normalized decision matrix.
Next, using Equations (19) and (20), we determine PIS and NIS as below:
| PIS | |||
| NIS |
These benchmarks now allow us to calculate the separation distances for each supplier in the next step.
Now, we obtain separation measures:
To complete the supplier ranking process, we compute the separation measures between each supplier and the ideal solution using Equations (20) and (21):
Based on the relative closeness to the ideal solution, Supplier S1 is identified as the most appropriate choice.
5.2. Comparative and Sensitivity Analyses (Example 2)
This subsection reports a comparative analysis and a sensitivity analysis for Case Study 2 (supplier selection). The comparative analysis contrasts the proposed FNGA–TOPSIS–ANP results with Classical TOPSIS, VIKOR, and ELECTRE I using the defuzzified weighted-normalized matrix. The sensitivity analysis examines the stability of the rankings under ±10% variations applied individually to each criterion column of the weighted-normalized matrix (all criteria are costs).
5.2.1. Comparative Analysis—Example 2
Table 19 summarizes the rankings across methods. The proposed approach identifies S1 as the best supplier. VIKOR and ELECTRE I are consistent with this conclusion. Classical TOPSIS, computed from the same weighted-normalized matrix treating all criteria as costs, ranks S2 slightly higher than S1. This disparity is expected because Classical TOPSIS does not explicitly capture interdependencies among criteria and is sensitive to how cost-type criteria are scaled and aggregated. Overall, three out of four methods agree on S1 as the best alternative.

Table 19.
Comparative analysis—Example 2.
5.2.2. Sensitivity Analysis—Example 2
Table 20 reports the impact of ±10% perturbations applied to each criterion column of the weighted-normalized matrix (cost-type). In all scenarios, the Classical TOPSIS ranking remains stable (S2 S1 S3), indicating that the small variations in the column magnitudes do not change the relative order under this aggregation scheme. This stability complements the comparative findings and supports the robustness of the overall decision-making outcome reported in the manuscript.

Table 20.
Sensitivity analysis under ±10% perturbations—Example 2.
6. Conclusions
This study proposed a novel hybrid decision-making framework that integrates the Fuzzy Normal Geometric Average (FNGA) with the TOPSIS and ANP methodologies for multi-criteria decision-making (MCDM) problems under uncertainty. The main objective was to overcome the limitations of conventional fuzzy normalization and to provide a more robust and mathematically consistent approach for deriving criteria weights and ranking alternatives. The application of the proposed model to two case studies demonstrated its effectiveness in capturing decision-makers’ preferences and ensuring consistent rankings. Comparative analyses with other established MCDM techniques further confirmed the validity and reliability of the method. The primary contributions of this research are threefold. First, it introduces a normalization technique that avoids the inconsistencies found in conventional methods. Second, it integrates this normalization into the FNGA–TOPSIS–ANP framework, thereby enhancing the precision of weight derivation and ranking. Third, it validates the proposed approach through practical examples and comparative analysis against Classical TOPSIS, VIKOR, and ELECTRE I. These contributions strengthen the applicability of the method to real-world decision-making contexts such as supplier selection, logistics, and resource allocation. Despite its advantages, this study has several limitations. The empirical validation was limited to two case studies: future research should expand the application to larger datasets and more diverse domains. Furthermore, the method assumes static criteria weights, whereas in practice, preferences may evolve dynamically over time. Another limitation is the computational complexity when the number of criteria and alternatives becomes large, which may challenge implementation in highly complex systems. Future research could address these limitations by extending the framework to dynamic environments, incorporating group decision-making with heterogeneous preferences, and exploring synergies with machine learning approaches for automated weight estimation. In addition, testing the model in different industrial sectors and cross-cultural decision-making contexts would enhance its generalizability.
Author Contributions
Conceptualization, A.K.Y.; Methodology, K.O.; Software, A.K.Y.; Validation, A.J.; Formal analysis, A.J.; Investigation, A.K.Y.; Resources, K.O.; Data curation, A.J.; Writing—original draft, K.O. and A.H.-V.; Writing—review & editing, A.J.; Visualization, K.O.; Supervision, A.H.-V.; Project administration, A.H.-V. All authors have read and agreed to the published version of the manuscript.
Funding
Amir Karbassi Yazdi thanks the financial support from Fortalecimiento Grupos de Investigación UTA N° 8764-25.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to sincerely thank the four anonymous reviewers for their insightful comments and constructive suggestions, which have greatly contributed to improving the quality and clarity of this manuscript.
Conflicts of Interest
All authors confirm that they have no conflict of interest to declare.
References
- Yazdi, A.K.; Özaydin, G.; Tan, Y.; Ishizaka, A.; Li, J. Decarbonisation in supply chain management with blockchain technology: Using multi-criteria decision-making in industry 4.0. Ann. Oper. Res. 2025. [Google Scholar] [CrossRef]
- Hao, E.; Ma, J. Enhanced Managerial Decision Optimization in Financial Accounting Using the Picture Fuzzy MARCOS-Based MCGDM Approach. IEEE Access 2024, 12, 178171–178190. [Google Scholar] [CrossRef]
- Komasi, H.; Yazdi, A.K.; Jamini, D.; Tan, Y.; Ocampo, L. Sustainable industrial development potential of Iranian provinces using the integration of MEREC and TRUST methods. J. Manag. Anal. 2025, 1, 1–33. [Google Scholar] [CrossRef]
- Bashiri, M.; Jalili, M. Interactive permutation decision making based on genetic algorithm. In Proceedings of the 2010 IEEE International Conference on Industrial Engineering and Engineering Management, Macao, China, 7–10 December 2010; pp. 84–88. [Google Scholar]
- Aldawood, F.K. Multi-criteria optimization of polymer selection for biomedical additive manufacturing using analytic hierarchy process. Mater. Des. 2025, 256, 114369. [Google Scholar] [CrossRef]
- Nafei, A.; Azizi, S.P.; Edalatpanah, S.A.; Huang, C.-Y. Smart TOPSIS: A Neural Network-Driven TOPSIS with Neutrosophic Triplets for Green Supplier Selection in Sustainable Manufacturing. Expert. Syst. Appl. 2024, 255, 124744. [Google Scholar] [CrossRef]
- Han, F.; Alkhawaji, R.N.; Shafieezadeh, M.M. Evaluating sustainable water management strategies using TOPSIS and fuzzy TOPSIS methods. Appl. Water Sci. 2025, 15, 4. [Google Scholar] [CrossRef]
- Sadabadi, S.A.; Hadi-Vencheh, A.; Jamshidi, A.; Jalali, M. A New Index for TOPSIS based on Relative Distance to Best and Worst Points. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 695–719. [Google Scholar] [CrossRef]
- Theilig, K.; Vollmer, M.; Lang, W.; Albus, J. Multi-criteria decision-making for energy building renovation: Comparing exterior wall structures with the AHP, ANP, utility analysis, and TOPSIS. Build. Environ. 2025, 280, 113075. [Google Scholar] [CrossRef]
- Abootalebi, S.; Hadi-Vencheh, A.; Jamshidi, A. Ranking the Alternatives with a Modified TOPSIS Method in Multiple Attribute Decision Making Problems. IEEE Trans. Eng. Manag. 2022, 69, 1800–1805. [Google Scholar] [CrossRef]
- Roy, P.K.; Shaw, K.; Ishizaka, A. Developing an integrated fuzzy credit rating system for SMEs using fuzzy-BWM and fuzzy-TOPSIS-Sort-C. Ann. Oper. Res. 2023, 325, 1197–1229. [Google Scholar] [CrossRef]
- Singh, Y.; Bisht, D.C.S. Pythagorean fuzzy-based integration of ANP with TOPSIS -VIKOR-SAW techniques for hospital service quality evaluation. OPSEARCH 2025. [Google Scholar] [CrossRef]
- Sadabadi, S.A.; Hadi-Vencheh, A.; Jamshidi, A.; Jalali, M. An Improved Fuzzy TOPSIS Method with a New Ranking Index. Int. J. Inf. Technol. Decis. Mak. 2022, 21, 615–641. [Google Scholar] [CrossRef]
- Baral, S.P.; Parida, P.K.; Sahoo, D. Fuzzy TOPSIS technique for multi-criteria group decision-making: A study of crude oil price. Results Control Optim. 2025, 19, 100565. [Google Scholar] [CrossRef]
- Chang, W.; Fu, C. A multi-criteria group decision-making method based on consistency of interval-valued distributed preference relations. Inf. Fusion 2024, 107, 102315. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, W.; Li, D.; Zhan, J. Multiple attribute group decision making based on multigranulation probabilistic models, MULTIMOORA and TPOP in incomplete q-rung orthopair fuzzy information systems. Int. J. Approx. Reason. 2022, 143, 102–120. [Google Scholar] [CrossRef]
- Sarfaraz, A.H.; Yazdi, A.K.; Wanke, P.; Nezhad, E.A.; Hosseini, R.S. A novel hierarchical fuzzy inference system for supplier selection and performance improvement in the oil & gas industry. J. Decis. Syst. 2022, 32, 356–383. [Google Scholar] [CrossRef]
- Guerra, M.L.; Stefanini, L. Approximate fuzzy arithmetic operations using monotonic interpolations. Fuzzy Sets Syst. 2005, 150, 5–33. [Google Scholar] [CrossRef]
- Asady, B.; Zendehnam, A. Ranking fuzzy numbers by distance minimization. Appl. Math. Model. 2007, 31, 2589–2598. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Luo, Y.; Hua, Z. On the extent analysis method for fuzzy AHP and its applications. Eur. J. Oper. Res. 2008, 186, 735–747. [Google Scholar] [CrossRef]
- Arman, H.; Hadi-Vencheh, A. The revised extent analysis method. Concurr. Comput. 2021, 33, e6319. [Google Scholar] [CrossRef]
- Chen, S.-J.; Hwang, C.-L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1992; pp. 289–486. [Google Scholar]
- Wang, Y.-M.; Elhag, T. On the normalization of interval and fuzzy weights. Fuzzy Sets Syst. 2006, 157, 2456–2471. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Mohamadghasemi, A. A fuzzy AHP-DEA approach for multiple criteria ABC inventory classification. Expert Syst. Appl. 2011, 38, 3346–3352. [Google Scholar] [CrossRef]
- Arman, A.; Arman, H.; Hadi-Vencheh, A. The Homogeneous MADM Methods: Is Trade-Off between Attributes Important? Comput. Intell. Neurosci. 2022, 2022, 8629986. [Google Scholar] [CrossRef]
- Arman, H.; Hadi-Vencheh, A.; Kiani Mavi, R.; Khodadadipour, M.; Jamshidi, A. Revisiting the interval and fuzzy TOPSIS methods: Is Euclidean distance a suitable tool to measure the differences between fuzzy numbers? Complexity 2022, 2022, 7032662. [Google Scholar] [CrossRef]
- Arman, H. Fuzzy analytic hierarchy process for pentagonal fuzzy numbers and its application in sustainable supplier selection. J. Clean. Prod. 2023, 409, 137190. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Mohamadghasemi, A. An integrated AHP–NLP methodology for facility layout design. J. Manuf. Syst. 2013, 32, 40–45. [Google Scholar] [CrossRef]
- Liu, R.B.; Ruan, C.Y.; Li, D.F.; Xu, H. Hesitant fuzzy multi-attribute decision making method based on signed correlation and prioritization relationship. J. Nonlinear Convex Anal. 2019, 20, 1241–1252. [Google Scholar]
- Zhang, B.; Xu, L.; Shu, H.; Gao, S.; Li, M.; Liang, J.; Xu, K.; Xu, K. A Cloud Model-Based Optimal Combined Weighting Framework for the Comprehensive Reliability Evaluation of Power Systems with High Penetration of Renewable Energies. Sustainability 2025, 17, 2273. [Google Scholar] [CrossRef]
- Yang, M.; Lim, M.K.; Qu, Y.; Ni, D.; Xiao, Z. Supply chain risk management with machine learning technology: A literature review and future research directions. Comput. Ind. Eng. 2023, 175, 108859. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).