Dynamic Analysis of China’s Urban Economic Spatial Network and Its Multidimensional Impact on Building Carbon Emissions

Abstract

With the continuous development of cities, the network connections between Chinese cities have rapidly strengthened, and cities are gradually transforming from traditional production bases into economic platforms within dynamic spaces. In this process, urban building carbon emissions are not only determined by the city’s own resource and industrial advantages but are increasingly influenced by its position within the urban economic space network. This study constructs an urban economic spatial network using the gravity model, and based on dynamic data of building carbon emissions in Chinese cities from 2008 to 2020, develops a new analytical framework from the perspective of dynamic network evolution to examine the impact mechanisms of urban network position and residential activity intensity on building carbon emissions. The findings indicate that both residents’ activity intensity and city’s network position have a significant positive impact on per capita building carbon emissions, The impact coefficient between residential activity intensity and per capita building carbon emissions is 0.278 (p < 0.01). This conclusion remains valid after robustness and endogeneity tests. The city’s network position can mitigate the detrimental impact that residents’ activity intensity has on per capita building carbon emissions, particularly in the dynamic decision-making process, where cities can adjust their strategies based on their network position. The influence of city’s network position on per capita building carbon emissions exhibits multidimensional heterogeneity, with its effect being more significant in megalopolis and metropolis compared to large city and medium & small city. Specifically, in megalopolis, the network position impact coefficient is 0.22, significantly higher than 0.039 in medium & small city. These findings provide new perspectives for reducing building carbon emissions at the urban-level in the context of dynamic spatial mobility.

1. Introduction

With the increasing severity of global climate change, carbon reduction has become an important issue for countries to address environmental challenges [1,2]. In the context of accelerated urbanization, urban building carbon emissions (BCEs) have become one of the major sources of global carbon emissions [3]. Particularly in China, carbon emissions from the building sector account for a significant proportion [4]. According to data from the International Energy Agency (IEA), the building sector accounts for 30% of global final energy consumption and contributes 26% of global energy-related emissions [5]. With economic development and the ongoing urbanization process, the carbon emission pressure in the building sector is gradually increasing [6,7].

In response to this challenge, many countries and regions worldwide have adopted proactive measures. For instance, the European Union has set a target of achieving carbon neutrality by 2050 in its European Green Deal, with the building sector identified as one of the key areas for reducing carbon emissions [8]. In addition, Japan revised its building regulations in 2022, requiring all new buildings to achieve zero energy consumption by 2030, and all existing buildings to reach zero energy consumption by 2050. In 2023, the European Union amended the Energy Performance of Buildings Directive (EPBD), further supporting the goal of achieving climate neutrality in the building sector by 2050. In China, the Ministry of Housing and Urban-Rural Development implemented the “General Code for Building Energy Efficiency and Utilization of Renewable Energy”, which mandates that all new, expanded, or renovated buildings must comply with energy-efficient design standards [9]. According to the Research Report on Carbon Emissions in the Urban and Rural Construction Sector of China (2024 Edition) published by the China Building Energy Conservation Association [10], the total carbon emissions from buildings and the construction industry in 2022 were 5.13 billion tons of carbon dioxide (CO₂), accounting for 48.3% of the country’s energy-related carbon emissions. The high level of BCEs not only has a significant impact on the environment but also poses a severe challenge to the sustainable development of cities. Therefore, exploring and analyzing the factors influencing urban BCEs, particularly how to achieve a low-carbon transition based on urban economic structure and spatial layout, has become a key focus for both academics and policymakers.

With the ongoing urban development, the network connections between Chinese cities have expanded rapidly, and cities are progressively evolving from traditional production hubs into economic platforms within dynamic spaces. This transformation has made the geographical boundaries of urban economies more open. Compared to traditional agglomeration economies, network economies have become a key factor in understanding urban economic development and sustainability [11]. The closer economic connections between cities through networks have driven the restructuring of industrial chains and specialized production [12], while also promoting the flow of knowledge, technology, and resources across a broader spatial range [13].

In the process of urban development, the level of BCEs is no longer solely dependent on the city’s own resource endowments and industrial structure but is increasingly influenced by its position within the economic spatial correlation network [14]. The network position of a city determines its ability to exchange resources, collaborate on technologies, and facilitate the flow of information with other cities [15,16]. Therefore, studying the impact of city’s network position on BCEs becomes particularly important. It not only reveals the traditional influencing factors of geographic location and industrial structure but also emphasizes a city’s ability to interact and integrate resources within the economic spatial correlation network, thus providing a new perspective for developing more precise low-carbon policies and measures.

BCEs are a significant component of urban carbon emissions. With the increasing severity of global climate change, research on urban BCEs has gradually increased within the international community [17,18]. These studies aim to provide scientific evidence for urban climate governance and promote greater progress in cities’ efforts to achieve sustainable development goals. For example, Wang et al. [19] calculated urban BCEs using the City Statistical Data Method (CSD-M) and the Provincial Energy Balance Sheet Method (PEB-M) and calibrated the PEB-M using the results from CSD-M, reducing the error to 12.8%. They established a BCE database covering 362 cities in China and analyzed the spatiotemporal characteristics of urban BCEs. Chen et al. [20] focused on Hubei Province as a case study to investigate the feasibility of reaching peak emissions and emission reduction potential in advance at the prefecture-level cities. By combining statistical data and energy use estimates, they explored the relationship between building energy consumption and socioeconomic variables, generating spatial distribution factors to provide theoretical support for low-carbon development. Liu et al. [21] developed a model for setting the Carbon Emission Peak Target (CEPT) in the construction industry based on scenario analysis and Monte Carlo simulation. The model was applied to China’s construction sector, detailing CEPT from building types, emission sources, and indicators, and formulating a more detailed carbon peak roadmap. Zhan et al. [22] conducted a carbon emission assessment in an industrial area of China, covering four cities and three building types. They developed and compared four popular machine learning models, applying the best model for interpretability analysis. Uncertainty analysis was used to identify key factors influencing carbon emissions.

In addition, existing studies on the factors influencing BCEs have comprehensively analyzed the impact of various factors, including economic output [23], industrial structure [24], population size [25,26], and urbanization rate [27], on BCEs. For example, Luo et al. [28] proposed an integrated framework combining econometrics and machine learning algorithms to identify key influencing factors during the building operation phase and used scenario analysis methods to predict future building carbon emissions. Building operation phase are the main source of BCEs; therefore, A research framework addressing the influencing factors and driving mechanisms of carbon emissions during the building operation phase was developed by Chen et al. [29]. They conducted an empirical analysis of the spatiotemporal changes in building elements throughout this phase and proposed a roadmap for achieving carbon neutrality in the building industry. In addition, some studies have analyzed the spatiotemporal characteristics and influencing factors of carbon emissions of different building types from a meso level perspective. Xu et al. [30] studied the impact of demographic factors on residential building carbon emissions in Chongqing and constructed a system dynamics model to explore the transmission mechanism of demographic factors’ impact on residential carbon emissions, comparing the future impact of changes in various demographic factors on emissions. Wang et al. [31] explored the spatiotemporal characteristics of carbon emissions in China’s construction industry, analyzing the contribution of each province to the carbon emissions in the industry and their spatiotemporal heterogeneity. They further investigated the main factors influencing carbon emissions. In addition, the multi-factor model for urban BCE proposed by Wei et al. [32] provides a comprehensive and general carbon emission prediction system for the urban construction industry. The practical application of the model was demonstrated through a case study in Heilongjiang Province, China. Xiang et al. [33] analyzed the spatiotemporal evolution of carbon emissions from public buildings in China from 2010 to 2020, revealing regional differences in public BCEs. They further examined the spatial spillover effects of carbon emissions from public buildings in the tertiary sector.

Some studies have also used more complex models and methods [34]. For example, Wang et al. [35] employed the Generalized Dynamic Input-Output Model method, combined with a decoupling model, to analyze the relationship between income growth and carbon emissions. They predicted the peak time and trends of building operational carbon emissions in the Yangtze River Delta region through scenario analysis and the Monte Carlo method. Yu et al. [36] combined top-down and bottom-up accounting methods to calculate the building operational carbon emissions of 321 cities in China from 2015 to 2020, providing further carbon emission management tools at the urban-level.

In addition, with the flow of population, technology, information, and other factors between cities, an increasing number of scholars are beginning to explore the impact of urban spatial network on carbon emissions [37,38]. For example, Dong et al. [39] combined the modified gravity model with social network analysis techniques to study the spatial correlation network structure characteristics of carbon emissions in urban agglomerations as a whole and each urban agglomeration and analyzed the interaction mechanisms between cities and urban agglomerations. Social network analysis methods have also been widely applied in studying the carbon productivity of the livestock industry and its driving factors. A panel data model was developed by Li et al. [40] spanning from 2006 to 2021, employing social network analysis to quantitatively evaluate the spatial correlation network structure of livestock carbon productivity and to identify its driving factors. In addition, research on urban spatial network structures has garnered widespread attention. Scholars have explored the potential of urban networks in carbon emissions management by revealing the connections and interactions between cities. In this context, Sheng et al. [12] constructed an urban network using investment data from Chinese manufacturing enterprises and investigated the mechanisms and characteristics of how the position of cities in the network affects total factor carbon emission efficiency. These studies provide important insights into the impact of urban spatial network structures on carbon emissions. However, existing research is still focused on specific sectors or regions and has not incorporated a broader range of urban factors into the analysis.

These studies provided important references for understanding the spatiotemporal variation characteristics, influencing factors, and regional differences in BCEs. They also offer theoretical support for the formulation and implementation of carbon reduction policies. However, despite certain progress, existing studies mainly focus on macro-level analyses and lack in-depth exploration of BCEs at the urban level. This limits their reference value for implementing low-carbon buildings in most cities. In addition, existing studies mostly overlook non-externality factors within the urban economic spatial correlation network, such as the impact of a city’s network position and residents’ activity intensity on BCEs. Therefore, research should further focus on these non-externality factors and their interrelationships at larger spatial scales, particularly how to balance economic growth with building carbon reduction. As a result, the impact mechanism of the urban economic spatial correlation network on BCEs remains unclear and requires further in-depth study.

Based on this, the key bottleneck that needs to be addressed is how to identify and understand the main factors influencing urban BCEs in dynamic spaces, and to formulate more targeted emission reduction policies through in-depth analysis of these factors. By conducting precise carbon accounting and incorporating the perspective of the urban economic spatial correlation network, a more comprehensive exploration of the factors influencing BCEs can be achieved. Such research not only helps cities formulate tailored building carbon reduction policies based on local conditions but also provides critical support for achieving carbon neutrality goals. Overall, an in-depth study of the factors influencing BCEs from the perspective of urban economic spatial correlation network will provide dual support for carbon reduction in the building sector, serving as an essential component in driving green and high-quality development.

Building upon existing literature, this study conducts innovative exploration. Based on accurate carbon accounting, the study focuses on the urban-level in China, constructs an urban economic spatial correlation network using an improved gravity model, and incorporates the concept of networks into the regression model of BCE influencing factors. A new analytical framework is established to analyze the impact of residents’ activity intensity on urban BCEs and to examine whether the position of a city within the urban economic spatial correlation network affects this relationship. Finally, by setting up group dummy variables in the regression model, the study tests the multidimensional heterogeneity of the impact of city’s network position on BCEs. The research framework is shown in Figure 1.

Therefore, compared to previous studies, the main contributions of this research are as follows:

(1) The study explores the impact of residents’ activity intensity on urban BCEs and further analyzes how city’s network position affects this relationship. While existing literature widely examines the impact of factors such as urban economy, urbanization level, and population size on BCEs, few studies consider the relationship between residents’ activity intensity, city’s network position, and BCEs, particularly those focusing on the urban-level.

(2) A framework has been developed to analyze the relationship between urban economic spatial correlation network and BCEs. The study theoretically explains the impact mechanism of city’s network position on building carbon reduction, enriching the theoretical connotations and application scenarios of urban economic spatial correlation network. It expands the understanding of building carbon reduction in the context of networked spatial environments, bridging the gap between the fields of urban economic spatial correlation network and BCEs.

(3) A multidimensional heterogeneity regression model was used to examine the impact of city’s network position on BCEs in different types of cities. This study clarifies the role of urban economic spatial correlation network in promoting building carbon reduction and provides new strategic options for advancing the green and high-quality development of the urban building sector. It also offers scientific evidence for formulating context-specific urban building carbon reduction strategies in networked environments.

The remainder of this study is organized as follows: Section 2 introduces the research methods and data. The results are provided in Section 3. Section 4 presents discussion. Section 5 summarizes the conclusions.

2. Method and Data

2.1. Urban Economic Spatial Correlation Network

Based on extant scholarly literature, a predominant approach employed by researchers to ascertain the spatial correlation across cities involves the utilization of vector autoregressive (VAR) models and gravity models [42,43]. Nevertheless, the VAR model lacks the ability to accurately depict the interdependence among variables and is highly susceptible to variations in the lag order [24]. Consequently, this drawback can significantly undermine the characteristics of the network structure. By contrast, gravity models can provide a thorough understanding of the economic, geographical, and other attributes of cities. Furthermore, they may effectively uncover the evolutionary characteristics of spatial relationships among cities throughout time. However, conventional gravity models fail to account for the directional aspect of spatial correlation, leading to a uniform gravity intensity across cities [44]. However, it is important to acknowledge that variations in economic growth, levels of openness, and levels of innovation among cities can result in notable bidirectional and asymmetric spatial connections between them [45]. This study aims to expand upon the conventional gravity model by incorporating the concept of urban spatial correlation. This expansion is informed by the research conducted by many experts [24,44,45], as illustrated below,

$$F_{ij}={\displaystyle \frac{G_i}{G_i+G_j}}\cdot {\displaystyle \frac{\sqrt{P_i\cdot C_i}·\sqrt{P_j\cdot C_j}}{{\left(\frac{D_{ij}}{q_i-q_j}\right)}^2}}.$$

(1)

where $i$ and $j$ represent city. $G$ denotes GDP. $P$ denotes openness. $C$ denotes innovation. City innovation and openness are measured by the proportion of scientific expenditure and the amount of foreign investment in each city. In a general sense, the spatial correlation of cities is influenced by both economic and geographical distance variables. It is important to note that solely evaluating geographical distance considerations may result in variations within spatial correlation relationships. Therefore, this study uses the difference between geographical distance ($D_{ij}$) and per capita GDP ($q_i-q_j$) to denote the geographical economic “distance” between cities [45].

Through Formula (1), we can obtain the gravitational matrix between cities. The average value of each row in the matrix is used as a threshold. If $F_{ij}$ is greater than or equal to the threshold, the corresponding value of the spatial correlation matrix is 1, indicating that city $i$ and city $j$ have spatial correlation. If $F_{ij}$ is less than the threshold, the corresponding value of the spatial correlation matrix is 0, indicating that there is no spatial correlation between the two cities. Based on this, the study uses Gephi software (version 0.9.2) to visualize and analyze the urban economic spatial correlation network.

In this study, degree centrality, betweenness centrality, and eigenvector centrality are used to comprehensively and deeply assess the position and influence of cities in the economic spatial correlation network [46]. These indicators not only help reveal the economic connections between cities but also clarify the functions and roles of different cities within the network. Therefore, the selection of these centrality indicators is crucial to this study, and their necessity is reflected in the following aspects:

(1) Degree Centrality

Degree Centrality (DC) describes the importance of a city from the perspective of its direct connections. Specifically, it measures the number of direct links a city has with other cities, reflecting its connectivity and frequency of interaction within the network. Cities with high degree centrality are typically “hubs” in the network, maintaining direct economic ties with more cities, indicating that these cities play an important role in the regional economy. DC reflects the city’s economic activity level, and cities with high DC are often important commercial or logistics hubs. According to existing studies [45,46], the specific calculation formula is as follows.

$$C_D(v)={\displaystyle \frac{d(v)}{N-1}}.$$

(2)

where $d(v)$ is the number of edges connected to node $v$. $N$ is the total number of nodes in the urban economic spatial network.

(2) Betweenness Centrality

Betweenness Centrality (BC) describes the importance of a city in the network from the perspective of its role as an intermediary or bridge. It measures the frequency with which a city appears on the shortest paths between other cities, reflecting its role as a hub for the flow of information or resources within the network. Cities with high betweenness centrality typically connect multiple cities, controlling the flow of resources and information. These cities play a key intermediary role and are core nodes that facilitate and control interactions among other cities in the network. According to existing studies [45,46], the specific calculation formula is as follows.

$$C_B(v)={\displaystyle {\sum }_{s\ne v\ne t}\frac{{\sigma }_{st}(v)}{{\sigma }_{st}}}.$$

(3)

where ${\sigma }_{st}(v)$ is the number of those paths that pass-through node $v$. ${\sigma }_{st}$ is the total number of shortest paths from node $s$ to node $t$. $s$, $t$, and $v$ are nodes in the urban economic spatial network.

(3) Eigenvector Centrality

Eigenvector Centrality (EC) describes the importance of a city in the network from the perspective of its overall influence. It not only considers the number of direct connections a city has with other cities but also focuses on the quality of these connections, i.e., the importance of the cities it is connected to. Cities with high eigenvector centrality are typically closely linked with other important cities, placing them at the core of the network and giving them greater economic and social influence. Consequently, cities with high EC often serve as centers of attraction for international business and high-tech investments. According to existing studies [45,46], the specific calculation formula is as follows.

$$C_E(v)={\displaystyle \frac{1}{\lambda }}{\displaystyle {\sum }_{t\in M(v)}{C}_E(t)}.$$

(4)

where $C_E(t)$ is the eigenvector centrality of node $t$. $M(v)$ is the set of all nodes directly connected to node $v$. $\lambda$ is a scaling factor associated with the largest eigenvalue of the adjacency matrix.

In summary, these indicators reveal the position and role of cities in the economic spatial network from different perspectives: degree centrality reflects connectivity, betweenness centrality reveals intermediary roles, and eigenvector centrality showcases overall influence. By integrating the analysis of these three measures, this study is able to provide a comprehensive assessment of the multidimensional influence of cities within urban economic spatial correlation network.

2.2. Regression Model

The development of urban economic spatial correlation networks enhances the external connections of cities and fosters the circulation of resources across different regions. As discussed in the introduction, existing literature has primarily focused on the impact of urban inherent attributes on BCEs. The influence of urban networks on BCEs has been overlooked.

Additionally, as an important component of the urban system, the activity intensity of residents has a significant impact on the sustainable development of cities. Nighttime lights directly indicate the degree of industrial development and urban expansion at the local level [47,48]. It may also serve as an indicator of the spatial distribution of the population [49]. Nighttime lights can somewhat characterize the intensity of human activity. Consequently, this study employs nighttime light data to assess the residents’ activity intensity.

A new building carbon accounting method combines top-down and bottom-up carbon emission accounting approaches, aiming to quantitatively analyze carbon emissions at each stage of the building lifecycle. Within this accounting framework, we conducted a detailed calculation of BCEs for 291 cities in China from 2008 to 2020 in our previous research [41].

Per capita building carbon emissions (PCBCEs) help evaluate the construction industry’s environmental impact and guide the development of emission reduction strategies. In this study, we define the per capita building carbon emissions of a city as the total building carbon emissions of the city divided by its resident population.

$$PCBC{E}_y^c={\displaystyle \frac{BC{E}_y^c}{PO{P}_y^c}}.$$

(5)

where $PCBC{E}_y^c$ denotes per capita building carbon emissions of city $c$ in the year $y$. $BC{E}_y^c$ is building carbon emissions of city $c$ in the year $y$. $PO{P}_y^c$ is the permanent resident population of city $c$ in the year $y$.

Based on this, this study analyzes whether the residents’ activity intensity affects PCBCEs and how the city’s network position affects their relationship. The Ordinary Least Squares (OLS) regression model is used to estimate the impact of each indicator on the dependent variable, ensuring the accuracy and reliability of the regression results. Therefore, OLS regression model [50] was used to depict the influence relationship between them, as shown below.

$$PCBC{E}_y^c=\delta M_y^c+\gamma H_y^c\times M_y^c+\alpha H_y^c+\beta X_{i,y}^c+a.$$

(6)

where $M$ denotes residents’ activity intensity. $H$ denotes city’s network position. $H\times M$ denotes interaction term. $X_{i,y}^c$ is control variables, which are the traditional variables used as main factors affecting PCBCEs. $a$ is constant term.

The critical parameters in this study are $\delta$ and $\gamma$, which explain whether PCBCEs are affected by residents’ activity intensity and whether this affects the city’s network position. According to existing studies [50], the differential equation regarding residents’ activity intensity is as follows.

$${\displaystyle \frac{\partial C{E}_y^c}{\partial M_y^c}}=\delta +\gamma H_y^c.$$

(7)

If $\gamma$ is significant, this indicates that the impact of residents’ activity intensity on PCBCEs depends on the city’s network position. If $\delta >0$ and $\gamma <0$, it means that the residents’ activity intensity is not conducive to building carbon reduction, the city’s network position can mitigate this adverse effect.

2.3. Data Sources

The data used in this study mainly consists of two types: (1) indicator data for constructing the urban economic spatial correlation network, and (2) data on control variables and the dependent variable for regression model. For the former, the level of urban innovation and openness is measured by the proportion of scientific expenditures to fiscal expenditures and the amount of foreign investment in each city. The data for urban GDP, per capita GDP, the proportion of scientific expenditure, and the amount of foreign investment are sourced from the China City Statistical Yearbook. Data on urban BCEs comes from existing research [41]. Additionally, to characterize residents’ activity intensity, this study uses city nighttime light data obtained from the Visible Infrared Imaging Radiometer and the Defense Meteorological Satellite Program [51].

The representativeness and reliability of the data are crucial to this study. The data on urban GDP, per capita GDP, the proportion of scientific expenditures to fiscal expenditures, and the amount of foreign investment are all sourced from the China City Statistical Yearbook, which provides authoritative statistical data nationwide and is highly reliable. The data on urban BCEs is based on existing research [41], making it highly representative. In addition, nighttime light data, as an indirect indicator of residential activity intensity, has been widely used in urban studies. The data obtained through satellite remote sensing technology has high spatial resolution and accuracy. In addition, this study uses Gephi software (version 0.9.2) to visualize the urban economic spatial association network and employs the OLS regression method for regression analysis. Gephi is a widely used network analysis tool that can effectively handle large-scale network data and visually display network structures. The data sample covers 266 cities from 2008 to 2020, used for network construction and regression estimation.

To gain a deeper understanding of the heterogeneity among cities, this study categorizes cities based on geographic location and population size and explores the impact of city’s network position on BCEs in different types of cities. Given the significant differences across cities in various aspects, city classification is crucial when analyzing the influence of city’s network position on BCEs. We divided the 266 cities into seven main regions based on geographic location: North, Northeast, East, Central, South, Southwest, Northwest regions. Additionally, we considered the population size of cities, classifying them into Megalopolis, Metropolis, Large city, Medium and small city, to further examine the impact of city’s network position on BCEs in cities of different sizes. Specific classification and criteria are provided in Supplementary Material Tables S1 and S2.

This classification method helps formulate and implement targeted carbon reduction policies based on the characteristics of each region, ensuring precise policy implementation. Through this analysis, the study explores in-depth the impact of city’s network position on BCEs in cities of different types and provides strong policy recommendations for low-carbon city development.

3. Results

3.1. Analysis of Network Structural Characteristics

This study constructs an urban economic space correlation matrix based on the gravity model and uses a 0–1 matrix to build the economic spatial correlation network for 266 cities from 2008 to 2020. Through this analysis, the aim is to visually demonstrate the development trends of the urban economic space structure of China’s 266 cities between 2008 and 2020. Due to space limitations, this study does not present the urban economic space correlation network diagrams for each year from 2008 to 2020. Instead, the network diagram for 2020 is chosen as an example to illustrate the urban economic spatial correlation network.

Using the network analysis and visualization software Gephi, the economic spatial correlation network diagram for 266 cities in China in 2020 was plotted. As shown in Figure 2, where the circles represent the 266 cities, and the lines indicate economic connections between cities. The size of the circle reflects the influence of the city; the larger the circle, the closer the city is to the center of the network and the stronger its economic correlation with other cities. It is worth noting that, over time, although the network has undergone dynamic evolution, the cities at the network’s core have remained largely unchanged. From the diagram, distinct network structural features can be observed, especially with large cities such as Shanghai, Beijing, Hangzhou, Nanjing, Shenzhen, and Guangzhou at the center. Other cities are more closely connected to these core cities, demonstrating strong economic radiation effects and spatial agglomeration characteristics. These cities not only occupy important geographic positions but also play a key role in the economic network, guiding economic interactions with surrounding cities.

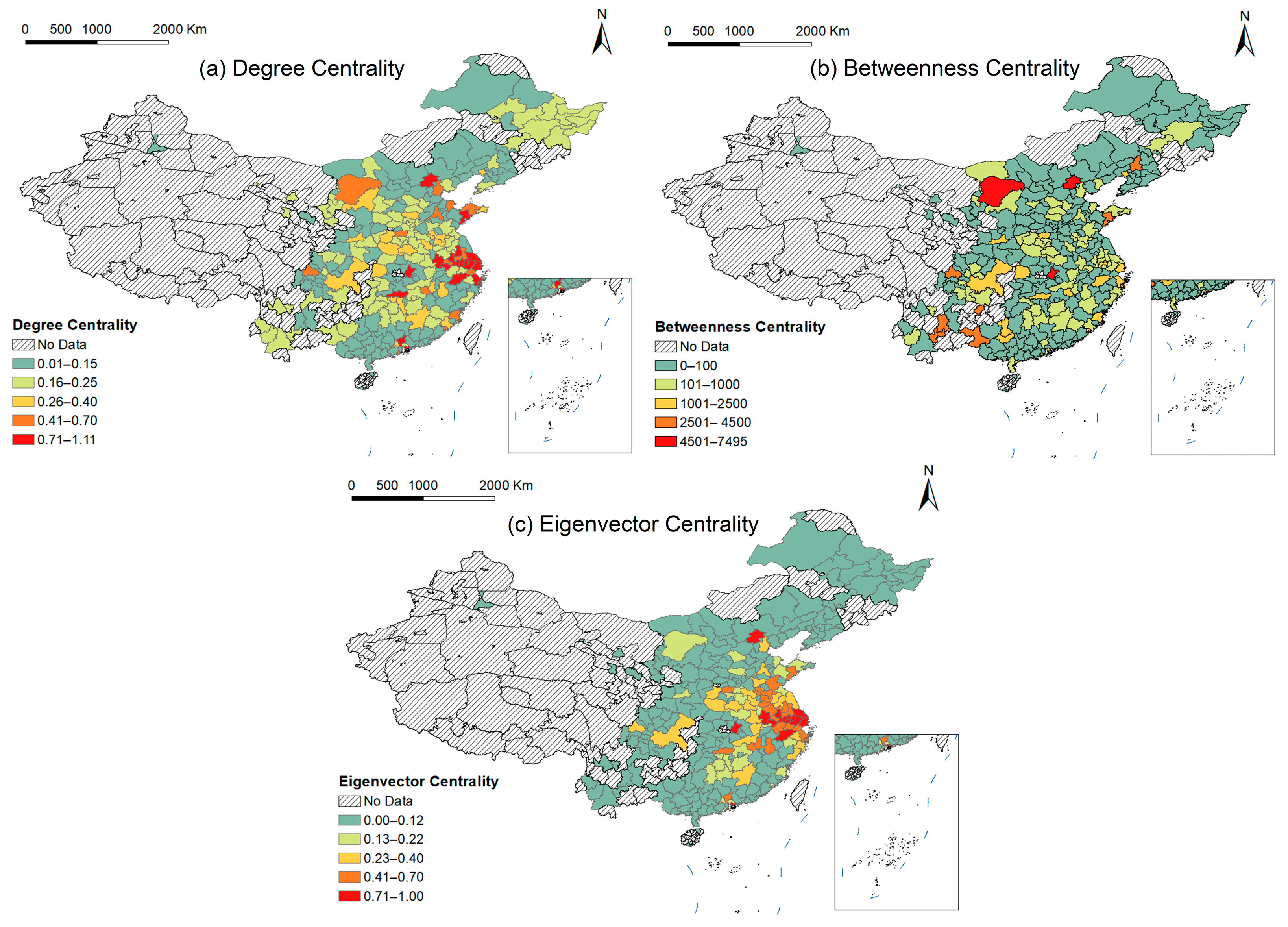
By analyzing degree centrality, betweenness centrality, and eigenvector centrality, this study examines the position of each city in the urban economic spatial correlation network in 2020. The specific results are shown in Figure 3, which illustrates the performance of cities in the network under different centrality indicators.

Firstly, degree centrality reflects the number of direct connections between cities. High-degree centrality cities, such as Beijing, Shanghai, Guangzhou, Hangzhou, Nanjing, and Shenzhen, with values of 1.11, 1.10, 1.06, 1.05, 1.02, and 0.98, respectively, play key roles in economic interactions and occupy central positions in the urban economic spatial correlation network. These cities, as core nodes of economic activity, drive resource flow and economic growth in surrounding areas. In contrast, cities in remote regions, such as Heihe and Xianning, have lower degree centrality values of 0.05 and 0.06, indicating limited direct economic connections and lower participation in overall economic activity. These cities are typically on the periphery of the regional economic system and less involved in large-scale interregional economic interactions. High-degree centrality cities, with strong economic connections, are central to regional economic development, while low-degree centrality cities tend to play more marginal roles, with limited economic interactions and resource flow.

Secondly, betweenness centrality measures a city’s role as an intermediary, indicating its importance in connecting other cities. Cities such as Beijing, Wuhan, Chengdu, Qingdao, and Xiamen have high betweenness centrality, meaning they serve as key hubs in economic interactions and play an important role in cross-regional economic activities, promoting economic flow and cooperation. In contrast, some inland cities, especially in the northwest, have low betweenness centrality, indicating they are on the periphery of the urban economic spatial correlation network with limited cross-regional economic interactions. High-betweenness cities facilitate regional cooperation and resource flow, breaking economic barriers, while low-betweenness cities are more isolated with less economic influence on other regions.

Additionally, eigenvector centrality measures a city’s influence within the overall urban economic spatial correlation network. High eigenvector centrality cities are mainly concentrated in the economically developed eastern and southern coastal regions, such as Beijing, Shanghai, Shenzhen, Hangzhou, and Nanjing, with values of 0.99, 1.10, 0.98, 1.02, and 1.05, respectively. These cities are not only regional economic hubs but also central to national economic activity, reflecting their key position and far-reaching impact on the network. They play a significant role in resources, information, and technology flow, with strong economic connections and network effects. In contrast, cities in the central and western regions, such as those in Tibet, Gansu, and Qinghai, have lower eigenvector centrality, indicating their peripheral position in the urban economic spatial correlation network. These cities experience less economic interaction, and their resource flow is less active compared to coastal cities, limiting their influence on the overall urban economic spatial correlation network. High eigenvector centrality cities play a more crucial role in economic activities, connecting various regions and promoting cross-regional resource flow and development, while low eigenvector centrality cities are more marginalized with weaker economic influence and interaction capabilities.

Therefore, the three indicators—degree centrality, betweenness centrality, and eigenvector centrality—provide a comprehensive view of the different positions of cities in the economic spatial correlation network. Degree centrality highlights the density of connections, betweenness centrality reflects the city’s role as an intermediary in cross-regional economic activities, and eigenvector centrality demonstrates the city’s centrality in the network and its efficiency in information flow. These analyses help to understand the position of each city within China’s economic space and their influence on national economic interactions.

3.2. Impact Relationship Analysis

The results based on regression are given in

Table 1. BCEs, Residents’ activity intensity, and City’s network position: OLS regression estimates.

Dependent Variable: PCBCEs
	(1)	(2)	(3)
Residents’ activity intensity	0.278 *** (10.25)	0.080 *** (3.79)	0.117 *** (5.15)
Residents’ activity intensity × DC	−0.489 *** (−12.75)
Residents’ activity intensity × BC		−0.043 * (−1.86)
Residents’ activity intensity × EC			−0.377 *** (−11.72)
DC	0.400 *** (14.29)
BC		0.075 *** (3.63)
EC			0.463 *** (17.93)
Population	−0.150 *** (−7.18)	−0.070 *** (−3.36)	−0.185 *** (2.40)
GDP	0.195 *** (6.25)	0.102 *** (3.43)	0.174 *** (5.75)
PCGDP	0.306 *** (12.41)	0.413 *** (16.40)	0.319 *** (13.69)
UR	0.066 *** (3.43)	0.095 *** (4.86)	0.080 *** (4.17)
Observations	3458	3458	3458
R2	0.418	0.382	0.433

Note: t-statistics are shown in parentheses under the coefficient estimates; *** indicates significant at the 1% level, * indicates significant at the 10% level.

. The city’s network position contains DC, BC, and EC. Considering the strong association between them, to avoid potential covariance problems, this paper analyzes these three variables. The effect of the residents’ activity intensity on the PCBCEs and whether the city’s network position impacts this influence relationship are obtained through the Formulas (6) and (7).

Findings indicate that control variables have intuitive signs. Indeed, the data demonstrate that rapid economic growth and urbanization have a positive impact on PCBCEs. In contrast, population size has a significant negative effect. The existing literature indicates that economic growth and urbanization encourage BCEs, and the impact of these factors has been verified.

The impact between residents’ activity intensity, the city’s network position, and PCBCEs are a significant finding of our study. The primary barrier to PCBCE reduction, as seen in Table 1, is the residents’ activity intensity. Furthermore, the city’s network position has positive and significant coefficients. In other words, the city’s network position positively impacts the PCBCEs, meaning that the PCBCEs rise with DC, BC, and EC.

The most important part of this study is to present the interaction effect between the residents’ activity intensity and the city’s network position, which is at the heart of the research question of this study. The interaction term ($H\times M$) coefficients are statistically significant at conventional levels. This suggests that the city’s network position affects the relationship between residents’ activity intensity and PCBCEs. The negative values of the coefficients indicate that as the city’s network position increases, the impact of residents’ activity intensity on PCBCEs decreases.

3.3. Robustness and Endogeneity Test

We conducted robustness and endogeneity tests to evaluate the sensitivity of research results. Testing with additional estimates using alternative measures of PCBCEs. We treat the energy consumption in buildings as the dependent variable rather than the PCBCEs used in the previous estimation. The intuition behind this is that the energy consumption can approximate PCBCEs in recent years.

Table 2. Robustness test.

Dependent Variable: Per Capita Energy Consumption in Buildings
	(1)	(2)	(3)
Residents’ activity intensity	0.229 *** (10.73)	0.106 *** (4.90)	0.139 *** (5.99)
Residents’ activity intensity × DC	−0.479 *** (−12.18)
Residents’ activity intensity × BC		−0.029 * (−1.23)
Residents’ activity intensity × EC			−0.377 *** (−11.46)
DC	0.410 *** (14.29)
BC		0.077 *** (3.63)
EC			0.482 *** (18.24)
Population	−0.116 *** (−5.42)	−0.036 * (−1.70)	−0.156 *** (−7.22)
GDP	0.146 *** (4.57)	0.054 * (1.77)	0.129 *** (4.18)
PCGDP	0.279 *** (11.04)	0.389 *** (15.06)	0.291 *** (12.19)
UR	0.069 *** (3.51)	0.097 *** (4.84)	0.084 *** (4.25)
Observations	3458	3458	3458
R2	0.388	0.352	0.406

Note: t-statistics are shown in parentheses under the coefficient estimates; *** indicates significant at the 1% level, * indicates significant at the 10% level.

below displays the results. Overall, the estimations in Table 2 support the findings in Table 1.

One of the study’s primary concerns is whether the negative impact of the interaction term is misleading because of certain confounding factors. This study employed the lagged value of the city’s network position as an explanatory variable and reran the model to account for any endogeneity problems that might arise from reverse causality. This can increase the dependability of the model’s results and lessen the impact of noise variables on the interaction term’s coefficient.

Table 3. Endogeneity test.

Dependent Variable: PCBCEs
	(1)	(2)	(3)
Residents’ activity intensity	0.283 *** (10.01)	0.094 *** (4.24)	0.124 *** (5.20)
Residents’ activity intensity × DC	−0.465 *** (−11.56)
Residents’ activity intensity × BC		−0.019 * (−0.77)
Residents’ activity intensity × EC			−0.346 *** (−10.27)
DC	0.389 *** (13.32)
BC		0.067 *** (3.06)
EC			0.438 *** (16.25)
Population	−0.141 *** (−6.60)	−0.058 *** (−2.76)	−0.172 *** (−7.91)
GDP	0.212 *** (6.37)	0.110 *** (3.45)	0.184 *** (5.72)
PCGDP	0.306 *** (12.00)	0.413 *** (15.68)	0.331 *** (13.76)
UR	0.066 *** (3.30)	0.094 *** (4.62)	0.077 *** (3.86)
Observations	3192	3192	3192
R2	0.432	0.400	0.444

Note: t-statistics are shown in parentheses under the coefficient estimates; *** indicates significant at the 1% level, * indicates significant at the 10% level.

displays the lagged variable model’s robustness test results. The robustness of the model results is maintained even after accounting for endogeneity concerns, by the observation that the city’s network position regression coefficients are still significantly positive and the interaction term is significant and negative.

3.4. Multidimensional Heterogeneity Analysis

This study further divides cities into North, Northeast, East, Central, South, Southwest, Northwest, and Megalopolis, Metropolis, Large City, Medium and Small City, respectively, based on geographic location and population size, to analyze the multidimensional heterogeneity of the impact of city’s network positions on PCBCEs. The multidimensional heterogeneity of the effect of the city’s network position on PCBCEs is examined by adding a cross-term of the city’s network position with the grouping dummy variables in the regression equation. Considering space constraints, we only present the results of the spatial heterogeneity test using DC to characterize the city’s network position.

The spatial heterogeneity test results for the city’s network position, represented by DC, are displayed in

Table 4. Results of heterogeneity test by geographical location.

Dependent Variable: PCBCE
	North	Northeast	East	Central	South	Southwest	Northwest
DC	0.160 *** (7.31)	0.158 *** (7.25)	0.068 *** (2.72)	0.200 *** (9.07)	0.190 *** (8.94)	0.168 *** (7.78)	0.174 *** (8.04)
DC × North	0.063 *** (4.51)
DC × Northeast		0.089 *** (6.63)
DC × East			0.149 *** (8.51)
DC × Central				−0.079 *** (−2.15)
DC × South					−0.175 *** (−12.42)
DC × Southwest						−0.081 *** (−5.87)
DC × Northwest							−0.054 *** (−1.48)
Population	−0.049 ** (−2.51)	−0.042 *** (−2.12)	−0.058 *** (−2.95)	−0.037 * (−1.85)	−0.090 *** (−4.59)	−0.033 * (−1.66)	−0.054 *** (−4.01)
GDP	0.020 * (0.70)	0.027 *** (0.97)	0.048 * (1.72)	0.013 * (0.46)	0.081 *** (2.93)	0.030 * (1.10)	0.024 * (0.85)
PCGDP	0.386 *** (15.97)	0.391 *** (16.23)	0.382 *** (15.92)	0.386 *** (16.01)	0.381 *** (16.03)	0.387 *** (16.01)	0.386 *** (15.95)
UR	0.117 *** (6.29)	0.123 *** (6.60)	0.116 *** (6.28)	0.111 *** (5.99)	0.140 *** (7.61)	0.107 *** (5.74)	0.123 *** (6.56)
Observations	3458	3458	3458	3458	3458	3458	3458
R2	0.394	0.398	0.403	0.396	0.416	0.396	0.393

Note: t-statistics are shown in parentheses under the coefficient estimates; *** indicates significant at the 1% level, ** indicates significant at the 5% level, and * indicates significant at the 10% level.

. According to Table 4, the fitting coefficients of DC × North, DC × Northeast, and DC × East are all significant and positive. At the same time, DC × Central, DC × South, DC × Southwest, and DC × Northwest are all significant and positive. It indicates that the city’s network position contributes significantly more to the PCBCEs of the North, Northeast, and East cities than the other cities. In contrast, it contributes considerably less to the PCBCEs of the Central, South, and Southwest cities than others.

Table 5. Results of heterogeneity test by population size.

Dependent Variable: PCBCEs
	Megalopolis	Metropolis	Large City	Medium and Small City
DC	0.220 *** (9.50)	0.098 *** (4.11)	0.082 *** (4.07)	0.039 *** (2.47)
DC × Megalopolis	0.119 *** (5.38)
DC × Metropolis		0.121 *** (7.74)
DC × Large City			−0.065 *** (−3.43)
DC × Medium and small city				−0.005 ** (−0.35)
Population	−0.069 *** (−3.46)	−0.089 *** (−4.43)	−0.065 *** (−3.23)	−0.063 *** (−3.13)
GDP	0.118 *** (3.61)	0.080 *** (2.80)	0.078 *** (2.84)	0.106 *** (4.04)
PCGDP	0.345 *** (13.52)	0.382 *** (15.86)	0.470 *** (18.81)	0.444 *** (18.62)
UR	0.121 *** (6.50)	0.108 *** (5.83)	0.099 *** (5.12)	0.114 *** (5.98)
Observations	3458	3458	3458	3458
R2	0.395	0.401	0.382	0.380

Note: t-statistics are shown in parentheses under the coefficient estimates; *** indicates significant at the 1% level, ** indicates significant at the 5% level.

reports the test results using DC to portray the city’s network position. As indicated by Table 5, the fit coefficients of DC × Megalopolis and DC × Metropolis are significantly positive, while DC × Large City and DC × Medium and Small City are significantly negative. The test results show that the city’s network position substantially contributes to BCEs in Megalopolis and Metropolis. Stated differently, a city’s contribution to PCBCEs increases with its position within the network.

4. Discussion

There are significant differences in degree centrality, betweenness centrality, and eigenvector centrality across different regions of China (as shown in Figure 3), which can be analyzed from the perspective of regional heterogeneity. The Northeast region shows notable differences in economic development, industrial structure, and urbanization processes compared to the Eastern and Southern coastal regions. This regional heterogeneity is reflected in the centrality indicators.

Firstly, the economic development level in the Northeast region differs significantly from the Eastern coastal areas, especially in industrial structure. Traditional heavy industries dominate the Northeast’s economy, while the development of innovation and high-tech industries lags behind. The weak connectivity between industries results in a more marginal position in the economic network, with fewer intercity connections, affecting centrality and network interaction. Secondly, the urbanization process and population movement in the Northeast also reflect regional heterogeneity. Compared to the high population density and rapid urbanization in the Eastern coastal cities, the Northeast has experienced population outflow in recent years, limiting participation in innovation activities and reducing interaction and connectivity within the economic network, thus suppressing centrality. Additionally, infrastructure development and regional connectivity contribute to the lower centrality in the Northeast. Despite improvements in transportation infrastructure, it remains weaker compared to the developed Eastern and Southern regions, limiting intercity connectivity, cross-regional collaboration, and resource flow, leading to lower betweenness and eigenvector centrality.

BCEs play a crucial role in cities development and are one of the key factors in achieving urban sustainability. Exploring the factors influencing urban BCEs is vital for cities to develop effective low-carbon policies and achieve carbon neutrality goals. As the introduction noted, most research to date on the subject of factors influencing BCEs has concentrated on the macro-level effects of urban areas, primarily examining factors like population size, economic level, and urbanization rate. However, as the main body of mobile space, urban areas’ BCEs depend not only on their own attributes but also on their ability to dominate, absorb, and utilize network resources. Unfortunately, existing studies have failed to pay attention to the profound impact of the rapid development of urban economic spatial correlation networks on BCEs. Therefore, this study introduces the concept of networking into research on the influencing factors of BCEs based on existing research. The results of the research show that BCEs are significantly impacted by residents’ activity intensity as well as the city’s network position. Moreover, the impact of residents’ activity intensity on BCEs is influenced by the city’s position. Firstly, cities, with their higher levels of economic and social development, have greater resources to improve urban infrastructure and implement environmental protection measures, leading to a reduction in carbon emissions. For instance, governments can adopt cleaner energy sources such as solar and wind energy, thereby reducing carbon emissions from urban buildings. Secondly, cities with higher positions in the network often have larger populations, which creates favorable conditions for implementing sharing economy practices. Additionally, these cities tend to have more public facilities, such as parks and sports centers, which encourage people to engage in outdoor activities, reducing the need for indoor activities and thus mitigating the impact of residents’ activity intensity on BCEs. In summary, the economic and social development level, as well as the population density characteristics, of cities enable them to effectively reduce carbon emissions from buildings and residential activities. This explains why cities with higher positions have a lower impact of the residents’ activity intensity on BCEs.

According to the above analysis, this study discovered that the urban economic spatial correlation network provides the foundation for cities to balance building carbon reduction with economic expansion on a broader spatial scale. This indicates that in a network space setting, cities are able to overcome geographic constraints, access vital resources from the urban economic spatial network, and create mutually beneficial conditions for both building carbon reduction and urban economic development. Therefore, relative to geographical location, the city’s position in the network is becoming increasingly important.

Moreover, this study divides cities based on geographical location and population size, respectively, and analyzes the multidimensional heterogeneity of the impact of cities’ positions on BCEs. The findings reveal that the impact of the city’s position on urban BCEs varies widely in different dimensions, such as geographic location and population size. Due to different geographical locations, cities have varying energy requirements, leading to different impacts on BCEs. The size of a city’s population also affects its BCEs since larger cities tend to have higher energy consumption. In the past, small and medium-sized cities have commonly faced problems with wasteful and inefficient buildings and infrastructure in urban construction. Therefore, to reduce BCEs, government policies cannot be generalized or implemented in a one-size-fits-all manner. Instead, in order to develop emission reduction policies that take into account the variability of carbon emissions from urban buildings, policymakers must take into account the emission characteristics and potential of various urban groups. Furthermore, targeted measures to reduce BCEs can challenge the conventional development mode of “high consumption, high fees, and high emissions” prevalent in the construction sector of small and medium-sized cities.

In this study, we analyze the relationship between urban BCEs and the urban economic spatial correlation network. Unlike similar studies, our research focuses on how the position of cities within the network space influences their BCEs, rather than solely on urbanization or economic development levels. For example, studies using the spatiotemporal geographically weighted regression (GTWR) model to analyze panel data from 30 Chinese provinces have explored the impact of urbanization on residential BCEs [52]. It reveals the spatiotemporal heterogeneity of urbanization’s impact on carbon emissions across different regions and periods, considering five dimensions: population, economy, land, lifestyle, and ecology. In contrast, our study focuses on how city’s network position provides favorable resources and conditions, thereby effectively reducing BCEs.

Although both studies explore the factors influencing BCEs, our study offers a novel perspective. Our study introduces the concept of networks, demonstrating how cities’ interactions and resource acquisition in the network space, through their network position, can reduce BCEs. This research framework offers a more systematic and multidimensional understanding, helping policymakers to consider the advantages and resource distribution of cities on a broader spatial scale when designing low-carbon policies, thus enabling more precise and effective emission reduction measures. This perspective differs from the existing studies by emphasizing the role of the urban economic spatial correlation network, rather than focusing solely on traditional factors such as population size or economic development in the process of reducing BCEs.

5. Conclusions

This study, based on building carbon emission data from 266 cities and urban economic spatial correlation network between 2008 and 2020, explores the impact mechanism of residents’ activity intensity and the city’s position within the spatially related network on building carbon emissions. The study focuses on analyzing the interactive effects between residents’ activity intensity and city’s network position and further examines the multidimensional heterogeneity of the impact of city’s network position on per capita building carbon emissions. Based on the analysis above, the following conclusions and policy implications are drawn:

(1) The residents’ activities intensity and the city’s network position have a significant positive impact on per capita building carbon emissions, which are the main obstacles to reducing building carbon emissions. This conclusion holds even after robustness and endogeneity tests are conducted.

(2) The city’s network position can mitigate the detrimental impact that residents’ activity intensity has on per capita building carbon emissions. As the city’s network position improves, the influence of residents’ activity intensity on per capita building carbon emissions diminishes. This suggests that the urban economic spatial correlation networks provide a foundation for balancing economic growth and creating carbon emissions reduction at a larger spatial scale.

(3) The influence of city’s network positions on per capita building carbon emissions is characterized by heterogeneity in multiple aspects, including population size and geographic location. For instance, the city’s network position has positive impacts on building carbon emissions in Metropolis and Megalopolis.

To effectively promote the achievement of carbon reduction targets, provinces and cities should develop scientifically sound and reasonable carbon reduction goals based on their population size, geographical characteristics, and economic development status. Building on the experiences of pilot cities, the carbon reduction efforts should be progressively advanced. This initiative is crucial for achieving the sustainable development of cities. Given the differences in building carbon emissions across cities, the central government should strengthen coordination between cities, particularly enhancing large-scale coordination across administrative regions. This will ensure the optimal allocation of resources and promote resource sharing and collaboration between urban clusters.

The network position of a city plays a key role in building carbon emissions. The network position of different cities determines their advantages and challenges in low-carbon development. To better leverage the network position of cities for optimizing carbon emission management, the government should consider placing greater emphasis on inter-city collaboration and the flow of resources in policy development, particularly in fostering innovative carbon reduction capabilities in eastern and larger cities. Eastern cities should prioritize the development of low-carbon technologies, green knowledge, and innovative resources, while facilitating the inflow of these resources, thereby strengthening their radiating and driving role within the urban economic spatial network. At the same time, western and smaller cities should receive more support to enhance their absorptive capacity within the urban economic spatial network. This not only helps strengthen the low-carbon technology innovation and development capabilities of these cities but also enables better utilization of the shared economy model within urban agglomeration networks, driving carbon reduction efforts.

This study has certain limitations. For example, using different indicators to depict a city’s position in urban economic spatial correlation network may yield different results regarding the impact mechanism on building carbon emissions. Therefore, future research needs to further examine the impact of other network indicators, such as closeness centrality, on building carbon emissions. Nevertheless, the current findings provide valuable insights for formulating context-specific and scientific urban building carbon reduction policies and lay a foundation for future related research.