Abstract
The sensor coverage problem is a well-known combinatorial optimization problem that continues to attract the attention of many researchers. The existing game-based algorithms mainly pursue a feasible solution when solving this problem. This problem is described as a potential game, and a memory-based greedy learning (MGL) algorithm is proposed, which can ensure convergence to Nash equilibrium. Compared with existing representative algorithms, our proposed algorithm performs the best in terms of average coverage, best value, and standard deviation within within a suitable time. In addition, increasing memory length helps to generate a better Nash equilibrium.
Keywords:
sensor area coverage; potential game; distributed optimization; greedy learning; memory length MSC:
68W15
1. Introduction
The sensor area coverage problem is a fundamental optimization problem in wireless sensor systems, which has been proven to be NP-hard, with the goal of efficiently utilizing limited sensors to cover the largest area with minimal cost [1]. This problem is also a typical engineering application optimization problem, such as military reconnaissance [2,3], unmanned autonomous intelligent systems [4,5], Internet of Things [6,7], disaster relief [8,9], etc.
Due to the wide application of sensor area coverage problem, it has attracted the attention of many researchers who are committed to developing various optimization approaches for solving this problem. Early well-known approaches include genetic algorithm [10,11], particle swarm algorithm [12,13], simulated annealing algorithm [14,15], ant colony algorithm [16,17], etc. Those algorithms have long been proven to solve optimization problems and ensure that at least one feasible solution can be obtained. However, with the rapid development of science and technology, sensors have been mass-produced, especially when hundreds or thousands of sensors cooperate to perform this problem, the above algorithms are not applicable [18]. The reason is that those algorithms are essentially centralized algorithms, requiring a central manager to make decisions for all sensors [19]. This requirement not only causes a heavy computational burden on the sensor system, but also results in high communication requirements, and the robustness of the system will also be poor [20].
Therefore, how to develop distributed approaches to solve the sensor area coverage problem is the current research trend, and the most common one currently available is local search algorithm [21]. This algorithm starts from an initial solution, generates neighboring solutions through neighborhood actions, determines the quality of neighboring solutions, and repeats the above process until the termination condition is reached [22]. Although the local search algorithm is simple and easy to implement, it also has a drawback that it is prone to getting stuck in local optima, and the quality of the final solution is closely related to the choice of the initial solution. Note that a local optimal solution is usually not a global optimal solution and may not even reach an approximate optimal solution [23]. Therefore, in recent years, researchers have turned their attention to game theory.
Game theory is a theory that studies how individuals make reasonable strategies in complex interactions [24,25]. By establishing a game model for optimization problems and designing corresponding game algorithms, an equilibrium solution can be obtained [26]. As a special type of game, potential game has been widely applied. In a potential game, there exists a potential function, and the individual utility changes caused by changing strategies can be mapped to this potential function. By optimizing this potential function, the equilibrium state (i.e., Nash equilibrium) of the game can be achieved [27]. For optimization problems that can be modeled as potential games, various game algorithms have emerged, such as log-linear learning algorithm [28], binary log-linear learning algorithm [29], fictitious play algorithm [30], etc. The above algorithms all have a common point, that is, at each time step, each player only uses the information from the most recent past time step (i.e., local information) to make decisions. The goal of those algorithms is to obtain a feasible solution, but this feasible solution is usually far from the approximate optimal solution.
For this, for the sensor area coverage problem, we present a potential game model, where the potential function reflects the global objective, and a player’s utility function is the wonderful life utility. Then, we propose a random memory algorithm (RMA), in which each player has a memory length that can store past step strategies, and make decisions based on local information. Subsequently, we verify that our proposed RMA can converge to a Nash equilibrium under any memory length. Numerical simulation will further demonstrate the value of our proposed RMA.
The main contributions of this paper are summarized as follows.
(1) We present a potential game for the sensor area coverage problem, where player’s utility function is the wonderful life utility.
(2) We proposes a game-based distributed algorithm, i.e., the RMA, which can converge to a Nash equilibrium under any memory length.
(3) Numerical simulations demonstrate the effectiveness and superiority of our proposed RMA by comparing with the existing representative optimization algorithms. In addition, we found through numerical simulations that increasing the memory length can achieve better sensor area coverage.
The rest of this paper is organized as follows. Section 2 describes the sensor area coverage problem and presents a potential game model for this problem. Section 3 presents our proposed RMA in detail and provides theoretical analysis on its convergence. Section 4 provides numerical simulations to verify the performance of our proposed RMA. Section 5 summarizes this article and provides prospects for future research directions. The main notations of this article are listed in Abbreviations.
2. Preliminaries and Game Model
2.1. Sensor Area Coverage Problem
Consider a set of sensors, forming a set , which are randomly deployed to monitor (cover) a area . Each sensor can cover the effective area of a circle under a coverage radius when it is in working condition. The location of the ith sensor can be denoted by . Without loss of generality, assume that the communication radius c of all sensors is the same. The set composed of neighbors of sensor i can be defined as
Then, the sensor area coverage problem is whether each sensor chooses a coverage decision that collectively maximizes the global objective function
where is the union of all areas covered by the sensors, is the cost function of sensor i under the coverage radius , and is expressed as
where is the maximum area covered by sensor i, is the penalty value, and is expressed as
2.2. Potential Game
In this subsection, we present the sensor area coverage problem as a game and prove that this game is a potential game.
Definition 1.
The sensor area coverage problem can be defined as a game , where
(i) is the set of all players (sensors);
(ii) is the strategy space, is the strategy set of player i, , and , , .
(iii) is the set of utility (i.e., payoff) functions, where is the utility function of player i, .
Based the Definition 1, is the strategy profile, is the strategy of player i, and . Thus, we have . Then, we will provide the definition of potential game.
Definition 2
([31]). Consider a game with individual utility function , if there exists a function φ satisfies
then the game is called potential game, and φ is the corresponding potential function.
Considering that when a pair of sensors are covered, once there is coverage overlap, they are within the communication range of each other. Thus, the communication radius . The utility function of player i is designed as
Theorem 1.
A game with individual utility function in (6) is potential game, and the corresponding potential function is expressed as
Proof.
By (2), we have
Further, for , we have
Remark 1.
The sensor coverage problem is an important application problem in sensor system, (2) transforms this problem into a combinatorial optimization problem, whose optimal solution is equivalent to an optimal sensor area coverage solution. In addition, (2) serves as the bridge that casts this problem into a potential game, which can be solved within a distributed optimization framework. Note that for any optimization problem that can be modeled as a potential game, there must exist at least one Nash equilibrium.
3. Distributed Algorithm Designed and Analysis
3.1. Algorithm Design
For an optimization problem that can be modeled as a potential game, it is crucial to design a suitable distributed algorithm, which requires a reasonable balance between the solution quality of the algorithm’s convergence and the runtime. For this, we propose a dynamic fictitious play (DFP) distributed algorithm, in which each player can dynamically adjust their own strategy in parallel based on local information. The procedure of our proposed DFP distributed algorithm is described as follows.
Step 1: At each time step t, each player randomly chooses its current strategy for the next time step or chooses to update its strategy.
Step 2: Each player i involved in updating strategy calculates its utility and best response , then records strategy and into a set .
Step 3: Each player i involved in updating strategy choose a strategy from the set for the next time step-based dynamic selection rule, i.e., .
In Step 2, is expressed as
In Step 3, the dynamic selection rule
where is expressed as
Remark 2.
(1) There exists multiple distributed algorithm used to solve potential game optimization problems, such as log-linear learning algorithm [28], binary log-linear learning algorithm [29], etc. Those algorithms have one point in common, which is that at each time step, only one player has the opportunity to update its strategy, while the remaining players keep their strategies unchanged. This sequential update strategy mechanism can cause those algorithms needing a long time to obtain a satisfactory solution in large-scale systems.
(2) Although there exist algorithms that allow each player to update their strategies at every time step, such as fictitious play algorithm [30]. In this algorithm, is set to a fixed value, which can cause this algorithm to easily fall into inefficient local optimal solution. In contrast, in our proposed DFP algorithm, is not limited to a fixed value, but dynamically changes based on local information.
(3) Our proposed DFP distributed algorithm is simple and easy to understand, and each player can independently update their strategy based on local information synchronization at each time step. This algorithm is suitable for multiple application fields. Especially in hostile environments, multiple drones collaborate in combat, and the sensors on each drone can autonomously monitor the target, as the sensors consume energy during operation. Therefore, in order to maximize efficiency and quickly execute monitoring tasks, we hope that each sensor can make independent decisions, and the DFP algorithm is suitable.
3.2. Convergence Analysis
For an algorithm, its convergence is crucial. Without convergence, the algorithm is difficult to apply in practice. Thus, in this subsection, we further analysis the convergence of this algorithm. First, we present the definition of Nash equilibrium.
Definition 3
([32]). A Nash equilibrium is such such a strategy profile where no player can unilaterally change its strategy to increase its utility, i.e.,
where .
Theorem 2.
Consider a potential game with individual utility function in (4), our proposed DFP distributed algorithm can converge to a Nash equilibrium with probability 1.
Proof.
Since the number of sensors is finite and each player i have finite strategy set, i.e., . Thus, the number of Nash equilibrium is finite, and they form a set , g is the number of all Nash equilibriums, i.e., . We will divide into two steps to prove the convergence of our proposed DFP algorithm. Firstly, we will prove that this algorithm can ensure that each strategy profile will touch a Nash equilibrium, and then prove that once touched, it locks onto this Nash equilibrium.
Part I: At each time step t, strategy profile is not a Nash equilibrium. Thus, there must exists at least a player i that satisfies . Then, according to Step 2 and Step 3 of our proposed DFP algorithm, there exists a positive probability for player i updating its strategy to , and all its neighbors will keep their strategies, , i.e.,
Similarly, there exists a positive probability for the strategy profile transform into the strategy profile , i.e.,
where is the set of player involved in updating strategies, and their neighbors keep their strategies.
Further, we have
where .
Thus, the value of the potential function strictly increases with a positive probability over time step t. Since the limited number of players, the value of the potential function is also finite. Thus, there must exist a time step such that , where , and . This means that our proposed DFP algorithm can ensure that each strategy profile will touch a Nash equilibrium with a positive probability.
If the probability of an event E occurring with a positive probability at any time step t, i.e., . Then, the event E will eventually occur due to . This means that our proposed DFP algorithm can ensure that each strategy profile must touch a Nash equilibrium in infinite time.
Part II: At time step t, if strategy profile is a Nash equilibrium, then we have , and , . Thus, we have . Similarly, we have . This means that any Nash equilibrium must touch this Nash equilibrium and lock it in.
Based on the analysis of part I and II, our proposed DFP distributed algorithm can converge to an Nash equilibrium with probability 1. Then, the proof of Theorem 2 is completed. □
Remark 3.
(1) Theorem 2 shows that our proposed DFP distributed algorithm can ensure that a Nash equilibrium can be obtained. A Nash equilibrium can be obtained through other ways. For example, any non-Nash equilibrium transforms into a Nash equilibrium within a time step.
(2) For common distributed game algorithms used to solve sensor coverage problems, such as log-linear learning algorithm [28], binary log-linear learning algorithm [29], etc. Although these algorithms can usually obtain a feasible solution, they theoretically cannot converge. For the FP algorithm, is a fixed value, and this algorithm is not affected by the strategy during the decision-making process.
4. Numerical Simulation
To evaluate the performance of our proposed DFP distributed algorithm, we compared it numerically with representative algorithms that can be modeled as potential games. Let us consider such a scenario: in a wireless sensor network composed of sensors from multiple unmanned aerial vehicles, the main requirement is to allow some sensors to monitor (i.e., sense) and collect effective information about the target area. Since sensors consume energy when in working, and the area the monitored area, the more energy is consumed. Therefore, how the sensor decides (to work or to turn off) to maximize the global objective value can be regarded as the sensor coverage problem of this paper. For fairness, each algorithm runs independently 1000 times to calculate the average value under each setting. All numerical simulations are realized on the MATLAB R2023a and the same computer with 3.20 GHz CPU and 16.0 G RAM.
4.1. Simulation Set
In this subsection, the area can be discretized as a two-dimensional grid represented by the Cartesian product . The area length d is set from 20 to 200, and the number n of agents is set to 20, 50, 100, 200, respectively. The strategy set of player is set to , i.e., , . the communication radius . In other words, if a sensor i does not work, its sensing radius and the communication radius c are both 0. If a sensor i is working, its sensing radius is 5, and the communication radius c is 10. A visual diagram as shown in Figure 1, where n is 15 and d is 20. In Figure 1, each solid circle represents a sensor, and the black dots indicate sensors in the turn off state, meaning its strategy is 0; the orange-red solid dots represent sensors in working state, the orange-red solid dots represent sensors in 5. We can clearly see that within a given area, active (working) sensors near the center can cover a complete circle area, while active sensors near the periphery do not cover a complete circle area. Due to the possible overlap in coverage area between active sensors, it can be seen from (6) that the benefits brought by each active sensor coverage are its own unique coverage area, and its cost is only related to the coverage radius. Therefore, our proposed MGL algorithm allows each active sensor to access the strategies of neighboring sensors for decision-making, with the expectation of achieving global goal maximization. The k in (4) is set to 0.2. For each 1000 independent runs of the algorithm, we calculate its the corresponding average value , best value , standard deviation , and average runtime .
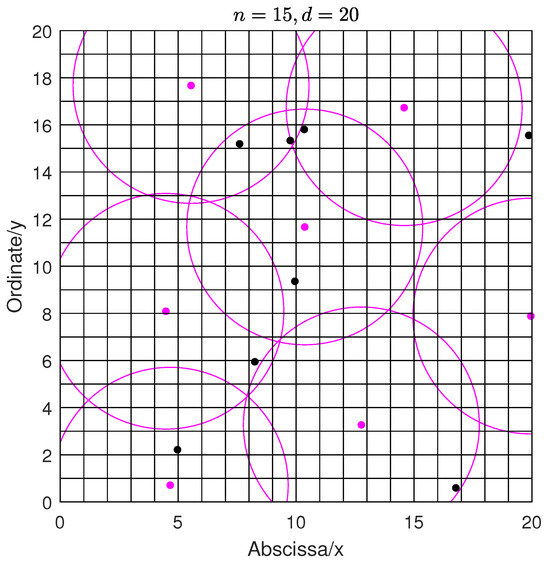
Figure 1.
Schematic diagram of sensor coverage. The coordinates of the fifteen sensors are (13.43,24.27), (16.63,53.01), (14.91,6.64), (43.73,50.18), (31.02,47.42), (50.31,1.78), (13.98,2.13), (38.30,9.81), (59.58,46.66), (29.84,28.08), (31.09,35.00), (59.85,23.66), (22.81, 45.58), (29.25,46.00), and (24.75,17.84), respectively.
4.2. Compared with the Existing Representative Algorithms
Typical representative algorithms that participate in numerical simulation comparisons include log-linear learning (LLL) algorithm [28], fictitious play (FP) algorithm [30], best response (BR) algorithm [33], and genetic algorithm (GA) [34]. The simple process of those algorithms are as follows:
LLL algorithm: This is a typical distributed algorithm that can be used to solve problems that can be modeled as potential games. The main idea of this algorithm is that, at each time step t, a player i is randomly selected to choose a strategy from its strategy profile with the probability for the next time step, and the probability is expressed as
where . When , player i is randomly selects a strategy from its strategy set for the next time step. When shows a tendency towards positive infinity, player i selects the best response for the next time step. Note that regardless of the given task value of , the LLL algorithm cannot converge. Therefore, for the LLL algorithm, we will sample at the time step, and is set 1000.
FP algorithm: This is a commonly distributed algorithm that can be used to solve problems that can be modeled as potential games. This algorithm has the characteristics of simplicity and fast convergence. The main idea of this algorithm is that, at each time step t, each player i chooses strategy with probability or selects the best response with probability for the next time step. Since a small induce a better solution, is thus set to 0.1. This algorithm can converge to a Nash equilibrium.
BR algorithm: This is also a distributed algorithm that can be used to solve problems that can be modeled as potential games. The main idea of this algorithm is that, at each time step t, a player i is randomly selected to choose the best response . This algorithm can converge to a Nash equilibrium.
GA: This is a classic metaheuristic algorithm, a centralized optimization algorithm that simulates natural selection and genetic mechanisms and belongs to the branch of evolutionary computation. This algorithm has been applied to various fields, with main operations including selection, crossover, and mutation. In this section, the fitness function adopts (2).
The numerical simulation results are shown in Table 1. From this Table, we can see the following:

Table 1.
Comparison results among different algorithms: Average value /Best value /Standard deviation /Average runtime (Unit: Seconds).
(1) When we observe the solution quality, i.e., average value and standard deviation , our proposed DFP algorithm performs the best result by comparing with other algorithms, followed by the GA, LLL algorithm, BR algorithm and FP algorithm. Specifically, compared to the FP algorithm, the reason why our proposed DF algorithm performs better in this regard is that our algorithm has dynamic probability in strategy selection, while in the FP algorithm, each player tends to choose the best response.
(2) When we further observe the best value , under all experimental settings (that is n and l), our proposed DFP algorithm can achieve the best values by comparing with other algorithms. In some cases, other algorithms can also achieve optimal values, such as in small-scale systems, i.e., , the GA can also achieve the best values. It is worth noting that under various settings, we have found through extensive simulation testing that for a given setting of , our proposed algorithm reaches its optimal value every 1000 runs.
(3) When we observe the average runtime , FP algorithm performs the best result by comparing with other algorithms, followed by the GA, DFP algorithm, BR algorithm, and LLL algorithm. The reason why the LLL algorithm performs poorly in terms of average runtime is that its update strategy mechanism is essentially a serial update strategy mechanism, and its average running time is related to the system size (i.e., the number of sensors), while other algorithms are essentially parallel update strategy mechanism. Note that the average runtime of our proposed DFP algorithm is very close to that of the FP algorithm.
In sum, our proposed DFP algorithm can obtain a satisfactory solution within a suitable time.
5. Conclusions and Future Research Directions
This paper investigates the issue of the multi-agent area coverage problem and addresses it within a distributed framework. We have treated each sensor as a player and use the game theory approach to solve it. We have established a potential game for this problem and designed a novel dynamic fictitious play distributed algorithm, which theoretically demonstrates that this algorithm can ensure obtaining a Nash equilibrium. Simulation results have shown that compared with typical optimization algorithms, our proposed algorithm can obtain the best results in terms of average coverage, best value, and standard deviation in a suitable time.
For future research directions, we will consider the following three aspects: (i) developing a novel distributed optimization method to achieve the optimal solution of sensor area coverage problem; (ii) researching a sensor area coverage problem in more complex environments, such as sensors being able to move, exit, or join; (iii) explore applying the developed optimization approaches to real-world scenarios.
Author Contributions
Software, X.X.; Validation, J.C.; Formal analysis, R.D.; Investigation, J.H.; Resources, J.H. and S.X.; Data curation, X.X. and S.X.; Writing—original draft, J.H.; Writing—review & editing, J.C. and R.D.; Project administration, R.D.; Funding acquisition, S.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the high-level talent fund No. 22-TDRCJH-02-013.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| Notation | Definitions |
| the area covered by sensor i under coverage radius | |
| the cost function of sensor i under coverage radius | |
| V | the set of players (sensors) |
| n | the number of players |
| F | the set of cost functions |
| X | the strategy space |
| the strategy set of player i | |
| x | the strategy profile (solution) |
| the Nash equilibrium | |
| the set of all Nash equilibriums | |
| the strategy of player i | |
| the strategy profile of all players expect player i | |
| the best response of player i at time step t | |
| the coverage radius of player i | |
| c | the communication radius of all sensors |
| the utility of player i | |
| the best value in a set of data | |
| the potential function | |
| the neighbor set of player i |
References
- Zhou, E.; Liu, Z.; Zhou, W.; Lan, P.; Dong, Z. Position and orientation planning of the uav with rectangle coverage area. IEEE Trans. Veh. Technol. 2025, 74, 1719–1724. [Google Scholar] [CrossRef]
- Li, X.; Lu, X.; Chen, W.; Ge, D.; Zhu, J. Research on uavs reconnaissance task allocation method based on communication preservation. IEEE Trans. Consum. Electron. 2024, 70, 684–695. [Google Scholar] [CrossRef]
- Shaofei, M.; Jiansheng, S.; Qi, Y.; Wei, X. Analysis of detection capabilities of leo reconnaissance satellite constellation based on coverage performance. J. Syst. Eng. Electron. 2018, 29, 98–104. [Google Scholar] [CrossRef]
- Chen, J.; Ling, F.; Zhang, Y.; You, T.; Liu, Y.; Du, X. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Hu, B.-B.; Zhang, H.-T.; Liu, B.; Ding, J.; Xu, Y.; Luo, C.; Cao, H. Coordinated navigation control of cross-domain unmanned systems via guiding vector fields. IEEE Trans. Control Syst. Technol. 2024, 32, 550–563. [Google Scholar] [CrossRef]
- Zhu, C.; Fan, X.; Deng, X.; Liu, S.; Yin, D.; Gao, H.; Yang, L.T. Area coverage reliability evaluation for collaborative intelligence and meta-computing of decentralized industrial internet of things. IEEE Internet Things J. 2025, 12, 13734–13745. [Google Scholar] [CrossRef]
- Yang, F.; Shu, L.; Duan, N.; Yang, X.; Hancke, G.P. Complete area c-probability coverage in solar insecticidal lamps internet of things. IEEE Internet Things J. 2023, 10, 22764–22774. [Google Scholar] [CrossRef]
- Gui, J.; Cai, F. Coverage probability and throughput optimization in integrated mmwave and sub-6 ghz multi-uav-assisted disaster relief networks. IEEE Trans. Mob. Comput. 2024, 23, 10918–10937. [Google Scholar] [CrossRef]
- Shi, K.; Peng, X.; Lu, H.; Zhu, Y.; Niu, Z. Application of social sensors in natural disasters emergency management: A review. IEEE Trans. Comput. Soc. Syst. 2023, 10, 3143–3158. [Google Scholar] [CrossRef]
- Cao, Y.; Feng, W.; Quan, Y.; Bao, W.; Dauphin, G.; Song, Y.; Ren, A.; Xing, M. A two-step ensemble-based genetic algorithm for land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 409–418. [Google Scholar] [CrossRef]
- Hanh, N.T.; Binh, H.T.T.; Hoai, N.X.; Palaniswami, M.S. An efficient genetic algorithm for maximizing area coverage in wireless sensor networks. Inf. Sci. 2019, 488, 58–75. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, A. Leader prediction for multiobjective particle swarm optimization. IEEE Trans. Evol. Comput. 2024, 29, 1356–1370. [Google Scholar] [CrossRef]
- Bonnah, E.; Ju, S.; Cai, W. Coverage maximization in wireless sensor networks using minimal exposure path and particle swarm optimization. Sens. Imaging 2020, 21, 4. [Google Scholar] [CrossRef]
- He, Y.; Huang, J.; Li, W.; Zhang, L.; Wong, S.-W.; Chen, Z.N. Hybrid method of artificial neural network and simulated annealing algorithm for optimizing wideband patch antennas. IEEE Trans. Antennas Propag. 2024, 72, 944–949. [Google Scholar] [CrossRef]
- Wu, X.; Yang, Y.; Xie, Y.; Ma, Q.; Zhang, Z. Multiregion mission planning by satellite swarm using simulated annealing and neighborhood search. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1416–1439. [Google Scholar] [CrossRef]
- Dai, L.-L.; Pan, Q.-K.; Miao, Z.-H.; Suganthan, P.N.; Gao, K.-Z. Multi-objective multi-picking-robot task allocation: Mathematical model and discrete artificial bee colony algorithm. IEEE Trans. OnIntelligent Transp. Syst. 2024, 25, 6061–6073. [Google Scholar] [CrossRef]
- Xie, X.; Yan, Z.; Zhang, Z.; Qin, Y.; Jin, H.; Xu, M. Hybrid genetic ant colony optimization algorithm for full-coverage path planning of gardening pruning robots. Intell. Serv. Robot. 2024, 17, 661–683. [Google Scholar] [CrossRef]
- Aga, R.S.; Duncan, L.; Davidson, L.; Ouchen, F.; Aga, R.; Heckman, E.M.; Bartsch, C.M. Design and fabrication of a metal resistance strain sensor with enhanced sensitivity. IEEE Sens. Lett. 2024, 8, 2504004. [Google Scholar] [CrossRef]
- Zhou, X.; Rao, W.; Liu, Y.; Sun, S. A decentralized optimization algorithm for multi-agent job shop scheduling with private information. Mathematics 2024, 12, 971. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, S.; Li, F.; Trajanovski, S.; Zhou, P.; Hui, P.; Fu, X. Video content placement at the network edge: Centralized and distributed algorithms. IEEE Trans. Mob. Comput. 2023, 22, 6843–6859. [Google Scholar] [CrossRef]
- Luo, C.; Xing, W.; Cai, S.; Hu, C. Nusc: An effective local search algorithm for solving the set covering problem. IEEE Trans. OnCybernetics 2024, 54, 1403–1416. [Google Scholar] [CrossRef]
- Seyedkolaei, A.A.; Nasseri, S.H. Facilities location in the supply chain network using an iterated local search algorithm. Fuzzy Inf. Eng. 2023, 15, 14–25. [Google Scholar] [CrossRef]
- Zeng, L.; Chiang, H.-D.; Liang, D.; Xia, M.; Dong, N. Trust-tech source-point method for systematically computing multiple local optimal solutions: Theory and method. IEEE Trans. Cybern. 2022, 52, 11686–11697. [Google Scholar] [CrossRef]
- Guo, C.; Song, Y. Multi-subject decision-making analysis in the public opinion of emergencies: From an evolutionary game perspective. Mathematics 2025, 13, 1547. [Google Scholar] [CrossRef]
- Liu, S.; Li, L.; Zhang, L.; Shen, W. Game theory based dynamic event-driven service scheduling in cloud manufacturing. IEEE Trans. Autom. Sci. Eng. 2024, 21, 618–629. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, Z. Nash equilibrium solutions for switched nonlinear systems: A fuzzy-based dynamic game method. IEEE Trans. Fuzzy Syst. 2025, 33, 2006–2015. [Google Scholar] [CrossRef]
- Varga, B.; Inga, J.; Hohmann, S. Limited information shared control: A potential game approach. IEEE Trans. Hum.-Mach. Syst. 2023, 53, 282–292. [Google Scholar] [CrossRef]
- Li, Z.; Liu, C.; Tan, S.; Liu, Y. A timestamp-based log-linear algorithm for solving locally-informed multi-agent finite games. Expert Syst. Appl. 2024, 249, 123677. [Google Scholar] [CrossRef]
- Yan, K.; Xiang, L.; Yang, K. Cooperative target search algorithm for uav swarms with limited communication and energy capacity. IEEE Commun. Lett. 2024, 28, 1102–1106. [Google Scholar] [CrossRef]
- Dumitrescu, R.; Leutscher, M.; Tankov, P. Linear programming fictitious play algorithm for mean field games with optimal stopping and absorption. ESAIM: Math. Model. Numer. Anal. 2023, 57, 953–990. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential games. Games Econ. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Nash, J.F., Jr. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Thiran, G.; Stupia, I.; Vandendorpe, L. Best response dynamics convergence for generalized nash equilibrium problems: An opportunity for autonomous multiple access design in federated learning. IEEE Internet Things J. 2024, 11, 18463–18482. [Google Scholar] [CrossRef]
- Kim, Y.; Khir, R.; Lee, S. Enhancing genetic algorithm with explainable artificial intelligence for last-mile routing. IEEE Trans. Evolutionary Comput. 2025, 1–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).