Abstract
The main motivation of this research is the semi-analytical exploration of the dynamics of an asteroid that is attacked while approaching a planet (with an inelastic collision of the projectile normally to the surface of the asteroid occurring just before approaching). Namely, the particular case of the spin dynamics of the asteroid that has been struck by a projectile almost perpendicularly to the maximal-inertia principal axis, with further perturbing the dynamics of rotation due to gravitational torques during close approach to the planet, is investigated. The initial surface of the asteroid is assumed to be a rubble pile, but preferably with a quasi-rigid internal structure, with circa constant distances between various parts of the asteroid as a first approximation. As a result of an inelastic collision with the surface of the asteroid, the rubble-pile material should be thrown off the surface into outer space in large amounts; thus, the mass of the asteroid and the moments of inertia along its principal axes should be changed (as well as the regime of angular rotation around its maximal-inertia principal axis). The updated Euler’s equations, stemming from the conservation of angular momentum, have been presented with gravitational torques acting during the approach of the asteroid to the planet (taking into account the impact on the asteroid that occurs just before it enters the zone of close approach). The evolution of the non-linear spin dynamical state is studied, along with kinematical findings for Euler angles via the governing equations, in accordance with two main rotational stages: first, immediately after the impact on the asteroid’s surface; and second, at the regime of asteroid rotation during its close approach to the planet, with perturbations caused by gravitational torques (just after being struck by the projectile).
MSC:
70F15; 70F07
1. Introduction
Investigation of the dynamics of asteroid rotation, which is governed mainly by the influence of the direct gravitational effects [1], indirect effects of non-gravitational nature (YORP effect [2,3]), or external perturbing effects (acting permanently or instantly at the moment, like impact by a projectile or cosmic billiard), falls within the sphere of attention of the celestial mechanics community. Herein, the combination of the first and third types of direct external effects influencing the dynamics of an asteroid’s rotation during close approach to a planet (considered most significant during such an approach) is studied. Let us recall [1] that the first type of the aforementioned effects is produced by the non-uniform influence of the gravitational field on various parts of asteroids, with anisotropic spatial reflected response from them forming the general combined dynamical angular momentum of the asteroid.
The evolution of non-linear spin dynamical state is studied alongside kinematical findings for Euler angles via governing equations, in accordance with the two main rotational stages: first, immediately after the attack of the asteroid’s surface; and second, at the regime of asteroid rotation during close approach to the planet, with perturbations caused by gravitational torques (just after being struck by the projectile). The external surface of the asteroid is assumed to be a rubble-pile [4,5] (loose and non-rigid), whereas the internal structure is preferably quasi-rigid (with almost constant distances between various parts of the asteroid inside, as a first approximation). It is assumed that the inelastic collision of the projectile normally to the surface of the asteroid takes place just before it approaches the planet. Namely, the particular case of the spin dynamics of the asteroid that has been struck by a projectile (with mass much less than that of the asteroid) almost perpendicularly to the maximal-inertia principal axis, with further perturbing the dynamics of rotation due to gravitational torques during close approach to the planet, is investigated.
We will assume the conservation of dynamical angular momentum as the first approximation (although the inelastic collision of the projectile with the rubble-pile external surface of the asteroid would have caused non-uniform heating [6] of the surface locally, with partial absorption of angular momentum). The spin-state of the asteroid before collision with the projectile (and before entering the zone of sufficient gravitational influence by the planet) is assumed as follows [1]: asteroid rotates due to the process of nutation relaxation [2], preferably about its maximal-inertia axis I1, with an almost constant rate of rotation Ω1, outside the zone of close approach to the planet, with small oscillations of other components of angular velocities {Ω2, Ω3} around other axes (I1 ≥ I2 ≥ I3).
2. The System of Equations
In accordance with the basic model reported in [7,8], let us present Euler’s equations, including the externally applied gravitational torques during the close approach of the asteroid to the planet (in a frame of reference fixed to the rotating body [7,8]) as follows:
where is the mass of Earth, G is the Gaussian constant of the gravitational law; is the “asteroid–Earth” distance (here, we consider the case of e > 1 for hyperbolic orbits of an asteroid [8]); a is the semimajor axis of the geocentric orbit; f is the true anomaly; α, β, and γ are the direction cosines of the main axes of inertia relative to the direction to the Earth [7,8].
In addition, system of Equation (1) should be completed with the kinematic equations of Euler angles {ψ, θ, φ} presented in (2) below (which transform the components of angular velocity in the co-rotating frame fixed in the rotating body to the absolute Cartesian coordinate system [1]; the description of Euler angles is standard, see [2] for details):
with appropriate expressions (3) for {α, β, γ} [7,8] used in the formulation of (1)
In addition, the true anomaly’s dynamics with respect to time t is governed by Equation [1]:
where the unit of time is chosen so that constant G equals 1, whereas the unit of length is chosen so that (just for simplicity of presentation of (4)).
3. Semi-Analytical Solution for Kinematic Equations (After Impact of Projectile on Surface)
As mentioned above, the dynamical state of stable rotation of asteroid before collision with the projectile is assumed to be as follows [1]: the asteroid rotates due to the process of nutation relaxation [2], preferably about its maximal-inertia axis I1, with an almost constant rate of rotation Ω1 (outside the zone of close approach to the planet), with small oscillations of the other components of angular velocities {Ω2, Ω3} around the other axes. This is possible because inelastic dissipation (mainly tidal [2,3]), which reduces the kinetic energy of the asteroid, causes its spin to evolve towards rotation about the maximal-inertia axis I1, with rate of rotation Ω1 (I1 ≥ I2 ≥ I3) as follows:
{Ω2, Ω3} ≪ Ω1 ⟹ {(Ω2/Ω1), (Ω3/Ω1)} ⟶ 0
On the other hand, after the impact of the projectile M on the surface, the evolution of the rate of rotation Ω1 should be changed according to the results reported in [9] as follows:
- -
- First, the mass of the asteroid is decreased (6) (due to ejecting of ‘rubble-pile’ material after the impact by projectile) on the amount of the thrown ‘rubble-pile’ material into the outer space after collision (nevertheless, with further possible partial returning of it to the surface of asteroid).
- -
- Second, the component of angular velocity Ω1 should linearly increase as follows:
Taking the further assumptions (5) and (7) as valid and physically self-consistent, let us assume the following as a first approximation in (2):
The third, second, and first equations of system (8) yield the appropriate system as follows (where sin ψ ≠ 0, sin θ ≠ 0):
So, we can conclude the following from the first and third Equations of (9):
Thus, using the second Equation of (10) with the help of Equations (7) and (11) (where C1 = const), we obtain:
where the last equation in (12) and (13) yields (see Figure 1, Figure 2 and Figure 3) the following:
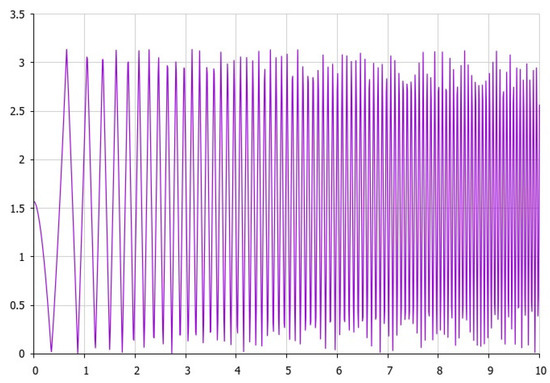
Figure 1.
Schematic approximation of the dynamics of angle θ according to (14) (the vertical axis), with time t depicted on the horizontal axis.
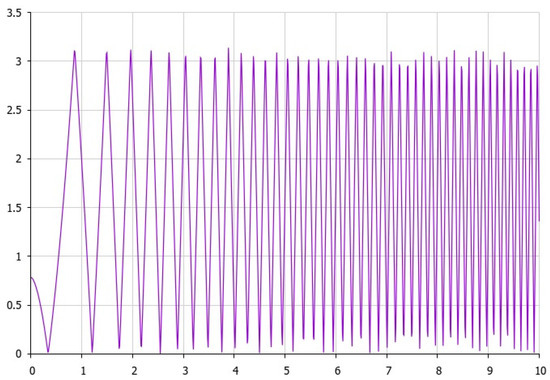
Figure 2.
Schematic approximation of the dynamics of angle θ according to (14) (the vertical axis) or (17), with time t depicted on the horizontal axis with other chosen constants as pointed below.
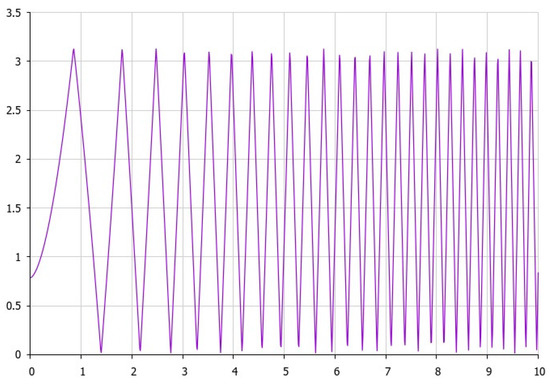
Figure 3.
Schematic approximation of the dynamics of angle θ according to (14) (the vertical axis) or (17), with time t depicted on the horizontal axis.
So, taking into account (14), we can conclude from (11) that
whereas the last equation in (9) yields the following (using both (14) and (15)):
(angle φ characterizes the inclination of the rotation axis to the orbital plane [8]). It is apparent that Equation (16) can be solved via numerical methods only.
Here on Figure 1, we have chosen constants as follows:
Here on Figure 2, constants are as follows:
Here on Figure 3, constants are as follows:
4. Semi-Analytical Solution of Euler’s Equations with Gravitational Torques (During Close Approach of Asteroid to Planet)
Let us investigate the simplified system of Equation (1), where we can use (as a first approximation) the expressions for the angles (14) and (16) obtained earlier from the first stage of free rotation of the asteroid outside the zone of effective attraction by the planet. Meanwhile, since angle φ characterizes the inclination of the rotation axis to the orbital plane [8], we can conclude from (16) that φ = φ(0) = 0 if we choose ψ(0) = 0 in (11) (with the aim of simplifying the presentation of the obtained partial solutions). Then, from (15), we conclude that ψ = 0 in this case, whereas expression (14) for angle θ should be given as follows:
So, we can further conclude from (3) that γ = 0 if we choose {φ = 0, ψ = 0} as above.
Following the ansatz reported in [3], let us present Equation (1) in a form for investigating the dynamics of non-rigid asteroid rotation:
where = {Ii Ωi} (i = 1, 2, 3), and is the total sum of applied external torques.
Then, from the first equation of (18) (see also (1) and (3)), and taking into account the approximation (5), we can conclude that K1 ≅ const = K1 (0) (since on the left side of that equation, and also since γ = 0 on the right side for the component of gravitational torques). This conclusion is consistent with those obtained earlier in (6) and (7) (taking into account that the main contribution to the changes in the asteroid’s principal moments of inertia stems from the changes in the asteroid’s mass). The second equation of (18) yields
whereas the third equation in (18) should be considered, along with (4), as a complete system, as follows:
where, in (20), the true anomaly f can be considered, within a limited range of time t, to be an almost constant (or at least very slowly variable) parameter.
The non-dimensionless parameters are introduced below for Equations (19) and (20):
Since the main contribution to the changes in the asteroid’s principal moments of inertia stems from the changes in the asteroid’s mass, we can transform system (20) into the equation below, with the help of (19) and (21):
where we used the expressions obtained earlier in (7) and (17) as follows:
(The expression given above for Ω1 has been approximated from (7) using a Taylor expansion, not taking into account the terms of second-order smallness).
At the final stage of ejecting the ‘rubble-pile’ material after the impact of a projectile on the asteroid’s surface, Equation (22) can be approximated by the equation of forced oscillations [12] (since Ω1 should be considered circa constant as a first approximation).
5. Discussion
The semi-analytical investigation of asteroid rotational dynamics during its close approach to a planet is presented. Two main stages of this process have been considered: first, when an asteroid is struck by a projectile far from the zone of significant gravitational influence by a planet (a Hill zone [12]); and second, when the asteroid enters the zone where its spin state is perturbed by gravitational torques, as represented on the right side of Equation (1).
In the first stage, the asteroid’s spin is preferably oriented along its rotation about the maximal-inertia axis I1, with an almost constant rate of rotation Ω1 (I1 ≥ I2 ≥ I3). It is then suddenly struck by a projectile in a direction perpendicular to the surface of the maximal-inertia axis I1, causing the rubble-pile material of the asteroid’s surface to be thrown off into outer space (6), and thus the rate of rotation Ω1 (t) is changed according to (7). Such instant perturbation also causes changes in the Euler angle kinematics (2), under the physically reasonable assumptions (5) of small oscillations along the two other principal axes (described by the semi-analytical formulae (8) and (16)), with zero gravitational torques at this stage for such a regime of rotation. As for providing the error bounds for the assumption in (5), such as {Ω2, Ω3} << Ω1, let us assume {(Ω2/Ω1), (Ω3/Ω1)} ~ 0.001.
The second stage (17) and (22) is governed by gravitational torques, depending on the direction cosines (3) of the asteroid’s main axes of inertia relative to the direction to Earth (this stage is fully described by the system of Equation (1), in a frame of reference fixed in the rotating body); also, the dependence (4) of time t on true anomaly f for the asteroid’s hyperbolic orbit should be taken into account.
Thus, we have obtained a particular semi-analytical solution to the system (1), which physically stems from the changed rotational dynamics of the asteroid due to a sudden impact by a projectile almost perpendicular to the maximal-inertia axis I1, which previously had an almost constant rate of rotation Ω1(0), with subsequent orbital evolution to the stage when gravitational torques govern further regimes of the asteroid’s rotation (1) (including rotation about two other principal axes, with their rates of rotation assumed to be negligible with respect to the rate of rotation Ω1(t)). Then, we have chosen simplification aimed at a semi-analytical presentation of a partial solution. Namely, since angle φ characterizes the inclination of the rotation axis to the orbital plane [8], we can choose from (16) that φ = φ(0) = 0 by assuming ψ(0) = 0 in (11), so we conclude from (15) that ψ = 0. Thus, the kinematics of the Euler angles, as well as the dynamics of all three components of angular velocity, have been fully described by the coupled system of Equations (20) or (22), with approximated solutions derived from (18) and (19) and assumption (21) (due to fact that the main contribution to the changes in the asteroid’s principal moments of inertia stems from the changes in the asteroid’s mass). We should especially note that among all possible solutions, especially when considering a more general case of system (18) than that presented in (19) and (20) (i.e., without simplifications {φ = 0, ψ = 0}), we should only choose those which are compatible with assumption (5).
Let us also highlight that the resulting Equation (22), which governs the regime of asteroid rotation during close approach to the planet after being struck by a projectile, can be approximated as an equation of forced oscillations in the suggested scenario (since Ω1 should be considered circa constant as a first approximation during the final stage of ejecting the ‘rubble-pile’ material after the impact on the asteroid’s surface). So, physical disintegration of the asteroid is possible due to its self-destruction if internal stress states exceed its material strength during such forced oscillations. We should mention useful studies [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] related to our study.
6. Conclusions
The main motivation of this research is the semi-analytical exploration of the dynamics of the attacked asteroid that is approaching a planet (with an inelastic collision of the projectile normally to the surface of the asteroid occurring just before approaching). Namely, the particular case of the spin dynamics of the asteroid that has been struck by a projectile almost perpendicularly to the maximal-inertia principal axis, with further perturbation of the dynamics of rotation by gravitational torques during close approach to the planet, is investigated. The initial surface of the asteroid is assumed to be a rubble-pile, but preferably with a quasi-rigid state of its internal structure with circa constant distances between various parts of the asteroid inside, as a first approximation. As a result of an inelastic collision with the surface of the asteroid, rubble-pile material should be thrown outside the surface into outer space in large amounts; thus, the mass of the asteroid and the moments of inertia of the principal axes should be changed (and also, the regime of angular rotation around its maximal-inertia principal axis). The updated Euler’s equations stemming from the conservation of angular momentum have been presented with the acting gravitational torques during the approach of the asteroid to the planet (taking into account the impact on the asteroid occurring just before it enters the zone of close approach). The evolution of the non-linear spin dynamical state is studied along with kinematical findings for Euler angles via governing equations, in accordance with the two main rotation stages: first, immediately after the impact of the asteroid’s surface; and second, at the regime of asteroid rotation during its close approach to the planet, with perturbations caused by gravitational torques (just after being struck by the projectile). Thus, we conclude that various scenarios may happen during an asteroid flyby near the planet. Herein, the particular case of choosing the initial data has been presented, which may also occur during, e.g., the Apophis flyby near the Earth in 2029.
Let us outline that physical disintegration of asteroids due to forced oscillations in the suggested scenario may take place, which requires their internal stress states to exceed their material strength [26] (which is beyond the scope of our study).
As a final remark, let us outline the restrictions to the model such that the influence of multiple immediate impact ejecta has been ignored in our model (as well as the partial returning of ejected material to the surface of the asteroid); the density of the rubble-pile asteroid’s material in (6) and (7) is supposed to be substantially less than the “mean” (bulk) density of the internal structure of the asteroid. Let us also declare that testing other rubble-pile media with the aim of preventing the penetration inside them at impact by a hypervelocity projectile or testing them for inventing active armor for the defense of the human body does not relate to the subject, method, or results of our research (which is also beyond the scope of our study).
In astrophysics and space science, the kinematics between an asteroid and a planet have been investigated in the literature [1,7,8,20,21,23,29,36,39]. In comparison with the past studies, the novel insights first found in this work and the originality are as follows: the work is devoted to the behavior of an asteroid approaching the planet, which was struck by a projectile. Equations for angular velocity have been considered by specifying angular velocity in terms of Euler angles, and applying them to the case of pure rotation of a body around the largest inertia axis with the given time-variable frequency (7) (due to perturbation caused by the projectile attack). Thus, Euler angles change over time during stationary rotation around the largest axis. Then, simplification with the aim of semi-analytical presentation of the partial solution with appropriate approximation has been used to eliminate the third component of angular velocity from the remaining Euler equations, resulting in novel equations of second order for the first and second components of angular velocity. Namely, kinematics of Euler angles as well as dynamics of all three components of angular velocity have been approximated by solutions stemming from the dynamics of non-rigid asteroid rotation and the assumption that the main contribution to changes in the asteroid’s principal moments of inertia stems from the change in the asteroid’s mass (due to the ejecting of ‘rubble-pile’ material after the impact by the projectile). All the results are compatible with assumptions that inelastic dissipation reduces the kinetic energy of the asteroid during orbital long-term evolution, resulting in the evolution of its spin towards almost constant rotation about the maximal-inertia axis I1 with close to zero-value components of angular velocity about the axes I2, I3. The main conclusion is that the resulting Equation (22) governing the regime of asteroid rotation in close approach to a planet (perturbed by the projectile’s impact) can be approximated by an equation of forced oscillations in the suggested scenario.
According to the descriptions in Section 1 and Section 2, the setups yielding the semi-analytic results are too complicated and specific. Euler’s equations to describe the system are also analyzed in Section 3. A non-linear spin dynamical state is also argued. In fact, in general, it is too difficult to obtain the correct results by including the non-linear effects using even a semi-analytic method. It is also recognized that it is too hard to explore the dynamics of the system consisting of an asteroid and a planet analytically. Indeed, since one can use numerical simulations, the physical advantages of considering the dynamics in a semi-analytical way are necessary. The obvious point is that since the setups are complicated, the limit of applicability for the current approach must exist. The limit is that among all possible solutions, especially when considering a more general case of system (18) than that presented in (19) and (20) (even without simplifications {φ = 0, ψ = 0}), we should choose solutions that are compatible with assumption (5). If we find, as a result of the solving procedure for the equation of forced oscillations stemming from Equation (22), that the components of angular velocity about axes I2 and I3 are no longer negligible compared to rotation about the maximal-inertia axis I1, the solving procedure should be stopped, since an untrue solution may arise.
7. Remarks (With Highlights)
- -
- A new physical model is suggested for asteroid rotation, consisting of two stages.
- -
- An asteroid with stable rotation about the maximal-inertia axis is struck by a projectile.
- -
- A projectile (much less massive than the asteroid) strikes it normally to the asteroid’s surface.
- -
- The second stage is governed by gravitational torques during the approach to the planet.
- -
- Gravitational torque-assisted energy dissipation reduces the kinetic energy of the asteroid’s spin.
- -
- The regime of rotation of Ω1 (with small components Ω2 and Ω3) is studied for both stages.
- -
- A semi-analytical ansatz is developed for modeling regimes of asteroid rotation.
- -
- The system of Euler equations for asteroid rotation has been investigated.
- -
- The asteroid experiences a regime of rotations with forced oscillations, which may disrupt it.
Funding
The study was conducted under the state assignment of Lomonosov Moscow State University.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Sergey Ershkov is thankful to Dmytro Leshchenko for conducting the literature survey on rigid body rotation.
Conflicts of Interest
The author declares that there are no conflicts of interest regarding the publication of the article.
References
- Ershkov, S.V. Semi-analytical Ansatz for Approximating Dynamics of Asteroid Rotation Approaching Planet. J. Appl. Comput. Mech. 2025, in press. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Shamin, R.V. The dynamics of asteroid rotation, governed by YORP effect: The kinematic ansatz. Acta Astronaut. 2018, 149, 47–54. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Leshchenko, D. On the dynamics OF NON-RIGID asteroid rotation. Acta Astronaut. 2019, 161, 40–43. [Google Scholar] [CrossRef]
- Walsh, K.J. Rubble pile asteroids. Annu. Rev. Astron. Astrophys. 2018, 56, 593–624. [Google Scholar] [CrossRef]
- Chapman, C.R.; Morrison, D.; Zellner, B. Surface properties of asteroids: A synthesis of polarimetry, radiometry, and spectrophotometry. Icarus 1975, 25, 104–130. [Google Scholar] [CrossRef]
- Kartashov, E.M. Developing generalized model representations of thermal shock for local non-equilibrium heat transfer processes. Russ. Technol. J. 2023, 11, 70–85. [Google Scholar] [CrossRef]
- Melnikov, A.V. Rotational Dynamics of Asteroids Approaching Planets. Sol. Syst. Res. 2022, 56, 241–251. [Google Scholar] [CrossRef]
- Lobanova, K.S.; Melnikov, A.V. Disturbances in the Rotational Dynamics of Asteroid (99942) Apophis at its Approach to the Earth in 2029. Sol. Syst. Res. 2024, 58, 208–219. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D. Inelastic Collision Influencing the Rotational Dynamics of a Non-Rigid Asteroid (of Rubble Pile Type). Mathematics 2023, 11, 1491. [Google Scholar] [CrossRef]
- de Goede, T.C.; de Bruin, K.G.; Bonn, D. High-velocity impact of solid objects on non-Newtonian fluids. Sci. Rep. 2019, 9, 1250. [Google Scholar] [CrossRef]
- Waitukaitis, S.R.; Jaeger, H.M. Impact-activated solidification of dense suspensions via dynamic jamming fronts. Nature 2012, 487, 205–209. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Rachinskaya, A. Note on the trapped motion in ER3BP at the vicinity of barycenter. Arch. Appl. Mech. 2021, 91, 997–1005. [Google Scholar] [CrossRef]
- Walsh, K.J.; Richardson, D.C.; Michel, P. Spin-up of rubble-pile asteroids: Disruption, satellite formation, and equilibrium shapes. Icarus 2012, 220, 514–529. [Google Scholar] [CrossRef]
- Melnikov, A.V.; Shevchenko, I.I. Unusual rotation modes of minor planetary satellites. Sol. Syst. Res. 2007, 41, 483–491. [Google Scholar] [CrossRef]
- Melnikov, A.V. Resonant and Chaotic Phenomena in the Dynamics of Celestial Bodies; GAO Pulkovo Observatory: Saint Petersburg, Russia, 2016. [Google Scholar]
- Vokrouhlicky, D.; Bottke, W.F.; Chesley, S.R.; Scheeres, D.J.; Statler, T.S. The Yarkovsky and YORP Effects. arXiv 2015, arXiv:1502.01249. [Google Scholar] [CrossRef]
- Chernous’ko, F.L. On the Motion of a Satellite about Its Center of Mass under the Action of Gravitational Torques. Prikl. Mat. Mekh. 1963, 27, 474–483. (In Russian) [Google Scholar]
- Chernousko, F.L.; Akulenko, L.D.; Leshchenko, D.D. Evolution of Motions of a Rigid Body About Its Center of Mass; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Beletsky, V.V. Motion of an Artificial Satellite About Its Center of Mass; Israel Program for Scientific Translation: Jerusalem, Israel, 1966. [Google Scholar]
- Benson, C.J.; Scheeres, D.J.; Brozović, M.; Chesley, S.R.; Pravec, P.; Scheirich, P. Spin state evolution of (99942) Apophis during its 2029 Earth encounter. Icarus 2023, 390, 115324. [Google Scholar] [CrossRef]
- Souchay, J.; Lhotka, C.; Heron, G.; Herve, Y.; Puente, V.; Lopez, M.F. Changes of spin axis and rate of the asteroid (99942) Apophis during the 2029 close encounter with Earth: A constrained model. Astron. Astrophys. 2018, 617, A74. [Google Scholar] [CrossRef]
- Holsapple, K.A.; Michel, P. Tidal disruptions: A continuum theory for solid bodies. Icarus 2006, 183, 331–348. [Google Scholar] [CrossRef]
- Hirabayashi, M.; Kim, Y.; Brozović, M. Finite element modeling to characterize the stress evolution in asteroid (99942) Apophis during the 2029 Earth encounter. Icarus 2021, 365, 114493. [Google Scholar] [CrossRef]
- Kartashov, E.M. Model representations of heat shock in terms of dynamic thermal elasticity. Russ. Technol. J. 2020, 8, 85–108. (In Russian) [Google Scholar] [CrossRef]
- Deriglazov, A.A. Rigid Body as a Constrained System: Lagrangian and Hamiltonian Formalism; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2024. [Google Scholar]
- Klavetter, J.J. Rotation of Hyperion. 2. Dynamics. Astron. J. 1989, 98, 1855. [Google Scholar] [CrossRef]
- Wisdom, J.; Peale, S.J.; Mignard, F. The chaotic rotation of Hyperion. Icarus 1984, 58, 137–152. [Google Scholar] [CrossRef]
- Pravec, P.; Harris, A.W.; Michalowski, T. Asteroid rotations. In Asteroids III; Bottke, W.F., Jr., Cellino, A., Paolicchi, P., Binzel, R.P., Eds.; University of Arizona Press: Tucson, AL, USA, 2002; pp. 113–122. [Google Scholar]
- Scheeres, D.J. Orbital Motion in Strongly Perturbed Environments; Applications to Asteroid, Comet and Planetary Satellite Orbiters; Springer: Berlin/Heidelberg, Germany; Praxis Publishing: Chichester, UK, 2012. [Google Scholar]
- Szebehely, V. Theory of Orbits. The Restricted Problem of Three Bodies; Yale University: New Haven, CT, USA; Academic Press: New York, NY, USA; London, UK, 1967. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics, Mechanics, 3rd ed.; §37 (“The Asymmetrical Top”); Heinemann, B., Ed.; Linacre House: Oxford, UK, 1976; Volume 1. [Google Scholar]
- Deriglazov, A.A. Lagrangian and Hamiltonian formulations of asymmetric rigid body, considered as a constrained system. Eur. J. Phys. 2023, 44, 065001. [Google Scholar] [CrossRef]
- Amer, T.S.; Elneklawy, A.H.; El-Kafly, H.F. Dynamical motion of a spacecraft containing a slug and influenced by a gyrostatic moment and constant torques. J. Low Freq. Noise Vib. Act. Control 2025, 44, 1708–1725. [Google Scholar] [CrossRef]
- Rivkin, A.S.; Cheng, A.F. Planetary defense with the Double Asteroid Redirection Test (DART) mission and prospects. Nat. Commun. 2023, 14, 1003. [Google Scholar] [CrossRef]
- Ballouz, R.-L.; Walsh, K.J.; Sánchez, P.; Holsapple, K.A.; Michel, P.; Scheeres, D.J.; Zhang, Y.; Richardson, D.C.; Barnouin, O.S.; Nolan, M.C.; et al. Modified granular impact force laws for the OSIRIS-REx touchdown on the surface of asteroid (101955) Bennu. Mon. Not. R. Astron. Soc. 2021, 507, 5087–5105. [Google Scholar] [CrossRef]
- Sánchez, P.; Scheeres, D.J. Dynamics of a granular asteroid after a subsonic DART-like impact. Icarus 2025, 442, 116741. [Google Scholar] [CrossRef]
- Stickle, A.M.; Kumamoto, K.M.; Graninger, D.M.; DeCoster, M.E.; Caldwell, W.K.; Pearl, J.M.; Owen, J.M.; Barnouin, O.; Collins, G.S.; Daly, R.T.; et al. Dimorphos’s Material Properties and Estimates of Crater Size from the DART Impact. Planet. Sci. J. 2025, 6, 38. [Google Scholar] [CrossRef]
- Trógolo, N.; Bagatin, A.C.; Parro, L.M.; Leiva, A.M.; Moreno, F.; Millas, C.; Benavidez, P.G. Evolution of ejecta in the (65803) Didymos system driven by the fast-spin primary-Stability conditions, mass transfer, and orbiting disk. Astron. Astrophys. 2025, 700, A164. [Google Scholar] [CrossRef]
- Naidu, S.P.; Chesley, S.R.; Moskovitz, N.; Thomas, C.; Meyer, A.J.; Pravec, P.; Scheirich, P.; Farnocchia, D.; Scheeres, D.J.; Brozovic, M.; et al. Orbital and Physical Characterization of Asteroid Dimorphos Following the DART Impact. Planet. Sci. J. 2024, 5, 74. [Google Scholar] [CrossRef]
- Chabot, N.; Adams, E.; Rivkin, A.; Kalirai, J. DART: Latest results from the Dimorphos impact and a look forward to future planetary defense initiatives. Acta Astronaut. 2024, 220, 118–125. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Q.; Long, R.; Ren, J.; Li, J.; Gong, Z.; Wu, Q.; Ren, S. Experimental and Numerical Simulation of Ejecta Size and Velocity of Hypervelocity Impact Rubble-Pile Asteroid. Aerospace 2024, 11, 621. [Google Scholar] [CrossRef]
- Akulenko, L.; Leshchenko, D.; Kushpil, T.; Timoshenko, I. Problems of Evolution of Rotations of a Rigid Body under the Action of Perturbing Moments. Multibody Syst. Dyn. 2001, 6, 3–16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).