Degenerate Fractals: A Formal and Computational Framework for Zero-Dimension Attractors

Abstract

This paper analyzes the extreme limit of iterated function systems (IFSs) when the number of contractions drops to one and the resulting attractors reduce to a single point. While classical fractals have a strictly positive fractal dimension, the degenerate case $D=0$ has been little explored. Starting from the question “what happens to a fractal when its complexity collapses completely?”, Moran’s similarity equation becomes tautological ($r^s=1$ with solution $s={dim}_M=0$) and that only the Hausdorff and box-counting definitions allow an exact calculation. Based on Banach’s fixed point theorem and these definitions, we prove that the attractor of a degenerate IFS is a singleton with ${dim}_H={dim}_B=0$. We develop a reproducible computational methodology to visualize the collapse in dimensions 1–3 (the Iterated Line Contraction—1D/Iterated Square Contraction—2D/Iterated Cube Contraction—3D families), including deterministic and stochastic variants, and we provide a Python script 3.9. The theoretical and numerical results show that the covering box-counting retains unity across all generations, confirming the zero-dimension element and the stability of the phenomenon under moderate perturbations. We conclude that degenerate fractals are an indispensable benchmark for validating fractal dimension estimators and for studying transitions to attractors with positive dimensions.

1. Introduction

Fractality has become over recent decades a fundamental framework for describing and analyzing complex, self-similar structures in mathematics and the applied sciences [1,2]. The fractal dimension, in particular, offers a bridge between classical geometry and natural phenomena, enabling a quantitative characterization of objects that do not fit traditional paradigms. Canonical examples such as the Cantor set, the Sierpiński triangle or carpet, and the Menger sponge have become landmarks in the literature [3,4].

What happens to a fractal when its complexity collapses completely? In this paper, we start from this apparent paradox and investigate the extreme limit where IFS attractors reduce to a point.

Following Mandelbrot [1], a convenient working definition is that a set is “fractal” when its Hausdorff (scaling) dimension D differs from its topological dimension $d_{\mathrm{top}}$, i.e., $D\ne d_{\mathrm{top}}$. For nonempty $X\subset {\mathbb{R}}^d$, the classical bounds $d_{\mathrm{top}}\le D\le d$ hold (here, d is the ambient/embedding dimension); hence, $D\ne d_{\mathrm{top}}$ actually implies $D>d_{\mathrm{top}}$ (see [2]).

A typical fractal regime is $D>d_{\mathrm{top}}$ with $D<d$, as illustrated by the Koch curve ($d_{\mathrm{top}}=1$, $D=log4/log3\approx 1.26$, $d=2$) or the Cantor set ($d_{\mathrm{top}}=0$, $D=log2/log3\approx 0.63$, $d=1$). (A space-filling curve (Peano/Hilbert) is a continuous surjection $f:[0,1]\to {[0,1]}^2$ whose image set equals the unit square; hence, $d_{\mathrm{top}}=D=d=2$ [5,6]. While these curves are often discussed within fractal geometry due to their iterative, self-similar construction, the resulting set does not satisfy Mandelbrot’s criterion $D\ne d_{\mathrm{top}}$. This is because the topological dimension is invariant under homeomorphisms (not under arbitrary continuous surjections), so a space-filling image remains a two-dimensional continuum even though it is generated from a one-dimensional parameter space. By contrast, the Hausdorff dimension is generally not invariant under homeomorphisms (it is preserved under bi-Lipschitz maps), see, e.g., [2].)

This work studies the degenerate boundary case $D=d_{\mathrm{top}}=0$ in ${\mathbb{R}}^d$ ($d\in \{1,2,3\}$), where the iterative construction retains fractal-like features despite dimensional collapse (e.g., for IFSs with $N=1$, the attractor is a singleton and ${dim}_H={dim}_B=0$).

The contributions of this article are twofold. On the one hand, we propose a rigorous and minimal formalization of situations in which trivial IFSs lead to FD = 0 attractors, explicitly proving the equality between the Hausdorff and box-counting dimensions in these cases. On the other hand, we develop and illustrate several “inverse” constructions inspired by classical models (e.g., Cantor, Sierpiński, Menger), where at each step only the central element is retained. The result is a class of degenerate fractals that inevitably collapse to a single point, yet provide a progressive visualization of this structural reduction process.

Beyond theoretical interest, these FD = 0 sets also have didactic value: they offer a strong contrast with canonical “positive” examples and can be used to test algorithms for estimating the fractal dimension, checking whether they correctly return the null value. In addition, they clarify how classical relationships between similarity, self-similarity, and the fractal dimensions behave in limit regimes [7].

Thus, this article seeks to integrate these perspectives—mathematical formalization, constructive visualizations, and didactic implications—into a unified and accessible framework.

1.1. Theoretical Framework: Comparative Analysis of Fractal Dimension Definitions

The mathematical characterization of the fractal dimension has evolved through several distinct formulations, each with specific theoretical foundations and practical implications. In this study, we consider three principal definitions and justify our selection of Moran’s approach for analyzing degenerate iterated function systems.

• Hausdorff Dimension

The Hausdorff dimension ${dim}_H$ represents the most general and theoretically rigorous approach. Defined through Hausdorff measure:

$${\mathcal{H}}^s\left(E\right)=\underset{\delta \downarrow 0}{lim}inf\left\{\sum _{i=1}^{\infty }{\left(diam{U}_i\right)}^s:E\subset \bigcup _{i=1}^{\infty }{U}_i,diam{U}_i<\delta \right\}.$$

(1)

$${dim}_H\left(E\right)=inf\{s\ge 0:{\mathcal{H}}^s\left(E\right)=0\}.$$

(2)

While this definition applies to arbitrary sets and provides deep mathematical insights, its computational implementation is often challenging, requiring optimization over all possible coverings. Here, $diam\left(U_i\right)$ denotes the diameter of the set $U_i$.

• Box-Counting Dimension

The box-counting dimension ${dim}_B$ offers greater computational tractability:

$${\overline{dim}}_B\left(E\right)=\underset{\epsilon \to 0}{lim\; sup}{\displaystyle \frac{logN\left(\epsilon \right)}{log(1/\epsilon )}},{\underline{dim}}_B\left(E\right)=\underset{\epsilon \to 0}{lim\; inf}{\displaystyle \frac{logN\left(\epsilon \right)}{log(1/\epsilon )}}.$$

(3)

When these agree, we write ${dim}_B\left(E\right)$ for their common value. Here $N\left(\epsilon \right)$ is the minimal number of $\epsilon$-boxes needed to cover E. This definition is suitable for empirical data and computational experiments but may not always equal the Hausdorff dimension, especially for sets with complex small-scale structure.

• Moran’s Similarity Dimension

For strictly self-similar sets satisfying the open set condition, Moran’s dimension ${dim}_M$ provides an algebraic formulation through the similarity equation.

Notation. 

We denote by ${dim}_M\left(E\right)$ the (Moran) similarity dimension of a set E. In formulas we solve ${\sum }_{i=1}^N{r}_i^s=1$ and then identify $s={dim}_M\left(E\right)$. We never use D inside Moran’s equation.

$$\sum _{i=1}^N{r}_i^s=1,$$

(4)

where $r_i$ are contraction ratios and N is the number of similarity transformations.

• Role of Moran’s Dimension in Our Framework

We employ Moran’s similarity dimension for this study based on the following considerations:

(a)

Mathematical Appropriateness: Our work exclusively addresses strictly self-similar sets generated by iterated function systems, precisely the domain where Moran’s definition is most natural and theoretically grounded.

(b)

Analytical Transparency: The algebraic nature of Moran’s equation provides clear insight into the degenerate case $N=1$, where it reduces to $r^s=1$ with the unique solution $s=0$. This transparency facilitates our analysis of the limit behavior.

(c)

Computational Advantages: For our constructive families (ILC, ISC, ICC) with exact similarity ratios, Moran’s dimension can be computed directly without the limit processes required by Hausdorff or box-counting definitions.

(d)

Theoretical Consistency: Under the open set condition—satisfied by our non-overlapping constructions—Moran’s dimension coincides with both Hausdorff and box-counting dimensions [2,3]:

$${dim}_H\left(E\right)={dim}_B\left(E\right)={dim}_M\left(E\right)$$

(5)

This equivalence ensures that our results remain consistent with the broader fractal theory.

(e)

Historical Context: Moran’s 1946 formulation [8] specifically addresses the dimensional properties of self-similar sets, making it the natural choice for our investigation of fractal degeneracy.

• Comprehensive Dimensional Verification

Despite our primary use of Moran’s definition, we provide comprehensive verification using all three approaches:

• For the Hausdorff dimension, we employ direct covering arguments demonstrating that ${\mathcal{H}}^s\left(A\right)=0$ for all $s>0$ when A is a singleton, confirming ${dim}_H\left(A\right)=0$.
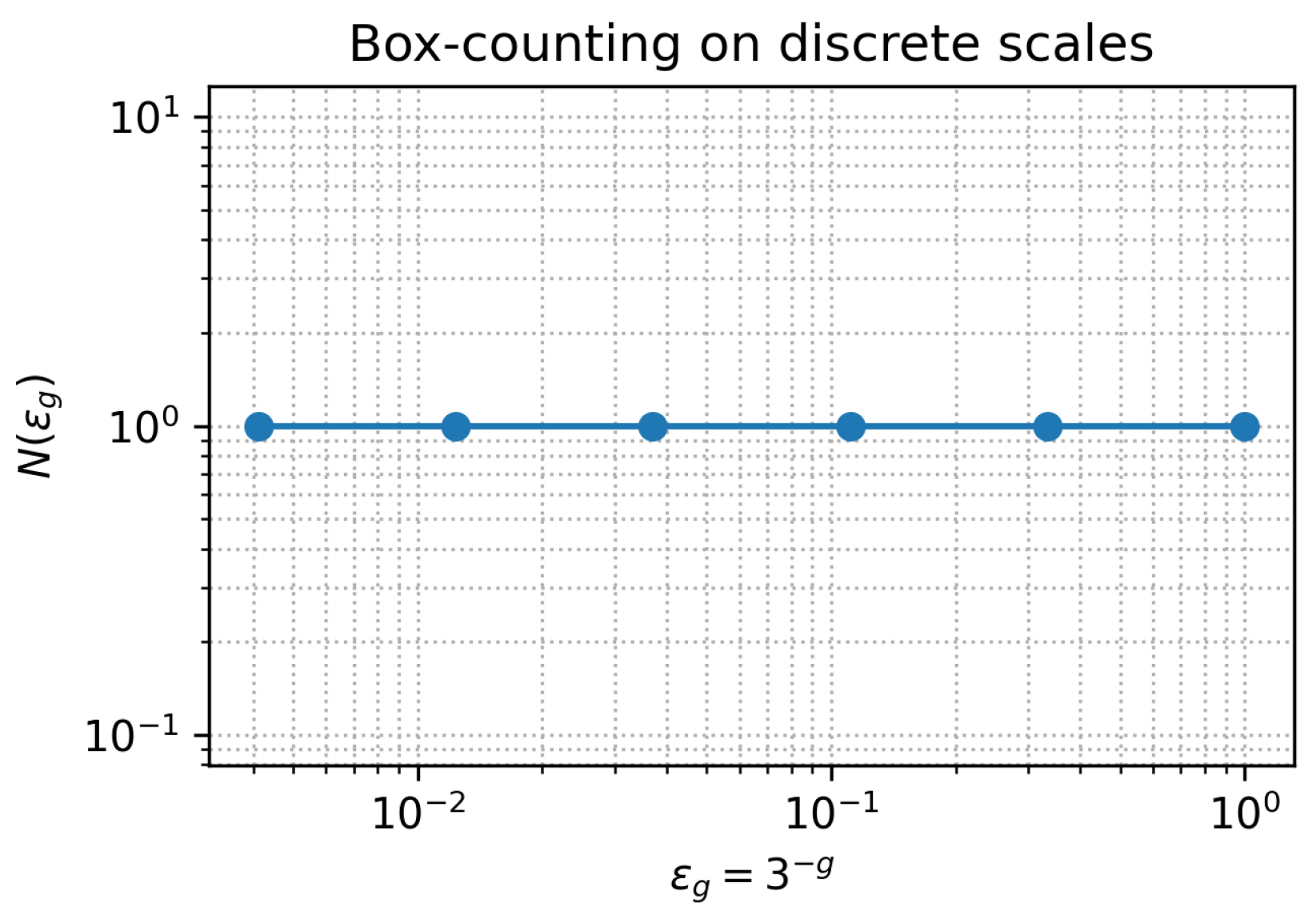
• For the Box-counting dimension, we use discrete box-counting on scales ${\epsilon }_g=3^{-g}$, showing $N\left({\epsilon }_g\right)=1$ for all generations g, yielding ${dim}_B\left(A\right)=0$.
• For the Moran’s dimension, we solve the similarity equation for $N=1$, obtaining the unique solution $s=0$.

This multi-method approach ensures rigorous dimensional analysis while leveraging the specific advantages of Moran’s formulation for our self-similar systems. The consistent results across all three definitions provide strong validation of our findings.

1.2. Related Work and Position in the Literature

To set the context, we recall two fundamental facts. (i) Banach’s fixed point theorem states that any contraction on a complete metric space admits a unique fixed point. Consequently, a degenerate IFS with a single contraction has a unique attractor, which justifies the topic of this article. (ii) The box-counting dimension of a set is defined by

$${dim}_B\left(E\right)=\underset{\epsilon \to 0}{lim}{\displaystyle \frac{logN\left(\epsilon \right)}{log(1/\epsilon )}},$$

(6)

where $N\left(\epsilon \right)$ is the minimal number of boxes of side $\epsilon$ needed to cover E. This definition, revisited in Section 2, provides an essential tool to prove that degenerate attractors have dimension zero. Such fundamental landmarks are often tacitly assumed in advanced works, and stating them explicitly facilitates a self-contained reading.

Although the problem $N=1$ is mentioned in classical texts, there is no monograph dedicated to this limit. Most studies focus on IFSs with two or more contractions, where Moran’s equation provides a unique solution and transversality methods become sophisticated tools [2,3,9,10]. By contrast, the degenerate case is often treated as a footnote; therefore, we devote this work to a detailed and systematic analysis of this conceptual limit. To contextualize our contribution, we provide a brief summary of the relevant literature. The term fractal was introduced by Mandelbrot [1] to describe sets whose fractal (scaling) dimension differs from their topological dimension, i.e., $D\ne d_{\mathrm{top}}$. Since for nonempty subsets of ${\mathbb{R}}^d$ one always has $d_{\mathrm{top}}\le D\le d$, the meaningful regimes are $d_{\mathrm{top}}<D<d$ (classical self-similar sets) and the limit case $d_{\mathrm{top}}<D=d$ (space-filling images); cases with $D<d_{\mathrm{top}}$ do not occur. Subsequently, Hutchinson formulated the general framework of iterated function systems (IFSs) and proved the existence of self-similar attractors [3]. Falconer developed the foundations of Hausdorff and box dimensions for self-similar sets and showed that, under separation conditions, the Hausdorff dimension coincides with the solution to the similarity equation [2]. Recent research has extended to IFSs with overlaps, graph-directed Markov systems, and applications in dislocated geometries [10,11,12,13,14,15]. In all these works, it is implicitly assumed that the number of contractions $N\ge 2$ and that the attractors have a non-trivial fractal structure. From our perspective, attractors with ${dim}_H=0$ appear only marginally: for example, generalized Cantor sets with super-exponential contractions can have zero Hausdorff dimension yet remain perfect and uncountable [16]. Cases where an IFS with a single contraction leads to a finite attractor (fixed point) are mentioned only for completeness. This work fills the gap by systematizing the situation $N=1$ and by providing examples, algorithms, and discussions regarding the relevance of this limit case.

Map of contributions. (i) We formulate a unified formal framework for degenerate IFSs ($N=1$) and show how the classical identities of dimensions (Hausdorff, box-counting, similarity) collapse to 0, clarifying the limit-case role of these attractors; (ii) we propose a taxonomy of constructive families in 1D/2D/3D (Iterated Line Contraction—ILC/Iterated Square Contraction—ISC/Iterated Cube Contraction—ICC) with minimal degeneracy criteria and elementary results about attraction to singletons; (iii) we offer a reproducible guide (definitions, short theorems, figures) that connects degenerate cases (FD $=0$) with classical constructions with $N\ge 2$.

2. Materials and Methods

2.1. Metric Spaces, Contractions, and IFSs

Let $(X,d)$ be a complete metric space. A map $f:X\to X$ is called a contraction if there exists $0\le r<1$ such that

$$d\left(f\left(x\right),f\left(y\right)\right)\le rd(x,y)\mathrm{for}\mathrm{all}x,y\in X.$$

(7)

Banach’s fixed point theorem guarantees that any contraction has a unique fixed point $x^{*}$ and, for any $x_0\in X$, the sequence $x_{n+1}=f\left(x_n\right)$ converges to $x^{*}$ [3].

An iterated function system (IFS) on X is a finite family of contractions $\mathcal{F}={\left\{f_i\right\}}_{i=1}^N$. We associate the operator on the set $\mathcal{K}\left(X\right)$ of nonempty compact subsets of X,

$${\Phi }_{\mathcal{F}}\left(A\right)=\bigcup _{i=1}^N{f}_i\left(A\right),A\in \mathcal{K}\left(X\right).$$

(8)

Then ${\Phi }_{\mathcal{F}}$ is a contraction for the Hausdorff distance; hence, it admits a unique fixed point A, called the attractor of the IFS. Classically, for $N\ge 2$, it has a fractal structure [2,4,7].

2.2. Dimensions: Hausdorff, Box-Counting, and Similarity

For a set $E\subset {\mathbb{R}}^d$, we write ${dim}_H\left(E\right)$ for the Hausdorff dimension (see Equations (1) and (2)) and ${\underline{dim}}_B\left(E\right),{\overline{dim}}_B\left(E\right)$ for the lower and upper box-counting dimensions; when these limits coincide, we denote the common value by ${dim}_B\left(E\right)$. The box-counting dimension is defined in Equation (6), and the limsup/liminf variants are recalled in Equation (3).

For self-similar IFSs with contraction ratios $r_i\in (0,1)$ satisfying standard separation (e.g., the open set condition), the similarity dimension s is defined by Moran’s equation (Equation (4)). In many such cases one has ${dim}_H\left(E\right)={dim}_B\left(E\right)={dim}_M\left(E\right)=s$. In the limit case $N=1$, Equation (4) becomes $r^s=1$, hence $s=0$.

This form of the similarity equation was comprehensively treated by Crownover [17] in the context of fractal geometry education, providing an accessible formulation suitable for computational implementation. In the classical literature one can show that the function $f\left(s\right)={\sum }_{i=1}^N{r}_i^s$ is strictly decreasing for $s>0$, with $f\left(0\right)=N$ and ${lim}_{s\to \infty }f\left(s\right)=0$, so the equation above admits a unique solution s for $N\ge 2$ (see [2]). For a detailed treatment and a complete proof of uniqueness for the similarity equation, including the trivial case $N=1$ and an exemplification of convexity properties of $f\left(s\right)$, see also [18]. In many cases ${dim}_H\left(E\right)={dim}_B\left(E\right)={dim}_M\left(E\right)=s$ (under standard conditions; cf. [8]). Our important limit case appears at $N=1$, when the equation becomes $r^s=1$; hence, $s=0$.

2.3. The Degenerate Case ($N=1$): Singleton Attractor and $dim=0$

We call degenerate an IFS with a single element, $\mathcal{F}=\left\{f\right\}$, where f is a contraction. Then the operator $\Phi \left(A\right)=f\left(A\right)$ has as its unique fixed point the set $A=\left\{x^{*}\right\}$, where $x^{*}$ is the fixed point of f (for example, in ${\mathbb{R}}^d$, for $f\left(x\right)=Rx+t$ with $\parallel R\parallel =r<1$, we have $x^{*}={(I-R)}^{-1}t$). Therefore:

$${dim}_H\left(A\right)={dim}_B\left(A\right)=0\mathrm{for}A=\left\{x^{*}\right\}.$$

(9)

and the Hausdorff measure ${\mathcal{H}}^0\left(A\right)=\#A=1$ [2,3]. Thus, the identities between dimensions in classical theory collapse to the value 0; this is why we interpret these attractors as a limit case in fractal geometry (cf. [1]).

Illustrative example. To make the above framework concrete, consider a contractive map $f:\mathbb{R}\to \mathbb{R}$ given by $f\left(x\right)=\lambda x$ with $\left|\lambda \right|<1$ (e.g., $\lambda =\frac{1}{2}$). Banach’s fixed point theorem guarantees the existence of a unique fixed point $p=0$ with $f\left(p\right)=p$, and the iteration $x_{n+1}=f\left(x_n\right)$ converges to 0 for any $x_0\in \mathbb{R}$. The degenerate iterated system $\left\{f\right\}$ thus has as its attractor the set $\left\{0\right\}$, which satisfies ${dim}_H={dim}_B=0$ and measure ${\mathcal{H}}^0\left(\left\{0\right\}\right)=1$. This is an elementary example of a the “degenerate fractal”: although the collapse to a point does not meet the classical criterion $D>d$, we use the term fractal in a broad sense to emphasize continuity with the $N\ge 2$ cases and to highlight the transition between non-trivial self-similarity and discrete structures.

2.4. Notations and Conventions

Throughout the paper (see

Table 1. Notation used throughout the paper.

Symbol	Meaning
N	Linear resolution per axis (pixels/voxels); ideally $N=3^G$.
G	Number of generations/iterations.
r	Contraction ratio per generation (default $r=\frac{1}{3}$).
$S_g$	Retained side length at generation g (discrete).
$L_g$	Retained segment length in 1D (ILC) at generation g.
${\epsilon }_g$	Observation scale at generation g (e.g., ${\epsilon }_g=3^{-g}$).
$A_g$	Discrete active set at generation g; $A={lim}_{g\to \infty }{A}_g$.
c	Central index (2D/3D: $(c,c)$/$(c,c,c)$, with $c=\lfloor N/2\rfloor$).
${dim}_H$, ${dim}_B$	Hausdorff and box-counting dimensions, respectively.
s (= ${dim}_M\left(E\right)$)	Similarity (Moran) dimension; unique solution of ${\sum }_i{r}_i^s=1$ for E.

for a summary):

• $d\in \mathbb{N}$ is the ambient dimension, typically $d=1,2,3$.
• In ${\mathbb{R}}^d$, we denote affine maps of the form $f\left(x\right)=Rx+t$, where R is a linear contraction ($\parallel R\parallel =r<1$) and $t\in {\mathbb{R}}^d$.
• For a finite family of contractions ${\left\{f_i\right\}}_{i=1}^N$ we use the operator $\Phi \left(A\right)={\bigcup }_i{f}_i\left(A\right)$ on $\mathcal{K}\left({\mathbb{R}}^d\right)$.
• Limit case FD = 0. We will call collapsed attractors those IFS attractors that are singletons, and degenerative constructions those deterministic procedures that converge (in a natural sense) to such sets. Canonical examples and constructive families appear in Section 5.
• $d_{\mathrm{top}}$ denotes the topological dimension of the set/attractor; we reserve d for the ambient space dimension in ${\mathbb{R}}^d$.

Notation. 

We denote by ${dim}_M\left(E\right)$ the (Moran) similarity dimension of a set E. In formulas we solve ${\sum }_{i=1}^N{r}_i^s=1$ and then identify $s={dim}_M\left(E\right)$. We never use D inside Moran’s equation.

2.5. Examples of Dimensional Relations

To illustrate the relations between the embedding dimension (d), the topological dimension of the resulting set ($d_{\mathrm{top}}$), and its Hausdorff (fractal) dimension (D), we recall a few canonical examples (see

Table 2. Representative examples (values standard in the literature).

Set	d	${\mathit{d}}_{\mathbf{top}}$	D	Relation
Middle–third Cantor set	1	0	$log2/log3\approx 0.6309$	$d_{\mathrm{top}}<D<d$
Koch curve	2	1	$log4/log3\approx 1.2619$	$d_{\mathrm{top}}<D<d$
Sierpiński triangle	2	1	$log3/log2\approx 1.5850$	$d_{\mathrm{top}}<D<d$
Sierpiński carpet	2	1	$log8/log3\approx 1.8928$	$d_{\mathrm{top}}<D<d$
Menger sponge	3	1	$log20/log3\approx 2.7268$	$d_{\mathrm{top}}<D<d$
Peano/Hilbert (image)	2	2	2	$D=d_{\mathrm{top}}=d$
Filled square (ref.; not fractal)	2	2	2	$D=d_{\mathrm{top}}=d$
Singleton ($N=1$)	$1,2,3$	0	0	$D=d_{\mathrm{top}}<d$

).

• Reading guide.

Classical self-similar fractals satisfy $d_{\mathrm{top}}<D<d$; space-filling images realize the limit $d_{\mathrm{top}}<D=d$ but do not satisfy $D\ne d_{\mathrm{top}}$; Euclidean references have $D=d_{\mathrm{top}}=d$; degenerate IFSs ($N=1$) yield singletons with $D=d_{\mathrm{top}}=0$.

2.6. Complementary Definitions

To formalize the notions used above we introduce the following definitions.

Definition 1 (Degenerate attractor). 

Let $f:X\to X$ be a contraction on a complete metric space $(X,d)$ and $\mathcal{F}=\left\{f\right\}$ the iterated system with a single contraction. We call degenerate attractor the set $A\subset X$ satisfying $\Phi \left(A\right)=f\left(A\right)=A$. In this case, A is a singleton $\left\{x^{*}\right\}$, where $x^{*}$ is the unique fixed point of f (cf. Theorem 1).

Definition 2 (Geometric collapse). 

Consider a discrete family ${\left\{A_g\right\}}_{g\ge 0}$ of finite subsets of ${\mathbb{R}}^d$ obtained by an iterative constructive procedure across successive generations. We say that a geometric collapse occurs if the diameter ${\delta }_g:=diam\left(A_g\right)$ of the smallest ball containing $A_g$ tends to zero as $g\to \infty$. In particular, for the “central-only” constructions in Section 5, we have ${\delta }_g=S_g$, and the condition $S_g\to 1$ (on the discrete scale) guarantees that the limit set is a singleton with ${dim}_H={dim}_B=0$.

2.7. Limit-Case Role in Fractal Geometry

The degenerate model ($N=1$) clarifies the components of classical identities:

(a)

The similarity dimension drops to $s=0$ (Moran’s equation).

(b)

The Hausdorff and box dimensions coincide and are 0 (Equation (9)).

(c)

Associated measures reduce to point count (${\mathcal{H}}^0$), suggesting a boundary between “fractality” and discrete structures.

In the following sections we exploit this framework to define and catalog deterministic families that degenerate to FD $=0$, providing examples in $d=1,2,3$ and bridges to classical cases ($N\ge 2$) [2,7].

General context of self-similar dimensions. The modern literature extensively investigates self-similar sets with $N\ge 2$, including cases with overlaps and weak separation conditions. Graf introduced the notion of statistically self-similar fractals and showed the existence of a well-defined dimension for sets generated by IFSs even without the open set condition [12]. Mauldin and Urbański developed the theory of graph-directed Markov systems to study the dimensions of attractors in complex situations [11], and Feng and Hu investigated self-similar measures and the conditions for the coincidence of Hausdorff and box dimensions [13]. Further contributions, such as multifractal analysis for countable Markov shifts [16] and Hochman’s overlap theorems for self-similar sets with overlap [14], highlight the complexity of behavior for $N\ge 2$ compared with the degenerate cases analyzed here.

Definition 3 (Open Set Condition (OSC)). 

We say that a family of contractions $\left\{S_{n,i}\right\}$ satisfies OSC if there exists a nonempty open set U such that $S_{n,i}\left(U\right)\subset U$ and the images $S_{n,i}\left(U\right)$ are disjoint (for each level n).

$$\prod _{n=1}^g\left(\sum _{i=1}^{m_n}{r}_{n,i}^s\right)\approx 1(\mathrm{heuristic}\mathrm{balance}\mathrm{as}g\to \infty ).$$

(10)

A rigorous determination of s for level-dependent systems uses the (sub)additive thermodynamic formalism: s is the unique value with pressure $\mathcal{P}\left(s\right)=0$; see [11,12,13].

3. Results

Theoretical Results

In this section we explicitly formulate several statements and proofs that consolidate the results discussed in the Preliminaries, providing numbered references for future citation. In addition to the basic theorems, we also introduce general criteria for identifying sets with a zero box-counting dimension and a characterization of transitions between degenerate behavior and that with positive dimension.

Theorem 1 (Degenerate attractor is a singleton). 

Let $(X,d)$ be a complete metric space and $f:X\to X$ a contraction. Then the degenerate IFS $\left\{f\right\}$ has as its unique attractor a set $\left\{x^{*}\right\}$, where $x^{*}$ is the fixed point of f. In particular, ${dim}_H\left(\left\{x^{*}\right\}\right)={dim}_B\left(\left\{x^{*}\right\}\right)=0$.

Proof. 

The result follows directly from Banach’s fixed point theorem and standard properties of fractal dimensions: any contraction admits a unique fixed point $x^{*}$, and a singleton has both Hausdorff and box-counting dimensions equal to zero, according to the definitions (see Lemma 2). In the spirit of [2,3], the similarity dimension is not useful here because Moran’s equation becomes tautological.

Finally, note that the zero-dimensional Hausdorff measure of a singleton is ${\mathcal{H}}^0\left(\left\{x^{*}\right\}\right)=1$, which mirrors the identity ${dim}_H\left(\left\{x^{*}\right\}\right)={dim}_B\left(\left\{x^{*}\right\}\right)=0$.    □

Proposition 1 (General criterion for zero box-counting dimension). 

Let $E\subset {\mathbb{R}}^d$ be a bounded set. Suppose there exists a discrete scale ${\left\{{\epsilon }_g\right\}}_{g\ge 0}$ with ${\epsilon }_g\to 0$ and a constant $C>0$ such that the number $N\left({\epsilon }_g\right)$ of cubes of side ${\epsilon }_g$ needed to cover E satisfies $N\left({\epsilon }_g\right)\le C$ for all g. Then ${dim}_B\left(E\right)=0$.

Proof. 

By definition, the upper box-counting dimension is

$${\overline{dim}}_B\left(E\right)=\underset{g\to \infty }{lim\; sup}{\displaystyle \frac{logN\left({\epsilon }_g\right)}{-log{\epsilon }_g}}.$$

(11)

The hypothesis implies $N\left({\epsilon }_g\right)\le C$ for a constant independent of g; hence,

$$0\le {\displaystyle \frac{logN\left({\epsilon }_g\right)}{-log{\epsilon }_g}}\le {\displaystyle \frac{logC}{-log{\epsilon }_g}}\underset{g\to \infty }{\to }0,$$

(12)

since $-log{\epsilon }_g\to \infty$. It follows that ${\overline{dim}}_B\left(E\right)=0$; similarly, the lower dimension is zero; hence, ${dim}_B\left(E\right)=0$.    □

Proposition 2 (Near-degenerate transition). 

Consider a central-only procedure in which, at each generation g, one retains $k_g$ disjoint sub-blocks of side proportional to $3^{-g}$ (e.g., $k_g$ segments in 1D or $k_g$ squares in 2D). Suppose $k_g\ge 1$ for all g. Then:

(i) 

if $log{k}_g=o\left(g\right)$, then ${dim}_B=0$;

(ii) 

if there exists a constant $\alpha \in (0,1]$ and positive constants $c_1,c_2$ such that $c_1{3}^{\alpha g}\le k_g\le c_2{3}^{\alpha g}$ for g large enough, then ${dim}_B=\alpha$.

Proof. 

On the discrete scale ${\epsilon }_g\sim 3^{-g}$, the number of boxes of side ${\epsilon }_g$ needed to cover the active set is proportional to $k_g$. In case (i) we have $log{k}_g/(glog3)\to 0$, which implies ${dim}_B=0$ by definition. In case (ii), we have

$$\underset{g\to \infty }{lim}{\displaystyle \frac{log{k}_g}{glog3}}=\alpha ,$$

(13)

by the comparability hypothesis; hence, ${dim}_B=\alpha$ (cf. [2]). In particular, we return to the degenerate case $\alpha =0$ when $k_g$ is uniformly bounded.    □

Proposition 3 (Similarity dimension at N = 1). 

Consider a degenerate iterated function system $\mathcal{F}=\left\{f\right\}$ on a complete metric space, with f a contraction with factor $r\in (0,1)$. The similarity dimension s of the attractor satisfies the identity equation $r^s=1$. The unique real solution is $s=0$.

Proof. 

Moran’s similarity equation for a self-similar IFS with $N=1$ becomes $r^s=1$. Since $r\in (0,1)$, the exponent s must satisfy $r^s=1$, which occurs only for $s=0$; if $s<0$ then $r^s>1$, and for $s>0$ we obtain $r^s<1$. Therefore, the unique solution is $s=0$.    □

Lemma 1 (Hausdorff dimension of finite sets). 

Let E be a finite set of points in ${\mathbb{R}}^d$. Then ${dim}_H\left(E\right)=0$ and ${dim}_B\left(E\right)=0$.

Proof. 

For a finite set $E=\{x_1,\dots ,x_m\}$ we can cover E with m balls of radius $\epsilon$ for any $\epsilon >0$. The associated s-Hausdorff mass of this cover is $m{\epsilon }^s$, which tends to zero as $\epsilon \to 0$ for any $s>0$, implying ${dim}_H\left(E\right)=0$. Also, the number $N\left(\epsilon \right)$ of cubes of side $\epsilon$ needed to cover E is m; hence, ${dim}_B\left(E\right)={lim}_{\epsilon \to 0}{\displaystyle \frac{logm}{-log\epsilon }}=0$.    □

Lemma 2 (Discrete box dimension). 

For the “central-only” constructions described in Section 5, at generation g a single block of side $S_g$ is retained, and on the discrete scale ${\epsilon }_g=3^{-g}$ the number of boxes needed to cover the active set is $N\left({\epsilon }_g\right)=1$. Consequently, ${dim}_B=0$.

Proof. 

By the definition of the ILC/ISC/ICC procedures, at each generation g there is a single segment/square/cube of side $S_g$ filled; the rest of the pixels/voxels are background. If we choose ${\epsilon }_g$ proportional to $3^{-g}$ (corresponding to the block scale), one cube of side ${\epsilon }_g$ covers the entire active set, so $N\left({\epsilon }_g\right)=1$ for all g and, by the formula in the Preliminaries, ${dim}_B=0$.    □

Theorem 2 (Stability of the collapse under moderate variations). 

Consider a sequence of deterministic or stochastic constructions characterized by discrete sides $S_g^x,S_g^y,S_g^z$ (with $S_g^i\in \mathbb{N}$ and ${lim}_{g\to \infty }{S}_g^i=1$ for each axis i) and translations of the center $(c_g^x,c_g^y,c_g^z)$ perturbed by noises ${\delta }_g^i$ such that ${\sum }_{g=0}^{\infty }\left|{\delta }_g^i\right|<\infty$ (or $\mathbb{E}\left[{\left({\delta }_g^i\right)}^2\right]\to 0$). Then the attractor is a singleton and ${dim}_B=0$.

Proof idea. 

Define the discrete scale ${\epsilon }_g:=max\{S_g^x,S_g^y,S_g^z,|{\delta }_g^x|,|{\delta }_g^y|,|{\delta }_g^z\left|\right\}$. Since ${\sum }_{g\ge 0}\left|{\delta }_g^i\right|<\infty$, the cumulative displacement of the center is bounded; hence, for large g the active set remains within a ball of vanishing radius. Together with ${lim}_{g\to \infty }{S}_g^i=1$, this implies that for g sufficiently large the active set is contained in a single box of side ${\epsilon }_g$, so $N\left({\epsilon }_g\right)=1$. Therefore, by the box-counting formula it follows that ${dim}_B=0$.    □

Definition 4 (Nonuniform Moran set, FD = 0 but nontrivial). 

On each level $n\ge 1$ let there be a number $m_n\in \{2,\dots ,M\}$ of disjoint copies (OSC), with similar contractions $S_{n,i}$ with ratios $r_{n,i}\in (0,1)$. Define

$$E=\bigcap _{g\ge 1}\bigcup _{(i_1,\dots ,i_g)}{S}_{1,i_1}\circ \dots \circ S_{g,i_g}\left(K_0\right),$$

(14)

where $K_0$ is an initial compact set (e.g., a cube), and the union at level g covers all choices ${\left(i_k\right)}_{k\le g}$.

Theorem 3 (FD = 0 with infinite branching). 

Assume (i) OSC, (ii) $1\le m_n\le M$ for all n, with $m_n\ge 2$ for infinitely many n, and (iii) there exists $c>0$ with $r_{n,i}\le e^{-c{n}^2}$ for all $n,i$. Then ${dim}_H\left(E\right)={dim}_B\left(E\right)=0$. Moreover, under OSC and branching at infinitely many levels (i.e., $m_n\ge 2$ for infinitely many n), E is uncountable, perfect (no isolated points), and totally disconnected.

Lemma 3 (Contrast with singleton/finite union). 

If there exists $N_0$ with $m_n=1$ for all levels $n\ge N_0$, then the attractor is finite (the singleton case included). In our setting (Theorem 3), branching occurs at infinitely many levels, so this case is excluded.

Remark 1 (Examples of perfect uncountable sets with zero dimension). 

The construction in Theorem 3 belongs to the broader class of Moran-type sets with super-exponential contractions. In the classical literature, there are variants of the Cantor set in which the lengths removed per level decay fast enough so that $2^n{a}_n^{1/n}\to 0$; these sets remain perfect and uncountable, yet have zero Hausdorff dimension. Such examples emphasize that ${dim}_H=0$ does not imply topological triviality.

Sketch of Theorem 3. 

For any cylinder at level g,

$$diam\left({\mathrm{cyl}}_g\right)\le \prod _{n\le g}{e}^{-c{n}^2}=exp\left(-c\frac{g(g+1)(2g+1)}{6}\right)\le e^{-c{g}^3/3}.$$

The number of level-g cylinders is $\le {\prod }_{n\le g}{m}_n\le M^g$. Thus for any $s>0$,

$$\sum _{{\mathrm{cyl}}_g}{\left(diam\left({\mathrm{cyl}}_g\right)\right)}^s\le M^g·e^{-sc{g}^3/3}\underset{g\to \infty }{\to }0,$$

so ${\mathcal{H}}^s\left(E\right)=0$ and hence ${dim}_H\left(E\right)=0$. For the box dimension, take ${\epsilon }_g:=e^{-c{g}^3/3}$; then $N\left({\epsilon }_g\right)\le M^g$ and

$${\displaystyle \frac{logN\left({\epsilon }_g\right)}{log(1/{\epsilon }_g)}}\le {\displaystyle \frac{glogM}{(c/3)g^3}}\underset{g\to \infty }{\to }0,$$

which gives ${dim}_B\left(E\right)=0$.

For the topological properties: OSC yields disjointness of cylinders at each level and $diam\left({\mathrm{cyl}}_g\right)\to 0$. Since $m_n\ge 2$ for infinitely many n, the coding space contains a full binary subtree, hence has cardinality of the continuum; therefore E is uncountable. No point is isolated: if $x\in E$, at arbitrarily large levels there is a branching inside any neighborhood of x, producing distinct points of E arbitrarily close to x. Finally, distinct points differ at some first level of branching and lie in disjoint closed cylinders, so connected components are singletons; hence E is totally disconnected and perfect.    □

Proposition 4 (Nonzero generalized Hausdorff measure; sketch). 

There exists a gauge $h:(0,1)\to (0,\infty )$, of the type $h\left(t\right)=exp(-\sqrt{|logt|})$ (or $h\left(t\right)={|logt|}^{-\alpha }$ chosen appropriately), such that

$$0<{\mathcal{H}}^h\left(E\right)<\infty .$$

(15)

Proof sketch. (We will state Proposition 5 below, which provides the required sub-polynomial bound on $N\left(\epsilon \right)$.) Using Proposition 5, we have a sub-polynomial covering bound $logN\left(\epsilon \right)\le {A|log\epsilon |}^{\beta }$ as $\epsilon \downarrow 0$ for some $A>0$ and $0<\beta <1$. Choosing a slowly varying gauge, e.g., $h\left(t\right)=exp(-\sqrt{|logt|})$, the corresponding Hausdorff sums are finite but nonzero, yielding $0<{\mathcal{H}}^h\left(E\right)<\infty$.

Remark 2 (Context for gauges). 

The condition in Proposition 4 is not an isolated peculiarity. In fractal theory, there are classical examples of sets with zero Hausdorff dimension or with zero standard measure that nevertheless admit a nonzero Hausdorff measure if an appropriate gauge function is used. For instance, Brownian trajectories have Hausdorff dimension 2, yet the associated 2-dimensional Hausdorff mass is zero; however, by choosing the gauge $h\left(t\right)=t^{2}loglog(1/t)$ one obtains a finite and nonzero measure. This type of adjustment highlights the fineness of small-scale structure and motivates the qualitative use of h in our case to detect nontriviality of sets with FD = 0.

Proposition 5 (Covering bound). 

There exist $A>0$ and $\beta \in (0,1)$ such that, for $\epsilon \downarrow 0$,

$$N\left(\epsilon \right)\le exp\left({A|log\epsilon |}^{\beta }\right).$$

(16)

In particular, ${\displaystyle \frac{logN\left(\epsilon \right)}{log(1/\epsilon )}}\to 0$ (cf. Equation (6)), with a sub-polynomial rate.

4. Methods and Implementation

4.1. Formal Framework: IFS with a Single Contraction

Consider $f:{\mathbb{R}}^d\to {\mathbb{R}}^d$ a similarity (or a composition with a rotation) that is strictly contractive,

$$f\left(x\right)=rRx+t,0<r<1,R\in SO\left(d\right),t\in {\mathbb{R}}^d.$$

(17)

By Banach’s theorem, there exists a unique fixed point p with $f\left(p\right)=p$, and the attractor of the IFS with a single map is $A=\left\{p\right\}$. Consequently,

$${dim}_H\left(A\right)={dim}_B\left(A\right)=0.$$

(18)

The similarity equation ${\sum }_i{r}_i^s=1$ is informative only for $N\ge 2$; for $N=1$ it becomes $r^s=1$ (hence $s={dim}_M=0$); hence, we use direct definitions (box-counting/Hausdorff).

4.2. Nomenclature, Parameters, and Notation

Standard acronyms: ILC (1D), ISC (2D), ICC (3D). Parameters: G (generations), N (ideally $N=3^G$), $r=\frac{1}{3}$ implicit, center $(c,c)$/$(c,c,c)$ with $c=\lfloor N/2\rfloor$, colors $bg=0$, $fg=255$. See Table 1 for a comprehensive summary of notation used throughout the paper.

4.3. “Central-Only” Discrete Construction (1D/2D/3D)

For $g=0,\dots ,G$ we retain only the central element, with geometric scaling.

• 1D (ILC): strip $h\times N$; length $L_g=max\{1,\lfloor N·r^g\rfloor \}$; fill $[s:s+L_g]$.
• 2D (ISC): grid $N\times N$; side $S_g=max\{1,\lfloor N/3^g\rfloor \}$; fill ${[s:s+S_g]}^2$.
• 3D (ICC): volume $N^3$; side $S_g$ as above; fill ${[s:s+S_g]}^3$; save XY/XZ/YZ slices and MIP (maximum intensity projection) projections.

Visual control: fixed windows/axes for all g (no autoscaling); white background, black object.

4.4. Algorithm (Pseudocode)

The core algorithm for generating degenerate fractals across all dimensions is presented in Listing 1. This pseudocode implements the central-only construction for ILC/ISC/ICC families. The complete pseudocode is provided in Appendix A.2 (Listing A1).

Listing 1. Central-only algorithm for ILC/ISC/ICC constructions

# Parameters: N (grid size), G (number of generations), r = 1/3  # mode in {"ILC", "ISC", "ICC"}, center = (c_x, c_y, c_z)  # optional: noise sigma and anisotropy (r_x, r_y, r_z)  # Default values: bg = 0 (background), fg = 255 (object)  for g in range(G + 1): if mode == "ILC":  # length of the 1D segment  Lg = max(1, int(N * (r ** g))) s = (N - Lg) // 2 img[:, :] = bg img[:, s:s + Lg] = fg else: # ISC/ICC  # side length of the square/cube in 2D/3D  Sg = max(1, N // (3 ** g)) # exact for r = 1/3  s = (N - Sg) // 2 # set background to bg  img[...] = bg # fill the central square/cube with value fg  fill_central_block(s, Sg, fg) # save the images; in ICC mode also save XY/XZ/YZ slices and the MIP projection.

4.5. Reproducibility (Reference Implementation)

To ensure full reproducibility of our results, we provide a reference implementation and specific commands (Listing 2). The full Python script (fd0_generator.py) is available as Supplementary Material. Script: fd0_generator.py (Python 3.9.18; numpy 1.26.4; Pillow 10.2.0; optional tqdm 4.66.4). Representative commands for reproducing all results are provided in Listing 2.

Note: include from pathlib import Path for directory creation

Listing 2. Representative commands for reproduction (script fd0_generator.py)

python fd0_generator.py --mode isc --size 512 --iters 6 --ratio 0.333 \ --outdir out_isc --fmt png python fd0_generator.py --mode icc --size 128 --iters 6 --ratio 0.333 \ --outdir out_icc --mip --slice-step 8 python fd0_generator.py --mode ilc --size 800 --iters 6 --ratio 0.333 \ --outdir out_ilc --strip-height 64

4.6. Verification of ${dim}_B=0$

For ${\epsilon }_g=3^{-g}$, $N\left({\epsilon }_g\right)=1$ for all g; hence,

$${dim}_{B}A=\underset{g\to \infty }{lim}{\displaystyle \frac{log1}{glog3}}=0,$$

(19)

and similarly ${dim}_{H}A=0$. This dimensional collapse is visually confirmed by the log-log plot in Figure 1, which shows a constant $N\left(\epsilon \right)=1$ across all scales ${\epsilon }_g=3^{-g}$, resulting in a zero slope that unequivocally demonstrates ${dim}_B=0$.

4.7. Pitfalls and Best Practices

Autoscaling masks the collapse (fix the windows); use $S_g=N/3^g$ (with $\lfloor ·\rfloor$) for $r=\frac{1}{3}$; report slices and MIP in 3D.

4.8. Extensions (Optional)

Near-degenerate cases: parameters can be modified without losing the collapse. For example, one may choose ratios $r\ne \frac{1}{3}$ or shift the block to an off-center position or add small noise; these variations do not change the conclusion for $N=1$. More generally, if at generation g one retains $k_g$ sub-blocks (e.g., $k_g$ segments in 1D), then Proposition 2 shows that $log{k}_g=o\left(g\right)$ implies ${dim}_B=0$, while an exponential growth of $k_g$ leads to a positive dimension. Thus, extending the parameter $k_g$ provides a natural mechanism for transitioning between the degenerate case and classical fractals.

4.9. Summary

Formal ⇒ discrete ⇒ numerical ⇒ reproducible: singleton A, central element at each generation, images/slices/MIP, standard parameters/classification.

5. Constructive Families

In this section we catalogue constructive families that produce degenerative attractors with ${dim}_H={dim}_B=0$, in the spirit of the methodology in Section 4. All models below converge, in the limit, to a singleton; discretely, they are implementable on a grid by retaining only a central sub-block (or its deterministic equivalent). The progressive dimensional collapse across generations is visually documented in Figure 2.

Notation clarification: here N denotes the grid size (e.g., $N=3^G$), not the number of IFS maps.

5.1. The ILC Family (1D)

Definition. At generation g, only the central segment of length $L_g=max\{1,\lfloor N{r}^g\rfloor \}$ is retained on a strip $h\times N$. Parameters: $N,G,r,h$. Limit: singleton. Implementation: implemented in Listing 1 and reproducible via fd0_generator.py with –mode ilc (Listing 2). The complete Python code is available in Supplementary Material. The visual progression of this collapse is shown in the top panel of Figure 2.

As the generation g increases, the remaining central segments define a sequence of lengths $L_g$ that decrease geometrically, analogous to a centralized variant of the Cantor set but without branching. The final attractor is a single point, and the resulting image series provides a visual illustration of the collapse to $D=0$. Choosing $N=3^G$ ensures that the lengths $L_g$ follow exactly the triadic scale $3^{-g}$; other values of N may introduce minor rounding without altering the limit. This family can serve as a benchmark for fractal dimension estimators, checking that $N\left({\epsilon }_g\right)=1$ at each scale [2,4].

5.2. The ISC Family (2D)

Definition. At generation g, only the central square of side $S_g=max\{1,\lfloor N/3^g\rfloor \}$ is retained (exact for $r=\frac{1}{3}$). Parameters: $N,G,r$. Limit: singleton. Implementation: –mode isc. The complete implementation is provided in Supplementary Material. The sequence of contracting squares is illustrated in the middle panel of Figure 2.

In 2D, the central square $[s:s+S_g]\times [s:s+S_g]$ survives at generation g; this produces a sequence of concentric squares that shrink by a factor of approximately $3^{-g}$. The model can be viewed as a degenerate variant of the Cantor dust or the Sierpiński carpet, in which only a single sub-block is retained, so that the entire set reduces to a point in the limit. Choosing $N=3^G$ maintains the exact triadic scale, while other resolutions introduce only rounding. The visualizations in Figure 2 (2D panel) illustrate these nested squares. For a detailed discussion of the differences between classical self-similar sets and degenerate variants, see [2].

5.3. The ICC Family (3D)

Definition. At generation g, only the central cube $S_g=max\{1,\lfloor N/3^g\rfloor \}$ is retained. Parameters: $N,G,r$. Limit: singleton. Implementation: –mode icc; XY/XZ/YZ slices and MIP are saved optionally. The complete 3D implementation is available in Supplementary Material. The 3D volumetric collapse is demonstrated in the bottom panel of Figure 2.

In 3D, the analogue is achieved by retaining at each generation the central cube of side $S_g$. The active volume forms a sequence of nested cubes; the visual representations (XY/XZ/YZ sections and MIP projections) show how the entire volume contracts to a single voxel as g increases. This family can be seen as a degenerate variant of the Menger sponge, in which only one sub-cube survives. Choosing $N=3^G$ ensures exact contraction at each generation; deviations from this value change only the intermediate resolution. Such 3D visualizations are useful for testing rendering algorithms and methods for measuring the fractal dimension in volume [2].

5.4. Deterministic Variations (Near-Degenerate)

Near-degenerate deterministic constructions can be grouped into three scenarios that do not change the point limit. In the deterministic off-center variant, the same side $S_g$ is maintained, but the center is shifted to a fixed position $c^{\prime }$. Although the position of the block changes, the convergence remains toward a single point; hence, ${dim}_B=0$. In the anisotropic step-down variant, the sides are reduced separately on each axis, $S_g^x,S_g^y,S_g^z$, with ratios $r_x,r_y,r_z$; as long as $S_g^{•}$ tends to 1 in each direction, the attractor is still a singleton. In the multi-pass shrink (“k-keep”) variant, the central sub-block is retained multiple times within the same generation, which changes only the intermediate visual scale without altering the limit.

5.5. Terminological Clarifications

Notation. Throughout the paper, D denotes a (fractal) dimension (Hausdorff or box-counting, as specified), while ${\delta }_g:=diam\left(A_g\right)$ denotes the diameter (at generation g) of the active set. In the fractal literature, the term degenerate can be used in different contexts. In this paper we use it to designate cases in which the IFS attractor is a finite set (usually a singleton). It should not be confused with the notion of trivial fractals used in some works for sets without non-trivial self-similarity. The essential difference is that the degenerate objects discussed here appear as limits of constructions with $N\ge 2$ when the number of contractions drops to one, and the process of degeneration is of interest in itself.

To position these objects within the broader framework of fractal geometry, recall the working definition (Mandelbrot) that fractals exhibit a mismatch between fractal and topological dimensions, i.e., $D\ne d_{\mathrm{top}}$ [1]. Since $d_{\mathrm{top}}\le D\le d$ for nonempty sets in ${\mathbb{R}}^d$, the umbrella covers $d_{\mathrm{top}}<D<d$ (e.g., Koch, Sierpiński, Menger) and, as a limit, $d_{\mathrm{top}}<D=d$ (space-filling images). It does not include any cases with $D<d_{\mathrm{top}}$. The cases analyzed here, with $D=0$, mark the frontier where scaling complexity collapses and thus motivate the term “degenerate” for this conceptual limit.

We will also use the expression geometric collapse to describe the phenomenon by which the diameter of the active set decreases to zero as the generation g increases. Formally, if $S_g$ is the side of the central block retained at generation g, we say that a geometric collapse occurs if $S_g\to 1$ (on the discrete scale) and the diameter of the active set tends to zero in the usual topology. In this sense, the Hausdorff measure of the limit set is zero and the fractal dimension is 0 (cf. Equation (9)).

5.6. Controlled Stochastic Variations

Stochastic variations introduce randomness without destroying the collapse. In the center jitter variant, the center of the block is perturbed by a deviation ${\delta }_g$ whose variances decrease with g; if ${\delta }_g\to 0$, the sequence of blocks still converges to a point. In the rare drop variant, the retention of the central block at generation g occurs with probability $1-{\epsilon }_g$; if the series ${\sum }_g{\epsilon }_g$ converges and the errors are controlled, the attraction to a singleton is maintained (Borel–Cantelli intuition).

5.7. Cartesian Products and Hybrids

Regarding Cartesian products, combining two 1D constructions produces a strip equivalent to the ILC family in two dimensions, and 1D × 2D or 2D × 1D combinations essentially reduce to the ISC or ICC constructions. It is useful to emphasize that the “skeleton-only” variant (retaining only the contour) is not discussed here: such a procedure would preserve a curve or a surface and would change the dimensional class; the constructions analyzed in this study always retain a filled sub-block that contracts to a point.

5.8. Comparative Summary

Table 3. Synopsis of constructive families for the degenerate case ${dim}_B=0$. The stability column indicates sufficient conditions for the limit set to remain a singleton.

Family	Domain	Block Retained at g	Stability (Conditions)	Implementation
ILC	1D (strip $h\times N$)	segment $L_g=max\{1,\lfloor N{r}^g\rfloor \}$	Y (always)	–mode ilc
ISC	2D ($N\times N$)	square $S_g$	Y (always)	–mode isc
ICC	3D ($N^3$)	cube $S_g$	Y (always)	–mode icc
Off-center det.	2D/3D	block $S_g$ with center $c^{\prime }$	Y if $\left(c_g\right)$ is Cauchy	custom (center)
Anisotropic det.	2D/3D	sides $S_g^x,S_g^y,S_g^z$	Y if $S_g^i\to 1$	custom ($r_x,r_y,r_z$)
Off-center stoch.	2D/3D	block $S_g$ with center $c_g+{\delta }_g$	Y if ${\sum }_g\left|{\delta }_g\right|<\infty$	custom (random)
Anisotropic stoch.	2D/3D	sides $S_g^x,S_g^y,S_g^z$ with noise	Y if $var\left({\delta }_g^i\right)\to 0$	custom (random)

summarizes the key parameters. In all cases, $\#\mathrm{boxes}\left({\epsilon }_g\right)=1$ on the scale ${\epsilon }_g=3^{-g}$; hence, ${dim}_B=0$.

5.9. Numerical Results

In this section we present the results obtained for the ILC/ISC/ICC families described in Section 5, over generations $g=0\to 5$, together with an elementary numerical verification that ${dim}_B=0$. All results were generated using the Python script provided in Supplementary Material. The dimensional collapse is graphically illustrated in Figure 1, which shows the characteristic zero slope of the log-log plot, confirming the theoretical prediction of zero box-counting dimension.

5.10. Generation-Wise Visualizations

For each family (1D/2D/3D) we generated frames at generations $g=0\to 5$ using the script from Supplementary Material. In each case, the retained element contracts geometrically toward the center, consistent with the “central-only” construction. Figure 2 summarizes representative examples (1D left, 2D middle, 3D right), clearly illustrating the progressive dimensional collapse across all families.

5.11. Numerical Verification of ${dim}_B=0$

On the discrete scale ${\epsilon }_g=3^{-g}$, the cover by boxes of side ${\epsilon }_g$ always has a single nonzero element (the central block).

Table 4. Numerical verification (box-counting) on the scale ${\epsilon }_g=3^{-g}$: $N\left({\epsilon }_g\right)=1$; hence, ${dim}_B=0$.

Generation g	Scale ${\mathit{\epsilon }}_{\mathit{g}}$	Number of Boxes $\mathit{N}\left({\mathit{\epsilon }}_{\mathit{g}}\right)$
0	$3^0$	1
1	$3^{-1}$	1
2	$3^{-2}$	1
3	$3^{-3}$	1
4	$3^{-4}$	1
5	$3^{-5}$	1

shows that $N\left({\epsilon }_g\right)=1$ for all g, which directly implies ${dim}_B=0$.

5.12. Reproducibility of Results

The results can be reproduced with fd0_generator.py (Supplementary Material), using the same parameters across all generations and fixed visualization windows (no autoscaling). Representative commands are provided in Listing 2.

6. Discussion

This paper treats the degenerate case of contractive systems with a single map (IFS), for which the attractor is a singleton and, consequently, ${dim}_H={dim}_B=0$. Recent studies confirm that iterated geometric models may degenerate into attractors with Hausdorff dimension zero, illustrating the broader mathematical landscape of FD=0 constructions [19,20]. In Section 4 we showed a discrete, reproducible method to simulate this limit: retaining only the central sub-block (“central-only”) over successive generations, in 1D/2D/3D. In Section 5 we organized the constructive families (ILC/ISC/ICC and their variations), and in Section 3 we numerically verified that the number of boxes remains $N\left({\epsilon }_g\right)=1$ on the scale ${\epsilon }_g=3^{-g}$, which directly implies ${dim}_B=0$. As Lemma 3 shows, the eventually-constant case $m_n=1$ yields a finite attractor.

6.1. Implications for Materials with Dimensional Reduction

The degenerate fractal framework provides a mathematical analogy for analyzing materials that undergo progressive structural simplification during processing or degradation. While natural systems rarely achieve perfect mathematical degeneracy, the progression toward homogeneity follows similar scaling principles.

In thermal degradation of polymers [21], complex molecular architectures experience topological simplification through chain scission and cross-link breakdown. This collapse from branched, entangled networks toward linear fragments or monomer units parallels the dimensional reduction in our framework. The parameter $k_g$—representing the number of retained structural features at scale ${\epsilon }_g$—can be experimentally quantified using techniques like dynamic light scattering or rheological measurements tracking the loss of relaxation modes.

Similarly, sintering processes [22] demonstrate how porous frameworks with rough interfaces (surface fractal dimension $D_s\in (2,3)$) evolve toward smoother, nearly Euclidean surfaces ($D_s\to 2$) as densification proceeds. In the notation of Proposition 2, if the number of distinct pore features $k_g$ decreases faster than the observation scale shrinks (i.e., $log{k}_g=o\left(g\right)$ along ${\epsilon }_g\sim 3^{-g}$), the microstructure approaches effective homogeneity. Advanced tomography can track this progression by measuring the narrowing of the pore-size distribution and the reduction of the surface-fractal scaling range.

These analogies highlight that while true mathematical degeneracy ($D=0$) may not occur in material systems, the progression toward structural simplicity follows quantifiable scaling laws. Our framework provides the mathematical language to characterize these transitions, distinguishing between mere coarsening (preserving fractal characteristics) and genuine architectural collapse.

Experimental validation: In situ scattering experiments during polymer degradation could track the evolution of $N\left(\epsilon \right)$ across length scales, testing whether the scaling approaches the degenerate limit of scale-independent structure.

Takeaway: Our degenerate fractal model offers quantitative scaling criteria to characterize structural simplification in materials, providing mathematical rigor to distinguish between different modes of dimensional reduction.

6.2. Discriminating Between Degenerate and Near-Degenerate Cases from Experimental Data

A key advantage of our formal framework is its ability to distinguish true degeneracy (FD = 0) from near-degeneracy in experimental systems where data may be non-geometric. For instance, in analyzing scattering data from nanomaterials [23] or impedance spectroscopy in porous electrodes [24], the signature of degeneracy would manifest as a complete loss of multiscale characteristics. Specifically, our Proposition 2 provides a quantitative criterion: if the number of structural features $k_g$ at different scales grows sub-exponentially ($log{k}_g=o\left(g\right)$), the system is approaching true degeneracy. In contrast, near-degenerate systems would exhibit weak but detectable scale-invariant behavior with $k_g$ growing polynomially, yielding a small but positive fractal dimension. This discrimination is crucial in applications like battery aging analysis [25], where the collapse of pore networks (approaching true degeneracy) must be distinguished from mere coarsening (near-degeneracy with FD > 0).

Experimental validation: The box-counting results in Table 4 and the visualizations in Figure 2 demonstrate the clear signature of degeneracy ($N\left({\epsilon }_g\right)=1$ across scales), providing a template for identifying similar collapse in experimental systems. Our computational methodology can be adapted to fit experimental scaling laws, providing a clear diagnostic for structural collapse even when direct imaging is unavailable.

Takeaway: The clear mathematical distinction between degenerate and near-degenerate cases provides experimentalists with quantitative criteria for identifying structural collapse in complex systems.

6.3. Connections to Dynamical Systems and Structural Transitions

Our degenerate fractal framework naturally aligns with bifurcation theory in dynamical systems [26], where complex attractors collapse to fixed points at critical parameter values. This analogy is particularly relevant for modeling the mechanical collapse of lightweight lattice structures under critical loads [27]. In such systems, the transition from a complex, energy-absorbing microstructure to a collapsed state mirrors the mathematical transition from a non-trivial fractal (FD > 0) to a degenerate one (FD = 0). Our formalization can describe the final collapsed state and, when extended to near-degenerate cases, can model the progression towards collapse. For example, in lattice structures used for energy absorption, the sequential buckling of structural elements can be viewed as a stepwise reduction in effective fractal dimension, culminating in complete collapse (FD = 0). This perspective provides a new quantitative language for describing failure mechanisms in architected materials and could inform the design of structures with controlled collapse behavior for impact protection applications.

Takeaway: The connection to dynamical systems theory enriches our understanding of collapse phenomena across disciplines, from mathematical bifurcations to mechanical failure.

6.4. Implications for AI and Machine Learning

Our work provides essential benchmarks for validating AI-driven approaches that characterize complex structures. In reinforcement learning and evolutionary algorithms used for materials discovery [28] or pattern recognition [29], it is crucial to distinguish between truly complex patterns (non-trivial dimensionality) and trivial or collapsed structures. Our degenerate fractals with FD = 0 serve as critical test cases: any competent dimensionality estimation algorithm should correctly identify these singleton attractors as zero-dimensional. Conversely, failure to do so indicates fundamental flaws in the method. Furthermore, the transition from non-degenerate to degenerate fractals can be used to test whether AI models can detect subtle changes in structural complexity. This is particularly important in applications like automated microstructure classification [30], where the ability to distinguish between intact and collapsed cellular materials is essential for quality control and failure analysis in manufacturing.

Takeaway: The FD=0 case serves as an essential null test for AI algorithms claiming to characterize structural complexity, providing a rigorous benchmark for model validation.

6.5. Application to Cavitation in Ultrasonic Micro-Injection Molding

Cavitation dynamics in ultrasonic processing presents a physical system where iterative collapse phenomena share mathematical similarities with our degenerate fractal framework, though important distinctions must be noted.

During ultrasonic micro-injection molding [31], cavitation bubbles undergo repetitive formation and collapse across successive acoustic cycles [32]. Each collapse event represents a local reduction in structural complexity: from intricate, possibly fractal-like bubble interfaces to nearly spherical interfaces or complete disappearance. The progression over multiple cycles mirrors the iterative contraction in our mathematical model.

However, unlike our deterministic constructions, cavitation is inherently stochastic and energy-driven. A more appropriate analogy is to consider the size distribution of bubble populations across scales, rather than deterministic retention rules. In this context, an approach toward degenerative states would manifest as:

• convergence (narrowing) of bubble size distributions toward monodispersity;
• loss of multiscale characteristics in acoustic-emission spectra;
• reduction in the scaling range of bubble-interface complexity.

Our framework suggests monitoring how an effective dimension $D_{\mathrm{eff}}$ of the cavitation process evolves with processing parameters. High-speed imaging combined with box-counting (on binary bubble masks) or multifractal analysis (on interfaces or acoustic signals) could quantify whether the system approaches scale-independent behavior—the experimental signature analogous to mathematical degeneracy.

This perspective may inform process optimization by identifying parameter regions where cavitation transitions from beneficial mixing (preserving multiscale characteristics) to potentially damaging collapse (approaching degenerative regimes). The analogy provides a conceptual framework for these transitions, though direct quantitative mapping requires additional physical modeling.

Takeaway: Cavitation offers a physical analogy for iterative collapse; our mathematical framework provides conceptual tools to analyze transitions in structural complexity, with potential applications in process optimization.

6.6. Significance of the Degenerate Case $D=0$

The situation $D=0$ is a useful landmark for two reasons: (i) mathematically, it clarifies that a single contraction does not produce higher-order fractal structure; (ii) computationally, it provides a baseline for visualization and pipeline testing (rendering, slices/MIP, measurement). Some usual ambiguities arise from autoscaling: if the viewing window is reframed at each generation, the collapse may appear stationary. Fixing the window/axes across all g (see Section 4) removes this artifact.

6.7. On the Similarity Equation and the Case $N=1$

The classical similarity equation ${\sum }_i{r}_i^s=1$ is suitable when $N\ge 2$ contractions act in parallel. … For $N=1$, the relation reduces to $r^s=1$, i.e., a tautology that does not inform s (the similarity dimension). Therefore our proofs use direct definitions (Hausdorff/box-counting) and simple numerical checks (Section 3).

Proposition 6 (Singleton attractor for a single strict contraction). 

Let $(X,d)$ be a complete metric space and $f:X\to X$ a strict contraction, i.e., $\exists 0<c<1$ such that $d\left(f\right(x),f(y\left)\right)\le cd(x,y)$ for all $x,y\in X$. Then the IFS $\left\{f\right\}$ has a unique attractor $A=\left\{x^{*}\right\}$, where $x^{*}$ is the Banach fixed point of f. In particular, ${dim}_H\left(A\right)={dim}_B\left(A\right)=0$.

Proof. 

By Banach’s fixed point theorem, any contraction has a unique fixed point $x^{*}$; hence, the attractor of the IFS $\left\{f\right\}$ is the singleton $A=\left\{x^{*}\right\}$. For a singleton one has ${\mathcal{H}}^0\left(A\right)=\#A=1$ and ${\mathcal{H}}^s\left(A\right)=0$ for all $s>0$, so ${dim}_H\left(A\right)=0$; moreover $N\left(\epsilon \right)\equiv 1$ for $\epsilon$ small; hence, ${dim}_B\left(A\right)=0$ (cf. Lemma 2). In the spirit of [2,3], the similarity equation is tautological at $N=1$.    □

6.8. Deterministic and Stochastic Variations: What Remains Invariant

The variations proposed in Section 5 (off-center, anisotropic, multi-pass) preserve the point limit as long as the block side $S_g$ decreases to 1 on each axis. Introducing a center jitter or a probabilistic “rare drop” mechanism does not change the conclusion as long as the perturbations diminish sufficiently (e.g., variance $\to 0$) and do not permanently interrupt block retention; intuitively, these conditions are compatible with convergence to a single active voxel/pixel.

6.9. Limitations and Practical Considerations

The limitations and useful extensions of our framework can be summarized in a few ideas. First, the apparent size of the collapse depends on the graphics window: for correct comparisons between generations, it is necessary to maintain the same axes and windows; otherwise the collapse may appear stationary. Second, choosing resolutions N different from $3^G$ introduces rounding and discrepancies; although these are benign and do not change the theoretical argument, it is recommended that they be reported and discussed. Third, near-degenerate cases with two or more contractions ($N\ge 2$) can produce $D>0$, and the models presented here should be seen as minimalist baselines for transition studies toward non-trivial structures. Finally, generalizations—such as adaptive off-center blocks, generation-dependent anisotropic contractions, or controlled noise—can be used to build experimental trajectories toward $D>0$ without substantially changing the base code.

While our framework provides mathematical insights into degenerative processes, several limitations should be noted when applying it to real-world systems. First, natural phenomena rarely exhibit the perfect self-similarity of mathematical fractals; most show statistical self-similarity with cutoffs at small and large scales. Second, the clear distinction between degenerate and near-degenerate cases in our theoretical model may be blurred in experimental data due to measurement noise and finite resolution. Third, the timescales of collapse in physical systems (e.g., milliseconds in cavitation vs. hours in material degradation) introduce dynamical aspects not captured by our static fractal framework. These limitations highlight the need for careful interpretation when bridging between mathematical idealizations and physical reality.

6.10. Implications and Applications

Although degenerate attractors are simple singletons, their study has several useful implications. First, these limit sets serve as a benchmark for fractal dimension estimators: any algorithm that returns a nonzero value for a singleton must be revised. Second, the contraction processes presented here offer a didactic example of checking the definitions: the geometric collapse clearly illustrates how the Hausdorff and box dimensions are defined via the number of boxes needed for coverage. Third, the fact that degenerate attractors are fixed points of contractive maps connects them to the generalized theory of iterated function systems and fixed point theory. Recent studies in the literature show that generalized Hutchinson-type operators in dislocated metric spaces have applications in variational problems, integral equations, and control systems, highlighting the importance of common attractors in modern research [10]. This framework offers opportunities to extend studies toward non-trivial attractions and to generalizations of contraction conditions [9]. In addition, sets with $D=0$ can be used as a visual benchmark for developing rendering tools, MIP projections in 3D, or comparisons with classical fractals. Beyond the theoretical framework, contraction-based fractal schemes have found applications in image reconstruction and segmentation. For instance, hybrid evolutionary methods successfully reconstruct fractal-coded images from sparse data [33], while fractal dimension measures have been combined with deep learning for the segmentation of thin, crack-like patterns in engineering materials [34]. These examples highlight the potential applicability of degenerate and sparse fractal structures in computational practice.

An article by Nazir and Silvestrov explores a class of generalized F-IFS systems in G-metric spaces and proves the existence of common attractors for a triplet of contractions, offering a modern perspective on attraction theories and justifying the continued interest in the notions discussed here [15].

6.11. Reproducibility and Best Practices

Fix the parameters ($N,G,r$), keep the windows constant, use fd0_generator.py with the documented options, and in 3D obligatorily save the three central sections (XY/XZ/YZ) and MIP projections. For traceability, state the Python/package versions and the structure of the output folders.

7. Conclusions

We presented a minimal yet complete framework for the degenerate case of contractive systems with a single map (IFS), in which the attractor is a singleton and, consequently, ${dim}_H={dim}_B=0$. Our methodology (Section 4) provides a discrete, reproducible procedure in 1D/2D/3D—retaining only the central block (“central-only”) over successive generations—and the constructive families (Section 5) and results (Section 3) numerically confirm the expected behavior. As a boundary case, the $N=1$ setting clarifies the lower end of the dimensional spectrum and serves as a rigorous null benchmark for validating algorithms near dimensional collapse.

7.1. Main Contributions

• Formal clarification. We rigorously show that an IFS with a single contraction has a singleton attractor; the case $N=1$ is not resolved by the similarity equation, but via direct definitions (Hausdorff/box-counting). In Mandelbrot’s working sense, such sets are not fractal ($D=d_{\mathrm{top}}=0$), yet they remain informative as precise limiting configurations that complement the usual $D>0$ self-similar cases.
• Unitary discrete method. We provide a unified implementation for ILC/ISC/ICC, with standard parameters ($N=3^G$, $r=\frac{1}{3}$), fixed windows, and a reporting pipeline that includes images, sections, and MIP projections.
• Reproducibility. We provide concrete CLI commands and an operational checklist; the reference script fd0_generator.py allows the recreation of all figures and numerical checks.
• Atlas of variations. We catalogue deterministic variations (off-center, anisotropic, multi-pass) and stochastic ones (jitter, rare drop) that preserve the point limit, offering examples and discussions on stability.

7.2. Future Directions

A natural direction is to investigate transitions to $D>0$ by introducing two or more contractions, with control over separation and scaling ratios, and to carry out a comparative study with the $D=0$ baseline. Also, near-degenerate regimes can be analyzed via adaptive center shifts, generation-dependent anisotropic contractions, and controlled noise, to evaluate collapse speed and to test dimension-estimation methods. Finally, developing easy-to-install software packages (e.g., via pip) and reproducible archives (e.g., Zenodo) would facilitate the reproduction of results and their extension by the community. A practical objective is to establish decision rules that reliably distinguish “$D\approx 0$” from the true degenerate case $D=0$ under finite, noisy data, using the $D=0$ baseline as ground truth.

7.3. Key Message

The case $D=0$ is an indispensable benchmark: it offers theoretical clarity and a practical baseline for visualization and measurement. Around this landmark, one can build controlled experiments toward classes with $D>0$. Placed at this lower bound, the $D=0$ case complements the usual focus on $D>0$ self-similar sets and anchors comparative experiments and validation pipelines.