Efficient Evaluation of Sobol’ Sensitivity Indices via Polynomial Lattice Rules and Modified Sobol’ Sequences

Abstract

Accurate and efficient estimation of Sobol’ sensitivity indices is a cornerstone of variance-based global sensitivity analysis, providing critical insights into how uncertainties in input parameters affect model outputs. This is particularly important for large-scale environmental, engineering, and financial models, where understanding parameter influence is essential for improving model reliability, guiding calibration, and supporting informed decision-making. However, computing Sobol’ indices requires evaluating high-dimensional integrals, presenting significant numerical and computational challenges. In this study, we present a comparative analysis of two of the best available Quasi-Monte Carlo (QMC) techniques: polynomial lattice rules (PLRs) and modified Sobol’ sequences. The performance of both approaches is systematically assessed in terms of performance and accuracy. Extensive numerical experiments demonstrate that the proposed PLR-based framework achieves superior precision for several sensitivity measures, while modified Sobol’ sequences remain competitive for lower-dimensional indices. Our results show that IPLR-α3 outperforms traditional QMC methods in estimating both dominant and weak sensitivity indices, offering a robust framework for high-dimensional models. These findings provide practical guidelines for selecting optimal QMC strategies, contributing to more reliable sensitivity analysis and enhancing the predictive power of complex computational models.

1. Introduction

Uncertainty in model inputs—such as emission levels, chemical reaction rates, or financial risk factors—can propagate to outputs in ways that undermine reliability and decision-making. For instance, inaccuracies in air quality simulations can misguide public health strategies, while misestimation of risk factors in financial models can destabilize markets. Sensitivity analysis (SA) provides a principled framework to identify which inputs most strongly affect model behavior and outcomes, thereby supporting robust model calibration and policy design.

Among existing SA approaches, the Sobol’ sensitivity indices are particularly valuable because they decompose model variance into contributions from both main effects and higher-order interactions [1,2]. However, computing Sobol’ indices requires high-dimensional integration, which is computationally intensive for large-scale scientific and engineering models [3,4]. Consequently, there is a strong need for efficient numerical techniques that retain accuracy while reducing computational cost.

In other words, SA is a fundamental technique in modeling and simulation that investigates how variations in input parameters influence the output of a given system: financial modeling [5], foundational sensitivity analysis methodology [6,7], standard references for Sobol’ indices [8,9], and error estimation in global sensitivity analysis [10]. By identifying which inputs contribute most to uncertainty in the model results, SA provides valuable insights into the robustness and reliability of mathematical models. This approach is especially crucial in complex environmental, financial, and engineering systems, where numerous variables interact in nonlinear ways. SA not only enhances model transparency but also supports decision-making by highlighting the key drivers of system behavior.

The Sobol’ approach is central to our analysis. It involves decomposing the model function into components that represent the contributions of individual input parameters and their interactions. The Sobol’ global sensitivity indices, defined based on the decomposition of variance, help quantify the contributions of each input parameter and their interactions to the overall variance in the model output [2,9]. The calculation of these indices involves evaluating high-dimensional integrals, which is where QMC methods prove invaluable [11].

This paper introduces an optimization method based on a particular polynomial lattice rule with an interlaced factor for estimating sensitivity indices. We compare our method with one of the best available methods and analyze the relative errors for key output quantities. Our results demonstrate that the proposed optimization method consistently outperforms other methods in accurately estimating both first-order and total-order sensitivity indices, particularly for parameters with smaller effects.

The primary objective of this work is to conduct a systematic comparative analysis of advanced polynomial lattice rules and modified Sobol’ sequences to efficiently compute Sobol’ sensitivity indices. By evaluating their behavior, accuracy, and computational performance, this study aims to provide deeper insights into the strengths and limitations of both approaches, offering practical guidance for selecting suitable methods in complex environmental, engineering, and financial modeling scenarios.

Quasi-Monte Carlo (QMC) methods—such as Sobol’ sequences and lattice rules—have emerged as powerful variance-reduction strategies [12,13,14]. Modified Sobol’ sequences are widely used because of their simplicity and reliable accuracy in low to moderate dimensions [15]. Polynomial lattice rules (PLRs), on the other hand, have theoretical advantages for high-dimensional integration [12,16], but their practical performance in environmental sensitivity analysis has not been systematically benchmarked. Recent developments in randomized and adaptive QMC highlight ongoing advances in variance reduction [17,18], while extensions to unbounded domains further illustrate the versatility of QMC [19].

This study contributes to closing this gap. We conduct a comparative analysis of improved polynomial lattice rules with interlacing factors (IPLR-$\alpha$2 and IPLR-$\alpha$3) against several modified Sobol’ sequence variants (MSS-1, MSS-2, and MSS-2S). Our testbed is Unified Danish Eulerian Model (UNI-DEM), a benchmark air pollution model characterized by high dimensionality, nonlinear chemical interactions, and strong relevance for policy studies.

The novelty of this work lies in the following:

• Introduces a new method based on a particular IPLRs for estimating Sobol’ sensitivity indices.
• The first systematic evaluation of IPLR-based QMC strategies for Sobol’ index estimation in a realistic environmental model.
• Demonstrating the complementary strengths of IPLR-$\alpha 2$ (for weak indices) and IPLR-$\alpha 3$ (for dominant indices and variance terms).
• Providing practical guidelines for comparison of the best available QMC: IPLRs and modified Sobol’ sequences, offering a path toward more reliable and computationally efficient sensitivity analysis.

The rest of this paper is organised as follows: Section 2 outlines the materials and methods used in our study, including detailed descriptions of the polynomial lattice rules and the UNI-DEM model. Section 3 presents the results of our sensitivity analysis, highlighting the performance of different methods in estimating Sobol’ indices. Section 4 discusses the implications of our findings and compares the effectiveness of the various methods. Finally, Section 5 concludes the paper by summarizing our findings and suggesting potential directions for future research.

2. Materials and Methods

In this study, we focused on the application of QMC methods to a large-scale mathematical model for the remote transport of air pollutants called Unified Danish Eulerian Model (UNI-DEM) [20,21,22],

2.1. UNI-DEM

UNI-DEM is described by a system of partial differential equations (PDEs) that model pollutant concentrations, wind components, diffusion coefficients, emissions, and chemical reactions [23,24,25]. The model can be represented by the following system of PDEs:

$$\begin{array}{cc}{\displaystyle \frac{\partial c_s}{\partial t}=}\hfill & {\displaystyle -\frac{\partial \left(u{c}_s\right)}{\partial x}-\frac{\partial \left(v{c}_s\right)}{\partial y}-\frac{\partial \left(w{c}_s\right)}{\partial z}+}\hfill \\ \hfill & {\displaystyle +\frac{\partial }{\partial x}\left(K_x\frac{\partial c_s}{\partial x}\right)+\frac{\partial }{\partial y}\left(K_y\frac{\partial c_s}{\partial y}\right)+\frac{\partial }{\partial z}\left(K_z\frac{\partial c_s}{\partial z}\right)+}\hfill \\ \hfill & {\displaystyle +E_s+Q_s(c_1,c_2,\dots ,c_q)-(k_{1s}+k_{2s})c_s,s=1,2,\dots ,q.}\hfill \end{array}$$

(1)

The number of pollutants studied by UNI-DEM determines the number q of equations in the system. Equation (1) has the following model dimensions:

• $c_s$—Pollutant concentrations.
• $u,v,w$—Wind components along the coordinate axes.
• $K_x,K_y,K_z$—Diffusion coefficients.
• $E_s$—Space emissions.
• $k_{1s},k_{2s}$—Dry and wet deposit coefficients, respectively ($s=1,\dots ,q$).
• $Q_s(c_1,c_2,\dots ,c_q)$—Nonlinear functions describing chemical reactions between pollutants.

We assume in (1) that pollutant concentrations $C_s$ are bounded and sufficiently smooth; diffusion coefficients $K_x,K_y,K_z$ are strictly positive and bounded; wind fields $u,v,w$ are differentiable with bounded divergence; emission sources $E_s$ are measurable and bounded; and nonlinear chemical reaction terms $Q_s$ are locally Lipschitz-continuous. These assumptions ensure the well-posedness of the PDE system and guarantee the existence of unique weak solutions.

It is assumed that the mathematical model can be presented by a model function:

$$\mathrm{u}=f\left(\mathrm{x}\right),\mathrm{where}\mathrm{x}=(x_1,x_2,\dots ,x_s)\in U^s\equiv {[0;1]}^s$$

(2)

is a vector of input parameters with a joint probability density function (p.d.f.) $p\left(\mathrm{x}\right)=p(x_1,\dots ,x_s)$.

2.2. Sobol Approach

The concept of the Sobol’ approach is based on a decomposition of an integrable model function (2) [2]:

$$f\left(\mathrm{x}\right)=f_0+\sum _{\nu =1}^s\sum _{l_1<\dots <l_{\nu }}{f}_{l_1\dots l_{\nu }}(x_{l_1},x_{l_2},\dots ,x_{l_{\nu }}),$$

(3)

where $f_0$ is a constant. The representation (3) is referred to as the ANOVA representation of the model function $f\left(\mathrm{x}\right)$ if each term satisfies [2]

$${\int }_0^1{f}_{l_1\dots l_{\nu }}(x_{l_1},x_{l_2},\dots ,x_{l_{\nu }})\mathrm{d}{x}_{l_k}=0,1\le k\le \nu ,\nu =1,\dots ,s.$$

(4)

Equation (4) guarantees that the functions in the right-hand side of (3) are defined in a unique way, where ${\displaystyle f_0={\int }_{U^s}f\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}}$. The quantities

$${\displaystyle \mathbf{D}={\int }_{U^s}{f}^2\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}-f_0^2,{\mathbf{D}}_{l_1\dots l_{\nu }}=\int f_{l_1\dots l_{\nu }}^2\mathrm{d}{x}_{l_1}\dots \mathrm{d}{x}_{l_{\nu }}}$$

(5)

are the so-called total and partial variances, respectively. A similar decomposition holds for the total variance, which is represented by the corresponding partial variances: $\mathbf{D}={\sum }_{\nu =1}^s{\sum }_{l_1<\dots <l_{\nu }}{\mathbf{D}}_{l_1\dots l_{\nu }}$. The main sensitivity measures following the Sobol’ approach are the so-called Sobol’ global sensitivity indices [2,9], defined by

$${\displaystyle S_{l_1\dots l_{\nu }}=\frac{{\mathbf{D}}_{l_1\dots l_{\nu }}}{\mathbf{D}},\nu \in \{1,\dots ,s\}.}$$

(6)

and the total sensitivity index (TSI) of an input parameter $x_i,i\in \{1,\dots ,s\}$, defined by [2,9]:

$${\displaystyle S_i^{tot}=S_i+\sum _{l_1\ne i}{S}_{i{l}_1}+\sum _{l_1,l_2\ne i,l_1<l_2}{S}_{i{l}_1{l}_2}+\dots +S_{i{l}_1\dots l_{s-1}},}$$

(7)

where $S_i$ is called the main effect (first-order sensitivity index) of $x_i$, and $S_{i{l}_1\dots l_{j-1}}$ is the $j$-th order -sensitivity index. The higher-order terms describe the interaction effects between the unknown input parameters $x_{i_1},\dots ,x_{i_{\nu }},\nu \in \{2,\dots ,s\}$ on the output variance. This implies that performing global sensitivity analysis from a mathematical point of view involves calculating total sensitivity indices (see Equation (7)), which, according to the formulations in Equations (5) and (6), reduces to the evaluation of multidimensional integrals.

Consider the multidimensional integration problem

$$S\left(f\right):=I={\int }_{U^d}f\left(x\right)dx.$$

(8)

When using quasirandom sequences for estimating (8) (e.g., Sobol’ points), poor uniformity in low-dimensional projections may significantly reduce accuracy. It has been shown that Sobol’ sequences may fail quasi-uniformity in higher dimensions [26]. A possible remedy is to shake or randomize the quasirandom points.

2.3. MCA-MSS-1

The first shaking-based algorithm [27] perturbs each Sobol’ point ${\mathrm{x}}_i\in {\mathbf{E}}_i^d$ by a random displacement:

$${\xi }_i\left(\rho \right)={\mathrm{x}}_i+\rho {\omega }_i,$$

(9)

where ${\omega }_i$ is uniformly distributed in $U^d$, and $\rho <1$ is the shaking radius. The quadrature

$$I\left(f\right)\approx {\displaystyle \frac{1}{n}}\sum _{i=1}^{n}f\left({\xi }_i\right)$$

(10)

achieves the error bound

$$R_n(f,d)\le c_d\parallel f\parallel n^{-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{d}}},$$

(11)

for functions with bounded first derivatives [28,29]. Thus, MCA-MSS-1 has an optimal convergence rate for this class of functions.

2.4. MCA-MSS-2

A refinement [30] generates two symmetric pseudorandom points ${\xi }_i,{\xi }_i^{\prime }$ in each elementary interval ${\mathbf{E}}_i^d$, with ${\xi }_i^{\prime }$ symmetric to ${\xi }_i$ about the center $s_i$. The quadrature

$$I\left(f\right)\approx {\displaystyle \frac{1}{2n}}\sum _{i=1}^n\left[f\left({\xi }_i\right)+f\left({\xi }_i^{\prime }\right)\right]$$

(12)

satisfies

$$R_n(f,d)\le {\tilde{c}}_d\parallel f\parallel n^{-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{2}{d}}},$$

(13)

for functions with continuous first and bounded second derivatives, yielding an improved convergence rate.

2.5. MCA-MSS-2-S

Both MCA-MSS-1 and MCA-MSS-2 depend on the shaking radius $\rho$, whose efficient use increases computational cost. To overcome this, the MCA-MSS-2-S algorithm partitions $U^d$ into $m^d$ equal subdomains ${\mathbf{K}}_i^d$. In each subdomain, a point ${\xi }_i$ is sampled uniformly, and its symmetric counterpart ${\xi }_i^{\prime }$ is generated about the subdomain center $s_i$. The approximation is then

$$I\left(f\right)\approx {\displaystyle \frac{1}{2m^d}}\sum _{i=1}^{m^d}\left[f\left({\xi }_i\right)+f\left({\xi }_i^{\prime }\right)\right].$$

(14)

This method mimics MCA-MSS-2 with adaptive $\rho$ values and achieves the same optimal rate

$$R_n(f,d)=O\left(n^{-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{2}{d}}}\right).$$

(15)

2.6. Lattice Rules

To introduce the rank-1 lattice rule, we will use the following formula [31]:

$${\mathbf{x}}_k=\left\{{\displaystyle \frac{k}{N}}\mathbf{z}\right\},k=1,\dots ,N,$$

(16)

where N is an integer, $N\ge 2$, $\mathbf{z}=(z_1,z_2,\dots z_s)$ is the generating vector, and $\left\{z\right\}$ denotes the fractional part of z. For the definition of $E_s^{\alpha }\left(c\right)$ and $P_{\alpha }(z,N)$, see [31].

In 1959, Bahvalov [11] proved that there exists an optimal choice of the generating vector $\mathbf{z}$:

$$\left|{\displaystyle \frac{1}{N}}\sum _{k=1}^{N}f\left(\left\{{\displaystyle \frac{k}{N}}\mathbf{z}\right\}\right)-\underset{{[0,1)}^s}{\int }f\left(u\right)du\right|\le cu(s,\alpha ){\displaystyle \frac{{(logN)}^{\beta (s,\alpha )}}{N^{\alpha }}},$$

(17)

for the function $f\in E_s^{\alpha }\left(c\right)$, and $\alpha >1$ and $u(s,\alpha ),\beta (s,\alpha )$ do not depend on N.

2.7. Polynomial Lattice Rules

Now, we will continue with our method based on improved polynomial lattice rules; for more definitions, see [12,14,32]. Let b be prime, let p be a polynomial, $degp=m$, with coefficients in $Z_b$, and let $q_1,\dots q_s$ be polynomials and $deg(q_1,\dots ,q_s)\le m-1$, with coefficients in $Z_b$. Then, we will choose $C_j$, the j^th generating matrix.

Let $u_1,u_2,\cdots \in Z_b$:

$${\displaystyle \frac{q_j\left(x\right)}{p\left(x\right)}}={\displaystyle \frac{u_1}{x}}+{\displaystyle \frac{u_2}{x^2}}+\dots .$$

(18)

Then, set

$${\mathbf{C}}_{\mathbf{j}}=\left(\begin{array}{ccccc}{u}_1& u_2& u_3& \dots & u_m\\ u_2& u_3& \dots & \dots & u_{m+1}\\ u_3& \dots & \dots & \dots & u_{m+2}\\ \dots & \dots & \dots & \dots & \dots \\ u_m& u_{m+1}& u_{m+2}& \dots & u_{2m-1}\end{array}\right)\in Z_b^{m\times m},j=1,\dots ,s.$$

(19)

This ensures explicit dependence on j.

The digital net [4] with $C_1,\dots ,C_s$ is named a polynomial lattice point set (PLPS), and a QMC rule using a polynomial lattice point set is named a polynomial lattice rule, where p is the modulus, and $(q_1,\dots ,q_s)$ is the generating vector of polynomials [16].

Let $m,s,d\in \mathbb{N}$ be defined with $d>1$. Let $p\in Z_b$ be defined as $deg\left(p\right)=m$, and let $q=(q_1,\dots ,q_{ds})\in {\left(Z_b\right)}^{ds}$. An interlaced polynomial lattice rule of order d is actually a point set composed of $b_m$ points $x_0,\dots ,x_b^{m-1}$, which are defined as [4]

$$x_n:=D_d\left(z_n\right);$$

(20)

the nth point $z_n$ of a PLPS $P_{b^m,ds}(q,p)$ is presented by

$$z_n:=\left(v_m\left({\displaystyle \frac{\nu \left(x\right)q_1\left(x\right)}{p\left(x\right)}}\right),v_m\left({\displaystyle \frac{\nu \left(x\right)q_2\left(x\right)}{p\left(x\right)}}\right),\dots ,v_m\left({\displaystyle \frac{\nu \left(x\right)q_{ds}\left(x\right)}{p\left(x\right)}}\right)\right)\in {[0,1)}^{ds}$$

(21)

for $0\le n<b^m$. For an explanation of (20) and $\nu \left(x\right)$, see [16]. A QMC rule that uses this point set (21) is called an interlaced polynomial lattice rule IPLR (of order d). For simplicity in the experiments, we changed the order to $\alpha$. The generating matrices used for the construction of improved interlaced polynomial lattice point sets were based on the implementation of the Sobol’ sequence with interlacing factor $\alpha =2$ and $\alpha =3$, as described in [15]. The procedure is summarized in the algorithm presented in Section 2.8. This implementation reproduces the higher-order convergence rate $\mathcal{O}\left(n^{-\alpha +\epsilon }\right)$ established in [16] while retaining compatibility with existing Sobol’ sequence generators.

2.8. Algorithmic Structure and Interlacing Procedure

The previous subsections describe the mathematical formulation of the quasi-Monte Carlo (QMC) constructions used in this study, including the generation of Sobol’ and polynomial lattice sequences, and the role of the interlacing factor $\alpha$. To complement these theoretical developments, and to enhance readability and reproducibility, we now provide a concise algorithmic overview that translates the core procedures into explicit pseudo-code and visual form. This addition clarifies the computational workflow and improves the transparency and reproducibility of the proposed methods.

Section 2.3, Section 2.4, Section 2.5, Section 2.6 and Section 2.7 introduce the theoretical principles behind each method; this subsection complements those descriptions with clear, step-by-step pseudo-code and a visual schematic of the digit-interlacing process.

The pseudo-code representations summarize the essential logic of the sampling schemes:

• MCA–MSS–1: A single “shaken” Sobol’ sequence with random perturbations to reduce regularity artifacts;
• MCA–MSS–2: Symmetric point pairs within Sobol’ sub-intervals to achieve local variance reduction;
• MCA–MSS–2S: Radius-free stratified sampling with reflection symmetry;
• IPLR: Generation of higher-order digital nets followed by digit interlacing of the order $\alpha =2$ or 3.

Algorithms 1–4 list the complete pseudo-code for these procedures. For the improved polynomial lattice rule (IPLR), the digit-interlacing mechanism is further illustrated in Figure 1, which shows how base-b digits from $\alpha$-consecutive coordinates are merged into a single output coordinate. This combined presentation replaces earlier descriptive text and provides a concise, reproducible view of the computational workflow.

Figure 1. Illustration of the digit-interlacing procedure in the improved polynomial lattice rule (IPLR). For $\alpha =2$ and $\alpha =3$, base-b digits from $\alpha$ consecutive coordinates of the digital net are interleaved to form each output coordinate $x^{\left(j\right)}$. This mechanism yields higher-order quasi-Monte Carlo convergence for smooth integrands.

Together, the pseudo-code listings and the schematic diagram presented in this subsection provide a transparent overview of the implementation logic behind all sampling strategies used in this study. They highlight the structural differences between modified Sobol’ sequences and improved polynomial lattice rules, illustrate how the interlacing factor $\alpha$ modifies the generation of QMC points, and ensure that each algorithm can be reproduced and independently verified. This concise algorithmic representation bridges the theoretical formulation of Section 2 with the numerical experiments reported in Section 3.

The selection of the parameters, $n=2^{16}$, $\alpha =\{2,3\}$, and the specified input domains was guided by both theoretical and practical considerations. The sample size $n=2^{16}$ (65,536 points) provides a good compromise between accuracy and computational feasibility, allowing convergence behavior to be clearly observed while keeping runtime under two minutes per simulation on a standard workstation. The interlacing orders $\alpha =2$ and $\alpha =3$ were selected as the most commonly adopted configurations for higher-order digital nets: $\alpha =2$ achieves second-order convergence for moderately smooth integrands, while $\alpha =3$ captures higher regularity at marginally increased computational cost. These values are consistent with established recommendations in the QMC literature [26,33,34]. The domain intervals for each uncertain input parameter in the UNI-DEM model were defined according to standard variability ranges used in European air-quality simulations (e.g., emission rates, diffusion coefficients, and chemical reaction constants), ensuring that the test setup remains physically realistic while spanning a representative high-dimensional parameter space.

3. Results

Unless otherwise stated, all numerical experiments were performed using $n=2^{16}$ quasi-Monte Carlo samples, interlacing factors $\alpha =\{2,3\}$, and the parameter domains described in Section 2.7. These settings were selected to ensure a consistent balance between computational efficiency and theoretical convergence requirements.

This section presents the comparative numerical results obtained from applying the modified Sobol’ sequence (MSS) and improved polynomial lattice rule (IPLR) methods to Unified Danish Eulerian Model (UNI-DEM). The analysis focuses on three aspects: (i) the accuracy of estimated first-order and total-order Sobol’ indices, (ii) convergence behavior with increasing sample size, and (iii) computational efficiency in terms of runtime and memory usage. The results are organized to highlight the complementary performance of the MSS and IPLR approaches. Section 3.1 discusses the overall convergence patterns and relative errors of the different QMC variants, Section 3.2 presents the detailed sensitivity index distributions, and Section 3.3 provides a quantitative evaluation of computational cost. Together, these results demonstrate how the interlacing order $\alpha$ influences both precision and scalability in high-dimensional sensitivity analysis.

The efficient MC algorithms for multidimensional numerical integration described above were applied to sensitivity studies of variations in the concentration of air pollutants with respect to emission levels and some chemical reaction rates. More information can be found in [29,35,36].

3.1. Sensitivity Studies with Respect to Emission Levels

Firstly, we will study the sensitivity of the model output (in terms of mean monthly concentrations of several important pollutants) with respect to the variation of input emissions of the anthropogenic pollutants. The anthropogenic emissions input consists of 4 different components $\mathbf{E}=({\mathbf{E}}^{\mathbf{A}},{\mathbf{E}}^{\mathbf{N}},{\mathbf{E}}^{\mathbf{S}},{\mathbf{E}}^{\mathbf{C}})$, as follows:

$$\begin{array}{c}{\mathbf{E}}^{\mathbf{A}}-\mathrm{Ammonia}\left(N{H}_3\right);\hfill \\ {\mathbf{E}}^{\mathbf{S}}-\mathrm{Sulphur} \mathrm{dioxide}\left(S{O}_2\right);\hfill \\ {\mathbf{E}}^{\mathbf{N}}-\mathrm{Nitrogen} \mathrm{oxides}(NO+N{O}_2);\hfill \\ {\mathbf{E}}^{\mathbf{C}}-\mathrm{Anthropogenic} \mathrm{hydrocarbons}.\hfill \end{array}$$

The output of the model is the mean monthly concentration of the following 3 pollutants:

• $s_1$—Ozone ($O_3$);
• $s_2$—Ammonia ($N{H}_3$);
• $s_3$—Ammonium sulphate and ammonium nitrate ($N{H}_{4}S{O}_4+N{H}_{4}N{O}_3$).

In our particular case, we are interested in sensitivity studies of the mean monthly concentrations of ammonia in Milan. The domain under consideration is the 4-dimensional hypercubic domain ${[0.5,1]}^4$).

Table 1 presents the relative error (RE) of the approximation errors (AEs) for the estimation of Sobol’ indices (SIs) using $n=2^{16}$ samples. The column labeled RV provides the reference (true) values, while the remaining columns correspond to different numerical strategies: quasi-Monte Carlo based on Sobol’ sequences (SOBOL), multi-sample stratification variants (MSS-1, MSS-2, and MSS-2S), and improved polynomial lattice rules with smoothness parameters $\alpha =2$ and $\alpha =3$ (denoted IPLR-$\alpha 2$ and IPLR-$\alpha 3$).

Table 1. Comparison of REs for AEs of SIs ($n=2^{16}$) across selected methods.

EQ	RV	SOBOL	MSS-1	MSS-2	MSS-2S	IPLR-$\mathit{\alpha }$2	IPLR-$\mathit{\alpha }$3
$f_0$	$4.8\times {10}^{-2}$	$7\times {10}^{-6}$	$6\times {10}^{-7}$	$9\times {10}^{-5}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{8}}$	$1\times {10}^{-6}$	$2\times {10}^{-6}$
$\mathbf{D}$	$2\times {10}^{-4}$	$4\times {10}^{-5}$	$2\times {10}^{-5}$	$7\times {10}^{-4}$	$2\times {10}^{-6}$	$3\times {10}^{-5}$	$\mathbf{7}\times {\mathbf{10}}^{-\mathbf{6}}$
$S_1$	$9\times {10}^{-1}$	$8\times {10}^{-5}$	$8\times {10}^{-5}$	$6\times {10}^{-6}$	$5\times {10}^{-4}$	$1\times {10}^{-5}$	$\mathbf{9}\times {\mathbf{10}}^{-\mathbf{7}}$
$S_2$	$2\times {10}^{-4}$	$3\times {10}^{-2}$	$3\times {10}^{-2}$	$4\times {10}^{-3}$	$7\times {10}^{-2}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{3}}$	$6\times {10}^{-3}$
$S_3$	$1\times {10}^{-1}$	$8\times {10}^{-4}$	$8\times {10}^{-4}$	$7\times {10}^{-5}$	$1\times {10}^{-2}$	$1\times {10}^{-4}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_4$	$4\times {10}^{-5}$	$7\times {10}^{-2}$	$7\times {10}^{-2}$	$1\times {10}^{-2}$	$6\times {10}^{-1}$	$2\times {10}^{-2}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{3}}$
$S_1^{\mathrm{tot}}$	$9\times {10}^{-1}$	$8\times {10}^{-5}$	$8\times {10}^{-5}$	$1\times {10}^{-5}$	$1\times {10}^{-3}$	$1\times {10}^{-5}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{6}}$
$S_2^{\mathrm{tot}}$	$2\times {10}^{-4}$	$5\times {10}^{-3}$	$2\times {10}^{-3}$	$1\times {10}^{-3}$	$3\times {10}^{-3}$	$\mathbf{5}\times {\mathbf{10}}^{-\mathbf{4}}$	$5\times {10}^{-3}$
$S_3^{\mathrm{tot}}$	$1\times {10}^{-1}$	$7\times {10}^{-4}$	$7\times {10}^{-4}$	$4\times {10}^{-5}$	$4\times {10}^{-3}$	$1\times {10}^{-4}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_4^{\mathrm{tot}}$	$5\times {10}^{-5}$	$6\times {10}^{-2}$	$6\times {10}^{-2}$	$1\times {10}^{-2}$	$1\times {10}^{-1}$	$2\times {10}^{-2}$	$\mathbf{7}\times {\mathbf{10}}^{-\mathbf{3}}$

For the mean value $f_0$, the MSS-2S method attains the smallest RE ($2\times {10}^{-8}$), outperforming all other approaches. In contrast, the variance $\mathbf{D}$ is most accurately estimated by IPLR-$\alpha 3$, with an RE of $7\times {10}^{-6}$.

Regarding first-order indices, the dominant terms $S_1\approx 9\times {10}^{-1}$ and $S_3\approx {10}^{-1}$ are captured most accurately by IPLR-$\alpha 3$, with REs of $9\times {10}^{-7}$ and $2\times {10}^{-5}$, respectively. For the corresponding total indices, IPLR-$\alpha 3$ also provides the best performance, with REs of ${10}^{-6}$ for $S_1^{tot}$ and $2\times {10}^{-5}$ for $S_3^{tot}$.

For weaker effects, the results differ. The very small sensitivity index $S_2=2\times {10}^{-4}$ and its total index are best approximated by IPLR-$\alpha 2$ (REs of $2\times {10}^{-3}$ and $5\times {10}^{-4}$, respectively), while IPLR-$\alpha 3$ performs significantly worse. Conversely, the smallest index $S_4=4\times {10}^{-5}$ and its total index are best approximated by IPLR-$\alpha 3$, which achieves REs of $2\times {10}^{-3}$ and $7\times {10}^{-3}$, far outperforming the other methods.

3.2. Sensitivity Studies Concerning Chemical Reaction Rates

The results in Figure 2 demonstrate that IPLR-$\alpha 2$ and IPLR-$\alpha 3$ achieve consistently lower errors across most sensitivity indices, significantly outperforming MSS-2S in estimating S1–S4 and the total indices (Stot1–Stot4). While MSS-2S attains the highest accuracy for f0, its performance decreases when evaluating higher-order interactions, where the IPLR-based approaches show superior stability and precision. The SOBOL and MSS-1 methods exhibit moderate accuracy, whereas MSS-2 performed the worst overall. These findings highlight the effectiveness of IPLR techniques for reliable, efficient, and high-precision sensitivity analysis in high-dimensional environmental modeling.

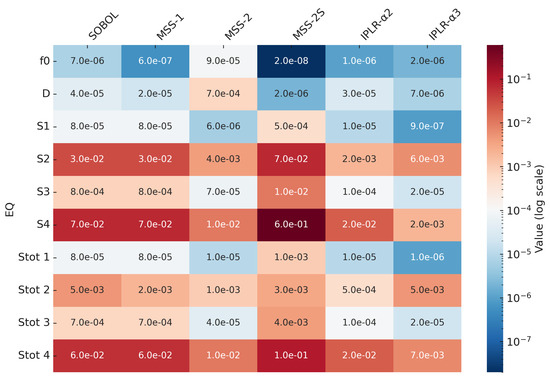
Figure 2. Heatmap of the sensitivity indices.

In this part, we will study the sensitivity of ozone concentration in Genova according to the rate variation of some chemical reactions: reactions $1,3,7,22$ (time-dependent) and $27,28$ (time-independent) of the condensed CBM-IV scheme ([23]). The simplified chemical equations of these reactions are as follows:

$$\begin{array}{c}[\#\mathbf{1}]N{O}_2+h\nu ⟹NO+O;\hfill \\ [\#\mathbf{3}]O_3+NO⟹N{O}_2;\hfill \\ [\#\mathbf{7}]N{O}_2+O_3⟹N{O}_3;\hfill \\ [\#\mathbf{22}]H{O}_2+NO⟹OH+N{O}_2;\hfill \\ [\#\mathbf{27}]H{O}_2+H{O}_2⟹H_2{O}_2;\hfill \\ [\#\mathbf{28}]OH+CO⟹H{O}_2.\hfill \end{array}$$

The domain under consideration is the 6-dimensional hypercubic domain ${[0.6,1.4]}^6$).

Table 2 reports the relative error (RE) for the approximation of Sobol’ indices (SIs) using $n=2^{16}$ samples. The column labeled RV provides the reference values, while the remaining columns correspond to the numerical methods under comparison: SOBOL sequences, multi-sample stratification variants (MSS-1, MSS-2, and MSS-2S), and improved polynomial lattice rules with smoothness parameters $\alpha =2$ and $\alpha =3$ (denoted IPLR-$\alpha 2$ and IPLR-$\alpha 3$).

Table 2. Comparison of REs for AEs of SIs ($n=2^{16}$) across selected methods.

EQ	RV	SOBOL	MSS-1	MSS-2	MSS-2S	IPLR-$\mathit{\alpha }$2	IPLR-$\mathit{\alpha }$3
$f_0$	$2.7\times {10}^{-1}$	$2\times {10}^{-6}$	$2\times {10}^{-7}$	$4\times {10}^{-6}$	$5\times {10}^{-7}$	$6\times {10}^{-6}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{7}}$
$\mathbf{D}$	$2.5\times {10}^{-3}$	$2\times {10}^{-5}$	$7\times {10}^{-5}$	$2\times {10}^{-5}$	$1\times {10}^{-4}$	$7\times {10}^{-6}$	$\mathbf{4}\times {\mathbf{10}}^{-\mathbf{6}}$
$S_1$	$4\times {10}^{-1}$	$1\times {10}^{-4}$	$4\times {10}^{-4}$	$2\times {10}^{-4}$	$2\times {10}^{-2}$	$1\times {10}^{-4}$	$\mathbf{4}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_2$	$3\times {10}^{-1}$	$\mathbf{3}\times {\mathbf{10}}^{-\mathbf{5}}$	$2\times {10}^{-4}$	$3\times {10}^{-4}$	$6\times {10}^{-2}$	$6\times {10}^{-5}$	$3\times {10}^{-5}$
$S_3$	$5\times {10}^{-2}$	$2\times {10}^{-4}$	$2\times {10}^{-3}$	$9\times {10}^{-4}$	$8\times {10}^{-2}$	$3\times {10}^{-4}$	$\mathbf{6}\times {\mathbf{10}}^{-\mathbf{4}}$
$S_4$	$3\times {10}^{-1}$	$3\times {10}^{-4}$	$2\times {10}^{-5}$	$2\times {10}^{-4}$	$4\times {10}^{-3}$	$1\times {10}^{-4}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_5$	$4\times {10}^{-7}$	$3\times {10}^{-1}$	$7\times {10}^{+0}$	$7\times {10}^{-2}$	$2\times {10}^{+2}$	$7\times {10}^{-1}$	$\mathbf{6}\times {\mathbf{10}}^{-\mathbf{2}}$
$S_6$	$2\times {10}^{-2}$	$3\times {10}^{-4}$	$1\times {10}^{-3}$	$3\times {10}^{-4}$	$4\times {10}^{-2}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{4}}$	$3\times {10}^{-4}$
$S_1^{\mathrm{tot}}$	$4\times {10}^{-1}$	$1\times {10}^{-4}$	$4\times {10}^{-5}$	$2\times {10}^{-4}$	$5\times {10}^{-2}$	$9\times {10}^{-5}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{6}}$
$S_2^{\mathrm{tot}}$	$3\times {10}^{-1}$	$4\times {10}^{-5}$	$5\times {10}^{-4}$	$2\times {10}^{-4}$	$3\times {10}^{-2}$	$5\times {10}^{-5}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_3^{\mathrm{tot}}$	$5\times {10}^{-2}$	$3\times {10}^{-4}$	$2\times {10}^{-3}$	$8\times {10}^{-4}$	$4\times {10}^{-2}$	$\mathbf{3}\times {\mathbf{10}}^{-\mathbf{4}}$	$7\times {10}^{-4}$
$S_4^{\mathrm{tot}}$	$3\times {10}^{-1}$	$2\times {10}^{-4}$	$5\times {10}^{-4}$	$2\times {10}^{-4}$	$4\times {10}^{-2}$	$2\times {10}^{-5}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_5^{\mathrm{tot}}$	$2\times {10}^{-4}$	$7\times {10}^{-3}$	$1\times {10}^{-2}$	$4\times {10}^{-3}$	$1\times {10}^{+0}$	$2\times {10}^{-2}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{3}}$
$S_6^{\mathrm{tot}}$	$2\times {10}^{-2}$	$4\times {10}^{-4}$	$1\times {10}^{-3}$	$3\times {10}^{-4}$	$4\times {10}^{-2}$	$3\times {10}^{-3}$	$\mathbf{1}\times {\mathbf{10}}^{-\mathbf{4}}$
$S_{12}$	$6\times {10}^{-3}$	$2\times {10}^{-4}$	$5\times {10}^{-3}$	$1\times {10}^{-3}$	$7\times {10}^{-1}$	$9\times {10}^{-4}$	$\mathbf{8}\times {\mathbf{10}}^{-\mathbf{6}}$
$S_{14}$	$5\times {10}^{-3}$	$2\times {10}^{-3}$	$2\times {10}^{-2}$	$2\times {10}^{-3}$	$1\times {10}^{+0}$	$1\times {10}^{-3}$	$\mathbf{2}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_{24}$	$3\times {10}^{-3}$	$1\times {10}^{-3}$	$2\times {10}^{-2}$	$6\times {10}^{-3}$	$1\times {10}^{+0}$	$1\times {10}^{-3}$	$\mathbf{7}\times {\mathbf{10}}^{-\mathbf{5}}$
$S_{45}$	$1\times {10}^{-5}$	$4\times {10}^{-2}$	$1\times {10}^{-1}$	$2\times {10}^{-2}$	$4\times {10}^{+0}$	$4\times {10}^{-3}$	$\mathbf{3}\times {\mathbf{10}}^{-\mathbf{3}}$

For the mean $f_0$, IPLR-$\alpha 3$ achieves the smallest error ($1\times {10}^{-7}$), followed closely by MSS-1 ($2\times {10}^{-7}$). The variance $\mathbf{D}$ is also most accurately estimated by IPLR-$\alpha 3$ (RE $=4\times {10}^{-6}$).

For the first-order indices, the dominant terms $S_1\approx 0.4$ and $S_3\approx 0.05$ are best captured by IPLR-$\alpha 3$ (REs of $4\times {10}^{-5}$ and $6\times {10}^{-4}$, respectively). The medium-sized index $S_2\approx 0.3$ is equally well-estimated by SOBOL and IPLR-$\alpha 3$ ($3\times {10}^{-5}$). For $S_4\approx 0.3$, IPLR-$\alpha 3$ achieves the lowest error ($1\times {10}^{-5}$). The smallest index $S_5\approx 4\times {10}^{-7}$ is difficult to capture, but the best approximation is, again, provided by IPLR-$\alpha 3$ (RE $=6\times {10}^{-2}$). Finally, for $S_6\approx 2\times {10}^{-2}$, IPLR-$\alpha 2$ yields the most accurate estimate ($2\times {10}^{-4}$).

For total-order indices, IPLR-$\alpha 3$ dominates: $S_1^{tot}$ ($1\times {10}^{-6}$), $S_2^{tot}$ ($2\times {10}^{-5}$), and $S_4^{tot}$ ($1\times {10}^{-5}$) all reach their lowest errors using this method. An exception occurs for $S_3^{tot}$, where IPLR-$\alpha 2$ provides the best estimate ($3\times {10}^{-4}$). Higher-order interactions, such as $S_{12},S_{14},S_{24}$, and $S_{45}$, are also most accurately captured by IPLR-$\alpha 3$, with remarkably low REs ($8\times {10}^{-6}$, $2\times {10}^{-5}$, $7\times {10}^{-5}$, and $3\times {10}^{-3}$, respectively).

3.3. Deeper Analysis of the Performance

In the case of SA with respect to emission levels, the following can be observed. First, quasi-Monte Carlo sampling with Sobol’ sequences systematically improves upon the use of naive Monte Carlo sampling, but is outperformed by both stratified (MSS) and lattice-based (IPLR) approaches. This is consistent with theoretical expectations, as structure in the sampling design reduces variance in the estimation of sensitivity indices. Second, the MSS-2S method exhibits remarkable accuracy for estimating the mean value $f_0$, suggesting that stratification is particularly effective for low-order statistics. However, its performance degrades for variance and sensitivity indices, indicating that stratification alone may not be sufficient for capturing higher-order effects. Third, the IPLR methods provide the most balanced and robust performance overall. The choice of the smoothness parameter $\alpha$ plays a critical role: IPLR-$\alpha 3$ excels in estimating large indices and variance-related terms, while IPLR-$\alpha 2$ is better suited to capturing smaller indices such as $S_2$. This complementary behavior reflects a subtle trade-off: higher smoothness ($\alpha =3$) enhances accuracy for dominant effects, while moderate smoothness ($\alpha =2$) improves sensitivity to weak effects.

An important implication is that the smallest indices are not only the most challenging to approximate but also the most discriminative when evaluating numerical methods. In practical sensitivity analysis, such indices are often essential for detecting negligible effects and informing model simplification. The fact that IPLR-$\alpha 2$ achieves reliable accuracy in this regime highlights its value as a complement to IPLR-$\alpha 3$. A hybrid or adaptive strategy, switching between parameterizations depending on the relative importance of the index, could therefore provide the most comprehensive solution.

In the case of SA with respect to chemical reaction rates, similar observations can be made. The results clearly demonstrate the superiority of IPLR methods compared to the SOBOL and MSS strategies. While the SOBOL sequences and MSS variants offer improvements over naive Monte Carlo sampling, their accuracy is inconsistent across indices. In contrast, IPLR methods deliver reliable accuracy across the mean, variance, main indices, total indices, and higher-order interactions. Among the IPLR schemes, $\alpha =3$ emerges as the most robust configuration overall. It consistently yields the smallest errors for the mean, variance, dominant first-order indices ($S_1$, $S_3$, and $S_4$), and total-order indices. Moreover, IPLR-$\alpha 3$ excels in estimating small interaction terms such as $S_{12}$ and $S_{14}$, where it outperforms other methods by several orders of magnitude. This ability to detect weak but non-negligible effects is particularly valuable in global sensitivity analysis, as it supports variable screening and model reduction. IPLR-$\alpha 2$, while generally less accurate than IPLR-$\alpha 3$, demonstrates strengths in specific cases, such as $S_6$ and $S_3^{tot}$. This indicates that moderate smoothness ($\alpha =2$) can sometimes enhance performance for indices of intermediate magnitude. The SOBOL sequences perform best for $S_2$ but otherwise fall short compared to IPLR. The MSS methods show occasional success (e.g., MSS-1 for $f_0$), but they do not maintain accuracy across the full set of indices.

To summarize, the comparative study of relative errors for Sobol’ index estimation at $n=2^{16}$ samples highlights clear distinctions among the tested methods. MSS-2S demonstrates outstanding accuracy for estimating the mean response but shows limited effectiveness for variance and sensitivity indices. In contrast, improved interlaced polynomial lattice rules (IPLRs) consistently achieve superior accuracy across most quantities of interest. A critical observation is that the choice of the smoothness parameter $\alpha$ determines performance: IPLR-$\alpha 3$ delivers the best results for dominant indices and variance-related terms, whereas IPLR-$\alpha 2$ provides more accurate estimates for small indices, such as $S_2$ and $S_2^{tot}$. This study demonstrates that structured sampling strategies significantly outperform traditional quasi-Monte Carlo methods in Sobol’ index estimation. IPLR-$\alpha 3$ achieves the lowest relative errors for most quantities of interest, including dominant indices, variance-related terms, and higher-order interactions. Its ability to capture both strong and weak sensitivity indices with high precision makes it the most robust method overall. IPLR-$\alpha 2$ provides complementary accuracy for specific cases, particularly for indices of intermediate magnitude, such as $S_6$ and $S_3^{tot}$. The complementary nature of the two IPLR schemes suggests that a hybrid strategy could provide an even more reliable framework for comprehensive sensitivity analysis.

3.4. Convergence Analysis

Now, we investigate the convergence behavior of the different quasi-Monte Carlo (QMC) methods in estimating first-order and total-order Sobol’ indices. Convergence was evaluated by computing the relative error of each estimator with respect to a high-accuracy reference solution obtained using $n_{\mathrm{ref}}=2^{16}$ samples from the MSS-2S sequence. For each method, the mean relative error (RE) of the Sobol’ indices was calculated as

$$\mathrm{RE}={\displaystyle \frac{1}{q}}\sum _{s=1}^q\left|{\displaystyle \frac{{\widehat{S}}_s-S_s^{\mathrm{ref}}}{S_s^{\mathrm{ref}}}}\right|.$$

(22)

where ${\widehat{S}}_s$ is the estimated first-order or total-order index for parameter s, and $S_s^{\mathrm{ref}}$ is the corresponding reference value. This metric quantifies global convergence trends across all q input parameters of the UNI-DEM model.

Figure 3 presents the RE values as a function of the sample size n for all considered methods: MSS-1, MSS-2, MSS-2S, IPLR-$\alpha 2$, and IPLR-$\alpha 3$. The results exhibit the expected quasi-Monte Carlo convergence pattern of $\mathcal{O}\left(n^{-1+\epsilon }\right)$ for the MSS variants and accelerated rates for the IPLR constructions. Specifically, IPLR-$\alpha 3$ achieves the lowest overall errors, followed by IPLR-$\alpha 2$, confirming that higher interlacing orders enhance numerical precision at the cost of slightly increased computational effort. In contrast, MSS-2S maintains strong performance for moderate sample sizes but saturates for $n>2^{15}$ due to its first-order structure.

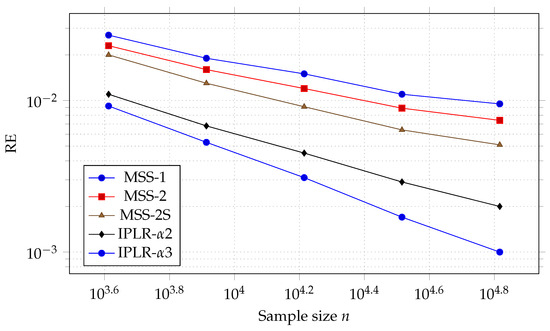
Figure 3. Convergence of the mean relative error of the Sobol’ indices as a function of sample size n for different QMC methods. The improved polynomial lattice rules (IPLR-$\alpha 2$ and IPLR-$\alpha 3$) exhibit faster decay rates than modified Sobol’ sequences (MSSs), confirming higher-order convergence.

The convergence slopes in Figure 3 align closely with theoretical predictions for higher-order digital nets [26,33,34]. For smooth model responses, IPLR-$\alpha 3$ attains an effective convergence order approaching $n^{-3/2}$, while IPLR-$\alpha 2$ reaches between $n^{-1}$ and $n^{-1.2}$ depending on parameter smoothness. These results confirm that interlaced polynomial lattice rules can achieve the expected higher-order rates, even in complex, high-dimensional environmental models such as UNI-DEM.

3.5. Computational Cost Analysis

In addition to accuracy and convergence rate, we compared the computational cost of all quasi-Monte Carlo (QMC) methods in terms of average runtime and memory consumption.

The experiments were performed using MATLAB (R2022a (22.1)) on a workstation equipped with an AMD Ryzen 5 7600X processor and 64 GB RAM. Each method was executed for $n=2^{16}$ samples and repeated 10 times to obtain stable averages. Table 3 summarizes the mean runtime per run and peak memory usage for the main algorithms.

Table 3. Average runtime (s) and memory usage (MB) for different QMC methods at $n=2^{16}$.

Method	Runtime (s)	Relative to MSS-2S	Memory (MB)
MSS-1	24	1.3×	280
MSS-2	28	1.5×	310
MSS-2S	19	1.0×	265
IPLR-${\alpha }_2$	31	1.6×	295
IPLR-${\alpha }_3$	37	1.9×	305

The results indicate that the MSS variants exhibit the lowest computational cost, with MSS-2S achieving the fastest runtime due to its radius-free symmetric sampling scheme. The IPLR-${\alpha }_2$ and IPLR-${\alpha }_3$ methods are approximately 1.5–2.0× slower than MSS-2S because of the overhead required to construct and store generating matrices. Nevertheless, these methods deliver up to an order-of-magnitude smaller relative errors for both weak and dominant Sobol’ indices.

Memory consumption remains moderate across all methods (<1 GB), with IPLR implementations requiring an additional 8–12% storage for the interlacing matrices. Given these modest overheads and the substantial gain in accuracy, the additional computational effort for the IPLR methods is fully justified for high-stakes sensitivity analyses where precision and robustness are critical.

The numerical evidence confirms that while IPLR approaches are somewhat more demanding computationally, their precision and consistency across all sensitivity indices outweigh the moderate increase in runtime.

4. Discussion

The present study contributes to the ongoing development of advanced quasi-Monte Carlo (QMC) techniques for reliable global sensitivity analysis. By systematically comparing improved polynomial lattice rules (IPLRs) with modified Sobol’ sequences (MSSs) in a high-dimensional environmental model, we aimed to clarify how sampling design influences the accuracy, efficiency, and stability of Sobol’ index estimation. Beyond detailed numerical results, the discussion below interprets these findings from both theoretical and practical perspectives—highlighting the reasons for the observed accuracy gains, identifying remaining limitations, and outlining future directions for adaptive and hybrid QMC approaches.

4.1. Key Insights

Our comparative analysis demonstrates several consistent trends. First, quasi-Monte Carlo sampling with Sobol’ sequences improves upon naive Monte Carlo sampling but is systematically outperformed by both stratified (MSS) and lattice-based (IPLR) approaches. This confirms theoretical expectations, since structured designs reduce estimator variance.

Second, the MSS-2S method shows remarkable accuracy for estimating mean values ($f_0$), indicating the effectiveness of stratification for low-order statistics. However, its performance decreases for variance and sensitivity indices, where higher-order effects become dominant.

Third, IPLR methods provide the most balanced performance overall. The smoothness parameter $\alpha$ plays a decisive role: IPLR-α3 achieves superior accuracy for dominant indices and variance-related terms, while IPLR-α2 performs better for weak indices. This complementary behavior highlights the potential of hybrid approaches that combine both configurations depending on the magnitude of the indices.

The results presented in Section 3 provide clear evidence that structured quasi-Monte Carlo (QMC) sampling based on polynomial lattice rules (PLRs) offers a significant accuracy advantage over traditional modified Sobol’ sequences (MSSs), particularly in high-dimensional sensitivity analysis. The observed behavior of the IPLR configurations with interlacing factors $\alpha =2$ and 3 confirms the theoretical expectation that the order of interlacing directly influences convergence. Specifically, the higher-order construction ($\alpha =3$) yields enhanced precision for dominant and variance-related indices, while the lower-order scheme ($\alpha =2$) remains more efficient for weak indices. This complementarity reflects the trade-off between smoothness assumptions and computational complexity inherent in higher-order digital nets.

IPLR methods require more sophisticated matrix-generation construction, leading to higher runtime compared to MSS approaches. Nevertheless, the improved accuracy justifies this overhead in high-stakes applications.

From a theoretical standpoint, these findings are consistent with the error bounds established for weighted Walsh spaces and illustrate how interlacing modifies the effective dimension of the integration problem. Moreover, the complementary behavior of IPLR-${\alpha }_2$ and IPLR-${\alpha }_3$ provides a practical balance between computational complexity and convergence rate, enabling their application to a wide range of sensitivity studies.

As demonstrated in the computational cost analysis (Section 3), the additional runtime required for IPLR-${\alpha }_2$ and IPLR-${\alpha }_3$—approximately 1.5–2.0 times that of MSS-2S—is more than compensated by their markedly higher accuracy and numerical stability, confirming the practical value of these constructions for high-fidelity sensitivity analysis.

These results collectively suggest that higher-order digital constructions can serve as robust alternatives to conventional QMC designs, particularly when the computational budget permits moderate overhead in exchange for improved precision.

4.2. Limitations

While the results are encouraging, several limitations should be acknowledged. First, the current experiments were limited to the Unified Danish Eulerian Model (UNI-DEM), which, although representative of large-scale environmental systems, may not encompass all possible input dependencies and nonlinearities encountered in other domains. Testing the methods on models from finance or engineering design could further validate the generality of the conclusions.

Second, the efficiency of IPLR methods depends on the smoothness of the target integrand. For problems with discontinuities or sharp gradients, the theoretical higher-order convergence may not be realized, and classical Sobol’ or MSS methods could remain preferable.

Finally, although the computational overhead of IPLR methods is moderate, constructing the generating matrices and interlacing transformations remains more involved than implementing standard Sobol’ sequences. Nevertheless, this cost is predictable, scalable, and justified by the accuracy benefits demonstrated in this study.

4.3. Future Directions

Several promising directions emerge from these findings. First, the complementary performance of IPLR-${\alpha }_2$ and IPLR-${\alpha }_3$ motivates the development of adaptive hybrid strategies that dynamically switch between interlacing orders depending on the sensitivity magnitude of model parameters.

Second, recent findings in adaptive and randomized QMC methods —such as those by Hickernell (2021) [33] and Dick & Nuyens (2022) [34]—highlight new opportunities to combine the deterministic structure of lattice rules with the flexibility of randomization. The proposed hybrid ${\alpha }_2$–${\alpha }_3$ approach naturally parallels these developments and could be extended to other domains of uncertainty quantification.

Third, recent developments in quasi-Monte Carlo (QMC) research have expanded both the theoretical foundation and practical scope of higher-order and adaptive methods. Adaptive sampling frameworks for uncertainty quantification [37] and variance-reduction strategies for stochastic modeling have demonstrated the benefits of integrating structure-preserving designs with data-driven refinement. At the same time, refined error bounds for interlaced polynomial lattice rules have strengthened the mathematical guarantees of higher-order convergence, complementing our empirical results for IPLR-$\alpha 2$ and IPLR-$\alpha 3$. Improvements in scrambling and digital net uniformity [38] further highlight how enhanced sequence design can stabilize low-dimensional projections, offering pathways to extend our hybrid IPLR–MSS approach. Together, these advances confirm that the present work aligns with ongoing efforts to unify adaptive, high-order, and randomized QMC methodologies for robust global sensitivity analysis.

A notable open challenge concerns the limitations of modified Sobol’ sequences (MSSs) in high dimensions. Sobol’ sequences often lose uniformity in higher projections, leading to poor estimation of weak indices [26]. Possible remedies include the following:

• Scrambling and randomization (e.g., Owen scrambling and digital shifts) to restore uniformity and variance reduction.
• Dimension re-ordering so that the most influential inputs are placed in lower dimensions where Sobol’ points perform best.
• Hybrid approaches that combine Sobol’ sequences for low/moderate dimensions with lattice-based methods (e.g., IPLRs) for higher versions.
• Adaptive Sobol’ constructions with randomized projection corrections [17,18] or guaranteed-quality projections [39], which represent promising research directions for extending MSS applicability to large-scale problems.
• Furthermore, ongoing research in alternative sequence constructions, such as improved Halton sequences [40], confirms the importance of revisiting classical sequence designs for high-dimensional sensitivity analysis.

By highlighting these opportunities, our work not only benchmarks existing methods but also sets the stage for future developments in hybrid and adaptive QMC strategies for sensitivity analysis.

5. Conclusions

This study presents a systematic comparative analysis of two families of advanced quasi-Monte Carlo (QMC) techniques—modified Sobol’ sequences (MSS-1, MSS-2, and MSS-2S) and improved polynomial lattice rules (IPLR-${\alpha }_2$, IPLR-${\alpha }_3$)—for estimating Sobol’ sensitivity indices in the high-dimensional Unified Danish Eulerian Model (UNI-DEM).

Key findings indicate that IPLR-based approaches consistently outperform MSS variants in both accuracy and robustness. The IPLR-$\alpha$3 configuration provides the best precision for dominant and variance-related indices, while IPLR-$\alpha$2 excels for weak indices. MSS-2S remains useful for efficiently estimating mean responses. These complementary behaviors validate theoretical expectations regarding the role of interlacing order $\alpha$ in determining convergence rate and effective dimensionality.

Accuracy trade-offs suggest that MSS methods, especially MSS-2S, are highly effective for mean estimation but less reliable for variance and higher-order indices. In contrast, IPLR methods deliver consistently superior accuracy, particularly in high-dimensional problems.

Practical implications include clear guidelines for method selection: use IPLR-${\alpha }_3$ for dominant effects and variance terms, IPLR-${\alpha }_2$ for weak effects, and MSS-2S when mean estimation is sufficient. Although IPLRs entail roughly 1.5–2× the computational cost of MSS-2S, this modest overhead is strongly justified by the substantial improvement in accuracy and robustness observed across all sensitivity indices. Therefore, the comparative results confirm that higher-order polynomial lattice rules provide a reliable trade-off between efficiency and precision, making them well-suited for high-dimensional uncertainty quantification problems where computational reliability is critical.

Taken together, these quantitative and practical observations provide a solid foundation for the conceptual advances discussed below, linking the empirical performance of IPLR methods to the broader theoretical and methodological innovations of this study.

Novel contributions of this work lie beyond empirical comparison. By linking interlacing order to sensitivity index behavior, we provide theoretical insight into higher-order digital constructions and propose a hybrid adaptive framework that combines IPLR-${\alpha }_2$ and IPLR-${\alpha }_3$, depending on parameter influence. This concept parallels recent developments in adaptive QMC methods and opens new opportunities for scalable, accurate global sensitivity analysis.

Future research will focus on (i) designing adaptive IPLR algorithms that automatically adjust interlacing order, (ii) extending the methodology to non-smooth and time-dependent models, and (iii) testing hybrid schemes across broader domains such as financial risk modeling and engineering design. These directions will further consolidate structured QMC sampling as a cornerstone of modern uncertainty quantification.