MIDS-GAN: Minority Intrusion Data Synthesizer GAN—An ACON Activated Conditional GAN for Minority Intrusion Detection
Abstract
1. Introduction
- Class-conditional generation with ACGAN to produce label-consistent minority samples.
- Trainable activation (ACON) to adaptively model complex, imbalanced intrusion manifolds.
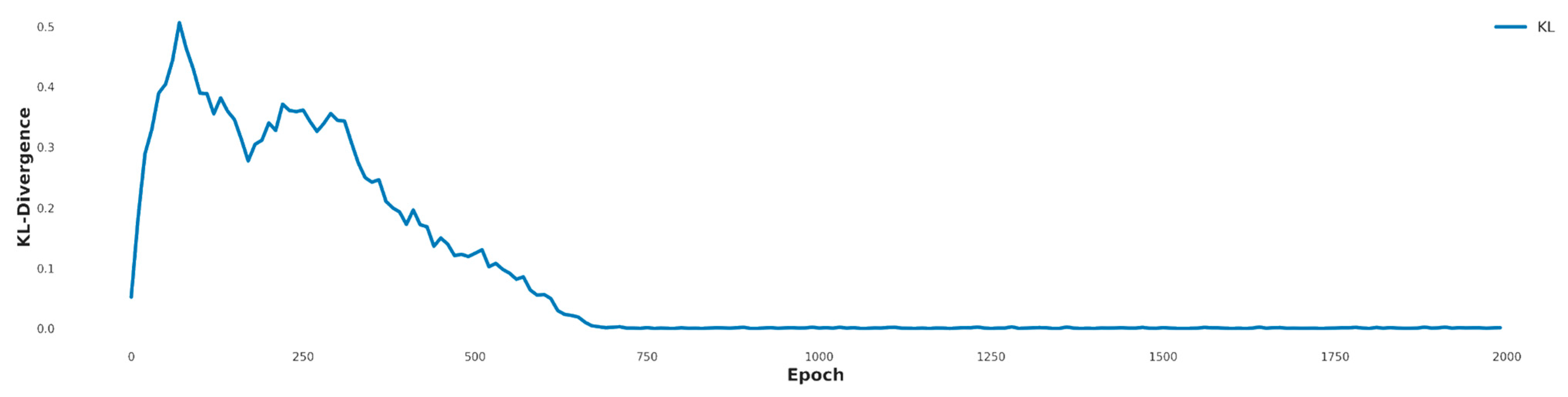
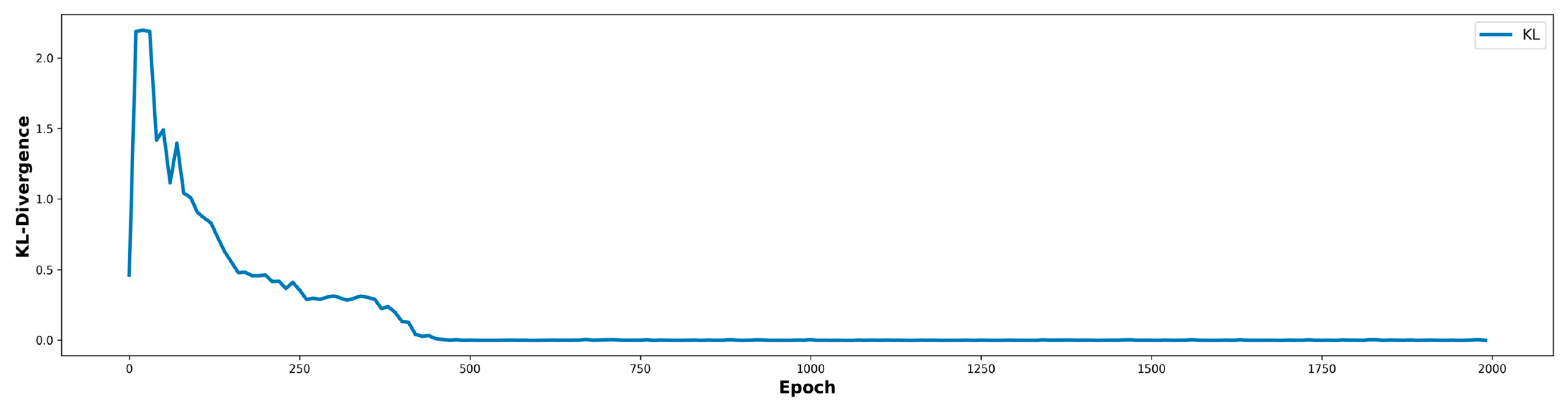
- Structured feature selection with KL-divergence alignment to preserve distributional fidelity and mitigate mode dropping.
2. Related Work
2.1. Oversampling Techniques
2.2. Generative Adversarial Networks (GANs) for Intrusion Detection
2.3. Summary and Motivation
- (1)
- Effectiveness of adversarial generation—GANs can synthesize minority-class traffic patterns that traditional oversampling fails to capture, thereby improving minority detection rates.
- (2)
- Technical challenges—Training instability, mode collapse, and the absence of strict label fidelity remain significant obstacles, especially for ultra-minority classes (e.g., R2L, U2R).
- (3)
- Limitations of conventional oversampling—Although computational efficient, methods such as SMOTE and ADASYN rely on geometric heuristics and cfail to preserve the behavioral semantics of cyberattacks.
3. Proposed Methodology
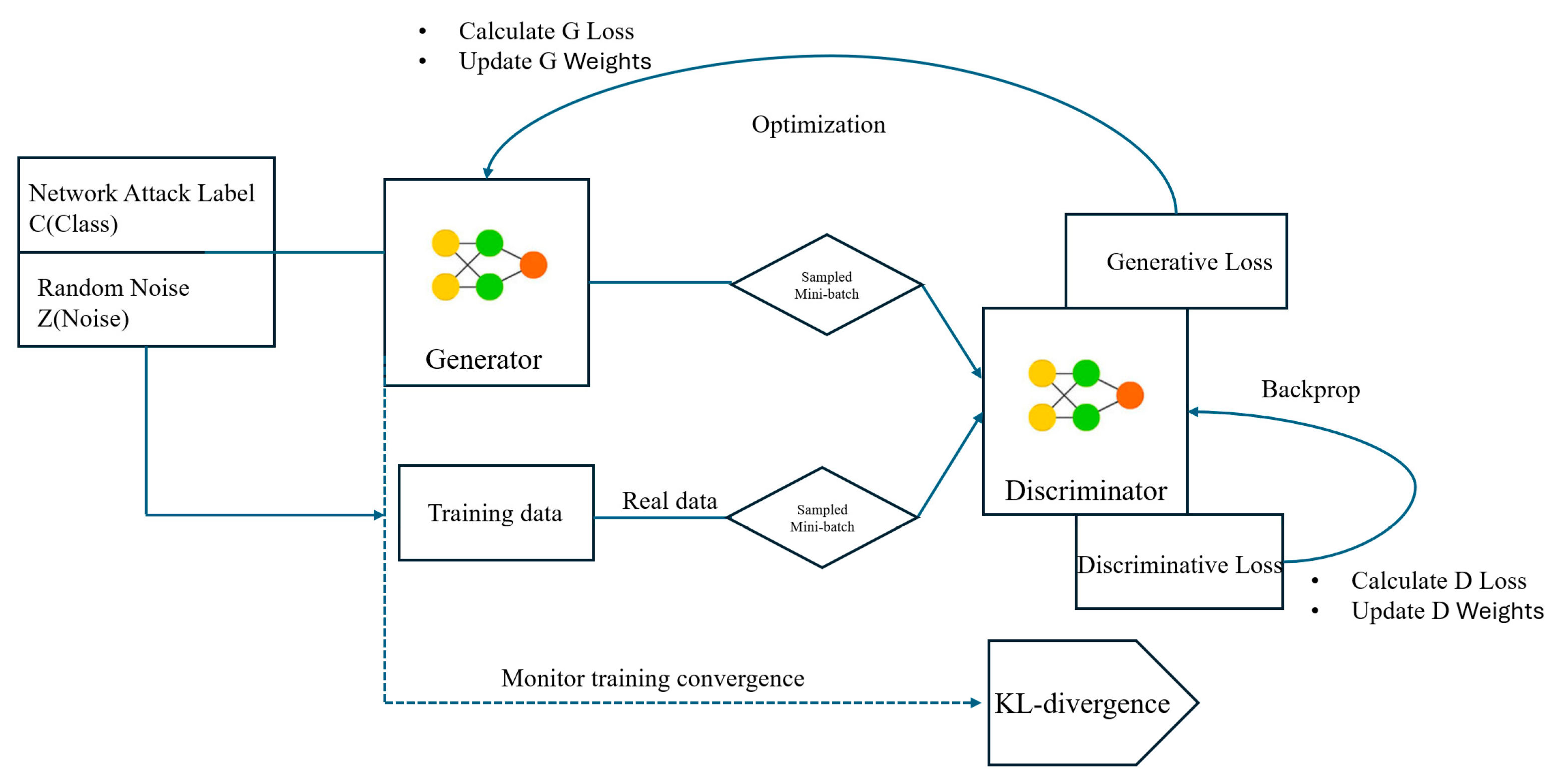
3.1. Overview of the MIDS-GAN Augmentation Module (Train-Time Only)
3.2. Feature-Driven Preprocessing
3.2.1. Encoding of Categorical Features
3.2.2. Normalization and Scaling
3.2.3. Constant Feature Removal
3.3. Structured Feature Selection: Correlation-Based Filtering (SFS)
3.4. Conditional Generation via ACGAN with ACON Activation
3.4.1. Full Loss Function Formulation
3.4.2. Trainable Activation: ACON
- Discriminator Update: Minimize using real data and synthetic data
- Generator Update: Minimize , focusing on fooling and generating label-consistent samples
3.4.3. Minimax Training Objective
| Algorithm 1. Training mechanism of ACON-Activated ACGAN with SFS based on minibatch stochastic gradient descent. |
|
| , (initialized), SFS-selected features. |
|
| for number of training iterations do |
| for steps do |
|
|
|
|
|
| end for |
|
|
| end for |
3.5. Rationale for Determining the Number of Synthetic Samples per Minority Class
3.5.1. Computation of Minority-to-Majority Ratio
3.5.2. Theoretical Target for Full Balance
3.5.3. Adjusted Target with Heuristic Constraints
- Class complexity: complex classes, such as Shellcode, require more diversity.
3.6. Machine Learning Classifier
3.7. Computational Complexity (Concise)
4. Experimental and Results
4.1. System and Tool Requirements
4.2. Dataset Information
4.2.1. NSL-KDD
4.2.2. UNSW-NB15
4.2.3. Dataset Challenges (Imbalance and Overlap)
4.2.4. Relevance to This Study
4.3. Implementation Details
4.4. Model Hyperparameter Configuration
4.5. Evaluation Criteria
- TP = True Positives.
- FP = False Positives.
- FN = False Negatives.
- = Number of true instances in class
- = F1-score of class
- = Total number of classes.
4.6. Comparative Results and Effectiveness of MIDS-GAN
4.6.1. NSL-KDD Results
4.6.2. 2 UNSW-NB15 Results
4.6.3. Weighted F1-Score Comparison
5. Discussion
5.1. Portability and Scope
5.2. Limitations
5.3. Significance of Recall Improvement on Ultra-Minority Classes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. t-SNE Visualization of Real Data
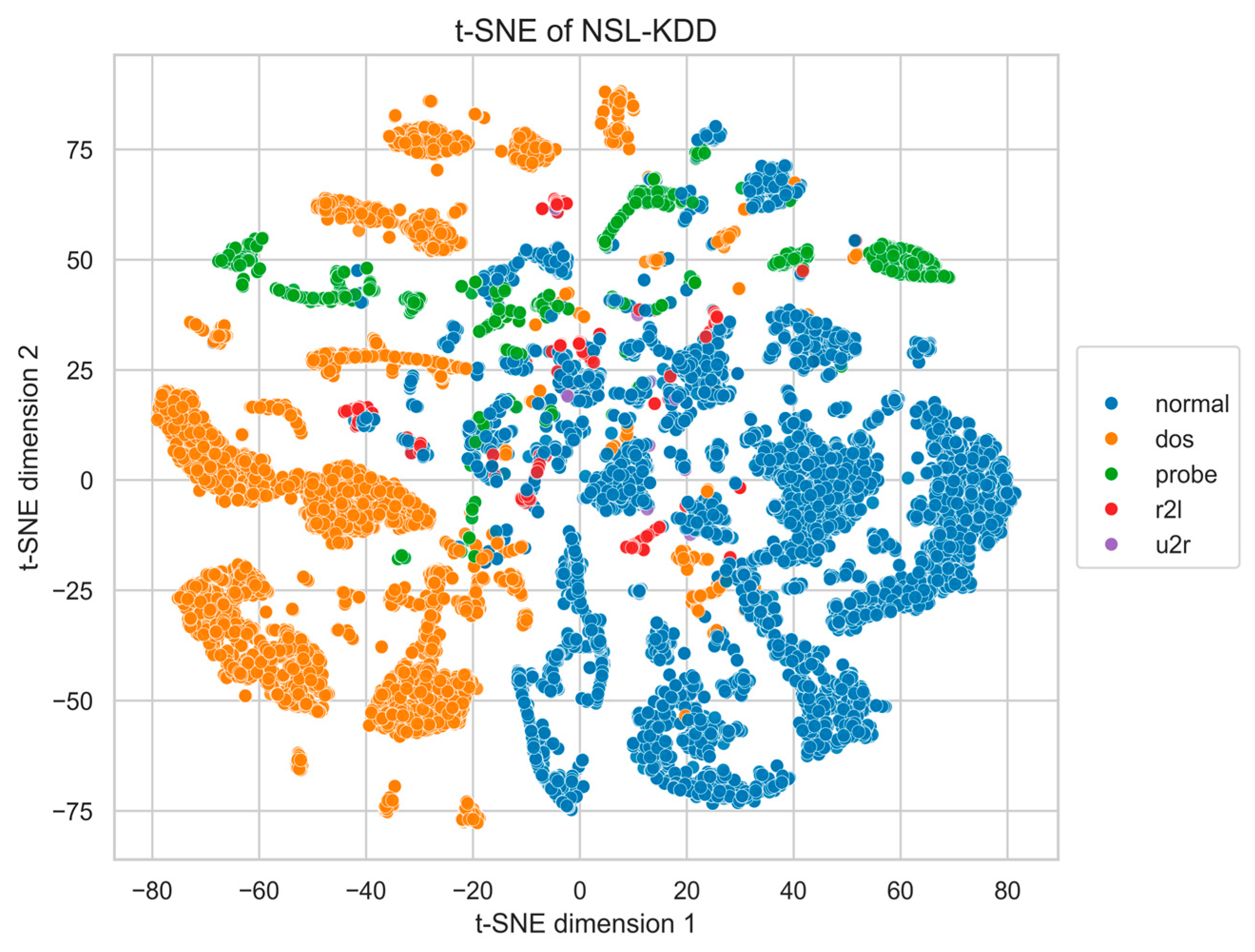
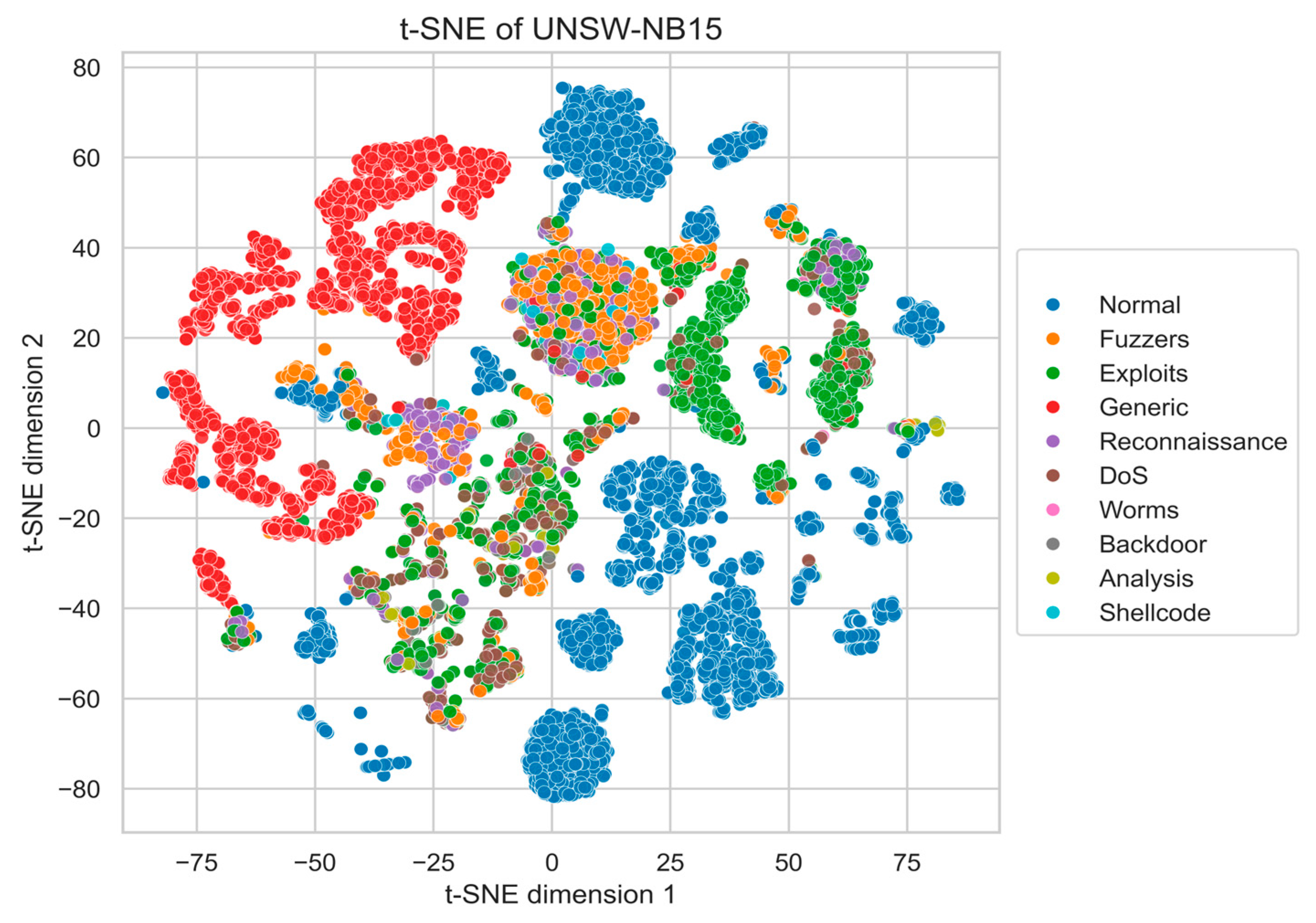
References
- Buczak, A.L.; Guven, E. A Survey of Data Mining and Machine Learning Methods for Cyber Security Intrusion Detection. IEEE Commun. Surv. Tutor. 2016, 18, 1153–1176. [Google Scholar] [CrossRef]
- Ring, M.; Wunderlich, S.; Scheuring, D.; Landes, D.; Hotho, A. A Survey of Network-Based Intrusion Detection Data Sets. Comput. Secur. 2019, 86, 147–167. [Google Scholar] [CrossRef]
- Dunmore, A.; Jang-Jaccard, J.; Sabrina, F.; Kwak, J. A Comprehensive Survey of Generative Adversarial Networks (GANs) in Cybersecurity Intrusion Detection. IEEE Access 2023, 11, 76071–76093. [Google Scholar] [CrossRef]
- Thakkar, A.; Lohiya, R. A Review on Challenges and Future Research Directions for Machine Learning-Based Intrusion Detection System. Arch. Comput. Methods Eng. 2023, 30, 4245–4269. [Google Scholar] [CrossRef]
- Goldschmidt, P.; Chudá, D. Network Intrusion Datasets: A Survey, Limitations, and Recommendations. Comput. Secur. 2025, 156, 104510. [Google Scholar] [CrossRef]
- Park, C.; Lee, J.; Kim, Y.; Park, J.-G.; Kim, H.; Hong, D. An Enhanced AI-Based Network Intrusion Detection System Using Generative Adversarial Networks. IEEE Internet Things J. 2023, 10, 2330–2345. [Google Scholar] [CrossRef]
- Apicella, A.; Donnarumma, F.; Isgrò, F.; Prevete, R. A Survey on Modern Trainable Activation Functions. Neural Netw. 2021, 138, 14–32. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Liu, M.; Sun, J. Activate or Not: Learning Customized Activation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8028–8038. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Batista, G.; Prati, R.; Monard, M.-C. A study of the behavior of several methods for balancing machine learning training data. SIGKDD Explor. Newsl. 2004, 1, 20–29. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. In Advances in Intelligent Computing; Huang, D.S., Zhang, X.P., Huang, G.B., Eds.; ICIC 2005. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3644. [Google Scholar] [CrossRef]
- Napierala, K.; Stefanowski, J. Types of minority class examples and their influence on learning classifiers from imbalanced data. J. Intell. Inf. Syst. 2016, 46, 563–597. [Google Scholar] [CrossRef]
- Guo, J.; Wu, H.; Chen, X.; Lin, W. Adaptive SV-Borderline SMOTE-SVM Algorithm for Imbalanced Data Classification. Appl. Soft Comput. 2024, 150, 110986. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 2672–2680. Available online: https://proceedings.neurips.cc/paper/2014/file/f033ed80deb0234979a61f95710dbe25-Paper.pdf (accessed on 10 September 2025).
- Yin, C.; Zhu, Y.; Fei, J.; He, X. A Deep Learning Approach for Intrusion Detection Using Recurrent Neural Networks. IEEE Access 2017, 5, 21954–21961. [Google Scholar] [CrossRef]
- Yang, J.; Li, T.; Liang, G.; He, W.; Zhao, Y. A Simple Recurrent Unit Model Based Intrusion Detection System With DCGAN. IEEE Access 2019, 7, 83286–83296. [Google Scholar] [CrossRef]
- Shahriar, M.H.; Haque, N.I.; Rahman, M.A.; Alonso, M. G-IDS: Generative Adversarial Networks Assisted Intrusion Detection System. In Proceedings of the 2020 IEEE 44th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 13–17 July 2020; pp. 376–385. [Google Scholar] [CrossRef]
- Dlamini, G.; Fahim, M. DGM: A data generative model to improve minority class presence in anomaly detection domain. Neural Comput. Appl. 2021, 33, 13635–13646. [Google Scholar] [CrossRef]
- Alotaibi, F.; Rassam, M. Adversarial Machine Learning Attacks against Intrusion Detection Systems: A Survey on Strategies and Defense. Future Internet 2023, 15, 62. [Google Scholar] [CrossRef]
- Klinkhamhom, C.; Wuttidittachotti, P.; Boonyopakorn, P. Comparative Evaluation of GAN, CGAN, and ACGAN for Intrusion Detection in Cybersecurity. In Proceedings of the 2025 International Technical Conference on Circuits/Systems, Computers, and Communications (ITC-CSCC), Seoul, Republic of Korea, 7–10 July 2025; pp. 1–4. [Google Scholar] [CrossRef]
- Lee, G.-C.; Li, J.-H.; Li, Z.-Y. A Wasserstein Generative Adversarial Network–Gradient Penalty-Based Model with Imbalanced Data Enhancement for Network Intrusion Detection. Appl. Sci. 2023, 13, 8132. [Google Scholar] [CrossRef]
- Gul, S.; Arshad, S.; Saeed, S.M.U.; Akram, A.; Azam, M.A. WGAN-DL-IDS: An Efficient Framework for Intrusion Detection System Using WGAN, Random Forest, and Deep Learning Approaches. Computers 2025, 14, 4. [Google Scholar] [CrossRef]
- Strickland, C.; Zakar, M.; Saha, C.; Soltani Nejad, S.; Tasnim, N.; Lizotte, D.J.; Haque, A. DRL-GAN: A Hybrid Approach for Binary and Multiclass Network Intrusion Detection. Sensors 2024, 24, 2746. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Odena, A.; Olah, C.; Shlens, J. Conditional Image Synthesis with Auxiliary Classifier GANs. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; JMLR.org: Sydney, Australia, 2017; pp. 2642–2651. [Google Scholar]
- Zhang, K.; Qin, H.; Jin, Y.; Wang, H.; Yu, X. Auxiliary Classifier Generative Adversarial Network Assisted Intrusion Detection System. In Proceedings of the 2022 4th International Conference on Intelligent Information Processing (IIP), Guangzhou, China, 14–16 October 2022; pp. 307–311. [Google Scholar] [CrossRef]
- Yang, H.; Xu, J.; Xiao, Y.; Hu, L. SPE-ACGAN: A Resampling Approach for Class Imbalance Problem in Network Intrusion Detection Systems. Electronics 2023, 12, 3323. [Google Scholar] [CrossRef]
- Dahouda, M.K.; Joe, I. A Deep-Learned Embedding Technique for Categorical Features Encoding. IEEE Access 2021, 9, 114381–114391. [Google Scholar] [CrossRef]
- Borisov, V.; Leemann, T.; Seßler, K.; Haug, J.; Pawelczyk, M.; Kasneci, G. Deep Neural Networks and Tabular Data: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7499–7519. [Google Scholar] [CrossRef]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling tabular data using conditional GAN. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019; pp. 7335–7345. [Google Scholar] [CrossRef]
- Zhao, Z.; Kunar, A.; Birke, R.; Van der Scheer, H.; Chen, L.Y. CTAB-GAN+: Enhancing tabular data synthesis. Front. Big Data 2024, 6, 1296508. [Google Scholar] [CrossRef]
- Allagi, S.; Pawan, T.; Leong, W.Y. Enhanced Intrusion Detection Using Conditional-Tabular-Generative-Adversarial-Network-Augmented Data and a Convolutional Neural Network: A Robust Approach to Addressing Imbalanced Cybersecurity Datasets. Mathematics 2025, 13, 1923. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Khan, J.; Elfakharany, R.; Saleem, H.; Pathan, M.; Shahzad, E.; Dhou, S.; Aloul, F. Can Machine Learning Enhance Intrusion Detection to Safeguard Smart City Networks from Multi-Step Cyberattacks? Smart Cities 2025, 8, 13. [Google Scholar] [CrossRef]
- Sabilla, M.S.; Rahmat, B.; Maulana, D.S. Optimizing Threshold Using Pearson Correlation for Selecting Features of Electronic Nose Signals. Int. J. Intell. Eng. Syst. 2019, 12, 82–90. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, University of Waikato, Hamilton, New Zealand, 1999. Available online: https://ml.cms.waikato.ac.nz/publications/1999/99MH-Thesis.pdf (accessed on 2 September 2025).
- Nasir, I.M.; Khan, M.A.; Yasmin, M.; Shah, J.H.; Gabryel, M.; Scherer, R.; Damaševičius, R. Pearson Correlation-Based Feature Selection for Document Classification Using Balanced Training. Sensors 2020, 20, 6793. [Google Scholar] [CrossRef]
- Ozkan-Okay, M.; Samet, R.; Aslan, Ö.; Kosunalp, S.; Iliev, T.; Stoyanov, I. A Novel Feature Selection Approach to Classify Intrusion Attacks in Network Communications. Appl. Sci. 2023, 13, 11067. [Google Scholar] [CrossRef]
- Yin, Y.; Jang-Jaccard, J.; Xu, W.; Singh, A.; Zhu, J.; Sabrina, F.; Kwak, J. IGRF-RFE: A hybrid feature selection method for MLP-based network intrusion detection on UNSW-NB15 dataset. J. Big Data 2023, 10, 15. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Rajathi, C.; Rukmani, P. AccFIT-IDS: Accuracy-Based Feature Inclusion Technique for Intrusion Detection System. Syst. Sci. Control Eng. 2025, 13, 2460429. [Google Scholar] [CrossRef]
- Psychogyios, K.; Papadakis, A.; Bourou, S.; Nikolaou, N.; Maniatis, A.; Zahariadis, T. Deep Learning for Intrusion Detection Systems (IDSs) in Time Series Data. Future Internet 2024, 16, 73. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. KDD Cup 1999 Data Set. UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/130/kdd+cup+1999+data (accessed on 4 September 2025).
- Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A.A. A detailed analysis of the KDD CUP 99 data set. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, 8–10 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Canadian Institute for Cybersecurity (CIC). NSL-KDD Dataset. Available online: https://www.unb.ca/cic/datasets/nsl.html (accessed on 12 September 2025).
- Moustafa, N.; Slay, J. UNSW-NB15: A comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set). In Proceedings of the 2015 Military Communications and Information Systems Conference (MilCIS), Canberra, Australia, 10–12 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- UNSW Canberra. UNSW-NB15 Dataset. Available online: https://research.unsw.edu.au/projects/unsw-nb15-dataset (accessed on 4 September 2025).

| Class | Training Set | Test Set | Raw Ratio | Required Multiplier |
Applied Multiplier |
Final Target | Class Type |
|---|---|---|---|---|---|---|---|
| Normal | 67,342 | 9710 | 1.0000 | 1.0 | - | 0 | Major |
| DoS | 45,927 | 7457 | 0.6819 | 1.5 | - | 0 | Major |
| Probe | 11,656 | 2421 | 0.1731 | 5.8 | 0.43 | 5000 | Minor |
| R2L | 995 | 2754 | 0.0148 | 67.7 | 3 | 3000 | Minor |
| U2R | 52 | 200 | 0.0008 | 1294.7 | 38 | 2000 | Rare |
| Class |
Training Set | Test Set |
Raw Ratio |
Required Multiplier |
Applied Multiplier |
Final Target | Class Type |
|---|---|---|---|---|---|---|---|
| Analysis | 2000 | 667 | 0.0357 | 28.0 | 1.5 | 3000 | Minor |
| Backdoor | 1746 | 583 | 0.0312 | 32.1 | 1.7 | 3000 | Minor |
| DoS | 12,264 | 4089 | 0.2197 | 4.5 | 0.24 | 3000 | Minor |
| Exploits | 33,393 | 11,132 | 0.5963 | 1.7 | - | 0 | Major |
| Fuzzers | 18,184 | 6062 | 0.3240 | 3.1 | 0.27 | 5000 | Minor |
| Generic | 40,000 | 18,871 | 0.7143 | 1.4 | - | 0 | Major |
| Normal | 56,000 | 37,000 | 1.0000 | 1.0 | - | 0 | Major |
| Reconnaissance | 10,491 | 3494 | 0.1873 | 5.3 | 0.48 | 5000 | Minor |
| Shellcode | 1133 | 378 | 0.0202 | 49.4 | 2.6 | 3000 | Minor |
| Worms | 130 | 44 | 0.0023 | 430.8 | 15.4 | 2000 | Rare Avoid overfitting (×15 is sufficient) |
| Component | Specification |
|---|---|
| Operating System | Ubuntu 20.04 LTS |
| Development IDE | Visual Studio Code 1.105.1 |
| Programming Lang. | Python 3.x |
| Deep Learning | TensorFlow-GPU 2.4, Keras 2.4.3 |
| Machine Learning | scikit-learn 0.24.0 |
| Data Processing | Pandas 1.1.5, NumPy 1.19.5 |
| Utilities | tqdm 4.50.0, Matplotlib 3.3, Seaborn 0.11 |
| Hardware | Intel Core i5 CPU, 16 GB RAM, NVIDIA RTX 3060 Ti GPU (8 GB VRAM) |
| Class | Type | Training Set | Test Set | Total | Ratio (%) |
|---|---|---|---|---|---|
| Normal | Major | 67,342 | 9710 | 77,052 | 51.88% |
| DoS | Major | 45,927 | 7457 | 53,384 | 35.95% |
| Probe | Minor | 11,656 | 2421 | 14,077 | 9.48% |
| R2L | Minor | 995 | 2754 | 3749 | 2.52% |
| U2R | Rare | 52 | 200 | 252 | 0.17% |
| Class | Type | Training Set | Test Set | Total | Ratio (%) |
|---|---|---|---|---|---|
| Analysis | Minor | 2000 | 667 | 2667 | 1.04% |
| Backdoor | Minor | 1746 | 583 | 2329 | 0.90% |
| DoS | Minor | 12,264 | 4089 | 16,353 | 6.35% |
| Exploits | Major | 33,393 | 11,132 | 44,525 | 17.28% |
| Fuzzers | Minor | 18,184 | 6062 | 24,246 | 9.41% |
| Generic | Major | 40,000 | 18,871 | 58,871 | 22.85% |
| Normal | Major | 56,000 | 37,000 | 93,000 | 36.09% |
| Reconnaissance | Minor | 10,491 | 3494 | 13,985 | 5.43% |
| Shellcode | Minor | 1133 | 378 | 1511 | 0.59% |
| Worms | Rare | 130 | 44 | 174 | 0.07% |
| Parameter | NSL–ACON | NSL–ReLU | UNSW–ACON | UNSW–ReLU |
|---|---|---|---|---|
| Epochs | 2000 | 2000 | 2000 | 2000 |
| Batch size | 128 | 128 | 128 | 128 |
| Latent dim (z) | 100 | 100 | 100 | 100 |
| Optimizer (G/D) | Adam | Adam | Adam | Adam |
| LR (G/D) | 2 × 10−4 | 2 × 10−4 | 2 × 10−4 | 2 × 10−4 |
| Layers (G/D) | 4/4 | 4/4 | 4/4 | 4/4 |
| Hidden units (G) | 128 → 64 → 32 → | 128 → 64 → 32 → | 128 → 64 → 32 → | 128 → 64 → 32→ |
| Hidden units (D) | 128 → 64 → 32 → | 128 → 64 → 32 → | 128 → 64 → 32 → | 128 → 64 → 32 → |
| Activation | ACON (trainable α,β,γ) | ReLU | ACON (trainable α,β,γ) | ReLU |
| Dropout | 0.2 | 0.2 | 0.2 | 0.2 |
| Update Ratio (D:G) | 1:3 | 1:3 | 1:3 | 1:3 |
| Validation | 5-fold CV | 5-fold CV | 5-fold CV | 5-fold CV |
| Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) | ||
|---|---|---|---|---|---|---|---|
| Class | Classifier | Original Data | MIDS | ||||
| DoS | Random forest | 96 | 78 | 86 | 93 | 87 | 90 |
| DoS | Decision tree | 95 | 79 | 86 | 90 | 75 | 82 |
| DoS | Neural network | 96 | 81 | 88 | 92 | 83 | 87 |
| DoS | SVM | 96 | 78 | 86 | 95 | 82 | 88 |
| Probe | Random forest | 84 | 62 | 72 | 44 | 86 | 58 |
| Probe | Decision tree | 81 | 65 | 72 | 41 | 86 | 56 |
| Probe | Neural network | 73 | 60 | 66 | 43 | 83 | 56 |
| Probe | SVM | 80 | 2 | 67 | 42 | 87 | 57 |
| R2L | Random forest | 96 | 2 | 5 | 67 | 27 | 39 |
| R2L | Decision tree | 71 | 5 | 9 | 41 | 86 | 55 |
| R2L | Neural network | 85 | 9 | 16 | 43 | 82 | 56 |
| R2L | SVM | 97 | 8 | 16 | 42 | 87 | 57 |
| U2R | Random forest | 62 | 1 | 3 | 60 | 17 | 26 |
| U2R | Decision tree | 60 | 6 | 11 | 44 | 23 | 30 |
| U2R | Neural network | 72 | 8 | 15 | 61 | 30 | 40 |
| U2R | SVM | 57 | 1 | 2 | 35 | 26 | 30 |
| Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) | ||
|---|---|---|---|---|---|---|---|
| Class | Classifier | Original Data | MIDS | ||||
| Analysis | Random forest | 0 | 0 | 0 | 0 | 0 | 0 |
| Analysis | Decision tree | 1 | 7 | 3 | 2 | 8 | 4 |
| Analysis | Neural network | 0 | 0 | 0 | 0 | 0 | 0 |
| Analysis | SVM | 0 | 0 | 0 | 0 | 0 | 0 |
| Backdoor | Random forest | 2 | 12 | 3 | 2 | 1 | 4 |
| Backdoor | Decision tree | 2 | 10 | 3 | 3 | 1 | 5 |
| Backdoor | Neural network | 2 | 1 | 1 | 3 | 2 | 2 |
| Backdoor | SVM | 6 | 5 | 11 | 8 | 1 | 2 |
| DoS | Random forest | 57 | 10 | 17 | 28 | 33 | 30 |
| DoS | Decision tree | 29 | 19 | 23 | 27 | 30 | 28 |
| DoS | Neural network | 28 | 5 | 9 | 31 | 64 | 42 |
| DoS | SVM | 32 | 34 | 33 | 32 | 70 | 44 |
| Exploits | Random forest | 60 | 79 | 68 | 78 | 66 | 71 |
| Exploits | Decision tree | 62 | 68 | 65 | 73 | 61 | 66 |
| Exploits | Neural network | 56 | 88 | 68 | 74 | 64 | 69 |
| Exploits | SVM | 81 | 49 | 61 | 83 | 52 | 64 |
| Fuzzers | Random forest | 30 | 57 | 39 | 86 | 70 | 77 |
| Fuzzers | Decision tree | 27 | 47 | 35 | 91 | 65 | 75 |
| Fuzzers | Neural network | 31 | 52 | 39 | 80 | 61 | 69 |
| Fuzzers | SVM | 22 | 51 | 31 | 71 | 50 | 59 |
| Generic | Random forest | 100 | 96 | 98 | 100 | 96 | 98 |
| Generic | Decision tree | 98 | 97 | 98 | 99 | 97 | 98 |
| Generic | Neural network | 99 | 95 | 97 | 99 | 95 | 97 |
| Generic | SVM | 99 | 94 | 97 | 99 | 95 | 97 |
| Reconnaissance | Random forest | 92 | 80 | 86 | 89 | 82 | 86 |
| Reconnaissance | Decision tree | 89 | 78 | 83 | 88 | 80 | 84 |
| Reconnaissance | Neural network | 68 | 82 | 75 | 80 | 81 | 80 |
| Reconnaissance | SVM | 44 | 79 | 57 | 50 | 85 | 63 |
| Shellcode | Random forest | 39 | 71 | 50 | 40 | 75 | 52 |
| Shellcode | Decision tree | 36 | 69 | 47 | 38 | 71 | 49 |
| Shellcode | Neural network | 22 | 64 | 33 | 30 | 59 | 40 |
| Shellcode | SVM | 7 | 69 | 14 | 16 | 37 | 22 |
| Worms | Random forest | 57 | 18 | 27 | 69 | 44 | 53 |
| Worms | Decision tree | 52 | 52 | 52 | 45 | 63 | 52 |
| Worms | Neural network | 50 | 15 | 24 | 43 | 10 | 17 |
| Worms | SVM | 4 | 72 | 7 | 7 | 16 | 25 |
| Model | Random Forest | Decision Tree | Neural Network | SVM |
|---|---|---|---|---|
| Original | 70 | 71 | 71 | 68 |
| SMOTE | 71 | 72 | 70 | 71 |
| ADASYN | 72 | 66 | 70 | 71 |
| SMOTEENN | 73 | 70 | 71 | 71 |
| Borderline-SMOTE | 73 | 70 | 70 | 71 |
| MIDS-ACON | 72 | 69 | 70 | 71 |
| MIDS-RELU | 72 | 71 | 70 | 71 |
| Model | Random Forest | Decision Tree | Neural Network | SVM | ||||
|---|---|---|---|---|---|---|---|---|
| Original | 76 | 76 | 67 | 58 | ||||
| SMOTE | 77 | 75 | 73 | 70 | ||||
| ADASYN | 77 | 75 | 73 | 69 | ||||
| SMOTEENN | 73 | 73 | 67 | 68 | ||||
| Borderline-SMOTE | 77 | 75 | 72 | 69 | ||||
| MIDS-ACON | 78 | 77 | 77 | 73 | ||||
| MIDS-RELU | 71 | 77 | 77 | 73 | ||||
| Weighted F1-scores | UNSW-NB15 | NSL-KDD | UNSW-NB15 | NSL-KDD | UNSW-NB15 | NSL-KDD | UNSW-NB15 | NSL-KDD |
| Original | 76 | 70 | 76 | 71 | 67 | 71 | 58 | 68 |
| SMOTE | 77 | 71 | 75 | 72 | 73 | 70 | 70 | 71 |
| ADASYN | 77 | 72 | 75 | 66 | 73 | 70 | 69 | 71 |
| SMOTEENN | 73 | 73 | 73 | 70 | 67 | 71 | 68 | 71 |
| Borderline-SMOTE | 77 | 73 | 75 | 70 | 72 | 70 | 69 | 71 |
| MIDS-ACON | 78 | 72 | 77 | 69 | 77 | 70 | 73 | 71 |
| MIDS-RELU | 71 | 72 | 77 | 71 | 77 | 70 | 73 | 71 |
| Dataset | Class | Classifier | Recall | Recall | ∆Recall (%) |
|---|---|---|---|---|---|
| (Original) (%) | (MIDS-GAN) (%) | ||||
| NSL-KDD | R2L | Random Forest | 2 | 27 | 25 |
| NSL-KDD | U2R | SVM | 1 | 26 | 25 |
| UNSW-NB15 | Worms | Random Forest | 18 | 44 | 26 |
| Dataset | Class | MIDS-GAN | Best Classifier | DGM [19] | Best Classifier | Advantage (pp) |
|---|---|---|---|---|---|---|
| NSL-KDD | R2L | +25 (2→27) | Random Forest | +17 (9→26) | SVM | +8 |
| NSL-KDD | U2R | +25 (1→26) | SVM | +8 (9→17) | Random Forest | +17 |
| UNSW-NB15 | Worms | +26 (18→44) | Random Forest | +1 (0→1) | Random Forest | +25 |
| Average Improvement (Δ pp) | ≈+16.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klinkhamhom, C.; Boonyopakorn, P.; Wuttidittachotti, P. MIDS-GAN: Minority Intrusion Data Synthesizer GAN—An ACON Activated Conditional GAN for Minority Intrusion Detection. Mathematics 2025, 13, 3391. https://doi.org/10.3390/math13213391
Klinkhamhom C, Boonyopakorn P, Wuttidittachotti P. MIDS-GAN: Minority Intrusion Data Synthesizer GAN—An ACON Activated Conditional GAN for Minority Intrusion Detection. Mathematics. 2025; 13(21):3391. https://doi.org/10.3390/math13213391
Chicago/Turabian StyleKlinkhamhom, Chalerm, Pongsarun Boonyopakorn, and Pongpisit Wuttidittachotti. 2025. "MIDS-GAN: Minority Intrusion Data Synthesizer GAN—An ACON Activated Conditional GAN for Minority Intrusion Detection" Mathematics 13, no. 21: 3391. https://doi.org/10.3390/math13213391
APA StyleKlinkhamhom, C., Boonyopakorn, P., & Wuttidittachotti, P. (2025). MIDS-GAN: Minority Intrusion Data Synthesizer GAN—An ACON Activated Conditional GAN for Minority Intrusion Detection. Mathematics, 13(21), 3391. https://doi.org/10.3390/math13213391






