Null Space Properties of Neural Networks with Applications to Image Steganography

Abstract

This paper advances beyond adversarial neural network methods by considering whether the underlying mathematics of neural networks contains inherent properties that can be exploited to fool neural networks. In broad terms, this paper will consider a neural network to be composed of a series of linear transformations between layers of the network, interspersed with nonlinear stages that serve to compress outliers. The input layer of the network is typically extremely high-dimensional, yet the final classification is in a space of a much lower dimension. This dimensional reduction leads to the existence of a null space, and this paper will explore how that can be exploited. Specifically, this paper explores the null space properties of neural networks by extending the null space definition from linear to nonlinear maps and discussing the presence of a null space in neural networks. The null space of a neural network characterizes the component of input data that makes no contribution to the final prediction so that we can exploit it to trick the neural network. One application described here leads to a method of image steganography. Through experiments on image data sets such as MNIST, it has been shown that the null space components can be used to force the neural network to choose a selected hidden image class, even though the overall image can be made to look like a completely different image. The paper concludes with comparisons between what a human viewer would see and the part of the image that the neural network is actually using to make predictions, hence showing that what the neural network “sees” is completely different than what we would expect.

1. Introduction

Despite their remarkable success in various tasks, neural networks (NNs) can sometimes behave in unexpectedly fragile ways, particularly in image recognition. One well-known problem is the existence of adversarial examples, where even small, carefully crafted perturbations to the input can lead to incorrect outputs [1,2]. While adversarial examples highlight an important class of vulnerabilities, they are not the only cause of unreliability. Such behaviors are not merely the result of noisy inputs or training data limitations but may reflect deeper issues rooted in the architecture of the neural networks. In this work, we take a different perspective to examine a structural property of neural networks, namely their null space, as a potential source of fragility.

Many existing studies attribute the vulnerability of neural networks to input-level manipulations. In 2014, Szegedy et al. [3] first discovered an intriguing weakness of deep neural networks. They showed that neural networks for image classification can be easily fooled by small perturbations. Following this observation, numerous studies have been carried out to find different ways to generate adversarial examples (see, for example, [2,4,5,6]). It is observed that adversarial examples have good transferability across models, which suggests that the existence of adversarial examples is also a property of data sets [7]. Thus, adversarial examples are not restricted to the given model.

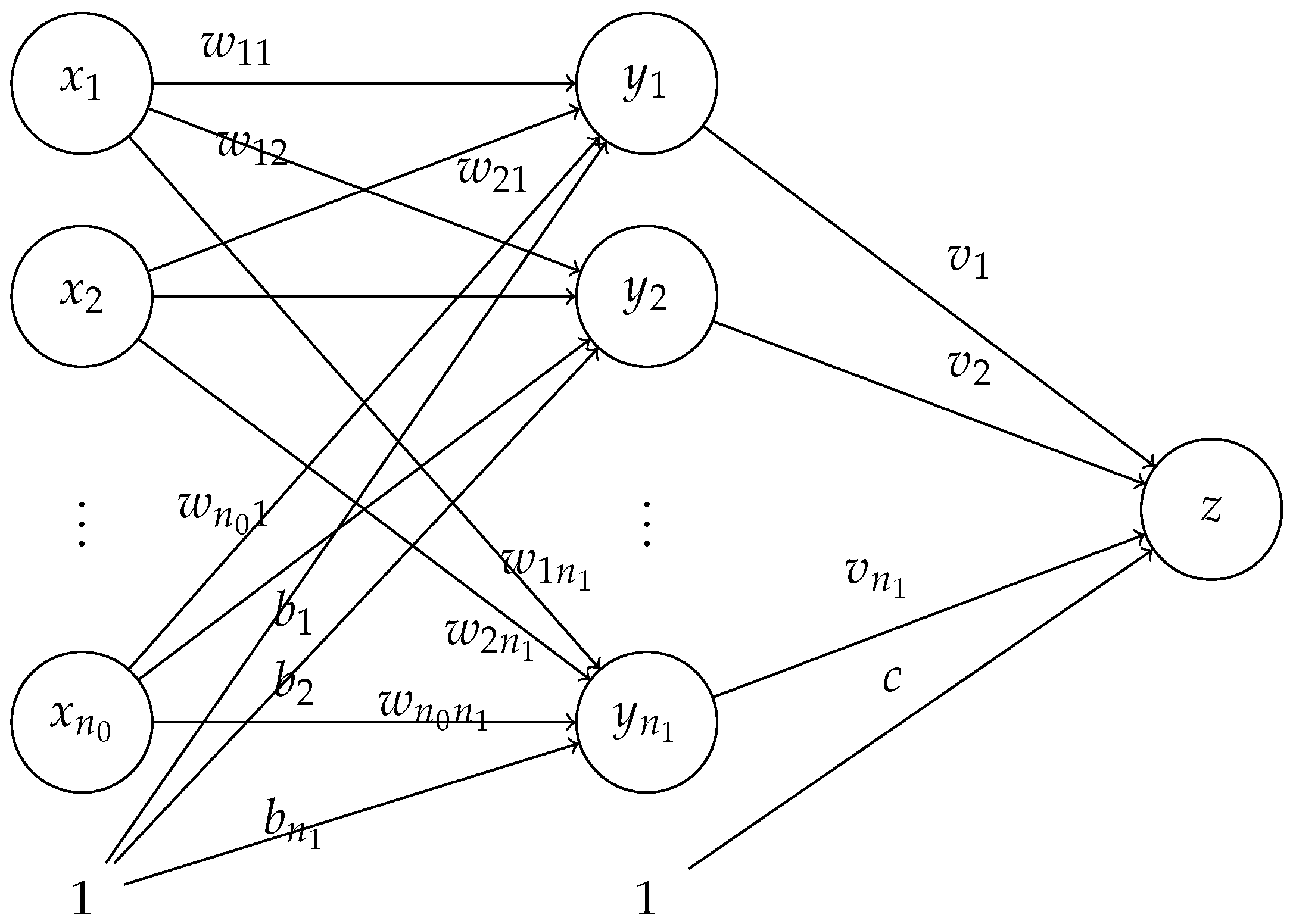
Unlike the adversarial examples, our study focuses on a structural property of neural networks: the null space of neural networks. The null space is a well-established concept in linear algebra, but its connection to neural networks may not be obvious. If one were to consider a standard neural network from the perspective of a mathematician, the input can be considered a vector, generally in a high-dimensional space. Considering Figure 1, each entry $x_i$ in the input vector $\overrightarrow{x}$ is placed in an open circle in the input layer. If we ignore for the moment the unitary node indicated by the 1 at the bottom of the first layer, the weights $w_{ij}$ are multiplied by the entries in the input vector to produce the intermediate values $y_j$, where $y_j={\sum }_{i=1}^{n_0}{w}_{ij}{x}_i$ at the nodes in the middle layer. Hence, the mathematical structure is basically a matrix multiplication of a weight matrix W times the input vector $\overrightarrow{x}$, so the presence of a null space associated with the weight matrix is very possible. Further, in the case of an NN, the known information is in the input vector and the weight matrix is to be determined via the training process. Note that the number of degrees of freedom in W is much greater than the dimension of the input vector; thus the training process can lead to underdetermined systems and high-dimensional null spaces.

In the simplest examples of NNs, the transformation from one layer to the next may be a linear transformation, but a bias term, as indicated by the unitary node labeled 1 at the bottom of the input layer, is usually introduced, which then converts the transformations into affine transformations. The affine form will introduce some complications, and this paper will explore the impact of this on the null space characteristics of the linear transformation component of NNs. When all of the layers are considered, along with the activation functions, we say that we have a fully connected neural network (FCNN) with $n_0$ nodes in the first layer, $n_1$ nodes in the second layer, and so on. This FCNN is also referred to as an $(n_0,n_1,\cdots ,n_k)$-FCNN. Finally, it should be mentioned that a nonlinear activation function is usually applied to the data in an intermediate layer, such as a sigmoid function or ReLU function, but these functions can be thought of as a compressing or compactifying function that diminishes the impact of outlier results or, in the case of ReLU, negative-valued intermediate results. While these nonlinear activation functions can obfuscate the impact of the null space effects, this paper will separate out the stages to show that the null space properties, extended to consider the nonlinear effects, can be used to fool the NN and cause it to give unexpected classification results. A detailed analysis will be given in Section 2.

As a primary goal, we discuss how the null space of a neural network affects classification outcomes, revealing it to be a critical factor that may inherently limit a model’s ability to make reliable predictions. The approach takes advantage of the (nonlinear) null space properties of the neural network and generates examples to fool the neural network by adding a large difference to images without changing the predictions. More importantly, to the naked eye, the large differences will look like completely different objects than those that will be recognized by the neural network, achieved via image steganography. Considered from a broader perspective, only a few studies have analyzed the null space properties of neural network functions. Cook et al. [8] integrated the null space analysis on weight matrices with the loss function to detect out-of-distribution inputs rather than analyzing the reliability of NN predictions. Rezaei et al. [9] used the null space of the last layer weight matrix to quantify overfitting. Beyond these, some studies have investigated the null space structure of the parameter space. Sonoda et al. [10] showed that the parameter spaces of overparameterized NNs inherently contain null components that do not affect training loss but may impact generalization. In addition, a few studies have worked on the null space associated with the input data itself  [11,12,13].

However, there is still a lack of understanding regarding the global effects of null space properties for NNs. In this study, inspired by the null space of linear maps, we introduce the concept of a null space for nonlinear maps and discuss how the null space applies to fully connected neural networks (FCNNs). We show how the null space is generally an intrinsic property of NNs. Further, in most cases, once the NN’s architecture is determined, the dimension of the null space of the NN is also determined. To illustrate this in concrete terms, we use null space-based methods to fool an image recognition NN, demonstrating an application of image steganography.

Image steganography is a technique to hide an image inside another image [14,15]. Traditional image steganography methods can be categorized into two main types: methods operating in the spatial domain [16] and the transform domain [17]. Among methods operating in the transform domain, discrete orthogonal moment transforms have been widely used in image analysis and image steganography [18,19,20,21,22]. In addition to traditional steganography methods, approaches based on NNs have also been employed for image steganography, using several different approaches [23,24,25,26,27,28,29,30,31]. In this paper, inspired by the null space analysis of NNs, we propose a null space-based method for image steganography. Our approach shares some similarity with discrete orthogonal moment-based steganography, as both methods decompose images with respect to a chosen basis. However, while moment methods rely on polynomial bases (e.g., Tchebichef, Krawtchouk), our method employs basis vectors from the null space of a neural network. In addition, although conceptually related to other steganographic methods, the null space-based method presented in this paper provides new degrees of freedom and a clear process for creating steganographic images for NNs. The main goal is to hide an image and recognize the correct class of the hidden image while presenting to the (human) viewer an image that is completely different to the hidden image that will be recognized by the NN.

In summary, the main contributions of this paper are as follows:

• We introduce a novel perspective on NN reliability by analyzing the role of the null space structure for the NN and showing that its dimension is architecture-dependent.
• We propose a null space-based steganographic method that generates visually different images while hiding images that are recognized with high certainty by the model.

The rest of this paper is organized as follows: Section 2 introduces the (nonlinear) null space of NNs. Inspired by null space analysis, an image steganography method based on the null space of FCNNs is introduced in Section 3. Section 4 presents a series of experiments on different image data sets. In Section 5, we offer some discussion and conclusions about the advantages and limitations of the null space method and the differences between the null space image steganography method and adversarial examples. Additionally, more examples are presented to emphasize that what the NN is seeing and using to make classification decisions is not what we humans might perceive it to be seeing.

2. Methodology and Theory

In this section, we introduce the null space of nonlinear maps and discuss the null space of neural networks (NNs). In order to keep the flow of ideas consistent, detailed proofs will be placed in the appendix.

2.1. Null Space of Linear and Nonlinear Maps

In linear algebra, the null space of an $m\times n$ matrix A is $\mathrm{Null}\left(A\right)=\{\overrightarrow{x}\in {\mathbb{R}}^n:A\overrightarrow{x}=\overrightarrow{0}\}$ and $\mathrm{Null}\left(A\right)$ is a subspace of ${\mathbb{R}}^n$. Consider a linear map $T:{\mathbb{R}}^n\to {\mathbb{R}}^m,T\left(\overrightarrow{x}\right)=A\overrightarrow{x}$ with $\mathrm{Null}\left(A\right)$ nontrivial. By the definition of a null space, it is not difficult to see that for any $\overrightarrow{x}\in {\mathbb{R}}^n$ and ${\overrightarrow{x}}_{null}\in \mathrm{Null}\left(A\right)$, $T(\overrightarrow{x}+{\overrightarrow{x}}_{null})=T\overrightarrow{x}$. That is, adding any vector in $\mathrm{Null}\left(A\right)$ to any input $\overrightarrow{x}$ will not change the output since the transformation is a linear map.

In most cases, null space in nonlinear maps is not defined as described above. The set $\{\overrightarrow{x}:f\left(\overrightarrow{x}\right)=0\}$ for a nonlinear map $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is not a subspace of ${\mathbb{R}}^n$. Moreover, the property of linearity $f(\overrightarrow{x}+\overrightarrow{y})=f\left(\overrightarrow{x}\right)+f\left(\overrightarrow{y}\right)$ does not hold for the nonlinear map f. Although we can still find the set $\{{\overrightarrow{x}}_{\alpha }:f\left({\overrightarrow{x}}_{\alpha }\right)=0\}$, the property $f(\overrightarrow{x}+{\overrightarrow{x}}_{\alpha })=f\left(\overrightarrow{x}\right)$ is no longer true for all $\overrightarrow{x}\in {\mathbb{R}}^n$. To preserve this useful property, the concept of null space can be adapted to nonlinear maps by identifying a set of vectors ${\overrightarrow{x}}_{null}$ that satisfy the condition $f(\overrightarrow{x}+a{\overrightarrow{x}}_{null})=f\left(\overrightarrow{x}\right)$ for any $\overrightarrow{x}\in {\mathbb{R}}^n,a\in \mathbb{R}$:

Definition 1

(Null space of a nonlinear map). The null space of a nonlinear map $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$, denoted as $N\left(f\right)$, is the set of all vectors in which, by adding these vectors to any input, the image under the map, or output, will not change:

$$N\left(f\right):=\{\overrightarrow{v}\in {\mathbb{R}}^n:f\left(\overrightarrow{x}\right)=f(\overrightarrow{x}+a\overrightarrow{v})\mathrm{for}\mathrm{all}\overrightarrow{x}\in {\mathbb{R}}^n,a\in \mathbb{R}\}.$$

(1)

When this definition is applied to linear maps, it is equivalent to the null space concept in linear algebra. However, for the purposes of this paper, we will use the term “null space” in a broader sense, extending its application to include affine maps, nonlinear maps, etc. Similarly to the null space in linear algebra, $N\left(f\right)$ is a subspace of ${\mathbb{R}}^n$ (Proposition A1). Furthermore, as demonstrated in Proposition A2, all the vectors in $N\left(f\right)$ are mapped to a single point by f. More specifically, for any $\overrightarrow{x},\overrightarrow{y}\in N\left(f\right),f\left(\overrightarrow{x}\right)=f\left(\overrightarrow{y}\right)$. Further properties about null spaces of nonlinear maps are provided in Appendix B. One difference between null spaces of linear and nonlinear maps is that a nonlinear map will not always map null space vectors to zeros.

The definition of the null space for nonlinear maps is straightforward. However, in practice, it is difficult to find a null space explicitly by following this definition. Next, we will introduce an alternative yet equivalent definition for the null space of nonlinear maps, which provides a more accessible way with which to find the null space of a nonlinear map.

To begin with, given a nonlinear map $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$, let us consider the subspaces of $N\left(f\right)$. Suppose f has a decomposition; then, f can be expressed as the composition of two functions $f=f_2\circ f_1$ and $f_1$ is linear. It follows that $\mathrm{Null}\left(f_1\right)$ is a subspace of $N\left(f\right)$. This is straightforward to see, since for any ${\overrightarrow{x}}_{null}\in \mathrm{Null}\left(f_1\right)$, $f_1\left(\overrightarrow{x}\right)=f_1(\overrightarrow{x}+{\overrightarrow{x}}_{null})$ holds for every $\overrightarrow{x}\in {\mathbb{R}}^n$, and so $f(\overrightarrow{x}+{\overrightarrow{x}}_{null})=f_2\circ f_1(\overrightarrow{x}+{\overrightarrow{x}}_{null})=f_2\circ f_1\left(\overrightarrow{x}\right)=f\left(\overrightarrow{x}\right)$. Therefore, we now have a method to find a subspace of $N\left(f\right)$. Hence, we define a partial null space as follows:

Definition 2

(Partial null space of a map). Given a nonlinear map, $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$. If f has a decomposition $f=f_2\circ f_1$, where $f_1:{\mathbb{R}}^n\to {\mathbb{R}}^d$ is a linear map, then the null space of $f_1$ is defined as a partial null space of f (given by $f_1$). We denote it as $P{N}_{f_1}\left(f\right)$.

Then, the question of how to find the null space with partial null spaces and the decomposition of maps remains. In the following lemmas, we present some results regarding partial null spaces and the null space of a nonlinear map. Detailed proofs are provided in Appendix B.

Lemma 1.

Let $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a nonlinear map. Every partial null space $PN\left(f\right)$ is a subspace of $N\left(f\right)$, $dimPN\left(f\right)\le dimN\left(f\right)$.

Lemma 2.

For every nonlinear map $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$, there exists a decomposition $f=f_2\circ f_1$, where $f_1$ is a linear map such that $P{N}_{f_1}\left(f\right)=\mathrm{Null}\left(f_1\right)=N\left(f\right)$, i.e., the partial null space given by $f_1$ is equal to $N\left(f\right)$.

Note that $P{N}_{f_1}\left(f\right)=\mathrm{Null}\left(f_1\right)=N\left(f\right)$ is not always true for any arbitrary decomposition $f=f_2\circ f_1$. In the following corollary, we further discuss the conditions under which this equation holds.

Corollary 1.

Let $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a nonlinear map. The null space of f is the largest partial null space of f. That is, $N\left(f\right)=P{N}_{f_1}\left(f\right)$ if $f=f_2\circ f_1$, $f_1$ is a linear map, and $P{N}_{f_1}\left(f\right)$ has the largest dimension among all decompositions of f.

Directly from Lemmas 1 and 2, Corollary 1 gives an equivalent definition of $N\left(f\right)$ in terms of its partial null space. Consequently, instead of searching for all possible vectors that satisfy Equation (1), we have turned the null space problem into a problem of finding a decomposition of f that yields the largest partial null space.

2.2. Null Space of Fully Connected Neural Networks

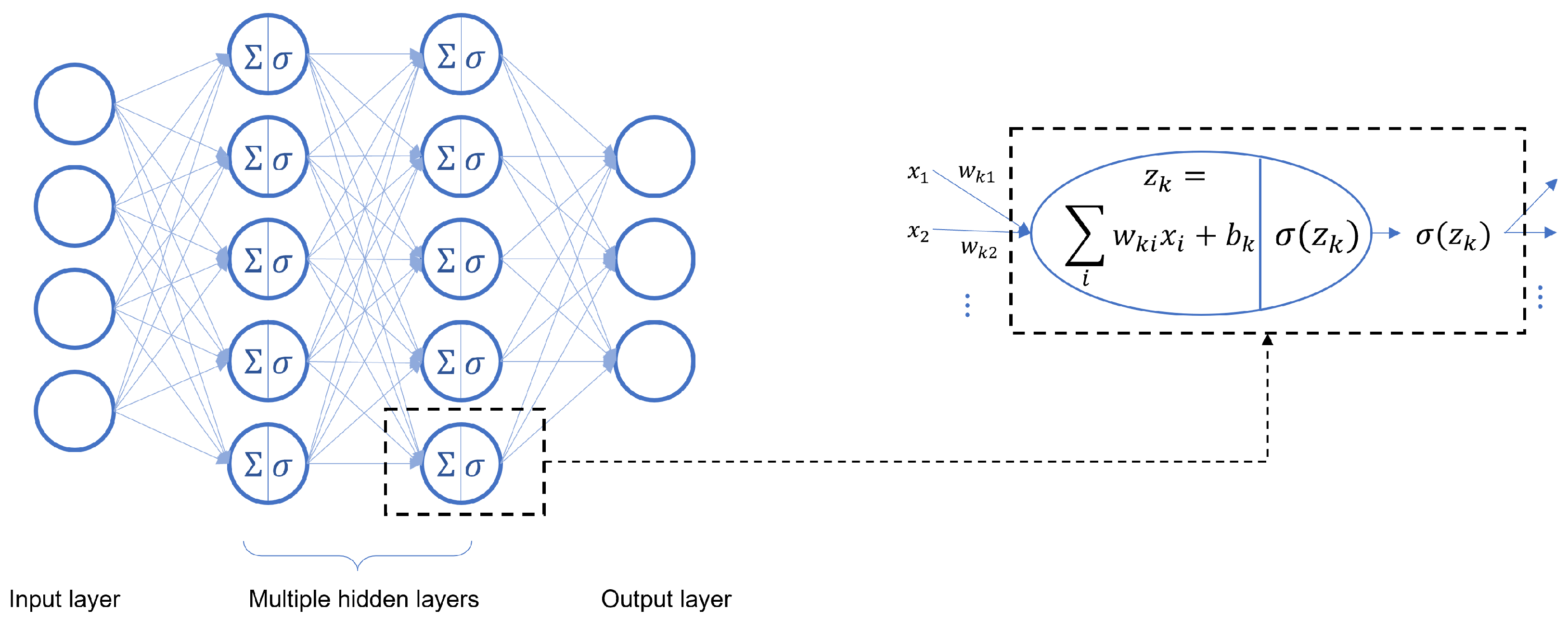
Consider a fully connected neural network $f:{\mathbb{R}}^{n_0}\to {\mathbb{R}}^{n_{K+1}}$, where $K\in \mathbb{N}$ denotes the number of hidden layers of f, with $n_1,n_2,\dots ,n_K\in \mathbb{N}$ representing widths of the hidden layers, i.e., the number of nodes in each hidden layer. $n_0,n_{K+1}\in \mathbb{N}$ are the input and output dimensions, respectively. f is called a $(K+1)-$layer fully connected neural network (FCNN). In this paper, we refer to this FCNN architecture as a $(n_0,n_1,\dots ,n_K)-$FCNN.

As shown in Figure 2, assume the input values are $\left\{x_i\right\}$ and the activation functions are denoted by $\sigma$; then the output of the k^th neuron in the j^th layer is given by $\sigma \left(z_k^{\left[j\right]}\right)={\displaystyle \sum _i}{W}_j(k,i)x_i+{\overrightarrow{b}}_j\left(k\right),$ and the outputs of the j^th layer can be written in a compact matrix form $\sigma \left({\overrightarrow{z}}^{\left[j\right]}\right)=W_j\overrightarrow{x}+{\overrightarrow{b}}_j.$ The function represented by this neural network is

$$f\left(\overrightarrow{x}\right)=W_{K+1}\sigma (W_K\sigma (\cdots W_2\sigma (W_1\overrightarrow{x}+{\overrightarrow{b}}_1)+{\overrightarrow{b}}_2\cdots )+{\overrightarrow{b}}_K)+{\overrightarrow{b}}_{K+1}.$$

Define a sequence of linear and affine transformations as $T_i\left(\overrightarrow{x}\right)=W_i\overrightarrow{x},A_i\left(\overrightarrow{x}\right)=\overrightarrow{x}+{\overrightarrow{b}}_i$ for $i=1,\dots ,k+1$, respectively. The function of FCNN f can also be represented by a composition of maps:

$$f=A_{k+1}\circ T_{k+1}\circ \sigma \circ A_k\circ T_k\circ \cdots \circ A_2\circ T_2\circ \sigma \circ A_1\circ T_1.$$

(2)

Common activation functions include sigmoid activation function and Rectified Linear Unit (ReLU). We refer to the $(n_0,n_1,\dots ,n_K)$-FCNN with ReLU activation as a $(n_0,n_1,\dots ,n_K)$-ReLU NN.

According to Corollary 1, we can conduct null space analysis on FCNNs using the composite function form (Equation (2)). An FCNN can be naturally decomposed into two parts, $(A_{K+1}\circ T_{K+1}\circ \sigma \circ T_K\circ \cdots \circ A_2\circ T_2\circ \sigma \circ A_1)$ and $T_1$, where $T_1$ is linear. Thus, $\mathrm{Null}\left(T_1\right)$ is a partial null space of FCNN f which, in most cases, is also the null space $N\left(f\right)$.

As will be shown in Section 3, input images can be decomposed into null space and non-null space components, which can be used to fool the neural networks in an image steganography application.

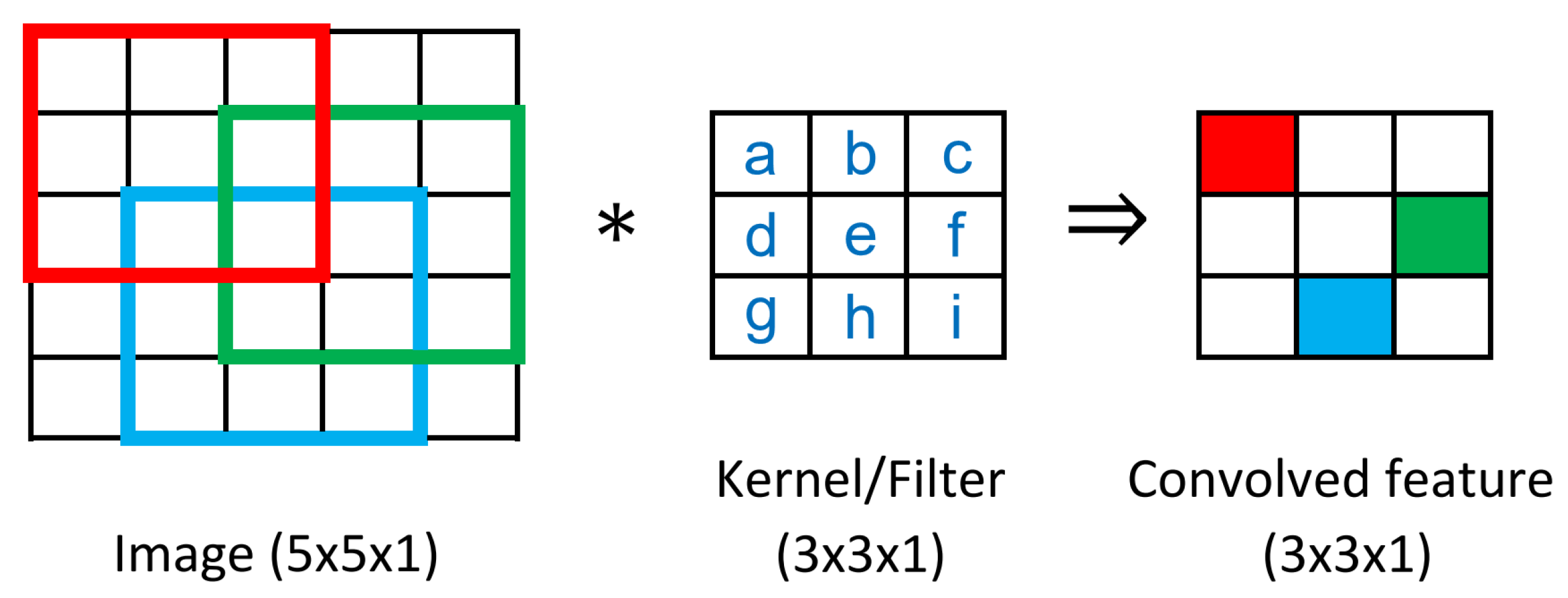
2.3. Null Space of Convolutional Neural Networks

Similarly, a convolutional neural network (CNN) can also be represented by the composition of maps. Instead of having only affine transformations and activation functions, the early layers of a CNN allow two additional types of computation: convolution, denoted as C, and pooling, denoted as S. To determine the null space of a CNN f, we can first decompose f into the composition of maps $f=T_{k+1}\circ \sigma \circ \cdots \circ \sigma \circ C$. So, in most cases, the first convolution operation C is the maximum linear map of f, and $N\left(f\right)=\mathrm{Null}\left(C\right)$.

The null space of a CNN is significantly more complex than an FCNN. In this paper, we will only give an overview of the null space analysis for CNN in a simple case. Consider the case when the input image of a CNN only has one channel, for example the grayscale number images in the MNIST data set (a color image typically has three channels).

A typical convolutional layer in a CNN comprises multiple kernels. To find the null space of the entire convolutional layer $\mathrm{Null}\left(C\right)$, we can initially determine the null space of a single kernel $\mathrm{Null}\left(K\right)$ corresponding to one convolution operation. As shown in Appendix C, given one kernel, if the convolution operation keeps the output image with the same dimensions as the input image (same padding), then $N\left(f\right)=\left\{0\right\}$ in most cases. If the output image of the first convolution operation has fewer dimensions than the input image (valid padding), $N\left(f\right)$ can be nontrivial. According to Lemma A1, in most cases, the null space of a given kernel has a dimension that is equal to the difference between the dimensions of the input and output image. For example, given a $28\times 28$ image and a $3\times 3$ kernel, the dimension of the null space of this convolution operation is $28\times 28-26\times 26=108$ in most cases.

Assume that the first convolutional layer C has n kernels $K_1,\cdots ,K_n$; then $N\left(f\right)=N\left(C\right)={\displaystyle \bigcap _{i=1}^n}\mathrm{Null}\left(K_i\right)$. For instance, if the input is a $28\times 28$ image and the first convolutional layer has six $3\times 3$ kernels, then the null space of the CNN is the intersection of six $109-$dimensional subspaces of ${\mathbb{R}}^{784}$. The likelihood of there being a non-trivial intersection between 109-dimensional subspaces of a 784-dimensional space is low, but care must be taken when designing the kernels.

Compared to FCNNs, CNNs can achieve a trivial null space with fewer unknown parameters in the first weight matrix and perhaps greater robustness.

3. Photo Steganography Based on the Null Space of a Neural Network

In considering the task of hiding secret information inside another image, a natural idea emerges from our previous discussions on the null space properties of FCNNs. To this end, in this section we propose a method for creating steganographic images, referred to as “stego images”, to fool FCNNs and pass on secret classification information.

In terms of a pre-trained FCNN f, for any input image X, the FCNN f gives a decomposition,

$$X=\widehat{X}+X_{\perp },$$

where $\widehat{X}\in N\left(f\right)$ is the projection of X onto the null space of f and $X_{\perp }$ is the orthogonal complement that determines the prediction. Since $f\left(\widehat{X}\right)=0$, the output depends solely on $X_{\perp }$; that is, $f\left(X\right)=f\left(X_{\perp }\right)$. This decomposition provides the idea for controlling the predicted label/classification independently of the image’s appearance.

Consider two images H and C: H is the hidden image which carries the secret label. C is the cover image which determines the visual appearance. Our goal is to pass a new image S that visually looks like C but secretly hides the classification information of H, i.e., which is classified the same as the hidden image by f. This can be achieved by decomposing both H and C with respect to the null space $N\left(f\right)$: the null space projections, denoted by $\widehat{H}$ and $\widehat{C}$, which lie in the null space and do not affect the prediction; and the orthogonal complements, denoted by $H_{\perp }$ and $C_{\perp }$, which contribute to the output of f. Importantly, this method does not involve retraining the network; instead, the null space $N\left(f\right)$ is computed directly from the first layer of a pre-trained neural network f. By combining the null space projection of C, denoted by $\widehat{C}$, with the prediction-relevant component of H, denoted by $H_{\perp }$, we construct

$$S={\alpha }_1{H}_{\perp }+{\alpha }_2\widehat{C},{\alpha }_1,{\alpha }_2\in (0,1),$$

so that S appears similar to C but satisfies $f\left(S\right)=f\left(H\right)$ if the f is trained on grayscale images to correctly classify the scaled inputs, such as $\alpha H$ for $\alpha \in (0,1)$. The pseudocode of the proposed image steganography method is provided in Appendix A.

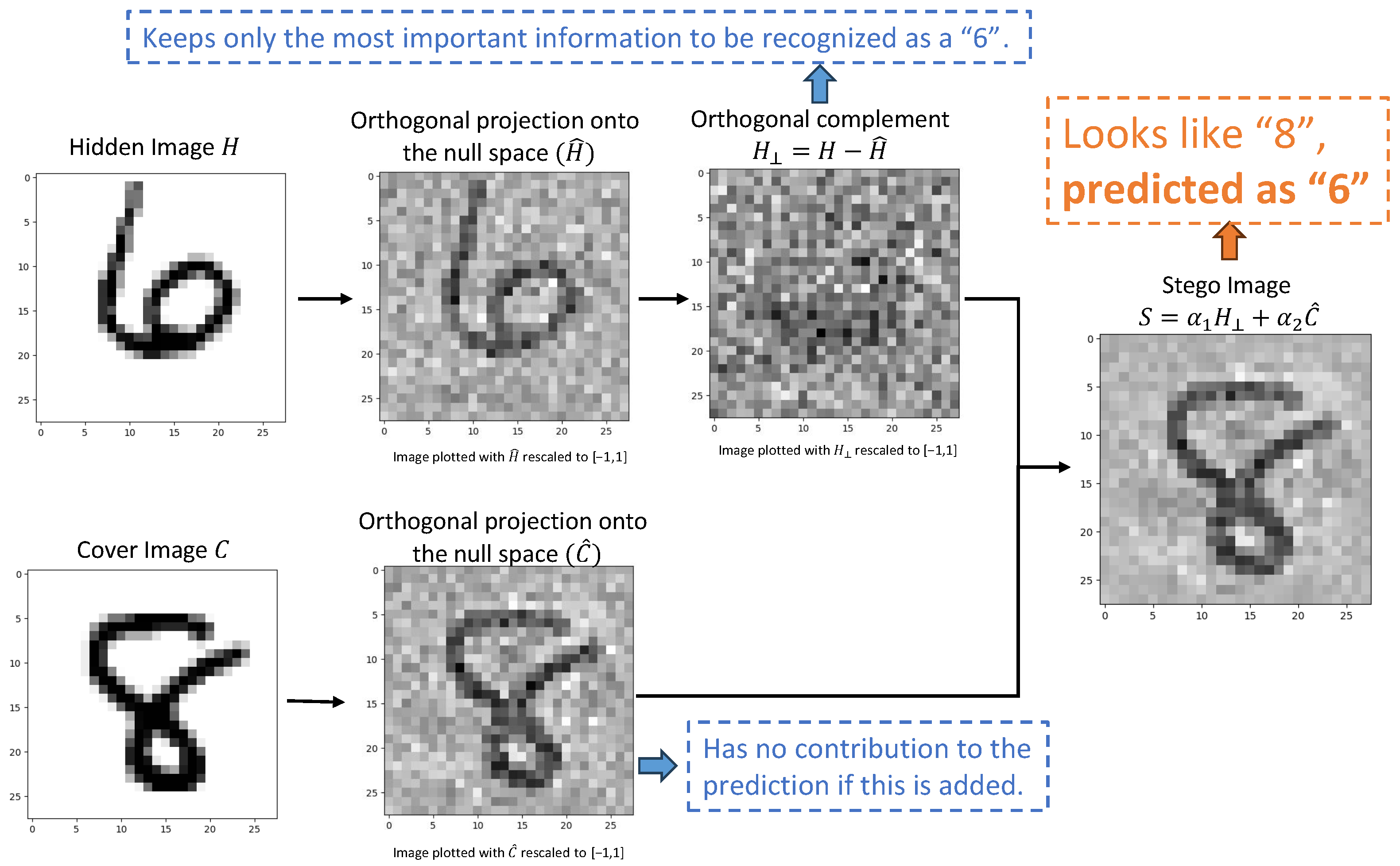
Figure 3 provides a visualization of the whole process. We consider a data set ${\left\{(X_i,y_i)\right\}}_{i=1}^N$, where $X_i$ are $28\times 28$ grayscale images normalized to the range $[-1,1]$ and $y_i$ are class labels. First, a fully connected ReLU network f is trained on both the original images $X_i$ and their rescaled versions $\alpha X_i$, where $\alpha \in (0,1)$, to create “headroom” for linear combinations. Then, the null space $N\left(f\right)$ is obtained by computing the singular value decomposition (SVD) of the first hidden layer weight matrix $W_1=US{V}^T$ and extracting the columns of V associated with zero singular values, which form an orthonormal basis for the null space $N\left(f\right)$. These columns form the matrix $V_2$. If H and C are column vectors in the form of neural network inputs, we compute $H_{\perp }$ and $\widehat{C}$ as follows:

$$H_{\perp }=H-V_2{V}_2^{T}H,\widehat{C}=V_2{V}_2^{T}C,$$

where $V_2^{T}H$ and $V_2^{T}C$ give the coefficients (dot products) of H and C along the null space basis vectors, respectively. Multiplying by $V_2$ reconstructs the projection within the null space. Thus, $\widehat{C}$ is composed only of null space vectors, while $H_{\perp }$ has all null space components removed. Finally, we construct the stego image $S={\alpha }_1{H}_{\perp }+{\alpha }_2\widehat{C}$. Note that the resulting stego image S must remain within the normalized range $[-1, 1]$, consistent with the range of the neural network inputs. This condition constrains the choice of ${\alpha }_1$ and ${\alpha }_2$: ${\alpha }_1$ cannot be too large (otherwise some entries of S may fall outside $[-1, 1]$) or too small (otherwise the hidden component becomes too weak to carry sufficient information from the hidden image). Also, guaranteeing the visual quality of the cover image requires ${\alpha }_2$ to be as large as possible.

In this example, the network classifies S as the digit eight based on the hidden image H while ignoring the visual features of the cover image C. So, for the example in Figure 3, the stego image looks like an “8”, but when presented to the NN, it is classified as a “6”.

In the next section, we will show experiments using the MNIST, Fashion-MNIST (FMNIST), and Extended MNIST (EMNIST) data sets. For simplification, we present experiment results using ${\alpha }_1=0.2$. Other values of ${\alpha }_1$ may also be used as long as the stego image remains within the range $[-1, 1]$. Further discussion on the choice of parameters ${\alpha }_1$ and ${\alpha }_2$ can be found in Appendix D.

4. Experimental Results

All experiments presented in this section were implemented in TensorFlow. The data sets used in these experiments include MNIST [32], Fashion-MNIST [33], Extended MNIST (EMNIST) [34], and CIFAR-10 [35].

4.1. Hide the Digits

In this section, we use the MNIST data set to conduct experiments in image steganography. For these experiments, we trained a (784, 32, 16, 10) − ReLU NN, i.e., the ReLU NN has $28\times 28$ images as the input vector ${28}^2=784$ in length, 32 nodes in the first hidden layer, 16 nodes in the second hidden layer, and 10 nodes in the output layer. The training was based on an expanded image training data set that included the original data set and the data set rescaled with ${\alpha }_1=0.2$, with a prediction accuracy of $99.79\%$ on the original training data. For the original training data correctly predicted, the average confidence level is $99.98\%$. When evaluated on the rescaled training data, this ReLU NN maintained a high prediction accuracy of $99.78\%$ with an average confidence of $99.77\%$ on correctly predicted data. Expanding the data set to include the rescaled training data slightly reduced the training accuracy; the accuracy remains high and still provides a large pool of correctly classified images for constructing steganographic images. Notably, this ReLU NN has a 752-dimensional null space. This large null space plays a crucial role in the steganographic capabilities of the network.

We then filter out only the correctly predicted images to create a new data set. This data set comprises a total of 50,000 images, with each class having 5000 examples. The (784, 32, 16, 10) − ReLU NN can correctly predict both original and rescaled data from this new data set. The main purpose of this process is to ensure that for any chosen hidden image H from the new data set, feeding $0.2H$ into the ReLU NN does not create scaling issues and yields a correct classification. Next, we will show some representative results with stego images produced by $S=0.2H_{\perp }+{\alpha }_2\widehat{C}$, where ${\alpha }_2$ can be chosen in the range of $(0, 1)$ and is generally set to around $0.5$.

Figure 4 and Figure 5 present stego images generated using the images from the new data set. For each set of three images, the first is the cover image, the second is the hidden image, and the third, the stego image, combines parts of the cover and the hidden image. Additionally, Figure 4 annotates the combination weights ${\alpha }_1, {\alpha }_2$ of stego images and the predictions and their corresponding confidence levels. In each case, the ReLU NN predicts the hidden digit with high confidence.

As shown in the figures, we can barely see the hidden digits in the stego images, which have patterns extremely similar to the cover images, even if the cover image is from another data set. However, these stego images are not predicted to be in the same classes as the cover images; rather, they are identified as the hidden images with high confidence. The cover image’s portion within the stego image falls entirely in the null space of the ReLU NN, giving the stego image a visible pattern that resembles the cover image (plus some noise-like structure) but makes no contribution to the prediction with the ReLU NN. On the other hand, the part of the hidden image included in the stego image appears as noise (as shown in Figure 3), but it is this portion that carries the most important information for prediction with the ReLU NN.

4.2. Results on Other Data Sets

This proposed image steganography method is general and can be applied to any image data set. In addition to the MNIST data set, we also applied our method to other image data sets: FMNIST, EMNIST, and CIFAR-10.

For the FMNIST data set, we trained a $(784,32,16,10)$-ReLU NN with a 752-dimensional null space. To generate stego images, we first created a new data set comprising both the correctly predicted original and rescaled images (also scaled by a factor of 0.2). This new data set has an average confidence of $99.74\%$ for the original images and $97.22\%$ for the rescaled images. Examples of stego images created from the new data set are shown in Figure 6 and Figure 7.

Similarly, as expected, the stego images have the look of cover images (as seen in the first column) but are recognized as the same categories as their corresponding hidden images (shown in the second column) with high confidence.

To continue this investigation, we also perform experiments on the EMNIST Balanced data set (Figure 8) and CIFAR-10 data set (Figure 9), where the same technique works. The figures suggest that the null space-based image steganography method is also applicable to more complicated and colorful images. To guarantee the capability of concealing an image within any chosen cover image, we can train a neural network model with a sufficiently large null space. As observed in the experiments, when simple digit or letter images are used as cover images, their null space components $\widehat{C}$ tend to preserve most of their visual information under projection, while more complex and colorful images, such as the images in the CIFAR-10 data set, may appear more “noisy” after being projected onto the null space, therefore requiring a larger null space to maintain visual fidelity.

4.3. Analysis of Reduced Confidence in Stego Images

While most stego images constructed by our method are classified the same as the hidden image with nearly 100% confidence, in a few cases, a reduced confidence is observed. In this regard, it is worthwhile to look at these outliers.

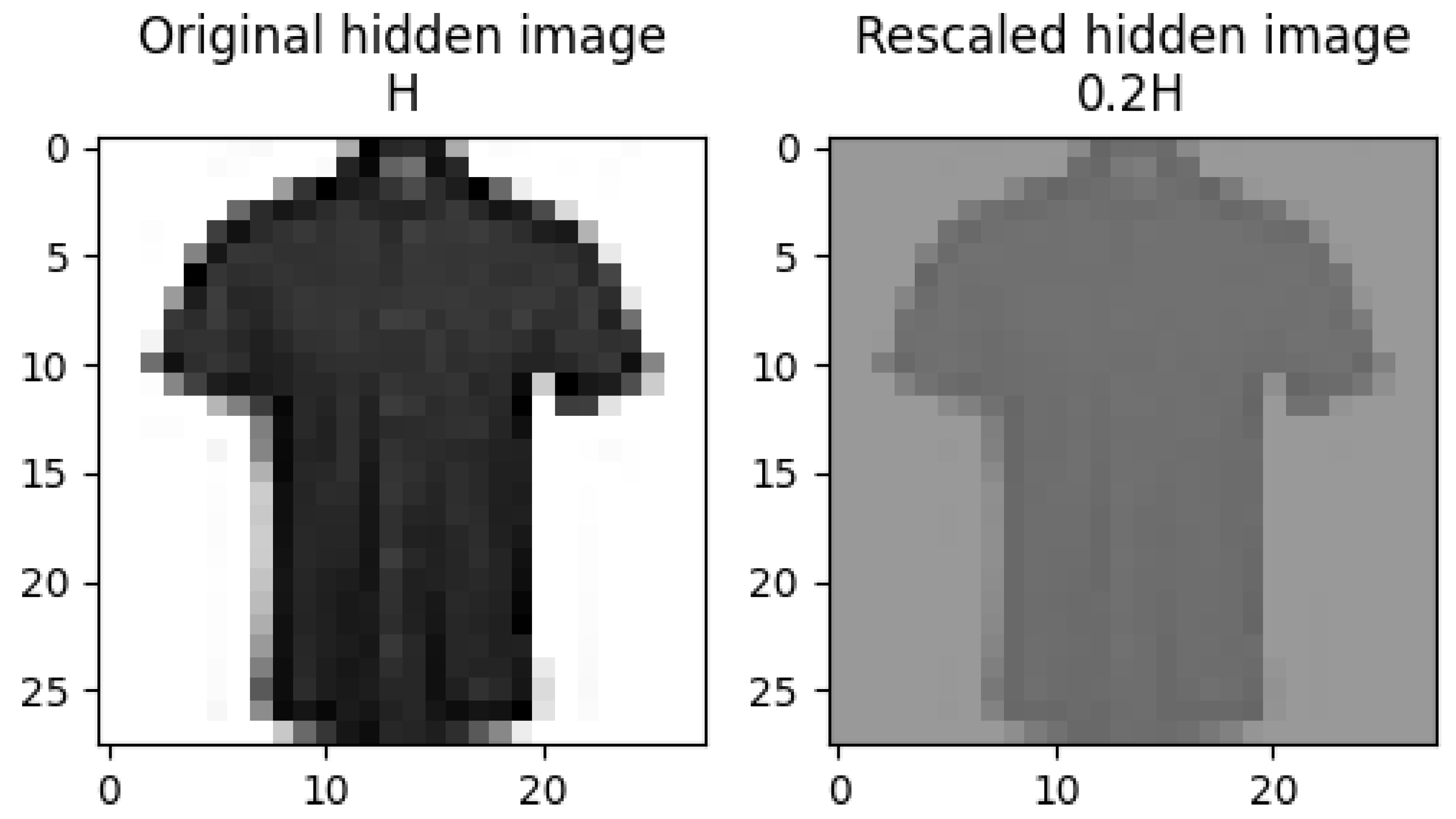
One such outlier result is shown in Figure 6a. While the original hidden image H is predicted to be a “shirt” with confidence close to 1, the stego image $S=0.2H_{\perp }+0.68\widehat{C}$ is predicted to be a “shirt” with a lower confidence of $86.4\%$. The reduced confidence level is caused by the rescaled hidden image. According to the null space method, the prediction and confidence level for the stego image S should align with those for $0.2H_{\perp }$ and, consequently, $0.2H$. Consistent with this analysis, the rescaled hidden image $0.2H$ is also predicted to be “shirt” with 86.4% confidence. Therefore, the confidence drop reflects the effect of rescaling rather than a limitation of the null space method.

Unlike the experiment with the MNIST data set, it is more common to see lower confidence stego image examples in the experiment with the FMNIST data set. In Figure 10, we compare the original hidden image H and rescaled hidden image $0.2H$ in Figure 6a. For the rescaled image $0.2H$, the NN gave a reduced confidence of $86.4\%$ for the correct prediction of “shirt”, but it also predicted the related category of “T-shirt/Top” with a confidence of $13.4\%$. As shown in Figure 10, the rescaling operation reduces contrast and leads to the loss of some visual details, which causes lower confidence. For instance, the buttons and collar cannot be clearly observed in the rescaled image, so it is also more likely to be identified as a “T-shirt/Top”.

Therefore, the achievement of high confidence in steganographic images depends on having “good” hidden images with high confidence on both original and rescaled data. Essentially, the prediction confidence level of the hidden images will be no better than the prediction confidence of the original images after rescaling has been applied.

5. Discussions and Conclusions

This study discusses the fundamental role of null space in NNs, the reliability issues it may introduce, and how it can be exploited. The null space is a structural property inherent to the architecture of the NN itself, which is independent of the input data. By extending the null space concept from linear transformations to complex NN architectures, we demonstrate that this hidden structure can lead to serious reliability concerns. More specifically, if a neural network has a high-dimensional null space, it remains vulnerable, no matter how well it is trained, because one can always construct inputs to fool the model. In this regard, CNNs tend to be more robust than FCNNs from the null space perspective, as their architectures typically induce a much smaller or even trivial null space. However, the null space property can also be used for beneficial applications, including but not limited to image steganography.

These findings have implications for model interpretability and reliability. The following discussion elaborates on what the NN actually "sees" and broader concerns like reliability in AI systems.

5.1. What We See and What NNs See

From the analysis and experimental results presented above, it is evident that NNs do not perceive visual information in the same way as humans. Figure 11 compares what we see and what the NN “sees”. After removing null space components, the remaining crucial parts for prediction have fewer visual patterns than their initial appearance. Without this, distinct neural networks would see the same image differently, even when they have null spaces of the same dimensions, as illustrated in Figure 12, where the null space orthogonal components of the same images are shown as they are seen by different NNs.

5.2. Null Space of NNs and Reliability Issue

Ball [36] pointed out that there are reproducibility and reliability issues with AI. Previously, studies have found that neural network models could pick up on irrelevant features to succeed in classification tasks, raising questions about their reliability. In this paper, the null space analysis on neural networks provides additional insights into these reliability concerns and shows that the NN may pick up on hidden features that are not just irrelevant but that are crafted to confuse the NN. In addition to being too focused on aligning with the particular patterns in the training data, the design of neural network architectures may also raise risks that cannot be solved by merely increasing the data set size. Importantly, it is the architecture that leads to the null space weaknesses shown in this paper.

In addition, stego images created by null space methods cannot be used to improve training. As described in [1], the adversarial example/image is a modified version of a clean image that is intentionally perturbed to mislead machine learning models, such as deep neural networks. Some studies have shown that it may be possible to harden NNs against adversarial attacks. Further, it was observed by Szegedy et al. that the robustness of deep neural networks against adversarial examples could be improved by adversarial training, where the idea is to include adversarial examples in the training data [3]. It is crucial to note that while adversarial examples using previous techniques may improve the training, they cannot solve the problem caused by the null space of a neural network. There are some interesting applications in adversarial attacks [4,37] that might be combined with null space ideas to produce an efficient, reliable way to fool neural networks, and this could be a fruitful direction for future research.

The null space analysis of NNs is not limited to the NNs in image classification tasks. In this study, image steganography is selected as an application to better visualize the impact of the null space. The existence of the null space, inherent in the neural network’s architecture, implies that one can always use the null space vectors to fool a neural network or the user of a neural network, at least when the input data projected onto the null space is close enough to the original to fool a human viewer. Recently, the development of large language models has advanced rapidly. However, these models sometimes produce incorrect or unreasonable outputs. Many researchers have focused on detecting and quantifying the extent of hallucinations in such models [38,39,40]. Through the analysis of the null space of neural networks, the null space may potentially be a contributing cause for these hallucinations. This also suggests a potential future direction for exploring the underlying reasons for hallucinations in large language models.