Highly Efficient and Light NTRU-Based Key Encapsulation Mechanisms with Small Moduli

Abstract

In this paper, we present CTRU-Light, an IND-CCA-secure key encapsulation mechanism (KEM) derived from NTRU and RLWE (and RLWR in variant) assumptions over power-of-two cyclotomic rings. Our CTRU-Light employs a compact NTT-compatible modulus $q=641$ while maintaining minimal public key and ciphertext dimensions with negligible error probability. Specifically, the design yields public key and ciphertext sizes of 1206 bytes under an error probability bound of $\le 2^{-110}$. When benchmarked against Kyber (NIST’s sole standardized KEM), CTRU-Light demonstrates 23.0–30.0% lower bandwidth consumption, accelerates key generation by at least 6.0%, and achieves over 1.3× speed enhancement in both encapsulation and decapsulation procedures.

1. Introduction

Most contemporary public-key cryptosystems depend on the computational difficulty of integer factorization or discrete logarithm problems. These mathematical challenges, however, become vulnerable to efficient resolution through Shor’s quantum algorithm, driving the advancement of post-quantum cryptography (PQC) [1].

The U.S. National Institute of Standards and Technology (NIST) PQC standardization initiative has categorized five principal classes of PQC primitives: code-based, hash-based, multivariate-based, isogeny-based, and lattice-based constructions [2]. Lattice-based approaches emerge as particularly advantageous due to their optimal balance between security assurances, communication economy, and operational efficiency [3].

Originally introduced in 1998, the NTRU cryptosystem [4] maintains its security integrity and continues to serve as a foundation for numerous cryptographic protocols. NTRU-based designs received consideration during the NIST PQC competition, exemplified by the Falcon signature scheme [5,6] and NTRUEncrypt KEMs [7]. While Kyber (an MLWE-based construction) ultimately secured standardization, NTRU persists within established standards including IEEE 1363.1 [8] and X9.98 [9], alongside implementations in protocols such as OpenSSH [10].

Developing an NTRU-based KEM that surpasses existing solutions in performance metrics presents an ongoing research challenge [11]. Prior solutions exhibit limitations in design efficiency despite supporting compact moduli and reduced bandwidth. Building upon foundational work in high-dimensional lattice constructions, this paper introduces CTRU-Light—a novel variant engineered to maintain robust security and operational efficiency while utilizing a significantly minimized modulus ($q=641$). In the post-quantum era, ensuring the confidentiality and integrity of sensitive data in critical sectors like healthcare is a major challenge [12], for which our proposed algorithm offers an effective security mechanism.

Our Contributions

In detail, our contributions are summarized as follows:

• We introduce CTRU-Light, a cryptographic framework derived from the CTRU foundation [13]. This construction integrates an IND-CPA-secure public-key encryption scheme with an IND-CCA-secure key encapsulation mechanism, leveraging NTRU and RLWE assumptions over power-of-two cyclotomic rings.
• We establish a parameter configuration for CTRU-Light targeting NIST security level I. This design employs a compact NTT-compatible modulus $q=641$, achieving minimized public key and ciphertext dimensions with negligible error probabilities. A compression methodology [14] further reduces key and ciphertext sizes by 5.7%.
• We develop C-based implementations of CTRU-Light and conduct comprehensive benchmarking against leading KEM schemes. Experimental validation confirms that CTRU-Light surpasses NEV [15] in security robustness, bandwidth efficiency, and error resilience. Compared to Kyber, CTRU-Light achieves 23.0–30.0% bandwidth reduction with computational speedups exceeding 1.3× in encapsulation/decapsulation and 6.0% in key generation.

2. Preliminaries

2.1. Notations and Definitions

Let n and q be positive integers. Denote ${\mathbb{Z}}_q=\mathbb{Z}/q\mathbb{Z}\cong \{0,1,\dots ,q-1\}$. Define the power-of-two cyclotomic rings $\mathcal{R}=\mathbb{Z}\left[x\right]/(x^n+1)$ and ${\mathcal{R}}_q={\mathbb{Z}}_q\left[x\right]/(x^n+1)$, where $n=2^k$ for some integer k. Elements in these rings are polynomials, denoted $f,g\in \mathcal{R}$ or ${\mathcal{R}}_q$.

Each polynomial $f\in \mathcal{R}$ (or ${\mathcal{R}}_q$) can be written as:

$$f\left(x\right)=\sum _{i=0}^{n-1}{f}_i{x}^i,\mathrm{where}{f}_i\in \mathbb{Z}(\mathrm{or}{\mathbb{Z}}_q).$$

We adopt notation from [13]. For a number $r\in \mathbb{R}$ and modulus q, define:

• $r^{\prime }=rmod\pm q$: the representative of r in $[-{\displaystyle \frac{q}{2}},{\displaystyle \frac{q}{2}})$
• $r^{\prime }=rmodq$: the representative of r in $[0,q)$
• ${\parallel w\parallel }_{q,\infty }=|wmod\pm q|$: ${\ell }_{\infty }$ norm
• ${\parallel w\parallel }_{q,2}=\sqrt{{\sum }_i{\parallel w_i\parallel }_{q,\infty }^2}$: ${\ell }_2$ norm for vector w

• Random sampling notations.

• $x\leftarrow D$: sample x from distribution D.
• $x\stackrel{\$}{\leftarrow }D$: uniform random sample from finite set D.

• Distributions.

• Centered Binomial Distribution ${\mathcal{B}}_{\eta }$: Sample $(a_1,\dots ,a_{\eta },b_1,\dots ,b_{\eta })\stackrel{\$}{\leftarrow }{\{0,1\}}^{2\eta }$ and output ${\sum }_{i=1}^{\eta }(a_i-b_i)$.
• Ternary Distribution ${\mathcal{T}}_{\mu }$: $x\in \{-1,0,1\}$ with $Pr[x=\pm 1]=\mu$ and $Pr[x=0]=1-2\mu$.

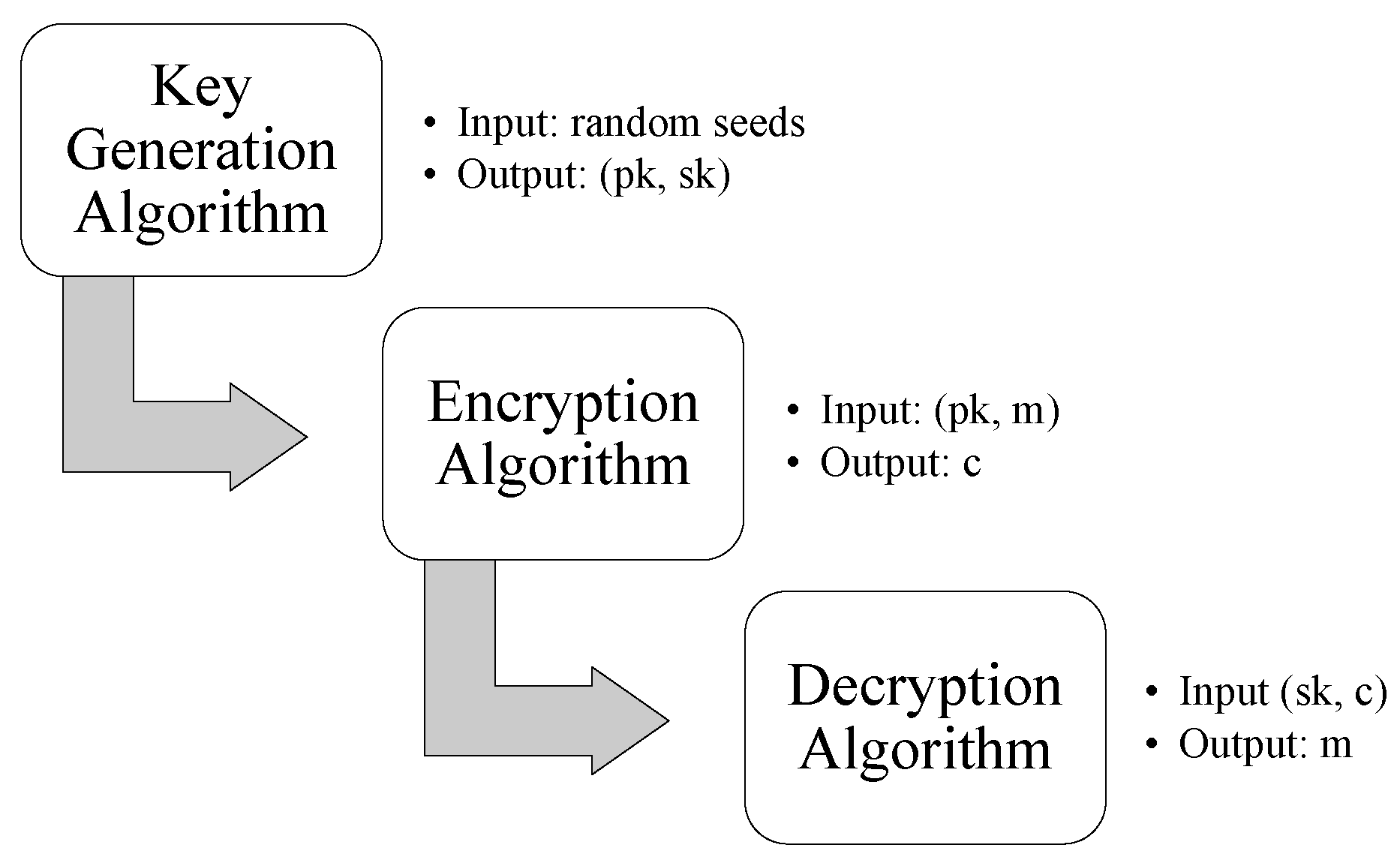
2.2. Cryptographic Primitives

Public-Key Encryption (PKE).

A PKE scheme is a triple $(\mathtt{KeyGen},\mathtt{Enc},\mathtt{Dec})$.

• $(\mathtt{pk},\mathtt{sk})\leftarrow \mathtt{KeyGen}\left(\right)$
• $\mathtt{ct}\leftarrow \mathtt{Enc}(\mathtt{pk},m)$
• $m\leftarrow \mathtt{Dec}(\mathtt{sk},\mathtt{ct})$ or ⊥

The error probability $\delta$ is:

$$\delta ={\mathbb{E}}_{(\mathtt{pk},\mathtt{sk})\leftarrow \mathtt{KeyGen}}\left[\underset{m\in \mathcal{M}}{max}Pr[\mathtt{Dec}(\mathtt{sk},\mathtt{Enc}(\mathtt{pk},m))\ne m]\right]$$

Key Encapsulation Mechanism (KEM).

A KEM scheme is $(\mathtt{KeyGen},\mathtt{Encaps},\mathtt{Decaps})$ with key space $\mathcal{K}$.

$$\begin{array}{cc}\hfill & (\mathtt{pk},\mathtt{sk})\leftarrow \mathtt{KeyGen}\left(\right),(\mathtt{ct},K)\leftarrow \mathtt{Encaps}\left(\mathtt{pk}\right),\hfill \\ \hfill & K^{\prime }\leftarrow \mathtt{Decaps}(\mathtt{sk},\mathtt{ct})\in \mathcal{K}\cup \{\perp \}\hfill \end{array}$$

The error probability is:

$$\delta =Pr\left[\mathtt{Decaps}\right(\mathtt{sk},\mathtt{ct})\ne K]$$

2.3. Hardness Assumptions

Definition 1

(NTRU Assumption [4]). Let Ψ be a distribution over $\mathcal{R}$ and $p\in \mathcal{R}$ an invertible element. Sample $f^{\prime }$, $g\leftarrow \Psi$, set $f=p{f}^{\prime }+1$, and $h=g/f$. The decisional NTRU problem is to distinguish h from uniform in $\mathcal{R}$. The advantage of adversary $\mathcal{A}$ is:

$${Adv}_{NTRU}^{\mathcal{R},\Psi }\left(\mathcal{A}\right)=\left|Pr\left[\mathcal{A}\right(h)=1]-Pr\left[\mathcal{A}\right(u)=1]\right|,$$

where $u\stackrel{\$}{\leftarrow }\mathcal{R}$.

Definition 2

(RLWE Assumption [16]). Let Ψ be a distribution over $\mathcal{R}$. The decisional RLWE problem is to distinguish:

$$(h,c=hr+e)from(h,u),wherer,e\leftarrow \Psi ,u\stackrel{\$}{\leftarrow }\mathcal{R}$$

Definition 3

(RLWR Assumption [17]). Let $q>p\ge 2$ and Ψ be a distribution over $\mathcal{R}$. Define $c=⌊{\displaystyle \frac{p}{q}}·hr⌉modp$ for $r\leftarrow \Psi$. The RLWR problem is to distinguish:

$$(h,c)from(h,u),whereh\stackrel{\$}{\leftarrow }{\mathcal{R}}_q,u\stackrel{\$}{\leftarrow }{\mathcal{R}}_p$$

2.4. Number Theoretic Transform (NTT)

The Number Theoretic Transform (NTT) is a special case of the Fast Fourier Transform (FFT) defined over a finite field. It is widely used for efficient polynomial multiplication due to its quasi-linear time complexity $\mathcal{O}(nlogn)$.

Given polynomials f and g in ${\mathcal{R}}_q$, their product can be efficiently computed using:

$$f·g=\mathrm{INTT}\left(\mathrm{NTT}\right(f)\circ \mathrm{NTT}(g\left)\right),$$

where ∘ denotes point-wise multiplication, and INTT is the inverse transform.

2.5. Scalable $E_8$ Lattice Code

We use the scalable $E_8$ lattice code defined in [13], which is constructed from the 8-dimensional Extended Hamming Code. For a 4-bit input $k\in {\{0,1\}}^4$, the encoding algorithm outputs a lattice point $\lambda ·(kHmod2)$, where H is a standard generator matrix. The decoding algorithm takes $v\in {\mathbb{R}}^8$, solves the closest vector problem in $E_8$, and returns k. From [13], Theorem 1: decoding succeeds if the Euclidean norm of the error vector, computed after reducing coefficients into $[-\lambda ,\lambda )$, is less than $\lambda$.

2.6. The CTRU Framework

CTRU, introduced by Liang et al. [13], is a framework for constructing compact KEMs from NTRU lattices. Its design philosophy differs from module-based schemes like Kyber by building primitives directly over a single polynomial ring ${\mathcal{R}}_q$. This architectural choice is central to its efficiency and compactness.

Core Structure: A standard CTRU scheme consists of a public key $h=g/f\in {\mathcal{R}}_q$ and a ciphertext $c=\lfloor {\displaystyle \frac{q_2}{q}}(hr+e+M)\rceil \in {\mathcal{R}}_{q_2}$, where $f,g,r,e$ are polynomials and M is the encoded message. The core advantage lies in this simplicity: both the public key and ciphertext are single ring elements, whereas Module-LWE schemes require vectors of polynomials, increasing bandwidth.

Advantages and Trade-offs: Compared to other NTRU/RLWR-based schemes, CTRU’s primary advantage is its communication efficiency. The single-polynomial structure inherently leads to smaller public keys and ciphertexts. However, this simplicity presents a trade-off. While module-based schemes can easily scale to different security levels by adjusting the module’s rank (i.e., the number of polynomials in vectors), CTRU’s security scaling is primarily tied to the ring dimension n. This makes parameterization for a wide range of security levels less flexible. Our work, CTRU-Light, builds on this compact foundation, further optimizing it with a smaller modulus and refined techniques.

3. Our Scheme: CTRU-Light

We now introduce CTRU-Light, comprising an IND-CPA-secure public-key encryption scheme (CTRU-Light.PKE) and an IND-CCA-secure key encapsulation mechanism (CTRU-Light.KEM). Figure 1 provides a high-level overview of the scheme’s operations.

3.1. Proposal Description

The CTRU-Light.PKE scheme is defined in Algorithms 1–5. Let n denote a power of two and q an NTT-compatible prime. We define $p=1-x^{512}$. Secret polynomials $f^{\prime },g$ are sampled from distribution ${\Psi }_1$, while randomness $r,e$ originate from ${\Psi }_2$. Messages $m\in \mathcal{M}$ are represented as binary polynomials of degree 255 ($\left|m\right|=256$).

Algorithm 1 CTRU-Light.PKE.KeyGen$\left(1^{\kappa }\right)$

1: repeat 2:     $f^{\prime },g\leftarrow {\Psi }_1$ 3:     $f:=p{f}^{\prime }+1$ 4: until $f^{-1}$ exists in ${\mathcal{R}}_q$ 5: $h:=g/f$ 6: return $(\mathtt{pk}:=h,\mathtt{sk}:=f)$

Algorithm 2 CTRU-Light.PKE.Enc$(\mathtt{pk}=h,m\in \mathcal{M})$

1: $r,e\leftarrow {\Psi }_2$ 2: $c:=hr+e+\mathtt{PolyEncode}\left(m\right)$ 3: return c

Algorithm 3 CTRU-Light.PKE.Dec$(\mathtt{sk}=f,c)$

1: $\tilde{m}:=c·f$ 2: $m:=\mathtt{PolyDecode}\left(\tilde{m}\right)$ 3: return m

Algorithm 4 PolyEncode$(m={\sum }_{i=0}^{\left|m\right|-1}{m}_i{x}^i\in \mathcal{M})$

1: for $i=0$ to $\left|m\right|/4-1$ do 2:     $k_i:=(m_{4i},m_{4i+1},m_{4i+2},m_{4i+3})\in {\{0,1\}}^4$ 3:     $(v_{8i},\dots ,v_{8i+7}):={\mathtt{Encode}}_{E_8}\left(k_i\right)$ 4: end for 5: $v:={\sum }_{i=0}^{2\left|m\right|-1}{v}_i{x}^i$ 6: return v

Algorithm 5 PolyDecode$(v={\sum }_{i=0}^{n-1}{v}_i{x}^i\in {\mathcal{R}}_q)$

1: for $i=0$ to $\left|m\right|/4-1$ do 2:     $x_i:=(v_{8i},\dots ,v_{8i+7})\in {\mathbb{R}}^8$ 3:     $(m_{4i},m_{4i+1},m_{4i+2},m_{4i+3}):={\mathtt{Decode}}_{E_8}\left(x_i\right)$ 4: end for 5: $m:={\sum }_{i=0}^{\left|m\right|-1}{m}_i{x}^i$ 6: return m

3.2. CTRU-Light.KEM Construction

We employ the ${\mathtt{FO}}_{\perp }^{\mathtt{ID}\left(pk\right),m}$ transform [18] to derive IND-CCA security from our IND-CPA secure PKE. Let $\iota ,\gamma \ge 256$ provide adequate security. Define $H:{\{0,1\}}^{*}\to \mathcal{K}\times \mathtt{COINS}$, where $\mathcal{K}$ is the shared key domain and COINS is the PKE randomness domain. Let $H_1$ extract $\mathcal{K}$ from H’s output, and $\mathtt{ID}:\mathtt{PK}\to {\{0,1\}}^{\gamma }$ as a deterministic identifier. To provide a clear, high-level overview of our KEM constructions, the operational flow is visualized in Figure 2. This flowchart details the three core procedures: key generation (KeyGen), encapsulation (Encaps), and decapsulation (Decaps). Given that the CTRU-Light and CTRU-Light-RLWR schemes are structurally identical aside from the handling of ciphertext, we present a unified diagram for conciseness. The steps marked in red are specific to the CTRU-Light-RLWR variant. All other steps in the process are common to both schemes.

Figure 2. Unified flowchart of the KeyGen, Encaps, and Decaps steps for CTRU-Light.KEM, which are formally described in Algorithms 6–8. The steps highlighted in red are unique to the CTRU-Light-RLWR variant. The remaining steps are identical for both schemes.

Figure 2. Unified flowchart of the KeyGen, Encaps, and Decaps steps for CTRU-Light.KEM, which are formally described in Algorithms 6–8. The steps highlighted in red are unique to the CTRU-Light-RLWR variant. The remaining steps are identical for both schemes.

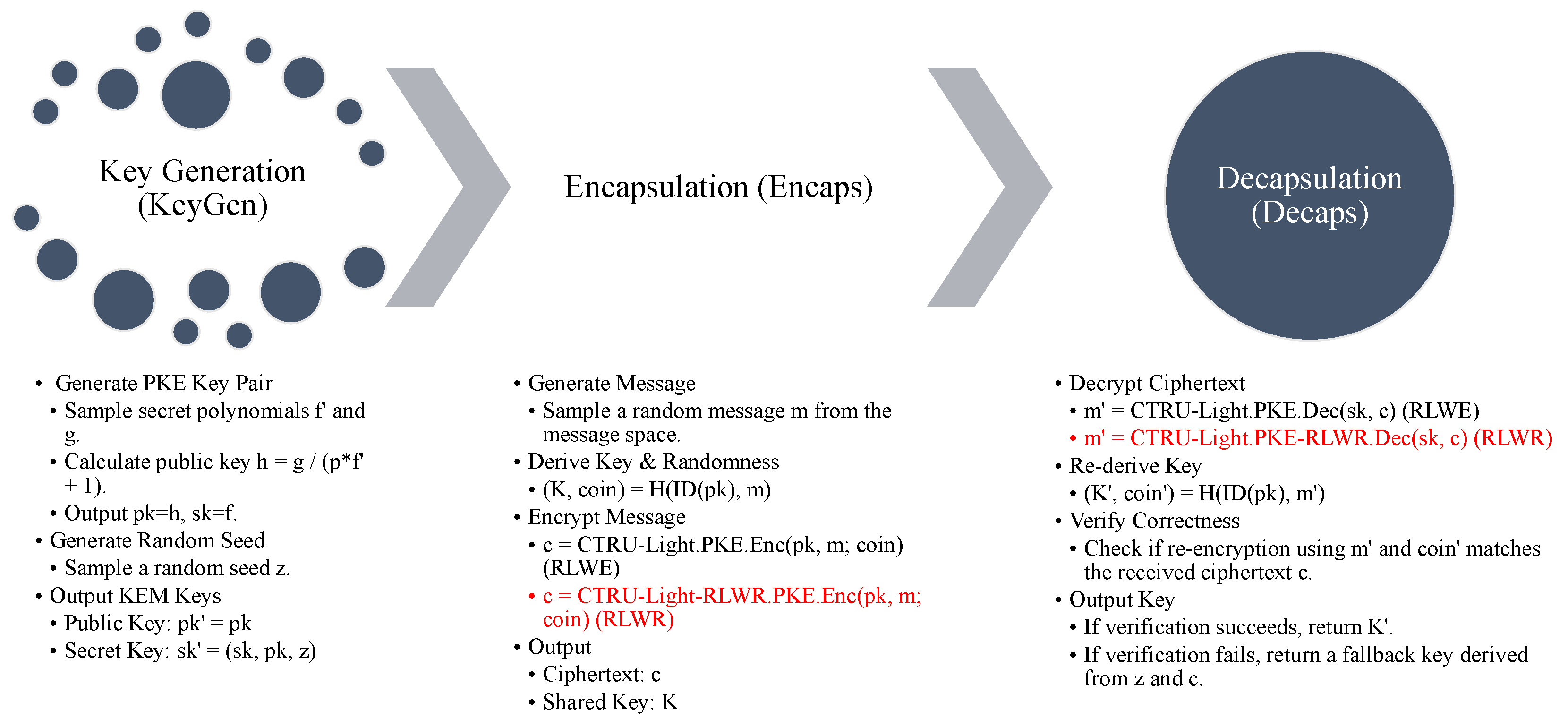
Algorithm 6 CTRU-Light.KEM.KeyGen$\left(1^{\kappa }\right)$

1: $(\mathtt{pk},\mathtt{sk})\leftarrow \mathtt{CTRU}-\mathtt{Light}.\mathtt{PKE}.\mathtt{KeyGen}\left(1^{\kappa }\right)$ 2: $z\stackrel{\$}{\leftarrow }{\{0,1\}}^{\iota }$ 3: return $({\mathtt{pk}}^{\prime },{\mathtt{sk}}^{\prime }):=(\mathtt{pk},(\mathtt{sk},\mathtt{pk},z))$

Algorithm 7 CTRU-Light.KEM.Encaps$\left({\mathtt{pk}}^{\prime }\right)$

1: $m\stackrel{\$}{\leftarrow }\mathcal{M}$ 2: $(K,\mathtt{coin}):=H\left(\mathtt{ID}\right(\mathtt{pk}),m)$ 3: $c:=\mathtt{CTRU}-\mathtt{Light}.\mathtt{PKE}.\mathtt{Enc}(\mathtt{pk},m;\mathtt{coin})$ 4: return $(c,K)$

Algorithm 8 CTRU-Light.KEM.Decaps$({\mathtt{sk}}^{\prime },c)$

1: $m^{\prime }:=\mathtt{CTRU}-\mathtt{Light}.\mathtt{PKE}.\mathtt{Dec}(\mathtt{sk},c)$ 2: $(K^{\prime },{\mathtt{coin}}^{\prime }):=H(\mathtt{ID}\left(\mathtt{pk}\right),m^{\prime })$ 3: $\tilde{K}:=H_1(\mathtt{ID}\left(\mathtt{pk}\right),z,c)$ 4: if $m^{\prime }\ne \perp$ and $c=\mathtt{CTRU}-\mathtt{Light}.\mathtt{PKE}.\mathtt{Enc}(\mathtt{pk},m^{\prime };{\mathtt{coin}}^{\prime })$ then 5:      return $K^{\prime }$ 6: else 7:      return $\tilde{K}$ 8: end if

3.3. Correctness Analysis

Correctness hinges on the noise term $gr+ef+s{f}^{\prime }$ remaining small enough for the $E_8$ decoder to function correctly. This is ensured with high probability by the small coefficients of the sampled polynomials. The detailed proof sketch can be found in the original manuscript.

4. Parameter Sets

Table 1. Parameter configurations for CTRU-Light.

n	q	$({\mathbf{\Psi }}_1,{\mathbf{\Psi }}_2)$	$\left|\mathit{pk}\right|$	$\left|\mathit{ct}\right|$	B.W.	NTRU-(C, Q)	RLWE-(C, Q)	$\mathit{\delta }$
512	641	$(B_1,B_1)$	603	603	1206	(129,117)	(129,117)	$2^{-113}$

summarizes the cryptographic parameters for our CTRU-Light scheme, targeting NIST security level I. All size measurements are reported in bytes.

5. Provable Security Reduction

Our security analysis establishes that CTRU-Light.PKE achieves IND-CPA security under both the NTRU and RLWE assumptions.

Theorem 1

(IND-CPA security of CTRU-Light.PKE). For any probabilistic polynomial-time adversary $\mathsf{A}$, there exist adversaries $\mathsf{B}$ and $\mathsf{C}$ with comparable running times satisfying:

$${\mathbf{Adv}}_{\mathrm{CTRU}-\mathrm{Light}.\mathrm{PKE}}^{\mathrm{IND}-\mathrm{CPA}}\left(\mathsf{A}\right)\le {\mathbf{Adv}}_{{\mathcal{R}}_q,{\Psi }_1}^{\mathrm{NTRU}}\left(\mathsf{B}\right)+{\mathbf{Adv}}_{{\mathcal{R}}_q,{\Psi }_2}^{\mathrm{RLWE}}\left(\mathsf{C}\right).$$

The proof follows a standard game-hopping argument. The IND-CCA security of CTRU-Light.KEM follows directly from the generic ${\mathrm{FO}}_{ID\left(pk\right),m}^f$ transformation [19] in the quantum random oracle model.

6. Concrete Security

We analyze the concrete security against the primal attack, which formulates cryptanalysis as a unique-Short Vector Problem (u-SVP) [20,21]. We use the core-SVP methodology [22] to estimate the costs of solving u-SVP using BKZ algorithms, with cost models of $2^{0.292b}$ (classical) and $2^{0.265b}$ (quantum) [23]. Our security estimates derive from adapted Python implementations of [13,24], with results in Table 1. We omit analysis of dual and overstretched NTRU attacks [25,26] as they are not practical for our parameter choices.

7. RLWR-Based Variant: CTRU-Light-RLWR

This section introduces CTRU-Light-RLWR, which uses rounding to further compress ciphertexts. The modified encryption and decryption procedures appear in Algorithms 9 and 10.

Algorithm 9 CTRU-Light-RLWR.PKE.Enc($pk=h$, $m\in \mathcal{M}$)

1: $r\leftarrow {\Psi }_2$ 2: $c:=\lfloor {\displaystyle \frac{q_2}{q}}(hr+\mathrm{PolyEncode}\left(m\right))\rceil mod{q}_2$ 3: return c

Algorithm 10 CTRU-Light-RLWR.PKE.Dec($sk=f$, c)

1: $\tilde{c}:=\lfloor {\displaystyle \frac{q}{q_2}}c\rceil modq$ 2: $\tilde{m}:=\tilde{c}f$ 3: $m:=\mathrm{PolyDecode}\left(\tilde{m}\right)$ 4: return m

The IND-CPA security of this variant reduces to the NTRU and RLWR assumptions.

Table 2. Parameter configuration for CTRU-Light-RLWR.

n	q	${\mathit{q}}_2$	$({\mathbf{\Psi }}_1,{\mathbf{\Psi }}_2)$	$\left|\mathit{pk}\right|$	$\left|\mathit{ct}\right|$	B.W.	NTRU-(C, Q)	RLWR-(C, Q)	$\mathit{\delta }$
512	641	$2^8$	$(B_1,B_1)$	603	512	1115	(129,117)	(130,118)	$2^{-102}$

presents its optimized parameter configuration.

8. Implementation Details

8.1. Polynomial Compression Techniques

We employ space-efficient compression for public key polynomials h [14]. For coefficient pairs $(h_i,h_{i+1})$, we compute $h_i+q·h_{i+1}mod{q}^2$. This technique leverages the 10-bit representation of $q=641$ coefficients, saving 37 bytes (5.7% reduction) per polynomial for $n=512$. The computational overhead of these compression and decompression operations is negligible. They primarily involve bitwise shifts and additions, which are orders of magnitude faster than the dominant operations in the scheme, such as NTT-based polynomial multiplication and SHA-3 hashing. Therefore, their impact on the overall performance benchmarks is minimal.

8.2. Optimized NTT Arithmetic

We implement incomplete NTT transformations for polynomial multiplication [27], as $q=641$ precludes full NTT for $n=512$. We exploit the property $q\equiv 1mod128$ to apply 6 levels of radix-2 FFT, decomposing the computation into products in 8-dimensional rings, which are then handled by optimized schoolbook and Karatsuba algorithms.

8.3. Cryptographic Primitives

We instantiate all hash functions using SHA-3 primitives (SHA3-512, SHAKE-256) for hashing, key derivation, and randomness expansion.

9. Performance Evaluation and Comparative Analysis

We present benchmarking results for our C implementations against prominent lattice-based KEMs.

Table 3. Comparative analysis of KEM schemes.

Scheme	Assumptions	n	q	$\left|\mathit{pk}\right|$	$\left|\mathit{ct}\right|$	B.W.	(C, Q)	$\mathit{\delta }$
CTRU-Light	NTRU, RLWE	512	641	603	603	1206	(129,117)	$2^{-113}$
CTRU-Light-RLWR	NTRU, RLWR	512	641	603	512	1115	(129,117)	$2^{-102}$
NEV	NTRU, RLWE	512	769	615	615	1230	(120,109)	$2^{-138}$
Kyber-512	MLWE	512	3329	800	768	1568	(118,107)	$2^{-139}$

provides a comparative analysis of the fundamental parameters of these schemes. The performance of these schemes is dominated by three main components: polynomial multiplication (typically via NTT), cryptographic hashing, and random sampling from specified distributions. The asymptotic complexity of the core multiplication operation is $O(nlogn)$. While a detailed breakdown of cycles per operation is highly platform-dependent, the total cycle counts presented in

Table 4. Computational performance (kilo cycles).

Scheme	KeyGen	Encaps	Decaps
CTRU-Light-512	59.5	43.5	85.0
CTRU-Light-RLWR-512	60.0	41.9	77.8
Kyber-512	65.0	72.3	111.7
Saber-512 [28]	35.0	40.6	55.0

provide a holistic and practical measure of the overall efficiency.

Benchmarks were conducted on an Intel Core i7-10510U @ 2.3GHz running Ubuntu 20.04 LTS with gcc 9.4.0 and flags -O3 -march=native.

9.1. Comparison with NEV

When evaluating against NEV, CTRU-Light demonstrates measurable improvements. It reduces total bandwidth by approximately 2% due to the smaller modulus and enhanced compression. From a security perspective, CTRU-Light provides stronger theoretical guarantees, offering 9-bit and 8-bit improvements in classical and quantum security estimates, respectively, positioning it as a more robust alternative.

9.2. Comparison with Kyber

The comparative analysis with Kyber reveals several fundamental advantages of CTRU-Light. It reduces bandwidth requirements by 23%, primarily due to its single-polynomial structure compared to Kyber’s matrix-based approach. This also translates to performance benefits, with 1.6× faster encapsulation and 1.3× faster decapsulation. CTRU-Light also provides 11-bit and 10-bit stronger security in classical and quantum settings, respectively.

This highlights a key design trade-off in lattice-based cryptography. Kyber’s Module-LWE framework offers high flexibility, allowing security levels to be scaled by changing the module’s dimensions (e.g., Kyber-512, Kyber-768, Kyber-1024). In contrast, CTRU-Light’s NTRU approach over a single ring offers a simpler, more compact design, leading to superior bandwidth and performance for a given ring dimension. For applications where bandwidth and speed are paramount, CTRU-Light presents a compelling alternative.

A consolidated summary of these comparisons, highlighting the trade-offs between bandwidth, performance, and failure probability, is presented in

Table 5. Comparative Analysis of KEMs at NIST Security Level I.

Scheme	Security Assumption	Bandwidth (Bytes)	Performance (k-Cycles)	Decryption Failure ($\mathit{\delta }$)
		PK + CT = Total	KeyGen/Encaps/Decaps
CTRU-Light-512	NTRU, RLWE	603 + 603 = 1206	59.5/43.5/85.0	$2^{-113}$
Kyber-512	MLWE	800 + 768 = 1568	65.0/72.3/111.7	$2^{-139}$
Saber-512	MLWR	672 + 736 = 1408	35.0/40.6/55.0	$2^{-120}$
NEV-512	NTRU, RLWE	615 + 615 = 1230	(See Note)	$2^{-138}$

Note on NEV Performance: The provided performance table does not include NEV. The NEV paper claims its KEM is 1.42–1.74× faster than Kyber. To avoid mixing data from different benchmarking environments, its specific values are omitted here.

.

10. Conclusions

This work presents CTRU-Light, a high-performance NTRU-based KEM that advances the state-of-the-art. Through careful parameter optimization, we have demonstrated that NTRU-based constructions can surpass MLWE-based alternatives like Kyber in both performance and bandwidth efficiency. The scheme’s compact size, efficient implementation, and strong security foundations position it as a viable candidate for deployment.

Future research directions should focus on expanding the scheme’s applicability beyond power-of-two cyclotomic rings, potentially exploring other cyclotomic fields that could provide better flexibility for intermediate security levels. Additional investigations into side-channel resistant implementations would further strengthen the scheme’s practical security profile. The extension of these techniques to other cryptographic primitives, particularly digital signatures, represents another promising avenue for research. These developments would help establish a more comprehensive NTRU-based cryptographic ecosystem, providing alternatives to current lattice-based standards. The results presented in this work suggest that NTRU-based constructions remain competitive in the post-quantum landscape and warrant continued investigation as the field evolves toward standardization and widespread adoption.