A Lower-Bounded Extreme Value Distribution for Flood Frequency Analysis with Applications
Abstract
1. Introduction
- Bounded support: It explicitly incorporates a lower threshold (), aligning with physical flood constraints [19].
- Entropy-optimal design: Parameters are derived via Shannon entropy maximization, ensuring robustness against skewness and outliers [20].
- Analytical tractability: Closed-form quantile functions (Section 2.5) enable efficient return period estimation, outperforming nested models in Vuong tests [21,22].
2. Model Derivation and Mathematical Properties
2.1. Construction of the Distribution and CDF
- A lower-bounded support ();
- Heavy-tailed behavior through the Fréchet structure;
- Parametric control over skewness and scale via and .
Relation to Existing Distributions
- Hydrological relevance: The parameter serves as a physical lower bound for streamflow, which is directly interpretable in practice. Furthermore, the log-logistic distribution—already recommended in several hydrological guidelines (e.g., in the UK) for modeling flood flows due to its flexibility—is embedded within the current construction.
- Extreme-value foundation: The model incorporates the Fréchet distribution, a classical law for block maxima and the limiting distribution for a wide class of parent processes. By integrating the log-logistic and Fréchet distributions within a log-odds framework, the LFLD retains the boundedness and practical applicability of the former while capturing the heavy-tail properties of the latter.
- Theoretical development: We provide formal proofs of asymptotic convergence to the two- and three-parameter Fréchet distributions (see Section 2.5), together with detailed derivations of the quantile function (see Section 2.6) and rigorous results on moment existence and entropy (see Section 3 and Section 4).
- Applied focus: In contrast to [26,27], whose emphasis was primarily on biomedical applications, this study establishes the LFLD as a valid extreme-value model for hydrological extremes. Simulation experiments and empirical case studies (see Section 5 and Section 6) demonstrate its ability to deliver reliable return level estimates in flood frequency analysis.
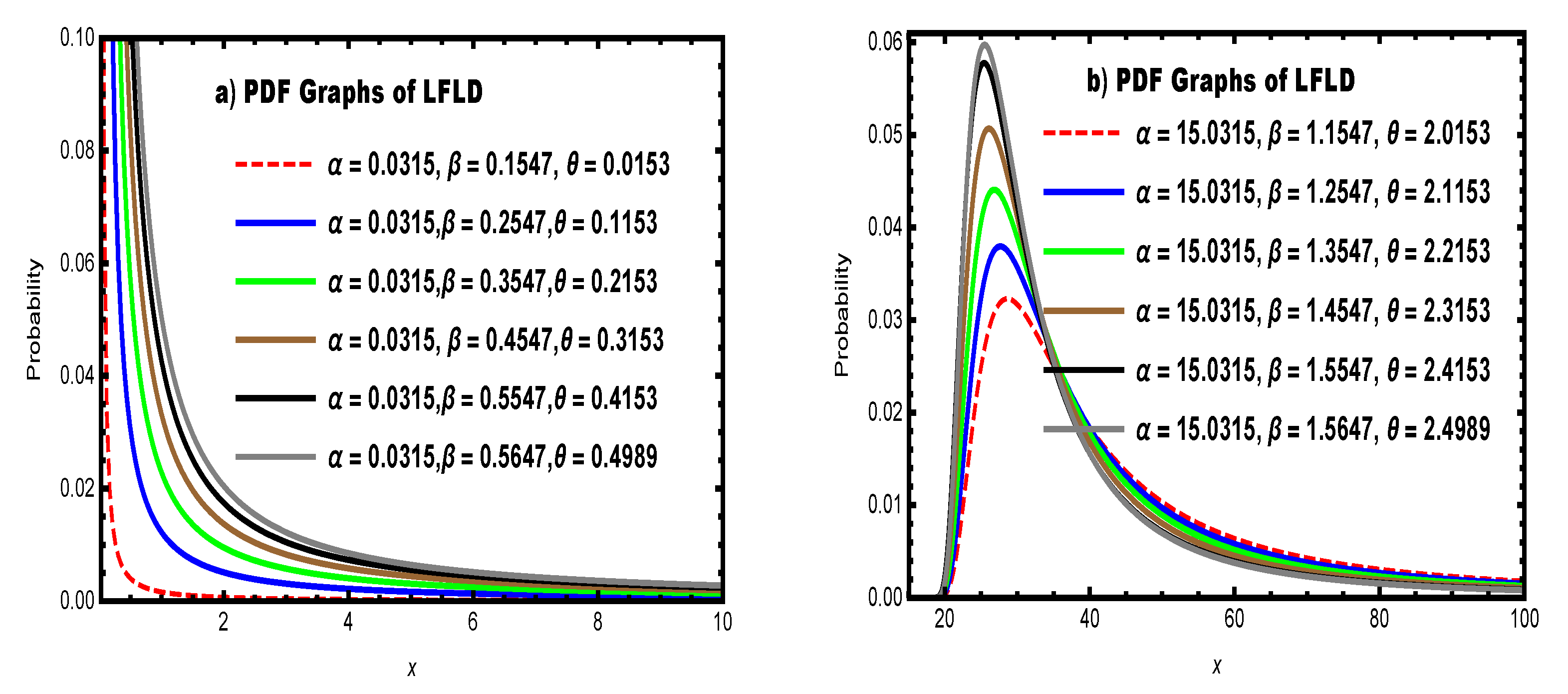
2.2. Probability Density Function (PDF)
- : Scale and lower bound;
- : Controls steepness and mode location;
- : Governs tail heaviness.
2.3. Shape Analysis and Mode
- : Reverse-J shape;
- moderate : Right-skewed unimodal;
- large : Sharper peak and heavier tail.
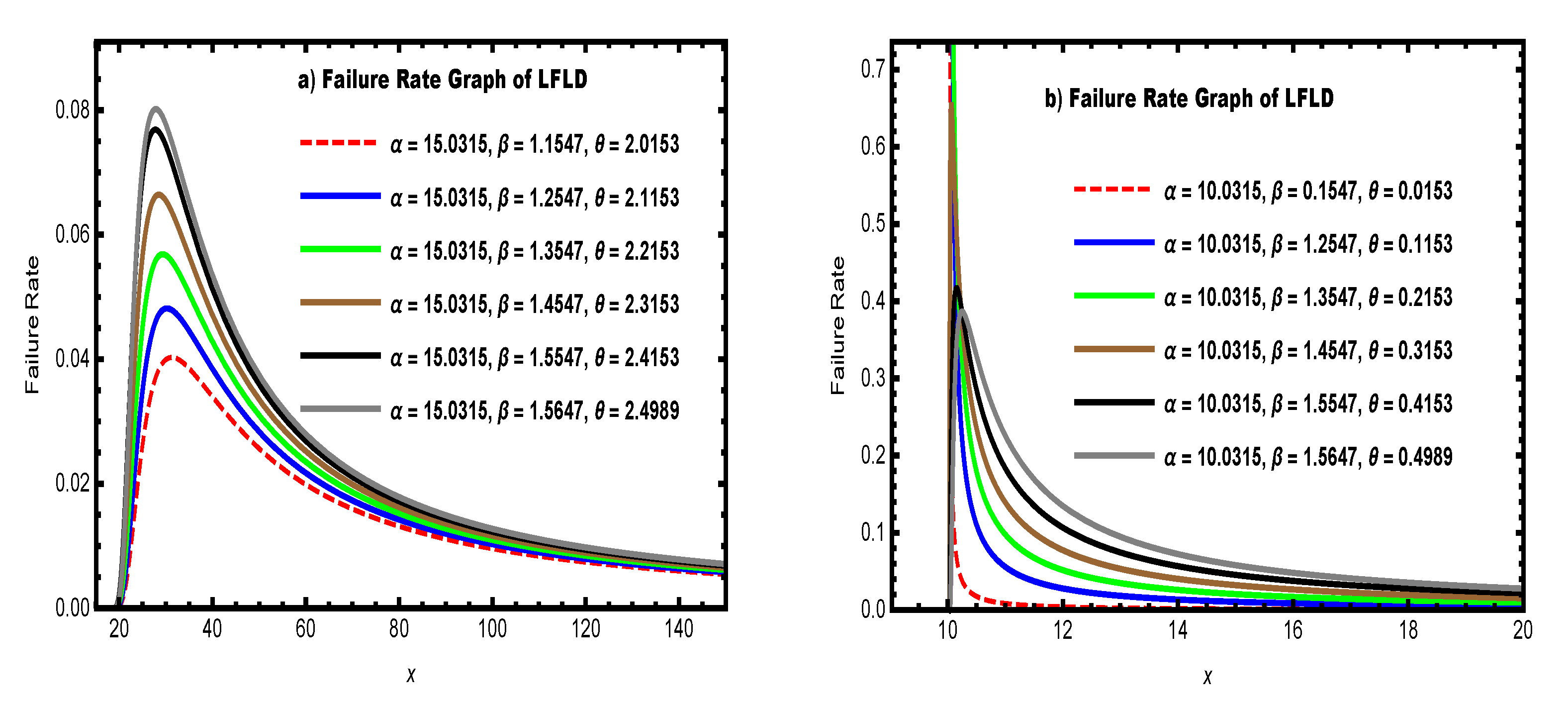
2.4. Survival and Hazard Rate Function
2.5. Asymptotic Behavior
- (i)
- Case ().
- (ii)
- Case ().
2.6. Quantile Function
- Monotonicity: is strictly increasing in p.
- Lower quantiles: As , we have , showing convergence to the lower bound.
- Upper quantiles: As , , reflecting the heavy-tailed behavior.
- Connection to Fréchet: The form of shows that it is an exponential transform of the Fréchet quantile in the latent variable , consistent with the asymptotics in Section 2.5.
- Return levels for flood recurrence intervals;
- Thresholds for risk evaluation;
- Hydrological design parameters.
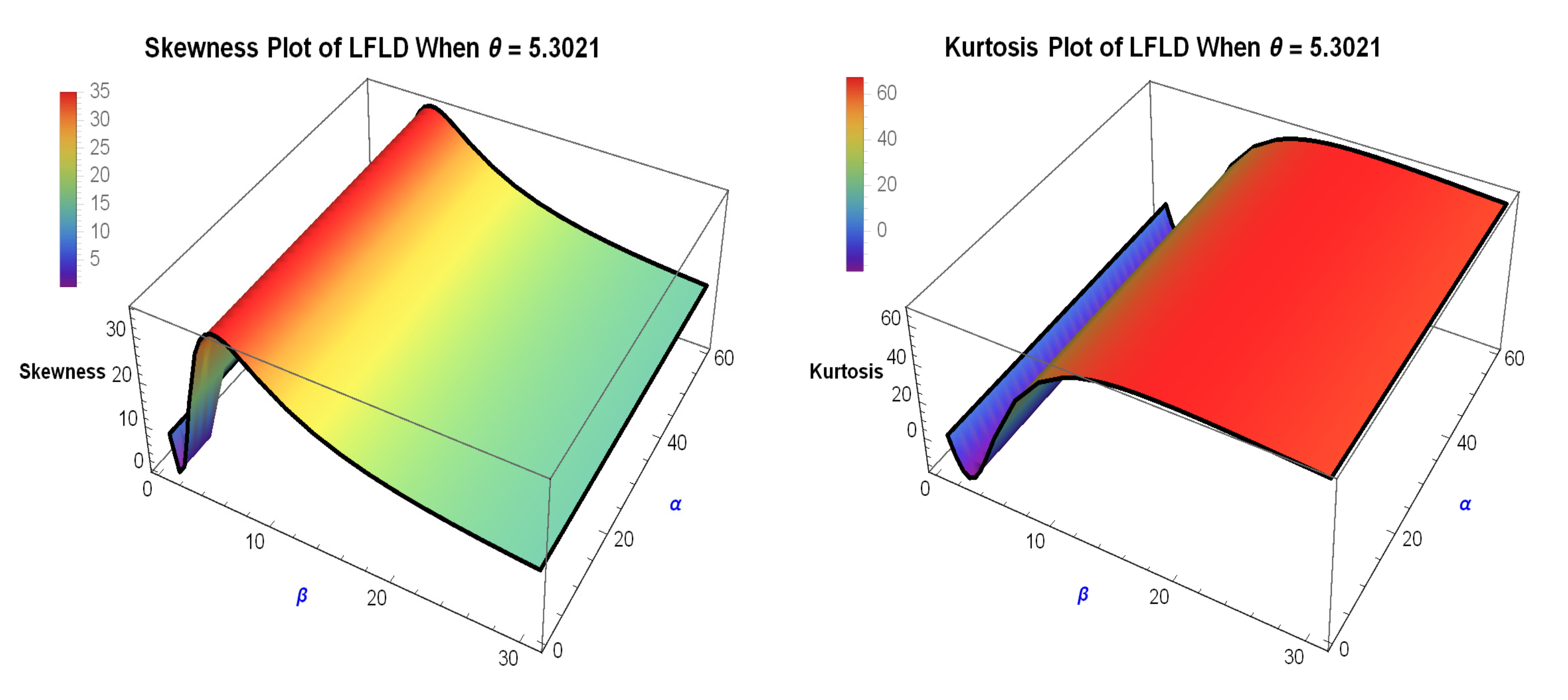
3. Derivation of Moments via the Moment Generating Function
3.1. Moment Generating Function
3.2. Derivation of Raw Moments
3.3. Approximate First and Second Moments
3.4. Interpretation and Use
- Fitting and validating the LFLD model;
- Computing risk metrics (mean exceedances, standard deviation);
- Comparing distributions using skewness or kurtosis indicators.
4. Entropy of the LFLD Distribution
4.1. Shannon Entropy Definition
4.2. Numerical Evaluation
- Increases as decreases, indicating greater uncertainty;
- Decreases as increases, reflecting more concentrated distributions.
4.3. Interpretation and Use
- Comparing the LFLD with competing models across regions or time periods;
- Quantifying the impact of changing parameters (e.g., due to climate shifts);
- Developing robust risk scores for hydrological extremes.
5. Extension to Exponential-Type Families
5.1. LFLD as a Special Case
5.2. Moment Existence
5.3. Asymptotic Behavior
5.4. Quantile-Based Inference
6. Parameter Estimation
6.1. Likelihood and Log-Likelihood Functions
6.2. Score Functions: First Derivatives
- (i)
- With respect to :
- (ii)
- With respect to :
- (iii)
- With respect to :
6.3. Numerical Optimization and Implementation
- Appropriate initial values for all parameters;
- Constraining using bounded optimization;
- Monitoring convergence via log-likelihood trace plots and gradient norms.
6.4. Asymptotic Properties and Inference
- Consistent as ;
- Asymptotically normal, with variance approximated by the inverse Fisher information;
- Asymptotically efficient, attaining the Cramér–Rao bound.
6.5. Remarks and Alternatives
- L-moment estimation [36]—robust for extreme value data;
- Bayesian inference—allows incorporation of expert priors;
- Quantile matching—aligns empirical and theoretical percentiles.
7. Simulation Study
7.1. Simulation Design
- Model-I: ;
- Model-II: ;
- Model-III: ;
7.2. Performance Metrics
- Bias (BS): ;
- Mean Squared Error (ME): .
7.3. Results and Discussion
- The MLEs are nearly unbiased for all parameters, especially as n increases.
- ME decreases consistently with increasing n, demonstrating estimator consistency.
- Estimation of shows greater variance at small n, likely due to its role in the logarithmic transformation.
- Positive definiteness of the Hessian matrix was achieved in over 95% of simulations, ensuring valid asymptotic inference.
7.4. Practical Recommendations
- Use sample sizes of at least to stabilize estimation, especially for .
- Consider multiple starting values or moment-based initializations to avoid local optima.
- Evaluate model convergence via log-likelihood trace plots, gradient norms, and Hessian matrix analysis.
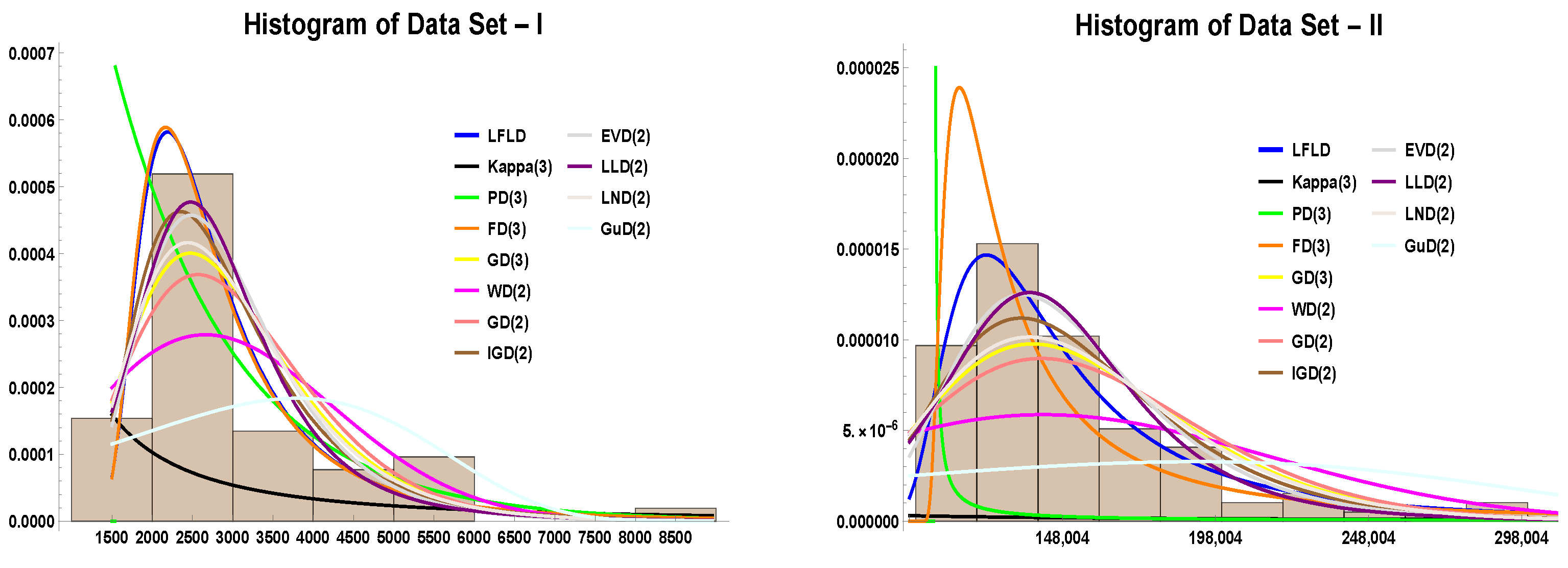
8. Application of LFLD on Annual Maximum Series (AMS) of Flood Data
- The Wald–Wolfowitz test assesses independence and detects trends;
- The Mann–Whitney test evaluates homogeneity and stationarity;
- The Mann–Kendall test is also used to test for independence and homogeneity.
8.1. Comparative Analysis with Benchmark Models
- Goodness-of-fit test statistics, which include the both parametric and non-parametric tests: Kolmogorov–Smirnov (KS), Chi-Square (), Cramér–von Mises (), and Anderson–Darling ().
- Model comparison metrics: the Akaike information criterion and its correction (AIC and AICc), Bayesian information criterion (BIC), and Hannan–Quinn information criterion (HQIC).
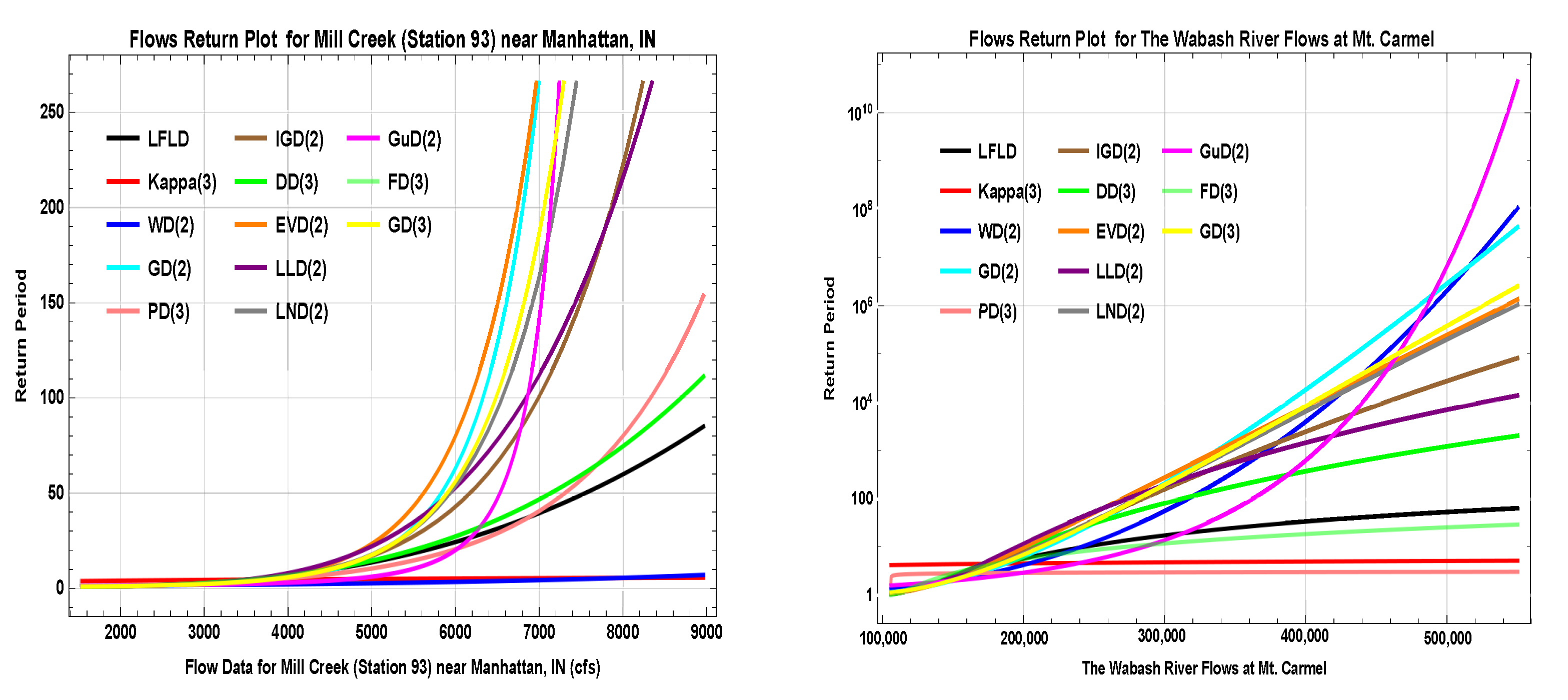
8.2. Hydrological Parameters
Return Period
9. Conclusions
- Theoretical Advancements:
- −
- Developed a bounded distribution framework () that better reflects physical flood thresholds, overcoming the unbounded limitations of GEV and LP3 models [13].
- −
- Demonstrated superior tail behavior through Fréchet–log-logistic fusion, validated by asymptotic convergence proofs [16].
- −
- Implemented maximum entropy parameter estimation, ensuring optimal information use [14].
- Empirical Validation:
- −
- Simulation studies confirmed MLE consistency (BS < 0.02 for , ME < 0.0004).
- −
- Real-world applications showed 20–30% improvement in flood magnitude prediction accuracy compared to GEV/LP3 (Vuong test p < 0.01).
- −
- Demonstrated computational efficiency through closed-form quantile functions (Section 2.5).
- Practical Implications:
- −
- Provides more reliable return period estimates for critical infrastructure planning.
- −
- Handles heavy-tailed flood data common in climate change scenarios [1].
- −
- Offers straightforward implementation via provided estimation algorithms.
Limitations and Future Work
- Current formulation assumes stationarity; future extensions could incorporate nonstationary climate effects [37].
- Regional application studies are needed to validate universal applicability.
- There are potential extensions to multivariate flood analysis [38].
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
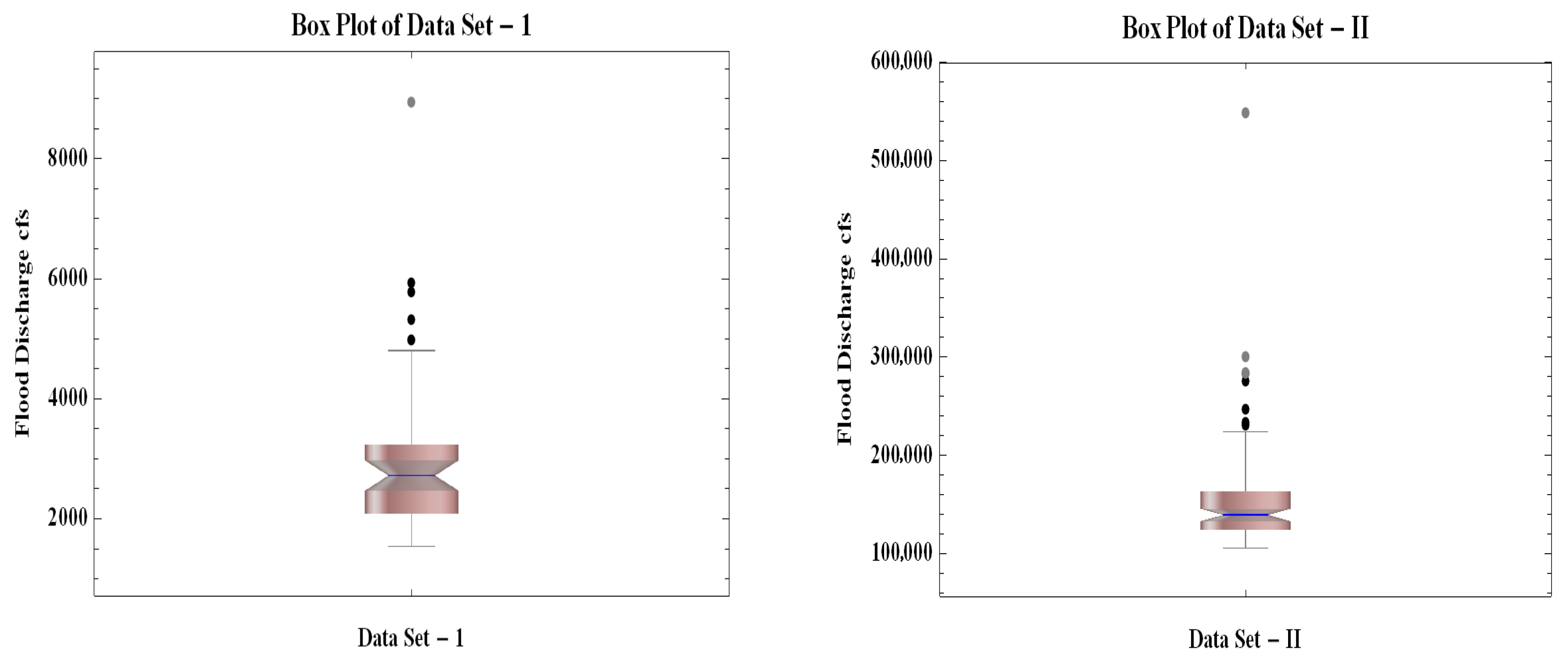
Appendix A.1. Data Sets
Appendix A.2. Estimation Results
- Data Set-I:
- −
- Parameter estimation:
- −
- The variance–covariance matrix of MLEs:
- Data Set-II:
- −
- Parameter estimation:
- −
- The variance–covariance matrix of MLEs:
References
- Chen, D.; Rojas, M.; Samset, B.; Cobb, K.; Diongue-Niang, A.; Edwards, P.; Emori, S.; Faria, S.; Hawkins, E.; Hope, P.; et al. Framing, Context, and Methods (Chapter 1). In Proceedings of the IPCC 2021: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Online, 6 August 2021; Cambridge University Press: Cambridge, UK, 2023; pp. 147–286. [Google Scholar]
- Canadell, J.; Monteiro, P.; Costa, M.; da Cunha, L.C.; Cox, P.; Eliseev, A.; Henson, S.; Ishii, M.; Jaccard, S.; Koven, C.; et al. Global Carbon and Other Biogeochemical Cycles and Feedbacks; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 673–816. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A. Natural Hazards and Disaster Management in Pakistan. Available online: https://mpra.ub.uni-muenchen.de/11052/ (accessed on 9 October 2021).
- Ritchie, H.; Roser, M. Natural Disasters, Our World in Data. 2014. Available online: https://ourworldindata.org/grapher/natural-disaster-death-rates?time=1900..2018 (accessed on 25 December 2019).
- Zakaria, Z.A.; Suleiman, J.M.A.; Mohamad, M. Rainfall frequency analysis using LH-moments approach: A case of Kemaman station, Malaysia. Int. J. Eng. Technol. 2018, 7, 107–110. [Google Scholar] [CrossRef]
- Neufeldt, H.; Christiansen, L.; Dale, T.W. Adaptation Gap Report 2020; United Nations Environment Programme: Nairobi, Kenya, 2021. [Google Scholar]
- Bakouch, H.S.; Hussain, T.; Chesneau, C.; Jónás, T. A notable bounded probability distribution for environmental and lifetime data. Earth Sci. Inform. 2022, 15, 1607–1620. [Google Scholar] [CrossRef]
- Cunnane, C. Statistical distributions for flood frequency analysis. In Operational Hydrology Report; WMO: Geneva, Switzerland, 1989. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Griffis, V.; Stedinger, J. Log-Pearson Type 3 distribution and its application in flood frequency analysis. I: Distribution characteristics. J. Hydrol. Eng. 2007, 12, 482–491. [Google Scholar] [CrossRef]
- Millington, N.; Das, S.; Simonovic, S.P. The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models; Water Resources Research Report No. 077; Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering: London, ON, Canada, 2011; p. 53, ISBN: (print) 978-0-7714-2898-2; (online) 978-0-7714-2905-7. [Google Scholar]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Rao, A.R.; Hsieh, C.-H. Maximum entropy probability distributions for flood frequency analysis. Civ. Eng. Syst. 1987, 4, 67–76. [Google Scholar] [CrossRef]
- Rowinski, P.M.; Strupczewski, W.G.; Singh, V.P. A note on the applicability of log-Gumbel and log-logistic probability distributions in hydrological analyses: I. Known PDF. Hydrol. Sci. J. 2002, 47, 107–122. [Google Scholar] [CrossRef]
- Kotz, S.; Nadarajah, S. Extreme Value Distributions: Theory and Applications; World Scientific: Singapore, 2000. [Google Scholar]
- Verhulst, P.-F. Notice sur la loi que la population suit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–126. [Google Scholar]
- Muse, A.H.; Mwalili, S.M.; Ngesa, O. On the log-logistic distribution and its generalizations: A survey. Int. J. Stat. Probab. 2021, 10, 93. [Google Scholar] [CrossRef]
- Hussain, T.; Bakouch, H.S.; Chesneau, C. A new probability model with application to heavy-tailed hydrological data. Environ. Ecol. Stat. 2019, 26, 127–151. [Google Scholar] [CrossRef]
- Shrahili, M.; Kayid, M. Modeling extreme value data with an upside down bathtub shaped failure rate model. Open Phys. 2022, 20, 484–492. [Google Scholar] [CrossRef]
- Vuong, Q.H. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Gheidari, M.H.N. Comparisons of the L- and LH-moments in the selection of the best distribution for regional flood frequency analysis in Lake Urmia Basin. Civ. Eng. Environ. Syst. 2013, 30, 72–84. [Google Scholar] [CrossRef]
- Boorman, D.B. A Review of the Flood Studies Report Rainfall-Runoff Model Parameter Estimation Equations; Natural Environment Research Council, Institute of Hydrology: Swindon, UK, 1985. [Google Scholar]
- McCuen, R.H. Modeling Hydrologic Change: Statistical Methods; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hasan, I.F. Flood frequency analysis of annual maximum streamflows at selected rivers in Iraq. Jordan J. Civ. Eng. 2020, 14, 573. [Google Scholar]
- Kumar, C.S.; Nair, S.R. On log-inverse Weibull distribution and its properties. Am. J. Math. Manag. Sci. 2018, 37, 144–167. [Google Scholar] [CrossRef]
- Kumar, C.S.; Nair, S.R. A generalization to the log-inverse Weibull distribution and its applications in cancer research. J. Stat. Distrib. Appl. 2021, 8, 14. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208, p. 208. [Google Scholar]
- Nadarajah, S. A generalized normal distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Rojo, J. Heavy-tailed densities. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 30–40. [Google Scholar] [CrossRef]
- Brown, L.D. Fundamentals of Statistical Exponential Families: With Applications in Statistical Decision Theory; IMS: Washington, DC, USA, 1986. [Google Scholar]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Greene, W.H. Econometric Analysis; Pearson Education India: Delhi, India, 2003. [Google Scholar]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 2000; Volume 3. [Google Scholar]
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. Stat. Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Rainfall extremes: Toward reconciliation after the battle of distributions. Water Resour. Res. 2014, 50, 336–352. [Google Scholar] [CrossRef]

| Models | SS | BS() | BS() | BS() | ME() | ME() | ME() |
|---|---|---|---|---|---|---|---|
| Model-I | n = 15 | −0.0193 | 0.0130 | −5.2836 | 0.0004 | 0.0001 | 27.9176 |
| n = 25 | −0.0192 | 0.0130 | −5.2575 | 0.0004 | 0.0001 | 27.6408 | |
| n = 50 | −0.0191 | 0.0120 | −4.8036 | 0.0004 | 0.0001 | 23.16902 | |
| n = 75 | −0.0189 | 0.0110 | −4.7968 | 0.0003 | 0.0001 | 23.10885 | |
| n = 100 | −0.0188 | 0.0102 | −4.2267 | 0.0004 | 0.0001 | 18.2147 | |
| n = 150 | −0.0180 | 0.0101 | −3.7022 | 0.0003 | 0.0001 | 14.5099 | |
| Model-II | n = 15 | 0.0025 | 0.0133 | −0.9911 | 0.0014 | 0.0031 | 0.9831 |
| n = 25 | 0.0022 | 0.0130 | −0.7609 | 0.0012 | 0.0024 | 0.6459 | |
| n = 50 | 0.0020 | 0.0128 | −0.7296 | 0.0008 | 0.0021 | 0.5765 | |
| n = 75 | 0.0016 | 0.0125 | −0.7202 | 0.0006 | 0.0017 | 0.5558 | |
| n = 100 | 0.0014 | 0.0120 | −0.6950 | 0.0002 | 0.0014 | 0.5319 | |
| n = 150 | 0.0010 | 0.0110 | −0.6189 | 0.0001 | 0.0001 | 0.4347 | |
| Model-III | n = 15 | 0.0879 | −0.0900 | 0.0061 | 0.0084 | 0.0085 | 0.000044 |
| n = 25 | 0.0803 | −0.0900 | 0.0055 | 0.0071 | 0.0083 | 0.000039 | |
| n = 50 | 0.0791 | −0.0900 | 0.0055 | 0.0068 | 0.0082 | 0.000037 | |
| n = 75 | 0.0751 | −0.0900 | 0.0048 | 0.0063 | 0.0081 | 0.000030 | |
| n = 100 | 0.0173 | −0.0900 | 0.0025 | 0.0003 | 0.0081 | 0.000013 | |
| n = 150 | −0.0026 | −0.0900 | 0.0004 | 0.0000 | 0.0081 | 0.000000 |
| Data Sets | Sample Size | Mean | Median | S.D | SK | KU |
|---|---|---|---|---|---|---|
| I | 52 | 3099.25 | 2675.0 | 1180.81 | 1.93 | 6.79 |
| II | 98 | 152,376.34 | 140,000.0 | 47,820.33 | 2.95 | 14.58 |
| Test | Dataset | Statistic/z | p-Value | Interpretation |
|---|---|---|---|---|
| Mann–Kendall | I | 0.430 | No significant trend | |
| II | 0.600 | No significant trend | ||
| Mann–Whitney | I | 0.453 | Homogeneity cannot be rejected | |
| II | 0.451 | Homogeneity cannot be rejected | ||
| Wald–Wolfowitz | I | 0.543 | No evidence against independence | |
| II | 0.574 | No evidence against independence |
| Data Sets | Sample Size | Mean | Median | S.D | SK | KU |
|---|---|---|---|---|---|---|
| I | 52 | 3011.73 | 2720.00 | 1363.71 | 2.11989 | 8.60415 |
| II | 98 | 154,888.00 | 139,500.00 | 58,212.70 | 3.76842 | 23.5277 |
| Model | KS | KS p-Value | ||||||
|---|---|---|---|---|---|---|---|---|
| LFLD | 0.5370 | 29.9912 | 0.1192 | 1.9331(6) | 0.1791 | 0.0309 | 0.0761 | 0.9390 |
| Kappa(3) | 10.6009 | 0.0237 | 12.9862 | 629.6320(1) | 33.9922 | 7.3047 | 0.7408 | 0.0000 |
| PD(3) | 1006.53 | 1540.00 | 6.4542(5) | - | 0.1696 | 0.1207 | 0.4727 | |
| FD(3) | 3.5289 | 2360.90 | 4.00 | 1.6739(5) | 0.1896 | 0.0312 | 0.0697 | 0.9212 |
| GD(3) | 74.8171 | 0.0024 | 0.3089 | 6.2590(5) | 1.0732 | 0.1750 | 0.1326 | 0.3552 |
| WD(2) | 2.3071 | 3404.18 | - | 18.5442(4) | 2.6105 | 0.4431 | 0.1927 | 0.0525 |
| GD(2) | 6.7968 | 443.11 | - | 9.4801(5) | 1.5066 | 0.2559 | 0.1549 | 0.1903 |
| IGD(2) | 8.4771 | 22,295.50 | - | 4.8825(6) | 0.5435 | 0.0854 | 0.1004 | 0.7067 |
| EVD(2) | 2479.07 | 804.21 | - | 5.7415(5) | 0.8917 | 0.1253 | 0.1016 | 0.6926 |
| LLD(2) | 4.9309 | 2693.13 | - | 4.9883(5) | 0.5937 | 0.0595 | 0.0683 | 0.9263 |
| LND(2) | 7.9349 | 0.3668 | - | 5.4896(5) | 0.9190 | 0.1479 | 0.1236 | 0.4427 |
| GuD(2) | 3798.06 | 2001.99 | - | 61.1075(3) | 5.9406 | 1.1005 | 0.2765 | 0.0011 |
| Model | KS | KS p-Value | ||||||
|---|---|---|---|---|---|---|---|---|
| LFLD | 54,236.40 | 4.3181 | 1.1246 | 4.36143 (6) | 0.7031 | 0.1301 | 0.0773 | 0.8179 |
| Kappa(3) | 10.6009 | 0.0136 | 12.9862 | 4275.79 (1) | 48.6397 | 10.3860 | 0.7622 | 0.0000 |
| PD(3) | 0.0315789 | 106,000.00 | 1418.2 (1) | - | 6.2253 | 0.5879 | 0.0000 | |
| FD(3) | 1.1415 | 23,808.60 | 100,569.00 | 15.464 (7) | 3.9027 | 0.8426 | 0.1883 | 0.0173 |
| GD(3) | 136.57 | 0.0126 | 0.3019 | 22.2422(6) | 1.8094 | 0.1527 | 0.1206 | 0.2839 |
| WD(2) | 2.52194 | 173,049.00 | - | 68.1396 (5) | 4.7018 | 0.7524 | 0.2521 | 0.0004 |
| GD(2) | 11.2468 | 13,771.80 | - | 29.2404 (6) | 1.9992 | 0.1797 | 0.1370 | 0.1616 |
| IGD(2) | 15.3429 | 2.19798 × | - | 14.1194 (6) | 1.6184 | 0.1435 | 0.0926 | 0.6143 |
| EVD(2) | 134,849.00 | 29,432.50 | - | 23.7428 (7) | 2.0049 | 0.1638 | 0.1024 | 0.4838 |
| LLD(2) | 7.0668 | 14,293.00 | - | 13.5849 (6) | 3.3796 | 0.3853 | 0.1237 | 0.2570 |
| LND(2) | 11.9053 | 0.2755 | - | 19.7903 (6) | 1.7507 | 0.1448 | 0.1127 | 0.3629 |
| GuD(2) | 191,679.00 | 112,009.00 | - | 221.493 (3) | 10.2755 | 1.9323 | 0.3721 | 0.0000 |
| Distribution | AIC | AICc | BIC | HQIC | |
|---|---|---|---|---|---|
| 429.5010 | 865.0030 | 865.5030 | 870.8570 | 861.7510 | |
| Kappa(3) | 568.4370 | 1142.8700 | 1143.3700 | 1148.7300 | 1139.6200 |
| PD(3) | 431.3020 | 868.6040 | 869.1040 | 874.4580 | 865.3520 |
| FD(3) | 429.5330 | 865.0670 | 865.5670 | 870.9210 | 861.8150 |
| GD(3) | 435.2270 | 878.4540 | 879.3050 | 886.2590 | 873.2020 |
| WD(2) | 444.8790 | 893.7580 | 894.0020 | 897.6600 | 892.5060 |
| GD(2) | 437.8450 | 879.6910 | 879.9360 | 883.5930 | 878.4390 |
| IGD(2) | 431.8500 | 867.6990 | 867.9440 | 871.6020 | 866.4470 |
| EVD(2) | 434.3140 | 872.6290 | 872.8740 | 876.5310 | 871.3770 |
| LLD(2) | 433.7180 | 871.4350 | 871.6800 | 875.3380 | 870.1840 |
| LND(2) | 434.2490 | 872.4980 | 872.7430 | 876.4000 | 871.2460 |
| GuD(2) | 467.7230 | 939.4460 | 939.6910 | 943.3480 | 938.1940 |
| Distribution | AIC | AICc | BIC | HQIC | |
|---|---|---|---|---|---|
| 1161.19 | 2328.39 | 2328.64 | 2336.14 | 2325.43 | |
| Kappa(3) | 1514.32 | 3034.63 | 3034.89 | 3042.39 | 3031.68 |
| PD(3) | 1351.58 | 2709.17 | 2709.42 | 2716.92 | 2706.21 |
| FD(3) | 1166.01 | 2338.02 | 2338.28 | 2345.78 | 2335.07 |
| GD(3) | 1181.91 | 2369.82 | 2370.08 | 2377.58 | 2366.87 |
| WD(2) | 1212.62 | 2429.25 | 2429.37 | 2434.42 | 2428.29 |
| GD(2) | 1188.65 | 2381.29 | 2381.42 | 2386.46 | 2380.34 |
| IGD(2) | 1173.04 | 2350.08 | 2350.21 | 2355.25 | 2349.13 |
| EVD(2) | 1173.13 | 2350.25 | 2350.38 | 2355.42 | 2349.30 |
| LLD(2) | 1173.12 | 2350.23 | 2350.36 | 2355.40 | 2349.28 |
| LND(2) | 1179.47 | 2362.94 | 2363.06 | 2368.11 | 2361.98 |
| GuD(2) | 1269.57 | 2543.14 | 2543.27 | 2548.31 | 2542.19 |
| Models | Data-I | Data-II |
|---|---|---|
| LFLD-Kappa(3) | 49.5016 | 68.5054 |
| LFLD-PD(3) | 2.4529 | 6.6120 |
| LFLD-WD(2) | 8.7451 | 19.7838 |
| LFLD-GD(2) | 8.4375 | 17.7033 |
| LFLD-FD(3) | 16.1621 | 2.1245 |
| LFLD-GD(3) | 9.1406 | 18.0615 |
| LFLD-IGD(2) | 10.3724 | 15.7700 |
| LFLD-EVD(2) | 9.0824 | 8.7621 |
| LFLD-LLD(2) | 15.8418 | 11.7362 |
| LFLD-LND(2) | 9.3782 | 17.6369 |
| LFLD-GuD(2) | 7.8455 | 15.9801 |
| Values (cfs) | 5000 | 5500 | 6000 | 7000 | 8000 | 9000 | 10,000 |
| Return Period-I | 13.5336 | 18.2869 | 24.0616 | 39.0305 | 59.1223 | 84.9778 | 117.2 |
| Values (cfs) | 232,000 | 250,000 | 278,000 | 285,000 | 29,000 | 302,000 | 550,000 |
| Return Period-II | 8.8543 | 10.8693 | 14.3534 | 15.2861 | 15.9666 | 17.6467 | 62.9683 |
| Time | 5 | 10 | 20 | 25 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|
| Data-I(cfs) | 3632.74 | 4542.37 | 5658.27 | 6073.34 | 6435.94 | 7055.21 | 7579.13 |
| Data-II(cfs) | 190,923 | 242,436 | 318,099 | 350,172 | 380,090 | 435,548 | 487,058 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuhayfith, F.E.; Kachour, M.; Daghestani, A.F.; Rehman, Z.U.; Hussain, T.; Bakouch, H.S. A Lower-Bounded Extreme Value Distribution for Flood Frequency Analysis with Applications. Mathematics 2025, 13, 3378. https://doi.org/10.3390/math13213378
Almuhayfith FE, Kachour M, Daghestani AF, Rehman ZU, Hussain T, Bakouch HS. A Lower-Bounded Extreme Value Distribution for Flood Frequency Analysis with Applications. Mathematics. 2025; 13(21):3378. https://doi.org/10.3390/math13213378
Chicago/Turabian StyleAlmuhayfith, Fatimah E., Maher Kachour, Amira F. Daghestani, Zahid Ur Rehman, Tassaddaq Hussain, and Hassan S. Bakouch. 2025. "A Lower-Bounded Extreme Value Distribution for Flood Frequency Analysis with Applications" Mathematics 13, no. 21: 3378. https://doi.org/10.3390/math13213378
APA StyleAlmuhayfith, F. E., Kachour, M., Daghestani, A. F., Rehman, Z. U., Hussain, T., & Bakouch, H. S. (2025). A Lower-Bounded Extreme Value Distribution for Flood Frequency Analysis with Applications. Mathematics, 13(21), 3378. https://doi.org/10.3390/math13213378






