Efficient Single-Server Private Information Retrieval Based on LWE Encryption
Abstract
1. Introduction
- We propose an SM3-PRF-based shuffling algorithm that leverages the SM3 hash function and a pseudorandom function to preprocess the database. This preprocessing strategy is compatible with any single-server client and requires the storage of only a -sized hint. In addition, SM3 cryptographic security chips are integrated into the server to enable hardware–software co-processing, thereby accelerating the SM3-PRF shuffling process and enhancing resistance to physical and side-channel attacks.
- A parallel encryption algorithm is developed based on the Regev LWE (Learning With Errors) scheme. The algorithm transforms scalar LWE encryption into matrix-based encryption, significantly reducing computational overhead from O(N) to O(1) operations for database encryption/decryption. Performance evaluations demonstrate substantial improvements: encryption time is reduced by 85–92% for long-bit data processing (>1000 bits) while maintaining equivalent security guarantees. Specifically, for a 16 GB database with 1 MB records, the parallel scheme achieves 9903 MB/s throughput, compared to the 1516 MB/s of existing schemes, representing a 6.5× performance improvement.
- Extensive simulations demonstrate that the single-server ShufflePIR protocol achieves high performance, with a peak throughput of 9903 MB/s on a 16 GB database with 1 MB records—representing an six-fold improvement over the best-performing existing single-server PIR scheme, the Spiral family. Furthermore, we formally prove the protocol’s security under polynomial-time adversaries. Therefore, the protocol provides a practical and secure solution for high-throughput information retrieval in privacy-sensitive applications.
2. Relatedwork
3. Background
3.1. Learn with Errors (LWE)
3.2. Private Information Retrieval with Preprocessing
4. Main Construction
4.1. ShufflePIR
- : The preprocessing phase is responsible for generating and storing the hint tables ( and ).
- Initialization.The client retrieves the complete database () from the server, constructs an initial master table (), and initializes all parity bits () in to zero. Subsequently, the client constructs a corresponding replacement table () to support future updates.
- Setup of the Master Table . Generate an SM3-PRF key () for each row () in the master table. The shuffling algorithm is applied to permute the database indices according to the rule expressed as . The key point is such that if is known, both and can be deterministically derived. This permutation uniformly redistributes the database records, ensuring that each record is equally likely to occupy any position in the table. The parity bits are then updated as
- Setup of the Replacement Table . Random indices () are selected from each of the blocks, and tuples of the form are subsequently sampled and stored. These tuples are then used to construct the replacement table (), which facilitates efficient record updates during future queries.
- Delete Local Database. Remove the locally stored database.
- : The client obtains a hint table through a preprocessing phase. The preprocessing algorithm performs a single linear scan of the database while requiring only local storage. In the ShufflePIR scheme, this preprocessing incurs communication and computation overhead and must be executed once every queries. Thus, the amortized cost per query remains . During each query, the client utilizes the stored . To retrieve a specific record (), the client performs a single query based on the stored , sends the query (), and records the state ().
- The position () is extracted from the hint information. Given a query index (), the client first computes , then derives the position mapping () using the master table ().
- The state value is recorded. The corresponding value () is retrieved:The next available replacement pair () is selected from the replacement table () and is used to replace the -th data record associated with index . The resulting modified set is denoted as . The state () is recorded.
- The retrieval ciphertext is sent. Set is encrypted using an LWE-based cryptosystem. Set is transformed into a matrix of the form . In Section 4.2, the selection of parameters for the LWE-based cryptographic scheme is discussed. The resulting retrieval ciphertext () is sent to the server:
- : After receiving the ciphertext () from the client, the server decrypts it to recover the corresponding plaintext index, executes a query and performs the required computation over the database (), and returns the response ().
- Decrypt the ciphertext.The server uses the secret key () to decrypt the ciphertext () and recovers the index set from the resulting matrix:
- Retrieve. The corresponding data records are retrieved from the database, and the result () is computed as . Finally, the computed result () is transmitted to the client.
- : Using the ciphertext () returned by the server and the local state (), the client computes the value of the queried message ().
- The client computes :If the procedure fails, the client assigns a value of 0 to the retrieval result ().
4.2. Parameter Selection
4.3. Extensions
4.4. Hardware Support
4.5. Quantitative Analysis of SM3-PRF Shuffling Algorithm
5. Security Analysis
- Security of the LWE-based Encryption:
- In the scheme, the only public parameter that contains the private key (ss) is the public key . Since , , and are sampled independently, the security of the LWE encryption scheme ensures that the components of are computationally indistinguishable from encodings of random matrices. The remaining parameters of the LWE encryption scheme are publicly shared, and it is computationally infeasible to exploit encodings of random values to compromise the security of the LWE encryption scheme (see Section 3.1). The LWE problem is widely believed to be computationally hard, implying that no polynomial-time adversary can feasibly recover the plaintext from the ciphertext without access to the secret key. Consequently, the encrypted queries generated by the client do not reveal any information about the queried indices to any third party.
- SM3-PRF Shuffling Algorithm:
- During the preprocessing phase, the SM3-based pseudorandom function (PRF) shuffling algorithm randomly permutes the database indices, ensuring that the true query index is not transmitted to the server. The output of the pseudorandom function is computationally indistinguishable from a truly random index to any polynomial-time adversary. As a result, the shuffled indices stored in the master and replacement tables do not reveal any information about the original indices.
6. Evaluation
6.1. Experimental Setup
- 256 B: Corresponding to ultra-short voice snippets (e.g., 0.03 s of speech), representing minimal voice data units such as keyword triggers in voice assistants;
- 30 KB: Corresponding to short voice clips (e.g., 3–5 s of speech), typical of voice messages in messaging applications;
- 100 KB: Corresponding to medium-length voice recordings (e.g., 10–15 s of speech), such as voice notes or short voice commands;
- 1 MB: Corresponding to long voice segments (e.g., 2–3 min of speech), representing extended recordings like conference snippets or interview excerpts.
6.2. Impact of Database Configuration on Throughput
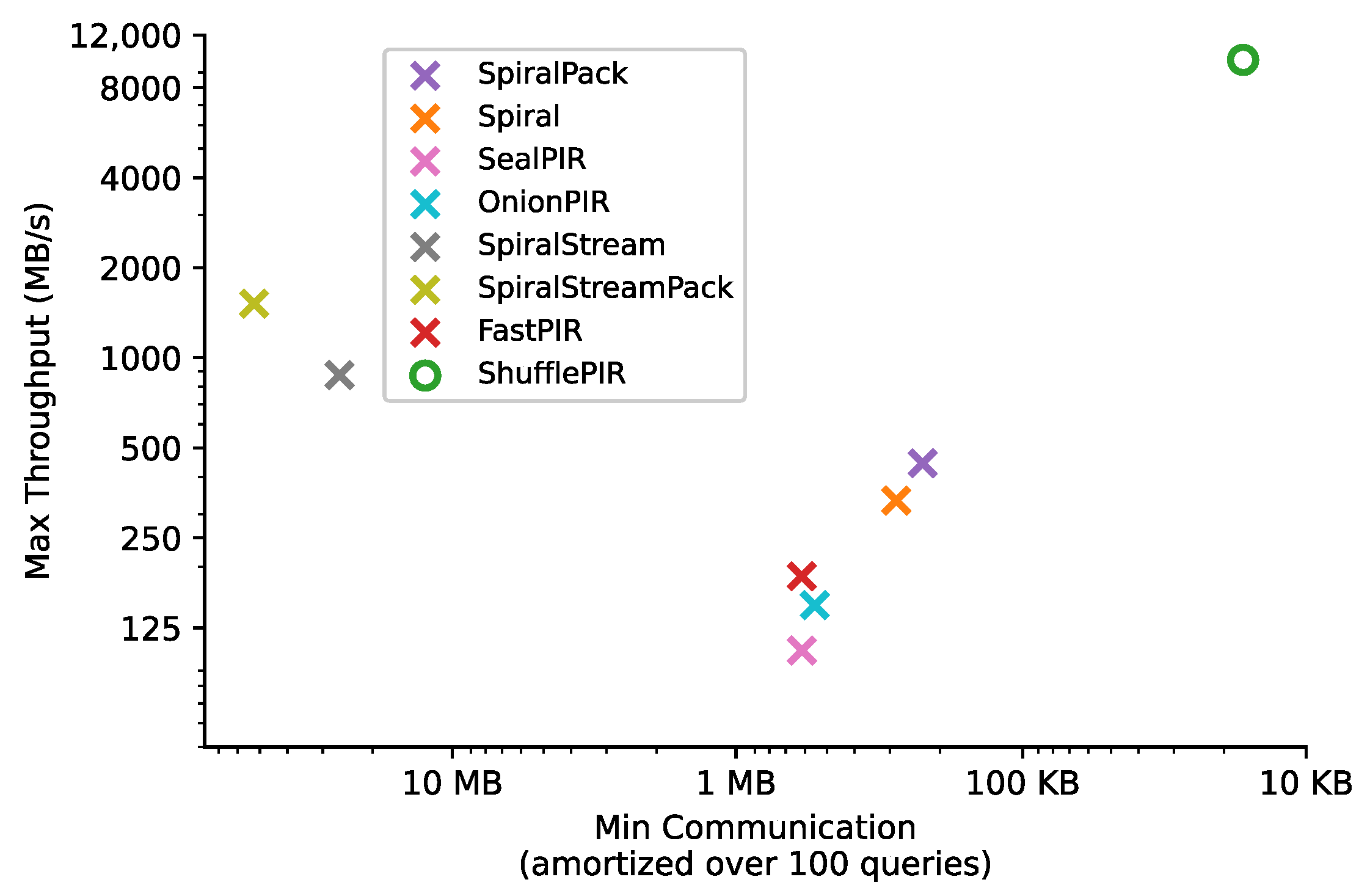
6.3. Comparative Analysis of Overall Performance
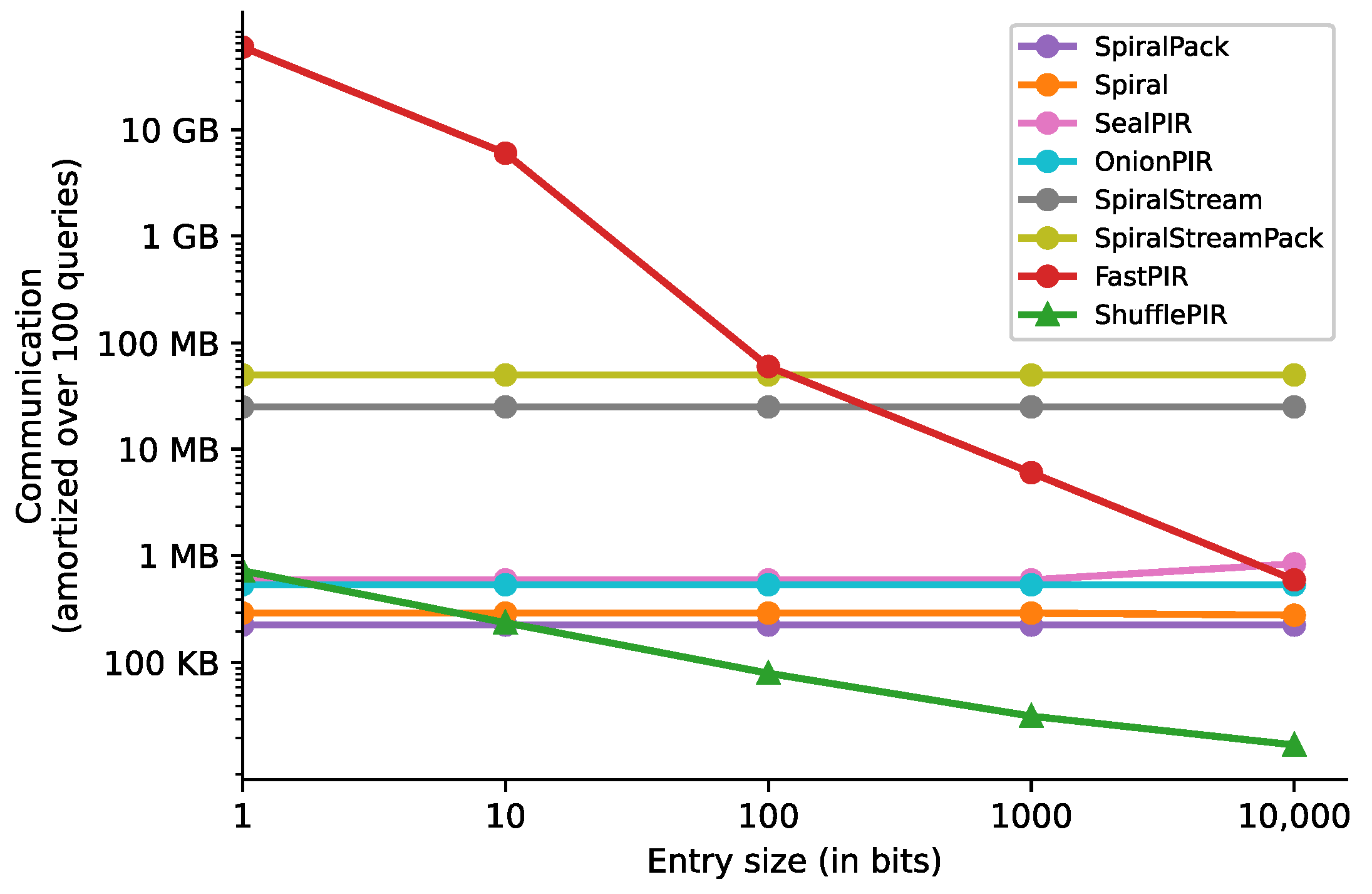
6.4. Trade-Off Between Throughput and Communication Overhead
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Yu, H.; Liu, Z.; Li, Y. MI-VFDNN: An Efficient Vertical Federated Deep Neural Network with Multi-Layer Interaction. IEEE Trans. Inf. Forensics Secur. 2024, 19, 7435–7448. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Jia, X.; Liu, Z. APFed: Anti-poisoning attacks in privacy-preserving heterogeneous federated learning. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5749–5761. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Jia, X.; Li, Y. pSafety: Privacy-preserving safety monitoring in online ride hailing services. IEEE Trans. Dependable Secur. Comput. 2023, 20, 209–224. [Google Scholar] [CrossRef]
- Yu, H.; Jia, X.; Zhang, H.; Li, Y. Efficient and privacy-preserving ride matching using exact road distance in online ride hailing services. IEEE Trans. Serv. Comput. 2022, 15, 1841–1854. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, H.; Li, X.; Zhang, H. PFind: Privacy-preserving lost object finding in vehicular crowdsensing. World Wide Web 2024, 27, 64. [Google Scholar] [CrossRef]
- Kapileswar, N.; Simon, J. Quantum-Resilient Consensus Mechanisms for Scalable Blockchain Networks using Lattice-based Cryptography. In Proceedings of the 6th International Conference on Intelligent Communication Technologies and Virtual Mobile Networks (ICICV 2025), Tirunelveli, India, 17–19 June 2025; pp. 1849–1854. [Google Scholar] [CrossRef]
- Wang, F.; Yun, C.; Goldwasser, S.; Vaikuntanathan, V.; Zaharia, M. Splinter: Practical Private Queries on Public Data. In Proceedings of the 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17), Boston, MA, USA, 27–29 March 2017; pp. 299–313. [Google Scholar]
- Liu, L.; Du, Q.; Gao, X. Device Independent Quantum Private Queries Based on Quantum Key Distribution. Mathematics 2025, 13, 951. [Google Scholar] [CrossRef]
- Kogan, D.; Corrigan-Gibbs, H. Private Blocklist Lookups with Checklist. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Boston, MA, USA, 11–13 August 2021; pp. 875–892. [Google Scholar]
- Pal, B.; Islam, M.; Ristenpart, T.; Chatterjee, R. Might I Get Pwned: A Second-Generation Password Breach Alerting Service. In Proceedings of the 31st USENIX Security Symposium (USENIX Security 22), Boston, MA, USA, 10–12 August 2022; pp. 2249–2266. [Google Scholar]
- Wang, K.C.; Reiter, M.K. Detecting Stuffing of a User’s Credentials at Her Own Accounts. In Proceedings of the 29th USENIX Security Symposium (USENIX Security 20), Virtual Event, 12–14 August 2020; USENIX Association: Berkeley, CA, USA, 2020; pp. 2201–2218. [Google Scholar]
- Servan-Schreiber, S.; Hogan, K.; Devadas, S. AdVeil: A Private Targeted Advertising Ecosystem. Cryptology ePrint Archive (Preprint); Report 2021/1032. Available online: https://ia.cr/2021/1032 (accessed on 8 March 2021).
- Chor, B.; Goldreich, O.; Kushilevitz, E.; Sudan, M. Private information retrieval. J. ACM 1998, 45, 965–981. [Google Scholar] [CrossRef]
- Kushilevitz, E.; Ostrovsky, R. Replication is not needed: Single database, computationally-private information retrieval. In Proceedings of the 38th Annual IEEE Symposium on Foundations of Computer Science (FOCS 1997), Miami Beach, FL, USA, 20–22 October 1997; IEEE Computer Society: Washington, DC, USA, 1997; pp. 364–373. [Google Scholar] [CrossRef]
- Gasarch, W. A survey on private information retrieval. Bull. EATCS 2004, 82, 113. [Google Scholar]
- Ostrovsky, R.; Skeith, W.E., III. A survey of single-database private information retrieval: Techniques and applications. In Proceedings of the 10th International Workshop on Public Key Cryptography (PKC 2007), Beijing, China, 16–20 April 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 393–411. [Google Scholar] [CrossRef]
- Corrigan-Gibbs, H.; Henzinger, A.; Kogan, D. Single-Server Private Information Retrieval with Sublinear Amortized Time. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT 2022), Trondheim, Norway, 30 May–3 June 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 3–33. [Google Scholar] [CrossRef]
- Corrigan-Gibbs, H.; Kogan, D. Private Information Retrieval with Sublinear Online Time. In Proceedings of the Advances in Cryptology-EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Part I, Zagreb, Croatia, 10–14 May 2020; pp. 44–75. [Google Scholar] [CrossRef]
- Shi, E.; Aqeel, W.; Chandrasekaran, B.; Maggs, B. Puncturable Pseudorandom Sets and Private Information Retrieval with Near-Optimal Online Bandwidth and Time. In Proceedings of the Springer Annual International Cryptology Conference (CRYPTO 2021), Santa Barbara, CA, USA, 16–20 August 2021; pp. 641–669. [Google Scholar] [CrossRef]
- Zhou, M.; Lin, W.K.; Tselekounis, Y.; Shi, E. Optimal Single-Server Private Information Retrieval. In Proceedings of the Advances in Cryptology-EUROCRYPT 2023: 42nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Part II, Lyon, France, 23–27 April 2023; pp. 395–425. [Google Scholar] [CrossRef]
- Boyle, E.; Ishai, Y.; Pass, R.; Wootters, M. Can We Access a Database Both Locally and Privately? In Proceedings of the Theory of Cryptography Conference (TCC 2017, Part II), Baltimore, MD, USA, 12–15 November 2017; pp. 662–693. [Google Scholar] [CrossRef]
- Canetti, R.; Holmgren, J.; Richelson, S. Towards Doubly Efficient Private Information Retrieval. In Proceedings of the Theory of Cryptography Conference (TCC 2017, Part II), Baltimore, MD, USA, 12–15 November 2017; pp. 694–726. [Google Scholar] [CrossRef]
- Menon, S.J.; Wu, D.J. Spiral: Fast, High-Rate Single-Server PIR via FHE Composition. In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP 2022), San Francisco, CA, USA, 22–26 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 930–947. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On Ideal Lattices and Learning with Errors over Rings. J. ACM 2013, 60, 43. [Google Scholar] [CrossRef]
- Angel, S.; Chen, H.; Laine, K.; Setty, S. PIR with Compressed Queries and Amortized Query Processing. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP 2018), San Francisco, CA, USA, 21–23 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 962–979. [Google Scholar] [CrossRef]
- Melchor, C.A.; Barrier, J.; Fousse, L.; Killijian, M.O. XPIR: Private Information Retrieval for Everyone. Proc. Priv. Enhanc. Technol. 2016, 2016, 155–174. [Google Scholar]
- Ahmad, I.; Yang, Y.; Agrawal, D.; El Abbadi, A.; Gupta, T. Addra: Metadata-Private Voice Communication over Fully Untrusted Infrastructure. In Proceedings of the 15th USENIX Symposium on Operating Systems Design and Implementation (OSDI 21), Virtual Event, 14–16 July 2021; USENIX Association: Berkeley, CA, USA, 2021; pp. 603–622. [Google Scholar]
- Ali, A.; Lepoint, T.; Patel, S.; Raykova, M.; Schoppmann, P.; Seth, K.; Yeo, K. Communication-Computation Trade-Offs in PIR. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Virtual Event, 11–13 August 2021; USENIX Association: Berkeley, CA, USA, 2021; pp. 1811–1828. [Google Scholar]
- Mughees, M.H.; Chen, H.; Ren, L. OnionPIR: Response-Efficient Single-Server PIR. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security (CCS 2021), Virtual Event, 15–19 November 2021; ACM: New York, NY, USA, 2021; pp. 2292–2306. [Google Scholar] [CrossRef]
- Gentry, C. Fully Homomorphic Encryption Using Ideal Lattices. In Proceedings of the 41st Annual ACM Symposium on Theory of Computing (STOC 2009), Bethesda, MD, USA, 31 May–2 June 2009; ACM: New York, NY, USA, 2009; pp. 169–178. [Google Scholar] [CrossRef]
- Gentry, C.; Halevi, S. Compressible FHE with Applications to PIR. In Proceedings of the Theory of Cryptography: 17th International Conference, TCC 2019, Part I, Nuremberg, Germany, 1–5 December 2019; Springer: Cham, Switzerland, 2019; pp. 438–464. [Google Scholar] [CrossRef]
- Boyle, E.; Gilboa, N.; Ishai, Y. Function Secret Sharing: Improvements and Extensions. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS 2016), Vienna, Austria, 24–28 October 2016; ACM: New York, NY, USA, 2016; pp. 1292–1303. [Google Scholar] [CrossRef]
- Kales, D.; Omolola, O.; Ramacher, S. Revisiting User Privacy for Certificate Transparency. In Proceedings of the 2019 IEEE European Symposium on Security and Privacy (EuroS&P 2019), Stockholm, Sweden, 17–19 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 432–447. [Google Scholar] [CrossRef]
- Beimel, A.; Ishai, Y.; Malkin, T. Reducing the Server’s Computation in Private Information Retrieval: PIR with Preprocessing. J. Cryptol. 2004, 17, 125–151. [Google Scholar] [CrossRef]
- Davidson, A.; Pestana, G.; Celi, S. FrodoPIR: Simple, Scalable, Single-Server Private Information Retrieval. Proc. Priv. Enhanc. Technol. 2023, 365–383. [Google Scholar] [CrossRef]
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. J. ACM 2009, 56, 34. [Google Scholar] [CrossRef]
- Amazon EC2 Reserved Instances Pricing. Available online: https://aws.amazon.com/ec2/pricing/reserved-instances/pricing/ (accessed on 28 June 2025).

| Scheme | Servers | Communication | Client Storage | Polylog Compute Overhead | Max. Achievable Throughput/Core |
|---|---|---|---|---|---|
| DPF PIR [34] | 2 | logN | × | ✓ | 5381 MB/s |
| XOR PIR [26] | 2 | × | ✓ | 6067 MB/s | |
| XOR PIR fast [26] | 2 | × | ✓ | 11,797 MB/s | |
| SealPIR [25] | 1 | ✓ | ✓ | 105 MB/s | |
| FastPIR [27] | 1 | N | ✓ | ✓ | 186 MB/s |
| MulPIR [28] | 1 | ✓ | ✓ | 69 MB/s | |
| OnionPIR [29] | 1 | log N | ✓ | ✓ | 149 MB/s |
| FrodoPIR [35] | 1 | × | ✓ | 1256 MB/S | |
| Spiral family [23] | 1 | log N | ✓ | ✓ | 1516 MB/s |
| ShufflePIR (Ours) | 1 | ✓ | ✓ | 9903 MB/S |
| Metric | ||||
|---|---|---|---|---|
| log n | 10 | 9 | 7 | 7 |
| log m | 10 | 9 | 7 | 7 |
| log q | 32 | 32 | 32 | 32 |
| log p | 9 | 16 | 18 | 21 |
| Metric | Traditional Random Permutation | SM3-PRF Shuffling |
|---|---|---|
| Computational Complexity | ||
| Security Level (bits) | 256 (constant) | |
| Throughput (MB/s) | 45 | 3750 |
| Cache Miss Rate | 23.4% | 7.8% |
| Side-channel Resistance | Low | High |
| Hardware Acceleration | NO | YES(RSP S20G) |
| Scheme | Database Size | Max. Achievable Throughput/core (MB/s) | |
|---|---|---|---|
| N | d | ||
| Prior two-server PIR | |||
| DPF PIR [34] | 32 B | 5381 MB/s | |
| XOR PIR [26] | 1 bit | 6067 MB/s | |
| XOR PIR fast [26] | 1 bit | 11,797 MB/s | |
| Prior single-server PIR | |||
| SealPIR [25] | 30 KB | 105 MB/s | |
| MulPIR [28] | 40 KB | 69 MB/s | |
| FastPIR [27] | 1024 B | 186 MB/s | |
| OnionPIR [29] | 30 KB | 149 MB/s | |
| FrodoPIR [35] | 1 KB | 1256 MB/s | |
| Spiral [23] | 100 KB | 333 MB/s | |
| SpiralPack [23] | 30 KB | 444 MB/s | |
| SpiralStream [23] | 30 KB | 874 MB/s | |
| SpiralStreamPack [23] | 30 KB | 1516 MB/s | |
| ShufflePIR (Ours) | 1 MB | 9903 ± 198 MB/s | |
| Scheme | SealPIR | FastPIR | OnionPIR | Spiral Family | ShufflePIR (Ours) |
|---|---|---|---|---|---|
| Param. Size | 3 MB | 1 MB | 5 MB | 16–24 MB | 0.125–8 MB |
| Database: (268 MB) | |||||
| Query Size | 66 KB | 33 MB | 63 KB | 16 MB | 11.94 KB |
| Response Size | 328 KB | 66 KB | 127 KB | 71 KB | 4.31 KB |
| Computation | 3.19 s | 1.44 s | 1.69 s | 0.42 s | 0.00044 s |
| Rate | 0.0008 | 0.0039 | 0.0122 | 0.0036 | 0.05939 |
| Throughput | 84 MB/s | 186 MB/s | 81 MB/s | 635 MB/s | 554 MB/s |
| Server Cost | $0.0000258 | $0.0000107 | $0.0000130 | $0.0000036 | $0.000004 |
| Database: (7.9 GB) | |||||
| Query Size | 66 KB | 8 MB | 63 KB | 30 MB | 11.94 KB |
| Response Size | 3 MB | 262 KB | 127 KB | 96 KB | 35.29 KB |
| Computation | 74.91 s | 50.52 s | 52.73 s | 5.33 s | 0.003964 s |
| Rate | 0.0092 | 0.1144 | 0.2363 | 0.3117 | 0.85 |
| Throughput | 105 MB/s | 156 MB/s | 149 MB/s | 1.48 GB/s | 7250 MB/s |
| Server Cost | $0.0005550 | $0.0003546 | $0.0003683 | $0.0000380 | $0.0000036 |
| Database: (1.6 GB) | |||||
| Query Size | 66 KB | 524 KB | 63 KB | 30 MB | 11.94 KB |
| Response Size | 11 MB | 721 KB | 508 KB | 150 KB | 108.2 KB |
| Computation | 19.03 s | 23.27 s | 14.38 s | 1.21 s | 0.011769 s |
| Rate | 0.0092 | 0.1387 | 0.1969 | 0.6677 | 0.92421 |
| Throughput | 86 MB/s | 70 MB/s | 114 MB/s | 1.35 GB/s | 8103 MB/s |
| Server Cost | $0.0002420 | $0.0001692 | $0.0001046 | $0.0000099 | $0.00000109 |
| Database Configuration | Metric | ShufflePIR | Spiral Family |
|---|---|---|---|
| Rate | 0.05939 | 0.0036 | |
| Throughput (MB/s) | 554 | 635 | |
| Query Size (KB) | 11.94 | 15,360 | |
| Rate | 0.85 | 0.3117 | |
| Throughput (MB/s) | 7250 | 1516 | |
| Query Size (KB) | 5.97 | 30,720 | |
| Rate | 0.92421 | 0.6677 | |
| Throughput (MB/s) | 8103 | 1382.4 | |
| Query Size (KB) | 1.49 | 30,720 | |
| Rate | 0.93404 | 0.7750 | |
| Throughput (MB/s) | 9903 | 1382.4 | |
| Query Size (KB) | 1.49 | 90,112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Guan, Z.; Yu, B.; Li, X.; Ge, M.; Ma, C.; Ma, X. Efficient Single-Server Private Information Retrieval Based on LWE Encryption. Mathematics 2025, 13, 3373. https://doi.org/10.3390/math13213373
Huang H, Guan Z, Yu B, Li X, Ge M, Ma C, Ma X. Efficient Single-Server Private Information Retrieval Based on LWE Encryption. Mathematics. 2025; 13(21):3373. https://doi.org/10.3390/math13213373
Chicago/Turabian StyleHuang, Hai, Zhibo Guan, Bin Yu, Xiang Li, Mengmeng Ge, Chao Ma, and Xiangyu Ma. 2025. "Efficient Single-Server Private Information Retrieval Based on LWE Encryption" Mathematics 13, no. 21: 3373. https://doi.org/10.3390/math13213373
APA StyleHuang, H., Guan, Z., Yu, B., Li, X., Ge, M., Ma, C., & Ma, X. (2025). Efficient Single-Server Private Information Retrieval Based on LWE Encryption. Mathematics, 13(21), 3373. https://doi.org/10.3390/math13213373







