Wave Scattering and Trapping by C-Type Floating Breakwaters in the Presence of Bottom-Standing Perforated Semicircular Humps
Abstract
1. Introduction
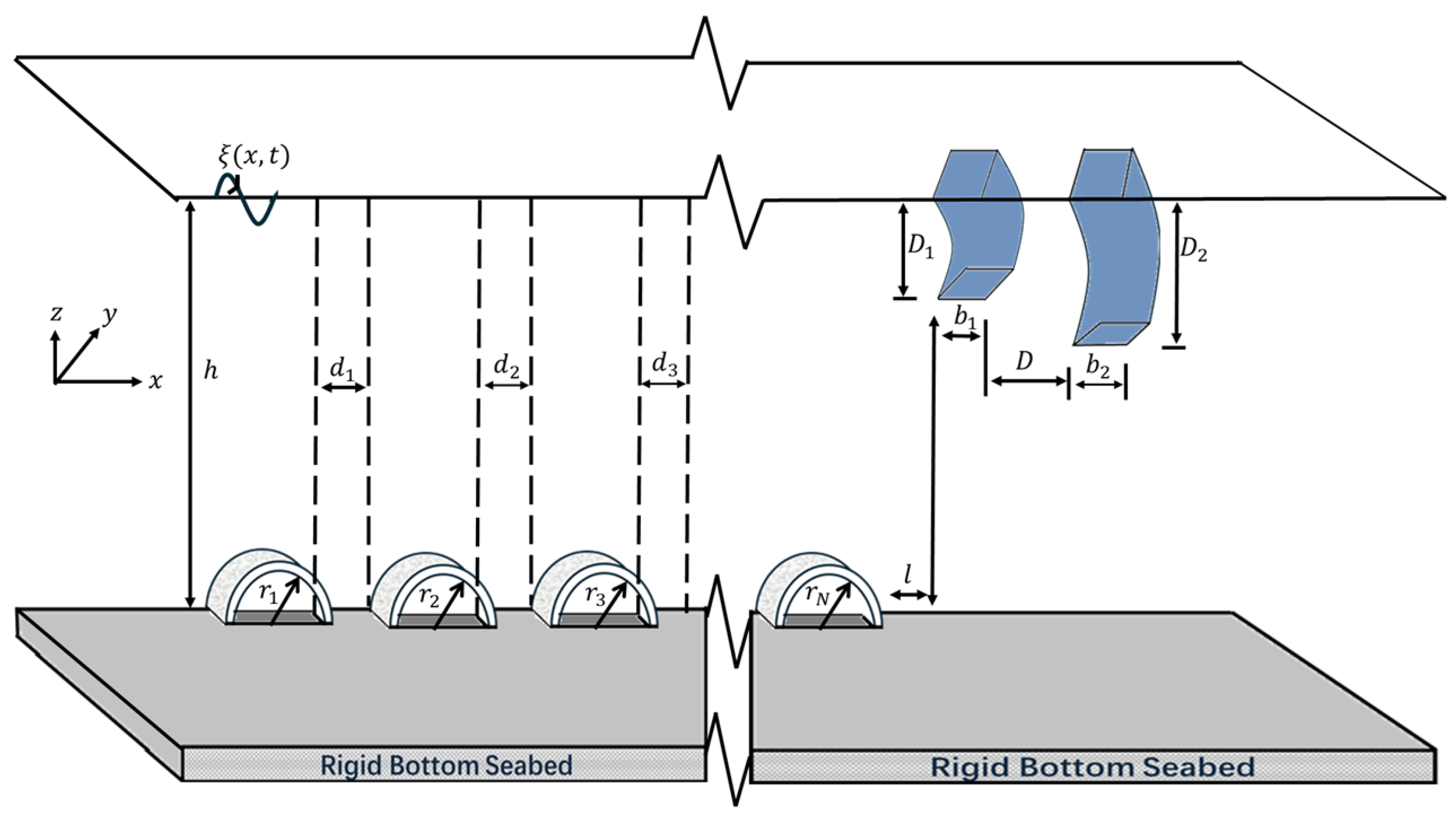
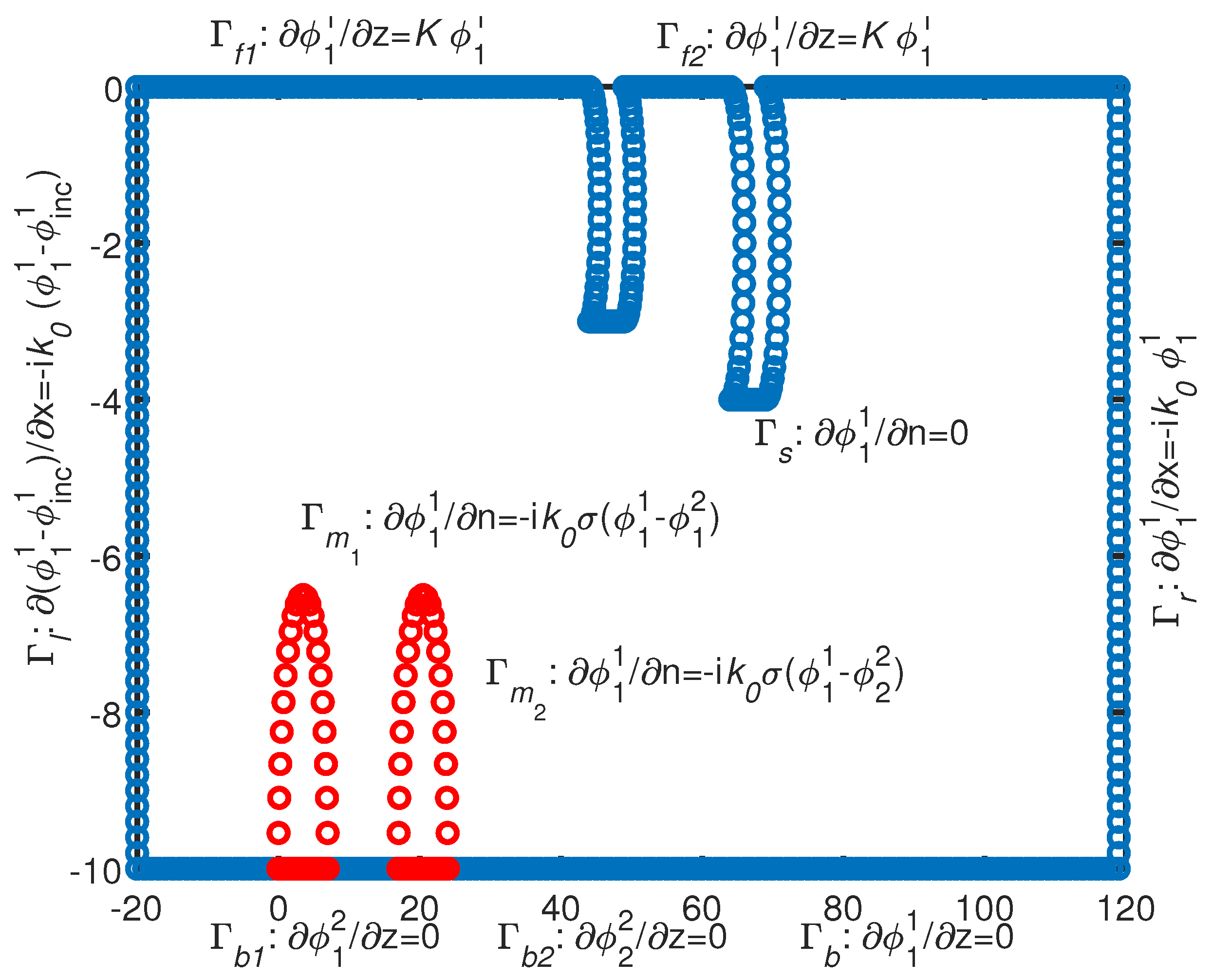
2. Mathematical Formulation
2.1. Methodology: BEM
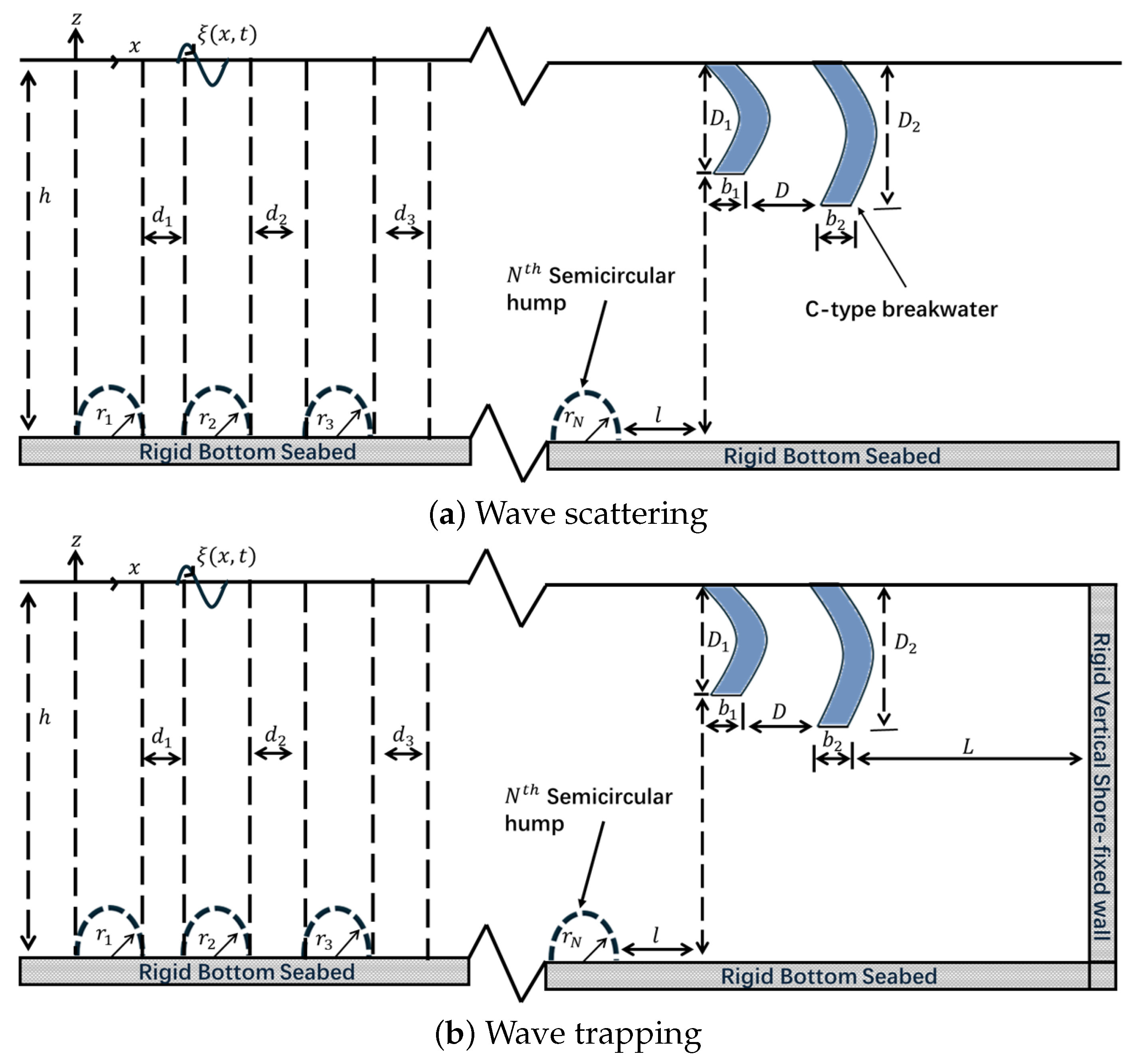
2.2. Wave Scattering
2.3. Wave Trapping
2.4. Wave Forces
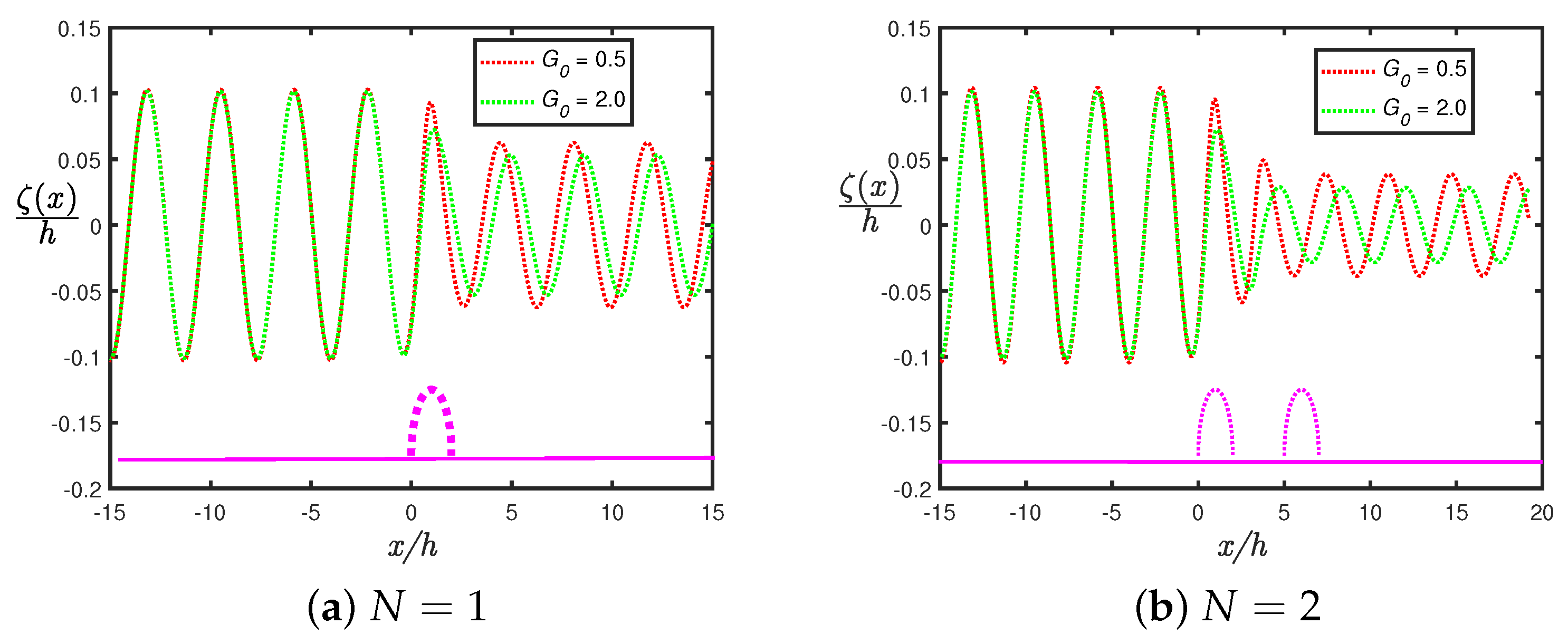
2.5. Free-Surface Elevation
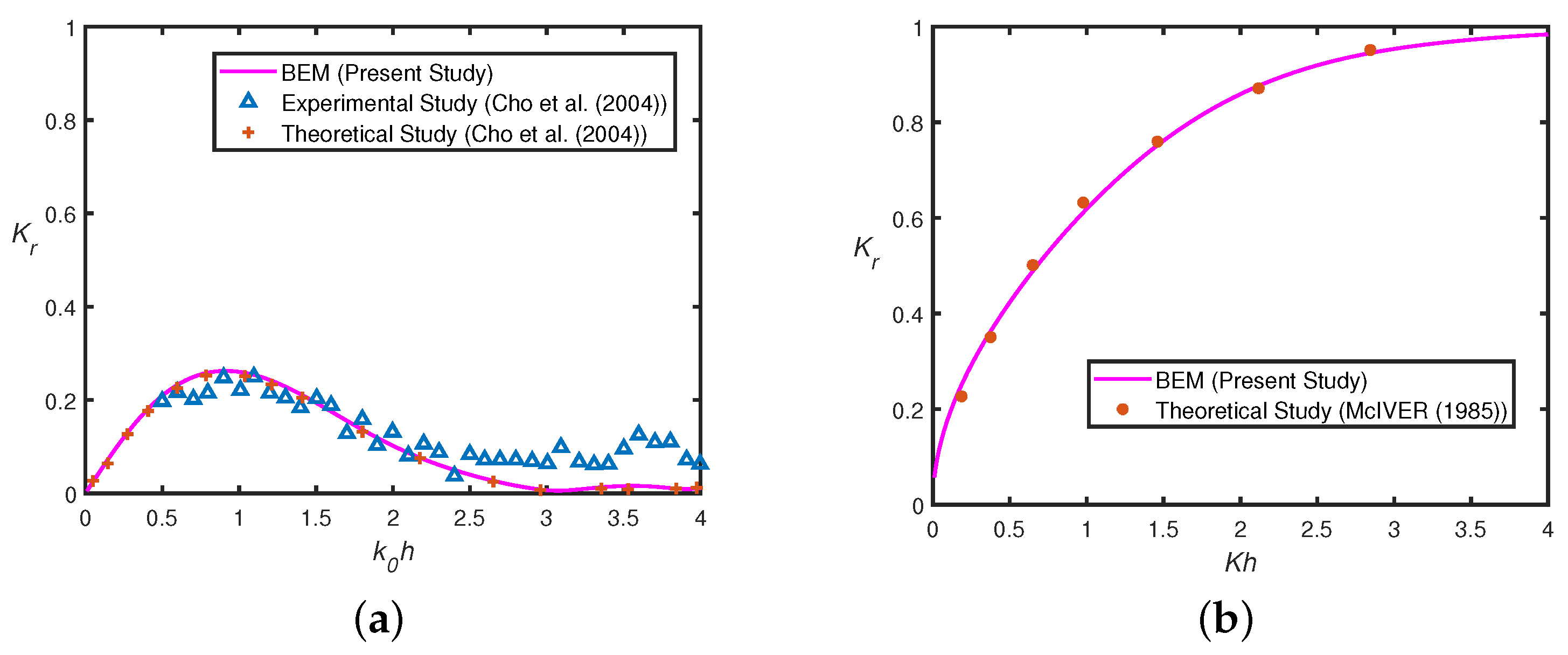
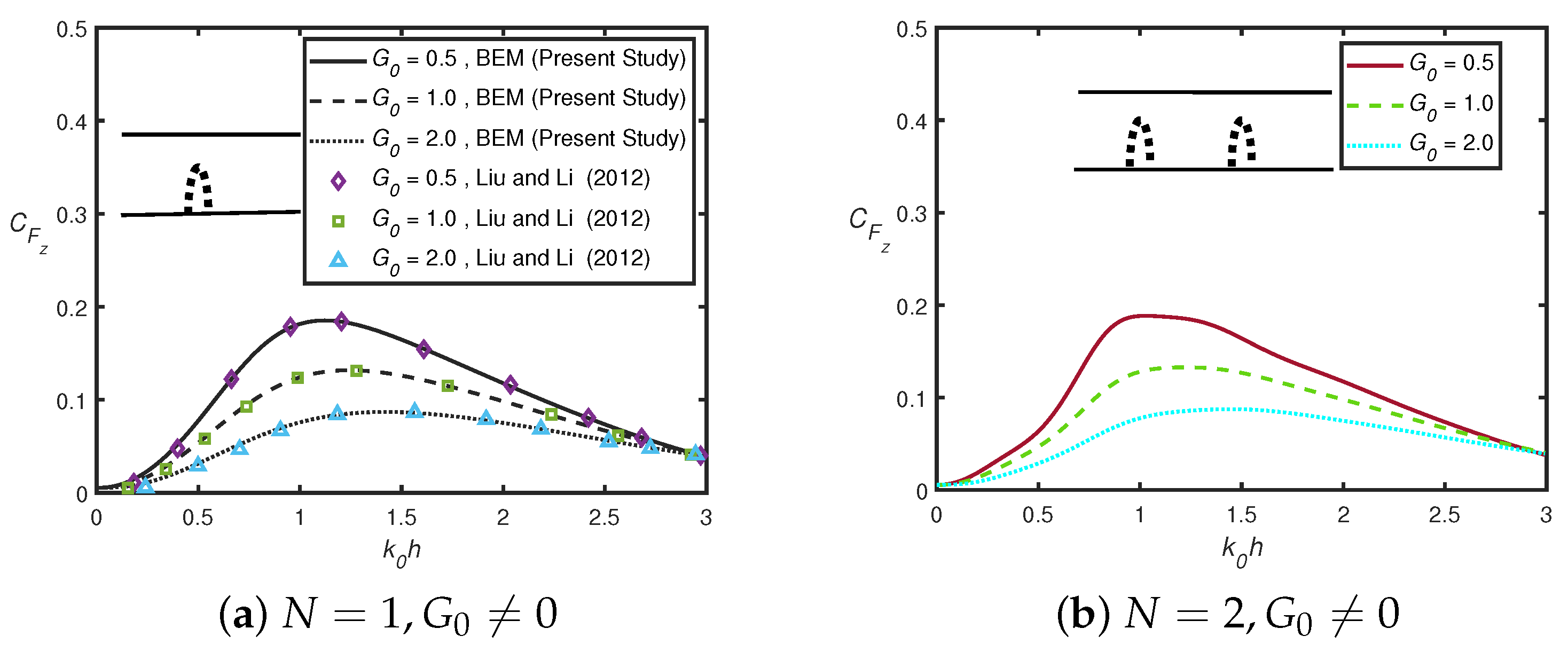
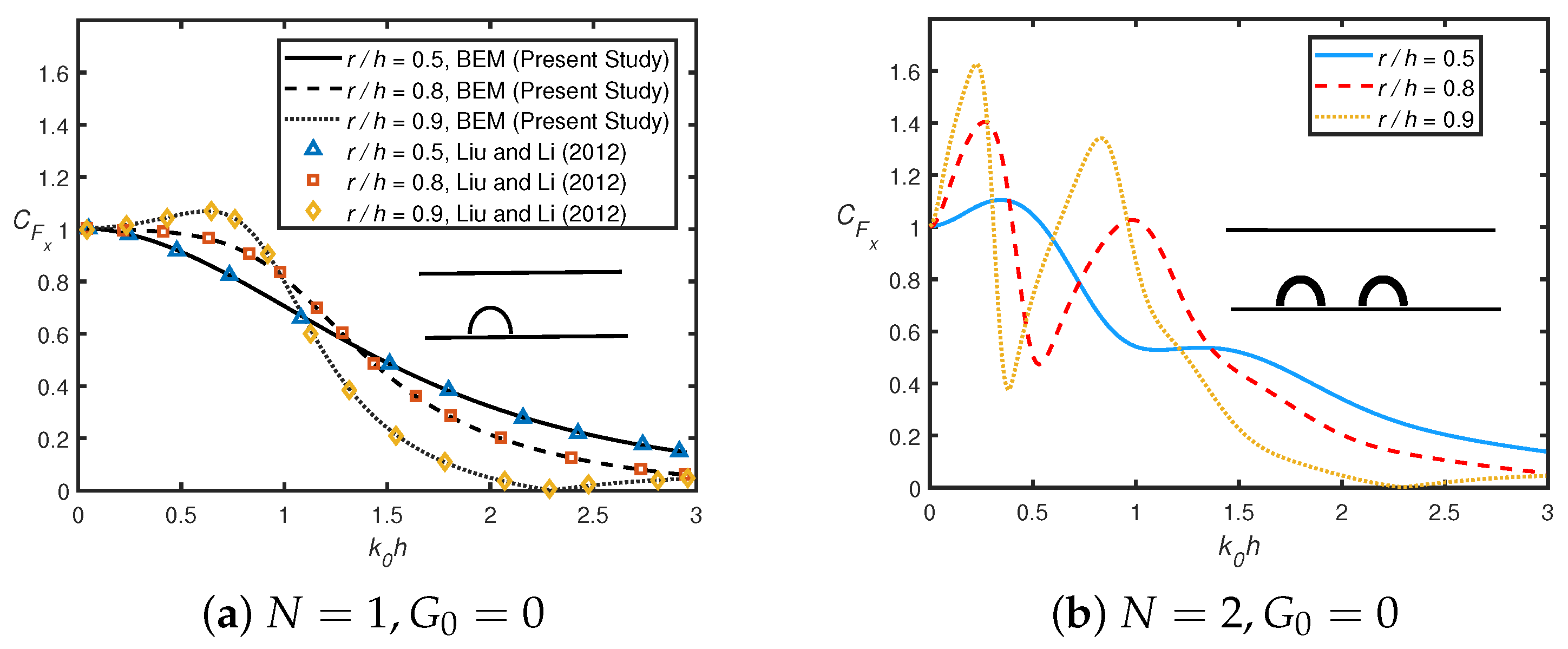
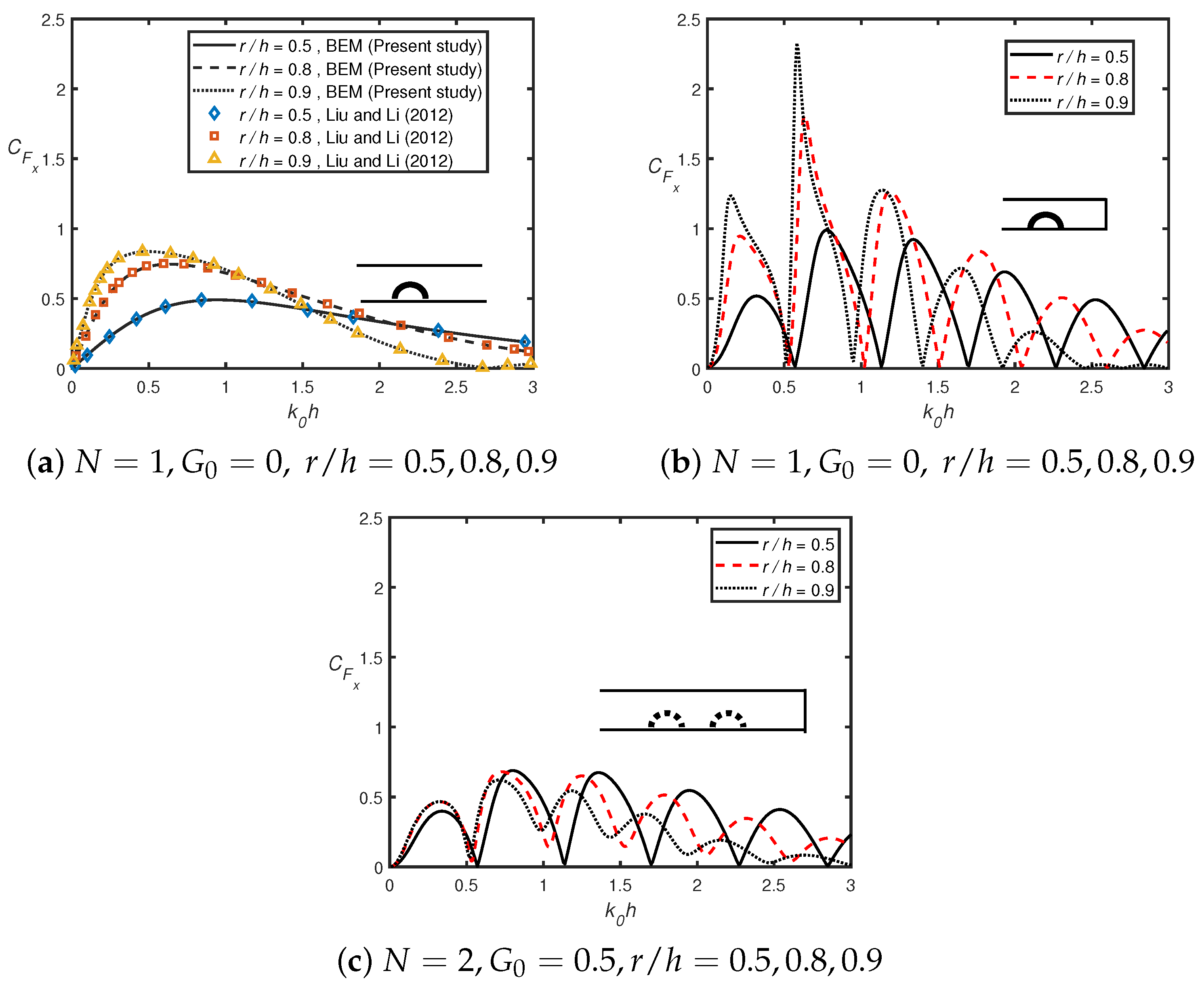
3. Convergence of Numerical Solution and Validation
4. Results and Discussion
4.1. Wave Scattering
4.1.1. In the Absence of -Type Breakwater
4.1.2. In the Presence of -Type Floating Breakwater
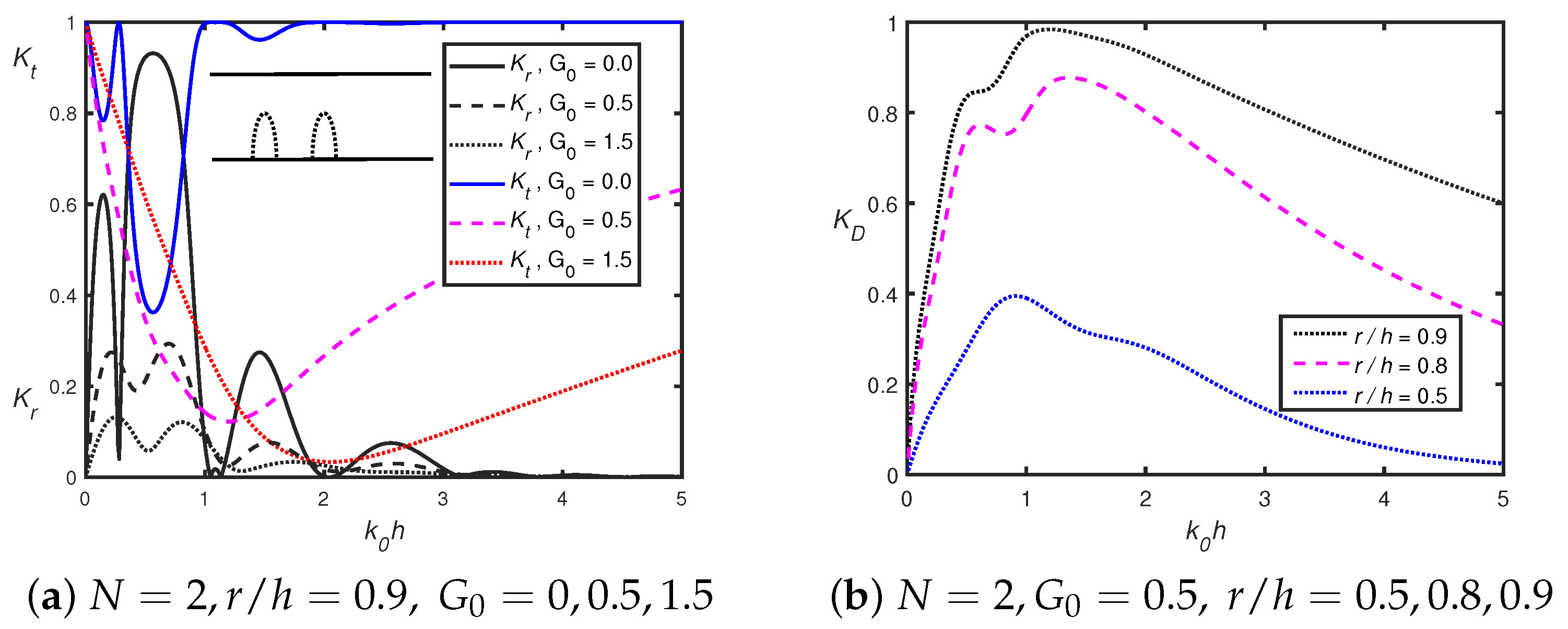
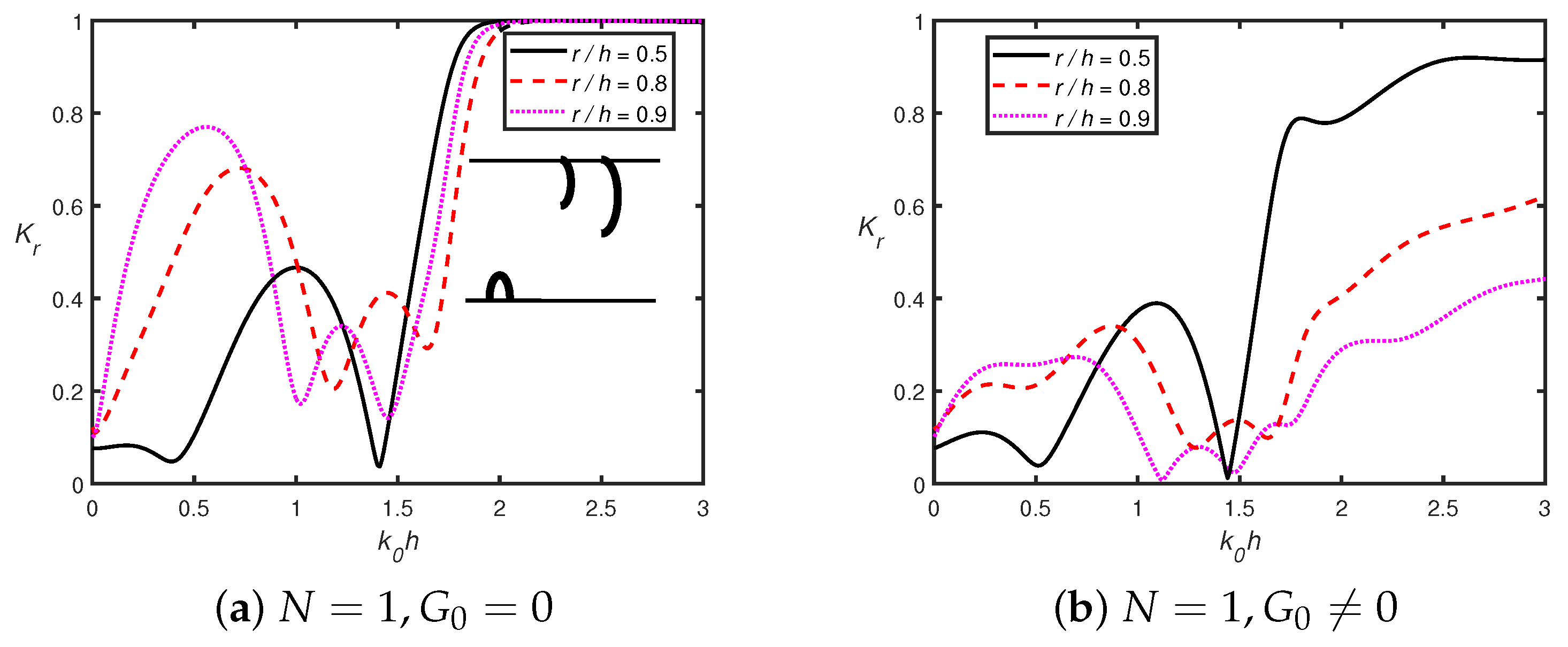
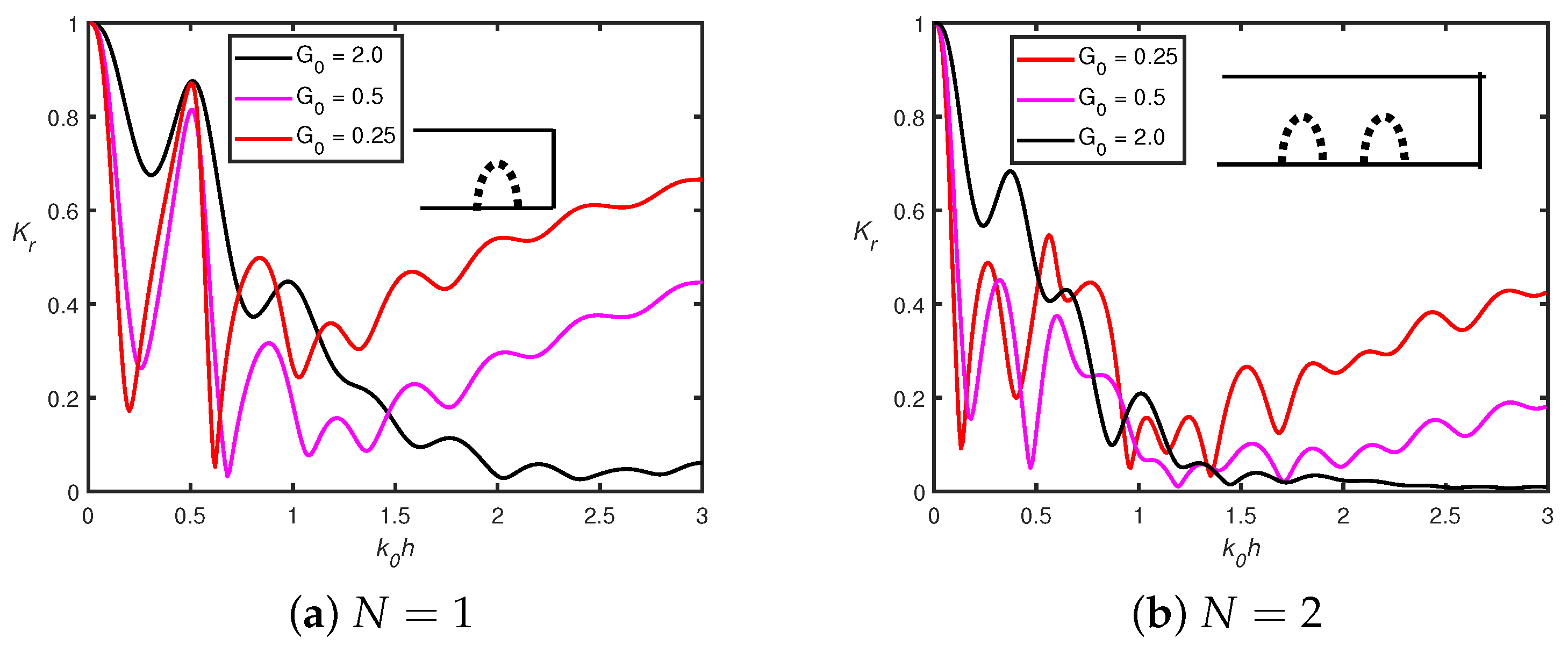
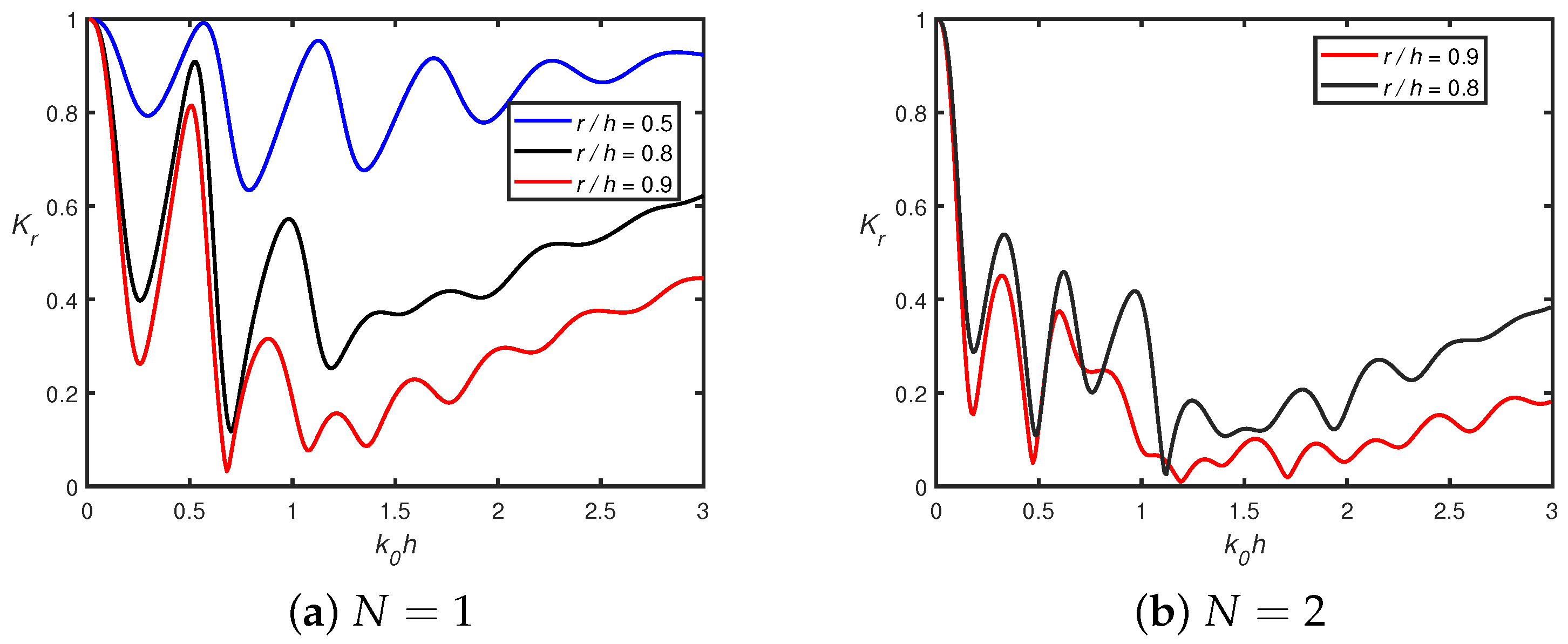
4.2. Wave Trapping
4.2.1. In the Absence of -Type Floating Breakwater
4.2.2. In the Presence of -Type Floating Breakwater
5. Conclusions
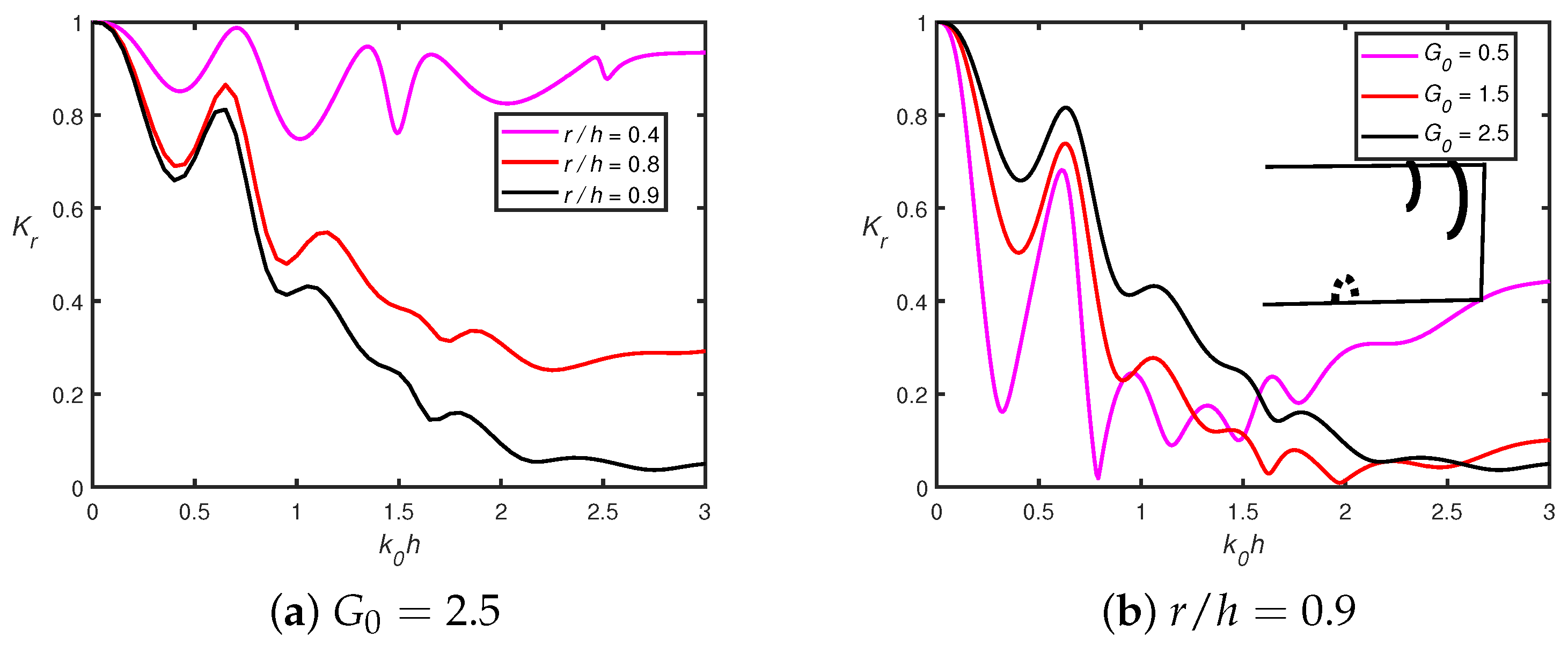
- In the presence of a shore-fixed wall, the higher Bragg reflection occurs for smaller wavenumbers, which is due to constructive interference between the semicircles and the rigid wall. The peak amplitude in the reflection coefficient decreases as the number of semicircles increases.
- The wave reflection decreases as the radius of the perforated semicircle becomes larger. Therefore, the radius of the perforated semicircle is crucial in diminishing the energy of the incoming waves.
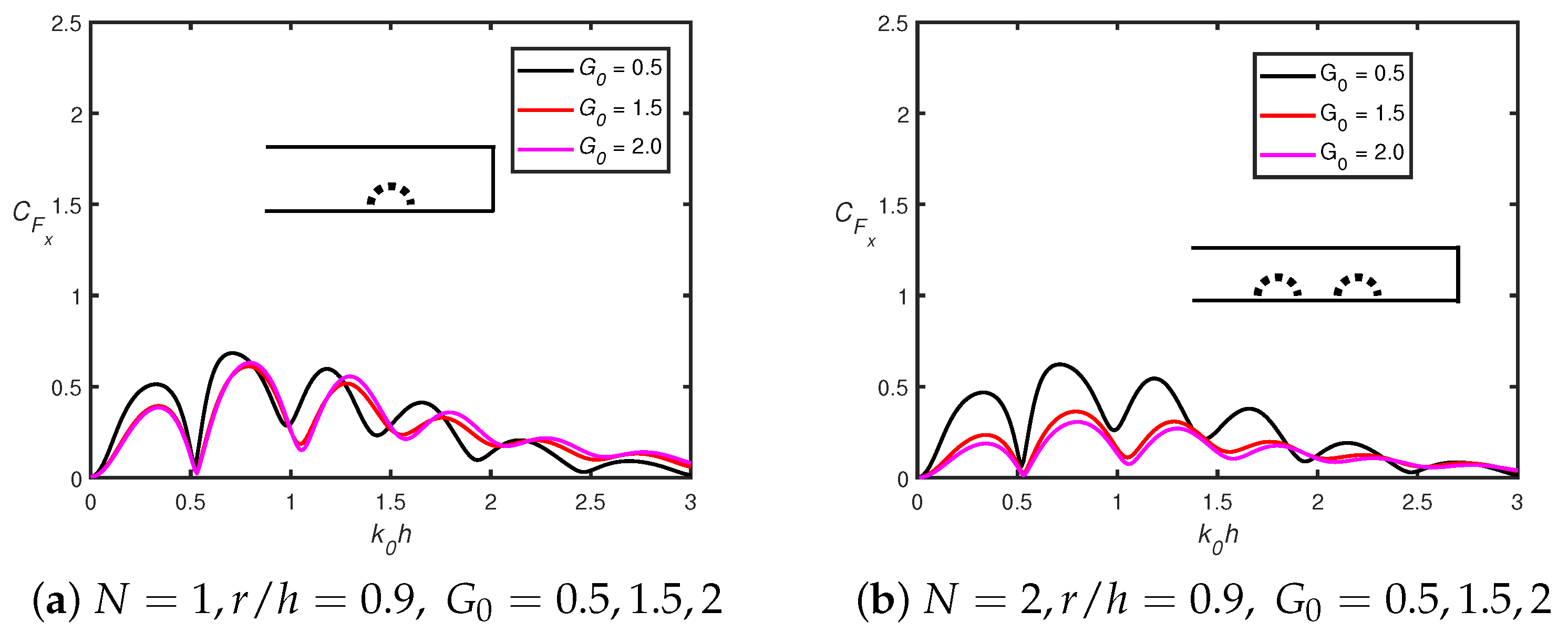
- Horizontal force acting on the first semicircular hump follows the Bragg resonance pattern in the presence of a shore-fixed wall, whilst it is not observed in the absence of a shore-fixed wall.
- Moreover, the horizontal force acting on the shore-fixed wall drastically decreases in the presence of porosity as compared to its absence.
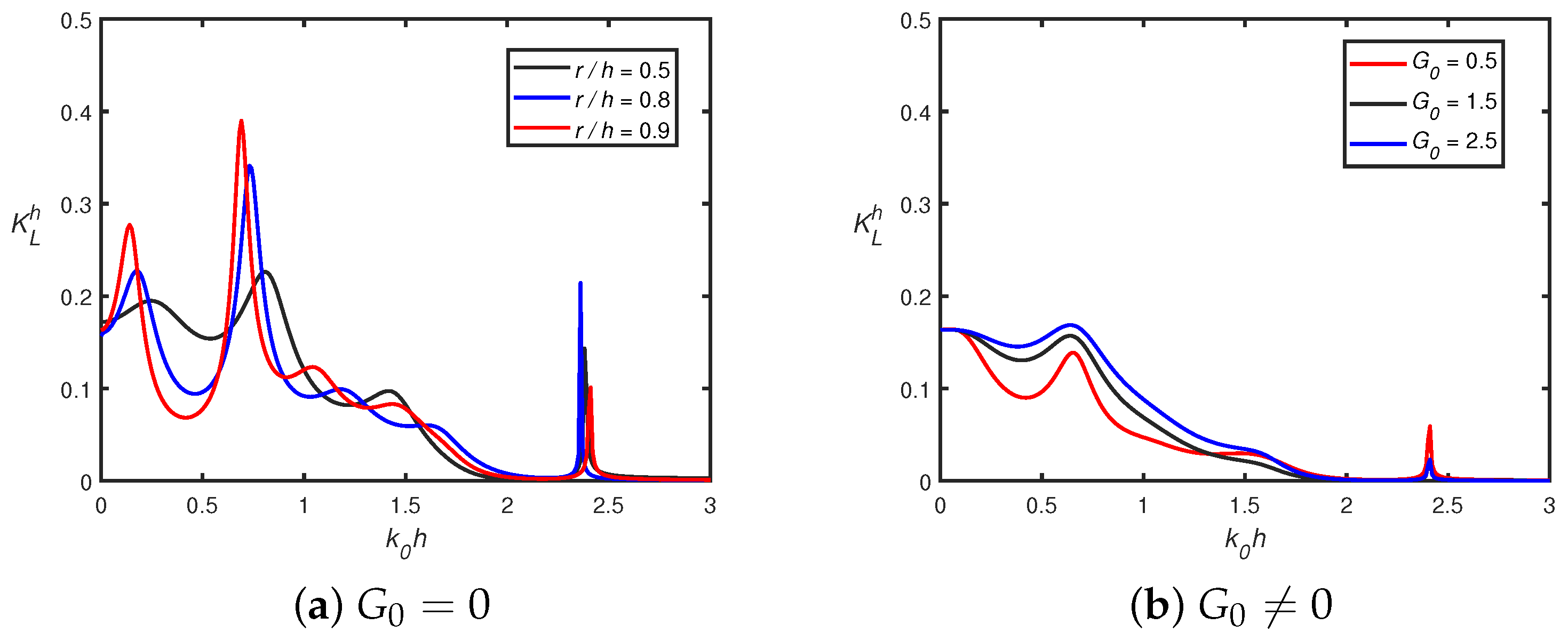
- In addition, when wavenumbers shift to zero, the vertical force converges to zero for multiple permeable semicircular humps, whilst it converges to unity in the case of multiple impermeable semicircular humps.
- The amplitude of wave attenuation decreases when the number of perforated bottom-standing semicircular humps increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mei, C.C.; Black, J.L. Scattering of surface waves by rectangular obstacles in waters of finite depth. J. Fluid Mech. 1969, 38, 499–511. [Google Scholar] [CrossRef]
- Porter, R.; Porter, D. Interaction of water waves with three-dimensional periodic topography. J. Fluid Mech. 2001, 434, 301–335. [Google Scholar] [CrossRef]
- Xie, J.J.; Liu, H.W. Analytical study of Bragg resonances by a finite periodic array of congruent trapezoidal bars or trenches on a sloping seabed. Appl. Math. Model. 2023, 119, 717–735. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.J.; Zhu, L. Bragg reflection of water waves by multiple submerged semi-circular breakwaters. Appl. Ocean Res. 2016, 56, 67–78. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, H.W.; Lin, P. Quantitative Expression of the Modified Bragg’s Law for Bragg resonances of water waves excited by five types of artificial bars. Phys. Fluids 2024, 36, 047130. [Google Scholar] [CrossRef]
- Akarni, H.; Mabchour, H.; Aarabi, L.; Mordane, S. Wave reflection by rectangular breakwaters for coastal protection. Fluid Dyn. Mater. Process. 2024, 20, 579. [Google Scholar] [CrossRef]
- Goyal, D.; Martha, S. Optimal allocation of multiple rigid bars with unequal draft to enhance Bragg reflection of surface gravity waves. Ships Offshore Struct. 2025, 1–10. [Google Scholar] [CrossRef]
- Anilkumar, S.; Panduranga, K. Analysis of Bragg reflection phenomenon induced by an array of submerged twin-wing breakwaters. Phys. Fluids 2025, 37, 077184. [Google Scholar] [CrossRef]
- Teng, B.; Zhang, X.; Ning, D. Interaction of oblique waves with infinite number of perforated caissons. Ocean Eng. 2004, 31, 615–632. [Google Scholar] [CrossRef]
- Dhinakaran, G.; Sundar, V.; Sundaravadivelu, R. Review of the research on emerged and submerged semicircular breakwaters. Proc. Inst. Mech. Eng. M J. Eng. Marit. Environ. 2012, 226, 397–409. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.C.; Teng, B. Interaction between oblique waves and perforated caisson breakwaters with perforated partition walls. Eur. J. Mech. B Fluids 2016, 56, 143–155. [Google Scholar] [CrossRef]
- Koley, S.; Sahoo, T. Wave interaction with a submerged semicircular porous breakwater placed on a porous seabed. Eng. Anal. Bound. Elem. 2017, 80, 18–37. [Google Scholar] [CrossRef]
- Li, A.j.; Liu, Y.; Liu, X.; Zhao, Y. Analytical and experimental studies on Bragg scattering of water waves by multiple submerged perforated semi-circular breakwaters. Ocean Eng. 2020, 209, 107419. [Google Scholar] [CrossRef]
- Sharma, M.; Kaligatla, R.; Sahoo, T. Wave interaction with a submerged floating tunnel in the presence of a bottom mounted submerged porous breakwater. Appl. Ocean Res. 2020, 96, 102069. [Google Scholar] [CrossRef]
- Khan, M.B.; Behera, H. Analysis of wave action through multiple submerged porous structures. J. Offshore Mech. Arct. Eng. 2020, 142, 011101. [Google Scholar] [CrossRef]
- Li, A.j.; Sun, X.l.; Liu, Y.; Li, H.j. Analysis of water wave interaction with multiple submerged porous reef balls. J. Eng. Math. 2021, 127, 26. [Google Scholar] [CrossRef]
- Vijay, K.; Venkateswarlu, V.; Sahoo, T. Bragg scattering of surface gravity waves by an array of submerged breakwaters and a floating dock. Wave Motion 2021, 106, 102807. [Google Scholar] [CrossRef]
- Ni, Y.l.; Teng, B. Bragg resonant reflection of water waves by a Bragg breakwater with porous trapezoidal bars on a sloping permeable seabed. Appl. Ocean Res. 2021, 114, 102770. [Google Scholar] [CrossRef]
- Han, M.; Wang, C. Potential flow theory-based analytical and numerical modelling of porous and perforated breakwaters: A review. Ocean Eng. 2022, 249, 110897. [Google Scholar] [CrossRef]
- Pan, D.; Xu, L.; Chen, H. Experimental study on seabed-fixed cylinders with truncated porous shells. Ocean Eng. 2025, 311, 117902. [Google Scholar]
- Venkateswarlu, V.; Vijay, K.; Sannasiraj, S.A. Enhancement in Hydrodynamic Performance of a Quarter-Circular Breakwater Using a Porous Shield. J. Offshore Mech. Arct. Eng. 2025, 147, 051204. [Google Scholar] [CrossRef]
- Sahoo, G.; Venkateswarlu, V.; Martha, S. Mitigation of structural response on a floating elastic plate in the presence of multiple porous structures. Appl. Ocean Res. 2025, 154, 104412. [Google Scholar] [CrossRef]
- Penney, W.G.; Price, A.T.; Martin, J.; Moyce, W.; Penney, W.G.; Price, A.; Thornhill, C. Part I. The diffraction theory of sea waves and the shelter afforded by breakwaters. Philos. Trans. R. Soc. A Math. Phy. Sci. 1952, 244, 236–253. [Google Scholar]
- Chang, J.Y.; Tsai, C.C. Wave forces on a partially reflecting wall by oblique Bragg scattering with porous breakwaters over uneven bottoms. J. Mar. Sci. Eng. 2022, 10, 409. [Google Scholar] [CrossRef]
- Halvorson, B.; Huang, Z. Study of effects of perforation layouts on wave energy dissipation caused by a submerged perforated breakwater in front of a vertical seawall. Ocean Eng. 2024, 311, 119025. [Google Scholar] [CrossRef]
- Swami, K.C.; Koley, S. Wave trapping by porous breakwater near a rigid wall under the influence of ocean current. Sci. Rep. 2024, 14, 17325. [Google Scholar] [CrossRef]
- Dora, R.R.; Mondal, R.; Mohanty, S.K. Wave trapping by porous breakwater near a wall under the influence of ocean current. Ocean Eng. 2024, 303, 117820. [Google Scholar] [CrossRef]
- Matsui, T.; Kato, K.; Shirai, T. A hybrid integral equation method for diffraction and radiation of water waves by three-dimensional bodies. Comput. Mech. 1987, 2, 119–135. [Google Scholar] [CrossRef]
- Hess, J.; Smith, A. Calculation of nonlifting potential flow about arbitrary three-dimensional bodies. J. Ship Res. 1964, 8, 22–44. [Google Scholar] [CrossRef]
- Magkouris, A.; Bonovas, M.; Gerostathis, T.; Belibassakis, K. A 3D BEM Model for the Hydrodynamic Analysis and Design of Heaving WEC Arrays Attached to a Breakwater. Sustainability 2023, 15, 12777. [Google Scholar] [CrossRef]
- Brebbia, C.A.; Dominguez, J.; Tassoulas, J.L. Boundary Elements: An Introductory Course. J. Appl. Mech. 1991, 3, 860. [Google Scholar] [CrossRef]
- Sauter, S.; Schwab, C. Boundary Element Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mei, C. The Applied Dynamics of Ocean Surface Waves; World Scientific: Singapore, 1989. [Google Scholar]
- Show, T.K.; Hirdaris, S.; Datta, R. A Fully Coupled Time-Domain BEM-FEM Method for the Prediction of Symmetric Hydroelastic Responses of Ships with Forward Speed. Shock Vib. 2022, 2022, 4564769. [Google Scholar] [CrossRef]
- Evans, D.; Linton, C. Trapped modes in open channels. J. Fluid Mech. 1991, 225, 153–175. [Google Scholar] [CrossRef]
- Linton, C.; McIver, P. Embedded trapped modes in water waves and acoustics. Wave Motion 2007, 45, 16–29. [Google Scholar] [CrossRef]
- Barman, S.; Das, S.; Sahoo, T.; Meylan, M. Scattering of flexural-gravity waves by a crack in a floating ice sheet due to mode conversion during blocking. J. Fluid Mech. 2021, 916, A11. [Google Scholar] [CrossRef]
- Yu, X.; Chwang, A. Wave-induced oscillation in harbor with porous breakwaters. J. Waterw. Port Coast 1994, 120, 125–144. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.J. Analysis of wave interaction with submerged perforated semi-circular breakwaters through multipole method. Appl. Ocean Res. 2012, 34, 164–172. [Google Scholar] [CrossRef]
- Kar, P.; Koley, S.; Sahoo, T. Scattering of surface gravity waves over a pair of trenches. Appl. Math. Model. 2018, 62, 303–320. [Google Scholar] [CrossRef]
- Tsai, C.C.; Behera, H.; Hsu, T.W. Analysis of water wave interaction with multiple submerged semi-circular porous structures. Arch. Appl. Mech. 2023, 93, 2693–2709. [Google Scholar] [CrossRef]
- Cho, Y.S.; Lee, J.I.; Kim, Y.T. Experimental study of strong reflection of regular water waves over submerged breakwaters in tandem. Ocean Eng. 2004, 31, 1325–1335. [Google Scholar] [CrossRef]
- McIVER, M. Diffraction of water waves by a moored, horizontal, flat plate. J. Eng. Math. 1985, 19, 297–319. [Google Scholar] [CrossRef]



| 0.1104 | 0.8326 | 0.2945 | 0.0214 | 0.3922 | 0.8456 | 0.0100 | 0.1917 | 0.9631 | |
| 0.1104 | 0.8326 | 0.2945 | 0.0213 | 0.3922 | 0.8456 | 0.0102 | 0.1917 | 0.9631 | |
| 0.1104 | 0.8326 | 0.2945 | 0.0213 | 0.3922 | 0.8456 | 0.0102 | 0.1916 | 0.9631 |
| 0.3031 | 0.0315 | 0.3434 | 0.0866 | 0.1499 | 0.0568 | |
| 0.3035 | 0.0307 | 0.3434 | 0.0867 | 0.1498 | 0.0569 | |
| 0.3034 | 0.0306 | 0.3434 | 0.0866 | 0.1498 | 0.0568 |
| Liu and Li [39] | 0.3162 | 0.6103 | 0.0631 | 0.3975 | 0.0185 | 0.6041 |
| BEM (present study) | 0.3161 | 0.6106 | 0.0633 | 0.3975 | 0.0185 | 0.6043 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Sea-side breakwater depth | 0.24 | Porosity | 0.5 |
| Lee-side breakwater depth | 0.28 | Water depth h | 10 (m) |
| Gap between breakwaters | 1 | Radius of semicircle | 0.5 |
| Breakwaters thickness | 0.1 | Gap from breakwater to semicircle | 1 |
| Gap between the semicircles | 1 | Gap from vertical wall to breakwater | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kar, P.; Behera, H.; Ning, D. Wave Scattering and Trapping by C-Type Floating Breakwaters in the Presence of Bottom-Standing Perforated Semicircular Humps. Mathematics 2025, 13, 3372. https://doi.org/10.3390/math13213372
Kar P, Behera H, Ning D. Wave Scattering and Trapping by C-Type Floating Breakwaters in the Presence of Bottom-Standing Perforated Semicircular Humps. Mathematics. 2025; 13(21):3372. https://doi.org/10.3390/math13213372
Chicago/Turabian StyleKar, Prakash, Harekrushna Behera, and Dezhi Ning. 2025. "Wave Scattering and Trapping by C-Type Floating Breakwaters in the Presence of Bottom-Standing Perforated Semicircular Humps" Mathematics 13, no. 21: 3372. https://doi.org/10.3390/math13213372
APA StyleKar, P., Behera, H., & Ning, D. (2025). Wave Scattering and Trapping by C-Type Floating Breakwaters in the Presence of Bottom-Standing Perforated Semicircular Humps. Mathematics, 13(21), 3372. https://doi.org/10.3390/math13213372








