Sharp Functional Inequalities for Starlike and Convex Functions Defined via a Single-Lobed Elliptic Domain

Abstract

In this paper, we introduce two novel subclasses of analytic functions, namely, starlike and convex functions of Ma–Minda-type, associated with a newly proposed domain. We set sharp bounds on the basic coefficients of these classes and provide sharp estimates of the second- and third-order Hankel determinants, demonstrating the power of our analytic approach, the clarity of its results, and its applicability even in unconventional domains.

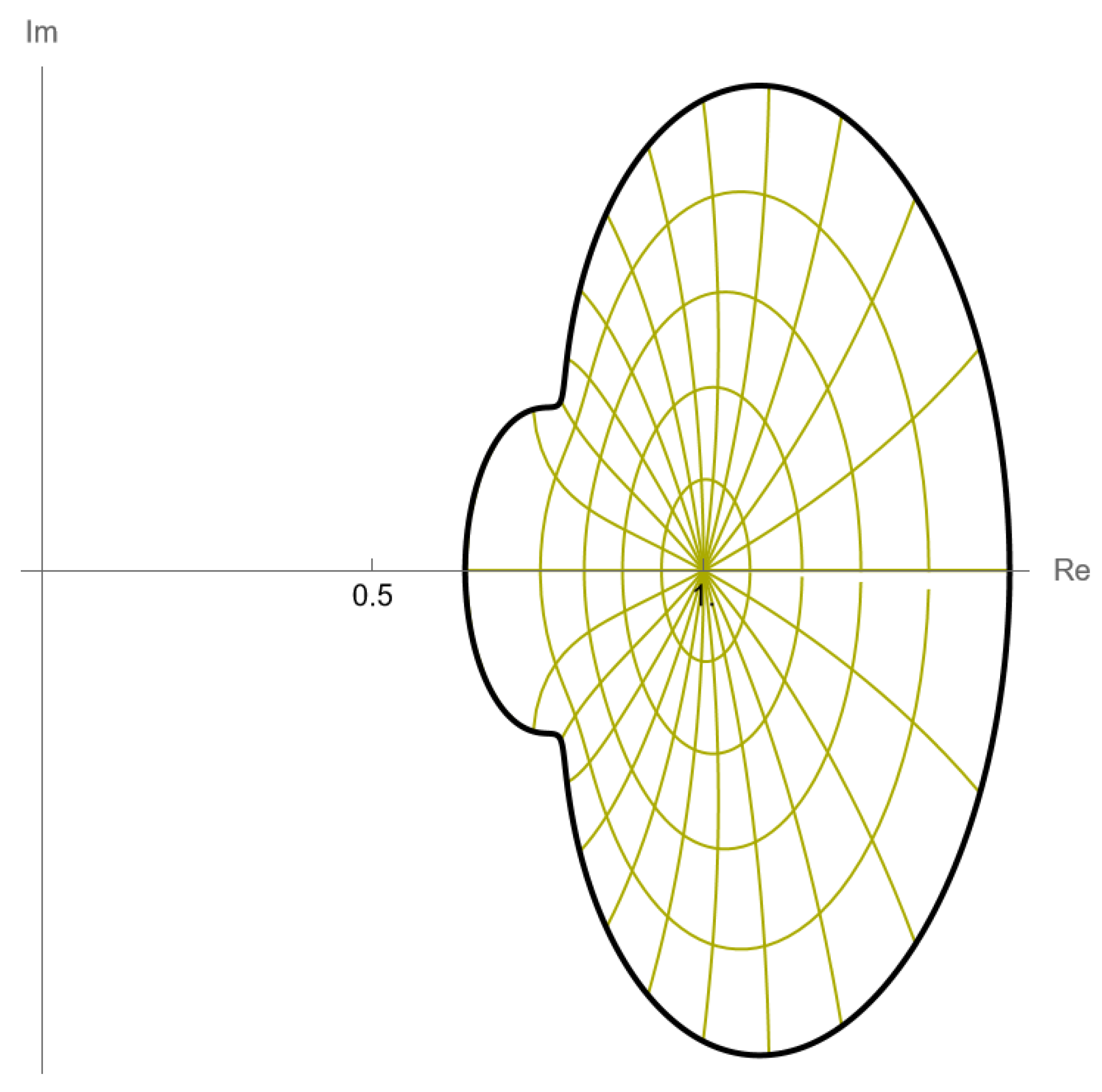
1. Introduction

Let $\mathbb{A}$ denote the class of normalized analytic functions in the open unit disk $\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\},$ which admit the Taylor series expansion

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n,z\in \mathbb{D}.$$

(1)

In this setting, we denote by $\mathsf{S}$ the subclass of $\mathbb{A}$ consisting of functions that are univalent in $\mathbb{D}$.

It is worth noting that the study of the class $\mathsf{S}$ has a rich history in geometric function theory. One of the most celebrated problems in this area was the Bieberbach conjecture, proposed in 1916, which asserted that if $f\in \mathsf{S}$, then $|a_n|\le n$ for every $n\ge 2$. The first cases were settled gradually: $|a_2|\le 2$ was established by Bieberbach himself, while the case $n=3$ was proved by Löwner using the differential equations that now bear his name. Subsequent contributions by Schaeffer, Spencer, Jenkins, Garabedian, Schiffer, Pedersen, and Ozawa extended the range of verified cases through a variety of analytic and variational techniques. The conjecture remained in full generality for decades until de Branges, in 1985, settled the problem for all $n\ge 2$ by employing methods involving hypergeometric functions. This landmark result highlights the deep significance of coefficient problems in the theory of univalent functions.

An analytic function f is said to be subordinate to another analytic function g, denoted by $f\prec g$, if there exists a Schwarz function w, analytic in $\mathbb{D}$ with $w\left(0\right)=0$ and $|w(z)|<1$, such that $f\left(z\right)=g\left(w\right(z\left)\right)$. In the special case when g is univalent and $f\left(0\right)=g\left(0\right)$, the subordination relation ensures that $f\left(\mathbb{D}\right)\subset g\left(\mathbb{D}\right)$.

Let $\varphi$ be an analytic and univalent function in $\mathbb{D}$ such that $\varphi \left(0\right)=1$, ${\varphi }^{\prime }\left(0\right)>0$, and whose image is symmetric with respect to the real axis. Under these assumptions, Ma and Minda [1] extended the notion of classical starlike and convex functions by introducing the subclasses

$${\mathsf{S}}^{*}\left(\varphi \right):=\left\{f\in \mathbb{A}:{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec \varphi \left(z\right)\right\},\mathcal{C}\left(\varphi \right):=\left\{f\in \mathbb{A}:1+{\displaystyle \frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}}\prec \varphi \left(z\right)\right\}.$$

To position the present work within the existing literature and highlight its novelty, we provide a brief overview of selected starlike function classes in

Table 1. Examples of starlike function classes with their associated functions.

${\mathsf{S}}^{*}\left(\mathit{\phi }\right)$	$\mathit{\phi }\left(\mathit{z}\right)$	References
${\mathsf{S}}_e^{*}$	$e^z$	[2]
${\mathsf{S}}_{SG}^{*}$	${\displaystyle \frac{2}{1+e^{-z}}}$	[3]
${\mathsf{S}}_{RL}^{*}$	$\sqrt{2}-(\sqrt{2}-1)\sqrt{{\displaystyle \frac{1-z}{1+2(\sqrt{2}-1)z}}}$	[4]
${\mathsf{S}}_{☾}^{*}$	$z+\sqrt{1+z^2}$	[5]
${\mathsf{S}}_C^{*}$	$1+{\displaystyle \frac{4z}{3}}+{\displaystyle \frac{2z^2}{3}}$	[6]
${\mathsf{S}}_H^{*}$	$1+z+{\displaystyle \frac{1}{3}}{z}^2-{\displaystyle \frac{1}{9}}{z}^3$	[7]
${\mathsf{S}}_{\varrho }^{*}$	$cosh\sqrt{z}$	[8]
${\mathsf{S}}_k^{*}$	$2-\sqrt[3]{{\displaystyle \frac{4}{{(1+e^{2z})}^2}}}$	[9]

. These classes are constructed by choosing specific functions and include notable examples such as the various Ma–Minda-type classes introduced in recent years [2,3,4,5,6,7,8,9]. Table 1 summarizes these classes, their defining functions, and key references. This overview illustrates the research gaps that motivated the present study and emphasizes how our approach, focusing on a single-lobed elliptic domain and combining geometric analysis with computational tools, extends and advances the state-of-the-art methods.

In the present work, instead of choosing $\varphi \left(z\right)$ to map onto the right half-plane, we consider a univalent function $\varphi \left(z\right)$ that maps the unit disk $\mathbb{D}$ onto a domain resembling a single-lobed elliptical region. Based on this choice, we introduce two classes of functions, which can be seen as particular instances of this general setting.

$${\mathsf{S}}_{LE}^{*}:=\left\{f\in \mathbb{A}:{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec {\varphi }_{LE}\left(z\right),z\in \mathbb{D}\right\},$$

(2)

and

$${\mathcal{C}}_{LE}:=\left\{f\in \mathbb{A}:1+{\displaystyle \frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}}\prec {\varphi }_{LE}\left(z\right),z\in \mathbb{D}\right\}.$$

(3)

where these classes are characterized via the analytic function ${\varphi }_{LE}:\mathbb{D}\to \mathbb{C}$, which satisfies the following formula:

$${\varphi }_{LE}\left(z\right)=2-\sqrt{{\displaystyle \frac{2-z^2}{2\left(1+{sin}^{-1}\left(\frac{2z}{3}\right)\right)}}}=1+{\displaystyle \frac{z}{3}}+{\displaystyle \frac{z^2}{12}}+{\displaystyle \frac{11z^3}{324}}-{\displaystyle \frac{5z^4}{864}}+\dots ,z\in \mathbb{D}.$$

(4)

It is clear from Figure 1 that the curves do not intersect themselves, which supports the fact that the function is univalent. This observation can be easily verified using computational software such as Mathematica or Maple, since our function is somewhat complicated and providing a formal proof of univalence is challenging.

Motivated by these challenges, the present work aims to introduce two specific subclasses of univalent functions associated with a single-lobed elliptical domain, denoted as ${\mathsf{S}}_{LE}^{*}$ and ${\mathcal{C}}_{LE}$, and to determine sharp bounds for their coefficients and the third-order Hankel determinant. This study extends the classical framework of starlike and convex functions by incorporating geometric considerations of the image domain. Meanwhile, the next two results establish explicit representation formulas for functions belonging to the classes ${\mathsf{S}}_{LE}^{*}$ and ${\mathcal{C}}_{LE}$.

Theorem 1.

Let f be analytic in $\mathbb{D}$. Then $f\in {\mathsf{S}}_{LE}^{*}$ if and only if

$$f\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathcal{N}\left(\varsigma \right)-1}{\varsigma }}d\varsigma \right),z\in \mathbb{D},$$

(5)

for some analytic function $\mathcal{N}\left(z\right)$ satisfying the subordination $\mathcal{N}\left(z\right)\prec {\varphi }_{LE}\left(z\right)$.

Proof. 

Assume $f\in {\mathsf{S}}_{LE}^{*}$. Define the functions

$$\mathcal{N}\left(\varsigma \right):={\displaystyle \frac{\varsigma f^{\prime }\left(\varsigma \right)}{f\left(\varsigma \right)}},\mathrm{and}r\left(\varsigma \right):={\displaystyle \frac{f\left(\varsigma \right)}{\varsigma }}.$$

Then, it follows that $\mathcal{N}\left(\varsigma \right)\prec {\varphi }_{LE}$ and $r\left(\varsigma \right)\ne 0$. Applying logarithmic differentiation to $r\left(\varsigma \right)$, we obtain

$${\displaystyle \frac{r^{\prime }\left(\varsigma \right)}{r\left(\varsigma \right)}}={\displaystyle \frac{\mathcal{N}\left(\varsigma \right)-1}{\varsigma }},\varsigma \in \mathbb{D}.$$

(6)

Integrating Equation (6) from 0 to z yields the representation in Equation (5). □

Corollary 1.

Let g be analytic in $\mathbb{D}$. Then, $g\in {\mathcal{C}}_{LE}$ if and only if

$$g\left(z\right)={\int }_0^{z}exp\left({\int }_0^w{\displaystyle \frac{\mathcal{N}\left(\varsigma \right)-1}{\varsigma }}d\varsigma \right)dw,z\in \mathbb{D},$$

(7)

for some analytic function $\mathcal{N}\left(z\right)$ subordinate to ${\varphi }_{LE}$.

Proof. 

This result is an immediate consequence of the classical Alexander relation between the classes ${\mathsf{S}}_{LE}^{*}$ and ${\mathcal{C}}_{LE}$. □

Below, we provide examples to demonstrate that the introduced classes are non-empty. These examples also serve to support the sharpness of the conjectures that will be presented in the coefficient estimation section.

Example 1.

Let us define the following analytic functions:

$${\mathcal{N}}_1\left(z\right)=1+{\displaystyle \frac{zsinz}{5}},{\mathcal{N}}_2\left(z\right)=1+{\displaystyle \frac{z{e}^z}{7}},{\mathcal{N}}_3\left(z\right)=1+{\displaystyle \frac{3z-z^3}{15}}.$$

It can be readily verified that ${\mathcal{N}}_i\left(0\right)=1$ and the image of ${\mathcal{N}}_i$ over the unit disk satisfies ${\mathcal{N}}_i\left(\mathbb{D}\right)\subseteq {\varphi }_{LE}\left(\mathbb{D}\right)$ for $i=1,2,3$. Given that ${\varphi }_{LE}\in S$, this inclusion implies that ${\mathcal{N}}_i\prec {\varphi }_{LE}$ for $i=1,2,3$. Consequently, by invoking Theorem 1 and Corollary 1, it follows that the corresponding functions $f_i\left(z\right)$ (or $g_i\left(z\right)$), $i=1,2,3$, defined accordingly, lie within the classes ${\mathsf{S}}_{LE}^{*}$ (or ${\mathcal{C}}_{LE}$) (as illustrated in Figure 2). The corresponding functions are given by

$$\begin{array}{cc}\hfill f_1\left(z\right)& =zexp\left({\displaystyle \frac{1-cosz}{5}}\right)=z+{\displaystyle \frac{z^3}{10}}-{\displaystyle \frac{z^5}{300}}-{\displaystyle \frac{7z^7}{18000}}+\dots ,\hfill \\ \hfill f_2\left(z\right)& =zexp\left({\displaystyle \frac{e^z-1}{7}}\right)=z+{\displaystyle \frac{z^2}{7}}+{\displaystyle \frac{4z^3}{49}}+{\displaystyle \frac{71z^4}{2058}}+{\displaystyle \frac{243z^5}{19208}}+\dots ,\hfill \\ \hfill f_3\left(z\right)& =zexp\left({\displaystyle \frac{9z-z^3}{45}}\right)=z+{\displaystyle \frac{z^2}{5}}+{\displaystyle \frac{z^3}{50}}-{\displaystyle \frac{47z^4}{2250}}-{\displaystyle \frac{197z^5}{45000}}+\dots .\hfill \end{array}$$

Furthermore,

$$\begin{array}{cc}\hfill g_1\left(z\right)& =z+{\displaystyle \frac{z^3}{30}}-{\displaystyle \frac{z^5}{1500}}-{\displaystyle \frac{z^7}{18000}}+\dots ,\hfill \\ \hfill g_2\left(z\right)& =z+{\displaystyle \frac{z^2}{14}}+{\displaystyle \frac{4z^3}{147}}+{\displaystyle \frac{71z^4}{8232}}+{\displaystyle \frac{243z^5}{96040}}+\dots ,\hfill \\ \hfill g_3\left(z\right)& =z+{\displaystyle \frac{z^2}{10}}+{\displaystyle \frac{z^3}{150}}-{\displaystyle \frac{47z^4}{9000}}-{\displaystyle \frac{197z^5}{225000}}+\dots .\hfill \end{array}$$

Figure 2 below illustrates the required inclusion, demonstrating that the introduced function classes are non-empty.

Example 2.

The following formula yields an infinite number of functions:

$$s_n\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{1-\sqrt{(2-{\varsigma }^{2n})/2\left(1+{sin}^{-1}\left(2{\varsigma }^n/3\right)\right)}}{\varsigma }}d\varsigma \right),z\in \mathbb{D},n=1,2,3,\dots ,$$

(8)

belonging to ${\mathsf{S}}_{LE}^{*}$. In particular,

$$\begin{array}{cc}\hfill s_1\left(z\right)& =z+{\displaystyle \frac{z^2}{3}}+{\displaystyle \frac{7z^3}{72}}+{\displaystyle \frac{61z^4}{1944}}+{\displaystyle \frac{281z^5}{46656}}+\dots ,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill s_2\left(z\right)& =z+{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{5z^5}{144}}+{\displaystyle \frac{77z^7}{7776}}+\dots ,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill s_3\left(z\right)& =z+{\displaystyle \frac{z^4}{9}}+{\displaystyle \frac{13z^7}{648}}+{\displaystyle \frac{97z^{10}}{17496}}+\dots ,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill s_4\left(z\right)& =z+{\displaystyle \frac{z^5}{12}}+{\displaystyle \frac{z^9}{72}}+\dots .\hfill \end{array}$$

(12)

Example 3.

The following formula yields an infinite number of functions:

$$c_n\left(z\right)={\int }_0^{z}exp\left({\int }_0^w{\displaystyle \frac{1-\sqrt{(2-{\varsigma }^{2n})/2\left(1+{sin}^{-1}\left(2{\varsigma }^n/3\right)\right)}}{\varsigma }}d\varsigma \right)dw,z\in \mathbb{D},n=1,2,3,\dots ,$$

(13)

belonging to ${\mathcal{C}}_{LE}$, and

$$\begin{array}{cc}\hfill c_1\left(z\right)& =z+{\displaystyle \frac{z^2}{6}}+{\displaystyle \frac{7z^3}{216}}+{\displaystyle \frac{61z^4}{7776}}+{\displaystyle \frac{281z^5}{233280}}+\dots ,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill c_2\left(z\right)& =z+{\displaystyle \frac{z^3}{18}}+{\displaystyle \frac{z^5}{144}}+{\displaystyle \frac{11z^7}{7776}}+\dots ,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill c_3\left(z\right)& =z+{\displaystyle \frac{z^4}{36}}+{\displaystyle \frac{13z^7}{4536}}+{\displaystyle \frac{97z^{10}}{174960}},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill c_4\left(z\right)& =z+{\displaystyle \frac{z^5}{60}}+{\displaystyle \frac{z^9}{648}}+\dots .\hfill \end{array}$$

(17)

The qth Hankel determinant for analytic functions $f\in \mathbb{A}$ was introduced by Pommerenke [10] and is defined as

$$H_{q,n}\left(f\right):=\left|\begin{array}{cccc}{a}_n& a_{n+1}& \dots & a_{n+q-1}\\ a_{n+1}& a_{n+2}& \dots & a_{n+q}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n+q-1}& a_{n+q}& \dots & a_{n+2q-2}\end{array}\right|,n\ge 1,q\ge 1.$$

In general, sharp bounds for the second Hankel determinant

$$|H_{2,2}\left(f\right)|=\left|\begin{array}{cc}{a}_2\hfill & a_3\hfill \\ a_3\hfill & a_4\hfill \end{array}\right|=\left|a_2{a}_4-a_3^2\right|,$$

for various subclasses of univalent functions can often be derived relatively easily using standard techniques (see, e.g., [11,12,13,14,15,16,17,18,19,20]). However, determining sharp bounds for the third Hankel determinant

$$|H_{3,1}\left(f\right)|=\left|\begin{array}{ccc}{a}_1\hfill & a_2\hfill & a_3\hfill \\ a_2\hfill & a_3\hfill & a_4\hfill \\ a_3\hfill & a_4\hfill & a_5\hfill \end{array}\right|.$$

Since $a_1=1$ in this case, the formula simplifies to

$$|H_{3,1}\left(f\right)|=\left|a_3\left(a_2{a}_4-a_3^2\right)-a_4\left(a_4-a_2{a}_3\right)+a_5\left(a_3-a_2^2\right)\right|.$$

(18)

The study of Hankel determinants, particularly of higher order, has gained increasing attention in geometric function theory due to their deep connections with coefficient problems and complex analytic structures. While the second Hankel determinant has been extensively analyzed for various subclasses of univalent functions, sharp bounds for the third-order determinant remain more challenging, motivating further investigation. Moreover, recent advances in defining univalent functions through image domains with specific geometric properties, such as elliptical regions, provide new opportunities to extend classical results (see [21,22,23]). To date, only a few sharp bounds have been obtained, while several non-sharp bounds for $H_{3,1}\left(f\right)$ have been reported in the literature, e.g., [24,25,26,27,28,29]. Recently, some authors [30,31,32,33,34,35] have successfully established sharp estimates for $H_{3,1}\left(f\right)$ in certain subclasses of univalent functions.

Despite previous studies providing both sharp and non-sharp estimates for the third-order Hankel determinant in various subclasses, precise bounds for functions associated with single-lobed elliptical domains remain unexplored. This motivates the present work, which aims to establish accurate coefficient bounds and determinant estimates, thereby contributing to a deeper understanding of univalent function theory in geometrically defined domains and laying the groundwork for further investigations.

2. Fundamental Lemmas

The fundamental lemmas serve as essential analytical tools for establishing the subsequent results. They provide core estimates and inequalities for the coefficients of functions belonging to the Carathéodory class $\mathsf{P}$, as given by the expression

$$p\left(z\right)=1+\sum _{n=1}^{\infty }{c}_n{z}^n,z\in \mathbb{D},$$

(19)

which will be employed in proving the main results.

Lemma 1

([36]). Let $p\in \mathsf{P}$ with Equation (19). Then,

$$|c_k|\le 2,k\in \mathbb{N},$$

(20)

$$|c_{k+n}-\mu c_k{c}_n|\le 2,\mu \in (0,1],k,n\in \mathbb{N},$$

(21)

$$|c_2-\eta c_1^2|\le 2max\{1,|2\eta -1|\},\eta \in \mathbb{C}.$$

(22)

Lemma 2

([37]). Let $p\in \mathsf{P}$ with Equation (19), and suppose $R\in [0,1]$ satisfies $R(2R-1)\le S\le R$. Then,

$$|S{c}_1^3-2R{c}_1{c}_2+c_3|\le 2.$$

(23)

Lemma 3

([38]). Let $\alpha ,\beta ,\gamma ,$ and ζ satisfy $\alpha ,\zeta \in (0,1)$ with

$$8\zeta (1-\zeta )\left[{(\alpha \beta -2\gamma )}^2+{(\alpha (\zeta +\alpha )-\beta )}^2\right]+\alpha (1-\alpha ){(\beta -2\zeta \alpha )}^2\le 4\zeta {\alpha }^2{(1-\alpha )}^2(1-\zeta ).$$

Then, for $p\in \mathsf{P}$ with Equation (19), we have

$$\left|\gamma c_1^4+\zeta c_2^2+2\alpha c_1{c}_3-{\displaystyle \frac{3}{2}}\beta c_1^2{c}_2-c_4\right|\le 2.$$

(24)

Lemma 4

([39,40,41]). Let $p\in \mathsf{P}$ with Equation (17). Then,

$$2c_2=c_1^2+\zeta (4-c_1^2),$$

(25)

$$4c_3=c_1^3+2(4-c_1^2)c_1\zeta -(4-c_1^2)c_1{\zeta }^2+2(4-c_1^2){(1-|\zeta |}^2)\eta ,$$

(26)

$$\begin{array}{cc}\hfill 8c_4& =c_1^4+(4-c_1^2)\zeta \left(c_1^2({\zeta }^2-3\zeta +3)+4\zeta \right)\hfill \\ \hfill & -4(4-c_1^2){(1-|\zeta |}^2)\left(c_1(\zeta -1)\eta +\overline{\zeta }{\eta }^2{-(1-|\eta |}^2)\rho \right),\hfill \end{array}$$

(27)

for some $\rho ,\zeta ,\eta$ such that $max\{|\rho |,|\zeta |,|\eta |\}\le 1$.

3. Estimate of 2nd Hankel Determinant

In this section, we aim to compute the initial coefficients $a_n$ for $n=2,3,4,5$ by determining their sharp bounds for both our classes.

Theorem 2.

Let $f\in {\mathsf{S}}_{LE}^{*}$. Then

$$|a_2|\le {\displaystyle \frac{1}{3}},|a_3|\le {\displaystyle \frac{1}{6}},|a_4|\le {\displaystyle \frac{1}{9}},|a_5|\le {\displaystyle \frac{1}{12}}.$$

These estimates are sharp by Equations (9)–(12).

Proof. 

Let $f\in {\mathsf{S}}_{LE}^{*}$. Then,

$${\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}=2-\sqrt{{\displaystyle \frac{2-{\left(\omega \left(z\right)\right)}^2}{2\left(1+{sin}^{-1}\left(\frac{2\omega \left(z\right)}{3}\right)\right)}}},z\in \mathbb{D},$$

(28)

for some Schwarz function $\omega \left(z\right)$.

It is possible to assume the existence of a function $p\in \mathsf{P}$. Then, a well-known relation connects it to a Schwarz function, which can be expressed as follows:

$$p\left(z\right)={\displaystyle \frac{1+\omega \left(z\right)}{1-\omega \left(z\right)}}=1+c_{1}z+c_2{z}^2+c_3{z}^3+\dots .$$

Hence,

$$\begin{array}{cc}\hfill \omega \left(z\right)& ={\displaystyle \frac{1}{2}}{c}_{1}z+\left({\displaystyle \frac{1}{2}}{c}_2-{\displaystyle \frac{1}{4}}{c}_1^2\right)z^2+\left({\displaystyle \frac{1}{8}}{c}_1^3-{\displaystyle \frac{1}{2}}{c}_1{c}_2+{\displaystyle \frac{1}{2}}{c}_3\right)z^3\hfill \\ & +\left({\displaystyle \frac{1}{2}}{c}_4-{\displaystyle \frac{1}{2}}{c}_1{c}_3-{\displaystyle \frac{1}{4}}{c}_2^2-{\displaystyle \frac{1}{16}}{c}_1^4+{\displaystyle \frac{3}{8}}{c}_1^2{c}_2\right)z^4+\dots .\hfill \end{array}$$

(29)

Substituting Equation (29) into Equation (28), and performing some simplifications, we obtain

$$\begin{array}{cc}\hfill & 1+a_{2}z+(-a_2^2+2a_3)z^2+\left(-a_2^3+2a_2(a_2^2-a_3)-a_2{a}_3+3a_4\right)z^3\hfill \\ \hfill & +\left(a_2^4-3a_2^2{a}_3+3(a_2^2-a_3)a_3+a_3^2+2a_2(-a_2^3+2a_2{a}_3-a_4)-2a_2{a}_4+4a_5\right)z^4+\dots \hfill \\ \hfill & =1+{\displaystyle \frac{c_{1}z}{6}}+{\displaystyle \frac{-3c_1^2+8c_2}{48}}{z}^2+\left({\displaystyle \frac{11c_1^3}{2592}}-{\displaystyle \frac{1}{48}}{c}_1(c_1^2-2c_2)+{\displaystyle \frac{c_1^3-4c_1{c}_2+4c_3}{24}}\right)z^3\hfill \\ \hfill & +(-{\displaystyle \frac{5c_1^4}{13824}}-{\displaystyle \frac{11c_1^2(c_1^2-2c_2)}{1728}}+{\displaystyle \frac{3c_1^4-12c_1^2{c}_2+4c_2^2+8c_1{c}_3}{192}}\hfill \\ \hfill & +{\displaystyle \frac{-c_1^4+6c_1^2{c}_2-4c_2^2-8c_1{c}_3+8c_4}{48}})z^4+\dots ,\hfill \end{array}$$

(30)

Now, by comparing the coefficients of both sides of Equation (30), it follows that

$$\begin{array}{cc}\hfill & a_2={\displaystyle \frac{1}{6}}{c}_1,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & a_3={\displaystyle \frac{1}{12}}(c_2-{\displaystyle \frac{5}{24}}{c}_1^2),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & a_4={\displaystyle \frac{1}{18}}({\displaystyle \frac{61}{864}}{c}_1^3-{\displaystyle \frac{432}{864}}{c}_1{c}_2+c_3),\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & a_5={\displaystyle \frac{1}{746496}}(7776c_1^2{c}_2-9072c_2^2-16416c_1{c}_3+31104c_4-1123c_1^4),\hfill \end{array}$$

(34)

These formulas express the initial coefficients $a_2,a_3,a_4,a_5$ explicitly in terms of the coefficients $c_1,c_2,c_3,c_4$ of the auxiliary function $p\left(z\right)$ defined in Equation (29).

From Equations (20) and (31), it follows that

$$|a_2|\le {\displaystyle \frac{1}{3}}.$$

Also, from Equations (22) and (32), we obtain

$$|a_3|\le {\displaystyle \frac{1}{6}}.$$

We can also rewrite Equation (33) in the following form:

$$a_4={\displaystyle \frac{1}{18}}\left({\displaystyle \frac{61}{864}}{c}_1^3-2·{\displaystyle \frac{216}{864}}{c}_1{c}_2+c_3\right).$$

Assuming $R={\displaystyle \frac{216}{864}}\in [0,1]$ and $S={\displaystyle \frac{61}{864}}$, the inequality $R(2R-1)\le S\le R$ is satisfied. Accordingly, using Equation (23), we obtain

$$|a_4|\le {\displaystyle \frac{1}{9}}.$$

We can rewrite Equation (34) as follows:

$$a_5=-{\displaystyle \frac{1}{24}}\left(\gamma c_1^4+\zeta c_2^2+2\alpha c_1{c}_3-{\displaystyle \frac{3}{2}}\beta c_1^2{c}_2-c_4\right),$$

where

$$\gamma ={\displaystyle \frac{1123}{31104}},\zeta ={\displaystyle \frac{7}{24}},\alpha ={\displaystyle \frac{19}{72}},\beta ={\displaystyle \frac{1}{6}}.$$

Since

$$8\zeta (1-\zeta )\left[{(\alpha \beta -2\gamma )}^2+{(\alpha (\zeta +\alpha )-\beta )}^2\right]+\alpha (1-\alpha ){(\beta -2\zeta \alpha )}^2=0.002\dots ,$$

and

$$4\zeta {\alpha }^2{(1-\alpha )}^2(1-\zeta )=0.031\dots ,$$

then, applying Equation (24) in Lemma 3, we obtain

$$|a_5|\le {\displaystyle \frac{1}{12}}.$$

The desired estimates are thus established. □

Motivated by the sharp bounds obtained for the initial coefficients, we propose the following conjecture for higher-order coefficients:

Conjecture 1.

Let $f\in {\mathsf{S}}_{LE}^{*}$. Then,

$$|a_k|\le {\displaystyle \frac{1}{3(k-1)}},k=2,3,\dots .$$

Theorem 3.

Let $f\in {\mathcal{C}}_{LE}$. Then,

$$|a_2|\le {\displaystyle \frac{1}{6}},|a_3|\le {\displaystyle \frac{1}{18}},|a_4|\le {\displaystyle \frac{1}{36}},|a_5|\le {\displaystyle \frac{1}{60}}.$$

These estimates are sharp by Equations (14)–(17).

Proof. 

Let $f\in {\mathcal{C}}_{LE}$. Then,

$$1+{\displaystyle \frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}}=2-\sqrt{{\displaystyle \frac{2-{\left(\omega \left(z\right)\right)}^2}{2\left(1+{sin}^{-1}\left(\frac{2\omega \left(z\right)}{3}\right)\right)}}},z\in \mathbb{D},$$

(35)

for some Schwarz function $\omega \left(z\right)$ satisfying Equation (29). Substituting Equation (29) into Equation (35), followed by algebraic simplification, leads to

$$\begin{array}{cc}\hfill & 1+2z{a}_2+z^2(-4a_2^2+6a_3)+2z^3(4a_2^3-9a_2{a}_3+6a_4)\hfill \\ \hfill & +z^4\left(6(4a_2^2-3a_3)a_3+2a_2(-8a_2^3+12a_2{a}_3-4a_4)-24a_2{a}_4+20a_5\right)+\dots \hfill \\ \hfill & =1+{\displaystyle \frac{c_{1}z}{6}}+{\displaystyle \frac{-3c_1^2+8c_2}{48}}{z}^2+\left({\displaystyle \frac{11c_1^3}{2592}}-{\displaystyle \frac{1}{48}}{c}_1(c_1^2-2c_2)+{\displaystyle \frac{c_1^3-4c_1{c}_2+4c_3}{24}}\right)z^3\hfill \\ \hfill & +(-{\displaystyle \frac{5c_1^4}{13824}}-{\displaystyle \frac{11c_1^2(c_1^2-2c_2)}{1728}}+{\displaystyle \frac{3c_1^4-12c_1^2{c}_2+4c_2^2+8c_1{c}_3}{192}}\hfill \\ \hfill & +{\displaystyle \frac{-c_1^4+6c_1^2{c}_2-4c_2^2-8c_1{c}_3+8c_4}{48}})z^4+\dots .\hfill \end{array}$$

(36)

By comparing the corresponding coefficients of both sides in Equation (36), the following relations are obtained:

$$\begin{array}{cc}\hfill & a_2={\displaystyle \frac{c_1}{12}},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & a_3={\displaystyle \frac{1}{36}}(c_2-{\displaystyle \frac{5}{24}}{c}_1^2),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & a_4={\displaystyle \frac{1}{72}}({\displaystyle \frac{61}{864}}{c}_1^3-{\displaystyle \frac{432}{864}}{c}_1{c}_2+c_3),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & a_5={\displaystyle \frac{1}{3732480}}(-1123c_1^4-9072c_2^2-16416c_1{c}_3+7776c_1^2{c}_2+31104c_4),\hfill \end{array}$$

(40)

The remaining steps of the proof follow precisely the same framework employed in the proof of Theorem 2. In particular, the argument is completed by applying Lemmas 1–3 in the same logical order and deductive sequence. Hence, the structure of the proof is finalized, and its validity is thus established. □

We conclude this section by presenting the following conjecture, which arises naturally from the estimates established in the above theorem, reflecting the sharp estimates obtained for the initial coefficients and generalizing them to higher-order coefficients.

Conjecture 2.

Let $f\in {\mathcal{C}}_{LE}$. Then

$$|a_k|\le {\displaystyle \frac{1}{3k(k-1)}},k=2,3,\dots .$$

In subsequent estimates, we examined sharp bounds of the second-order Hankel determinant for analytic classes (starlike and convex).

Theorem 4.

Let $f\in {\mathsf{S}}_{LE}^{*}$. Then

$$|a_2{a}_4-a_3^2|\le {\displaystyle \frac{1}{36}}.$$

The sharpness is attained for the function given by Equation (10).

Proof. 

Starting from the established coefficient relationships, we can express

$$a_2{a}_4-a_3^2={\displaystyle \frac{263}{746496}}{c}_1^4-{\displaystyle \frac{1}{576}}{c}_1^2{c}_2-{\displaystyle \frac{1}{144}}{c}_2^2+{\displaystyle \frac{1}{108}}{c}_1{c}_3.$$

By applying Lemma 4 with the substitutions $c_1=c$, $|\eta |=1$, and $y=|\delta |$, we obtain

$$\begin{array}{cc}\hfill |a_2{a}_4-a_3^2|& =|{\displaystyle \frac{47}{746496}}{c}^4-{\displaystyle \frac{1}{432}}(4-c^2)c^2{\delta }^2+{\displaystyle \frac{1}{3456}}(4-c^2)c^2\delta \hfill \\ \hfill & +{\displaystyle \frac{1}{216}}c(4-c^2){(1-|\delta |}^2)\eta -{\displaystyle \frac{1}{576}}{(4-c^2)}^2{\delta }^2|.\hfill \end{array}$$

Applying the triangle inequality and taking absolute values leads to

$$\begin{array}{cc}\hfill |a_2{a}_4-a_3^2|& \le {\displaystyle \frac{47}{746496}}{c}^4+{\displaystyle \frac{1}{432}}(4-c^2)c^2{y}^2+{\displaystyle \frac{1}{3456}}(4-c^2)c^{2}y\hfill \\ \hfill & +{\displaystyle \frac{1}{216}}c(4-c^2)(1-y^2)+{\displaystyle \frac{1}{576}}{(4-c^2)}^2{y}^2\hfill \\ \hfill & :=M(y,c).\hfill \end{array}$$

In order to proceed, we aim to maximize $M(y,c)$. Differentiating $M(y,c)$ with respect to y, we obtain

$$\begin{array}{cc}\hfill M_y& ={\displaystyle \frac{1}{216}}(4-c^2)c^{2}y+{\displaystyle \frac{1}{3456}}(4-c^2)c^2-{\displaystyle \frac{1}{108}}c(4-c^2)y+{\displaystyle \frac{1}{288}}{(4-c^2)}^{2}y\hfill \\ \hfill & ={\displaystyle \frac{1}{3456}}(4-c^2)\left(48y+4y{c}^2-32cy+c^2\right).\hfill \end{array}$$

It is easy to verify that $M_y\ge 0$ for $y\in [0,1]$. Therefore, the function $M(y,c)$ attains its maximum at $y=1$, which gives

$$M\left(c\right)\equiv M(1,c)={\displaystyle \frac{47}{746496}}{c}^4+{\displaystyle \frac{1}{384}}(4-c^2)c^2+{\displaystyle \frac{1}{576}}{(4-c^2)}^2.$$

Next, we determine the value of c that maximizes $M\left(c\right)$. Differentiating $M\left(c\right)$ with respect to c, we find

$$M^{\prime }\left(c\right)=-{\displaystyle \frac{1}{186624}}c(1296+601c^2).$$

Setting $M^{\prime }\left(c\right)=0$ yields three roots: $c=0$ and two complex roots. Since $c=0$ is the only root in the interval $[0,2]$ and $M^{\prime \prime }\left(0\right)<0$, the maximum occurs at $c=0$. Thus, we obtain

$$|a_2{a}_4-a_3^2|\le M(1,0)={\displaystyle \frac{1}{36}}.$$

This completes the argument, confirming the stated inequality. □

By adopting a reasoning analogous to that employed for the class ${\mathsf{S}}_{LE}^{*}$, the proof for the class ${\mathcal{C}}_{LE}$ follows similarly. Hence, we state the result without providing the full proof.

Theorem 5.

Let $f\in {\mathcal{C}}_{LE}$. Then

$$|a_2{a}_4-a_3^2|\le {\displaystyle \frac{1}{324}}.$$

The bound is sharp and is attained by the function given in Equation (15).

After obtaining precise estimates for the initial coefficients and the second-order Hankel determinants, we naturally proceed to study the third-order Hankel determinants. This transition reflects the direct connection between the function coefficients and the associated geometric analyses, allowing for more complete and accurate results.

4. Third Hankel Determinants

In this section, we present a precise and systematic methodology for establishing the sharp upper bounds of the third-order Hankel determinants for both classes ${\mathsf{S}}_{LE}^{*}$ and ${\mathcal{C}}_{LE}$. The approach adopted here carefully combines analytical techniques and the application of previously developed lemmas, aiming to provide a rigorous and comprehensive treatment of these extremal problems.

Theorem 6.

Let $f\in {\mathsf{S}}_{LE}^{*}$. Then,

$$|H_{3,1}\left(f\right)|\le {\displaystyle \frac{1}{81}}.$$

This upper bound is sharp by Equation (11).

Proof. 

Let $f\in {\mathsf{S}}_{LE}^{*}$. Given the rotational invariance of the class ${\mathsf{S}}_{LE}^{*}$ and the functional $H_{3,1}\left(f\right)$, it is permissible to restrict $c_1$ to the interval $[0,2]$ without loss of generality. Substituting Equations (31)–(34) into Equation (18), we arrive at

$$\begin{array}{cc}\hfill H_{3,1}\left(f\right)& ={\displaystyle \frac{1}{483729408}}(16957c_1^6-88668c_1^4{c}_2+113832c_1^3{c}_3+113724c_1^2{c}_2^2-909792c_1^2{c}_4\hfill \\ \hfill & +1353024c_1{c}_2{c}_3-769824c_2^3+1679616c_2{c}_4-1492992c_3^2).\hfill \end{array}$$

(41)

By making use of Equations (25)–(27) and simplifying the expressions, we obtain

$$\begin{array}{cc}\hfill 88668c_1^4{c}_2& =44334\left(c_1^6+(4-c_1^2)c_1^4\zeta \right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill 113832c_1^3{c}_3& =-28458(4-c_1^2)c_1^4{\zeta }^2+56916c_1^3(4-c_1^2){(1-|\zeta |}^2)\eta \hfill \\ \hfill & +56916(4-c_1^2)c_1^4\zeta +28458c_1^6\hfill \end{array}$$

$$\begin{array}{cc}\hfill 113724c_1^2{c}_2^2& =28431c_1^6+56862(4-c_1^2)c_1^4\zeta +28431{(4-c_1^2)}^2{c}_1^2{\zeta }^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill 909792c_1^2{c}_4& ={-454896(1-|\zeta |}^2)(4-c_1^2)c_1^2{\eta }^2\overline{\zeta }-341172(4-c_1^2)c_1^4{\zeta }^2\hfill \\ \hfill & {+454896(1-|\zeta |}^2)(4-c_1^2)c_1^3\eta +454896(4-c_1^2)c_1^2{\zeta }^2\hfill \\ \hfill & +113724(4-c_1^2)c_1^4{\zeta }^3+113724c_1^6\hfill \\ \hfill & {+454896(1-|\eta |}^2\left)\right(1-{|\zeta |}^2)(4-c_1^2)c_1^2\rho +341172(4-c_1^2)c_1^4\zeta \hfill \\ \hfill & {-454896(1-|\zeta |}^2)(4-c_1^2)c_1^3\zeta \eta \hfill \end{array}$$

$$\begin{array}{cc}\hfill 1353024c_1{c}_2{c}_3& =-169128{(4-c_1^2)}^2{c}_1^2{\zeta }^3-169128(4-c_1^2)c_1^4{\zeta }^2\hfill \\ \hfill & +338256{(4-c_1^2)}^2{(1-|\zeta |}^2)c_1\zeta \eta +338256{(4-c_1^2)}^2{c}_1^2{\zeta }^2\hfill \\ \hfill & +338256(4-c_1^2){(1-|\zeta |}^2)c_1^3\eta +507384(4-c_1^2)c_1^4\zeta +169128c_1^6\hfill \end{array}$$

$$\begin{array}{cc}\hfill 769824c_2^3& =96228c_1^6+288684(4-c_1^2)c_1^4\zeta +288684{(4-c_1^2)}^2{c}_1^2{\zeta }^2+96228{(4-c_1^2)}^3{\zeta }^3\hfill \end{array}$$

$$\begin{array}{cc}\hfill 1679616c_2{c}_4& =104976c_1^6+104976{(4-c_1^2)}^2{c}_1^2{\zeta }^4+419904{(4-c_1^2)}^2{\zeta }^3\hfill \\ & -314928{(4-c_1^2)}^2{c}_1^2{\zeta }^3+104976(4-c_1^2)c_1^4{\zeta }^3-419904(4-c_1^2)\hfill \\ & {(1-|\zeta |}^2)c_1^2{\eta }^2\overline{\zeta }-419904{(4-c_1^2)}^2{(1-|\zeta |}^2)\zeta {\eta }^2\overline{\zeta }+419904(4-c_1^2)\hfill \\ & {(1-|\zeta |}^2\left)\right(1-{|\eta |}^2)c_1^2\rho +419904{(4-c_1^2)}^2{(1-|\zeta |}^2\left)\right(1-{|\eta |}^2)\zeta \rho -419904{(4-c_1^2)}^2\hfill \\ & {(1-|\zeta |}^2)c_1{\zeta }^2{\eta +419904(1-|\zeta |}^2)(4-c_1^2)c_1^3\eta +419904(4-c_1^2)c_1^4\zeta \hfill \\ \hfill & -419904(4-c_1^2){(1-|\zeta |}^2)c_1^3{\zeta \eta +419904(1-|\zeta |}^2){(4-c_1^2)}^2{c}_1\zeta \eta \hfill \\ & -419904(4-c_1^2)c_1^2{\zeta }^2-104976(4-c_1^2)c_1^4{\zeta }^2+524880{(4-c_1^2)}^2{c}_1^2{\zeta }^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill 1492992c_3^2& =93312c_1^6+93312{(4-c_1^2)}^2{c}_1^2{\zeta }^4-373248{(4-c_1^2)}^2{c}_1^2{\zeta }^3\hfill \\ & {+373248(1-|\zeta |}^2{)}^2{(4-c_1^2)}^2{\eta }^2+373248(4-c_1^2)c_1^4\zeta -186624(4-c_1^2)c_1^4{\zeta }^2\hfill \\ & +373248{(4-c_1^2)}^2{c}_1^2{\zeta }^2{+373248(1-|\zeta |}^2)(4-c_1^2)c_1^3{\eta +746496(1-|\zeta |}^2)\hfill \\ & {(4-c_1^2)}^2{c}_1{\zeta \eta -373248(1-|\zeta |}^2){(4-c_1^2)}^2{c}_1{\zeta }^2\eta \hfill \end{array}$$

Before presenting the final expressions for $H_{3,1}\left(f\right)$, we decompose each contributing term by substituting the identities from Lemma 4 and the coefficient relations, resulting in the following detailed components:

$$\begin{array}{cc}\hfill H_{3,1}\left(f\right)& ={\displaystyle \frac{1}{483729408}}\left(I_0(c,\zeta )+I_1(c,\zeta )\eta +I_2(c,\zeta ){\eta }^2+\Psi (c,\zeta ,\eta )\rho \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_0(c,\zeta )& =352c_1^6+(4-c_1^2)[(4-c_1^2)(11664{\zeta }^4{c}_1^2+229635{\zeta }^2{c}_1^2+34992{\zeta }^3-14580{\zeta }^3{c}_1^2)\hfill \\ \hfill & +(-6372\zeta c_1^4-8748{\zeta }^3{c}_1^4+225234{\zeta }^2{c}_1^4-874800{\zeta }^2{c}_1^2)],\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_1(c,\zeta )& =(4-c_1^2){(1-|\zeta |}^2)\left[(11664\zeta c_1-46656{\zeta }^2{c}_1)(4-c_1^2)-13068c_1^3+34992\zeta c_1^3\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_2(c,\zeta )& ={(1-|\zeta |}^2)(4-c_1^2)\left[{(-46656|\zeta |}^2-373248)(4-c_1^2)+34992\overline{\zeta }{c}_1^2\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Psi (c,\zeta ,\eta )& ={(1-|\eta |}^2\left)\right(1-{|\zeta |}^2)(4-c_1^2)\left[-34992c_1^2+419904(4-c_1^2)\zeta \right],\hfill \end{array}$$

for some $\rho ,\zeta ,\eta$ such that $max\{|\rho |,|\zeta |,|\eta |\}\le 1$.

After replacing $|\zeta |$ with x, $|\eta |$ with y,and setting $c:=c_1$. Since the assumption that $|\rho |\le 1$, then the expression simplifies to the following:

$$\begin{array}{cc}\hfill |H_{3,1}\left(f\right)|& \le {\displaystyle \frac{1}{483729408}}\left(|I_0(c,\zeta )|+|I_1(c,\zeta )|y+|I_2(c,\zeta )|y^2+|\Psi (c,\zeta ,\eta )|\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{483729408}}T(c,x,y),\hfill \end{array}$$

where

$$T(c,x,y)=v_0(c,x)+v_1(c,x)y+v_2(c,x)y^2+v_3(c,x)(1-y^2),$$

with

$$\begin{array}{cc}\hfill v_0(c,x)& =352c^6+(4-c^2)[(4-c^2)(11664x^4{c}^2+229635x^2{c}^2+34992x^3+14580x^3{c}^2)\hfill \\ \hfill & +(6372x{c}^4+8748x^3{c}^4+225234x^2{c}^4+874800x^2{c}^2)],\hfill \\ \hfill v_1(c,x)& =(4-c^2)(1-x^2)\left[(11664xc+46656x^{2}c)(4-c^2)+13068c^3+34992x{c}^3\right],\hfill \\ \hfill v_2(c,x)& =(1-x^2)(4-c^2)\left[(46656x^2+373248)(4-c^2)+34992x{c}^2\right],\hfill \\ \hfill v_3(c,x)& =(1-x^2)(4-c^2)\left[34992c^2+419904(4-c^2)x\right].\hfill \end{array}$$

To accomplish this, the analysis must be conducted in three distinct parts: first, within the interior of the domain $S=[0,2]\times [0,1]\times [0,1]$; second, on its boundary faces; and finally, along its edges.

Case I: In order to examine how the function $T(c,x,y)$ changes as y varies, we proceed by evaluating its partial derivative with respect to y:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial T}{\partial y}}& =(4-c^2)(1-x^2)[-108(-432cx(1+4x)+c^3(-121-216x+432x^2)\hfill \\ \hfill & -3456(8-9x+x^2)y+216c^2(35-39x+4x^2)y\left)\right].\hfill \end{array}$$

Imposing the condition ${\displaystyle \frac{\partial T}{\partial y}}=0$, we obtain

$$y={\displaystyle \frac{c\left(121c^2+1296x+216x\left(4-c^2\right)(2x-1)\right)}{216(x-1)\left(4\left(4-c^2\right)(8-x)-3c^2\right)}}=y_p.$$

If $y_p$ is a critical point within $\mathrm{\Lambda }$, which possible only if

$$\begin{array}{c}\hfill 121c^3+1296xc+216\left(4-c^2\right)cx(-1+2x)+864(1-x)\left(4-c^2\right)(8-x)<648(1-x)c^2\end{array}$$

(42)

and

$$\begin{array}{c}\hfill c^2>{\displaystyle \frac{16(8-x)}{(35-4x)}}.\end{array}$$

(43)

Now, only a solution that can meet both the inequalities in Equations (42) and (43) will be accepted as a critical point. Assuming $\hslash \left(x\right)={\displaystyle \frac{16(8-x)}{(35-4x)}}$ and ${\hslash }^{\prime }\left(x\right)=-{\displaystyle \frac{48}{{(35-4x)}^2}}<0$, which yields to $\hslash \left(x\right)$ is decreasing function, that is

$$c^2>{\displaystyle \frac{112}{31}}.$$

Suppose $\hslash \left(x\right)={\displaystyle \frac{16(8-x)}{(35-4x)}}$. Thus, $\hslash \left(x\right)$ decreases over $(0,1)$. Thus, $c^2>0$, and a straightforward task illustrates that Equation (42) will not hold for all values of $x\in (0,1)$. This implies that we have not found a critical point for T in $(0,2)\times (0,1)\times (0,1)$.

Case II: Interior of all six faces of the cuboid

(i) If $c=0$, the function T reduces

$$h_1(x,y)=559872x^3+6718464\left(1-x^2\right)x\left(1-y^2\right)+16\left(1-x^2\right)\left(46656x^2+373248\right)y^2,$$

then

$${\displaystyle \frac{\partial h_1}{\partial y}}=32\left(1-x^2\right)\left(46656x^2+373248\right)y-13436928x\left(1-x^2\right)y\ne 0\mathrm{for}y\in (0,1),$$

which implies that $h_1$ has no optimal points in $(0,1)\times (0,1).$

(ii) If $c=2$, we obtain

$$T(2,x,y)=22528.$$

(iii) If $x=0$, we get

$$h_2(c,y)=352c^6+34992\left(4-c^2\right)c^2\left(1-y^2\right)+373248{\left(4-c^2\right)}^2{y}^2+13068\left(4-c^2\right)c^{3}y,$$

then ${\displaystyle \frac{\partial h_2}{\partial y}}=0$ gives

$$y={\displaystyle \frac{121c^3}{216\left(35c^2-128\right)}}.$$

The range of $y\in (0,1)$, if $c>c_0\approx 1.94313$ Also ${\displaystyle \frac{\partial h_2}{\partial c}}=0$ gives

$$\begin{array}{cc}\hfill 2112c^5& -26136c^{4}y-69984c^3\left(1-y^2\right)-1492992\left(4-c^2\right)c{y}^2\hfill \\ & +69984\left(4-c^2\right)c\left(1-y^2\right)+39204\left(4-c^2\right)c^{2}y.\hfill \end{array}$$

Putting the value of y gives

$$3637095c^9-369172968c^7+3240787200c^5-9602924544c^3+9172942848c=0.$$

Solving c within the range $(0,2)$, we have $c\approx 1.42775$. This indicates that the function $T(c,0,y)$ has no optimal solution.

(iv) If $q=1$, then the function T reduces

$$h_3(c,1,y)=15877c^6-1925424c^4+7313328c^2+559872$$

then ${\displaystyle \frac{\partial h_3}{\partial c}}=0$ gives the critical point $c\approx 1.39499$, which yields that the maximum value of $h_3$ is $7.6171.$ (i.e., ($h_3\le 7.6171\left)\right).$

(v) If $y=0$, the function T reduces

$$\begin{array}{cc}\hfill h_4(c,x)& =139968c^2-34992c^4+352c^6+6718464x-3359232c^{2}x+445392c^{4}x-6372c^{6}x\hfill \\ & +7033392c^2{x}^2-1775952c^4{x}^2+4401c^6{x}^2-6158592x^3+3312576c^2{x}^3\hfill \\ & -466560c^4{x}^3+5832c^6{x}^3+186624c^2{x}^4-93312c^4{x}^4+11664c^6{x}^4.\hfill \end{array}$$

Thus

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial h_4}{\partial c}}& =69984c^5{x}^4+34992c^5{x}^3+26406c^5{x}^2-38232c^{5}x+2112c^5-373248c^3{x}^4\hfill \\ & -1866240c^3{x}^3-7103808c^3{x}^2+1781568c^{3}x-139968c^3+373248c{x}^4+6625152c{x}^3\hfill \\ & +14066784c{x}^2-6718464cx+279936c\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial h_4}{\partial x}}& =46656c^6{x}^3+17496c^6{x}^2+8802c^{6}x-6372c^6-373248c^4{x}^3-1399680c^4{x}^2\hfill \\ & -3551904c^{4}x+445392c^4+746496c^2{x}^3+9937728c^2{x}^2+14066784c^{2}x-3359232c^2\hfill \\ & -18475776x^2+6718464.\hfill \end{array}$$

Computation shows that the system of equations ${\displaystyle \frac{\partial h_4}{\partial c}}=0$ and ${\displaystyle \frac{\partial h_4}{\partial x}}=0$ have no exact solution in $(0,2)\times (0,1).$

(vi) on the face $y=1$, the function T reduces

$$\begin{array}{cc}\hfill h_5(c,x)& =11664c^6{x}^4+5832c^6{x}^3+4401c^6{x}^2-6372c^{6}x+352c^6-46656c^5{x}^4+23328c^5{x}^3\hfill \\ & +59724c^5{x}^2-23328c^{5}x-13068c^5-139968c^4{x}^4-11664c^4{x}^3-2137536c^4{x}^2-9504c^{4}x\hfill \\ & +373248c^4+373248c^3{x}^4-46656c^3{x}^3-425520c^3{x}^2+46656c^{3}x+52272c^3+559872c^2{x}^4\hfill \\ & -186624c^2{x}^3+9786096c^2{x}^2+139968c^{2}x-2985984c^2-746496c{x}^4-186624c{x}^3\hfill \\ & +746496c{x}^2+186624cx-746496x^4+559872x^3-5225472x^2+5971968.\hfill \end{array}$$

Thus

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial h_5}{\partial c}}& =69984c^5{x}^4+34992c^5{x}^3+26406c^5{x}^2-38232c^{5}x+2112c^5-233280c^4{x}^4\hfill \\ & +116640c^4{x}^3+298620c^4{x}^2-116640c^{4}x-65340c^4-559872c^3{x}^4-46656c^3{x}^3\hfill \\ & -8550144c^3{x}^2-38016c^{3}x+1492992c^3+1119744c^2{x}^4-139968c^2{x}^3\hfill \\ & -1276560c^2{x}^2+139968c^{2}x+156816c^2+1119744c{x}^4-373248c{x}^3+19572192c{x}^2\hfill \\ & +279936cx-5971968c-746496x^4-186624x^3+746496x^2+186624x\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial h_5}{\partial x}}& =186624c+139968c^2+46656c^3-9504c^4-23328c^5-6372c^6-10450944x\hfill \\ & +1492992cx+19572192c^{2}x-851040c^{3}x-4275072c^{4}x+119448c^{5}x+8802c^{6}x\hfill \\ & +1679616x^2-559872c{x}^2-559872c^2{x}^2-139968c^3{x}^2-34992c^4{x}^2\hfill \\ & +69984c^5{x}^2+17496c^6{x}^2-2985984x^3-2985984c{x}^3+2239488c^2{x}^3\hfill \\ & +1492992c^3{x}^3-559872c^4{x}^3-186624c^5{x}^3+46656c^6{x}^3.\hfill \end{array}$$

Similar computation indicates that the system of equations ${\displaystyle \frac{\partial h_4}{\partial c}}=0$ and ${\displaystyle \frac{\partial h_4}{\partial x}}=0$ have no exact solution in $(0,2)\times (0,1).$

Case III: 12 edges of the cuboid

(i) If $x=y=0$, then

$$h_6\left(c\right)=352c^6-34992c^4+139968c^2,$$

for ${\displaystyle \frac{\partial h_6}{\partial c}}=0$ gives the critical point $c\approx 1.43677$, where the max value is achieved as follows

$$h_6\left(c\right)\le 142920.$$

(ii) $x=0,y=1$, then

$$h_7\left(c\right)=352c^6-13068c^5+373248c^4+52272c^3-2985984c^2+5971968,$$

It is readily to show that ${\displaystyle \frac{\partial h_7}{\partial c}}\le 0$, which indicates that the function is decreasing. Furthermore, the maximum value is accurate at $c=0$

$$h_7\left(c\right)\le 5971968.$$

(iii) If $c=x=0$, then

$$h_8\left(y\right)=5971968y^2,$$

It is clear that ${\displaystyle \frac{\partial h_8}{\partial c}}>0$, which shows that $h_8$ is increasing function and the max value is obtained, when $y=1$

$$h_8\left(y\right)=5971968.$$

(iv) For $x=y=1$ and $x=1,y=0$, it follows that

$$h_9\left(c\right)=T(c,1,1)=T(c,1,0)=15877c^6-1925424c^4+7313328c^2+559872,$$

Setting ${\displaystyle \frac{\partial h_9}{\partial c}}=0$, we obtain a critical point $c=1.39499$. At this value of c, the function $h_9\left(c\right)$ reaches its highest value, which is

$$h_9\left(c\right)\le 7.61719.$$

(v) If $c=0$ and $x=1$, then

$$h_{1}0\left(y\right)=T(0,1,y)=559872.$$

(vi) On $c=2$, it follows that

$$T(2,0,y)=T(2,1,y)=T(2,x,0)=T(2,x,1)=22528.$$

(vii) If $c=0$ and $y=0$, then

$$h_{11}\left(x\right)=-559872x\left(11x^2-12\right),$$

and computation generates that ${\displaystyle \frac{\partial h_{11}}{\partial x}}\le 0$, which means $h_{1}1$ is decreasing function and its maximum value achieves when $x=0$; that is,

$$h_{11}\left(x\right)\le 0.$$

(viii) On the edge $c=0$ and $y=1$, then

$$h_{12}\left(x\right)=-746496x^4+559872x^3-5225472x^2+5971968,$$

For ${\displaystyle \frac{\partial h_{12}}{\partial x}}=0$, we obtain a critical value $x=0$, where the maximum value of $h_{12}\left(x\right)$ is

$$h_{12}\left(x\right)\le 5971968.$$

Hence, we deduce that

$$T(c,x,y)\le 5971968.$$

Then, the value of inequality $H_{3,1}\left(f\right)$ is

$$|H_{3,1}\left(f\right)|\le {\displaystyle \frac{1}{81}}=0.01234.$$

Thus, the inequality stands proven. □

Theorem 7.

Let $f\in {\mathcal{C}}_{LE}$. Then,

$$\left|H_{3,1}\left(f\right)\right|\le {\displaystyle \frac{1}{1296}}.$$

This upper bound is sharp by Equation (16).

Proof. 

Assume that $f\in {\mathcal{C}}_{LE}$. Due to the rotational invariance of both the class ${\mathcal{C}}_{LE}$ and the functional $H_{3,1}\left(f\right)$, one may restrict the first coefficient to the range $c_1\in [0,2]$ without loss of generality. By substituting Equations (37)–(40) into Equation (18), the expression for the Hankel determinant takes the form

$$\begin{array}{cc}\hfill H_{3,1}\left(f\right)& ={\displaystyle \frac{1}{19349176320}}(40963c_1^6-247968c_1^4{c}_2+297216c_1^3{c}_3+422496c_1^2{c}_2^2\hfill \\ \hfill & -2052864c_1^2{c}_4+2612736c_1{c}_2{c}_3-1721088c_2^3+4478976c_2{c}_4-3732480c_3^2).\hfill \end{array}$$

Proceeding in a manner similar to the computations carried out in the proof of Theorem 6, and upon substituting $|\zeta |=x$, $|\eta |=y$, and $c:=c_1$, we arrive at

$$|H_{3,1}\left(f\right)|\le {\displaystyle \frac{1}{19349176320}}T(c,x,y),$$

where

$$T(c,x,y)=v_0(c,x)+v_1(c,x)y+v_2(c,x)y^2+v_3(c,x)(1-y^2),$$

with

$$\begin{array}{cc}\hfill v_0(c,x)& =1589c^6+(4-c^2)[(4-c^2)\left(259200x^3+2539512x^2{c}^2+18144x^3{c}^2+46656x^4{c}^2\right)\hfill \\ \hfill & +2146176x^2{c}^2+769824c^4+12960x{c}^4+867456x^2{c}^4+23328x^3{c}^4],\hfill \\ \hfill v_1(c,x)& =(4-c^2)(1-x^2)\left[(4-c^2)(93312xc+186624x^{2}c)+38016c^3+93312x{c}^3\right],\hfill \\ \hfill v_2(c,x)& =(1-x^2)(4-c^2)\left[(933120+186624x^2)(4-c^2)+93312c^{2}x\right],\hfill \\ \hfill v_3(c,x)& =(4-c^2)(1-x^2)\left[93312c^2+1119744(4-c^2)x\right].\hfill \end{array}$$

By performing the calculations for the above equations and using the techniques adopted in Theorem 6, we arrive at

$$|H_{3,1}|\le {\displaystyle \frac{1}{19349176320}}T(0,x,1)={\displaystyle \frac{1}{1296}}.$$

The proof is now complete. □

5. Conclusions

In this work, within the framework of Ma and Minda’s differential subordination and by introducing a novel lobed elliptical domain for the function $\varphi \left(z\right)$, we have developed new subclasses of starlike and convex functions. Our analysis included deriving precise estimates for the initial coefficients up to the fifth order and determining sharp bounds for the second- and third-order Hankel determinants, verifying the sharpness of these results for both classes. Figure illustrations and analytical computations confirmed the non-emptiness of the introduced classes, highlighting the practical relevance of our approach. These results offer potential applications in geometric function theory, particularly in studying coefficient problems for complex analytic functions, as well as in computational and geometric modeling of analytic mappings. Furthermore, this study opens avenues for future research, including the exploration of additional subclasses associated with similar or more generalized domains, the investigation of higher-order Hankel determinants, and the integration of computational tools for broader experimental validation. The proposed domain can also be applied to other topics, such as those discussed in [42,43,44]. Overall, our findings contribute to advancing the understanding of geometric structures in analytic function theory and provide a foundation for subsequent theoretical and applied developments.