A PDE Model of Glioblastoma Progression: The Role of Cell Crowding and Resource Competition in Proliferation and Diffusion ^†

Abstract

Glioblastoma is the most aggressive and treatment-resistant form of primary brain tumors, characterized by rapid invasion and a poor prognosis. Its complex behavior continues to challenge both clinical interventions and research efforts. Mathematical modeling provides a valuable approach to unraveling a tumor’s spatiotemporal dynamics and supporting the development of more effective therapies. In this study, we built on the existing literature by refining and adapting mathematical models to better capture glioblastoma infiltration, using a partial differential equation (PDE) framework to simulate how cancer cell density evolves across both time and space. In particular, the role of cell diffusion and growth in tumor progression and their limitations due to cell crowding and competition were investigated. Experimental data of glioblastoma taken from the literature were exploited for the identification of the model parameters. The improved data reproduction when the limitations of cell diffusion and growth were taken into account proves the relevant impact of the considered mechanisms on the spread of the tumor population, which underscores the potential of the proposed framework.

1. Introduction

Glioblastoma, the most aggressive form of primary brain tumors, remains one of the most challenging malignancies to address in both clinical practice and biomedical research [1]. This cancer is distinguished by its rapid proliferation, diffuse infiltration into healthy brain tissue, and marked resistance to conventional therapeutic modalities [2,3,4]. Despite significant efforts to improve the treatment strategies, including a maximal surgical resection, temozolomide-based chemotherapy, and radiotherapy, the median survival for glioblastoma patients remains dismally low, rarely exceeding 15 months [5]. Factors contributing to this grim prognosis include the tumor’s remarkable heterogeneity, its ability to evade immune surveillance, and its reliance on complex interactions within the tumor microenvironment. Collectively, these challenges highlight an urgent need for innovative approaches that go beyond traditional therapeutic paradigms [6,7,8,9].

A critical aspect of glioblastoma’s complexity lies in its invasive nature. Unlike many solid tumors, glioblastoma cells infiltrate diffusely into surrounding brain tissue, often migrating far beyond the visible tumor margins observed through imaging [10,11]. This behavior severely limits the efficacy of surgical resection and contributes to inevitable tumor recurrence. Additionally, glioblastoma exhibits significant intratumoral heterogeneity at the genetic, epigenetic, and phenotypic levels, leading to varied responses to therapy and the emergence of treatment-resistant subpopulations. Understanding and addressing this intricate biological behavior necessitate advanced tools capable of capturing its underlying dynamics [12,13].

In this regard, mathematical modeling and computational simulation have emerged as powerful frameworks for studying glioblastoma. By leveraging mathematical abstractions, these approaches enable researchers to synthesize biological data into coherent models that describe the tumor behavior at multiple scales, from molecular signaling pathways to macroscopic tumor growth. These models serve several critical purposes: they provide insights into the mechanisms driving tumor progression, offer predictive capabilities for treatment outcomes, and suggest novel therapeutic targets. Importantly, mathematical models are not confined to theoretical exploration, but can also be directly integrated with experimental data to refine hypotheses, improve the model accuracy, and support clinical decision-making [14,15,16,17,18,19].

Numerous researchers have made significant contributions to the mathematical modeling of glioblastoma, developing a diverse array of frameworks to study its growth, invasion, and therapeutic responses. For example, Stein et al. [20] proposed a two-population model that quantitatively describes the evolution of both the invasive and central regions of glioblastoma over time, linking the tumor morphology to its underlying dynamics. This work laid a foundation for understanding how macroscopic tumor growth reflects biological processes at smaller scales. Conte and Surulescu [21] advanced this field further by presenting a multiscale model that incorporates tissue anisotropy, capturing the heterogeneous nature of the brain environment and its impact on glioblastoma invasion. Such models illustrate the importance of integrating spatial and structural complexities into computational frameworks.

Reviews of the glioblastoma modeling efforts have further enriched the field by synthesizing the existing approaches and identifying gaps in knowledge. For instance, Falco et al. [22] provided a comprehensive analysis of various mathematical models, categorizing them based on their biological assumptions and computational methodologies. Their work highlighted the progress achieved in areas such as reaction–diffusion models, agent-based simulations, and multiscale modeling, while also emphasizing the need for more refined models that account for tumor–microenvironment interactions and adaptive resistance mechanisms. Similarly, studies by Hatzikirou et al. [19], Engwer et al. [23], Kumar et al. [24], and Jørgensen et al. [25] have introduced novel frameworks that address specific aspects of glioblastoma dynamics, including the stochastic nature of cell migration [26], angiogenesis, and the impact of therapeutic interventions. Regarding the modeling of the angiogenic mechanisms supporting tumor invasion, we mention the fine model developed by Gandolfi et al. [27], which accounts for vessel co-option and chemotaxis stimulated by pro-angiogenic factors.

Beyond theoretical advancements, mathematical models have practical implications for glioblastoma research and treatment. By simulating various therapeutic scenarios, these models can identify optimal dosing regimens, predict the likelihood of recurrence, and evaluate the efficacy of combination therapies. Furthermore, they provide a platform for testing hypotheses about glioblastoma biology, such as the role of hypoxia in driving tumor invasion or the impact of phenotypic plasticity on resistance. As experimental techniques continue to generate high-resolution data, from single-cell transcriptomics to the live imaging of tumor growth, mathematical models are poised to integrate these data sets into predictive tools for precision oncology. By synthesizing biological knowledge with mathematical rigor, these approaches offer a unique perspective on the complex interplay of factors driving glioblastoma progression and resistance. The continued refinement of these models, coupled with advances in experimental and clinical research, holds great promise for transforming our understanding of this devastating disease and improving the outcomes for patients.

In this work, we address the mathematical modeling and simulation of the glioblastoma spread. Building upon our previous studies [28,29], we aimed to advance the current understanding of glioblastoma dynamics through a more robust theoretical framework. The work by Pompa et al. [28] introduced an agent-based model (ABM) to simulate glioblastoma infiltration into healthy brain tissue, accounting for the cell motility and proliferation rates influenced by internal energy levels. In the subsequent study by Borri et al. [29], glioblastoma infiltration was described by means of a continuum-scale PDE-based approach, comparing different probability distributions in reproducing experimental data on the spatial spread of grioblastoma cells. In the present study, we deepened the PDE-based data analysis introduced by Borri et al. [29], improving the model formulation and focusing on different aspects of cell physiology. The main focus of this work was to evaluate the impact of cell diffusion and cell proliferation, two fundamental aspects of tumor progression. We highlighted such an impact by separating the contribution of the two physiological processes, proposing models of increasing complexity: the first accounts only for cell diffusion, the second adds cell growth to cell diffusion, and the third introduces a general modulation factor of both processes, possibly attributable to cell crowding and competition. In addition to the improved reaction–diffusion PDE model that captures the essential features of glioblastoma growth and diffusion, we introduced a model-based characterization of the tumor core and invasion front, which is necessary to reproduce the available experimental data retrieved from [20].

The investigation proposed in this paper is quite different from the study carried out in [20]. Indeed, in that paper, the authors formulated a more sophisticated model accounting for two distinct tumor populations: one belonging to the core of the tumor mass—proliferative, but not motile—and the second one being extremely motile and belonging to the external invasive rim. They focused on different mobility aspects of the invasive population, showing how the combination of diffusion, advection, and shedding contribute to the tumor spread. Conversely, here, we propose a simplified model structure that accounts for only one general population, with the aim of focusing our attention on the physiological aspects mentioned above, evaluating their contribution to the tumor spread.

Organization: This paper is structured as follows. Section 2 introduces the mathematical tools and concepts used throughout the work. Section 3 presents the glioblastoma infiltration modeling framework and the experimental data employed. Section 4 outlines the optimization problem for parameter identification. The simulation results and their discussion are provided in Section 5. Finally, Section 6 offers concluding remarks.

Notation: In this paper, we adopted the following notation. We denote by ${\mathbb{R}}_{+}$ the set of nonnegative real numbers. Given a vector field $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$, the divergence operator in Cartesian coordinates is defined by $\mathrm{div}\left(F\right)={\sum }_{i=1}^n{\displaystyle \frac{\partial F_i}{\partial x_i}}$, while the Laplace operator of a function $f:{\mathbb{R}}^n\to \mathbb{R}$ is defined by ${\nabla }^{2}f={\sum }_{i=1}^n{\displaystyle \frac{{\partial }^{2}f}{\partial x_i^2}}$. We define by $\delta (x-x^0)$ the Dirac delta function centered at $x^0\in {\mathbb{R}}^n$. If x is a vector in ${\mathbb{R}}^n$, then its Euclidean norm is given by $\parallel x\parallel$, namely $x^{\top }x={\parallel x\parallel }^2$. We denote by I the identity matrix of the appropriate dimension.

2. Mathematical Framework

We illustrate in this section the mathematical framework for describing higher-dimensional/complexity models that exhibit certain properties of symmetry and/or isotropy, similar to those explored later in this study.

2.1. Stochastic Differential Equations and the Fokker–Planck Equation

A stochastic differential equation (SDE) of an n-dimensional Itô process $X\left(t\right)=(X_1\left(t\right),\dots ,X_n\left(t\right))$ is given by

$$\mathrm{d}X\left(t\right)=-b\left(X\left(t\right)\right)\mathrm{d}t+\sigma \mathrm{d}W\left(t\right),X\left(0\right)\sim p_0,$$

(1)

where $W\left(t\right)$ is an n-dimensional Wiener process, $b\left(x\right):{\mathbb{R}}^n\to {\mathbb{R}}^n$ is the drift term, $\sigma :=\sqrt{2D}$ with $D>0$ is the so-called diffusion coefficient, and $p_0\left(x\right)$ is a multidimensional initial ($t=0$) probability density function with $x={[x_1\dots x_n]}^{\top }\in {\mathbb{R}}^n$, the vector of Cartesian coordinates in the n-dimensional space ($n\in \{1,2,3\}$). At each subsequent time $t>0$, the particles are observed to be distributed non-uniformly throughout space, according to a probability density function $p:{\mathbb{R}}_{+}\times {\mathbb{R}}^n\to {\mathbb{R}}_{+}$. Such a probability density function $p(t,x)$, which describes the distribution of the state variable governed by the stochastic differential Equation (1), is known to satisfy the Fokker–Planck equation [30]:

$${\displaystyle \frac{\partial p(t,x)}{\partial t}}=\mathrm{div}(\left(b\left(x\right)p(t,x)\right)+D{\nabla }^{2}p(t,x),p(0,x)=p_0\left(x\right).$$

(2)

Since the solution $p(t,x)$ to (2) is a probability density on ${\mathbb{R}}^n$ for almost every fixed time t, then $p(t,x)\ge 0$ for almost every $(t,x)\in {\mathbb{R}}_{+}\times {\mathbb{R}}^n$ and ${\int }_{{\mathbb{R}}^n}p(t,x)d{x}_1\dots d{x}_n=1$ for every $t\ge 0$.

In some particular cases, it is possible to give the explicit expression of the stationary probability density function satisfying the Fokker–Planck Equation (2). For instance, if the drift coefficient is given by a vector field $b\left(x\right)=\nabla \mathsf{\Psi }\left(x\right)$ [31], where $\mathsf{\Psi }:{\mathbb{R}}^n\to {\mathbb{R}}_{+}$ is a smooth function that meets suitable conditions [30], there exists a unique stationary solution $p_s\left(x\right)$ to the Fokker–Planck equation, which is given by the Gibbs density function:

$$p_s\left(x\right)=Z^{-1}exp (-D^{-1}\mathsf{\Psi }\left(x\right)),$$

(3)

where the coefficient Z is given by the expression

$$Z:={\int }_{{\mathbb{R}}^n}\exp (-D^{-1}\mathsf{\Psi }\left(x\right))dx<+\infty .$$

(4)

Furthermore, if the drift term is zero, namely $b\left(x\right)=0$, and the diffusion is still constant as in (2), the process $\left\{X\right(t\left)\right\}$ in (1) is given by

$$\mathrm{d}X\left(t\right)=\sigma \mathrm{d}W\left(t\right),X^0\sim p_0,$$

(5)

and it is a shifted n-dimensional Wiener process if $p_0\left(x\right)=\delta (x-x^0)$, with $x^0\in {\mathbb{R}}^n$. As a consequence, the condition (4) for the existence and uniqueness of the stationary solution fails, and the solution to the Fokker–Planck Equation (2), which reduces to

$${\displaystyle \frac{\partial p(t,x)}{\partial t}}=D{\nabla }^{2}p(t,x),p(0,x)=\delta (x-x^0),$$

(6)

is the Gaussian density

$$p(t,x)={\displaystyle \frac{1}{{\left(2\pi {\sigma }^{2}t\right)}^{n/2}}}{e}^{-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\parallel x-x^0{\parallel }^2}{{\sigma }^{2}t}}},$$

(7)

describing a continuous-time random walk with mean $x^0$ and covariance ${\sigma }^{2}tI$, linearly increasing with time. It is clear that, since the independent variable x is the vector of the Cartesian coordinates, the latter model implicitly assumes spherical symmetry, as the density centered at $x^0$ exhibits such a kind of symmetry.

The stochastic model reported in this section provides the basic mathematical framework describing the mechanism underlying the ensemble diffusion process characterizing a population with random mobility of the single individuals, which we will extend to more refined models in the remainder of this paper.

2.2. Fisher Equation

In this section, we present another PDE model that is typically used to describe the spread of a cell population: the Fisher equation [32,33]. This model is actually an extension of the one given above in Equation (2), since, in addition to the diffusion process, it accounts for the net balance between mass production and elimination. In an n-dimensional space, it is given by

$${\displaystyle \frac{\partial u(t,x)}{\partial t}}=\mathrm{div}(\left(v\left(x\right)u(t,x)\right)+D{\nabla }^{2}u(t,x)+gu(t,x)\left(1-{\displaystyle \frac{u(t,x)}{u_{\max }}}\right),u(0,x)=u_0\left(x\right),$$

(8)

where the solution $u:{\mathbb{R}}_{+}\times {\mathbb{R}}^n\to \mathbb{R}$ is the scalar field representing, for example, the population density or concentration at position $x\in {\mathbb{R}}^n$ and time $t>0$. Similarly to before, the vector $v\left(x\right):{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a drift term and the constant $D>0$ is the diffusion coefficient, while $g>0$ is the proliferation rate constant and $u_{\max }$ is the local carrying capacity of the cells, representing the maximal cell density that can be reached by the solution u (at any point), which is related to environmental and nutrient conditions as well as to cell competition. Unlike the Fokker–Planck equation, which is a partial differential equation (PDE) describing the evolution of a probability density function typically derived from an underlying Itô process that accounts only for motility aspects, the Fisher equation is a reaction–diffusion equation that models both the spread and proliferation of a biological population. This is essentially obtained by considering the additive logistic-type growth term to the previous Fokker–Planck equation (suitably scaling the probability density to the cell/mass density).

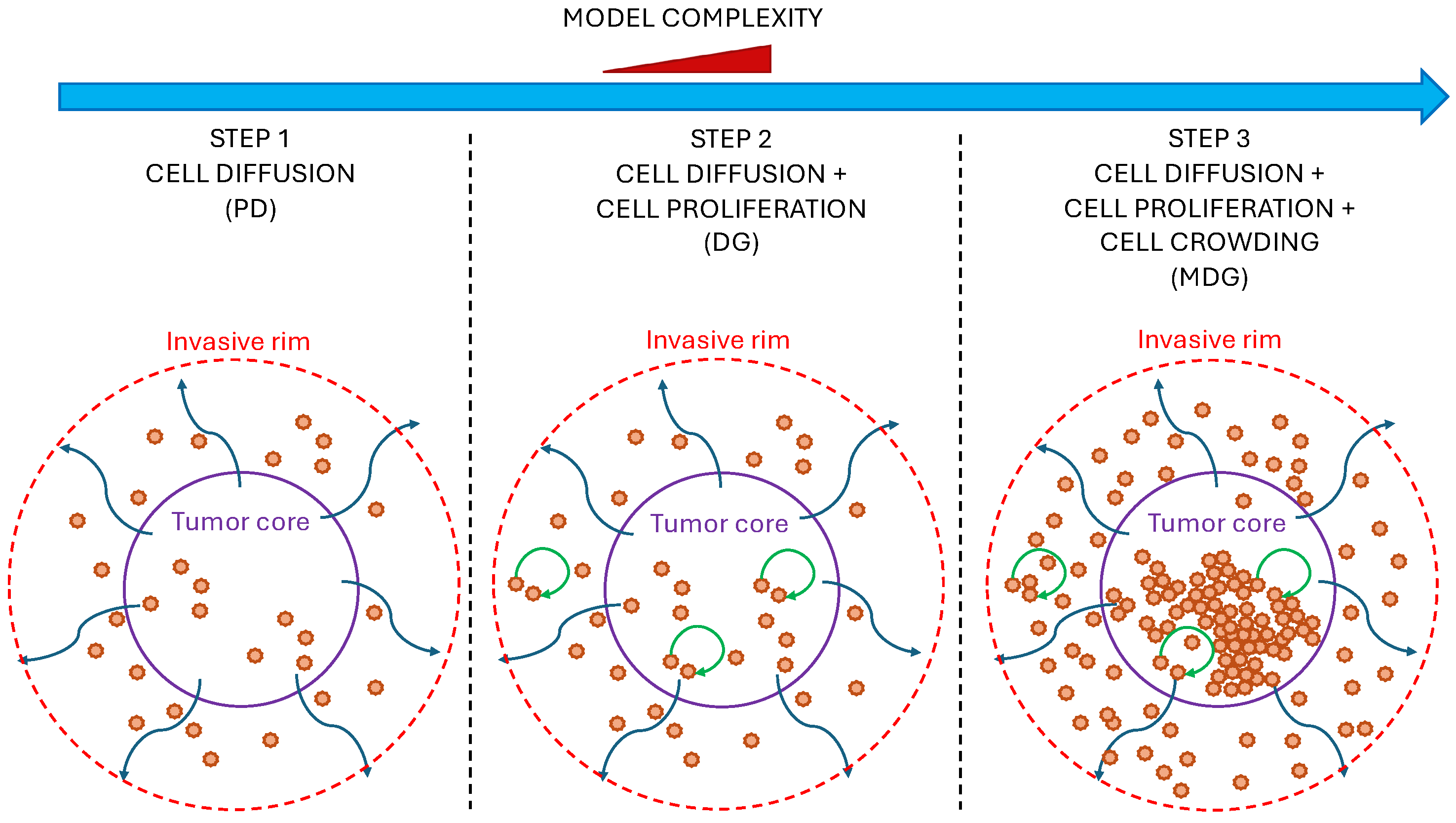
3. Glioblastoma Infiltration Modeling

We then leveraged the mathematical framework developed in the preceding section to formulate suitable macroscopic/mesoscopic models that capture the experimental time behavior of a glioblastoma tumor mass. In particular, from the paper by Stein et al. [20], we retrieved experimental data on cell density and two radii characterizing the time-volution of the tumor mass. So, we propose three different models with the aim of explicitly reproducing these kinds of variables. The main focus of this study was to evaluate the impact of cell diffusion and cell proliferation on glioblastoma spread. We tried to better highlight such an impact by separating their contribution, thus proposing three models of increasing complexity (from the one given in Section 3.2.1 to the last one in Section 3.2.3): the first one accounts only for cell diffusion, the second one adds cell growth to cell diffusion, and the last one introduces a general modulation factor for both processes, which can be attributable to cell crowding and competition. Figure 1 shows a scheme of the incremental steps followed in this investigation.

All the proposed models incorporate the following key features:

• Polar coordinate formulation: Because of the assumption of symmetry and the isotropy of cell movements (already assumed in Pompa et al. [28]) within the tumor mass, we can reduce the spatial dependency to only the radial coordinate.
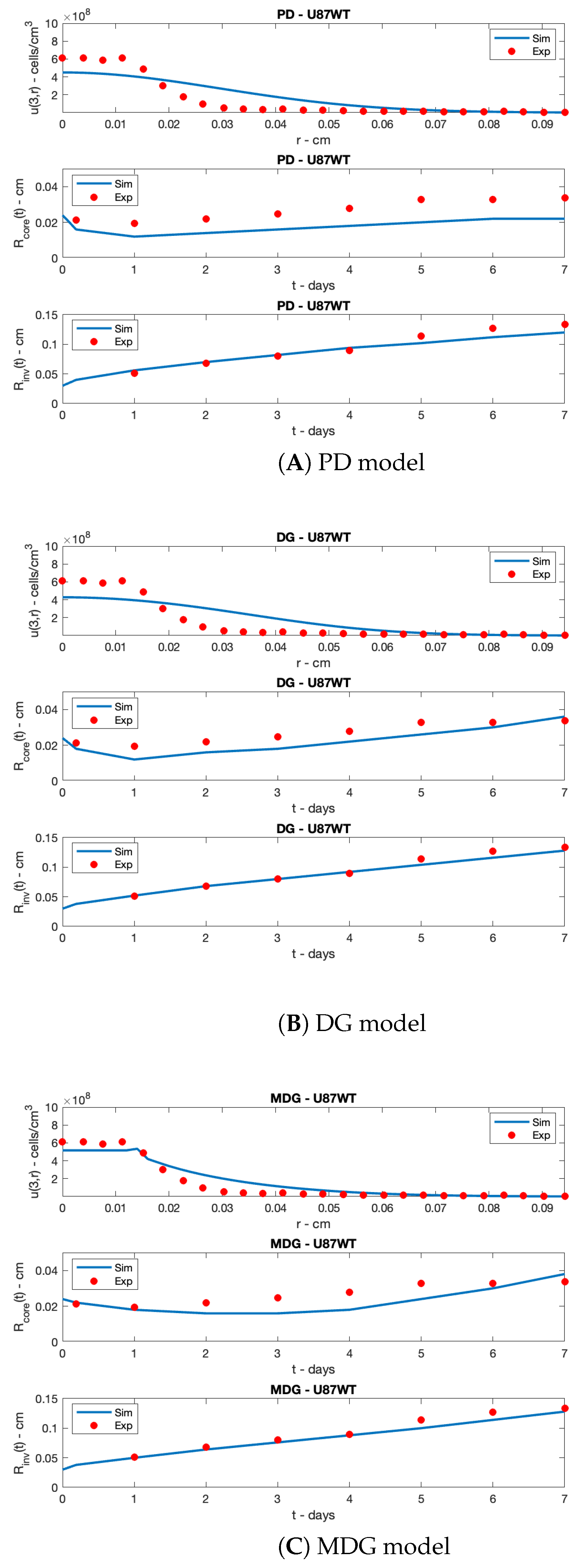
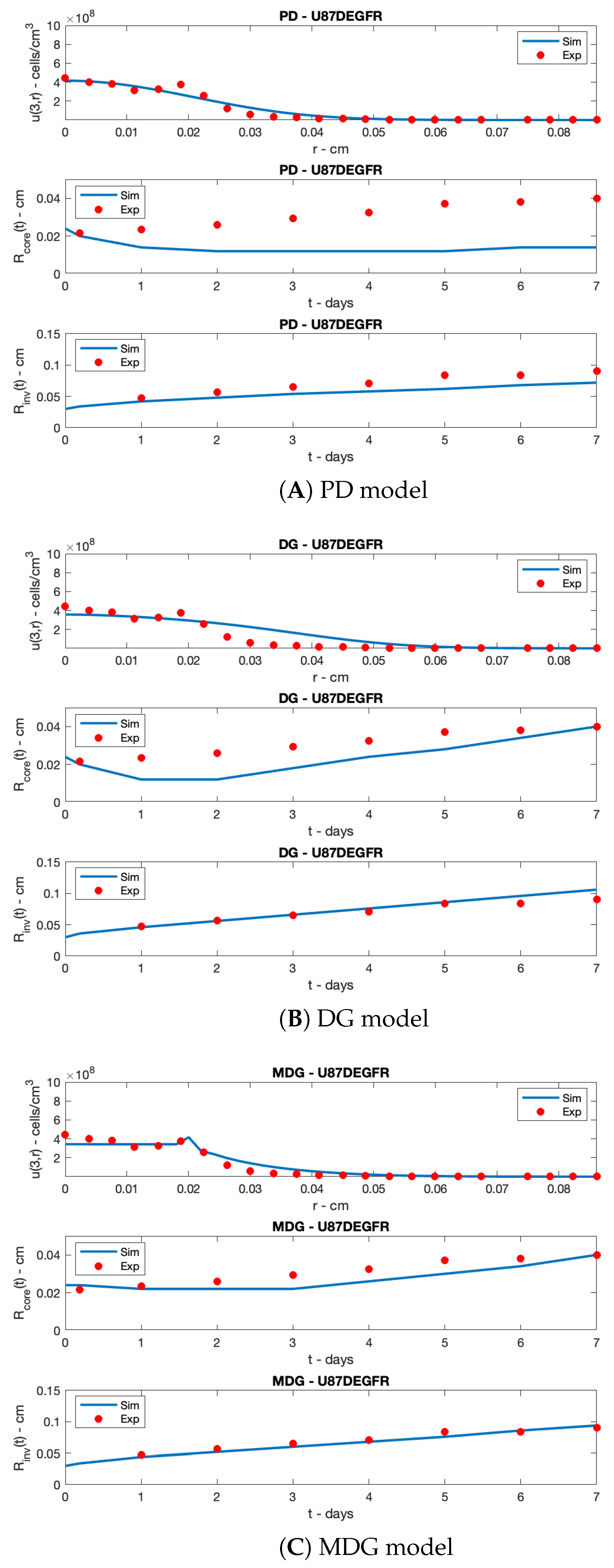
• Model outputs reproducing the available data on two different cell lines: U87WT (already considered in [28]) and U87$\Delta$EGFR, which is a common mutation (data reported in Stein et al. [20], see the next subsection); the proposed models are specified to the different cell lines by means of a suitable parameter estimation.

3.1. Data Collection

In this study, we utilized the experimental data reported by Stein et al. [20], which are related to the two glioblastoma cell lines U87WT and U87$\Delta$EGFR (a common mutation variant). As mentioned in the “External background” section of that paper, the data were extracted through the image processing of digital photomicrographs taken at the mid-plane of spheroids. We considered the following data:

• The invasive radius, ${\overline{R}}_{\mathrm{inv}}$, of a tumor, which represents the maximum distance that a single tumor cell or a small group of tumor cells can migrate from the primary tumor mass into the surrounding tissue. The extension of the invasive region is a key parameter in cancer invasion studies, as it reflects the ability of malignant cells to infiltrate the extracellular matrix (ECM), evade immune responses, and establish metastases, thus increasing the probability of recurrences and a poor prognosis [34]. The image-based definition reported in Stein et al. [20] defines the invasive radius as the farthest distance from the center at which the modulus of the azimuthally averaged gradient of the gray intensity reaches half of its maximum value.
• The core radius, ${\overline{R}}_{\mathrm{core}}$, which refers to the central region of the tumor where cell proliferation is significantly reduced or halted due to limited nutrient and oxygen availability. This region is often characterized by hypoxia, necrosis, or quiescence, depending on the severity of the nutrient and waste diffusion limitations. Again, according to the image-based definition reported in Stein et al. [20], the region is defined as the collection of pixels exhibiting an intensity level of $0.12$ on a grayscale—where 0 corresponds to the darkest pixel and 1 to the brightest—centered around the tumor spheroid.
• The radial cell density at day 3 (expressed in [cells/cm³]), a function of the radius $r>0$, which is denoted by $\overline{u}(\overline{t},r)$ with $\overline{t}=3$; it is extracted based on the concentration of darker pixels observed in the digital photomicrograph data.

Specifically, we aimed to replicate the experimental trends shown in Figure 2 (panels A–C) of Stein et al. [20], which include the following: the temporal evolution of the invasive radius (panel A) and the core radius (panel B) of the tumor from day 0 to day 7, and the radial cell density profile at day 3 (panel C).

3.2. Radial Distribution Models of Invasive Cells

In this section, we propose three different models for the radial position of the invasive tumor cells in a three-dimensional space ($n=3$), under the hypothesis of spherical symmetry. In particular, we describe by means of PDEs the spatial distribution of the cell density $u(t,r)$ (measurement unit: [cells/cm³]), with $u:{\mathbb{R}}_{+}\times \mathbb{R}\to \mathbb{R}$, where the spatial dependence of u is reduced to the single radial coordinate r, because of the spherical symmetry hypothesis. Under this simplifying assumption, the Laplace operator in the 3D space becomes

$${\nabla }^{2}u(t,r)={\displaystyle \frac{2}{r}}{\displaystyle \frac{\partial u(t,r)}{\partial r}}+{\displaystyle \frac{{\partial }^{2}u(t,r)}{\partial r^2}},$$

(9)

because the derivatives with respect to the angle coordinates are trivially zero ($\partial \theta /\partial r=\partial \varphi /\partial r=0$). All the proposed models have zero drift terms.

The models are then complemented by initial and boundary conditions as follows. Concerning the initial condition, we set $u(0,r)=u_0\left(r\right)$ with

$$u_0\left(r\right)=\left\{\begin{array}{cc}\overline{u},\hfill & \mathrm{for}r\le R_0,\hfill \\ 0,\hfill & \mathrm{for}r>R_0,\hfill \end{array}\right.$$

(10)

where $R_0$ is the initial radius of the implanted tumor mass and $\overline{u}>0$ is the related (constant) cell density. As far as the boundary conditions are concerned, the cell density is subject to the common zero flux conditions at $r=0$ because of the domain symmetry, i.e., ${{\displaystyle \frac{\partial u(t,r)}{\partial r}}|}_{r=0}=0$. Assuming also that the cell density is zero far from the tumor mass, we imposed the second boundary condition $u(t,\infty )=0$.

According to the definition reported in Section 3.1, the core and invasive radii were measured from the experimental images based on a grayscale intensity. Therefore, reasonably assuming that higher gray intensities are related to higher cell densities, we provide a mathematical definition of the core radius $R_{\mathrm{core}}\left(t\right)$ and of the invasive radius $R_{\mathrm{inv}}\left(t\right)$ at time $t>0$ on the basis of a heuristic on $u(t,r)$, which could be valid for all the proposed models. In particular, we define the following:

$$R_{\mathrm{core}}\left(t\right):=min\left\{\overline{r}:\left(1-{\displaystyle \frac{u(t,\overline{r})}{u(t,0)}}\right)\ge 0.12\right\},R_{\mathrm{inv}}\left(t\right):=min\left\{\overline{r}:\left(1-{\displaystyle \frac{u(t,\overline{r})}{u(t,0)}}\right)\ge 0.98\right\}.$$

(11)

Note that, according to Equations (10) and (11), we have $R_{\mathrm{core}}\left(0\right)=R_{\mathrm{inv}}\left(0\right)=R_0$ at the initial time (tumor implantation).

Remark 1. 

The intuition behind Equation (11) is that, at each time t, the core and invasive radii are defined as the radial coordinates at which the cell density decreases to $88\%$ and $2\%$, respectively, of the cell density $u(t,0)$ in the tumor center. The threshold $0.12$ that we chose for the core radius definition in Equation (11) matches the one related to the normalized light intensity reported in [20], which was used to identify the core region from the grayscale of the digital photomicrographs of the spheroids (see also Section 3.1). Conversely, the threshold for the invasive radius definition was calibrated in this work; however, note that the chosen value is in agreement with the ones identified in [20] (ranging in the interval $(0.98,1)$) extrapolated from the experimental data.

Remark 2. 

To the best of our knowledge, the approach proposed in this paper to describe the time behavior of the core and invasive radii is new from a mathematical point of view and tries to adhere to the grayscale-based method adopted in [20] for the processing of the experimental images. This definition is different from those adopted in [20,29]. In particular, in [29], these quantities were defined according to thresholds on the percentile of the tumor cell cumulative distribution function. Conversely, in [20], linear growth was assumed for the core radius (where the growth velocity was directly estimated from the related experimental data), while two different cutoff thresholds of the cell density tail were set to identify the extension of the invasive radius of the two cell lines; these line-dependent thresholds were identified by crossing the experimental data on the cell density distribution at day 3 and the related experimental measure of the invasive radius. So the definitions given here by Equation (11) are mathematically different from those adopted in the mathematical framework proposed in [20] and are independent of the experimental data.

As mentioned in Section 3.1, the core and the invasive radii increase in the observation period, so a steady-state model of cell distribution would not be realistic. Therefore, we focused on three different time-varying models for the cell density $u(t,r)$: (i) a pure diffusive (PD) model (i.e., the Fokker–Planck equation); (ii) a model combining diffusion and growth (DG), with a standard logistic-type limitation factor of cell growth due to nutrient availability (i.e., the Fisher equation); and (iii) a more refined model accounting for limitations of both diffusion and growth, which introduces more general modulation factors representing the impact of cell crowding and resource competition (modulated growth and diffusion model, MDG).

3.2.1. Pure Diffusion Model (PD)

The simplest non-stationary model we can define for the position of tumor cells, defined by a process $\left\{X\right(t\left)\right\}$, is the pure diffusive case exploited in (5) (no drift or cell proliferation), where we assume that the origin of the Cartesian frame is set in the center of the tumor spheroid. Thus, under the symmetry hypothesis of the 3D domain, the associated PDE in radial coordinates describing the cell density distribution is given by

$${\displaystyle \frac{\partial u}{\partial t}}=D\left({\displaystyle \frac{2}{r}}{\displaystyle \frac{\partial u(t,r)}{\partial r}}+{\displaystyle \frac{{\partial }^{2}u(t,r)}{\partial r^2}}\right),$$

(12)

with the initial and boundary conditions reported in Section 3.2. For this model, the parameters to be identified are ${\mathsf{\Theta }}^{\mathrm{PD}}:=\{D,\overline{u}\}$, where $\overline{u}$ is defined in (10), and they are computed through an optimization problem (see Section 4). In the following, we denote by $u^{PD}(t,r)$ the solution to the pure diffusion equation.

Notice that, in view of the pure diffusion process considered, the total number of cells M (i.e., the tumor mass) is constant over time (since no cell birth/death processes are taken into account by the model) and it is given by the relation $M:={\int }_{{\mathbb{R}}^n}u(t,r)dV={\int }_{{\mathbb{R}}^n}u(0,r)dV$, where $dV$ is the infinitesimal volume element in spherical coordinates and $n=3$ (i.e., $dV=r^{2}sin\theta d\theta d\varphi dr$, where $\theta$ and $\varphi$ are the angle coordinates). According to the previous definition, we have $M=4\pi {\int }_0^{R_0}\overline{u}{r}^{2}dr=\left({\displaystyle \frac{4}{3}}\pi R_0^3\right)\overline{u}$. It is also interesting to notice that, as the corresponding probability density function of the tumor population $p(t,r)$ is characterized by the basic property ${\int }_{{\mathbb{R}}^n}p(t,r)dV=1$, the total number of cells M represents a constant coefficient for rescaling the cell density to the probability density function (and vice versa), i.e., $p(t,r)=u(t,r)/M$. Although the model (12) provides a simple basis for comparison and allows for approximate computations over a short time horizon, its underlying behavior is not realistic given the invasive and reproductive nature of tumor cells. In the following subsections, the model will be properly extended to account for the growing cancer cell population.

3.2.2. Diffusion and Growth Model (DG)

A more detailed model involves considering the reaction–diffusion equation by Fisher, given above in Section 2.2. According to the assumptions given in Section 3.2 and neglecting additional cell movement sources out of the diffusion (i.e., $v=0$), the Fisher equation in radial coordinates becomes

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u(t,r)}{\partial t}}& =D\left({\displaystyle \frac{2}{r}}{\displaystyle \frac{\partial u(t,r)}{\partial r}}+{\displaystyle \frac{{\partial }^{2}u(t,r)}{\partial r^2}}\right)+gu(t,r)\left(1-{\displaystyle \frac{u(t,r)}{u_{\max }}}\right),\hfill \end{array}$$

(13)

with the initial and boundary conditions reported in Section 3.2. In the following, we denote by $u^{DG}(t,r)$ the solution to the Fisher model Equation (13), which depends on the parameters ${\mathsf{\Theta }}^{\mathrm{DG}}:=\{D,\overline{u},g,u_{max}\}$ that are computed through an optimization problem (see Section 4). Note that this model (13) extends the simple pure-diffusion one (12) because of the presence of the logistic term, reproducing the net cell proliferation coming from a birth/death balance.

3.2.3. Modulated Diffusion and Growth Model (MDG)

The final model we propose is an enhanced version of the previous Fisher model, extending the modulation of the proliferation rate constant g (already present in Equation (13)) and introducing a further modulation of the diffusion constant D. As explained in the seminal paper [27], in crowded environments, there is an increasing impairment of cell movement and an increasing inhibition of cell proliferation as the cell density increases. Such phenomena are likely to follow different laws with respect to cell density. As implemented in [27,35], in the last proposed model, we took both of these phenomena into account by multiplying the proliferation rate constant and the diffusion coefficient by means of the following limiting factor:

$${\left(1-{\displaystyle \frac{u}{u_{max}}}\right)}^{\alpha },\alpha >0.$$

However, we assumed that the extent of the limitation can be different for diffusion and proliferation, and then we assumed that the exponent $\alpha$ can be different (in principle) for the two mechanisms. According to this modeling setting, we give the following modified Fisher equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u(t,r)}{\partial t}}& =D{\left(1-{\displaystyle \frac{u(t,r)}{u_{m}ax}}\right)}^{{\alpha }_D}\left({\displaystyle \frac{2}{r}}{\displaystyle \frac{\partial u(t,r)}{\partial r}}+{\displaystyle \frac{{\partial }^{2}u(t,r)}{\partial r^2}}\right)+gu(t,r){\left(1-{\displaystyle \frac{u(t,r)}{u_{m}ax}}\right)}^{{\alpha }_g},\hfill \end{array}$$

(14)

with the initial and boundary conditions reported in Section 3.2. In the following, we denote by $u^{MDG}(t,r)$ the solution to Equation (14), depending on the parameters ${\mathsf{\Theta }}^{\mathrm{MDG}}=\{D,\overline{u},g,u_{max},{\alpha }_g,{\alpha }_D\}$ that are computed through an optimization problem (see Section 4).

Note that the extended model (14) falls beyond the mathematical framework considered in the previous section, representing a new formulation.

Remark 3. 

As a final remark on the proposed modeling framework, we highlight that, as already mentioned above, the pure diffusion model (12) does not incorporate any aspects of cell proliferation, so we expect a worse performance in the fitting of the time-varying quantities, such as the core and invasive radii. We also note that the extended modulation of cell proliferation and diffusion introduced in model (14) (due to cell crowding and competition for resources) gives to this model more degrees of freedom w.r.t. Model (13) in reproducing the experimental data.

4. Parameter Identification

In this section, we discuss the optimization problem used to identify the model parameters. We considered the following three sets of data:

(i)

$m_u={\left\{\overline{u}(\overline{t},r_k)\right\}}_{k=1}^{N_u}$, representing the radial distribution of cell density on days $t=\overline{t}=3$, measured at different spatial points $r_k$ with a sample size $N_u$;

(ii)

$m_{core}={\left\{{\overline{R}}_{c}ore\left(t_k\right)\right\}}_{k=1}^{N_{core}}$, representing the core radius at different times $t_k$, with a sample size $N_{core}$;

(iii)

$m_{inv}={\left\{{\overline{R}}_{i}nv\left(t_k\right)\right\}}_{k=1}^{N_{inv}}$, representing the invasive radius at different times $t_k$, with a sample size $N_{inv}$.

Denoting by $u^{\mathsf{\Sigma }}(t,r)$ the solution of model $\mathsf{\Sigma }$, with $\mathsf{\Sigma }\in \{\mathrm{PD},\mathrm{DG},\mathrm{MDG}\}$, for any time $t>0$ and radius $r>0$, as well as by ${\mathsf{\Theta }}^{\mathsf{\Sigma }}$ and by $R_{\mathrm{core}}^{\mathsf{\Sigma }}$, $R_{\mathrm{inv}}^{\mathsf{\Sigma }}$ the vector of related parameters and, respectively, the core and invasive radii (computed according to Equation (11) and to the solution $u^{\mathsf{\Sigma }}(t,r)$), we define the following optimization problem for the estimation of ${\mathsf{\Theta }}^{\mathsf{\Sigma }}$:

$$\begin{array}{cc}\hfill \underset{{\mathsf{\Theta }}^{\mathsf{\Sigma }}}{min}{\epsilon }_u^{\mathsf{\Sigma }}\sum _{k=1}^{N_u}& ∥\overline{u}(\overline{t},r_k)-u^{\mathsf{\Sigma }}(\overline{t},r_k)∥+{\epsilon }_{\mathrm{core}}^{\mathsf{\Sigma }}\sum _{k=1}^{N_{core}}∥{\overline{R}}_{\mathrm{core}}\left(t_k\right)-R_{\mathrm{core}}^{\mathsf{\Sigma }}\left(t_k\right)∥\hfill \\ \hfill & +{\epsilon }_{\mathrm{inv}}^{\mathsf{\Sigma }}\sum _{k=1}^{N_{inv}}∥{\overline{R}}_{\mathrm{inv}}\left(t_k\right)-R_{\mathrm{inv}}^{\mathsf{\Sigma }}\left(t_k\right)∥.\hfill \end{array}$$

(15)

As the available experimental data were characterized by large differences in magnitude orders and cardinality, the factors weighting the square errors in (15) were set as equal to the squared inverse of the product between the cardinality and the mean value of each data set, i.e.,

$${\epsilon }_u^{\mathsf{\Sigma }}={\displaystyle \frac{1}{{\left(N_u\langle m_u\rangle \right)}^2}},{\epsilon }_{\mathrm{core}}^{\mathsf{\Sigma }}={\displaystyle \frac{1}{{\left(N_{core}\langle m_{core}\rangle \right)}^2}},{\epsilon }_{i}n{v}^{\mathsf{\Sigma }}={\displaystyle \frac{1}{{\left(N_{inv}\langle m_{inv}\rangle \right)}^2}},$$

(16)

where $\langle ·\rangle$ is the arithmetic mean operator.

5. Simulation Results

The proposed PDE models were numerically solved in the domain $\mathsf{\Omega }=[0,R_{\infty }]$, where $R_{\infty }$ was chosen far from the center of the tumor mass. In particular, we set $R_{\infty }=1$ cm, i.e., about one order of magnitude larger than the highest radius at which the 3-day cell density was measured (that is, about 0.1 cm for both cell lines) and substantially larger than the available measurements of the core and invasive radii (which are always lower than about 0.15 cm for both cell lines). A non-uniform spatial mesh was adopted for the computation of the numerical solution in $\mathsf{\Omega }$, using a shorter radial step in the region $[0,R_d]$ containing the experimental data, where the data upper bound $R_d$ was set to 0.2 cm, and a larger step was used outside of this region. In particular, we divided the internal region $[0,R_d]$ into 100 intervals (spatial step $\Delta r_1=R_d/100=0.002$ cm) and the external one $[R_d,R_{\infty }]$ into 10 intervals (spatial step $\Delta r_2=(R_{\infty }-R_d)/10=0.08$ cm).

Concerning the time span, we computed the numerical solutions of the three models at the same time instants of the available data on the core and invasive radii, i.e., a solution for each day in the interval $[0,7]$ days plus a solution at 4.5 h (time of the first measurement of the core radius for both cell lines).

The numerical solutions to the PDE models were obtained by exploiting the MATLAB solver pdepe (MATLAB^® R2024b), which is based on the spatial discretization method for parabolic equations in one space dimension proposed by Skeel and Berzins in 1990 [36]. The initial tumor radius $R_0$ was fixed at 250 $\mathsf{\mu }$m (value directly measured from the spheroid images of the two cell lines reported in [20]).

The three least-squares problems described in Section 4 (minimization of the weighted sum of the squared differences between the observed and predicted variables) were solved using the MATLAB^® routine fminsearch for both the available data sets, which is based on the Nelder-Mead simplex algorithm (see [37]). This is a very efficient non-linear optimization routine, but a good initial guess is required. Therefore, we preliminarily set the initial values of the model parameters, based on indications from the literature [20,27] and a trial-and-error procedure. The same initial guess was used for all the proposed models and for both cell lines, except for the maximal value $\overline{u}$ of the initial cell density distribution (10), which was set according to the mean value of the first three points of the experimental distributions of the two cell lines, and $u_{max}$, initially set equal to $\overline{u}$. This tuned initial guess is reported in the caption of

Table 1. Estimated values of the model parameters. Initial guess: $D=4.4\times {10}^{-6}$ cm² · h⁻¹, $g=3\times {10}^{-2}$ h⁻¹, ${\alpha }_g=0.5$, ${\alpha }_D=1.5$; $\overline{u}=u_{max}=6\times {10}^8$ cells · cm⁻³ for U87WT and $\overline{u}=u_{max}=4\times {10}^8$ cells · cm⁻³ for U87$\Delta$EGFR. Notation: PD—pure diffusion; DG—diffusion and growth; MDG—modulated diffusion and growth.

(A) U87WT cell line
Parameter	m.u.	PD	DG	MDG
D	cm2 · h−1	$4.96\times {10}^{-6}$	$3.61\times {10}^{-6}$	$4.82\times {10}^{-6}$
$\overline{u}$	cells · cm−3	$2.63\times {10}^9$	$6.84\times {10}^8$	$4.97\times {10}^8$
g	h−1	-	$2.82\times {10}^{-2}$	$2.71\times {10}^{-2}$
$u_{max}$	cells · cm−3	-	$6.74\times {10}^8$	$5.16\times {10}^8$
${\alpha }_g$	-	-	-	0.6
${\alpha }_D$	-	-	-	1.9
(B) U87$\Delta$EGFR cell line
Parameter	m.u.	PD	DG	MDG
D	cm2 · h−1	$1.46\times {10}^{-6}$	$1.75\times {10}^{-6}$	$2.07\times {10}^{-6}$
$\overline{u}$	cells · cm−3	$6.92\times {10}^8$	$6.10\times {10}^8$	$3.42\times {10}^8$
g	h−1	-	$3.32\times {10}^{-2}$	$2.65\times {10}^{-2}$
$u_{max}$	cells · cm−3	-	$3.42\times {10}^8$	$3.42\times {10}^8$
${\alpha }_g$	-	-	-	0.4
${\alpha }_D$	-	-	-	2.4

.

Table 1 also reports the values of the estimated model parameters and the solutions to the three optimization problems, while Figure 2 and Figure 3 show the corresponding best fit of the experimental data (cell density function at $t=3$ days, $R_{\mathrm{core}}\left(t\right)$ and $R_{\mathrm{inv}}\left(t\right)$ for $t=0.19,1,\dots ,7$ days) for both cell lines, obtained for the three models with optimal parameters.

From the estimated model parameters in Table 1, we note that the estimated diffusion coefficients agree with the values reported in the literature, which reports data ranging in the interval of ($4.17\times {10}^{-7},8.33\times {10}^{-6}$) cm²/h [38,39]. Also, the estimated proliferation rate constants were basically in agreement with the literature, where the doubling time estimation increases to 20 h (proliferation rate estimates belonging to the range (0, 0.035) h⁻¹ [20]). We also note some common features related to the two parameter sets reported in Table 1: (i) when increasing the model complexity (from PD to MDG), the parameters $\overline{u}$, g, and $u_{max}$ decreased (this trend was not appreciable for $u_{max}$ related to U87$\Delta$EGFR due to the rounded values), and (ii) the conditions ${\alpha }_D>1$ and ${\alpha }_g<1$ held for both cell lines.

From the fitting results reported in Figure 2 and Figure 3, as expected, the PD model showed some limitations in following the time behavior of the experimental radii (especially for the line U87$\Delta$EGFR), while the other two models showed better performances in the fitting of the data ensemble. The obtained goodness of fit and the model potential in reproducing the experimental data were evaluated by computing three indexes: (i) the weighted squared error (WSE), which is the value of the cost index of Equation (15); (ii) the coefficient of determination (R²); and (iii) the Akaike information criterion (AIC). R² is a dimensionless measure representing how firmly the data cluster around the regression plane, and it is given by

$$R^2=1-{\displaystyle \frac{S{S}_{res}}{S{S}_{tot}}},$$

where $S{S}_{res}$ is the sum of the squared residuals while $S{S}_{tot}$ is the total sum of the squared differences between the data and their mean value [40]. Conversely, the AIC is a statistical indicator of the goodness of a model (exploited in model comparisons) that evaluates the relative amount of information lost by a given model, and it is given by

$$AIC=2k-2\ln \left(\widehat{L}\right),$$

where k is the number of model parameters while $\widehat{L}$ is the maximized value of the likelihood function of the model [41,42]. Therefore, the WSE gives the (weighted) raw distance of the model prediction from the data, R² relates the data variability to the model capacity in following such variation, and the AIC evaluates the model quality based on a tradeoff between the goodness of fit (data prediction error) and the model simplicity (number of model parameters). Obviously, the model quality and the goodness of fit increase when the WSE decreases, R² increases (tending to 1), and the AIC decreases, which indicates a more parsimonious and better model. All these trends can be appreciated in

Table 2. Goodness of fit. Notation: PD—pure diffusion; DG—diffusion and growth; MDG—modulated diffusion and growth; WSE—weighted squared error; R²—coefficient of determination; AIC—Akaike information criterion.

(A) U87WT cell line
Metrics	PD	DG	MDG
$WSE$	$0.040$	$0.033$	$0.017$
$R^2$	$0.79$	$0.83$	$0.91$
$AIC$	−163.39	−168.25	−192.18
(B) U87$\Delta$EGFR cell line
Metrics	PD	DG	MDG
$WSE$	$0.057$	$0.029$	$0.009$
$R^2$	$0.65$	$0.82$	$0.95$
$AIC$	−134.22	−157.16	−199.48

for both cell lines when the model complexity is increased, going from the PD to the MGD model. In particular, it can be appreciated that the MDG model fit all of the data (cell densities and radii of both lines) better than the other models. This means that accounting for both cell proliferation and diffusion, as well as their modulation, decisively improves the goodness of fit of the experimental data.

Remark 4. 

As noted in [20], a simple model accounting for only one population shows some limitations in following the evolution of both core and invasive regions in small tumors. This is also confirmed in this study, especially for the U87ΔEGFR cell line, and it was the main reason that the authors of [20] suggested a more realistic double population model. However, this limitation is certainly reduced when modulated growth and diffusion is taken into account, as can be appreciated from the improvement in the MGD data fitting shown by Figure 2 and Figure 3 and highlighted by the related goodness of fit reported in Table 2. The increased potential of the MGD model was also confirmed by a direct comparison with the more complex model proposed in [20]. Indeed, by implementing the mentioned two-population model (a linearly increasing core region with a constant cell density plus an invasive spreading population ruled by Equation (2) in [20]) and estimating its parameters (D, g, $v_i$, s, $u_{max}$, $v_c$) by fitting all the data (of each cell line) using the same identification procedure reported in Section 4, we obtained numerical results comparable to the MGD model. In particular, the obtained metric values were as follows: WSE = 0.017, R² = 0.91, and AIC = −191.82 for U87WT, and WSE = 0.019, R² = 0.89, and AIC = −169.97 for U87ΔEGFR. Note that the calculated metrics were substantially equivalent for the two models when the U87WT cell line was fitted, while the MGD model showed a better performance in fitting the mutant U87ΔEGFR (compare the metric values given above with the ones reported in Table 2 for the MGD model). We finally note that the comparison of the two models is quite fair, since the same number of model parameters were estimated for both models.

6. Conclusions

Glioblastoma remains a significant challenge in both clinical practice and research due to its aggressive nature and resistance to current treatments. Mathematical modeling provides a valuable tool for understanding the complex dynamics of this disease and supporting the development of new therapeutic strategies. In this study, we introduced a simple single-population mathematical model for glioblastoma infiltration, which captures both the proliferative and diffusion aspects of the tumor mass, particularly focusing on their limitations due to cell crowding and competition. The main focus of this work was to evaluate the impact of the considered physiological processes on tumor progression by separating their contribution within models of increasing complexity. This work also introduces a new model-based definition of the tumor core and invasion front that tries to adhere to the grayscale-based definition used for processing the digital photomicrographs of the tumor spheroids.

The obtained numerical simulations show that the presence of both proliferation and diffusion in the modeling framework, as well as the considered modulation factor, decisively improves the goodness of fit of the experimental data (see Table 2). In particular, the model quality and the goodness of fit increase when the model complexity increases, the WSE decreases, R² increases (tending to 1), and the AIC decreases. Also, a qualitative inspection of the data reproduction reported in the figures confirms this quantitative analysis.

The proposed theoretical framework can help improve the understanding of tumor progression and guide the development of potential therapeutic approaches. The model is designed to be flexible and can be extended to the study of different cell physiology mechanisms and different types of cell subpopulations, interactions between a tumor and the immune system, and personalized treatment strategies. In particular, this modeling framework can be useful for predicting tumor evolution in relation to vascularization. Since angiogenesis is a key factor in glioblastoma progression, providing oxygen and nutrients that sustain tumor growth and invasion, future studies could include vascularization dynamics in the model to better quantify how the tumor adapts to its microenvironment. This extension would enhance the model’s predictive ability and support the design of more effective treatments that target both tumor cells and their vascular network.

Another important extension of the model could be the introduction of cell heterogeneity, simultaneously describing the evolution of different cell subpopulations. Indeed, two-population models allow the different behavior of core and invasive regions for small glioblastoma tumors to be better described, as proved in [20].