An Algorithm for Finding Approximate Symbolic Pole/Zero Expressions

Abstract

The approximate pole/zero expressions are computed starting from the state or the “state-like” matrix. The attempts of open-circuit and short-circuit replacement of circuit elements are combined with those to cut row and column groups of the state matrix for poles or the “state-like” matrix for zeros, and with LR iterations. The expressions of all poles and zeros of a wide-band amplifier and an RLC band-stop filter are computed, obtaining significantly better results than those given by the best approach available, implemented in the Analog Insydes package.

1. Introduction

A circuit function, F(s) = N(s)/D(s), is a ratio of polynomials in s, with the coefficients of D(s) and N(s) depending on circuit parameters. The poles are the roots of D(s), while the zeros are the roots of N(s). Since the degrees of D(s) and N(s) often exceed four, exact symbolic p/z (pole/zero) expressions generally do not exist. Because these formulas are very useful in designing various circuits like amplifiers and filters, approximate p/z expressions are necessary.

Some approaches to calculating these expressions involve working with symbolic circuit functions. A detailed explanation of these methods is provided in [1,2,3]. The simplest method is pole splitting, which assumes that the first one or two roots of D(s) or N(s) have moduli much smaller than the other roots; the approximate p/z expressions are obtained by solving a first- or second-degree equation. These expressions can be refined using Newton iterations [4], starting from a formula that is close enough in value to the exact p/z. However, this formula is only available in specific cases, such as those involving pole splitting. Other methods involve the simplification after generation (SAG) of F(s), including cancelation of entries in the determinant form of N(s) and D(s), which can result in factored expressions. However, these factors are not always simple enough to extract the targeted p/z [3]. These methods, along with simpler ones that use the SAG of F(s) as a whole, can lead to significant modifications or the loss of some p/z values [2].

Aiming to calculate more p/z expressions, a symbolic state matrix or an equivalent matrix has been used. The time constant matrix is utilized in [1], and the approximate symbolic expressions for its first and second largest eigenvalues, τ₁ and τ₂, are obtained by solving a quadratic equation; the other eigenvalues are ignored. The first two dominant poles are p₁ = −1/τ₁ and p₂ = −1/τ₂. For an RC circuit, the remaining poles are calculated similarly, shifting p₁ and p₂ to the origin by short-circuiting two capacitors.

Writing the nodal admittance matrix as Y_N(s) = A − s ∙ B, where A and B are matrices with symbolic entries in terms of circuit parameters, the poles of any circuit function are the roots of

$$det\left(A-s·B\right)=0$$

(1)

which corresponds to the generalized eigenvalues of the matrix pencil (A, B). The simplification of the symbolic expression (1) until it can be expressed as a product of second-degree polynomials in s is used for calculating the symbolic expression of a p/z with its modulus near a user-specified value s₀ [2]. This calculation is performed with a maximum user-defined relative error on the p/z modulus and is implemented in the commercial package Analog Insydes [5].

The symbolic LR algorithm involves the following steps: writing the symbolic state matrix A₀, reducing the order of A₀ through pole cluster identification, rearranging A₀ so that its diagonal elements are in decreasing order of their magnitude, and performing LR iterations (A₀ = L₁ ∙ R₁, R₁ ∙ L₁ = A₁, A₁ = L₂ ∙ R₂, …). These iterations ultimately converge to a matrix with real poles on the diagonal and complex poles as the eigenvalues of 2 × 2 diagonal blocks, with the remaining entries close to zero. As the symbolic LR iterations proceed, the entries in A_i develop increasingly complex expressions that may exceed the available computational resources. This occurs because some simplifications that could slow the convergence rate are made. This method is effective for sixth-order matrices of moderate complexity [6].

For a linear circuit $\dot{x}=Ax+Bu+E\dot{u}$, $y=Cx+du$, where x is the state variable vector, A is the state matrix, u is the input vector with one component, y is the output vector with one component, and B, E, C, and d are matrices of appropriate dimensions. A is computed starting from a hybrid matrix with symbolic entries by the reduction to the row echelon form [7]. If d ≠ 0, the zeros are the eigenvalues of the “state-like” matrix A’:

$$A\prime =(A-B\cdot C/d)(I+E\cdot C/d{)}^{-1}$$

(2)

Since (2) is invalid for d = 0, the Sandberg-So [8] and Davison [9] algorithms, which can find A’ in this case, have been implemented in the MAPLE software [7]. The symbolic LR algorithm has been improved in [10] by using matrices without an initial ordering of the diagonal elements (which may lead to additional iterations) and by replacing the eigenvalue cluster search with matrix order reduction through the elimination of one or two rows and columns (corresponding to a real eigenvalue or a complex pair of eigenvalues) during symbolic LR iterations.

The circuit size manageable with our algorithms [6,7,10] is extended in this paper by considering the replacement of some circuit elements with open or short circuits and performing simplifications focused solely on the error of the targeted real eigenvalue (or pair of complex eigenvalues). Section 2 introduces the new algorithm, while Section 3 provides two examples worked out with the proposed algorithm.

2. Algorithm

This algorithm calculates the approximate symbolic expression of a pole $p_k$ or a zero $z_k$ that is valid around a design point defined by the nominal values of the circuit parameters. If $p_k$ is a real p/z, the relative error of this expression at the design point is

$${\epsilon }_1=(p_{kn}-p_k^{*})/p_k^{*}$$

(3)

where $p_{kn}$ is the numerical value of the expression of $p_k$ in the design point, and $p_k^{*}$ is the exact value of $p_k$ (calculated as the eigenvalue of the state matrix with numerical entries). If $p_k$ is a complex p/z, the similar errors ${\epsilon }_{1m}$ and ${\epsilon }_{1ph}$ for the pole modulus and phase are used.

The approximate symbolic expression of $p_k$ is computed as the eigenvalue of the state matrix using the following steps:

• Starting from a SPICE–like netlist [7], the symbolic state matrix, which contains all parameters as symbols, is written. The numerical values of the poles are then calculated as eigenvalues of the state matrix, where the entries are replaced with their respective parameter values.
• The symbolic parameters ${\alpha }_1$, …, ${\alpha }_M$, are selected in order of decreasing relative differential sensitivities of the $p_k$ modulus with respect to ${\alpha }_m$:

  $$S_{p_k}^{{\alpha }_m}=(\partial |p_k|/\partial {\alpha }_m)/\left(\right|p_k|/{\alpha }_m)$$

  (4)

  their number M is set by the user. For a complex pole, the sensitivity of the $p_k$ phase, defined similarly, is also used. Any other choice of the set of symbolic parameters may be adopted, depending on the specific design problem.
• Attempts to simplify the circuit equations by replacing a circuit element with parameter ${\alpha }_m$ by an open circuit are made; these attempts are performed for all non-symbolic parameters, in the increasing order of the $S_{p_k}^{{\alpha }_m}$ moduli. An attempt is validated if ${\epsilon }_o<{\epsilon }_{oM}$, where ${\epsilon }_o$ is computed with (3), $p_{kn}$ being the value with the above simplification, and ${\epsilon }_{oM}$ is user-defined. The new form of the symbolic state matrix is generated after each successful attempt.
• Attempts to simplify circuit equations, replacing a circuit element with parameter ${\alpha }_m$ by a short circuit are made; these attempts are performed for all non-symbolic parameters, in the increasing order of the $S_{p_k}^{{\alpha }_m}$ moduli. An attempt is validated if ${\epsilon }_{sh}<{\epsilon }_{shM}$, where ${\epsilon }_{sh}$ is computed with (3), $p_{kn}$ being the value with the above simplification, and ${\epsilon }_{shM}$ is user-defined. The new form of the symbolic state matrix is generated after each successful attempt.
• Attempts to cut an as-large-as-possible group of the same index rows and columns are made, the remaining matrix having $p_{kn}$ as an eigenvalue. Each attempt is validated if ${\epsilon }_{cut}<{\epsilon }_{cutM}$, where ${\epsilon }_{cut}$ is computed with (3), $p_{kn}$ being the value with the above simplification, and ${\epsilon }_{cutM}$ is user-defined. A reduced-order symbolic state matrix is generated after each successful attempt. If this matrix has order 1 or 2, the $p_k$ expression can be found straightforwardly.
• The symbolic LR iterations are performed using a simplified matrix from steps three to five. These iterations stop if ${\epsilon }_{it}<{\epsilon }_{itM}$, where ${\epsilon }_{it}$ is calculated using (3), $p_{kn}$ is the numerical value of the symbolic expression of the $p_k$ modulus obtained after that iteration, and ${\epsilon }_{itM}$ is user-defined. For complex eigenvalues, a similar phase error is used along with the modulus error. The user-defined simplification error during the LR iterations is ${\epsilon }_{itS}$. Attempts to cut groups of the same index rows and columns, as in step 5, are made after each LR iteration.

At first glance, steps three to five only involve numerical calculations, making step 2 seem unnecessary. However, the symbolic HYBRID algorithm [7], used in the second step, generates a minimum-complexity symbolic hybrid matrix, which then produces a minimum-complexity state matrix. This is very important because the complexity of symbolic calculations in LR iterations can exceed available computational resources.

A flowchart illustrating the logical relationships within the algorithm and the execution sequence of each step described in the text above is shown in Figure 1.

To acquire a more comprehensive understanding of the method’s details, the pseudo-code of the symbolic pole/zero extraction method is provided in Algorithm 1, for a pole $p_k$. A zero $z_k$ can be derived using the same algorithm starting from the “state-like” matrix A’.

Algorithm 1. Symbolic Pole/Zero Extraction for a pole $p_k$

Read the SPICE–like netlist    Generate the symbolic and the numeric state matrix A    Calculate the numerical values of the poles as eigenvalues of A    Select symbolic parameters ${\alpha }_1$, …, ${\alpha }_M$ in the decreasing order of $S_{p_k}^{{\alpha }_m}$   The circuit equations are simplified:       for $m=1\dots M$,$\mathrm{replace} {\alpha }_m$ by open-circuit          if $\left({\epsilon }_o<{\epsilon }_{oM}\right)$             validate simplification             $\mathrm{go} \mathrm{to} \mathrm{next} {\alpha }_m$          else             reject simplification             $\mathrm{go} \mathrm{to} \mathrm{next} {\alpha }_m$          end if       end for       for $m=1\dots M$,$\mathrm{replace} {\alpha }_m$ by short-circuit          if $\left({\epsilon }_{sh}<{\epsilon }_{shM}\right)$            validate simplification            $\mathrm{go} \mathrm{to} \mathrm{next} {\alpha }_m$          else            reject simplification            $\mathrm{go} \mathrm{to} \mathrm{next} {\alpha }_m$          end if       end for       for $k=1\dots size\left(A\right)$, cut row and column of the same index          if $\left({\epsilon }_{cut}<{\epsilon }_{cutM}\right)$            validate cut            try another cut          else            reject cut            try another cut         end if   end for   The symbolic pole ${\mathit{p}}_{\mathit{k}}$ is obtained:     if $size\left(A\right)=1$       $p_k$ = $A$     else if $size\left(A\right)=2$       $p_k$ and $p_{k+1}$ are $\mathrm{eigenvalues} \mathrm{of} A$     else       symbolic LR iterations are performed     end if

Either from the initial data or after the simplifications in the second and third steps, a circuit with excess elements may result. Consider a circuit without inductors having capacitors C₁, …, C_n, C_n+1, where only C_n+1 is an excess element. The equations of C₁, …, C_n are $y=-\Delta \dot{x}$, where x is the state vector, Δ = diag(C₁, …, C_n), and y contains the capacitor currents [11,12]. Let $y^{*}=-{\Delta }^{*}{\dot{x}}^{*}$ for C_n+1, $x^{*}=k_{3}x$ from the Kirchhoff’s second law, and $y=k_{0}x+k_2{y}^{*}$ given by the superposition theorem, where $k_0$ and $k_2$ have symbolic entries [12] and can be computed with the symbolic HYBRID software [7]. After some matrix algebra, it follows that

$$A=-{\left(I-{\Delta }^{-1}{k}_2{\Delta }^{*}{k}_3\right)}^{-1}{\Delta }^{-1}{k}_0$$

(5)

where I is the unity matrix of the appropriate order. This expression is valid for a circuit having many excess elements, too.

The approximate symbolic expression of $z_k$ is computed as the eigenvalue of the “state-like” matrix [7]. The procedures implementing this algorithm have been written in the MAPLE software.

Each parameter $p_k$ has a minimum tolerance $t_k^{-}$ and a maximum tolerance $t_k^{+}$ so that $p_k\in [p_k^{-},p_k^{+}]$, where $p_k^{-}=p_{kn}(1-t_k^{-}/100)$ and $p_k^{+}=p_{kn}(1+t_k^{+}/100)$. The errors of the p/z expressions are computed in the design point and in the corners corresponding to all combinations of the extreme values of $p_k$. For example, a two-parameter formula is tested in $(p_{1n},p_{2n})$, $(p_1^{+},p_2^{+})$, $(p_1^{-},p_2^{-})$, $(p_1^{+},p_2^{-})$, and $(p_1^{-},p_2^{+})$. Two expressions of the same p/z are compared using the following relative errors: the error in the design point e_n, the average error in all corners e_ac, the minimum error in a corner e_mc, and the maximum error in a corner e_Mc.

3. Application Cases

To evaluate the efficacy of the proposed method, it has been applied to two distinct circuits: a wide-band amplifier and a third-order band-stop Butterworth filter.

3.1. Wide-Band Amplifier

The approximate p/z expressions of the wide-band amplifier in Figure 2 are calculated using the proposed algorithm (PR) and the Analog Insydes method (AI). The small-signal transistor equivalent circuit is shown in Figure 3. The design parameters are C1 = 33 nF, R1 = 100 kΩ, C2 = 5.1 nF, R2 = 7.5 kΩ, C3 = 3.3 µF, R3 = 1 kΩ, R4 = 75 kΩ, R5 = 75 kΩ, R6 = 100 kΩ, R7 = 1 GΩ, Cbe = 100 pF, Rbe = 1 kΩ, Cbc = 3 fF, Rce = 80 kΩ, F = 50, and RE = 5Ω, and Vin is an AC voltage source with an amplitude of 1 V and zero-degree phase.

The symbolic parameters have been chosen so that both algorithms can produce expressions containing them. These parameters are listed in

Table 1. Pole sensitivities and errors.

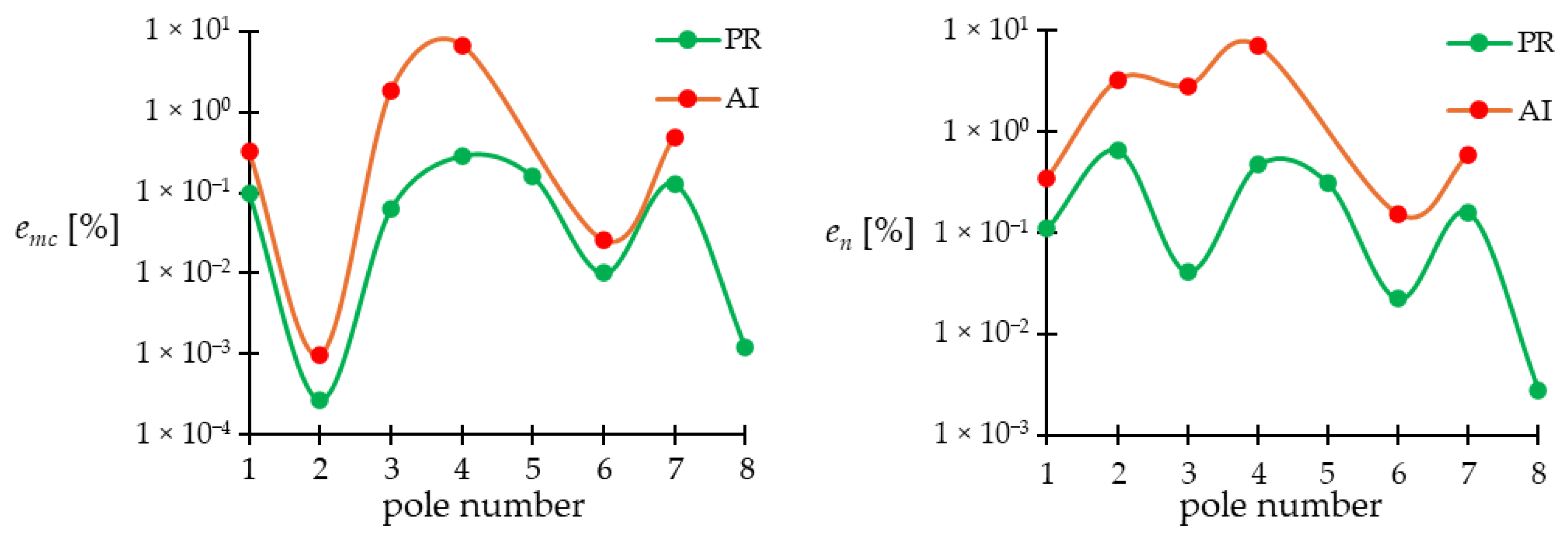
Pole	Parameters/ Sensitivities	Alg.	emc [%]	en [%]	eMc [%]	eac [%]
p1	C1, R1, R6/ 1.00, 0.85, 0.15	PR	1.0 × 10−1	1.1 × 10−1	1.2 × 10−1	1.1 × 10−1
		AI	3.2 × 10−1	3.4 × 10−1	3.7 × 10−1	3.4 × 10−1
p2	C2, Rbe3, F2, R5, R3, R4, R2, F3, R6, R1, RE3/ 1.03, 0.83, 0.72, 0.72, 0.72, 0.66, 0.65, 0.52, 0.37, 0.35, 0.20	PR	2.7 × 10−4	6.6 × 10−1	5.5	1.34
		AI	9.9 × 10−4	3.2	9.5	2.92
p3	Cbe2, Rbe2/ 1.04, 1.03	PR	6.3 × 10−2	4.1 × 10−2	2.0 × 10−1	1.3 × 10−1
		AI	1.81	2.81	4.21	2.86
p4	Cbe1, Rbe1, F1, R5, R1/ 0.98, 0.98, 0.92, 0.38, 0.30	PR	0.29	0.47	0.78	0.51
		AI	6.69	6.94	7.34	6.99
p5	Cbe3, RE3, Rbe3, F3/ 0.98, 0.80, 0.20, 0.19	PR	0.16	0.31	0.44	0.28
		AI	-	-	-	-
p6	Cbc1, R5, Rce1, R2, R1, R6/ 0.98, 0.29, 0.28, 0.14, 0.13, 0.13	PR	1.0 × 10−2	2.2 × 10−2	3.7 × 10−2	2.1 × 10−2
		AI	2.6 × 10−2	1.5 × 10−1	4.5	1.66
p7	Cbc2, R3, Rce2/ 0.99, 0.97, 0.01	PR	1.3 × 10−1	1.6 × 10−1	1.8 × 10−1	1.6 × 10−1
		AI	4.9 × 10−1	5.9 × 10−1	6.8 × 10−1	5.8 × 10−1
p8	Cbc3, RE2/ 1.00, 0.99	PR	1.2 × 10−3	2.8 × 10−3	4.8 × 10−3	2.6 × 10−3
		AI	-	-	-	-

and

Table 2. Zero sensitivities and errors.

Zero	Parameters/ Sensitivities	Alg.	emc [%]	en [%]	eMc [%]	eac [%]
z2	R6, F2/ 0.57, 0.57	PR	8.6 × 10−1	8.1 × 10−1	2.48	1.44
		AI	-	-	-	-
z3	Cbe2, Rbe2, F2, R6, C2, R5, R2, R4, Rbe3, F3/ 0.62, 0.62, 0.44, 0.44, 0.43, 0.42, 0.39, 0.39, 0.35, 0.35	PR	3.09	4.95	8.79	5.32
		AI	-	-	-	-
z4	Cbe1, Rbe1, F1/ 1.01, 1.01, 0.99	PR	4.0 × 10−2	6.9 × 10−1	5.6 × 10−1	3.6 × 10−1
		AI	1.8 × 10−1	9.0 × 10−1	1.22	8.3 × 10−1
z5	Cbe3, RE3, Rbe3, F3/ 0.98, 0.80, 0.20, 0.19	PR	1.17	1.54	1.88	1.53
		AI	-	-	-	-
z6	Cbc1, R2/ 1.00, 0.84	PR	4.7 × 10−6	7.6 × 10−6	1.2 × 10−5	8.0 × 10−6
		AI	4.7 × 10−6	7.6 × 10−6	1.2 × 10−5	8.0 × 10−6
z7	RE2, Cbc2, Cbc3/ 1.00, 0.50, 0.50	PR	4.9 × 10−3	7.4 × 10−3	1.0 × 10−2	7.4 × 10−3
		AI	9.5 × 10−3	1.4 × 10−2	1.9 × 10−2	1.4 × 10−2

, together with the relative differential p/z sensitivities with respect to them, and the errors e_n, e_mc, e_Mc, and e_ac. The corner errors are computed considering the usual tolerances as $t_k^{\pm }=\pm 5$ for all resistors in Figure 2, $t_k^{\pm }=\pm 30$ for all resistors in the small-signal equivalent circuit for transistors, $t_k^{\pm }=\pm 10$ for all capacitors, and $t_k^{\pm }=\pm 5$ for F.

The approximate symbolic expressions of all poles and zeros of the voltage gain $A_v=V_{out}/V_{in}$ are computed with the PR and AI algorithms.

The 9th-order state matrix of the small-signal equivalent circuit has one simple null eigenvalue, with the remaining ones being (−2.564 × 10², −5.131 × 10⁵, −9.726 × 10⁶, −1.802 × 10⁸, −2.549 × 10⁹, −1.521 × 10¹⁰, −3.394 × 10¹¹, and −6.701 × 10¹³). These are the pole numerical values for $A_v$, which, except for the greater-modulus one, have been obtained with HSPICE, also.

To improve the readability of this table, we incorporate graphical comparisons of PR errors versus AI errors for all the computed poles in Figure 4. Since the numerical values of the errors vary by several orders of magnitude, the best way to plot the graphs is to use a logarithmic scale on the y-axis.

As is easy to see, all the PR errors are smaller than the AI errors. Similar patterns can be observed for the zero errors, leading to the same conclusion.

The 8th-order “state-like” matrix for the computation of $A_v$ zeros has a double-null eigenvalue. As one null pole of $A_v$ is simplified with one null zero of $A_v$, the zero values are (0.00, 2.108 × 10⁷, −3.424 × 10⁷, −4.676 × 10⁸, −2.549 × 10⁹, −5.309 × 10¹⁰, and −3.334 × 10¹³). These are the zero numerical values for $A_v$, which, except for the greater-modulus one, have been obtained with HSPICE, also.

As the p/z expressions with more than three symbols cannot be easily displayed because of their huge dimensions, the p/z expressions containing those two or three symbols with the greatest-sensitivity moduli are given in

Table 3. Pole symbolic expressions and simplification errors.

Pole	Alg.	Symbolic Expression			ens [%]
p1	PR	${\displaystyle \frac{-5.62\times {10}^{-3}-4.22\times {10}^{-10} R6}{5.62\times {10}^{-3} C1 R1+C1+4.22\times {10}^{-10} C1 R1 R6+1.01\times {10}^{-3} C1 R6}}$			0.1
	AI	$-{\displaystyle \frac{1.00}{0.18 C1 R6+C1 R1}}$			0.3
p2	PR	$-{\displaystyle \frac{3.25}{2.55\times {10}^2 C2+C2 Rbe3}}$	or	${\displaystyle \frac{-1.00-4.49\times {10}^{-2} F2}{2.55\times {10}^2 C2+C2 Rbe3}}$	1.0
	AI	${\displaystyle \frac{-9.23\times {10}^7 C2 {Rbe3}^2-0.25 Rbe3-62}{C2 {Rbe3}^2}}+{\displaystyle \frac{\sqrt{-5.55\times {10}^8 C2 Rbe3+1.16\times {10}^{11} C2+8.52\times {10}^{15} {C2}^2 {Rbe3}^2}}{C2 Rbe3}}$			3.2
p3	PR	$-{\displaystyle \frac{1.00}{Cbe2 Rbe2}}$			2.8
	AI	$-{\displaystyle \frac{1.00}{Cbe2 Rbe2}}$			2.8
p4	PR	$-{\displaystyle \frac{18.40}{Rbe1 Cbe1+1.53\times {10}^{-9}}}$	or	${\displaystyle \frac{-0.35 F1-0.94}{Rbe1 Cbe1+3.06\times {10}^{-11} F1}}$	0.87
	AI	${\displaystyle \frac{-25.50-8.96\times {10}^9 Rbe1 Cbe1}{Rbe1 Cbe1}}+{\displaystyle \frac{\sqrt{1.06\times {10}^{11} Rbe1 Cbe1+8.03\times {10}^{19}{Rbe1}^2 {Cbe1}^2}}{Rbe1 Cbe1}}$			8.87
p5	PR	${\displaystyle \frac{-2.00 RE3 Rbe3-51.00 {RE3}^2-1.96\times {10}^{-2} {Rbe3}^2}{Rbe3 {RE3}^2 Cbe3+1.96\times {10}^{-2} {Rbe3}^2 RE3 Cbe3}}$			1.54
	AI	-			-
p6	PR	${\displaystyle \frac{-1.59\times {10}^{-4}-{10}^{-8} R5-8.99\times {10}^4 Cbc1 R5-1.57\times {10}^{-13} {R5}^2}{Cbc1+1.98\times {10}^{-4} Cbc1 R5+5.23\times {10}^{-9} Cbc1 {R5}^2}}$			0.74
	AI	${\displaystyle \frac{-5.00\times {10}^{-5} R5-\sqrt{1.27\times {10}^{-10} {R5}^2+1.12\times {10}^{-5} R5}}{Cbc1 R5}}$			10
p7	PR	${\displaystyle \frac{-0.50-1.67\times {10}^{14} Cbc2}{R3 Cbc2}}$	or	${\displaystyle \frac{-0.50 Rce2-0.50 R3-1.67\times {10}^{14} Rce2 Cbc2}{R3 Rce2 Cbc2}}$	1.8 1.2
	AI	$-{\displaystyle \frac{1.00}{R3 Cbc2}}$	or	${\displaystyle \frac{-R3-Rce2}{R3 Rce2 Cbc2}}$	1.8 0.6
p8	PR	${\displaystyle \frac{-R3-0.50 RE2}{R3 Cbc3 RE2}}$			0.3
	AI	-			-

and

Table 4. Zero symbolic expressions and simplification errors.

Zero	Alg.	Symbolic Expression			ens [%]
z2	PR	${\displaystyle \frac{1.03\times {10}^7-10.4 R6 F2+4.97\times {10}^{-6} {R6}^2 {F2}^2-1.33\times {10}^{-12} {R6}^3 {F2}^3}{1.00-1.01\times {10}^{-6} R6 F2+3.27\times {10}^{-13} {R6}^2 {F2}^2}}$			3.03
	AI	-			-
z3	PR	${\displaystyle \frac{-0.50-1.21\times {10}^3 \sqrt{Rbe2 Cbe2 F2}}{Rbe2 Cbe2}}$			6.5
	AI	-			-
z4	PR	${\displaystyle \frac{-1.00-0.92 F1-1.78\times {10}^{-5} Rbe1}{Rbe1 Cbe1}}$			0.07
	AI	${\displaystyle \frac{-3.26\times {10}^{-5} {Rbe1}^2-0.91 F1 Rbe1-Rbe1}{{Rbe1}^2 Cbe1}}$			0.9
z5	PR	${\displaystyle \frac{-1.00-5.10\times {10}^{-2} RE3}{RE3 Cbe3}}$	or	${\displaystyle \frac{-Rbe3-51.00 RE3}{Rbe3 RE3 Cbe3}}$	1.5
	AI	-			-
z6	PR	${\displaystyle \frac{-0.50-1.29\times {10}^{-5} R2-\sqrt{0.25+1.29\times {10}^{-5} R2}}{Cbc1 R2}}$			0.7
	AI	${\displaystyle \frac{-0.50-1.29\times {10}^{-5} R2-\sqrt{0.25+1.29\times {10}^{-5} R2}}{Cbc1 R2}}$			0.7
z7	PR	${\displaystyle \frac{-6.38\times {10}^{-14} RE2-1.25\times {10}^{-5} RE2 Cbc3-Cbc3-2.55\times {10}^{-9}}{2.55\times {10}^{-9} Cbc2 RE2+RE2 Cbc3 Cbc2+2.55\times {10}^{-9} RE2 Cbc3}}$			7 × 10−3
	AI	${\displaystyle \frac{-{10}^{10} Cbc2-{10}^{10} Cbc3-1.00}{Cbc2 RE2+RE2 Cbc3}}$			1 × 10−2

. These formulas are obtained from those described in Table 1 and Table 2, using a simplification procedure. This procedure eliminates the least significant term in the numerator and in the denominator if it does not lead to a relative error of the p/z value, which is greater than the simplification error e_ns in the design point [6]. In this way, as many terms as possible are removed. The maximum relative error of a p/z symbolic expression in the design point is e_n if this formula results from those described in Table 1 and Table 2, replacing some symbolic parameters by their nominal values, or e_ns if it is obtained using the above simplification procedure.

Table 3 and Table 4 contain the approximate p/z expressions in increasing order of the p/z moduli. These tables contain both three-symbol formulas (3f) and two-symbol formulas (2f). If the 3fs, obtained with relatively small simplification errors, are simple enough to be displayed for both algorithms, their display has been preferred to that of 2fs.

If a 3f is too intricate (as that of p₂ calculated with AI) or is obtained with a significantly greater e_ns than the corresponding 2f (as that of p₃ calculated with PR), then the 2f is preferred. In general, the 2f and 3f expressions are obtained with different e_ns (as for p₇).

The PR algorithm used the following errors to compute the symbolic expressions: ε_oM $\in$ [1 × 10⁻³, 5 × 10⁻²], ε_shM $\in$ [5 × 10⁻⁴, 1 × 10⁻³], ε_cutM $\in$ [5 × 10⁻⁵, 5 × 10⁻²], ε_itM $\in$ [1 × 10⁻², 1 × 10⁻¹], and ε_itS $\in$ [2 × 10⁻², 3 × 10⁻²]. The AI algorithm allows users to set only the relative error “MaxError” in the nominal point; in this example, the values “MaxError” $\in$ [1 × 10⁻³, 1.1 × 10⁻¹] have been employed. The 2fs and 3fs displayed in Table 3 and Table 4 have been simplified with e_ns $\in$ [7 × 10⁻⁵, 6.5 × 10⁻²] for the PR algorithm and with e_ns $\in$ [1 × 10⁻⁴, 1 × 10⁻¹] for the AI algorithm. In order to illustrate how our program works, the computation of three p/z expressions (p₁, p₆, z₂) is described in detail in the following paragraph:

(p₁) Cbc1, Cbc2, Cbc3, Cbe1, Cbe2, and Rce1 are replaced by open circuits using ε_oM = 1 × 10⁻³, and RE3 is replaced by a short circuit using ε_shM = 5 × 10⁻⁴. The third-order state matrix of the new circuit has been written, and one row–column pair of it has been removed using ε_cutM = 5 × 10⁻³. One LR iteration has been performed with the remaining second-order matrix using ε_itM = 1 × 10⁻² and ε_itS = 0; the symbolic pole expression, as described in Table 1, is its diagonal entry with the corresponding numerical value at the design point. The expression in Table 3 has been obtained with e_ns = 0.1%. This computation required 2.33 min. Setting ε_shM = 1 × 10⁻⁴ and using the same other errors, no short-circuit replacement has been made; the simplified pole symbolic expression obtained in 2.8 min is practically the same (a coefficient in the numerator is changed from −5.62 10⁻³ to −5.61 10⁻³). Still, the errors (computed with the non-simplified expression) are smaller: e_n = 0.073%, e_mc = 0.07%, e_Mc = 0.078%, and e_ac = 0.073%.

Many similar results show that, in general, the short-circuit replacement leads to a more significant error in the p/z expression than the open-circuit one.

(p₆) C2, Cbe2, Cbc3, Rbe2, Rbe3, Rce2, Rce3, F2, and F3 are replaced by open circuits, working with ε_oM = 1 × 10⁻³. The fifth-order state matrix of the new circuit has been written. Furthermore, RE2 and RE3 have been replaced by short circuits, considering ε_shM = 5 × 10⁻⁴, with a new fifth-order state matrix being written. Three row–column pairs have been cut from this matrix using ε_cutM = 5 × 10⁻³. One LR iteration with ε_itM = 1 × 10⁻² and ε_itS = 0 has been performed on the remaining second-order state matrix, obtaining the formula described in Table 1 with the simplified form in Table 3. A CPU time of 9.134 s has been used to obtain this result. A variant in which no element is replaced by an open circuit has also been considered. The short-circuit replacement of Rce3 has been performed using ε_shM = 1 × 10⁻³. A capacitor loop containing C2, Cbe3 || Cbc3, and Cbe2 resulted, with C2 being considered as the excess capacitor. The seventh-order state matrix of the modified circuit has been derived using Equation (5), where the matrices k₀ and k₂ were computed using the program reported in [7]. Six row–column pairs of this matrix have been cut considering ε_cutM = 5 × 10⁻², and the expression of p₆ has been found in 2.59 s as the remaining diagonal entry. The errors are two orders of magnitude greater than those in Table 1 (e_n = 0.15%, e_mc = 1.64%, e_Mc = 2.43%, e_ac = 2.00%).

(z₂) Replacing R3, Rce2, Cbc1, Rce3, and Cbe3 by open circuits using ε_oM = 1 × 10⁻², a sixth order “state-like” matrix is obtained with the Sandberg-So algorithm. For ε_shM = 1 × 10⁻³, no short-circuit replacement has been accepted. Using ε_cutM = 5 × 10⁻², two row–column pairs have been cut. Four LR iterations have been performed with the remaining fourht-order matrix using ε_itM = 1 × 10⁻² and ε_itS = 3 × 10⁻². This computation lasted for 22.9 s.

All procedures were implemented in the MAPLE software on a computer with an I7 at 3.5 GHz processor and 8GB RAM (with a maximum of 2 GB used). The CPU times of AI are at least 50% smaller than those of the proposed algorithm.

The AI algorithm gives no formula for p₅, p₈, z₂, z₃, and z₅. As can be observed from the above p/z numerical values, p₅ and z₅ have almost identical values (their computation with 50 digits gives p₅ = −2.549188 × 10⁹ and z₅ = −2.549361 × 10⁹). The AI algorithm cannot compute the approximate symbolic expressions of p₅ and z₅, which have almost identical values, due to the transfer function simplification. A term corresponding to p₅ in the denominator is simplified with the term corresponding to z₅ in the numerator. The p/z expressions computed by the AI for p₈, z₂, and z₃ have e_n error greater than 100% and are omitted. The absolute value of z₂ and z₃ is almost the same, which is most likely the reason why AI cannot calculate their correct expressions. In some cases, the same 2f is computed with both algorithms (p₃, z₆). All formulas given by PR have smaller errors than those provided by AI, or the same ones.

For F₁ = F₂ = F₃ = 400, p₂ and p₃ are a complex pair, whose sensitivities and errors are given in

Table 5. Sensitivities and errors for |p₂| = |p₃|.

Pole	Parameters/Sensitivities	Alg.	${\mathit{e}}_{\mathit{m}\mathit{c}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{n}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{M}\mathit{c}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{a}\mathit{c}}^{\mathit{M}}$ [%]
p2, p3	R5, C2, F2, Cbe2, Rbe2, R3, R4, R2, RE3, R1, R6, Rbe3, F3/ 0.58, 0.58, 0.57, 0.57, 0.57, 0.56, 0.53, 0.53, 0.38, 0.29, 0.29, 0.20, 0.20	PR	1.34	1.75	2.35	1.79

and

Table 6. Sensitivities and errors for arg(p₂) = −arg(p₃).

Pole	Parameters/Sensitivities	Alg.	${\mathit{e}}_{\mathit{m}\mathit{c}}^{\mathit{A}}$ [%]	${\mathit{e}}_{\mathit{n}}^{\mathit{A}}$ [%]	${\mathit{e}}_{\mathit{M}\mathit{c}}^{\mathit{A}}$ [%]	${\mathit{e}}_{\mathit{a}\mathit{c}}^{\mathit{A}}$ [%]
p2, p3	R5, C2, F2, Cbe2, Rbe2, R3, R4, R2, RE3, R1, R6, Rbe3, F3/ 0.58, 0.58, 0.57, 0.57, 0.57, 0.56, 0.53, 0.53, 0.38, 0.29, 0.29, 0.20, 0.20	PR	9.79 × 10−5	0.127	0.497	0.157

, where $e_n^M$ is the error module in the design point, $e_{ac}^M$ is the average module error in all corners, $e_{mc}^M$ is the minimum module error in a corner, and $e_{Mc}^M$ is the maximum module error in a corner. The errors with “A” superscript are for the argument. Their simplified symbolic expressions are written in

Table 7. Symbolic expressions for p₂ and p₃.

Pole	Alg.	Symbolic Expression	${\mathit{e}}_{\mathit{n}\mathit{s}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{n}\mathit{s}}^{\mathit{A}}$ [%]
p2, p3	PR	${\displaystyle \frac{-5\times {10}^6 C2 R5\pm I \sqrt{2.40\times {10}^{10} C2 R5-2.50\times {10}^{13} {C2}^2 {R5}^2}}{C2 R5}}$	1.61	0.127

, where $I=\sqrt{-1}$.

In many cases, a unique formula cannot be valid for a zone covering all intervals $[p_k^{-},p_k^{+}]$, k = 1, 2, …, with a set of formulas being needed. For example, if F₁ = F₂ = F₃ = 154, no formula with an acceptable validity range for p₂ and p₃ can be obtained around the design point D₀ (F₂ = 154, Rbe1 = 1 kΩ). This is because in this region, we have both the real and complex values for p₂ and p₃. But some useful expressions in terms of F₂ and Rbe1 can be found by considering two other design points, D₁ (F₂ = 140, Rbe1 = 1 kΩ) and D₂ (F2 = 160, Rbe1 = 1 kΩ). The results are given in

Table 8. Sensitivities and errors around D₁.

Pole	Parameters/Sensitivities	Alg.	${\mathit{e}}_{\mathit{m}\mathit{c}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{n}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{M}\mathit{c}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{a}\mathit{c}}^{\mathit{M}}$ [%]
p2	F2, F3, F1, Rbe1/ 1.68, 0.99, 2.91 × 10−2, 1.23 × 10−2	PR	3.48	4.01	5.12	4.08
p3	F2, F3, Rbe1, F1/ 0.75, 0.45, 1.28 × 10−2, 5.65 × 10−3	PR	0.08	0.23	1.27	0.44

,

Table 9. Symbolic expressions around D₁.

Pole	Alg.	Symbolic Expression	ens [%]
p2 p3	PR	${\displaystyle \frac{-5.09\times {10}^6-0.76 Rbe1-184 F2\pm \sqrt{2.48\times {10}^{13}-1.51\times {10}^{11} F2}}{1.50\times {10}^{-7} Rbe1+1.00}}$	4.054 0.248

,

Table 10. Sensitivities and errors for |p₂| = |p₃| around D₂.

Pole	Parameters/Sensitivities	Alg.	${\mathit{e}}_{\mathit{m}\mathit{c}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{n}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{M}\mathit{c}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{a}\mathit{c}}^{\mathit{M}}$ [%]
p2, p3	F2, F3, F1, Rbe1/ 2.52, 1.42, 2.78 × 10−2, 2.73 × 10−2	PR	1.18	3.48	2.84	1.87

,

Table 11. Sensitivities and errors for arg(p₂) = −arg(p₃) around D₂.

Pole	Parameters/Sensitivities	Alg.	${\mathit{e}}_{\mathit{m}\mathit{c}}^{\mathit{A}}$ [%]	${\mathit{e}}_{\mathit{n}}^{\mathit{A}}$ [%]	${\mathit{e}}_{\mathit{M}\mathit{c}}^{\mathit{A}}$ [%]	${\mathit{e}}_{\mathit{a}\mathit{c}}^{\mathit{A}}$ [%]
p2, p3	F2, F3, F1, Rbe1/ 2.52, 1.42, 2.78 × 10−2, 2.73 × 10−2	PR	0.000	0.997	1.958	0.718

and

Table 12. Symbolic expressions around D₂.

Pole	Alg.	Symbolic Expression	${\mathit{e}}_{\mathit{n}\mathit{s}}^{\mathit{M}}$ [%]	${\mathit{e}}_{\mathit{n}\mathit{s}}^{\mathit{A}}$ [%]
p2 p3	PR	${\displaystyle \frac{-5.09\times {10}^6-0.67 Rbe1-174 F2\pm I \sqrt{1.63\times {10}^{11} F2-2.48\times {10}^{13}}}{1.31\times {10}^{-7} Rbe1+1.00}}$	3.51	0.99

.

The modulus and the argument of each pole around D₀ are shown in Figure 5, Figure 6, Figure 7 and Figure 8. Although a set of formulas for real poles around D₁ is used along with another set for complex poles around D₂, the errors in the numerical values are negligible.

3.2. Band-Stop Filter

Although the algorithm for calculating p/z symbolic expressions was initially developed for amplifiers, it can be adapted and modified to compute the p/z symbolic expressions of filters, such as the circuit shown in Figure 9 [13].

The following third-order band-stop Butterworth filter was simulated with HSPICE and an earlier version of the PR algorithm. The circuit parameters are C1 = 3.18 µF, C2 = 1.593 nF, C3 = 3.18 µF, L1 = 7.966 µH, L2 = 15.9 mH, L3 = 7.966 µH, RS = 50 Ω, and RL = 50 Ω, and Vin is an AC voltage source with a magnitude of 1 V and zero-degree phase.

The state matrix of the circuit is 6 × 6, indicating that this circuit has six poles. The numerical results obtained with these programs are summarized in

Table 13. Pole values.

Pole	PR [ω]	HSPICE [ω]
p1	−3.138 × 103 + 5.446 × 103 I	−3.138 × 103 + 5.446 × 103 I
p2	−3.138 × 103 − 5.446 × 103 I	−3.138 × 103 − 5.446 × 103 I
p3	−6.295 × 103 + 0.000 I	−6.295 × 103 + 0.000 I
p4	−6.270 × 106 + 0.000 I	−6.270 × 106 + 0.000 I
p5	−3.135 × 106 + 5.441 × 106 I	−3.135 × 106 + 5.441 × 106 I
p6	−3.135 × 106 − 5.441 × 106 I	−3.135 × 106 − 5.441 × 106 I

and

Table 14. Zero values.

Zero	PR [ω]	HSPICE [ω]
z1, z3, z5	0.000 + 1.987 × 105 I	1.818 × 101 + 1.986 × 105 I
z2, z4, z6	0.000 − 1.987 × 105 I	1.818 × 101 − 1.986 × 105 I

.

The approximate symbolic expressions for the poles are listed in

Table 15. The approximate symbolic expressions of poles.

Pole	Symbolic Expressions
p1	$-{\displaystyle \frac{0.5( L2+RS C3 RL)}{C3 RL L2}}+{\displaystyle \frac{\sqrt{L{2}^2-2 L2 RS C3 RL+R{S}^2 C{3}^2 R{L}^2-4 C3 R{L}^2 L2}}{C3 RL L2}}$
p2	$-{\displaystyle \frac{0.5( L2+RS C3 RL)}{C3 RL L2}}-{\displaystyle \frac{\sqrt{L{2}^2-2 L2 RS C3 RL+R{S}^2 C{3}^2 R{L}^2-4 C3 R{L}^2 L2}}{C3 RL L2}}$
p3	$-{\displaystyle \frac{RL RS (L1+L3)}{L1 \left(RS+RL\right) L3}}$
p4	$-{\displaystyle \frac{0.5 R{S}^3-1.25\times {10}^5 R{L}^2 R{S}^3 C3}{RS RL \left(R{S}^2 C3+RS RL C3\right)}}+{\displaystyle \frac{\sqrt{1.57\times {10}^{10} R{L}^4 R{S}^6 C{3}^2-2.51\times {10}^5 R{S}^5 R{L}^3 C3-1.25\times {10}^5 R{L}^4 R{S}^4 C3}}{RS RL (R{S}^2 C3+RS RL C3)}}$
p5	$-{\displaystyle \frac{12.5 C2 L1+5\times {10}^{-3} L3 L1-12.5 C2 L3}{C2 L3 L1}}+{\displaystyle \frac{\sqrt{3.13\times {10}^{-2} C{2}^2 L{1}^2-75 L3 C2 L{1}^2+5\times {10}^{-3} L{3}^2 L{1}^2-25 L{3}^2 L1 C2-2.19\times {10}^5 C{2}^2 L{3}^2}}{C2 L3 L1}}$
p6	$-{\displaystyle \frac{12.5 C2 L1+5\times {10}^{-3} L3 L1-12.5 C2 L3}{C2 L3 L1}}-{\displaystyle \frac{\sqrt{3.13\times {10}^{-2} C{2}^2 L{1}^2-75 L3 C2 L{1}^2+5\times {10}^{-3} L{3}^2 L{1}^2-25 L{3}^2 L1 C2-2.19\times {10}^5 C{2}^2 L{3}^2}}{C2 L3 L1}}$

, and the approximate symbolic expressions for the zeros are presented in

Table 16. The approximate symbolic expressions of zeros.

Zero	Symbolic Expressions
z1, z3, z5	${\displaystyle \frac{1}{\sqrt{-L2 C2}}}$
z2, z4, z6	$-{\displaystyle \frac{1}{\sqrt{-L2 C2}}}$

.

Additional information about the settings used to obtain the p/z approximate symbolic expressions of this third-order band-stop Butterworth filter can be found in [13].

4. Discussion

Starting from a state or a “state-like” matrix with symbolic entries, the LR algorithm can, in principle, generate approximate p/z expressions containing at most one square root [6]. Writing this kind of matrix with symbols representing parameters for which the sensitivities of the targeted p/z are significant is not a difficult task, as the state matrix of the µA741 op-amp with 20 to 40 symbolic parameters has been obtained.

The main limitation of the LR algorithm is the increasing complexity of its matrix entries as the iterations progress, which can lead to exceeding available computational resources. Building on our previous work [6,7,8], we propose replacing certain circuit elements with open or short circuits and applying simplifications that focus solely on the error of the targeted eigenvalue, or complex pair of eigenvalues.

These techniques enabled the computation of approximate symbolic expressions for all eight poles and six zeros of the voltage gain of a three-transistor amplifier, as well as for all six poles and six zeros of a third-order band-stop Butterworth filter. Their p/z numerical values are in good agreement with those obtained using HSPICE software. In the case of the three-transistor amplifier, the approximate symbolic expressions of p/z were compared with those provided by the most advanced available algorithm [2], implemented in the Analog Insydes package, which could compute only six poles and three zeros. The errors relative to the exact numerical values were calculated for all symbolic expressions at the design point and at some corners defined by the maximum and minimum values of the symbolic parameters. The errors e_n, e_ac, e_mc, and e_Mc of our symbolic expressions are smaller than those from the Analog Insydes solutions. Additionally, our algorithm successfully computed the symbolic expressions for a pole and a zero with neighboring values, whereas the Analog Insydes algorithm was unable to do so. When both algorithms produced correct solutions, the Analog Insydes algorithm was at least twice as fast as ours. It was demonstrated how a set of formulas can be used when only one fails to cover a sufficiently large region in the parameter space; however, this technique is not generally valid. These results can be explained by considering the following factors:

-

The elimination of all terms containing a circuit parameter in $det\left(A-s·B\right)$ is more or less equivalent to the replacement of the corresponding circuit element by an open circuit or by a short circuit.

-

The controlled cutting of some row–column pairs and the convergent LR iterations performed on moderate-complexity matrices are efficient procedures, having no correspondence in the Analog Insydes algorithm, which simplifies the symbolic expression $det\left(A-s·B\right)$ “hoping that it will become” a first- or second-order polynomial in s [2].

-

The numerical value of the targeted p/z modified by a simplification attempt is computed by a fast iterative method in the Analog Insydes algorithm. At the same time, a more time-consuming standard procedure for eigenvalue computation is employed in the proposed algorithm for this purpose.

Even though we did not compare our results with those provided by the algorithm in [1], it is evident that

-

The transresistance computation in [1] is equivalent to our hybrid matrix computation [7].

-

The computation of two poles, followed by the short-circuit replacement of two capacitors, etc. [1], is a technique that can be used for some exceptional cases only, similar to the pole splitting, unlike the LR iterations and the associated techniques in our algorithm.

-

While in [1] a capacitor can be replaced by a short circuit only, our algorithm may replace any circuit element by a short circuit or an open circuit (which, in general, leads to less significant modifications of the p/z values—see the computation of p₆ in our example).

It follows that our algorithm is more powerful than those in [1,2] and is also more time-consuming compared to the Analog Insydes one.

A program for the automatic symbolic simplification of analog circuits containing MOSFETs, utilizing modified nodal analysis (MNA) and ant colony optimization (ACO), is described in [14]. The circuit is analyzed using symbolic MNA to obtain the exact symbolic expressions. Some simplified symbolic expressions are obtained by minimizing the numerical mean square error between the exact expression and the simplified one, corresponding to a specific set of frequencies. In this way, the final simplification error rate can be controlled by the user. In [15], a mathematical circuit root simplification using an ensemble heuristic–metaheuristic algorithm is presented. The algorithm is capable of computing the symbolic expressions for the three poles and two zeros of a three-stage amplifier. All these symbolic computations in [14,15] are performed in MATLAB R2020b.

A methodology for modeling and optimizing power supply rejection (PSR) in low-dropout regulator (LDO) system-on-chip (SoC) applications is presented in [16]. The Power Management Unit becomes crucial for meeting the multiple requirements of various blocks. The supply ripple, which has a significant impact on analog/RF blocks, needs to be reduced to obtain an optimal PSR performance. Two design cases are studied: a PSR of −50 dB at 100 kHz and a full-spectrum PSR of −50 dB.

The paper [17] presents both the consistent and causal derivations of the Level 1 MOSFET behavior from a few equations, along with explanations that facilitate an understanding of this behavior, while minimizing reliance on the extensive formulas commonly found in semiconductor technology books. The MOSFET behavior, considering usual formulas such as those describing the BSIM model, may lead to interpretation problems. A combination of BSIM with a modified SPICE Level 3 AC model can solve this issue.

For manual analysis, the calculations in [16,17] are too complex, so using a computer program is practical. Therefore, a conversion was implemented for the symbolic analysis tool Analog Insydes [5], which is based on Mathematica.

These papers, published in recent years [14,15,16,17], along with their applications of symbolic computation, present the diversity of tool options in the field of circuit symbolic computation. Our work does not contrast or complement these other methodologies, instead it can be seen as a different approach to the same problem. Ultimately, the choice of a symbolic tool always remains at the researcher’s discretion.

5. Conclusions

An algorithm implemented in MAPLE that computes both numeric and p/z approximate symbolic expressions is presented in this paper. The pole symbolic expressions are computed starting from the state matrix, and the zero symbolic expressions are computed starting from the “state-like” matrix. The attempts of open-circuit and short-circuit replacement of circuit elements are combined with those to cut row and column groups of the state matrix or the “state-like” matrix, and with LR iterations. The numerical results are compared with those obtained using HSPICE software, while the symbolic expressions are compared with those obtained with Analog Insydes software. Besides the advantage of calculating the expressions of all poles and zeros of a circuit, the proposed method has the disadvantage of being more time-consuming compared to the Analog Insydes one.

The symbolic expressions of poles and zeros are beneficial for designers of analog circuits. These p/z expressions can be applied in many situations, such as solving stability problems, identifying circuit parameters, computing symbolic formulas for the settling time of Op-Amps, calculating the symbolic phase margin for Op-Amps [18], or deriving the symbolic expressions for damping factor and damping resistance in passive filters [19].

Future research will address the calculation of symbolic p/z expressions for other types of circuits, of larger sizes and with more symbols, along with their applications in circuit design.