Deep Learning-Based Back-Projection Parameter Estimation for Quantitative Defect Assessment in Single-Framed Endoscopic Imaging of Water Pipelines
Abstract
1. Introduction
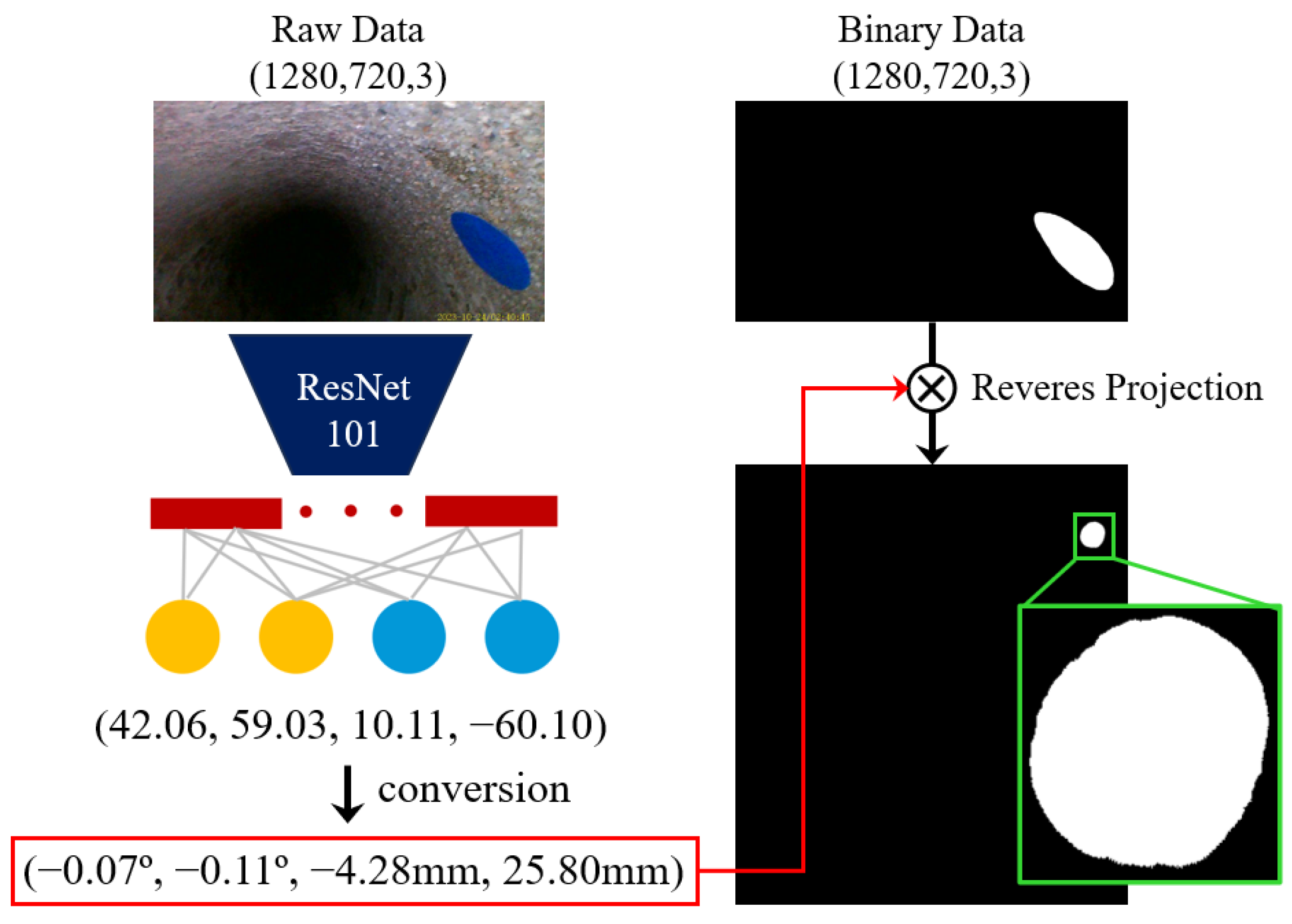
2. AI-Based Back-Projection Parameter Estimation for Quantitative Assessment of Internal Defects in Water Pipelines
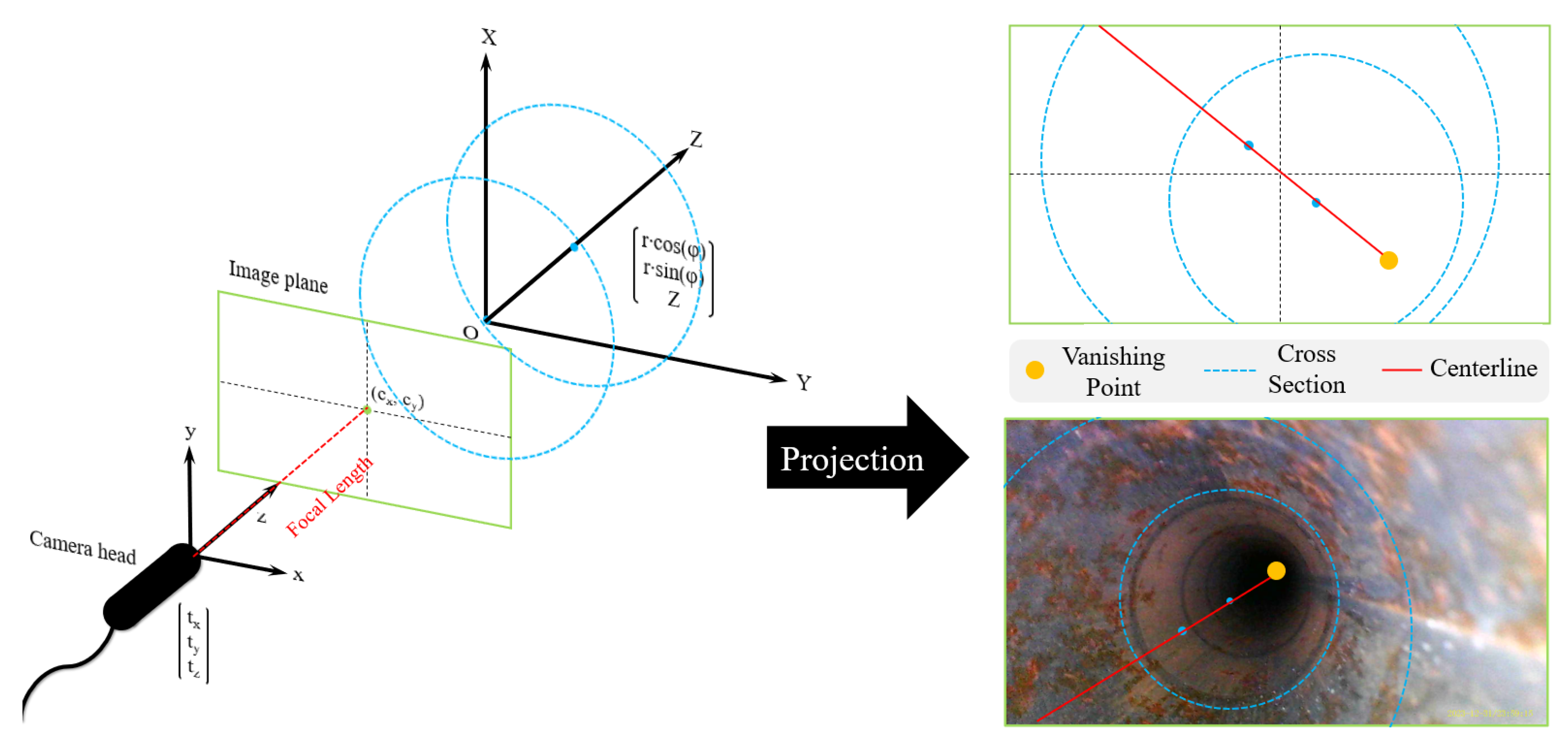
2.1. Analysis of the Relationship Between Back-Projection Parameters and Image Features
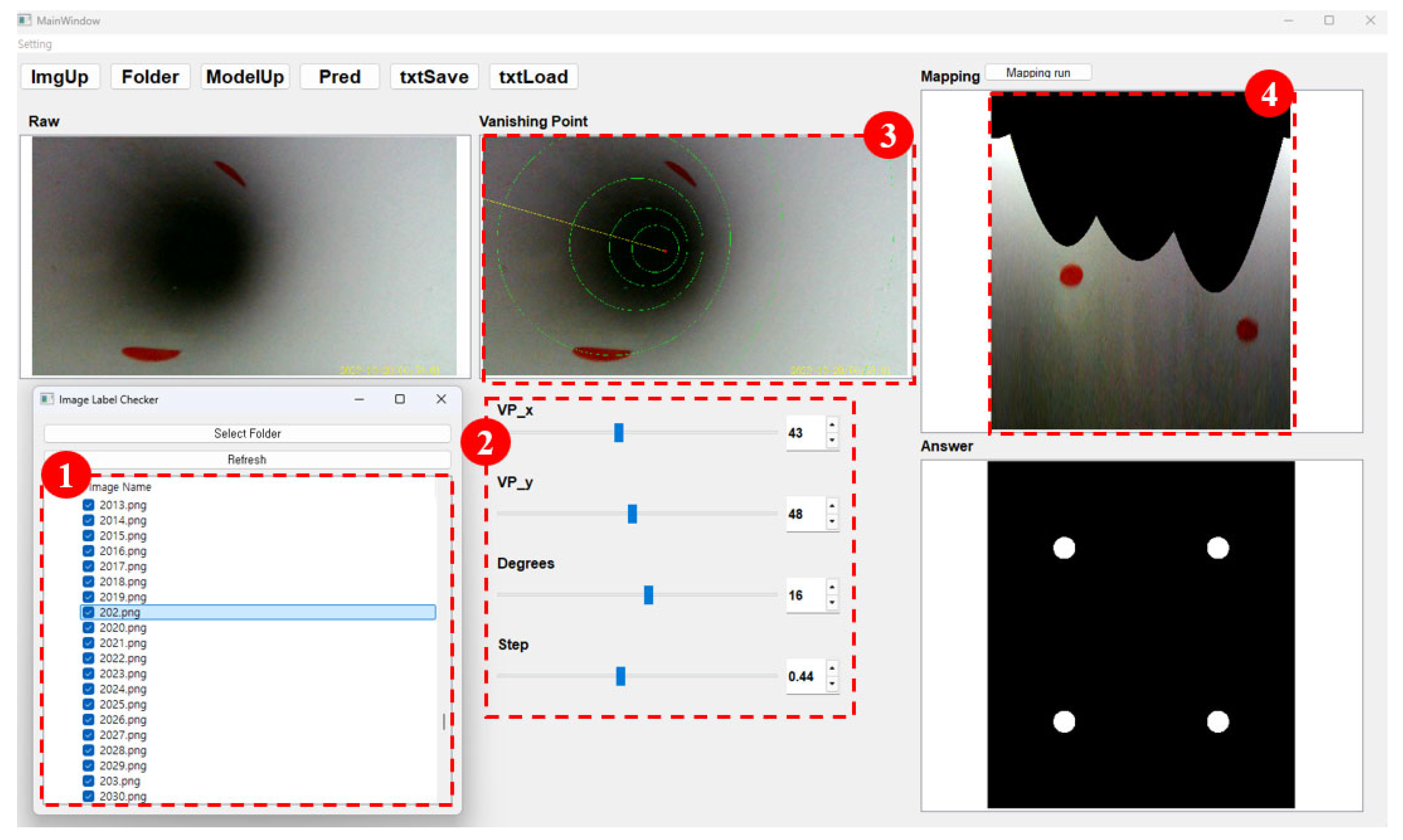
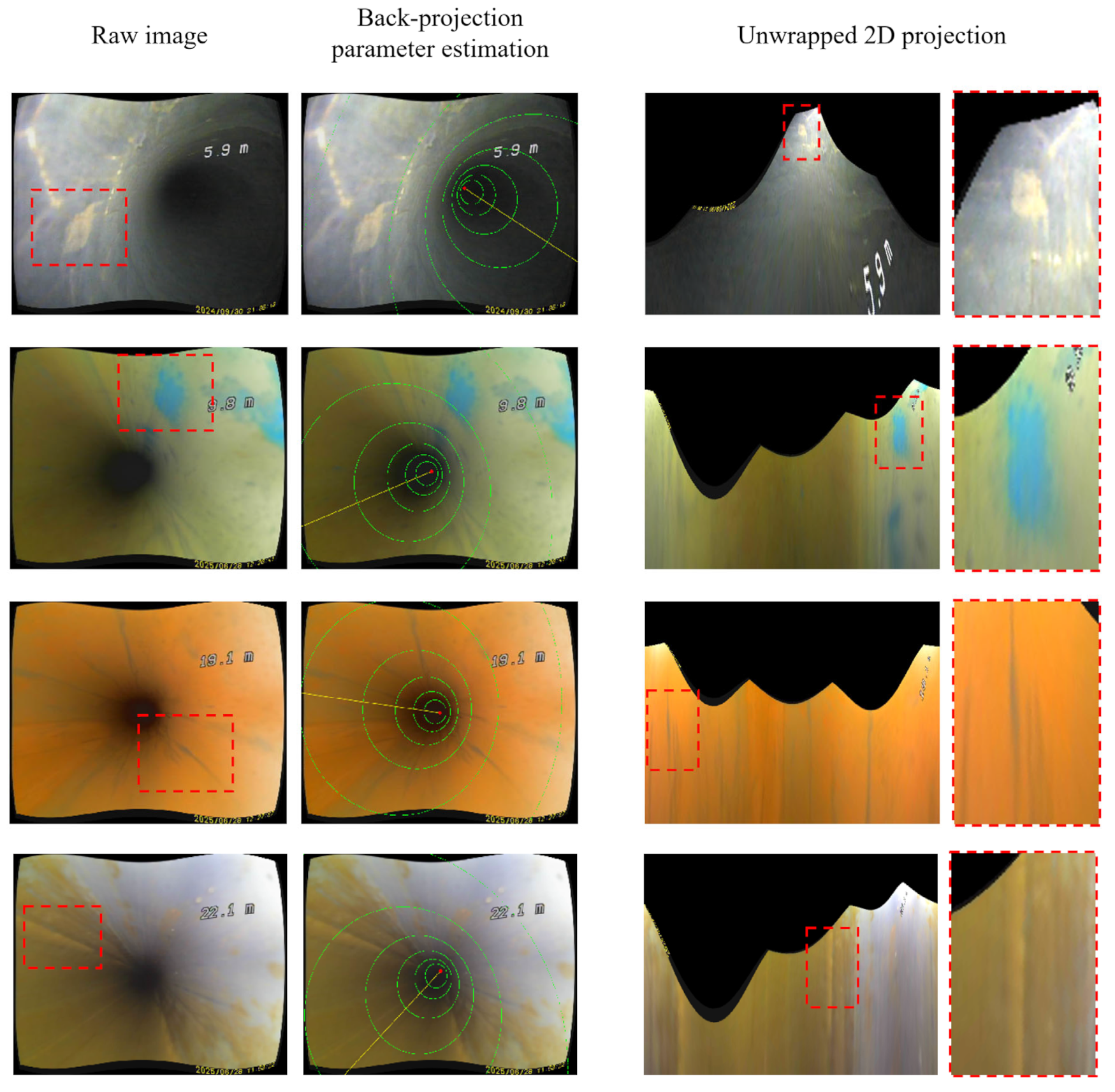
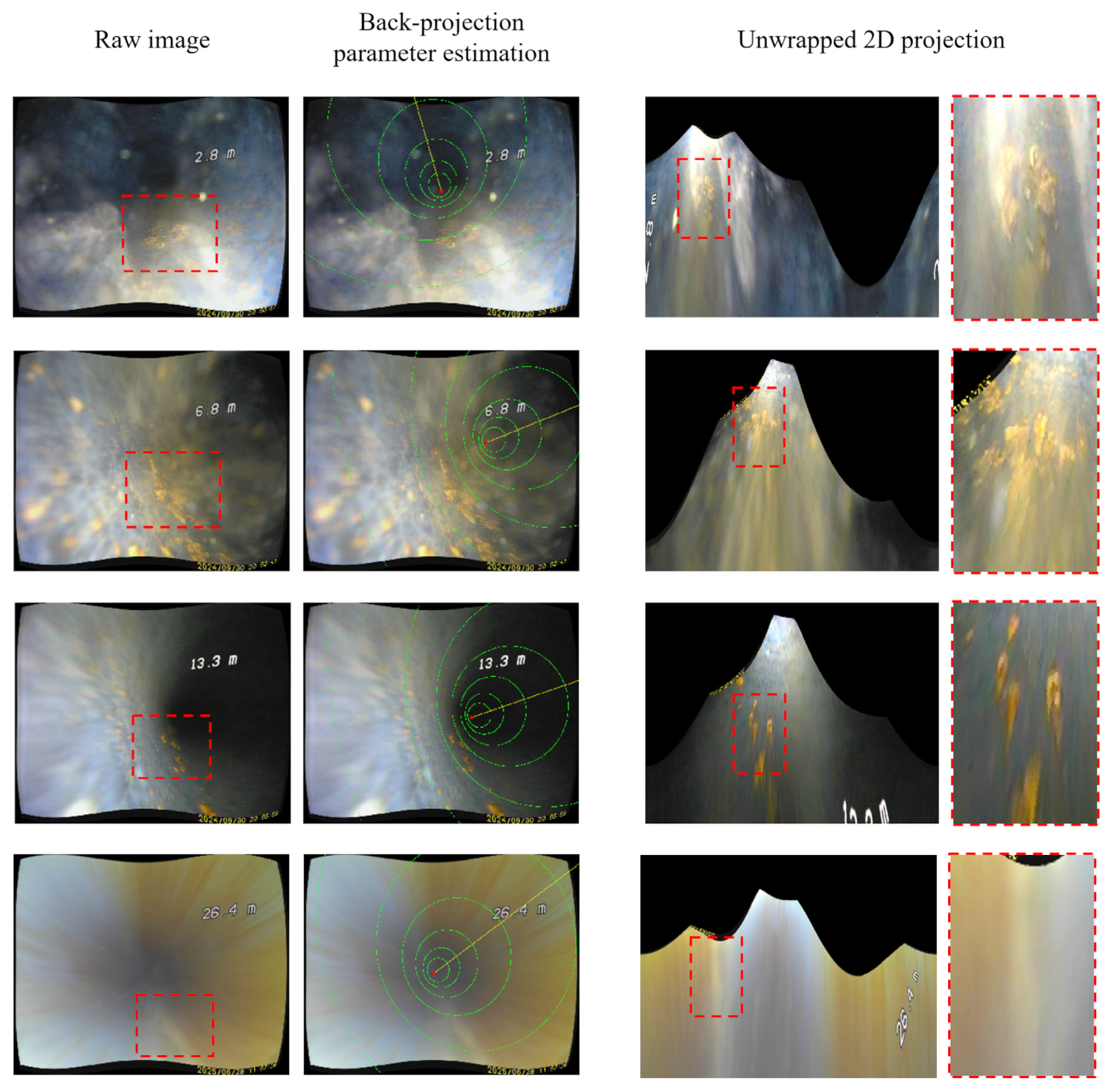
2.2. Endoscopic Inspection Data
- ➀
- A window displaying the current state of the inspection dataset.
- ➁
- Scrollbars and text boxes for inputting numerical values of the parameters.
- ➂
- A rendered image frame highlighting annotated features such as vanishing points.
- ➃
- Unwrapped 2D projection of cylindrical pipe, aiding in the visual consistency of the annotation.
2.3. AI-Based Back-Projection Parameter Estimation Model
3. Experiments and Results
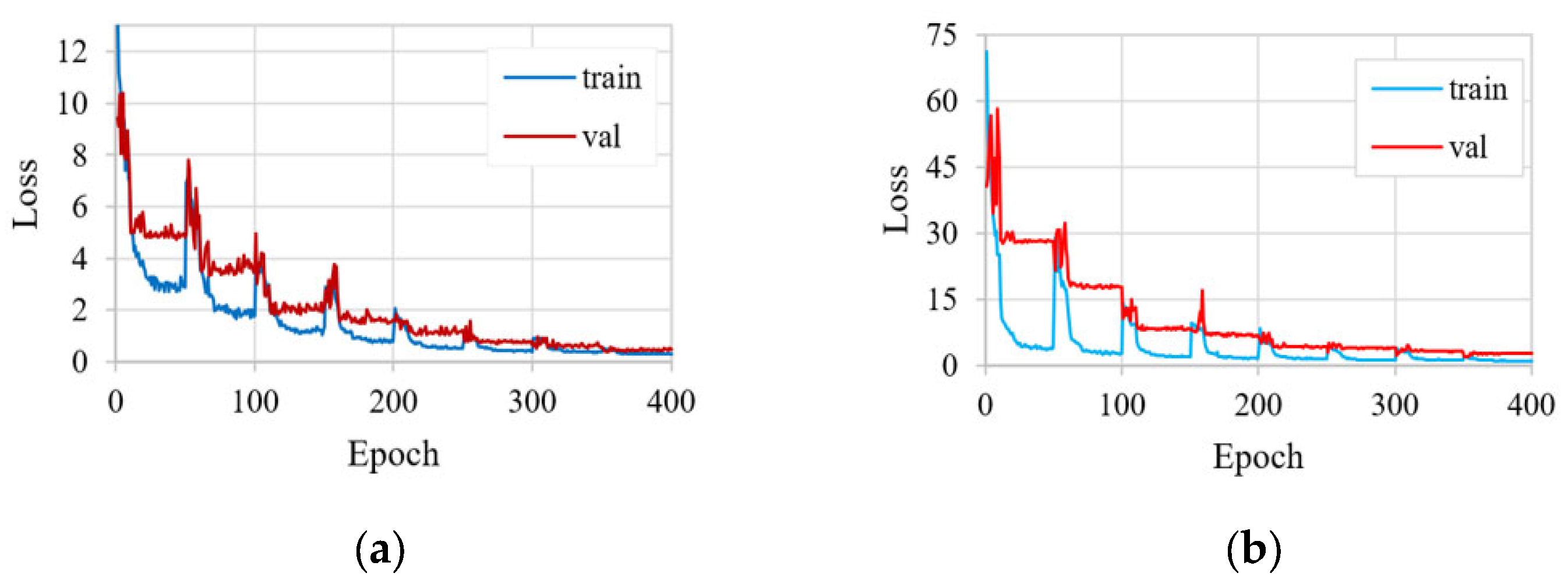
3.1. Training Results for the Back-Projection Parameter Estimation Model
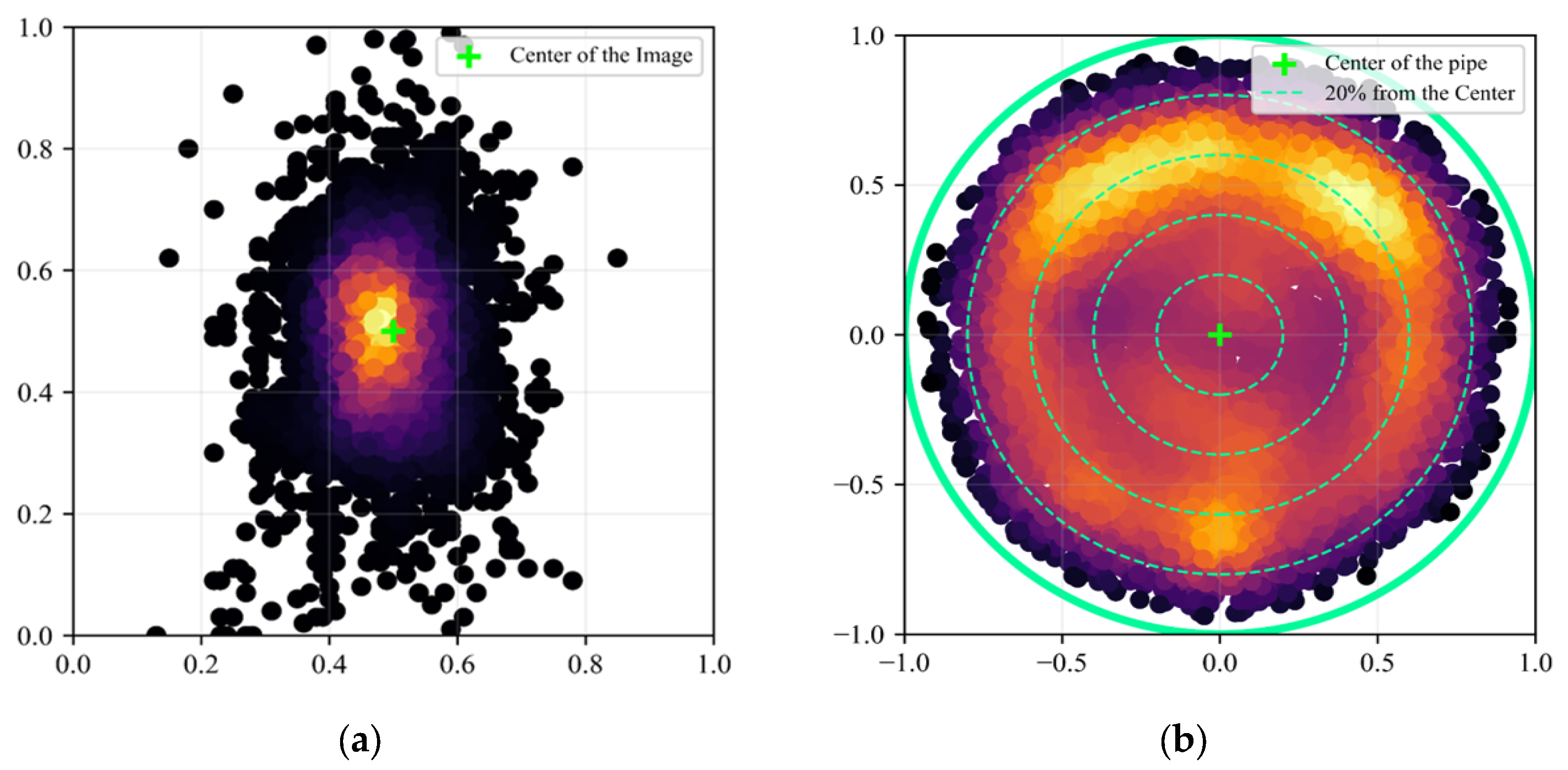
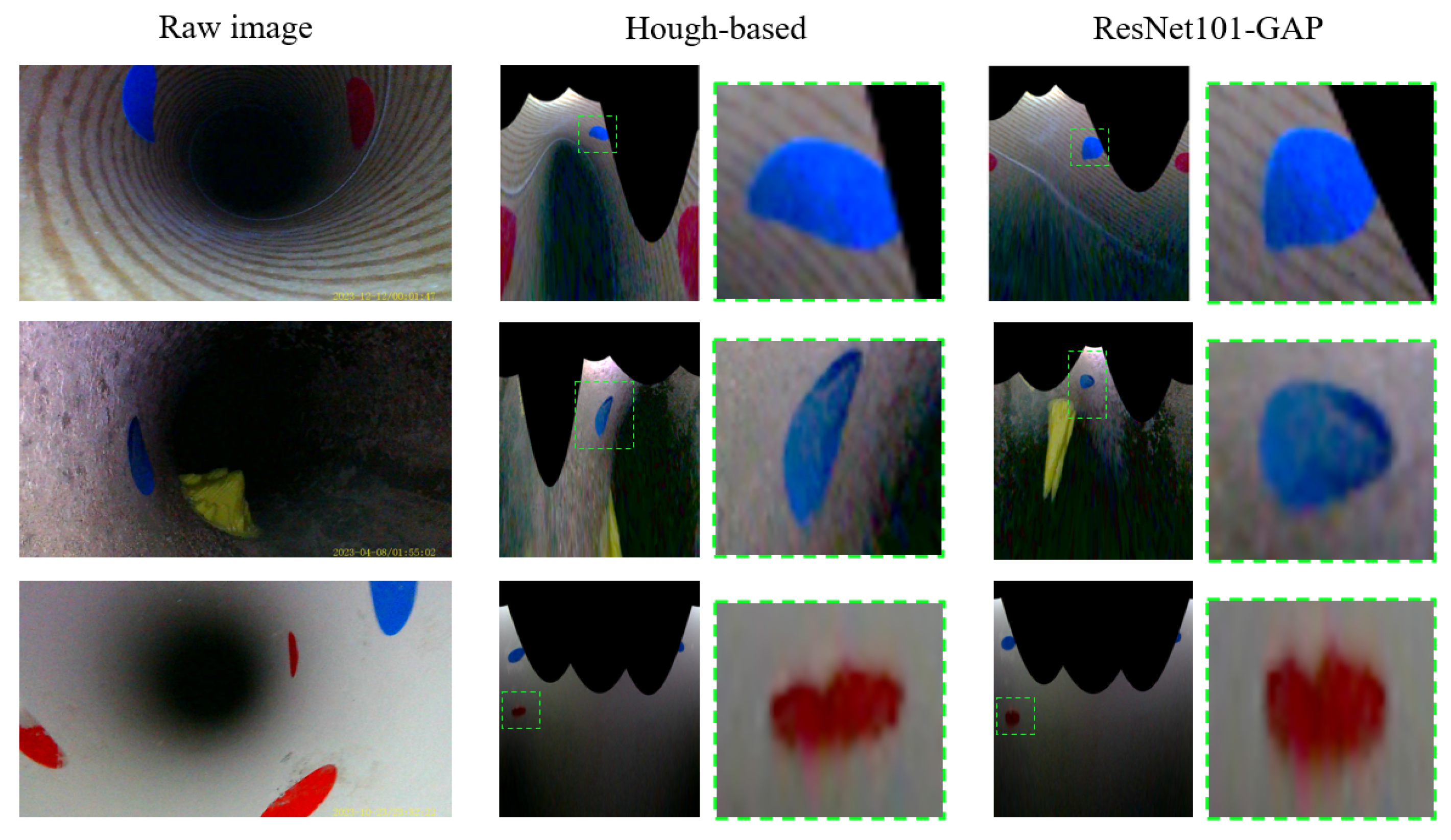
3.2. Accuracy Verification of Back-Projection Parameter Estimation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministry of Environment Korea. Water Supply Statistics; Ministry of Environment Korea: Sejong, Republic of Korea, 2023. [Google Scholar]
- Jun, H.J.; Park, J.K.; Bae, C.H. Factors affecting steel water-transmission pipe failure and pipe-failure mechanisms. J. Environ. Eng. 2020, 146, 04020034. [Google Scholar] [CrossRef]
- Taiwo, R.; Shaban, I.A.; Zayed, T. Development of sustainable water infrastructure: A proper understanding of water pipe failure. J. Clean. Prod. 2023, 398, 136653. [Google Scholar] [CrossRef]
- Mukunoki, T.; Kumano, N.; Otani, J.; Kuwano, R. Visualization of three dimensional failure in sand due to water inflow and soil drainage from defective underground pipe using X-ray CT. Soils Found. 2009, 49, 959–968. [Google Scholar] [CrossRef]
- Cui, J.; Liu, F.; Chen, R.; Wang, S.; Pu, C.; Zhao, X. Effects of internal pressure on urban water supply pipeline leakage-induced soil subsidence mechanisms. Geofluids 2024, 2024, 9577375. [Google Scholar] [CrossRef]
- Jacobsz, S.W. Responsive Pipe Networks; Water Research Commission Report; Water Research Commission: Pretoria, South Africa, 2019. [Google Scholar]
- Zhao, R.; Li, L.; Chen, X.; Zhang, S. Mechanical response of pipeline leakage to existing tunnel structures: Insights from numerical modeling. Buildings 2025, 15, 1771. [Google Scholar] [CrossRef]
- Rajani, B.; Kleiner, Y. Non-destructive inspection techniques to determine structural distress indicators in water mains. Eval. Control. Water Loss Urban Water Netw. 2004, 47, 21–25. [Google Scholar]
- Mazumder, R.K.; Salman, A.M.; Li, Y.; Yu, X. Performance evaluation of water distribution systems and asset management. J. Infrastruct. Syst. 2018, 24, 03118001. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A review of recent distributed optical fiber sensors applications for civil engineering structural health monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Abegaz, R.; Wang, F.; Xu, J.; Pierce, T. Developing soil internal erosion indicator to quantify erosion around defective buried pipes under water exfiltration. Geotech. Test. J. 2025, 48, 623–641. [Google Scholar]
- Jahnke, S.I. Pipeline Leak Detection Using in-situ Soil temperature and Strain Measurements. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2018. [Google Scholar]
- Dave, M.; Juneja, A. Erosion of soil around damaged buried water pipes a critical review. Arab. J. Geosci. 2023, 16, 317. [Google Scholar] [CrossRef]
- Kumar, S.S.; Abraham, D.M.; Jahanshahi, M.R.; Iseley, T.; Starr, J. Automated defect classification in sewer closed circuit television inspections using deep convolutional neural networks. Automat. Construct. 2018, 91, 273–283. [Google Scholar] [CrossRef]
- Meijer, D.; Scholten, L.; Clemens, F.; Knobbe, A. A defect classification methodology for sewer image sets with convolutional neural networks. Automat. Construct. 2019, 104, 281–298. [Google Scholar] [CrossRef]
- Dang, L.M.; Kyeong, S.; Li, Y.; Wang, H.; Nguyen, T.N.; Moon, H. Deep learning-based sewer defect classification for highly imbalanced dataset. Comput. Ind. Eng. 2021, 161, 107630. [Google Scholar] [CrossRef]
- Moradi, S.; Zayed, T. Defect Detection and Classification in Sewer Pipeline Inspection Videos Using Deep Neural Networks. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2020. [Google Scholar]
- Shen, D.; Liu, X.; Shang, Y.; Tang, X. Deep learning-based automatic defect detection method for sewer pipelines. Sustainability 2023, 15, 9164. [Google Scholar] [CrossRef]
- Sun, L.; Zhu, J.; Tan, J.; Li, X.; Li, R.; Deng, H.; Zhang, X.; Liu, B.; Zhu, X. Deep learning-assisted automated sewage pipe defect detection for urban water environment management. Sci. Total Environ. 2023, 882, 163562. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, X.; Zhang, X.; Xi, Z.; Wang, S. Automatic detection method of sewer pipe defects using deep learning techniques. Appl. Sci. 2023, 13, 4589. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Dang, L.M.; Piran, M.J.; Moon, H. A robust instance segmentation framework for underground sewer defect detection. Measurement 2022, 190, 110727. [Google Scholar] [CrossRef]
- Jung, J.T.; Reiterer, A. Improving sewer damage inspection: Development of a deep learning integration concept for a multi-sensor system. Sensors 2024, 24, 7786. [Google Scholar] [CrossRef]
- Mostafa, K.; Hegazy, T. Review of image-based analysis and applications in construction. Automat. Construct. 2021, 122, 103516. [Google Scholar] [CrossRef]
- Liu, J.C.; Tan, Y.; Wang, Z.Y.; Long, Y.Y. Experimental and numerical investigation on internal erosion induced by infiltration of defective buried pipe. Bull. Eng. Geol. Environ. 2025, 84, 38. [Google Scholar] [CrossRef]
- Pridmore, T.P.; Cooper, D.; Taylor, N. Estimating camera orientation from vanishing point location during sewer surveys. Automat. Construct. 1997, 6, 393–401. [Google Scholar]
- Kolesnik, M.; Baratoff, G. 3D interpretation of sewer circular structures. In Proceedings of the 2000 ICRA, IEEE International Conference on Robotics and Automation, Paris, France, 31 May–4 June 2020; IEEE: New York, NY, USA, 2020; Volume 4, pp. 3770–3775. [Google Scholar]
- Kwon, G.O.; Kwon, H.G.; Choi, Y.H. Development of computer vision-based water pipe internal defect quantification technique. J. Korea Water Resour. Assoc. 2024, 57, 835–845. [Google Scholar]
- Hengmeechai, J. Automated Analysis of Sewer Inspection Closed Circuit Television Videos Using Image Processing Techniques. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2013. [Google Scholar]
- Brammer, K. Feasibility of Active Vision for Inspection of Continuous Concrete Pipes. Ph.D. Thesis, Sheffield Hallam University, Sheffield, UK, 2003. [Google Scholar]
- Dawson-Howe, K.M.; Vernon, D. Simple pinhole camera calibration. Int. J. Imaging Syst. Technol. 1994, 5, 1–6. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; IEEE: New York, NY, USA, 2016; pp. 770–778. [Google Scholar]
- Fan, R.; Wang, Y.; Qiao, L.; Yao, R.; Han, P.; Zhang, W.; Pitas, I.; Liu, M. PT-ResNet: Perspective transformation-based residual network for semantic road image segmentation. In Proceedings of the 2019 IEEE International Conference on Imaging Systems and Techniques (IST), Abu Dhabi, United Arab Emirates, 8–10 December 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Hoang, T.M.; Nam, S.H.; Park, K.R. Enhanced detection and recognition of road markings based on adaptive region of interest and deep learning. IEEE Access 2019, 7, 109817–109832. [Google Scholar] [CrossRef]
- Choi, H.S.; An, K.; Kang, M. Regression with residual neural network for vanishing point detection. Image Vision Comput. 2019, 91, 103797. [Google Scholar] [CrossRef]
- Li, X.; Zhu, L.; Yu, Z.; Guo, B.; Wan, Y. Vanishing point detection and rail segmentation based on deep multi-task learning. IEEE Access 2020, 8, 163015–163025. [Google Scholar] [CrossRef]
- Cheng, J.C.; Wang, M. Automated detection of sewer pipe defects in closed-circuit television images using deep learning techniques. Automat. Construct. 2018, 95, 155–171. [Google Scholar]
- Halfawy, M.R.; Hengmeechai, J. Integrated vision-based system for automated defect detection in sewer closed circuit television inspection videos. J. Comput. Civil Eng. 2015, 29, 04014065. [Google Scholar] [CrossRef]
- Kagami, S.; Taira, H.; Miyashita, N.; Torii, A.; Okutomi, M. 3D pipe network reconstruction based on structure from motion with incremental conic shape detection and cylindrical constraint. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 1345–1352. [Google Scholar]
- Zheng, Z.; Zhang, H.; Li, X.; Liu, S.; Teng, Y. ResNet-based model for cancer detection. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 15–17 January 2021; IEEE: New York, NY, USA, 2021; pp. 325–328. [Google Scholar]
- Praveen, S.P.; Srinivasu, P.N.; Shafi, J.; Wozniak, M.; Ijaz, M.F. ResNet-32 and FastAI for diagnoses of ductal carcinoma from 2D tissue slides. Sci. Rep. 2022, 12, 20804. [Google Scholar]
- Mehnatkesh, H.; Jalali, S.M.J.; Khosravi, A.; Nahavandi, S. An intelligent driven deep residual learning framework for brain tumor classification using MRI images. Exp. Syst. Appl. 2023, 213, 119087. [Google Scholar] [CrossRef]
- Gopi, A.; Sudha, L.R.; Thanakumar, J.S.I. Resnet for blood sample detection: A study on improving diagnostic accuracy. AG Salud 2025, 3, 193. [Google Scholar] [CrossRef]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]




| Type | Steel Pipe (SP) | Polyvinyl Chloride Pipe (PVC) | 3D Printing Pipe | Paper Pipe (PP) | Cost Iron Pipe (CIP) | Polyethylene Pipe (PE) |
|---|---|---|---|---|---|---|
| Diameter (mm) | 23 | 84, 116 | 84 | 34 | 86, 150 | 52 |
| Layer Name | ResNet-18 | ResNet-34 | ResNet-50 | ResNet-101 | ResNet-152 |
|---|---|---|---|---|---|
| Parameters | 11.4 M | 21.5 M | 23.9 M | 42.8 M | 58.5 M |
| FLOPs | 1.8 × 109 | 3.6 × 109 | 3.8 × 109 | 7.6 × 109 | 11.3 × 109 |
| Hardware | Specification | Software | Specification |
|---|---|---|---|
| CPU | Inter Core i7-13700 | Python | 3.11.7 |
| GPU | NVIDIA GeForce RTX 3060 12 GB | Pytorch | 2.1.2 |
| Memory capacity | 32 GB | Operation System | Windows 10 |
| Optimizer | Learning Rate | Epoch | Decrease rate |
| Adam | 1 × 10−3 | 400 | 0.8/50 Epoch |
| Type | Diameter | Number of Data | Hough-Based | ResNet101-GAP | |||||
|---|---|---|---|---|---|---|---|---|---|
| MAPE | Top5 | Bottom5 | Miss Rate | MAPE | Top5 | Bottom5 | |||
| CIP | 86 mm | 100 | 181 | 3.2 | 1056.8 | 53/100 | 10.7 | 0.7 | 26.4 |
| SP | 34 mm | 30 | 132.9 | 2.6 | 558.4 | 0/30 | 6.2 | 0.9 | 14.6 |
| PVC | 84 mm | 91 | 26.6 | 6.1 | 50.4 | 12/91 | 7.0 | 0.1 | 28.5 |
| PP | 32 mm | 87 | 97.8 | 1.0 | 854.2 | 8/87 | 6.7 | 0.4 | 23.9 |
| Summary | 308 | 109.6 | 3.2 | 630.0 | 7.7 | 0.5 | 23.4 | ||
| Inference speed | 2000 ms | 8 ms | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, G.; Choi, Y.H. Deep Learning-Based Back-Projection Parameter Estimation for Quantitative Defect Assessment in Single-Framed Endoscopic Imaging of Water Pipelines. Mathematics 2025, 13, 3291. https://doi.org/10.3390/math13203291
Kwon G, Choi YH. Deep Learning-Based Back-Projection Parameter Estimation for Quantitative Defect Assessment in Single-Framed Endoscopic Imaging of Water Pipelines. Mathematics. 2025; 13(20):3291. https://doi.org/10.3390/math13203291
Chicago/Turabian StyleKwon, Gaon, and Young Hwan Choi. 2025. "Deep Learning-Based Back-Projection Parameter Estimation for Quantitative Defect Assessment in Single-Framed Endoscopic Imaging of Water Pipelines" Mathematics 13, no. 20: 3291. https://doi.org/10.3390/math13203291
APA StyleKwon, G., & Choi, Y. H. (2025). Deep Learning-Based Back-Projection Parameter Estimation for Quantitative Defect Assessment in Single-Framed Endoscopic Imaging of Water Pipelines. Mathematics, 13(20), 3291. https://doi.org/10.3390/math13203291






