Review of Physics-Informed Neural Networks: Challenges in Loss Function Design and Geometric Integration
Abstract
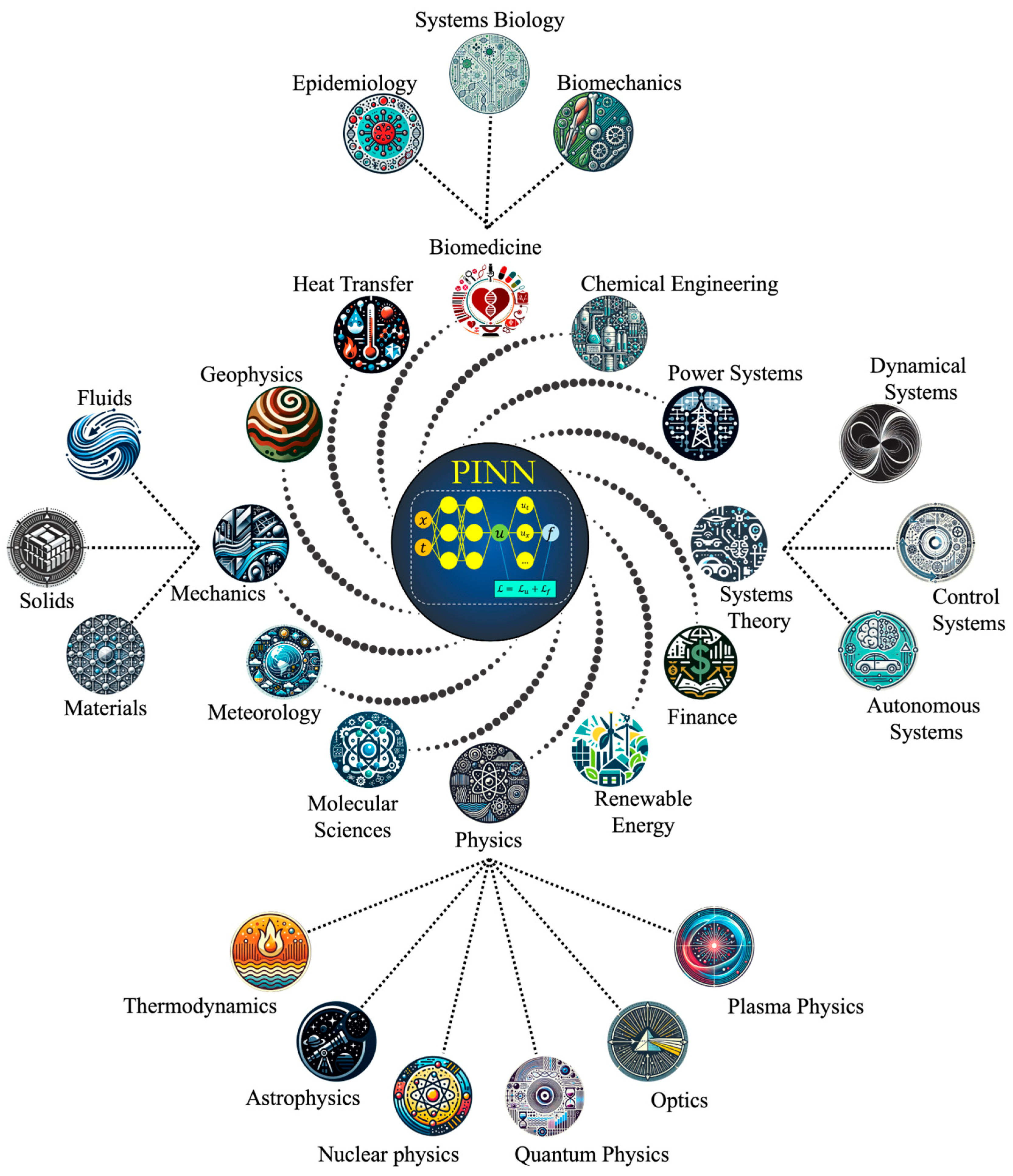
1. Introduction
- balancing error components (loss functions)—the total error to be minimized in most studies is the sum of heterogeneous terms with different scales and physical units, which can lead to significant errors;
- accounting for geometry and complex domain topologies—classical PINNs are built on Euclidean coordinates and do not account for complex or parameterized geometries, limiting their application;
- incorporating boundary conditions—in traditional approaches, boundary conditions are imposed through mean-squared penalties, which are “soft” conditions and lead to poor satisfaction at boundaries. Methods for hard enforcement of boundary conditions are not always universal and require complex analytical forms.
2. Research Methodology
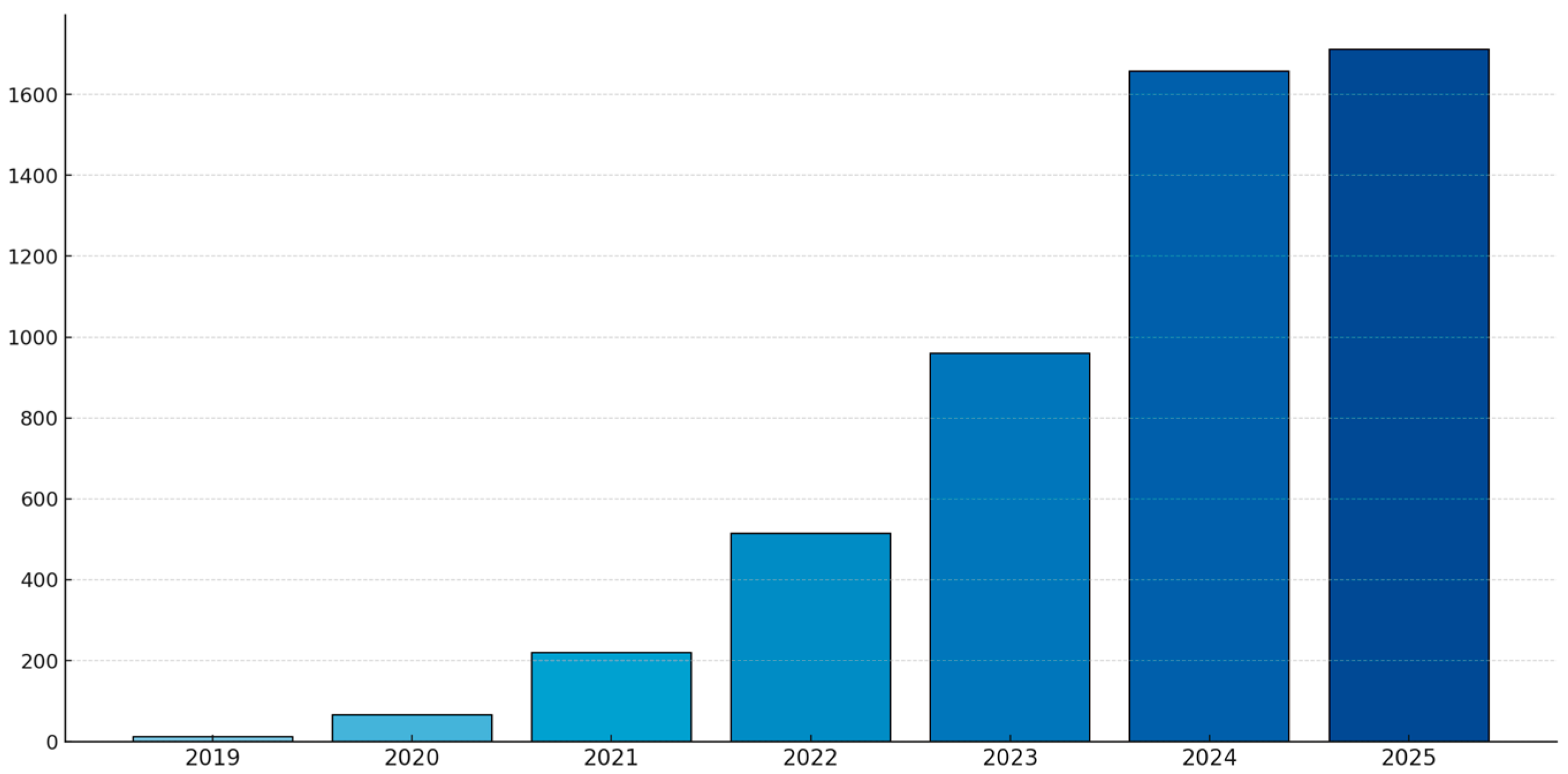
2.1. Sources and Coverage
2.2. Time Window
2.3. Query Design and Exact Search Strings
- PINN family (core):TITLE-ABS-KEY(“physics-informed neural network*” OR “physics informed neural network*” OR “PINN*” W/0 (PDE OR “boundary condition*” OR physics OR “governing equation*”))
- Variational/energy:TITLE-ABS-KEY(“variational physics-informed neural network*” OR “VPINN*” OR “energy-based PINN*” OR “energy PINN*”)
- Operator learning in physics-informed settings:TITLE-ABS-KEY(“physics-informed operator*” OR PINO OR “DeepONet” OR “Fourier Neural Operator” OR “FNO”)
- KAN/PIKAN:TITLE-ABS-KEY(“Kolmogorov–Arnold network*” OR “Kolmogorov Arnold network*” OR KAN OR PIKAN OR “physics-informed KAN” OR “physics informed KAN”)
- Geometry and BC encoding:TITLE-ABS-KEY((“signed distance function*” OR SDF OR “phi-function*” OR “phi function*” OR “R-function*” OR “R function*” OR “transfinite barycentric coordinate*” OR TFC) AND (PINN OR “physics-informed”))
- PINN family (core):TS = (“physics-informed neural network*” OR “physics informed neural network*” OR PINN) AND TS = (PDE OR “boundary condition*” OR physics OR “governing equation*”)
- Variational/energy:TS = (“variational physics-informed neural network*” OR VPINN* OR “energy-based PINN*” OR “energy PINN*”)
- Operator learning:TS = (“physics-informed operator*” OR PINO OR DeepONet OR “Fourier Neural Operator” OR FNO)
- KAN/PIKAN:TS = (“Kolmogorov–Arnold network*” OR “Kolmogorov Arnold network*” OR KAN OR PIKAN) AND TS = (“physics-informed” OR “physics informed”)
- Geometry and BC encoding:TS = ((“signed distance function*” OR SDF OR “phi-function*” OR “R-function*” OR “transfinite barycentric coordinate*” OR TFC) AND (PINN OR “physics-informed”))
- Consolidated query across titles and abstracts:all:(“physics-informed neural network” OR “variational physics-informed neural network” OR “energy-based PINN” OR “physics-informed operator” OR PINO OR DeepONet OR “Fourier Neural Operator” OR FNO OR “Kolmogorov–Arnold network” OR KAN OR PIKAN) AND submittedDate: [1 January 2019 TO 30 September 2025]
- For geometry-specific streams:all:((PINN OR “physics-informed”) AND (“signed distance function” OR SDF OR “phi-function” OR “R-function” OR “transfinite barycentric coordinate” OR TFC)) AND submittedDate: [1 January 2019 TO 30 September 2025]
2.4. Inclusion Criteria
- Presented methodological contributions to physics-informed learning (e.g., adaptive loss weighting; variational/energy formulations; geometry/BC encoding; sampling and domain decomposition; hard-constraint constructions; hybrid FEM–PINN/operator pipelines).
- Provided technical detail sufficient for reuse (derivations, algorithmic steps, loss definitions, or implementation sketches).
- Related directly to PDE-based modeling or boundary-value problems in engineering or applied physics.
- Were journal or major-venue conference papers; preprints were included when they introduced novel methods subsequently adopted or discussed by the community.
- Addressed operator learning or KAN/PIKAN in a physics-informed capacity (e.g., PINO with PDE constraints; KAN variants embedding physics in the objective or architecture).
2.5. Exclusion Criteria
- Reported pure application case studies with routine PINN usage and no methodological novelty.
- Focused primarily on non-PDE ML or image-only tasks without physical constraints.
- Were editorials, short abstracts, theses, or lacked sufficient methodological detail.
- Were duplicates across sources or minor versions of the same preprint without substantive changes.
- Used the acronym PINN in unrelated contexts (e.g., “pinning” phenomena) despite keyword matches.
2.6. Screening and De-Duplication Workflow
2.7. Data Extraction and Synthesis
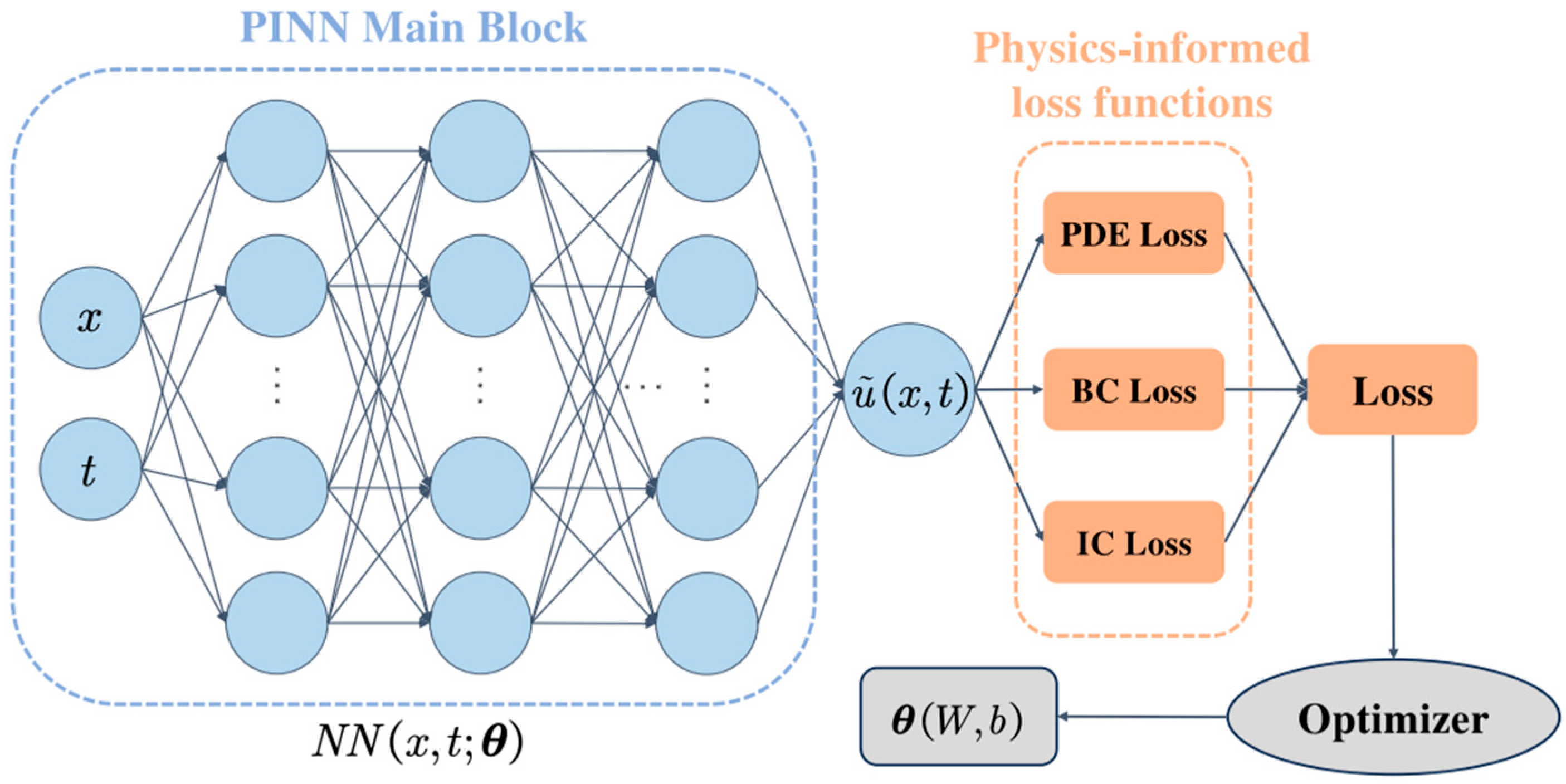
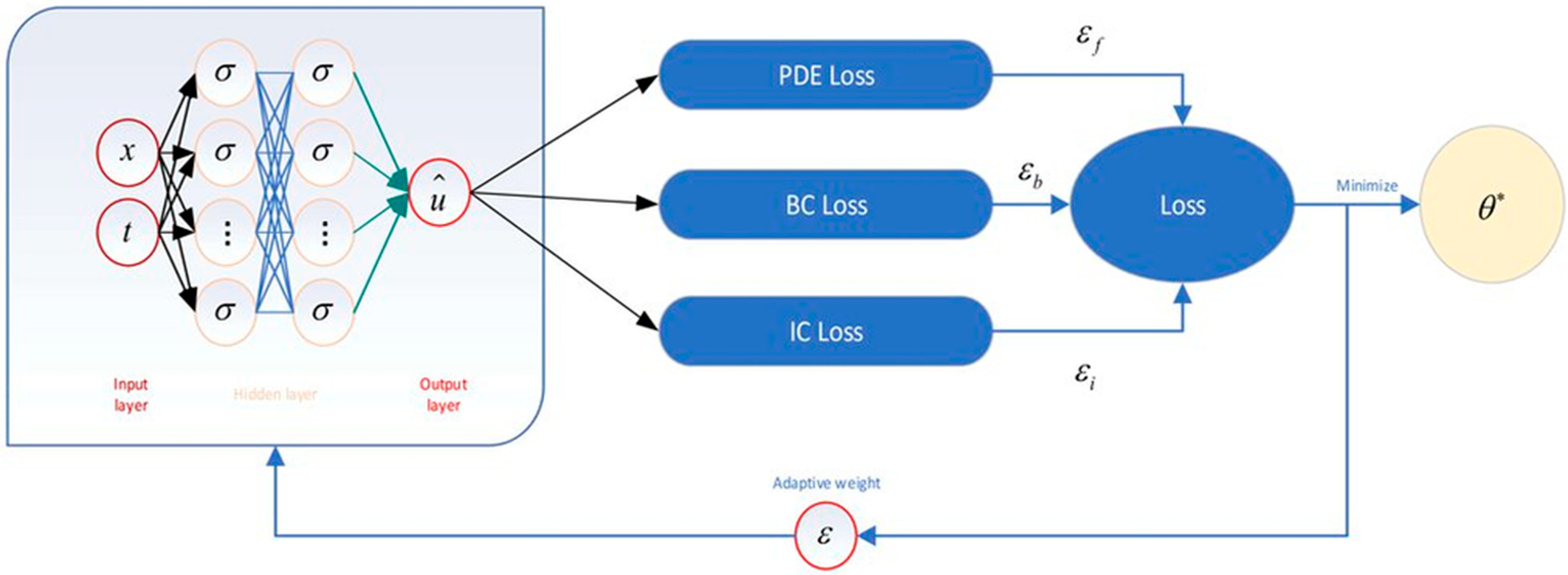
3. Loss Functions for PINNs: Concept and Evolution
3.1. Methods for Balancing Loss Function Components
3.2. Application of Variational and Energy Formulations in PINNs
4. Incorporating Geometry and Boundary Conditions in PINNs
- definition of domain geometry and boundary: the computational domain is described, and the boundary is divided into parts for different types of boundaries conditions;
- generation and filtering of collocation points inside the domain and on its boundary, removal from the selection of points that are outside the selection or outside , division of boundary points by types of boundaries conditions;
- integration of geometry into the loss function, if necessary—construction of functions for strict enforcement of defined types of boundary conditions.
4.1. Methods for Incorporating Geometric Information in PINN
- -continuous (first derivative exists) but not smooth in sign-change zones;
- for is smooth almost everywhere, approximates the distance function without singularities; parameter controls the “thickness” of medial zones;
- m-times differentiable everywhere with vanishing derivatives in singularities.
4.2. Sampling of Collocation Point for Physics-Informed Neural Networks
4.3. Enforcement of Boundary Conditions in PINNs
- 1.
- Construction of normalized equations using one of the complete systems of R-functions (17), (19)–(21) and expressions (23)–(25) to describe the boundary of the computational domain and boundary segments with different boundary conditions. The order to which and are normalized is determined by the order of the governing differential equation.
- 2.
- Extension of boundary conditions defined only on the domain boundary to the entire computational domain. In addition to the operator (25), which extends n-fold differentiation along the normal to into the domain [92], the following operators are used:defined everywhere in , and on , it represents the m-th order tangential derivative, anddefined everywhere in , and on , it represents the order derivative along the boundary curve.
- 3.
- Extension of nonhomogeneous boundary conditions to the computational domain. For nonhomogeneous boundary conditions of the form , the function satisfying these conditions can be written aswhere is defined as in (24). This function is defined throughout the computational domain. Similarly, functions extending boundary conditions (e.g., ,) involving derivatives or mixed derivatives of higher orders are constructed.
- 4.
- Construction of the solution structure. For a governing PDE of order m, the solution structure, which identically satisfies the boundary conditions and includes arbitrary components, is constructed aswhere is normalized to order m, and are arbitrary functions.
- 5.
- Construction of solution structures for boundary conditions defined by systems of equations. When a system of conditions of the form is specified on and expressed as differential equations of different orders , the solution structure can be constructed as follows. First, a bundle of functions is constructed to satisfy the boundary condition of the highest order . Substituting this into the condition , terms containing the product vanish. Then, it is sufficient to choose to satisfy the corresponding condition, i.e.,
- 6.
- For cases with multiple boundaries and systems of equations of the form on each , bundles of functions , are constructed to satisfy all conditions on with the highest degree . The solution structure satisfying the conditions on takes the following form:
5. Future Directions and Opportunities
5.1. Development of Physics-Informed Kolmogorov–Arnold Neural Networks
5.2. Operator Learning and Meta-Learning
5.3. Automation of Geometry and Boundary Condition Information Generation in CAE Packages
5.4. Development of Hybrid Methods for Engineering Modeling
5.5. Standardization and Infrastructure Development
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PINN | Physics-Informed Neural Network |
| PDE | Partial differential equation |
| FEM | Finite element method |
| AI | Artificial intelligence |
| PDD | Progressive domain decomposition |
| SDF | Signed distance function |
| TFC | Transfinite barycentric coordinates |
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep learning with TensorFlow: A review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Novac, O.C.; Chirodea, M.C.; Novac, C.M.; Bizon, N.; Oproescu, M.; Stan, O.P.; Gordan, C.E. Analysis of the application efficiency of TensorFlow and PyTorch in convolutional neural network. Sensors 2022, 22, 8872. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. A review of physics-informed machine learning in fluid mechanics. Energies 2023, 16, 2343. [Google Scholar] [CrossRef]
- Hu, H.; Qi, L.; Chao, X. Physics-informed Neural Networks (PINN) for computational solid mechanics: Numerical frameworks and applications. Thin-Walled Struct. 2024, 205, 112495. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Pawar, N.M.; Fernandes, C.; Raissi, M.; Das, S.; Kalantari, N.K.; Kourosh Mahjour, S. Physics-guided, physics-informed, and physics-encoded neural networks and operators in scientific computing: Fluid and solid mechanics. J. Comput. Inf. Sci. Eng. 2024, 24, 040802. [Google Scholar] [CrossRef]
- Herrmann, L.; Kollmannsberger, S. Deep learning in computational mechanics: A review. Comput. Mech. 2024, 74, 281–331. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Du, Z.; Lu, R. Physics-informed neural networks for advanced thermal management in electronics and battery systems: A review of recent developments and future prospects. Batteries 2025, 11, 204. [Google Scholar] [CrossRef]
- Abdelraouf, O.A.; Ahmed, A.; Eldele, E.; Omar, A.A. Physics-Informed Neural Networks in electromagnetic and nanophotonic design. arXiv 2025, arXiv:2505.03354. [Google Scholar] [CrossRef]
- Tkachenko, D.; Tsegelnyk, Y.; Myntiuk, S.; Myntiuk, V. Spectral methods application in problems of the thin-walled structures deformation. J. Appl. Comput. Mech. 2022, 8, 641–654. [Google Scholar] [CrossRef]
- Ilyunin, O.; Bezsonov, O.; Rudenko, S.; Serdiuk, N.; Udovenko, S.; Kapustenko, P.; Plankovskyy, S.; Arsenyeva, O. The neural network approach for estimation of heat transfer coefficient in heat exchangers considering the fouling formation dynamic. Therm. Sci. Eng. Prog. 2024, 51, 102615. [Google Scholar] [CrossRef]
- Toscano, J.D.; Oommen, V.; Varghese, A.J.; Zou, Z.; Ahmadi Daryakenari, N.; Wu, C.; Karniadakis, G.E. From PINNs to PIKANs: Recent advances in physics-informed machine learning. Mach. Learn. Comput. Sci. Eng. 2025, 1, 15. [Google Scholar] [CrossRef]
- Khanolkar, P.M.; Vrolijk, A.; Olechowski, A. Mapping artificial intelligence-based methods to engineering design stages: A focused literature review. Artif. Intell. Eng. Des. Anal. Manuf. 2023, 37, e25. [Google Scholar] [CrossRef]
- Ulan Uulu, C.; Kulyabin, M.; Etaiwi, L.; Martins Pacheco, N.M.; Joosten, J.; Röse, K.; Petridis, F.; Bosch, J.; Olsson, H.H. AI for better UX in computer-aided engineering: Is academia catching up with industry demands? A multivocal literature review. arXiv 2025, arXiv:2507.16586. [Google Scholar] [CrossRef]
- Montáns, F.J.; Cueto, E.; Bathe, K.J. Machine learning in computer aided engineering. In Machine Learning in Modeling and Simulation; Rabczuk, T., Bathe, K.J., Eds.; Springer: Cham, Switzerland, 2023; pp. 1–83. [Google Scholar] [CrossRef]
- Zhao, X.W.; Tong, X.M.; Ning, F.W.; Cai, M.L.; Han, F.; Li, H.G. Review of empowering computer-aided engineering with artificial intelligence. Adv. Manuf. 2025. [Google Scholar] [CrossRef]
- Chuang, P.Y.; Barba, L.A. Experience report of physics-informed neural networks in fluid simulations: Pitfalls and frustration. arXiv 2022, arXiv:2205.14249. [Google Scholar] [CrossRef]
- Ren, Z.; Zhou, S.; Liu, D.; Liu, Q. Physics-informed neural networks: A review of methodological evolution, theoretical foundations, and interdisciplinary frontiers toward next-generation scientific computing. Appl. Sci. 2025, 15, 8092. [Google Scholar] [CrossRef]
- Ciampi, F.G.; Rega, A.; Diallo, T.M.; Patalano, S. Analysing the role of physics-informed neural networks in modelling industrial systems through case studies in automotive manufacturing. Int. J. Interact. Des. Manuf. 2025. [Google Scholar] [CrossRef]
- Nadal, I.V.; Stiasny, J.; Chatzivasileiadis, S. Physics-informed neural networks in power system dynamics: Improving simulation accuracy. arXiv 2025, arXiv:2501.17621. [Google Scholar] [CrossRef]
- Nath, D.; Neog, D.R.; Gautam, S.S. Application of machine learning and deep learning in finite element analysis: A comprehensive review. Arch. Comput. Methods Eng. 2024, 31, 2945–2984. [Google Scholar] [CrossRef]
- Li, C.; Yang, S.; Zheng, H.; Zhang, Y.; Wu, L.; Xue, W.; Shen, D.; Lu, W.; Ni, Z.; Liu, M.; et al. Integration of machine learning with finite element analysis in materials science: A review. J. Mater. Sci. 2025, 60, 8285–8307. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Farea, A.; Yli-Harja, O.; Emmert-Streib, F. Understanding physics-informed neural networks: Techniques, applications, trends, and challenges. AI 2024, 5, 1534–1557. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Ahmadi, N.; Karniadakis, G.E. Physics-informed neural networks and extensions. arXiv 2024, arXiv:2408.16806. [Google Scholar] [CrossRef]
- Ganga, S.; Uddin, Z. Exploring physics-informed neural networks: From fundamentals to applications in complex systems. arXiv 2024, arXiv:2410.00422. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Lai, D.T.C.; Che Idris, A. Physics-informed neural network (PINN) evolution and beyond: A systematic literature review and bibliometric analysis. Big Data Cogn. Comput. 2022, 6, 140. [Google Scholar] [CrossRef]
- Luo, K.; Zhao, J.; Wang, Y.; Li, J.; Wen, J.; Liang, J.; Soekmadji, H.; Liao, S. Physics-informed neural networks for PDE problems: A comprehensive review. Artif. Intell. Rev. 2025, 58, 323. [Google Scholar] [CrossRef]
- Krishnapriyan, A.; Gholami, A.; Zhe, S.; Kirby, R.; Mahoney, M.W. Characterizing possible failure modes in physics informed neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 26548–26560. [Google Scholar]
- Rohrhofer, F.M.; Posch, S.; Gößnitzer, C.; Geiger, B.C. Data VS. physics: The apparent Pareto front of physics-informed neural networks. IEEE Access 2023, 11, 86252–86261. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. Multi-fidelity physics-constrained neural network and its application in materials modeling. J. Mech. Des. 2019, 141, 121403. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. A dual-dimer method for training physics-constrained neural networks with minimax architecture. Neural Netw. 2021, 136, 112–125. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-adaptive loss balanced physics-informed neural networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Dong, X.; Cao, F.; Yuan, D. Self-adaptive weight balanced physics-informed neural networks for solving complex coupling equations. In Proceedings of the International Conference on Mechatronic Engineering and Artificial Intelligence (MEAI 2024), Shenyang, China, 13–15 December 2024; Volume 13555, pp. 917–926. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Zheng, X.; Zhao, X.; Yao, W. Self-adaptive loss balanced physics-informed neural networks for the incompressible Navier-Stokes equations. arXiv 2021, arXiv:2104.06217. [Google Scholar] [CrossRef]
- McClenny, L.D.; Braga-Neto, U.M. Self-adaptive physics-informed neural networks. J. Comput. Phys. 2023, 474, 111722. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, H.; Zhu, F.; Chen, Y. Dasa-PINNs: Differentiable adversarial self-adaptive pointwise weighting scheme for physics-informed neural networks. SSRN 2023, 4376049. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.J.; Toscano, J.D.; Stergiopulos, N.; Karniadakis, G.E. Residual-based attention and connection to information bottleneck theory in PINNs. arXiv 2023, arXiv:2307.00379. [Google Scholar] [CrossRef]
- Song, Y.; Wang, H.; Yang, H.; Taccari, M.L.; Chen, X. Loss-attentional physics-informed neural networks. J. Comput. Phys. 2024, 501, 112781. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Meng, X.; Karniadakis, G.E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114823. [Google Scholar] [CrossRef]
- Son, H.; Jang, J.W.; Han, W.J.; Hwang, H.J. Sobolev training for physics informed neural networks. arXiv 2021, arXiv:2101.08932. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended physics-informed neural networks (XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Commun. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar] [CrossRef]
- Moseley, B.; Markham, A.; Nissen-Meyer, T. Finite basis physics-informed neural networks (FBPINNs): A scalable domain decomposition approach for solving differential equations. Adv. Comput. Math. 2023, 49, 62. [Google Scholar] [CrossRef]
- Luo, D.; Jo, S.H.; Kim, T. Progressive domain decomposition for efficient training of physics-informed neural network. Mathematics 2025, 13, 1515. [Google Scholar] [CrossRef]
- Mangado, N.; Piella, G.; Noailly, J.; Pons-Prats, J.; González Ballester, M. Analysis of uncertainty and variability in finite element computational models for biomedical engineering: Characterization and propagation. Front. Bioeng. Biotechnol. 2016, 4, 60. [Google Scholar] [CrossRef]
- Sun, X. Uncertainty quantification of material properties in ballistic impact of magnesium alloys. Materials 2022, 15, 6961. [Google Scholar] [CrossRef]
- Berggren, C.C.; Jiang, D.; Jack Wang, Y.F.; Bergquist, J.A.; Rupp, L.C.; Liu, Z.; MacLeod, R.S.; Narayan, A.; Timmins, L.H. Influence of material parameter variability on the predicted coronary artery biomechanical environment via uncertainty quantification. Biomech. Model. Mechanobiol. 2024, 23, 927–940. [Google Scholar] [CrossRef]
- Segura, C.L., Jr.; Sattar, S.; Hariri-Ardebili, M.A. Quantifying material uncertainty in seismic evaluations of reinforced concrete bridge column structures. ACI Struct. J. 2022, 119, 141–152. [Google Scholar] [CrossRef] [PubMed]
- Jo, J.; Jeong, Y.; Kim, J.; Yoo, J. Thermal conductivity estimation using Physics-Informed Neural Networks with limited data. Eng. Appl. Artif. Intell. 2024, 137, 109079. [Google Scholar] [CrossRef]
- Li, D.; Yan, B.; Gao, T.; Li, G.; Wang, Y. PINN model of diffusion coefficient identification problem in Fick’s laws. ACS Omega 2024, 9, 3846–3857. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resour. Res. 2020, 56, e2019WR026731. [Google Scholar] [CrossRef]
- Teloli, R.D.O.; Tittarelli, R.; Bigot, M.; Coelho, L.; Ramasso, E.; Le Moal, P.; Ouisse, M. A physics-informed neural networks framework for model parameter identification of beam-like structures. Mech. Syst. Signal Process. 2025, 224, 112189. [Google Scholar] [CrossRef]
- Kamali, A.; Sarabian, M.; Laksari, K. Elasticity imaging using physics-informed neural networks: Spatial discovery of elastic modulus and Poisson’s ratio. Acta Biomater. 2023, 155, 400–409. [Google Scholar] [CrossRef]
- Lee, S.; Popovics, J. Applications of physics-informed neural networks for property characterization of complex materials. RILEM Tech. Lett. 2022, 7, 178–188. [Google Scholar] [CrossRef]
- Mitusch, S.K.; Funke, S.W.; Kuchta, M. Hybrid FEM-NN models: Combining artificial neural networks with the finite element method. J. Comput. Phys. 2021, 446, 110651. [Google Scholar] [CrossRef]
- Yang, S.; Peng, S.; Guo, J.; Wang, F. A review on physics-informed machine learning for monitoring metal additive manufacturing process. Adv. Manuf. 2024, 1, 0008. [Google Scholar] [CrossRef]
- Zhou, M.; Mei, G.; Xu, N. Enhancing computational accuracy in surrogate modeling for elastic–plastic problems by coupling S-FEM and physics-informed deep learning. Mathematics 2023, 11, 2016. [Google Scholar] [CrossRef]
- Meethal, R.E.; Kodakkal, A.; Khalil, M.; Ghantasala, A.; Obst, B.; Bletzinger, K.U.; Wüchner, R. Finite element method-enhanced neural network for forward and inverse problems. Adv. Model. Simul. Eng. Sci. 2023, 10, 6. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. Variational physics-informed neural networks for solving partial differential equations. arXiv 2019, arXiv:1912.00873. [Google Scholar] [CrossRef]
- Berrone, S.; Canuto, C.; Pintore, M. Variational physics informed neural networks: The role of quadratures and test functions. J. Sci. Comput. 2022, 92, 100. [Google Scholar] [CrossRef]
- Berrone, S.; Canuto, C.; Pintore, M. Solving PDEs by variational physics-informed neural networks: An a posteriori error analysis. Ann. Univ. Ferrara 2022, 68, 575–595. [Google Scholar] [CrossRef]
- Khodayi-Mehr, R.; Zavlanos, M. VarNet: Variational neural networks for the solution of partial differential equations. Proc. Mach. Learn. Res. 2020, 120, 298–307. [Google Scholar]
- Zang, Y.; Bao, G.; Ye, X.; Zhou, H. Weak adversarial networks for high-dimensional partial differential equations. J. Comput. Phys. 2020, 411, 109409. [Google Scholar] [CrossRef]
- Berrone, S.; Pintore, M. Meshfree Variational-Physics-Informed neural networks (MF-VPINN): An adaptive training strategy. Algorithms 2024, 17, 415. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Samaniego, E.; Anitescu, C.; Goswami, S.; Nguyen-Thanh, V.M.; Guo, H.; Hamdia, K.; Zhuang, X.; Rabczuk, T. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Comput. Methods Appl. Mech. Eng. 2020, 362, 112790. [Google Scholar] [CrossRef]
- Bai, J.; Rabczuk, T.; Gupta, A.; Alzubaidi, L.; Gu, Y. A physics-informed neural network technique based on a modified loss function for computational 2D and 3D solid mechanics. Comput. Mech. 2023, 71, 543–562. [Google Scholar] [CrossRef]
- Roehrl, M.A.; Runkler, T.A.; Brandtstetter, V.; Tokic, M.; Obermayer, S. Modeling system dynamics with physics-informed neural networks based on Lagrangian mechanics. IFAC-PapersOnLine 2020, 53, 9195–9200. [Google Scholar] [CrossRef]
- Kaltsas, D.A. Constrained Hamiltonian systems and physics-informed neural networks: Hamilton-Dirac neural networks. Phys. Rev. E 2025, 111, 025301. [Google Scholar] [CrossRef]
- Baldan, M.; Di Barba, P. Energy-based PINNs for solving coupled field problems: Concepts and application to the multi-objective optimal design of an induction heater. IET Sci. Meas. Technol. 2024, 18, 514–523. [Google Scholar] [CrossRef]
- Liu, C.; Wu, H. cv-PINN: Efficient learning of variational physics-informed neural network with domain decomposition. Extrem. Mech. Lett. 2023, 63, 102051. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Zhao, Z.; Zhou, X. Energy-based PINNs using the element integral approach and their enhancement for solid mechanics problems. Int. J. Solids Struct. 2025, 313, 113315. [Google Scholar] [CrossRef]
- ASTM A370-24; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM International: West Conshohocken, PA, USA, 2024. [CrossRef]
- ASTM D3039/D3039M-14; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2014. [CrossRef]
- ASTM C39/C39M-21; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- Skala, V. Point-in-convex polygon and point-in-convex polyhedron algorithms with O (1) complexity using space subdivision. AIP Conf. Proc. 2016, 1738, 480034. [Google Scholar] [CrossRef]
- Žalik, B.; Kolingerova, I. A cell-based point-in-polygon algorithm suitable for large sets of points. Comput. Geosci. 2001, 27, 1135–1145. [Google Scholar] [CrossRef]
- Sethian, J.A. Fast marching methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Sethian, J.A. Evolution, implementation, and application of level set and fast marching methods for advancing fronts. J. Comput. Phys. 2001, 169, 503–555. [Google Scholar] [CrossRef]
- Fayolle, P.A. Signed distance function computation from an implicit surface. arXiv 2021, arXiv:2104.08057. [Google Scholar] [CrossRef]
- Basir, S. Investigating and mitigating failure modes in physics-informed neural networks (PINNS). arXiv 2022, arXiv:2209.09988. [Google Scholar] [CrossRef]
- Jones, M.W.; Bærentzen, J.A.; Sramek, M. 3D distance fields: A survey of techniques and applications. IEEE Trans. Vis. Comput. Graph. 2006, 12, 581–599. [Google Scholar] [CrossRef]
- Kraus, M.A.; Tatsis, K.E. SDF-PINNs: Joining physics-informed neural networks with neural implicit geometry representation. In Proceedings of the GNI Symposium & Expo on Artificial Intelligence for the Built World Technical University of Munich, Munich, Germany, 10–12 September 2024; pp. 97–104. [Google Scholar] [CrossRef]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning continuous signed distance functions for shape representation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 165–174. [Google Scholar] [CrossRef]
- Atzmon, M.; Lipman, Y. SAL: Sign agnostic learning of shapes from raw data. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2562–2571. [Google Scholar] [CrossRef]
- Ma, B.; Han, Z.; Liu, Y.S.; Zwicker, M. Neural-pull: Learning signed distance functions from point clouds by learning to pull space onto surfaces. arXiv 2020, arXiv:2011.13495. [Google Scholar] [CrossRef]
- Sukumar, N.; Srivastava, A. Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks. Comput. Methods Appl. Mech. Eng. 2022, 389, 114333. [Google Scholar] [CrossRef]
- Rvachev, V.L. Theory of R-Functions and Some Applications; Naukova Dumka: Kiev, Ukraine, 1982. (In Russian) [Google Scholar]
- Plankovskyy, S.; Shypul, O.; Tsegelnyk, Y.; Tryfonov, O.; Golovin, I. Simulation of surface heating for arbitrary shape’s moving bodies/sources by using R-functions. Acta Polytech. 2016, 56, 472–477. [Google Scholar] [CrossRef]
- Shapiro, V. Semi-analytic geometry with R-functions. Acta Numer. 2007, 16, 239–303. [Google Scholar] [CrossRef]
- Stoyan, Y. Mathematical methods for geometric design. In Advances in CAD/CAM, Proceedings of PROLAMAT82; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1983; pp. 67–86. [Google Scholar]
- Chernov, N.; Stoyan, Y.; Romanova, T. Mathematical model and efficient algorithms for object packing problem. Comput. Geom. 2010, 43, 535–553. [Google Scholar] [CrossRef]
- Stoyan, Y.; Pankratov, A.; Romanova, T. Quasi-phi-functions and optimal packing of ellipses. J. Glob. Optim. 2016, 65, 283–307. [Google Scholar] [CrossRef]
- Stoyan, Y.; Romanova, T. Mathematical models of placement optimisation: Two- and three-dimensional problems and applications. In Modeling and Optimization in Space Engineering; SOIA; Fasano, G., Pintér, J., Eds.; Springer: New York, NY, USA, 2012; Volume 73, pp. 363–388. [Google Scholar] [CrossRef]
- Romanova, T.; Litvinchev, I.; Pankratov, A. Packing ellipsoids in an optimized cylinder. Eur. J. Oper. Res. 2020, 285, 429–443. [Google Scholar] [CrossRef]
- Romanova, T.; Bennell, J.; Stoyan, Y.; Pankratov, A. Packing of concave polyhedra with continuous rotations using nonlinear optimisation. Eur. J. Oper. Res. 2018, 268, 37–53. [Google Scholar] [CrossRef]
- Pankratov, A.; Romanova, T.; Litvinchev, I. Packing oblique 3D objects. Mathematics 2020, 8, 1130. [Google Scholar] [CrossRef]
- Romanova, T.; Pankratov, A.; Litvinchev, I.; Dubinskyi, V.; Infante, L. Sparse layout of irregular 3D clusters. J. Oper. Res. Soc. 2023, 74, 351–361. [Google Scholar] [CrossRef]
- Romanova, T.; Pankratov, A.; Litvinchev, I.; Plankovskyy, S.; Tsegelnyk, Y.; Shypul, O. Sparsest packing of two-dimensional objects. Int. J. Prod. Res. 2021, 59, 3900–3915. [Google Scholar] [CrossRef]
- Romanova, T.; Stoyan, Y.; Pankratov, A.; Litvinchev, I.; Plankovskyy, S.; Tsegelnyk, Y.; Shypul, O. Sparsest balanced packing of irregular 3D objects in a cylindrical container. Eur. J. Oper. Res. 2021, 291, 84–100. [Google Scholar] [CrossRef]
- Romanova, T.; Stoyan, Y.; Pankratov, A.; Litvinchev, I.; Avramov, K.; Chernobryvko, M.; Yanchevskyi, I.; Mozgova, I.; Bennell, J. Optimal layout of ellipses and its application for additive manufacturing. Int. J. Prod. Res. 2021, 59, 560–575. [Google Scholar] [CrossRef]
- Romanova, T.; Pankratov, A.; Litvinchev, I.; Strelnikova, E. Modeling nanocomposites with ellipsoidal and conical inclusions by optimized packing. In Computer Science and Health Engineering in Health Services; LNICST; Marmolejo-Saucedo, J.A., Vasant, P., Litvinchev, I., Rodriguez-Aguilar, R., Martinez-Rios, F., Eds.; Springer: Cham, Switzerland, 2021; Volume 359, pp. 201–210. [Google Scholar] [CrossRef]
- Duriagina, Z.; Pankratov, A.; Romanova, T.; Litvinchev, I.; Bennell, J.; Lemishka, I.; Maximov, S. Optimized packing titanium alloy powder particles. Computation 2023, 11, 22. [Google Scholar] [CrossRef]
- Scheithauer, U.; Romanova, T.; Pankratov, O.; Schwarzer-Fischer, E.; Schwentenwein, M.; Ertl, F.; Fischer, A. Potentials of numerical methods for increasing the productivity of additive manufacturing processes. Ceramics 2023, 6, 630–650. [Google Scholar] [CrossRef]
- Yamada, F.M.; Gois, J.P.; Batagelo, H.C.; Takahashi, H. Reinforcement learning for circular sparsest packing problems. In New Trends in Intelligent Software Methodologies, Tools and Techniques; Fujita, H., Hernandez-Matamoros, A., Watanobe, Y., Eds.; IOS Press: Amsterdam, The Netherlands, 2025; pp. 135–148. [Google Scholar] [CrossRef]
- Belyaev, A.G.; Fayolle, P.A. Transfinite barycentric coordinates. In Generalized Barycentric Coordinates in Computer Graphics and Computational Mechanics; CRC Press: Boca Raton, FL, USA, 2017; pp. 43–62. [Google Scholar] [CrossRef]
- Jenis, J.; Ondriga, J.; Hrcek, S.; Brumercik, F.; Cuchor, M.; Sadovsky, E. Engineering applications of artificial intelligence in mechanical design and optimization. Machines 2023, 11, 577. [Google Scholar] [CrossRef]
- Anton, D.; Wessels, H. Physics-informed neural networks for material model calibration from full-field displacement data. arXiv 2022, arXiv:2212.07723. [Google Scholar] [CrossRef]
- Anton, D.; Tröger, J.A.; Wessels, H.; Römer, U.; Henkes, A.; Hartmann, S. Deterministic and statistical calibration of constitutive models from full-field data with parametric physics-informed neural networks. Adv. Model. Simul. Eng. Sci. 2025, 12, 12. [Google Scholar] [CrossRef]
- Valente, M.; Dias, T.C.; Guerra, V.; Ventura, R. Physics-consistent machine learning: Output projection onto physical manifolds. arXiv 2025, arXiv:2502.15755. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, M.; Tan, Q.; Kartha, Y.; Lu, L. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2023, 403, 115671. [Google Scholar] [CrossRef]
- Florido, J.; Wang, H.; Khan, A.; Jimack, P.K. Investigating guiding information for adaptive collocation point sampling in PINNs. In Computational Science, Proceedings of the ICCS 2024, Malaga, Spain, 2–4 June 2024; LNCS; Franco, L., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A., Eds.; Springer: Cham, Switzerland, 2024; Volume 14834, pp. 323–337. [Google Scholar] [CrossRef]
- Mao, Z.; Meng, X. Physics-informed neural networks with residual/gradient-based adaptive sampling methods for solving partial differential equations with sharp solutions. Adv. Appl. Math. Mech. 2023, 44, 1069–1084. [Google Scholar] [CrossRef]
- Tang, K.; Wan, X.; Yang, C. DAS-PINNs: A deep adaptive sampling method for solving high-dimensional partial differential equations. J. Comput. Phys. 2023, 476, 111868. [Google Scholar] [CrossRef]
- Lin, S.; Chen, Y. Causality-guided adaptive sampling method for physics-informed neural networks solving forward problems of partial differential equations. Phys. D 2025, 481, 134878. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Ding, J. Grad-RAR: An adaptive sampling method based on residual gradient for physical-informed neural networks. In Proceedings of the 2022 International Conference on Automation, Robotics and Computer Engineering (ICARCE), Wuhan, China, 16–17 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Subramanian, S.; Kirby, R.M.; Mahoney, M.W.; Gholami, A. Adaptive self-supervision algorithms for physics-informed neural networks. arXiv 2022, arXiv:2207.04084. [Google Scholar] [CrossRef]
- Visser, C.; Heinlein, A.; Giovanardi, B. PACMANN: Point adaptive collocation method for artificial neural networks. arXiv 2024, arXiv:2411.19632. [Google Scholar] [CrossRef]
- Lu, R.; Jia, J.; Lee, Y.J.; Lu, Z.; Zhang, C. R-PINN: Recovery-type a-posteriori estimator enhanced adaptive PINN. arXiv 2025, arXiv:2506.10243. [Google Scholar] [CrossRef]
- Li, C.; Yu, W.; Wang, Q. Energy dissipation rate guided adaptive sampling for physics-informed neural networks: Resolving surface-bulk dynamics in Allen-Cahn systems. arXiv 2025, arXiv:2507.09757. [Google Scholar] [CrossRef]
- Lau, G.K.R.; Hemachandra, A.; Ng, S.K.; Low, B.K.H. PINNACLE: PINN adaptive collocation and experimental points selection. arXiv 2024, arXiv:2404.07662. [Google Scholar] [CrossRef]
- Sukumar, N.; Bolander, J.E. Distance-based collocation sampling for mesh-free physics-informed neural networks. Phys. Fluids 2025, 37, 077190. [Google Scholar] [CrossRef]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Point set surfaces. In Proceedings of the Proceedings Visualization, 2001. VIS’01, San Diego, CA, USA, 21–26 October 2001; pp. 21–29. [Google Scholar] [CrossRef]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Computing and rendering point set surfaces. IEEE Trans. Vis. Comput. Graph. 2003, 9, 3–15. [Google Scholar] [CrossRef]
- Calakli, F.; Taubin, G. SSD: Smooth signed distance surface reconstruction. Comput. Graph. Forum 2011, 30, 1993–2002. [Google Scholar] [CrossRef]
- Ma, B.; Liu, Y.S.; Han, Z. Reconstructing surfaces for sparse point clouds with on-surface priors. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6305–6315. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Vinod, A.; Bhattacharya, S.; Koganti, A.; Ellendula, A.S.; Reddy, B. Curvature informed furthest point sampling. arXiv 2024, arXiv:2411.16995. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural. Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Lu, L.; Pestourie, R.; Yao, W.; Wang, Z.; Verdugo, F.; Johnson, S.G. Physics-informed neural networks with hard constraints for inverse design. SIAM J. Sci. Comput. 2021, 43, B1105–B1132. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Zhang, W.; Yang, J. A hard-constraint wide-body physics-informed neural network model for solving multiple cases in forward problems for partial differential equations. Appl. Sci. 2023, 14, 189. [Google Scholar] [CrossRef]
- Lai, M.C.; Song, Y.; Yuan, X.; Yue, H.; Zeng, T. The hard-constraint PINNs for interface optimal control problems. SIAM J. Sci. Comput. 2025, 47, C601–C629. [Google Scholar] [CrossRef]
- Berrone, S.; Canuto, C.; Pintore, M.; Sukumar, N. Enforcing Dirichlet boundary conditions in physics-informed neural networks and variational physics-informed neural networks. Heliyon 2023, 9, e18820. [Google Scholar] [CrossRef]
- Wang, J.; Mo, Y.L.; Izzuddin, B.; Kim, C.W. Exact Dirichlet boundary physics-informed neural network EPINN for solid mechanics. Comput. Methods Appl. Mech. Eng. 2023, 414, 116184. [Google Scholar] [CrossRef]
- Tian, X.; Wang, J.; Kim, C.W.; Deng, X.; Zhu, Y. Automated machine learning exact dirichlet boundary physics-informed neural networks for solid mechanics. Eng. Struct. 2025, 330, 119884. [Google Scholar] [CrossRef]
- Straub, C.; Brendel, P.; Medvedev, V.; Rosskopf, A. Hard-constraining Neumann boundary conditions in physics-informed neural networks via Fourier feature embeddings. arXiv 2025, arXiv:2504.01093. [Google Scholar] [CrossRef]
- Rvachev, V.L.; Sheiko, T.I. R-functions in boundary value problems in mechanics. Appl. Mech. Rev. 1995, 48, 151–188. [Google Scholar] [CrossRef]
- Rvachev, V.L.; Slesarenko, A.P. Application op logic-algebraic and numerical methods to multidimensional heat exchange problems in regions op complex geometry pilled with uniform or composite media. In Proceedings of the International Heat Transfer Conference 7, Munich, Germany, 6–10 September 1982; pp. 35–39. [Google Scholar] [CrossRef]
- Biswas, A.; Shapiro, V. Approximate distance fields with non-vanishing gradients. Graph. Models 2004, 66, 133–159. [Google Scholar] [CrossRef]
- Sobh, N.; Gladstone, R.J.; Meidani, H. PINN-FEM: A hybrid approach for enforcing Dirichlet boundary conditions in physics-informed neural networks. arXiv 2025, arXiv:2501.07765. [Google Scholar] [CrossRef]
- Shukla, K.; Toscano, J.D.; Wang, Z.; Zou, Z.; Karniadakis, G.E. A comprehensive and FAIR comparison between MLP and KAN representations for differential equations and operator networks. Comput. Methods Appl. Mech. Eng. 2024, 431, 117290. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; Bai, J.; Anitescu, C.; Eshaghi, M.S.; Zhuang, X.; Rabczuk, T. Kolmogorov–Arnold-Informed neural network: A physics-informed deep learning framework for solving forward and inverse problems based on Kolmogorov–Arnold Networks. Comput. Methods Appl. Mech. Eng. 2025, 433, 117518. [Google Scholar] [CrossRef]
- Jacob, B.; Howard, A.; Stinis, P. SPIKANs: Separable physics-informed Kolmogorov-Arnold networks. Mach. Learn. Sci. Technol. 2024, 6, 035060. [Google Scholar] [CrossRef]
- Rigas, S.; Papachristou, M.; Papadopoulos, T.; Anagnostopoulos, F.; Alexandridis, G. Adaptive training of grid-dependent physics-informed kolmogorov-arnold networks. IEEE Access 2024, 12, 176982–176998. [Google Scholar] [CrossRef]
- Gong, Y.; He, Y.; Mei, Y.; Zhuang, X.; Qin, F.; Rabczuk, T. Physics-Informed Kolmogorov-Arnold Networks for multi-material elasticity problems in electronic packaging. arXiv 2025, arXiv:2508.16999. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Pang, G.; Zhang, Z.; Karniadakis, G.E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 2021, 3, 218–229. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, H.; Kovachki, N.; Jin, D.; Chen, H.; Liu, B.; Azizzadenesheli, K.; Anandkumar, A. Physics-informed neural operator for learning partial differential equations. ACM/IMS J. Data Sci. 2024, 1, 9. [Google Scholar] [CrossRef]
- Hao, Z.; Wang, Z.; Su, H.; Ying, C.; Dong, Y.; Liu, S.; Cheng, Z.; Song, J.; Zhu, J. Gnot: A general neural operator transformer for operator learning. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 12556–12569. [Google Scholar]
- Zhong, W.; Meidani, H. Physics-informed geometry-aware neural operator. Comput. Methods Appl. Mech. Eng. 2025, 434, 117540. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Choy, C.; Li, B.; Kossaifi, J.; Otta, S.; Nabian, M.A.; Stadler, M.; Hundt, C.; Azizzadenesheli, K.; et al. Geometry-informed neural operator for large-scale 3d PDEs. Adv. Neural. Inf. Process. Syst. 2023, 36, 35836–35854. [Google Scholar]
- Eshaghi, M.S.; Anitescu, C.; Thombre, M.; Wang, Y.; Zhuang, X.; Rabczuk, T. Variational physics-informed neural operator (VINO) for solving partial differential equations. Comput. Methods Appl. Mech. Eng. 2025, 437, 117785. [Google Scholar] [CrossRef]
- Sunil, P.; Sills, R.B. FE-PINNs: Finite-element-based physics-informed neural networks for surrogate modeling. arXiv 2024, arXiv:2412.07126. [Google Scholar] [CrossRef]
- Zhang, N.; Xu, K.; Yin, Z.Y.; Li, K.Q.; Jin, Y.F. Finite element-integrated neural network framework for elastic and elastoplastic solids. Comput. Methods Appl. Mech. Eng. 2025, 433, 117474. [Google Scholar] [CrossRef]
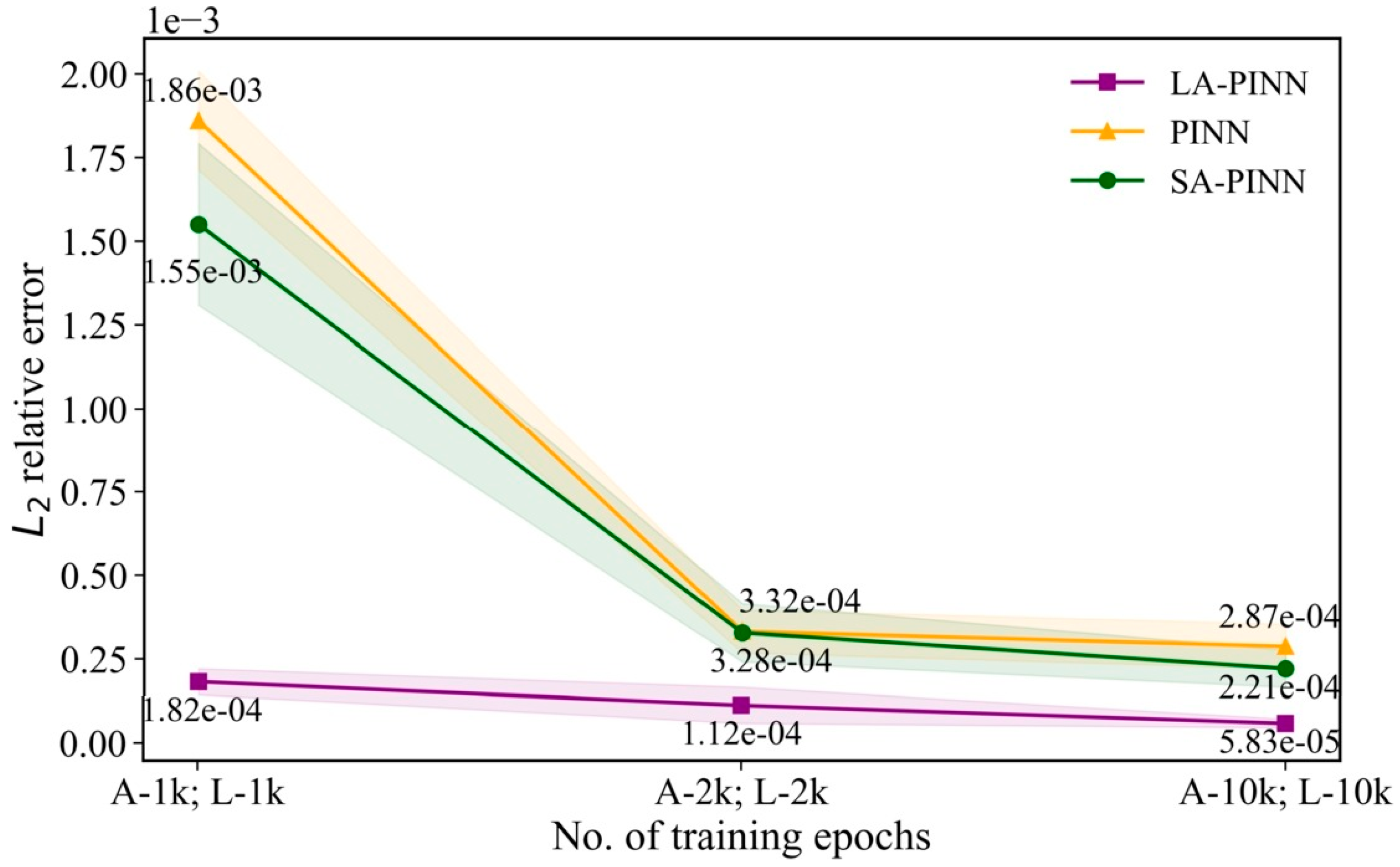
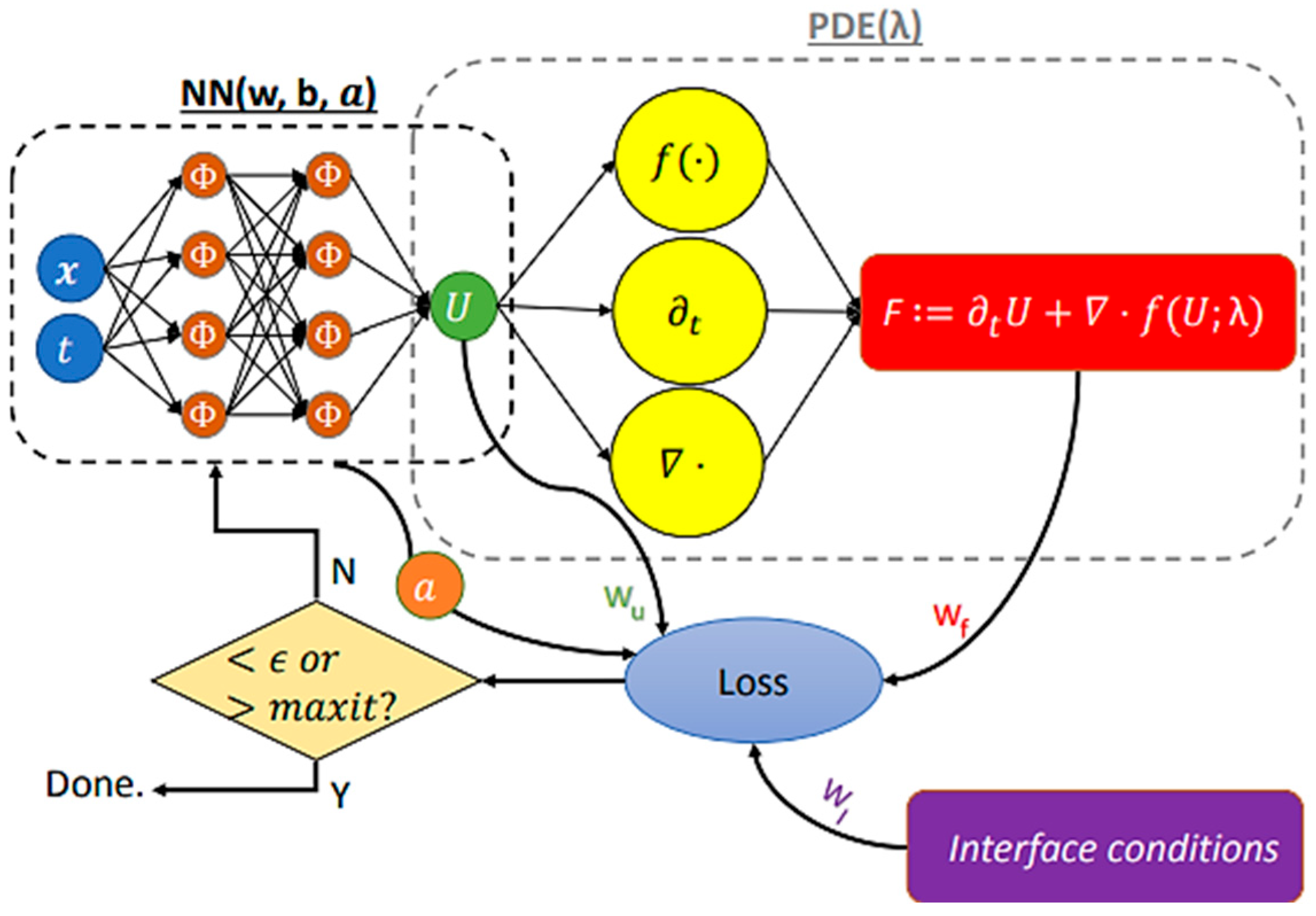
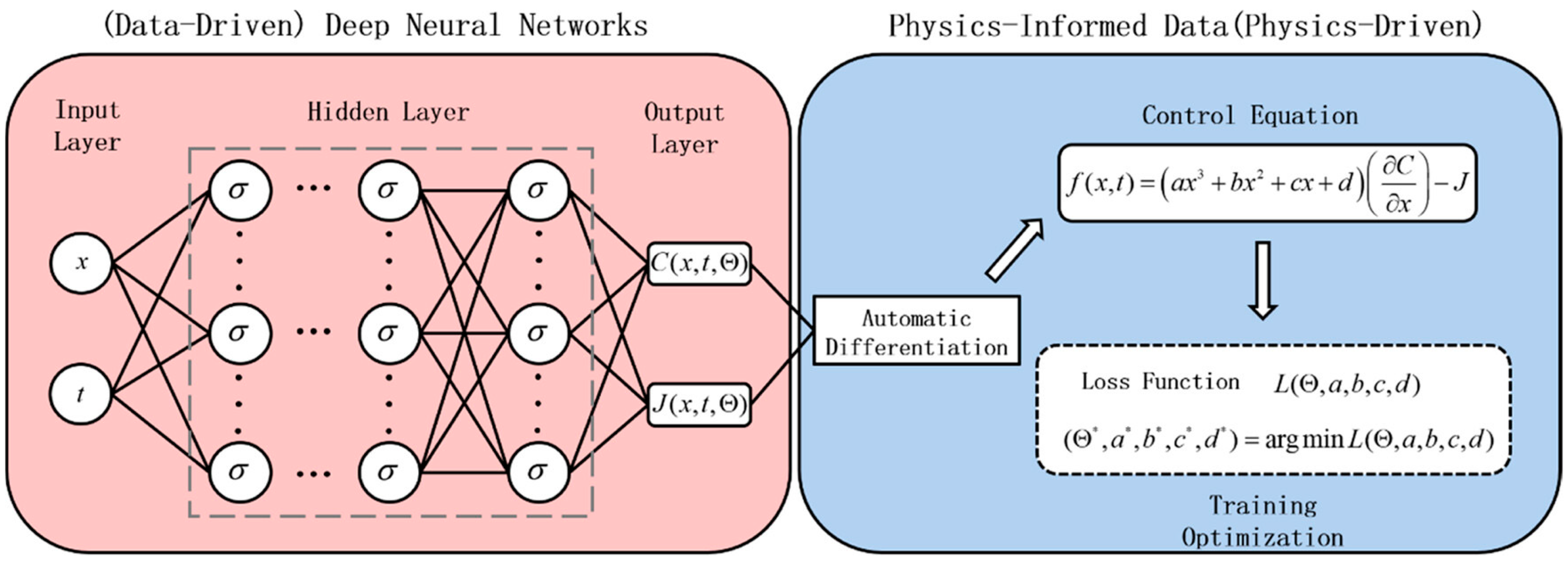
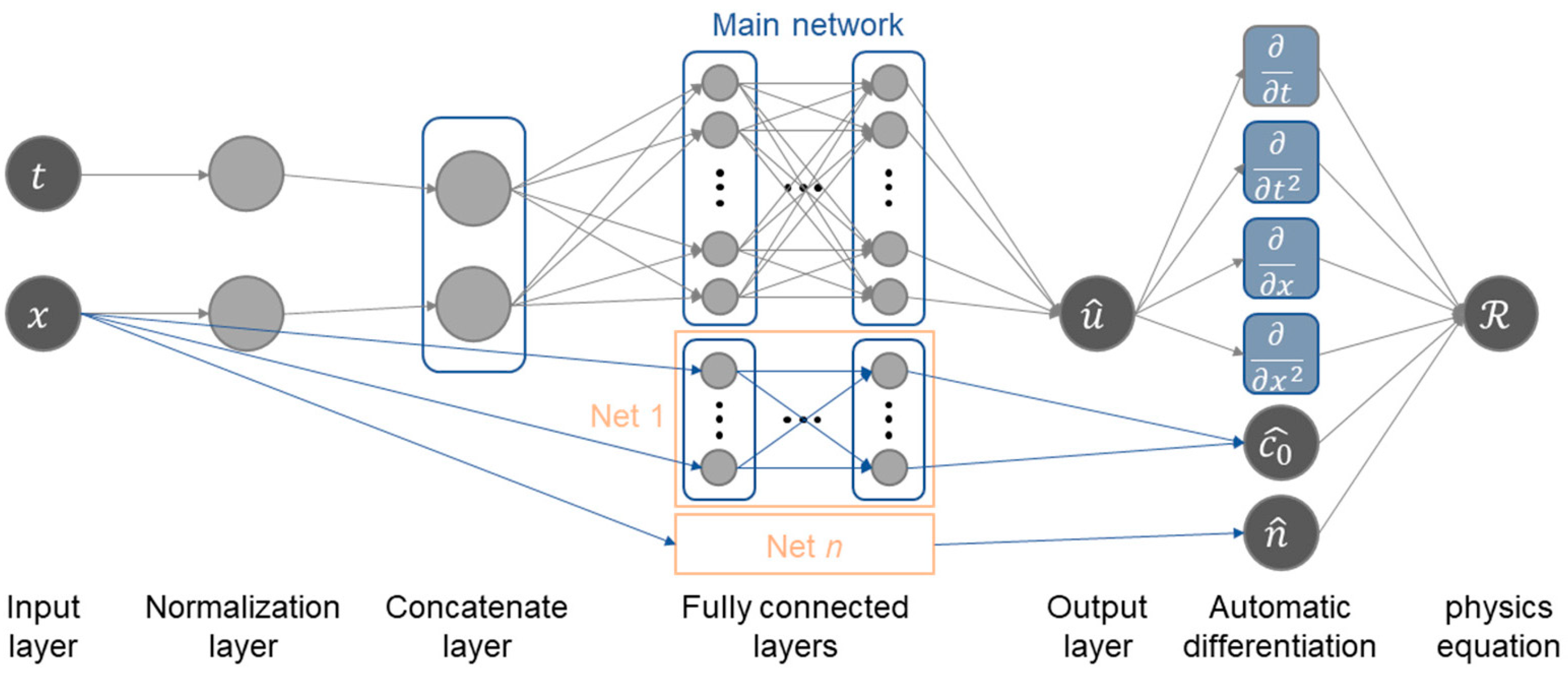
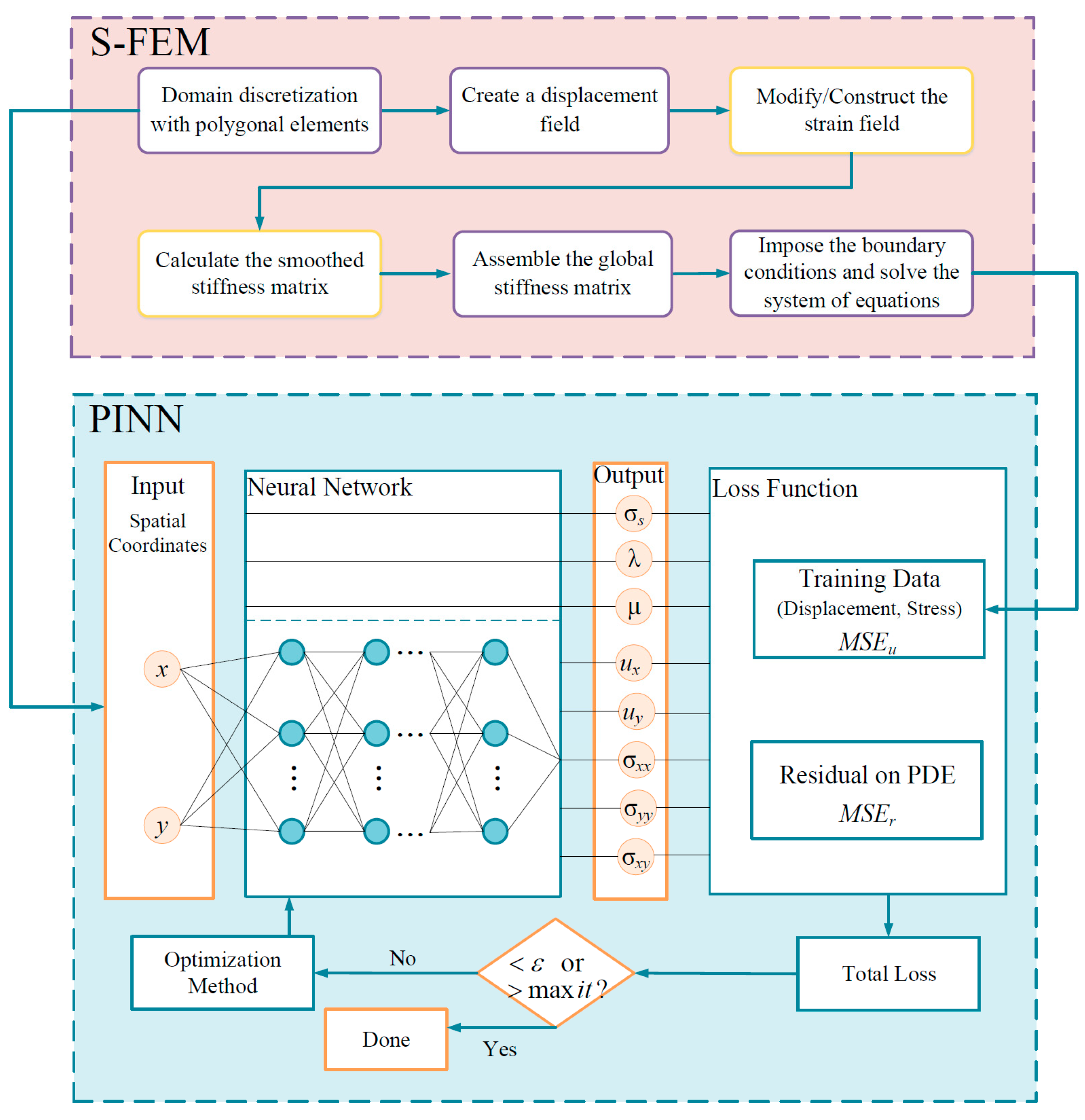
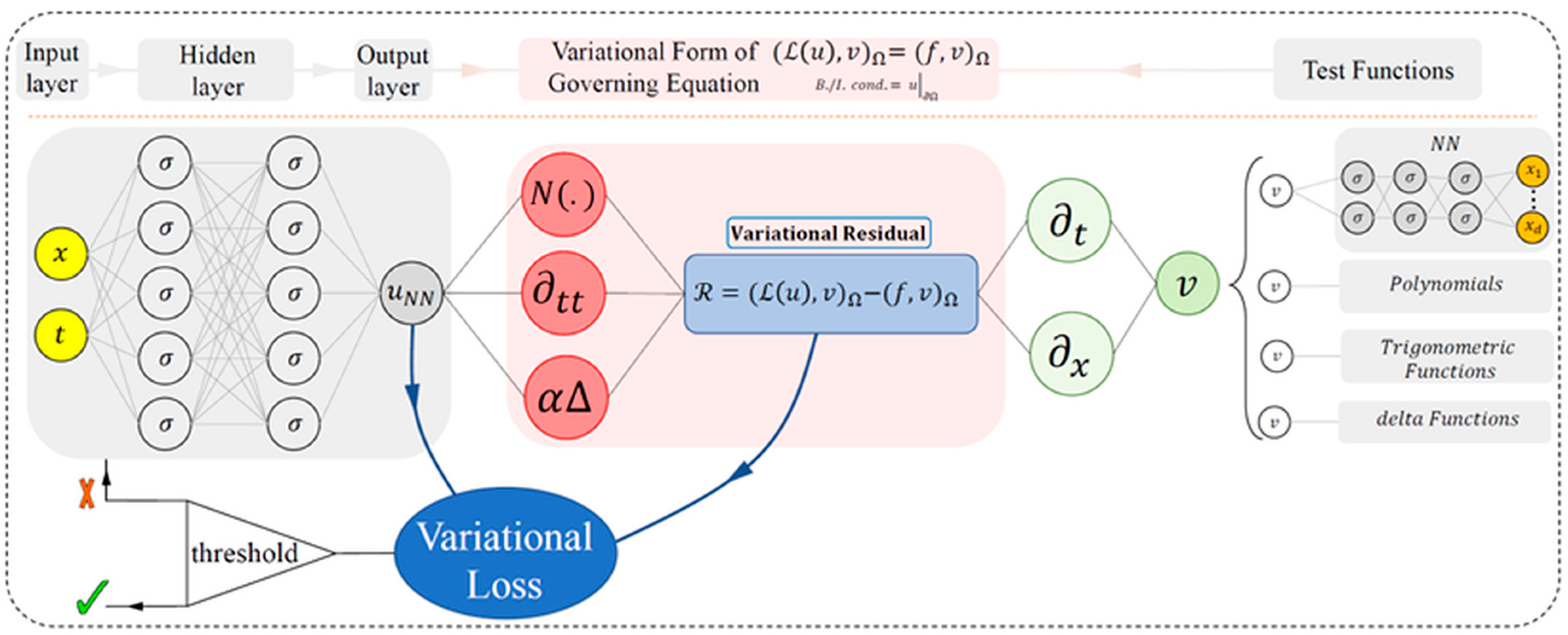
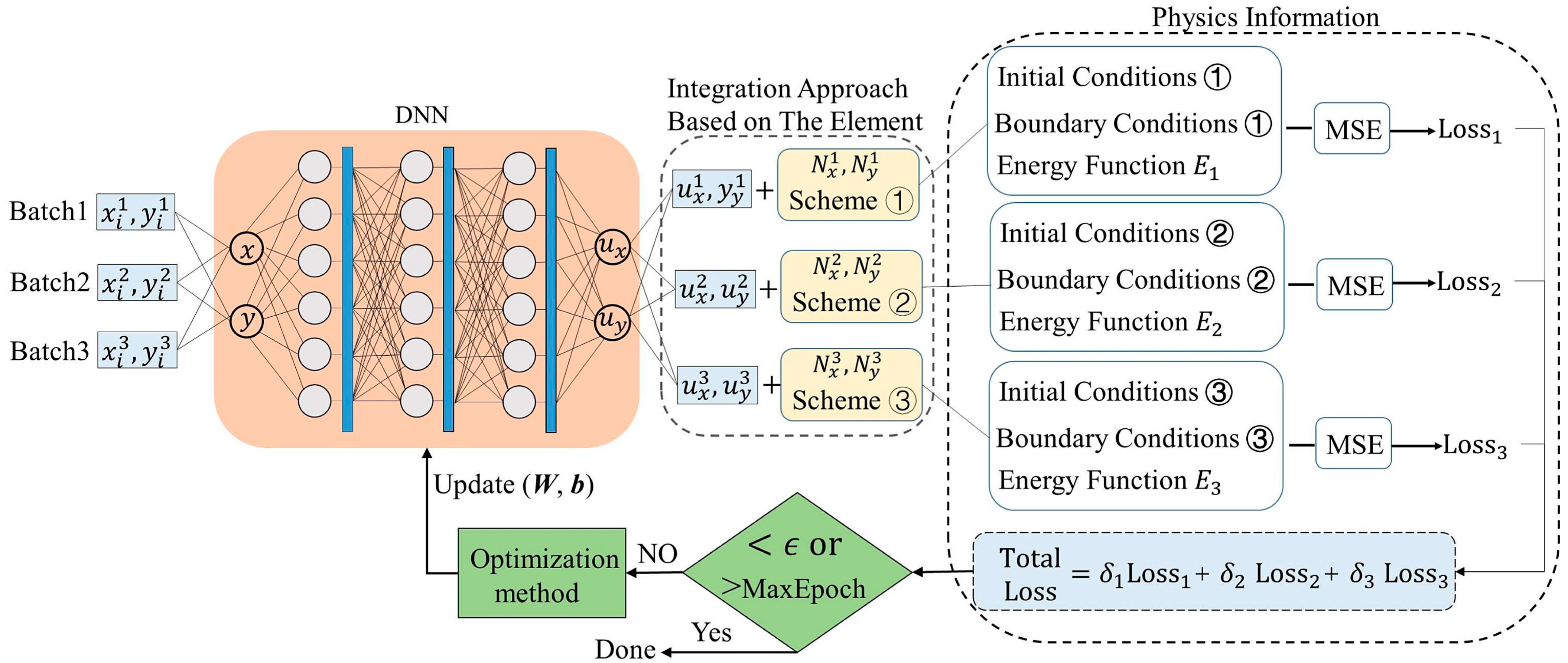


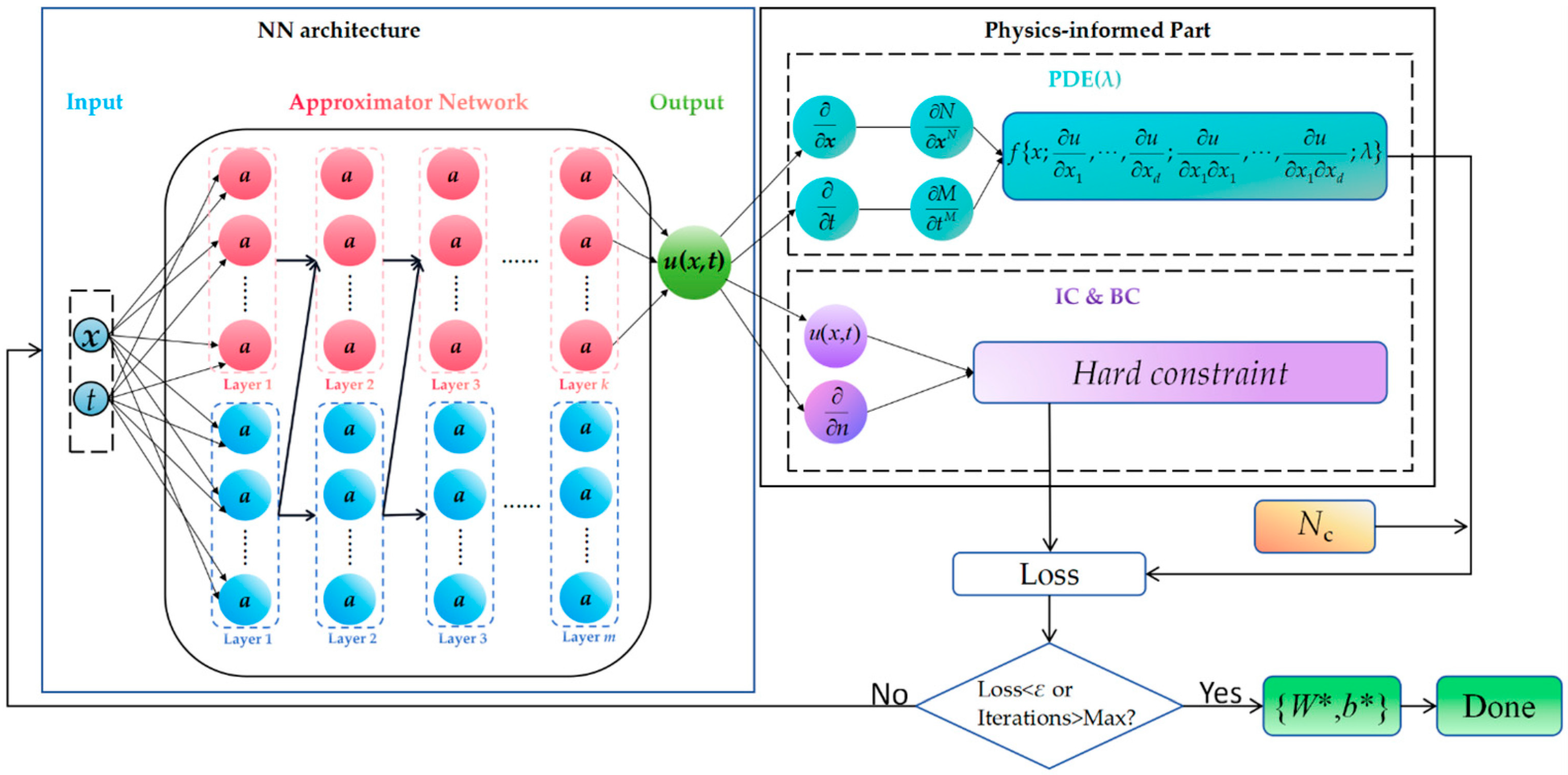
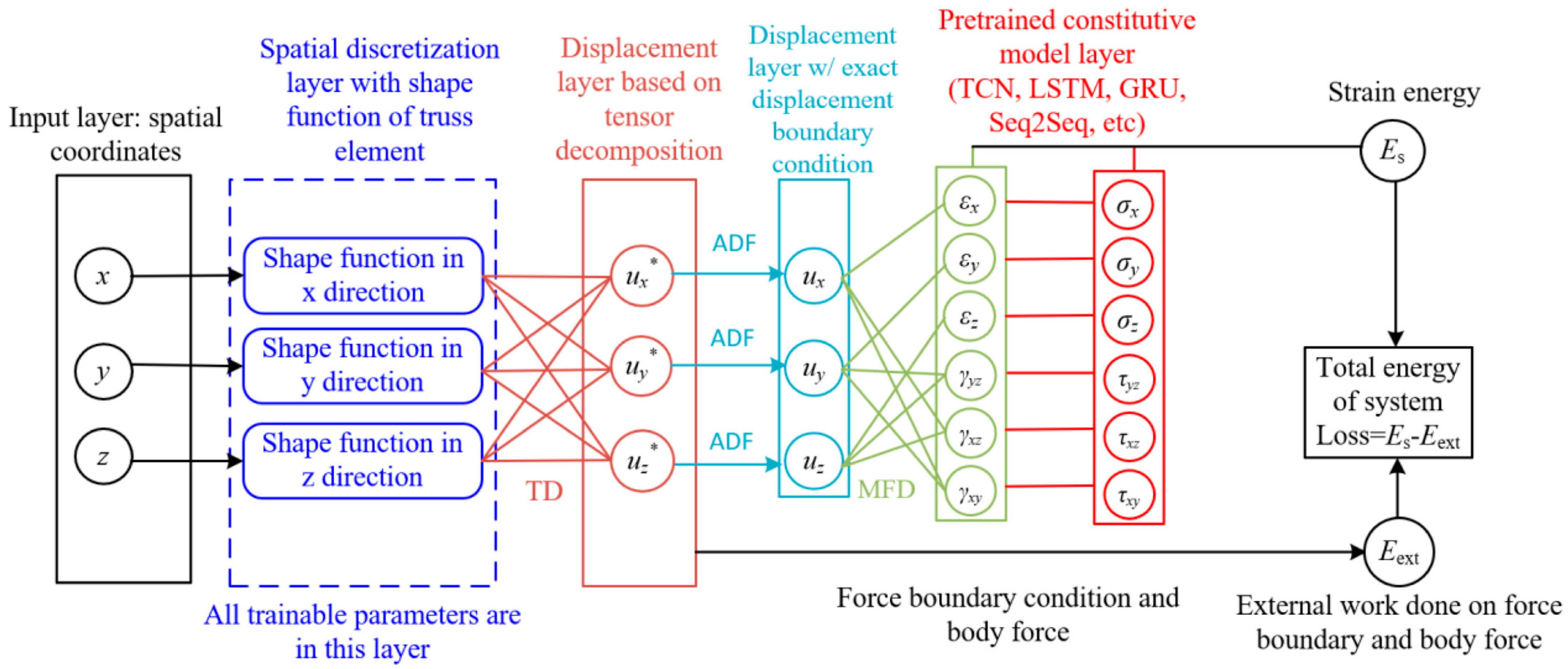
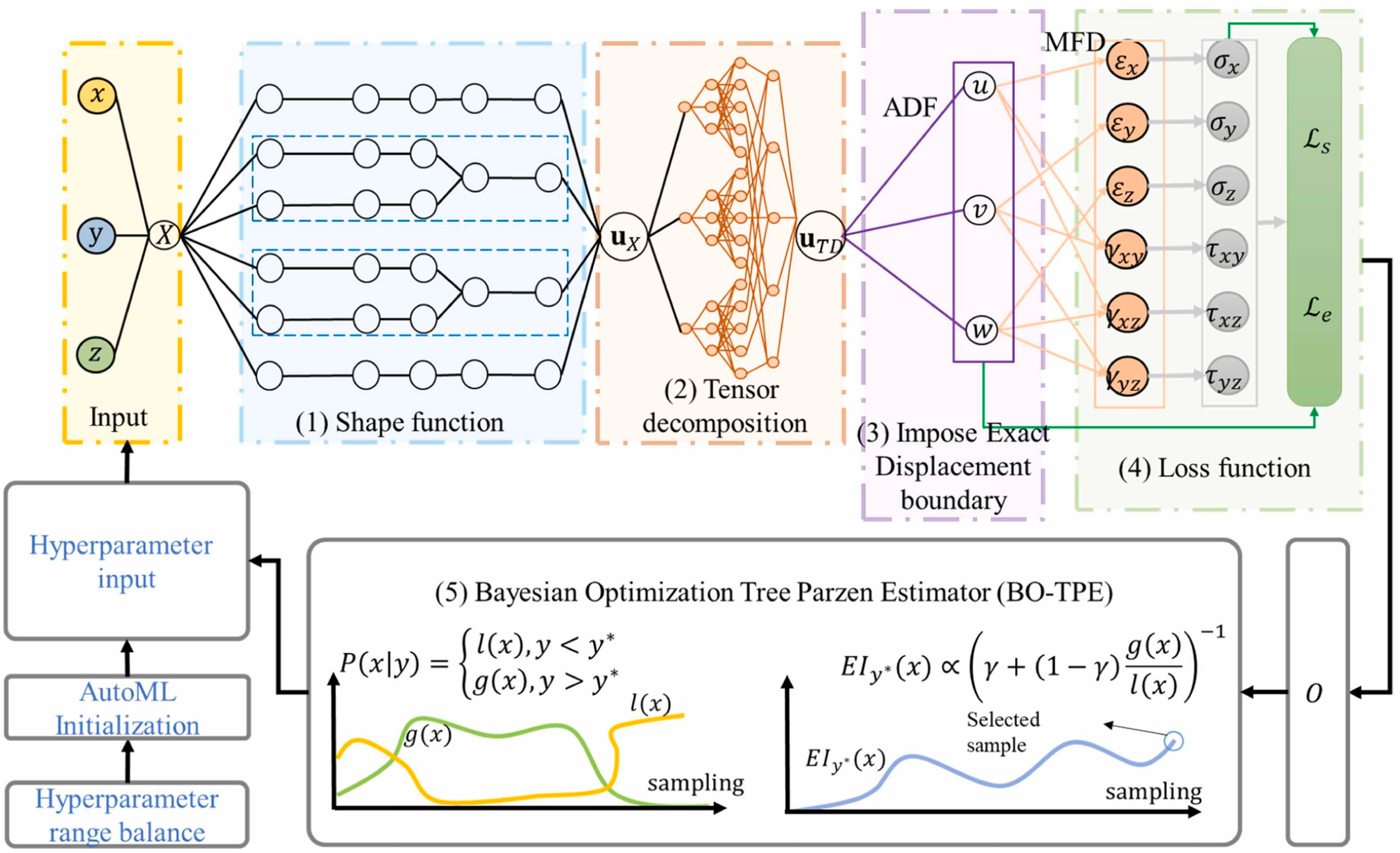


| Architecture Type | Core Concept | Advantages | Limitations |
|---|---|---|---|
| Basic MLP-PINN | Classical multilayer perceptron architecture; loss includes PDE residuals + initial and boundary conditions | Simplicity of implementation; versatility; no mesh required; automatic differentiation | Imbalance of loss function components (different scales of quantities); low convergence for complex PDE; sensitivity to hyperparameters |
| MLP-PINN with adaptive weight determination (lbPINN, SA-PINN, LA-PINN, etc.) | Weight coefficients in the loss functions are determined dynamically (minimax optimization, softmax, attention mechanisms, probabilistic models) | Automatic balancing of PDE/BC/IC; reduced risk of any single term dominating; improved convergence for nonlinear PDEs; effective for multiphysics problems | Increase in optimization complexity; need for additional parameters (attention models, masks); increased computational cost |
| MLP-PINN with domain decomposition (cPINN, XPINN, FBPINN, PDD, etc.) | Division of the area into subdomains; separate networks for each subdomain; additional matching conditions on interfaces | Parallelization of calculations; scalability for complex geometries and multiscale tasks; better accuracy | Choice of decomposition principles not always obvious; matching on interfaces complex; possible numerical instabilities |
| Variational/energy PINN (VPINN, E-PINN, etc.) | Use of weak form PDE (Petrov–Galerkin) or minimization of energy functional instead of PDE residuals | Better interpretability; fewer hyperparameters; more stable optimization; efficiency for multiphysics problems | Need for numerical integration (quadrature rules); dependence of accuracy on test space; possibility of null spaces |
| Variational/energy PINN with domain decomposition (hp-VPINN, E-PINN with local integrals, etc.) | Decomposition of the area into subdomains with local test functions or local energy integrals | Fewer correlated gradients; more stable training; effective parallel implementation; high accuracy for complex PDE | Increased implementation complexity; need for correct subdomain localization; additional costs for integration |
| Material | Property | Typical Uncertainty (COV, %) | Standard |
|---|---|---|---|
| Steel (structural) | Yield strength | ≈7–8% | ASTM A370-24. Standard Test Methods and Definitions for Mechanical Testing of Steel Products [77] |
| Composites (fiber-reinforced polymers) | Tensile strength along fibers | ≈10–20% | ASTM D3039/D3039M-14. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials [78] |
| Concrete | Compressive strength | ≈15–25% | ASTM C39/C39M-21. Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens [79] |
| Architecture Type | Suitability for Multiphysics | Advantages |
|---|---|---|
| Basic MLP-PINN |  Limited Limited | Simplicity; quick start for simple PDEs |
| MLP-PINN with adaptive weight determination (lbPINN, SA-PINN, LA-PINN, …) |  High High | Automatic balancing of losses of different physical nature; improved convergence; capability for nonlinear and coupled PDEs |
| MLP-PINN with domain decomposition (cPINN, XPINN, FBPINN, PDD, …) |  High High | Separate networks can be assigned for different physics in different regions; good scalability and parallelism |
| Variational/energy PINN (VPINN, E-PINN, …) |  Very high Very high | A single energy functional naturally integrates different physics; physically consistent formulation |
| Variational/energy PINN with domain decomposition (hp-VPINN, E-PINN) |   Highest Highest | Combine the physical interpretability of energy-based loss with local adaptation; work well in strongly coupled systems |
| Criterion | SDF | Phi-Function |
|---|---|---|
| Meaning | Distance from point to boundary (with positive/negative sign). | Continuous function of mutual position of two bodies (intersection, tangency, separation). |
| Ease of Geometry Specification | Suitable for single objects or smooth boundaries. | Ideal for multi-object systems and complex combinations (intersections, unions). |
| Local Geometry | Provides surface normal via gradient (∇SDF). | Normals not directly extracted; boundary defined implicitly via Φ = 0. |
| Smoothness | Smooth and well-differentiable with proper approximation. | Piecewise smooth function. Contains operations (min-max), less suitable for backpropagation. |
| Applicability in PINNs | Excellent for boundary conditions (Dirichlet/Neumann). | Better for global geometric constraints (non-intersection, object placement). |
| Interpretation | Metric: “distance to boundary.” | Phi-function: “degree of intersection/ separation”. Normalized phi-function: Euclidean distance between objects. |
| Flexibility for Complex Domains | Requires specialized methods (e.g., CSG with SDF, implicit surfaces). | Naturally describes combinations and relative objects positions. |
| Computational Properties | Direct approximation, good training stability. | More complex computations, potential gradient instability. |
| Method | Key Idea/Essence | Advantages | Disadvantages |
|---|---|---|---|
| PIP algorithms (Ray Casting, Winding Number, mesh-based) | Use predicate functions to test whether a point belongs to the domain/boundary | Simplicity; basic point-membership checks; integrates with sampling | Do not provide smooth information; limited use inside loss functions; ignore curvature |
| Analytical SDF from geometric primitives | Build complex shapes by combining simple analytic SDFs (min/max) | Simple implementation; high accuracy; low computational cos | Limited to primitives with analytic SDF; non-smoothness at switching surfaces (min/max) |
| SDF from triangular meshes (STL-based) | Distance computed from CAD mesh facets; sign from (pseudo)normals | CAD/CAE compatibility; high accuracy; library support (Open3D, libigl) | High computational cost; challenging for very large/fine meshes |
| SDF via Eikonal (Fast Marching, Fast Sweeping) | Numerical solution of with φ = 0 on | Smooth fields without gradient blow-up | Limited to polygon/polyhedron-type domains |
| Neural SDF approaches (DeepSDF, SAL, Neural-Pull) | Train a neural network to approximate a continuous SDF from point samples/unsigned data | Highest flexibility; handles complex shapes; smooth differentiable fields; fast inference after training | High training cost; large datasets needed; potential overfitting |
| R-functions | Construct implicit geometry via algebraic functions with logical-algebra properties | Universality; analyticity; can form solution structures respecting boundary conditions | Mathematical complexity; limited CAD/CAE integration at present |
| Phi-functions | Continuous functions encoding the mutual position of two bodies (intersection, tangency, separation); usable as penalties in loss or as analytical building blocks for hard-constraint trial forms | Natural for multi-object configurations and optimization/packing; enforce non-overlap and placement constraints; pair well with SDF in hybrid schemes | No local metric (normals) like SDF; piecewise-smooth due to min/max → can hinder backpropagation; requires smoothing (e.g., R-operators/soft-min) |
| Transfinite Barycentric Coordinates (TFC) | Mean-value/harmonic-coordinate–based analytic fields; domain defined as an analytical combination of local primitives; smooth everywhere | Analytically smooth (reduces gradient-explosion risk) | Applicable only to polygon/polyhedron-type domains; expensive for complex STL with many faces |
| Method of Collocation Point Generation | Disadvantages | Accuracy and Convergence | Integration with CAD/CAE |
|---|---|---|---|
| Non-adaptive methods (uniform grid, random sampling, Latin hypercube, etc.) | Inefficient for complex geometries, may require many points, limited adaptivity, risks of incomplete coverage of gradient zones | Average, stable, but slow convergence | High for grids, average for others (use of bounding box or CAD meshes) |
| Based on PDE residuals (residual-based, including DAS-PINNs) | Risk of overfitting, noisiness in early stages | High | High (integration with CAE for dynamic reconstruction) |
| Causality-guided (for unsteady problems) | More complex implementation, dependence on hyperparameters | High for dynamic systems | High (compatible with CAE for time simulations) |
| Based on PDE residual gradient | High differentiation cost, gradient noisiness, risk of local overfitting, loss of global coverage | High, better for fixed quantity | Average (can integrate with CAD for anisotropic strategies) |
| Based on loss-function residuals or energy functionals | Less common, depends on loss structure | High for multiphysics problems | High (integration with energy-based CAE methods) |
| Using SDF or R-functions (rejection sampling, projection methods, hard constraints) | Costs for computing SDF/R-functions, rejection, limitations for non-analytical forms | High, identical satisfaction of BCs for R-functions | High (integration with CAD/CAE for implicit geometry and BCs) |
| Method of Boundary Condition Integration | Key Idea | Advantages | Integration with CAD/CAE |
|---|---|---|---|
| Soft-constraint PINN | Boundary conditions are added to the loss function as penalty terms | Simplicity of implementation; universality | Low (no direct link to CAD geometries) |
| Hard-constraint PINN | Solution represented as a sum: one part exactly satisfies boundary conditions, the other is approximated by NN | Guaranteed enforcement of Dirichlet conditions; improved accuracy | Medium (CAD analytics can be integrated for simple geometries) |
| HC-PINN with SDF/ADF | Use of signed/approximate distance functions to enforce conditions on arbitrary geometries | Applicability to complex domains; guaranteed enforcement of Dirichlet, Neumann, and Robin conditions | High (SDF can be generated from STL/CAD meshes) |
| Domain Decomposition Methods (FBPINN-HC, PINN-FEM) | Decomposition into overlapping subdomains, with interface conditions enforced | Scalability, combining strengths of FEM and PINN | High (CAD → mesh → easy integration with PINN) |
| Hard-constraint with R-functions | Construction of solution structures that analytically satisfy various boundary conditions | Universality; suitability for complex and combined conditions | Highest (provided R-function construction is automated with CAD data) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plankovskyy, S.; Tsegelnyk, Y.; Shyshko, N.; Litvinchev, I.; Romanova, T.; Velarde Cantú, J.M. Review of Physics-Informed Neural Networks: Challenges in Loss Function Design and Geometric Integration. Mathematics 2025, 13, 3289. https://doi.org/10.3390/math13203289
Plankovskyy S, Tsegelnyk Y, Shyshko N, Litvinchev I, Romanova T, Velarde Cantú JM. Review of Physics-Informed Neural Networks: Challenges in Loss Function Design and Geometric Integration. Mathematics. 2025; 13(20):3289. https://doi.org/10.3390/math13203289
Chicago/Turabian StylePlankovskyy, Sergiy, Yevgen Tsegelnyk, Nataliia Shyshko, Igor Litvinchev, Tetyana Romanova, and José Manuel Velarde Cantú. 2025. "Review of Physics-Informed Neural Networks: Challenges in Loss Function Design and Geometric Integration" Mathematics 13, no. 20: 3289. https://doi.org/10.3390/math13203289
APA StylePlankovskyy, S., Tsegelnyk, Y., Shyshko, N., Litvinchev, I., Romanova, T., & Velarde Cantú, J. M. (2025). Review of Physics-Informed Neural Networks: Challenges in Loss Function Design and Geometric Integration. Mathematics, 13(20), 3289. https://doi.org/10.3390/math13203289








