An Analytical Solution to the 1D Drainage Problem

Abstract

We derive an analytical solution to the one-dimensional linearized Boussinesq equation with mixed boundary conditions (Dirichlet–Neumann), formulated to describe drainage in porous media. The solution is obtained via the unified transform method (Fokas method), extending its previous applications in infiltration problems and illustrating its utility in soil hydrology. An explicit integral representation is constructed, considering different types of initial conditions. Numerical examples are presented to demonstrate the accuracy of the solution, with direct comparisons to the classical Fourier series approach.

1. Introduction

Drainage is the redistribution or removal of water that is already in the soil profile, usually after saturation. Water is frequently moving downward through a saturated or nearly saturated zone by gravity but it experiences variations in hydraulic head, conductivity, and moisture content. The application and interpretation of the common mathematical models in practice are influenced by these variations in boundary conditions and initial moisture states. In a one-dimensional context, drainage is the vertical flow of water through soil, mostly due to gravity, after the soil has saturated or after a wetting event like irrigation or rainfall. This process is essential for controlling plant-available water, groundwater recharge, and soil moisture [1].

The mathematical modeling of soil drainage fundamentally relies on Boussinesq equation [2], which governs variably saturated water flow in porous media and provides a unified framework for describing drainage. Theoretically, the connection between heat conduction and water flow, as outlined in Carslaw and Jaeger’s classic work [3], have provided the mathematical basis for many solution techniques applied to drainage modeling.

Analytical works exist mainly for the linearized Boussinesq equation, such as [4,5,6,7], where exact or approximate solutions were derived for specific drainage scenarios, offering insights into water movement under varying conditions. On the other hand, numerical solutions based on the finite difference method exist for both the linear and non-linear case, see, e.g., [8,9,10,11]. Together, these studies demonstrate that a combination of analytical solutions, scaling approaches, and numerical methods form the fundamentals of mathematical modeling for soil drainage processes.

Mathematical formulations of infiltration and drainage processes share fundamental similarities, and Richards’ equation [12] is widely used to model both of them. Using the Fokas method [13], the authors derived an analytical solution of the linearized Richards’ equation for various infiltration scenarios in a bounded soil profile [14,15]. Although the physical environments in which these mechanisms occur differ significantly, in their linearized and simplified form, the solution for one process can also be applied to describe the other.

The potential of extending this work to more physically relevant problems, involving nonlinear and inverse problems, is clear: First, the Fokas method, introduced as the unified transform (UT) [13,16,17], initially targeted initial-boundary value problems (IBVPs) for integrable nonlinear partial differential equations (PDEs). This development provided the foundation for a natural extension of the powerful Inverse Scattering Transform (IST) [18], originally introduced for initial value problems (IVPs) associated with integrable PDEs. Second, the UT has also been systematically developed for linear PDEs, with a rigorous framework established in [19], where the method was shown to yield explicit and unified integral representations of the solution. It is precisely this linear theory that underpins the present work. Third, the integral representations obtained for linear PDEs have also played a key role in revisiting the theory of IBVPs for nonlinear PDEs. In particular, they have been used to establish well-posedness results by rigorously proving the existence and uniqueness of solutions; see, for instance, [20,21,22,23]. Fourth, the Fokas method has also inspired new approaches in inverse problems. These include, on one hand, applications to control theory, where boundary controllability and stabilization problems have been analyzed [24,25,26], and on the other hand, parameter identification problems in applied settings, such as soil and groundwater characterization [15,27], as well as recent contributions to inverse problems for the wave equation [28].

The scope of this work is to present an analytical solution to the one-dimensional linearized Boussinesq equation, a diffusion-type formulation, within a bounded domain representing the drain axis. The analysis is carried out under a range of initial conditions, including both constant and polynomial forms, and incorporates mixed Dirichlet–Neumann boundary conditions. The solution can be derived easily from the formulation obtained for the Richards’ equation under Robin–Robin boundary conditions, as shown in [14]. To test its validity and performance, we compare our solution with the classical Fourier series solution constructed through the method of separation of variables [3].

The structure of the paper is as follows: In Section 2 we present the mathematical model and the necessary equations and initial/boundary conditions. The assumptions resulting in a diffusion-type PDE are discussed. The form of the analytical solution is given in Section 3. Simplifications under different initial conditions are also presented. In Section 4 numerical examples are addressed, and the analytical solution is compared with well-known series solutions.

2. A Physical Problem Formulation

Subsurface unconfined flow in a homogeneous bounded medium is modelled through the Boussinesq equation [2]

$$S{\displaystyle \frac{\partial h}{\partial t}}-K{\displaystyle \frac{\partial }{\partial x}}\left(h{\displaystyle \frac{\partial h}{\partial x}}\right)=0,\mathrm{f}\mathrm{o}\mathrm{r}0<x<L,t>0,$$

(1)

where h is the height of the water table from the impermeable lower boundary, x the horizontal spatial coordinate, S a storage coefficient (specific yield), and K the saturated hydraulic conductivity.

Equation (1) is considered together with the initial condition

$$h(x,0)=f_0\left(x\right),0<x<L,$$

(2)

and the boundary conditions

$$\begin{array}{ccc}\hfill h(0,t)& =g\left(t\right),\hfill & \hfill t>0,\\ \hfill {\displaystyle \frac{\partial h}{\partial x}}(L,t)& =0,\hfill & \hfill t>0,\end{array}$$

(3)

where $f_0$ is a known initial function and g the given height of the stream surface at $x=0.$

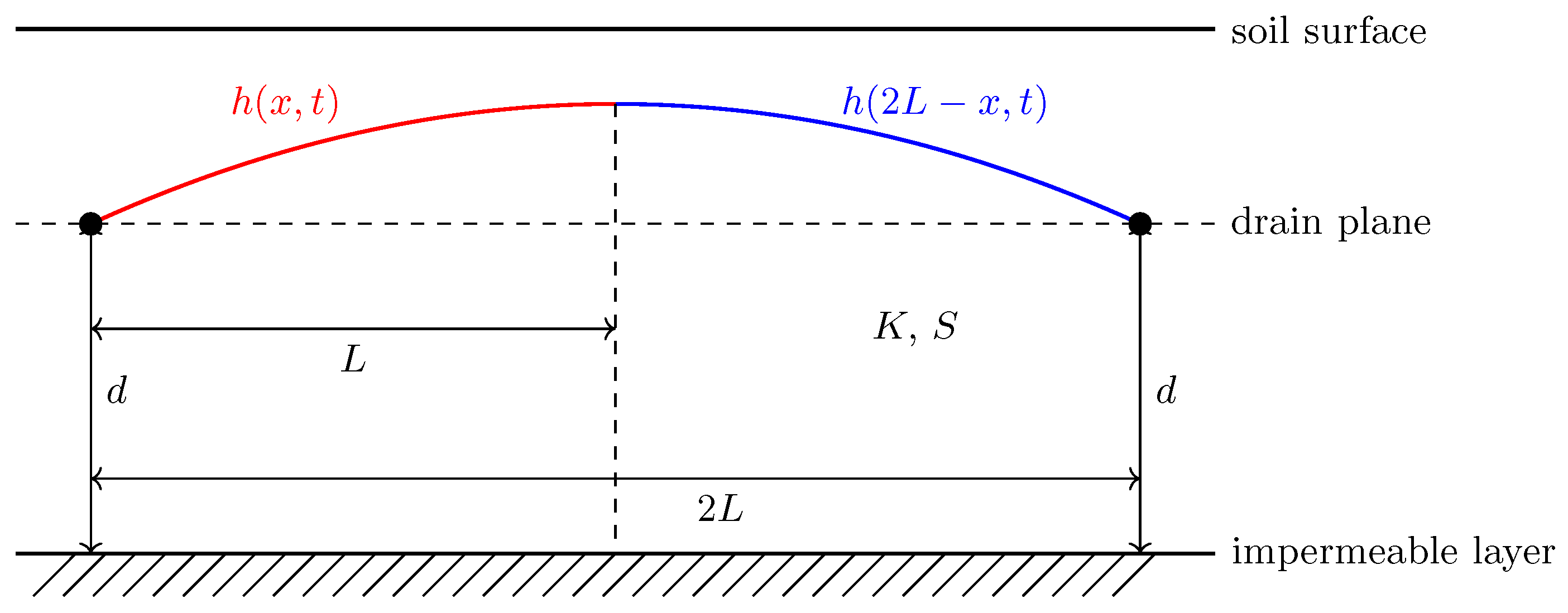
In practice, this model originates from considering a symmetric domain such that $h(0,t)=h(2L,t)=g\left(t\right)$ with the requirement of even solutions with respect to x around $x=L$, which leads to ${\displaystyle \frac{\partial h}{\partial x}}(L,t)=0$. The solution of the “full” problem is then given by

$$H(x,t)=\left\{\begin{array}{cc}h(x,t),\hfill & x\in [0,L],t\ge 0,\hfill \\ h(2L-x,t),\hfill & x\in [L,2L],t\ge 0.\hfill \end{array}\right.$$

(4)

Furthermore, the physically relevant solutions are increasing in $x\in (0,L)$, namely ${\displaystyle \frac{\partial h}{\partial x}}(x,t)\ge 0,x\in (0,L)$ and decreasing with respect to time $t>0.$ In Figure 1 we present the geometry of the problem and the corresponding solutions.

By expanding the spatial operator, we rewrite (1) in the form

$${\displaystyle \frac{{\partial }^{2}h}{\partial x^2}}={\displaystyle \frac{S}{Kh}}{\displaystyle \frac{\partial h}{\partial t}}-{\displaystyle \frac{1}{h}}{\left({\displaystyle \frac{\partial h}{\partial x}}\right)}^2,$$

(5)

where we place the non-linear terms on the right-hand side. For this non-linear PDE there is no clear association to a linear heat-type PDE. However, in the soil physics literature [29,30] there exist physical approximations which make this simplification possible.

The last term in the right-hand side of (5) becomes significant only when the slope of the water table is large. Assuming small slopes, it becomes negligible. In addition, the assumption of small water table fluctuations around an average depth, replaces h in the denominator with its mean value (i.e., the constant $\overline{h}$) resulting in the heat equation

$${\displaystyle \frac{\partial h}{\partial t}}-D{\displaystyle \frac{{\partial }^{2}h}{\partial x^2}}=0,$$

(6)

where $D={\displaystyle \frac{K\overline{h}}{S}}$ is an effective diffusivity.

We summarize the initial boundary value problem (IBVP) modelling the 1D drainage problem:

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial h}{\partial t}}& =D{\displaystyle \frac{{\partial }^{2}h}{\partial x^2}},\hfill & & 0<x<L,t>0,\hfill \end{array}$$

(7a)

$$\begin{array}{cccc}\hfill h(x,0)& =f_0\left(x\right),\hfill & & 0<x<L,\hfill \end{array}$$

(7b)

$$\begin{array}{cccc}\hfill h(0,t)& =g\left(t\right),\hfill & & t>0,\hfill \end{array}$$

(7c)

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial h}{\partial x}}(L,t)& =0,\hfill & & t>0.\hfill \end{array}$$

(7d)

As shown in Figure 1, the drain plane is placed at a certain height $\left(d\right)$ above the impenetrable layer, resulting in the conditions $f_0\left(x\right)=d+{\phi }_0\left(x\right)$ and $g\left(t\right)=d,$ for a constant $d>0.$ We define

$$u(x,t)=h(x,t)-d,$$

(8)

which satisfies

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial u}{\partial t}}& =D{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}},\hfill & & 0<x<L,t>0,\hfill \end{array}$$

(9a)

$$\begin{array}{cccc}\hfill u(x,0)& ={\phi }_0\left(x\right),\hfill & & 0<x<L,\hfill \end{array}$$

(9b)

$$\begin{array}{cccc}\hfill u(0,t)& =0,\hfill & & t>0,\hfill \end{array}$$

(9c)

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial u}{\partial x}}(L,t)& =0,\hfill & & t>0.\hfill \end{array}$$

(9d)

The first step is to obtain an analytical solution of (9a)–(9d) and then compare it with numerical results.

3. Analytical Solution of the IBVP (9a)–(9d)

In [15], the authors considering the problem of vertical infiltration and derived the solution of the IBVP

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial \theta }{\partial t}}+K_0{\displaystyle \frac{\partial \theta }{\partial x}}& =D_0{\displaystyle \frac{{\partial }^2\theta }{\partial x^2}},\hfill & & 0<x<L,t>0,\hfill \end{array}$$

(10a)

$$\begin{array}{cccc}\hfill \theta (x,0)& ={\theta }_0\left(x\right),\hfill & & 0<x<L,\hfill \end{array}$$

(10b)

$$\begin{array}{cccc}\hfill \theta (0,t)-a{\displaystyle \frac{\partial \theta }{\partial x}}(0,t)& =f\left(t\right),\hfill & & t>0,\hfill \end{array}$$

(10c)

$$\begin{array}{cccc}\hfill \theta (L,t)-\beta {\displaystyle \frac{\partial \theta }{\partial x}}(L,t)& =g\left(t\right),\hfill & & t>0.\hfill \end{array}$$

(10d)

Comparing (10a)–(10d) with (9a)–(9d), we observe that the linearized Richards Equation (10a) reduces to the heat Equation (9a), while the Robin boundary conditions (10c) and (10d) simplify to Dirichlet and Neumann conditions, respectively. Thus, the first three equations of (10a)–(10d) reduce to the first three equations of (9a)–(9d) by setting $K_0=0,D_0=D,a=0,$ and $f\left(t\right)=0$. Then, set $g\left(t\right)=-\beta g_N\left(t\right),$ and write (10d) as

$${\displaystyle \frac{1}{\beta }}\theta (L,t)-{\displaystyle \frac{\partial \theta }{\partial x}}(L,t)=-{\displaystyle \frac{1}{\beta }}\beta g_N\left(t\right)=-g_N\left(t\right),$$

since the limiting case $\beta \to \infty$, along with $g_N\equiv 0$, yields (9d).

Employing this terminology (for general $\beta$ and $g_N$), we get (see [15], Equation (16))

$$\begin{array}{cc}\hfill u_{\beta }(x,t)& ={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}{e}^{i\lambda x-D{\lambda }^{2}t}{\widehat{\phi }}_0\left(\lambda \right)d\lambda -{\displaystyle \frac{i}{\pi }}{\int }_{C_{+}}{\displaystyle \frac{e^{-D{\lambda }^{2}t}}{{\mathsf{\Delta }}_{\beta }\left(\lambda \right)}}\left[-sin\left(\lambda x\right)\left({\displaystyle \frac{1}{\beta }}-i\lambda \right)e^{i\lambda L}{\widehat{\phi }}_0\left(\lambda \right)\right.\hfill \\ \hfill & \left.\phantom{=}+\left({\displaystyle \frac{1}{\beta }}sin\left(\lambda (x-L)\right)+\lambda cos\left(\lambda (x-L)\right)\right){\widehat{\phi }}_0(-\lambda )+2i\lambda Dsin\left(\lambda x\right){\tilde{g}}_N(\alpha {\lambda }^2,t)\right]d\lambda ,\hfill \end{array}$$

(11)

where

$${\mathsf{\Delta }}_{\beta }\left(\lambda \right)=e^{-i\lambda L}\left({\displaystyle \frac{1}{\beta }}+i\lambda \right)-e^{i\lambda L}\left({\displaystyle \frac{1}{\beta }}-i\lambda \right).$$

Thus ${\displaystyle u(x,t)=\underset{\beta \to \infty }{lim}{u}_{\beta }(x,t)}$ and for ${\tilde{g}}_N=0$ we derive

$$\begin{array}{cc}\hfill u(x,t)& ={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}{e}^{i\lambda x-D{\lambda }^{2}t}{\widehat{\phi }}_0\left(\lambda \right)d\lambda \hfill \\ \hfill & \phantom{=}-{\displaystyle \frac{1}{2\pi }}{\int }_{C_{+}}{\displaystyle \frac{e^{-D{\lambda }^{2}t}}{cos\left(\lambda L\right)}}\left[isin\left(\lambda x\right)e^{i\lambda L}{\widehat{\phi }}_0\left(\lambda \right)+cos\left(\lambda (x-L)\right){\widehat{\phi }}_0(-\lambda )\right]d\lambda ,\hfill \end{array}$$

(12)

where we have used the simplification ${\mathsf{\Delta }}_{\infty }\left(\lambda \right)=2i\lambda cos\left(\lambda L\right)$.

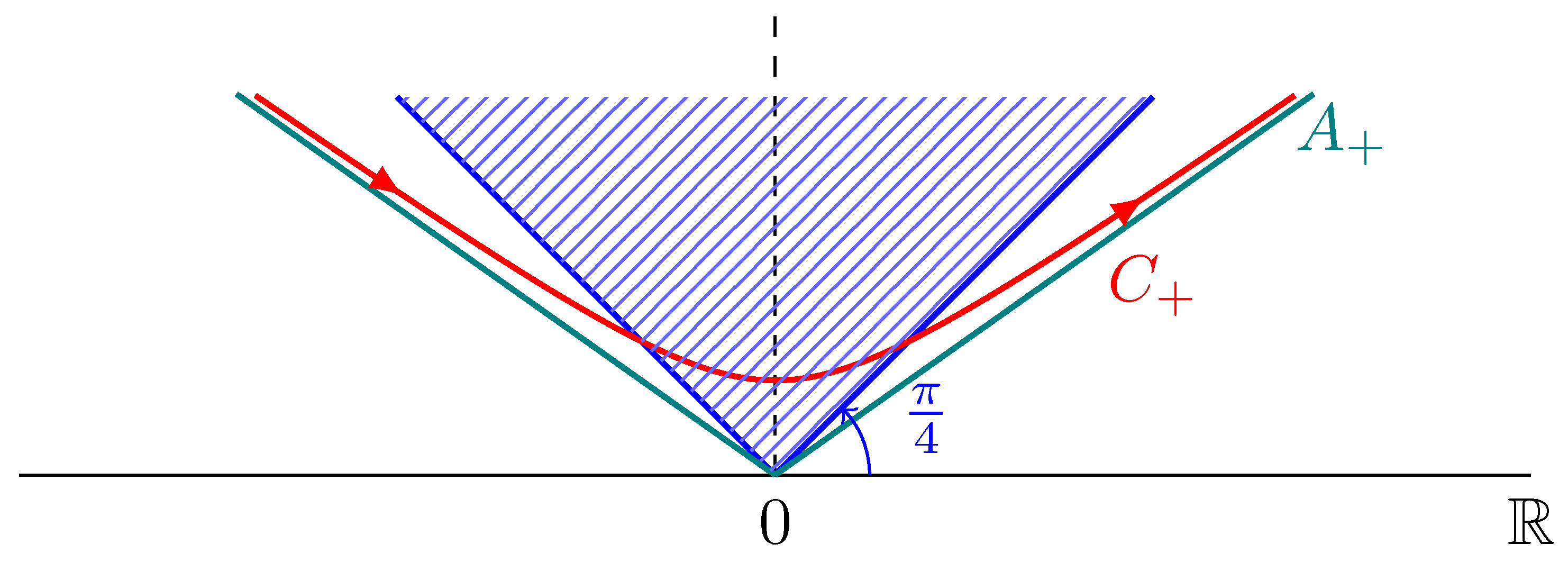
Remark 1.

The curve of integration, $C_{+}$, can be chosen to be any simply connected open (and infinite) curve of the upper half plane with two (linear) asymptotes that are defined by $A_{+}=\left\{\lambda \in \mathbb{C}:Im\left(\lambda \right)=c_{1,2}Re\left(\lambda \right),c_1\in [-1,0],c_2\in [0,1],Im\left(\lambda \right)\ge 0\right\}$; for an example, see Figure 2. This is useful if one would wish to avoid the computation of any pole contribution occurring in the process described in the remaining part of this section.

Equation (12) constitutes the integral representation of the solution of (9a)–(9d) that depends on the initial shape of the water table (${\phi }_0$). In what follows, we specify the initial condition and we derive simplified forms of the solution.

3.1. Quadratic Function

Let

$${\phi }_0\left(x\right)=h_0\left({\displaystyle \frac{2x}{L}}-{\displaystyle \frac{x^2}{L^2}}\right),$$

(13)

so that the boundary conditions (9c) and (9d) are satisfied. Then,

$$\begin{array}{cc}\hfill {\widehat{\phi }}_0\left(\lambda \right)& ={\int }_0^L{e}^{-i\lambda x}{\varphi }_0\left(x\right)dx=h_0{\int }_0^L{e}^{-i\lambda x}\left({\displaystyle \frac{2x}{L}}-{\displaystyle \frac{x^2}{c^2}}\right)dx\hfill \\ \hfill & =h_0{\displaystyle \frac{-2(i+\lambda L)+i{e}^{-i\lambda L}\left(2+{\lambda }^2{L}^2\right)}{{\lambda }^3{L}^2}}.\hfill \end{array}$$

(14)

The first integral in the right-hand side of (12) admits the decomposition

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}{e}^{i\lambda x-D{\lambda }^{2}t}{\widehat{\phi }}_0\left(\lambda \right)d\lambda & =-{\displaystyle \frac{h_0}{2\pi }}{\int }_{C_{+}}{e}^{i\lambda x-D{\lambda }^{2}t}{\displaystyle \frac{2(i+\lambda L)}{{\lambda }^3{L}^2}}d\lambda \hfill \\ \hfill & \phantom{=}-{\displaystyle \frac{h_0}{2\pi }}{\int }_{C_{-}}{e}^{-i\lambda (L-x)-D{\lambda }^{2}t}{\displaystyle \frac{i\left(2+{\lambda }^2{L}^2\right)}{{\lambda }^3{L}^2}}d\lambda \hfill \\ \hfill & \phantom{=}-{\displaystyle \frac{h_0}{2\pi }}2\pi i{Res}_{\lambda =0}\left\{e^{-i\lambda (L-x)-D{\lambda }^{2}t}{\displaystyle \frac{i\left(2+{\lambda }^2{L}^2\right)}{{\lambda }^3{L}^2}}\right\}\hfill \\ \hfill & =-{\displaystyle \frac{h_0}{2\pi }}{\int }_{C_{+}}{\displaystyle \frac{e^{-D{\lambda }^{2}t}}{{\lambda }^3{L}^2}}\left[e^{i\lambda x}2(i+\lambda L)+e^{i\lambda (L-x)}i(2+{\lambda }^2{L}^2)\right]d\lambda \hfill \\ \hfill & \phantom{=}+{\displaystyle \frac{h_0(2Lx-2Dt-x^2)}{L^2}}.\hfill \end{array}$$

(15)

In view of Remark 1, the above integral, as well as the second integral in the right-hand side of Equation (12), can be directly computed by choosing the curve of integration to avoid the poles, which occur on the real line.

3.2. Constant Function

In this section, we assume that the free water table is parallel to the drain axis at a distance $h_0:$

$${\phi }_0\left(x\right)=h_0>0.$$

In this case, the solution (12) can be further simplified by defining

$$\tilde{u}(x,t)=u(x,t)-h_0,$$

(16)

that solves

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial \tilde{u}}{\partial t}}& =D{\displaystyle \frac{{\partial }^2\tilde{u}}{\partial x^2}},\hfill & & 0<x<L,t>0,\hfill \end{array}$$

(17a)

$$\begin{array}{cccc}\hfill \tilde{u}(x,0)& =0,\hfill & & 0<x<L,\hfill \end{array}$$

(17b)

$$\begin{array}{cccc}\hfill \tilde{u}(0,t)& =-h_0,\hfill & & t>0,\hfill \end{array}$$

(17c)

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial \tilde{u}}{\partial x}}(L,t)& =0,\hfill & & t>0.\hfill \end{array}$$

(17d)

In view of [15] (Equation (16)) and the simplifications discussed previously we obtain

$$\tilde{u}(x,t)=-{\displaystyle \frac{i}{\pi }}{\int }_{C_{+}}{\displaystyle \frac{e^{-D{\lambda }^{2}t}}{cos\left(\lambda L\right)}}D\lambda cos\left(\lambda (x-L)\right)\tilde{f}(D{\lambda }^2,t)d\lambda ,$$

(18)

where

$$\tilde{f}(D{\lambda }^2,t)=-h_0{\int }_0^t{e}^{D{\lambda }^2\tau }d\tau =h_0{\displaystyle \frac{1-e^{D{\lambda }^{2}t}}{D{\lambda }^2}}.$$

Then, from (8) and (16), we get

$$h(x,t)=d+h_0+i{\displaystyle \frac{h_0}{\pi }}{\int }_{C_{+}}{\displaystyle \frac{1-e^{-D{\lambda }^{2}t}}{\lambda cos\left(\lambda L\right)}}cos\left(\lambda (x-L)\right)d\lambda .$$

(19)

In view of Remark 1, the above integral can be further simplified to

$$h(x,t)=d+h_0-i{\displaystyle \frac{h_0}{\pi }}{\int }_{C_{+}}{\displaystyle \frac{e^{-D{\lambda }^{2}t}}{\lambda cos\left(\lambda L\right)}}cos\left(\lambda (x-L)\right)d\lambda .$$

(20)

4. Numerical Examples

In this section we compare the analytical solution given as an integral representation here, as opposed to the Fourier series solution, which was obtained by using separation of variables [3], for the two specific initial conditions. We note that this analysis employs a specific type of Fourier series, which incorporates the x-evenness of the solution in $x\in [0,2L]$.

Considering the numerical computation of our analytical solution, we recall that one needs to evaluate only one integral along the curve $C_{+}$, with properties of Remark 1; the integrand displays exponential decay (along $C_{+}$) for all $(x,t)$ including the boundaries of the domain. Hence, one only needs a parametrisation of the curve: $C_{+}=\left\{\left(r,c\left(r\right)=c_R\left(r\right)+i{c}_I\left(r\right)\right),r\in \mathcal{M}\subset \mathbb{R}\right\}$, which reads

$$\begin{array}{cc}\hfill u(x,t)& ={\int }_{C_{+}}V(\lambda ;x,t)d\lambda ={\int }_{\mathcal{M}}V(\lambda \left(r\right);x,t){\displaystyle \frac{d\lambda \left(r\right)}{dr}}dr\hfill \\ \hfill & ={\int }_{\mathcal{M}}W(r;x,t)dr={\int }_{\mathcal{M}}\mathrm{Re}\left\{W(r;x,t)\right\}dr,\hfill \end{array}$$

where the last equality comes from the natural fact that $\mathrm{Im}\left\{W\right(r;x,t\left)\right\}$, even if it is non-trivial, yields zero contribution to the real-valued solution, $u(x,t)$, of the physical problem (real IBVP). For example, $c\left(r\right)=bsinhr+iacoshr,b>a>0,$ and $\mathcal{M}\equiv \mathbb{R}$ parametrises a proper hyperbola $C_{+}$. The implementation here was straightforward, by using the command NIntegrate, with the default choice of Method; the exponential decay of the integrand reassures that this simple implementation is adequate.

Example 1.

The series solution of the IBVP (9a)–(9d) with initial condition given by (13) admits the form

$$h_N(x,t)=d+{\displaystyle \frac{32h_0}{{\pi }^3}}\sum _{n=1}^N{\displaystyle \frac{1}{{(2n-1)}^3}}sin\left({\displaystyle \frac{(2n-1)\pi x}{2L}}\right)e^{-{\left(\frac{(2n-1)\pi }{2L}\right)}^{2}Dt},N\in \mathbb{N}.$$

(21)

As discussed above, the term $2L$ appears in the formula because the solution is derived over the entire interval $[0,2L]$, but for comparison we plot it on $[0,L]$.

We set the soil parameters $K=0.25$ m/day and $S=0.05$ and the heights $h_0=1.5$ m and $d=5$ m. The mean value of h is usually approximated by $\overline{h}=d+\frac{h_0}{2}=5.75$ m.

We present the integral solution (12) and the series solution (21) with $N=10$ for $L=50$ m in Figure 3. We observe that the two solutions fit perfectly.

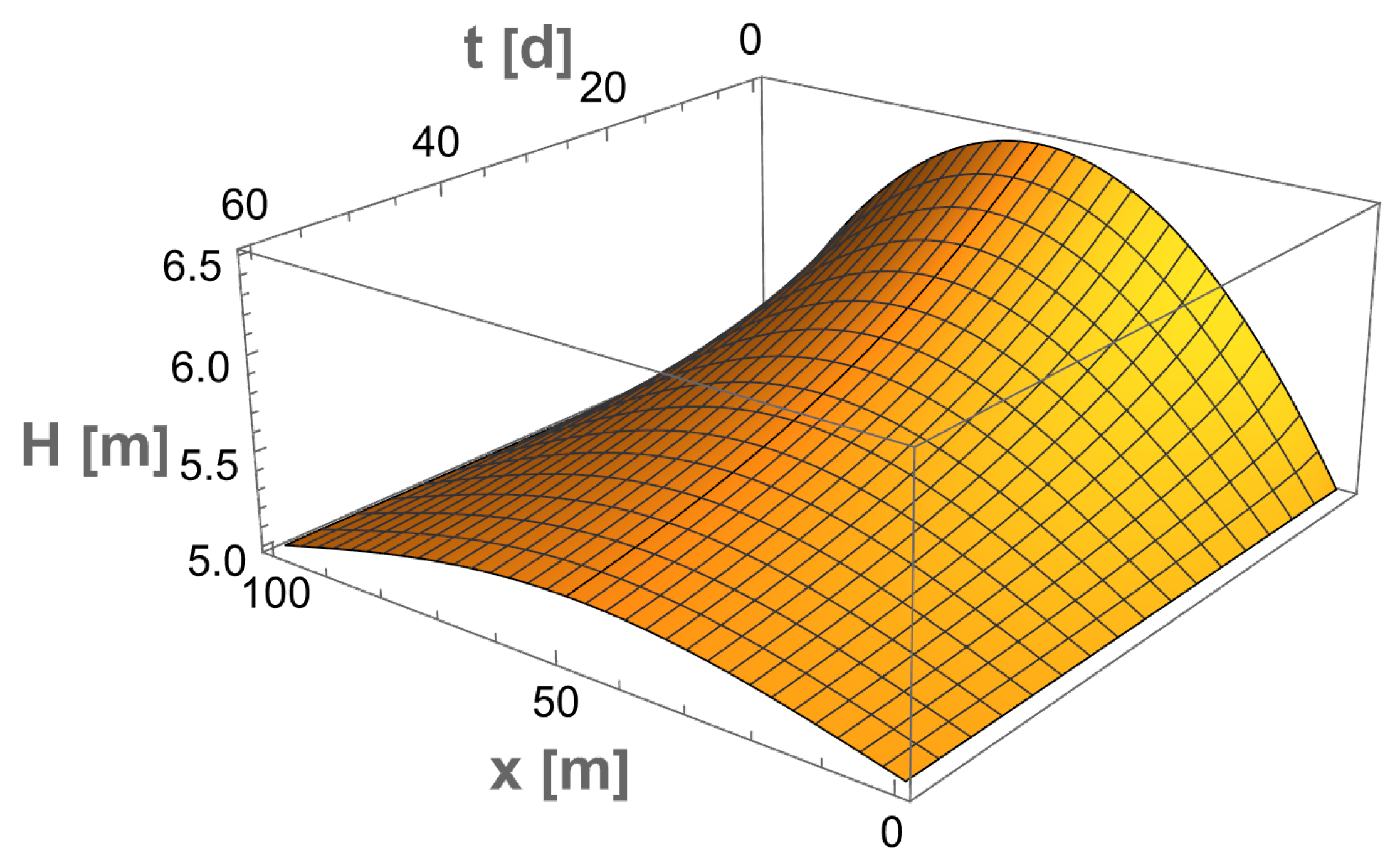
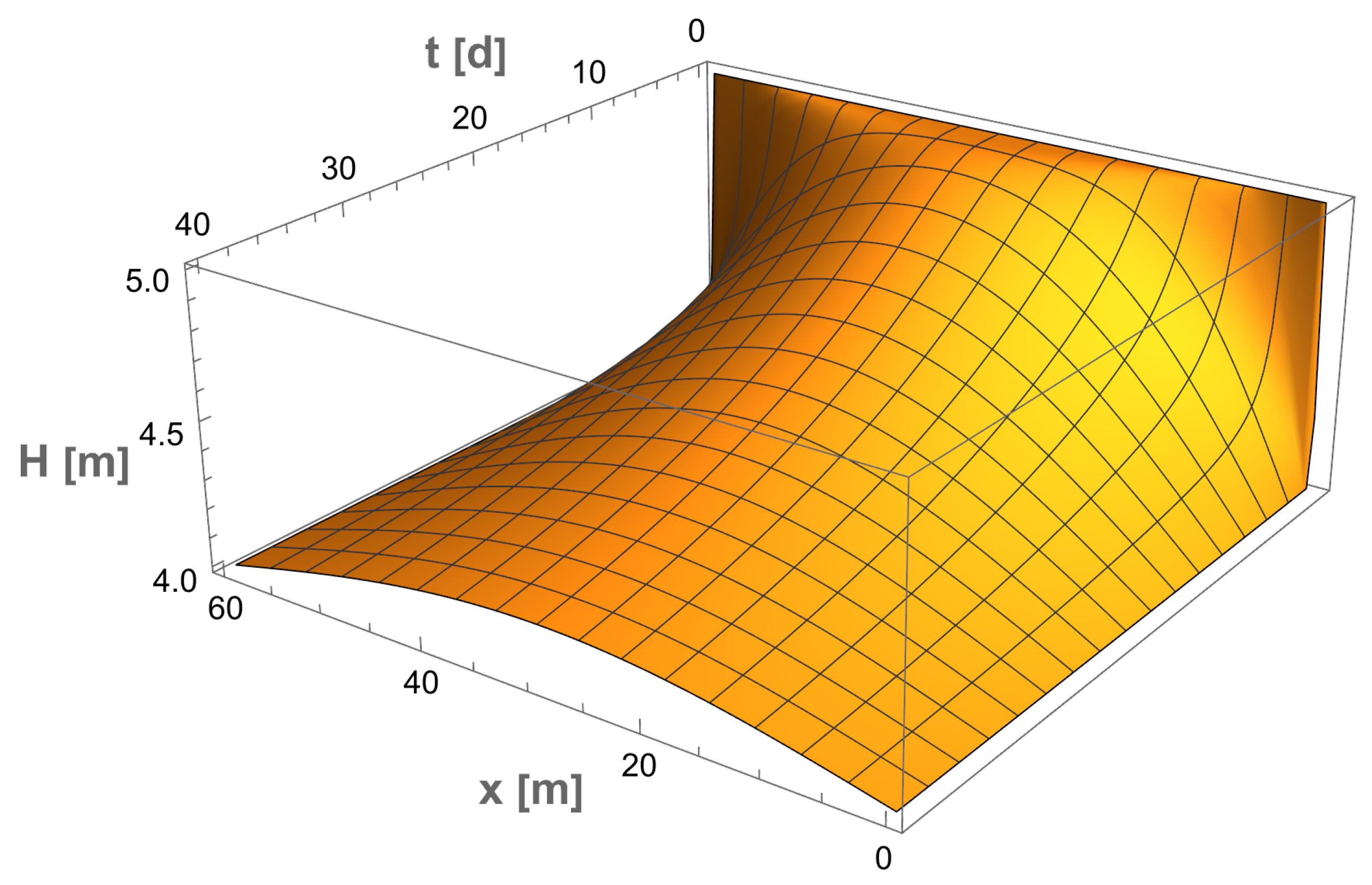
In Figure 4 we present the solution $H(x,t)$ given by (4) where $h(x,t)$ defined by (12) solves (9a)–(9d) with initial function the quadratic function (13) for $x\in [0,2L]$ and $t=[0,60]$ days. The expected physically meaningful behavior is clearly observed.

Example 2.

Using separation of variables, the solution for constant initial condition is given by

$$h_N(x,t)=d+{\displaystyle \frac{4h_0}{\pi }}\sum _{n=1}^N{\displaystyle \frac{1}{2n-1}}sin\left({\displaystyle \frac{(2n-1)\pi x}{2L}}\right)e^{-{\left(\frac{(2n-1)\pi }{2L}\right)}^{2}Dt},N\in \mathbb{N}.$$

(22)

We set the soil parameters $K=0.2$ m/day and $S=0.05$ and the heights $h_0=1$ m and $d=4$ m. The mean value of h is given by $\overline{h}=d+\frac{h_0}{2}=4.5$ m.

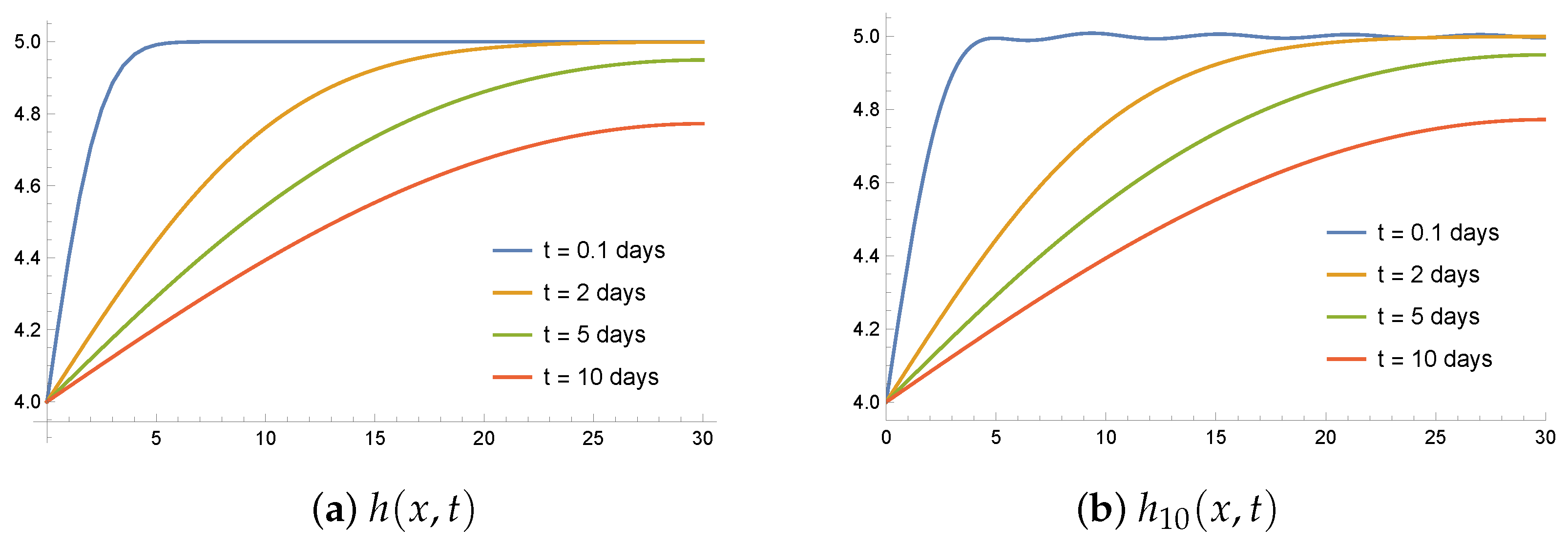
In Figure 5 we present the integral solution (19) and the series solution (22) with $N=10$ for $L=30$ m. We observe that more terms in the series are required to accurately capture the behavior at short times, whereas for larger times, the series and integral solutions match almost perfectly. This happens because the initial $u(x,0)=h_0>0$ and boundary $u(0,t)=0$ conditions are not compatible, resulting in a non-smooth solution at the boundary as $t\to 0.$

In Figure 6, the influence of short times and/or small values of x is evident in the series solution, whereas the integral solution does not exhibit such limitations. The reason for that is the uniform convergence of the solution to the initial and boundary conditions at $t=0$, and $x=0$ and L, respectively. This is also transparent if one tries to verify the initial condition, namely $h(x,0)=d+h_0$, from (19) and (22), respectively: In the former representation, substituting $t=0$ vanishes the integral and yields the desired result, whereas in the latter representation we obtain

$$h_{\infty }(x,0)=d+{\displaystyle \frac{4h_0}{\pi }}\sum _{n=1}^{\infty }{\displaystyle \frac{1}{2n-1}}sin\left({\displaystyle \frac{(2n-1)\pi x}{2L}}\right),$$

(23)

where the computation of the above series is needed for the desired result. The same observation is also true for the example with quadratic initial condition (13), $h(x,0)=d+{\phi }_0\left(x\right)$, when comparing (21) with (12) in view of (15). In the latter representation, for $t=0$ all the integrals vanish due to analyticity, whereas the former one involves the computation of a Fourier series, in analogy with (23).

The solution $H(x,t)$ (see (4)) with $h(x,t)$ given by (19) for $x\in [0,2L]$ m and $t=[0,40]$ days is plotted in Figure 7. As in the first example, the solution behaves as expected.