D-Finite Discrete Generating Series and Their Sections
Abstract
1. Introduction and Notation
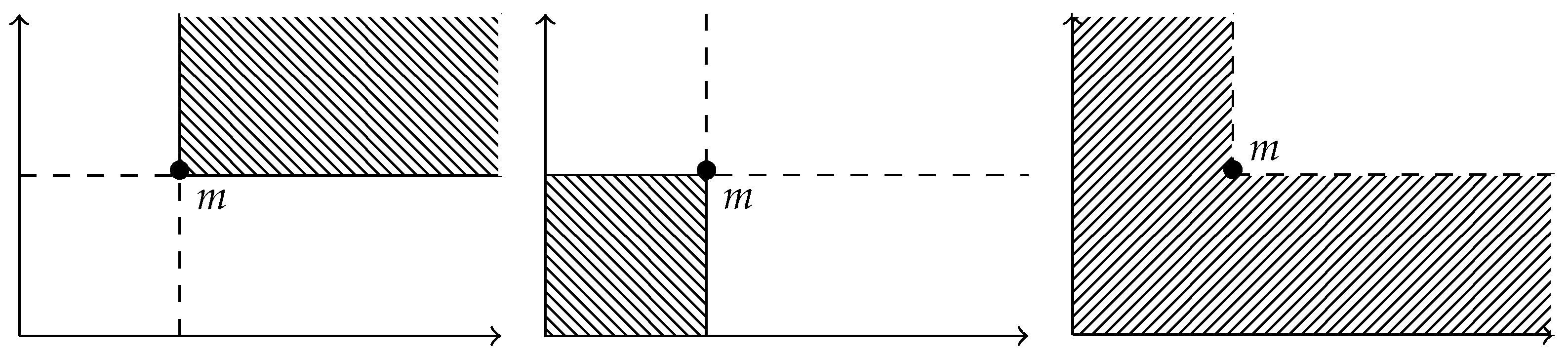
2. D-Finite Discrete Generating Functions
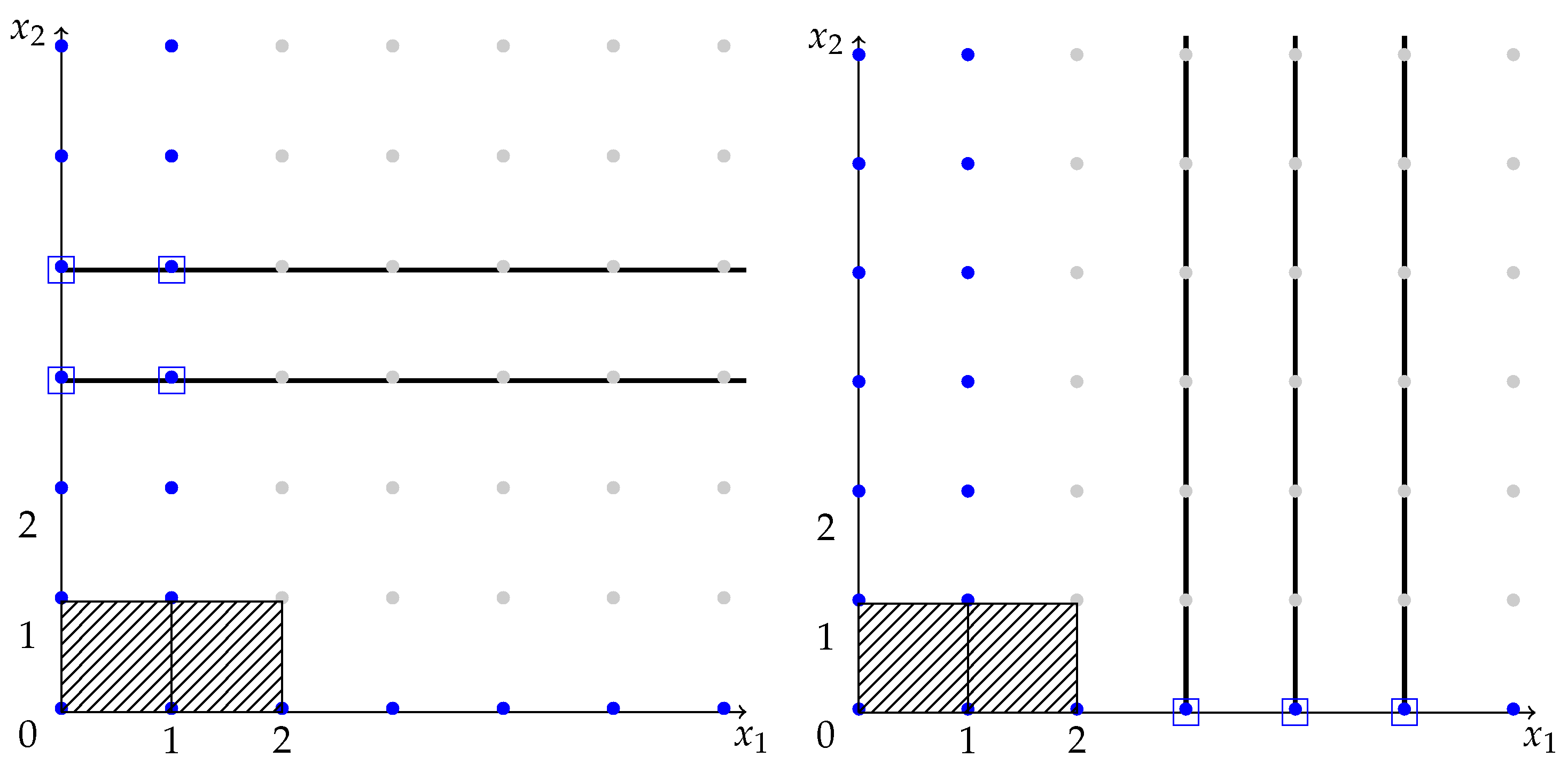
3. Sections of the Discrete Generating Bi-Variate Series
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stanley, R.P. Differentiably Finite Power Series. Eur. J. Comb. 1980, 1, 175–188. [Google Scholar] [CrossRef]
- Lipshitz, L. D-Finite Power Series. J. Algebra 1989, 122, 353–373. [Google Scholar] [CrossRef]
- Leinartas, E.; Yakovleva, T. The Cauchy Problem for Multidimensional Difference Equations and the Preservation of the Hierarchy of Generating Functions of Its Solutions. J. Sib. Fed. Univ. Math. Phys. 2018, 11, 712–722. [Google Scholar] [CrossRef]
- Akhtamova, S.S.; Alekseev, V.S.; Lyapin, A.P. Discrete Generating Functions. Math. Notes 2023, 114, 1087–1093. [Google Scholar] [CrossRef]
- Akhtamova, S.; Cuchta, T.; Lyapin, A. An Approach to Multidimensional Generating Series. Mathematics 2024, 12, 143. [Google Scholar] [CrossRef]
- Bohner, M.; Cuchta, T. The Generalized Hypergeometric Difference Equation. Demonstr. Math. 2018, 51, 62–75. [Google Scholar] [CrossRef]
- Bohner, M.; Cuchta, T. The Bessel Difference Equation. Proc. Am. Math. Soc. 2017, 145, 1567–1580. [Google Scholar] [CrossRef]
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales: An Introduction with Applications; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Riordan, J. Combinatorial Identities; John Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Bousquet-Mélou, M.; Petkovšek, M. Linear Recurrences with Constant Coefficients: The Multivariate Case. Discret. Math. 2000, 225, 51–75. [Google Scholar] [CrossRef]
- Trishin, P.V. Necessary and Sufficient Conditions for the Existence of Rational Solutions to Homogeneous Difference Equations with Constant Coefficients. Bull. Irkutsk State Univ. Ser. Math. 2024, 47, 47–62. [Google Scholar] [CrossRef]
- Apanovich, M.S.; Leinartas, E.K. Correctness of a Two-Dimensional Cauchy Problem for a Polynomial Difference Operator with Constant Coefficients. J. Sib. Fed. Univ. Math. Phys. 2017, 10, 199–205. [Google Scholar] [CrossRef]
- Chandragiri, S. Counting Lattice Paths by Using Difference Equations with Non-constant Coefficients. Bull. Irkutsk State Univ. Ser. Math. 2023, 44, 55–70. [Google Scholar] [CrossRef]
- Leinartas, E.K.; Passare, M.; Tsikh, A.K. Multidimensional Versions of Poincaré’s Theorem for Difference Equations. Sb. Math. 2008, 199, 1505–1521. [Google Scholar] [CrossRef]
- Krasikov, V.A. A Survey on Computational Aspects of Polynomial Amoebas. Math. Comput. Sci. 2023, 17, 16. [Google Scholar] [CrossRef]
- Leinartas, E.; Nekrasova, T. Constant Coefficient Linear Difference Equations on the Rational Cones of the Integer Lattice. Sib. Math. J. 2016, 57, 74–85. [Google Scholar] [CrossRef]
- Lyapin, A.; Akhtamova, S. Recurrence Relations for the Sections of the Generating Series of the Solution to the Multidimensional Difference Equation. Vestn. Udmurtsk. Univ. Mat. Mekh. Komp. Nauki 2021, 31, 414–423. [Google Scholar] [CrossRef]
- Lyapin, A.; Cuchta, T. Sections of the Generating Series of a Solution to the Multidimensional Difference Equation. Bull. Irkutsk State Univ. Ser. Math. 2022, 42, 75–89. [Google Scholar] [CrossRef]
- Luzón, A.; Morón, M.A. Recurrence Relations for Polynomial Sequences via Riordan Matrices. Linear Algebra Appl. 2010, 433, 1422–1446. [Google Scholar] [CrossRef][Green Version]
- Andrica, D.; Bagdasar, O. Some Remarks on the Coefficients of Cyclotomic Polynomials. In New Frontiers in Number Theory and Applications; Trends in Mathematics; Guàrdia, J., Minculete, N., Savin, D., Vela, M., Zekhnini, A., Eds.; Birkhäuser: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Kızılateş, C.; Polatlı, E.; Terzioğlu, N.; Du, W.-S. On Higher-Order Generalized Fibonacci Hybrid Numbers with q-Integer Components: New Properties, Recurrence Relations, and Matrix Representations. Symmetry 2025, 17, 584. [Google Scholar] [CrossRef]
- Kostić, M.; Koyuncuoğlu, H.C. Multi-Dimensional Almost Automorphic Type Sequences and Applications. Georgian Math. J. 2024, 31, 453–471. [Google Scholar] [CrossRef]
- Kostić, M. Almost Periodic Type Solutions to Integro-Differential-Difference Equations; De Gruyter: Berlin, Germany, 2025. [Google Scholar]
- Leinartas, E.K.; Shishkina, O.A. The Euler–Maclaurin Formula in the Problem of Summation over Lattice Points of a Simplex. J. Sib. Fed. Univ. Math. Phys. 2022, 15, 108–113. [Google Scholar] [CrossRef]
- Grigoriev, A.A.; Leinartas, E.K.; Lyapin, A.P. Summation of Functions and Polynomial Solutions to a Multidimensional Difference Equation. J. Sib. Fed. Univ. Math. Phys. 2023, 16, 153–161. [Google Scholar]
- Kruchinin, D.; Kruchinin, V.; Shablya, Y. On some properties of generalized Narayana numbers. Quaest. Math. 2021, 45, 1949–1963. [Google Scholar] [CrossRef]
- Shabiya, Y.; Kruchinin, V.; Kruchinin, D. Enumeration of Words Derived from Unambiguous Context-Free Grammars Based on Powers of Generating Functions. Proc. Jangjeon Math. Soc. 2025, 28, 299–317. [Google Scholar] [CrossRef]
- Abramov, S.A.; Barkatou, M.A.; van Hoeij, M.; Petkovsek, M. Subanalytic Solutions of Linear Difference Equations and Multidimensional Hypergeometric Sequences. J. Symb. Comput. 2011, 46, 1205–1228. [Google Scholar] [CrossRef]
- Abramov, S.A.; Barkatou, M.A.; Petkovšek, M. Linear Difference Operators with Coefficients in the Form of Infinite Sequences. Comput. Math. Math. Phys. 2021, 61, 1582–1589. [Google Scholar] [CrossRef]
- Abramov, S.A.; Petkovsek, M.; Ryabenko, A.A. Hypergeometric Solutions of First-order Linear Difference Dystems with Rational-function Coefficients. In International Workshop on Computer Algebra in Scientific Computing; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9301, pp. 1–14. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhtamova, S.S.; Alekseev, V.S.; Lyapin, A.P. D-Finite Discrete Generating Series and Their Sections. Mathematics 2025, 13, 3259. https://doi.org/10.3390/math13203259
Akhtamova SS, Alekseev VS, Lyapin AP. D-Finite Discrete Generating Series and Their Sections. Mathematics. 2025; 13(20):3259. https://doi.org/10.3390/math13203259
Chicago/Turabian StyleAkhtamova, Svetlana S., Vitaly S. Alekseev, and Alexander P. Lyapin. 2025. "D-Finite Discrete Generating Series and Their Sections" Mathematics 13, no. 20: 3259. https://doi.org/10.3390/math13203259
APA StyleAkhtamova, S. S., Alekseev, V. S., & Lyapin, A. P. (2025). D-Finite Discrete Generating Series and Their Sections. Mathematics, 13(20), 3259. https://doi.org/10.3390/math13203259





