Topology and Algebra of Bonded Knots and Braids
Abstract
1. Introduction
2. Bonded Knots and Links
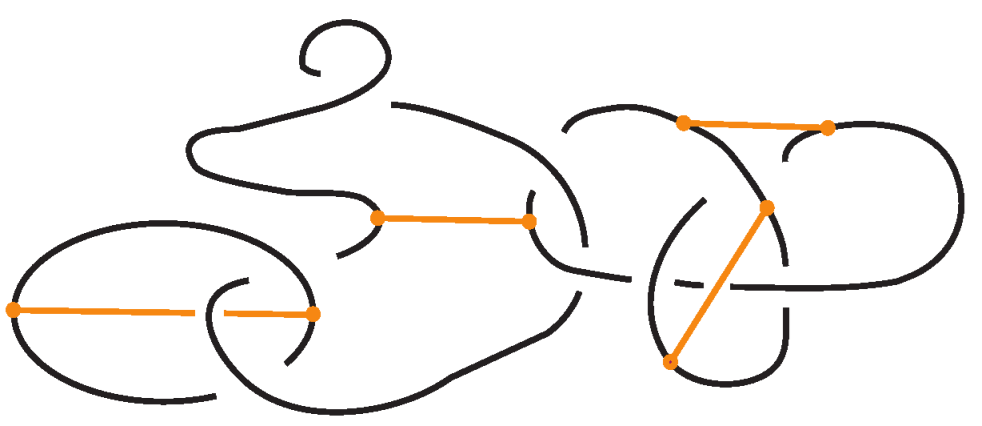
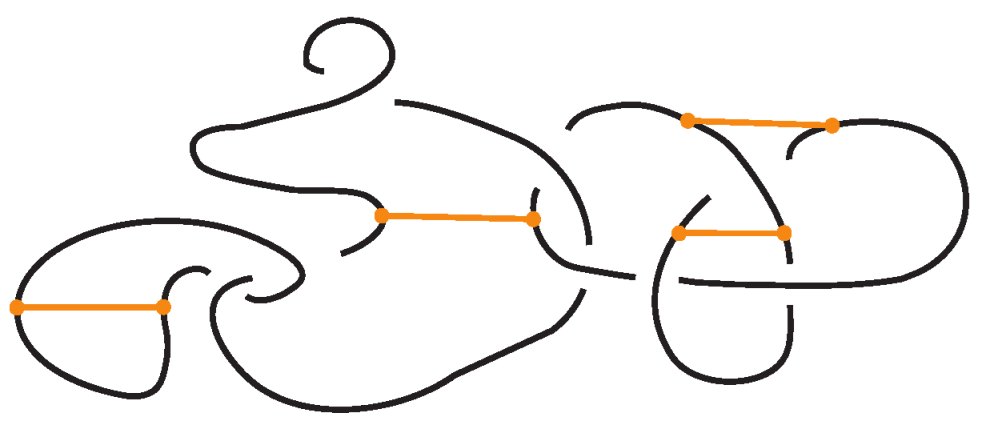
2.1. Definition of Bonded Knots and Links
2.2. Bonded Isotopy and Allowed Moves
- i.
- Planar isotopies of link arcs, bonded arcs, or nodes, as shown in Figure 3.
- ii.
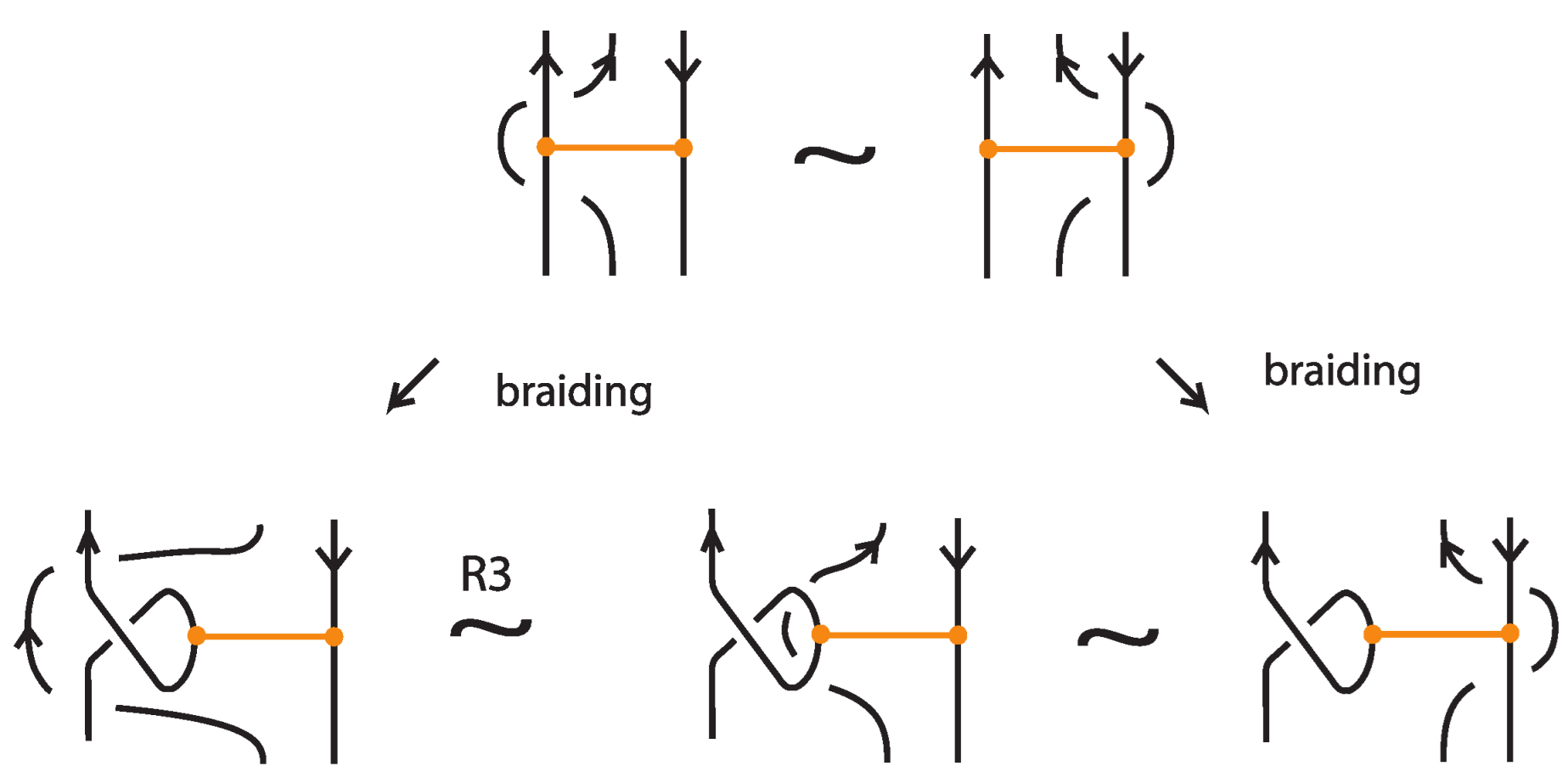
- Classical Reidemeister moves (R1, R2, R3) acting on link arcs away from nodes, as exemplified in Figure 4.
- iii.
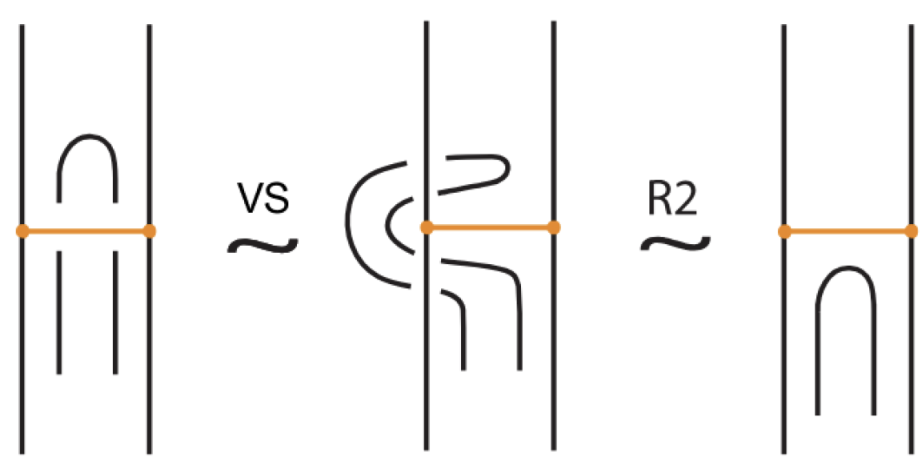
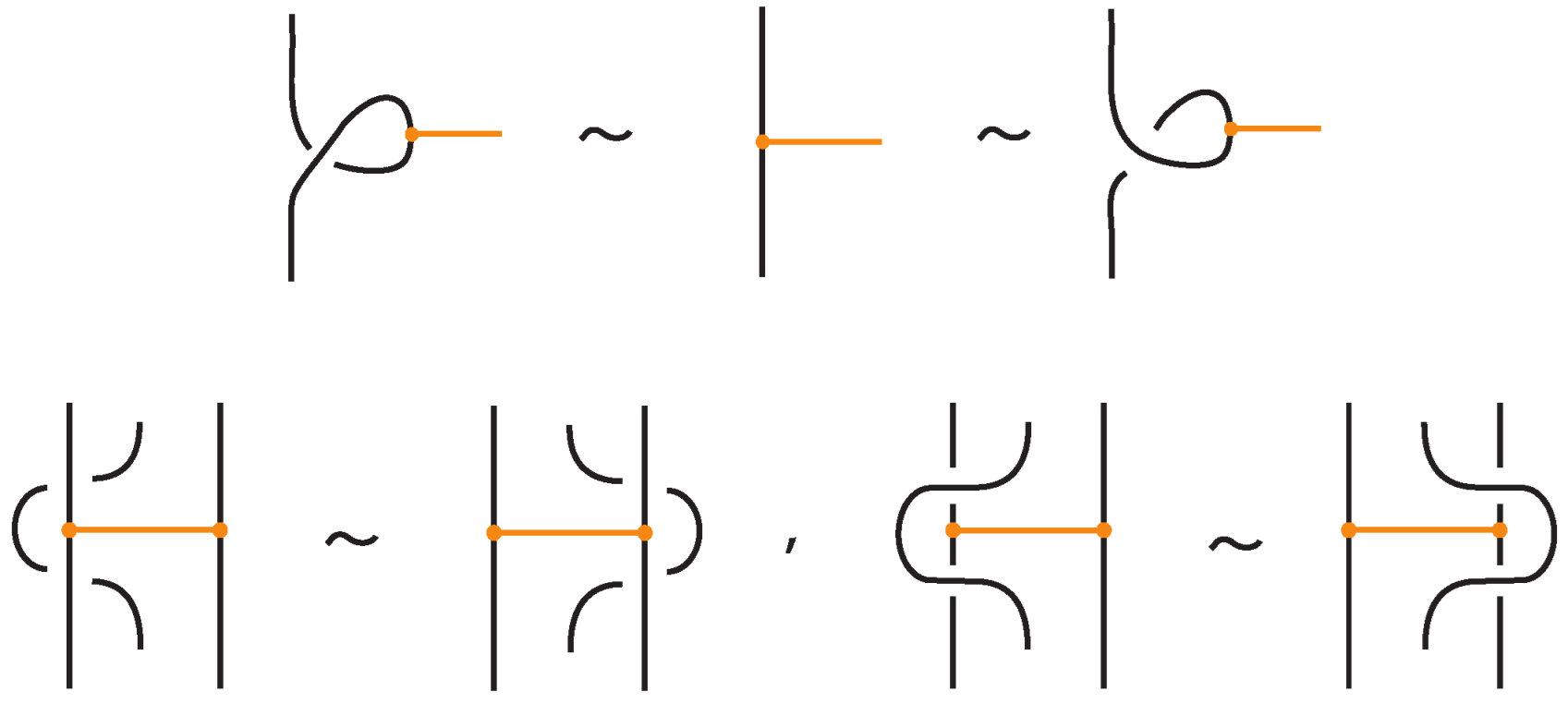
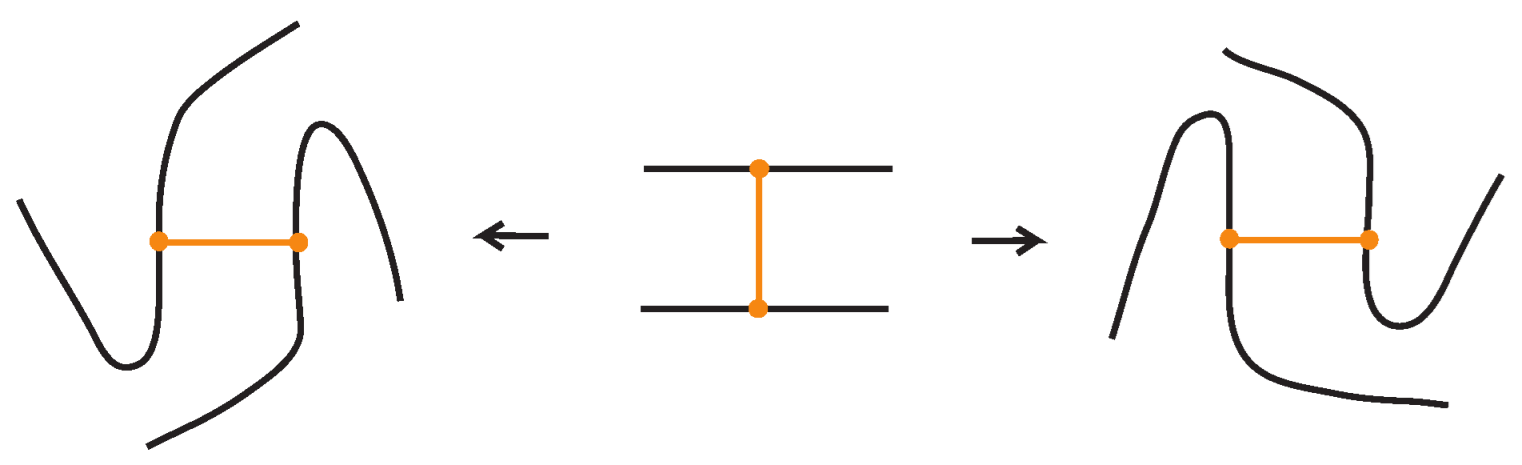
- Reidemeister-type moves acting only on bonded arcs, as shown in Figure 5.
- iv.
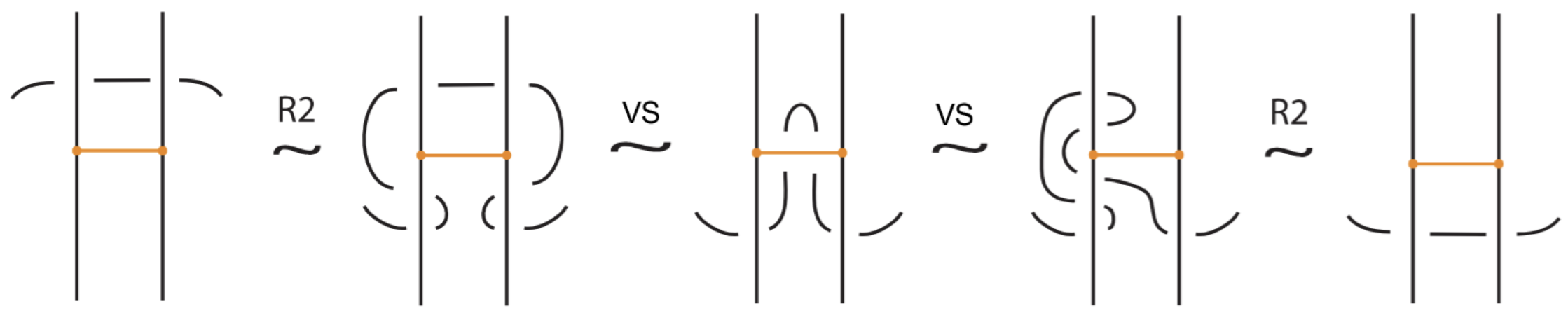
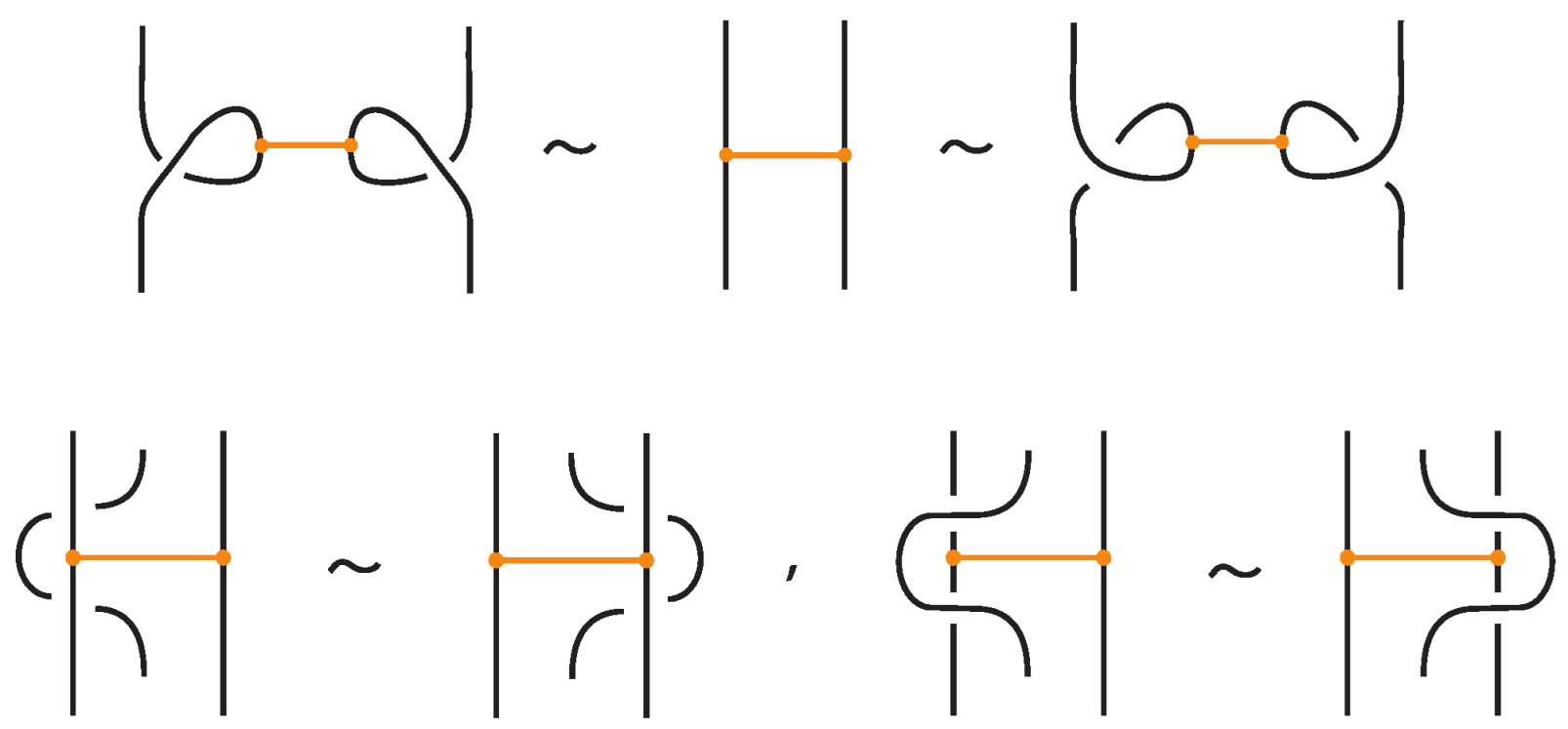
- Reidemeister-type moves involving both link arcs and bonded arcs, as exemplified in Figure 6.
- v.
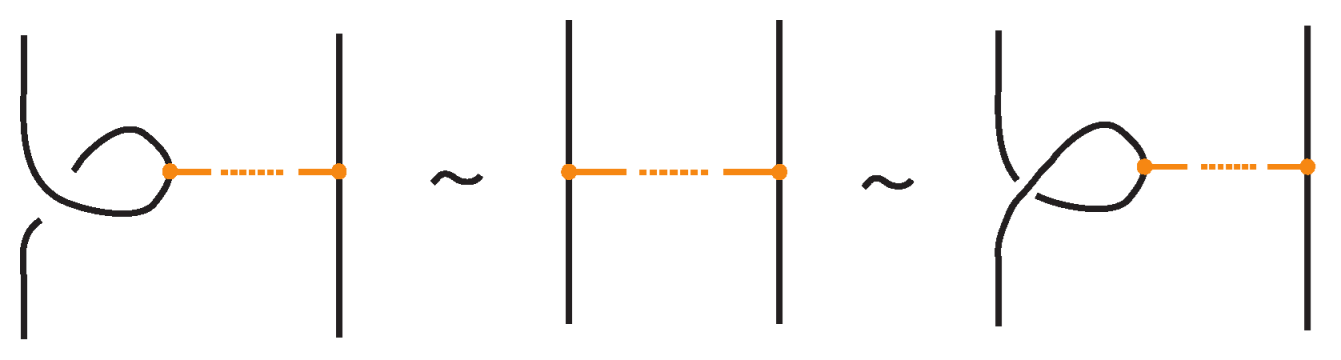
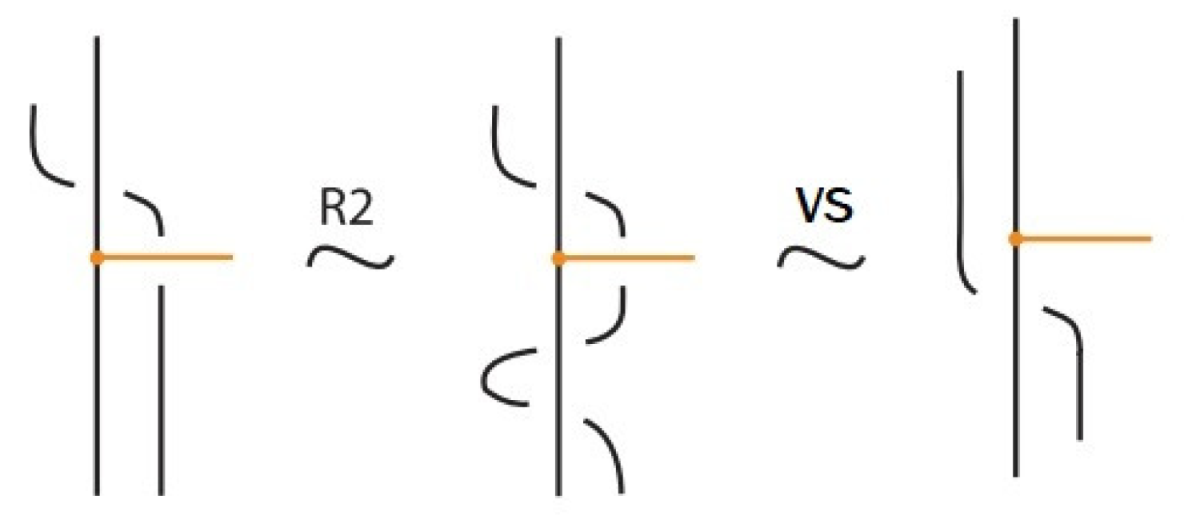
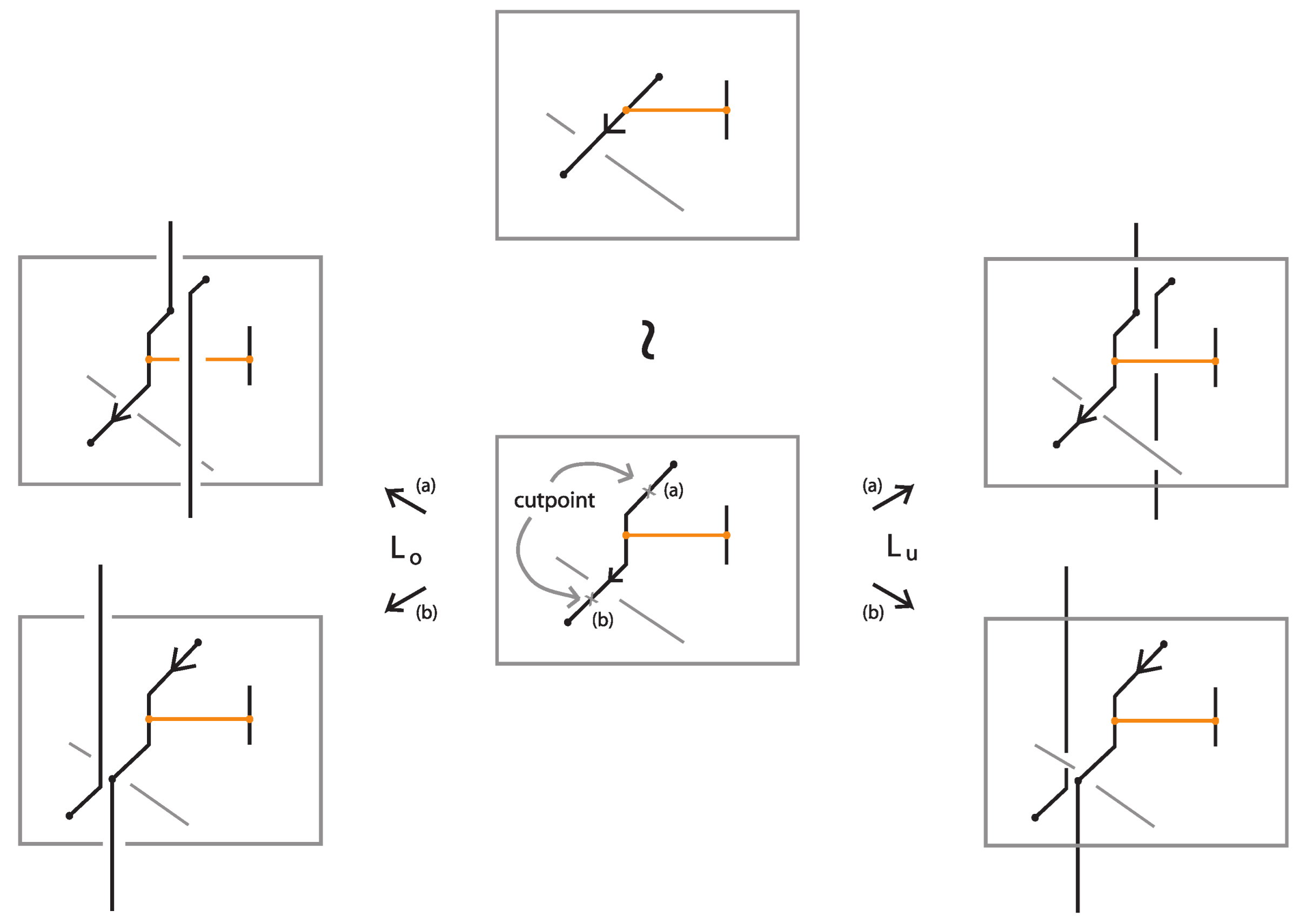
- Vertex slide moves, allowing a bond endpoint to slide along the link to a new position, exemplified in Figure 7.
- vi.
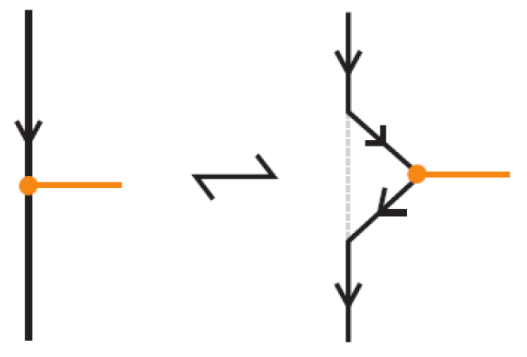
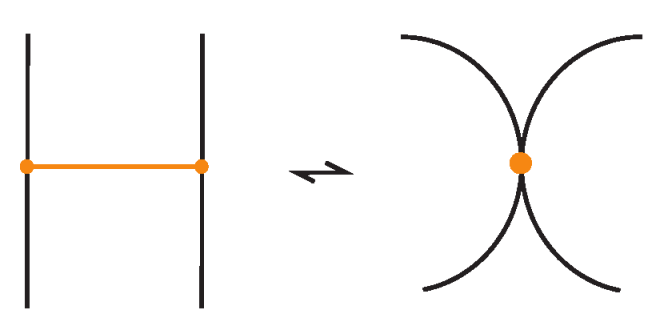
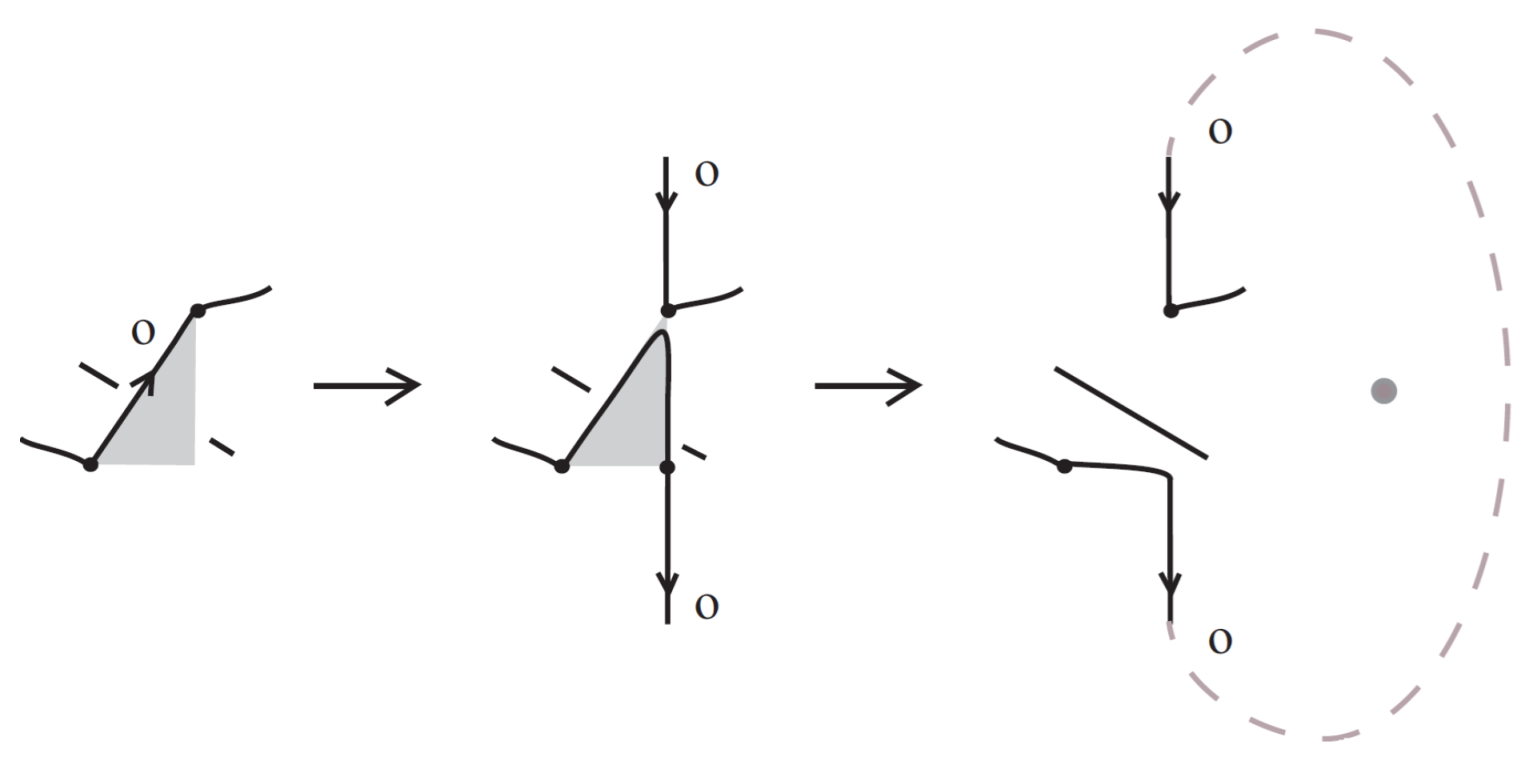
- Topological vertex twist moves (TVT), as exemplified in Figure 8.
- Similarly, two (oriented) bonded links and are equivalent as bonded links via rigid vertex isotopy if corresponding diagrams of theirs differ by a finite sequence of the moves (i)–(v) above together with the rigid vertex twists (RVT) shown in Figure 9, excluding the TVT moves (Figure 8). Rigid vertex isotopy moves are illustrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 9.
2.3. More Diagrammatic Moves for Bonded Links
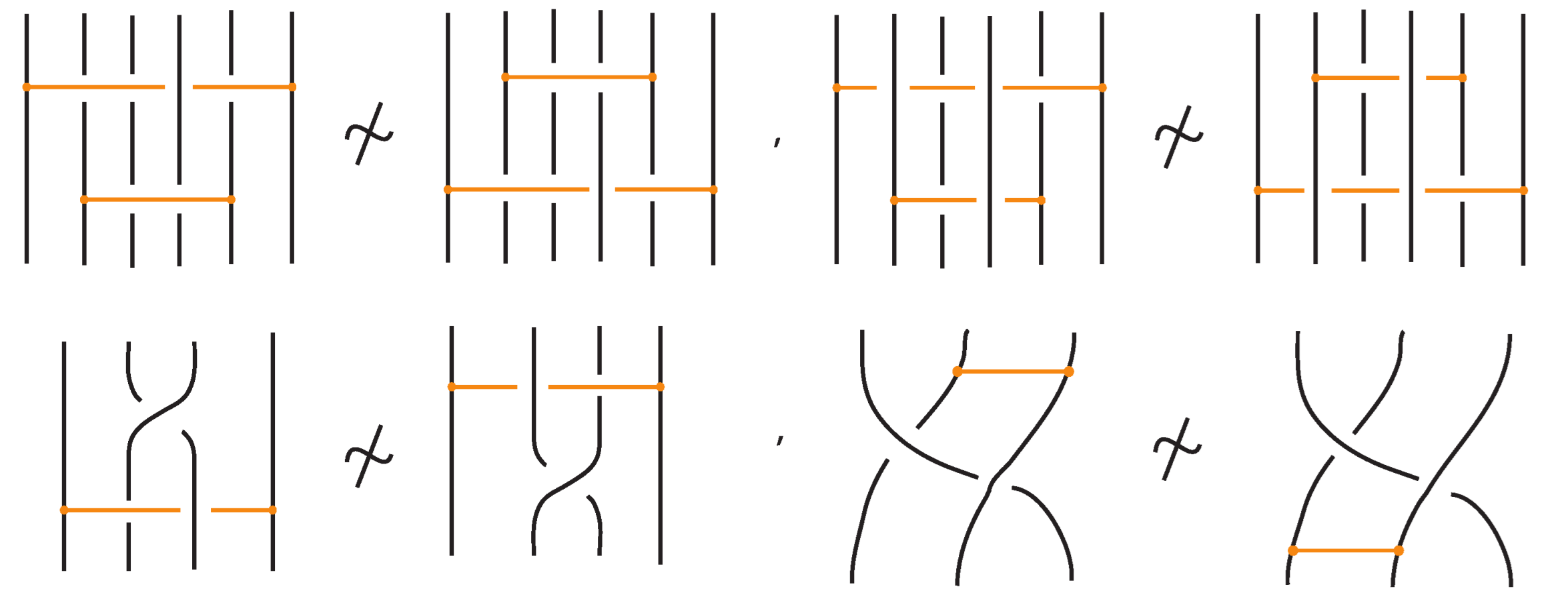
- Moves involving the interaction of a bonded arc with a link arc or another bond,
- Moves involving the interaction of a bonded arc with a crossing.
2.4. Some Restrictions and Forbidden Moves
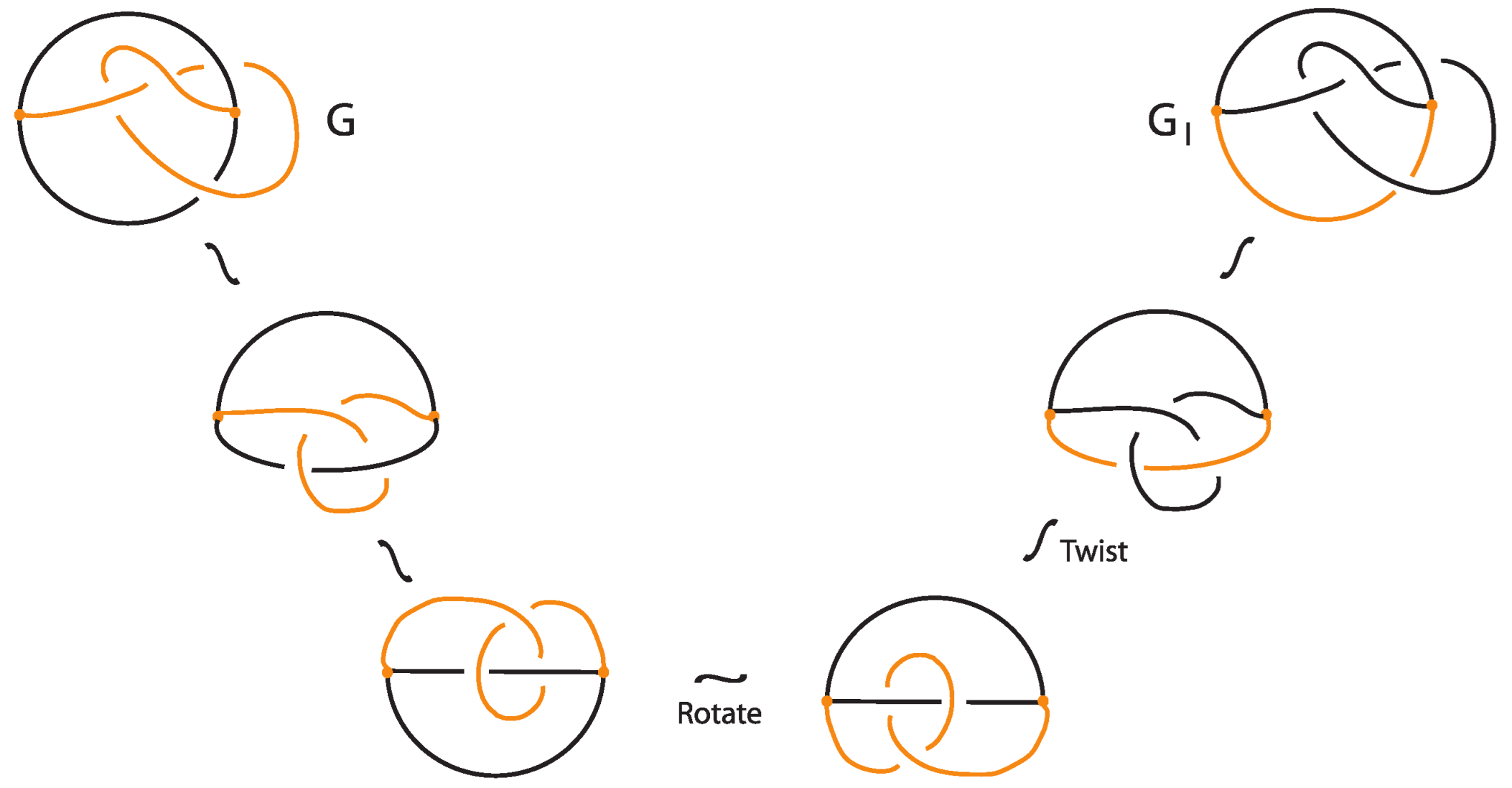
3. Standard Bonded Links
4. Tight Bonded Links
5. Invariants of Topological and Rigid Vertex Bonded Links
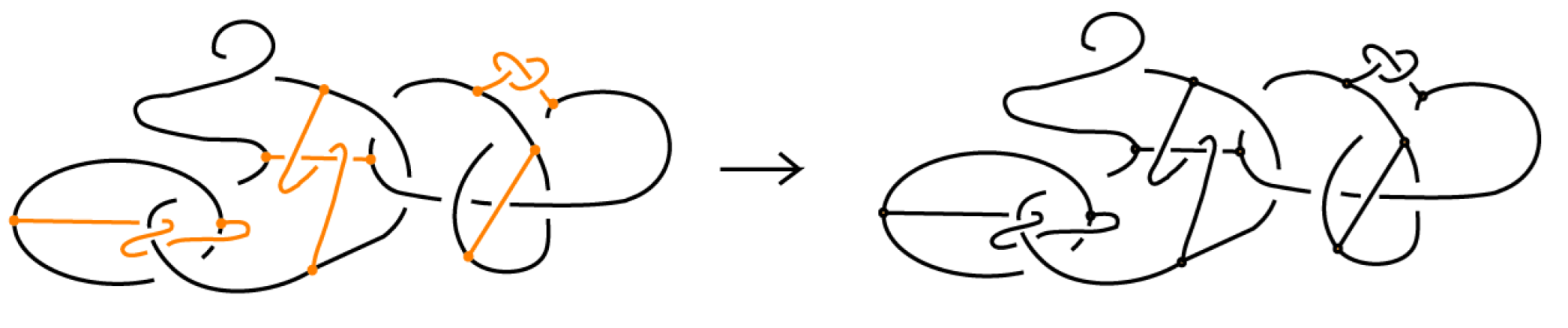
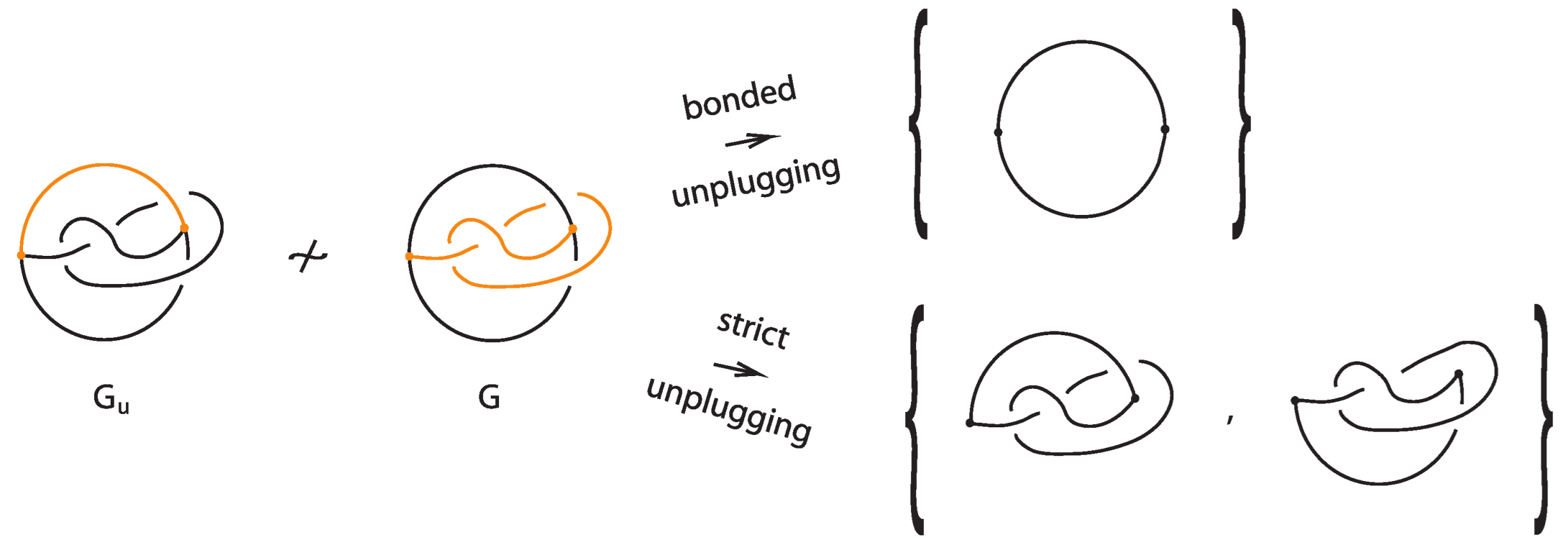
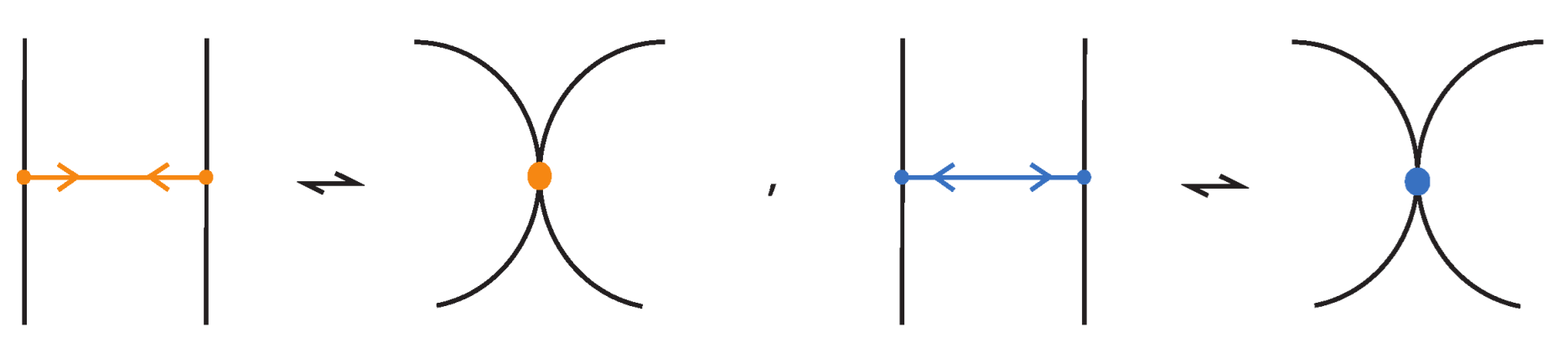
5.1. Topological Bonded Links: Unplugging Operations
- The set of classical links derived from all possible vertex unpluggings is a topological vertex isotopy invariant of .
- Consequently, any ambient isotopy invariant applied to is also a topological vertex isotopy invariant of .
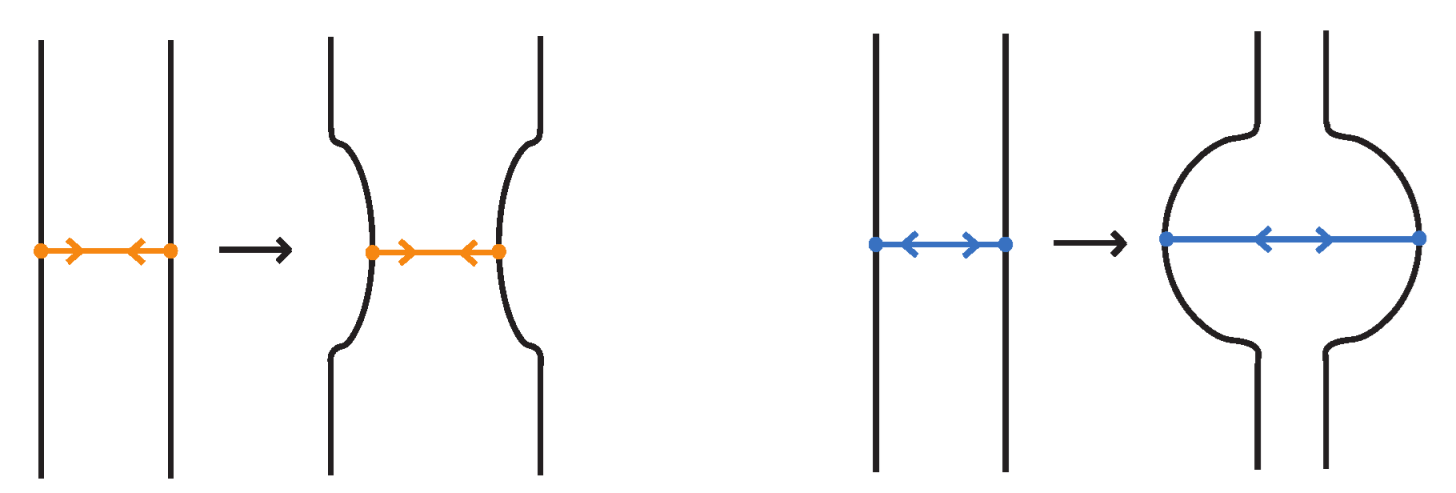
5.2. Rigid Standard Bonded Links: Tangle Insertions
- Replace each bond by a properly embedded band connecting its two nodes.
- Into each band, insert a properly embedded two-tangle chosen from a fixed family of tangles.
- The result is a classical link diagram whose isotopy class depends only on the rigid isotopy class of and the choice of tangles.
- The set of classical links obtained from all possible tangle insertions is a rigid vertex isotopy (resp. rigid vertex regular isotopy) invariant of .
- For any fixed choice of tangles, the ambient (resp. regular) isotopy class of the resulting classical link is a rigid vertex (resp. rigid vertex regular) isotopy invariant of .
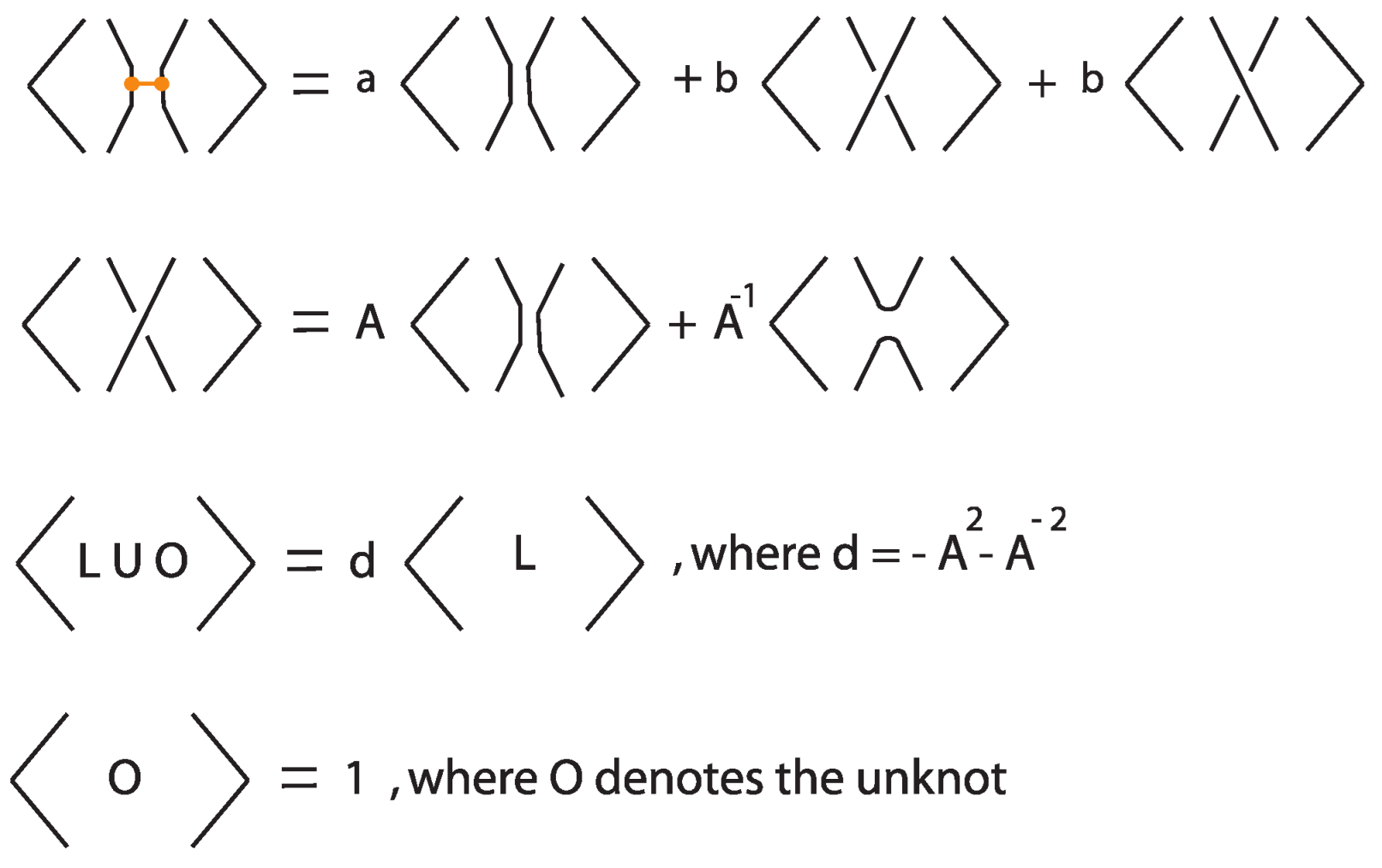
5.3. Rigid Tight Bonded Links: The Bonded Bracket Polynomial
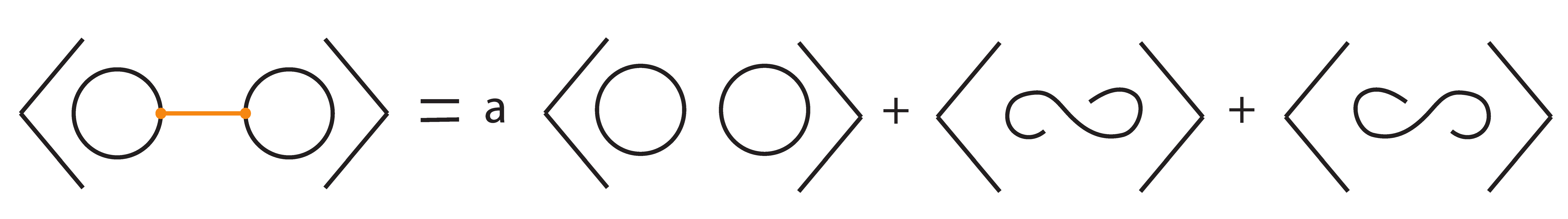
6. Bonded Braids
6.1. Bonded Braid Definition
6.2. Bonded Braid Isotopy
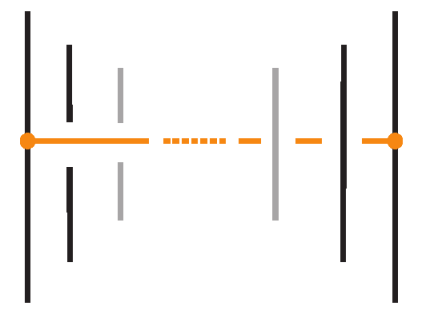
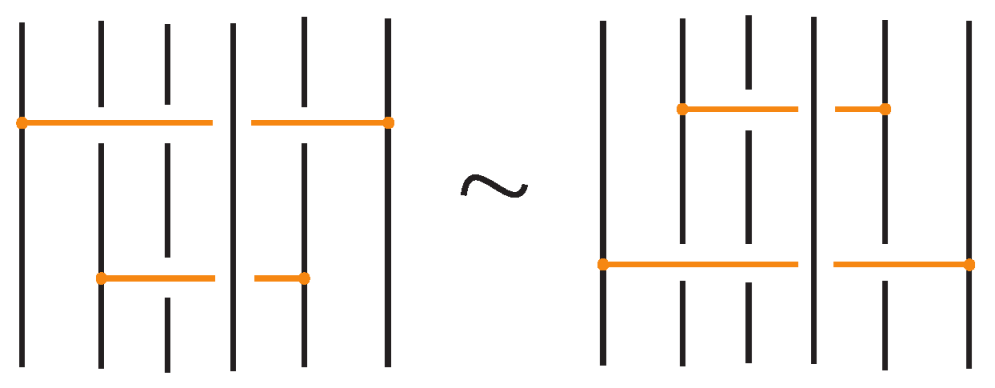
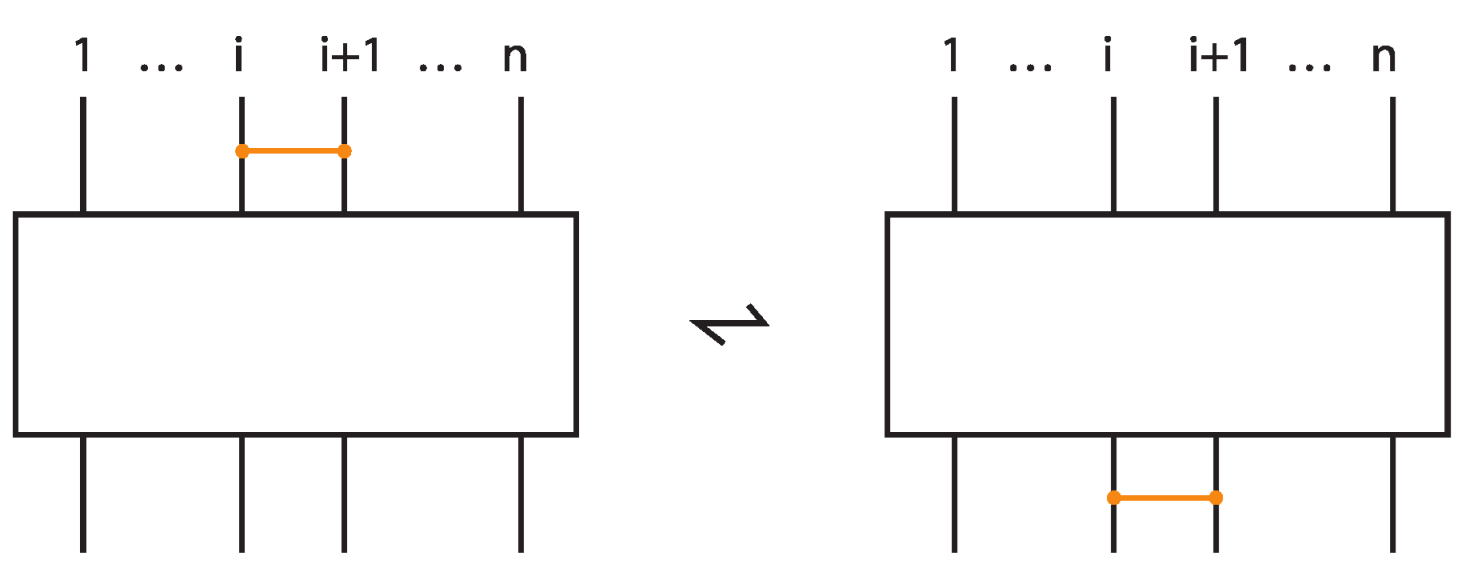
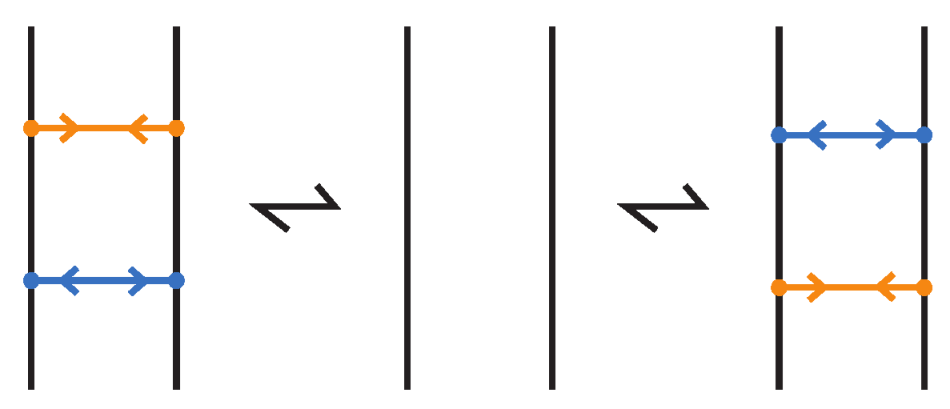
- If two bonds and are sufficiently far apart so that their threading paths do not overlap or interact, that is , they commute freely. For an example see Figure 46.
- Two bonds and also commute if and is a uniform over/under, that is, it passes either over or under all its intermediate strands, which include the set of intermediate strands of . In this case, the configuration of the sequence of u’s and o’s of the bond does not matter. For an example, see Figure 47.
- Furthermore, the two bonds and commute if , the sequence of crossings of coincides with a subsequence of the sequence of crossings of for the strands and the markings in the bigger sequence before and after the subsequence agree, i.e., they are both ‘over’ or both ‘under’. For example, if forms the sequence with its intermediate strands, the bond must contain either the subsequence or the subsequence for the bonds to commute. We call this configuration the matching crossing sequences. For an illustration see Figure 48.
- If the strands forming the crossing do not interact with the bond , i.e., or , then the bond and the crossing commute freely (see Figure 50 for an example).
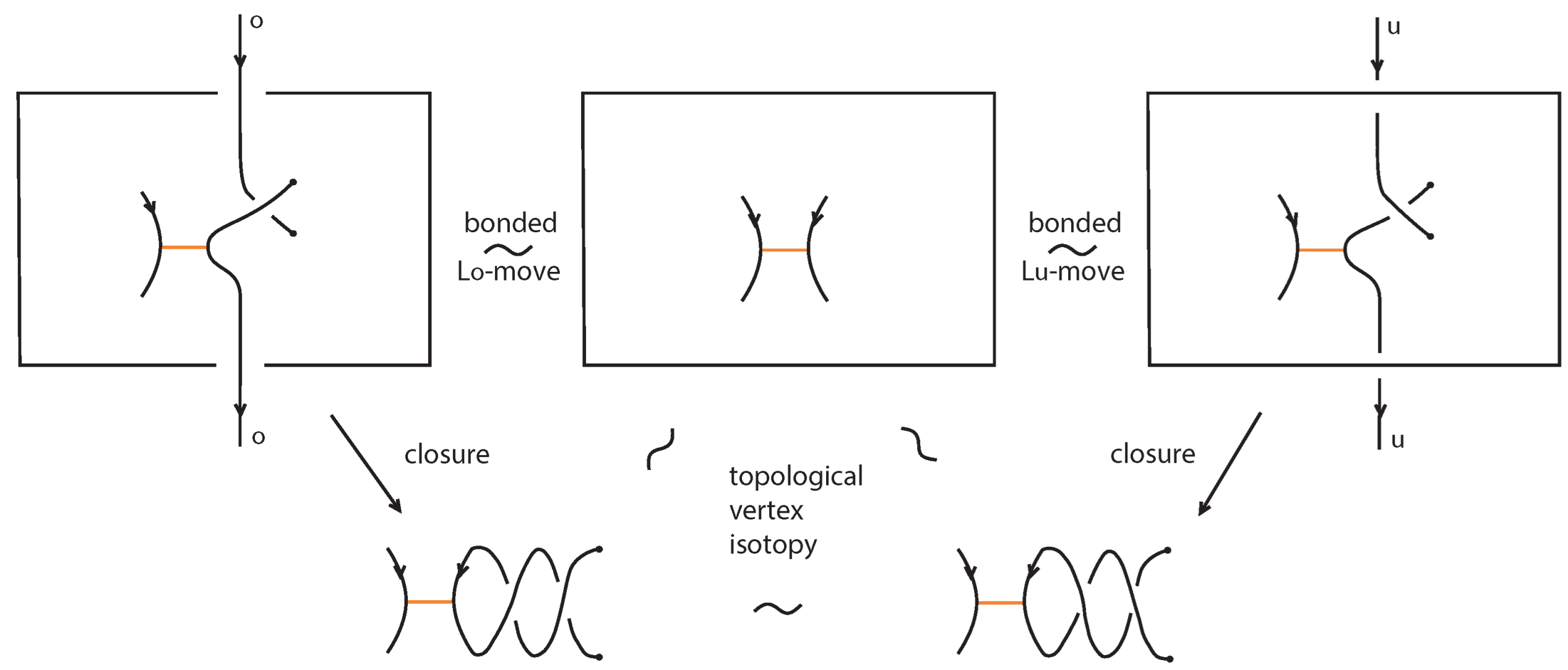
- If the nodes of the bond lie on two strands that form a crossing, the bond and the crossing commute, i.e., commutes with (see Figure 51). This is the bonded flype move.
- A bond and a crossing commute if the bond passes entirely over or entirely under both strands that form the crossing. We call this configuration, the uniform position of the bond. For an illustration of this case, see the left-hand side of Figure 52.
- A bond and a crossing also commute if the over-strand of the crossing lies above the bond and the under-strand lies below it. In this case, the bond effectively ‘threads through’ the crossing without disrupting its configuration. We refer to this move as the bonded R3 move. For an illustration of this case, see the right-hand side of Figure 52.
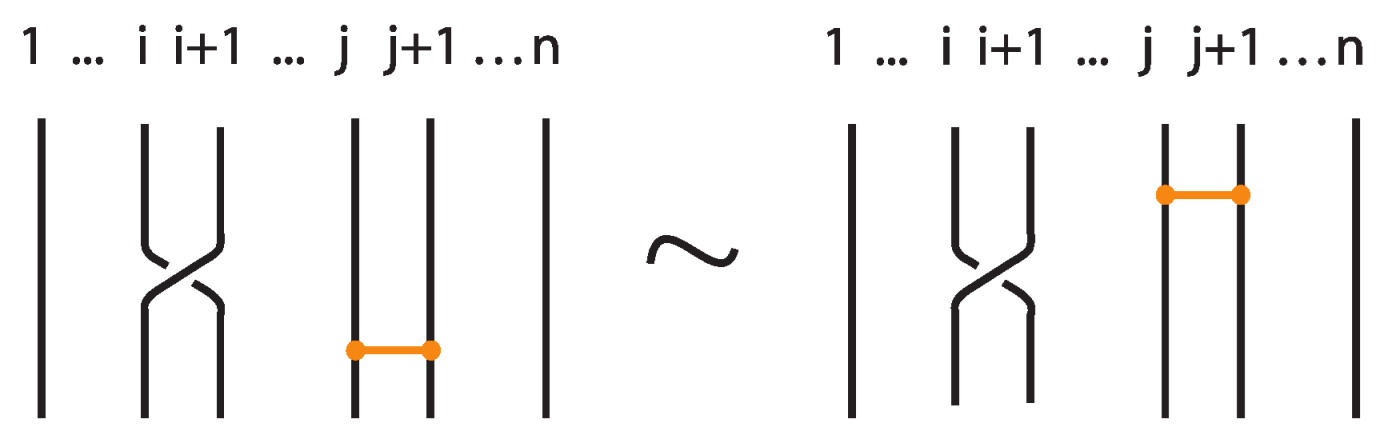


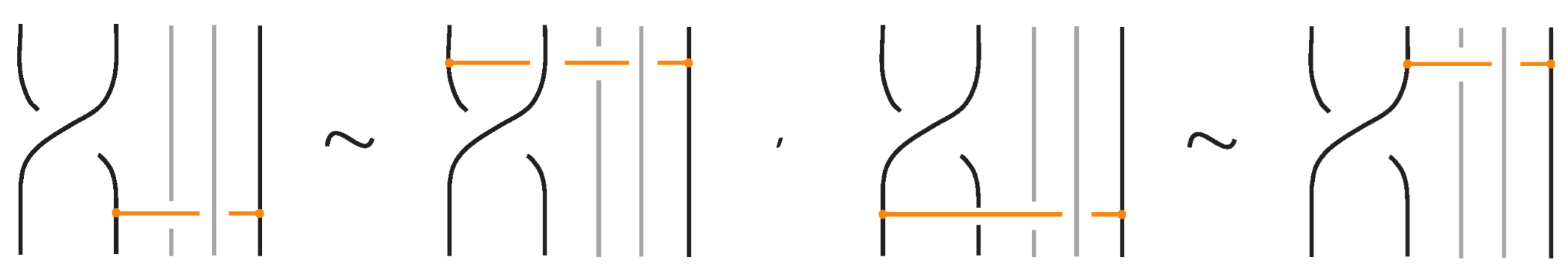
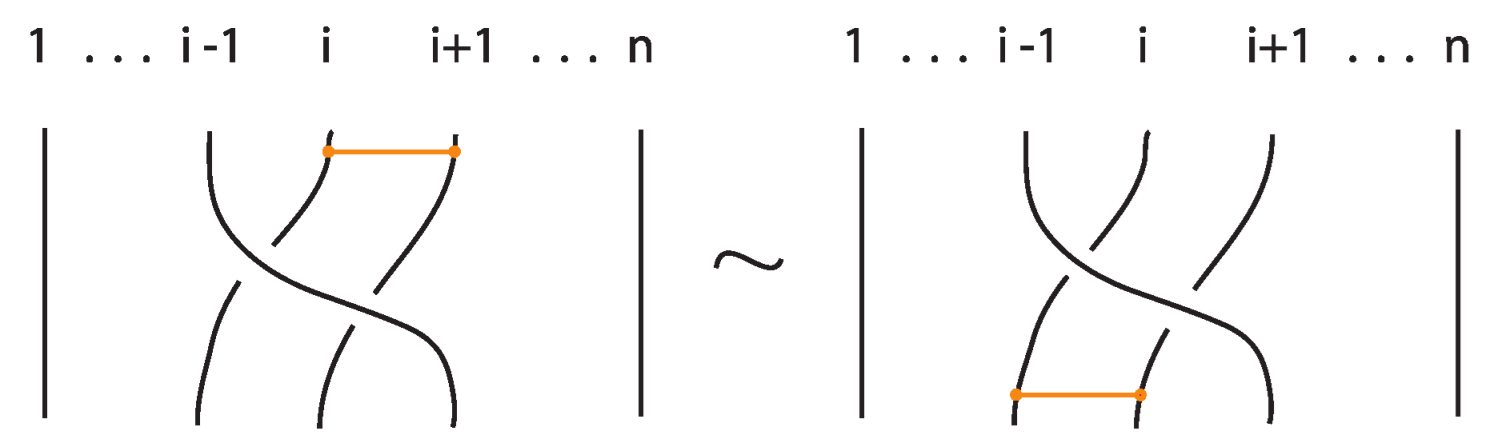
6.3. The Bonded Braid Monoid
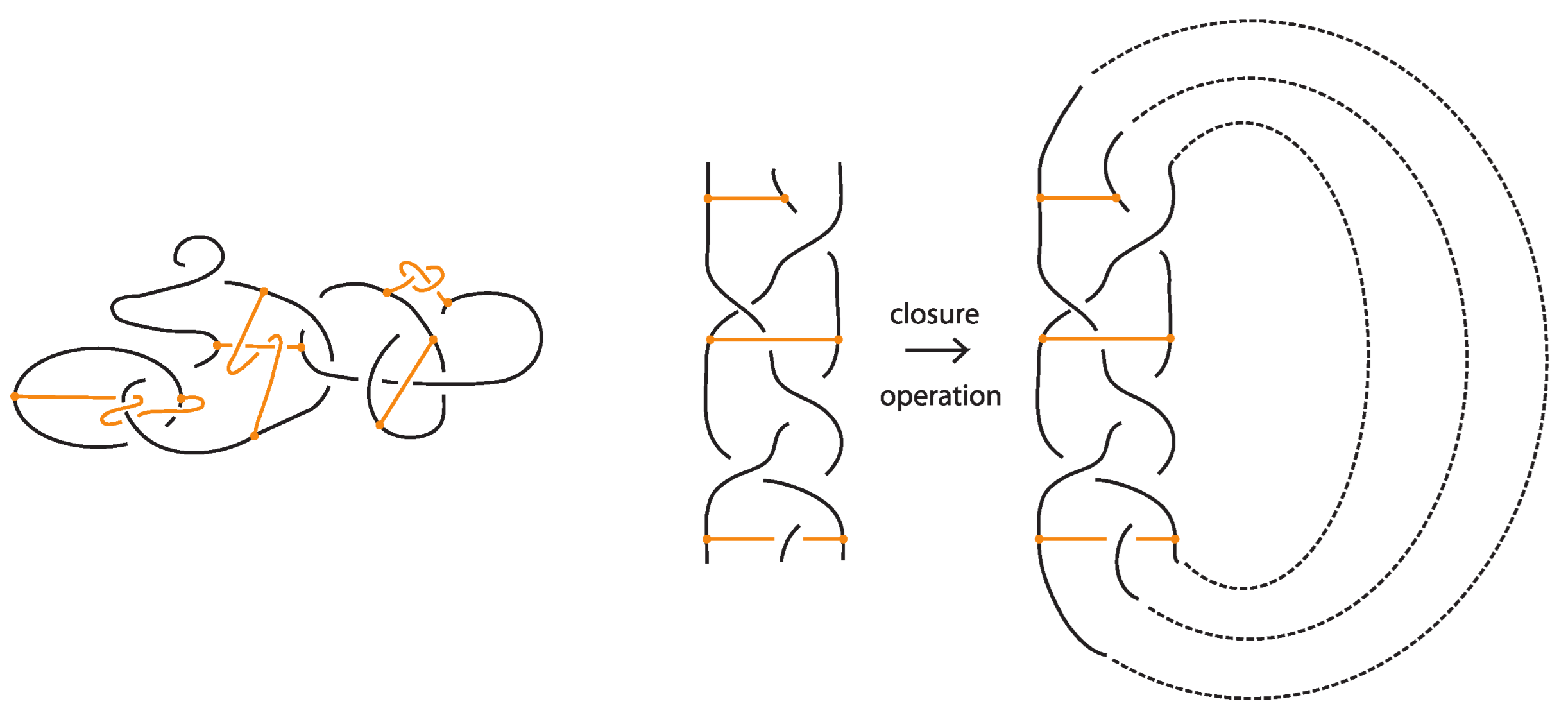
7. An Analogue of the Alexander Theorem for Bonded Links
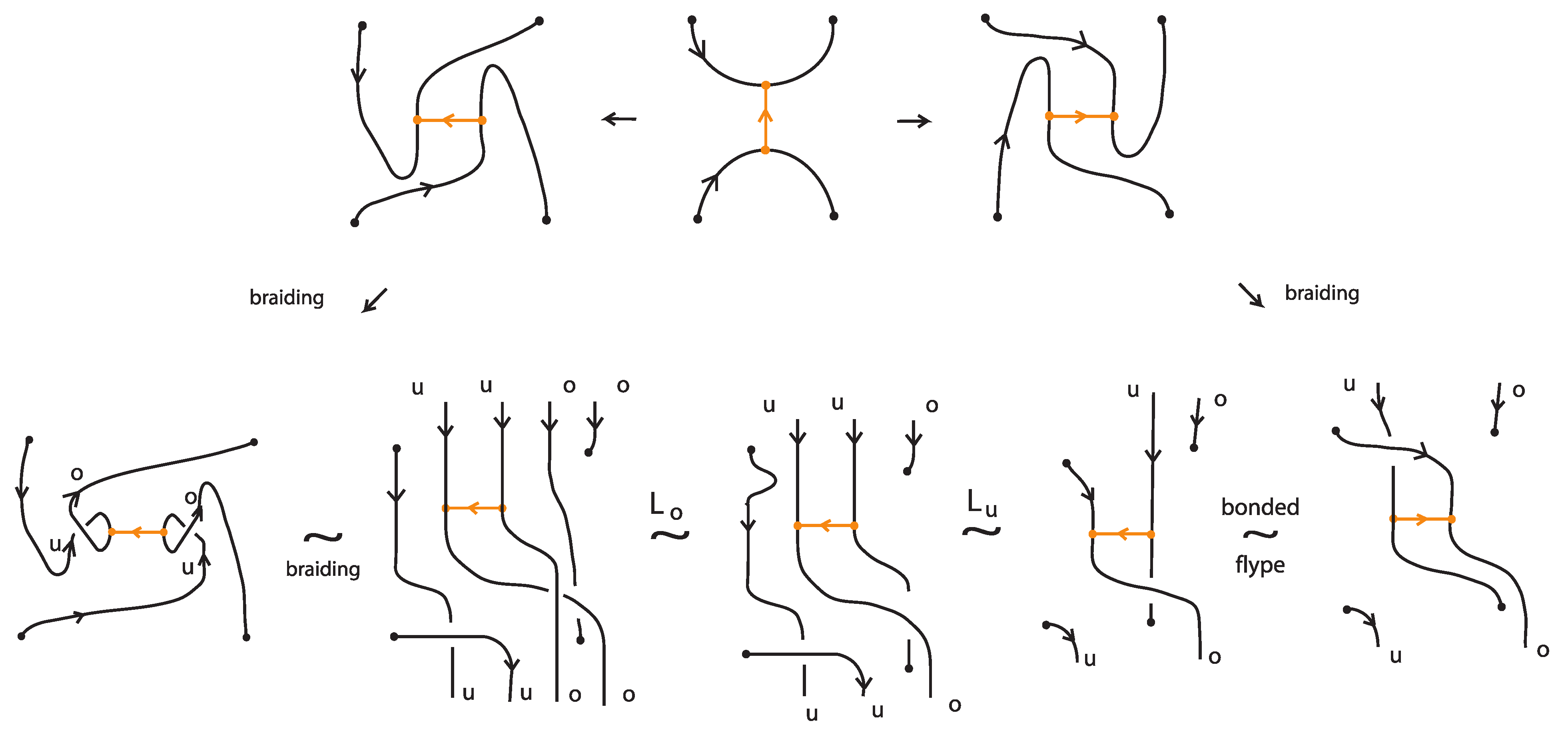
- Step 1:
- We first bring all bonds to horizontal position using (bonded) planar isotopy, observing the general position rules. See Figure 61.
- Step 2:
- We next deal with up-arcs in the diagram that contain at least one node of a bond, standard or tight. For this we apply the isotopy moves TVT or RVT as exemplified in Figure 62 and Figure 63, according to whether the two joining arcs are antiparallel or parallel upward arcs. Note that the braiding preparation of a bonded region with two parallel upward arcs can also be achieved with planar isotopy, by performing a 180-degree rotation on the plane. Then the bonds will only lie on down-arcs, so that the braiding algorithm will not affect them.
- Step 3:
- Finally, we apply the braiding algorithm of [7] for the link diagram, ignoring the bonds. After eliminating all up-arcs, we obtain a standard bonded braid, the closure of which is—by construction—isotopic to the original oriented bonded link diagram.
- Step 4:
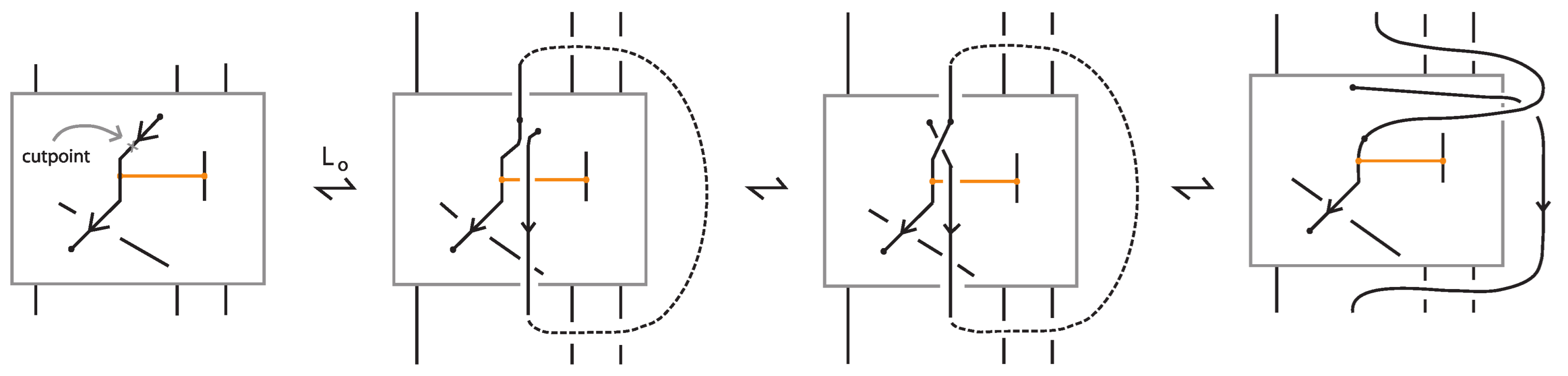
- In the end of the process some braid strands may cross over or under some bonds. Using the braided vertex slide moves (recall Figure 57) we bring them to tight form. The algorithm above provides a proof of Theorem 9.
- (a)
- Note that in the rigid vertex category it is not possible to braid two antiparallel strands that are connected by a bond. This is because braiding such strands necessarily requires the use of a topological vertex twist at one of the nodes, a move that is forbidden in the rigid vertex category. For this reason we restricted our focus to the topological vertex category.
- (b)
- The vertex slide moves for bringing the bonds to tight form (recall Figure 28) could have been already applied after Step 1 or Step 2. In the end we might still need to apply the braided vertex slide moves for new braid strands.
8. Bonded Braid Equivalences
- Conjugation: ;
- Stabilization move: .
- 1.
- L-moves,
- 2.
- Bonded L-moves,
- 3.
- Bond Commuting: .
- 1.
- Tight L-moves,
- 2.
- Tight bonded L-moves,
- 3.
- Elementary Bond Commuting: .
9. The Theory of Enhanced Bonded Links and Braids
9.1. Enhanced Bonds: Attracting vs. Repelling
9.2. The Enhanced Bonded Braid Group
9.3. Analogues of the Alexander and Markov Theorems for Enhanced Bonded Braids
- 1.
- L-moves,
- 2.
- Bonded L-moves,
- 3.
- Enhanced Bond Conjugation: .
- 1.
- Tight L-moves,
- 2.
- Tight Bonded L-moves,
- 3.
- Enhanced Elementary Bond Conjugation: .
10. Conclusions and Further Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kauffman, L.H. Invariants of graphs in three-space. Trans. Am. Math. Soc. 1989, 311, 697–710. [Google Scholar] [CrossRef]
- Kauffman, L.H.; Magarshak, Y. Vassiliev knot invariants and the structure of RNA foldings. In Knots and Applications; Kauffman, L.H., Ed.; World Scientific: Singapore, 1995; pp. 343–394. [Google Scholar]
- Baez, J.C. Link invariants of finite type and perturbation theory. Lett. Math. Phys. 1992, 26, 43–51. [Google Scholar] [CrossRef]
- Alexander, J.W. A lemma on systems of knotted curves. Proc. Natl. Acad. Sci. USA 1923, 9, 93–95. [Google Scholar] [CrossRef] [PubMed]
- Markov, A.A. Über die freie Äquivalenz geschlossener Zöpfe. Recl. Math. Moscou 1935, 1, 73–78. [Google Scholar]
- Jones, V.F.R. Hecke algebra representations of braid groups and link polynomials. Ann. Math. 1987, 126, 335–388. [Google Scholar] [CrossRef]
- Lambropoulou, S.; Rourke, C.P. Markov’s theorem in 3-manifolds. Topol. Its Appl. 1997, 78, 95–122. [Google Scholar] [CrossRef]
- Turaev, V. Knotoids. Osaka J. Math. 2012, 49, 195–223. [Google Scholar]
- Gügümcü, N.; Kauffman, L.H. New invariants of knotoids. Eur. J. Combin. 2017, 65, 186–229. [Google Scholar] [CrossRef]
- Gügümcü, N.; Lambropoulou, S. Braidoids. Isr. J. Math. 2021, 242, 955–995. [Google Scholar] [CrossRef]
- Goundaroulis, D.; Dorier, J.; Benedetti, F.; Stasiak, A. Studies of global and local entanglements of individual protein chains using the concept of knotoids. Sci. Rep. 2017, 7, 6309. [Google Scholar] [CrossRef]
- Skolnick, J.; Gao, M. The role of local versus nonlocal physicochemical restraints in determining protein native structure. Curr. Opin. Struct. Biol. 2021, 68, 1–8. [Google Scholar] [CrossRef]
- Mugler, A.; Tans, S.; Mashaghi, A. Circuit topology of self-interacting chains: Implications for folding and unfolding dynamics. Phys. Chem. Chem. Phys. R. Soc. Chem. 2014, 16, 22537–22544. [Google Scholar] [CrossRef]
- Dombkowski, A.A.; Sultana, K.Z.; Craig, D.B. Protein disulfide engineering. FEBS Lett. 2014, 588, 206–212. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sulkowska, J.I. KnotProt 2.0: A database of proteins with knots and other entangled structures. Nucleic Acids Res. 2018, 47, D367–D375. [Google Scholar] [CrossRef]
- Goundaroulis, D.; Gügümcü, N.; Lambropoulou, S.; Dorier, J.; Stasiak, A.; Kauffman, L.H. Topological models for open-knotted protein chains using the concepts of knotoids and bonded knotoids. Polymers 2017, 9, 444. [Google Scholar] [CrossRef]
- Gabrovšek, B. An invariant for colored bonded knots. Stud. Appl. Math. 2021, 146, 586–604. [Google Scholar] [CrossRef]
- Adams, C.; Devadoss, J.; Elhamdadi, M.; Mashaghi, A. Knot theory for proteins: Gauss codes, quandles and bondles. J. Math. Chem. 2020, 58, 1711–1736. [Google Scholar] [CrossRef]
- Lambropoulou, S. L-moves and Markov theorems. J. Knot Theory Its Ramif. 2007, 16, 1459–1468. [Google Scholar] [CrossRef]
- Kauffman, L.H.; Lambropoulou, S. Virtual braids and the L-moves. J. Knot Theory Ramif. 2006, 15, 773–811. [Google Scholar] [CrossRef]
- Kreimer, D. Knots and Feynman Diagrams; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Niemi, A. Are glueballs knotted closed strings? In Proceedings of the International Conference on Color Confinement and Hadrons in Quantum Chromodynamics (Confinement 2003), Wako, Japan, 21–24 July 2003; pp. 127–139. [Google Scholar]
- Buniy, R.; Kephart, T. Universal energy spectrum of tight knots and links in physics. In Physical and Numerical Models in Knot Theory Including Applications to the Life Sciences; Calvo, J., Millett, K.C., Rawdon, E.J., Stasiak, A., Eds.; World Scientific: Singapore, 2005; pp. 45–63. [Google Scholar]
- Jonoska, N.; Winfree, E. (Eds.) Visions of DNA Nanotechnology at 40 for the Next 40: A Tribute to Nadrian C. Seeman; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Aicardi, F.; Juyumaya, J. Tied links. J. Knot Theory Ramif. 2016, 25, 1641001. [Google Scholar] [CrossRef]
- Diamantis, I. Tied pseudo links & pseudo knotoids. Mediterr. J. Math. 2021, 18, 201. [Google Scholar] [CrossRef]
- Birman, J.S. New points of view in knot theory. Bull. Amer. Math. Soc. (New Ser.) 1993, 28, 253–287. [Google Scholar] [CrossRef]
- Fenn, R.; Keyman, E.; Rourke, C.P. The singular braid monoid embeds in a group. J. Knot Theory Ramif. 1998, 7, 881–892. [Google Scholar] [CrossRef]
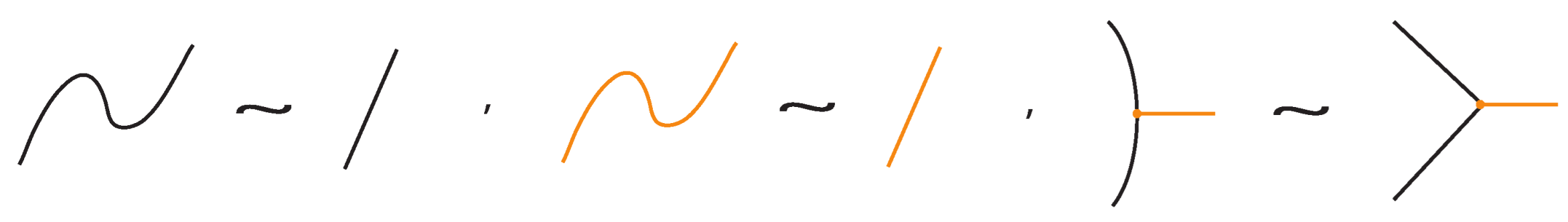
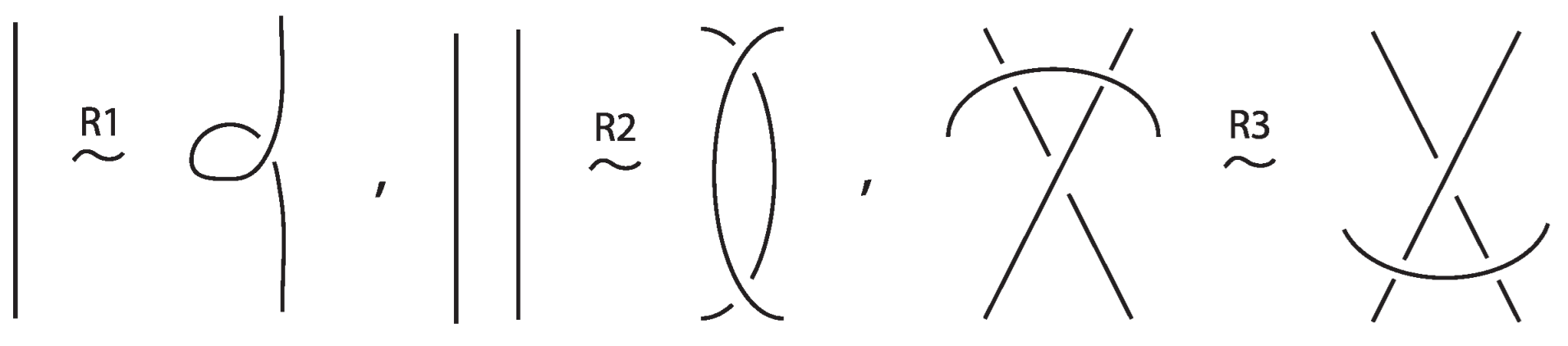
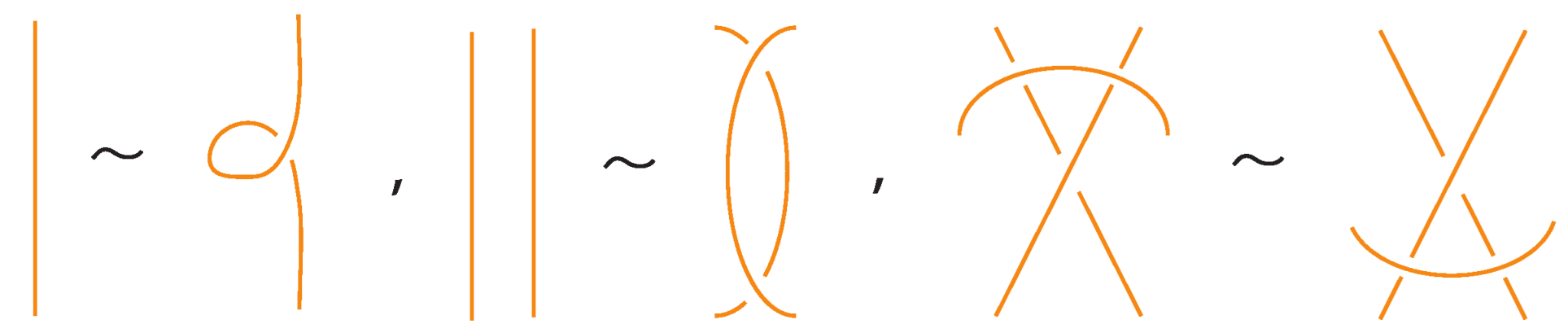
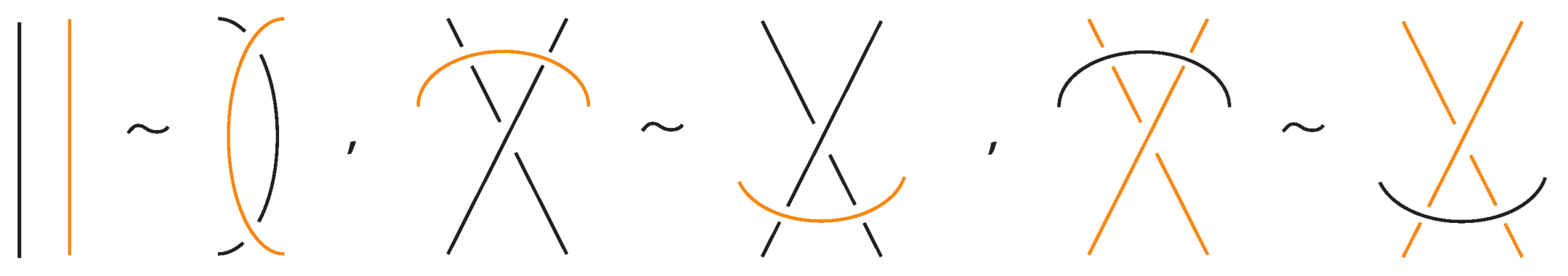








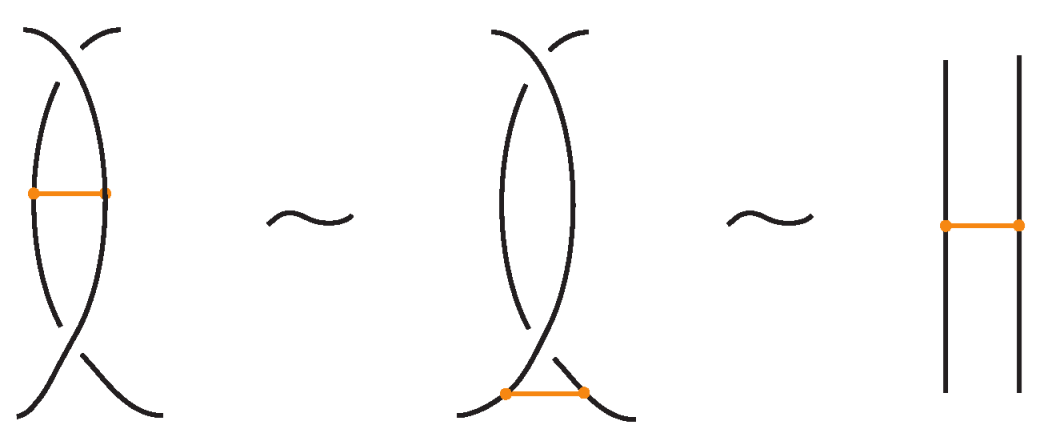
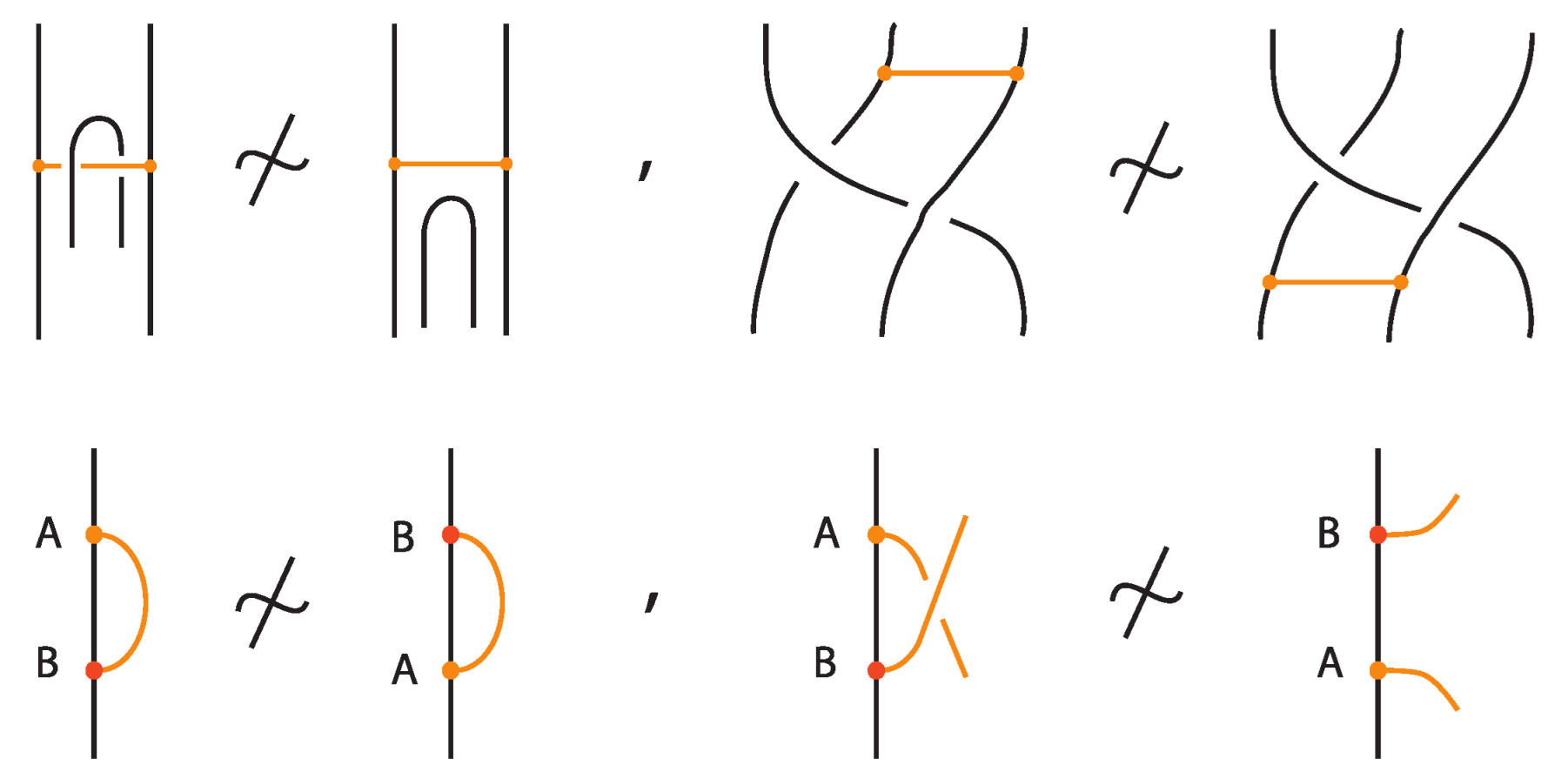

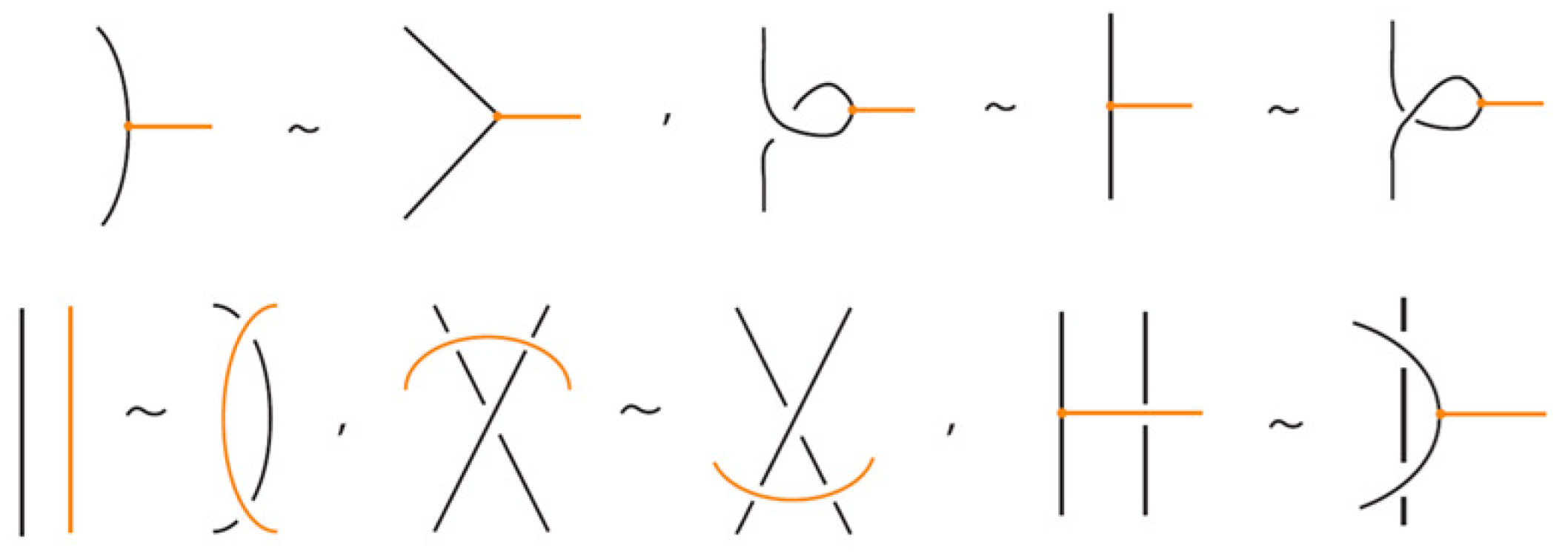







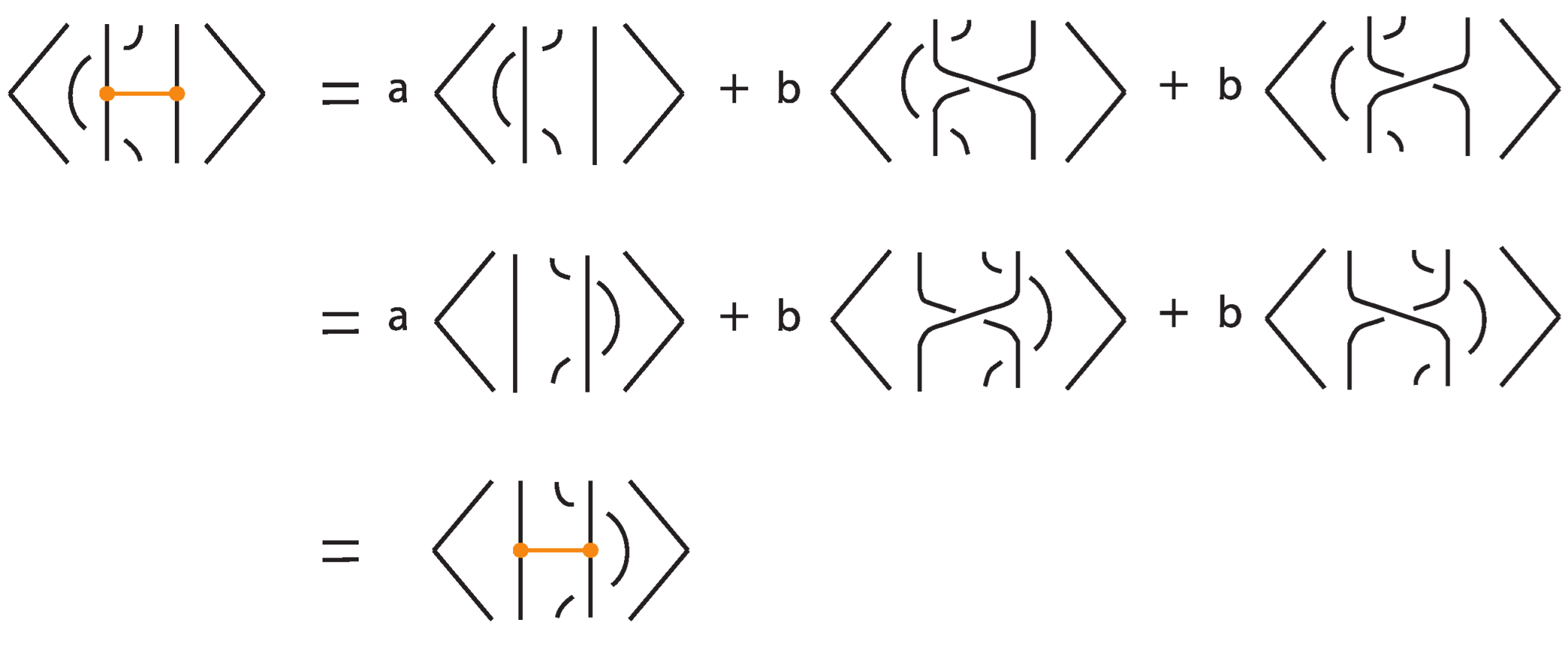

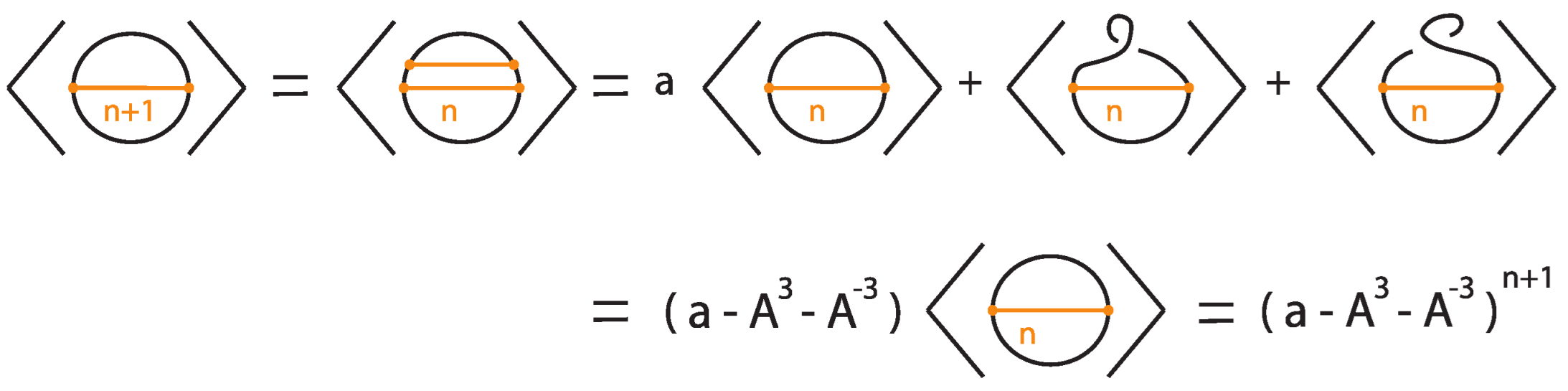













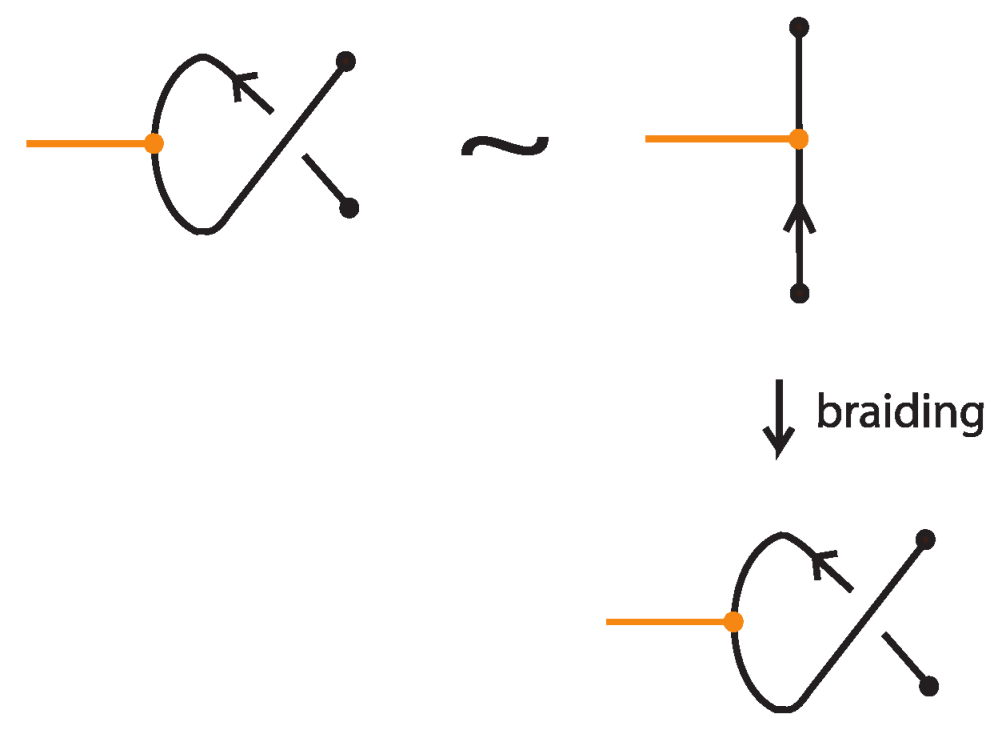




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diamantis, I.; Kauffman, L.H.; Lambropoulou, S. Topology and Algebra of Bonded Knots and Braids. Mathematics 2025, 13, 3260. https://doi.org/10.3390/math13203260
Diamantis I, Kauffman LH, Lambropoulou S. Topology and Algebra of Bonded Knots and Braids. Mathematics. 2025; 13(20):3260. https://doi.org/10.3390/math13203260
Chicago/Turabian StyleDiamantis, Ioannis, Louis H. Kauffman, and Sofia Lambropoulou. 2025. "Topology and Algebra of Bonded Knots and Braids" Mathematics 13, no. 20: 3260. https://doi.org/10.3390/math13203260
APA StyleDiamantis, I., Kauffman, L. H., & Lambropoulou, S. (2025). Topology and Algebra of Bonded Knots and Braids. Mathematics, 13(20), 3260. https://doi.org/10.3390/math13203260






