Perspectives on Dynamic Hardy–Littlewood Inequalities in Time Scale Analysis
Abstract
1. Introduction
2. Preliminaries on Time Scales
3. Main Results
4. Applications
4.1. Stability Analysis
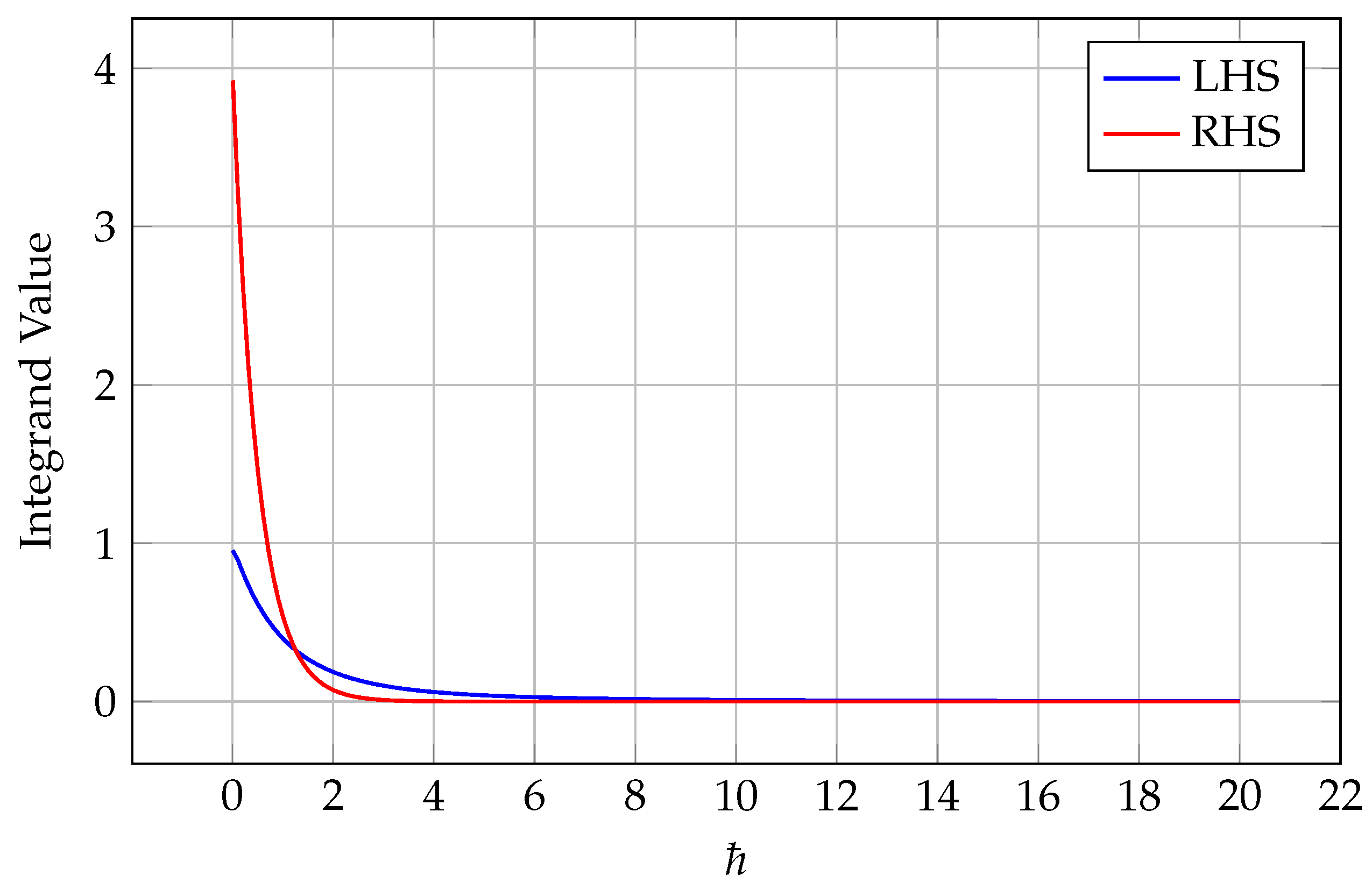
4.2. Example
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hardy, G.H. Note on a Theorem of Hilbert. Math. Z. 1920, 6, 314–317. [Google Scholar] [CrossRef]
- Hardy, G.H. Notes on some points in the integral calculus (LX). Messenger Math. 1925, 54, 150–156. [Google Scholar]
- Littlewood, J.E.; Hardy, G.H. Elementary Theorems concerning power series with positive coefficients and moment constants of positive functions. J. Reine Angew. Math. 1927, 157, 141–158. [Google Scholar] [CrossRef]
- Hardy, G.H. Notes on some points in the integral calculus (LXI). Messenger Math. 1928, 57, 12–16. [Google Scholar]
- Hilger, S. Analysis on measure chains—A unified approach to continuous and discrete calculus. Results Math. 1990, 18, 18–56. [Google Scholar] [CrossRef]
- García García, V.; Ortega Salvador, P. Some new weighted weak-type iterated and bilinear modified Hardy inequalities. Ann. Funct. Anal. 2024, 15, 26. [Google Scholar] [CrossRef]
- Orazbayev, A.; Suragan, D. Improved Lp–Lq Hardy inequalities. Math. Inequal. Appl. 2024, 27, 981–990. [Google Scholar]
- Bianchi, F.; Brasco, L.; Sk, F.; Zagati, A.C. A note on the supersolution method for Hardy’s inequality. Rev. Mat. Complut. 2024, 37, 323–340. [Google Scholar] [CrossRef]
- Zakarya, M.; AlNemer, G.; El-Hamid, H.A.A.; Butush, R.; Rezk, H.M. On refinements of multidimensional inequalities of Hardy-type via superquadratic and subquadratic functions. J. Math. 2022, 2022, 7668860. [Google Scholar] [CrossRef]
- Kufner, A.; Maligranda, L.; Persson, L.-E. The Hardy Inequality: About Its History and Some Related Results; Vydavatelský Servis: Plzeň, Czech Republic, 2007. [Google Scholar]
- Persson, L.-E.; Kufner, A.; Samko, N. Weighted Inequalities of Hardy Type; World Scientific Publishing Company: Singapore, 2017. [Google Scholar]
- Řehák, P. Hardy inequality on time scales and its application to half-linear dynamic equations. J. Inequal. Appl. 2005, 2005, 495–507. [Google Scholar] [CrossRef]
- Bohner, M.; Georgiev, S.G. Multivariable Dynamic Calculus on Time Scales; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Agarwal, R.P.; O’Regan, D.; Saker, S.H. Hardy Type Inequalities on Time Scales; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Bohner, M.; Jadlovská, I.; Saied, A.I. Some new Hardy-type inequalities with negative parameters on time scales. Qual. Theory Dyn. Syst. 2025, 24, 72. [Google Scholar] [CrossRef]
- Kayar, Z.; Kaymakçalan, B. Converses of nabla Pachpatte-type dynamic inequalities on arbitrary time scales. Demonstr. Math. 2025, 58, 20250114. [Google Scholar] [CrossRef]
- Saqib, M.; Saleem, M.; Hasnain, S. New generalized extended Hardy-type dynamic inequalities on time scales. Babyl. J. Math. 2024, 2024, 178–197. [Google Scholar] [CrossRef]
- Aly, E.S.; Madani, Y.A.; Gassem, F.; Saied, A.I.; Rezk, H.M.; Mohammed, W.W. Some dynamic Hardy-type inequalities with negative parameters on time scales nabla calculus. AIMS Math. 2024, 9, 5147–5170. [Google Scholar] [CrossRef]
- Hasan, W.M.; El-Owaidy, H.M.; El-Deeb, A.A.; Rezk, H.M. A generalization of some integral inequalities similar to Hardy inequality on time scales. Kuwait J. Sci. 2024, 51, 100124. [Google Scholar] [CrossRef]
- Rezk, H.M.; El-Owaidy, H.M.; Hasan, W.M.; El-Deeb, A.A. Dynamic Hardy-type inequalities with convex and non-convex functions on time scales. J. Math. Sci. 2025. [Google Scholar] [CrossRef]
- Essam Awwad, A.; Saied, I. Some weighted dynamic inequalities of Hardy type with kernels on time scales nabla calculus. J. Math. Inequal. 2024, 18, 457–475. [Google Scholar] [CrossRef]
- Saker, S.H.; Mahmoud, R.R.; Osman, M.M.; Agarwal, R.P. Some new generalized forms of Hardy’s type inequality on time scales. Math. Inequal. Appl. 2017, 20, 459–481. [Google Scholar] [CrossRef]
- Bohner, M.; Peterson, A. Advances in Dynamic Equations on Time Scales; Birkhäuser Boston, Inc.: Boston, MA, USA, 2003. [Google Scholar]
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales: An Introduction with Applications; Birkhäuser Boston, Inc.: Boston, MA, USA, 2001. [Google Scholar]
- Agarwal, R.P.; Pang, P.Y. Opial Inequalities with Applications in Differential and Difference Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, T.S.; Hasan, W.M.; Popa, I.-L.; Mesmouli, M.B.; Ali, A.; Rezk, H.M. Perspectives on Dynamic Hardy–Littlewood Inequalities in Time Scale Analysis. Mathematics 2025, 13, 2176. https://doi.org/10.3390/math13132176
Hassan TS, Hasan WM, Popa I-L, Mesmouli MB, Ali A, Rezk HM. Perspectives on Dynamic Hardy–Littlewood Inequalities in Time Scale Analysis. Mathematics. 2025; 13(13):2176. https://doi.org/10.3390/math13132176
Chicago/Turabian StyleHassan, Taher S., Wafy M. Hasan, Ioan-Lucian Popa, Mouataz Billah Mesmouli, Akbar Ali, and Haytham M. Rezk. 2025. "Perspectives on Dynamic Hardy–Littlewood Inequalities in Time Scale Analysis" Mathematics 13, no. 13: 2176. https://doi.org/10.3390/math13132176
APA StyleHassan, T. S., Hasan, W. M., Popa, I.-L., Mesmouli, M. B., Ali, A., & Rezk, H. M. (2025). Perspectives on Dynamic Hardy–Littlewood Inequalities in Time Scale Analysis. Mathematics, 13(13), 2176. https://doi.org/10.3390/math13132176









