Improved Sampled-Data Consensus Control for Multi-Agent Systems via Delay-Incorporating Looped-Functional

Abstract

This paper addresses the problem of achieving consensus control for homogeneous multi-agent systems (MASs) under aperiodic sampled data and communication delays. By incorporating additional delay information, this paper introduces two novel delay-incorporating integral terms, an enhanced two-sided looped functional, and a novel discontinuous function to further exploit system state responses observed during sampling and data transmission. In addition, this paper introduces two additional zero equalities to derive less conservative stability and stabilization conditions. Based on these, sufficient conditions for guaranteeing consensus in MASs under this context are derived as linear matrix inequalities (LMIs). Finally, the effectiveness and superiority of the proposed method are validated through a numerical example.

1. Introduction

In recent years, the study of MASs has gained significant traction due to their widespread applications in fields such as robotics, unmanned aerial vehicles, intelligent transportation systems, and distributed sensor networks [1,2,3,4]. MASs consist of multiple interconnected agents that collaborate to achieve common objectives, typically in a decentralized manner. This decentralized nature makes MASs highly resilient, scalable, and adaptable to dynamic environments. One of the core objectives in MAS research is to achieve consensus, which aims to direct a group of agents toward reaching a unified state, a process known as leaderless consensus control [5], or to ensure that agents track the trajectory of a designated leader, referred to as leader-following consensus control [6]. In this context, numerous modern control strategies have been explored and implemented to address the consensus problem in MAS, such as the sampled-data control (SDC) [7,8,9], event-triggered control [10,11,12], and impulsive control [13,14]. Especially, this consensus problem becomes more complex when considering SDC strategies and networked communication, which are common in practical scenarios involving processing latencies and time delays.

With advancements in technology, research on digital networked control systems has gained significant attention in the field of control systems (see [15,16,17,18]). Among these studies, SDC has emerged as an effective technique for addressing the consensus challenge in MASs, providing notable advantages in terms of robustness and resource efficiency. By updating control inputs at discrete time intervals rather than continuously, SDC significantly reduces the demand on communication and computational resources (refer to [19]). This approach makes SDC particularly well-suited for large-scale MASs and distributed networks, where continuous feedback may be impractical. Therefore, there has been a significant amount of research aimed at dealing with the sampled-data consensus problem in MASs [20,21]. Three main methods have been proposed for the mathematical modeling of sampled-data systems: the input-delay method [22], the discrete-time method [23], and the impulsive method [24]. The input delay method, Ref. [25] addressed the aperiodic sampled-data consensus control problem of MASs through the free-matrix-based inequality approach. Subsequently, Ref. [26] introduced a memory-based SDC framework for the consensus problem in MASs with time delays, employing a looped-functional approach. More recently, Ref. [27] designed a sampled-data consensus controller for MASs by deriving a two-sided looped functional that incorporates system state information between two consecutive sampling instants. Although both [26] and [27] address the problem of sampled-data consensus with time delays, their approaches incorporate time delay information solely within the time-delay-dependent Lyapunov function framework, which does not fully exploit the delay information to accurately capture the system dynamics in the sampled-data context. This study aims to address this limitation by directly incorporating delay information into the looped-functional framework, thereby enabling a more accurate representation of the system state in sampled data and transmission processes.

Building on the above discussion, this paper focuses on the problem of aperiodic sampled-data consensus control for homogeneous MASs with communication delay. In particular, this paper focuses on extending the maximized allowable sampling interval, which is crucial for achieving an optimal balance between system performance and communication efficiency. To achieve this objective, the paper makes the following significant contributions:

• Unlike [26,27], this paper introduces two novel delay-incorporating integral terms, which are used to establish an improved looped-functional. These enhancements enable a more precise characterization of sampling-induced and network-induced delays, effectively capturing their impacts on system stability and performance.
• Based on the free-matrix-based inequality approach, this paper introduces a novel discontinuous function to improve the extraction of system state information from the most recent transmitted data.
• To strengthen the connections between the novel delay-incorporating integral terms and other elements, this paper introduces two new zero equalities. Furthermore, by incorporating two additional slack variables, the conservatism of the stability and stabilization conditions is effectively reduced.

The rest of this paper is organized as follows: Section 2 presents the system model and problem formulation, providing the mathematical foundation for the consensus control design. Section 3 details the main theoretical results, including the derivation of the stability conditions and the design of the sampled-data controller gain. Section 4 offers numerical simulations to validate the proposed methodology. Finally, Section 5 concludes the paper and outlines future research directions.

Notations: Throughout this paper, the set $N_0$ indicates the natural numbers including zero, the sets ${\mathbb{R}}^n$ and $R^{n\times m}$ are the sets of n-dimensional vectors, and $n\times m$ real matrices, respectively. The notation $P>0$ indicates that square matrix P is positive definite, $P^{-1}$ is the inverse of P, $P^T$ is the transpose of P, and $\mathrm{He}\left\{P\right\}$ stands for $P+P^T$. In symmetric matrices, the symbol (*) is used to denote terms that arise from the symmetry of the matrix structure. The operator ⊗ indicates the Kronecker product. The notation $I_n$ denotes the n-dimensional identity matrix, $0_{n\times m}$ is the $n\times m$ zero matrix, $\mathrm{diag}\{·\}$ stands for the block-diagonal matrix, $\mathrm{col}\{·\}$ is the column matrix, ${\left[a_{ij}\right]}_{N\times N}$ is $N\times N$ matrix with $a_{ij}$ at the respective position $(i,j)$.

2. Problem Statement

Let $\mathcal{G}=\{\mathcal{V},\mathcal{E},\mathcal{A}\}$ denote a directed weighted graph with the set of nodes $\mathcal{V}=\left\{v_1,v_2,\dots ,v_N\right\}$, the set of directed edges $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$, and the adjacency matrix $\mathcal{A}={\left[a_{ij}\right]}_{N\times N}$ with $a_{ii}=0$. It is assumed that the graph $\mathcal{G}$ contains a directed spanning tree. If node $v_i$ can receive information from node $v_j$, then node $v_j$ is called a neighbor of node $v_i$, that is, $a_{ij}>0$; otherwise, $a_{ij}=0$. The Laplacian matrix $\mathcal{L}={\left[{\ell }_{ij}\right]}_{N\times N}$ of the directed graph $\mathcal{G}$ is defined as ${\ell }_{ii}={\sum }_{j\ne i}{a}_{ij}$ and ${\ell }_{ij}=-a_{ij}$.

This paper considers a homogeneous MAS given by the following dynamics:

$$\begin{array}{c}\hfill {\dot{z}}_i\left(t\right)=A{z}_i\left(t\right)+B{u}_i\left(t\right)\end{array}$$

(1)

where $A\in {\mathbb{R}}^{n_z\times n_z}$ and $B\in {\mathbb{R}}^{n_z\times n_u}$ are constant matrices; $z_i\left(t\right)\in {\mathbb{R}}^{n_z}$ is the state of node $v_i$, for $i\in \{1,2,\dots ,N\}$, and $u_i\left(t\right)\in {\mathbb{R}}^{n_u}$ is the control input.

Definition 1 

([28]). The consensus of MAS (1) is achieved if and only if, for any $i,j\in \{1,2,\dots ,N\}$; the states of nodes $v_i$ and $v_j$ satisfy the equality

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\left|\right|z_i\left(t\right)-z_j\left(t\right)\left|\right|=0.\end{array}$$

As shown in Figure 1, this paper addresses the problem of sampling the state of all nodes at specific instants $t_k$ where $t_0=0$ and $t_k<t_{k+1}$, for $k\in {\mathbb{N}}_0$, and the sampling interval $h_k=t_{k+1}-t_k$ is bounded by $h_m$ and $h_M$. Then, the sampled-data controller for node $v_i$ with constant transmission delay $\tau$ is given as

$$\begin{array}{cc}\hfill u_i\left(t\right)=& -K\sum _{j=1}^N{a}_{ij}\left[z_i(t_k-\tau )-z_j(t_k-\tau )\right]\hfill \end{array}$$

(2)

where K is the sampled-data controller gain to be designed. Let the error variable be denoted by $x_i\left(t\right)=z_1\left(t\right)-z_{i+1}\left(t\right)$. From (1) and (2), the closed-loop error system is obtained as

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& \overline{A}x\left(t\right)-(\overline{\mathcal{L}}\otimes BK)x(t_k-\tau )+\overline{C}f\left(x\left(t\right)\right)\hfill \end{array}$$

(3)

where

$$\begin{array}{cc}\hfill & x\left(t\right)=col\left\{x_1\left(t\right),x_2\left(t\right),\dots ,x_{N-1}\left(t\right)\right\}\in {\mathbb{R}}^n,n=(N-1)n_z\hfill \\ \hfill & f\left(x\left(t\right)\right)=col\left\{f\left(x_1\left(t\right)\right),f\left(x_2\left(t\right)\right),\dots ,f\left(x_{N-1}\left(t\right)\right)\right\}\hfill \\ \hfill & \overline{A}=I_{N-1}\otimes A,\overline{\mathcal{L}}={\Gamma }_1\mathcal{L}{\Gamma }_2,\overline{C}=I_{N-1}\otimes C\hfill \\ \hfill & {\Gamma }_1=[1_{N-1} -I_{N-1}],{\Gamma }_2=[0_{N-1} -I_{N-1}{]}^T.\hfill \end{array}$$

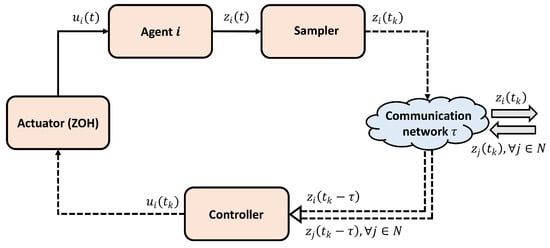
Figure 1. Diagram of SDC of MASs.

3. Control Synthesis

Let us establish the following Lyapunov–Krasovskii-based functional:

$$\begin{array}{c}\hfill V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right),t\in [t_k,t_{k+1}),\forall k\in {\mathbb{N}}_0\end{array}$$

(4)

where

$$\begin{array}{cc}\hfill & V_1\left(t\right)=x^T\left(t\right)Px\left(t\right)+{\int }_{t-\tau }^t{\eta }_1^T\left(s\right)W{\eta }_1\left(s\right)ds+{\int }_{-\tau }^0{\int }_{t+\theta }^t{\dot{x}}^T\left(s\right)S\dot{x}\left(s\right)dsd\theta \hfill \\ \hfill & V_2\left(t\right)=d_2\left(t\right)2{\eta }_2^T\left(t\right)X_1{\eta }_3\left(t\right)+d_1\left(t\right)2{\eta }_4^T\left(t\right)X_2{\eta }_5\left(t\right)+d_1\left(t\right)d_2\left(t\right){\eta }_6^{T}U{\eta }_6\hfill \\ \hfill & +d_2\left(t\right){\int }_{t_k-\tau }^{t-\tau }{\dot{x}}^T\left(s\right)R_1\dot{x}\left(s\right)ds-d_1\left(t\right){\int }_{t-\tau }^{t_{k+1}-\tau }{\dot{x}}^T\left(s\right)R_2\dot{x}\left(s\right)ds\hfill \\ \hfill & V_3\left(t\right)=h_M{\eta }_7^T\left(t\right)Q_1{\eta }_7\left(t\right)+2\left(x^T(t-\tau )-x^T(t_k-\tau )\right)Q_2{\eta }_7\left(t\right)+{\int }_{t_k-\tau }^{t-\tau }{\dot{x}}^T\left(s\right)Q_3\dot{x}\left(s\right)ds\hfill \end{array}$$

in which

$$\begin{array}{cc}\hfill & d_1\left(t\right)=t-t_k,d_2\left(t\right)=t_{k+1}-t,{\eta }_1\left(t\right)=\mathrm{col}\left\{x\left(t\right),\dot{x}\left(t\right)\right\}\hfill \\ \hfill & {\eta }_2\left(t\right)=\mathrm{col}\left\{x(t-\tau )-x(t_k-\tau ),{\int }_{t_k-\tau }^{t-\tau }x\left(s\right)ds,{\int }_{t_k-\tau }^{t-\tau }(t-s)\dot{x}\left(s\right)ds\right\}\hfill \\ \hfill & {\eta }_3\left(t\right)=\mathrm{col}\left\{x(t-\tau ),x(t_k-\tau ),{\int }_{t_k-\tau }^{t-\tau }x\left(s\right)ds,{\int }_{t_k-\tau }^{t-\tau }(t-s)\dot{x}\left(s\right)ds\right\}\hfill \\ \hfill & {\eta }_4\left(t\right)=\mathrm{col}\left\{x(t_{k+1}-\tau )-x(t-\tau ),{\int }_{t-\tau }^{t_{k+1}-\tau }x\left(s\right)ds,{\int }_{t-\tau }^{t_{k+1}-\tau }(t-s)\dot{x}\left(s\right)ds\right\}\hfill \\ \hfill & {\eta }_5\left(t\right)=\mathrm{col}\left\{x(t-\tau ),x(t_{k+1}-\tau ),{\int }_{t-\tau }^{t_{k+1}-\tau }x\left(s\right)ds,{\int }_{t-\tau }^{t_{k+1}-\tau }(t-s)\dot{x}\left(s\right)ds\right\}\hfill \\ \hfill & {\eta }_6=\mathrm{col}\left\{x(t_k-\tau ),x(t_{k+1}-\tau )\right\},{\eta }_7\left(t\right)=\mathrm{col}\left\{x(t-\tau ),x(t_k-\tau )\right\}\hfill \\ \hfill & P=P^T\in {\mathbb{R}}^{n\times n},W=W^T\in {\mathbb{R}}^{2n\times 2n},S=S^T\in {\mathbb{R}}^{n\times n},X_1,X_2\in {\mathbb{R}}^{3n\times 4n}\hfill \\ \hfill & R_1=R_1^T,R_2=R_2^T\in {\mathbb{R}}^{n\times n},Q_1=Q_1^T\in {\mathbb{R}}^{2n\times 2n},Q_2\in {\mathbb{R}}^{n\times 2n},Q_3=Q_3^T\in {\mathbb{R}}^{n\times n}\hfill \end{array}$$

subject to $P>0$, $W>0$, $S>0$, and

$$0<\left[\begin{array}{cc}{Q}_1& (\ast )\\ Q_2& Q_3\end{array}\right].$$

(5)

Given that $V_2\left(t\right)$ satisfies $V_2\left(t_k\right)=0$ and ${lim}_{t\to t_{k+1}^{-}}{V}_2\left(t\right)=0$, the positive definiteness of $V_2\left(t\right)$ can be omitted based on the looped-functional approach [29]. Then, since condition (5) ensures

$$\begin{array}{c}0<{\int }_{t_k-\tau }^{t-\tau }\left[\begin{array}{c}{\eta }_7\left(t\right)\\ \dot{x}\left(s\right)\end{array}{]}^T\right[\begin{array}{cc}{Q}_1& (\ast )\\ Q_2& Q_3\end{array}\left]\right[\begin{array}{c}{\eta }_7\left(t\right)\\ \dot{x}\left(s\right)\end{array}]ds\hfill \\ \begin{array}{c}\le h_M{\eta }_7^T\left(t\right)Q_1{\eta }_7\left(t\right)+2\left(x^T(t-\tau )-x^T(t_k-\tau )\right)Q_2{\eta }_7\left(t\right)+{\int }_{t_k-\tau }^{t-\tau }{\dot{x}}^T\left(s\right)Q_3\dot{x}\left(s\right)ds\end{array}\end{array}$$

follows that $V_3\left(t\right)\ge 0$ for all $t\in [t_k,t_{k+1})$. Furthermore, the term ${\int }_{t_k-\tau }^t{\dot{x}}^T\left(s\right)Q_3\dot{x}\left(s\right)ds$ disappears at $t=t_k$, i.e., $\underset{t\to t_k^{-}}{lim}{V}_3\left(t\right)\ge V_3\left(t_k\right)$. This indicates that the jump in discontinuous functional $V_3\left(t\right)$ at every sampling instance $t_k$ is diminished.

Remark 1. 

To capture the impacts of delay on system stability and performance, it is essential to fully exploit the delay information within a Lyapunov–Krasovskii-based functional. Distinct from [26] and [27], this paper proposes an improved looped-functional $V_2\left(t\right)$ and a novel discontinuous function $V_3\left(t\right)$, which incorporate more comprehensive delay information. Furthermore, two novel delay-incorporating integral terms, ${\int }_{t_k-\tau }^{t-\tau }(t-s)\dot{x}\left(s\right)ds$ and ${\int }_{t-\tau }^{t_{k+1}-\tau }(t-s)\dot{x}\left(s\right)ds$, are introduced into the looped-functional framework.

The following theorem establishes the stability condition for achieving consensus of homogeneous MASs.

Theorem 1. 

For given positive scalars ${\epsilon }_1$, ${\epsilon }_2$, τ, $h_m$, and $h_M$, the consensus of MAS (1) can be achieved, if there exist symmetric matrices $0<P=P^T\in {\mathbb{R}}^{n\times n}$, $0<W=W^T\in {\mathbb{R}}^{2n\times 2n}$, $0<S=S^T\in {\mathbb{R}}^{n\times n}$, $X_1$, $X_2\in {\mathbb{R}}^{3n\times 4n}$, $R_1=R_1^T$, $R_2=R_2^T\in {\mathbb{R}}^{n\times n}$, $U=U^T\in {\mathbb{R}}^{2n\times 2n}$, $Q_1=Q_1^T\in {\mathbb{R}}^{2n\times 2n}$, $Q_2\in {\mathbb{R}}^{n\times 2n}$, $Q_3=Q_3^T\in {\mathbb{R}}^{n\times n}$, $M\in {\mathbb{R}}^{n\times 2n}$, $N_1$, $N_2\in {\mathbb{R}}^{n\times 2n}$, $Z_1$, $Z_2\in {\mathbb{R}}^{n\times 4n}$, and $G\in {\mathbb{R}}^{n\times n}$ such that the following conditions are satisfied, for $h_k\in \{h_m,h_M\}$: LMI (5),

$$0>\left[\begin{array}{ccc}{\Psi }_1+{\Psi }_2\left(t_k\right)& (\ast )& (\ast )\\ \tau M{\Xi }_8& -\tau S& 0\\ h_k{N}_2{\Xi }_{10}& 0& -h_k{R}_2\end{array}\right]$$

(6)

$$0>\left[\begin{array}{ccc}{\Psi }_1+{\Psi }_2\left(t_{k+1}\right)& (\ast )& (\ast )\\ \tau M{\Xi }_8& -\tau S& 0\\ h_k{N}_1{\Xi }_9& 0& -h_k{R}_1\end{array}\right]$$

(7)

where

$$\begin{array}{cc}\hfill & {\Psi }_1=\mathrm{He}\left\{{\mathbf{e}}_1^{T}P{\mathbf{e}}_9-{\Xi }_2^T{X}_1{\Xi }_3+{\Xi }_4^T{X}_2{\Xi }_5\right\}+{\Xi }_1^{T}W{\Xi }_1-{\widehat{\Xi }}_1^{T}W{\widehat{\Xi }}_1+\tau {\mathbf{e}}_9^T{S\mathbf{e}}_9\hfill \\ \hfill & +\mathrm{He}\left\{h_M{\overline{\Xi }}_7^T{Q}_1{\Xi }_7+{\mathbf{e}}_{10}^T{Q}_2{\Xi }_7+\left({\mathbf{e}}_2^T-{\mathbf{e}}_3^T\right)Q_2{\overline{\Xi }}_7+{\mathbf{e}}_{10}^T{Q}_3{\mathbf{e}}_{10}\right\}\hfill \\ \hfill & +\mathrm{He}\left\{({\mathbf{e}}_1^T-{\mathbf{e}}_2^T)M{\Xi }_8+({\mathbf{e}}_2^T-{\mathbf{e}}_3^T)N_1{\Xi }_9+({\mathbf{e}}_4^T-{\mathbf{e}}_2^T)N_2{\Xi }_{10}\right\}\hfill \\ \hfill & +\mathrm{He}\{{\Xi }_{11}^T{Z}_1^T\left(\tau ({\mathbf{e}}_2-{\mathbf{e}}_3)+{\mathbf{e}}_5-{\mathbf{e}}_7\right)+{\Xi }_{12}^T{Z}_2^T\left(\tau ({\mathbf{e}}_4-{\mathbf{e}}_2)+{\mathbf{e}}_6-{\mathbf{e}}_8\right)\}\hfill \\ \hfill & +\mathrm{He}\left\{{\Xi }_{13}^T{G}^T\left(\overline{A}{\mathbf{e}}_1-(\overline{\mathcal{L}}\otimes BK){\mathbf{e}}_3+\overline{C}{\mathbf{e}}_{11}-{\mathbf{e}}_9\right)\right\}\hfill \\ \hfill & {\Psi }_2\left(t\right)=d_2\left(t\right)\mathrm{He}\left\{{\overline{\Xi }}_2^T{X}_1{\Xi }_3+{\Xi }_2^T{X}_1{\overline{\Xi }}_3+{\Xi }_6^{T}U{\Xi }_6+{\mathbf{e}}_{10}^T{R}_1{\mathbf{e}}_{10}-{\Xi }_{11}^T{Z}_1^T{\mathbf{e}}_3\right\}\hfill \\ \hfill & +d_1\left(t\right)\mathrm{He}\left\{{\overline{\Xi }}_4^T{X}_2{\Xi }_5+{\Xi }_4^T{X}_2{\overline{\Xi }}_5-{\Xi }_6^{T}U{\Xi }_6+{\mathbf{e}}_{10}^T{R}_2{\mathbf{e}}_{10}-{\Xi }_{12}^T{Z}_2^T{\mathbf{e}}_4\right\}\hfill \end{array}$$

in which

$$\begin{array}{cc}\hfill & {\mathbf{e}}_i=[0_{n\times (i-1)n} I_n 0_{n\times (11-i)n}],{\Xi }_1=\mathrm{col}\{{\mathbf{e}}_1,{\mathbf{e}}_9\},{\widehat{\Xi }}_1=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_{10}\}\hfill \\ \hfill & {\Xi }_2=\mathrm{col}\{{\mathbf{e}}_2-{\mathbf{e}}_3,{\mathbf{e}}_5,{\mathbf{e}}_7\},{\overline{\Xi }}_2=\mathrm{col}\{{\mathbf{e}}_{10},{\mathbf{e}}_2,\tau {\mathbf{e}}_{10}+{\mathbf{e}}_2-{\mathbf{e}}_3\}\hfill \\ \hfill & {\Xi }_3=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_3,{\mathbf{e}}_5,{\mathbf{e}}_7\},{\overline{\Xi }}_3=\mathrm{col}\{{\mathbf{e}}_{10},0,{\mathbf{e}}_2,\tau {\mathbf{e}}_{10}+{\mathbf{e}}_2-{\mathbf{e}}_3\}\hfill \\ \hfill & {\Xi }_4=\mathrm{col}\{{\mathbf{e}}_4-{\mathbf{e}}_2,{\mathbf{e}}_6,{\mathbf{e}}_8\},{\overline{\Xi }}_4=\mathrm{col}\{-{\mathbf{e}}_{10},-{\mathbf{e}}_2,-\tau {\mathbf{e}}_{10}+{\mathbf{e}}_4-{\mathbf{e}}_2\}\hfill \\ \hfill & {\Xi }_5=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_4,{\mathbf{e}}_6,{\mathbf{e}}_8\},{\overline{\Xi }}_5=\mathrm{col}\{{\mathbf{e}}_{10},0,-{\mathbf{e}}_2,-\tau {\mathbf{e}}_{10}+{\mathbf{e}}_4-{\mathbf{e}}_2\}\hfill \\ \hfill & {\Xi }_6=\mathrm{col}\{{\mathbf{e}}_3,{\mathbf{e}}_4\},{\Xi }_7=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_3\},{\overline{\Xi }}_7=\mathrm{col}\{{\mathbf{e}}_{10},0\},{\Xi }_8=\mathrm{col}\{{\mathbf{e}}_1,{\mathbf{e}}_2\}\hfill \\ \hfill & {\Xi }_9=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_3\},{\Xi }_{10}=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_4\},{\Xi }_{11}=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_3,{\mathbf{e}}_5,{\mathbf{e}}_7\}\hfill \\ \hfill & {\Xi }_{12}=\mathrm{col}\{{\mathbf{e}}_2,{\mathbf{e}}_4,{\mathbf{e}}_6,{\mathbf{e}}_8\},{\Xi }_{13}={\mathbf{e}}_1+{\epsilon }_1{\mathbf{e}}_3+{\epsilon }_2{\mathbf{e}}_9.\hfill \end{array}$$

Proof. 

The time derivatives of (4) are derived as follows:

$$\begin{array}{cc}\hfill & {\dot{V}}_1\left(t\right)=2x^T\left(t\right)P\dot{x}\left(t\right)+{\eta }_1^T\left(t\right)W{\eta }_1\left(t\right)-{\eta }_1^T(t-\tau )W{\eta }_1(t-\tau )\hfill \\ \hfill & +\tau {\dot{x}}^T(t)S\dot{x}\left(t\right){\underset{\_}{-{\int }_{t-\tau }^t{\dot{x}}^T\left(s\right)S\dot{x}\left(s\right)ds}}_{:=T_1\left(t\right)}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & {\dot{V}}_2\left(t\right)=d_2\left(t\right)\left(2{\dot{\eta }}_2^T\left(t\right)X_1{\eta }_3\left(t\right)+2{\eta }_2^T\left(t\right)X_1{\dot{\eta }}_3\left(t\right)+{\eta }_6^{T}U{\eta }_6\right)\hfill \\ \hfill & +d_1\left(t\right)\left(2{\dot{\eta }}_4^T\left(t\right)X_2{\eta }_5\left(t\right)+2{\eta }_4^T\left(t\right)X_2{\dot{\eta }}_5\left(t\right)-{\eta }_6^{T}U{\eta }_6\right)\hfill \\ \hfill & -2{\eta }_2^T\left(t\right)X_1{\eta }_3\left(t\right)+2{\eta }_4^T\left(t\right)X_2{\eta }_5\left(t\right)\hfill \\ \hfill & +d_2\left(t\right){\dot{x}}^T(t-\tau )R_1\dot{x}(t-\tau )+d_1\left(t\right){\dot{x}}^T(t-\tau )R_2\dot{x}(t-\tau )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\underset{\_}{-{\int }_{t_k-\tau }^{t-\tau }{\dot{x}}^T\left(s\right)R_1\dot{x}\left(s\right)ds}}_{:=T_2\left(t\right)}{\underset{\_}{-{\int }_{t-\tau }^{t_{k+1}-\tau }{\dot{x}}^T\left(s\right)R_2\dot{x}\left(s\right)ds}}_{:=T_3\left(t\right)}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\dot{V}}_3\left(t\right)=2h_M{\dot{\eta }}_7\left(t\right)Q_1{\eta }_7\left(t\right)+2{\dot{x}}^T(t-\tau )Q_2{\eta }_7\left(t\right)\hfill \\ \hfill & +2\left(x^T(t-\tau )-x^T(t_k-\tau )\right)Q_2{\dot{\eta }}_7\left(t\right)+{\dot{x}}^T(t-\tau )Q_3\dot{x}(t-\tau ).\hfill \end{array}$$

(10)

Since it is clear that

$$\begin{array}{cc}\hfill 0& \le {\int }_{\alpha }^{\beta }\left({\dot{x}}^T\left(s\right)R+{\eta }^T\left(t\right)M^T\right)R^{-1}\left(R\dot{x}\left(s\right)+M\eta \left(t\right)\right)ds\hfill \\ \hfill & ={\int }_{\alpha }^{\beta }{\dot{x}}^T\left(s\right)R\dot{x}\left(s\right)ds+(\beta -\alpha ){\eta }^T\left(t\right)M^T{R}^{-1}M\eta \left(t\right)+2(x^T\left(\beta \right)-x^T\left(\alpha \right))M\eta \left(t\right)\hfill \end{array}$$

the following inequalities is satisfied:

$$\begin{array}{cc}\hfill T_1\left(t\right)& \le \tau {\eta }_8^T\left(t\right)M^T{S}^{-1}M{\eta }_8\left(t\right)+2(x^T\left(t\right)-x^T(t-\tau ))M{\eta }_8\left(t\right)\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill T_2\left(t\right)& \le d_1\left(t\right){\eta }_9^T\left(t\right)N_1^T{R}_1^{-1}{N}_1{\eta }_9\left(t\right)+2(x^T(t-\tau )-x^T(t_k-\tau ))N_1{\eta }_9\left(t\right)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill T_3\left(t\right)& \le d_2\left(t\right){\eta }_{10}^T\left(t\right)N_2^T{R}_2^{-1}{N}_2{\eta }_{10}\left(t\right)+2(x^T(t_{k+1}-\tau )-x^T(t-\tau ))N_2{\eta }_{10}\left(t\right)\hfill \end{array}$$

(13)

where ${\eta }_8\left(t\right)=\mathrm{col}\left\{x\left(t\right),x(t-\tau )\right\}$, ${\eta }_9\left(t\right)=\mathrm{col}\left\{x(t-\tau ),x(t_k-\tau )\right\}$, ${\eta }_{10}\left(t\right)=\mathrm{col}\left\{x(t-\tau ),x(t_{k+1}-\tau )\right\}$. Next, using integration by parts, the following zero equalities hold:

$$\begin{array}{cc}\hfill 0& =2{\eta }_{11}^T\left(t\right)Z_1^T(-{\int }_{t_k-\tau }^{t-\tau }(t-s)\dot{x}\left(s\right)ds+\tau (x(t-\tau )-x(t_k-\tau ))\hfill \\ \hfill & -d_1\left(t\right)x(t_k-\tau )+{\int }_{t_k-\tau }^{t-\tau }x\left(s\right)ds)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill 0& =2{\eta }_{12}^T\left(t\right)Z_2^T(-{\int }_{t-\tau }^{t_{k+1}-\tau }(t-s)\dot{x}\left(s\right)ds+\tau (x(t_{k+1}-\tau )-x(t-\tau ))\hfill \\ \hfill & -d_2\left(t\right)x(t_{k+1}-\tau )+{\int }_{t-\tau }^{t_{k+1}-\tau }x\left(s\right)ds).\hfill \end{array}$$

(15)

Additionally, based on (3), we have

$$\begin{array}{cc}\hfill 0& =2{\eta }_{13}^T\left(t\right)G^T\left(\overline{A}x\left(t\right)-(\overline{\mathcal{L}}\otimes BK)x(t_k-\tau )+\overline{C}f\left(x\left(t\right)\right)-\dot{x}\left(t\right)\right).\hfill \end{array}$$

(16)

Subsequently, by combining (8)–(16), we can obtain

$$\begin{array}{c}\hfill \dot{V}\left(t\right)\le {\eta }^T\left(t\right)\Psi \left(t\right)\eta \left(t\right)\end{array}$$

(17)

where

$$\begin{array}{cc}\hfill & \eta \left(t\right)=\mathrm{col}\{x\left(t\right),x(t-\tau ),x(t_k-\tau ),x(t_{k+1}-\tau ),{\int }_{t_k-\tau }^{t-\tau }x\left(s\right)ds,{\int }_{t-\tau }^{t_{k+1}-\tau }x\left(s\right)ds,\hfill \\ \hfill & {\int }_{t_k-\tau }^{t-\tau }(t-s)\dot{x}\left(s\right)ds,{\int }_{t-\tau }^{t_{k+1}-\tau }(t-s)\dot{x}\left(s\right)ds,\dot{x}\left(t\right),\dot{x}(t-\tau ),f\left(x\left(t\right)\right)\}\hfill \\ \hfill & \Psi \left(t\right)={\Psi }_1+{\Psi }_2\left(t\right)+\tau {\Xi }_8^T{M}^T{S}^{-1}M{\Xi }_8+d_1\left(t\right){\Xi }_9^T{N}_1^T{R}_1^{-1}{N}_1{\Xi }_9+d_2\left(t\right){\Xi }_{10}^T{N}_2^T{R}_2^{-1}{N}_2{\Xi }_{10}.\hfill \end{array}$$

As a result, from $t\in [t_k,t_{k+1})$ and $h_k\in [h_m,h_M]$, the stability condition $\dot{V}\left(t\right)<0$ can be represented as the following linear convex combination, for $h_k\in \{h_m,h_M\}$:

$$\begin{array}{cc}\hfill & 0>{\Psi }_1+{\Psi }_2\left(t_k\right)+\tau {\Xi }_8^T{M}^T{S}^{-1}M{\Xi }_8+h_k{\Xi }_{10}^T{N}_2^T{R}_2^{-1}{N}_2{\Xi }_{10}^T\hfill \\ \hfill & 0>{\Psi }_1+{\Psi }_2\left(t_{k+1}\right)+\tau {\Xi }_8^T{M}^T{S}^{-1}M{\Xi }_8+h_k{\Xi }_9^T{N}_1^T{R}_1^{-1}{N}_1{\Xi }_9\hfill \end{array}$$

which are transformed into (6) and (7) using the Schur complement. □

Remark 2. 

The inclusion of new elements in the looped-functional requires careful consideration of the relationship between these elements. Compared to [26] and [27], this paper establishes two new zero equalities, (14) and (15), within the stability analysis framework. Building upon this, two slack variables, $Z_1$ and $Z_2$, are integrated into the stability condition, thereby reducing the conservatism of the results.

Based on the stability condition of Theorem 1, the corresponding sampled-data controller is provided in the following theorem.

Theorem 2. 

For given positive scalars ${\epsilon }_1$, ${\epsilon }_2$, τ, $h_m$, and $h_M$, the consensus of MAS (1) can be achieved, if there exist symmetric matrices $0<\overline{P}={\overline{P}}^T\in {\mathbb{R}}^{n\times n}$, $0<\overline{W}={\overline{W}}^T\in {\mathbb{R}}^{2n\times 2n}$, $0<\overline{S}={\overline{S}}^T\in {\mathbb{R}}^{n\times n}$, ${\overline{X}}_1$, ${\overline{X}}_2\in {\mathbb{R}}^{3n\times 4n}$, ${\overline{R}}_1={\overline{R}}_1^T$, ${\overline{R}}_2={\overline{R}}_2^T\in {\mathbb{R}}^{n\times n}$, $\overline{U}={\overline{U}}^T\in {\mathbb{R}}^{2n\times 2n}$, ${\overline{Q}}_1={\overline{Q}}_1^T\in {\mathbb{R}}^{2n\times 2n}$, ${\overline{Q}}_2\in {\mathbb{R}}^{n\times 2n}$, ${\overline{Q}}_3={\overline{Q}}_3^T\in {\mathbb{R}}^{n\times n}$, $\overline{M}\in {\mathbb{R}}^{n\times 2n}$, ${\overline{N}}_1$, ${\overline{N}}_2\in {\mathbb{R}}^{n\times 2n}$, ${\overline{Z}}_1$, ${\overline{Z}}_2\in {\mathbb{R}}^{n\times 4n}$, $0<\overline{G}=I_{N-1}\otimes \widehat{G}\in {\mathbb{R}}^{n\times n}$, and $\overline{K}\in {\mathbb{R}}^{n_u\times n_z}$, such that the following conditions are satisfied, for $h_k\in \{h_m,h_M\}$:

$$0<\left[\begin{array}{cc}{\overline{Q}}_1& (\ast )\\ {\overline{Q}}_2& {\overline{Q}}_3\end{array}\right]$$

(18)

$$0>\left[\begin{array}{ccc}{\overline{\Psi }}_1+{\overline{\Psi }}_2\left(t_k\right)& (\ast )& (\ast )\\ \tau \overline{M}{\Xi }_8& -\tau \overline{S}& 0\\ h_k{\overline{N}}_2{\Xi }_{10}& 0& -h_k{\overline{R}}_2\end{array}\right]$$

(19)

$$0>\left[\begin{array}{ccc}{\overline{\Psi }}_1+{\overline{\Psi }}_2\left(t_{k+1}\right)& (\ast )& (\ast )\\ \tau \overline{M}{\Xi }_8& -\tau \overline{S}& 0\\ h_k{\overline{N}}_1{\Xi }_9& 0& -h_k{\overline{R}}_1\end{array}\right]$$

(20)

where

$$\begin{array}{cc}\hfill & {\overline{\Psi }}_1=\mathrm{He}\left\{{\mathbf{e}}_1^T\overline{P}{\mathbf{e}}_9-{\Xi }_2^T{\overline{X}}_1{\Xi }_3+{\Xi }_4^T{\overline{X}}_2{\Xi }_5\right\}+{\Xi }_1^T\overline{W}{\Xi }_1-{\widehat{\Xi }}_1^T\overline{W}{\widehat{\Xi }}_1+\tau {\mathbf{e}}_9^T\overline{S}{\mathbf{e}}_9\hfill \\ \hfill & +\mathrm{He}\left\{h_M{\overline{\Xi }}_7^T{\overline{Q}}_1{\Xi }_7+{\mathbf{e}}_{10}^T{\overline{Q}}_2{\Xi }_7+\left({\mathbf{e}}_2^T-{\mathbf{e}}_3^T\right){\overline{Q}}_2{\overline{\Xi }}_7+{\mathbf{e}}_{10}^T{\overline{Q}}_3{\mathbf{e}}_{10}\right\}\hfill \\ \hfill & +\mathrm{He}\left\{({\mathbf{e}}_1^T-{\mathbf{e}}_2^T)\overline{M}{\Xi }_8+({\mathbf{e}}_2^T-{\mathbf{e}}_3^T){\overline{N}}_1{\Xi }_9+({\mathbf{e}}_4^T-{\mathbf{e}}_2^T){\overline{N}}_2{\Xi }_{10}\right\}\hfill \\ \hfill & +\mathrm{He}\{{\Xi }_{11}^T{\overline{Z}}_1^T\left(\tau ({\mathbf{e}}_2-{\mathbf{e}}_3)+{\mathbf{e}}_5-{\mathbf{e}}_7\right)+{\Xi }_{12}^T{\overline{Z}}_2^T\left(\tau ({\mathbf{e}}_4-{\mathbf{e}}_2)+{\mathbf{e}}_6-{\mathbf{e}}_8\right)\}\hfill \\ \hfill & +\mathrm{He}\left\{{\Xi }_{13}^T\left(\overline{A} \overline{G}{\mathbf{e}}_1-(\overline{\mathcal{L}}\otimes B\overline{K}){\mathbf{e}}_3+\overline{C} \overline{G}{\mathbf{e}}_{11}-\overline{G}{\mathbf{e}}_9\right)\right\}\hfill \\ \hfill & {\overline{\Psi }}_2\left(t\right)=d_2\left(t\right)\mathrm{He}\left\{{\overline{\Xi }}_2^T{\overline{X}}_1{\Xi }_3+{\Xi }_2^T{\overline{X}}_1{\overline{\Xi }}_3+{\Xi }_6^T\overline{U}{\Xi }_6+{\mathbf{e}}_{10}^T{\overline{R}}_1{\mathbf{e}}_{10}-{\Xi }_{11}^T{\overline{Z}}_1^T{\mathbf{e}}_3\right\}\hfill \\ \hfill & +d_1\left(t\right)\mathrm{He}\left\{{\overline{\Xi }}_4^T{\overline{X}}_2{\Xi }_5+{\Xi }_4^T{\overline{X}}_2{\overline{\Xi }}_5-{\Xi }_6^T\overline{U}{\Xi }_6+{\mathbf{e}}_{10}^T{\overline{R}}_2{\mathbf{e}}_{10}-{\Xi }_{12}^T{\overline{Z}}_2^T{\mathbf{e}}_4\right\}\hfill \end{array}$$

Then, the control gain is reconstructed by $K=\overline{K}{\widehat{G}}^{-1}$.

Proof. 

Let us construct several congruent transformation matrices ${\mathbf{G}}_2=I_2\otimes \overline{G}$, ${\mathbf{G}}_3=I_3\otimes \overline{G}$, ${\mathbf{G}}_4=I_4\otimes \overline{G}$, and ${\mathbf{G}}_{13}=I_{13}\otimes \overline{G}$. Then, using the subsequent replacement variables:

$$\begin{array}{cc}\hfill & G={\overline{G}}^{-1},\overline{K}=K\widehat{G},\overline{P}={\overline{G}}^{T}P\overline{G},\overline{W}={\mathbf{G}}_2^{T}W{\mathbf{G}}_2,\overline{S}={\overline{G}}^T\overline{S}\overline{G},{\overline{X}}_1={\mathbf{G}}_3^T{X}_1{\mathbf{G}}_4,{\overline{X}}_2={\mathbf{G}}_3^T{X}_2{\mathbf{G}}_4\hfill \\ \hfill & {\overline{R}}_1={\overline{G}}^T{R}_1\overline{G},{\overline{R}}_2={\overline{G}}^T{R}_2\overline{G},\overline{U}={\mathbf{G}}_2^T{U\mathbf{G}}_2,{\overline{Q}}_1={\mathbf{G}}_2^T{Q}_1{\mathbf{G}}_2,{\overline{Q}}_2={\overline{G}}^T{Q}_2{\mathbf{G}}_2,{\overline{Q}}_3={\overline{G}}^T{Q}_3\overline{G}\hfill \\ \hfill & \overline{M}={\overline{G}}^{T}M{\mathbf{G}}_2,{\overline{N}}_1={\overline{G}}^T{N}_1{\mathbf{G}}_2,{\overline{N}}_2={\overline{G}}^T{N}_2{\mathbf{G}}_2,{\overline{Z}}_1={\overline{G}}^T{Z}_1{\mathbf{G}}_4,{\overline{Z}}_2={\overline{G}}^T{Z}_2{\mathbf{G}}_4\hfill \end{array}$$

condition (18)–(20) are derived by pre- and post-multiplying (5)–(7) by ${\mathbf{G}}_3^T$, ${\mathbf{G}}_{13}^T$, and ${\mathbf{G}}_{13}^T$ and their transpose, respectively. □

Remark 3. 

The number of variables (NoVs) required for Theorems 1 and 2 are computed as follows: ${\mathrm{NoVs}}_{\mathrm{Th}1}=49.5$$n^2$+5.5 n and ${\mathrm{NoVs}}_{\mathrm{Th}2}=48.5$$n^2+5.5$n + $n_z^2+n_u{n}_z$, respectively.

4. Illuminate Examples

The simulation is performed using MATLAB R2023b software from MathWorks, Inc. [30]. The LMI conditions (18)–(20) in Theorem 2 are numerically solved by LMI solver in Robust Control Toolbox, MATLAB.

Consider a diode circuit system model with $N=5$, as described in [27].

$$\left\{\begin{array}{c}{\dot{z}}_{i1}\left(t\right)={\displaystyle \frac{0.2}{C}}{z}_{i1}\left(t\right)+{\displaystyle \frac{1}{C}}{z}_{i2}\left(t\right)\hfill \\ {\dot{z}}_{i2}\left(t\right)=-{\displaystyle \frac{1}{L}}{z}_{i1}\left(t\right)-{\displaystyle \frac{R}{L}}{z}_{i2}\left(t\right)+{\displaystyle \frac{1}{L}}{u}_i\left(t\right),i\in \{1,\dots ,5\}\hfill \end{array}\right.$$

where $z_{i1}\left(t\right)=v_D\left(t\right)$ represents the voltage across the diode (V) and $z_{i2}\left(t\right)=i_D\left(t\right)$ denotes the diode current (A). In particular, the system parameters are defined as capacitance $C=0.2\mathrm{F}$, resistance $R=2\Omega$, and inductance $L=0.1\mathrm{H}$. Accordingly, the diode circuit system model can be represented in the form (1) as follows:

$$A=\left[\begin{array}{cc}1& 5\\ -10& -20\end{array}\right],B=\left[\begin{array}{c}0\\ 10\end{array}\right].$$

Following [27], we consider the Laplacian matrix given below:

$$\begin{array}{c}\hfill \mathcal{L}=\left[\begin{array}{ccccc}2& -1& 0& 0& -1\\ -1& 2& -1& 0& 0\\ 0& -1& 2& -1& 0\\ 0& 0& -1& 2& -1\\ -1& 0& 0& -1& 2\end{array}\right]\end{array}$$

For comparison, Table 1 presents the maximized upper bound of the sampling interval $h_M$ corresponding to various communication delays $\tau$, as obtained from [25] (Theorem 3), [26] (Theorem 3.1), [27] (Corollary 1), and Theorem 2, with ${\epsilon }_1=1$, ${\epsilon }_2=1$, and $h_m={10}^{-4}$.

Table 1. Comparison of maximized $h_M$ for different $\tau$.

Method	$\mathit{\tau }=0.1$	$\mathit{\tau }=0.2$	$\mathit{\tau }=0.3$	$\mathit{\tau }=0.5$	NoVs
[25] (Theorem 3)	0.6480	0.4959	0.3448	0.0733	248
[26] (Theorem 3.1)	0.8004	0.6433	0.4862	0.1721	1280
[27] (Corollary 1)	0.8763	0.7299	0.5887	0.3479	2704
Theorem 2	1.5322	1.0671	0.8165	0.5874	3154

Table 1 demonstrates that Theorem 2 provides a larger maximized upper bound $h_M$ for all values of $\tau$ compared to [25] (Theorem 3), [26] (Theorem 3.1) and [27] (Corollary 1). Specifically, when compared to [27] (Corollary 1) for $\tau =0.5$, although Theorem 2 requires approximately $16.6\%$ more in the NoV, it yields an increase of about $68.8\%$ in the maximized upper bound $h_M$. This demonstrates that Theorem 2 provides a significantly larger maximized allowable sampling interval, despite the slightly higher computational complexity.

Then, by solving Theorem 2 with ε₁ = 1, ε₂ = 1, τ = 0.1, $h_m={10}^{-4}$, and $h_M=1.5322$, the sampled-data controller gain can be determined as follows:

$$\begin{array}{cc}\hfill K=[-0.0168& -0.0238].\hfill \end{array}$$

For the initial value $z_i\left(0\right)=\mathrm{col}\{2i-i^{-1},i\}$ for $i\in 1,2,\dots ,5$, $h_k\in [{10}^{-4},1.5322]$, and $\tau =0.1$, the sampled state $z_i\left(t_k\right)$ and the sampled state with time delay $z_i(t_k-\tau )$ for each agent are shown in Figure 2a and Figure 2b, respectively. Subsequently, the SDC input $u_i\left(t\right)$ is as illustrated in Figure 3a. Under this SDC input, the system state trajectories for each agent are shown in Figure 3b. As observed in Figure 3, the system state trajectories of agent i exhibit convergence to zero within a relatively brief time interval. Therefore, the proposed sampled-data controller effectively ensures the consensus of homogeneous MASs.

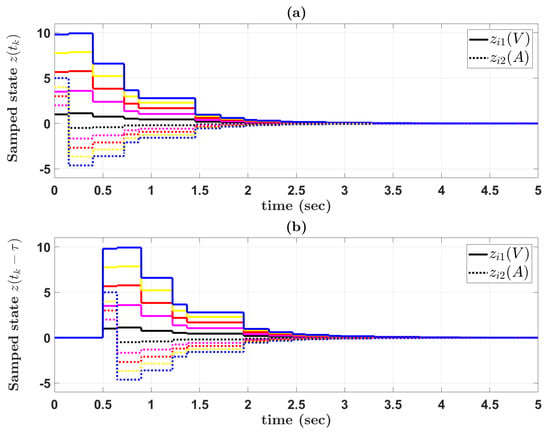
Figure 2. (a) Sampled state $z_i\left(t_k\right)$ and (b) sampled state with time delay $z(t_k-\tau )$.

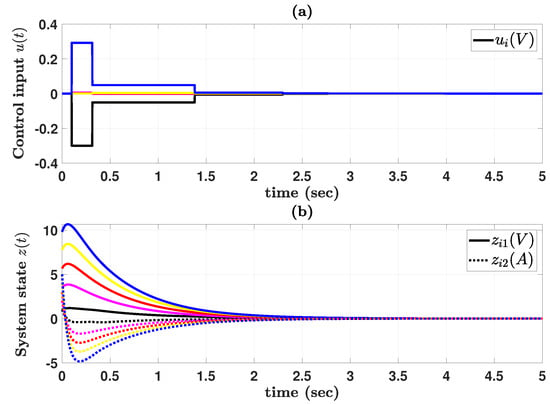
Figure 3. (a) Control input $u\left(t\right)$ and (b) system state $z_i\left(t\right)$.

5. Concluding Remarks

This paper presents an improved approach to designing a consensus controller for homogeneous MASs with aperiodic sampled data and communication delay. To exploit information about system state responses available during sampling and data transmission, we have introduced two novel delay-incorporating integral terms, an improved two-sided looped-functional, a novel discontinuous function, and two additional zero equalities into the stability process. Subsequently, conditions sufficient to ensure consensus among MASs in this context have been formulated as LMIs. Through simulation results, the efficiency of the proposed method has been verified in extending the maximized allowable sampling interval. In future work, we will focus on addressing more realistic problems, including heterogeneous MASs and time-varying time delays.