Accurate Sum and Dot Product with New Instruction for High-Precision Computing on ARMv8 Processor

Abstract

The accumulation of rounding errors can lead to unreliable results. Therefore, accurate and efficient algorithms are required. A processor from the ARMv8 architecture has introduced new instructions for high-precision computation. We have redesigned and implemented accurate summation and the accurate dot product. The number of floating-point operations has been reduced from $7n-5$ and $10n-5$ to $4n-2$ and $7n-2$, compared with the classic compensated precision algorithms. It has been proven that our accurate summation and dot algorithms’ error bounds are ${\gamma }_{n-1}{\gamma }_n\mathrm{cond}+u$ and ${\gamma }_n{\gamma }_{n+1}\mathrm{cond}+u$, where ‘cond’ denotes the condition number, ${\gamma }_n=n·u/(1-n·u)$, and u denotes the relative rounding error unit. Our accurate summation and dot product achieved a 1.69× speedup and a 1.14× speedup, respectively, on a simulation platform. Numerical experiments also illustrate that, under round-towards-zero mode, our algorithms are as accurate as the classic compensated precision algorithms.

1. Introduction

When computations have reached the maximum precision limit of the hardware or programming language and demand even greater accuracy, it is imperative to consider alternative methods, such as compensated summation and compensated dot. However, these algorithms will take more FLOPs.

After rounding, computers round away the significant bits that exceed the precision limit, often referred to as the ‘rounding error’. Compensated summation and compensated dot can reduce the rounding error but increase the FLOPs. The capacity to directly extract the rounding error has the potential to significantly reduce the FLOPs of accurate algorithms. This has led to the introduction of several high-precision instructions into the processors of the ARMv8 architecture.

Compensated summation and compensated dot, which traditionally utilize add, subtract, and multiplication instructions to compute the rounding error, are able to leverage new instructions for acceleration. Hence, there is a clear need for the development of novel algorithms that harness advanced instructions for accurate summation and dot product operations on the ARMv8 processor.

1.1. Previous Work

The inaugural compensated algorithm, FastTwoSum, was introduced by Kahan in 1965 [1]. This pioneering method effectively computes the sum of two floating-point numbers, concurrently accounting for their rounding errors. However, FastTwoSum is subject to constraints regarding the relative magnitudes of the operands, which necessitates the introduction of branching conditions. In 1970, Knuth proposed the TwoSum algorithm [2] to circumvent the impact of the branching conditions and enhance the computational efficiency of compensated summation on real platforms. Unlike its predecessor, TwoSum can accurately ascertain the rounding error without regard to the absolute values of the operands, a and b. This algorithm eschews branching and comprises six floating-point operations. When considering the computation of absolute values and comparisons as a single floating-point operation, the TwoSum algorithm demonstrates a 50% increase in speed over FastTwoSum when the number of floating-point operations is held constant, attributed to the elimination of branching conditions. In 2017, Boldo and Graillat revealed that these algorithms possess greater robustness than is commonly acknowledged [3].

The TwoProduct algorithm [4], proposed by Dekker, is designed to accurately calculate the rounding error associated with the product of two floating-point numbers. This method exhibited a marked enhancement in efficiency following acceleration with the fused multiply–add (fma) instruction. In 2020, Graillat introduced algorithms capable of computing “exact” products through arithmetic operations, all rounded either toward $-\infty$ or $+\infty$ [5]. This approach underscores the significance of employing specific instructions and alternative rounding models in computational practice.

Subsequent research in precision control has been dedicated to enhancing the velocity and parallelism of compensation summation algorithms. In 2005, Oishi, Ogita, and Rump first introduced the concept of error-free transformation [6]. Building upon the foundational work of Dekker and Knuth, Oishi developed a method for the accurate computation of the sum and dot product (inner product) of a sequence of floating-point numbers in 2008 [7,8]. Numerical results demonstrated that the efficiency in achieving the same level of precision was significantly improved compared to algorithms reliant on double–double improvements. In the same year, Yamanaka crafted a parallel algorithm for the accurate computation of the dot product (inner product) [9]. In 2011, K. Ozaki proposed an error-free transformation approach for matrix multiplication [10]. The following year, Graillat employed similar techniques to design and implement compensated precision summation, dot product, and polynomial algorithms within the complex domain [11]. In 2013, Kadric demonstrated the utilization of tree-reduce parallelism to compute correctly rounded floating-point sums in O(log(n)) depth [12], while Demmel proposed a technique for floating-point summation that ensured reproducibility, independent of the order of summation [13]. In 2014, Abdalla leveraged the single instruction multiple data (SIMD) paradigm found in modern CPUs to accelerate matrix multiplication calculations [14]. In 2015, Jankovic presented a solution for the accurate summation problem using a fixed-point accumulator [15]. The year 2016 saw Goodrich provide several efficient parallel algorithms for the summing of floating-point numbers, aimed at producing a faithfully rounded floating-point representation of the sum [16]. In 2022, Evstigneev improved parallel algorithms based on the work of Rump, Ogita, and Oishi [6,7,8], achieving higher precision in floating-point reduction-type operations for graphics processing units (GPUs) [17]. In the same year, Lange proposed the aaaSum algorithm [18], which exploits ideas from Zhu and Hayes’ OnlineExactSum [19]. Some research has been anchored in specific high-performance computer platforms, such as the ARMv8 platform. In 2017, Jiang designed, implemented, and optimized quad-precision (double-double) dense matrix multiplication (QGEMM) [20] based on the domestic ARMv8 64-bit multi-core processor, applying it to large-scale computations.

As reliability is paramount in compensation algorithms, a rigorous analysis of the error bounds is indispensable. Between 2017 and 2019, Lange, drawing on the study of standard Wilkinson-type error estimates for floating-point algorithms, developed novel a priori estimates for the summation of real numbers, where each sum is subject to perturbations [21,22]. In 2021, Muller demonstrated the implementation of a new “rounding direction” using current operations [23]. The following year, he utilized formal proofs to significantly refine the error bounds and generalize certain results, showing their validity under slight modifications to the rounding mode [24]. In 2023, they explored functions for which correctly rounded implementations are available, enabling the use of these functions for floating-point multiplication or division with tight error bounds measured in units in the last place (ulps) [25]. Recently, Hubrecht revealed that the use of fused arithmetic operators can enable more accurate calculations with smaller costs than traditional operations alone [26].

In this paper, we design more efficient algorithms for accurate summation and dot product operations on an ARMv8 architecture processor at the FPGA simulation stage. This processor is being designed and developed by the National University of Defense Technology. The architecture of this processor is similar to those of other ARMv8 processors, except that some instructions (such as the ones mentioned in this article) are added due to requirements. We provide the error bounds for our algorithms, along with their proofs, and describe numerical experiments on the FPGA simulation platform to assess the accuracy and performance of our algorithms.

1.2. Background

1.2.1. Notation

The working precision of our algorithms is double, and the rounding mode is round-towards-zero. All floating-point representations and operations follow the IEEE 754 floating-point standard [27]. It is assumed that overflow will not occur, but underflow is permitted. We denote the set of all floating-point numbers at this precision as $\mathbb{F}$. The relative rounding error unit is denoted as u, and the unit of underflow is denoted as $elow$. Double precision has 53 significant bits and an 11-bit exponent; thus, $elow=2^{-1074}$. When using the round-to-nearest mode, $u=2^{-53}$, and with the round-towards-zero mode, $u=2^{-52}$. Since the additional instructions only support round-towards-zero, in subsequent proofs, the value of u is $2^{-52}$.

$\mathrm{fl}(\circ )$ represents the result of floating-point computation, where ∘ denotes all operations performed in the working precision. This paper will employ parentheses to uniquely determine the order of computation. According to the IEEE 754 standard, the backward error for a single floating-point operation satisfies [27]

$$\begin{array}{c}\hfill \mathrm{fl}(a\circ b)=(a\circ b){(1+ϵ)}^{\pm 1},\\ \hfill \circ \in \{+,-\},\mathrm{and}\left|ϵ\right|\le u;\end{array}$$

(1)

and

$$\begin{array}{c}\hfill \mathrm{fl}(a\circ b)=(a\circ b){(1+ϵ)}^{\pm 1}+\eta ,\\ \hfill \circ \in \{·,/\},\mathrm{and}\left|ϵ\right|\le u,\left|\eta \right|\le elow\end{array}$$

(2)

This means that, for $\circ \in \{+,-\}$, the forward error satisfies

$$\begin{array}{c}\hfill |a\circ b-\mathrm{fl}(a\circ b\left)\right|\le u·|a\circ b|\\ \hfill |a\circ b-\mathrm{fl}(a\circ b\left)\right|\le u·\left|\mathrm{fl}\right(a\circ b\left)\right|\end{array}$$

(3)

Meanwhile, for $\circ \in \{·,/\}$, the forward error satisfies

$$\begin{array}{c}\hfill |a\circ b-\mathrm{fl}(a\circ b\left)\right|\le u·|a\circ b|\\ \hfill |a\circ b-\mathrm{fl}(a\circ b\left)\right|\le u·\left|\mathrm{fl}\right(a\circ b\left)\right|\end{array}$$

(4)

The quantities $\gamma$ are defined by

$${\gamma }_n:=n·u/(1-n·u),n·u<1$$

(5)

The following lemma is proven in [28].

Lemma 1

([28]). For floating-point numbers $a_i\in \mathbb{F},1\le i\le n$, the following inequality is true:

$$|\mathrm{fl}(\sum _{i=1}^n{a}_i)-\sum _{i=1}^n{a}_i| \le {\gamma }_{n-1}\sum _{i=1}^n\left|a_i\right|$$

(6)

When using ${\gamma }_n$, we assume that $n·u<1$ by default, and it will not be explicitly mentioned in subsequent expressions.

1.2.2. Error-Free Transformation

The compensated algorithm needs to extend the error-free transformation of two floating-point numbers to vector summation and dot product. Therefore, the following content will help in understanding this work. For the error-free transformation of addition, Knuth [2] proposed the TwoSum algorithm (Algorithm 1).

Algorithm 1 TwoSum [2]

$\mathrm{function}[x,y]=TwoSum(a,b)$ $x=\mathrm{fl}(a+b)$ $z=\mathrm{fl}(x-a)$ $y=\mathrm{fl}\left(\right(a-(x-z))+(b-z\left)\right)$

Algorithm 1 converts two inputs $a,b\in \mathbb{F}$ into two outputs $x,y\in \mathbb{F}$, satisfying

$$a+b=x+y\mathrm{and}x=\mathrm{fl}(a+b).$$

(7)

Since addition and subtraction are exact in this case, the proof in [2] also applies to cases of underflow.

For the error-free transformation of multiplication, the algorithm TwoProductFMA (Algorithm 2) is currently the best solution, because a Fused-Multiply-and-Add operation is available on the ARMv8 processor.

Algorithm 2 TwoProductFMA [6]

$\mathrm{function}[x,y]=TwoProductFMA(a,b)$ $x=\mathrm{fl}(a·b)$ $y=\mathrm{fl}\left(a·b-x\right)$

Algorithm 2 has no branches, with only a basic and optimizable sequence of floating-point operations. In the absence of underflow, the following equation is confirmed:

$$a·b=x+y\mathrm{and}x=\mathrm{fl}(a·b).$$

(8)

Therefore, the properties of the TwoSum and TwoProductFMA algorithms are as follows.

Theorem 1

([2]). If $a,b\in \mathbb{F}$, the result of Algorithm 1 (TwoSum) is $x,y$, even in the case of underflow:

$$\begin{array}{c}\hfill a+b=x+y,x=\mathrm{fl}(a+b),\\ \hfill \left|y\right|\le u·\left|x\right|,\left|y\right|\le u·|a+b|.\end{array}$$

Algorithm 1 requires 6 floating-point operations. If $a,b\in \mathbb{F}$, the result of Algorithm 2 (TwoProductFMA) is $x,y$. If underflow does not occur, then

$$\begin{array}{c}\hfill a·b=x+y,x=\mathrm{fl}(a·b),\\ \hfill \left|y\right|\le u·\left|x\right|,\left|y\right|\le u·|a·b|,\end{array}$$

In the case of underflow, the equation $a·b=x+y+5\eta , x=\mathrm{fl}(a·b), \left|y\right|\le u·\left|x\right|+5$ elow, $\left|y\right|\le u·|a·b|+5$ elow holds. Here, η satisfies $\left|\eta \right|\le elow$. Algorithm 2 requires 2 floating-point operations.

1.2.3. Compensated Summation and Dot

The compensated accurate sum (Algorithm 3) can be viewed as the vector form of $\mathrm{TwoSum}$ and also satisfies the condition of error-free transformation.

Algorithm 3 CompensatedSum [6]

$\mathrm{function}\mathrm{Res}=CompensatedSum\left(\mathbf{a}\right)$ ${\pi }_1=a_1$, $r_1=0$ for $i=2$ to n do    $[{\pi }_i,y_i]=\mathrm{TwoSum}({\pi }_{i-1},a_i)$    $r_i=\mathrm{fl}(r_{i-1}+y_i)$ end for $\mathrm{Res}={\pi }_n+r_n$

Ref. [6] showed the relative error bound of Algorithm 3 and proposed the following theorem.

Theorem 2

([6]). The variables in Algorithm 3 algorithm are all double-precision floating-point, and the rounding mode is round-towards-zero. The forward error of the result is $\left|E_n\right|=|\mathrm{Res}-s_n|$, where $s_n={\sum }_{i=1}^n{a}_i$, $S_n={\sum }_{i=1}^n\left|a_i\right|$, and the following inequality holds:

$$\left|E_n\right|/\left|s_n\right|\le {\gamma }_{n-1}^2\mathrm{cond}(\sum _{i=1}^n{a}_i)+u.$$

(9)

where $\mathrm{cond}\left({\sum }_{i=1}^n{a}_i\right)=S_n/\left|s_n\right|$.

The compensated accurate dot product (Algorithm 4) can be seen as a combination of Algorithms 2 and 3.

Algorithm 4 CompensatedDot [6]

$\mathrm{function}\mathrm{Res}=CompensatedDot(\mathbf{a},\mathbf{b})$ $[{\pi }_1,p_1]=\mathrm{TwoProductFMA}(a_1,b_1)$ for $i=2$ to n do    $[h_i,l_i]=\mathrm{TwoProductFMA}(a_i,b_i)$    $[{\pi }_i,r_i]=\mathrm{TwoSum}({\pi }_{i-1},h_i)$    $p_i=\mathrm{fl}(p_{i-1}+(r_i+l_i))$ end for $\mathrm{Res}={\pi }_n+p_n$

To show the relative error bound of Algorithm 4, ref. [6] also proposed the following theorem.

Theorem 3

([6]). The variables in Algorithm 3 algorithm are all double-precision floating-point, and the rounding mode is round-towards-zero. The forward error of the result is $\left|E_n\right|=|\mathrm{Res}-{\mathbf{a}}^T·\mathbf{b}|$, where $s_n={\mathbf{a}}^T·\mathbf{b}$, $S_n=|{\mathbf{a}}^T\left|\right|\mathbf{b}|$, and the following inequality holds:

$$\left|E_n\right|/{\mathbf{a}}^T·\mathbf{b}\le {\gamma }_{n-1}^2\mathrm{cond}({\mathbf{a}}^T·\mathbf{b})+u.$$

(10)

where $\mathrm{cond}\left({\sum }_{i=1}^n{a}_i\right)=S_n/\left|s_n\right|$.

2. Compensated Sum and Dot Product Algorithms Based on High-Precision Instructions

This section will first introduce the functions and technical details of the faddr and faddn instructions and describe accurate summation and dot with these two instructions. Then, the error bounds of the accurate summation and dot are presented.

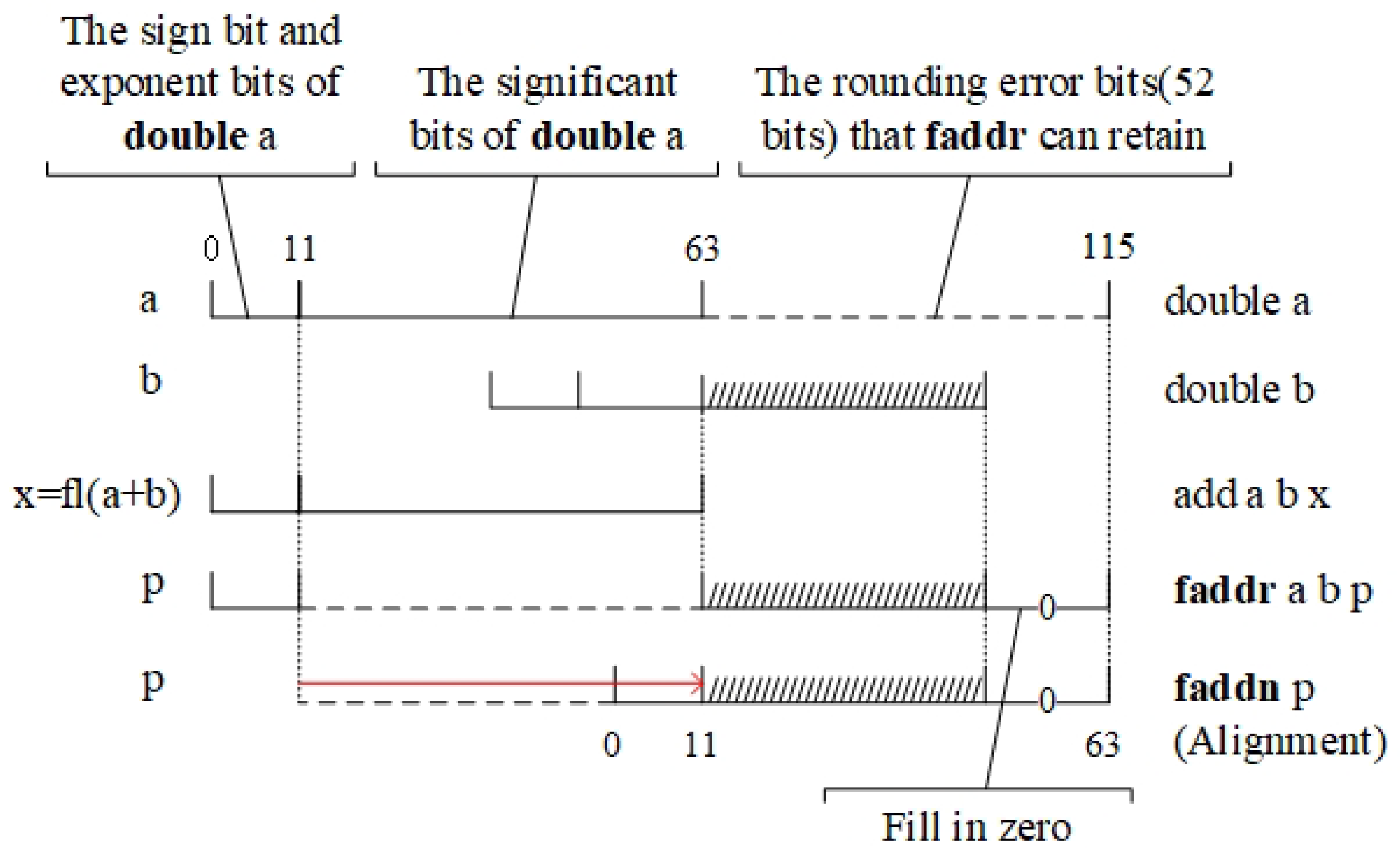
2.1. The Faddr and Faddn Instructions

The faddr and faddn instructions appear in pairs and aim to achieve the rounding error of $\mathrm{fl}(a+b)$ with a few floating-point operations. Assuming that no carry occurs in fl(a + b), the functions of faddn and faddr are as shown in Figure 1. The descriptions of the instructions’ functionalities are as follows.

$$\begin{array}{cc}\hfill \mathbf{FADD}& \mathbf{R}\mathbf{Instruction}\hfill \\ \hfill & \mathrm{FADDR}<\mathrm{Dn}\text{>},<\mathrm{Dm}\text{>},<\mathrm{Dd}\text{>}\hfill \\ \hfill & \mathbf{Assembly}\mathbf{Symbols}\hfill \\ \hfill & <\mathrm{Dd}\text{>}\mathrm{is}\mathrm{the}\mathrm{destination}\mathrm{double}\text{-}\mathrm{precision}\mathrm{register}.\hfill \\ \hfill & <\mathrm{Dn}\text{>}\mathrm{is}\mathrm{the}\mathrm{first}\mathrm{source}\mathrm{double}\text{-}\mathrm{precision}\mathrm{register}.\hfill \\ \hfill & <\mathrm{Dm}\text{>}\mathrm{is}\mathrm{the}\sec \mathrm{ond}\mathrm{source}\mathrm{double}\text{-}\mathrm{precision}\mathrm{register}.\hfill \\ \hfill & \mathbf{Operation}\hfill \\ \hfill & \mathrm{The}\mathrm{faddr}\mathrm{instruction}\mathrm{can}\mathrm{extract}\mathrm{the}\mathrm{significant}\mathrm{bits}\mathrm{that}\mathrm{are}\mathrm{rounded}\mathrm{away}\mathrm{during}\hfill \\ \hfill & \mathrm{floating}\text{-}\mathrm{point}\mathrm{addition}\mathrm{fl}(\mathrm{a}+\mathrm{b}),\mathrm{while}a\mathrm{in}\mathrm{register}<\mathrm{Dn}\text{>},b\mathrm{in}\mathrm{register}<\mathrm{Dm}\text{>}.\mathrm{This}\hfill \\ \hfill & \mathrm{instruction}\mathrm{adds}\mathrm{the}\mathrm{corresponding}\mathrm{elements}\mathrm{from}\mathrm{the}\mathrm{two}\mathrm{registers},\mathrm{extracts}\mathrm{the}\hfill \\ \hfill & \mathrm{significant}\mathrm{bits}\mathrm{that}\mathrm{are}\mathrm{rounded}\mathrm{away}\mathrm{from}\mathrm{the}\mathrm{floating}\text{-}\mathrm{point}\mathrm{operation},\mathrm{and}\mathrm{stores}\hfill \\ \hfill & \mathrm{them}\mathrm{in}\mathrm{the}\mathrm{destination}\mathrm{register}<\mathrm{Dd}\text{>},\mathrm{while}\mathrm{taking}\mathrm{the}\mathrm{sign}\mathrm{bit}\mathrm{and}\mathrm{exponent}\mathrm{bits}.\hfill \\ \hfill & \mathrm{This}\mathrm{instruction}\mathrm{is}\mathrm{for}\mathrm{double}\text{-}\mathrm{precision}\mathrm{operations}.\mathrm{In}\mathrm{the}\mathrm{original}\mathrm{addition}\mathrm{result},\mathrm{let}\hfill \\ \hfill & p\mathrm{denote}\mathrm{the}\mathrm{result}\mathrm{in}\mathrm{the}\mathrm{destination}\mathrm{register}<\mathrm{Dd}\text{>},\hfill \end{array}$$

$$p\approx 2^{\lfloor {log}_2\left|\mathrm{fl}(a+b)\right|\rfloor -\lfloor {log}_2|a+b-\mathrm{fl}(a+b)|\rfloor }(a+b-\mathrm{fl}(a+b)).$$

$$\begin{array}{cc}\hfill \mathbf{FADDN}& \mathbf{Instruction}\hfill \\ \hfill & \mathrm{FADDN}<\mathrm{Dd}\text{>}\hfill \\ \hfill & \mathbf{Assembly}\mathbf{Symbols}\hfill \\ \hfill & <\mathrm{Dd}\text{>}\mathrm{is}\mathrm{the}\mathrm{source}\mathrm{double}\text{-}\mathrm{precision}\mathrm{register}\mathrm{and}\mathrm{the}\mathrm{destination}\mathrm{double}\text{-}\mathrm{precision}\hfill \\ \hfill & \mathrm{register}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \mathbf{Operation}\hfill \\ \hfill & \mathrm{The}\mathrm{faddn}\mathrm{instruction}\mathrm{will}\mathrm{apply}\mathrm{the}\mathrm{appropriate}\mathrm{bias}\mathrm{to}\mathrm{the}\mathrm{exponent}\mathrm{bits}\mathrm{and}\hfill \\ \hfill & \mathrm{normalize}\mathrm{the}\mathrm{significand}\mathrm{of}\mathrm{the}\mathrm{element}\mathrm{in}\mathrm{register}<\mathrm{Dd}\text{>}.\mathrm{This}\mathrm{instruction}\mathrm{is}\mathrm{for}\hfill \\ \hfill & \mathrm{double}\text{-}\mathrm{precision}\mathrm{operations}.\mathrm{Let}p\mathrm{denote}\mathrm{the}\mathrm{result}\mathrm{in}\mathrm{the}\mathrm{destination}\mathrm{register}<\mathrm{Dd}\text{>},\hfill \end{array}$$

$$p\approx a+b-\mathrm{fl}(a+b).$$

Thus, with these two instructions, we can obtain round errors using fewer FLOPs. An example is the following Algorithm  5.

Algorithm 5 Err

$\mathrm{function}p=Err(a,b)$ $faddrabp$ $faddnp$

Here, $x=\mathrm{fl}(a+b)$, and we hope that the result p from the faddr and faddn instructions satisfies Equation (7). However, there is a limitation on the hardware. As shown in Figure 2, Figure 3, Figure 4 and Figure 5, when the working precision is double precision, $\mathrm{fl}(a+b)$ has 64 bits, with the last 52 bits as the signifcand. When using the faddr instruction to achieve the rounding error of $\mathrm{fl}(a+b)$ and directly round off the error, only the first 52 bits of the rounded significant bits will be preserved. Thus, p is an approximation of the rounding error, which satisfies

$$x+p\approx a+b$$

(11)

Under extreme conditions, some or even all of the rounding error will not be saved in p. Therefore, special processing is required when calculating the error bound. Several cases may arise.

Lemma 2.

Without loss of generality, assume $a>b$. Then, the relative size of b compared to $\mathrm{fl}(a+b)$ will affect the outcome of Algorithm 5. In the following four different cases, p has different properties.

(a) 

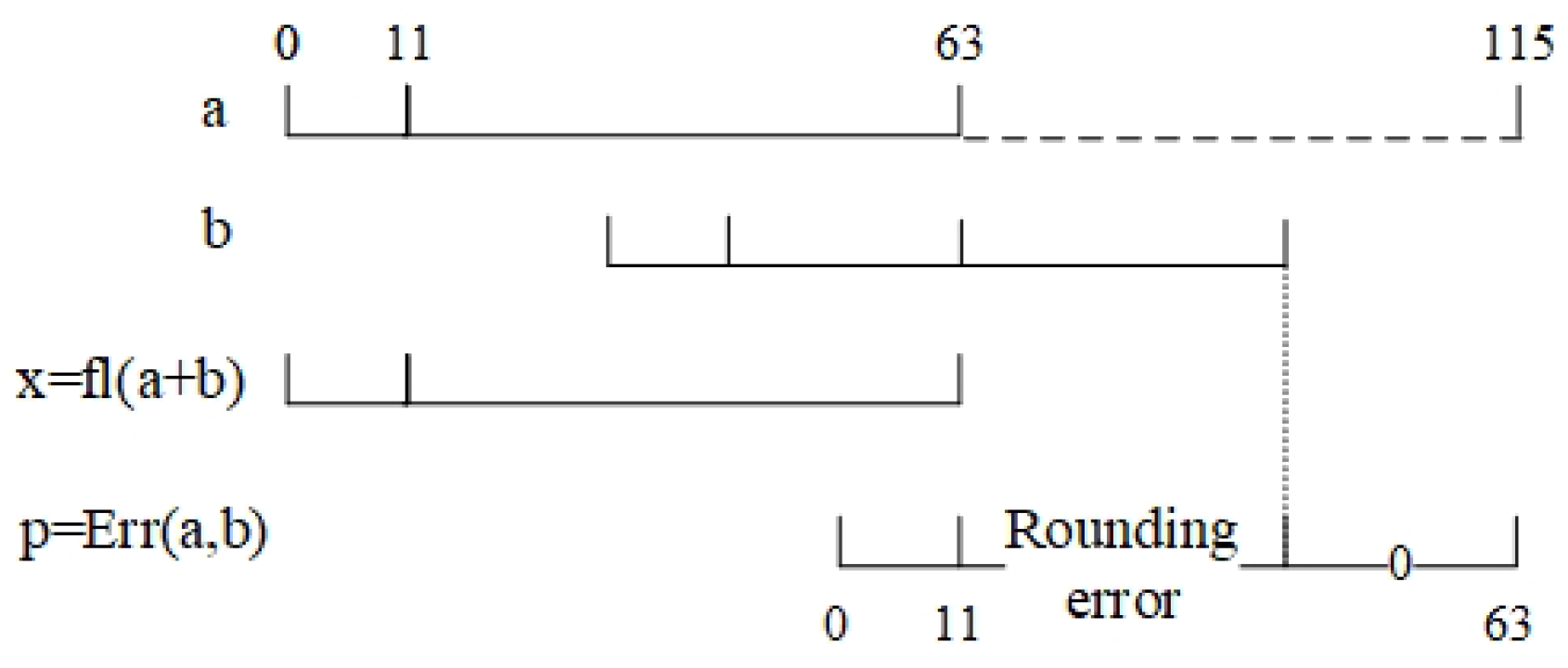
When $\left|b\right|\ge 2^{\lfloor {log}_2\left|x\right|\rfloor }$, there is no rounding error. p, the rounding error, and zero are equal, as shown in Figure 2.

Figure 2. In case of $\left|b\right|\ge 2^{\lfloor {log}_2\left|x\right|\rfloor }$, p equals zero.

Figure 2. In case of $\left|b\right|\ge 2^{\lfloor {log}_2\left|x\right|\rfloor }$, p equals zero.

(b) 

When $\left|b\right|<2^{\lfloor {log}_2\left|x\right|\rfloor }$ and $\left|b\right|\ge u·2^{\lfloor {log}_2\left|x\right|\rfloor }$, p will retain all rounding errors. Therefore, p equals the rounding error and satisfies Equation (7), as shown in Figure 3.

Figure 3. In case of $u·2^{\lfloor {log}_2\left|x\right|\rfloor }\le \left|b\right|<2^{\lfloor {log}_2\left|x\right|\rfloor }$, p equals rounding error.

Figure 3. In case of $u·2^{\lfloor {log}_2\left|x\right|\rfloor }\le \left|b\right|<2^{\lfloor {log}_2\left|x\right|\rfloor }$, p equals rounding error.

(c) 

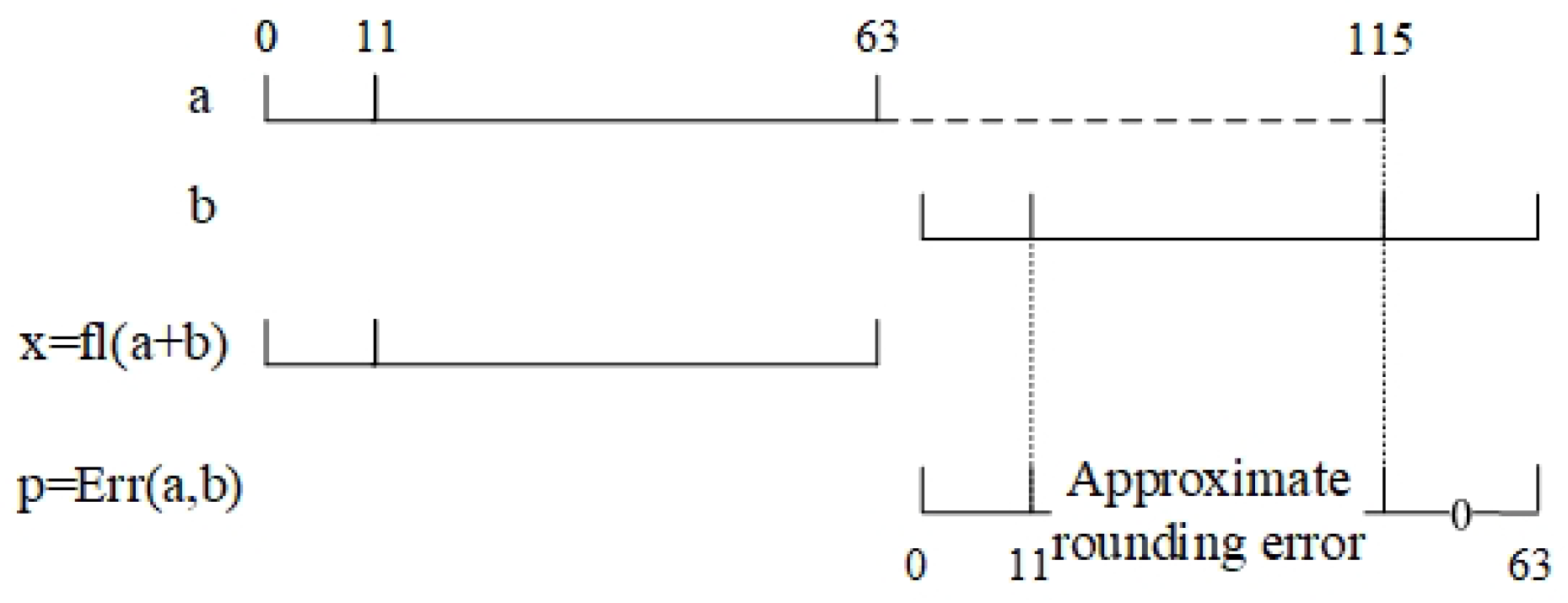
When $\left|b\right|<u·2^{\lfloor {log}_2\left|x\right|\rfloor }$ and $\left|b\right|\ge u^2·2^{\lfloor {log}_2\left|x\right|\rfloor }$, due to the limitation of the instructions, part of the rounding error will be truncated. Therefore, p is the approximation of the rounding error, as shown in Figure 4.

Figure 4. In case of $u^2·2^{\lfloor {log}_2\left|x\right|\rfloor }\le \left|b\right|<u·2^{\lfloor {log}_2\left|x\right|\rfloor }$, p is approximation of rounding error.

Figure 4. In case of $u^2·2^{\lfloor {log}_2\left|x\right|\rfloor }\le \left|b\right|<u·2^{\lfloor {log}_2\left|x\right|\rfloor }$, p is approximation of rounding error.

(d) 

When $\left|b\right|<u^2·2^{\lfloor {log}_2\left|x\right|\rfloor }$, the rounding error is too small to be retained. Therefore, p equals zero, as shown in Figure 5.

Figure 5. In case of $\left|b\right|<u^2·2^{\lfloor {log}_2\left|x\right|\rfloor }$, p equals zero.

Figure 5. In case of $\left|b\right|<u^2·2^{\lfloor {log}_2\left|x\right|\rfloor }$, p equals zero.

Let $q=a+b-x-p$. In all situations, $\left|p\right|\le u\left|x\right|,\left|q\right|\le u^2\left|x\right|$.

Proof. 

Because the rounding mode is rounding-towards-zero, $|p+q|=\left|p\right|+\left|q\right|$. By Theorem 1,

$$u\left|x\right|\ge |p+q|=\left|p\right|+\left|q\right|\ge \left|p\right|$$

In cases (a) and (b), x and p satisfy Equation (7), which means that $q=0$. In case (c), $\left|q\right|\le u\left|p\right|\le u^2\left|x\right|$. In case (d), $\left|q\right|=\left|b\right|\le u^2\left|x\right|$.

In summary, the lemma is established.    □

2.2. Compensated Summation and Dot Product Based on High-Precision Instructions

Algorithm 5 uses these two instructions to obtain the approximations of the rounding error. We take the result of Algorithm 5 as the rounding error. The improved algorithm is presented as Algorithm 6.

Algorithm 6 rnTwoSum

$\mathrm{function}[x,p]=rnTwoSum(a,b)$ $x=\mathrm{fl}(a+b)$ $p=Err(a,b)$

For floating-point numbers $a_i,i=1,2,\dots n$, $s_n={\sum }_{i=1}^n{a}_i$ represents the exact result of the summation. Let $S_n={\sum }_{i=1}^n\left|a_i\right|$, and ${\pi }_n=\mathrm{fl}\left({\sum }_{i=1}^n{a}_i\right)$ represents the floating-point sum result. Applying Algorithm 6 at each step of ${\sum }_{i=1}^n{a}_i$, and then accumulating all the error terms for compensation in the final summation result, we obtain Algorithm 7.

Algorithm 7 rnCompensatedSum

$\mathrm{function}\mathrm{Res}=rnCompensatedSum\left(\mathbf{a}\right)$ ${\pi }_1=a_1$;$r_1=0$ for $i=2$ to n do    $[{\pi }_i,p_i]=\mathrm{rnTwoSum}({\pi }_{i-1},a_i)$    $r_i=\mathrm{fl}(r_{i-1}+p_i)$ end for $\mathrm{Res}={\pi }_n+r_n$

Combining Algorithms  2 and 7, we achieve the compensated precision dot product based on the high-precision instructions (Algorithm 8).

Algorithm 8 rnCompensatedDot

$\mathrm{function}\mathrm{Res}=CompensatedDot(\mathbf{a},\mathbf{b})$ $[{\pi }_1,r_1]=\mathrm{TwoProductFMA}(a_1,b_1)$ for $i=2$ to n do    $[h_i,l_i]=\mathrm{TwoProductFMA}(a_i,b_i)$    $[{\pi }_i,p_i]=\mathrm{rnTwoSum}({\pi }_{i-1},h_i)$    $r_i=\mathrm{fl}(r_{i-1}+(p_i+l_i))$ end for $\mathrm{Res}={\pi }_n+r_n$

2.3. Error Analysis

Algorithms 7 and 8 reduce the number of floating-point operations for compensated summation and dot product, thus improving the computational efficiency. However, due to hardware limitations on the floating-point precision, there may be some loss of accuracy. Therefore, the applicability of Algorithms 7 and 8, i.e., whether these two algorithms can be applied in specific cases, depends on the analysis of the rounding error bounds for these algorithms. When the error meets the conditions, due to the efficiency of computation, the priority of these two algorithms will be higher than that of the traditional compensated summation and dot product.

In Algorithm 7, $p_i$ represents the part of the rounding error directly in the signifcand from the 64th to the 115th bit, and let $q_i$ represent the part beyond the 115th bit. Then, $(p_i+q_i)$ can be considered as the rounding error in the addition process. Consequently, we have $s_n={\sum }_{i=2}^n{p}_i+{\sum }_{i=2}^n{q}_i+{\pi }_n$. The result obtained by accumulating $a_i$ in Algorithm 7 is $res=\mathrm{fl}({\pi }_n+p_n)=\mathrm{fl}\left({\pi }_n+\left({\sum }_{i=2}^n{p}_i\right)\right)$.

To prove the conclusion about the relative error bound of Algorithm 7, we need to introduce a lemma.

Lemma 3.

Given floating-point numbers ${\pi }_0, a_i\in \mathbb{F},1\le i\le n$. ${\pi }_i,p_i\in \mathbb{F},1\le i\le n$, are the results of the following loop calculation:

$$[{\pi }_i,p_i]=rnTwoSum({\pi }_{i-1},a_i),i=1,\dots ,n$$

(12)

Let $q_i={\pi }_{i-1}+a_i-{\pi }_i-p_i$; then, the following inequalities are confirmed:

(a) 

$|q_i|\le u^2\left|{\pi }_i\right|$, $|p_i|\le u|{\pi }_i|$;

(b) 

When ${\pi }_0=0$, ${\sum }_{i=2}^n|p_i|\le {\gamma }_{n-1}{\sum }_{i=1}^n\left|a_i\right|={\gamma }_{n-1}{S}_n$; when ${\pi }_0\ne 0$, ${\sum }_{i=2}^n|p_i|\le {\gamma }_n{\sum }_{i=1}^n\left|a_i\right|={\gamma }_n{S}_n$;

(c) 

When ${\pi }_0=0$, ${\sum }_{i=2}^n|q_i|\le u{\gamma }_{n-1}{\sum }_{i=1}^n\left|a_i\right|=u{\gamma }_{n-1}{S}_n$; when ${\pi }_0\ne 0$, ${\sum }_{i=2}^n|q_i|\le u{\gamma }_n{\sum }_{i=1}^n\left|a_i\right|=u{\gamma }_n{S}_n$.

Proof. 

Due to Lemma 2, (a) is confirmed. To prove (b), we require the following.

First, when $n=2$, both sides of the inequality are 0. Assume that (b) is true for some $n-1\ge 2$; then,

$$\begin{array}{cc}\hfill \sum _{i=2}^n\left|p_i\right|& =\sum _{i=2}^{n-1}|p_i|+|p_n|\hfill \\ \hfill & \le {\gamma }_{n-2}\sum _{i=1}^{n-1}|a_i|+|p_n|={\gamma }_{n-2}{S}_{n-1}+\left|p_n\right|.\hfill \end{array}$$

(13)

By Lemmas 1 and 2,

$$|p_n|\le u|{\pi }_n|\le u(1+{\gamma }_{n-1})\sum _{i=1}^n\left|a_i\right|=u(1+{\gamma }_{n-1})S_n.$$

(14)

Combining Equations (13) and (14), we have

$$\begin{array}{cc}\hfill \sum _{i=2}^n\left|p_i\right|& \le {\gamma }_{n-2}{S}_{n-1}+u(1+{\gamma }_{n-1})S_n\hfill \\ \hfill & \le S_n({\gamma }_{n-2}+u(1+{\gamma }_{n-1}))\hfill \\ \hfill & \le {\gamma }_{n-1}{S}_n.\hfill \end{array}$$

(15)

Hence, (b) is true. Similarly, (c) is true as well.    □

Theorem 4.

All variables in Algorithm 7 are double-precision floating-point numbers, and the rounding mode is round-towards-zero. The absolute error bound of the sum obtained by this algorithm and $s_n$ is denoted as $\left|E_n\right|=|\mathrm{Res}-s_n|$. The following inequality holds:

$$\left|E_n\right|/\left|s_n\right|\le {\gamma }_{n-1}{\gamma }_n\mathrm{cond}(\sum _{i=1}^n{a}_i)+u.$$

(16)

where $\mathrm{cond}\left({\sum }_{i=1}^n{a}_i\right)={\displaystyle \frac{{\sum }_{i=1}^n\left|a_i\right|}{|{\sum }_{i=1}^n{a}_i|}}$.

Proof. 

In Algorithm 7, define $q_i={\pi }_{i-1}+a_i-{\pi }_i-p_i$. Then, by Equation (1),

$$\begin{array}{cc}\hfill \left|E_n\right|& =|\mathrm{fl}({\pi }_n+r_n)-s_n|\hfill \\ \hfill & =|(1+ϵ)({\pi }_n+r_n-s_n)+ϵs_n|\hfill \\ \hfill & =|(1+ϵ)({\pi }_n+\sum _{i=2}^n{p}_i-s_n)+(1+ϵ)(p_n-\sum _{i=2}^n{p}_i)+ϵs_n|\hfill \\ \hfill & =|(1+ϵ)\sum _{i=2}^n{q}_i+(1+ϵ)(p_n-\sum _{i=2}^n{p}_i)+ϵs_n|.\hfill \end{array}$$

(17)

In Equation (1), $\left|ϵ\right|\le u$

$$\begin{array}{cc}\hfill \left|E_n\right|& \le (1+u)\left(\right|\sum _{i=2}^n{q}_i|+|p_n-\sum _{i=2}^n{p}_i\left|\right)+u|s_n|.\hfill \end{array}$$

(18)

By Lemmas 1 and 3 we have

$$|p_n-\sum _{i=2}^n{p}_i| \le {\gamma }_{n-2}\sum _{i=2}^n|p_i| \le {\gamma }_{n-2}·{\gamma }_{n-1}\sum _{i=2}^n\left|a_i\right|.$$

Therefore, combining inequality (18), we obtain

$$\begin{array}{cc}\hfill \left|E_n\right|& \le (1+u)\left(\right|\sum _{i=2}^n{q}_i|+{\gamma }_{n-2}\sum _{i=2}^n|p_i\left|\right)+u|s_n|\hfill \\ \hfill & \le (1+u)|\sum _{i=2}^n{q}_i|+(1+u){\gamma }_{n-2}{\gamma }_{n-1}{S}_n+u|s_n|.\hfill \end{array}$$

(19)

It is not difficult to see that $(1+u){\gamma }_{n-2}\le {\gamma }_{n-1}$, and, by Lemma 3, $|{\sum }_{i=2}^n{q}_i| \le {\sum }_{i=2}^n\left|q_i\right| \le u{\gamma }_{n-1}{S}_n$. Therefore,

$$\begin{array}{cc}\hfill \left|E_n\right|& \le (1+u)u{\gamma }_{n-1}{S}_n+{\gamma }_{n-1}^2{S}_n+u|s_n| =({\gamma }_{n-1}+u+u^2){\gamma }_{n-1}{S}_n+u\left|s_n\right|.\hfill \end{array}$$

(20)

In Equation (20),

$${\gamma }_{n-1}+u+u^2<{\gamma }_{n-1}+u+u^2+u{\gamma }_{n-1}\le {\gamma }_{n-1}+u+u{\gamma }_n\le {\gamma }_n,$$

(21)

thus,

$$\begin{array}{cc}\hfill & \left|E_n\right|/|s_n| \le {\gamma }_{n-1}{\gamma }_n{S}_n/\left|s_n\right|+u={\gamma }_{n-1}{\gamma }_n\mathrm{cond}(\sum _{i=1}^n{a}_i)+u.\hfill \end{array}$$

(22)

   □

Theorem 4 shows that applying the error storage instruction in Algorithm 7 will affect the error bound of the final summation result. Similar conclusions hold for Algorithm 8.

Theorem 5.

All variables in Algorithm 8 are double-precision floating-point numbers, and the rounding mode is round-towards-zero. The absolute error bound of the algorithm’s result with respect to $s_n$ is denoted as $\left|E_n\right|=|\mathrm{Res}-{\mathbf{a}}^T\mathbf{b}|$; then, the following inequality holds:

$$\left|E_n\right|/\left|{\mathbf{a}}^T\mathbf{b}\right|\le {\gamma }_n{\gamma }_{n+1}\mathrm{cond}\left({\mathbf{a}}^T\mathbf{b}\right)+u.$$

(23)

where $\mathrm{cond}\left({\mathbf{a}}^T\mathbf{b}\right)={\displaystyle \frac{|{\mathbf{a}}^T\left|\right|\mathbf{b}|}{|{\mathbf{a}}^T\mathbf{b}|}}$.

Proof. 

In Algorithm 8, define $q_i={\pi }_{i-1}+h_i-{\pi }_i-p_i$. From Equations (1), (2), and (4), we have

$$\begin{array}{cc}\hfill |E_n|& =|\mathrm{fl}({\pi }_n+r_n)-{\mathbf{a}}^T\mathbf{b}|\hfill \\ \hfill & =|(1+ϵ)({\pi }_n+r_n)-{\mathbf{a}}^T\mathbf{b}|\hfill \\ \hfill & =|ϵ{\mathbf{a}}^T\mathbf{b}+(1+ϵ)({\pi }_n+r_n-{\mathbf{a}}^T\mathbf{b})|\hfill \\ \hfill & \le (1+u)|{\pi }_n+r_n-{\mathbf{a}}^T\mathbf{b}|+u|{\mathbf{a}}^T\mathbf{b}|.\hfill \end{array}$$

(24)

Moreover, $h_i,l_i,{\pi }_i,r_i$ for $2\le i\le n$ are intermediate variables after executing Algorithm 8. Combining the definition of $q_i$, we have the following equation:

$$\begin{array}{cc}\hfill & p_i+q_i+l_i=({\pi }_{i-1}+h_i-{\pi }_i)+(a_i{b}_i-h_i)=a_i{b}_i+{\pi }_{i-1}-{\pi }_i.\hfill \end{array}$$

(25)

Then,

$$\begin{array}{cc}\hfill & r_1+\sum _{i=2}^n(p_i+q_i+l_i)=(a_1{b}_1-{\pi }_1)+(\sum _{i=2}^n{a}_i{b}_i+{\pi }_1-{\pi }_n)={\mathbf{a}}^T\mathbf{b}-{\pi }_n.\hfill \end{array}$$

(26)

Substituting Equation (26) into Equation (24), we obtain

$$\begin{array}{cc}\hfill |E_n|& \le (1+u)|r_n-r_1-\sum _{i=2}^n(p_i+q_i+l_i)|+u|{\mathbf{a}}^T\mathbf{b}|\hfill \\ \hfill & =(1+u)|\mathrm{fl}(r_1+\sum _{i=2}^n(p_i+l_i))-r_1-\sum _{i=2}^n(p_i+q_i+l_i)|+u|{\mathbf{a}}^T\mathbf{b}|\hfill \\ \hfill & \le (1+u)|\mathrm{fl}(r_1+\sum _{i=2}^n(p_i+l_i))-r_1-\sum _{i=2}^n(p_i+l_i)|+(1+u)\sum _{i=2}^n|q_i|+u|{\mathbf{a}}^T\mathbf{b}|.\hfill \end{array}$$

(27)

where, from Lemma 1,

$$\begin{array}{cc}\hfill |r_1+\sum _{i=2}^n(p_i+l_i)-\mathrm{fl}(r_n+\sum _{i=2}^n(p_i+l_i))|& \le {\gamma }_{n-1}\left(\right|r_1|+\sum _{i=2}^n|\mathrm{fl}(p_i+l_i)\left|\right)\hfill \\ \hfill & \le {\gamma }_n\left(\right|r_1|+\sum _{i=2}^n|p_i+l_i\left|\right).\hfill \end{array}$$

(28)

From Equation (2) and Lemma 3, the following inequalities are confirmed:

$$\begin{array}{cc}\hfill & |r_1| \le u|a_1{b}_1|,\hfill \\ \hfill & \sum _{i=2}^n|l_i| \le u\sum _{i=2}^n\left|a_i{b}_i\right|,\hfill \\ \hfill & \sum _{i=2}^n\left(\right|p_i|+|q_i\left|\right)\le {\gamma }_{n-1}\left(\right|{\pi }_1|+\sum _{i=2}^n|h_i\left|\right)={\gamma }_{n-1}\sum _{i=1}^n|\mathrm{fl}(a_i·b_i|)\le (1+u){\gamma }_{n-1}|{\mathbf{a}}^T\left|\right|\mathbf{b}|.\hfill \end{array}$$

(29)

Substituting this into Equation (28), we obtain

$$|r_1+\sum _{i=2}^n(r_i+l_i)-\mathrm{fl}(r_1+\sum _{i=2}^n(r_i+l_i))| \le {\displaystyle \frac{{\gamma }_{n}n·u}{(1-(n-1\left)u\right)}}|{\mathbf{a}}^T\left|\right|\mathbf{b}|.$$

(30)

Combining Equation (27), we obtain

$$\begin{array}{cc}\hfill |E_n|& \le {\displaystyle \frac{(1+u)n·u{\gamma }_n}{(1-(n-1\left)u\right)}}|{\mathbf{a}}^T\left|\right|\mathbf{b}|+(1+u)\sum _{i=2}^n|q_i| + u|{\mathbf{a}}^T\mathbf{b}|\hfill \\ \hfill & \le {\gamma }_n^2|{\mathbf{a}}^T\left|\right|\mathbf{b}|+(1+u)\sum _{i=2}^n|q_i| + u|{\mathbf{a}}^T\mathbf{b}|.\hfill \end{array}$$

(31)

According to Lemma 3, ${\sum }_{i=2}^n|q_i| \le u{\gamma }_n{\sum }_{i=1}^n|a_i,b_i| \le u{\gamma }_n\left|{\mathbf{a}}^T\mathbf{b}\right|$. Combining Equation (31), we have

$$\begin{array}{cc}\hfill |E_n|& \le {\gamma }_n^2|{\mathbf{a}}^T\left|\right|\mathbf{b}|+u(1+u){\gamma }_n|{\mathbf{a}}^T\left|\right|\mathbf{b}|+u|{\mathbf{a}}^T\mathbf{b}|\hfill \\ \hfill & ={\gamma }_n({\gamma }_n+u+u^2){\mathbf{a}}^T\left|\right|\mathbf{b}|+u|{\mathbf{a}}^T\mathbf{b}|\hfill \end{array}$$

(32)

and by Equation (21), we obtain

$$\begin{array}{c}\hfill |E_n| \le {\gamma }_n{\gamma }_{n+1}{\mathbf{a}}^T\left|\right|\mathbf{b}|+u|{\mathbf{a}}^T\mathbf{b}|.\end{array}$$

(33)

Then,

$$\begin{array}{c}\hfill \left|E_n\right|/\left|{\mathbf{a}}^T\mathbf{b}\right|\le {\gamma }_n{\gamma }_{n+1}\mathrm{cond}\left({\mathbf{a}}^T\mathbf{b}\right)+u.\end{array}$$

(34)

   □

3. Numerical Experiment

When conducting simulation experiments on the FPGA platform, it may not fully reflect the program’s performance. For example, the HAPS platform, using real DDR, cannot accurately evaluate program performance when the program involves accessing DDR. The FPGA platform provides modeling capabilities for DDR controllers and memory. Users can use the tools and libraries provided by the FPGA platform to build DDR models, including configuring the memory parameters, setting the timing, delays, etc. After loading the design code onto the FPGA chip, the FPGA platform will simulate the behavior of the DDR controller and memory. During program execution, FPGA will simulate DDR read/write operations, timing delays, data transfers, etc., to accurately simulate the program’s performance. Therefore, the FPGA platform can not only test the correctness but also accurately reflect the performance. The high-precision instructions become ineffective under the round-to-nearest mode. Hence, it is necessary to switch the system’s rounding mode to round-towards-zero mode. The code to modify the rounding mode on the ARMv8 platform is as Listing 1.

Listing 1. The code to modify the rounding mode on the ARMv8 platform.

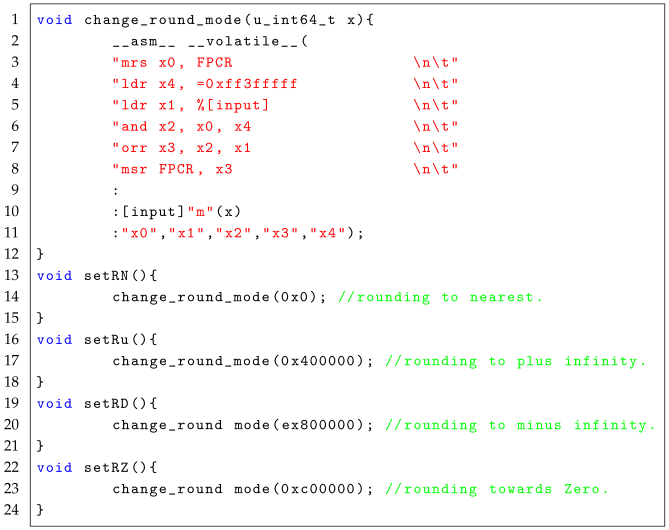3.1. FPGA Hardware Simulation Platform

The ARMv8 processor for this experiment is built on the FPGA simulation platform. The testing programs are compiled with the -O0 and -fno-fast-math options to avoid compiler optimization, because this may invalidate the accuracy of the algorithms. When testing the summation algorithm, let $a_0$ be a constant $\alpha$, with the rest of the numbers in the array generated by the sine function within the domain $(-\pi /2,\pi /2)$, ensuring that the exact sum of this portion of the numbers is 0, thus obtaining the exact solution of the array sum as $\alpha$. Similarly, when testing the dot product algorithm, let $a_0\ast b_0$ be a constant $\alpha$, with the remaining products being split into two halves that are opposite and equal in magnitude, resulting in the exact solution of the array sum as $\alpha$. This can help us to calculate the condition number and relative error. Since the current instructions only support round-towards-zero, the algorithm will fail under round-to-nearest mode. Therefore, all numerical experiments are conducted under the round-towards-zero mode.

3.2. Experiment for Accurate Summation

First, we observe the calculation results of Algorithms 3 and 7 and regular summation for multiple sets of different $\alpha$ and array sizes n. We calculate the relative errors, compare the precision of Algorithms 3 and 7 with regular summation, and verify the correctness of Theorem 4 based on the condition numbers. Second, we compare the time required for Algorithms 3 and 7 to compute problems of the same scale and verify the performance improvement of algorithm optimization.

3.2.1. Accuracy Comparison for Accurate Summation

The length of arrays ${\left\{a_i\right\}}_{i=0}^N$ is $N+1$ , $a_i=sin(\pi /2*(2i-1-N)/2N),i=1,2,\dots ,N$. $a_0=\alpha$, $\alpha$ takes the values ${10}^{-5},{10}^{-10}$, and ${10}^{-15}$. We calculate the sum of array $a_n$ using ordinary summation and Algorithms 3 and 7. The relative error of the algorithm is as follows:

$$\mathrm{relative}\mathrm{error}\mathrm{of}\mathrm{algorithm}=|\alpha -\mathrm{result}\mathrm{of}\mathrm{algorithm}|/\alpha .$$

(35)

where $\alpha$ is known to be the analytical solution of ${\sum }_{i=0}^N{a}_i$. The relative errors of each algorithm are shown in

Table 1. The condition numbers and the relative errors of each algorithm.

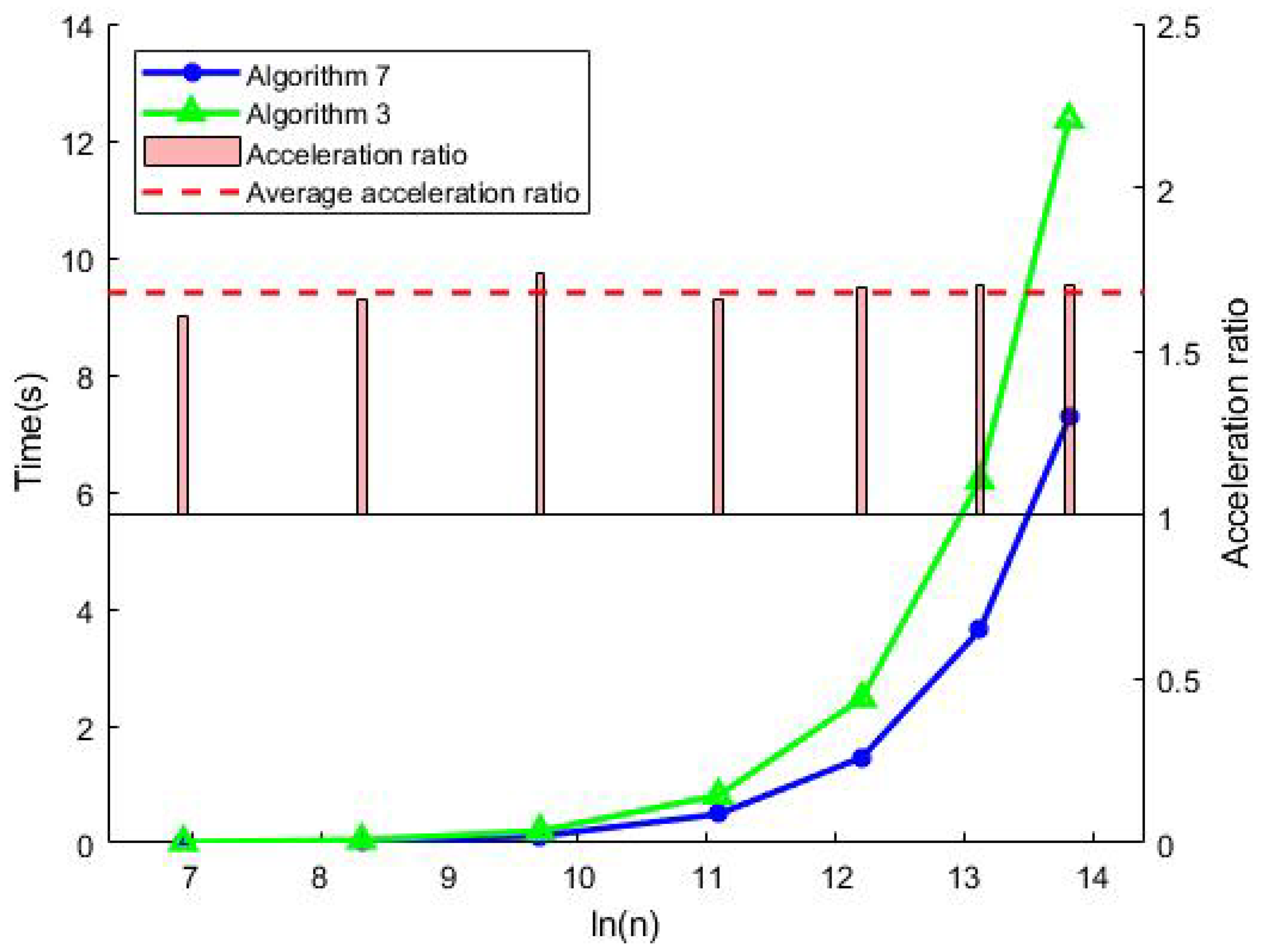
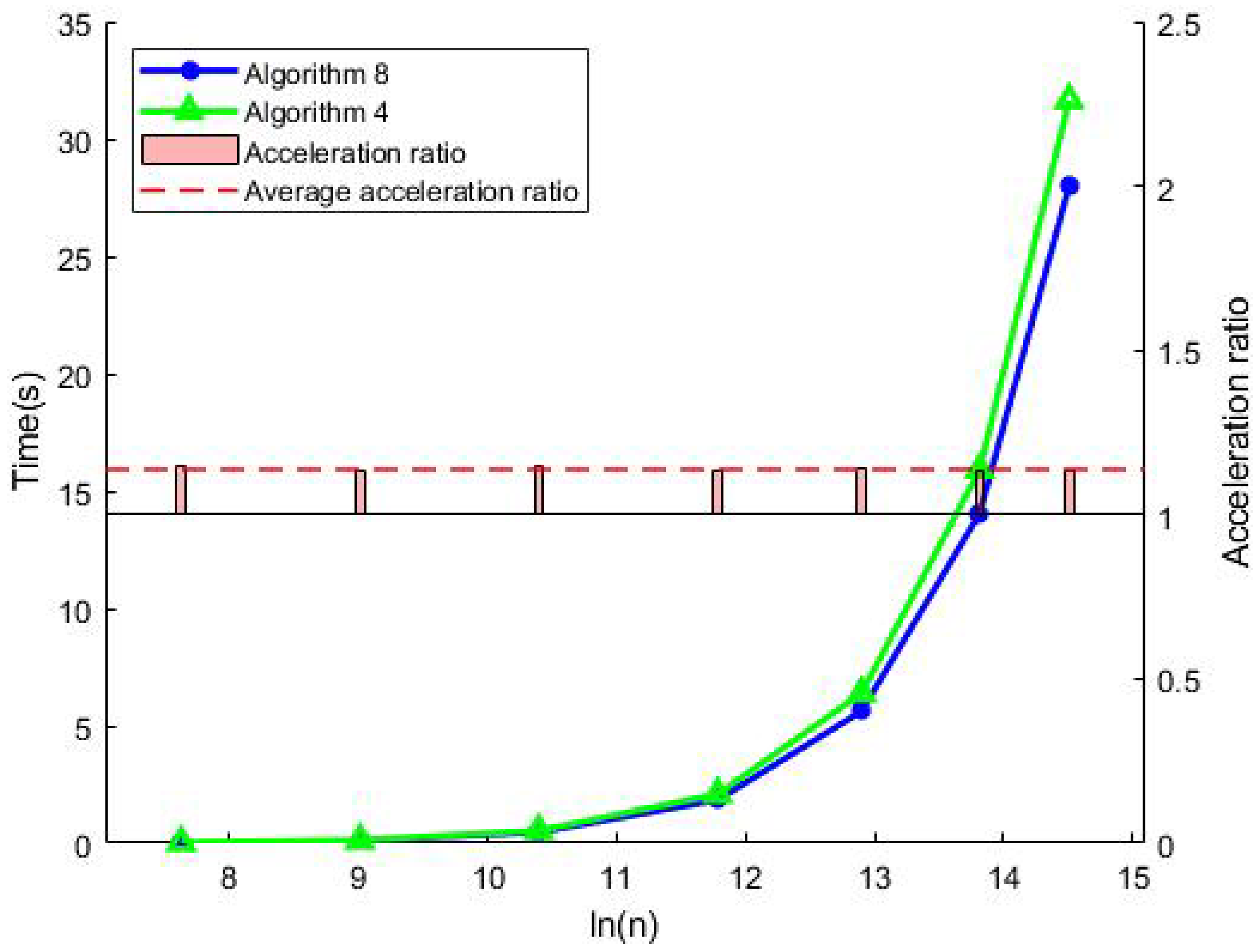
Condition Number	Relative Error of Algorithm 7 (Ours)	Relative Error of Algorithm 3 [6]	Relative Error of Classic Sum
6.51898903 $\times {10}^7$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	2.21007546 $\times {10}^{-7}$
2.60759465 $\times {10}^8$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	3.63575381 $\times {10}^{-6}$
1.04303784 $\times {10}^9$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	5.83473446 $\times {10}^{-5}$
4.17215134 $\times {10}^9$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	9.34421480 $\times {10}^{-4}$
1.27323954 $\times {10}^{10}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	7.02761044 $\times {10}^{-3}$
3.18309886 $\times {10}^{10}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	5.47924835 $\times {10}^{-2}$
6.36619772 $\times {10}^{10}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	2.19175222 $\times {10}^{-1}$
6.51898903 $\times {10}^{12}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	2.20868596 $\times {10}^{-2}$
2.60750465 $\times {10}^{13}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	3.63419377 $\times {10}^{-1}$
1.04303784 $\times {10}^{14}$	6.46234854 $\times {10}^{-16}$	6.46234854 $\times {10}^{-16}$	5.83543333 $\times {10}^0$
4.17215134 $\times {10}^{14}$	8.91804098 $\times {10}^{-15}$	8.91804098 $\times {10}^{-15}$	9.34405709 $\times {10}^1$
1.27323954 $\times {10}^{15}$	7.50024900 $\times {10}^{-14}$	7.50924900 $\times {10}^{-14}$	7.02764015 $\times {10}^2$
3.18309886 $\times {10}^{15}$	7.50024900 $\times {10}^{-14}$	7.50924900 $\times {10}^{-14}$	5.47923314 $\times {10}^3$
6.36619772 $\times {10}^{15}$	2.19267486 $\times {10}^{-12}$	2.19267486 $\times {10}^{-12}$	2.19175070 $\times {10}^4$
2.60759465 $\times {10}^{18}$	2.11611938 $\times {10}^{-12}$	9.57846791 $\times {10}^{-12}$	3.63533640 $\times {10}^4$
1.04303784 $\times {10}^{19}$	8.57846791 $\times {10}^{-12}$	1.11976044 $\times {10}^{-10}$	5.83497916 $\times {10}^5$
4.17215134 $\times {10}^{19}$	3.18771198 $\times {10}^{-10}$	3.18771198 $\times {10}^{-10}$	9.34401167 $\times {10}^6$
1.27323054 $\times {10}^{20}$	3.62749365 $\times {10}^{-9}$	3.62749365 $\times {10}^{-9}$	7.02763561 $\times {10}^7$
3.18309886 $\times {10}^{20}$	3.62749365 $\times {10}^{-9}$	1.09506612 $\times {10}^{-8}$	5.47925087 $\times {10}^8$
6.36619772 $\times {10}^{20}$	3.21264849 $\times {10}^{-7}$	3.21264849 $\times {10}^{-7}$	2.19175611 $\times {10}^9$

. With the rise in the condition number, the relative error follows an increasing tendency.

Consistent with theoretical analysis and intuition, as the condition number increases, the relative error of the algorithm also increases. Comparing the relative error of our algorithm and the classic sum, we can conclude that the precision of the results obtained by Algorithm 7 is higher compared to classic summation. Comparing the relative error of our algorithm and Algorithm 3 [6], it can be concluded that the computed results of Algorithms 3 and 7 are quite similar. For a few rows of data, the relative error of Algorithm 7 is lower. This may because of the features of the data. It also indirectly reflects that, at least for the computation of certain types of data, the precision of Algorithm 7 is as high as that of Algorithm 3.

3.2.2. Runtime Performance Comparison for Accurate Summation

The lengths of arrays n range from 1025 to 1,000,001. The left y-axis is the runtime. The right y-axis is the acceleration ratio. Due to the large range of values for n, the x-axis takes $ln\left(n\right)$. Comparing the runtimes of Algorithms 3 and 7, Algorithm 7 achieved a 1.69 speedup on average, as shown in Figure 6. Thus, we conclude that using Algorithm 7 can significantly improve the efficiency of accurate summation.

3.3. Experiment for Accurate Dot Product

Similar to accurate summation, we observe the calculation results of Algorithms 4 and 8 and the regular dot product for multiple sets of different $\alpha$ and array sizes n. We compare the accuracy of Algorithms 4 and 8 with that of regular summation and verify the correctness of the error bounding Theorem 5 based on the condition numbers. We compare the time required for Algorithms 4 and 8 to compute problems of the same scale and verify the performance improvement of algorithm optimization.

3.3.1. Accuracy Comparison for Accurate Dot Product

The lengths of $\mathbf{a}$ and $\mathbf{b}$ are $2N+1$. Let $d{r}_i\in \mathbb{F}$ be a random number from $0.5$ to $1.5$, $i=1,2,\dots ,N$. $a_i=sin(\pi /2\times (2i-1-N)/2N)/d{r}_i=a_{2N+1-i}$, $b_i=d{r}_i=-b_{2N+1-i}$, for $i=1,2,\dots ,N$. $a_0=\alpha$ and $b_0=1$ are constant, and $\alpha$ takes the values ${10}^{-3},{10}^{-6}$, and ${10}^{-9}$. We calculate the sum of array $a_n$ using ordinary summation and Algorithms 4 and 8. The analytical solution for ${\mathbf{a}}^T\mathbf{b}$ is known to be $\alpha$. Then, the relative error of the algorithm is also computed by Equation (35). As with the results of the sum algorithms, with the rise in the condition number, the relative error follows an increasing tendency. In

Table 2. The condition numbers and the relative errors of each algorithm.

Condition Number	Relative Error of Algorithm 8 (Ours)	Relative Error of Algorithm 4 [6]	Relative Error of Classic Dot
3.09609813 $\times {10}^9$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	3.64059902 $\times {10}^{-8}$
4.93847415 $\times {10}^{10}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	5.84336469 $\times {10}^{-7}$
7.78222147 $\times {10}^{11}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	9.34442157 $\times {10}^{-6}$
3.09609813 $\times {10}^{12}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	3.64271123 $\times {10}^{-5}$
1.24410327 $\times {10}^{13}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	1.49551930 $\times {10}^{-4}$
4.93847415 $\times {10}^{13}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	5.84243904 $\times {10}^{-4}$
3.09609813 $\times {10}^{15}$	0.00000000 $\times {10}^0$	0.00000000 $\times {10}^0$	3.64190617 $\times {10}^{-2}$
1.24410327 $\times {10}^{16}$	1.29172524 $\times {10}^{-14}$	5.23042845 $\times {10}^{-14}$	1.49552064 $\times {10}^{-1}$
1.15696185 $\times {10}^{17}$	2.97732081 $\times {10}^{-13}$	1.19008129 $\times {10}^{-12}$	1.12452736 $\times {10}^0$
7.22410536 $\times {10}^{17}$	5.95210052 $\times {10}^{-12}$	2.38306367 $\times {10}^{-11}$	8.76712204 $\times {10}^0$
2.89045729 $\times {10}^{18}$	4.76318389 $\times {10}^{-11}$	1.00464464 $\times {10}^{-10}$	3.50684910 $\times {10}^1$
1.24410327 $\times {10}^{19}$	1.31147418 $\times {10}^{-11}$	5.23462639 $\times {10}^{-11}$	1.49552170 $\times {10}^2$
1.15696185 $\times {10}^{20}$	2.97807148 $\times {10}^{-10}$	1.19010342 $\times {10}^{-9}$	1.12453110 $\times {10}^3$
7.22410535 $\times {10}^{20}$	5.95217559 $\times {10}^{-9}$	2.38305000 $\times {10}^{-8}$	8.76713306 $\times {10}^3$
2.89045729 $\times {10}^{21}$	4.76325403 $\times {10}^{-8}$	1.90464327 $\times {10}^{-7}$	3.50685311 $\times {10}^4$

, we compare the relative errors of each algorithm under the same circumstances.

Comparing the relative errors of our algorithm and the classic dot, it can be recognized that the precision of Algorithm 8 is higher than that of the classic dot product. By observing the relative errors of our algorithm and Algorithm 4 [6], it can be seen that even the relative error of Algorithm 7 is lower for a few rows. We can see that Algorithm 8 is as accurate as Algorithm 4.

3.3.2. Runtime Performance Comparison for Accurate Dot Product

The lengths of arrays n range from 2049 to 2,000,001. The left y-axis is the runtime. The right y-axis is the acceleration ratio. Due to the large range of values for n, the x-axis takes $ln\left(n\right)$. As shown in Figure 7, Algorithm 8 achieves a 1.14 speedup on average. Because it requires more multiplications and FMA instructions, the proportion of Algorithm 6 is lower. Therefore, the acceleration ratio that Algorithm 8 achieves is not as high as that of Algorithm 7. Thus, we conclude that using Algorithm 8 can slightly improve the efficiency of the accurate dot operation.

4. Conclusions

Considering the error analysis along with the results of the numerical experiments, the following conclusions can be drawn (

Table 3. Floating-point operations and error bounds for each algorithm.

Algorithm	FLOPs	Relative Error Bound
Algorithm 3	$7n-5$	${\gamma }_{n-1}^2\mathrm{cond}+u$ (Theorem 2)
Algorithm 7	$4n-2$	${\gamma }_{n-1}{\gamma }_n\mathrm{cond}+u$ (Theorem 4)
Algorithm 4	$10n-5$	${\gamma }_n^2\mathrm{cond}+u$ (Theorem 3)
Algorithm 8	$7n-2$	${\gamma }_n{\gamma }_{n+1}\mathrm{cond}+u$ (Theorem 5)

). When the rounding mode is round-towards-zero, the relative error bound of Algorithm 7 is ${\gamma }_{n-1}{\gamma }_n\mathrm{cond}+u$ and the relative error bound of Algorithm 8 (ours) is ${\gamma }_n{\gamma }_{n+1}\mathrm{cond}+u$ according to Theorems 4 and 5. The differences in the error bounds between our algorithms and the algorithms in [6] are not significant. The numerical experiments also indicate that the computed results of Algorithms 7 and 8 are very close in accuracy to those of Algorithms 3 and 4 [6]. Regarding the runtime performance, Algorithm 7 reduces the computation time by 40% compared to Algorithm 3 in [6]. Algorithm 8 reduces the computation time by 10% compared to Algorithm 4 in [6].