Umbral Interpolation: A Survey

Abstract

A survey on recent umbral polynomial interpolation is presented. Some new results are given, following a matrix-determinant approach. Some theoretical and numerical examples are provided.

1. Introduction

Interpolation is a very old theme [1,2,3]. The simple theorem of polynomial interpolation, on which much of practical numerical analysis is based, states that a straight line can pass through two points, a parabola through three, a cubic through four, and so on [4].

Modern interpolation theory is concerned with reconstructing functions on the basis of certain assumed known functional information [5,6]. In many cases, the functionals are linear. Hence, we consider the following general problem.

Let

• X be a linear space of real functions defined on the interval $[a,b]$, continuous and with continuous derivatives of all necessary orders;
• $\forall n\in \mathbb{N},{\mathcal{P}}_n$ be the space of polynomials of degree less than or equal to n;
• Q be a delta-operator (In [7,8] the authors use the notation $\delta$-operator, while in [9,10,11,12] the notation delta-operator) (see [13,14,15,16] and references therein), i.e.,

  $$\forall y\in X,Qy=\sum _{i=0}^{\infty }{c}_i{\displaystyle \frac{y^{\left(i\right)}}{i!}},c_0=0,c_1\ne 0,c_i\in \mathbb{R},i\ge 0;$$

  (1)
• L be a linear functional on X of the following type

  $$\begin{array}{cc}{\displaystyle L\left(y\right)=}\hfill & {\displaystyle {\int }_a^b\left[a_0\left(x\right)y\left(x\right)+\cdots +a_n\left(x\right)y^{\left(n\right)}\left(x\right)\right]dx}\hfill \\ \hfill & {\displaystyle +\sum _{i=1}^{m_0}{b}_{i,0}y\left(x_{i,0}\right)+\sum _{i=1}^{m_1}{b}_{i,1}{y}^{\prime }\left(x_{i,1}\right)+\cdots +\sum _{i=0}^{m_n}{b}_{i,n}{y}^{\left(n\right)}\left(x_{i,n}\right),}\hfill \end{array}$$

  (2)

  where the functions $a_i\left(x\right)$ are assumed to be piecewise continuous in $[a,b]$ and the points $x_{ij}$ to lie in $[a,b]$;
• ${\displaystyle X^{Q,n}=\left\{y\in X|Q^{i}y\in X,i=0,\dots ,n,\forall n\in \mathbb{N}\right\}}$, being $\mathbb{N}$ the set of natural numbers.

Then, for each $y\in X^{Q,n}$, we look for a polynomial $P_n\left[y\right]$, if it exists, of degree less than or equal to n such that

$$y=P_n\left[y\right]+R_n\left[y\right],$$

(3)

with

$$L\left(Q^i{P}_n\left[y\right]\right)=L\left(Q^{i}y\right),i=0,\dots ,n.$$

(4)

The polynomial $P_n\left[y\right]$ and $R_n\left[y\right]$ in (3) are called umbral interpolant and remainder, respectively. This problem is called umbral-interpolation problem for $(L,Q)$ (see [17,18] and references therein), and the conditions (4) are called umbral conditions for $(L,Q)$.

The term umbral interpolation is also used for other different topics (see [19,20] and references therein).

The paper is organized as follows: Section 2 contains the preliminaries, and Section 3 deals with the problem of umbral interpolation. In Section 4, some known and new examples of umbral interpolating polynomials associated with different types of delta operators are given. In Section 5, we compare the error in the approximation of some given function by many of these interpolating polynomials. Section 6 is dedicated to a brief conclusion. Finally, the Appendix A contains some tables that summarize the cases of umbral interpolation previously considered.

2. Preliminaries

Let the delta-operator Q be assigned.

Theorem 1 

(The Main Theorem [21]). There exists a unique polynomial sequence, denoted by ${\left\{p_n\right\}}_{n\in \mathbb{N}}$, such that

$$\left\{\begin{array}{c}{p}_0\left(x\right)=1,p_n\left(0\right)=0,\hfill \\ Q{p}_n=n{p}_{n-1}.\hfill \end{array}\right.$$

This polynomial sequence (p.s. in the following [22,23]) is said basic or associated with the operator Q, and it is of binomial type (see [13,14,16,24,25] and references therein).

For the proof of Theorem 1, we give some preliminary results.

Proposition 1 

(Numerical sequence and related matrix [16]). We consider the numerical sequence ${\left({\overline{b}}_i\right)}_{i\in \mathbb{N}}$ such that

$${\overline{b}}_i=c_i,i=0,1,\dots ,$$

with $c_i$ as in (1). Then we can build the nonsingular, lower triangular matrix ${\overline{B}}_n={\left({\overline{b}}_{i,k}\right)}_{i,k=0,\dots ,n}$ by the following algorithm ([16], p. 8):

$$\begin{array}{c}{\overline{b}}_{\ell ,0}={\delta }_{\ell ,0},{\overline{b}}_{\ell ,1}={\overline{b}}_{\ell },\ell =0,\cdots ,n,\hfill \\ {\displaystyle {\overline{b}}_{\ell ,k}=\frac{1}{k}\sum _{j=1}^{\ell -k+1}\left(\genfrac{}{}{0pt}{}{\ell }{j}\right){\overline{b}}_{j,1}{\overline{b}}_{\ell -j,k-1},\ell =2,\cdots ,n,k=2,\dots ,\ell ,}\hfill \\ {\overline{b}}_{\ell ,k}=0,\ell =0,\cdots ,n,k=\ell +1,\dots ,n.\hfill \end{array}$$

(5)

For $n\to \infty$ the matrix ${\overline{B}}_n$ is an infinite, lower triangular matrix [26,27], denoted by $\overline{B}$.

Proposition 2 

([16]). We consider the numerical sequence ${\left(b_i\right)}_{i\in \mathbb{N}}$ defined as

$$b_0=0,\sum _{k=1}^n{\overline{b}}_{n,k}{b}_k={\delta }_{n,1},n=1,2,\dots ,$$

with ${\overline{b}}_{n,k}$ as in (5). Then, by Algorithm (5), in which ${\overline{b}}_i$ is replaced with $b_i$, the numerical sequence ${\left(b_i\right)}_{i\in \mathbb{N}}$ generates the lower triangular matrix $B_n={\left(b_{j,k}\right)}_{j,k=0,\dots ,n}$. For $n\to \infty$ the matrix $B_n$ is an infinite lower triangular matrix, denoted by B.

Remark 1. 

We note that ${\overline{b}}_{i,i}={\overline{b}}_1^i\ne 0$ and $b_{i,i}=b_1^i\ne 0$. Hence, for every n the matrices $B_n\left(B\right)$ and ${\overline{B}}_n\left(\overline{B}\right)$ are nonsingular.

The matrices $B_n$ and ${\overline{B}}_n$ (B and $\overline{B}$, respectively, in the infinite case) are inverse of each other and are called matrices of binomial type ([16], p. 7).

The numerical sequences ${\left(b_i\right)}_{i\in \mathbb{N}}$ and ${\left({\overline{b}}_i\right)}_{i\in \mathbb{N}}$ generate the formal power series

$$f\left(t\right)=\sum _{i=0}^{\infty }{b}_i{\displaystyle \frac{t^i}{i!}},\overline{f}\left(t\right)=\sum _{i=0}^{\infty }{\overline{b}}_i{\displaystyle \frac{t^i}{i!}},$$

(6)

respectively. They are called δ-series [13,14], being $b_0={\overline{b}}_0=0$, and $b_1\ne 0,{\overline{b}}_1\ne 0$.

Proposition 3 

([16], p. 9). With the previous hypothesis and notation, we obtain

$$\begin{array}{c}{\displaystyle f\left(\overline{f}\left(t\right)\right)=t=\overline{f}\left(f\left(t\right)\right)}\hfill \\ {\displaystyle \frac{1}{k!}{\left(f\left(t\right)\right)}^k=\sum _{i=0}^{\infty }{b}_{i,k}\frac{t^i}{i!}}\hfill \\ {\displaystyle \frac{1}{k!}{\left(\overline{f}\left(t\right)\right)}^k=\sum _{i=0}^{\infty }{\overline{b}}_{i,k}\frac{t^i}{i!}.}\hfill \end{array}$$

Proof of Theorem 1.

Let us consider the matrix $B_n={\left(b_{j,k}\right)}_{j,k=0,\dots ,n}$ with elements as in Propositions 2 and 3. It defines the p.s. ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ with

$$p_0\left(x\right)=1,p_n\left(x\right)=\sum _{k=0}^n{b}_{n,k}{x}^k,\forall n\in \mathbb{N}.$$

(7)

It can be proved (see ([17], pp. 124–125)) that

$$e^{xf\left(t\right)}=\sum _{n=0}^{\infty }{p}_n\left(x\right){\displaystyle \frac{t^n}{n!}}.$$

with $f\left(x\right)$ as in (6).

It is easy to verify that

$$p_n\left(0\right)=b_{n,0}=0,n\ge 1.$$

Then, taking into account the linearity of Q and the previous relations, we obtain

$$\begin{array}{cc}{\displaystyle \sum _{n=0}^{\infty }Q{p}_n\left(x\right)\frac{t^n}{n!}}\hfill & {\displaystyle =Q\sum _{n=0}^{\infty }{p}_n\left(x\right)\frac{t^n}{n!}=Q{e}^{xf\left(t\right)}=\left({\overline{b}}_{1}f\left(t\right)+{\overline{b}}_2\frac{f^2\left(t\right)}{2!}+\dots +{\overline{b}}_n\frac{f^n\left(t\right)}{n!}+\cdots \right)e^{xf\left(t\right)}}\hfill \\ & {\displaystyle =t\sum _{n=0}^{\infty }{p}_n\left(x\right)\frac{t^n}{n!}=\sum _{n=0}^{\infty }n{p}_{n-1}\left(x\right)\frac{t^n}{n!}.}\hfill \end{array}$$

This implies $Q{p}_n=n{p}_{n-1}$.

Proposition 4 

([16], pp. 31–32). For the elements of ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ the following determinant form holds

$$\begin{array}{c}{\displaystyle p_0\left(x\right)=1,}\hfill \\ {\displaystyle p_n\left(x\right)=\frac{{\left(-1\right)}^{n+1}}{{\prod }_{i=0}^n{\overline{b}}_{i,i}}\left|\begin{array}{ccccc}x& x^2& \cdots & x^{n-1}& x^n\\ {\overline{b}}_{1,1}& {\overline{b}}_{2,1}& \cdots & {\overline{b}}_{n-1,1}& {\overline{b}}_{n,1}\\ 0& \ddots & \ddots & & ⋮\\ ⋮& & \ddots & \ddots & ⋮\\ 0& \cdots & 0& {\overline{b}}_{n-1,n-1}& {\overline{b}}_{n,n-1}\end{array}\right|,n>0.}\hfill \end{array}$$

(8)

Now, let L be a linear functional on X with L as in (2). We set

$${\beta }_n=L\left(p_n\right),n=0,1,\dots$$

(9)

The sequence ${\left({\beta }_n\right)}_{n\in \mathbb{N}}$ generates the numerical sequence ${\left({\alpha }_n\right)}_{n\in \mathbb{N}}$, called associated with ${\left({\beta }_k\right)}_{k\in \mathbb{N}}$, by the binomial convolution product (also called Hurwitz product) [28,29]:

$${\alpha }_0={\displaystyle \frac{1}{{\beta }_0}},\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\alpha }_k{\beta }_{n-k}=0.$$

(10)

In [30], sequences of type ${\left({\alpha }_n\right)}_{n\in \mathbb{N}}$ are called convolution sequences.

Then we build the p.s. ${\left\{a_n\right\}}_{n\in \mathbb{N}}$ with

$$a_0\left(x\right)={\alpha }_0\ne 0,a_n\left(x\right)=\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\alpha }_k{x}^{n-k}.$$

It is easy to verify that

$$\left\{\begin{array}{c}{a}_n^{\prime }\left(x\right)=n{a}_{n-1}\left(x\right),\hfill \\ a_n\left(0\right)={\alpha }_n,\hfill \end{array}\right.\forall n\in \mathbb{N}.$$

Furthermore, if we set

$$g\left(t\right)=\sum _{n=0}^{\infty }{\alpha }_n{\displaystyle \frac{t^n}{n!}},$$

we obtain

$$g\left(t\right)e^{xt}=\sum _{n=0}^{\infty }{a}_n\left(x\right){\displaystyle \frac{t^n}{n!}}$$

and

$${\displaystyle \frac{1}{g\left(t\right)}}·g\left(t\right)=1,{\displaystyle \frac{1}{g\left(t\right)}}=\sum _{n=0}^{\infty }{\beta }_n{\displaystyle \frac{t^n}{n!}}.$$

The p.s. ${\left\{a_n\right\}}_{n\in \mathbb{N}}$, so defined, is known as Appell p.s. (see [16,31,32] and references therein).

Taking into account that the set of polynomial sequences is a group with respect to the umbral composition ([17], p. 58), we can consider the umbral composition of the Appell p.s. ${\left\{a_n\right\}}_{n\in \mathbb{N}}$ and the binomial-type p.s. ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ as in (7). Thus, we obtain the p.s. ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ with

$$s_n\left(x\right)=\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\alpha }_k{p}_{n-k}\left(x\right),\forall n\in \mathbb{N}.$$

(11)

It is proved [33] that the p.s. ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ has the following determinant form

$$\begin{array}{c}{\displaystyle s_0\left(x\right)=\frac{1}{{\beta }_0},}\hfill \\ {\displaystyle s_n\left(x\right)=\frac{{\left(-1\right)}^n}{{\beta }_0^{n+1}}\left|\begin{array}{cccccc}{p}_0\left(x\right)& p_1\left(x\right)& p_2\left(x\right)& \cdots & p_{n-1}\left(x\right)& p_n\left(x\right)\\ {\beta }_0& {\beta }_1& {\beta }_2& \cdots & {\beta }_{n-1}& {\beta }_n\\ 0& {\beta }_0& \left(\genfrac{}{}{0pt}{}{2}{1}\right){\beta }_1& \cdots & \left(\genfrac{}{}{0pt}{}{n-1}{1}\right){\beta }_{n-2}& \left(\genfrac{}{}{0pt}{}{n}{1}\right){\beta }_{n-1}\\ ⋮& \ddots & \ddots & & ⋮& ⋮\\ ⋮& & \ddots & \ddots & ⋮& ⋮\\ 0& \cdots & \cdots & 0& {\beta }_0& \left(\genfrac{}{}{0pt}{}{n}{n-1}\right){\beta }_1\end{array}\right|,n>0,}\hfill \end{array}$$

(12)

with ${\beta }_i=L\left(p_i\right)$.

Moreover, the following recurrence form holds [33]:

$$s_n\left(x\right)={\displaystyle \frac{1}{{\beta }_0}}\left(p_n\left(x\right)-\sum _{i=0}^{n-1}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right){\beta }_{n-i}{s}_i\left(x\right)\right).$$

From (11) and Theorem 1 it follows that

$$Q{s}_n=n{s}_{n-1}.$$

(13)

Proposition 5 

([33]). We obtain

$$L\left(Q^i{s}_n\right)=i!\left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right){\delta }_{i,n},i=0,\dots ,n,$$

(14)

where ${\delta }_{i,n}$ is the Kroneker symbol.

Proof. 

From Theorem 1 we have

$$L\left(Q^i{s}_n\right)=n^{\underline{i}}L\left(s_{n-i}\right)=i!\left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right){\delta }_{i,n},$$

(15)

where $n^{\underline{i}}$ is the falling factorial [34]. In the second equality, we applied (11), (9) and (10).   □

We observe that the p.s. ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ is a Sheffer p.s. (see [16,17,21,33,35] and references therein). Then the set $\left\{s_0\left(x\right),\cdots ,s_n\left(x\right)\right\}$ is a basis for ${\mathcal{P}}_n$, and we call it umbral basis for $(L,Q)$ or simply umbral basis.

In summary, once a delta-operator Q and a linear functional L are assigned,

• there exists a unique p.s. ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ such that

  $$p_0\left(x\right)=1,p_n\left(0\right)=0,Q{p}_n=n{p}_{n-1};$$

  the p.s. ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ is of binomial-type;
• assuming ${\beta }_n=L\left(p_n\right)$ as in (9), there exists the numerical sequence ${\left({\alpha }_k\right)}_{k\in \mathbb{N}}$, such that

  $${\alpha }_0={\displaystyle \frac{1}{{\beta }_0}},{\beta }_0\ne 0,\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\alpha }_k{\beta }_{n-k}=0;$$
• there exists the p.s. ${\left\{a_n\right\}}_{n\in \mathbb{N}}$ such that

  $$a_n^{\prime }\left(x\right)=n{a}_{n-1}\left(x\right),a_n\left(0\right)={\alpha }_n;$$

  the p.s. ${\left\{a_n\right\}}_{n\in \mathbb{N}}$ is an Appell p.s. [31];
• finally, we consider the umbral composition

  $$s_n\left(x\right)=\left(a_n\circ p_n\right)\left(x\right)=\sum _{k=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\alpha }_k{p}_{n-k}\left(x\right).$$

  (16)
  The p.s. ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ is a Sheffer p.s. which satisfies

  $$Q{s}_n=n{s}_{n-1}.$$

  Hence, as the linear functional L, with L as in (2), varies, the set of polynomial sequences ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ in (16) is the set of Sheffer polynomial sequences associated with the delta-operator Q. It is an umbral basis for $(L,Q)$ [16,17,18].

3. Umbral Interpolation

Now, we consider the problem of umbral interpolation mentioned in the Introduction. We first extend the problem to the more general case.

Let L be a linear functional on X with L as in (2), Q a delta-operator on ${\mathcal{P}}_n$ and ${\omega }_i\in \mathbb{R},i=0,1,\dots ,n$, not all zero. We want to solve the following problem: determine, if it exists, the polynomial $P_n\in {\mathcal{P}}_n$ such that

$$L\left(Q^i{P}_n\right)=i!{\omega }_i,i=0,\dots ,n.$$

(17)

This problem is called umbral-interpolation problem in ${\mathcal{P}}_n$. The conditions (17) are called umbral-interpolant conditions.

Theorem 2 

([18]). Let ${\left\{s_k\right\}}_{k\in \mathbb{N}}$ be the umbral basis for $(L,Q)$. The polynomial

$$P_n\left(x\right)=\sum _{i=0}^n{\omega }_i{s}_i\left(x\right)$$

is the unique polynomial of degree less than or equal to n satisfying the umbral-interpolation problem, i.e., such that

$$L\left(Q^i{P}_n\right)=i!{\omega }_i,i=0,\dots ,n.$$

Proof. 

The proof is a straightforward consequence of Proposition 5 and the linearity of Q.    □

Corollary 1.

(Representation of polynomials). Each $P_n\in {\mathcal{P}}_n$ can be written as

$$P_n\left(x\right)=\sum _{i=0}^{n}L\left(Q^i{P}_n\right){\displaystyle \frac{s_i\left(x\right)}{i!}}.$$

(18)

Now, we extend the concept of umbral interpolation to the real space of functions X.

Theorem 3.

(The main Theorem). Let Q be a delta-operator on the linear space X. We set

$$X^{Q,n}=\left\{f\in X:Q^{i}f\in X,i=0,\dots ,n\right\},\forall n\in \mathbb{N}.$$

Let L be a linear functional on $X^{Q,n}$, with L as in (2). Let ${\left\{s_n\right\}}_{n\in \mathbb{N}}$ be the umbral basis for $\left(L,Q\right)$. Then, for every $f\in X^{Q,n}$, the polynomial

$$P_n\left[f\right]\left(x\right)=\sum _{i=0}^{n}L\left(Q^{i}f\right){\displaystyle \frac{s_i\left(x\right)}{i!}}$$

(19)

is the unique polynomial of degree less than or equal to n such that

$$L\left(Q^i{P}_n\left[f\right]\right)=L\left(Q^{i}f\right),i=0,1,\dots ,n.$$

(20)

Proof. 

The proof follows from Theorem 2 (for details see ([17], pp. 392–394)).    □

Definition 1. 

The polynomial $P_n\left[f\right]$ is called the  umbral interpolant  for the function f related to $\left(L,Q\right)$. The conditions (20) are known as  umbral interpolant conditions  of f for $\left(L,Q\right)$.

The difference 

$$R_n\left[f\right]\left(x\right)=f\left(x\right)-P_n\left[f\right]\left(x\right),x\in [a,b],$$

is called  truncation error  or  remainder  at the point x.

Theorem 4 

([18]). For any $g\in {\mathcal{P}}_n$, we obtain

$$R_n\left[g\right]\left(x\right)=0,\forall x\in [a,b].$$

If $q_{n+1}$ is a polynomial of degree $n+1$, then

$$\exists x\in [a,b]s.t.R_n\left[q_{n+1}\right]\left(x\right)\ne 0.$$

Proof. 

The proof follows from (8) and (13), taking into account the (15).    □

We say that $P_n\left[f\right]$ is an approximant of order n for f.

For every fixed x in $[a,b]$, we may consider the remainder $R_n\left[f\right]\left(x\right)$ as a linear functional which acts on f and annihilates all elements of ${\mathcal{P}}_n$. For any fixed x, it can be considered to be a linear functional as in (2). Therefore, we can apply Peano’s Theorem ([4], p. 69).

Theorem 5 

([18]). Let $f\in C^{n+1}[a,b]$. The following representation for $R_n\left[f\right]\left(x\right)$ holds:

$$R_n\left[f\right]\left(x\right)={\displaystyle \frac{1}{n!}}{\int }_a^b{K}_n(x,t)f^{\left(n+1\right)}\left(t\right)dt,\forall x\in [a,b],$$

where

$$K_n(x,t)=R_n\left[{\left(x-t\right)}_{+}^n\right]={\left(x-t\right)}_{+}^n-\sum _{i=0}^n{L}_x\left(Q^i{(x-t)}_{+}^n\right){\displaystyle \frac{s_i\left(x\right)}{i!}},$$

being ${\left(x\right)}_{+}^n$ the truncated power function ([4], p. 70).

Remark 2. 

From (19), if $f^{(n+1)}\in {\mathcal{L}}^p[a,b]$ and $K_n(x,t)\in {\mathcal{L}}^q[a,b]$ with ${\displaystyle \frac{1}{p}+\frac{1}{q}=1}$, then, by applying the known Holder’s inequality, classic bounds for $\left|R_n\left[f\right]\right|$ can be obtained.

Proposition 6. 

Let $T_n^a\left[f\right]\left(x\right)$ be the Taylor polynomial for the function f with initial point a. Then the following identity holds:

$$P_n\left[f\right]\left(x\right)=T_n^a\left[f\right]\left(x\right)-{\displaystyle \frac{1}{n!}}\sum _{i=0}^n{\displaystyle \frac{s_i\left(x\right)}{i!}}{\int }_a^b{L}_x\left(Q^i{(x-t)}_{+}^n\right)f^{(n+1)}\left(t\right)dt.$$

Moreover,

$$P_n\left[f\right]\left(x\right)⟶T_n^a\left[f\right]\left(x\right),x⟶a.$$

Proof. 

The proof follows from Theorem 5, after easy calculations.    □

In order to provide another umbral-interpolant for f, if z is a fixed point in $[a,b]$, we consider the polynomial

$${\overline{P}}_{n,z}\left[f\right]\left(x\right)\equiv P_n\left[f\right]\left(x\right)+f\left(z\right)-P_{n,z}\left[f\right]\left(z\right)=f\left(z\right)+\sum _{i=1}^{n}L\left(Q^{i}f\right){\displaystyle \frac{s_i\left(x\right)-s_i\left(z\right)}{i!}}.$$

Theorem 6 

([18]). The polynomial ${\overline{P}}_{n,z}\left[f\right]$ is an approximant of order n for f, i.e.,

$$f\left(x\right)={\overline{P}}_{n,z}\left[f\right]\left(x\right)+{\overline{R}}_{n,z}\left[f\right]\left(x\right),$$

with

$${\overline{R}}_{n,z}\left[q_i\right]\left(x\right)=0,i=0,\cdots ,n,q_i\in {\mathcal{P}}_i,{\overline{R}}_{n,z}\left[q_{n+1}\right]\left(x\right)\ne 0\mathrm{for}\mathrm{at}\mathrm{least}\mathrm{an}x\in [a,b].$$

Proof. 

The proof follows from Theorem 4.    □

Theorem 7 

([18]). The polynomial ${\overline{P}}_{n,z}\left[f\right]$ satisfies the following interpolating conditions

$${\overline{P}}_{n,z}\left[f\right]\left(z\right)=f\left(z\right),L\left(Q^i{\overline{P}}_n\left[f\right]\right)=L\left(Q^{i}f\right),i=1,\dots ,n.$$

${\overline{P}}_{n,z}\left[f\right]\left(x\right)$ is called the complementary umbral interpolating polynomial ([17], p. 394) for $f\in X^{Q,n}$.

The remainder is

$${\overline{R}}_n[f,z]\left(x\right)=f\left(x\right)-{\overline{P}}_n[f,z]\left(x\right),\forall x\in \left[a,b\right],$$

and it is exact on ${\mathcal{P}}_n$. It can be written as

$${\overline{R}}_n[f,z]\left(x\right)=R_n\left[f\right]\left(x\right)-R_n\left[f\right]\left(z\right).$$

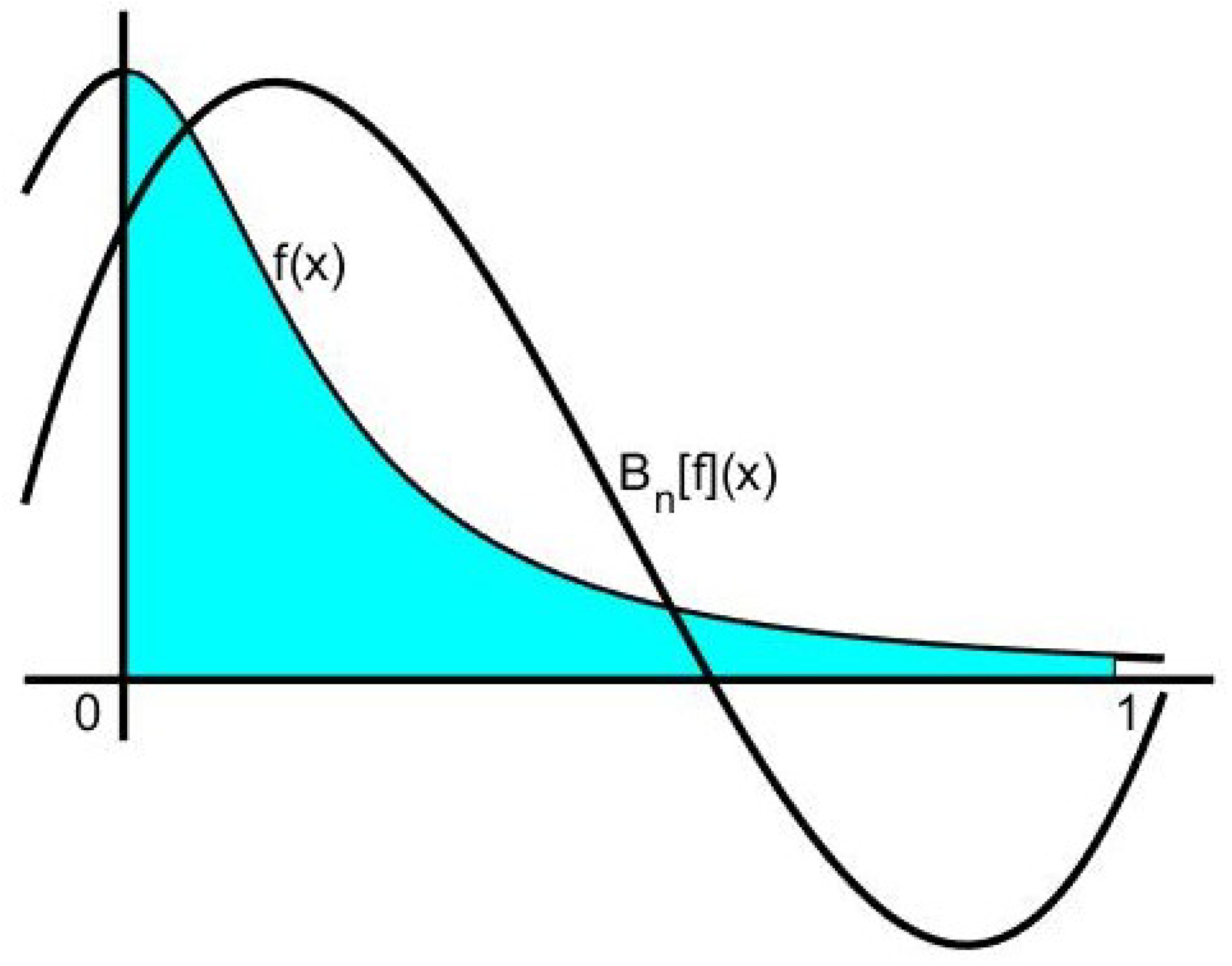
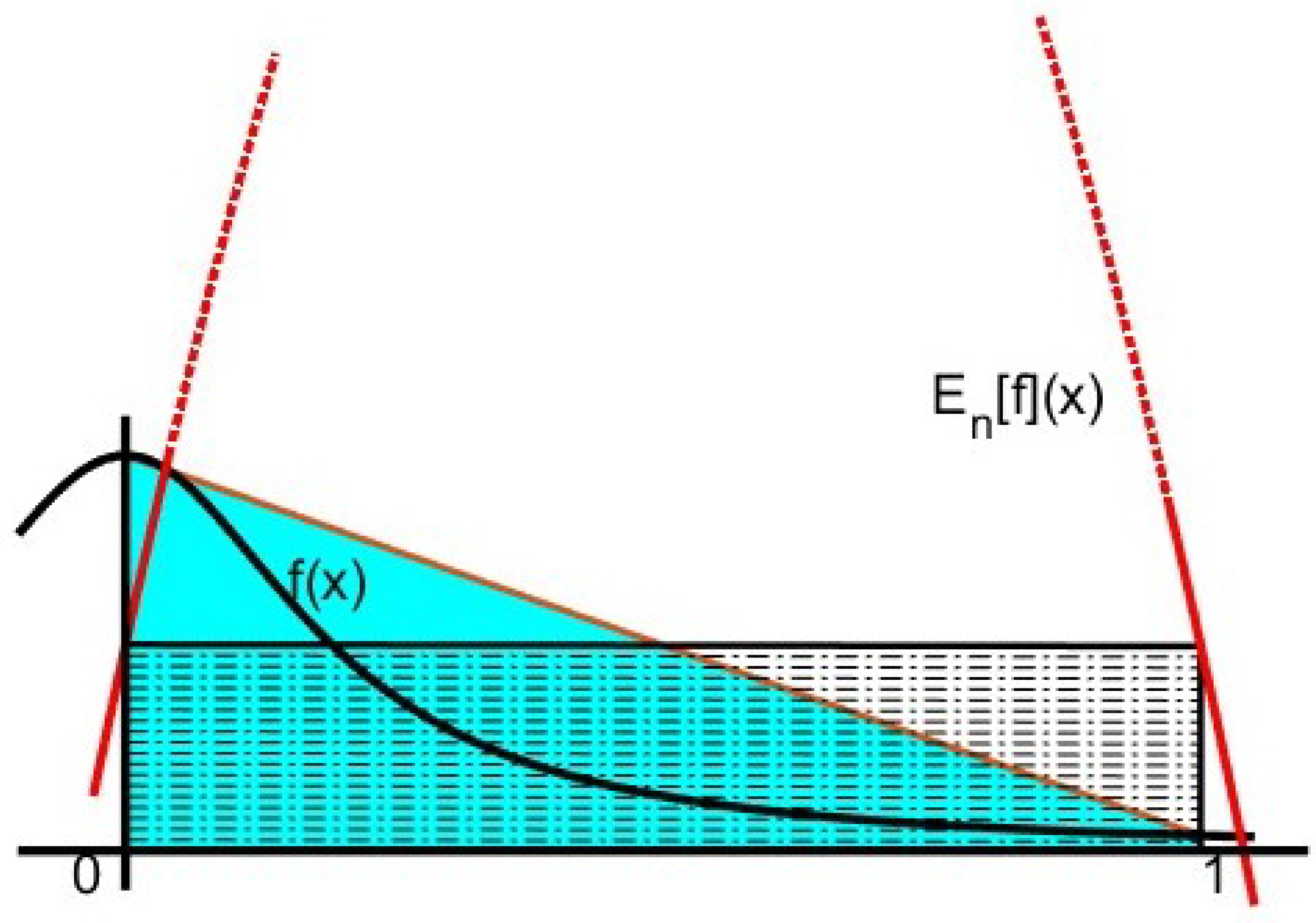
4. Examples

Now, we give some known and unknown examples of umbral interpolation. For the sake of brevity, in the examples, we do not consider the study of the remainder, referring to it in the cited bibliography.

4.1. Umbral Interpolation Related to $\mathit{Q}={\mathit{D}}_{\mathit{x}}$

Let us consider as delta-operator the classic operator of differentiation

$$Q=D_x.$$

For simplicity, in the following, we will use D instead of $D_x$ if there is no possibility of misunderstanding.

The associated sequence is the canonical basis ${\left\{x^n\right\}}_{n\in \mathbb{N}}$ and $X^{Q,n}=C^n[0,1]$.

If L is a linear functional on $X^{Q,n}$, with L as in (2), the umbral basis for $(D,L)$ is the Appell p.s. ${\left\{{\mathrm{a}}_{L,n}\right\}}_{n\in \mathbb{N}}$ such that

$$\begin{array}{cc}\hfill & {\mathrm{a}}_{L,0}\left(x\right)={\displaystyle \frac{1}{{\beta }_0}}\hfill \\ \hfill & {\mathrm{a}}_{L,n}\left(x\right)={\displaystyle \frac{{\left(-1\right)}^n}{{\displaystyle {\beta }_0^{n+1}}}}\left|\begin{array}{cccccc}1& x& x^2& \cdots & \cdots & x^n\\ {\beta }_0& {\beta }_1& {\beta }_2& \cdots & \cdots & {\beta }_n\\ 0& {\beta }_0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{1}}\right){\beta }_1& \cdots & \cdots & \left({\displaystyle \genfrac{}{}{0pt}{}{n}{1}}\right){\beta }_{n-1}\\ ⋮& \ddots & \ddots & \ddots & & ⋮\\ ⋮& & \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 0& {\beta }_0& \left({\displaystyle \genfrac{}{}{0pt}{}{n}{n-1}}\right){\beta }_1\end{array}\right|,\hfill \end{array}$$

(21)

with ${\beta }_i=L\left(x^i\right)$, $i\ge 0$.

In this case, the umbral interpolating polynomial and the related complementary polynomial for $f\in X^{Q,n}$ are, respectively,

$$\begin{array}{cc}\hfill & A_n\left[f\right]\left(x\right)=\sum _{i=0}^{n}L\left(f^{\left(i\right)}\right){\displaystyle \frac{{\mathrm{a}}_{L,i}\left(x\right)}{i!}},\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill & {\overline{A}}_n\left[f\right]\left(x\right)=f\left(z\right)+\sum _{i=1}^{n}L\left(f^{\left(i\right)}\right){\displaystyle \frac{{\mathrm{a}}_{L,i}\left(x\right)-{\mathrm{a}}_{L,i}\left(z\right)}{i!}}.\hfill \end{array}$$

(22b)

In (22b) z is any point in $[0,1]$. From now on, unless otherwise specified, we set $z=0$.

The interpolatory conditions are, respectively,

$$\begin{array}{cc}\hfill & L\left(A_n{\left[f\right]}^{\left(i\right)}\right)=L\left(f^{\left(i\right)}\right),i=0,\dots ,n\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill & {\overline{A}}_n\left[f\right]\left(0\right)=f\left(0\right),L\left({\overline{A}}_n{\left[f\right]}^{\left(i\right)}\right)=L\left(f^{\left(i\right)}\right),i=1,\dots ,n.\hfill \end{array}$$

(23b)

We call this type of interpolation Appell umbral interpolation [36].

4.1.1. Generalized Taylor Polynomial

Assuming

$$L\left(f\right)=f\left(x_0\right),x_0\in \left[0,1\right],$$

the umbral polynomial (22a) coincides with (22b) and becomes

$$A_n\left[f\right]\left(x\right)={\overline{A}}_n\left[f\right]\left(x\right)=f\left(x_0\right)+\sum _{i=1}^n{f}^{\left(i\right)}\left(x_0\right){\displaystyle \frac{{(x-x_o)}^i}{i!}},$$

that is, the well-known Taylor polynomial for f. Therefore, we call the polynomial (22b) generalized Taylor polynomial of degree n.

4.1.2. Bernoulli of the First Kind Umbral Interpolation

Assuming

$$L\left(f\right)={\int }_0^{1}f\left(x\right)dx,$$

we obtain

$${\beta }_k=L\left(x^k\right)={\displaystyle \frac{1}{k+1}},k\ge 0.$$

Then the umbral polynomial (22a) becomes the well-known Bernoulli polynomial of the first kind [36,37,38], $B_i\left(x\right)$. The umbral Bernoulli interpolant is (see [16,36] and references therein)

$$B_n\left[f\right]\left(x\right)={\int }_0^{1}f\left(x\right)dx+\sum _{i=1}^n\left[f^{(i-1)}\left(1\right)-f^{(i-1)}\left(0\right)\right]{\displaystyle \frac{B_i\left(x\right)}{i!}}.$$

(24)

It is also known as expansion in Bernoulli polynomials [39] or umbral Bernoulli interpolant [17].

The complementary polynomial is

$${\overline{B}}_n\left[f\right]\left(x\right)=f\left(0\right)+\sum _{i=1}^n\left[f^{(i-1)}\left(1\right)-f^{(i-1)}\left(0\right)\right]{\displaystyle \frac{B_i\left(x\right)-B_i\left(0\right)}{i!}}.$$

(25)

This polynomial appeared for the first time in [40], and then, it has been applied in several topics: interpolation of real functions [18], numerical solution of nonlinear equations [41], numerical solution of BVPs by collocation methods [42,43].

The umbral interpolatory conditions for (24) are

$${\int }_0^{1}f\left(x\right)dx={\int }_0^1{B}_n\left[f\right]\left(x\right)dx,$$

(26a)

$$f^{(i-1)}\left(1\right)-f^{(i-1)}\left(0\right)={\int }_0^1{B}_n{\left[f\right]}^{\left(i\right)}\left(x\right)dx,i=1,\dots ,n.$$

(26b)

Similarly, for the polynomial (24) the umbral interpolatory conditions are

$$f\left(0\right)={\overline{B}}_n\left[f\right]\left(0\right),f^{(i-1)}\left(1\right)-f^{(i-1)}\left(0\right)={\int }_0^1{\overline{B}}_n{\left[f\right]}^{\left(i\right)}\left(x\right)dx,i=1,\dots ,n.$$

Figure 1 shows the geometric interprestation of the interpolatory condition (26a) for $i=1$.

4.1.3. Euler Umbral Interpolation

Euler polynomials, introduced by Euler in 1740 [44], are Appell polynomials. Hence, they are often related to the theory of Bernoulli polynomials. There is a wide range of literature on them and several interesting applications.

Assuming

$$L\left(f\right)={\displaystyle \frac{f\left(0\right)+f\left(1\right)}{2}},$$

we obtain

$${\beta }_k=L\left(x^k\right)=\left\{\begin{array}{ccc}1,\hfill & & k=0\hfill \\ {\displaystyle \frac{1}{2}},\hfill & & k\ge 1\hfill \end{array}\right.\forall k\in \mathbb{N}.$$

Then the Appell p.s. (22a) is the well-known Euler p.s. ([16], p. 124, [36]) ${\left\{E_n\right\}}_{n\in \mathbb{N}}$, with

$$E_n\left(x\right)=\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)E_{n-k}\left(0\right)x^k,\forall n\in \mathbb{N}.$$

The umbral interpolating polynomial is

$$E_n\left[f\right]\left(x\right)={\displaystyle \frac{f\left(0\right)+f\left(1\right)}{2}}+\sum _{i=1}^n{\displaystyle \frac{f^{\left(i\right)}\left(0\right)+f^{\left(i\right)}\left(1\right)}{2}}{\displaystyle \frac{E_i\left(x\right)}{i!}}.$$

(27)

The related umbral complementary interpolant is

$${\overline{E}}_n\left[f\right]\left(x\right)=f\left(0\right)+\sum _{i=1}^n{\displaystyle \frac{f^{\left(i\right)}\left(0\right)+f^{\left(i\right)}\left(1\right)}{2}}{\displaystyle \frac{E_i\left(x\right)-E_i\left(0\right)}{i!}}.$$

(28)

The umbral interpolatory conditions are, respectively,

$${\displaystyle \frac{f^{\left(i\right)}\left(1\right)+f^{\left(i\right)}\left(0\right)}{2}}={\displaystyle \frac{E_n{\left[f\right]}^{\left(i\right)}\left(1\right)+E_n{\left[f\right]}^{\left(i\right)}\left(0\right)}{2}},i=0,\dots ,n,$$

(29)

and

$$f\left(0\right)={\overline{E}}_n\left[f\right]\left(0\right),{\displaystyle \frac{f^{\left(i\right)}\left(1\right)+f^{\left(i\right)}\left(0\right)}{2}}={\displaystyle \frac{{\overline{E}}_n{\left[f\right]}^{\left(i\right)}\left(1\right)+{\overline{E}}_n{\left[f\right]}^{\left(i\right)}\left(0\right)}{2}},i=1,\dots ,n.$$

Figure 2 shows the geometric interpretation of the interpolatory condition (29) for $i=0$ and $n=3$.

We observe that if we introduce the mean operator [39]

$$Mf={\displaystyle \frac{f(x+1)+f\left(x\right)}{2}},$$

we have ${L\left(f\right)=Mf|}_{x=0}$.

4.1.4. First Kind Bernoulli-Type Umbral Interpolation

Let L be the following linear functional on $[-1,1]$

$$L\left(f\right)={\displaystyle \frac{1}{2}}{\int }_{-1}^{1}f\left(x\right)dx.$$

We obtain

$${\beta }_k=L\left(x^k\right)=\left\{\begin{array}{ccc}1& & k=0,\hfill \\ 0& & oddk,\hfill \\ {\displaystyle \frac{1}{k+1},}& & evenk,\hfill \end{array}\right.\forall k\in \mathbb{N}.$$

The umbral basis for $(L,D)$ is the p.s. ${\left\{{\mathcal{B}}_n\right\}}_{n\in \mathbb{N}}$ with elements given by

$$\begin{array}{cc}\hfill & {\mathcal{B}}_0\left(x\right)=1,\hfill \\ \hfill & {\mathcal{B}}_n\left(x\right)={(-1)}^n\left|\begin{array}{cccccc}1& x& x^2& \cdots & \cdots & x^n\\ 1& 0& {\displaystyle \frac{1}{3}}& \cdots & \cdots & {\beta }_n\\ 0& 1& 0& \cdots & \cdots & \left({\displaystyle \genfrac{}{}{0pt}{}{n}{1}}\right){\beta }_{n-1}\\ ⋮& \ddots & \ddots & \ddots & & ⋮\\ ⋮& & \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 0& 1& 0\end{array}\right|.\hfill \end{array}$$

(30)

The first six polynomials of the p.s. ${\left\{{\mathcal{B}}_n\right\}}_{n\in \mathbb{N}}$ are

$${\mathcal{B}}_0\left(x\right)=1,{\mathcal{B}}_1\left(x\right)=x,{\mathcal{B}}_2\left(x\right)=x^2-{\displaystyle \frac{1}{3}},{\mathcal{B}}_3\left(x\right)=x^3-x,$$

$${\mathcal{B}}_4\left(x\right)=x^4-2x^2+{\displaystyle \frac{7}{15}},{\mathcal{B}}_5\left(x\right)=x^5-{\displaystyle \frac{10}{3}}{x}^3+{\displaystyle \frac{7}{3}}x.$$

Their plots are in Figure 3.

Observe that

$${\displaystyle {\mathcal{B}}_n\left(x\right)=2^n{B}_n\left(\frac{x+1}{2}\right),B_n\left(x\right)=\frac{1}{2^n}{\mathcal{B}}_n\left(\frac{2x-1}{2}\right).}$$

That is, the polynomials ${\mathcal{B}}_n\left(x\right)$ coincide, up to a constant, with the classical Bernoulli polynomials of the first kind, translated in the interval $[-1,1]$. Moreover, the subsequences ${\left\{{\mathcal{B}}_{2n}\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\mathcal{B}}_{2n+1}\right\}}_{n\in \mathbb{N}}$ are the even and odd Lidstone-type polynomial sequences, respectively, introduced in ([17], p. 238) (see also the reference therein). The p.s. ${\left\{{\mathcal{B}}_n\right\}}_{n\in \mathbb{N}}$ has been introduced in [10,11,45] by the classical theory of Rota et al. [13,14,46].

This theory is very different from the determinant approach used here.

The umbral interpolating polynomials is

$$B_n\left[f\right]\left(x\right)={\displaystyle \frac{1}{2}}{\int }_{-1}^{1}f\left(x\right)dx+{\displaystyle \frac{1}{2}}\sum _{i=1}^n\left[f^{(i-1)}\left(1\right)-f^{(i-1)}(-1)\right]{\displaystyle \frac{{\mathcal{B}}_i\left(x\right)}{i!}},$$

and the related complementary is

$${\overline{B}}_n\left[f\right]\left(x\right)=f\left(z\right)+{\displaystyle \frac{1}{2}}\sum _{i=1}^n\left[f^{(i-1)}\left(1\right)-f^{(i-1)}(-1)\right]{\displaystyle \frac{{\mathcal{B}}_i\left(x\right)-{\mathcal{B}}_i\left(z\right)}{i!}},z\in [-1,1].$$

The interpolatory conditions are

$${\int }_{-1}^1{f}^{\left(i\right)}\left(x\right)dx={\int }_{-1}^1{B}_n{\left[f\right]}^{\left(i\right)}\left(x\right)dx,i=0,\dots ,n$$

and

$${\overline{B}}_n\left[f\right]\left(z\right)=f\left(z\right),{\int }_{-1}^1{f}^{\left(i\right)}\left(x\right)dx={\int }_{-1}^1{\overline{B}}_n{\left[f\right]}^{\left(i\right)}\left(x\right)dx,i=1,\dots ,n.$$

4.2. Umbral Interpolation Related to $\mathit{Q}={\Delta }_{\mathit{h}}$

In this section, we look at some known and new examples of umbral interpolation related to the finite difference operator [26,39,47,48,49]

$$Q={\Delta }_{h}y\left(x\right)=y(x+h)-y\left(x\right),h>0,x\in [0,1].$$

(31)

It is a delta-operator.

For simplicity of notation, in the following, we omit showing the dependence on h in ${\Delta }_h$, unless absolutely necessary.

Let us define the finite difference operator of order i, $i\in \mathbb{N}$, as

$${\Delta }^{i}y\left(x\right)=\Delta \left({\Delta }^{i-1}y\left(x\right)\right)=\sum _{j=0}^i{(-1)}^{i-j}\left({\displaystyle \genfrac{}{}{0pt}{}{i}{j}}\right)y(x+jh),$$

(32)

with ${\Delta }^0=I$, ${\Delta }^1=\Delta$, being I the identity operator.

Moreover, let ${\Delta }^{-1}$ denote the indefinite summation operator, defined in ([39], pp. 100–101) as the linear operator inverse of the finite difference operator $\Delta$. It is related to the finite difference operator as the indefinite integral is related to the derivative operator.

From (31) we obtain [50]

$$\Delta y\left(x\right)=\sum _{i=1}^{\infty }{h}^i{\displaystyle \frac{y^{\left(i\right)}\left(x\right)}{i!}}.$$

Hence $\Delta$ is a delta-operator, with ${\overline{b}}_i=h^i,i=1,2,\dots$. It is known [50] that the elements of the associated p.s. are the generalized falling factorials ${\left(x\right)}_{n,h}\equiv {\left(x\right)}_n$([39], p. 45), that is,

$${\left(x\right)}_0=1,{\left(x\right)}_n=x\left(x-h\right)\left(x-2h\right)\cdots \left(x-(n-1)h\right),n\ge 1.$$

Then we obtain

$$\Delta {\left(x\right)}_n=nh{\left(x\right)}_{n-1}.$$

Let L be a linear functional on $X^{Q,n}$ with L as in (2). We set

$${\beta }_n=L\left({\left(x\right)}_n\right),n\ge 0.$$

Then the umbral basis for $(L,\Delta )$ is the p.s.

$$\begin{array}{cc}\hfill & {\mathcal{A}}_0^L\left(x\right)={\displaystyle \frac{1}{{\beta }_0}},\hfill \\ \hfill & {\mathcal{A}}_n^L\left(x\right)={\displaystyle \frac{{\left(-1\right)}^n}{{\beta }_0^{n+1}}}\left|\begin{array}{cccccc}1& {\left(x\right)}_1& {\left(x\right)}_2& \cdots & \cdots & {\left(x\right)}_n\\ {\beta }_0& {\beta }_1& {\beta }_2& \cdots & \cdots & {\beta }_n\\ 0& {\beta }_0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{1}}\right){\beta }_1& \cdots & \cdots & \left({\displaystyle \genfrac{}{}{0pt}{}{n}{1}}\right){\beta }_{n-1}\\ ⋮& \ddots & \ddots & \ddots & & ⋮\\ ⋮& & \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 0& {\beta }_0& \left({\displaystyle \genfrac{}{}{0pt}{}{n}{n-1}}\right){\beta }_1\end{array}\right|.\hfill \end{array}$$

(33)

The related umbral interpolant of $f\in X^{Q,n}$ is the polynomial

$$P_{L,n}\left[f\right]\left(x\right)=\sum _{i=0}^{n}L\left({\Delta }^{i}f\right){\displaystyle \frac{{\mathcal{A}}_i^L\left(x\right)}{h^{i}i!}},$$

(34)

and the complementary umbral interpolant is

$${\overline{P}}_{L,n}\left[f\right]\left(x\right)=f\left(0\right)+\sum _{i=1}^{n}L\left({\Delta }^{i}f\right){\displaystyle \frac{{\mathcal{A}}_i^L\left(x\right)-{\mathcal{A}}_i^L\left(0\right)}{h^{i}i!}}.$$

(35)

Remark 3. 

We observe that if $L\left(f\right)=f\left(0\right)$, the polynomial (34) coincides with the well-known Newton’s forward difference interpolating polynomial on the data points $\left(x_0+ih,f(x_0+ih)\right)$, $i=0,\dots ,n$.

Using relation (32) and the linearity of the operator L, the umbral interpolating conditions

$$L\left({\Delta }^i{P}_{L,n}\left[f\right]\right)=L\left({\Delta }^{i}f\right),i=0,1,\dots ,n$$

are equivalent to the following conditions

$$L\left(P_{L,n}\left[f\right](x_0+ih)\right)=L\left(f(x_0+ih)\right),i=0,1,\dots ,n.$$

(36)

Moreover, the polynomial $P_{L,n}\left[f\right]$ can be expressed in the form

$$P_{L,n}\left[f\right]\left(x\right)=\sum _{i=0}^{n}L\left(f(x_0+ih)\right){\widehat{\mathcal{A}}}_{n,i}\left(x\right),x_0\in [0,1],$$

where

$${\widehat{\mathcal{A}}}_{n,i}\left(x\right)={\displaystyle \frac{1}{i!}}\sum _{j=i}^n{(-1)}^{j-i}{\displaystyle \frac{{\mathcal{A}}_j^L\left(x\right)}{h^j(j-i)!}}.$$

For this reason, we can see the polynomial $P_{L,n}\left[f\right]$ as a generalization of the classical interpolating polynomial on equidistant points.

4.2.1. Generalized Bernoulli of the Second Kind Umbral Interpolation

Now we consider the linear functional L defined as [50]

$$L\left(f\right)={\left[D{\Delta }^{-1}f\right]}_{x=0}.$$

We obtain

$${\beta }_i={\left[D{\Delta }^{-1}{\left(x\right)}_i\right]}_{x=0}={\displaystyle \frac{{(-1)}^i}{i+1}}{h}^{i-1}i!,i\ge 0.$$

We call the related polynomial ${\mathcal{A}}_n^L$, given in (50) generalized Bernoulli polynomial of the second kind and denote it by $B_n^{II}$.

We observe that ${\displaystyle B_n^{II}\left(x\right)=n!h^{n+1}{\psi }_n\left(\frac{x}{h}\right)}$, where ${\psi }_n$ is the Bernoulli polynomial of the second kind, as defined in ([39] p. 265). Indeed, starting from the determinant definition, we can easily prove the following relationships:

$$\left\{\begin{array}{c}{\displaystyle \Delta B_n^{II}\left(x\right)=nh{B}_{n-1}^{II}\left(x\right)}\hfill \\ {\displaystyle D{B}_n^{II}\left(x\right)=nh{\left(x\right)}_{n-1},D{B}_n^{II}\left(0\right)=0,}\hfill \end{array}\right.$$

Which, in [39], for $h=1$ and up to a multiplicative factor, characterizes the sequence of Bernoulli polynomials of the second kind.

According to (34), the Bernoulli interpolating polynomial of the second kind is

$$\begin{array}{cc}{\displaystyle B_n^{II}\left[f\right]\left(x\right)}\hfill & {\displaystyle =\sum _{i=0}^n{\left[D{\Delta }^{-1}{\Delta }^{i}f\right]}_{x=0}\frac{B_i^{II}\left(x\right)}{h^{i}i!}}\hfill \\ \hfill & {\displaystyle =h{\left[{\Delta }^{-1}Df\right]}_{x=0}+\sum _{i=1}^n\sum _{j=0}^{i-1}\frac{1}{h^{i}i!}\left(\genfrac{}{}{0pt}{}{i-1}{j}\right){(-1)}^{i-1-j}{f}^{\prime }\left(jh\right)B_i^{II}\left(x\right),}\hfill \end{array}$$

or

$$B_n^{II}\left[f\right]\left(x\right)=h{\left[{\Delta }^{-1}Df\right]}_{x=0}+\sum _{i=0}^{n-1}{f}^{\prime }\left(ih\right){\mathcal{B}}_i^{II}\left(x\right),{\mathcal{B}}_i^{II}\left(x\right)=\sum _{j=i}^{n-1}\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{{(-1)}^{j-i}}{h^{j+1}(j+1)!}}{B}_{j+1}^{II}\left(x\right).$$

The related interpolating conditions, after calculations, can be expressed as

$${\left(B_n^{II}\left[f\right]\right)}^{\prime }\left(ih\right)=f^{\prime }\left(ih\right),i=0,\dots ,n.$$

According to (35), the complementary umbral-interpolant Bernoulli polynomial of the second kind is

$${\overline{B}}_n^{II}\left[f\right]\left(x\right)=f\left(0\right)+\sum _{i=1}^n\sum _{j=0}^{i-1}\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{j}}\right){(-1)}^{i-1-j}{f}^{\prime }\left(jh\right){\displaystyle \frac{B_i^{II}\left(x\right)-B_i^{II}\left(0\right)}{h^{i}i!}}.$$

(37)

By using the polynomials ${\mathcal{B}}_i^{II}\left[f\right]$, it becomes

$${\overline{B}}_n^{II}\left[f\right]\left(x\right)=f\left(0\right)+\sum _{i=0}^{n-1}{f}^{\prime }\left(ih\right)\left[{\mathcal{B}}_i^{II}\left(x\right)-{\mathcal{B}}_i^{II}\left(0\right)\right].$$

The polynomial ${\overline{B}}_n^{II}\left[f\right]$ satisfies the conditions [50]

$${\overline{B}}_n^{II}\left[f\right]\left(0\right)=f\left(0\right),{\left({\overline{B}}_n^{II}\left[f\right]\right)}^{\prime }\left(ih\right)=f^{\prime }\left(ih\right),i=1,\dots ,n.$$

For this interpolating polynomial, there is a nice expression of the remainder.

Theorem 8 

([50]). Let $f\in C^n[0,b]$, with $b=nh$, and suppose that $f^{(n+1)}$ exists at each point of $(0,b)$. Then we have

$${\overline{B}}_n^{II}\left[f\right]\left(x\right)-f\left(x\right)={\displaystyle \frac{1}{n!}}{\int }_0^x{\left(t\right)}_n{f}^{(n+1)}\left({\xi }_t\right)dt,\forall x\in [0,b],0<{\xi }_t<b.$$

Furthermore, the interpolating polynomial ${\overline{B}}_n^{II}\left[f\right]$ suggests an application to the initial value problem

$$\left\{\begin{array}{c}{y}^{\prime }=f(x,y\left(x\right)),x\in [0,b],\hfill \\ y\left(0\right)=y_0.\hfill \end{array}\right.$$

(38)

In fact, the polynomial

$$y_n\left(x\right)=y_0+\sum _{i=0}^{n-1}f\left(ih,y_n\left(ih\right)\right)\left[{\overline{B}}_i^{II}\left[f\right]\left(x\right)-{\overline{B}}_i^{II}\left[f\right]\left(0\right)\right]$$

is a collocation polynomial [42,51] for the problem (38).

4.2.2. Generalized Boole Umbral Interpolation

Let us consider the linear functional

$$L\left(f\right)={\left[Mf\right]}_{x=0},$$

where $Mf$ is the mean operator defined by ([39], p. 6)

$$Mf\left(x\right)={\displaystyle \frac{f\left(x\right)+f(x+h)}{2}}.$$

If we set ${\beta }_i=L\left({\left(x\right)}_i\right)$ we obtain

$${\beta }_i={\left[M{\left(x\right)}_i\right]}_{x=0}=\left\{\begin{array}{ccc}1& & i=0,\hfill \\ {\displaystyle \frac{h}{2}}& & i=1,\hfill \\ 0& & i\ge 2.\hfill \end{array}\right.$$

Substituting these values in (50), we obtain the polynomials ${\mathcal{A}}_n^L$ called generalized Boole polynomials and denoted by ${\left\{E_n^{II}\right\}}_{n\in \mathbb{N}}$. We observe that $E_n^{II}\left(x\right)=n!h^n{J}_n\left({\displaystyle \frac{x}{h}}\right)$, where $J_n\left(x\right)$ is the Boole polynomial defined in ([39], p. 317).

Indeed, starting from the determinant definition, we can easily prove the following relations

$$\left\{\begin{array}{c}\Delta E_n^{II}\left(x\right)=nh{E}_{n-1}^{II}\left(x\right),\hfill \\ {\displaystyle E_n^{II}\left(0\right)=\frac{{(-h)}^{n}n!}{2^n},}\hfill \end{array}\right.$$

(39)

$$E_n^{II}\left(x\right)=\sum _{j=0}^n{(-1)}^j{\displaystyle \frac{n!}{(n-j)!}}{\left({\displaystyle \frac{h}{2}}\right)}^j{\left(x\right)}_{n-j},n\ge 0.$$

The relations (39) in [39], for $h=1$ and up to a multiplicative constant, characterize the sequence of Boole polynomials.

Then, according to (34), the umbral Boole interpolant is

$$E_n^{II}\left[f\right]\left(x\right)=\sum _{i=0}^n{\displaystyle \frac{f\left(ih\right)+f\left(\right(i+1\left)h\right)}{2}}{\mathcal{E}}_i^{II}\left(x\right),$$

(40)

where

$${\mathcal{E}}_i^{II}\left(x\right)=\sum _{j=i}^n\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{{(-1)}^{j-i}}{h^{j}j!}}{E}_j^{II}\left(x\right).$$

The related complementary umbral interpolant is

$${\overline{E}}_n^{II}\left[f\right]\left(x\right)=f\left(0\right)+\sum _{i=0}^n{\displaystyle \frac{f\left(ih\right)+f\left(\right(i+1\left)h\right)}{2}}\left[{\mathcal{E}}_i^{II}\left(x\right)-{\mathcal{E}}_i^{II}\left(0\right)\right].$$

(41)

The interpolating conditions for the polynomials (40) and (41) are

$${\displaystyle \frac{E^{II}\left[f\right]\left(ih\right)+E^{II}\left[f\right]\left((i+1)h\right)}{2}}={\displaystyle \frac{f\left(ih\right)+f\left(\right(i+1\left)h\right)}{2}},i=0,\dots ,n,$$

$${\overline{E}}^{II}\left[f\right]\left(0\right)=f\left(0\right),{\displaystyle \frac{{\overline{E}}^{II}\left[f\right]\left(ih\right)+{\overline{E}}^{II}\left[f\right]\left((i+1)h\right)}{2}}={\displaystyle \frac{f\left(ih\right)+f\left(\right(i+1\left)h\right)}{2}},i=1,\dots ,n,$$

respectively.

4.3. Umbral Interpolation Related to $\mathit{Q}={\Delta }_{\mathit{p}}$

In [10,11,45,52] the authors introduced a new class of difference finite operators defined as

$${\Delta }_p\equiv {\Delta }_{p,h}={\displaystyle \frac{1}{h}}\sum _{k=\ell }^m{a}_k{T}^k,\ell ,m\in \mathbb{Z},\ell <m,p=m-\ell ,a_k\in \mathbb{R},h\in {\mathbb{R}}^{+},$$

(42)

where T is the shift-operator [39], i.e.,

$$Ty\left(x\right)=y(x+h).$$

In the following, we omit to show the dependence on h in ${\Delta }_{p,h}$, unless absolutely necessary.

We obtain

$${\Delta }_{p}y\left(x\right)={\displaystyle \frac{1}{h}}\sum _{k=\ell }^m{a}_k{T}^{k}y\left(x\right)={\displaystyle \frac{1}{h}}\sum _{k=\ell }^m{a}_{k}y(x+kh),\forall y\in C^{\infty }[0,1].$$

(43)

Using a Taylor expansion around $h=0$, we have

$${\Delta }_{p}y\left(x\right)={\displaystyle \frac{1}{h}}\sum _{j=0}^{\infty }{\displaystyle \frac{y^{\left(j\right)}\left(x\right)}{j!}}{h}^j\sum _{k=\ell }^m{a}_k{k}^j.$$

(44)

In order for ${\Delta }_p$ to be a delta-operator, it must satisfy

$$\sum _{k=\ell }^m{a}_k=0,\sum _{k=\ell }^{m}k{a}_k=1.$$

(45)

An operator of the form (42) that satisfies (45) is called a delta-operator of order $p=m-\ell$.

To fix all the constants $a_k$, $k=\ell ,\cdots ,m$, we must impose $m-\ell -1$ further conditions. A possible choice is, for instance [10,11],

$${\gamma }_p=\sum _{k=\ell }^m{k}^p{a}_k=0,p=2,3,\cdots ,m-\ell .$$

(46)

When the conditions (45) and (46) are satisfied, the operator (44) provides an approximation of order p for the continuous derivative $D_x$. In fact,

$${\Delta }_{p}y\approx y^{\prime }\left(x\right)+{\displaystyle \frac{h^{m-\ell }}{(m-\ell +1)!}}{y}^{(m-\ell +1)}\sum _{k=\ell }^m{a}_k{k}^{m-\ell +1},p=m-\ell .$$

We note that the delta-operator ${\Delta }_1$ obtained for $\ell =0$ and $m=1$, i.e., ${\Delta }_{1}y\left(x\right)={\displaystyle \frac{y(x+1)-y\left(x\right)}{h}}$, coincides with the operator defined in (31) up to ${\displaystyle \frac{1}{h}}$.

Setting

$${\overline{b}}_0=0,{\overline{b}}_j=h^{j-1}\sum _{k=\ell }^m{a}_k{k}^j,j\ge 1,$$

in (44), for the delta-operator ${\Delta }_p$ the following representation holds:

$${\Delta }_{p}y=\sum _{j=0}^{\infty }{\overline{b}}_j{\displaystyle \frac{y^{\left(j\right)}}{j!}}.$$

Then, by Theorem 1, we can determine the p.s. ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ associated with ${\Delta }_p$ whose elements satisfy

$$p_0\left(x\right)=1,p_n\left(0\right)=0,n\ge 1,{\Delta }_p{p}_n=n{p}_{n-1}.$$

Now, let L be a linear functional with L as in (2). Setting

$${\beta }_k=L\left(p_k\right),k\ge 0,$$

the umbral basis for $(L,{\Delta }_p)$ is the p.s. ${\left\{s_n^L\right\}}_{n\in \mathbb{N}}$ with elements given by (12).

Hence the umbral interpolant for $(L,{\Delta }_p)$ is the polynomial

$$s_n^L\left[y\right]\left(x\right)=\sum _{i=0}^{n}L\left({\Delta }_p^{i}y\right){\displaystyle \frac{s_i^L\left(x\right)}{i!}},$$

(47)

and the related complementary polynomial is

$${\overline{s}}_n^L\left[y\right]\left(x\right)=y\left(0\right)+\sum _{i=1}^{n}L\left({\Delta }_p^{i}y\right){\displaystyle \frac{s_i^L\left(x\right)-s_i^L\left(0\right)}{i!}},$$

(48)

where the operator ${\Delta }_p^i$ is defined by

$${\Delta }_p^{i}y={\Delta }_p\left({\Delta }_p^{i-1}y\right),i\ge 1,{\Delta }_p^0=I.$$

${\mathbf{\Delta }}_{\mathbf{2}}$-Umbral Interpolation

As an example, we can consider the case $p=2$, with $\ell =-1$ and $m=1$. In this case, we obtain the operator of order 2

$${\Delta }_{2,h}y\equiv {\Delta }_{2}y={\displaystyle \frac{y(x+h)-y(x-h)}{2h}}.$$

Observe that, with reference to formulas (42) and (45), ${\displaystyle a_{-1}=-\frac{1}{2},a_0=0,a_1=\frac{1}{2}}$.

We note that for $h={\displaystyle \frac{1}{2}}k$, we obtain the classic central difference operator [5], ([17], p. 191). Hence ${\Delta }_{2,h}$ is an actual generalization of the central difference operator.

By Taylor expansion, we obtain

$${\Delta }_{2}y=\sum _{i=1}^{\infty }{\overline{b}}_i{\displaystyle \frac{y^{\left(i\right)}}{i!}},$$

where

$${\overline{b}}_i=\left\{\begin{array}{ccc}{h}^{i-1}& & oddi,\hfill \\ 0& & eveni.\hfill \end{array}\right.$$

Hence we have

$${\Delta }_{2}y=\sum _{i=1}^{\infty }{h}^{2i-2}{\displaystyle \frac{y^{(2i-1)}}{(2i-1)!}}.$$

The power series associated with the operator ${\Delta }_2$ is

$$\overline{f}\left(t\right)=\sum _{i=1}^{\infty }{h}^{2i-2}{\displaystyle \frac{t^{2i-1}}{(2i-1)!}}={\displaystyle \frac{1}{h}}sinhht.$$

(49)

From the numerical sequence ${\left({\overline{b}}_i\right)}_{i\in \mathbb{N}}$, by Proposition 1, we obtain the lower triangular matrix ${\overline{B}}_n$ ($\overline{B}$ in the infinite case) with elements ${\overline{b}}_{i,j}$ as in (5).

Then, using Proposition 2, we obtain the related sequence of ${\left({\overline{b}}_i\right)}_{i\in \mathbb{N}}$, denoted by ${\left(b_i\right)}_{i\in \mathbb{N}}$, and the matrix $B_n$ (B in the infinite case), which is the inverse (conjugate) matrix of ${\overline{B}}_n$ ($\overline{B}$).

For instance, if $n=5$, we obtain

$${\overline{B}}_5=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& h^2& 0& 1& 0& 0\\ 0& 0& 4h^2& 0& 1& 0\\ 0& h^4& 0& 10h^2& 0& 1\end{array}\right),$$

$$b_0=0,b_1=1,b_2=0,b_3=-h^2,b_4=0,b_5=9h^4,$$

$$B_5=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& -h^2& 0& 1& 0& 0\\ 0& 0& -4h^2& 0& 1& 0\\ 0& 9h^4& 0& -10h^2& 0& 1\end{array}\right).$$

The numerical sequence ${\left(b_i\right)}_{i\in \mathbb{N}}$ generates the power series

$$f\left(t\right)=\sum _{i=1}^{\infty }{b}_i{\displaystyle \frac{t^i}{i!}},b_1\ne 0,$$

which is the compositional inverse of $\overline{f}\left(t\right)$, as in (49). In this case, taking into account that

$$\overline{f}\left(f\left(t\right)\right)=f\left(\overline{f}\left(t\right)\right)=t,$$

we obtain

$$f\left(t\right)={\displaystyle \frac{1}{h}}\mathrm{arcsinh}ht={\displaystyle \frac{1}{h}}\ln \left(ht+\sqrt{h^2{t}^2+1}\right).$$

Then, the generating function of the p.s. ${\left\{p_n\right\}}_{n\in \mathbb{N}}$ is

$${\left(ht+\sqrt{h^2{t}^2+1}\right)}^{{\displaystyle \frac{x}{h}}}=\sum _{n=0}^{\infty }{p}_n\left(x\right){\displaystyle \frac{t^n}{n!}}.$$

The matrix B allows us to write the expansion of $p_n\left(x\right)$ in classic monomials. Moreover, denoting by $p_n\left(x\right)={\left[x\right]}_{n,2}$, we obtain

$${\left[x\right]}_{n,2}=\sum _{k=0}^n{b}_{n,k}{x}^k,x^n=\sum _{k=0}^n{\overline{b}}_{n,k}{\left[x\right]}_{k,2}.$$

From the analogy of the previous formulas with the well-known formulas

$${\left(x\right)}_n=\sum _{k=0}^n{s}_{n,k}{x}^k,x^n=\sum _{k=0}^n{\overline{S}}_{n,k}{\left(x\right)}_k,$$

where ${\left(x\right)}_n=x(x-1)\cdots (x-n+1)$, the coefficients $b_{n,k}$ and ${\overline{b}}_{n,k}$, $k=0,\cdots ,n$, can be called, respectively, Stirling numbers of the first and second kind of order 2.

From (8) and Proposition 1, we obtain the following determinant form for the elements of this p.s.

$$\begin{array}{cc}\hfill & {\left[x\right]}_{0,2}=1,\hfill \\ \hfill & {\left[x\right]}_{n,2}={\displaystyle \frac{{\left(-1\right)}^{n+1}}{{\prod }_{k=0}^n{\overline{b}}_{k,k}}}\left|\begin{array}{ccccc}x& x^2& \cdots & x^{n-1}& x^n\\ {\overline{b}}_{1,1}& {\overline{b}}_{2,1}& \cdots & {\overline{b}}_{n-1,1}& {\overline{b}}_{n,1}\\ 0& {\overline{b}}_{2,2}& \cdots & {\overline{b}}_{n-1,2}& {\overline{b}}_{n,2}\\ ⋮& \ddots & & ⋮& ⋮\\ ⋮& & \ddots & \ddots & ⋮\\ 0& \cdots & 0& {\overline{b}}_{n-1,n-1}& {\overline{b}}_{n,n-1}\end{array}\right|\hfill \end{array}={\left(-1\right)}^{n+1}\left|\begin{array}{ccccc}x& x^2& \cdots & x^{n-1}& x^n\\ 1& 0& \cdots & {\overline{b}}_{n-1,1}& {\overline{b}}_{n,1}\\ 0& 1& \cdots & {\overline{b}}_{n-1,2}& {\overline{b}}_{n,2}\\ ⋮& \ddots & & ⋮& ⋮\\ ⋮& & \ddots & \ddots & ⋮\\ 0& \cdots & 0& 1& 0\end{array}\right|.$$

(50)

Hence, the p.s. ${\left\{{\left[x\right]}_{n,2}\right\}}_{n\in \mathbb{N}}$ is the (basic) p.s. associated with the delta-operator ${\Delta }_2$.

The p.s. ${\left\{{\left[x\right]}_{n,2}\right\}}_{n\in \mathbb{N}}$ can be considered to be a generalization of the falling factorial sequence of order 2.

The first polynomials ${\left[x\right]}_{n,2}$ are (see their graph in Figure 4)

$${\left[x\right]}_{0,2}=1,{\left[x\right]}_{1,2}=x,{\left[x\right]}_{2,2}=x^2,{\left[x\right]}_{3,2}=x^3-h^{2}x,$$

$${\left[x\right]}_{4,2}=x^4-4h^2{x}^2,{\left[x\right]}_{5,2}=x^5-10h^2{x}^3+9h^{4}x.$$

The polynomials ${\left[x\right]}_{n,2}$ can be written in the following form

$${\left[x\right]}_{0,2}=1,{\left[x\right]}_{1,2}=x,{\left[x\right]}_{n,2}=x\prod _{j=0}^{n-2}(x-(n-2j-2)h),n>1.$$

(51)

In fact, the polynomials ${\left[x\right]}_{n,2}$ satisfy Theorem 1 with delta-operator ${\Delta }_2$: ${\left[x\right]}_{0,2}=1$ and ${\left[x\right]}_{1,2}=x$ from (50); furthermore, after some calculations, we obtain ${\Delta }_2{\left[x\right]}_{n,2}=n{\left[x\right]}_{n-1,2}$.

From the second equality in (50) we have that ${\left[x\right]}_{n,2}$ is a symmetric sequence [17,53].

We note that for $h={\displaystyle \frac{1}{2}}$ the p.s. ${\left\{{\left[x\right]}_{n,2}\right\}}_{n\in \mathbb{N}}$ becomes the known central factorial p.s. ${\left\{x^{\left[n\right]}\right\}}_{n\in \mathbb{N}}$ ([16], p. 70, [53], p. 8). Therefore, we call ${\left\{{\left[x\right]}_{n,2}\right\}}_{n\in \mathbb{N}}$ central factorial p.s. of order 2.

A detailed study of this sequence will be published later.

Let L be a linear functional with $L\left(1\right)\ne 0$. The umbral basis for $(L,{\Delta }_2)$ is p.s. with elements

$$\begin{array}{cc}& d_0\left(x\right)={\displaystyle \frac{1}{{\beta }_0}},\hfill \\ & d_n\left(x\right)={\displaystyle \frac{{(-1)}^n}{{\beta }_0^{n+1}}}\left|\begin{array}{cccccc}{\left[x\right]}_{0,2}& {\left[x\right]}_{1,2}& \cdots & \cdots & {\left[x\right]}_{n-1,2}& {\left[x\right]}_{n,2}\\ {\beta }_0& {\beta }_1& {\beta }_2& \cdots & \cdots & {\beta }_n\\ 0& {\beta }_0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{1}}\right){\beta }_1& \cdots & \cdots & \left({\displaystyle \genfrac{}{}{0pt}{}{n}{1}}\right){\beta }_{n-1}\\ ⋮& \ddots & \ddots & \ddots & & ⋮\\ ⋮& & \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 0& {\beta }_0& \left({\displaystyle \genfrac{}{}{0pt}{}{n}{n-1}}\right){\beta }_1\end{array}\right|.\hfill \end{array}$$

where ${\beta }_k=L\left({\left[x\right]}_{k,2}\right).$

According to (47) and (48), the umbral interpolating polynomials for $(L,{\Delta }_2)$ are

$$d_n\left[y\right]\left(x\right)=\sum _{i=0}^{n}L\left({\Delta }_2^{i}y\right){\displaystyle \frac{d_i^L\left(x\right)}{i!}},$$

(52)

and

$${\overline{d}}_n\left[y\right]\left(x\right)=y\left(0\right)+\sum _{i=1}^{n}L\left({\Delta }_2^{i}y\right){\displaystyle \frac{d_i^L\left(x\right)-d_i^L\left(0\right)}{i!}}.$$

(53)

To give an explicit expression for $d_n\left[y\right]\left(x\right)$ and ${\overline{d}}_n\left[y\right]\left(x\right)$, we need the powers ${\Delta }_2^i$. After calculations, we obtain

$${\Delta }_2^{i}y\left(x\right)={\displaystyle \frac{1}{2^i{h}^i}}\sum _{j=-s}^s\left({\displaystyle \genfrac{}{}{0pt}{}{i}{|j+s|}}\right)\left\{\begin{array}{ccc}{(-1)}^{|j+s|+1}y(x+(2j+1)h)\hfill & & oddi,\hfill \\ {(-1)}^{|j+s|}y(x+2jh)\hfill & & eveni,\hfill \end{array}\right.$$

where $s=\lfloor {\displaystyle \frac{i+1}{2}}\rfloor$.

For example,

$$\begin{array}{cc}& {\Delta }_2^{2}y={\displaystyle \frac{1}{4h^2}}\left[y(x-2h)-2y\left(x\right)+y(x+2h)\right]\hfill \\ & {\Delta }_2^{3}y={\displaystyle \frac{1}{8h^3}}\left[-y(x-3h)+3y(x-h)-3y(x+h)+y(x+3h)\right]\hfill \\ & {\Delta }_2^{4}y={\displaystyle \frac{1}{16h^4}}\left[y(x-4h)-4y(x-2h)+6y\left(x\right)-4y(x+2h)+y(x+4h)\right].\hfill \end{array}$$

Assuming $L\left(y\right)=y\left(0\right)$ we have

$${\beta }_k=L\left({\left[x\right]}_{k,2}\right)=\left\{\begin{array}{ccc}{h}^{k-1}& & k=0,\hfill \\ 0& & k\ne 0.\hfill \end{array}\right.$$

In this case, we obtain

$$\begin{array}{cc}& d_0\left(x\right)=1,\hfill \\ & d_n\left(x\right)={(-1)}^n\left|\begin{array}{cccccc}{\left[x\right]}_{0,2}& {\left[x\right]}_{1,2}& \cdots & \cdots & {\left[x\right]}_{n-1,2}& {\left[x\right]}_{n,2}\\ 1& 0& \cdots & \cdots & \cdots & 0\\ 0& 1& 0& \cdots & \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & & ⋮\\ ⋮& & \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 0& 1& 0\end{array}\right|={\left[x\right]}_{n,2}.\hfill \end{array}$$

The umbral interpolating polynomial (52) becomes

$$d_n\left[y\right]\left(x\right)=\sum _{i=0}^{n}L\left({\Delta }_2^{i}y\right){\displaystyle \frac{{\left[x\right]}_{i,2}}{i!}}=y\left(0\right)+\sum _{i=1}^n{\Delta }_2^{i}y\left(0\right){\displaystyle \frac{{\left[x\right]}_{i,2}}{i!}}.$$

(54)

Taking into account that ${\left[x\right]}_{n,2}=0$ at $x=0$, the complementary umbral interpolating polynomial (53) coincides with $d_n\left[y\right]\left(x\right)$.

Formula (54) is like a Newton expansion ([39] p. 75), so we can call it generalized Newton expansion for polynomials.

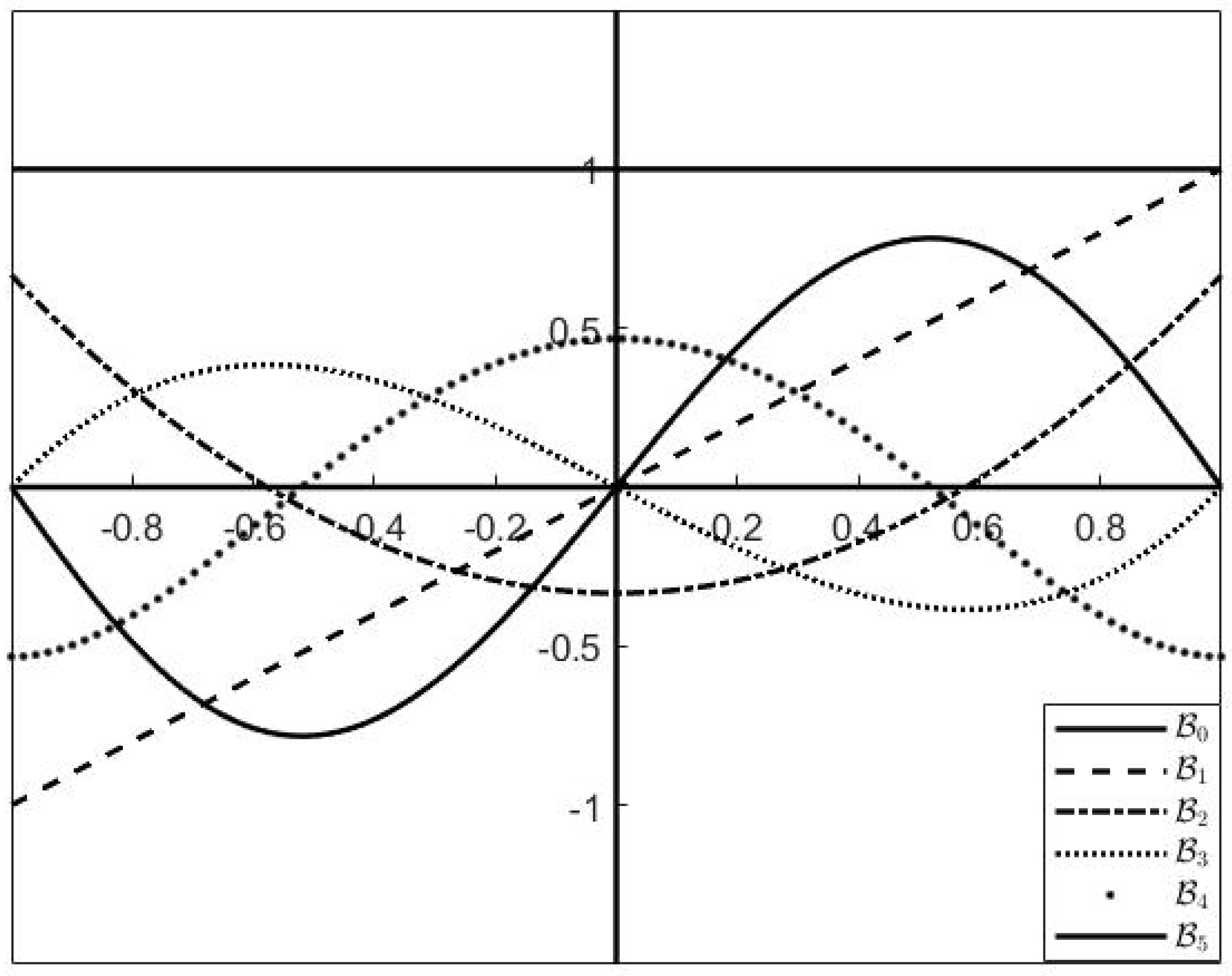
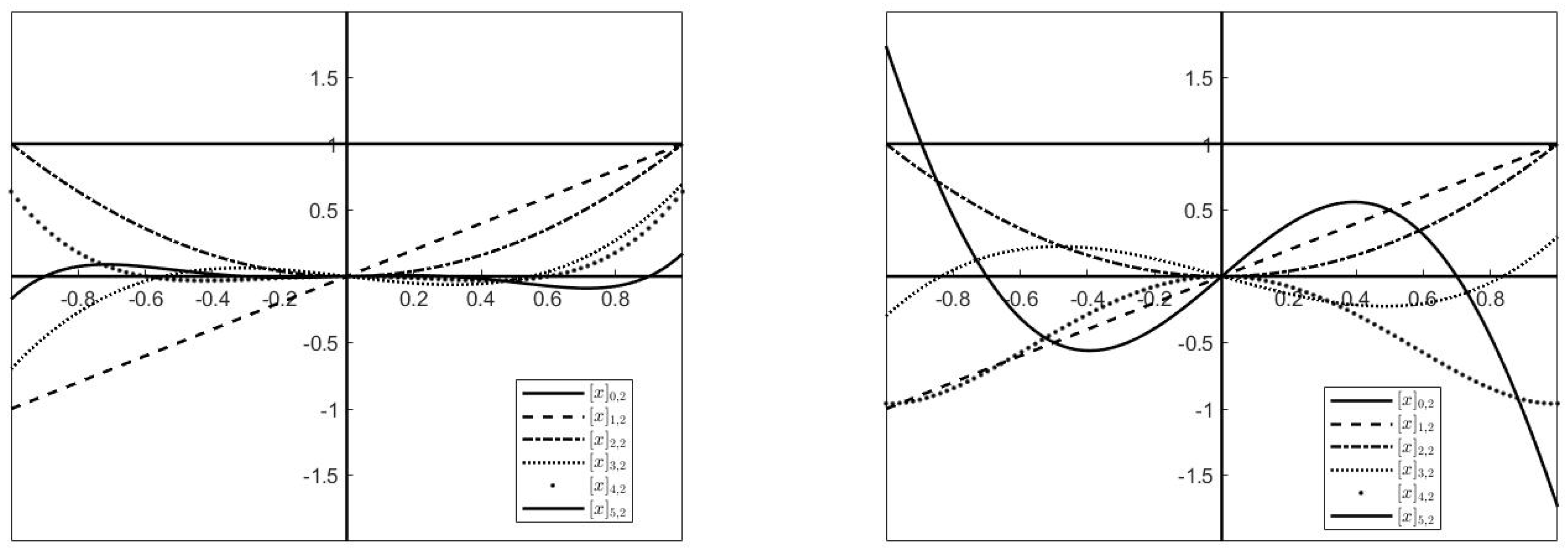
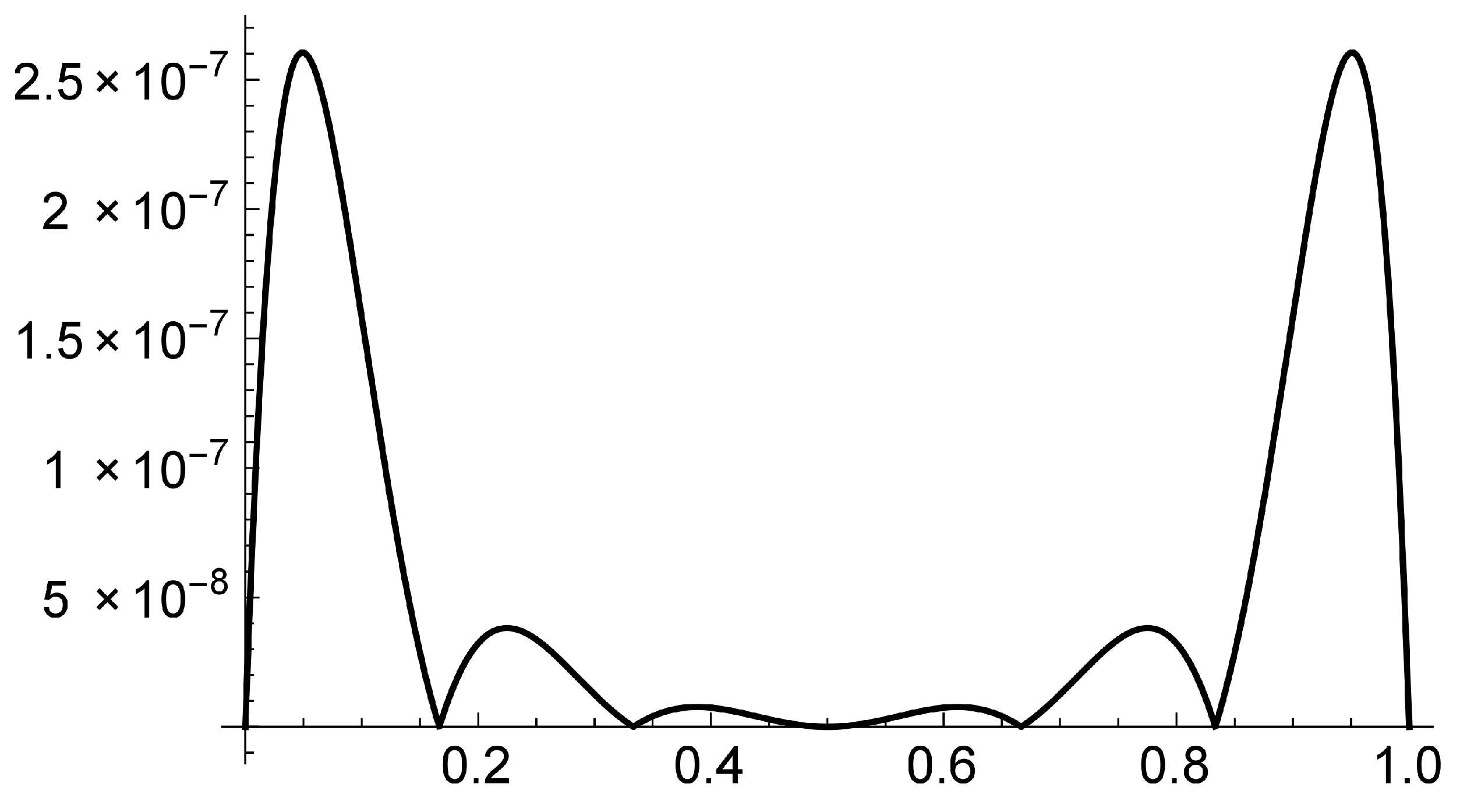
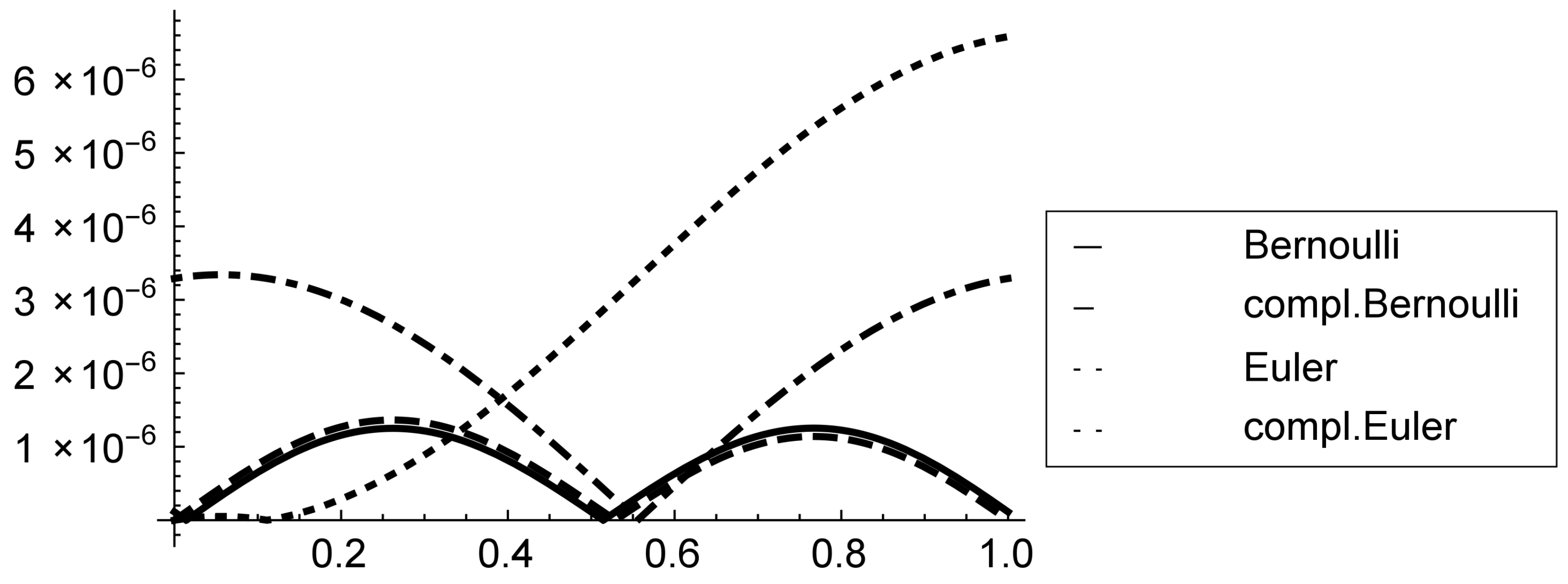
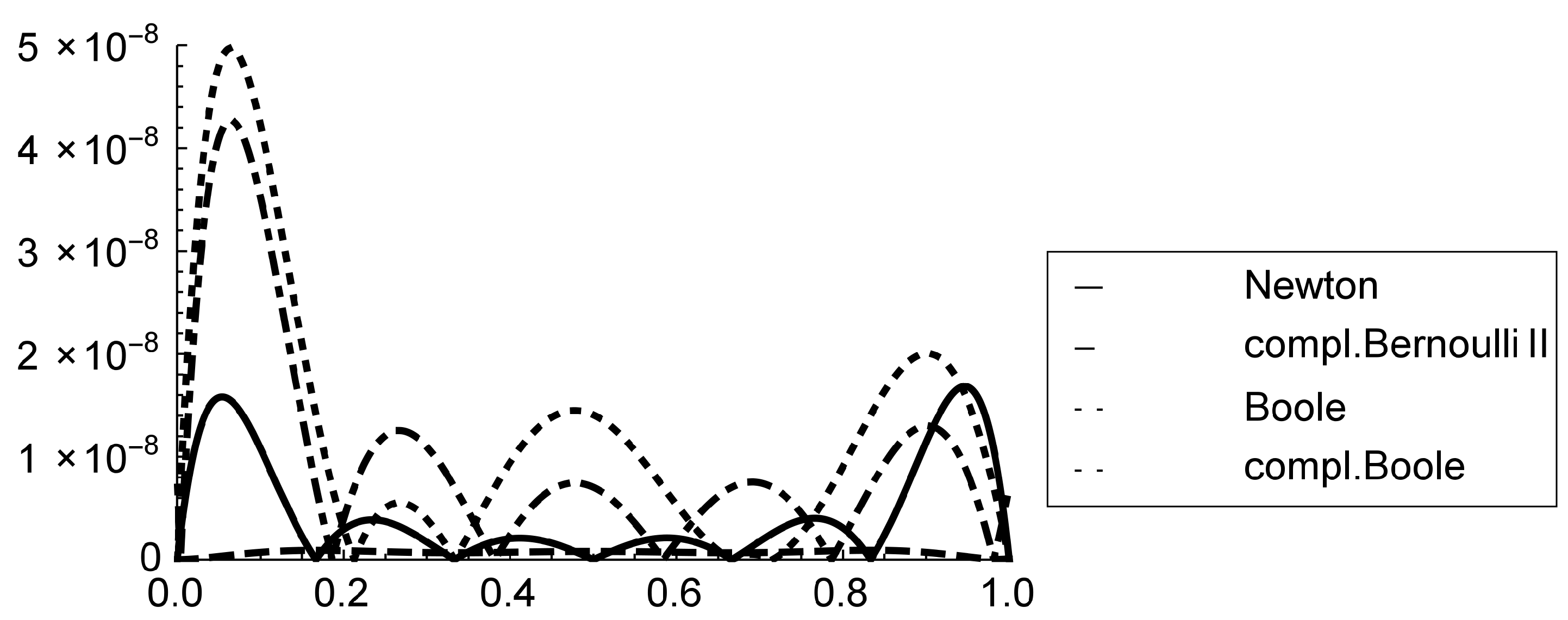
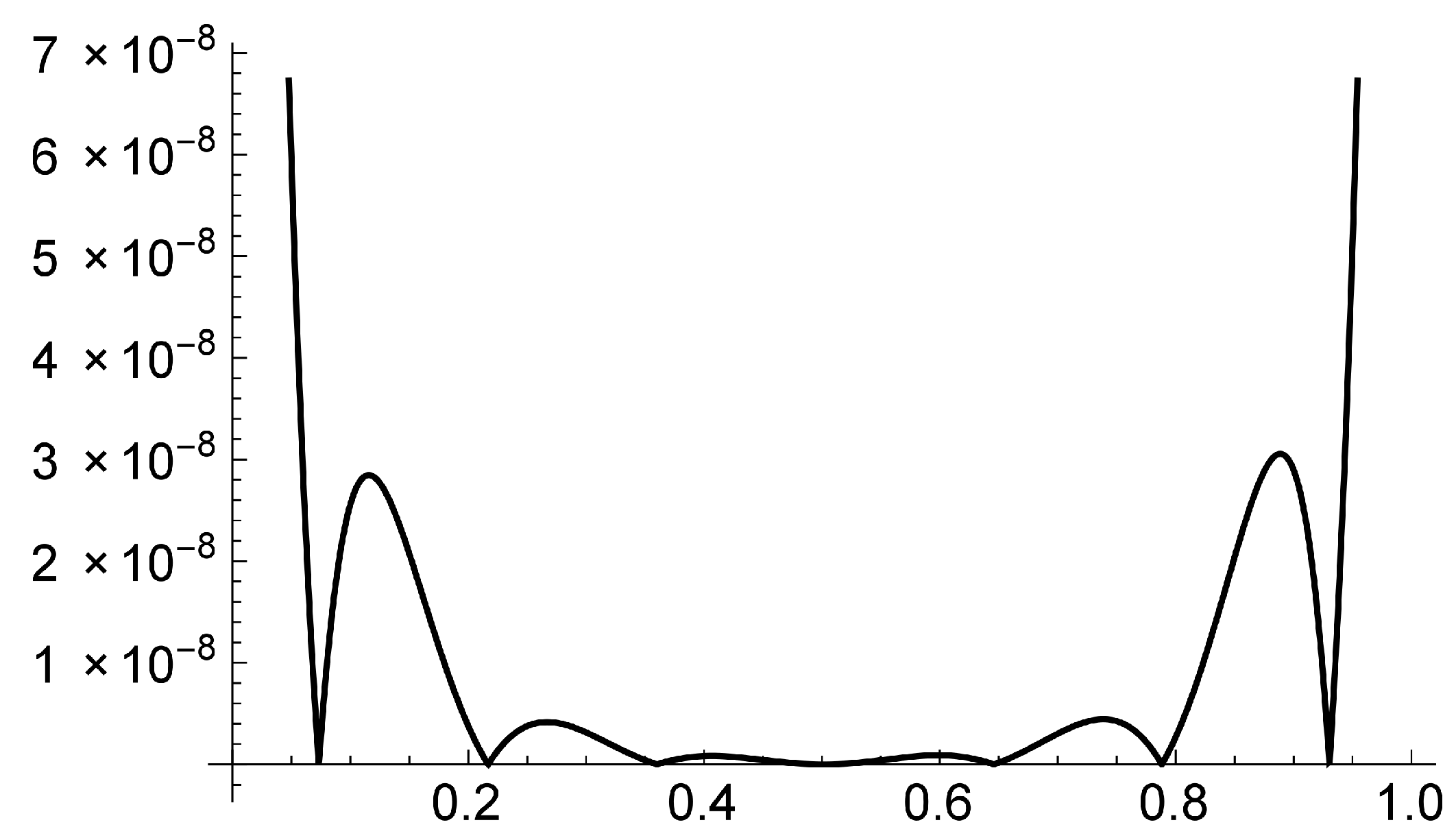
5. Numerical Examples

Now, we consider some test functions f. For each function, we plot the graph of the error function

$$e_n\left(x\right)=|f\left(x\right)-P_n\left[f\right]\left(x\right)|,x\in [0,1],$$

where $P_n\left[f\right]\left(x\right)$ is one of the umbral interpolating polynomials previously considered.

In particular, we compare the error in the approximation of the given function by the following interpolating polynomials: Bernoulli (24), complementary Bernoulli (25), Euler (28), complementary Euler (28), Newton [39], complementary Bernoulli of the second type (37), Boole (40), complementary Boole (41), ${\Delta }_2$ (54) interpolating polynomials.

The comparison is made by setting a tolerance $\epsilon$ and determining the minimum degree of the interpolating polynomial for which the required tolerance is reached.

The numerical results have been obtained using a Mathematica code.

Example 1. 

Let us consider the Bessel function

$$f\left(x\right)=J_0\left(x\right),x\in [0,1].$$

We fix the tolerance $\epsilon =10\times {10}^{-6}$.

Figure 5 contains the plot of the error functions in the approximation of the function by means of umbral interpolating polynomials related to the operator $Q=D_x$: Bernoulli, complementary Bernoulli, Euler and complementary Euler interpolating polynomials.

In the case of Bernoulli and complementary Bernoulli polynomials, we obtain an error less than or equal to the requested tolerance for $n=6$, while in the case of Euler and complementary Euler interpolation, we need polynomials of degree $n=10$ in order to reach the same tolerance.

Figure 6 shows the graph of the error functions in the case of umbral interpolating polynomials related to the operator $Q={\Delta }_h$: Newton, complementary Bernoulli of the second type, Boole, and complementary Boole interpolating polynomials $\left(h={\displaystyle \frac{1}{n}}\right)$. We obtain an absolute error less than the requested tolerance $\epsilon =10\times {10}^{-6}$ for $n=5$ with Newton and complementary Bernoulli polynomials of the second type and for $n=6$ in the other cases.

Figure 7 shows the graph of the error function in the case of umbral interpolating polynomial related to the operator $Q={\Delta }_{2,h}$ for $n=6$ and $h={\displaystyle \frac{1}{n}}$.

Example 2. 

Let us consider the function

$$f\left(x\right)=x{e}^{{\displaystyle \frac{x+1}{2}}},x\in [0,1].$$

Let $\epsilon =10\times {10}^{-7}$.

Figure 8 shows the plot of the error functions in the interpolation by Bernoulli, complementary Bernoulli, Euler and complementary Euler interpolating polynomials.

In the case of Bernoulli and complementary Bernoulli polynomials, we obtain an error less than or equal to the requested tolerance for $n=6$, while in the case of Euler and complementary Euler interpolation, we need polynomials of degree $n=8$ in order to reach the same value of ε.

Figure 9 contains the graph of the error functions in the case of Newton, complementary Bernoulli of the second type, Boole, and complementary Boole interpolating polynomials when $h={\displaystyle \frac{1}{n}}$. The absolute error is less than the fixed tolerance for $n=7$ with complementary Bernoulli polynomials of the second type and for $n=6$ in the other cases.

Figure 10 shows the graph of the error function in the case of umbral interpolating polynomial related to the operator $Q={\Delta }_{2,h}$ for $n=7$ and $h={\displaystyle \frac{1}{n}}$.

6. Conclusions

A survey on recent umbral interpolation based on a linear functional L and a delta-operator Q is given. This type of interpolation can be considered a wide subclass of general linear finite interpolating polynomials considered in [4]. To build the basis of the interpolating polynomials, we use a matrix-determinant approach, which is more flowing with respect to the classical theory of Rota et al. Relevant examples are given, some of which generalize the classic types of interpolation, such as Taylor and Newton interpolations. New cases of umbral interpolation are also considered. Numerical examples are given which confirm the efficiency of this type of umbral interpolation. Further theoretical and computational advances are possible. In fact, new examples and comparisons can be given. Problems like convergence, bounds of the remainder and numerical stability can be investigated.