On the Exponential Atom-Bond Connectivity Index of Graphs

Abstract

Several topological indices are possibly the most widely applied graph-based molecular structure descriptors in chemistry and pharmacology. The capacity of topological indices to discriminate is a crucial component of their study. In light of this, the literature has introduced the exponential vertex-degree-based topological index. The exponential atom-bond connectivity index is defined as follows: $e^{\mathcal{ABC}}=e^{\mathcal{ABC}}({\rm Y})={\displaystyle \sum _{v_i{v}_j\in E({\rm Y})}}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}},$ where $d_i$ is the degree of the vertex $v_i$ in ${\rm Y}$. In this paper, we prove that the double star $D{S}_{n-3,1}$ is the second maximal graph with respect to the $e^{\mathcal{ABC}}$ index of trees of order n. We give an upper bound on $e^{\mathcal{ABC}}$ of unicyclic graphs of order n and characterize the maximal graphs. The graph $K_1\vee (P_3\cup (n-4)K_1)$ gives the maximal graph with respect to the $e^{\mathcal{ABC}}$ index of bicyclic graphs of order n. We present several relations between $e^{\mathcal{ABC}}({\rm Y})$ and $ABC({\rm Y})$ of graph ${\rm Y}$. Finally, we provide a conclusion summarizing our findings and discuss potential directions for future research.

1. Introduction

Molecular descriptors are crucial in various fields, such as chemistry, pharmacology, and related sciences. These descriptors provide valuable information about the molecular structure and properties, aiding in the analysis and prediction of molecular behavior. Among these descriptors, topological indices are particularly significant [1]. Topological indices are numerical values derived from the graph representation of a molecule. They encapsulate information about the molecule’s topology, which refers to the spatial arrangement of its atoms and bonds. These indices play a pivotal role in Quantitative Structure–Property Relationships $\left(QSPR\right)$ and Quantitative Structure–Activity Relationships $\left(QSAR\right)$ studies, where they help in understanding and predicting the properties and activities of chemical compounds.

In the chemical literature, topological indices can be broadly categorized based on different criteria. One major category includes indices classified under graph distance. Graph distance-based indices are derived from the distances between pairs of vertices (atoms) in the molecular graph. These indices provide information on the overall shape and size of the molecule, as well as the spatial relationships between its parts and references therein. Another significant category consists of indices based on vertex degree. The vertex degree refers to the number of edges (bonds) connected to a vertex (atom) in the molecular graph. Vertex-degree-based topological indices focus on the connectivity and branching patterns within the molecule. These indices are particularly useful in identifying molecular features related to reactivity and interaction with other molecules (see [2] and references therein). Several vertex-degree-based topological indices have been developed and are extensively used in QSPR/QSAR studies. These indices help researchers in modeling and predicting the physical, chemical, and biological properties of compounds, facilitating drug discovery, environmental chemistry, and materials science. In summary, topological indices, whether based on graph distance or vertex degree, are invaluable tools in molecular research. They provide a bridge between the molecular structure and its properties, enabling a deeper understanding and more accurate predictions in various scientific domains.

In general, the vertex-degree-based (VDB) topological index is defined for any set of numbers ${\left\{{\phi }_{i,j}\right\}}_{(i,j)\in K}$ as

$$\begin{array}{c}\hfill \phi ({\rm Y})=\sum _{(i,j)\in K}{m}_{i,j}({\rm Y}){\phi }_{i,j}.\end{array}$$

(1)

Some of the most explored VDB topological indices are the first Zagreb index ${\mathcal{M}}_1$ [3], the Second Zagreb index ${\mathcal{M}}_2$ [3], the Randić index $\chi$ [4], the Harmonic index $\mathcal{H}$ [5], the Sum-Connectivity index $\mathcal{SC}$ [6,7], the neighborhood inverse sum indeg index $\mathcal{NI}$ [8], the Geometric-Arithmetic index $\mathcal{GA}$ [9], the Atom-Bond-Connectivity index $\mathcal{ABC}$ [10,11,12], the Atom-Bond Sum-Connectivity index [13], the Sombor index [14], and the Augmented Zagreb index $\mathcal{AZ}$ [15]. An analysis of the discrimination power and its crucial role in topological indices is discussed in [16,17,18]. Taking this into account, Rada [19] introduced exponential degree-based indices, significantly enhancing the discriminative power of topological indices. For a given vertex-degree-based topological index $\phi$ defined as in (1), the exponential of $\phi$, denoted by $e^{\phi }$, is defined as

$$\begin{array}{c}\hfill e^{\phi }({\rm Y})=\sum _{(i,j)\in K}{m}_{i,j}({\rm Y})e^{{\phi }_{i,j}}.\end{array}$$

(2)

For those interested in exploring further research on exponential degree-based indices, comprehensive sources include [20,21,22,23,24,25,26,27,28,29,30,31,32]. The current study focuses on the exponential atom-bond connectivity [19], which is defined as a refined topological index, offering new insights into the structure–property relationships of chemical compounds. The exponential atom-bond connectivity index is defined as follows:

$$e^{\mathcal{ABC}}=e^{\mathcal{ABC}}({\rm Y})={\displaystyle \sum _{v_i{v}_j\in E({\rm Y})}}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}=\sum _{v_i{v}_j\in E({\rm Y})}\Theta (d_i,d_j),$$

where $\Theta (d_i,d_j)=e^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}$, and $d_i$ is the degree of the vertex $v_i$ in ${\rm Y}$. For its basic mathematical properties, including various lower and upper bounds, see [23,33].

In this paper, all graphs are assumed to be finite and simple. Let ${\rm Y}$ be a graph with vertex set $V({\rm Y})=\{v_1,v_2,\dots ,v_n\}$ and edge set $E({\rm Y})$. The degree of a vertex $v_i\in V({\rm Y})$, denoted by $d_{{\rm Y}}\left(v_i\right)$ or simply $d_i$, is the number of vertices adjacent to $v_i$ in ${\rm Y}$. For a subset $E_0$ of $E({\rm Y})$, ${\rm Y}\setminus E_0$ denotes the subgraph obtained by deleting the edges in $E_0$. When $E_0=\left\{v_j{v}_k\right\}$, we abbreviate ${\rm Y}\setminus E_0$ as ${\rm Y}-v_j{v}_k$. For any two nonadjacent vertices $v_i$ and $v_j$ in ${\rm Y}$, ${\rm Y}+v_i{v}_j$ denotes the graph obtained by adding the edge $v_i{v}_j$ to ${\rm Y}$. We denote by $K_n$, $P_n$, $K_{1,n-1}$, and $C_n$ the complete graph, the path, the star, and the cycle on n vertices throughout this paper. Let $D{S}_{p,q}(p\ge q\ge 1,p+q=n-2)$ be a double star of order n obtained from joining the central vertices of the two stars $K_{1,p}$ and $K_{1,q}$. The join of the two graphs $G_1$ and $G_2$$(G_1\vee G_2)$ is a graph formed from disjoint copies of $G_1$ and $G_2$ by connecting every vertex of $G_1$ to every vertex of $G_2$. For additional notations and terminology related to graph theory that are not defined here, readers should consult [34]. Let $v_i{v}_j$ be an edge in ${\rm Y}$ such that $d_i\ge d_j$. Then, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\le {\displaystyle \frac{1}{2}}\mathrm{if}{d}_j\ge 2,\mathrm{and}{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}=1-{\displaystyle \frac{1}{d_i}}& \mathrm{if}{d}_j=1.\hfill \end{array}$$

(3)

The paper is organized as follows: In Section 2, we prove that the double star $D{S}_{n-3,1}$ is the second maximal graph with respect to the $e^{\mathcal{ABC}}$ index of trees of order n. In Section 3, we give an upper bound on $e^{\mathcal{ABC}}$ of unicyclic graphs of order n and characterize the maximal graphs. The graph $K_1\vee (P_3\cup (n-4)K_1)$ gives the maximal graph with respect to the $e^{\mathcal{ABC}}$ index of bicyclic graphs of order n. In Section 4, we present several relations between $e^{\mathcal{ABC}}({\rm Y})$ and $ABC({\rm Y})$ of graph ${\rm Y}$. Finally, in Section 5, we provide a conclusion summarizing our findings and discuss potential directions for future research.

2. On the Second Maximal Trees of Exponential Atom-Bond Connectivity Index

In their study, Cruz and Rada [22] established that among all trees of order n, the star graph maximizes the exponential atom-bond connectivity index $\left(e^{\mathcal{ABC}}\left(T\right)\right)$. In this section, we identify the second maximal tree for the $e^{\mathcal{ABC}}\left(T\right)$ index.

From Equation (3), it is evident that each term in $e^{\mathcal{ABC}}\left(T\right)$ reaches its maximum when the vertex with the highest degree is adjacent to a pendant vertex. Consequently, trees with a larger number of pendant edges achieve a higher $\left(e^{\mathcal{ABC}}\left(T\right)\right)$ index, as fewer non-pendant edges contribute to the sum. This insight forms the basis for the proof of the following result, which ranks trees by their $e^{\mathcal{ABC}}\left(T\right)$ index according to the number of non-pendant edges.

Theorem 1. 

Let $T(\ncong K_{1,n-1})$ be a tree of order n. Then,

$$e^{\mathcal{ABC}}\left(T\right)\le (n-3)\Theta (n-2,1)+2\Theta (2,1)<(n-1)\Theta (n-1,1).$$

(4)

Moreover, the first equality holds if and only if $T\cong D{S}_{n-3,1}$.

Proof. 

Let $v_i{v}_j\in E\left(T\right)$ be any edge in T with $d_T\left(v_i\right)\ge d_T\left(v_j\right)$. Let r be the number of non-pendant edges in T. Since $T\ncong K_{1,n-1}$, we have $r\ge 1$. We consider the following two cases:

Case 1. 

$r=1$. In this case, T is a double star $D{S}_{p,q}(p\ge q\ge 1,p+q=n-2)$. Let $v_1$ and $v_2$ be the non-pendant vertices in T such that $p+1=d_1\ge d_2=q+1$. Then, $q\le \lfloor {\displaystyle \frac{n-2}{2}}\rfloor$. Now,

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}\left(T\right)& =\sum _{v_i{v}_j\in E\left(T\right)}\Theta (d_i,d_j)\hfill \\ \hfill & =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_1{v}_j\in E\left(T\right),}{p=d_1-1\ge d_j=1}}}\Theta (d_1,d_j)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_2{v}_j\in E\left(T\right),}{q=d_2-1\ge d_j=1}}}\Theta (d_2,d_j)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_1{v}_2\in E\left(T\right),}{d_1\ge d_2\ge 2}}}\Theta (d_1,d_2)\hfill \\ \hfill & =p\Theta (p+1,1)+q\Theta (q+1,1)+\Theta (p+1,q+1)\hfill \\ \hfill & =(n-q-2)\Theta (n-q-1,1)+q\Theta (q+1,1)+\Theta (n-q-1,q+1)\hfill \\ \hfill & =f(n,q),\left(\mathrm{say}\right).\hfill \end{array}$$

(5)

If $q=1$, then $T\cong D{S}_{n-3,1}$ with

$$e^{\mathcal{ABC}}\left(T\right)=f(n,1)=(n-3)\Theta (n-2,1)+2\Theta (2,1)$$

and hence the equality holds in (4). Otherwise, $2\le q\le \lfloor {\displaystyle \frac{n-2}{2}}\rfloor$. One can easily see that

$$q+1\le n-q-1<n-2,\mathrm{that} \mathrm{is},{\displaystyle \frac{1}{q+1}}\ge {\displaystyle \frac{1}{n-q-1}}>{\displaystyle \frac{1}{n-2}},$$

$${\displaystyle \mathrm{that} \mathrm{is},\frac{q}{q+1}\le \frac{n-q-2}{n-q-1}<\frac{n-3}{n-2},\mathrm{that} \mathrm{is},\sqrt{\frac{q}{q+1}}\le \sqrt{\frac{n-q-2}{n-q-1}}<\sqrt{\frac{n-3}{n-2}}.}$$

Thus, we have

$$\begin{array}{c}\hfill \Theta (q+1,1)\le \Theta (n-q-1,1)<\Theta (n-2,1).\end{array}$$

(6)

We consider two cases:

Case 1.1. 

$n\le 46$. In this case, $2\le q\le \lfloor {\displaystyle \frac{n-2}{2}}\rfloor =22$. For each value of $n(6\le n\le 46)$, by Mathematica [35], we obtain the maximum value of $e^{\mathcal{ABC}}\left(D{S}_{n-q-2,q}\right)$ in the Table 1 and Table 2 (see Appendix A for more details):

Table 1. Maximum value of $e^{\mathcal{ABC}}\left(D{S}_{n-q-2,q}\right)$ and $f(n,1)$ for $6\le n\le 26$.

n	q	Maximum Value of	$\mathit{f}(\mathit{n},1)$
		${\mathit{e}}^{\mathcal{ABC}}$ (DSn−q−2,q)
6	2	10.998	11.189
7	2	13.564	13.84
8	[2,3]	16.191	16.514
9	[2,3]	18.848	19.2
10	[2,4]	21.523	21.894
11	[2,4]	24.208	24.594
12	[2,5]	26.9	27.297
13	[2,5]	29.598	30.003
14	[2,6]	32.299	32.711
15	[2,6]	35.004	35.421
16	[2,7]	37.71	38.132
17	[2,7]	40.418	40.843
18	[2,8]	43.128	43.556
19	[2,8]	45.838	46.269
20	[2,9]	48.55	48.983
21	[2,9]	51.262	51.697
22	[2,10]	53.975	54.412
23	[2,10]	56.688	57.127
24	[2,11]	59.402	59.843
25	[2,11]	62.116	62.558
26	[2,12]	64.831	65.274

Table 2. Maximum value of $e^{\mathcal{ABC}}\left(D{S}_{n-q-2,q}\right)$ and $f(n,1)$ for $27\le n\le 46$.

n	q	Maximum Value of	$\mathit{f}(\mathit{n},1)$
		${\mathit{e}}^{\mathcal{ABC}}$ (DSn−q−2,q)
27	[2,12]	67.546	67.99
28	[2,13]	70.261	70.706
29	[2,13]	72.976	73.423
30	[2,14]	75.692	76.139
31	[2,14]	78.408	78.856
32	[2,15]	81.124	81.572
33	[2,15]	83.84	84.289
34	[2,16]	86.556	87.006
35	[2,16]	89.272	89.723
36	[2,17]	91.989	92.44
37	[2,17]	94.705	95.157
38	[2,18]	97.422	97.875
39	[2,18]	100.139	100.592
40	[2,19]	102.856	103.309
41	[2,19]	105.573	106.027
42	[2,20]	108.29	108.744
43	[2,20]	111.007	111.461
44	[2,21]	113.724	114.179
45	[2,21]	116.441	116.897
46	[2,22]	119.159	119.614

From the above Table 1 and Table 2, we confirm that the result (4) strictly holds.

Case 1.2. 

$n\ge 47$. First, we assume that ${\displaystyle \frac{n-2}{(q+1)(n-q-1)}\le \frac{1}{12}}$. Then,

$$\Theta (n-q-1,q+1)\le e^{{\displaystyle \sqrt{\frac{1}{12}}}}<1.335$$

and hence

$$\Theta (q+1,1)+\Theta (n-q-1,q+1)<e+1.335<4.054<2\Theta (2,1).$$

Using the above results with (6) in (5), we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& \le (n-3)\Theta (n-q-1,1)+\Theta (q+1,1)+\Theta (n-q-1,q+1)\hfill \\ \hfill & <2\Theta (2,1)+(n-3)\Theta (n-2,1).\hfill \end{array}$$

The result (4) strictly holds.

Next, we assume that

$${\displaystyle \frac{n-2}{(q+1)(n-q-1)}}>{\displaystyle \frac{1}{12}},\mathrm{that} \mathrm{is},{(q+1)}^2-n(q+1)+12(n-2)>0,$$

that is,

$$\mathrm{either}q+1<{\displaystyle \frac{n-\sqrt{n^2-48(n-2)}}{2}}\mathrm{or}q+1>{\displaystyle \frac{n+\sqrt{n^2-48(n-2)}}{2}}.$$

Since $q\le \lfloor {\displaystyle \frac{n-2}{2}}\rfloor$, we obtain

$$q+1<{\displaystyle \frac{n-\sqrt{n^2-48(n-2)}}{2}}.$$

Since $f\left(x\right)=x-\sqrt{x^2-48(x-2)}$ is a strictly decreasing function on $x\ge 47$, we obtain

$$q+1<{\displaystyle \frac{n-\sqrt{n^2-48(n-2)}}{2}}\le {\displaystyle \frac{1}{2}}f\left(47\right)=20,\mathrm{that} \mathrm{is},q\le 18.$$

Case 1.2.1. 

$2\le q\le 9$. Since $n\ge 47$, one can easily see that $(n-q-1)(q+1)\ge 4(n-4)$ and hence

$${\displaystyle \frac{n-2}{(n-q-1)(q+1)}}\le {\displaystyle \frac{n-2}{4(n-4)}}={\displaystyle \frac{1}{4}}\left(1+{\displaystyle \frac{2}{n-4}}\right)\le {\displaystyle \frac{1}{4}}\left(1+{\displaystyle \frac{2}{43}}\right).$$

Thus, we have

$$e^{{\displaystyle \sqrt{\frac{n-2}{(n-q-1)(q+1)}}}}<e^{{\displaystyle \sqrt{\frac{1}{4}\left(1+\frac{2}{43}\right)}}}<1.668.$$

Since

$${\displaystyle \frac{q+1}{q}}=1+{\displaystyle \frac{1}{q}}\ge 1+{\displaystyle \frac{1}{9}}={\displaystyle \frac{10}{9}}\mathrm{and}{\displaystyle \frac{n-2}{n-3}}=1+{\displaystyle \frac{1}{n-3}}\le 1+{\displaystyle \frac{1}{44}}={\displaystyle \frac{45}{44}},$$

we obtain

$$e^{{\displaystyle \sqrt{\frac{q}{q+1}}}}\le e^{{\displaystyle \sqrt{\frac{9}{10}}}}<2.583\mathrm{and}{e}^{{\displaystyle \sqrt{\frac{n-3}{n-2}}}}\ge e^{{\displaystyle \sqrt{\frac{44}{45}}}}>2.688.$$

Using the above results with (6) in (5), we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& \le (n-5)\Theta (n-q-1,1)+3\Theta (q+1,1)+\Theta (n-q-1,q+1)\hfill \\ \hfill & <(n-5)\Theta (n-2,1)+3\times 2.583+1.668\hfill \\ \hfill & <2\Theta (2,1)+(n-3)\Theta (n-2,1)\hfill \end{array}$$

as $\Theta (2,1)>2.028$ and

$$\begin{array}{cc}\hfill & 2\Theta (2,1)+(n-3)\Theta (n-2,1)>(n-5)\Theta (n-2,1)+5.376+4.056\hfill \\ \hfill & >(n-5)\Theta \left(\right(n-2,1)+3\times 2.583+1.668.\hfill \end{array}$$

The result (4) strictly holds.

Case 1.2.2. 

$10\le q\le 18$. Since $n\ge 47$, one can easily see that $(n-q-1)(q+1)\ge 11(n-11)$ and hence

$${\displaystyle \frac{n-2}{(n-q-1)(q+1)}}\le {\displaystyle \frac{n-2}{11(n-11)}}={\displaystyle \frac{1}{11}}\left(1+{\displaystyle \frac{9}{n-11}}\right)\le {\displaystyle \frac{1}{11}}\left(1+{\displaystyle \frac{9}{36}}\right)<0.114.$$

Thus, we have

$$\Theta (n-q-1,q+1)<e^{{\displaystyle \sqrt{0.114}}}<1.402.$$

Since

$${\displaystyle \frac{q+1}{q}}=1+{\displaystyle \frac{1}{q}}\ge 1+{\displaystyle \frac{1}{18}}={\displaystyle \frac{19}{18}},$$

we obtain

$$e^{{\displaystyle \sqrt{\frac{q}{q+1}}}}\le e^{{\displaystyle \sqrt{\frac{18}{19}}}}<2.647\mathrm{and}{e}^{{\displaystyle \sqrt{\frac{1}{2}}}}>2.028.$$

Using the above results with (6) in (5), we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}\left(T\right)& \le (n-3)\Theta (n-q-1,1)+\Theta (q+1,1)+\Theta (n-q-1,q+1)\hfill \\ \hfill & <(n-3)\Theta (n-2,1)+2.647+1.402\hfill \\ \hfill & =(n-3)\Theta (n-2,1)+4.049<2\Theta (2,1)+(n-3)\Theta (n-2,1).\hfill \end{array}$$

The result (4) strictly holds.

Case 2. 

$r\ge 2$. In this case, $\Delta \le n-3$. For any non-pendant edge $v_i{v}_j\in E\left(T\right)$ with $d_i\ge d_j\ge 2$, we obtain

$${\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\le {\displaystyle \frac{1}{2}}.$$

For any pendant edge $v_i{v}_j\in E\left(T\right)$ with $\Delta \ge d_i\ge d_j=1$, we obtain

$${\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\le 1-{\displaystyle \frac{1}{n-3}}={\displaystyle \frac{n-4}{n-3}}<{\displaystyle \frac{n-3}{n-2}}.$$

Using the above results, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}\left(T\right)& =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_1{v}_j\in E\left(T\right),}{d_i\ge d_j=1}}}\Theta (d_i,d_j)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(T\right),}{d_i\ge d_j\ge 2}}}\Theta (d_i,d_j)\hfill \\ \hfill & <(n-r-1)\Theta (n-2,1)+r\Theta (2,1)\hfill \\ \hfill & =(n-3)\Theta (n-2,1)-(r-2)\Theta (n-2,1)-\Theta (2,1)+2\Theta (2,1)\hfill \\ \hfill & \le (n-3)\Theta (n-2,1)+2\Theta (2,1)\hfill \end{array}$$

as $\sqrt{{\displaystyle \frac{n-3}{n-2}}}\ge \sqrt{{\displaystyle \frac{1}{2}}}$. The result (4) strictly holds. This completes the proof of the theorem.

□

Remark 1. 

Theorem 1 establishes a sharp upper bound for the exponential atom-bond connectivity index of a tree T of order n, excluding the star $K_{1,n-1}$. This result highlights that among such trees, the double star $D{S}_{n-3,1}$ uniquely achieves the equality in (4), thereby demonstrating its extremal nature. This conclusion unifies the structural insights about trees and their exponential atom-bond connectivity index, providing a foundation for further exploration of extremal graph structures.

3. Upper Bounds on ${\mathit{e}}^{\mathcal{ABC}}\mathbf{(}\mathbf{{\rm Y}}\mathbf{)}$ of Unicyclic and Bicyclic Graphs

A unicyclic graph is a connected graph that contains exactly one cycle. For a graph $G=(V,E)$ with n vertices $\left(\right|V\left(G\right)|=n)$ and m edges $\left(\right|E\left(G\right)|=m)$, G is unicyclic if $m=n$ and G is connected. We establish an upper bound on $e^{\mathcal{ABC}}({\rm Y})$ for unicyclic graphs in terms of n and characterize the extremal graphs that achieve this bound. The key idea of the proof involves dividing the terms of $e^{\mathcal{ABC}}({\rm Y})$ into contributions from pendant edges and non-pendant edges. Using (3), the maximum contribution of each term to $e^{\mathcal{ABC}}({\rm Y})$ is evaluated separately for these two types of edges.

Theorem 2. 

Let ${\rm Y}$ be a unicyclic graph of order n. Then,

$$e^{\mathcal{ABC}}({\rm Y})\le 3\Theta (2,1)+(n-3)\Theta (n-1,1)$$

with equality if and only if ${\rm Y}\cong K_1\vee (K_2\cup (n-3)K_1)$.

Proof. 

For $d_i\ge d_j$, one can easily check that

$${\displaystyle \sqrt{\frac{d_i+d_j-2}{d_i{d}_j}}\le \sqrt{\frac{n-2}{n-1}}}$$

with equality if and only if $d_i=n-1$ and $d_j=1$. Moreover, for $d_i\ge d_j\ge 2$,

$${\displaystyle \sqrt{\frac{d_i+d_j-2}{d_i{d}_j}}\le \sqrt{\frac{1}{2}}}$$

with equality if and only if $d_i=2$ or $d_j=2$. Let $C_g$ be the cycle in ${\rm Y}$ and $V\left(C_g\right)=\{v_1,v_2,\dots ,v_g\}$. For $n\ge 3$,

$${\displaystyle \sqrt{\frac{n-2}{n-1}}\ge \sqrt{\frac{1}{2}}}$$

with equality if and only if $n=3$. Using the above results, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{v_i{v}_j\in E({\rm Y})}\Theta (d_i,d_j)\hfill \\ \hfill & =\sum _{v_i{v}_j\in E\left(C_g\right)}\Theta (d_i,d_j)+\sum _{v_i{v}_j\in E({\rm Y}\setminus E\left(C_g\right))}\Theta (d_i,d_j)\hfill \\ \hfill & \le g\Theta (2,1)+(n-g)\Theta (n-1,1)\hfill \\ \hfill & =3\Theta (2,1)+(g-3)\Theta (2,1)+(n-g)\Theta (n-1,1)\hfill \\ \hfill & \le 3\Theta (2,1)+(n-3)\Theta (n-1,1).\hfill \end{array}$$

Moreover, the equality holds if and only if $g=3$, $d_i=2$ or $d_j=2$ for $v_i{v}_j\in E\left(C_g\right)$ and $d_i=n-1$, $d_j=1$ for $v_i{v}_j\in E({\rm Y}\setminus E\left(C_g\right))$; that is, if and only if ${\rm Y}\cong K_1\vee (K_2\cup (n-3)K_1)$. □

Remark 2. 

Theorem 2 identifies a precise upper bound for the exponential atom-bond connectivity index of a unicyclic graph ${\rm Y}$ of order n. The extremal case is uniquely achieved by the graph ${\rm Y}\cong K_1\vee (K_2\cup (n-3)K_1)$, underscoring its special structural property. This result enriches the study of unicyclic graphs by characterizing those with maximal exponential atom-bond connectivity indices.

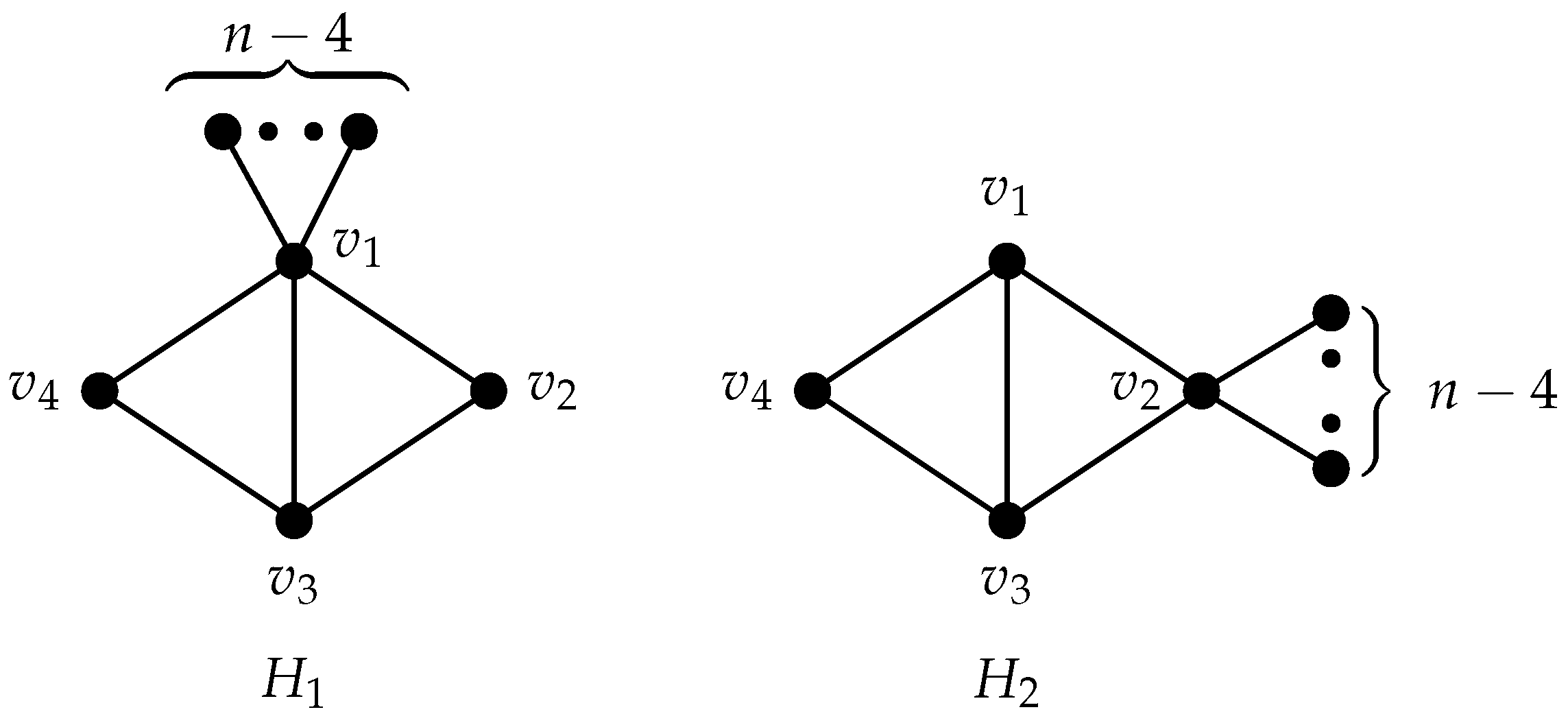
A bicyclic graph is a graph with n vertices and $n+1$ edges, containing exactly two independent cycles. Let $C_4^{\prime }$ be a graph of order 4 obtained from the complete graph $K_4$ by deleting one edge. Define $H_1$ as a graph obtained by attaching $n-4$ pendent edges to one of the vertices of degree 3 in $C_4^{\prime }$ (see Figure 1). Similarly, define $H_2$ as a graph obtained by attaching $n-4$ pendent edges to the vertex of degree 2 in $C_4^{\prime }$ (see Figure 1). We now present an upper bound on $e^{\mathcal{ABC}}({\rm Y})$ of bicyclic graphs in terms of n, and characterize the extremal graphs.

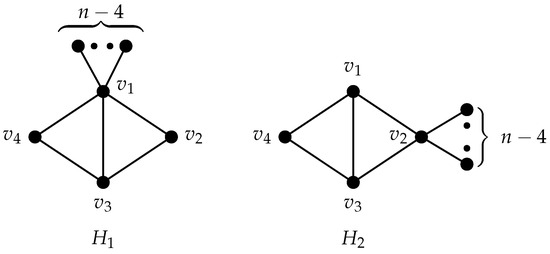
Figure 1. Two graphs $H_1$ and $H_2$.

From Equation (3), it is evident that any term in $e^{\mathcal{ABC}}\left(G\right)$ corresponding to a pendant edge is greater than or equal to a term corresponding to a non-pendant edge. Furthermore, each term in $e^{\mathcal{ABC}}\left(G\right)$ reaches its maximum value when the vertex with the highest degree is adjacent to a pendant vertex. Since the graph G has $n+1$ edges, graphs with a larger number of pendant edges achieve a higher $e^{\mathcal{ABC}}\left(G\right)$ index, as the contribution of non-pendant edges to the sum is minimized. Therefore, the proof of the following result is based on analyzing the number of non-pendant edges.

Theorem 3. 

Let ${\rm Y}$ be a bicyclic graph of order n. Then,

$$e^{\mathcal{ABC}}({\rm Y})\le (n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3)$$

(7)

with equality if and only if ${\rm Y}\cong H_1$ or ${\rm Y}\cong C_4^{\prime }$.

Proof. 

For $4\le n\le 9$, by Sage [36], one can easily check that the result (10) holds. So, now we can assume that $n\ge 10$. For $d_i\ge d_j$, one can easily check that

$${\displaystyle \sqrt{\frac{d_i+d_j-2}{d_i{d}_j}}\le \sqrt{\frac{n-2}{n-1}}}$$

with equality holding if and only if $d_i=n-1$ and $d_j=1$. Moreover, for $d_i\ge d_j\ge 2$,

$${\displaystyle \sqrt{\frac{d_i+d_j-2}{d_i{d}_j}}\le \sqrt{\frac{1}{2}}}$$

(8)

with equality if and only if $d_i=2$ or $d_j=2$. For $n\ge 3$,

$${\displaystyle \sqrt{\frac{n-2}{n-1}}\ge \sqrt{\frac{1}{2}}}$$

(9)

with equality if and only if $n=3$.

Let q be the number of non-pendant edges in ${\rm Y}$. Since ${\rm Y}$ is bicyclic, we have $q\ge 5$. We consider the following two cases:

Case 1. 

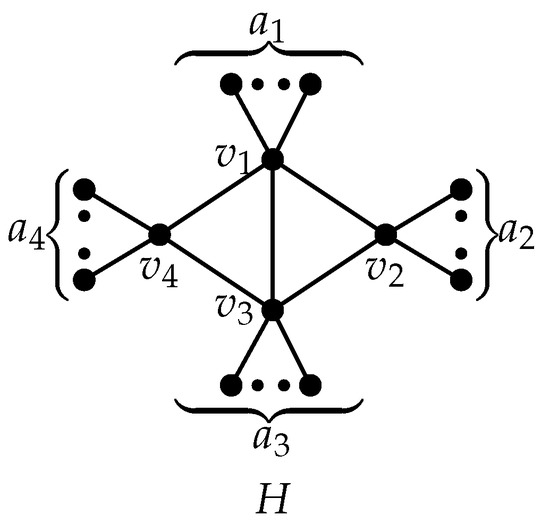
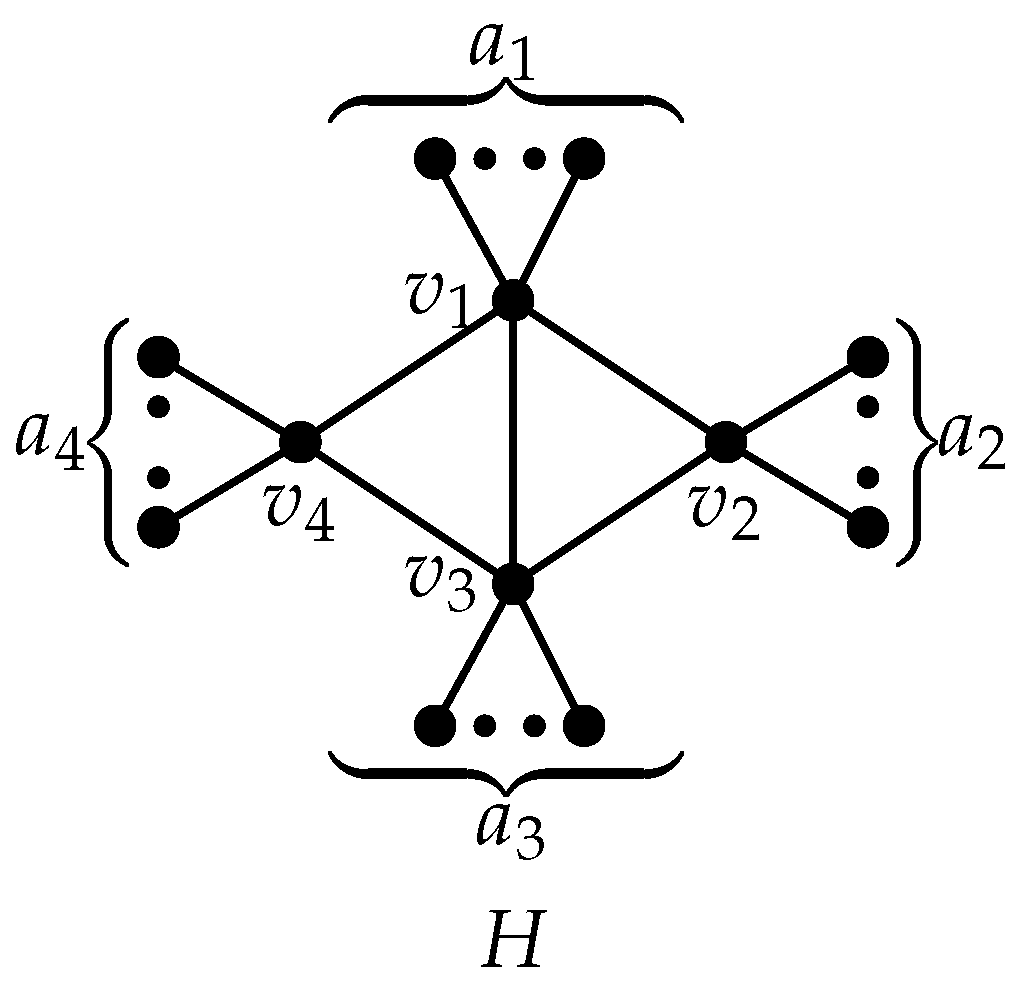
$q=5$. Since ${\rm Y}$ is bicyclic, in this case, ${\rm Y}\cong H$ (see, Figure 2). Let $v_1,v_2,v_3$, and $v_4$ be the non-pendant vertices of degrees $d_1,d_2,d_3,$ and $d_4$ in H, respectively, where $d_1=a_1+3,d_2=a_2+2,d_3=a_3+3$, and $d_4=a_4+2$. Without loss of generality, we can assume that $a_1\ge a_3$ and $a_2\ge a_4$. We consider the following four cases $a_1=0,a_2=0$; $a_1=0,a_2\ge 1$; $a_1\ge 1,a_2=0$; $a_1\ge 1,a_2\ge 1$.

Figure 2. A graph H.

Case 1.1. 

$a_1=0$, $a_2=0$. In this case, $a_3=a_4=0$. Then, ${\rm Y}\cong C_4^{\prime }$ with

$$e^{\mathcal{ABC}}({\rm Y})=4\Theta (2,1)+\Theta (3,3)$$

and hence the equality holds in (7).

Case 1.2. 

$a_1=0,a_2\ge 1$. We have $a_3=0$. First, we assume that $a_4=0$. Then, $a_2=n-4$ and hence ${\rm Y}\cong H_2$ (see, Figure 1).

Case 1. 

$$2\Theta (n-2,3)+\Theta (3,3)<2\Theta (2,1)+\Theta (n-1,3).$$

(10)

Proof of Claim 1.

For $10\le n\le 14$, by Mathematica [35], one can easily check that the result (10) holds. Otherwise, $n\ge 15$. Thus, we have ${\displaystyle \frac{1}{n-2}\le \frac{1}{13}<0.077}$, that is,

$$2\sqrt{{\displaystyle \frac{n-1}{n-2}}}=2\sqrt{1+{\displaystyle \frac{1}{n-2}}}<2.076<\sqrt{{\displaystyle \frac{n}{n-1}}}+\sqrt{{\displaystyle \frac{3}{2}}},$$

that is,

$$2\sqrt{{\displaystyle \frac{n-1}{3(n-2)}}}<\sqrt{{\displaystyle \frac{n}{3(n-1)}}}+\sqrt{{\displaystyle \frac{1}{2}}}.$$

By the arithmetic-geometric-mean inequality with the above result, we obtain

$${\left({\displaystyle \frac{\Theta (2,1)+\Theta (n-1,3)}{2}}\right)}^2\ge \Theta (2,1)\Theta (n-1,3),$$

that is,

$$\Theta (2,1)+\Theta (n-1,3)\ge 2e^{{\displaystyle \frac{1}{2}}\left(\sqrt{{\displaystyle \frac{1}{2}}}+\sqrt{{\displaystyle \frac{n}{3(n-1)}}}\right)}>2\Theta (n-2,3),$$

that is,

$$2\Theta (2,1)+\Theta (n-1,3)>\Theta (3,3)+2\Theta (n-2,3)$$

as ${\displaystyle \frac{2}{3}}<\sqrt{{\displaystyle \frac{1}{2}}}.$ This proves the Claim 1. □

Using Claim 1 with

$${\displaystyle \frac{n-3}{n-2}}<{\displaystyle \frac{n-2}{n-1}},$$

we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{v_i{v}_j\in E({\rm Y})}\Theta (d_i,d_j)\hfill \\ \hfill & =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_2{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_2,d_j)+\Theta (d_1,d_3)+\Theta (d_1,d_2)+\Theta (d_1,d_4)+\Theta (d_2,d_3)+\Theta (d_3,d_4)\hfill \\ \hfill & =(n-4)\Theta (n-2,1)+2\Theta (n-2,3)+\Theta (3,3)+2\Theta (2,1)\hfill \\ \hfill & <(n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3).\hfill \end{array}$$

The inequality (7) strictly holds.

Next, we assume that $a_4\ge 1$. We have $a_2+a_4=n-4$. Since $d_1=3=d_3$, $d_2=a_2+2\ge 3$ and $d_4=a_4+2\ge 3$, we obtain

$$\Theta (d_1,d_3)=\Theta (3,3),\Theta (d_1,d_4)=\Theta (d_4,3)\le \Theta (3,3),\Theta (d_3,d_4)\le \Theta (3,3),$$

$$\Theta (d_1,d_2)\le \Theta (3,3),\mathrm{and}\Theta (d_2,d_3)\le \Theta (3,3).$$

Moreover, we obtain

$$a_2\Theta (a_2+2,1)+a_4\Theta (a_4+2,1)<(a_2+a_4)\Theta (n-1,1)=(n-4)\Theta (n-1,1),$$

and

$$4\Theta (2,1)-\Theta (3,3)+\Theta (n-1,3)>e^{\sqrt{{\displaystyle \frac{1}{3}}}}+4\times 0.081>2.1>\Theta (3,3),$$

that is,

$$5\Theta (3,3)<4\Theta (2,1)+\Theta (n-1,3).$$

Using the above results, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})\left(G\right)& =\sum _{v_i{v}_j\in E({\rm Y})}\Theta (d_i,d_j)\hfill \\ \hfill & =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_2{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_2,d_j)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_4{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_4,d_j)+\Theta (d_1,d_3)\hfill \\ \hfill & +\Theta (d_1,d_2)+\Theta (d_1,d_4)+\Theta (d_2,d_3)+\Theta (d_3,d_4)\hfill \\ \hfill & \le a_2\Theta (a_2+2,1)+a_4\Theta (a_4+2,1)+5\Theta (3,3)\hfill \\ \hfill & <(n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3).\hfill \end{array}$$

The inequality (7) strictly holds.

Case 1.3. 

$a_1\ge 1,a_2=0$. We have $a_4=0$. If $a_3=0$, then $a_1=n-4$, ${\rm Y}\cong H_1$ with

$$e^{\mathcal{ABC}}({\rm Y})\left(G\right)=(n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3),$$

and hence the equality holds in (7). Otherwise, $a_3\ge 1$. We have $a_1+a_3=n-4$. Using this, we obtain $(a_1+3)(a_3+3)>3(n-1)$ as $a_1\ge a_3>0$. Thus, we have

$$\Theta (d_1,d_3)=\Theta (a_1+3,a_3+3)=e^{\sqrt{{\displaystyle \frac{n}{(a_1+3)(a_3+3)}}}}<\Theta (n-1,3).$$

Now,

$$\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_1{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_1,d_j)=a_1\Theta (a_1+3,1)\mathrm{and}\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_3{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_3,d_j)=a_3\Theta (a_3+3,1).$$

Using the above results, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{v_i{v}_j\in E({\rm Y})}\Theta (d_i,d_j)\hfill \\ \hfill & =\sum _{v_j:v_1{v}_j\in E({\rm Y})}\Theta (d_1,d_j)+\Theta (d_1,d_3)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_3{v}_j\in E({\rm Y}),}{j\ne 1}}}\Theta (d_3,d_j)\hfill \\ \hfill & =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_1{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_1,d_j)+\Theta (a_1+3,a_3+3)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_j:v_3{v}_j\in E({\rm Y}),}{d_j=1}}}\Theta (d_3,d_j)+4\Theta (2,1)\hfill \\ \hfill & <a_1\Theta (a_1+3,1)+\Theta (n-1,3)+a_3\Theta (a_3+3,1)+4\Theta (2,1)\hfill \\ \hfill & <(n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3)\hfill \end{array}$$

as

$$\sqrt{{\displaystyle \frac{a_1+2}{a_1+3}}}<\sqrt{{\displaystyle \frac{n-2}{n-1}}}\mathrm{and}\sqrt{{\displaystyle \frac{a_3+2}{a_3+3}}}<\sqrt{{\displaystyle \frac{n-2}{n-1}}}.$$

The inequality (7) strictly holds.

Case 1.4. 

$a_1\ge 1,a_2\ge 1$. In this case, we have $d_1\ge 4,d_2\ge 3,d_3\ge 3,d_4\ge 2$. Now,

$$\Theta (d_1,d_3)\le \Theta (4,3),\Theta (d_1,d_4)\le \Theta (4,2)=\Theta (2,1),\Theta (d_3,d_4)\le \Theta (3,2)=\Theta (2,1),$$

$$\Theta (d_1,d_2)\le \Theta (4,3),\mathrm{and}\Theta (d_2,d_3)\le \Theta (3,3).$$

Thus, we have

$$\begin{array}{cc}\hfill \Theta (d_1,d_3)+\Theta (d_1,d_2)+\Theta (d_2,d_3)& \le 2\Theta (4,3)+\Theta (3,3)\hfill \\ \hfill & <5.762<2\Theta (2,1)+e^{\sqrt{{\displaystyle \frac{1}{3}}}}<2\Theta (2,1)+\Theta (n-1,3).\hfill \end{array}$$

Since $q=5$, ${\rm Y}$ has $n-4$ pendant edges, and hence

$$\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E({\rm Y}),}{d_i\ge d_j=1}}}\Theta (d_i,d_j)\le (n-4)\Theta (n-1,1).$$

Using the above results, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{v_i{v}_j\in E({\rm Y})}\Theta (d_i,d_j)\hfill \\ \hfill & =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E({\rm Y}),}{d_i\ge d_j=1}}}\Theta (d_i,d_j)+\Theta (d_1,d_3)+\Theta (d_1,d_2)+\Theta (d_1,d_4)+\Theta (d_2,d_3)+\Theta (d_3,d_4)\hfill \\ \hfill & <(n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3).\hfill \end{array}$$

The inequality (7) strictly holds.

Case 2. 

$q\ge 6$. First, we have to prove that

$${\displaystyle \sqrt{\frac{n-2}{n-1}}}+{\displaystyle \sqrt{\frac{n}{3(n-1)}}}>\sqrt{2}.$$

(11)

Since ${\rm Y}$ is bicyclic, $n\ge 4$. If $n=4$, then

$${\displaystyle \sqrt{\frac{n-2}{n-1}}}+{\displaystyle \sqrt{\frac{n}{3(n-1)}}}=\sqrt{{\displaystyle \frac{2}{3}}}+{\displaystyle \frac{2}{3}}>\sqrt{2},$$

(11) holds. Otherwise, $n\ge 5$. We obtain

$${\displaystyle \frac{1}{n-1}}\le {\displaystyle \frac{1}{4}},\mathrm{that} \mathrm{is},\sqrt{1-{\displaystyle \frac{1}{n-1}}}\ge \sqrt{{\displaystyle \frac{3}{4}}},\mathrm{that} \mathrm{is},\sqrt{{\displaystyle \frac{n-2}{n-1}}}\ge \sqrt{{\displaystyle \frac{3}{4}}}.$$

Using this result, we obtain

$${\displaystyle \sqrt{\frac{n-2}{n-1}}}+{\displaystyle \sqrt{\frac{n}{3(n-1)}}}>\sqrt{{\displaystyle \frac{3}{4}}}+\sqrt{{\displaystyle \frac{1}{3}}}>\sqrt{2}.$$

Again, (11) holds.

By the arithmetic-geometric-mean inequality, we obtain

$${\left({\displaystyle \frac{\Theta (n-1,1)+\Theta (n-1,3)}{2}}\right)}^2\ge \Theta (n-1,1)\Theta (n-1,3),$$

that is,

$$\Theta (n-1,1)+\Theta (n-1,3)\ge 2{\left(e^{{\displaystyle \sqrt{\frac{n-2}{n-1}}}+{\displaystyle \sqrt{\frac{n}{3(n-1)}}}}\right)}^{1/2},$$

that is,

$$\Theta (n-1,1)+\Theta (n-1,3)\ge 2\Theta (2,1),$$

by (11). Using this result with (8), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(C_g\right),}{d_i\ge d_j\ge 2}}\Theta (d_i,d_j)\le q\sqrt{\frac{1}{2}}}& =(q-2)\Theta (2,1)+2\Theta (2,1)\hfill \\ \hfill & <(q-2)\Theta (2,1)+\Theta (n-1,1)+\Theta (n-1,3).\hfill \end{array}$$

Using the above results, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E({\rm Y}),}{d_i\ge d_j=1}}}\Theta (d_i,d_j)+\sum _{{\displaystyle \genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(C_g\right),}{d_i\ge d_j\ge 2}}}\Theta (d_i,d_j)\hfill \\ \hfill & <(n-q+1)\Theta (n-1,1)+(q-2)\Theta (2,1)+\Theta (n-1,1)+\Theta (n-1,3)\hfill \\ \hfill & \le (n-4)\Theta (n-1,1)+4\Theta (2,1)+\Theta (n-1,3)\hfill \end{array}$$

as $q\ge 6$ and by (9). The result (7) strictly holds.

□

Remark 3. 

Theorem 3 establishes an upper bound for the exponential atom-bond connectivity index of bicyclic graphs of order n. The equality in (7) is attained exclusively by the graphs ${\rm Y}\cong H_1$ or ${\rm Y}\cong C_4^{\prime }$, highlighting their extremal nature. This result contributes to the understanding of bicyclic graph structures and their influence on the exponential atom-bond connectivity indices.

4. Some Relations Between ${\mathit{e}}^{\mathcal{ABC}}\mathbf{(}\mathbf{{\rm Y}}\mathbf{)}$ and ABC($\mathbf{{\rm Y}}$) of Graphs

In this section, we present several lower and upper bounds on $e^{\mathcal{ABC}}({\rm Y})$ of graphs in terms of different graph parameters, and characterize the corresponding extremal graphs. We begin with some relations between $e^{\mathcal{ABC}}({\rm Y})$ and $ABC({\rm Y})$ of any graph ${\rm Y}$ as follows:

Proposition 1. 

Let ${\rm Y}$ be a graph with m edges. Then,

$$e^{\mathcal{ABC}}({\rm Y})\ge m{e}^{ABC({\rm Y})/m},$$

where $ABC({\rm Y})$ is the atom-bond connectivity index of the graph Υ. If Υ is connected, then the above equality holds if and only if for each vertex $v_i\in V({\rm Y})$, $d_i=2$, or $d_j=d_k$ for $v_j,v_k\in N_{{\rm Y}}\left(v_i\right)$.

Proof. 

By arithmetic-geometric-mean inequality, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})=\sum _{v_i{v}_j\in E({\rm Y})}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}& \ge m{\left(\prod _{v_i{v}_j\in E({\rm Y})}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}\right)}^{1/m}\hfill \\ \hfill & =m{\left(e^{\sum _{v_i{v}_j\in E({\rm Y})}\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}\right)}^{1/m}\hfill \\ \hfill & =m{e}^{ABC({\rm Y})/m}.\hfill \end{array}$$

Moreover, the equality holds if and only if

$${\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}={\displaystyle \frac{d_k+d_{\ell }-2}{d_k{d}_{\ell }}}\mathrm{for}\mathrm{any}\mathrm{edges}{v}_i{v}_j,v_k{v}_{\ell }\in E({\rm Y}),$$

that is, if and only if

$${\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}={\displaystyle \frac{d_i+d_k-2}{d_i{d}_k}},\mathrm{that}\mathrm{is},(d_i-2)(d_j-d_k)=0,$$

that is, if and only if $d_i=2$, or $d_j=d_k$ for $v_j,v_k\in N_{{\rm Y}}\left(v_i\right)$ as ${\rm Y}$ is connected. This completes the proof of the theorem. □

We now give two relations between $e^{\mathcal{ABC}}({\rm Y})$ and $ABC({\rm Y})$ of graph ${\rm Y}$.

Theorem 4. 

Let ${\rm Y}$ be a graph with m edges and maximum degree Δ. Then,

$$e^{\mathcal{ABC}}({\rm Y})>\left({\displaystyle \frac{{\Delta }^2+\Delta -1}{{\Delta }^2}}\right)m+\left({\displaystyle \frac{3{\Delta }^2+\Delta -1}{3{\Delta }^2}}\right)ABC({\rm Y})+{\displaystyle \frac{{(\Delta -1)}^2}{6{\Delta }^4}}.$$

Proof. 

Since

$${\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\ge {\displaystyle \frac{2(\Delta -1)}{{\Delta }^2}},$$

from the definition of $e^{\mathcal{ABC}}({\rm Y})$, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{v_i{v}_j\in E({\rm Y})}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}\hfill \\ \hfill & >\sum _{v_i{v}_j\in E({\rm Y})}[1+\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\right)}^{3/2}\hfill \\ \hfill & +{\displaystyle \frac{1}{24}}{\left({\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\right)}^2]\hfill \\ \hfill & =m+ABC({\rm Y})+\sum _{v_i{v}_j\in E({\rm Y})}{\displaystyle \frac{1}{2}}{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\left[1+{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}+{\displaystyle \frac{1}{12}}{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\right]\hfill \\ \hfill & \ge m+ABC({\rm Y})+{\displaystyle \frac{(\Delta -1)}{{\Delta }^2}}\sum _{v_i{v}_j\in E({\rm Y})}\left[1+{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}+{\displaystyle \frac{1}{12}}{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\right]\hfill \\ \hfill & =\left({\displaystyle \frac{{\Delta }^2+\Delta -1}{{\Delta }^2}}\right)m+\left({\displaystyle \frac{3{\Delta }^2+\Delta -1}{3{\Delta }^2}}\right)ABC({\rm Y})+{\displaystyle \frac{{(\Delta -1)}^2}{6{\Delta }^4}}.\hfill \end{array}$$

This completes the proof. □

Theorem 5. 

Let ${\rm Y}$ be a graph with m edges and maximum degree Δ. Then,

$$e^{\mathcal{ABC}}({\rm Y})<{\displaystyle \frac{24{\Delta }^2}{23{\Delta }^2+2\Delta -1}}\left({\displaystyle \frac{(3\Delta -1)}{2\Delta }}m+{\displaystyle \frac{(7\Delta -1)}{6\Delta }}ABC({\rm Y})\right).$$

Proof. 

Let $v_i{v}_j\in E({\rm Y})$ be any edge in ${\rm Y}$ with $d_i\ge d_j$. Since $\Delta$ is the maximum degree in ${\rm Y}$, one can easily see that

$$\begin{array}{c}\hfill {\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}\le 1-\frac{1}{\Delta }.}\end{array}$$

(12)

For any real number x,

$$\begin{array}{cc}\hfill e^x& =1+x+{\displaystyle \frac{x^2}{2}}+{\displaystyle \frac{x^3}{6}}+{\displaystyle \frac{x^4}{24}}+{\displaystyle \frac{x^5}{120}}+{\displaystyle \frac{x^6}{720}}+{\displaystyle \frac{x^7}{5040}}+\cdots \hfill \\ \hfill & =1+x+{\displaystyle \frac{x^2}{2}}+{\displaystyle \frac{x^3}{6}}+{\displaystyle \frac{x^4}{24}}\left(1+{\displaystyle \frac{x}{5}}+{\displaystyle \frac{x^2}{30}}+{\displaystyle \frac{x^3}{210}}+\cdots \right)\hfill \\ \hfill & <1+x+{\displaystyle \frac{x^2}{2}}+{\displaystyle \frac{x^3}{6}}+{\displaystyle \frac{x^4}{24}}\left(1+x+{\displaystyle \frac{x^2}{2!}}+{\displaystyle \frac{x^3}{3!}}+{\displaystyle \frac{x^4}{4!}}+\cdots \right)\hfill \\ \hfill & =1+x+{\displaystyle \frac{x^2}{2}}+{\displaystyle \frac{x^3}{6}}+{\displaystyle \frac{x^4}{24}}{e}^x.\hfill \end{array}$$

Using this result with (12), from the definition of $e^{\mathcal{ABC}}({\rm Y})$, we obtain

$$\begin{array}{cc}\hfill e^{\mathcal{ABC}}({\rm Y})& =\sum _{v_i{v}_j\in E({\rm Y})}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}\hfill \\ \hfill & <\sum _{v_i{v}_j\in E({\rm Y})}[1+\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}+{\displaystyle \frac{1}{6}}{\left({\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\right)}^{3/2}\hfill \\ \hfill & +{\displaystyle \frac{1}{24}}{\left({\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}\right)}^2{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}}]\hfill \\ \hfill & \le m+ABC({\rm Y})+{\displaystyle \frac{(\Delta -1)}{2\Delta }}m+{\displaystyle \frac{(\Delta -1)}{6\Delta }}ABC({\rm Y})+{\displaystyle \frac{{(\Delta -1)}^2}{24{\Delta }^2}}\sum _{v_i{v}_j\in E({\rm Y})}{e}^{\sqrt{{\displaystyle \frac{d_i+d_j-2}{d_i{d}_j}}}},\hfill \end{array}$$

that is,

$$e^{\mathcal{ABC}}({\rm Y})<{\displaystyle \frac{24{\Delta }^2}{23{\Delta }^2+2\Delta -1}}\left({\displaystyle \frac{(3\Delta -1)}{2\Delta }}m+{\displaystyle \frac{(7\Delta -1)}{6\Delta }}ABC({\rm Y})\right).$$

This completes the proof of the theorem. □

Remark 4. 

In Theorems 4 and 5, a compelling comparison is provided of $e^{\mathcal{ABC}}({\rm Y})$ and $ABC({\rm Y})$. These results emphasize the relationships and differences between the exponential atom-bond connectivity index and the classical atom-bond connectivity index. To further enrich the discussion and underline the value of the exponential weighting, it would be insightful to include a brief exploration of its unique advantages.

For example, a discussion could address scenarios where the exponential weighting in $e^{\mathcal{ABC}}({\rm Y})$ might offer superior discrimination among molecular graphs. Specifically, the exponential nature of the index may amplify subtle variations in graph topology or degree distributions, making it particularly effective in distinguishing between structurally similar molecules. Such insights would not only underscore the practical utility of the $e^{\mathcal{ABC}}({\rm Y})$ index but also offer guidance on its application in chemical and pharmacological research.

5. Conclusions and Future Work

Topological indices are among the most commonly used graph-based molecular structure descriptors in chemistry and pharmacology. The ability of these indices to differentiate between molecular structures is a key aspect of their utility. Recently, researchers have introduced the exponential atom-bond connectivity $\left(e^{\mathcal{ABC}}\right)$ index to enhance this discriminative power. In this paper, we establish that the double star $D{S}_{n-3,1}$ is the second-highest graph with respect to the exponential atom-bond connectivity $\left(e^{\mathcal{ABC}}\right)$ index among trees of order n. We provide an upper bound for the $e^{\mathcal{ABC}}$ index of unicyclic graphs of order n and identify the maximal graphs. The graph $K_1\vee (P_3\cup (n-4)K_1)$ is shown to be the maximal graph concerning the $e^{\mathcal{ABC}}$ index among bicyclic graphs of order n. Finally, we explore several relationships between $e^{\mathcal{ABC}}$ and $ABC({\rm Y})$ for the graph ${\rm Y}$. In this paper, we determine the maximal graphs for different classes of graphs. The characterization of minimal graphs for the $e^{\mathcal{ABC}}$ can be considered a future direction of research.