Minimum-Cost Shortest-Path Interdiction Problem Involving Upgrading Edges on Trees with Weighted l_∞ Norm

Abstract

Network interdiction problems involving edge deletion on shortest paths have wide applications. However, in many practical scenarios, the complete removal of edges is infeasible. The minimum-cost shortest-path interdiction problem for trees with the weighted $l_{\infty }$ norm (MCSPIT_∞) is studied in this paper. The goal is to upgrade selected edges at minimum total cost such that the shortest root–leaf distance is bounded below by a given value. We designed an $O(nlogn)$ algorithm based on greedy techniques combined with a binary search method to solve this problem efficiently. We then extended the framework to the minimum-cost shortest-path double interdiction problem for trees with the weighted $l_{\infty }$ norm, which imposes an additional requirement that the sum of root–leaf distances exceed a given threshold. Building upon the solution to (MCSPIT_∞), we developed an equally efficient $O(nlogn)$ algorithm for this variant. Finally, numerical experiments are presented to demonstrate both the effectiveness and practical performance of the proposed algorithms.

1. Introduction

Critical edge deletion in network interdiction problems typically involves two entities, a decision-maker (defender) and a disruptor (attacker), competing in a specific Stackelberg game. The decision-maker operates the network to optimize their objective function, such as shortest path, maximum flow, or minimum cost flow, whereas the disruptor attempts to degrade this performance by interdicting several arcs with limited resources [1].

The interdiction problem was first applied to the shortest-path problem by Corley and Sha in [2] in the shortest-path interdiction problem (denoted by (SPIP)). Ball et al. [3] proved that this problem is NP-hard. Israeli et al. [4] transformed this problem into a bilevel mixed integer programming problem. Khachiyan et al. [5] proved that this problem does not admit an approximation algorithm with a performance ratio of 2, which is the current best result. Chen et al. [6] provided an $O(m+nlogn)$ algorithm for the problem on undirected networks when $K=1$. Nardelli et al. [7] improved the time complexity to $O\left(m\alpha \right(m,n\left)\right)$, where $\alpha$ is the inverse Ackermann function, and m and n are the number of edges and nodes, respectively. Building upon classical deterministic frameworks, recent advances in SPIP have expanded into stochastic, temporal, and information-asymmetric settings while simultaneously enhancing our understanding of the problem’s computational complexity and solution methods. Henke et al. [8] established the NP-hardness of the bilevel SPIP, clearly delineating its intractability. Similarly, Boeckmann et al. [9] demonstrated that the temporal version remains NP-hard even when interdicting a single edge. To address uncertainty, Punla-Green et al. [10] and Azizi et al. [11] both developed models for SPIP with incomplete information; the former employed a max–min framework for asymmetric uncertainty, while the latter adopted a robust optimization approach. Nguyen et al. [12] further enriched the stochastic domain by incorporating the conditional value-at-risk (CVaR) metric to model asymmetric risk aversion in an uncertain environment. Beyond traditional mathematical programming, Huang et al. [13] pioneered a novel approach by solving the SPIP using reinforcement learning, demonstrating the potential of AI-based methods. Finally, previous research also clarifies strategic choices as Holzmann et al. [14] laid a key complexity foundation by proving that the problem with randomized interdiction strategies is generally NP-hard but can be solved in pseudo-polynomial time, while Borrero et al. [15] tackled sequential decision-making in a stochastic environment, proposing an approximate dynamic programming algorithm for optimal interdiction policies. Collectively, these studies significantly broaden the modeling landscape and clarify the hardness frontiers of SPIP under various complex conditions.

Currently, the majority of research in this area focuses on the SPIP under the assumption of critical edge deletion. However, factors such as rapid system recovery mechanisms and the presence of backup pathways often make complete edge deletion difficult or even infeasible in practical scenarios. For instance, in a military network scenario, available mobile forces may only be capable of interdicting support between K pairs of adjacent enemy positions. The objective is to choose which K pairs to disrupt so as to maximize the enemy’s support time [16]. This represents a typical application of the shortest-path interdiction problem in military operations. Classical interdiction models focus on completely severing support between enemy positions, that is, deleting edges between the K selected pairs to make communication impossible. However, in reality, adjacent positions may maintain connectivity through multiple alternative means, such as sea, rail, or air transport. As a result, interdiction efforts may only partially disrupt certain support channels rather than entirely eliminating all connections. Another example is shown in Figure 1 [17]: Once the disruptor attacks node $k_{10}$, a fire will break out at that node. The disruptor aims to delay the fire truck’s arrival by maximizing the shortest path from node $k_1$ to $k_{10}$ with a limited interdiction budget. In this case, the disruptor can only increase the length of certain arcs rather than deleting them entirely. Correspondingly, the decision-maker must proactively identify vulnerable arcs and preemptively plan safer alternative routes to ensure the fire truck can reach the incident as quickly as possible. Recent work on the quickest path reliability problem underlines a similar focus on optimizing path performance under resource constraints [18]. This connection highlights the broad applicability of our interdiction and upgrade framework to diverse network optimization scenarios, such as ensuring reliable flow transmission.

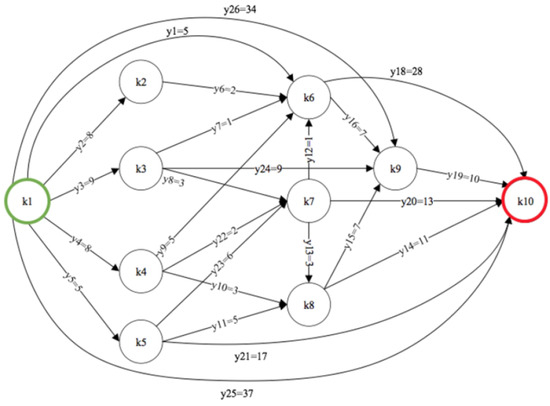
Figure 1. A terrorist network consisting of 10 nodes and 26 arcs, taken from [17], illustrating a shortest-path interdiction scenario. The disruptor aims to delay the fire truck’s arrival by increasing the travel time (length) of arcs from node $k_1$ to the target node $k_{10}$, subject to a limited budget. The interdiction cost for each relevant arc is annotated. This scenario motivates the study of interdiction models based on partial edge degradation (weight increase) rather than complete edge deletion.

Therefore, the classical SPIP with critical edge deletion has inherent limitations. To overcome these, refs. [19,20] introduced the concept of upgrading edges and investigated the maximum shortest-path interdiction problem involving upgrading edges on trees (denoted by MSPIT), which can be defined as follows. Let $T=(V,E,w)$ be an edge-weighted tree rooted at $v_1$, where $V:=\{v_1,v_2,\cdots ,v_n\}$, and $E:=\{e_2,e_3,\cdots ,e_n\}$ be the sets of nodes and edges, respectively. Let $Y:=\{t_1,\cdots$$,t_r\}$ be the set of leaves. Let $w\left(e\right)$ and $u\left(e\right)$ be the original weight and upper bounds of the upgraded weight for an edge $e\in E$, respectively, where $w\left(e\right)\le u\left(e\right)$. Let $c\left(e\right)>0$ be a cost to upgrade the edge $e\in E$. $\mathsf{\Delta }w\left(e\right):=u\left(e\right)-w\left(e\right)$ denotes the deviation between $u\left(e\right)$ and $w\left(e\right)$. $P_{v_i,v_j}$ denotes the unique path from $v_i$ to $v_j$ on the tree T and $P_k:=P_{v_1,t_k}$ the “root–leaf path” of the leaf node $t_k\in Y$ in brief. Define $f\left(P_k\right):={\sum }_{e\in P_k}f\left(e\right)$ as the “root–leaf distance” for a weight vector f and a root–leaf path $P_k$, where $t_k\in Y.$ The problem MSPIT involves finding an upgrade scheme $\overline{w}$ to maximize the shortest root–leaf distance of the tree on the premise that the total upgrade cost with some norm is upper bounded by a given value M. The mathematical model can be stated as follows.

$$\begin{array}{ccc}& {max}_{\overline{w}}& \underset{t_k\in Y}{min}\overline{w}\left(P_k\right)\hfill \\ \hfill \left(\mathrm{MSPIT}\right)& s.t.& \parallel \overline{w}\left(e\right)-w\left(e\right)\parallel \le M,\hfill \\ & & w\left(e\right)\le \overline{w}\left(e\right)\le u\left(e\right),e\in E.\hfill \end{array}$$

(1)

The corresponding minimum-cost shortest-path interdiction problem involving upgrading edges on trees (denoted by MCSPIT) entails upgrading some edges to minimize the total cost with measurement on the premise that the shortest root–leaf distance of the tree is bounded below by a given value D. The mathematical model can be stated as follows.

$$\begin{array}{ccc}& {max}_{\overline{w}}& \parallel \widehat{w}\left(e\right)-w\left(e\right)\parallel \hfill \\ \hfill \left(\mathrm{MCSPIT}\right)& s.t.& \widehat{w}\left(P_k\right)\ge D,t_k\in Y,\hfill \\ & & w\left(e\right)\le \widehat{w}\left(e\right)\le u\left(e\right),e\in E.\hfill \end{array}$$

(2)

Using the weighted $l_1$ norm, Zhang et al. [16] proposed primal–dual algorithms with time complexity $O\left(n^2\right)$ for both problems and with the unit $l_1$ norm and developed linear-time algorithms. Using the weighted Hamming distance, Zhang et al. [21] proved that both problems are NP-hard and designed dynamic programming algorithms with time complexities $O\left(n^4\right)$ and $O(n^{4}logn)$ for the problems MSPIT and MCSPIT with unit Hamming distance, respectively. Yi et al. [22] subsequently improved these algorithms with local optimizations for time complexities $O\left(n^3\right)$ and $O(n^{3}logn)$, respectively. Zhang et al. [23] also investigated the sum of the root–leaf distance interdiction problem involving upgrading edges on trees along with its corresponding minimum cost problem. Using the weighted $l_1$ norm, they provided linear-time algorithms for both problems. They showed the NP-hardness of the problems with the weighted Hamming distance and unit Hamming distance and designed a linear-time greedy algorithm and an $O(nlogn)$ time algorithm based on a binary search method for each problem. Furthermore, Li et al. [24] studied the problem with cardinality constraints and its corresponding minimum cost problem. Using the weighted $l_{\infty }$ norm, they provided two algorithms with time complexity $O(nlogn)$ and $O\left(N{n}^2\right)$ for the problems, respectively, where N denotes the cardinality budget as the maximum number of edges that can be upgraded. They proposed two algorithms using the weighted bottleneck Hamming distance, both in $O(nlogn)$ time.

Research on extensions of the shortest-path interdiction problem involving upgrading edges remains relatively limited. Mohammadi et al. [25] studied the maximum capacity path interdiction problem involving upgrading edges with the sum-type Hamming distance. Unlike the traditional shortest-path problem, where the weight of a path is defined as the sum of the weights of all edges along it, this problem uses the maximum edge weight along the path as its capacity. They provided a strongly polynomial-time algorithm for the case where the cost of reducing each arc’s capacity is fixed. Tayyebi et al. [26] studied the continuous maximum capacity path interdiction problem, where the capacity of each arc in the network can be reduced by any continuous amount. They proposed an efficient algorithm based on a binary search method and the discrete Newton method, solving the problem in polynomial time. Li et al. [27] introduced the minimum-cost shortest-path double interdiction problem involving upgrading edges on trees (MCDSPIT). They addressed the problem that measures the upgrade cost with both weighted $l_{\infty }$ and weighted sum Hamming distances. They showed that the problem is NP-hard and proposed a pseudo-polynomial time algorithm. Research on the shortest-path interdiction problem involving upgrading edges is highly significant and greatly enriches the theory of network interdiction problems.

In this paper, we concentrate on the problems MSPIT and MCSPIT with the weighted $l_{\infty }$ norm, denoted by MSPIT_∞ and MCSPIT_∞, respectively. They can be formulated as follows by applying the weighted $l_{\infty }$ norm to the $\parallel ·\parallel$ in models (1) and (2), respectively.

$$\begin{array}{ccc}& \underset{\overline{w}}{max}& D\left(\overline{w}\right):=\underset{t_k\in Y}{min}\overline{w}\left(P_k\right)\hfill \\ \hfill ({\mathrm{MSPIT}}_{\infty })& s.t.& \underset{e\in E}{max}c\left(e\right)(\overline{w}\left(e\right)-w\left(e\right))\le M,\hfill \\ & & w\left(e\right)\le \overline{w}\left(e\right)\le u\left(e\right),e\in E.\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& \underset{\overline{w}}{min}& C\left(\widehat{w}\right):=\underset{e\in E}{max}c\left(e\right)(\widehat{w}\left(e\right)-w\left(e\right))\hfill \\ \hfill ({\mathrm{MCSPIT}}_{\infty })& s.t.& \underset{t_k\in Y}{min}\widehat{w}\left(P_k\right)\ge D,\hfill \\ & & w\left(e\right)\le \widehat{w}\left(e\right)\le u\left(e\right),e\in E.\hfill \end{array}$$

(4)

We analyzed their models and properties and designed optimization algorithms with time complexity analysis. As summarized in Table 1, our study delineates the computational complexity of the MSPIT, MCSPIT, and MCDSPIT with various norms, including ${\mathsf{\ell }}_1$, Hamming distance, and ${\mathsf{\ell }}_{\infty }$. A key contribution of this work is the establishment of efficient algorithms with complexities of $O\left(n\right)$ and $O(nlogn)$ for the weighted ${\mathsf{\ell }}_{\infty }$ norm variants, thereby resolving previously open problems.

Table 1. Recent advances upgrading edges on trees in shortest-path interdiction problems.

Problem	Norms	Complexity	Reference
MSPIT	weighted ${\mathsf{\ell }}_1$	$O\left(n^2\right)$	[16]
	weighted Hamming	NP-hard	[21]
	unit Hamming	$O\left(n^4\right)$ & $O\left(n^3\right)$	[21,22]
	weighted ${\mathsf{\ell }}_{\infty }$	$O\left(n\right)$	Section 2
MCSPIT	weighted ${\mathsf{\ell }}_1$	$O\left(n^2\right)$	[16]
	weighted Hamming	NP-hard	[21]
	unit Hamming	$O(n^{4}logn)$ & $O(n^{3}logn)$	[21,22]
	weighted ${\mathsf{\ell }}_{\infty }$	$O(nlogn)$	Section 3
MCDSPIT	weighted ${\mathsf{\ell }}_{\infty }$ + Hamming	NP-hard	[27]
	weighted ${\mathsf{\ell }}_{\infty }$	$O(nlogn)$	Section 4

The paper is organized as follows. In Section 2, we propose an $O\left(n\right)$ time algorithm to solve the problem MSPIT_∞. In Section 3, we research the problem MCSPIT_∞ and propose a greedy algorithm in $O(nlogn)$ time based on a binary search method. In Section 4, based on the problem MCSPIT_∞, the  problem MCDSPIT_∞ is studied, and an $O(nlogn)$ time algorithm is proposed. In Section 5, we present some computational experiments to show the effectiveness of the algorithms. In Section 6, we conclude and present directions for future research.

2. Solving the Problem MSPIT_∞

In this section, we propose a linear time algorithm for the problem MSPIT_∞ based on the analysis of properties.

According to model (3) for the ${\mathrm{MSPIT}}_{\infty }$ problem, the optimal strategy for any edge $e\in E$ is to upgrade its weight to the maximum possible value. This upgrade is subject to the cost constraint M and the upper bound $u\left(e\right)$. The optimal increment for the edge weight can be determined with $min\left\{{\displaystyle \frac{M}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}$, where $\mathsf{\Delta }u\left(e\right)=u\left(e\right)-w\left(e\right)$. Thus an optimal solution is

$$\begin{array}{c}\hfill \overline{w}\left(e\right):=w\left(e\right)+min\left\{{\displaystyle \frac{M}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}(e\in E)\end{array}$$

(5)

and its relevant optimal objective value $D\left(\overline{w}\right)={min}_{t_k\in Y}\overline{w}\left(P_k\right).$

Theorem 1. 

The solution $\overline{w}$ defined as (5) is an optimal solution of the problem MSPIT_∞.

Proof. 

(1) For any edge $e\in E$, we have

$$w\left(e\right)\le \overline{w}\left(e\right)=w\left(e\right)+min\left\{{\displaystyle \frac{M}{c\left(e\right)}},u\left(e\right)-w\left(e\right)\right\}\le w\left(e\right)+u\left(e\right)-w\left(e\right)=u\left(e\right)$$

and

$$c\left(e\right)(\overline{w}\left(e\right)-w\left(e\right))=c\left(e\right)·min\left\{{\displaystyle \frac{M}{c\left(e\right)}},u\left(e\right)-w\left(e\right)\right\}\le c\left(e\right)·{\displaystyle \frac{M}{c\left(e\right)}}=M.$$

Therefore, $\overline{w}$ is a feasible solution of the problem MSPIT_∞.

(2) Suppose $\overline{w}$ is not optimal, but $w^{\ast }$ is. Then, $D\left(w^{\ast }\right)=w^{\ast }\left(P_{t^{\ast }}\right)>D\left(\overline{w}\right)=\overline{w}\left(P_{\overline{t}}\right)$.

(i) If $t^{\ast }=\overline{t}$, then there exists an edge $\widehat{e}\in P_{t^{\ast }}$ satisfying $u\left(\widehat{e}\right)\ge w^{\ast }\left(\widehat{e}\right)>\overline{w}\left(\widehat{e}\right)$ as $w^{\ast }\left(P_{t^{\ast }}\right)>\overline{w}\left(P_{t^{\ast }}\right)$. Then, we have

$$C\left(w^{\ast }\right)\ge c\left(\widehat{e}\right)(w^{\ast }\left(\widehat{e}\right)-w\left(\widehat{e}\right))>c\left(\widehat{e}\right)(\overline{w}\left(\widehat{e}\right)-w\left(\widehat{e}\right))=M,$$

which contradicts the feasibility of $w^{\ast }$.

(ii) If $t^{\ast }\ne \overline{t}$, then $w^{\ast }\left(P_{\overline{t}}\right)\ge w^{\ast }\left(P_{t^{\ast }}\right)>\overline{w}\left(P_{\overline{t}}\right)\le \overline{w}\left(P_{t^{\ast }}\right)$, and there is an edge $\widehat{e}\in P_{\overline{t}}$ satisfying $u\left(\widehat{e}\right)\ge w^{\ast }\left(\widehat{e}\right)>\overline{w}\left(\widehat{e}\right)$. Similarly, we have

$$C\left(w^{\ast }\right)\ge c\left(\widehat{e}\right)(w^{\ast }\left(\widehat{e}\right)-w\left(\widehat{e}\right))>c\left(\widehat{e}\right)(\overline{w}\left(\widehat{e}\right)-w\left(\widehat{e}\right))=M,$$

which contradicts the feasibility of $w^{\ast }$.

Hence, $\overline{w}$ is an optimal solution of the problem MSPIT_∞.    □

For a given tree $T(V,E)$ with a set Y of leaves, cost vector c, and two weight vectors w and u along with a given budget M, we can obtain an optimal solution $\overline{w}$ for the problem ${\mathrm{MSPIT}}_{\infty }$ using Formula (5). This solution allows us to determine the corresponding optimal objective value $D\left(\overline{w}\right)={min}_{t\in Y}\overline{w}\left(P_t\right)$. For convenience, we represent the above process with (6):

$$[\overline{w},D\left(\overline{w}\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M).$$

(6)

Theorem 2. 

The problem MSPIT_∞ can be solved using (6) in $O\left(n\right)$ time.

3. Solving the Problem MCSPIT_∞

In this section, we address the problem MCSPIT_∞. Through a series of property analyses and case discussions, we developed an efficient algorithm. The algorithm leverages greedy strategies and a binary search method to achieve a time complexity of $O(nlogn)$.

We begin by sorting $c\left(e\right)\mathsf{\Delta }u\left(e\right)$ in a non-decreasing order and removing any duplicates to obtain the sequence $\left\{{\alpha }_{n^{\ast }}\right\}$:

$$c\left(e_{{\alpha }_1}\right)\mathsf{\Delta }u\left(e_{{\alpha }_1}\right)<c\left(e_{{\alpha }_2}\right)\mathsf{\Delta }u\left(e_{{\alpha }_2}\right)<\cdots <c\left(e_{{\alpha }_{n^{\ast }}}\right)\mathsf{\Delta }u\left(e_{{\alpha }_{n^{\ast }}}\right)$$

(7)

Define $M_j:=c\left(e_{{\alpha }_j}\right)\mathsf{\Delta }u\left(e_{{\alpha }_j}\right)$ for $j:=1,2,\dots ,n^{\ast }$. We can then apply (6) using the assignment $[{\widehat{w}}^j,D\left({\widehat{w}}^j\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_j)$ to compute the value ${\widehat{w}}^j$ and the corresponding shortest root–leaf distance $D_j=D\left({\widehat{w}}^j\right)$. Since $M_j$ is increasing, the output $D_j$ is non-decreasing.

Specifically, for $j=n^{\ast }$ and $j=1$, the processes are defined as

$$[{\widehat{w}}^{n^{\ast }},D\left({\widehat{w}}^{n^{\ast }}\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_{n^{\ast }})\mathrm{with}{M}_{n^{\ast }}=c\left(e_{{\alpha }_{n^{\ast }}}\right)\mathsf{\Delta }u\left(e_{{\alpha }_{n^{\ast }}}\right)$$

and

$$[{\widehat{w}}^1,D\left({\widehat{w}}^1\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_1)\mathrm{with}{M}_1=c\left(e_{{\alpha }_1}\right)\mathsf{\Delta }u\left(e_{{\alpha }_1}\right).$$

These computations yield ${\widehat{w}}^{n^{\ast }}$ and ${\widehat{w}}^1$ along with their respective distances $D_{n^{\ast }}$ and $D_1$. Upon analysis, we derive the following two straightforward lemmas.

Lemma 1. 

The optimal objective value of the problem MCSPIT_∞ is in the range $[0,M_{n^{\ast }}]$.

Lemma 2. 

If $\widehat{w}$ is an optimal solution of the problem MCSPIT_∞, then its relevant length $D\left(\widehat{w}\right)$ of the shortest root–leaf distance satisfies $D\left(w\right)\le D\left(\widehat{w}\right)\le D_{n^{\ast }}$.

According to Lemma 2, the problem MCSPIT_∞ is infeasible for $D>D_{n^{\ast }}$ as all edges have been upgraded to their maximum capacity. For $D\le D\left(w\right)$, the optimal solution is conversely w with an optimal value 0 since w already satisfies the feasibility conditions. We can consequently state the following theorems.

Theorem 3.

(1) If $D>D_{n^{\ast }}$, the (MCSPIT_∞) is infeasible.

(2) If $D\le D\left(w\right)$, the optimal solution is w, and the optimal value is 0.

We next consider the problem MCSPIT_∞ when $D\left(w\right)<D\le D_1$. The optimal objective value is denoted by $M^{\ast }$. The optimal objective value $M^{\ast }$ of problem ${\mathrm{MCSPIT}}_{\infty }$ therefore satisfies $M^{\ast }\le M_1$. Consequently, the upgrade amount for any edge $e\in E$ is given by ${\displaystyle \frac{M^{\ast }}{c\left(e\right)}}$. Let $Y_{<}:=\{t_k\in Y|w\left(P_k\right)<D\}$ be the set of leaves with root–leaf distances of less than D. Then, for each path $P_k(t_k\in Y_{<})$, ${\sum }_{e\in P_k}{\displaystyle \frac{M^{\ast }}{c\left(e\right)}}+w\left(P_k\right)\ge D$ holds. Hence, we have the following theorem.

Theorem 4. 

When $D\left(w\right)<D\le D_1$, $M^{\ast }=\underset{t_k\in Y_{<}}{max}{\displaystyle \frac{D-w\left(P_k\right)}{{\sum }_{e\in P_k}\frac{1}{c\left(e\right)}}}$ is the optimal objective value of problem MCSPIT_∞, where $Y_{<}=\{t_k\in Y|w\left(P_k\right)<D\}$.

Proof. 

Let $\overline{w}\left(e\right)=w\left(e\right)+min\{{\displaystyle \frac{M^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\}=w\left(e\right)+{\displaystyle \frac{M^{\ast }}{c\left(e\right)}}$ be the corresponding optimal solution of the objective value $M^{\ast }$ as defined in the theorem.

(1) We show the feasibility of the solution $\overline{w}$. For any $t_k\in Y$,

$$\begin{array}{ccc}\hfill \overline{w}\left(P_k\right)& =& w\left(P_k\right)+\sum _{e\in P_k}{\displaystyle \frac{M^{\ast }}{c\left(e\right)}}\hfill \\ & =& w\left(P_k\right)+\underset{t_j\in Y}{max}{\displaystyle \frac{D-w\left(P_j\right)}{{\sum }_{e\in P_j}\frac{1}{c\left(e\right)}}}·\sum _{e\in P_k}{\displaystyle \frac{1}{c\left(e\right)}}\hfill \\ & \ge & w\left(P_k\right)+{\displaystyle \frac{D-w\left(P_k\right)}{{\sum }_{e\in P_k}\frac{1}{c\left(e\right)}}}·\sum _{e\in P_k}{\displaystyle \frac{1}{c\left(e\right)}}=D\hfill \end{array}$$

Hence, $\overline{w}$ is feasible.

(2) Next, we show the optimality. Suppose $\overline{w}$ is not an optimal solution, but $\widehat{w}\left(e\right)=w\left(e\right)+{\displaystyle \frac{\widehat{M}}{c\left(e\right)}}$ (for $e\in E$) is, where $\widehat{M}<M^{\ast }\le M_1$ is its corresponding objective value. Let $P_{\widehat{t}}$ be the shortest path with the weight $\widehat{w}$.

(2.1) If $P_{\widehat{t}}$ is also the shortest path with the weight $\overline{w}$, then $\overline{w}\left(P_{\widehat{t}}\right)=D$ according to the definition of $M^{\ast }$. We then have

$$\widehat{w}\left(P_{\widehat{t}}\right)=w\left(P_{\widehat{t}}\right)+\sum _{e\in P_{\widehat{t}}}{\displaystyle \frac{\widehat{M}}{c\left(e\right)}}<w\left(P_{\widehat{t}}\right)+\sum _{e\in P_{\widehat{t}}}{\displaystyle \frac{M^{\ast }}{c\left(e\right)}}=\overline{w}\left(P_{\widehat{t}}\right)=D,$$

which contradicts the fact that $\widehat{w}$ is feasible.

(2.2) If $P_{\widehat{t}}$ is not the shortest path with the weight $\overline{w}$, but $P_{\overline{t}}$ is, and $\overline{w}\left(P_{\overline{t}}\right)<\overline{w}\left(P_{\widehat{t}}\right)$, then we have

$$\widehat{w}\left(P_{\widehat{t}}\right)\le \widehat{w}\left(P_{\overline{t}}\right)<\overline{w}\left(P_{\overline{t}}\right)=D,$$

which contradicts the fact that $\widehat{w}$ is optimal.

In conclusion, $\overline{w}$ is an optimal solution to the problem with its relevant optimal objective value $M^{\ast }$.    □

When $D_1<D\le D_{n^{\ast }}$, we employ a binary search method to determine the range of the optimal solution for the problem MCSPIT_∞. We present the optimal solution by identifying the smallest cost among the infeasible paths and provide an $O(nlogn)$ time algorithm to solve the problem MCSPIT_∞.

Specifically, we first use a binary search method based on the ascending sequence in (7) to determine the index k satisfying $D_k<D\le D_{k+1}$. We call (6) to solve $[{\widehat{w}}^k,D\left({\widehat{w}}^k\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_k)$, obtaining ${\widehat{w}}^k$ and its corresponding shortest root–leaf path length $D_k=D\left({\widehat{w}}^k\right)$. Next, we call (6) to solve $[{\widehat{w}}^{k+1},D\left({\widehat{w}}^{k+1}\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_{k+1})$, obtaining ${\widehat{w}}^{k+1}$ and its corresponding shortest root–leaf path length $D_{k+1}=D\left({\widehat{w}}^{k+1}\right)$. When $D_{k+1}=D$, the current cost $M_{k+1}$ is just enough to satisfy the constraint, and the following theorem is obvious.

Theorem 5. 

If $D_{k+1}=D$, then $M_{k+1}$ is the optimal value to problem MCSPIT_∞, and the corresponding optimal solution is ${\widehat{w}}^{k+1}$.

Then, we have the following theorem to give the optimal solution.

Theorem 6. 

Suppose $D_k<D\le D_{k+1}$ for an index k based on the ascending sequence in (7). The optimal objective value of the problem MCSPIT_∞ is

$$\begin{array}{c}\hfill M^{\ast }=\underset{t_k\in Y_{<}}{max}{\displaystyle \frac{D-w\left(P_k\right)-{\sum }_{e\in P_k\setminus E_{>}}\mathsf{\Delta }u\left(e\right)}{{\sum }_{e\in P_k\cap E_{>}}\frac{1}{c\left(e\right)}}},\end{array}$$

(8)

where $Y_{<}:=\{t_k\in Y\mid w\left(P_k\right)<D\}$ and $E_{>}:=\{e\in E\mid c\left(e\right)\mathsf{\Delta }u\left(e\right)>M_k\}$. Then, the corresponding optimal solution is given by

$$\begin{array}{c}\hfill w^{\ast }\left(e\right)=w\left(e\right)+min\left\{{\displaystyle \frac{M^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}.\end{array}$$

(9)

Proof. 

We mainly show that $w^{\ast }$ is a feasible solution of the problem MCSPIT_∞. Notice that for any edge $e\in E_{>}$, we have $c\left(e\right)\mathsf{\Delta }u\left(e\right)>M_k$, and $c\left(e\right)\mathsf{\Delta }u\left(e\right)>M^{\ast }$ also holds. Otherwise, the case $M^{\ast }>c\left(e\right)\mathsf{\Delta }u\left(e\right)>M_k$ occurs, which contradicts $D_k<M\le D_{k+1}$, implying no values between $M_k$ and $M_{k+1}$ in sequence (7). Additionally, for any edge $e\in P_k\setminus E_{>}$, we obviously have $c\left(e\right)\mathsf{\Delta }u\left(e\right)\le M_k<M^{\ast }$.

For any $t_k\in Y_{<}$,

$$\begin{array}{ccc}\hfill w^{\ast }\left(P_k\right)=\sum _{e\in P_k}{w}^{\ast }\left(e\right)& =& \sum _{e\in P_k}\left(w\left(e\right)+min\left\{{\displaystyle \frac{M^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& w\left(P_k\right)+\sum _{e\in P_k\cap E_{>}}{\displaystyle \frac{M^{\ast }}{c\left(e\right)}}+\sum _{e\in P_k\setminus E_{>}}\mathsf{\Delta }u\left(e\right)\hfill \end{array}$$

(10)

$$\begin{array}{ccc}& \ge & w\left(P_k\right)+\sum _{e\in P_k\cap E_{>}}{\displaystyle \frac{\frac{D-w\left(P_k\right)-{\sum }_{e\in P_k\setminus E_{>}}\mathsf{\Delta }u\left(e\right)}{{\sum }_{e\in P_k\cap E_{>}}\frac{1}{c\left(e\right)}}}{c\left(e\right)}}+\sum _{e\in P_k\setminus E_{>}}\mathsf{\Delta }u\left(e\right)\hfill \\ & =& w\left(P_k\right)+D-w\left(P_k\right)-\sum _{e\in P_k\setminus E_{>}}\mathsf{\Delta }u\left(e\right)+\sum _{e\in P_k\setminus E_{>}}\mathsf{\Delta }u\left(e\right)\hfill \\ & =& D\hfill \end{array}$$

(11)

For any $t_k\in Y\setminus Y_{<}$, we have $w^{\ast }\left(P_k\right)\ge w\left(P_k\right)\ge D$.

The proof for the optimality of $M^{\ast }$ follows a similar argument to that in part (2) of Theorem 4, and we omit the details here.   □

Based on the analysis above, we have the following Algorithm 1 to solve the problem MCSPIT_∞.

Theorem 7. 

The problem MCSPIT_∞ can be solved with Algorithm 1 in $O(nlogn)$ time.

Proof. 

We analyze the time complexity of Algorithm 1 step by step to establish the $O(nlogn)$ bound. The algorithm begins by calculating the weight difference vector $\mathsf{\Delta }u=u-w$ in Line 1. This involves a simple subtraction operation for each of the $O\left(n\right)$ edges, which requires $O\left(n\right)$ time. In Line 2, sorting the edges based on the value of $c\left(e\right)\mathsf{\Delta }u\left(e\right)$ is a fundamental operation. Since there are $O\left(n\right)$ edges, sorting them requires $O(nlogn)$ time.

In Lines 4–5, the algorithm calls the MSPIT_∞ subroutine as (6) twice for the extreme values $M_1$ and $M_{n^{\ast }}$ in $O\left(n\right)$ time. Lines 6–13 handle special cases regarding the feasibility and triviality of the problem. The checks $D>D_{n^{\ast }}$ and $D\le D\left(w\right)$ involve simple comparisons. The calculation of $M^{\ast }$ for the case $D\left(w\right)<D\le D_1$ involves iterating over the paths to leaves in the set $Y_{<}$, which can be obtained from a breadth-first search in $O\left(n\right)$ time. Thus, this entire block runs in $O\left(n\right)$ time.

Algorithm 1 $[\overline{w},M^{\ast }]:={\mathrm{MCSPIT}}_{\infty }(T,Y,w,u,c,D)$

Input: The tree $T(V,E)$ rooted at a root node $v_1$,    The set Y of leaf nodes,    The cost vector c,    Two weight vectors w, u,    A given value D. Output: An optimal solution $\overline{w}$,     Its relevant objective value $M^{\ast }$.   1: Calculate $\mathsf{\Delta }u:=u-w$.   2: Sort edges $e\in E$ by $c\left(e\right)\mathsf{\Delta }u\left(e\right)$ in ascending order (remove duplicates).   3: Let the sorted distinct values be: $M_1\le M_2\le \cdots \le M_{n^{\ast }}$.   4: Call (6) $[{\widehat{w}}^{n^{\ast }},D_{n^{\ast }}]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_{n^{\ast }})$.   5: Call (6) $[{\widehat{w}}^1,D_1]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_1)$.   6: if $D>D_{n^{\ast }}$ then   7:  return “The problem is infeasible.”   8: else if $D\le D\left(w\right)$ then   9:  return $(w,0)$. 10: else if $D\left(w\right)<D\le D_1$ then 11:  $M^{\ast }:=\underset{t_k\in Y_{<}}{max}{\displaystyle \frac{D-w\left(P_k\right)}{{\sum }_{e\in P_k}\frac{1}{c\left(e\right)}}},$ where $Y_{<}:=\{t_k\in Y\mid w\left(P_k\right)<D\}$. 12:  Call (6) $[\overline{w},D\left(\overline{w}\right)]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M^{\ast })$. 13:  return $(\overline{w},M^{\ast })$. 14: else 15:  Initialize $a:=1$, $b:=n^{\ast }$, $k^{\ast }:=\mathrm{null}$ 16:  if $a=b$ then 17:   $k^{\ast }:=a$ 18:  end if 19:  while $k^{\ast }=\mathrm{null}$ do 20:   $k:=\lfloor {\displaystyle \frac{a+b}{2}}\rfloor$. 21:   Call (6) $[{\widehat{w}}^k,D_k]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_k)$. 22:   Call (6) $[{\widehat{w}}^{k+1},D_{k+1}]:={\mathrm{MSPIT}}_{\infty }(T,Y,w,u,c,M_{k+1})$. 23:   if $D_{k+1}<D$ then 24:    $a:=k$. 25:   else if $D_k\ge D$ then 26:    $b:=k$. 27:   else if $D_k<D\le D_{k+1}$ then 28:    $k^{\ast }:=k$. 29:   end if 30:  end while 31:  $Y_{<}:=\{t_k\in Y\mid w\left(P_k\right)<D\}$. 32:  $E_{>}:=\{e\in E\mid c\left(e\right)\mathsf{\Delta }u\left(e\right)>M_{k^{\ast }}\}$. 33:  Calculate $M^{\ast }$ as (8) and $w^{\ast }$ as (9). 34:  return $(w^{\ast },M^{\ast })$. 35: end if

The binary search loop in Lines 15–30 is the core component of the algorithm. The loop performs a binary search over the $n^{\ast }$ (which is $O\left(n\right)$) sorted $M_j$ values to find the critical interval $[M_k,M_{k+1}]$ such that $D_k<D\le D_{k+1}$. The number of iterations of this binary search is $O(logn)$. In each iteration, the algorithm makes two calls to the MSPIT_∞ subroutine (Lines 21 and 22) to compute $D_k$ and $D_{k+1}$ for the current pivot $M_k$ and its successor $M_{k+1}$. Since each call to MSPIT_∞ takes $O\left(n\right)$ time, the cost per iteration is $O\left(n\right)$. Therefore, the total time cost of the binary search loop is $O(logn)\times O\left(n\right)=O(nlogn)$.

After identifying the critical index $k^{\ast }$, the final solution is constructed. Lines 31–32 define the sets $Y_{<}$ and $E_{>}$, which can be determined by checking each leaf and each edge, taking $O\left(n\right)$ time. Line 33 calculates $M^{\ast }$ and the optimal weight vector $w^{\ast }$ according to (8) and (9) in $O\left(n\right)$ time.

To sum up, the overall time complexity is dominated by the sorting operation and the binary search loop, both of which are $O(nlogn)$. Hence, Algorithm 1 solves the MCSPIT_∞ problem in $O(nlogn)$ time.    □

4. Minimum-Cost Shortest-Path Double Interdiction Problem Involving Upgrading Edges on Trees with Weighted ${\mathit{l}}_{\infty }$ Norm

In this section, we consider an extended version of the problem MCSPIT_∞, referred to as the minimum-cost shortest-path double interdiction problem involving upgrading edges on trees (MCDSPIT) with the weighted $l_{\infty }$ norm (MCDSPIT_∞). Li et al. [27] introduced the MCDSPIT problem, which has significant implications in diverse areas such as transportation networks, military strategies, and counter-terrorism efforts. The objective is to find a minimum-cost upgrade scheme such that two constraints are satisfied: the shortest root–leaf distance is at least a given value D, and the sum of all root–leaf distances is no less than a given value B. The mathematical model can be stated as follows.

$$\begin{array}{ccc}& {min}_{\tilde{w}}& \parallel \tilde{w}\left(e\right)-w\left(e\right)\parallel \hfill \\ \hfill \left(\mathrm{MCDSPIT}\right)& s.t.& \tilde{w}\left(P_i\right)\ge D,t_i\in Y,\hfill \\ & & \sum _{t_i\in Y}\tilde{w}\left(P_i\right)\ge B,\hfill \\ & & w\left(e\right)\le \tilde{w}\left(e\right)\le u\left(e\right),e\in E.\hfill \end{array}$$

(12)

When the $l_{\infty }$ norm applies to $\parallel ·\parallel$ in model (12), we can obtain the problem MCDSPIT_∞, which is formulated as follows.

$$\begin{array}{ccc}& {min}_{\tilde{w}}& C\left(\tilde{w}\right):=\underset{e\in E}{max}c\left(e\right)(\tilde{w}\left(e\right)-w\left(e\right))\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill ({\mathrm{MCDSPIT}}_{\infty })& s.t.& \tilde{w}\left(P_i\right)\ge D,t_i\in Y,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & \sum _{t_i\in Y}\tilde{w}\left(P_i\right)\ge B,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}& & w\left(e\right)\le \tilde{w}\left(e\right)\le u\left(e\right),e\in E.\hfill \end{array}$$

(16)

It follows from the model of the problem MCDSPIT_∞ that if upgrading all edges to their upper bounds still cannot satisfy the conditions (14) or (15), then the problem is infeasible.

Theorem 8. 

If ${\sum }_{t_i\in Y}u\left(P_i\right)<B$ or ${min}_{t_i\in Y}u\left(P_i\right)<D$, then the problem MCDSPIT_∞ is infeasible.

Notice that (13), (14), and (16) are the problem MCSPIT_∞. An optimal solution of the problem MCDSPIT_∞ is thus a feasible solution of the problem MCSPIT_∞. Then, we have the following conclusion for the optimal objective values of the two problems. Note that for any $e\in E$, $\mathsf{\Delta }u\left(e\right)=u\left(e\right)-w\left(e\right).$

Lemma 3. 

We have $M^{\ast }\le K^{\ast }\le {max}_{e\in E}c\left(e\right)\mathsf{\Delta }u\left(e\right)$, where $K^{\ast }$ and $M^{\ast }$ are the optimal values of the problems MCDSPIT_∞ and MCSPIT_∞, respectively.

For any $K\ge 0$, define the weight vector $w_K$ as follows:

$$\begin{array}{c}\hfill w_K\left(e\right):=w\left(e\right)+min\left\{{\displaystyle \frac{K}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\},e\in E.\end{array}$$

(17)

Then, we have the following lemma to show the relationship between the optimal value $K^{\ast }$ of the problem MCDSPIT_∞ and any cost $K\ge 0$.

Lemma 4. 

The vector $w_K$ as (17) is feasible for MCDSPIT_∞ if and only if $K\ge K^{\ast }$, where $K^{\ast }$ is the optimal values of the problem MCDSPIT_∞. Moreover, if $K=K^{\ast }$, then $w_K$ is an optimal solution of the problem MCDSPIT_∞.

Proof. 

Necessity: Let $w_K$ be defined as (17), a feasible solution to the problem MCDSPIT_∞, and suppose $K<K^{\ast }$. This contradicts that $K^{\ast }$ is the optimal value of the problem MCDSPIT_∞.

Sufficiency: Suppose $w^{\ast }$ is an optimal solution to problem MCDSPIT_∞. We will prove that for any $e\in E$, $w_K\left(e\right)\ge w^{\ast }\left(e\right)$ holds. Suppose there exists $e_i\in E$, such that $w_K\left(e_i\right)=w\left(e_i\right)+min\left\{{\displaystyle \frac{K}{c\left(e_i\right)}},\mathsf{\Delta }u\left(e_i\right)\right\}<w^{\ast }\left(e_i\right)$.

(1) If ${\displaystyle \frac{K}{c\left(e_i\right)}}>\mathsf{\Delta }u\left(e_i\right)$, then $w_K\left(e_i\right)=w\left(e_i\right)+\mathsf{\Delta }u\left(e_i\right)=u\left(e_i\right)<w^{\ast }\left(e_i\right)$, which contradicts $w^{\ast }\left(e_i\right)\le u\left(e_i\right)$.

(2) If ${\displaystyle \frac{K}{c\left(e_i\right)}}\le \mathsf{\Delta }u\left(e_i\right)$, then $w_K\left(e_i\right)=w\left(e_i\right)+{\displaystyle \frac{K}{c\left(e_i\right)}}<w^{\ast }\left(e_i\right)$, which implies that $K^{\ast }\ge c\left(e_i\right)(w^{\ast }\left(e_i\right)-w\left(e_i\right))>c\left(e_i\right)(w_K\left(e_i\right)-w\left(e_i\right))=K.$ This contradicts $K^{\ast }\le K$.

Therefore, for any $e\in E$, $w_K\left(e\right)\ge w^{\ast }\left(e\right)$ holds so that constraints (14)–(16) hold for the vector $w_K$, confirming that $w_K$ is indeed feasible.    □

We can solve the problem MCDSPIT_∞ from the analysis above based on an optimal solution $\widehat{w}$ of MCSPIT_∞ with its corresponding optimal cost $M^{\ast }:=C\left(\widehat{w}\right)$. If the constraint for the sum of the root–leaf distance holds already, then $\widehat{w}$ is also optimal for the problem MCDSPIT_∞.

Theorem 9. 

If ${\sum }_{t_i\in Y}\widehat{w}\left(P_i\right)\ge B$, then $\tilde{w}:=\widehat{w}$ is an optimal solution of the problem MCDSPIT_∞, where $\widehat{w}$ is an optimal solution of the problem MCSPIT_∞.

Otherwise, we have the case when ${\sum }_{t_i\in Y}\widehat{w}\left(P_i\right)<B$, which is the most significant and difficult part of solving the problem MCSPIT_∞. To address this case, we first choose the sequence (7) by removing any duplicates and the values lower than $C\left(\overline{w}\right)$ to obtain the sequence $\left\{{\beta }_{\widehat{n}}\right\}$:

$$\widehat{K}\le c\left(e_{{\beta }_1}\right)\mathsf{\Delta }u\left(e_{{\beta }_1}\right)<c\left(e_{{\beta }_2}\right)\mathsf{\Delta }u\left(e_{{\beta }_2}\right)<\cdots <c\left(e_{{\beta }_{\widehat{n}}}\right)\mathsf{\Delta }u\left(e_{{\beta }_{\widehat{n}}}\right)$$

(18)

Define $K_0:=\widehat{K},K_j:=c\left(e_{{\beta }_j}\right)\mathsf{\Delta }u\left(e_{{\beta }_j}\right)$ for $j:=1,2,\dots ,\widehat{n}$. Then, the following lemma holds immediately.

Lemma 5. 

The optimal value $K^{\ast }$ of the problem MCDSPIT_∞ lies in $[K_0,k_{\widehat{n}}]$.

We can consequently determine the index k through a binary search method such that $K_k<K^{\ast }\le K_{k+1}$, that is, ${\sum }_{t_i\in Y}{w}_k\left(P_i\right)<B\le {\sum }_{t_i\in Y}{w}_{k+1}\left(P_i\right)$, where $w_k$ and $w_{k+1}$ are constructed as (17) with $K_k$ and $K_{k+1}$, respectively. For convenience, we introduce the following concept $Q\left(e\right)$ containing the leaf nodes controlled by an edge $e\in E.$

Definition 1 

([23]). Define $Q\left(e\right):=\left\{t_k\right|e\in P_k,k=1,\cdots ,r\}$ as the set of leaf nodes with root–leaf paths passing through e. If $t_k\in Q\left(e\right)$, then the leaf node $t_k$ is controlled by the edge $e\in E$.

Based on the index k with $K_k<K^{\ast }\le K_{k+1}$ in an non-decreasing sequence (18), we can then calculate the optimal value $K^{\ast }$ as the following theorem.

Theorem 10. 

The value

$$\begin{array}{c}\hfill K^{\ast }:={\displaystyle \frac{B-{\sum }_{t_i\in Y}{\sum }_{e\in P_i}w\left(e\right)-{\sum }_{e\in E_{\le }^k}\left|Q\left(e\right)\right|\mathsf{\Delta }u\left(e\right)}{{\sum }_{e\in E_{>}^k}\frac{\left|Q\right(e\left)\right|}{c\left(e\right)}}}\end{array}$$

(19)

is the optimal objective value of the (MCDSPIT_∞), where $E_{>}^k:=\{e\in E|c\left(e\right)\mathsf{\Delta }u\left(e\right)>K_k\}$ and $E_{\le }^k:=\{e\in E|c\left(e\right)\mathsf{\Delta }u\left(e\right)\le K_k\}$. Then, $w_{K^{\ast }}$ as (17) is an optimal solution.

Proof. 

(1) We first prove that $w_{K^{\ast }}$ is a feasible solution of the (MCDSPIT_∞). It is obvious that $w\left(e\right)\le w_{K^{\ast }}\left(e\right)\le u\left(e\right),$ for $e\in E$ because it is constructed as (17). We then need to show that $w_{K^{\ast }}$ satisfies the constraints (14) and (15).

For constraint (14), as $\widehat{K}\le K_k<K^{\ast }\le K_{k+1}$, then for any $t_i\in Y$, we have $w_{K^{\ast }}\left(P_i\right)>w_{\widehat{K}}\left(P_i\right)\ge D$.

For constraint (15), notice that for any edge $e\in E_{>}^k$, we have $c\left(e\right)\mathsf{\Delta }u\left(e\right)>K_k$ and $c\left(e\right)\mathsf{\Delta }u\left(e\right)>K^{\ast }$ also holds. Otherwise, the case $K^{\ast }>c\left(e\right)\mathsf{\Delta }u\left(e\right)>K_k$ occurs, which contradicts $K_k<K^{\ast }\le K_{k+1}$, implying no values between $K_k$ and $K_{k+1}$ in sequence (18). We also obviously have $c\left(e\right)\mathsf{\Delta }u\left(e\right)\le K_k<K^{\ast }$ for any edge $e\in E_{\le }^k$. Then, we have

$$\begin{array}{cc}\hfill \sum _{t_i\in Y}{w}_{K^{\ast }}\left(P_i\right)& =\sum _{t_i\in Y}\sum _{e\in P_i}{w}_{K^{\ast }}\left(e\right)\hfill \\ & =\sum _{t_i\in Y}\sum _{e\in P_i}\left(w\left(e\right)+min\left\{{\displaystyle \frac{K^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}\right)\hfill \\ & =\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)+\sum _{t_i\in Y}\sum _{e\in P_i}min\left\{{\displaystyle \frac{K^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}\hfill \\ & =\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)+\sum _{e\in E}\sum _{e\in P_i,t_i\in Y}min\left\{{\displaystyle \frac{K^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}\hfill \\ & =\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)+\sum _{e\in E}\left|Q\left(e\right)\right|min\left\{{\displaystyle \frac{K^{\ast }}{c\left(e\right)}},\mathsf{\Delta }u\left(e\right)\right\}\hfill \\ & =\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)+\sum _{e\in E_{>}^k}\left|Q\left(e\right)\right|{\displaystyle \frac{K^{\ast }}{c\left(e\right)}}+\sum _{e\in E_{\le }^k}\left|Q\left(e\right)\right|\mathsf{\Delta }u\left(e\right)\hfill \\ & =\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)+\left(B-\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)-\sum _{e\in E_{\le }^k}\left|Q\left(e\right)\right|\mathsf{\Delta }u\left(e\right)\right)+\sum _{e\in E_{\le }^k}\left|Q\left(e\right)\right|\mathsf{\Delta }u\left(e\right)\hfill \\ & =B\hfill \end{array}$$

Therefore, $w_{K^{\ast }}$ as (17) with $K^{\ast }$ is a feasible solution of the problem MCDSPIT_∞.

(2) We next prove that $K^{\ast }$ is the optimal value. Suppose that $K^{\prime }<K^{\ast }$ is the optimal value of the problem MCDSPIT_∞ and $w_{K^{\prime }}$ is a corresponding optimal solution; then, we have

$$\sum _{t_i\in Y}{w}_{K^{\prime }}\left(P_i\right)=\sum _{t_i\in Y}\sum _{e\in P_i}w\left(e\right)+\sum _{e\in E_{>}^k}\left|Q\left(e\right)\right|{\displaystyle \frac{K^{\prime }}{c\left(e\right)}}+\sum _{e\in E_{\le }^k}\left|Q\left(e\right)\right|\mathsf{\Delta }u\left(e\right)<B,$$

which contradicts the feasibility of $w_{K^{\prime }}$. Hence, $K^{\ast }$ is the optimal value of the problem MCDSPIT_∞.    □

From the above analysis, we have the following algorithm to solve the problem MCDSPIT_∞.

Theorem 11. 

The problem MCDSPIT_∞ can be solved using Algorithm 2 in $O(nlogn)$ time.

Algorithm 2 $[\overline{w},K^{\ast }]:={\mathrm{MCDSPIT}}_{\infty }(T,Y,w,u,c,D,B)$

Input: The tree $T(V,E)$ rooted at a root node $v_1$,    The set Y of leaf nodes,    The cost vector c,    Two weight vectors w, u,    Given values D and B. Output: An optimal solution $\overline{w}$,     Its relevant objective value $K^{\ast }$.   1: if ${\sum }_{t_k\in Y}u\left(P_k\right)<B$ or ${min}_{t_k\in Y}u\left(P_k\right)<D$ then   2:  return “The problem is infeasible.”   3: else   4:  Call $[\widehat{w},M^{\ast }]:={\mathrm{MCSPIT}}_{\infty }(T,Y,w,u,c,D)$.   5:  if ${\sum }_{t_k\in Y}\overline{w}\left(P_k\right)\ge B$ then   6:   return $(\widehat{w},M^{\ast })$.   7:  end if   8:  Calculate $\mathsf{\Delta }u:=u-w$.   9:  Construct the sequence $\left\{{\beta }_{\widehat{n}}\right\}$ by removing duplicates and values lower than $C\left(\overline{w}\right)$ from sequence (7): $$\overline{K}\le c\left(e_{{\beta }_1}\right)\mathsf{\Delta }u\left(e_{{\beta }_1}\right)<c\left(e_{{\beta }_2}\right)\mathsf{\Delta }u\left(e_{{\beta }_2}\right)<\cdots <c\left(e_{{\beta }_{\widehat{n}}}\right)\mathsf{\Delta }u\left(e_{{\beta }_{\widehat{n}}}\right).$$ 10:  Let $K_0:=\overline{K}$, $K_j:=c\left(e_{{\beta }_j}\right)\mathsf{\Delta }u\left(e_{{\beta }_j}\right)$ for $j:=1,2,\dots ,\widehat{n}$. 11:  Initialize $a:=0$, $b:=\widehat{n}$. 12:  while $b-a>1$ do 13:   $k:=\lfloor {\displaystyle \frac{a+b}{2}}\rfloor$. 14:   Construct $w_{K_k}$ as Formula (17). 15:   if ${\sum }_{t_i\in Y}{w}_{K_k}\left(P_i\right)<B$ then 16:    $a:=k$. 17:   else if ${\sum }_{t_i\in Y}{w}_{K_k}\left(P_i\right)>B$ then 18:    $b:=k$. 19:   end if 20:  end while 21:  Let $k:=a$. 22:  Determine $E_{>}:=\{e\in E\mid c\left(e\right)\mathsf{\Delta }u\left(e\right)>K_k\}$, $E_{\le }:=\{e\in E\mid c\left(e\right)\mathsf{\Delta }u\left(e\right)\le K_k\}$. 23:  Calculate $K^{\ast }$ as Formula (19). 24:  Determine optimal value $w_{K^{\ast }}$ as Formula (17). 25:  return $(w_{K^{\ast }},K^{\ast })$. 26: end if

Proof. 

We analyze the time complexity of Algorithm 2 step by step to establish the $O(nlogn)$ bound. The algorithm begins with a feasibility check in Lines 1–2. This involves computing the sum of path weights ${\sum }_{k\in Y}u\left(P_k\right)$ and finding the minimum path weight ${min}_{k\in Y}u\left(P_k\right)$ over all leaf nodes, which can be obtained from a breadth-first search in $O\left(n\right)$ time. In Line 3, the algorithm calls Algorithm 1 MCSPIT_∞. As established in Theorem 7, Algorithm 1 has a time complexity of $O(nlogn)$, which contributes significantly to the overall complexity.

Lines 4–5 perform a condition check ${\sum }_{k\in Y}\tilde{w}\left(P_k\right)\ge B$ and potentially return early. This operation involves summing path weights for all leaves, requiring $O\left(n\right)$ time. Line 6 calculates the weight difference vector $\mathsf{\Delta }u=u-w$, which is a simple subtraction operation over $O\left(n\right)$ edges, taking $O\left(n\right)$ time. The sequence construction in Lines 7–9 involves sorting and filtering operations. Constructing the sequence $\left\{{\beta }_{\widehat{n}}\right\}$ from the original sequence requires removing duplicates and values below $C\left(\tilde{w}\right)$. The sorting step dominates this process with $O(nlogn)$ time complexity, while the subsequent initialization of $K_j$ values takes $O\left(n\right)$ time.

The core of Algorithm 2 is the binary search loop in Lines 10–20. This loop performs a binary search over the $\widehat{n}$ (which is $O\left(n\right)$) sorted $K_j$ values, resulting in $O(logn)$ iterations. Within each iteration, the algorithm computes the midpoint ($O\left(1\right)$ time); constructs $w_{K_k}$ using Formula (17) which processes $O\left(n\right)$ edges ($O\left(n\right)$ time); and evaluates the condition ${\sum }_{i_l\in Y}{w}_{K_k}\left(P_i\right)$ which requires $O\left(n\right)$ time. Therefore, each iteration takes $O\left(n\right)$ time, and the entire binary search loop requires $O(logn)\times O\left(n\right)=O(nlogn)$ time.

Finally, Lines 21–24 handle the solution construction after the binary search. These steps include simple assignments ($O\left(1\right)$), set operations on edges ($O\left(n\right)$), and calculations using Formulas (19) and (17) ($O\left(n\right)$ each). The total time for these final steps is $O\left(n\right)$. To sum up, the  overall time complexity is dominated by the $O(nlogn)$ operations.    □

5. Computational Experiments

We used synthetic trees and enforced bit-level reproducibility within machine precision across typical environments to demonstrate the efficiency and reproducibility of our experimental results. All randomness was keyed with per-trial seeds, costs were median-normalized so that budget magnitudes do not drift with n, and all targets and path-sum budgets were calibrated on an instance-intrinsic, unit-free scale. These choices ensure that the results are comparable across sizes and that any observed differences reflect algorithmic behavior, not arbitrary units or sampling noise.

Instances were tested in the rooted recursive trees $T=(V,E)$: node i attaches uniformly to $\{1,\dots ,i-1\}$. Each edge e receives a base weight $w\left(e\right)\sim \mathrm{Uniform}[0,1]$ and an available slack $\mathsf{\Delta }u\left(e\right)\sim \mathrm{Uniform}[0,1]$, with the upper bound $u\left(e\right)=w\left(e\right)+\mathsf{\Delta }u\left(e\right)$. Raw costs $c_{\mathrm{raw}}\left(e\right)\sim \mathrm{Uniform}[0.5,2]$ are converted to unit-free costs via median normalization: $c\left(e\right)=c_{\mathrm{raw}}\left(e\right)/\mathrm{median}\left(c_{\mathrm{raw}}\right)$. For a budget $M\ge 0$, upgrading along an edge follows

$$w_M\left(e\right)=w\left(e\right)+min\{M/c\left(e\right),\mathsf{\Delta }u\left(e\right)\},$$

which in turn determines the minimum root–leaf distance $D\left(M\right)$. Let $M_{min}={min}_{e}c\left(e\right)\mathsf{\Delta }u\left(e\right)$ and $M_{max}={max}_{e}c\left(e\right)\mathsf{\Delta }u\left(e\right)$. We set the target distance at the midpoint,

$$D=\frac{1}{2}\left(D\left(M_{min}\right)+D\left(M_{max}\right)\right),$$

and quantify the instance difficulty with

$$\rho ={\displaystyle \frac{D-D\left(M_{min}\right)}{D\left(M_{max}\right)-D\left(M_{min}\right)}}\in (0,1],$$

so that $\rho$ measures how far the target lies between “no upgrades’’ and “maximal upgrades’’ on that specific instance. In the double-constraint setting, we analogously work with the aggregate path sum $S\left(M\right)$. Let $M^{★}$ be the MCSPIT_∞ solution that attains the chosen D, and define   

$$B=\frac{1}{2}\left(S\left(M^{★}\right)+S\left(M_{max}\right)\right),\beta ={\displaystyle \frac{B-S\left(M^{★}\right)}{S\left(M_{max}\right)-S\left(M^{★}\right)}}\in (0,1],$$

which pairs $(\rho ,\beta )$ as difficulty indices for distance and path-sum goals, respectively. Rare degeneracies in which the reachable interval collapses are resolved by a minimal backoff (e.g., $D\leftarrow D\left(M_{max}\right)-{10}^{-6}$). All feasibility checks and accept/reject outcomes were recorded so that third parties can replay the exact run list.

We evaluated the algorithms for the problems MSPIT_∞, MCSPIT_∞, and MCDSPIT_∞. Unless stated otherwise, problem MSPIT_∞ was parameterized by $M=\theta M_{max}$ with $\theta =0.5$ in the main results. Timing isolated the algorithms: instance generation and $(D,B)$ calibration occurred once per trial, after which inputs were frozen. Each routine received a single untimed warm-up call and was then timed with timeit; timed functions contained no internal random draws, guaranteeing byte-identical repeats with a fixed seed. We swept $n\in \{{10}^3,5\times {10}^3,{10}^4,2\times {10}^4,3\times {10}^4,5\times {10}^4\}$; ran 30 trials per size; and report the mean, maximum, and minimum wall-clock seconds in Table 2. To diagnose growth rates, we regressed time on n and on $nlogn$ and report $R^2$ in Table 3.

Table 2. Empirical CPU time (in seconds) for the proposed algorithms on tree instances of varying sizes (n denotes the number of edges). $T_1$, $T_2$, and $T_3$ report the average time for algorithms MSPIT_∞, MCSPIT_∞, and MCDSPIT_∞, respectively. For each algorithm, $T_{max}$ and $T_{min}$ denote the maximum and minimum observed times across test instances.

Complexity	n	1000	5000	10,000	20,000	30,000	50,000
$O\left(n\right)$	$T_1$	0.006	0.027	0.048	0.084	0.121	0.200
	$T_1^{\max }$	0.008	0.031	0.051	0.090	0.131	0.229
	$T_1^{\min }$	0.005	0.025	0.044	0.081	0.113	0.180
$O(nlogn)$	$T_2$	0.145	0.800	1.611	3.148	4.558	7.517
	$T_2^{\max }$	0.225	1.040	1.900	3.580	5.030	8.191
	$T_2^{\min }$	0.072	0.553	1.184	2.517	3.839	5.275
$O(nlogn)$	$T_3$	2.030	9.933	19.516	39.275	59.510	104.171
	$T_3^{\max }$	2.193	10.510	20.551	40.121	61.901	107.392
	$T_3^{\min }$	1.912	9.551	19.027	38.403	58.089	101.737

Table 3. Scaling diagnostics from least-squares fits and log–log slopes.

	${\mathit{R}}^2$ for $\mathit{t}\sim \mathit{an}+\mathit{b}$	${\mathit{R}}^2$ for $\mathit{t}\sim \mathit{a}(\mathit{n}log\mathit{n})+\mathit{b}$	log–log Slope
MSPIT∞	0.9987	0.9961	0.898
MCSPIT∞	0.9996	0.9971	1.007
MCDSPIT∞	0.9989	0.9998	1.001

All artifacts followed a strict provenance protocol. A manifest MANIFEST.csv enumerated every run by $(n,\mathtt{trial}\_\mathtt{id},\mathtt{seed},M,D,B,\rho ,\beta ,D_1,D_{\mathrm{all}},S_0,S_1)$, and optional per-instance .mat files stored $(T,w,u,c,D,B)$ for bit-level reproduction. Experiments were conducted in Matlab R2025a on a laptop (Intel^® Core™ i9-14900HX, 2.20 GHz; Windows 11). Absolute times naturally depend on hardware and BLAS/JIT settings, but our seeded, deterministic protocol ensures that relative comparisons and scaling trends are stable across environments. See the Supplementary Material (“Program_Result”) for the full experiment manifest, fixed seed list, and results for all experiments and figures.

The results align with the intended complexity interpretations. Across a $50\times$ increase in n, MSPIT_∞ grows by $\sim 34\times$, MCSPIT_∞ by $\sim 52\times$, and MCDSPIT_∞ by $\sim 51\times$, indicative of near-linear behavior over our range. Least-squares fits achieve $R^2\ge 0.996$ throughout; the log–log slope is $0.898\approx 1$ for MSPIT_∞ and ≈1.00 for MCSPIT_∞ and MCDSPIT_∞, with the latter showing a mild finite-size preference for $nlogn$ in the parametric regressions (Table 3). Together, these diagnostics suggest $O\left(n\right)$ versus $O(nlogn)$ behavior in practice for the studied algorithms.

The empirical scaling trends are further visualized in Figure 2, where each panel reports the mean CPU time (dots), the min–max range across instances (shaded band), a least-squares linear fit (solid line with $R^2$ value), and a reference curve proportional to the theoretical complexity (dashed line). The figure clearly demonstrates the linear growth for MSPIT_∞ and the $nlogn$ scaling for MCSPIT_∞ and MCDSPIT_∞.

Figure 2. Empirical scaling of the algorithms confirms the theoretical time complexities. CPU time is plotted against instance size n. Dots represent mean execution time, the shaded band shows the min-max range, the solid line is a least-squares fit (with $R^2$ value), and the dashed line is a reference curve proportional to the theoretical complexity ($O\left(n\right)$ for MSPIT_∞, $O(nlogn)$ for the others). The results validate the linear scaling of MSPIT_∞ and the linearithmic scaling of MCSPIT_∞ and MCDSPIT_∞.

Recent work studied related problems for the l₁ norm and Hamming distance. We do not report cross-norm runtime plots because changing the norm (for example, from the infinity norm to the l₁ norm or to Hamming distance) changes the problem class itself and leads to different algorithmic structures and complexity profiles. As is typical in combinatorial optimization, each norm induces its own objective geometry and constraints, which in turn invite specialized methods—for instance, decision-diagram dynamic programming for bottleneck-style objectives versus flow-based, knapsack-like, or budgeted-edit formulations for additive or Hamming-style objectives. Direct wall-clock comparisons across different norms would therefore mix modeling choices with implementation details and hardware/software constants and would not yield a fair apples-to-apples assessment. Our experiments instead focus on validating the predicted scaling behavior for the studied infinity-norm model using a deterministic and reproducible protocol. Table 1 situates the related problem families and summarizes their typical algorithmic landscapes to make the scope of our comparisons explicit.

6. Conclusions and Further Research

Three interdiction problems on trees with the weighted $l_{\infty }$ norm were investigated in this study: the maximum shortest-path interdiction problem MSPIT_∞, its corresponding minimum-cost shortest-path interdiction problem MCSPIT_∞, and the double-interdiction variant MCDSPIT_∞. The problems have wide applications in cybersecurity, logistics, and infrastructure resilience. For MSPIT_∞, we presented a linear-time greedy algorithm. For MCSPIT_∞, we developed an efficient $O(nlogn)$-time algorithm based on greedy selection and binary search. Building on this framework, we extended the methodology to handle the additional constraint in MCDSPIT_∞ and proposed an algorithm with the same asymptotic complexity. Numerical experiments on synthetic instances confirmed the scalability and practical effectiveness of the proposed methods.

Further research is needed to design more advanced approaches for extremely large-scale graphs with millions of edges and nodes, such as graph decomposition, to enhance scalability. It should also be noted that while our algorithms address the interdiction problems with the $l_{\infty }$ norm, they may not directly extend to other norms—a common challenge in combinatorial optimization, where tailored methods are often necessary. Nevertheless, the methodology developed in this work provides a foundation that can be adapted to related interdiction problems in alternative infinite-norm settings.

In summary, a comprehensive and efficient algorithmic framework for solving a class of critical interdiction problems on tree networks was established in this work, providing both theoretical guarantees and practical computational tools. Future research directions include extending the proposed models and algorithms to more general graph classes (e.g., series–parallel graphs or general directed acyclic graphs), as well as developing stochastic and robust variants where edge upgrade costs or capacity bounds are uncertain. Moreover, interdiction problems involving node upgrades—rather than edge upgrades— remain largely unexplored and present both theoretical and computational challenges. Finally, applying these models to real-world domains such as cybersecurity, logistics, and infrastructure resilience represents a promising avenue for empirical validation and practical impact.