Complex Variable Approach for Thermoelastic Boundary Value Problem Using Rational Mapping Techniques
Abstract
1. Introduction
2. Formulation of the Problem
- If and is a particular stress function, the problem indicates the displacement of the first boundary condition (first BVP) [21].
- If and denotes prescribed stress, the problem indicates a second boundary condition (second BVP) [22].Using the Cauchy integral formula, the solution is given by the following:, where includes the known boundary data and thermal terms derived from the boundary condition.
3. Conformal Rational Mapping
- : A translation constant shifts the entire mapped domain in the complex plane and does not introduce any deformation. It is important in relative positioning for multi-body interactions, e.g., tunnels or layered structures.
- : Represents a scaling and rotation. A larger increases the boundary area, potentially diluting stress over a wider zone. Rotation via reorients stress fields relative to thermal gradients.
- : A series of inverse power terms that introduce localized perturbations near the origin , and controls the strength and direction of the deformations such as lobes, bulges, or necking zones. Also, high values create more fine-grained geometric perturbations, useful for modeling engineered surfaces in heat-sensitive components.
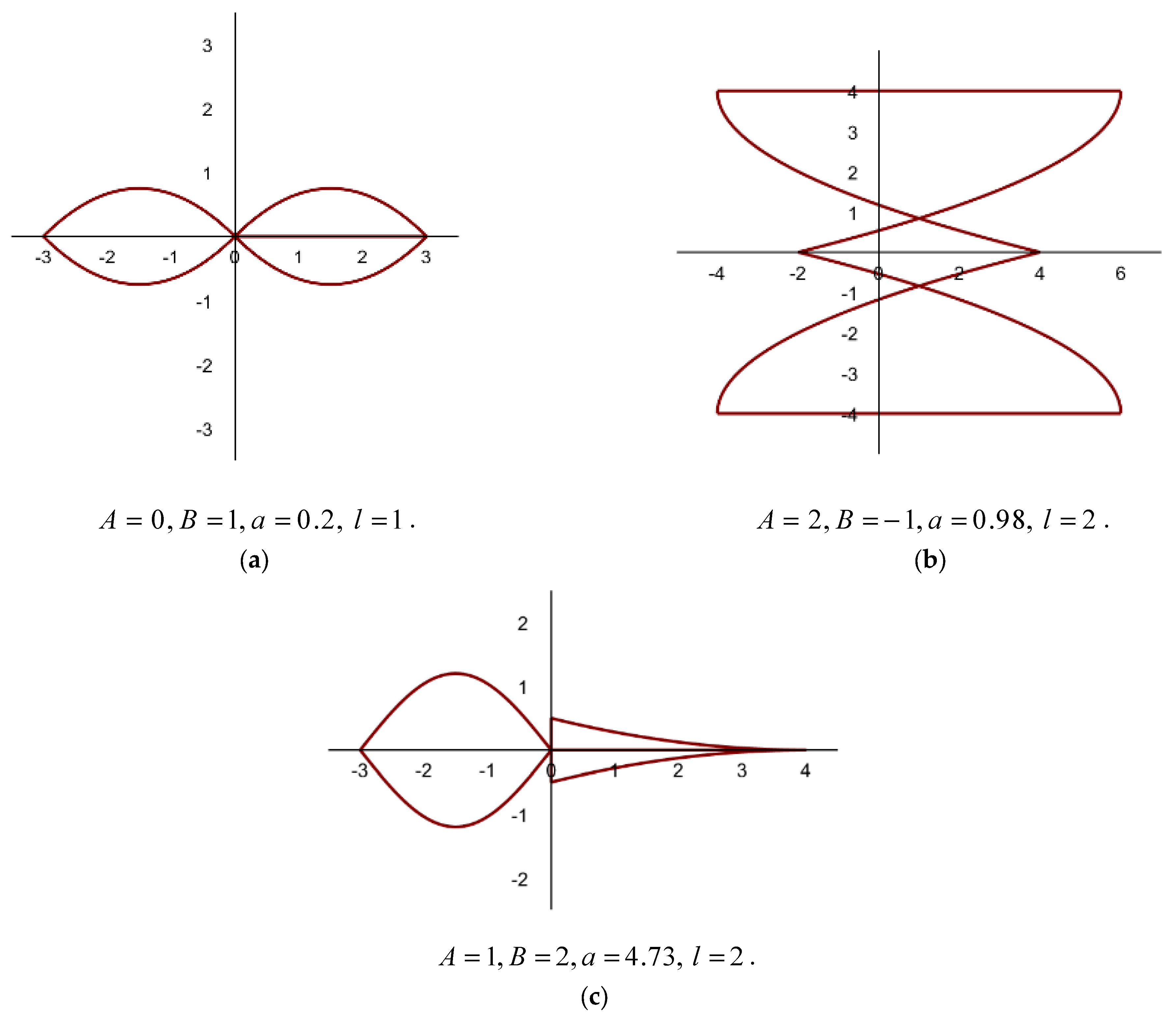
- Case (1): If are fractions and is an integer.
- Case (2): If are integers and is a fraction.
- Case (3): If are integers and is a complex number.
- These figures have smooth, closed, non-circular limits at different levels of symmetry and curvature. As a result of harmonic distortion, they usually show localized bulges, indentations, or lobes. Despite their diversity, each form of Figure 1 has a continuous border without a sharp corner, in particular (c), indicating that they are controlled by complex but fluid boundary transformations.
- The shapes in Figure 2 are curves that feature acute, symmetric, and piecewise-smooth edges that are distinctly non-circular and possess angular points. All shapes have a central axis, usually the horizontal axis, which suggests that they are mirror images of each other along one or both coordinate axes.
- The shapes in Figure 3 represent open curves that are smooth and symmetric and are spread out along the horizontal x-axis. These curves oscillate with decreasing amplitudes and commonly form lobes on both sides of the origin, especially Figure 3d, while others have smooth curves and gradual changes.
4. Complex Variable Approach
4.1. Series Representation of Gaursat Functions
4.2. Projection Method
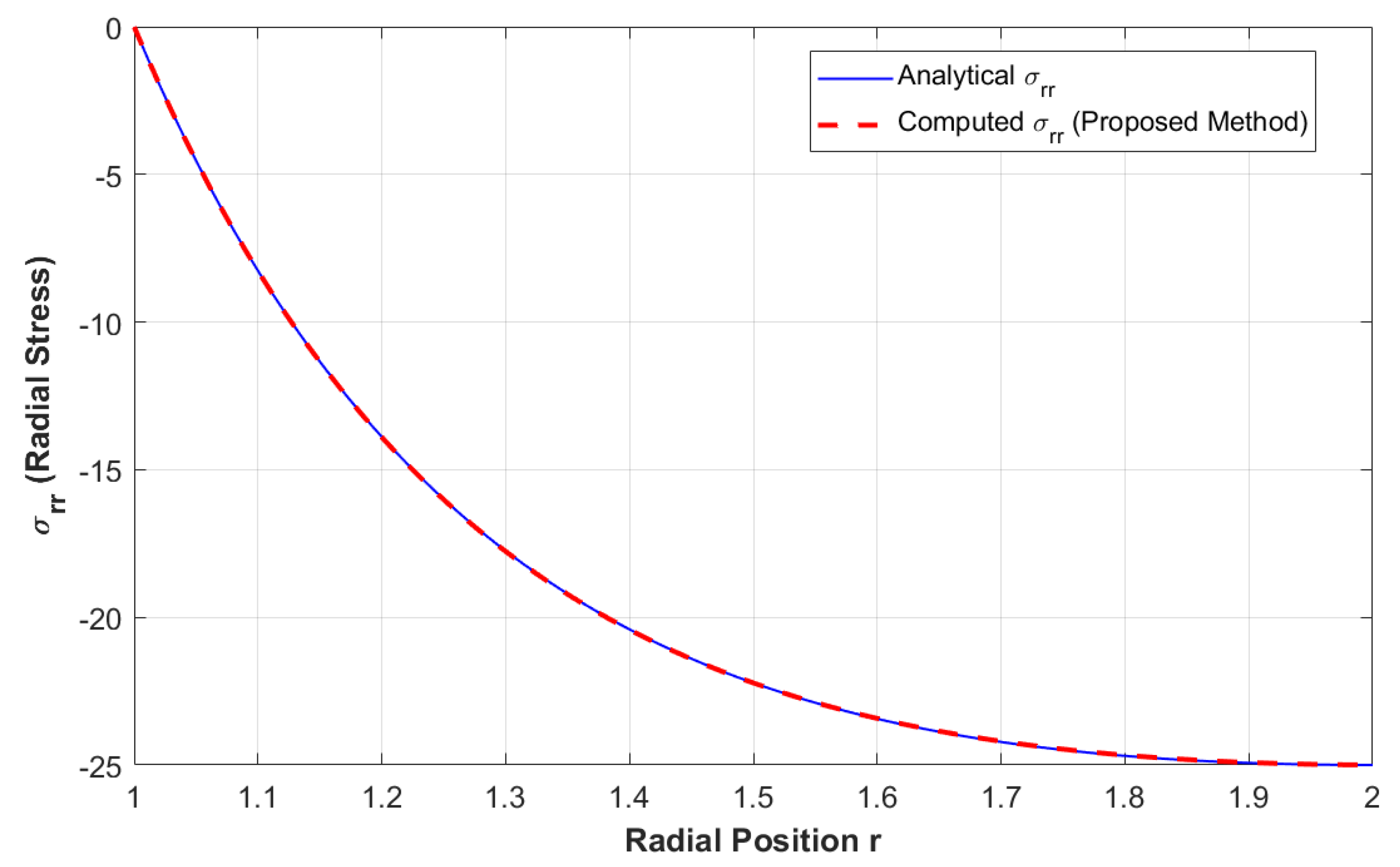
5. Application: Thermoelastic Stress in a Circular Annulus Under Radial Thermal Gradient
Discussion
- In Figure 5, showing the distribution behavior of , the inner boundary wants to expand radially, creating radial tension near the x-axis and compressive regions further out. The distribution behavior of is similar in structure to but rotated by 90°; tends to mirror but with slight differences due to the directionality of stress paths. The distribution behavior of components, representing the maximum shear, often appears near the “diagonal” directions (45°, 135°). Due to temperature gradients, different ring sectors want to move in different directions, producing internal shearing.
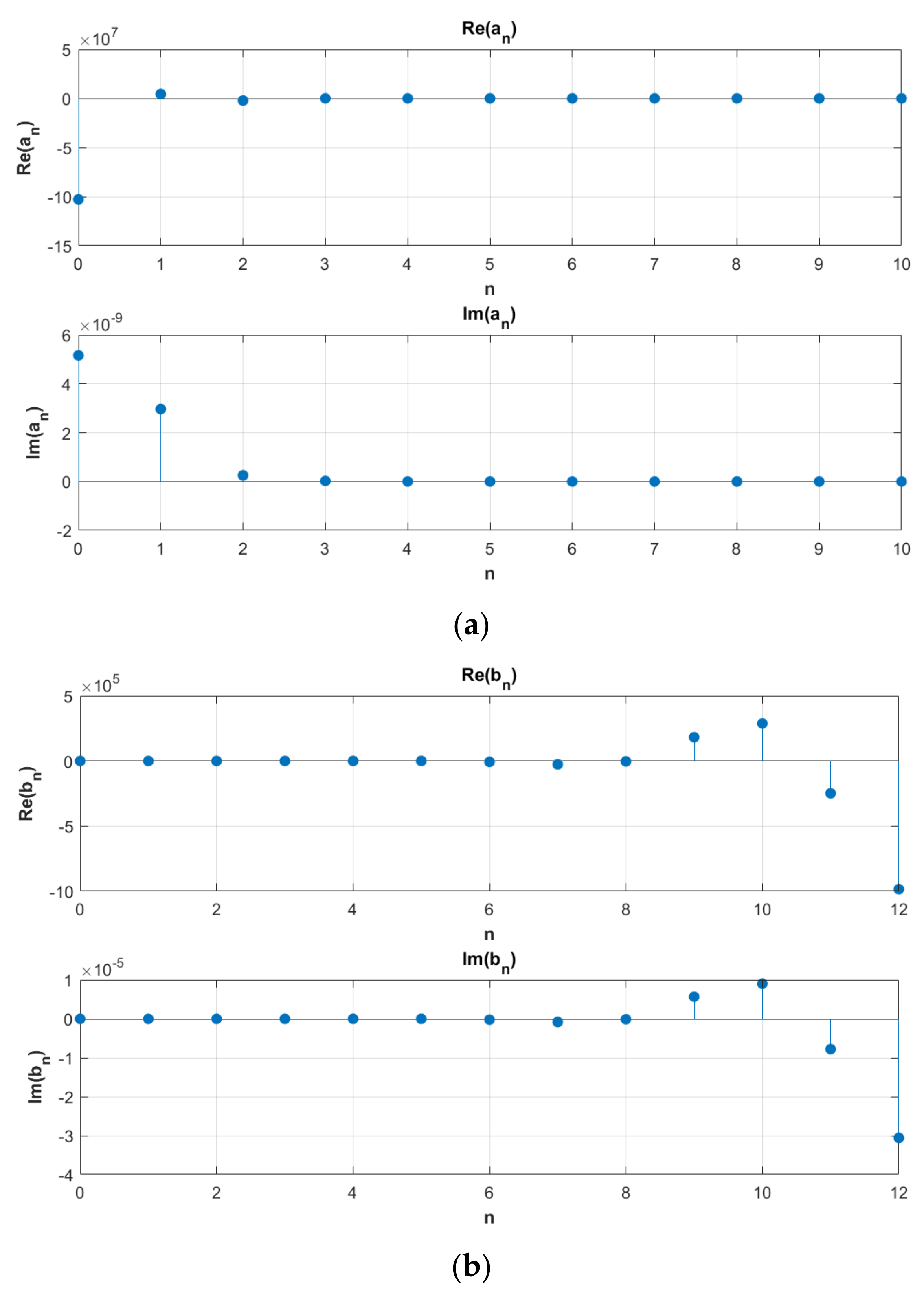
- In Figure 6a, real parts of typically peak at low values (), indicating the dominance of lower-order harmonics; imaginary parts are generally small or decay rapidly unless torsional or asymmetric loading is present. Figure 6b shows the real parts of that are usually smaller than those of , but are still meaningful in thermoelastic analyses. Imaginary components of become prominent in asymmetric geometries for .
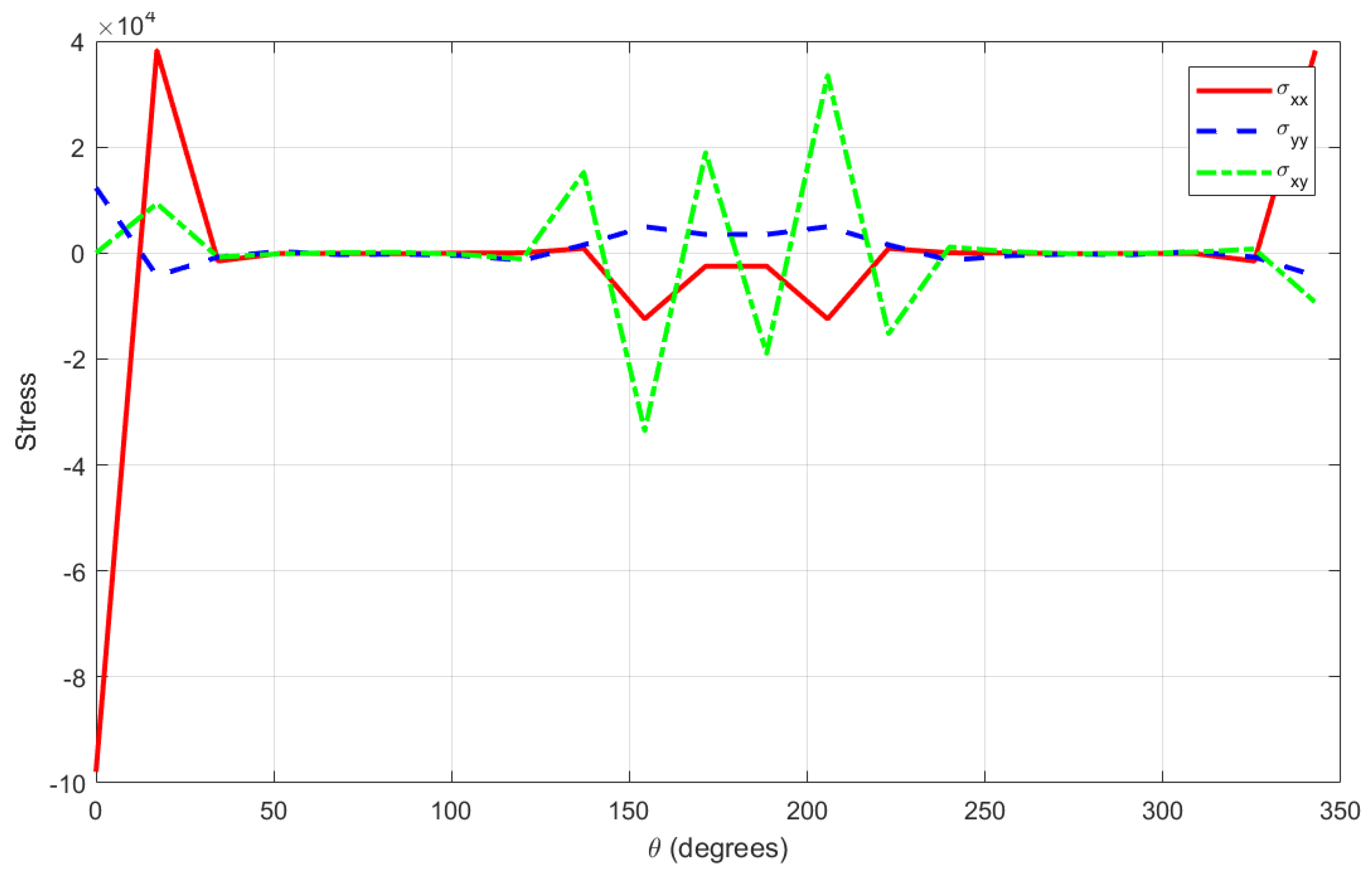
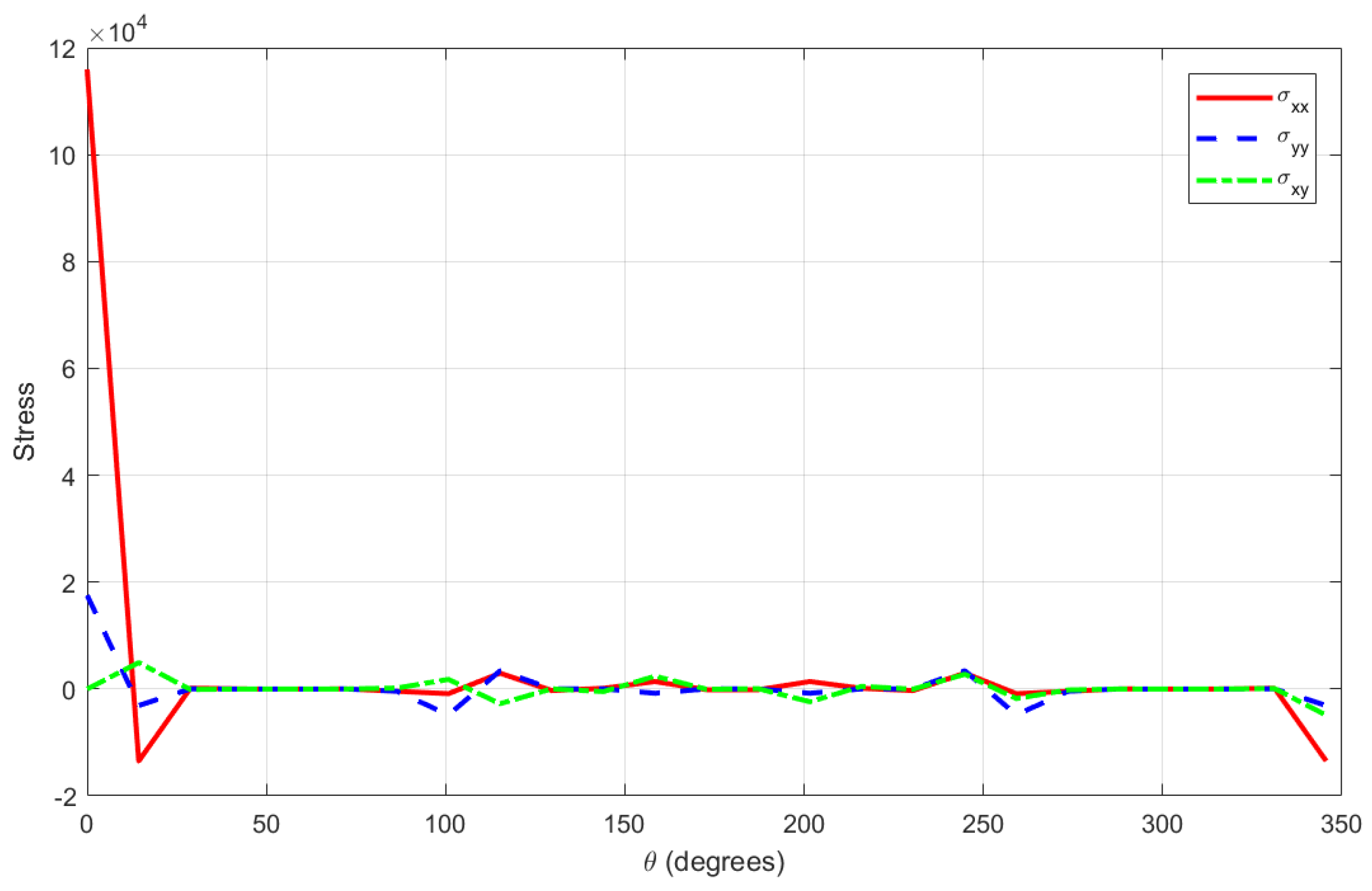
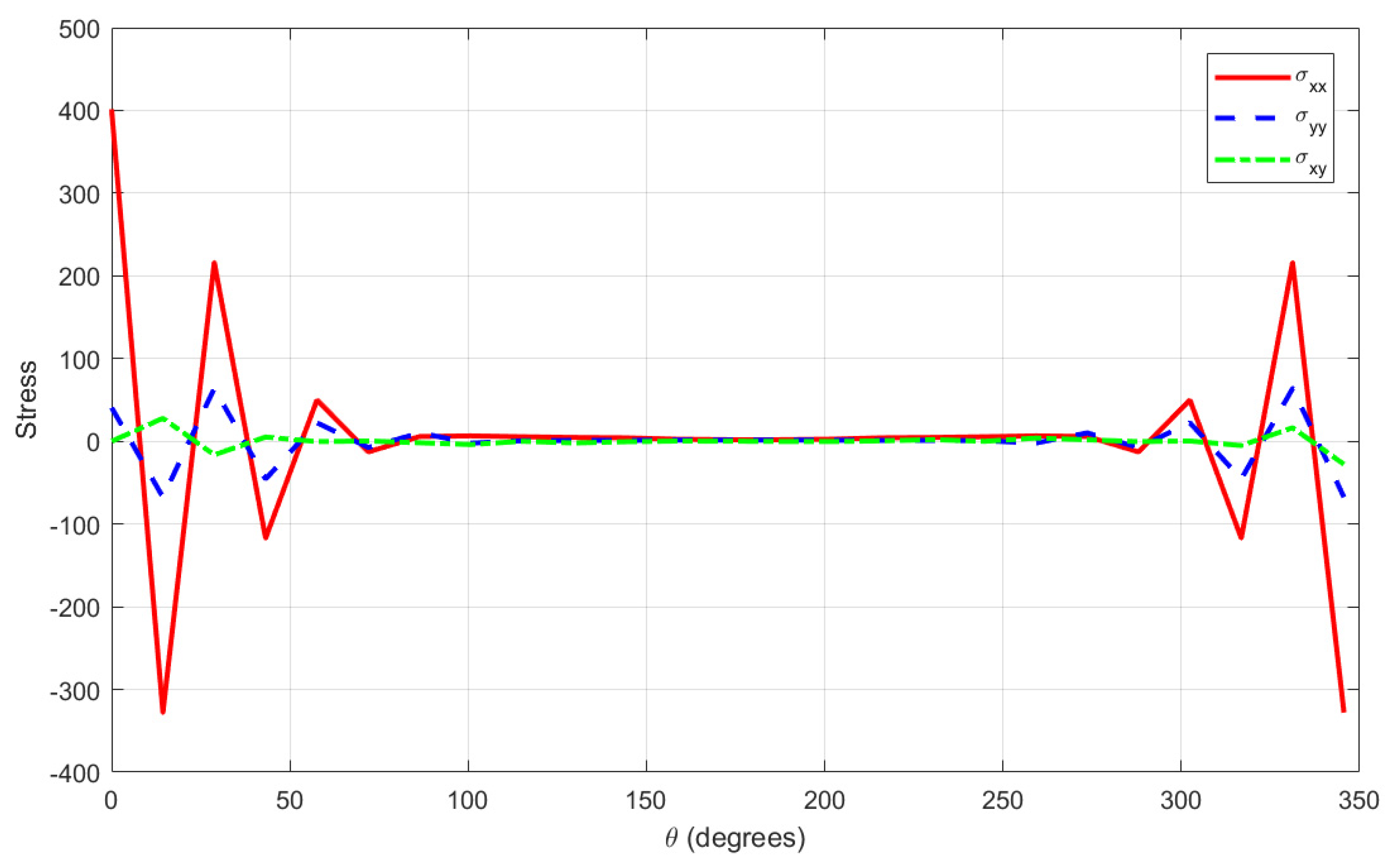
- The variation in each stress component around the annular boundary is shown in Figure 7, Figure 8 and Figure 9. Figure 7 shows a high perturbation and strong thermal gradient, and exhibits extremely high positive and negative peaks, particularly near and , indicating strong stress concentrations due to boundary lobes or sharp geometry. is smoother and oscillates slightly around a small positive value. has periodic fluctuations of moderate magnitude. Figure 8 shows mild perturbation and a weak thermal gradient; displays a notable initial spike but remains significantly lower overall, while and are very smooth, showing a low magnitude and being nearly flat across the boundary. Figure 9 shows an intermediate case, with having medium peaks and alternating, but not extreme, positive and negative values and and being bounded, smooth, and consistent.
- Table 2 refers to when we fixed and varied in the range between 25 and 60 for each value of . We computed the resulting stress fields and over the same physical geometry; the maximum relative difference in stress magnitudes between successive values of was found to decrease significantly, reaching less than 0.5% for , indicating a stable convergence.
- Acccording to Table 3, an elevation in Young’s modulus from 50 GPa to 200 GPa results in an approximate quadrupling of both and , in accordance with the linear elasticity principle that stress is directly proportional to stiffness. Fluctuations in Poisson’s ratio ranging from 0.2 to 0.4 result in minor alterations in while causing a significant redistribution of , indicating the increased impact of transverse coupling effects on thermal strain transfer in curved geometries. Conversely, increasing the thermal expansion coefficient from to leads to an approximate threefold escalation in both and , thereby confirming the direct proportionality between thermal stress and under constrained boundary conditions.
6. Conclusions
- Stress concentrations near the inner radius may be critical; the design must consider material yield strength (Figure 6).
- The stem plots of and in Figure 5 indicate a harmonic contribution to the stress field that arises from the first few harmonic terms, especially for . Thermal effects embedded in are more subtle but still influence the stress field meaningfully.
- We examined the residual norm for increasing truncation orders for as shown in Table 1. These results confirm the reliability of our method and endorse the application of mild truncation rules for precise practical computations.
- Table 3 shows how stress distributions evolve with varying material constants; these data generally indicate that and govern the overall stress magnitude, but exerts a secondary, although substantial, influence on the stress distribution.
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Muskhelishvili, N. Basic equations of the plane theory of elasticity. In Some Basic Problems of the Mathematical Theory of Elasticity: Fundamental Equations Plane Theory of Elasticity Torsion and Bending; Springer: Berlin/Heidelberg, Germany, 1977; pp. 89–104. [Google Scholar]
- Rubenfeld, L.A. A First Course in Applied Complex Variables; Dover Publications: New York, NY, USA, 1985. [Google Scholar]
- Erfanian, M.; Zeidabadi, H.; Mehri, R. Solving two-dimensional nonlinear volterra integral equations using rationalized haar functions in the complex plane. Adv. Sci. Eng. Med. 2020, 12, 409–415. [Google Scholar] [CrossRef]
- Carloni, C.; Piva, A.; Viola, E. An alternative complex variable formulation for an inclined crack in an orthotropic medium. Eng. Fract. Mech. 2003, 70, 2033–2058. [Google Scholar] [CrossRef]
- Schinzinger, R.; Laura, P.A. Conformal Mapping: Methods and Applications; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Al-Bugami, A. Numerical Treating of Mixed Integral Equation Two--Dimensional in Surface Cracks in Finite Layers of Materials. Adv. Math. Phys. 2022, 2022, 3398175. [Google Scholar] [CrossRef]
- Abdou, M. Fredholm–Volterra integral equation with singular kernel. Appl. Math. Comput. 2003, 137, 231–243. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Abdou, M.; Soliman, A. Solvability of quadratic integral equations with singular kernel. J. Contemp. Math. Anal. (Armen. Acad. Sci.) 2022, 57, 12–25. [Google Scholar]
- Abdou, M.A.; Jan, A.R. An infinite elastic plate weakened by a generalized curvilinear hole and Goursat functions. Appl. Math. 2014, 5, 728–743. [Google Scholar] [CrossRef][Green Version]
- Alhazmi, S.E.; Abdou, M.; Basseem, M. The stresses components in position and time of weakened plate with two holes conformally mapped into a unit circle by a conformal mapping with complex constant coefficients. AIMS Math 2023, 8, 11095–11112. [Google Scholar] [CrossRef]
- Jafari, M. Thermal stress analysis of orthotropic plate containing a rectangular hole using complex variable method. Eur. J. Mech. -A/Solids 2019, 73, 212–223. [Google Scholar] [CrossRef]
- Grigorenko, A.Y.; Pankrat’ev, S. Stress–strain state of complex-shaped orthotropic plates under variable load. Int. Appl. Mech. 2018, 54, 411–417. [Google Scholar] [CrossRef]
- Khechai, A.; Layachi, M.; Belarbi, M.-O.; Gohery, S.; Layachi, S.; Ruocco, E.; Gemi, L.; Liang, Q.Q. An extended Greszczuk’s analytical method for stress analysis of unsymmetrical laminated composite plates with a circular hole under axial, biaxial, and shear loads. Structures 2025, 71, 108169. [Google Scholar] [CrossRef]
- Gonenli, C.; Das, O. Free vibration analysis of circular and annular thin plates based on crack characteristics. Rep. Mech. Eng. 2022, 3, 158–167. [Google Scholar] [CrossRef]
- Șeremet, V.; Crețu, I. New Green’s functions for a thermoelastic unbounded parallelepiped under a point heat source and their application. Acta Mech. 2023, 234, 6515–6528. [Google Scholar] [CrossRef]
- Hetnarski, R.B.; Ignaczak, J. Mathematical theory of elasticity. J. Therm. Stress. 2006, 29, 505–506. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Alhendi, N.G. Influence of Heat Transfer on Stress Components in Metallic Plates Weakened by Multi-Curved Holes. Axioms 2025, 14, 369. [Google Scholar] [CrossRef]
- Mao, S.; Liu, W.; Zhou, T.; Xue, C.; Wei, D. Steady-state and transient thermal–hydraulic analysis for high temperature heat pipe cooled reactors. Nucl. Eng. Des. 2023, 412, 112479. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Liu, W.; Ma, Z. Unloading and reloading stress-strain relationship of recycled aggregate concrete reinforced with steel/polypropylene fibers under uniaxial low-cycle loadings. Cem. Concr. Compos. 2022, 131, 104597. [Google Scholar] [CrossRef]
- Abouelregal, A.E. Generalized thermoelastic MGT model for a functionally graded heterogeneous unbounded medium containing a spherical hole. Eur. Phys. J. Plus 2022, 137, 953. [Google Scholar] [CrossRef]
- Abdullaev, V.; Aida-Zade, K. Numerical method of solution to loaded nonlocal boundary value problems for ordinary differential equations. Comput. Math. Math. Phys. 2014, 54, 1096–1109. [Google Scholar] [CrossRef]
- Lamichhane, B.P.; Lindstrom, S.B.; Sims, B. Application of projection algorithms to differential equations: Boundary value problems. ANZIAM J. 2019, 61, 23–46. [Google Scholar]
- El-sirafy, I.H. Goursat Functions of Thermoelastic Problem of an Infinite Plate with Hypitrochoidal Hole. In Encyclopedia of Thermal Stresses; Springer: Berlin/Heidelberg, Germany, 2014; pp. 2006–2012. [Google Scholar]
- Bhullar, S.; Wegner, J. Thermal stresses in a plate with hyperelliptical hole. J. Eng. Technol. Res. 2009, 1, 152–170. [Google Scholar]
- Gavrilov, S.N.; Krivtsov, A.M. Steady-state kinetic temperature distribution in a two-dimensional square harmonic scalar lattice lying in a viscous environment and subjected to a point heat source. Contin. Mech. Thermodyn. 2020, 32, 41–61. [Google Scholar] [CrossRef]
- Filipov, S.M.; Gospodinov, I.D.; Faragó, I. Shooting-projection method for two-point boundary value problems. Appl. Math. Lett. 2017, 72, 10–15. [Google Scholar] [CrossRef]
- Alsulaiman, R.E.; Abdou, M.A.; ElBorai, M.M.; El-Sayed, W.G.; Youssef, E.M.; Taha, M. Qualitative Analysis for Solving a Fractional Integro-Differential Equation of Hyperbolic Type with Numerical Treatment Using the Lerch Matrix Collocation Method. Fractal Fract. 2023, 7, 599. [Google Scholar] [CrossRef]
- Mortari, D. Least-squares solution of linear differential equations. Mathematics 2017, 5, 48. [Google Scholar] [CrossRef]
- Solhi, E.; Mirzaee, F.; Naserifar, S. Enhanced moving least squares method for solving the stochastic fractional Volterra integro-differential equations of Hammerstein type. Numer. Algorithms 2024, 95, 1921–1951. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A. Elastic and Thermoelastic Problems in Nonlinear Dynamics of Structural Members; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
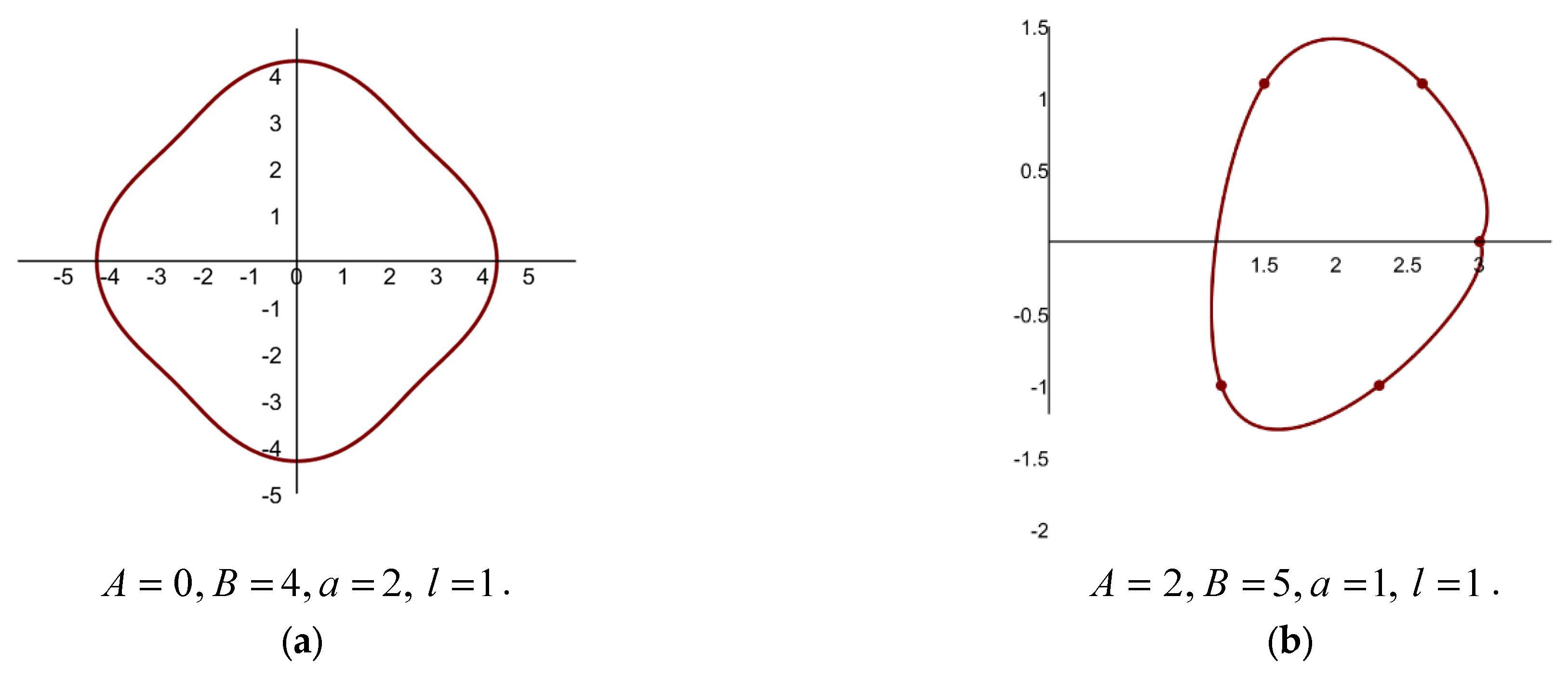
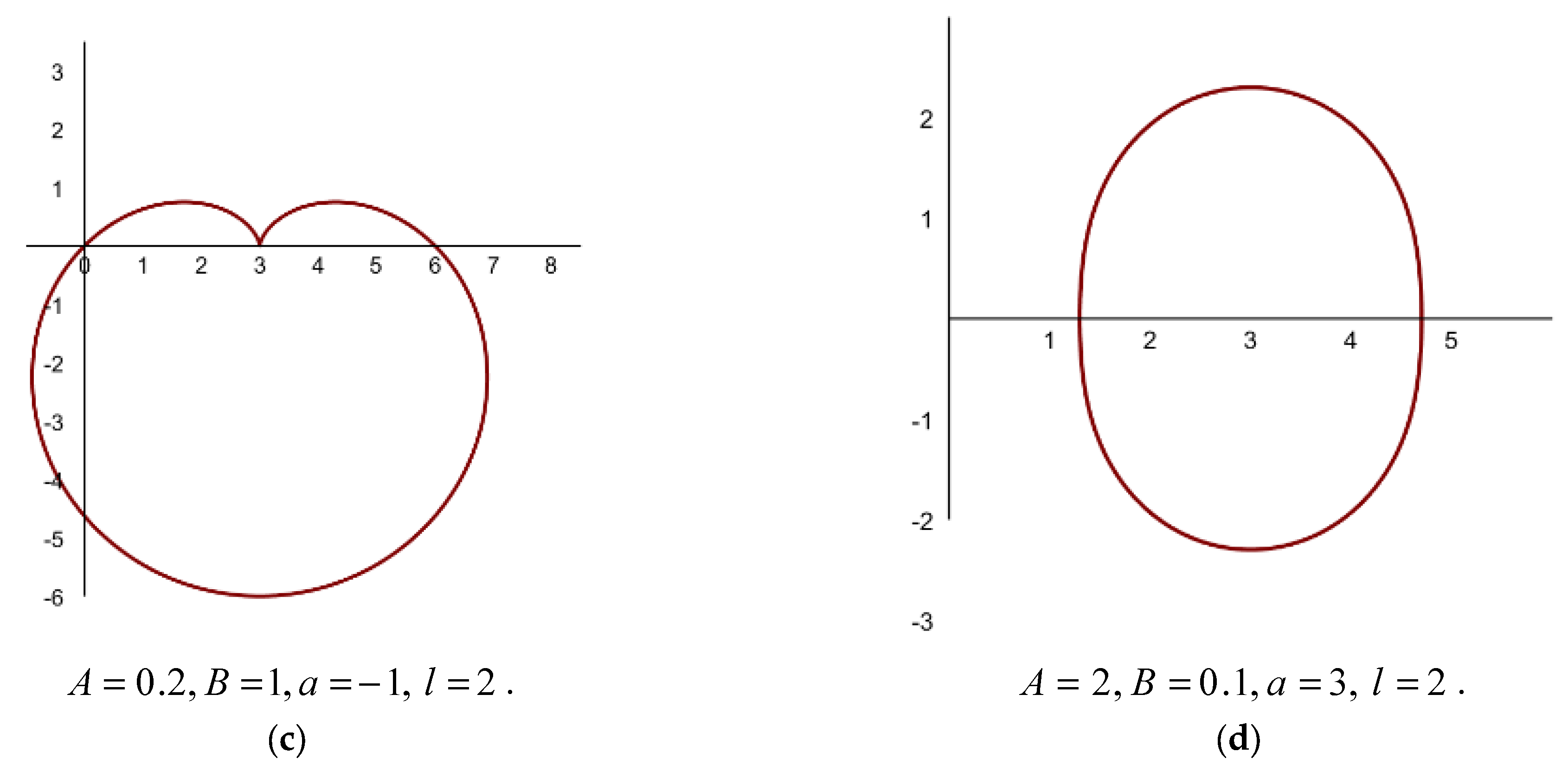



| Truncation Order | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
|---|---|---|---|---|---|---|---|
| Residual norm |
| Max. Difference vs. Prev. | |||
|---|---|---|---|
| 25 | 1.822 | 2.115 | – |
| 30 | 1.823 | 2.114 | 0.07% |
| 40 | 1.824 | 2.114 | 0.05% |
| 50 | 1.824 | 2.114 | 0.01% |
| 60 | 1.824 | 2.114 | <0.01% |
| Material Parameter | Value Range | Max σ_xx | Max σ_yy |
|---|---|---|---|
| E (GPa) | 50–200 | ↑ Linear (×4) | ↑ Linear (×4) |
| ν | 0.2–0.4 | Moderate variation | Noticeable redistribution |
| α (1/K) | 1 × 10−5–3 × 10−5 | ↑ ×3 | ↑ ×3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taha, M.; Abdou, M.A.; Shammaky, A.E.; Al-Dohiman, A.A.; Youssef, E.M. Complex Variable Approach for Thermoelastic Boundary Value Problem Using Rational Mapping Techniques. Mathematics 2025, 13, 3218. https://doi.org/10.3390/math13193218
Taha M, Abdou MA, Shammaky AE, Al-Dohiman AA, Youssef EM. Complex Variable Approach for Thermoelastic Boundary Value Problem Using Rational Mapping Techniques. Mathematics. 2025; 13(19):3218. https://doi.org/10.3390/math13193218
Chicago/Turabian StyleTaha, Mai, Mohamed A. Abdou, Amnah E. Shammaky, Abeer A. Al-Dohiman, and Eslam M. Youssef. 2025. "Complex Variable Approach for Thermoelastic Boundary Value Problem Using Rational Mapping Techniques" Mathematics 13, no. 19: 3218. https://doi.org/10.3390/math13193218
APA StyleTaha, M., Abdou, M. A., Shammaky, A. E., Al-Dohiman, A. A., & Youssef, E. M. (2025). Complex Variable Approach for Thermoelastic Boundary Value Problem Using Rational Mapping Techniques. Mathematics, 13(19), 3218. https://doi.org/10.3390/math13193218








