Multiple Positive Solutions of Nabla Fractional Equations with Summation Boundaries
Abstract
1. Introduction
2. Preliminaries
- (a)
- for and for ;
- (b)
- is decreasing in s for ζ in , . Moreover, it is increasing in ζ for ζ in , ;
- (c)
- .
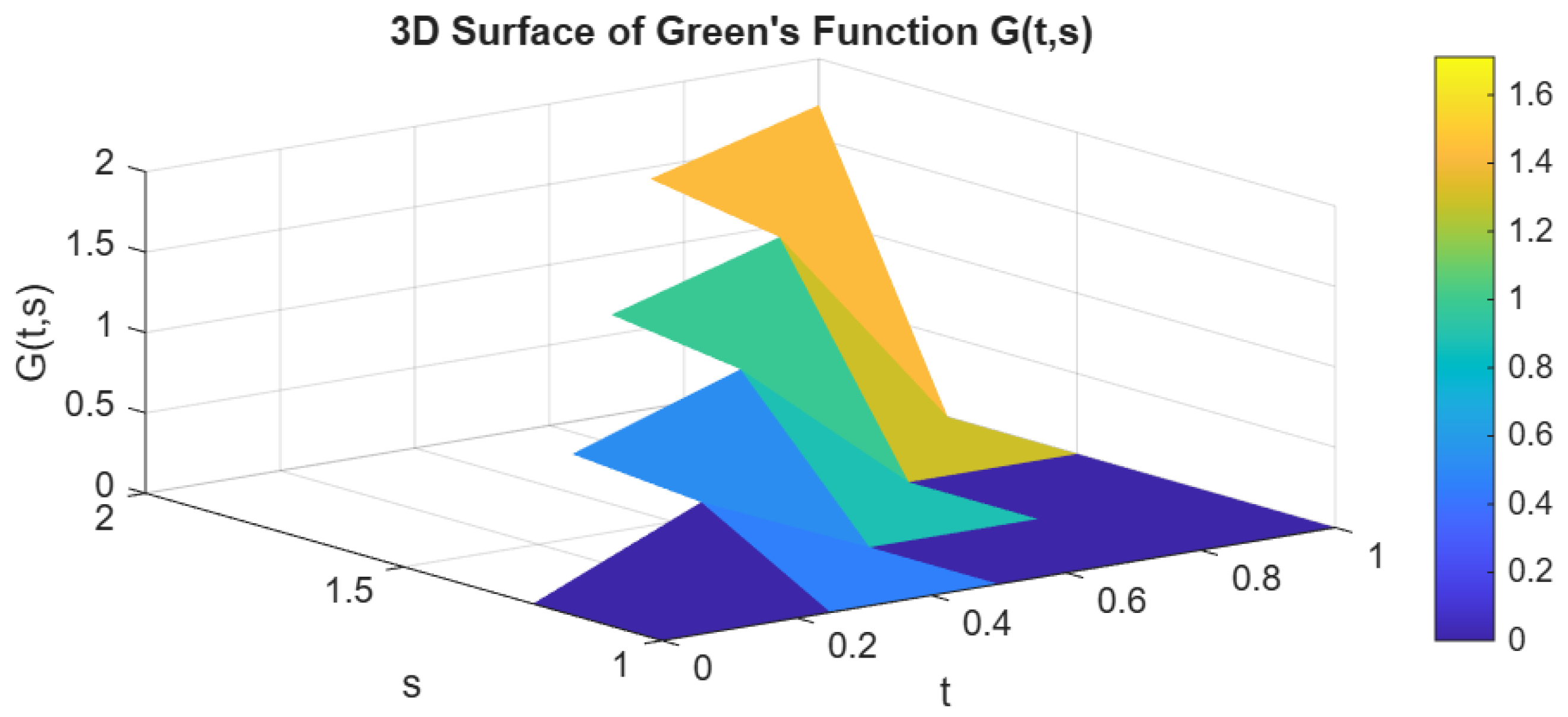
3. Green’s Function
4. Positive Solutions
- (A1)
- for and ;
- (A2)
- for and ,
- (B1)
- for and ;
- (B2)
- for and ,
5. Multiplicity Results
- (F1)
- for , and ;
- (F2)
- for , and ;
6. Examples
- (B1)
- for and ;
- (B2)
- for and ,
- (F11)
- for and ;
- (F12)
- for and ;
- (F2)
- for and ,
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Ferreira, R.A.C. Discrete Fractional Calculus and Fractional Difference Equations; Springer Briefs in Mathematics; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999. [Google Scholar]
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales: An Introduction with Applications, 1st ed.; Springer Science & Business Media: Boston, MA, USA, 2001. [Google Scholar]
- Hossein, H.; Zakieh, A.; Praveen, A.; Samrad, M.; Ebadi, M.J.; Shafi, D.M.; Eskandar, N. A study on fractional tumor-immune interaction model related to lung cancer via generalized Laguerre polynomials. BMC Med. Res. Methodol. 2023, 23, 189. [Google Scholar] [CrossRef]
- Ebadi, M. A Novel Approach to Nonlinear 2D Fractional Optimal Control Problems Via Generalized Lerch Polynomials. Math. Methods Appl. Sci. 2025, 48, 12738–12748. [Google Scholar] [CrossRef]
- Abdeljawad, T. On delta and nabla Caputo fractional differences and dual identities. Discret. Dyn. Nat. Soc. 2013, 2013, 406910. [Google Scholar] [CrossRef]
- Jia, B.; Erbe, L.; Peterson, A.C. Two monotonicity results for nabla and delta fractional differences. Arch. Math. 2015, 104, 589–597. [Google Scholar] [CrossRef]
- Jia, B.; Erbe, L.; Peterson, A. Convexity for nabla and delta fractional differences. J. Differ. Equ. Appl. 2015, 21, 360–373. [Google Scholar]
- Anastassiou, G.A. Nabla discrete fractional calculus and nabla inequalities. Math. Comput. Model. 2010, 51, 562–571. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Existence and uniqueness of solutions for nonlinear Caputo fractional difference equations. Turkish J. Math. 2020, 44, 857–869. [Google Scholar] [CrossRef]
- Ahrendt, K.; Kissler, C. Green’s function for higher-order boundary value problems involving a nabla Caputo fractional operator. J. Differ. Equ. Appl. 2019, 25, 788–800. [Google Scholar] [CrossRef]
- Ikram, A. Lyapunov inequalities for nabla Caputo boundary value problems. J. Differ. Equ. Appl. 2019, 25, 757–775. [Google Scholar] [CrossRef]
- Almusawa, M.Y.; Mohammed, P.O. Approximation of sequential fractional systems of Liouville-Caputo type by discrete delta difference operators. Chaos Solitons Fractals 2023, 176, 114098. [Google Scholar] [CrossRef]
- Peterson, A.; Hu, W. Caputo Nabla Fractional Boundary Value Problems. In Progress on Difference Equations and Discrete Dynamical Systems; Baigent, S., Bohner, M., Elaydi, S., Eds.; ICDEA 2019; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2020; Volume 341. [Google Scholar]
- Ardjouni, A.; Boulares, H.; Djoudi, A. Stability of nonlinear neutral nabla fractional difference equations. Commun. Optim. Theory 2018, 2018, 8. [Google Scholar]
- Atici, F.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 2009, 1–12. [Google Scholar] [CrossRef]
- Atici, F.; Eloe, P.W. Linear systems of fractional nabla difference equations. Rocky Mt. J. Math. 2011, 41, 353–370. [Google Scholar] [CrossRef]
- Ahrendt, K.; Castle, L.; Holm, M.; Yochman, K. Laplace transforms for the nabla-difference operator and a fractional variation of parameters formula. Commun. Appl. Anal. 2012, 16, 317–348. [Google Scholar]
- Bastos, N.; Torres, D. Combined delta-nabla sum operator in discrete fractional calculus. arXiv 2010, arXiv:1009.3883. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Atici, F.M. On the definitions of nabla fractional operators. Abstr. Appl. Anal. 2012, 2012, 406757. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Foundations of nabla fractional calculus on time scales and inequalities. Comput. Math. Appl. 2010, 59, 3750–3762. [Google Scholar] [CrossRef]
- Dassios, I.K.; Baleanu, D.I. On a singular system of fractional nabla difference equations with boundary conditions. Bound. Value Probl. 2013, 2013, 148. [Google Scholar] [CrossRef]
- Dimitrov, N.D.; Jonnalagadda, J.M. Existence of positive solutions for a class of nabla fractional boundary value problems. Fractal Fract. 2025, 9, 131. [Google Scholar] [CrossRef]
- Costabile, F.A.; Napoli, A. A multipoint Birkhoff type boundary value problem. J. Numer. Math. 2015, 23, 1–11. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. Fractional difference calculus. In Univalent Functions, Fractional Calculus and Their Applications; Ellis Horwood: Chichester, UK, 1989; pp. 139–152. [Google Scholar]
- Shah, K.; Abdalla, B.; Abdeljawad, T.; Gul, R. Analysis of multipoint impulsive problem of fractional-order differential equations. Bound Value Probl. 2023, 2023, 1. [Google Scholar] [CrossRef]
- Pu, R.; Zhang, X.Q.; Cui, Y.J.; Li, P.L.; Wang, W.W. Positive solutions for singular semipositone fractional differential equation subject to multipoint boundary conditions. J. Funct. Spaces 2017, 2017, 5892616. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, Y. Positive solutions for multipoint boundary value problem of fractional differential equations. J. Appl. Math. Comput. 2012, 38, 417–427. [Google Scholar] [CrossRef]
- Sevinik-Adıgüzel, R.; Aksoy, Ü.; Karapınar, E.; Erhan, İ.M. Uniqueness of solution for higher-order nonlinear fractional differential equations with multi-point and integral boundary conditions. RACSAM 2021, 115, 155. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Y.; Guan, Y.; Li, W. Stability analysis of multi-point boundary conditions for fractional differential equation with non-instantaneous integral impulse. Math. Biosci. Eng. 2023, 20, 7020–7041. [Google Scholar] [CrossRef]
- Al-khateeb, A.; Zureigat, H.; Ala’yed, O.; Bawaneh, S. Ulam–Hyers Stability and Uniqueness for Nonlinear Sequential Fractional Differential Equations Involving Integral Boundary Conditions. Fractal Fract. 2021, 5, 235. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Baleanu, D.; Rezapour, S.; Salehi, S. The existence of solutions for some fractional finite difference equations via sum boundary conditions. Adv. Differ. Equ. 2014, 2014, 282. [Google Scholar] [CrossRef]
- Haider, S.S.; Rehman, M.U. Ulam–Hyers–Rassias Stability and Existence of Solutions to Nonlinear Fractional Difference Equations with Multipoint Summation Boundary Condition. Acta Math. Sci. 2020, 40, 589–602. [Google Scholar] [CrossRef]
- Dimitrov, N.D.; Jonnalagadda, J.M. Existence, uniqueness and stability of solutions of a nabla fractional difference equations. Fractal Fract. 2024, 8, 591. [Google Scholar] [CrossRef]
- Dimitrov, N.D.; Jonnalagadda, J.M. Existence of Solutions for a Class of Nabla Fractional Difference Equations with Parameter Dependent Summation Boundary Conditions. Fractal Fract. 2025, 9, 513. [Google Scholar] [CrossRef]
- Agarwal, R.; Meehan, M.; O’Regan, D. Fixed Point Theory and Applications; Cambridge Univ. Press: Cambridge, UK, 2001. [Google Scholar]
- Cabada, A.; Dimitrov, N. Existence of solutions of nth-order nonlinear difference equations with general boundary conditions. Acta Math. Sci. 2020, 40, 226–236. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrov, N.D.; Jonnalagadda, J.M. Multiple Positive Solutions of Nabla Fractional Equations with Summation Boundaries. Mathematics 2025, 13, 3210. https://doi.org/10.3390/math13193210
Dimitrov ND, Jonnalagadda JM. Multiple Positive Solutions of Nabla Fractional Equations with Summation Boundaries. Mathematics. 2025; 13(19):3210. https://doi.org/10.3390/math13193210
Chicago/Turabian StyleDimitrov, Nikolay D., and Jagan Mohan Jonnalagadda. 2025. "Multiple Positive Solutions of Nabla Fractional Equations with Summation Boundaries" Mathematics 13, no. 19: 3210. https://doi.org/10.3390/math13193210
APA StyleDimitrov, N. D., & Jonnalagadda, J. M. (2025). Multiple Positive Solutions of Nabla Fractional Equations with Summation Boundaries. Mathematics, 13(19), 3210. https://doi.org/10.3390/math13193210





