Multiple Positive Solutions of Nabla Fractional Equations with Summation Boundaries

Abstract

The current work studies difference problems including two different nabla operators coupled with general summation boundary conditions that depend on a parameter. After we deduce the Green’s function, we obtain an interval of the parameter, where it is strictly positive. Then, we establish a lower and upper bound of the related Green’s function and we impose suitable conditions of the nonlinear part, under which, using the classical Guo–Krasnoselskii fixed point theorem, we deduce the existence of at least one positive solution of the studied equation. After that, we impose more restricted conditions on the right-hand side and we obtain the existence of n positive solutions again using fixed point theory, which is the main novelty of this research. Finally, we give particular examples as an application of our theoretical findings.

1. Introduction

In order to describe more precisely the dynamic of complex systems, more models of fractional order have emerged, and some previously given of integer order have been modified to fractional-order models. They have applications in numerous branches of engineering and science, such as signal processing, control theory, and mathematical modeling of phenomena in economics, biology, and physics, where discrete events or data points are paramount. We recommend to the reader References [1,2,3,4] for a detailed introduction to discrete fractional calculus and References [5,6] for some recent results in this direction.

Lately, interest in discrete fractional problems has surged [7,8,9,10]. Consequently, many articles on this topic appeared for both delta problems and nabla problems with Liouville–Caputo [11,12,13,14,15] or Riemann–Liouville operators [16,17,18] under different boundary conditions. In particular, some of the first works with nabla operators are referred to in [19,20,21,22,23].

Recently, in Ref. [24], the authors managed to ensure the existence results for the problem with two different nabla operators

$$\begin{array}{c}-\left({\nabla }_{d_1-1}^{\nu }w\right)\left(\zeta \right)=\lambda \mathfrak{f}\left(\zeta \right)g\left(w\left(\zeta \right)\right),\zeta \in {\mathbb{N}}_{d_1+2}^{d_2},\\ w\left(d_1\right)=\left({\nabla }_{d_1-1}^{\mu }w\right)\left(d_2\right)=0,\end{array}$$

where $\mathfrak{f}:{\mathbb{N}}_{d_1+2}^{d_2}\to (0,\infty )$ and $g:[0,\infty )\to [0,\infty )$ are continuous functions, and $0\le \mu \le 1<\nu <2$.

Since many mathematical models in different science areas and engineering areas, like elasticity, railway systems, power networks, telecommunication lines, thermodynamics, and others, may be expressed as multi-point boundary value problems [25,26,27,28,29] or problems with integral boundary conditions [30,31,32], the interest in studying such discrete fractional problems has increased lately. However, while there are a few results for discrete delta problems [33,34], for nabla fractional problems, similar results are almost not available. To the best of our knowledge, there are only two results about nabla problems with summation conditions. First, in Ref. [35], the following nabla problem

$$\begin{array}{c}-\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=\mathfrak{f}\left(\zeta ,w(\zeta \right)),1<\eta \le 2,\zeta \in {\mathbb{N}}_{k+2}^l,\\ w\left(k\right)=C,w\left(l\right)+\mu \sum _{s=k+1}^{l-1}w\left(s\right)=D,\mu >0,\end{array}$$

was studied and the authors managed to deduce existence, uniqueness, and stability results. This was the first result about a fractional problem with summation conditions in the nabla sense. We point out that no results about the the Green’s function’s sign were obtained, and the authors of the above work only managed to obtain the existence of a sign-changing solution based on the fact that the Green’s function there was also sign-changing.

In Ref. [36], it was found that the problem

$$\begin{array}{c}-\left({\nabla }_{k-1}^{\eta }w\right)\left(\zeta \right)=\mathfrak{f}\left(\zeta ,w(\zeta \right)),1<\eta \le 2,\zeta \in {\mathbb{N}}_{k+2}^l,\\ w\left(k\right)=0,w\left(l\right)=\mu \sum _{s=k+1}^{d}w\left(s\right),d\in {\mathbb{N}}_{k+1}^{l-1},\mu >0,\end{array}$$

admits a positive solution in a given interval, where $\mathfrak{f}:{\mathbb{N}}_{k+2}^l\times \mathbb{R}\to \mathbb{R}$ is a continuous function.

As we mentioned above, continuous fractional calculus has been well studied, but discrete versions, especially nabla-based, are more recent and still developing. Thus, studying nabla fractional problems is crucial both from a theoretical and applied perspective since it generalizes the concept of discrete difference equations by allowing non-integer order differences, and while delta fractional models are more commonly studied, nabla equations are often more appropriate when modeling is based on past data. The chosen methodology is commonly used along with variational methods, but the results obtained using fixed point theory allow us to prove existence under minimal assumptions, which is the main reason for us to choose such an approach.

For example, in economics, the economic behaviors often depend not just on current values but also on past states (e.g., inflation, investment, consumption). This is one of the main reasons why financial markets are often modeled in discrete time and nabla fractional models allow better modeling of volatility clustering, mean reversion, and memory-dependent risk. Time-series forecasting in stock markets using this methodology to incorporate past market trends is more effective.

The goal in this work is to expand the previously mentioned theoretical findings as we establish multiplicity results of the discrete nabla fractional problem

$$\begin{array}{c}-\left({\nabla }_{\rho \left(a\right)}^{\nu }u\right)\left(t\right)=\mathfrak{f}(t,u\left(t\right)),t\in {\mathbb{N}}_{a+2}^b,\end{array}$$

(1)

$$\begin{array}{c}u\left(a\right)=0,\left({\nabla }_{\rho \left(a\right)}^{\mu }u\right)\left(b\right)=\lambda \sum _{s=a+1}^{d}u\left(s\right),d\in {\mathbb{N}}_{a+1}^{b-1},\lambda >0,\end{array}$$

(2)

by an application of Guo–Krasnoselskii’s theorem as we deduce the existence of at least n positive solutions of the considered problems (1) and (2), with n being an arbitrary positive integer.

Above a and $b\in \mathbb{R}$ with $b-a\in {\mathbb{N}}_3$; $\mathfrak{f}:{\mathbb{N}}_{a+2}^b\times [0,\infty )\to [0,\infty )$ is a continuous function, $0<\mu <\nu -1<1$; ${\nabla }_{\rho \left(a\right)}^{\gamma }u$ is the ${\gamma }^{\mathrm{th}}$-order difference of u in the Riemann–Liouville sense, where $\gamma \in \{\nu ,\mu \}$.

We point out that this is the first research on a nabla fractional problem with summation boundary conditions where multiplicity results are deduced, which we might highlight as the main novelty. Usually, the existence results in such articles are based on the bounded Green’s function that might change sign, and as a result, the obtained solutions are also sign-changing. However, we manage to show that the related Green’s function is strictly positive in a given subinterval of the parameter, which allows us to obtain the existence of strictly positive solutions of the considered problem under some suitable conditions. Additionally, the multiplicity results in this direction almost every time show the existence of at least two or three positive solutions, based on some classical fixed point theorems, while we are able to deduce the existence of n positive solutions. Moreover, the boundary conditions include a second nabla operator and they are much more general than the ones in the above-mentioned papers. Apart from this theoretical achievement, our work also has real-world implications since usually positive solutions show outcomes that stay positive, such as population levels, disease counts, etc. In epidemiology, nabla fractional equations can represent memory effects in discrete-time disease models like the well-known SIR-type models that describe how infectious diseases spread through the population. For example, memory represents the lasting effects of immunity or past infection. Summation boundary conditions could represent average infection rates over time, while multiplicity means the same public health measures could lead to different disease spread scenarios depending on initial infection patterns. However, the current manuscript focuses mainly on the theoretical approach of this problem.

The manuscript has the following organization. In Section 2 we recall the preliminaries of this work. After that, in Section 3 we deduce the Green’s function, and obtain an interval of the parameter $\lambda$, where it is strictly positive, and deduce a lower and upper bound of it. Then, in Section 4, under some sufficient conditions, we obtain an existence result for (1) and (2) by using Guo–Krasnoselskii’s theorem. In Section 5, we deduce that (1) and (2) admit multiple positive solutions. Finally, we give some applications of our new theoretical results in Section 6, as we provide a few examples there, while in Section 7, we give a brief summary of our novel results in this work as well as offering some possible ideas for future work.

We add the schematic diagram in Figure 1 for a better illustration of the organization of this work mentioned above.

Figure 1. Schematic diagram of the organization of this article.

2. Preliminaries

To complete this work, we are going to use the notations and definitions given in [1]. Denote ${\mathbb{N}}_e=\{e,e+1,e+2,\dots \}$ and ${\mathbb{N}}_e^f=\{e,e+1,e+2,\dots ,f\}$ for any real e and f such that $f-e\in {\mathbb{N}}_1$.

Definition 1

([1]). For any a, $b\in \mathbb{R}$, the generalized rising function is

$$a^{\overline{b}}={\displaystyle \frac{\Gamma (a+b)}{\Gamma \left(a\right)}}.$$

Definition 2

([1]). For $\beta \in \mathbb{R}\setminus {\mathbb{Z}}^{-}$, the ${\beta }^{\mathrm{th}}$ fractional Taylor monomial in the nabla sense is

$$H_{\beta }(\zeta ,k)={\displaystyle \frac{{(\zeta -k)}^{\overline{\beta }}}{\Gamma (\beta +1)}}.$$

Lemma 1

([1,13]). For s in ${\mathbb{N}}_k$ and $\mu >-1$,

(a)

$H_{\mu }(\zeta ,s-1)\ge 0$ for $\zeta \in {\mathbb{N}}_{s-1}$ and $H_{\mu }(\zeta ,s-1)>0$ for $\zeta \in {\mathbb{N}}_s$;

(b)

$H_{\mu }(\zeta ,s-1)$ is decreasing in s for ζ in ${\mathbb{N}}_{s-1}$, $\mu >0$. Moreover, it is increasing in ζ for ζ in ${\mathbb{N}}_s$, $\mu >0$;

(c)

${\displaystyle H_{\mu }(\zeta ,k)-H_{\mu -1}(\zeta ,k)=H_{\mu }(\zeta ,k+1)}$.

Finally, let us recall the generalized power rule

Lemma 2

([1]). For $t\in {\mathbb{N}}_a$

$${\nabla }_a^{\nu }{H}_{\mu }(t,a)=H_{\mu -\nu }(t,a),$$

where $\nu \in {\mathbb{R}}^{+},\mu \in \mathbb{R}$ such that $\nu +\mu$ and $\mu -\nu$ are nonnegative.

Our main tool for all of our results will be the classical Guo–Krasnoselskii’s fixed point theorem in cones [37].

Theorem 1.

Let $B=\left(B,\parallel ·\parallel \right)$ be a Banach space, and let $K\subseteq B$ be a cone. Assume that ${\Omega }_1$ and ${\Omega }_2$ are bounded open subsets contained in B such that $0\in$ ${\Omega }_1$ and ${\Omega }_1\subseteq$${\Omega }_2$. Assume further that $T:K\cap \left(\overline{{\Omega }_2} \setminus {\Omega }_1\right)\to K$ is a completely continuous operator. Here, either

(i) $∥Ty∥\le ∥y∥$ for $y\in K\cap \partial {\Omega }_1$, and $∥Ty∥\ge ∥y∥$ for $y\in K\cap \partial {\Omega }_2$; or

(ii) $∥Ty∥\ge ∥y∥$ for $y\in K\cap \partial {\Omega }_1$, and $∥Ty∥\le ∥y∥$ for $y\in K\cap \partial {\Omega }_2$.

Then, T has at least one fixed point in $K\cap \left(\overline{{\Omega }_2} \setminus {\Omega }_1\right).$

3. Green’s Function

First, we are going to study the linear problem

$$-\left({\nabla }_{\rho \left(a\right)}^{\nu }u\right)\left(t\right)=h\left(t\right),t\in {\mathbb{N}}_{a+2}^b,$$

(3)

coupled with conditions (2) assuming that $0<\mu <\nu -1<1$ and $h:{\mathbb{N}}_{a+2}^b\to \mathbb{R}$. Set

$$\Omega =H_{\nu -\mu -1}(b,a)-\lambda H_{\nu }(d,a).$$

Theorem 2.

Assume $\Omega \ne 0$. For the linear problem (3)–(2), the expression

$$u\left(t\right)=\sum _{s=a+2}^{b}G(t,s)h\left(s\right),$$

(4)

for $t\in {\mathbb{N}}_a^b$, is the unique solution, as

$$G(t,s)=\left\{\begin{array}{c}{G}_1(t,s),s\le min\{t,d\},\hfill \\ G_2(t,s),s\in {\mathbb{N}}_{t+1}^d,\hfill \\ G_3(t,s),s\in {\mathbb{N}}_{d+1}^t,\hfill \\ G_4(t,s),s\ge max\{t+1,d+1\},\hfill \end{array}\right.$$

(5)

with

$$G_1(t,s)={\displaystyle \frac{H_{\nu -1}(t,a)H_{\nu -\mu -1}(b,\rho \left(s\right))}{\Omega }}-{\displaystyle \frac{\lambda H_{\nu -1}(t,a)H_{\nu }(d,\rho \left(s\right))}{\Omega }}-H_{\nu -1}(t,\rho \left(s\right)),$$

$$G_2(t,s)={\displaystyle \frac{H_{\nu -1}(t,a)H_{\nu -\mu -1}(b,\rho \left(s\right))}{\Omega }}-{\displaystyle \frac{\lambda H_{\nu -1}(t,a)H_{\nu }(d,\rho \left(s\right))}{\Omega }},$$

$$G_3(t,s)={\displaystyle \frac{H_{\nu -1}(t,a)H_{\nu -\mu -1}(b,\rho \left(s\right))}{\Omega }}-H_{\nu -1}(t,\rho \left(s\right))$$

and

$$G_4(t,s)={\displaystyle \frac{H_{\nu -1}(t,a)H_{\nu -\mu -1}(b,\rho \left(s\right))}{\Omega }}.$$

Proof. 

It is well known that (3) is equivalent to

$$u\left(t\right)=C_1{H}_{\nu -1}(t,\rho \left(a\right))+C_2{H}_{\nu -2}(t,\rho \left(a\right))-\sum _{s=a+2}^t{H}_{\nu -1}(t,\rho \left(s\right))h\left(s\right),t\in {\mathbb{N}}_a^b.$$

(6)

Using the first boundary condition $u\left(a\right)=0$ in the above Equation (6), we get

$$C_1+C_2=0.$$

(7)

Next, applying ${\nabla }_{\rho \left(a\right)}^{\mu }$ on both sides of (6) and using Lemma 2, we deduce

$$\begin{array}{c}\left({\nabla }_{\rho \left(a\right)}^{\mu }u\right)\left(t\right)=C_1{H}_{\nu -\mu -1}(t,\rho \left(a\right))+C_2{H}_{\nu -\mu -2}(t,\rho \left(a\right))\hfill \\ \hfill -\sum _{s=a+2}^t{H}_{\nu -\mu -1}(t,\rho \left(s\right))h\left(s\right),t\in {\mathbb{N}}_a^b.\end{array}$$

(8)

From the second boundary condition $\left({\nabla }_{\rho \left(a\right)}^{\mu }u\right)\left(b\right)=\lambda {\sum }_{s=a}^{d}u\left(s\right)$ and (6)–(8), we obtain

$$\begin{array}{c}{C}_1{H}_{\nu -\mu -1}(b,\rho \left(a\right))+C_2{H}_{\nu -\mu -2}(b,\rho \left(a\right))-\sum _{s=a+2}^b{H}_{\nu -\mu -1}(b,\rho \left(s\right))h\left(s\right)\hfill \\ \hfill =\lambda \sum _{s=a}^d\left[C_1{H}_{\nu -1}(s,\rho \left(a\right))+C_2{H}_{\nu -2}(s,\rho \left(a\right))-\sum _{r=a+2}^s{H}_{\nu -1}(s,\rho \left(r\right))h\left(r\right)\right].\end{array}$$

(9)

Now, after solving the linear system of (7) and (9) and simplifying, we have

$$C_1={\displaystyle \frac{1}{\Omega }}\left[\sum _{s=a+2}^b{H}_{\nu -\mu -1}(b,\rho \left(s\right))h\left(s\right)-\lambda \sum _{s=a+2}^d{H}_{\nu }(d,\rho \left(s\right))h\left(s\right)\right]$$

(10)

and

$$C_2=-{\displaystyle \frac{1}{\Omega }}\left[\sum _{s=a+2}^b{H}_{\nu -\mu -1}(b,\rho \left(s\right))h\left(s\right)-\lambda \sum _{s=a+2}^d{H}_{\nu }(d,\rho \left(s\right))h\left(s\right)\right].$$

(11)

Substituting the equalities (10) and (11) in (6), we obtain (4). □

Now, in the following interval of the parameter $\lambda$, we deduce our first new result.

Theorem 3.

Let

$${\displaystyle \frac{\nu -\mu -1}{2}}\le \lambda <{\displaystyle \frac{H_{\nu -\mu -1}\left(b,a\right)}{H_{\nu }\left(d,a\right)}},$$

(12)

then $G\left(t,s\right)$ is positive for all $\left(t,s\right)$ in ${\mathbb{N}}_{a+1}^b\times {\mathbb{N}}_{a+2}^b.$

Proof. 

From (5), using the expressions of the related Green’s function in all four possible cases, we have

$$G_1\left(t,s\right)<G_i\left(t,s\right),i=2,3,4,$$

$\left(t,s\right)$ in ${\mathbb{N}}_{a+1}^b\times {\mathbb{N}}_{a+2}^b$. Thus, we only need to check that $G_1\left(t,s\right)$ is positive in order to have $G\left(t,s\right)$ as positive for all $\left(t,s\right)$ in ${\mathbb{N}}_{a+1}^b\times {\mathbb{N}}_{a+2}^b.$ Note that the second inequality

$$\lambda <{\displaystyle \frac{H_{\nu -\mu -1}\left(b,a\right)}{H_{\nu }\left(d,a\right)}}$$

ensures us that $\Omega >0.$ Moreover, let us define the function

$$\varphi \left(s\right)=-\lambda H_{\nu }\left(d,\rho \left(s\right)\right)+H_{\nu -\mu -1}\left(b,\rho \left(s\right)\right),s\in {\mathbb{N}}_{a+2}^d.$$

One can show that $\varphi$ is an increasing function on ${\mathbb{N}}_{a+2}^d$. Indeed, a simple computation gives us

$$\begin{array}{ccc}\hfill \left(\nabla \varphi \right)\left(s\right)& =& -H_{\nu -\mu -2}\left(b+1,s-1\right)+\lambda H_{\nu -1}\left(d+1,s-1\right)\hfill \\ & \ge & -H_{\nu -\mu -2}\left(d+2,s-1\right)+\lambda H_{\nu -\mu -1}\left(d+1,s-1\right)\hfill \\ & =& {\displaystyle \frac{\Gamma \left(d-s+\nu -\mu +1\right)}{\Gamma \left(\nu -\mu -1\right)\Gamma \left(d-s+2\right)}}\left(-{\displaystyle \frac{1}{d-s+2}}+\lambda {\displaystyle \frac{1}{\nu -\mu -1}}\right)\hfill \\ & \ge & {\displaystyle \frac{\Gamma \left(d-s+\nu -\mu +1\right)}{\Gamma \left(\nu -\mu -1\right)\Gamma \left(d-b+3\right)}}\left(-{\displaystyle \frac{1}{2}}+\lambda {\displaystyle \frac{1}{\nu -\mu -1}}\right)\hfill \\ & \ge & 0,\hfill \end{array}$$

for $s\in {\mathbb{N}}_{a+3}^d$. Note that using Lemma 1, one can verify that

$$\begin{array}{ccc}\hfill G_1\left(t,s\right)& =& {\displaystyle \frac{H_{\nu -1}\left(t,a\right)\varphi \left(s\right)-H_{\nu -1}\left(t,s-1\right)\varphi \left(a+1\right)}{\Omega }}\hfill \\ & >& {\displaystyle \frac{H_{\nu -1}\left(t,s-1\right)}{\Omega }}\left(\varphi \left(s\right)-\varphi \left(a+1\right)\right)\hfill \\ & >& 0,\hfill \end{array}$$

(13)

which proves our claim since we have already shown that $\Omega >0$ and $\varphi$ is an increasing function, meaning that $\varphi \left(s\right)-\varphi \left(a+1\right)>0$. □

Theorem 4.

Assume that condition (12) holds. Then,

$$G(t,s)\in \left[g_1\left(s\right),g_2\left(s\right)\right],\left(t,s\right)\in {\mathbb{N}}_{a+1}^b\times {\mathbb{N}}_{a+2}^b,$$

(14)

with

$$g_1\left(s\right)=G_1\left(s,s\right),s\in {\mathbb{N}}_{a+1}^b,$$

and

$$g_2\left(s\right)={\displaystyle \frac{H_{\nu -1}(b,a)}{\Omega }}\times H_{\nu -\mu -1}(b,\rho \left(s\right)),s\in {\mathbb{N}}_{a+2}^b.$$

Proof. 

From (5), it is clear that

$$G_1\left(t,s\right)<G_i\left(t,s\right)<G_4\left(t,s\right),i=2,3,\left(t,s\right)\in {\mathbb{N}}_{a+1}^b\times {\mathbb{N}}_{a+2}^b.$$

Moreover, from (13), we have that

$$G_1\left(t,s\right)={\displaystyle \frac{H_{\nu -1}\left(t,a\right)\varphi \left(s\right)-H_{\nu -1}\left(t,s-1\right)\varphi \left(a+1\right)}{\Omega }}.$$

For s in ${\mathbb{N}}_{a+2}^b$, we have

$${\nabla }_t{G}_1\left(t,s\right)={\displaystyle \frac{H_{\nu -2}\left(t,a\right)\varphi \left(s\right)+H_{\nu -2}\left(t+1,s-1\right)\varphi \left(a+1\right)}{\Omega }},t\in {\mathbb{N}}_{a+2}^b.$$

From Theorem 3, we have that $\Omega >0$ and $\varphi \left(s\right)>0$ for all $s\in {\mathbb{N}}_{a+1}^b$. Moreover, from Lemma 1, we have that both $H_{\nu -2}\left(t+1,a\right)>0$ and $H_{\nu -2}\left(t+1,s-1\right)>0$ for $\left(t,s\right)$ in ${\mathbb{N}}_{a+2}^b\times {\mathbb{N}}_{a+2}^b$ with $s\le t$, which implies ${\nabla }_t{G}_1\left(t,s\right)>0$ for all $\left(t,s\right)$ in ${\mathbb{N}}_{a+2}^b\times {\mathbb{N}}_{a+2}^b$ with $s\le t$. Consequently, we have

$$G_1\left(t,s\right)\ge G_1\left(s,s\right)=g_1\left(s\right),s\in {\mathbb{N}}_{a+2}^b.$$

Finally, from the expression of $G_4\left(t,s\right)$ and Lemma 1 it is clear that $H_{\nu -1}\left(t,a\right)<H_{\nu -1}\left(b,a\right)$, giving us that

$$G_4\left(t,s\right)\le g_2\left(s\right).$$

Consequently, we obtain (14). □

4. Positive Solutions

With regard to this article, we assume that condition (12) holds. Set

$${\mathfrak{f}}_0=\underset{\xi \to 0^{+}}{lim}{\displaystyle \frac{\mathfrak{f}(t,\xi )}{\xi }},{\mathfrak{f}}_{\infty }=\underset{\xi \to +\infty }{lim}{\displaystyle \frac{\mathfrak{f}(t,\xi )}{\xi }},$$

for all $t\in {\mathbb{N}}_{a+2}^b$.

Theorem 2 implies the equivalence between the solutions of (1) and (2) and

$$u\left(t\right)=\sum _{s=a+2}^{b}G(t,s)\mathfrak{f}(s,u\left(s\right)),t\in {\mathbb{N}}_a^b.$$

Consider $(b-a+1)$-dimensional Banach space

$$\mathcal{B}=\left\{u:{\mathbb{N}}_a^b\to \mathbb{R}|u\left(a\right)=0,\left({\nabla }_{\rho \left(a\right)}^{\mu }u\right)\left(b\right)=\lambda \sum _{s=a+1}^{d}u\left(s\right),d\in {\mathbb{N}}_{a+1}^{b-1},\lambda >0\right\},$$

coupled with

$$∥u∥=\underset{t\in {\mathbb{N}}_a^b}{max}\left|u\left(t\right)\right|,$$

and cone

$$\mathcal{P}=\left\{u\in \mathcal{B}:u\left(t\right)\ge 0,t\in {\mathbb{N}}_a^b;u\left(t\right)\ge {\displaystyle \frac{L_1}{L_2}}∥u∥,t\in {\mathbb{N}}_{a+1}^b\right\},$$

where

$$L_1=\underset{s\in {\mathbb{N}}_{a+2}^b}{min}{g}_1\left(s\right)>0,L_2=\underset{s\in {\mathbb{N}}_{a+2}^b}{max}{g}_2\left(s\right)>0.$$

Let $S:\mathcal{B}\to \mathcal{B}$ be defined as

$$\left(Su\right)\left(t\right)=\sum _{s=a+2}^{b}G(t,s)\mathfrak{f}(s,u\left(s\right)),t\in {\mathbb{N}}_a^b.$$

(15)

Clearly, u is a fixed point of S if and only if u is a solution of (1) and (2).

Lemma 3.

$S:\mathcal{P}\to \mathcal{P}$ is completely continuous.

Proof. 

Let $u\in \mathcal{P}$. Clearly, using Theorem 3 and from (15), $\left(Su\right)\left(t\right)\ge 0$ for $t\in {\mathbb{N}}_a^b.$ Further,

$$\begin{array}{cc}\hfill \left(Su\right)\left(t\right)& \ge {\displaystyle \frac{L_1}{L_2}}\sum _{s=a+2}^b\left[\underset{s\in {\mathbb{N}}_{a+2}^b}{max}{g}_2\left(s\right)\right]\mathfrak{f}(s,u\left(s\right))\hfill \\ \hfill & ={\displaystyle \frac{L_1}{L_2}}\sum _{s=a+2}^b\left[\underset{t\in {\mathbb{N}}_{a+1}^b}{max}G(t,s)\right]\mathfrak{f}(s,u\left(s\right))\hfill \\ \hfill & \ge {\displaystyle \frac{L_1}{L_2}}\underset{t\in {\mathbb{N}}_{a+1}^b}{max}\left[\sum _{s=a+2}^{b}G(t,s)\mathfrak{f}(s,u\left(s\right))\right]\hfill \\ \hfill & ={\displaystyle \frac{L_1}{L_2}}∥Su∥.\hfill \end{array}$$

Thus, $Su\in \mathcal{P}$. Furthermore, the continuity of $\mathfrak{f}$ implies that S is completely continuous. □

Our first main result is as follows.

Theorem 5.

If there exist constants $0<r_1<r_2<\infty$ such that

(A1)

${\displaystyle \mathfrak{f}(x,\xi )\le \frac{r_1}{(b-a-1)L_2}}$ for $0\le \xi \le r_1$ and $x\in {\mathbb{N}}_{a+2}^b$;

(A2)

${\displaystyle \mathfrak{f}(x,\xi )\ge \frac{r_2}{(b-a-1)L_1}}$ for ${\displaystyle \frac{L_1}{L_2}{r}_2\le \xi \le r_2}$ and $x\in {\mathbb{N}}_{a+2}^b$,

then the boundary value problem (1) and (2) has at least one positive solution u with

$$r_1\le ∥u∥\le r_2.$$

Proof. 

Let $u\in \mathcal{P}$ and $∥u∥=r_1$. Then, from (15) and (A1),

$$\left(Su\right)\left(t\right)\le {\displaystyle \frac{r_1}{(b-a-1)L_2}}\sum _{s=a+2}^b{g}_2\left(s\right)\le r_1=∥u∥,$$

for all $t\in {\mathbb{N}}_a^b$. Now, if we choose ${\Omega }_1=\left\{u\in \mathcal{B}:∥u∥<r_1\right\}$, then $∥Su∥\le ∥u∥$ for $u\in \mathcal{P}\cap \partial {\Omega }_1$, giving us that condition (i) of Theorem 1 is satisfied. On the other hand, let ${\Omega }_2=\left\{u\in \mathcal{B}:∥u∥<r_2\right\}$. For $u\in \mathcal{P}$ with $∥u∥=r_2$,

$$\underset{t\in {\mathbb{N}}_{a+1}^b}{min}u\left(t\right)\ge {\displaystyle \frac{L_1}{L_2}}∥u∥={\displaystyle \frac{L_1}{L_2}}{r}_2.$$

Thus, if $s\in {\mathbb{N}}_{a+1}^b$, then ${\displaystyle \frac{L_1}{L_2}{r}_2\le u\left(s\right)\le r_2}$; using (15) and (A2), we obtain

$$\left(Su\right)\left(t\right)\ge {\displaystyle \frac{r_2}{(b-a-1)L_1}}\sum _{s=a+2}^b{g}_1\left(s\right)\ge r_2=∥u∥,$$

for all $t\in {\mathbb{N}}_a^b$, implying that $∥Su∥\ge ∥u∥$ for $u\in \mathcal{P}\cap \partial {\Omega }_2$. Therefore, condition (ii) of the classical Guo–Krasnoselskii’s fixed point theorem holds, implying that S has a fixed point in $\mathcal{P}\cap \left({\overline{\Omega }}_2\setminus {\Omega }_1\right)$, and as a consequence, the studied problem (1) and (2) admits a positive solution. □

Our second existence result is the following

Theorem 6.

If there exist constants $0<r_1<r_2<\infty$ such that

(B1)

${\displaystyle \mathfrak{f}(x,\xi )\ge \frac{r_1}{(b-a-1)L_2}}$ for $0\le \xi \le r_1$ and $x\in {\mathbb{N}}_{a+2}^b$;

(B2)

${\displaystyle \mathfrak{f}(x,\xi )\le \frac{r_2}{(b-a-1)L_1}}$ for ${\displaystyle \frac{L_1}{L_2}{r}_2\le \xi \le r_2}$ and $x\in {\mathbb{N}}_{a+2}^b$,

then the boundary value problem (1) and (2) has at least one positive solution u with

$$r_1\le ∥u∥\le r_2.$$

Proof. 

Let $u\in \mathcal{P}$ and $∥u∥=r_1$. Then, by (15) and (B1),

$$\left(Su\right)\left(t\right)\ge {\displaystyle \frac{r_1}{(b-a-1)L_2}}\sum _{s=a+2}^b{g}_2\left(s\right)\ge r_1=∥u∥,$$

for all $t\in {\mathbb{N}}_a^b$. Now, if we choose ${\Omega }_1=\left\{u\in \mathcal{B}:∥u∥<r_1\right\}$, then $∥Su∥\ge ∥u∥$ for $u\in \mathcal{P}\cap \partial {\Omega }_1$, giving us that condition (ii) of Theorem 1 holds. On the other hand, let ${\Omega }_2=\left\{u\in \mathcal{B}:∥u∥<r_2\right\}$. For $u\in \mathcal{P}$ with $∥u∥=r_2$,

$$\underset{t\in {\mathbb{N}}_{a+1}^b}{min}u\left(t\right)\ge {\displaystyle \frac{L_1}{L_2}}∥u∥={\displaystyle \frac{L_1}{L_2}}{r}_2.$$

Thus, if $s\in {\mathbb{N}}_{a+1}^b$, then ${\displaystyle \frac{L_1}{L_2}{r}_2\le u\left(s\right)\le r_2}$, and using (15) and (B2), we obtain

$$\left(Su\right)\left(t\right)\le {\displaystyle \frac{r_2}{(b-a-1)L_1}}\sum _{s=a+2}^b{g}_1\left(s\right)\le r_2=∥u∥,$$

for all $t\in {\mathbb{N}}_a^b$, implying that $∥Su∥\le ∥u∥$ for $u\in \mathcal{P}\cap \partial {\Omega }_2$. Thus, condition (i) of Theorem 1 is also met. As a consequence, it follows that S has a fixed point in $\mathcal{P}\cap \left({\overline{\Omega }}_2\setminus {\Omega }_1\right)$; hence, it is a positive solution of problem (1) and (2). □

5. Multiplicity Results

We point out that under condition (12), from Theorem 4, one has that the Green’s function satisfies condition $\left(P{g}_1\right)$ from [38] and using similar arguments to the ones established there, one can obtain the existence of at least two or three positive solutions. However, we will focus on a more general result.

The two lemmas presented below are sufficient in this section.

Lemma 4.

Assume that there exists $r>0$ and $0<A<1$ such that ${\displaystyle \mathfrak{f}(x,\xi )\le \frac{Ar}{(b-a-1)L_2}}$ for $0\le \xi \le r$ and $x\in {\mathbb{N}}_{a+2}^b$. If $u\in \mathcal{P}$ with $∥u∥=\rho$, where $Ar\le \rho \le r$, then $∥Su∥\le \rho$.

Proof. 

If $u\in \mathcal{P}$ with $∥u∥=\rho$, using (15)

$$\left(Su\right)\left(t\right)\le {\displaystyle \frac{Ar}{(b-a-1)L_2}}\sum _{s=a+2}^b{g}_2\left(s\right)\le Ar\le \rho ,$$

for all $t\in {\mathbb{N}}_a^b$. That is, $∥Su∥\le \rho$. □

Lemma 5.

Suppose that there exists $r>0$ and $0<A<1$ such that ${\displaystyle \mathfrak{f}(x,\xi )\ge \frac{r}{(b-a-1)L_1}}$ for ${\displaystyle \frac{A{L}_1}{L_2}r\le \xi \le r}$ and $x\in {\mathbb{N}}_{a+2}^b$. If $u\in \mathcal{P}$ with $∥u∥=\rho$, where $Ar\le \rho \le r$, then $∥Su∥\ge \rho$.

Proof. 

If $u\in \mathcal{P}$ with $∥u∥=\rho$, where $Ar\le \rho \le r$, then

$$\underset{t\in {\mathbb{N}}_{a+1}^b}{min}u\left(t\right)\ge {\displaystyle \frac{L_1}{L_2}}∥u∥={\displaystyle \frac{L_1}{L_2}}\rho .$$

Thus, if $s\in {\mathbb{N}}_{a+1}^b$, then

$${\displaystyle \frac{L_1}{L_2}}\rho \le u\left(s\right)\le \rho ,\mathrm{or}{\displaystyle \frac{A{L}_1}{L_2}}r\le u\left(s\right)\le r.$$

Therefore, from (15),

$$\left(Su\right)\left(t\right)\ge {\displaystyle \frac{r}{(b-a-1)L_1}}\sum _{s=a+2}^b{g}_2\left(s\right)\ge r\ge \rho ,$$

for all $t\in {\mathbb{N}}_a^b$. That is, $∥Su∥\ge \rho$. □

Now, we combine our two previous technical results in order to deduce our main multiplicity result.

Theorem 7.

Suppose that there exist constants $0<r_1<r_2<\cdots <r_n$ ($n\ge 3$) and $0<A<1$. Moreover, if

(F1)

${\displaystyle \mathfrak{f}(x,\xi )\le \frac{A{r}_{2i-1}}{(b-a-1)L_2}}$ for $0\le \xi \le r_{2i-1}$, $x\in {\mathbb{N}}_{a+2}^b$ and ${\displaystyle 1\le i\le ⌈\frac{n}{2}⌉}$;

(F2)

${\displaystyle \mathfrak{f}(x,\xi )\ge \frac{r_{2j}}{(b-a-1)L_1}}$ for ${\displaystyle \frac{A{L}_1}{L_2}{r}_{2j}\le \xi \le r_{2j}}$, $x\in {\mathbb{N}}_{a+2}^b$ and ${\displaystyle 1\le j\le ⌊\frac{n}{2}⌋}$;

then (1) and (2) has at least $n-1$ positive solutions $u_k$ with

$$r_k\le ∥u_k∥\le r_{k+1},1\le k\le n-1.$$

Proof. 

Let $l_m\in \left(A{r}_m,r_m\right)$ and $l_m>r_{m-1}$ with $2\le m\le n$. Define

$${\Omega }_m^{l_m}=\left\{u\in \mathcal{B}:∥u∥<l_m\right\},2\le m\le n,$$

and

$${\Omega }_q^{r_q}=\left\{u\in \mathcal{B}:∥u∥<r_q\right\},1\le q\le n.$$

Then, from conditions (F1) and (F2) and from Lemmas (4) and (5), we have

$$∥Su∥\le ∥u∥\mathrm{for}u\in \mathcal{P}\cap \partial {\Omega }_{2p-1}^{l_{2p-1}},2\le p\le ⌈{\displaystyle \frac{n}{2}}⌉,$$

$$∥Su∥\le ∥u∥\mathrm{for}u\in \mathcal{P}\cap \partial {\Omega }_{2i-1}^{l_{2i-1}},1\le i\le ⌈{\displaystyle \frac{n}{2}}⌉,$$

$$∥Su∥\ge ∥u∥\mathrm{for}u\in \mathcal{P}\cap \partial {\Omega }_{2j}^{l_{2j}},1\le j\le ⌊{\displaystyle \frac{n}{2}}⌋,$$

and

$$∥Su∥\ge ∥u∥\mathrm{for}u\in \mathcal{P}\cap \partial {\Omega }_{2i}^{l_{2i}},1\le i\le ⌊{\displaystyle \frac{n}{2}}⌋.$$

From Theorem 5, we deduce that S has a fixed point in each of the sets

$$\mathcal{P}\cap \left({\overline{\Omega }}_m^{l_m}\setminus {\Omega }_{m-1}^{r_m-1}\right),2\le m\le n.$$

Hence, the considered problem (1) and (2) has at least $n-1$ positive solutions. □

6. Examples

Here, we will highlight the applications of our theoretical findings using two examples.

Example 1.

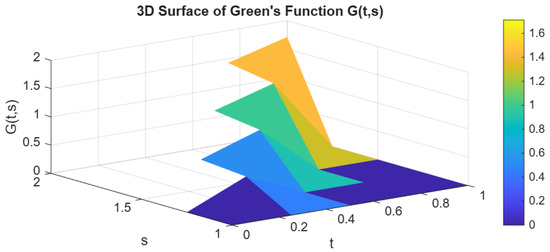
Consider (1) and (2) with $a=0$, $b=5$, $\nu =1.5$, $\mu =0.25$, $d=3$, $\lambda =0.25$, and $\mathfrak{f}\left(t,\xi \right)={\displaystyle \frac{t}{100}}+{\displaystyle \frac{{sin}^2\xi }{10}}$. Then, $\Omega =H_{0.25}(5,0)-\lambda H_{1.5}(3,0)=0.5250$. The corresponding Green’s function is given by

$$G(t,s)=\left\{\begin{array}{c}{G}_1(t,s),s\le min\{t,3\},\hfill \\ G_2(t,s),t+1\le s\le 3,\hfill \\ G_3(t,s),4\le s\le t,\hfill \\ G_4(t,s),s\ge max\{t+1,4\},\hfill \end{array}\right.$$

(16)

with

$$G_1(t,s)={\displaystyle \frac{H_{0.5}(t,0)H_{0.25}(5,\rho \left(s\right))}{0.5250}}-{\displaystyle \frac{\left(0.25\right)H_{0.5}(t,0)H_{1.5}(3,\rho \left(s\right))}{0.5250}}-H_{0.5}(t,\rho \left(s\right)),$$

$$G_2(t,s)={\displaystyle \frac{H_{0.5}(t,0)H_{0.25}(5,\rho \left(s\right))}{0.5250}}-{\displaystyle \frac{\left(0.25\right)H_{0.5}(t,0)H_{1.5}(3,\rho \left(s\right))}{0.5250}},$$

$$G_3(t,s)={\displaystyle \frac{H_{0.5}(t,0)H_{0.25}(5,\rho \left(s\right))}{0.5250}}-H_{0.5}(t,\rho \left(s\right)),$$

$$G_4(t,s)={\displaystyle \frac{H_{0.5}(t,0)H_{0.25}(5,\rho \left(s\right))}{0.5250}}.$$

Clearly, inequality (12) holds. Consequently, from Lemma 3, $G\left(t,s\right)$ is positive for all $\left(t,s\right)\in {\mathbb{N}}_1^5\times {\mathbb{N}}_2^5$ as it might be seen in Figure 2. Moreover, by computation

$$\begin{array}{cc}\hfill L_1& =\underset{s\in {\mathbb{N}}_2^5}{min}{g}_1\left(s\right)\hfill \\ & =\underset{s\in {\mathbb{N}}_2^5}{min}{G}_1(s,s)\hfill \\ & =\underset{s\in {\mathbb{N}}_2^5}{min}\left[{\displaystyle \frac{H_{0.5}(s,0)H_{0.25}(5,\rho \left(s\right))}{0.5250}}-{\displaystyle \frac{\left(0.25\right)H_{0.5}(s,0)H_{1.5}(3,\rho \left(s\right))}{0.5250}}-H_{0.5}(s,\rho \left(s\right))\right]\hfill \\ & =1.5670\hfill \end{array}$$

and

$$L_2=\underset{s\in {\mathbb{N}}_2^5}{max}{g}_2\left(s\right)=\underset{s\in {\mathbb{N}}_2^5}{max}\left[{\displaystyle \frac{H_{0.5}(5,0)H_{0.25}(5,\rho \left(s\right))}{0.5250}}\right]=7.1411.$$

If we choose $r_1=0.5$ and $r_2=1$ such that

Figure 2. Three-dimensional plot of $G(t,s)$.

(B1)

${\displaystyle \mathfrak{f}(x,\xi )\ge \left(0.0350\right)r_1}$ for $0\le \xi \le r_1$ and $x\in {\mathbb{N}}_2^5$;

(B2)

${\displaystyle \mathfrak{f}(x,\xi )\le \left(0.1595\right)r_2}$ for ${\displaystyle \left(0.2194\right)r_2\le \xi \le r_2}$ and $x\in {\mathbb{N}}_2^5$,

implying that all conditions of Theorem 6 hold, then (1) and (2) admits at least one positive solution u with

$$r_1\le ∥u∥\le r_2.$$

Example 2.

Consider (1) and (2) with $a=0$, $b=5$, $\nu =1.5$, $\mu =0.25$, $d=3$, $\lambda =0.25$, and

$$\mathfrak{f}\left(t,\xi \right)={\displaystyle \frac{1}{300(\zeta +1)}}\left\{\begin{array}{c}{\displaystyle \frac{1}{120}+sin\xi ,t\in {\mathbb{N}}_2^5,0\le \xi \le \frac{1}{35},}\hfill \\ {\displaystyle \frac{1}{120}+150\left(\xi -\frac{1}{35}\right)+sin\xi , t\in {\mathbb{N}}_2^5,\frac{1}{35}\le \xi \le \frac{1}{27},}\hfill \\ {\displaystyle \frac{1}{120}+\frac{80}{63}+sin\xi ,t\in {\mathbb{N}}_2^5,\frac{1}{27}\le \xi \le 360.}\hfill \end{array}\right.$$

As in Example 1, one can verify that $\Omega =0.5250$, inequality (12) holds, and by Lemma 3, $G\left(t,s\right)>0$ for all $\left(t,s\right)\in {\mathbb{N}}_1^5\times {\mathbb{N}}_2^5.$ Again, $L_1=1.5670$ and $L_2=7.1411$. Now, if we choose $A=0.5$, $r_1={\displaystyle \frac{1}{35}}$, $r_2={\displaystyle \frac{85}{216}}$, and $r_3=360$ such that

(F11)

${\displaystyle \mathfrak{f}(x,\xi )\le \left(0.0175\right)r_1}$ for $0\le \xi \le r_1$ and $x\in {\mathbb{N}}_2^5$;

(F12)

${\displaystyle \mathfrak{f}(x,\xi )\le \left(0.0175\right)r_3}$ for $0\le \xi \le r_3$ and $x\in {\mathbb{N}}_2^5$;

(F2)

${\displaystyle \mathfrak{f}(x,\xi )\ge \left(0.0798\right)r_2}$ for ${\displaystyle \left(0.1097\right)r_2\le \xi \le r_2}$ and $x\in {\mathbb{N}}_2^5$,

implying that the conditions of Theorem 7 hold, then (1) and (2) admits at least two positive solutions $u_1$ and $u_2$ with

$$r_1\le ∥u_1∥\le r_2\le ∥u_2∥\le r_3.$$

7. Conclusions

In this manuscript, we studied a class of nabla fractional difference problems with summation multi-point boundary conditions with two different nabla operators depending on a real parameter. We obtained the exact expression of the related Green’s function, we deduced specific bounds of the parameter in which the Green’s function is strictly positive, and we showed the existence of multiple positive solutions of the studied problem, which we consider to be the main novelty of this work. This has never been completed in the literature for such kinds of problem, and this new idea can be very helpful for other researchers in their attempts to deduce the existence and multiplicity of positive solutions of fractional problems with parameter dependence. Moreover, it can be extended in order to obtain nonexistence results or in the study of similar fractional problems of higher order. Another possible future approach would be applying this method to singular fractional order systems or to fractional difference multi-agent systems, since such systems are very common.