Structure-Preserving Numerical Methods for Fractional Nonlinear Schrödinger Equations with Wave Operators
Abstract
1. Introduction
2. Notations
3. Conservative Difference Schemes
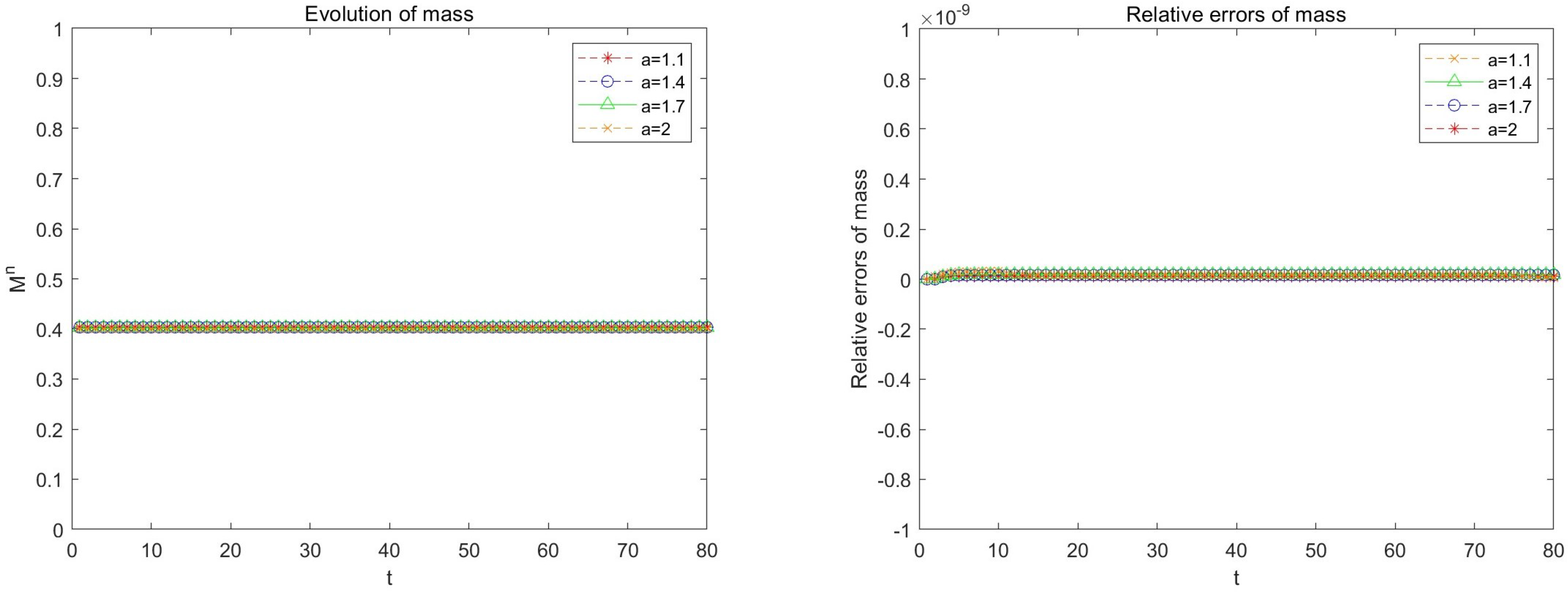
4. Mass and Energy Conservation
5. Convergence and Stability
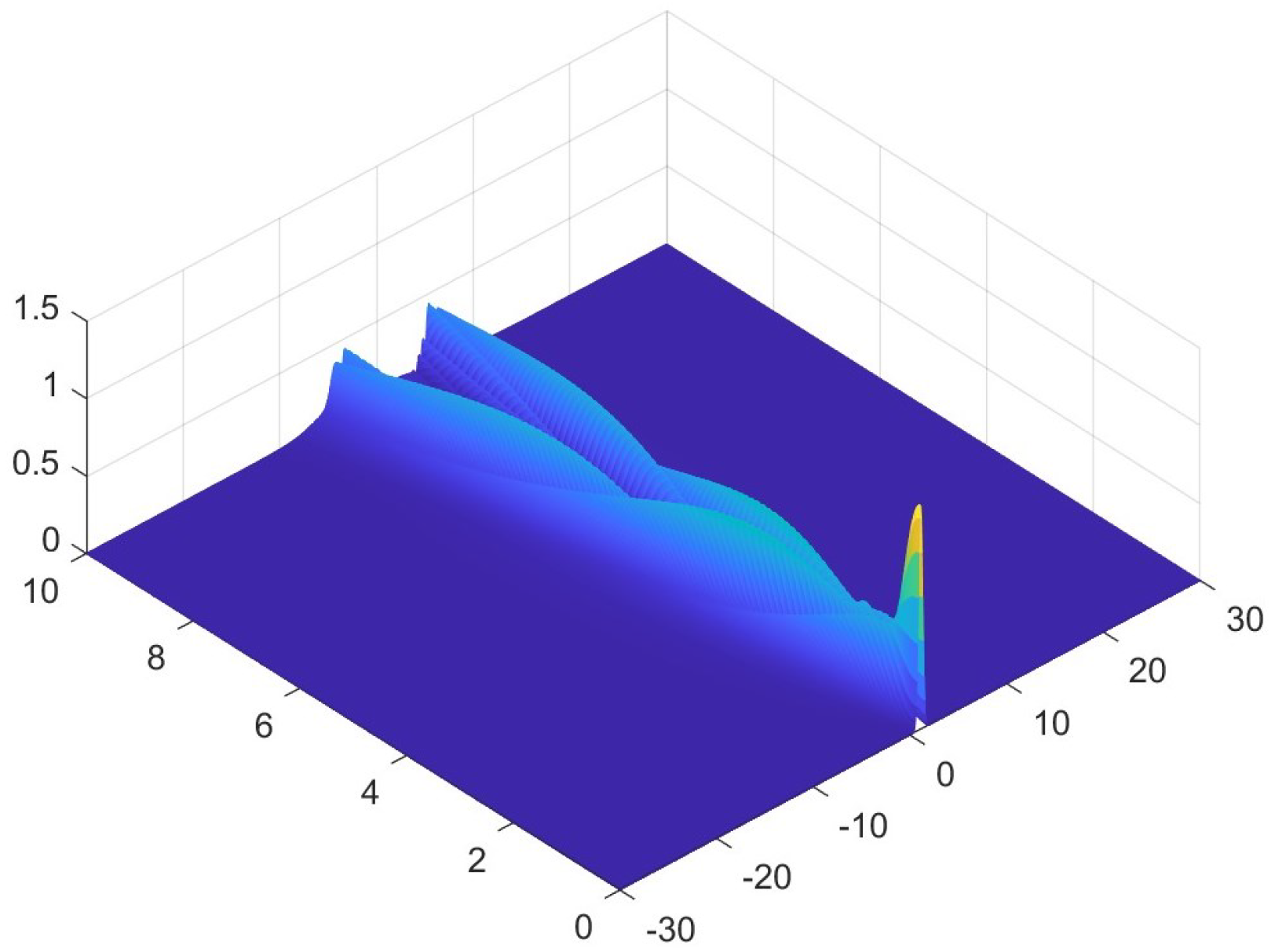
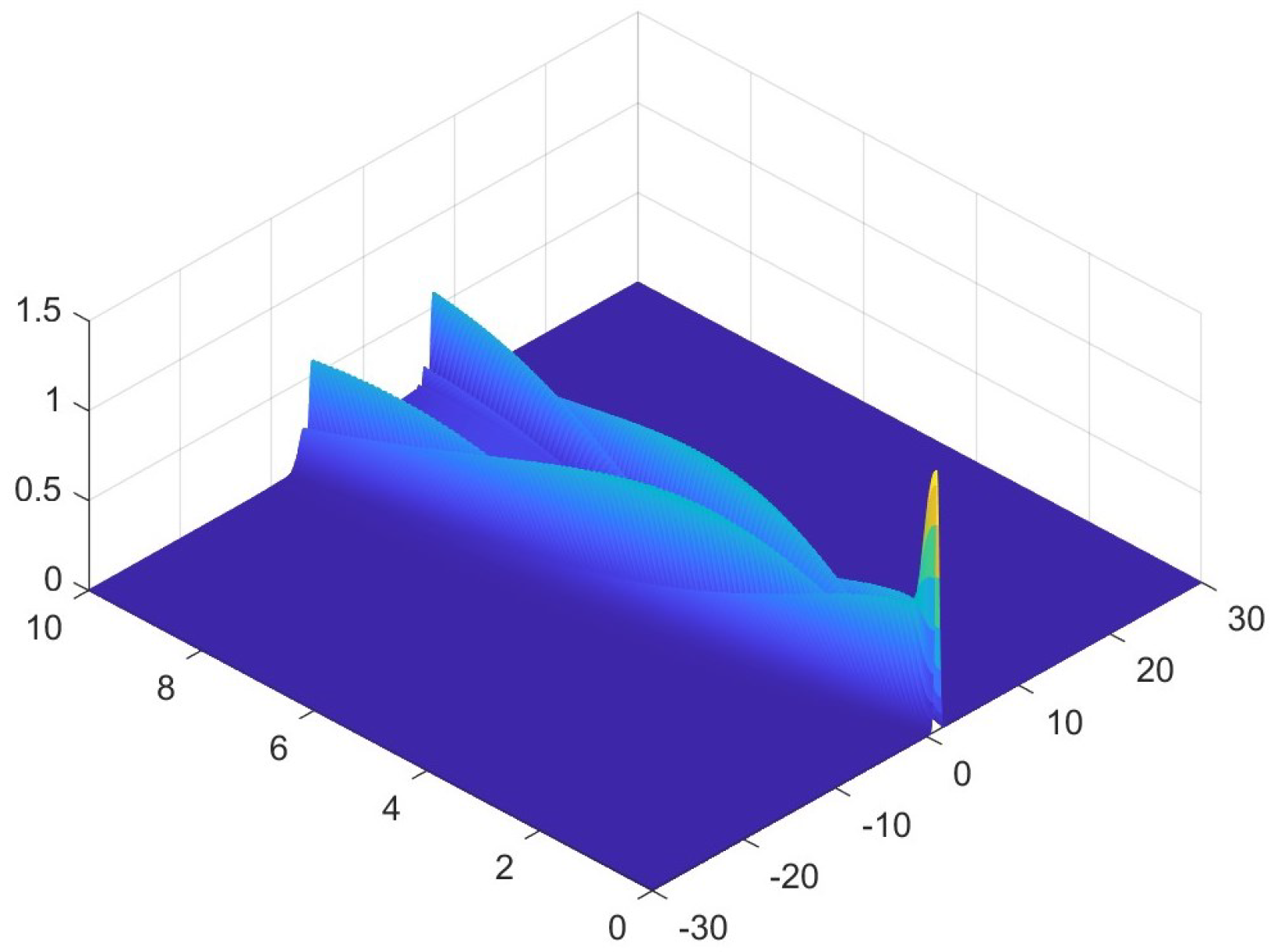
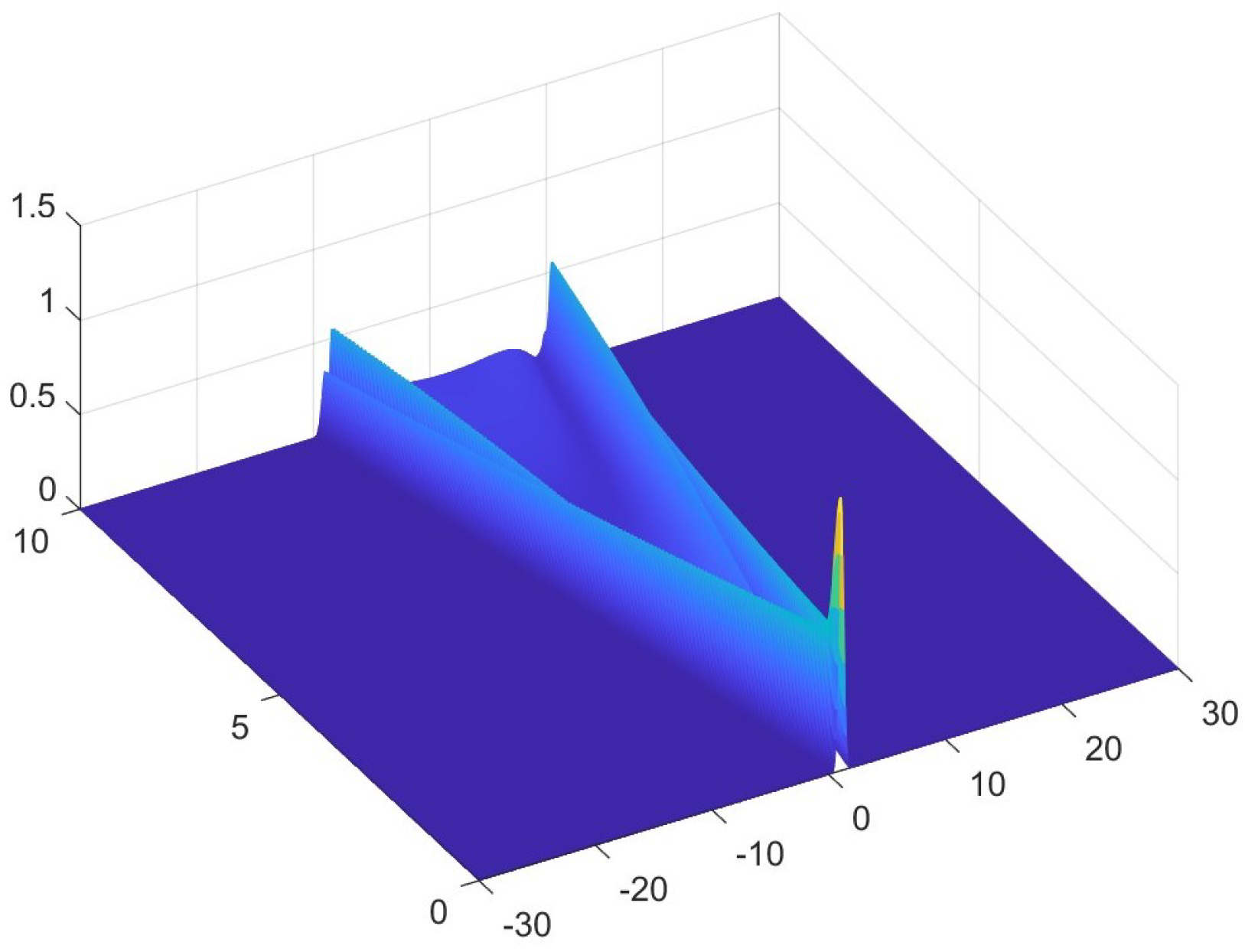
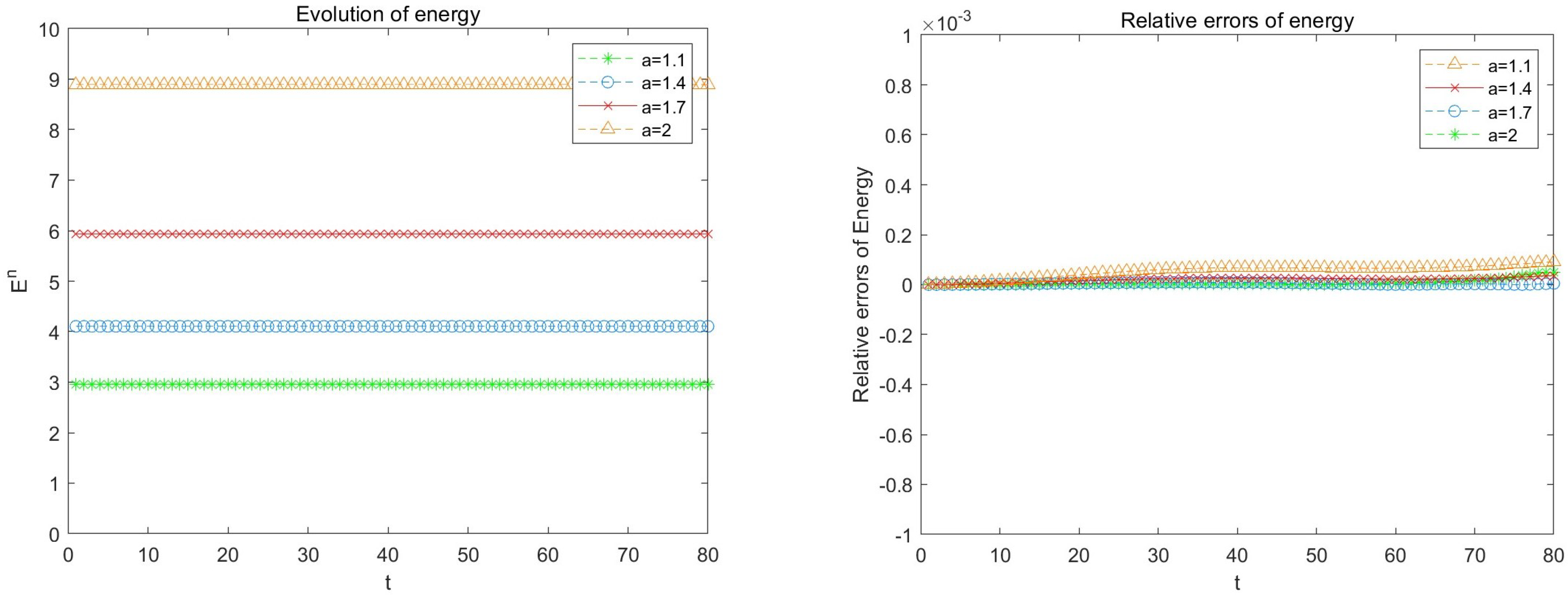
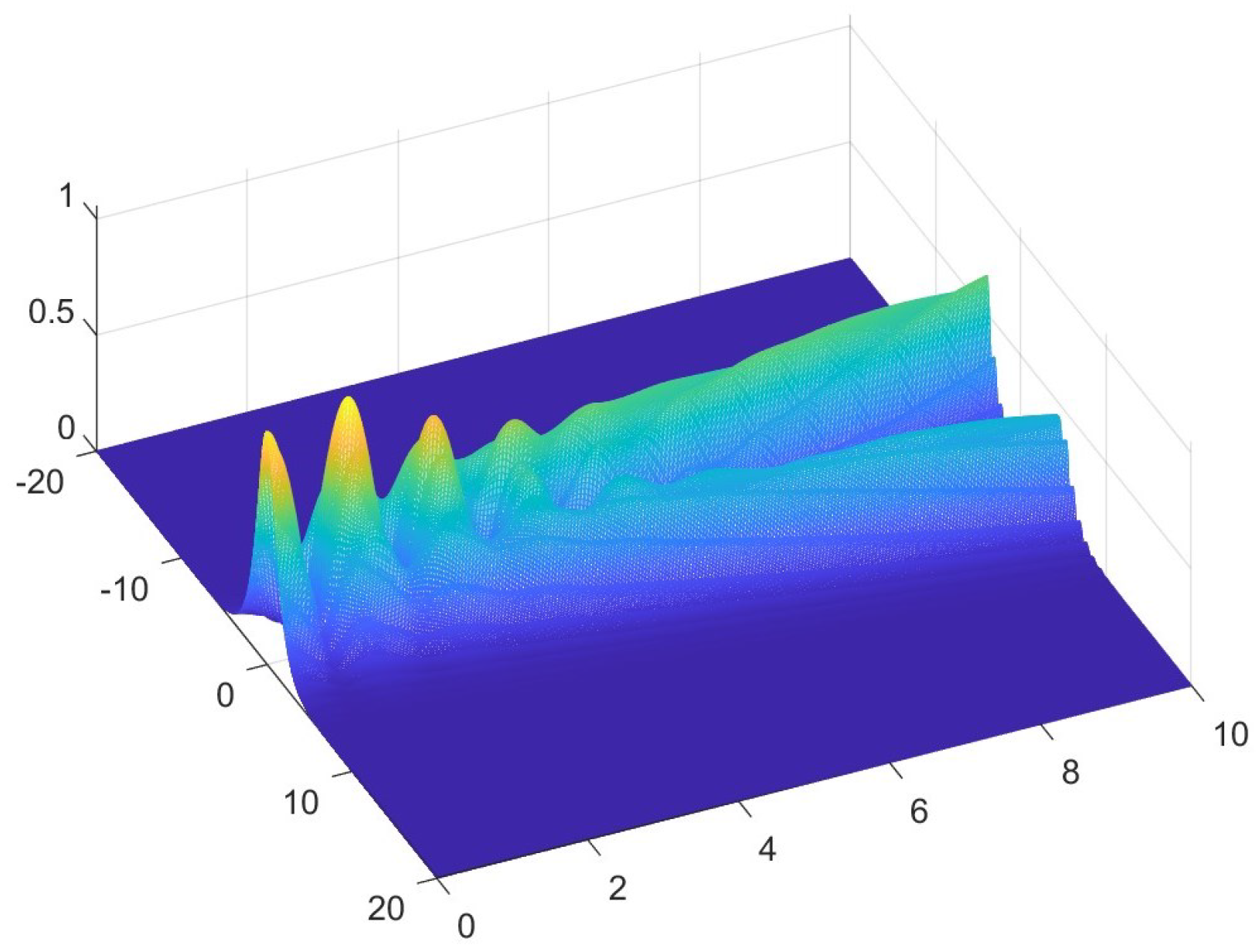
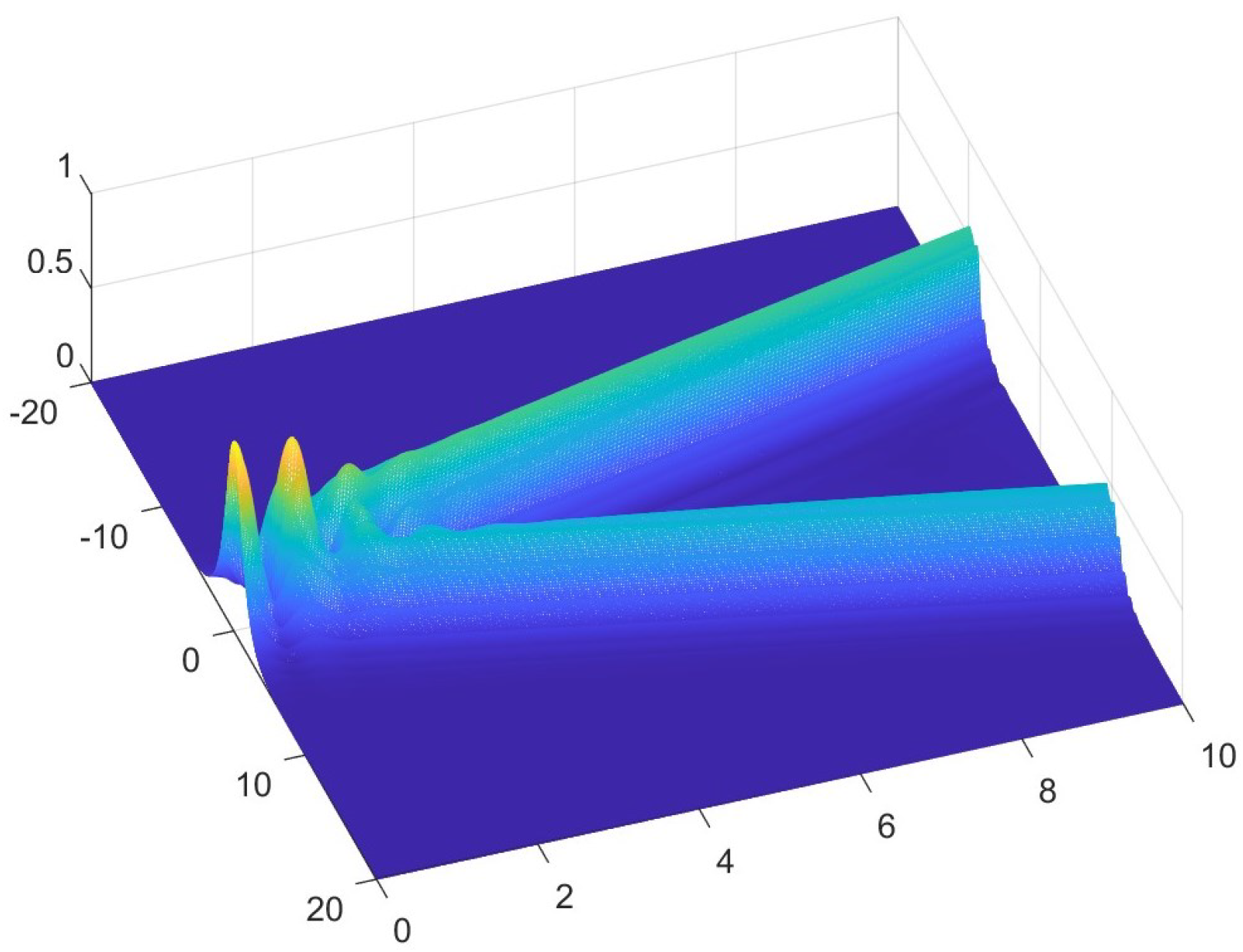
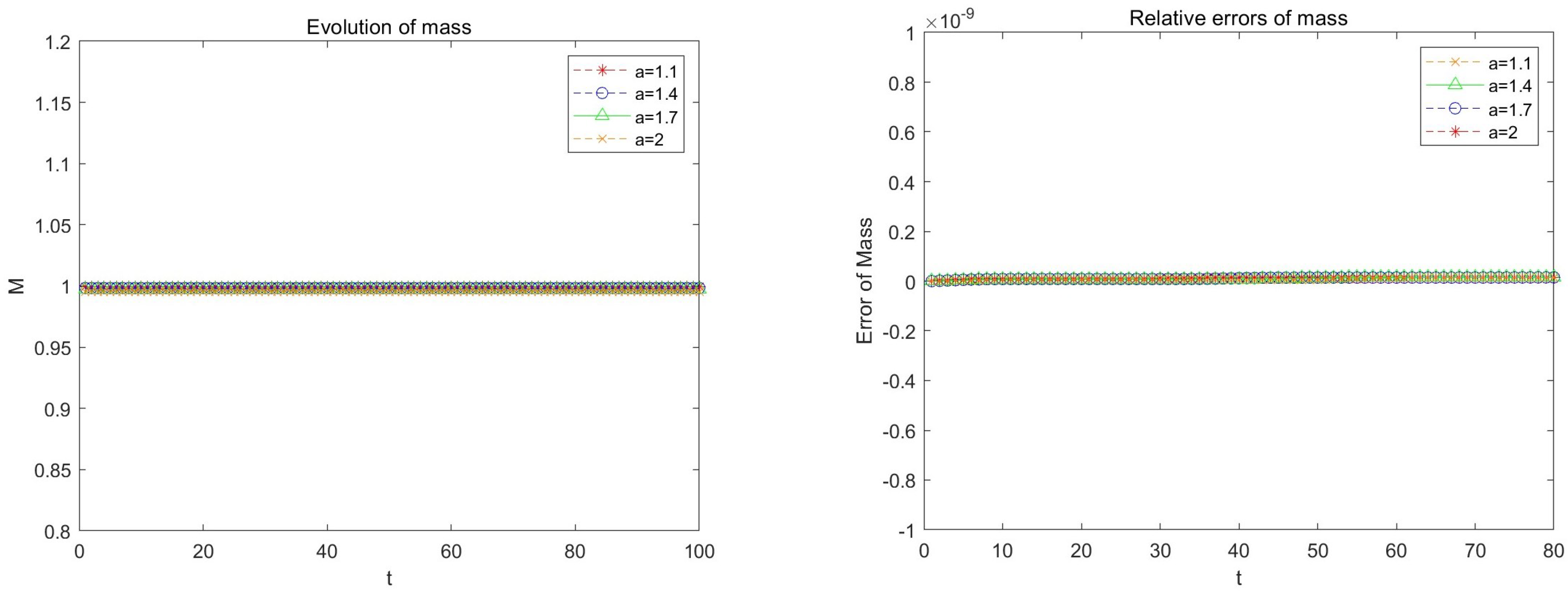
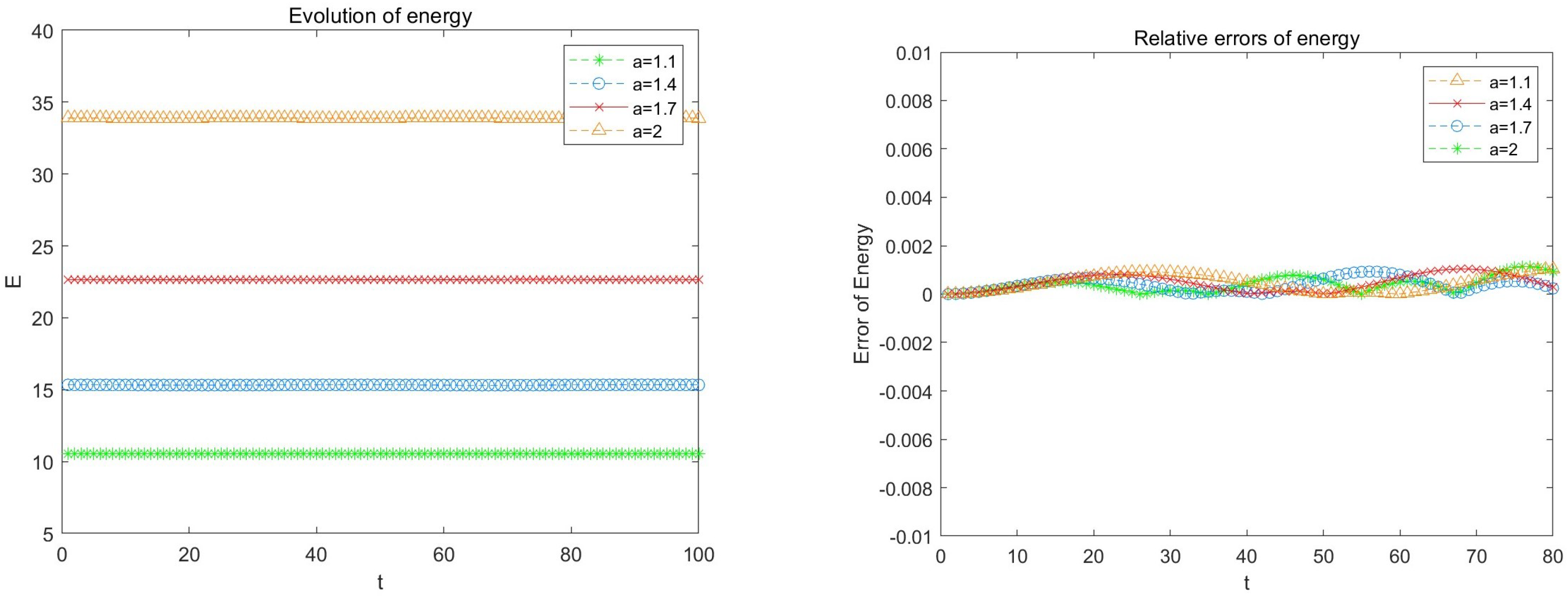
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Yang, B.; Wei, C.Z.; Luo, M.K. Quantization method and Schrödinger equation of fractional time and their weak effects on Hamiltonian: Phase transitions of energy and wave functions. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105531. [Google Scholar] [CrossRef]
- Deng, Y.B.; Liu, C.C.; Yang, X. Standing waves of fractional Schrödinger equations with critical nonlinearities and decaying potentials. Discret. Contin. Dyn. Syst. 2025, 45, 1248–1296. [Google Scholar] [CrossRef]
- Hu, D.D.; Hui, H.L.; Xu, Z.Z.; Wang, Y.S. On convergence of a novel linear conservative scheme for the two-dimensional fractional nonlinear Schrödinger equation with wave operator. Comput. Math. Appl. Int. J. 2023, 150, 254–266. [Google Scholar] [CrossRef]
- Faridi, W.A.; Asjad, M.I.; Jhangeer, A.; Yusuf, A.; Sulaiman, T.A. The weakly non-linear waves propagation for Kelvin–Helmholtz instability in the magnetohydrodynamics flow impelled by fractional theory. Opt. Quantum Electron. 2023, 55, 172. [Google Scholar] [CrossRef]
- Lashkarian, E.; Motamednezhad, A.; Hejazi, S.R. Invariance properties and conservation laws of perturbed fractional wave equation. Eur. Phys. J. Plus 2021, 136, 615. [Google Scholar] [CrossRef]
- Zhong, M.; Yan, Z.Y. Data-driven soliton mappings for integrable fractional nonlinear wave equations via deep learning with Fourier neural operator. Chaos Solitons Fractals 2022, 165, 112787. [Google Scholar] [CrossRef]
- Mohammad, M.; Sajjad, H.M.; Arzu, A.; Hamood, U.R.; Ifrah, I.; Mostafa, E. Dynamics of optical solitons in the extended(3+1)-dimensional nonlinear conformable Kudryashov equation with generalized anti-cubic nonlinearity. Math. Methods Appl. Sci. 2024, 47, 5355–5375. [Google Scholar]
- He, X.M.; Zou, W.M. Existence and concentration result for the fractional Schrödinger equations with critical nonlinearities. Calc. Var. Part. Differ. Equ. 2016, 55, 91. [Google Scholar] [CrossRef]
- Yan, J.Y.; Zhang, H.; Wei, Y.B.; Qian, X. High-order and mass-conservative regularized implicit-explicit relaxation Runge-Kutta methods for the low regularity Schrödinger equations. Appl. Numer. Math. 2025, 216, 210–221. [Google Scholar] [CrossRef]
- Wang, L.L.; Yan, J.Y.; Zhang, X.L. Error analysis of a first-order IMEX scheme for the logarithmic Schrödinger equation. SIAM J. Numer. Anal. 2024, 62, 119–137. [Google Scholar] [CrossRef]
- Deepika, R.; Muthunagai, K. A Novel Fractional Uncertainty Relation in Quaternionic Quantum Mechanics. Math. Methods Appl. Sci. 2025, 13, 12813–12818. [Google Scholar] [CrossRef]
- Varão, G.; Lobo, I.P.; Bezerra, V.B. Fractional quantum mechanics meets quantum gravity phenomenology. Europhys. Lett. 2024, 3, 30001. [Google Scholar] [CrossRef]
- Zhang, X.; Ran, M.H.; Liu, Y.; Zhang, L. A high-order structure-preserving difference scheme for generalized fractional Schrödinger equation with wave operator. Math. Comput. Simul. 2023, 210, 532–546. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef]
- Caffarelli, L. Non-local diffusions, drifts and games. In Nonlinear Partial Differential Equations. Abel Symposium; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7, pp. 37–52. [Google Scholar]
- Lischke, A.; Pang, G.; Gulian, M.; Song, F.; Glusa, C.; Zheng, X.; Mao, Z.; Cai, W.; Meerschaert, M.M.; Ainsworth, M.; et al. What is the fractional Laplacian? A comparative review with new results. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- D’Elia, M.; Du, Q.; Glusa, C.; Gunzburger, M.; Tian, X.; Zhou, Z. Numerical methods for nonlocal and fractional models. Acta Numer. 2020, 29, 1–124. [Google Scholar] [CrossRef]
- Bao, W.Z.; Cai, Y.Y. Uniform Error Estimates of Finite Difference Methods for the Nonlinear Schrödinger Equation with Wave Operator. SIAM J. Numer. Anal. 2012, 20, 492–521. [Google Scholar] [CrossRef]
- Wang, P.D.; Huang, C.M. An energy conservative difference scheme for the nonlinear fractional Schrödinger equations. J. Comput. Phys. 2015, 293, 238–251. [Google Scholar] [CrossRef]
- Yao, L.; Lei, S.L.; Sun, H.W. Efficient finite difference scheme for a hidden-memory variable-order time-fractional diffusion equation. Comput. Appl. Math. 2023, 42, 362. [Google Scholar]
- Li, M.; Huang, C.M.; Wang, P.D. Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer. Algorithms 2017, 74, 499–525. [Google Scholar] [CrossRef]
- Li, M.; Gu, X.M.; Huang, C.M.; Fei, M.F.; Zhang, G.Y. A fast linearized conservative finite element method for the strongly coupled nonlinear fractional Schrödinger equations. J. Comput. Phys. 2018, 258, 256–282. [Google Scholar] [CrossRef]
- Liang, X.; Khaliq, A.Q.M. An efficient Fourier spectral exponential time differencing method for the space-fractional nonlinear Schrödinger equations. Comput. Math. Appl. 2018, 75, 4438–4457. [Google Scholar] [CrossRef]
- Hui, Z.; Yun, X.J.; Chu, W.; Zhen, S.C. Crank-Nicolson Fourier spectral methods for the space fractional nonlinear Schrödinger equation and its parameter estimation. Int. J. Comput. Math. 2019, 96, 238–263. [Google Scholar]
- Bian, R.C.; Hua, Z.G. Regularized splitting spectral method for space-fractional logarithmic Schrödinger equation. Appl. Numer. Math. 2021, 167, 330–355. [Google Scholar] [CrossRef]
- Amore, P.; Fernandez, F.M.; Hofmann, C.P.; Saenz, R.A. Collocation method for fractional quantum mechanics. J. Math. Phys. 2010, 51, 122101. [Google Scholar] [CrossRef]
- Yan, C.; Chen, H.Z. Fourth-order finite difference scheme and efficient algorithm for nonlinear fractional Schrödinger equations. Adv. Differ. Equ. 2020, 2020, 4. [Google Scholar]
- Wang, J.J. High-order conservative schemes for the space fractional nonlinear Schrödinger equation. Appl. Numer. Math. 2021, 165, 248–269. [Google Scholar] [CrossRef]
- Li, X.X.; Wen, J.M.; Li, D.F. Mass- and energy-conserving difference schemes for nonlinear fractional Schrödinger equations. Appl. Math. Lett. 2021, 111, 106686. [Google Scholar] [CrossRef]
- Çelik, C.; Duman, M. Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J. Comput. Phys. 2012, 231, 1743–1750. [Google Scholar] [CrossRef]
- Bao, W.Z.; Cai, Y. Optimal error estimates of finite difference methods for the gross-pitaevskii equation with angular momentum rotation. Math. Comput. 2013, 82, 99–128. [Google Scholar] [CrossRef]
- Ye, H.P.; Gao, J.M.; Ding, Y.S. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Xie, S.S.; Li, G.X.; Yi, S. Compact finite difference schemes with high accuracy for one-dimensional nonlinear Schrödinger equation. Comput. Methods Appl. Mech. Eng. 2009, 198, 1052–1060. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, D. On the l∞ convergence of a difference scheme for coupled nonlinear Schrödinger equations. Comput. Math. Appl. 2010, 59, 3286–3300. [Google Scholar] [CrossRef]
- Lv, S.Q.; Nie, Z.H.; Liao, C.C. Stability and Convergence Analysis of Multi-Symplectic Variational Integrator for Nonlinear Schrödinger Equation. Mathematics 2023, 11, 3788. [Google Scholar] [CrossRef]
- Wang, D.; Xiao, A.; Yang, W. A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations. J. Comput. Phys. 2014, 272, 644–655. [Google Scholar] [CrossRef]
- Pan, K.J.; Zeng, J.L.; He, D.D.; Zhang, S.Y. A fourth-order difference scheme for the fractional nonlinear Schrodinger equation with wave operator. Appl. Anal. 2022, 101, 2886–2902. [Google Scholar] [CrossRef]




| Error | Rate | Error | Rate | Error | Rate | Error | Rate | |
|---|---|---|---|---|---|---|---|---|
| 0.2 | 7.69 × | 1.04 | 1.41 | 1.89 | ||||
| 0.1 | 2.15 × | 1.84 | 3.06 × | 1.76 | 4.56 × | 1.64 | 6.85 × | 1.46 |
| 0.05 | 5.29 × | 2.02 | 7.69 × | 1.99 | 1.19 × | 1.94 | 1.90 × | 1.85 |
| 0.025 | 1.07 × | 2.31 | 1.56 × | 2.30 | 2.43 × | 2.29 | 3.98 × | 2.25 |
| h | ||||||||
|---|---|---|---|---|---|---|---|---|
| Error | Rate | Error | Rate | Error | Rate | Error | Rate | |
| 0.2 | 1.17 | 7.86 × | 6.75 × | 4.64 × | ||||
| 0.1 | 3.29 × | 1.83 | 2.29 × | 1.78 | 1.83 × | 1.88 | 1.23 × | 1.91 |
| 0.05 | 7.88 × | 2.06 | 5.95 × | 1.95 | 4.75 × | 1.95 | 2.95 × | 2.06 |
| 0.025 | 1.96 × | 2.01 | 1.46 × | 2.02 | 1.22 × | 1.96 | 7.24 × | 2.03 |
| Error | Rate | Error | Rate | Error | Rate | Error | Rate | |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 3.50 × | 5.31 × | 7.75 × | 8.45 × | ||||
| 0.05 | 9.92 × | 1.82 | 1.52 × | 1.80 | 2.22 × | 1.80 | 2.20 × | 1.94 |
| 0.025 | 2.57 × | 1.95 | 3.65 × | 2.06 | 5.79 × | 1.94 | 5.64 × | 1.97 |
| 0.0125 | 6.23 × | 2.05 | 8.45 × | 2.11 | 1.45 × | 2.00 | 1.23 × | 2.20 |
| h | ||||||||
|---|---|---|---|---|---|---|---|---|
| Error | Rate | Error | Rate | Error | Rate | Error | Rate | |
| 0.1 | 3.07 × | 9.77 × | 9.92 × | 6.43 × | ||||
| 0.05 | 8.30 × | 1.89 | 2.47 × | 1.99 | 2.49 × | 2.00 | 1.62 × | 1.99 |
| 0.025 | 2.16 × | 1.94 | 5.97 × | 2.05 | 5.71 × | 2.12 | 4.18 × | 1.95 |
| 0.0125 | 5.36 × | 2.01 | 1.42 × | 2.07 | 1.14 × | 2.33 | 8.44 × | 2.31 |
| Error | Rate | Error | Rate | Error | Rate | Error | Rate | |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 7.52 × | 1.07 × | 1.12 × | 2.85 × | ||||
| 0.05 | 1.80 × | 2.07 | 2.60 × | 2.04 | 2.73 × | 2.03 | 6.89 × | 2.05 |
| 0.025 | 4.40 × | 2.03 | 6.45 × | 2.01 | 6.80 × | 2.01 | 1.60 × | 2.11 |
| 0.0125 | 1.09 × | 2.01 | 1.60 × | 2.01 | 1.70 × | 2.00 | 3.99 × | 2.00 |
| h | ||||||||
|---|---|---|---|---|---|---|---|---|
| Error | Rate | Error | Rate | Error | Rate | Error | Rate | |
| 0.1 | 1.35 × | 4.40 × | 3.92 × | 5.53 × | ||||
| 0.05 | 3.08 × | 2.14 | 1.01 × | 2.13 | 9.34 × | 2.07 | 1.29 × | 2.09 |
| 0.025 | 6.97 × | 2.14 | 2.24 × | 2.17 | 2.16 × | 2.11 | 3.13 × | 2.05 |
| 0.0125 | 1.64 × | 2.09 | 5.32 × | 2.07 | 4.96 × | 2.13 | 6.99 × | 2.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhou, X.; Liao, C. Structure-Preserving Numerical Methods for Fractional Nonlinear Schrödinger Equations with Wave Operators. Mathematics 2025, 13, 3187. https://doi.org/10.3390/math13193187
Zhang M, Zhou X, Liao C. Structure-Preserving Numerical Methods for Fractional Nonlinear Schrödinger Equations with Wave Operators. Mathematics. 2025; 13(19):3187. https://doi.org/10.3390/math13193187
Chicago/Turabian StyleZhang, Mengnan, Xinyu Zhou, and Cuicui Liao. 2025. "Structure-Preserving Numerical Methods for Fractional Nonlinear Schrödinger Equations with Wave Operators" Mathematics 13, no. 19: 3187. https://doi.org/10.3390/math13193187
APA StyleZhang, M., Zhou, X., & Liao, C. (2025). Structure-Preserving Numerical Methods for Fractional Nonlinear Schrödinger Equations with Wave Operators. Mathematics, 13(19), 3187. https://doi.org/10.3390/math13193187





