Two-Sided Matching with Bounded Rationality: A Stochastic Framework for Personnel Selection
Abstract
1. Introduction
2. Literature Review
Contributions of This Paper
- Integrating Bounded Rationality into Matching: Extends classical two-sided matching by incorporating Quantal Response Equilibrium (QRE) to account for incomplete information in organizational hiring decisions.
- Empirical Estimation of Parameters: Provides the first empirical calibration of bounded rationality in recruitment using three years of data, showing learning effects vary by position level.
- Computational Framework: Introduces a two-stage stochastic optimization approach to handle non-convexities from QRE, with particle swarm optimization outperforming other heuristics.
- Quantifying Costs of Bounded Rationality: Demonstrates a measurable cost premium (~26%) in optimal job packages due to bounded rationality, with implications for HR budgeting.
- Actionable Decision Support: Offers insights on package design, showing single-item packages are costlier and lower-priority roles rely more on bounded rational behavior, sometimes reducing costs.
- Dynamic Matching with Learning Effects: Models evolving organizational expertise across repeated hiring cycles through time-varying bounded rationality parameters.
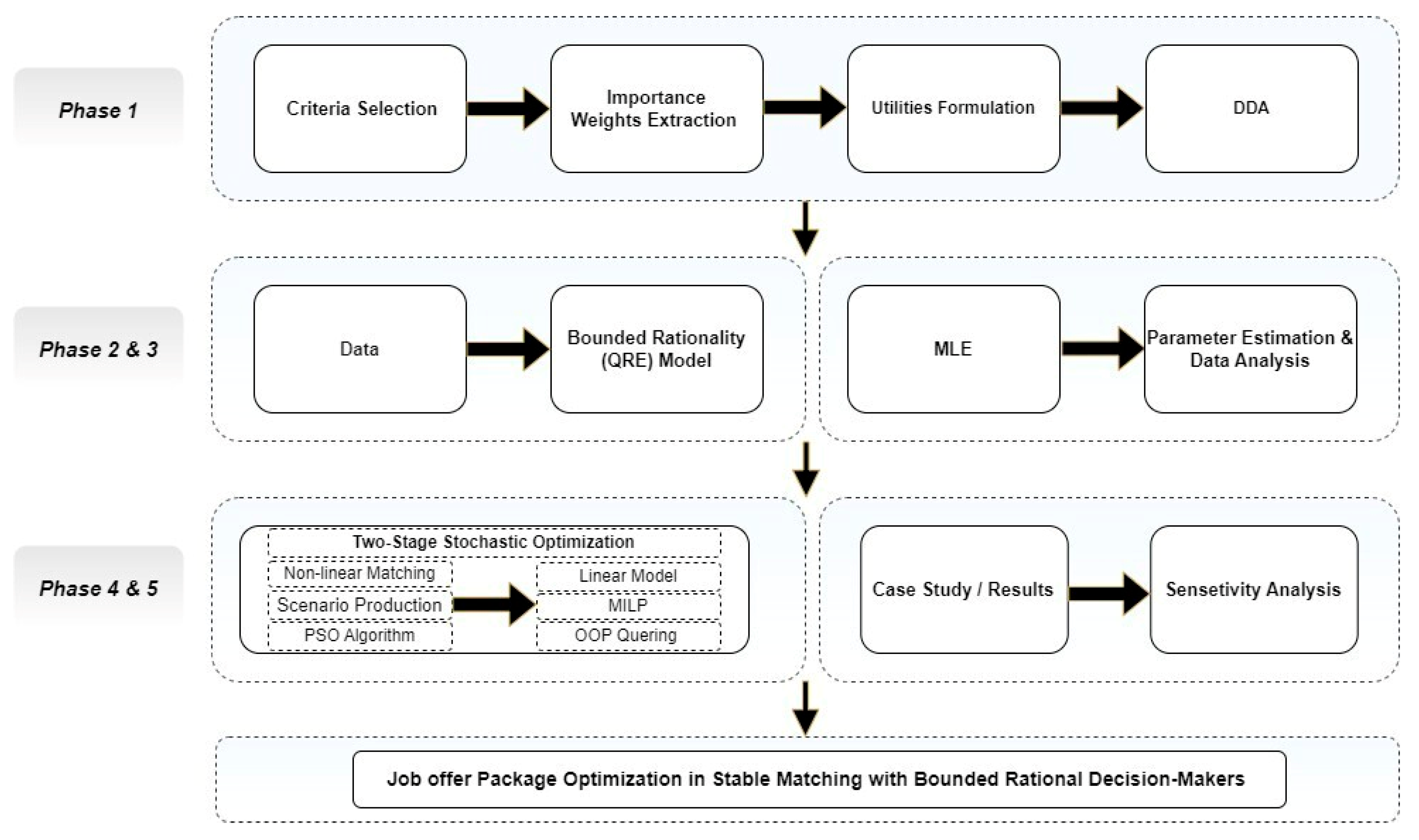
3. Materials and Methods
3.1. Problem Definition and Two-Sided Matching
3.1.1. Deferred Acceptance Algorithm (DAA)
3.1.2. Identification of Desired Criteria
3.1.3. Payoff Formulations
3.2. Bounded Rationality Model
3.2.1. Data
3.2.2. Bounded Rationality Based on QRE
3.3. Maximum Likelihood Estimation (MLE)
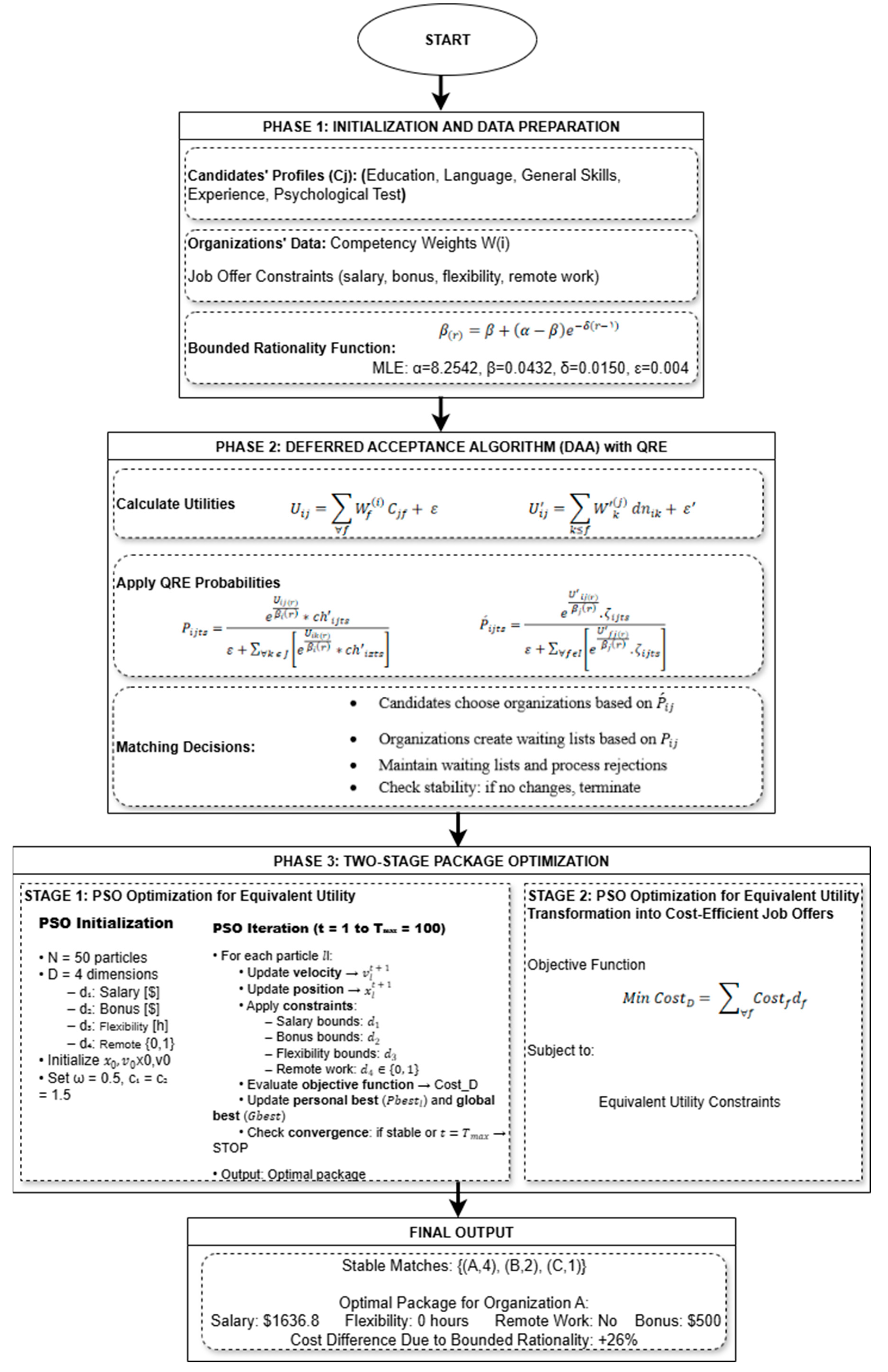
4. Modeling and Computational Study
4.1. First Stage: Two-Sided Matching and Equivalent Utility Based on Bounded Rationality
4.2. Second Stage: Cost-Efficient Job Offer Design
4.3. Particle Swarm Optimization
4.3.1. Algorithm Selection and Comparative Analysis
4.3.2. Model Limitations and Parameter Analysis
5. Discussion
5.1. Case Study
5.2. Results
5.2.1. Rational Mode
5.2.2. Bounded Rational Mode
5.3. Further Discussion
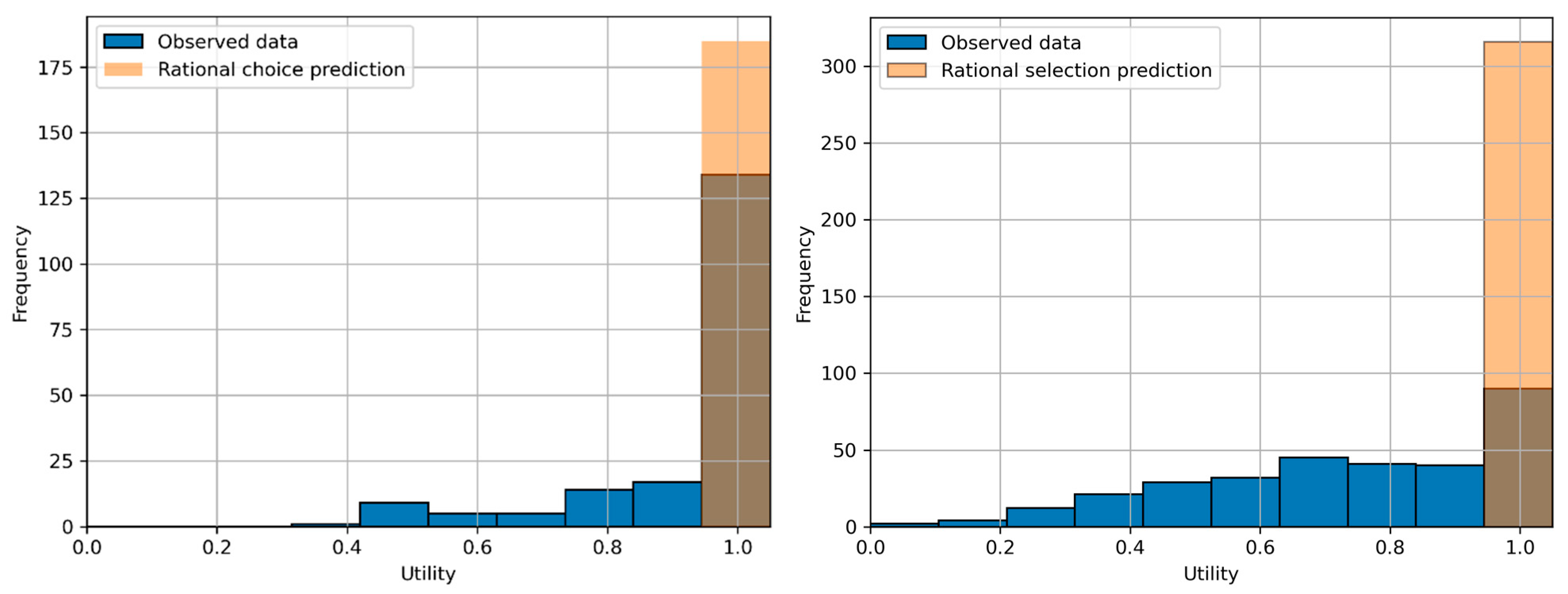
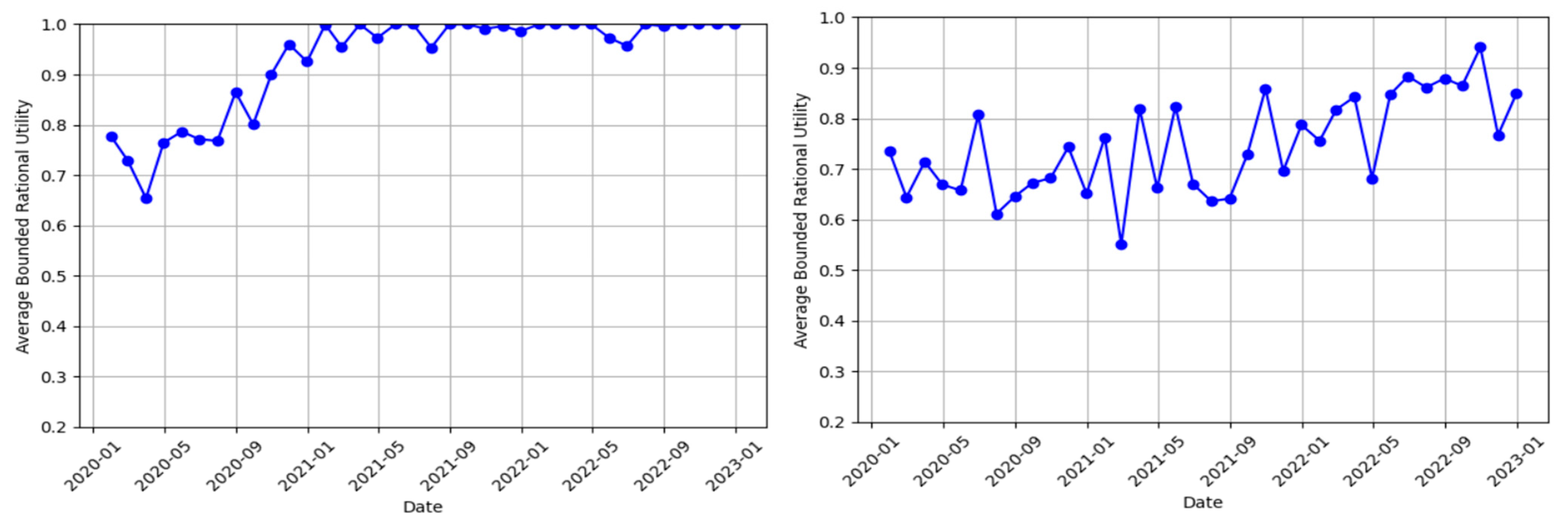
- As shown in Section 3.2 and Section 3.3, the behavior of the hiring manager, who serves as the final decision layer after technical and behavioral interviews, follows the QRE function. The collected data aligns well with this function, reflecting the manager’s incomplete information about the candidate’s utility. A candidate’s utility has both explicit and implicit components, and the manager’s rationality is constrained by limited knowledge of the implicit component. Moreover, analysis of the estimated beta functions shows evidence of a learning process over time, gradually reducing bounded rationality, although it never disappears completely.
- In organizations with bounded-rational decision-makers, perceived candidate utilities tend to decrease. Managers often select candidates with lower normalized utility rather than the optimal choice. This effect is more pronounced for lower-level or less critical positions. Because bounded rationality has a random component, there are occasional increases in perceived utility, but overall, a long-term decline is observed.
- Comparing the matching outcomes under rational and bounded rational modes, the organization’s utility fell slightly from 0.90 to 0.88. This minor change reflects the learning and improvement in the hiring manager’s decisions over time. The final match itself remained unchanged, but larger differences between rationality and bounded rationality could lead to different matches.
- The decline in utility translated into higher job-offer costs, rising from $1300 to $1636.8 to secure the best candidate. Essentially, the bounded rationality of decision-makers imposes additional costs on the organization.
6. Conclusions
6.1. Managerial Implications
6.2. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QRE | Quantal Response Equilibrium |
| MLE | Maximum Likelihood Estimation |
| PSO | Particle swarm optimization |
| LQRE | logit quantal response equilibrium |
| DAA | Deferred Acceptance Algorithm |
| FAHP | Fuzzy Analytic Hierarchy Process |
| MILP | Mixed-Integer Linear Programming |
Appendix A
| Title 1 | Title 2 | Title 3 | |
|---|---|---|---|
| Maximum utility of organization at time | Index of organizations | ||
| Utility of candidate for organization | Index of candidates | ||
| Utility of organization for candidate | Index of packages’ item | ||
| Importance weights of competencies for organization | Index of time | ||
| Importance weights of package items for candidate | Second index of time | ||
| Equivalent utility of the target organization | Set of Time Indexes | T | |
| Cost of organization i’s package item f | Index of job-offer items | ||
| -th package item of organization | Index variable for the organization under investigation | ||
| Index of package items of integer type | Index of package items of binary type | ||
| Set of Candidates | Set of Organizations | ||
| Normalized value of the f’th package item of organization i | Competencies of candidate j | ||
| Upper bound of the ’th item | Lower bound of the -th item | ||
| Binary variable for whether organization interviews candidate at time | maximum utility of candidate at time | ||
| Binary variable: organization chooses candidate at time | Binary variable: candidate chooses organization at time | ||
| Binary variable: candidate can choose organization at time | Sensitivity of organization ’s position |
References
- Najafi-Zangeneh, S.; Shams-Gharneh, N.; Arjomandi-Nezhad, A.; Zolfani, S.H. An improved machine learning-based employees attrition prediction framework with emphasis on feature selection. Mathematics 2021, 9, 1226. [Google Scholar] [CrossRef]
- Nabeeh, N.A.; Smarandache, F.; Abdel-Basset, M.; El-Ghareeb, H.A.; Aboelfetouh, A. An integrated neutrosophic-topsis approach and its application to personnel selection: A new trend in brain processing and analysis. IEEE Access 2019, 7, 29734–29744. [Google Scholar] [CrossRef]
- Wang, B.; Li, Z.; Wang, S.; Li, M.; Ji, A. Modeling bounded rationality in discretionary lane change with the quantal response equilibrium of game theory. Transp. Res. Part B Methodol. 2022, 164, 145–161. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Roth, A.E.; Sotomayor, M. Two-sided matching. In Handbook of Game Theory with Economic Applications; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1, pp. 485–541. [Google Scholar]
- Pu, D.; Yuan, G. Two-sided matching model considering multi-information fusion of stakeholders. Expert Syst. Appl. 2023, 212, 118784. [Google Scholar] [CrossRef]
- Jiang, P.; Guo, S.; Du, B.; Guo, J. Two-sided matching decision-making model for complex product system based on life-cycle sustainability assessment. Expert Syst. Appl. 2022, 208, 118184. [Google Scholar] [CrossRef]
- Manlove, D.F.; Irving, R.W.; Iwama, K. Guest editorial: Special issue on matching under preferences. Algorithmica 2010, 58, 1–4. [Google Scholar] [CrossRef]
- Bansal, N.; Gupta, A.; Li, J.; Mestre, J.; Nagarajan, V.; Rudra, A. When LP is the cure for your matching woes: Improved bounds for stochastic matchings. Algorithmica 2012, 63, 733–762. [Google Scholar] [CrossRef]
- Ashlagi, I.; Braverman, M.; Hassidim, A. Matching with couples revisited. In Proceedings of the 12th ACM Conference on Electronic Commerce, San Jose, CA, USA, 5–9 June 2011. [Google Scholar]
- Hatfield, J.; Kominers, S.D. Multilateral matching. In Proceedings of the 12th ACM Conference on Electronic Commerce, San Jose, CA, USA, 5–9 June 2011. [Google Scholar]
- Manlove, D. Algorithmics of Matching Under Preferences; World Scientific: Singapore, 2013; Volume 2. [Google Scholar]
- Rastegari, B.; Condon, A.; Immorlica, N.; Leyton-Brown, K. Two-sided matching with partial information. In Proceedings of the Fourteenth ACM Conference on Electronic Commerce, Philadelphia, PA, USA, 16–20 June 2013. [Google Scholar]
- Luce, R.D. Individual Choice Behavior; Wiley: New York, NY, USA, 1959; Volume 4. [Google Scholar]
- Chen, Y.; Su, X.; Zhao, X. Modeling bounded rationality in capacity allocation games with the quantal response equilibrium. Manag. Sci. 2012, 58, 1952–1962. [Google Scholar] [CrossRef]
- Simon, H.A. A behavioral model of rational choice. Q. J. Econ. 1955, 69, 99–118. [Google Scholar] [CrossRef]
- Nelson, R.R. An Evolutionary Theory of Economic Change; Harvard University Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Rubinstein, A. Modeling Bounded Rationality; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Canbolat, P.G. Bounded rationality in clearing service systems. Eur. J. Oper. Res. 2020, 282, 614–626. [Google Scholar] [CrossRef]
- McKelvey, R.D.; Palfrey, T.R. Quantal response equilibria for normal form games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Stochastic game theory for social science: A primer on quantal response equilibrium. In Handbook of Experimental Game Theory; Edward Elgar Publishing: Cheltenham, UK, 2020; pp. 8–47. [Google Scholar]
- Chen, H.-C.; Friedman, J.W.; Thisse, J.-F. Boundedly rational Nash equilibrium: A probabilistic choice approach. Games Econ. Behav. 1997, 18, 32–54. [Google Scholar] [CrossRef]
- Anderson, S.P.; Goeree, J.K.; Holt, C.A. The logit equilibrium: A perspective on intuitive behavioral anomalies. South. Econ. J. 2002, 69, 21–47. [Google Scholar] [PubMed][Green Version]
- Goeree, J.K.; Holt, C.A. Ten little treasures of game theory and ten intuitive contradictions. Am. Econ. Rev. 2001, 91, 1402–1422. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A. Asymmetric inequality aversion and noisy behavior in alternating-offer bargaining games. Eur. Econ. Rev. 2000, 44, 1079–1089. [Google Scholar] [CrossRef]
- Anderson, S.P.; Goeree, J.K.; Holt, C.A. Minimum-effort coordination games: Stochastic potential and logit equilibrium. Games Econ. Behav. 2001, 34, 177–199. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Quantal response equilibrium and overbidding in private-value auctions. J. Econ. Theory 2002, 104, 247–272. [Google Scholar] [CrossRef]
- Capra, C.M.; Goeree, J.K.; Gomez, R.; A Holt, C. Anomalous behavior in a traveler’s dilemma? Am. Econ. Rev. 1999, 89, 678–690. [Google Scholar] [CrossRef]
- Lim, N.; Ho, T.-H. Designing price contracts for boundedly rational customers: Does the number of blocks matter? Mark. Sci. 2007, 26, 312–326. [Google Scholar] [CrossRef]
- Ho, T.-H.; Zhang, J. Designing pricing contracts for boundedly rational customers: Does the framing of the fixed fee matter? Manag. Sci. 2008, 54, 686–700. [Google Scholar] [CrossRef]
- Su, X. Bounded rationality in newsvendor models. Manuf. Serv. Oper. Manag. 2008, 10, 566–589. [Google Scholar] [CrossRef]
- Liu, T.; Methapatara, C.; Wynter, L. Revenue management model for on-demand IT services. Eur. J. Oper. Res. 2010, 207, 401–408. [Google Scholar] [CrossRef]
- Shang, W.; Liu, L. Promised delivery time and capacity games in time-based competition. Manag. Sci. 2011, 57, 599–610. [Google Scholar] [CrossRef]
- Di, X.; Liu, H.X. Boundedly rational route choice behavior: A review of models and methodologies. Transp. Res. Part B Methodol. 2016, 85, 142–179. [Google Scholar] [CrossRef]
- Roemer, N.; Müller, S.; Voigt, G. A choice-based optimization approach for contracting in supply chains. Eur. J. Oper. Res. 2023, 305, 271–286. [Google Scholar] [CrossRef]
- Khanlarzade, N.; Farughi, H. Modeling the Stackelberg game with a boundedly rational follower in deterioration supply chain-based interaction with the leader’s hybrid pricing strategy. Expert Syst. Appl. 2024, 237, 121302. [Google Scholar] [CrossRef]
- Pais, J.; Pintér, Á. School choice and information: An experimental study on matching mechanisms. Games Econ. Behav. 2008, 64, 303–328. [Google Scholar] [CrossRef]
- Echenique, F.; Wilson, A.J.; Yariv, L. Clearinghouses for two-sided matching: An experimental study. Quant. Econ. 2016, 7, 449–482. [Google Scholar] [CrossRef]
- Dreyfuss, B.; Heffetz, O.; Rabin, M. Expectations-based loss aversion may help explain seemingly dominated choices in strategy-proof mechanisms. Am. Econ. J. Microecon. 2022, 14, 515–555. [Google Scholar] [CrossRef]
- Alcalde-Unzu, J.; Klijn, F.; Vorsatz, M. Constrained school choice: An experimental QRE analysis. Soc. Choice Welf. 2023, 61, 587–624. [Google Scholar] [CrossRef]
- Wallace, M.J.J.; Steuer, R.E. Multiple Objective Linear Programming in the Design of Internal Wage Structures. In Academy of Management Proceedings; Academy of Management Briarcliff Manor: New York, NY, USA, 1979; p. 10510. [Google Scholar]
- Kwak, N.; Allen, T.; Schniederjans, M. A multilevel salary compensation model using goal programming. RAIRO-Oper. Res. 1982, 16, 21–31. [Google Scholar] [CrossRef]
- Garcia-Diaz, A.; Hogg, G.L. A mathematical programming approach to salary administration. Comput. Ind. Eng. 1983, 7, 7–13. [Google Scholar] [CrossRef]
- Kassa, B.A. A decision support model for salary structure design. Compens. Benefits Rev. 2020, 52, 109–120. [Google Scholar] [CrossRef]
- Tremblay, F.-A.; Piché-Meunier, D.; Dubois, L. Multi-objective Optimization for the Design of Salary Structures. In Integration of Constraint Programming, Artificial Intelligence, and Operations Research; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Najafi-Zangeneh, S.; Shams-Gharneh, N.; Gossner, O.; Abbasi, E. Optimizing Job Offer Packages: How Can Organizations Enhance Personnel Selection. In Proceedings of the 33rd European Conference on Operational Research, Copenhagen, Denmark, 30 June–3 July 2024. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for search. In Technical Report SFI-TR-95-02-010; Santa Fe Institute: Santa Fe, NM, USA, 1995. [Google Scholar]
- Bo, Y.; Guo, X.; Liu, Q.; Pan, Y.; Zhang, L.; Lu, Y. Prediction of tunnel deformation using PSO variant integrated with XGBoost and its TBM jamming application. Tunn. Undergr. Space Technol. 2024, 150, 105842. [Google Scholar] [CrossRef]
- Jovanovic, L.; Bacanin, N.; Petrovic, A.; Zivkovic, M.; Antonijevic, M.; Gajic, V.; Elsayed, M.M.; Abouhawwash, M. Exploring artificial intelligence potential in solar energy production forecasting: Methodology based on modified PSO optimized attention augmented recurrent networks. Sustain. Comput. Inform. Syst. 2025, 47, 101174. [Google Scholar] [CrossRef]
- Haile, P.A.; Hortaçsu, A.; Kosenok, G. On the empirical content of quantal response equilibrium. Am. Econ. Rev. 2008, 98, 180–200. [Google Scholar] [CrossRef]
- Simon, H.A. Models of man: Social and rational. In Mathematical Essays on Rational Human Behavior in Society Setting; Wiley: New York, NY, USA, 1957. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA. [Google Scholar]
- Zhang, Y.; Balochian, S.; Agarwal, P.; Bhatnagar, V.; Houshia, O. Artificial Intelligence and Its Applications; Hindawi Publishing Corporation: Cairo, Egypt, 2014; p. 840491.

| Company | Final Interviews | Hiring Manager Recruits | Common Interviewees | High-Level Jobs | Low-Level Jobs |
|---|---|---|---|---|---|
| A | 1853 | 660 | 511 | 185 | 316 |
| B | 1358 | 539 | 427 | 142 | 282 |
| C | 1189 | 423 | 352 | 117 | 235 |
| Parameters | Log-Likelihood | ||||
|---|---|---|---|---|---|
| High-level job | 8.2542 | 0.0432 | 0.0150 | 0.004 | −166.20 |
| Low-level job | 10.248 | 0.1244 | 0.0047 | 0.005 | −551.19 |
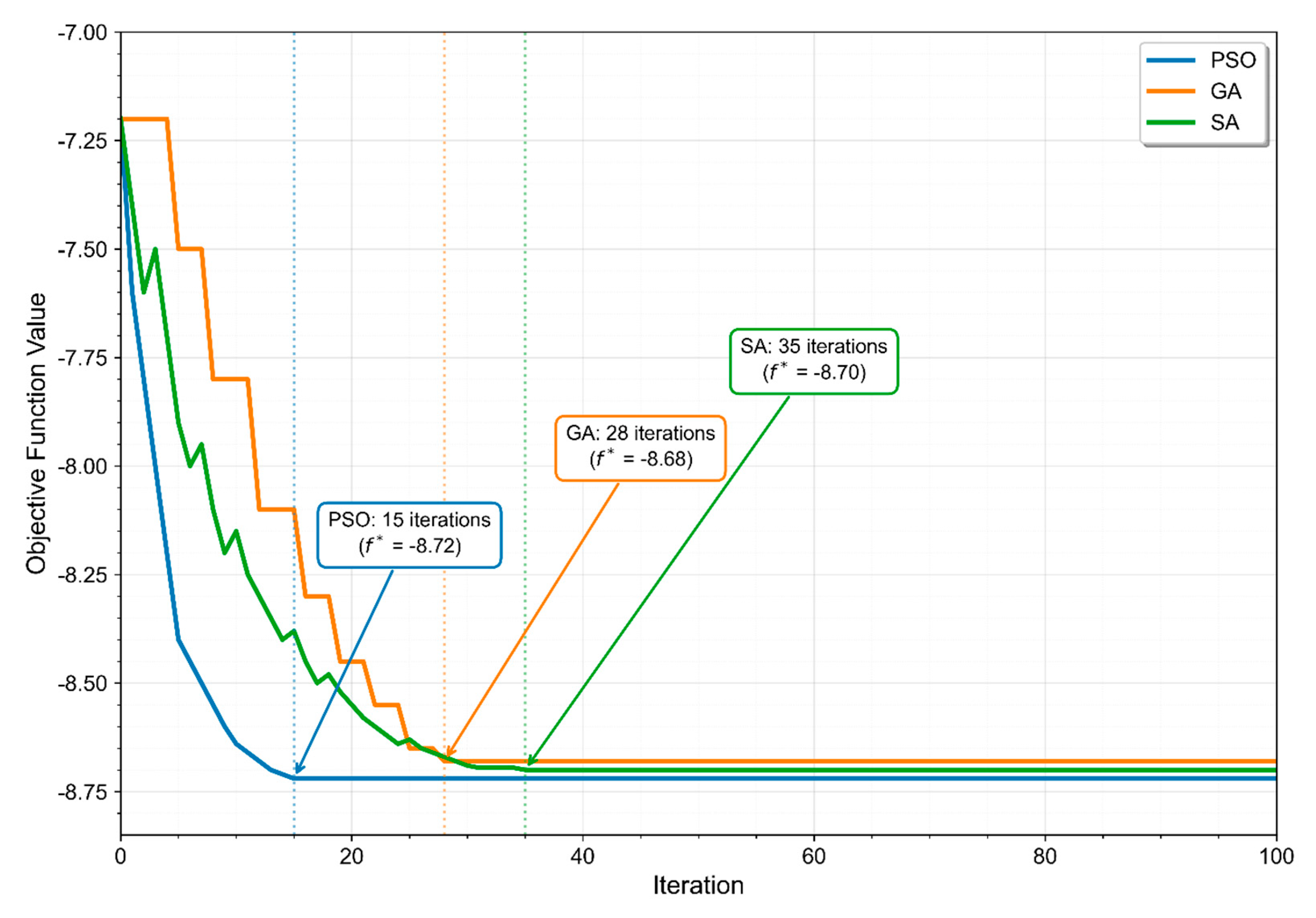
| Performance Metrics | PSO | GA | SA |
|---|---|---|---|
| Convergence Iteration | 15 | 28 | 35 |
| Final Objective Value | −8.72 | −8.68 | −8.70 |
| Initial Objective Value | −7.20 | −7.20 | −7.20 |
| Improvement Rate (First 10 Iterations) | 1.32 | 0.85 | 0.72 |
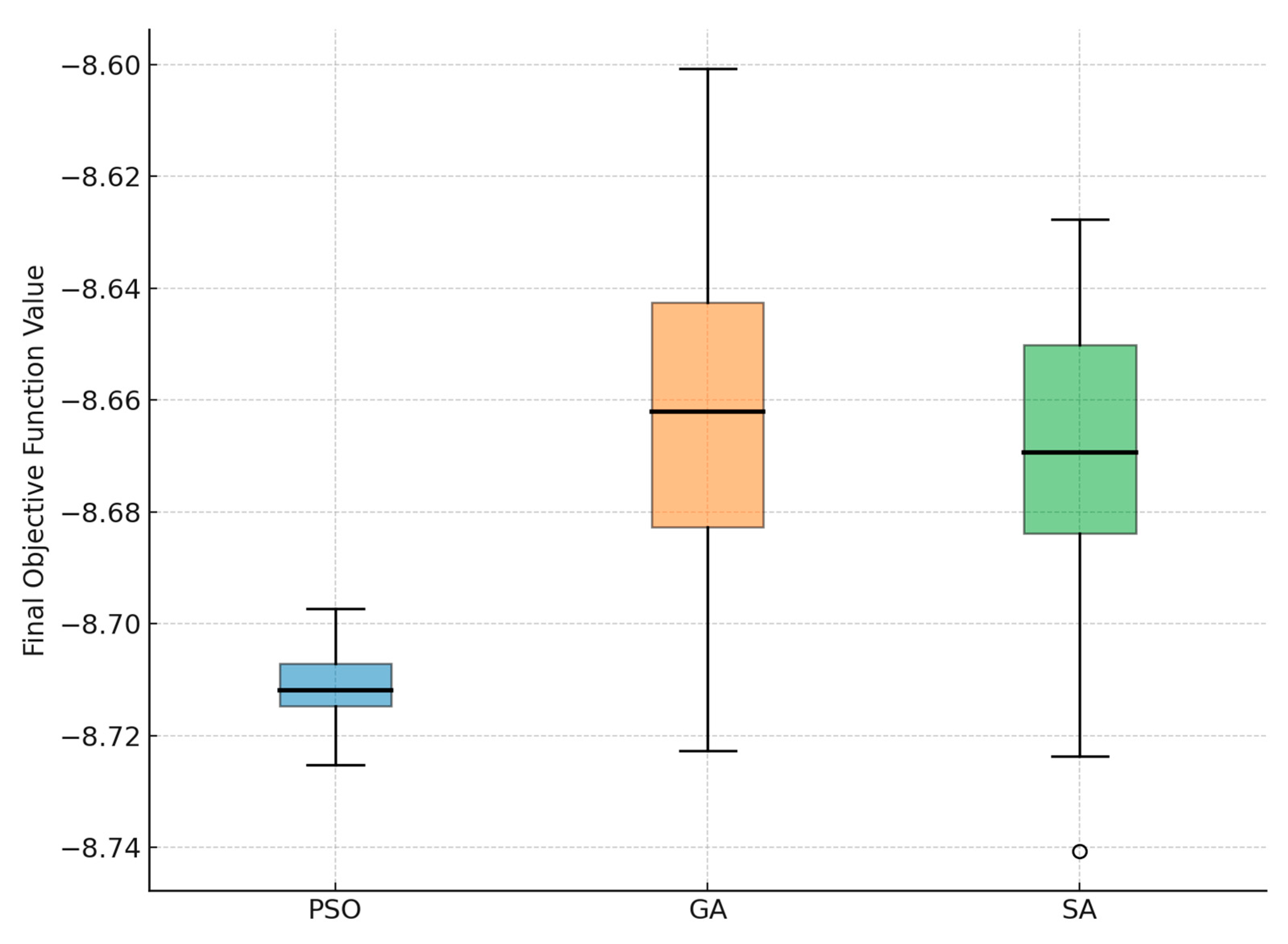
| Stability After Convergence | High | Medium | Low |
| Oscillation During Search | Minimal | Moderate | High |
| Average Final Value | −8.71 | −8.66 | −8.67 |
| Best Value Found | −8.72 | −8.70 | −8.71 |
| Worst Value Found | −8.69 | −8.58 | −8.61 |
| Standard Deviation | 0.008 | 0.032 | 0.027 |
| Parameter | Range Tested | Optimal Value | Impact on Performance |
|---|---|---|---|
| Inertia weight () | [0.2, 0.9] | 0.5 | Lower values (<0.4) cause premature convergence; higher values (>0.7) slow convergence |
| ) | [0.5, 2.5] | 1.5 | Values outside [1.0, 2.0] significantly degrade performance |
| ) | [0.5, 2.5] | 1.5 | ) work best |
| Population size | [20, 100] | 50 | <30 particles insufficient for exploration; >70 offers marginal improvement |
| Max iterations | [50, 200] | 100 | 95% of runs converge by iteration 50; 100 ensures robustness |
| # | Education | Language Proficiency | General Skills | Work Experience | Psychological Test |
|---|---|---|---|---|---|
| Candidate 1 | MSc | native | good | 0–5 | good |
| Candidate 2 | PHD | medium | medium | 10–15 | low |
| Candidate 3 | BSc | good | high | 0–5 | medium |
| Candidate 4 | PHD | advanced | advanced | 15–20 | excellent |
| Candidate 5 | BSc | advanced | high | 0–5 | good |
| # | Education | Language Proficiency | General Skills | Work Experience | Psychological Test |
|---|---|---|---|---|---|
| Organization A | 0.40 | 0.10 | 0.10 | 0.25 | 0.15 |
| Organization B | 0.36 | 0.04 | 0.20 | 0.30 | 0.10 |
| Organization C | 0.31 | 0.14 | 0.16 | 0.14 | 0.25 |
| # | Salary Level | Bonus Plans | Flexibility in Working Hours | Ability to Work Remotely | Salary Level |
|---|---|---|---|---|---|
| Candidate 1 | 0.50 | 0.20 | 0.20 | 0.10 | 0.50 |
| Candidate 2 | 0.40 | 0.20 | 0.15 | 0.25 | 0.40 |
| Candidate 3 | 0.35 | 0.10 | 0.25 | 0.30 | 0.35 |
| Candidate 4 | 0.60 | 0.10 | 0.20 | 0.10 | 0.60 |
| Candidate 5 | 0.55 | 0.15 | 0.15 | 0.15 | 0.55 |
| # | Salary ($) | Bonus ($) | Flexibility in Working Hours (h) | Working Remotely |
|---|---|---|---|---|
| Organization B | 900 | 400 | 2 | No |
| Organization C | 800 | 500 | 1 | Yes |
| # | Salary ($) | Bonus ($) | Flexibility in Working Hours (h) | Working Remotely | Stable Match |
|---|---|---|---|---|---|
| Organization A | 1300 | 500 | - | No | Candidate 4 |
| Organization B | 900 | 400 | 2 | No | Candidate 2 |
| Organization C | 800 | 500 | 1 | Yes | Candidate 1 |
| Organization A | Organization B | Organization C | |
|---|---|---|---|
| Candidate 1 | 0.525 | 0.36 | 0.34 |
| Candidate 2 | 0.46 | 0.30 | 0.54 |
| Candidate 3 | 0.327 | 0.27 | 0.54 |
| Candidate 4 | 0.42 | 0.30 | 0.339 |
| Candidate 5 | 0.50 | 0.30 | 0.419 |
| # | Candidate 1 | Candidate 2 | Candidate 3 | Candidate 4 | Candidate 5 |
|---|---|---|---|---|---|
| Organization A | 0.38 | 0.54 | 0.14 | 0.90 | 0.20 |
| Organization B | 0.32 | 0.54 | 0.18 | 0.90 | 0.21 |
| Organization C | 0.47 | 0.42 | 0.22 | 0.92 | 0.31 |
| Scenarios | Optimal Package | |||||
|---|---|---|---|---|---|---|
| # | Salary ($) | Bonus ($) | Flexibility (Hours) | Remote Work | Match | |
| 1 | = 1 | 1300 | 500 | 0 | No | {A,4}, {B,2}, {C,1} |
| 2 | = 0.5 | 500 | 0 | 0 | No | {A,2}, {B,4}, {C,1} |
| 3 | = 1 | 967 | 500 | 0 | Yes | {A,4}, {B,2}, {C,1} |
| 4 | Salary only, = 1 | 1634 | 0 | 0 | No | {A,4}, {B,2}, {C,1} |
| Parameters | Values |
|---|---|
| Population size | 50 |
| Number of iterations | 100 |
| Inertia weight | 0.5 |
| Cognitive coefficient | 1.5 |
| Social coefficient | 1.5 |
| # | Salary ($) | Bonus ($) | Flexibility in Working Hours (h) | Working Remotely | Stable Match |
|---|---|---|---|---|---|
| Organization A | 1636.8 | 500 | - | No | Candidate 4 |
| Organization B | 900 | 400 | 2 | No | Candidate 2 |
| Organization C | 800 | 500 | 1 | Yes | Candidate 1 |
| Candidate | Organization | ||
|---|---|---|---|
| 0.39 | Candidate 1 | Organization C | 0.47 |
| 0.35 | Candidate 2 | Organization B | 0.52 |
| 0.40 | Candidate 4 | Organization A | 0.88 |
| Scenarios | Optimal Package | ||||||
|---|---|---|---|---|---|---|---|
| # | Salary ($) | Bonus ($) | Flexibility (Hours) | Remote Work | Match | Cost vs. Rational | |
| 1 | = 1 | 1636.8 | 500 | 0 | No | {A,4}, {B,2}, {C,1} | +26% |
| 2 | = 0.5 | 380 | 0 | 0 | No | {A,2}, {B,4}, {C,1} | −24% |
| 3 | = 1 | 875 | 420 | 2 | Yes | {A,2}, {B,4}, {C,1} | −10% |
| 4 | Salary only, = 1 | 1925 | 0 | 0 | No | {A,4}, {B,2}, {C,1} | +18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafi-Zangeneh, S.; Shams-Gharneh, N.; Gossner, O. Two-Sided Matching with Bounded Rationality: A Stochastic Framework for Personnel Selection. Mathematics 2025, 13, 3173. https://doi.org/10.3390/math13193173
Najafi-Zangeneh S, Shams-Gharneh N, Gossner O. Two-Sided Matching with Bounded Rationality: A Stochastic Framework for Personnel Selection. Mathematics. 2025; 13(19):3173. https://doi.org/10.3390/math13193173
Chicago/Turabian StyleNajafi-Zangeneh, Saeed, Naser Shams-Gharneh, and Olivier Gossner. 2025. "Two-Sided Matching with Bounded Rationality: A Stochastic Framework for Personnel Selection" Mathematics 13, no. 19: 3173. https://doi.org/10.3390/math13193173
APA StyleNajafi-Zangeneh, S., Shams-Gharneh, N., & Gossner, O. (2025). Two-Sided Matching with Bounded Rationality: A Stochastic Framework for Personnel Selection. Mathematics, 13(19), 3173. https://doi.org/10.3390/math13193173







